Evaluation of the Fluid Model Approach for the Sizing of Energy Storage in Wave-Wind Energy Systems
Abstract
:1. Introduction
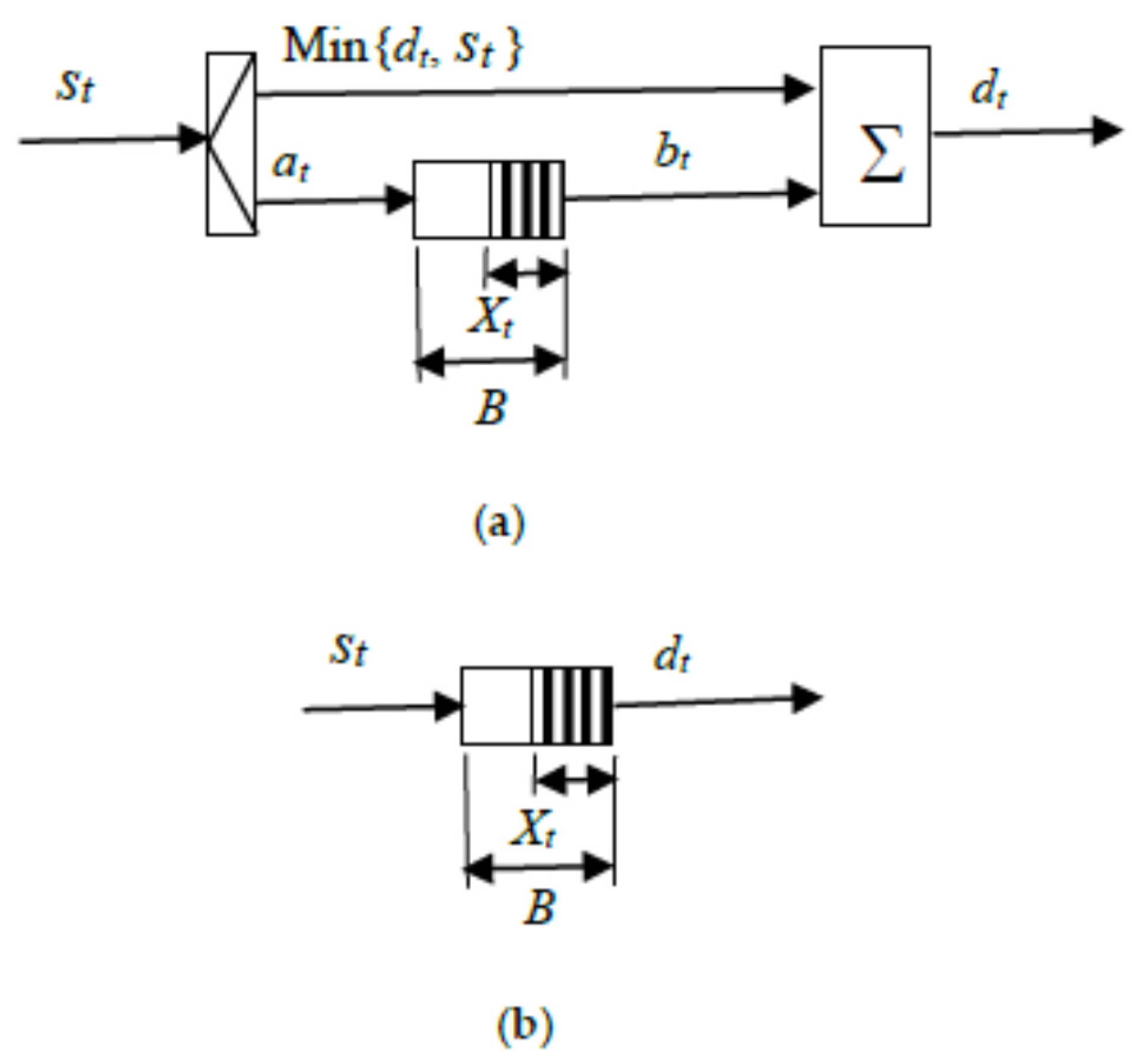
2. Fluid Approximation of Storage Systems
2.1. Regulated Brownian Model Approximation
L[k] = L[k − 1] + (lim_inf − (X[k] + L[k − 1] − U[k − 1]))
else L[k] = L[k − 1]
U[k] = U[k − 1] + ((X[k] + L[k − 1] − U[k − 1]) − lim_sup)
else U[k] = U[k − 1]
2.2. Optimal Sizing of Storage System Modelled by Regulated Brownian Motion
- E[], is the expected value of a stochastic variable.
- p, is the selling price of energy (€/kWh).
- S, is a stochastic variable with mean µ and standard deviation σ that represents the generated power (kW). Here, it is a normal distribution N (µ,σ).
- λ, is the interest rate.
- m, is the installation cost of (wind and wave) generators (€/kW).
- maxS, is the maximum power supplied by generators (kW).
- h2, is the installation cost of the storage system (€/kWh).
- B, is the energy capacity of the storage system (kWh).
- α, is the price of the loss of energy (€/kWh).
- β, is the price of the waste of energy (€/kWh).
- pb, payback time or number of years of amortization.
2.3. Optimal Converter Power Rating for the Storage System Modelled by Brownian Motion
3. Wind and Wave Generators Models
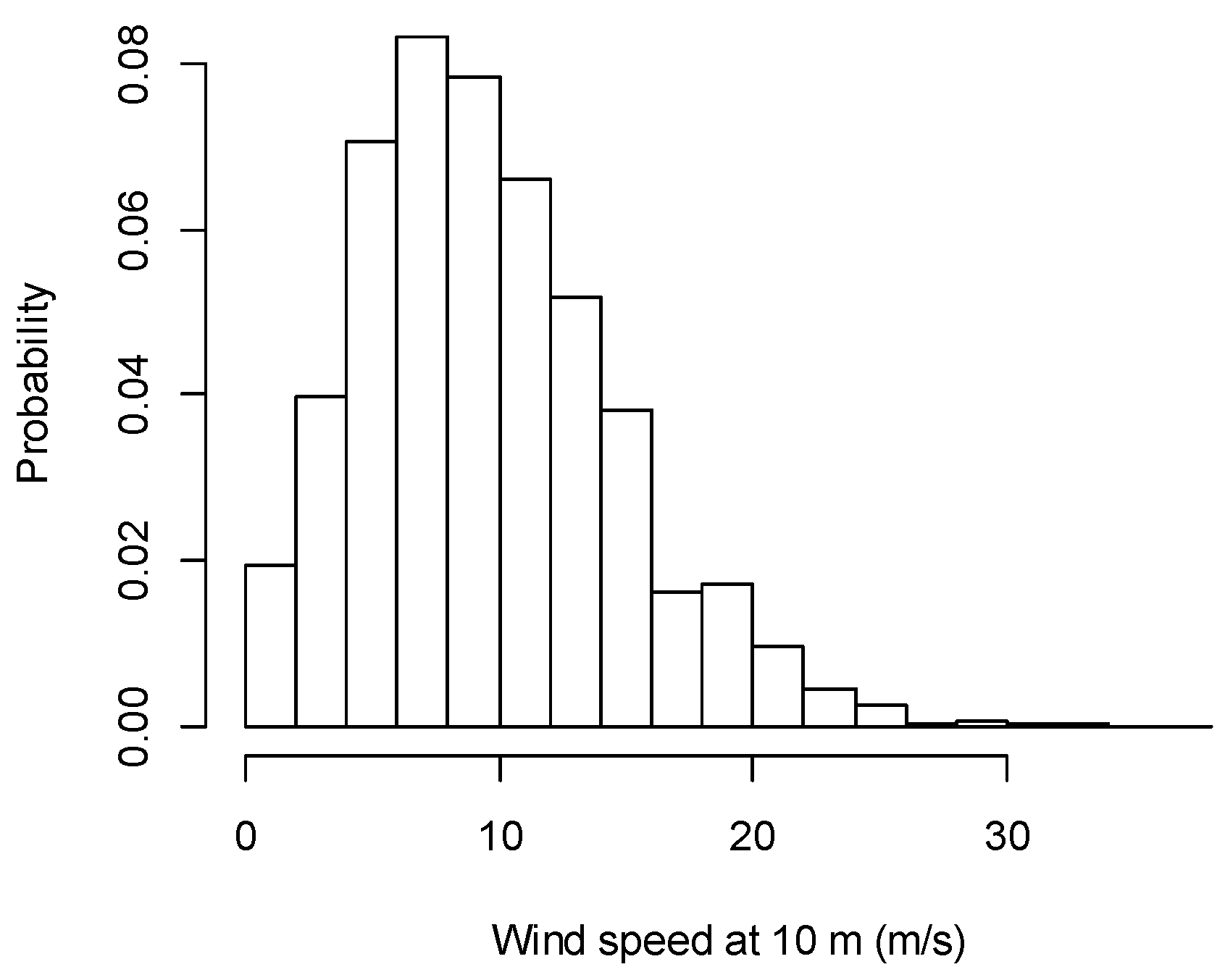
3.1. Wind Generator Model
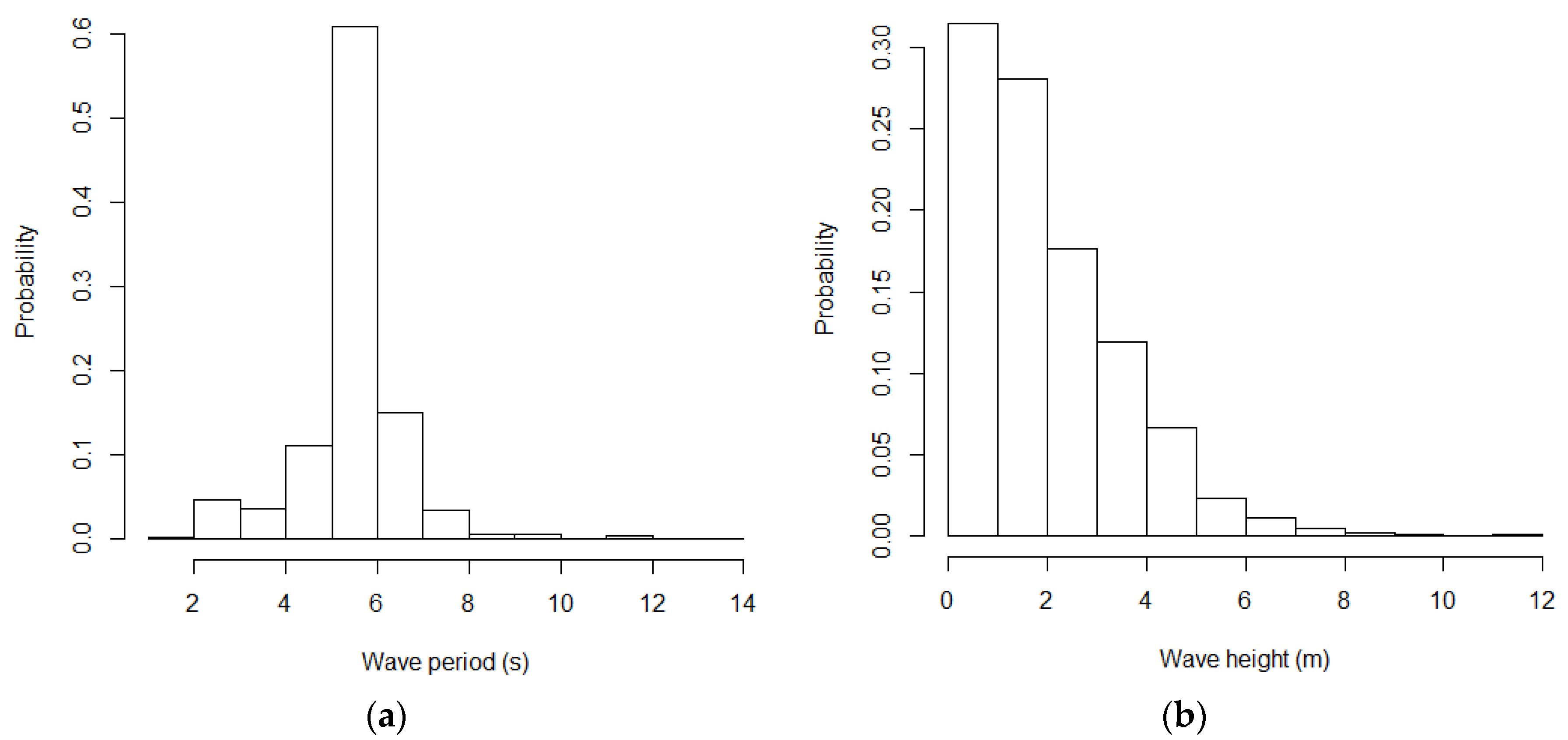
3.2. Wave Generator Model
3.3. Aggregate Power Output from the Wind–Wave Farm
- , is the wind farm efficiency.
- , is the number of wind generators.
- , is the wave farm efficiency.
- , is the number of wave generators.
4. Genetic Algorithm
Subject to: B > 0, psto > 0
5. Simulation Results
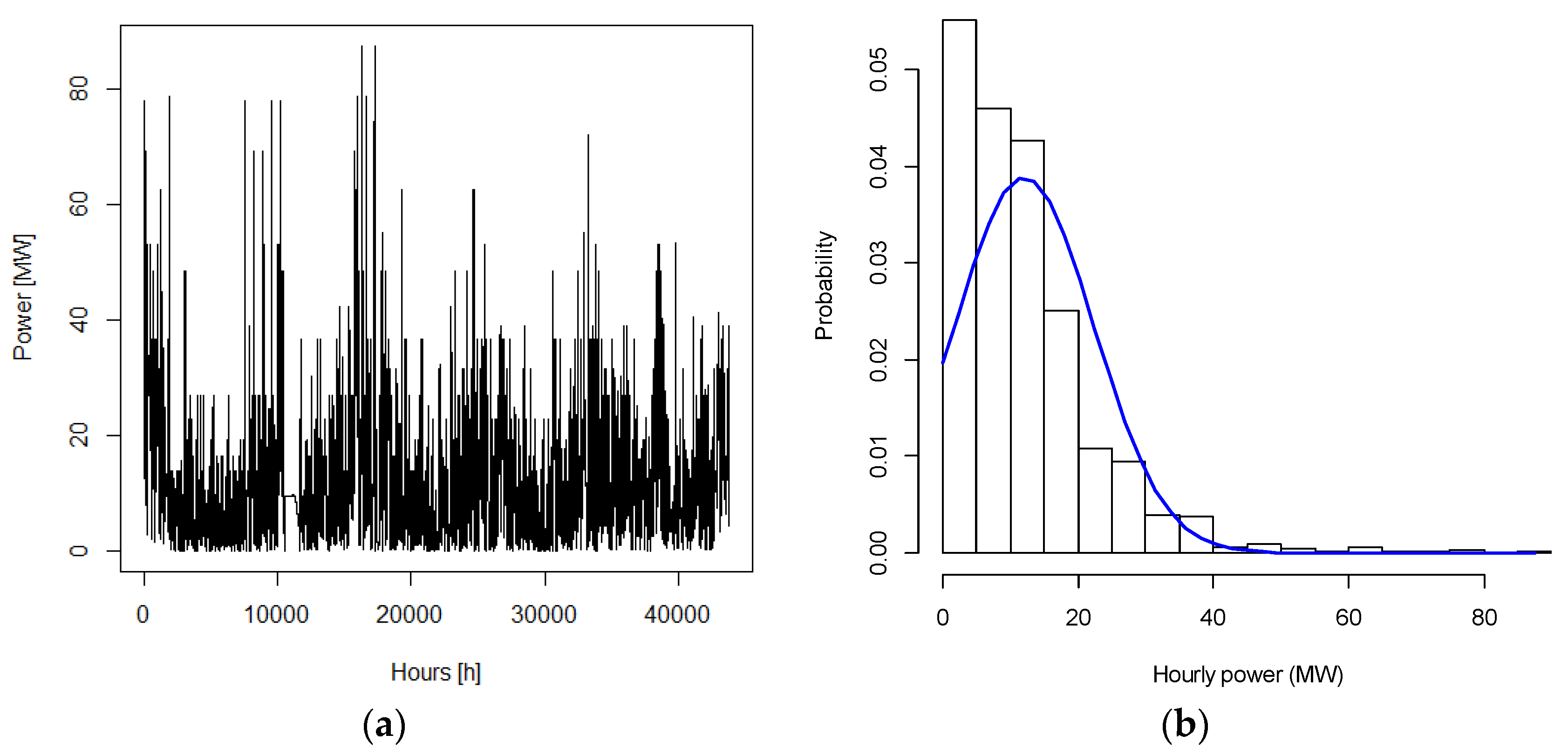
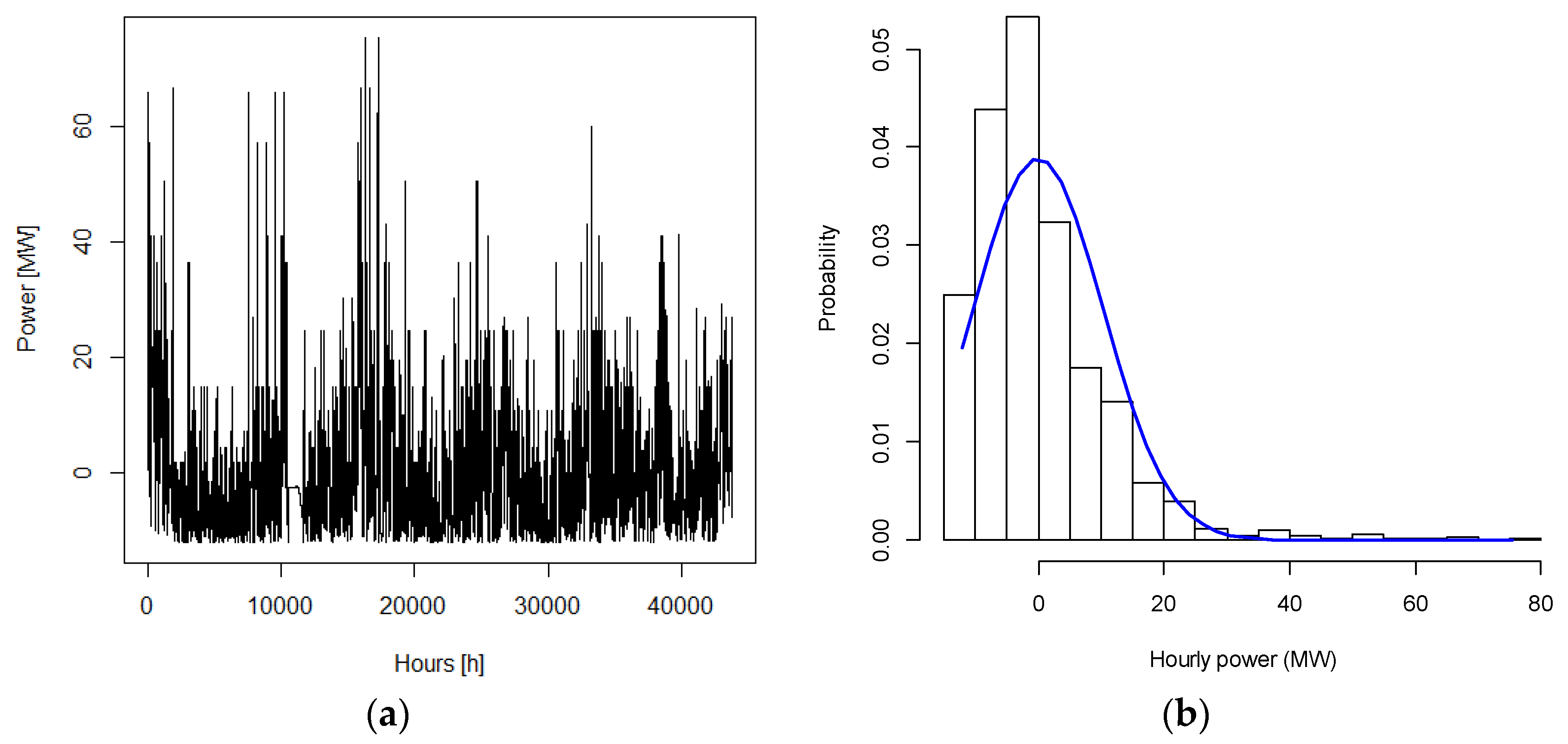
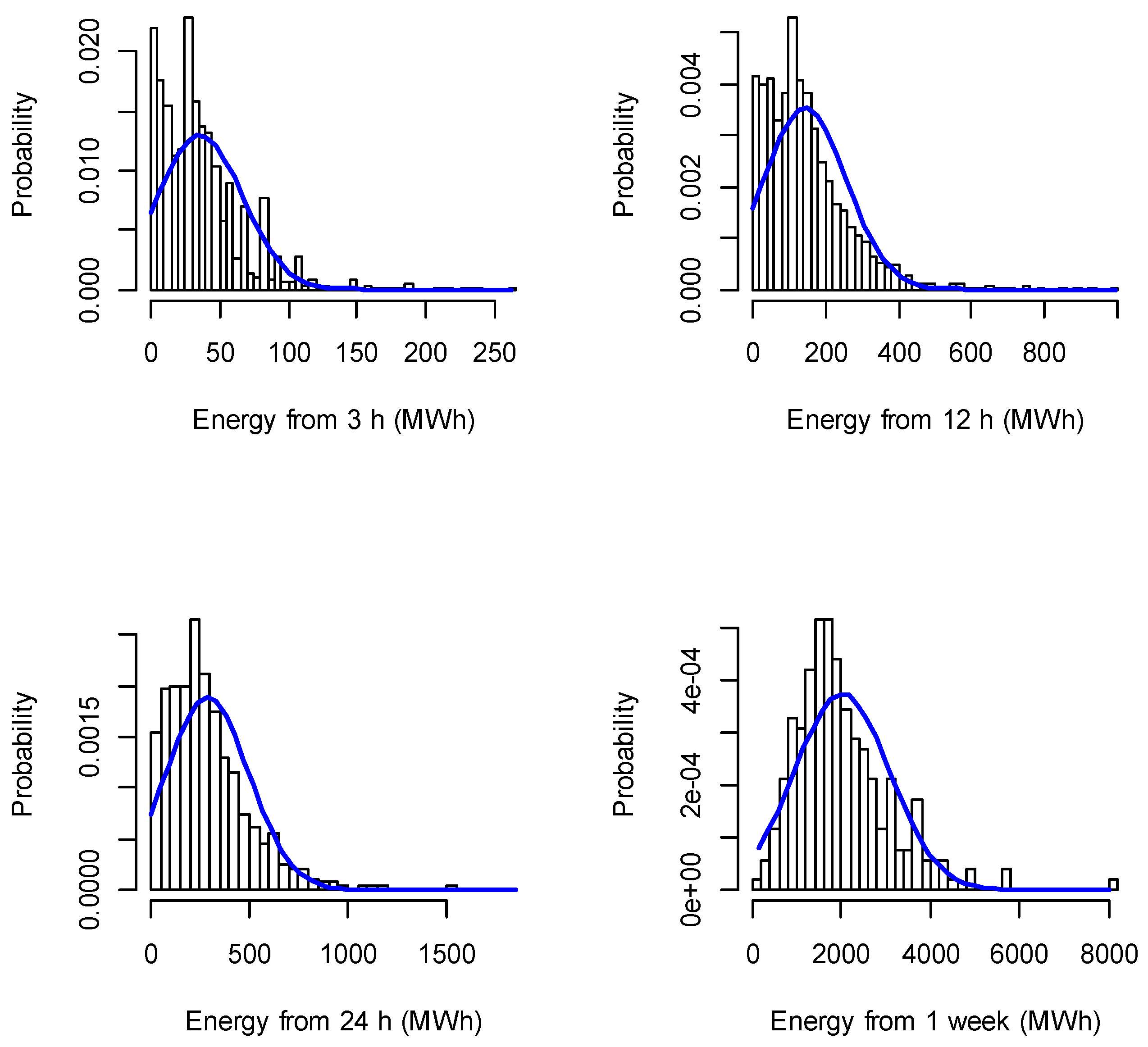
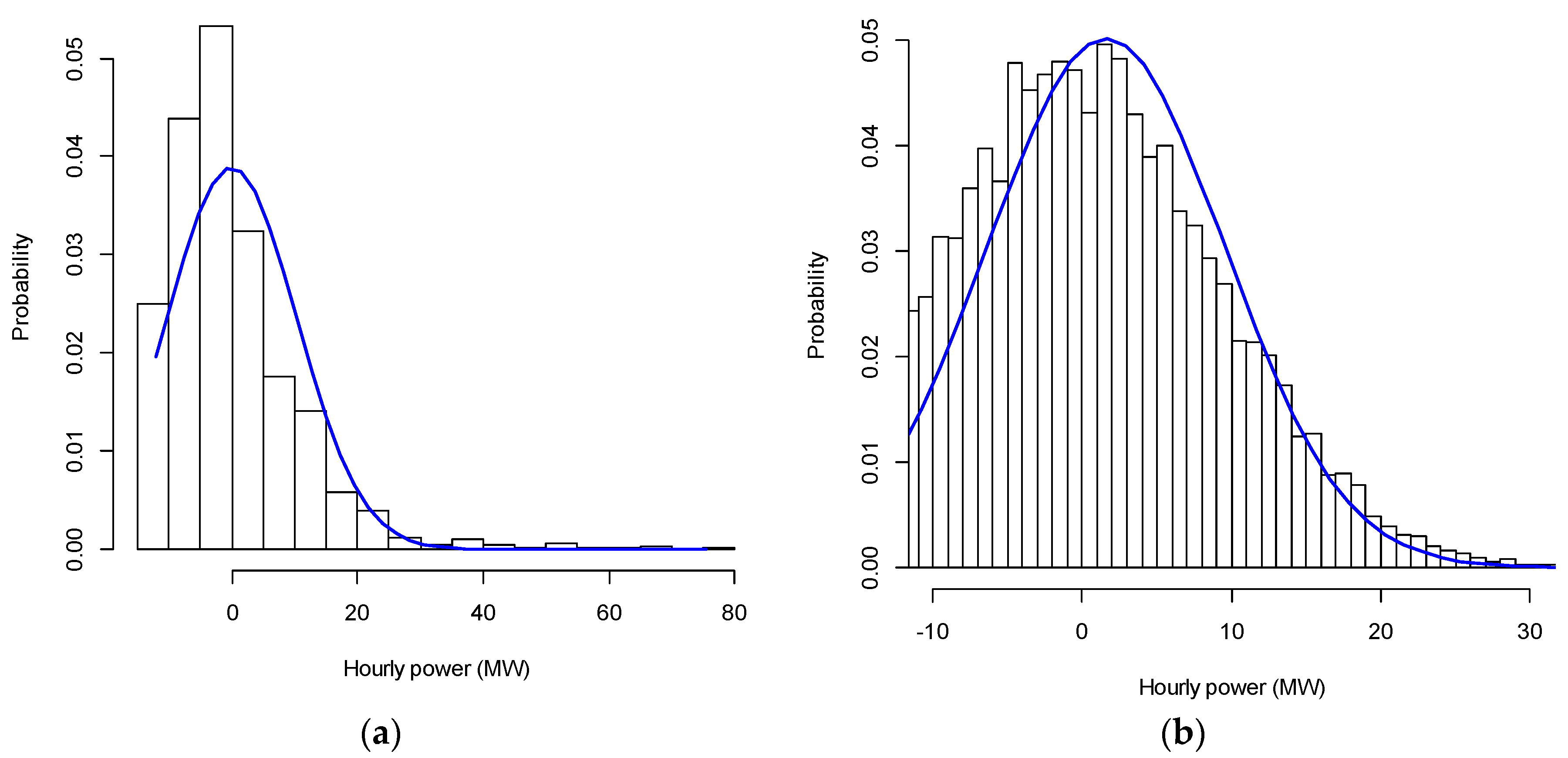
5.1. Description of Input Data
5.2. Studied Cases
- Case 1:
- Monte Carlo simulation of hybrid wave-wind generation system without storage and real data.
- Case 2:
- Monte Carlo simulation of hybrid wave-wind generation system without storage and approximated data.
- Case 3:
- Fluid model of hybrid wave-wind generation system without storage.
- Case 4:
- Optimal sizing of storage system with the Monte Carlo simulation and real data.
- Case 5:
- Optimal sizing of storage system with the Monte Carlo simulation and approximated data.
- Case 6:
- Optimal sizing of storage system with the fluid model.
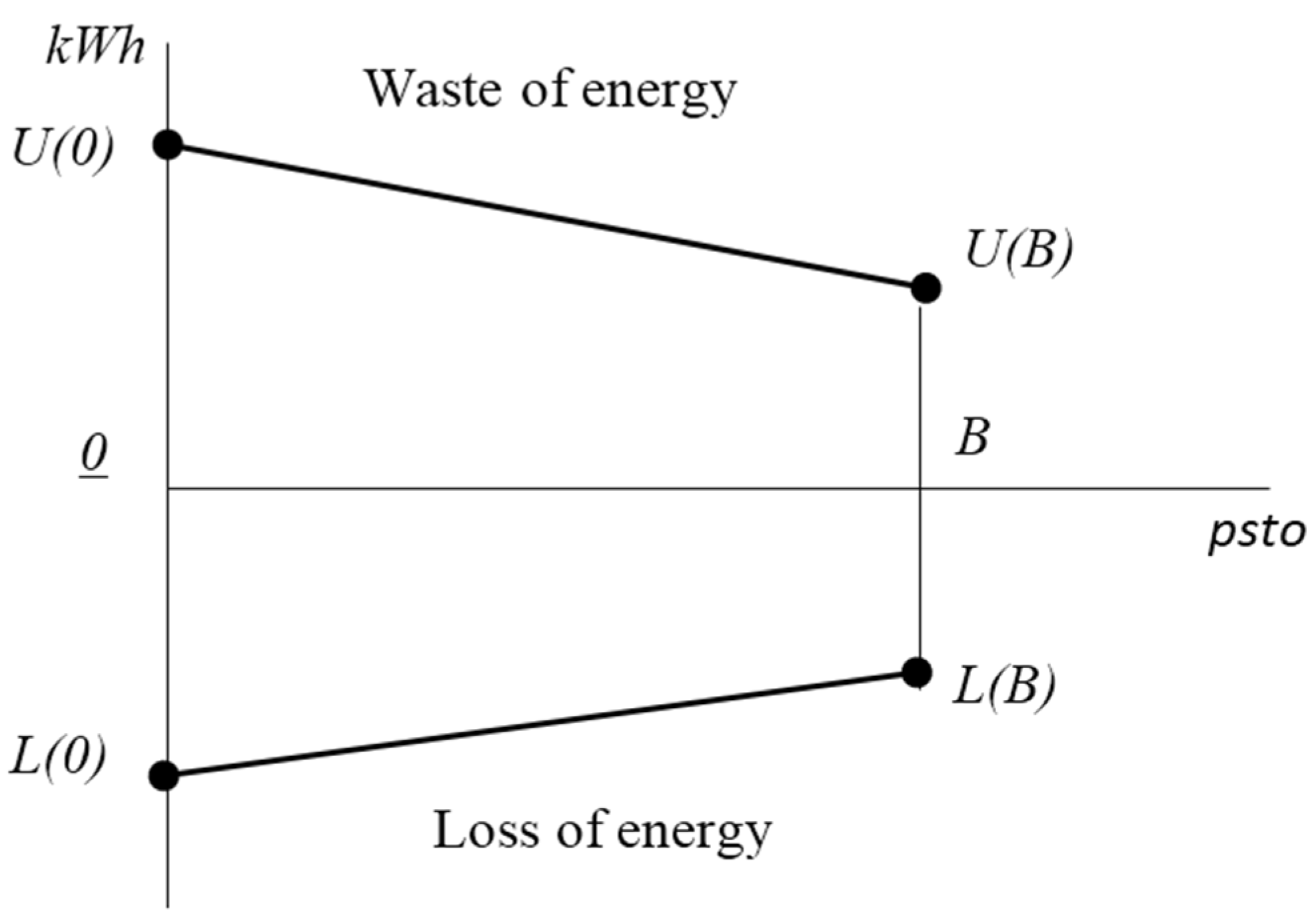
5.3. Sensitivity of the Wasted and Loss Energy to the Storage Sizing
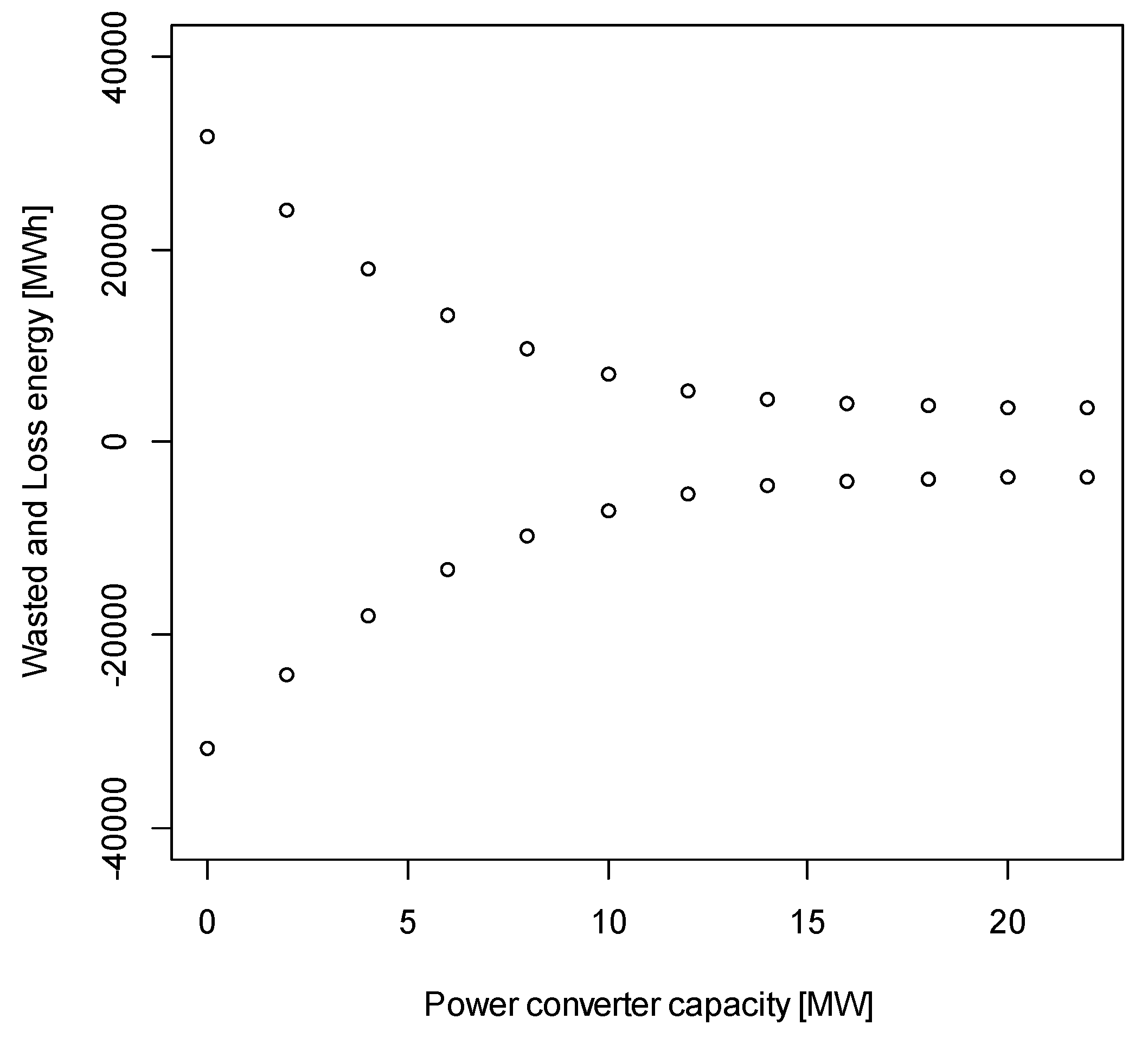
5.4. Sensitivity of the Wasted and Lost Energy to the Converter Power Rating
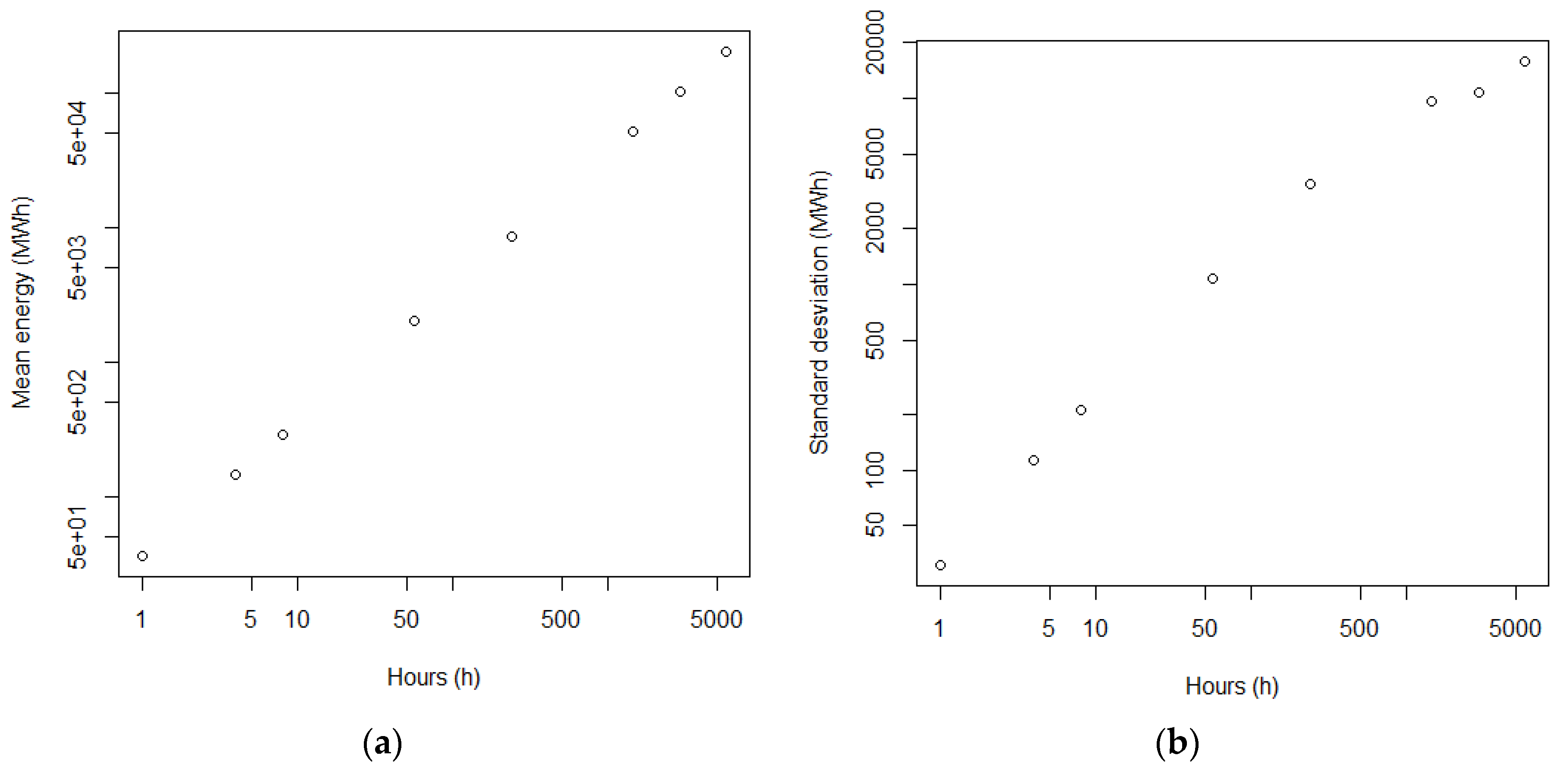
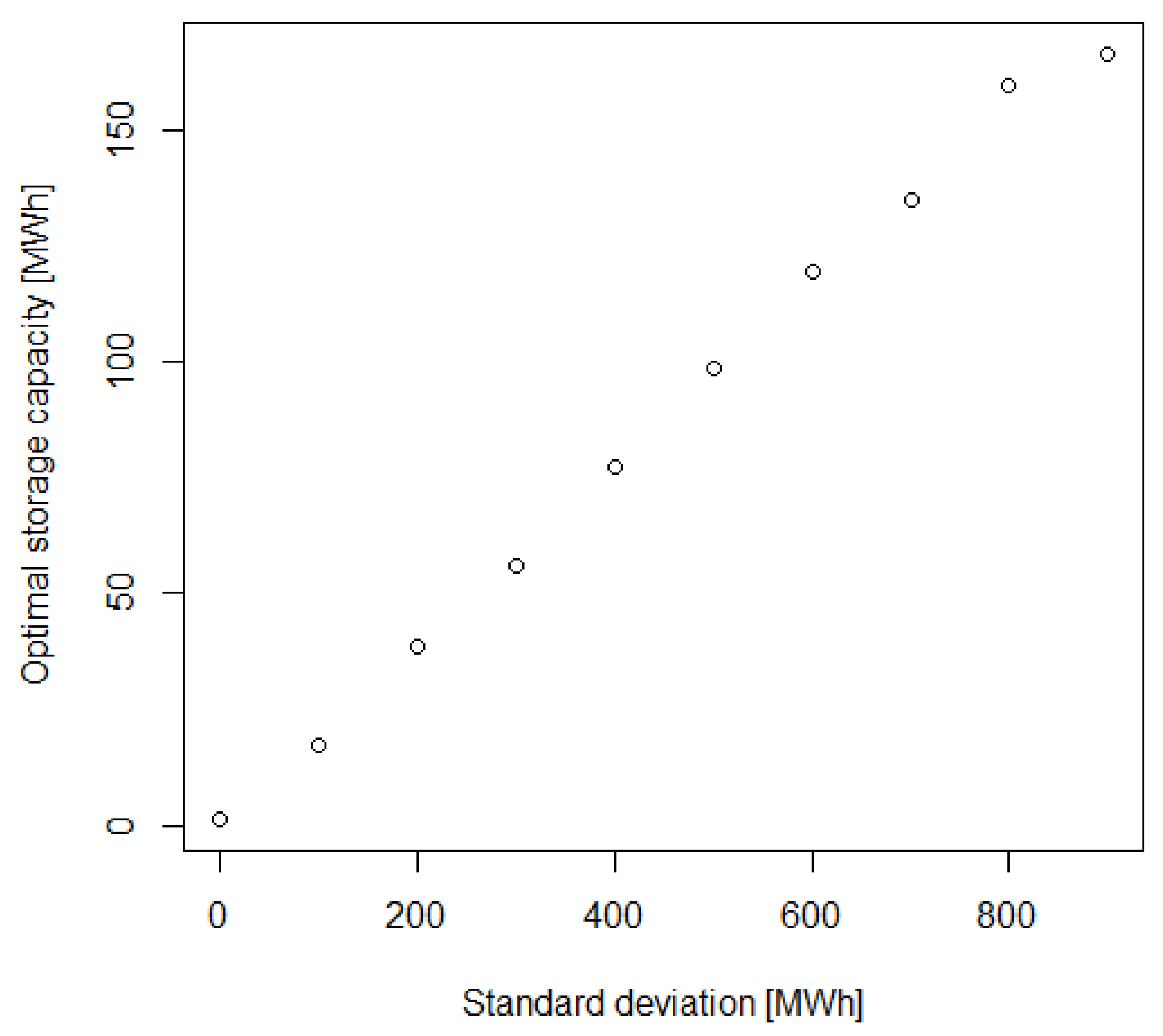
5.5. Sensitivity of the Storage Sizing to the Variability of the Input Power
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Pérez-Collazo, C.; Greaves, D.; Iglesias, G. A review of combined wave and offshore wind energy. Renew. Sustain. Energy Rev. 2015, 42, 141–153. [Google Scholar] [CrossRef]
- The European Wind Energy Association. The European offshore wind industry—key trends and statistics 2014. Available online: http://www.ewea.org/fileadmin/files/library/publications/statistics/EWEA-European-Offshore-Statistics-2014.pdf (accessed on 29 February 2016).
- Widén, J.; Carpman, N.; Castellucci, V.; Lingfors, D.; Olauson, J.; Remouit, F.; Bergkvist, M.; Grabbe, M.; Waters, R. Variability assessment and forecasting of renewables: A review for solar, wind, wave and tidal resources. Renew. Sustain. Energy Rev. 2015, 44, 356–375. [Google Scholar] [CrossRef]
- Stoutenburg, E.D.; Jenkins, N.; Jacobson, M.Z. Power output variations of co-located offshore wind turbines and wave energy converters in California. Renew. Energy 2010, 35, 2781–2791. [Google Scholar] [CrossRef]
- Soukissian, T.H. Probabilistic modeling of directional and linear characteristics of wind and sea states. Ocean Eng. 2014, 91, 91–110. [Google Scholar] [CrossRef]
- Güner, H.A.A.; Yüksel, Y.; Çevik, E.Ö. Estimation of wave parameters based on nearshore wind-wave correlations. Ocean Eng. 2013, 63, 52–62. [Google Scholar] [CrossRef]
- Fusco, F.; Nolan, G.; Ringwood, J.V. Variability reduction through optimal combination of wind/wave resources—An Irish case study. Energy 2010, 35, 314–325. [Google Scholar] [CrossRef]
- Tedeschi, E.; Robles, E.; Santos, M.; Duperray, O.; Salcedo, F. Effect of energy storage on a combined wind and wave energy farm. In Proceedings of the Energy Conversion Congress and Exposition, Raleigh, NC, USA, 15–20 September 2012; pp. 2798–2804.
- Astariz, S.; Perez-Collazo, C.; Abanades, J.; Iglesias, G. Towards the optimal design of a co-located wind–wave farm. Energy 2015, 84, 15–24. [Google Scholar] [CrossRef]
- Chozas, J.F.; Kramer, M.M.; Sørensen, H.C.; Kofoed, J.P. Combined Production of a Full-scale Wave Converter and a Full-scale Wind Turbine—A Real Case Study. Int. Conf. Ocean Energy 2012, 2012, 1–7. [Google Scholar]
- Hanssen, J.E.; Margheritini, L.; O’Sullivan, K.; Mayorga, P.; Martinez, I.; Arriaga, A.; Agos, I.; Steynor, J.; Ingram, D.; Hezari, R.; et al. Design and performance validation of a hybrid offshore renewable energy platform. In Proceedings of the 2015 10th International Conference on Ecological Vehicles and Renewable Energies, Monte-Carlo, Monaco, 31 March–2 April 2015; pp. 1–8.
- Zhou, Z.; Benbouzid, M.; Charpentier, J.F.; Scuiller, F.; Tang, T. A review of energy storage technologies for marine current energy systems. Renew. Sustain. Energy Rev. 2013, 18, 390–400. [Google Scholar] [CrossRef]
- Slocum, A.H. Symbiotic offshore energy harvesting and storage systems. Sustain. Energy Technol. Assess. 2014. [Google Scholar] [CrossRef]
- Aubry, J.; Bydlowski, P.; Multon, B.; Ahmed, H.B.; Borgarino, B. Energy Storage System Sizing for Smoothing Power Generation of Direct Wave Energy Converters. In Proceedings of the 3rd International Conference on Ocean Energy, Bilbao, Spain, 6–8 October 2010; pp. 1–7.
- O’Sullivan, D.; Murray, D.; Hayes, J.; Egan, M.G.; Lewis, A.W. The Benefits of Device Level Short Term Energy Storage in Ocean Wave Energy Converters. In Energy Storage in the Emerging Era of Smart Grids; Carbone, R., Ed.; InTech: Rijeka, Croatia, 2011; Available online: http://www.intechopen.com/books/energy-storage-in-the-emerging-era-of-smart-grids/the-benefits-of-device-level-short-term-energy-storage-in-ocean-wave-energy-converters (accessed on 29 February 2016).
- Tedeschi, E.; Santos-Mugica, M. Modeling and Control of a Wave Energy Farm Including Energy Storage for Power Quality Enhancement: The Bimep Case Study. IEEE Trans. Power Syst. 2014, 29, 1489–1497. [Google Scholar] [CrossRef]
- Kovaltchouk, T.; Blavette, A.; Ahmed, H.B.; Multon, B.; Aubry, J. Comparison between centralized and decentralized storage energy management for Direct Wave Energy Converter Farm. In Proceedings of the IEEE 10th International Conference on Ecological Vehicles and Renewable Energies, Monte-Carlo, Monaco, 31 March–2 April 2015.
- Marañon-Ledesma, H.; Tedeschi, E. Energy Storage Sizing by Stochastic Optimization for a combined Wind–wave-Diesel Supplied System. In Proceedings of the IEEE 4th International Conference on Renewable Energies and Applications, Palermo, Italy, 22–25 November 2015.
- Tedeschi, E.; Sjolte, J.; Molinas, M.; Santos, M. Stochastic rating of storage systems in isolated networks with increasing wave energy penetration. Energies 2013, 6, 2481–2500. [Google Scholar] [CrossRef]
- Rabiee, A.; Khorramdel, H.; Aghaei, J. A review of energy storage systems in microgrids with wind turbines. Renew. Sustain. Energy Rev. 2013, 18, 316–326. [Google Scholar] [CrossRef]
- Oudalov, A.; Cherkaoui, R.; Beguin, A. Sizing and optimal operation of battery energy storage system for peak shaving application. In Proceedings of the IEEE Lausanne Power Tech, Lausanne, Switzerland, 1–5 July 2007; pp. 621–625.
- Nick, M.; Cherkaoui, R.; Paolone, M. Optimal siting and sizing of distributed energy storage systems via alternating direction method of multipliers. Int. J. Electr. Power Energy Syst. 2015, 72, 33–39. [Google Scholar] [CrossRef]
- Chen, S.X.; Gooi, H.B.; Wang, M.Q. Sizing of energy storage for microgrids. IEEE Trans. Smart Grid 2012, 3, 142–151. [Google Scholar] [CrossRef]
- Barton, J.P.; Infield, D.G. A probabilistic method for calculating the usefulness of a store with finite energy capacity for smoothing electricity generation from wind and solar power. J. Power Sources 2006, 162, 943–948. [Google Scholar] [CrossRef]
- Bludszuweit, H.; Dominguez-Navarro, J.A. A Probabilistic Method for Energy Storage Sizing Based on Wind Power Forecast Uncertainty. IEEE Trans. Power Syst. 2011, 26, 1651–1658. [Google Scholar] [CrossRef]
- Song, J.; Krishnamurthy, V.; Kwasinski, A.; Sharma, R. Development of a markov-chain-based energy storage model for power supply availability assessment of photovoltaic generation plants. IEEE Trans. Sustain. Energy 2013, 4, 491–500. [Google Scholar] [CrossRef]
- Jones, G.L.; Harrison, P.G.; Harder, U.; Field, T. Fluid queue models of renewable energy storage. In Proceedings of the 6th International Conference on Performance Evaluation Methodologies and Tools, Cargese, France, 9–12 October 2012; pp. 224–225.
- Ghiassi-Farrokhfal, Y.; Keshav, S.; Rosenberg, C. Toward a Realistic Performance Analysis of Storage Systems in Smart Grids. IEEE Trans. Smart Grid 2015, 6, 402–410. [Google Scholar] [CrossRef]
- Wang, K.; Member, S.; Ciucu, F.; Lin, C.; Member, S.; Low, S.H. A Stochastic Power Network Calculus for Integrating Renewable Energy Sources into the Power Grid. IEEE J. Sel. Areas Commun. 2012, 30, 1037–1048. [Google Scholar] [CrossRef]
- Gautam, N.; Xu, Y.; Bradley, J.T. Meeting inelastic demand in systems with storage and renewable sources. In Proceedings of the IEEE International Conference on Smart Grid Communications, Venice, Italy, 3–6 November 2014.
- Yan, K. Fluid Models for Production-Inventory Systems. Ph.D. Dissertation, The University of North Carolina at Chapel Hill, Chapel Hill, NC, USA, 2006. Available online: http://www.unc.edu/~vkulkarn/PhD/YanDissertation.pdf (accessed on 29 February 2016). [Google Scholar]
- Aggarwal, V.; Gautam, N.; Kumara, S.R.T.; Greaves, M. Stochastic fluid flow models for determining optimal switching thresholds. Perform. Eval. 2005, 59, 19–46. [Google Scholar] [CrossRef]
- Jones, G.L.; Harrison, P.G.; Harder, U.; Field, T. Fluid queue models of battery life. In Proceedings of the 2012 IEEE 20th International Symposium on Modeling, Analysis and Simulation of Computer and Telecommunication Systems, Arlington, VA, USA, 7–9 August 2012; pp. 278–285.
- Mohammadi, S.; Mohammadi, A. Stochastic scenario-based model and investigating size of battery energy storage and thermal energy storage for micro-grid. Int. J. Electr. Power Energy Syst. 2014, 61, 531–546. [Google Scholar] [CrossRef]
- Ardakanian, O.; Keshav, S.; Rosenberg, C. On the use of teletraffic theory in power distribution systems. In e-Energy’12, Proceedings of the 3rd International Conference on Future Energy System: Where Energy, Computing and Communication Meet, Madrid, Spain, 9–11 May 2012; ACM: New York, NY, USA, 2012. [Google Scholar] [CrossRef]
- Harrison, J.M. Browmian Motion and Stochastic Flow Sytems; John Wiley and Son: Hoboken, NJ, USA, 1985. [Google Scholar]
- Fox, B.; Flynn, D.; Bryans, L.; Jenkins, N.; Milborrow, D.; O’Malley, M.; Watson, R.; Anaya-Lara, O. Wind Power Integration: Connection and System Operational Aspects; The Institution of Engineering Technology: Stevenage, UK, 2007. [Google Scholar]
- Smith, G.H.; Venugopal, V.; Fasham, J. Wave Spectral Bandwidth as a Measure of Available Wave Power. In Proceedings of the 25th International Conference on Offshore Mechanics and Artic Engineering, Hamburg, Gennany, 4–9 June 2006; pp. 1–9.
- Scrucca, L. GA: A Package for Genetic Algorithms in R. J. Stat. Softw. 2012, 53, 1–37. [Google Scholar]
- BADC. MIDAS Marine surface measurements. Available online: http://badc.nerc.ac.uk/home/ (accessed on 29 February 2016).
- International Renewable Energy Agency (IRENA). Battery storage for renewables: Market status and technology outlook. January 2015. Available online: http://www.irena.org/documentdownloads/publications/irena_battery_storage_report_2015.pdf (accessed on 29 February 2016).
- Fraunhofer Institute for Solar Energy Systems (ISE). Photovoltaics report. 2015. Available online: https://www.ise.fraunhofer.de/de/downloads/pdf-files/aktuelles/photovoltaics-report-in-englischer-sprache.pdf (accessed on 29 February 2016).



| Case 1 | Case 2 | Case 3 | Case 4 | Case 5 | Case 6 | |
|---|---|---|---|---|---|---|
| B (MWh) | – | – | – | 37.23 | 87.46 | 62.09 |
| psto (MW) | – | – | – | 9.43 | 22.82 | 15.09 |
| Convergence time of the algorithm | – | – | – | 5.84 min | 2.48 min | 5.71 s |
| Produced energy (GWh) | 105.12 | 105.12 | 105.12 | 105.12 | 105.12 | 105.12 |
| Waste of energy (GWh) | 32.42 | 31.64 | 35.80 | 26.48 | 3.38 | 2.87 |
| Loss of energy (GWh) | 32.42 | 31.64 | 35.81 | 26.49 | 3.42 | 2.90 |
| Extracted energy (GWh) | 72.70 | 73.48 | 69.31 | 78.63 | 101.70 | 102.22 |
| Wasted energy cost (%) | 31.72 | 30.96 | 35.03 | 25.91 | 3.31 | 2.81 |
| Lost energy cost (%) | 31.72 | 30.96 | 35.03 | 25.91 | 3.34 | 2.84 |
| Income (%) | 71.12 | 71.88 | 67.81 | 76.93 | 99.50 | 100.00 |
| Investment (%) | – | – | – | 3.89 | 9.15 | 6.47 |
| Profit (%) | 71.12 | 71.88 | 67.81 | 73.04 | 90.34 | 93.53 |
| Capacity factor | 0.691 | 0.698 | 0.659 | 0.748 | 0.967 | 0.972 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Domínguez-Navarro, J.A.; Tedeschi, E. Evaluation of the Fluid Model Approach for the Sizing of Energy Storage in Wave-Wind Energy Systems. Energies 2016, 9, 162. https://doi.org/10.3390/en9030162
Domínguez-Navarro JA, Tedeschi E. Evaluation of the Fluid Model Approach for the Sizing of Energy Storage in Wave-Wind Energy Systems. Energies. 2016; 9(3):162. https://doi.org/10.3390/en9030162
Chicago/Turabian StyleDomínguez-Navarro, José A., and Elisabetta Tedeschi. 2016. "Evaluation of the Fluid Model Approach for the Sizing of Energy Storage in Wave-Wind Energy Systems" Energies 9, no. 3: 162. https://doi.org/10.3390/en9030162
APA StyleDomínguez-Navarro, J. A., & Tedeschi, E. (2016). Evaluation of the Fluid Model Approach for the Sizing of Energy Storage in Wave-Wind Energy Systems. Energies, 9(3), 162. https://doi.org/10.3390/en9030162







