Comparison of Optimized Control Strategies of a High-Speed Traction Machine with Five Phases and Bi-Harmonic Electromotive Force
Abstract
:1. Introduction
2. Presentation and Characterization of the Five-Phase Machine
- For hybrid vehicles, the required volume density is high: permanent magnet machines are then preferred [43,44]; moreover, the use of high speeds allows obtaining, for a given power, lower torque and consequently a lower rotor diameter: speeds up to 14,000 rpm are currently considered in automotive applications; using a high number of poles also allows reducing the stator diameter: eight poles are common for automotive applications for speed range up to 14,000 rpm. The consequence of all of these previous choices is the need to take into account permanent magnet and iron losses due to the high frequency eddy currents found in the machine (normally up to 800 Hz and even 1800 Hz). For the studied machine, the number of slots per pole per phase Nppis equal to 0.5. The choice is motivated by the fact that among other concentrated tooth fractional windings, windings with Npp = 0.5 present low amplitude harmonics and subharmonics of magneto-motive forces [44,45] with a consequently low level of eddy current losses. It can be noticed that numerous commercial three-phase traction motors with a concentrated tooth winding and with approximately the same frequency range are used for hybrid automotive suppliers, such as Honda (24 slots/16 poles), Bosch (36 slots/24 poles), Hyundai (24 slots/16 poles) and Toyota (12 slots/8 poles): they all have the same Npp = 0.5. Finally, insertion of magnets also protects them from the all too important eddy currents and reduces mechanical constraints.
- For automotive applications, if efficiency is fundamental in steady states, the ability to achieve high torque during transient operations is also required: a machine that can produce torque with, not only one, but two harmonics of currents under constraints has been chosen in order to enlarge the number of degrees of freedom for the control. Moreover, at least two levels of current densities (5 and 10 A/mm) must also be considered during the design.
- In order to reduce the power (and the cost) of the voltage source inverter, the machine must be able to be controlled in a wide range of speeds at constant power under the voltage constraint: with a five-phase machine, the control can be simple, even if two harmonics are used.
3. Maximum Torque per Ampere Application under Constraints
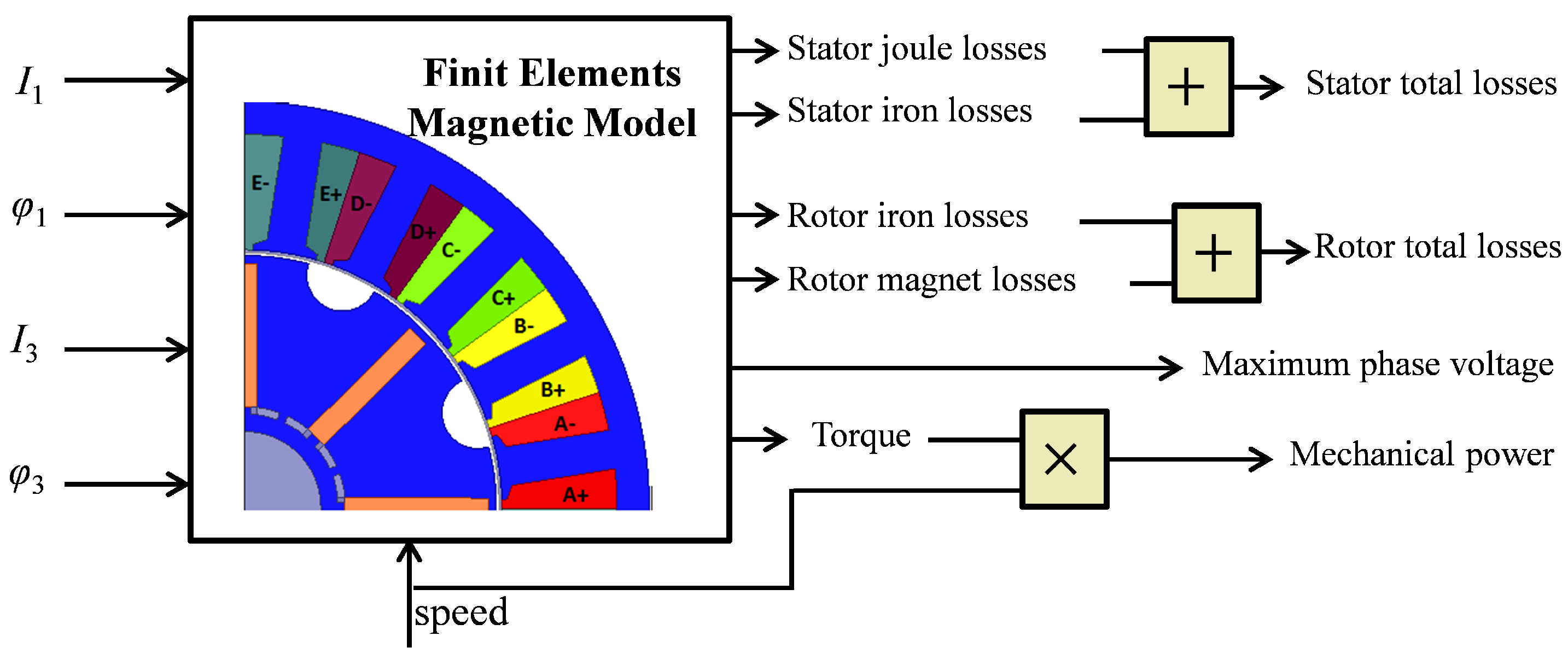
3.1. Modeling Description
3.2. MTPA Formulation under Constraint
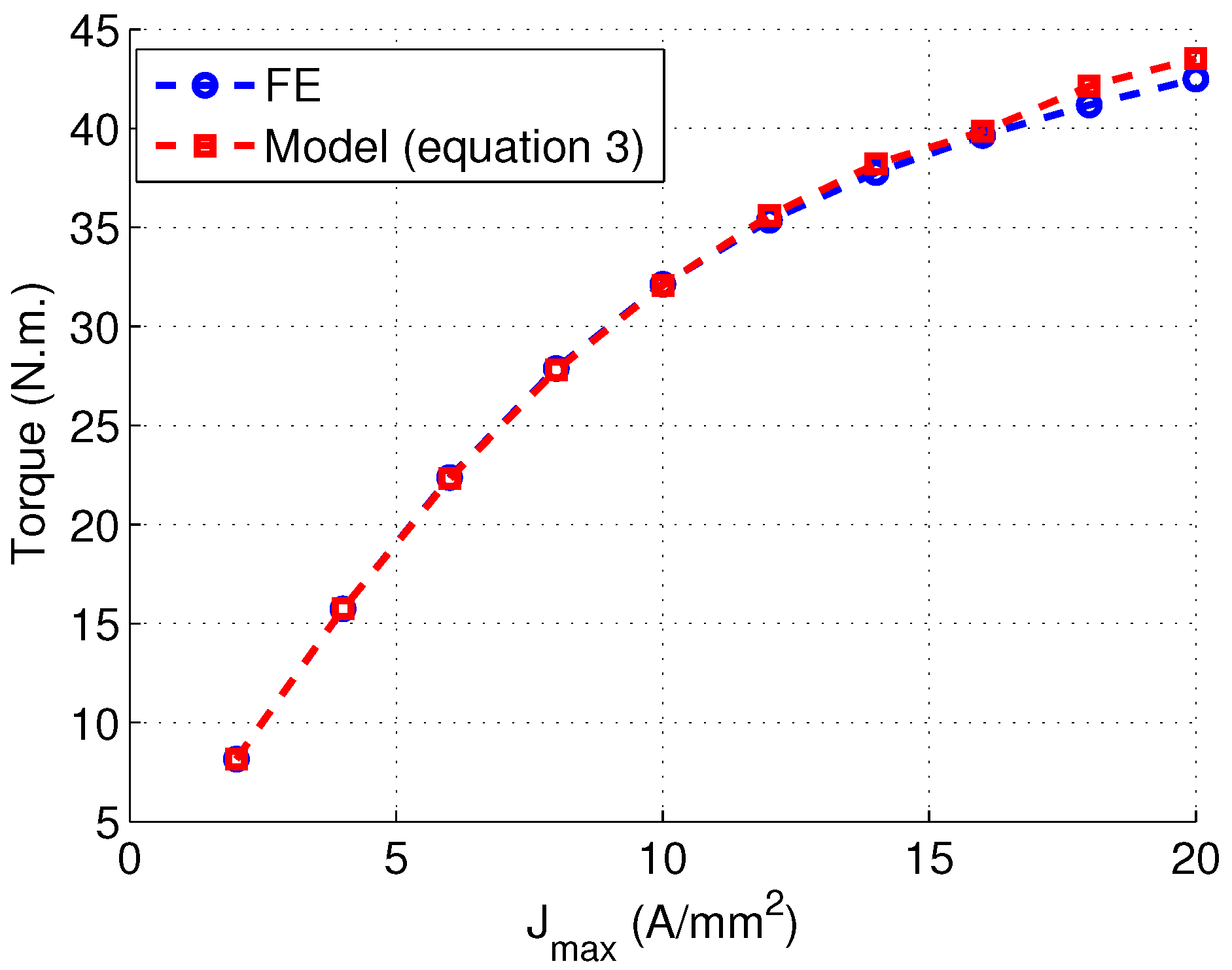
3.3. MTPA Results
4. Maximum Torque per Losses Strategies
4.1. Optimization Problem Formulation MTPL(I)
4.2. Optimization Problem Formulation at High Speeds MTPL(II)
4.3. Optimization Tool-EGO
- Initialization of the sampling plan: select the initial designs of the sampling plan using the Latin hypercube strategy (generally a good choice for this kind of surrogate model).
- Fine model evaluation: evaluate the designs of the sampling plane with the fine model.
- Kriging model construction: build the kriging models for each objective and constraint function.
- Improvement point search: find the improvement point using the Infill Criterion (IC), expressed in Equation (10).where is the Expected Improvement , which is the probability that the estimated response is smaller than the current minimal objective function; is the cumulative distribution function; is the inexpensive constraint in terms of the evaluation time.
- Infill point fine model evaluation: evaluate the infill point determined at the precedent iteration using the fine model (FEM).
- Best objective value: if the objective infill is lower than the best objective and the constraint violation is in acceptable tolerance, set this point as the new best point.
- Sampled data addition: add the infill point to the sampled dataset.
- Stop criterion verification: if the maximum iteration number is attained, the algorithm ends; otherwise, return to Step 3 and repeat.
4.4. MTPL Resolution
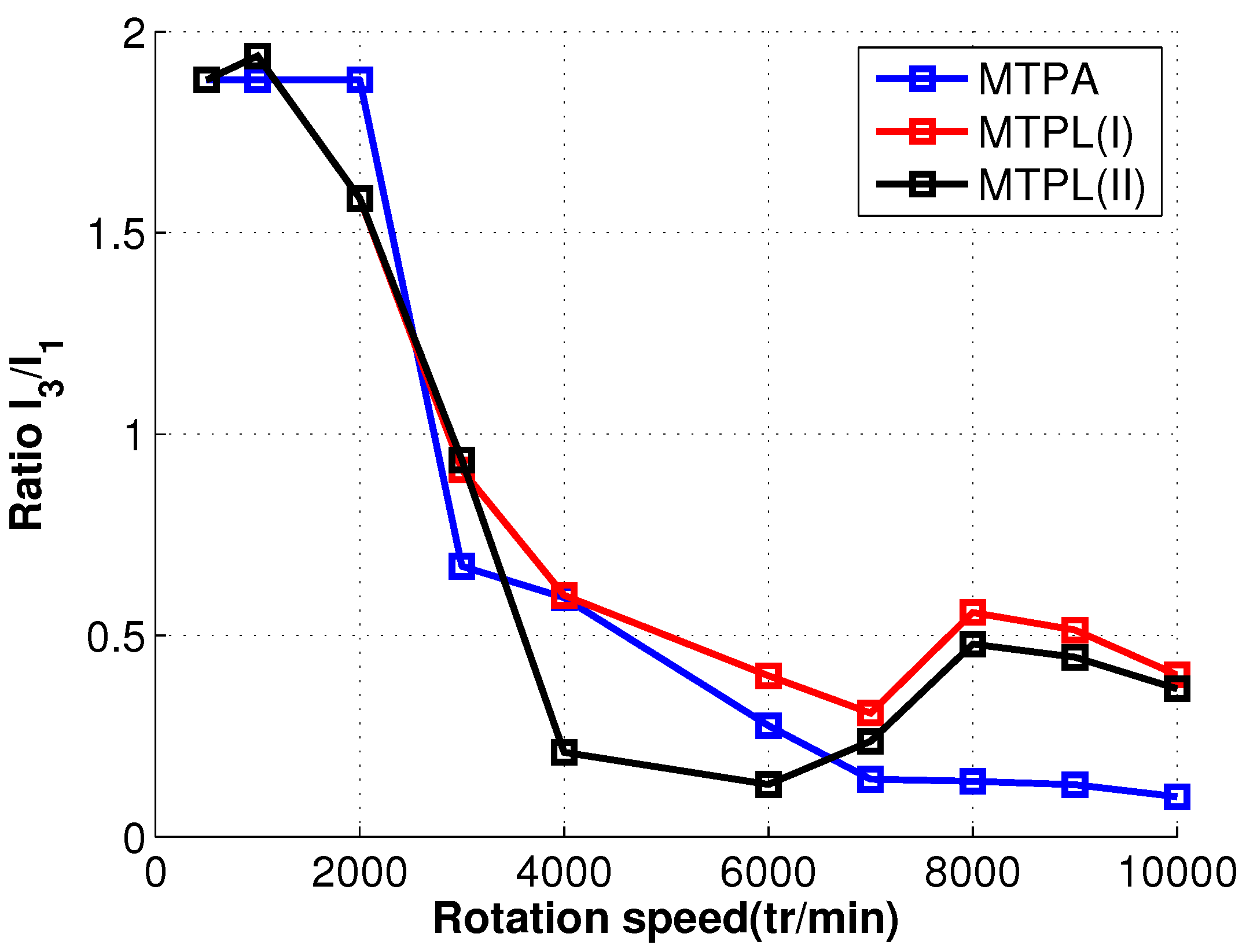
4.4.1. Optimal Currents at Low Speeds
4.4.2. Optimal Currents at High Speeds
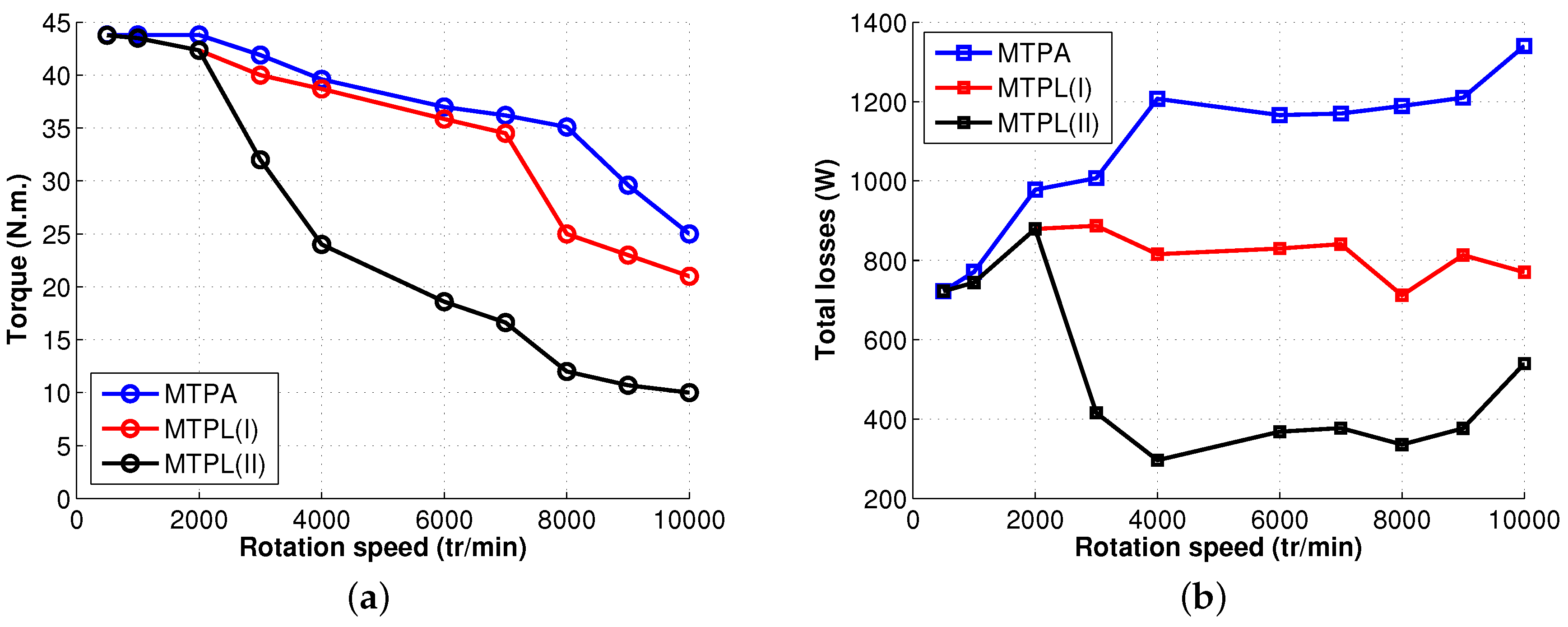
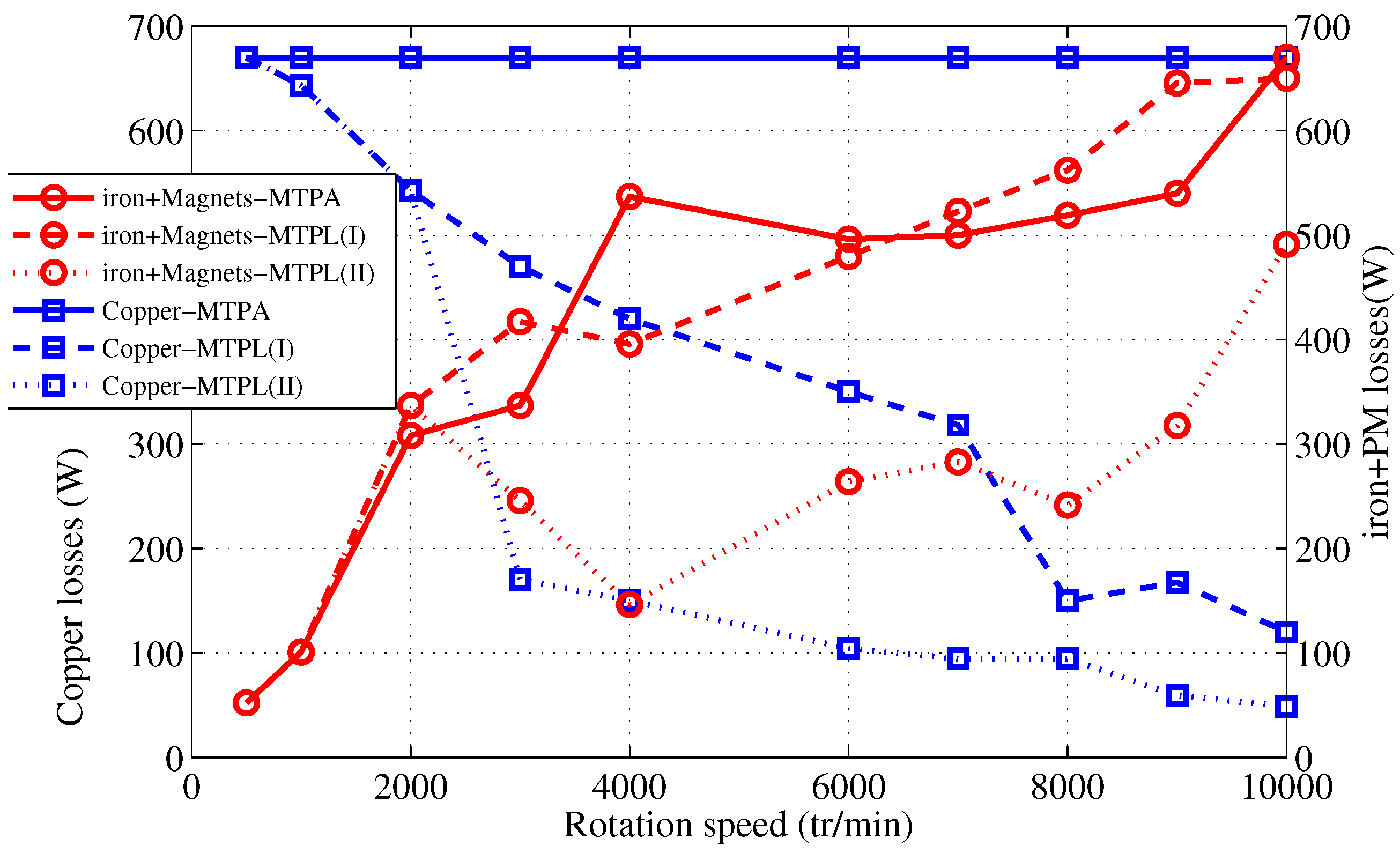
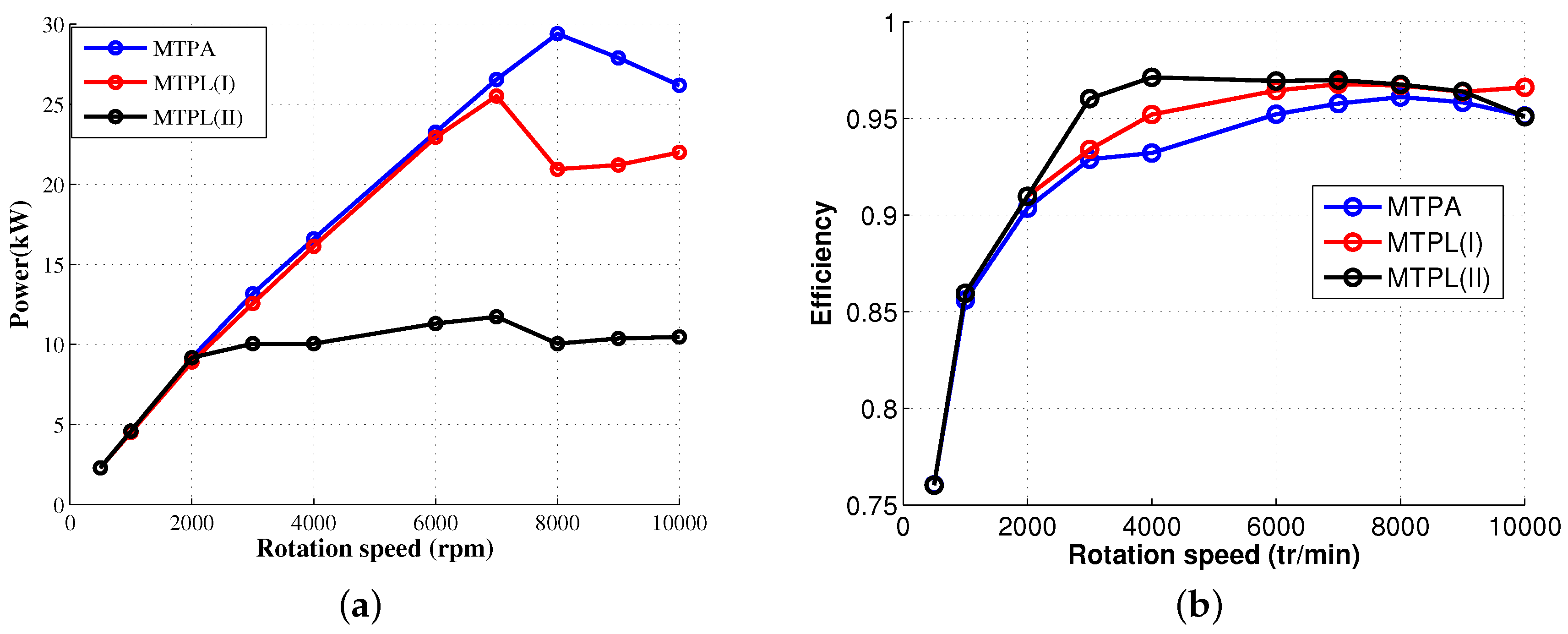
4.4.3. Torque, Losses and Efficiency
5. Conclusions
Author Contributions
Conflicts of Interest
Abbreviations
| subspace associated with the primary machine defined by Concordia transformation | |
| subspace associated with the secondary machine defined by Concordia transformation | |
| , | phase of first and third harmonic of current with first and third harmonic of electromotive force as references |
| Ψ | flux linked in a phase of the machine |
| Concordia matrix | |
| (resp. ) | first (resp. third) harmonic electromotive force amplitude |
| (resp. ) | first (resp. third) harmonic current force amplitude |
| IPM | Internal Permanent Magnet |
| SPM | Surface Permanent Magnet |
| J | RMS current density |
| torque produced by the machine | |
| PM | Permanent magnet |
| total losses in the stator (copper and iron losses) | |
| total losses in the rotor (iron and permanent magnet losses) | |
| number of slots per pole and per phase | |
| cumulative distribution function | |
| p | number of pairs of poles |
| the conductor area | |
| voltage across a phase of the machine | |
| DC bus voltage |
Appendix A. Iron Losses Calculation
References
- Levi, E. Multiphase electric machines for variable-speed applications. IEEE Trans. Ind. Electron. 2008, 55, 1893–1909. [Google Scholar] [CrossRef]
- Letellier, P. High Power Permanent magnet machines for electric propulsion drives. In Proceedings of the 3rd International Symposium on All Electric Ship, Paris, France, 26–27 October 2000; pp. 126–132.
- Thongam, J.; Tarbouchi, M.; Okou, A.; Bouchard, D.; Beguenane, R. Trends in naval ship propulsion drive motor technology. In Proceedings of the Electrical Power & Energy Conference (EPEC), Halifax, NS, Canada, 21–23 August 2013; IEEE: New York, NY, USA, 2013; pp. 1–5. [Google Scholar]
- Bennett, J.; Mecrow, B.C.; Atkinson, D.J.; Atkinson, G. Safety-critical design of electromechanical actuation systems in commercial aircraft. Electr. Power Appl. IET 2011, 5, 37–47. [Google Scholar] [CrossRef]
- Cao, W.; Mecrow, B.C.; Atkinson, G.J.; Bennett, J.W.; Atkinson, D.J. Overview of electric motor technologies used for more electric aircraft (MEA). IEEE Trans. Ind. Electron. 2012, 59, 3523–3531. [Google Scholar]
- Huang, X.; Goodman, A.; Gerada, C.; Fang, Y.; Lu, Q. Design of a five-phase brushless DC motor for a safety critical aerospace application. IEEE Trans. Ind. Electron. 2012, 59, 3532–3541. [Google Scholar] [CrossRef]
- Bojoi, R.; Cavagnino, A.; Tenconi, A.; Vaschetto, S. Control of Shaft-Line-Embedded Multiphase Starter/Generator for Aero-Engine. IEEE Trans. Ind. Electron. 2016, 63, 641–652. [Google Scholar] [CrossRef]
- Parsa, L.; Toliyat, H.A. Fault-tolerant interior-permanent-magnet machines for hybrid electric vehicle applications. IEEE Trans. Veh. Technol. 2007, 56, 1546–1552. [Google Scholar] [CrossRef]
- Mohammadpour, A.; Parsa, L. Global fault-tolerant control technique for multiphase permanent-magnet machines. IEEE Trans. Ind. Appl. 2015, 51, 178–186. [Google Scholar] [CrossRef]
- Chen, Q.; Liu, G.; Gong, W.; Zhao, W. A new fault-tolerant permanent-magnet machine for electric vehicle applications. IEEE Trans. Magn. 2011, 47, 4183–4186. [Google Scholar] [CrossRef]
- Zheng, P.; Wu, F.; Lei, Y.; Sui, Y.; Yu, B. Investigation of a novel 24-slot/14-pole six-phase fault-tolerant modular permanent-magnet in-wheel motor for electric vehicles. Energies 2013, 6, 4980–5002. [Google Scholar] [CrossRef]
- Arashloo, R.S.; Romeral Martinez, J.L.; Salehifar, M.; Moreno-Eguilaz, M. Genetic algorithm-based output power optimisation of fault tolerant five-phase brushless direct current drives applicable for electrical and hybrid electrical vehicles. Electr. Power Appl. IET 2014, 8, 267–277. [Google Scholar] [CrossRef]
- Scuiller, F.; Semail, E.; Charpentier, J.F.; Letellier, P. Multi-criteria-based design approach of multi-phase permanent magnet low-speed synchronous machines. Electr. Power Appl. IET 2009, 3, 102–110. [Google Scholar] [CrossRef]
- Aslan, B.; Semail, E.; Korecki, J.; Legranger, J. Slot/pole combinations choice for concentrated multiphase machines dedicated to mild-hybrid applications. In Proceedings of the IECON 2011—37th Annual Conference on IEEE Industrial Electronics Society, Melbourne, Australia, 7–10 November 2011; pp. 3698–3703.
- Sui, Y.; Zheng, P.; Wu, F.; Yu, B.; Wang, P.; Zhang, J. Research on a 20-slot/22-pole five-phase fault-tolerant pmsm used for four-wheel-drive electric vehicles. Energies 2014, 7, 1265–1287. [Google Scholar] [CrossRef]
- Bojoi, R.; Cavagnino, A.; Cossale, M.; Tenconi, A. Multiphase starter generator for 48 V mini-hybrid powertrain: Design and testing. In Proceedings of the 2014 International Symposium on Power Electronics, Electrical Drives, Automation and Motion (SPEEDAM), Ischia, Italy, 18–20 June 2014; pp. 1319–1324.
- Aslan, B.; Savinois, O.; Mipo, J.C.; Farah, P.S. Comparison between 5 and 6 Phases Claw Pole Alternator for Automotive Application. In Proceedings of the 2014 IEEE Vehicle Power and Propulsion Conference (VPPC), Delft, The Netherlands, 18–20 June 2014; pp. 1–5.
- Jordan, S.; Manolopoulos, C.D.; Apsley, J.M. Winding Configurations for Five-Phase Synchronous Generators with Diode Rectifiers. IEEE Trans. Ind. Electron. 2016, 63, 517–525. [Google Scholar] [CrossRef]
- Scuiller, F.; Zahr, H.; Semail, E. Maximum reachable torque, power and speed for five-phase SPM machine with low armature reaction. IEEE Trans. Energy Convers. 2016, 31, 959–969. [Google Scholar] [CrossRef]
- Kestelyn, X.; Semail, E. A vectorial approach for generation of optimal current references for multiphase permanent-magnet synchronous machines in real time. IEEE Trans. Ind. Electron. 2011, 58, 5057–5065. [Google Scholar] [CrossRef]
- Zhao, P.; Yang, G. Torque density improvement of five-phase PMSM drive for electric vehicles applications. J. Power Electron. 2011, 11, 401–407. [Google Scholar] [CrossRef]
- Gong, J.; Aslan, B.; Gillon, F.; Semail, E. High Speed Functionality Optimizaion of Five-Phase PM Machine Using 3rd Harmonic Current. Int. J. Comput. Math. Electr. Electron. Eng. 2014, 33, 879–893. [Google Scholar] [CrossRef]
- Wang, K.; Zhu, Z.; Ombach, G. Torque enhancement of surface-mounted permanent magnet machine using third-order harmonic. IEEE Trans. Magn. 2014, 50, 104–113. [Google Scholar] [CrossRef]
- Sadeghi, S.; Mohammadpour, A.; Parsa, L. Design optimization of a high performance five-phase slotless PMSM. In Proceedings of the 2014 International Symposium on Power Electronics, Electrical Drives, Automation and Motion (SPEEDAM), Ischia, Italy, 18–20 June 2014; pp. 6–11.
- Yu, F.; Cheng, M.; Chau, K.T.; Li, F. Control and Performance Evaluation of Multiphase FSPM Motor in Low-Speed Region for Hybrid Electric Vehicles. Energies 2015, 8, 10335–10353. [Google Scholar] [CrossRef]
- Barrero, F.; Duran, M.J. Recent Advances in the Design, Modeling, and Control of Multiphase Machines— Part I. IEEE Trans. Ind. Electron. 2016, 63, 449–458. [Google Scholar] [CrossRef]
- Sun, Z.; Wang, J.; Jewell, G.W.; Howe, D. Enhanced optimal torque control of fault-tolerant PM machine under flux-weakening operation. IEEE Trans. Ind. Electron. 2010, 57, 344–353. [Google Scholar]
- Xuelei, S.; Xuhui, W.; Wei, C. Research on field-weakening control of multiphase permanent magnet synchronous motor. In Proceedings of the 2011 International Conference on Electrical Machines and Systems (ICEMS), Beijing, China, 20–23 August 2011; pp. 1–5.
- Sadeghi, S.; Guo, L.; Toliyat, H.A.; Parsa, L. Wide operational speed range of five-phase permanent magnet machines by using different stator winding configurations. IEEE Trans. Ind. Electron. 2012, 59, 2621–2631. [Google Scholar] [CrossRef]
- Lu, L.; Aslan, B.; Kobylanski, L.; Sandulescu, P.; Meinguet, F.; Kestelyn, X.; Semail, E. Computation of optimal current references for flux-weakening of multi-phase synchronous machines. In Proceedings of the IECON 2012—38th Annual Conference on IEEE Industrial Electronics Society, Montreal, QC, Canada, 25–28 October 2012; pp. 3610–3615.
- Mengoni, M.; Zarri, L.; Tani, A.; Parsa, L.; Serra, G.; Casadei, D. High-Torque-Density Control of Multiphase Induction Motor Drives Operating Over a Wide Speed Range. IEEE Trans. Ind. Electron. 2015, 62, 814–825. [Google Scholar] [CrossRef]
- Grandi, G.; Loncarski, J. Analysis of peak-to-peak current ripple amplitude in seven-phase PWM voltage source inverters. Energies 2013, 6, 4429–4447. [Google Scholar] [CrossRef]
- Levi, E. Advances in converter control and innovative exploitation of additional degrees of freedom for multiphase machines. IEEE Trans. Ind. Electron. 2016, 63, 433–448. [Google Scholar] [CrossRef]
- Aslan, B.; Korecki, J.; Vigier, T.; Semail, E. Influence of Rotor Structure and Number of Phases on Torque and Flux Weakening Characteristics of V-shape Interior PM Electrical Machine. J. Energy Power Eng. 2012, 6, 1461. [Google Scholar]
- Aslan, B.; Semail, E. New 5-phase concentrated winding machine with bi-harmonic rotor for automotive application. In Proceedings of the 2014 International Conference on Electrical Machines (ICEM), Berlin, Germany, 2–5 September 2014; pp. 2114–2119.
- Legranger, J.; Semail, B.; Semail, E. Polyphase Rotary Electrical Machine Having at Least Five Phases with Optimised Control. European Patent EP 2866344 (A2), 5 August 2015. [Google Scholar]
- Zahr, H.; Semail, E.; Scuiller, F. Five-phase version of 12slots/8poles three-phase synchronous machine for marine-propulsion. In Proceedings of the 2014 IEEE Vehicle Power and Propulsion Conference (VPPC), Coimbra, Portugal, 27–30 October 2014; pp. 1–6.
- Lyra, R.O.; Lipo, T.A. Torque density improvement in a six-phase induction motor with third harmonic current injection. IEEE Trans. Ind. Appl. 2002, 38, 1351–1360. [Google Scholar] [CrossRef]
- Lipo, T.A.; Lyra, R.O. Multi-Phase Electric Motor with Third Harmonic Current Injection. U.S. Patent 6,710,495, 23 March 2004. [Google Scholar]
- Abdelkhalik, A.; Masoud, M.; Barry, W. Eleven-phase induction machine: steady-state analysis and performance evaluation with harmonic injection. Electr. Power Appl. IET 2010, 4, 670–685. [Google Scholar] [CrossRef]
- Giurgea, S.; Zire, H.; Miraoui, A. Two-stage surrogate model for finite-element-based optimization of permanent-magnet synchronous motor. IEEE Trans. Magn. 2007, 43, 3607–3613. [Google Scholar] [CrossRef]
- Berbecea, A.; Kreuawan, S.; Gillon, F.; Brochet, P. A parallel multiobjective efficient global optimization: The finite element method in optimal design and model development. IEEE Trans. Magn. 2010, 46, 2868–2871. [Google Scholar] [CrossRef]
- El-Refaie, A.M. Motors/generators for traction/propulsion applications: A review. IEEE Veh. Technol. Mag. 2013, 8, 90–99. [Google Scholar] [CrossRef]
- Dajaku, G.; Spas, S.; Dajaku, X.; Gerling, D. Comparison of Two FSCW PM Machines for Integrated Traction Motor/Generator. In Proceedings of the IEEE International Electric Machines & Drives Conference (IEMDC), Coeur d’Alene, ID, USA, 10–13 May 2015; pp. 187–194.
- Kestelyn, X.; Semail, E. Vectorial Modeling and Control of Multiphase Machines with Non-salient Poles Supplied by an Inverter. In Control of Non-conventional Synchronous Motors; ISTE Ltd.: London, UK; John Wiley & Sons: New York, NY, USA, 2012; Chapter 7. [Google Scholar]
- Scuiller, F.; Semail, E.; Charpentier, J.F. General modeling of the windings for multi-phase ac machines. Eur. Phys. J. Appl. Phys. 2010, 50, 31102. [Google Scholar] [CrossRef]
- Zahr, H.; Semail, E.; Aslan, B.; Scuiller, F. Maximum Torque Per Ampere strategy for a biharmonic five-phase synchronous machine. In Proceedings of the 2016 International Symposium on Power Electronics, Electrical Drives, Automation and Motion (SPEEDAM), Anacapri, Italy, 22–24 June 2016; pp. 91–97.
- Rathnayake, R.; Dutta, R.; Fletcher, J.; Xiao, D. Modified efficiency optimization control for fractional slot concentrated wound interior permanent magnet synchronous generators. In Proceedings of the IECON 2015—41st Annual Conference of the IEEE Industrial Electronics Society, Yokohama, Japan, 9–12 November 2015.
- Saur, M.; Lehner, B.; Hentschel, F.; Gerling, D.; Lorenz, R.D. DB-DTFC as loss minimizing control for synchronous reluctance drives. In Proceedings of the IECON 2015—41st Annual Conference of the IEEE Industrial Electronics Society, Yokohama, Japan, 9–12 November 2015.
- Lin, D.; Zhou, P.; Fu, W.; Badics, Z.; Cendes, Z. A dynamic core loss model for soft ferromagnetic and power ferrite materials in transient finite element analysis. IEEE Trans. Magn. 2004, 40, 1318–1321. [Google Scholar] [CrossRef]
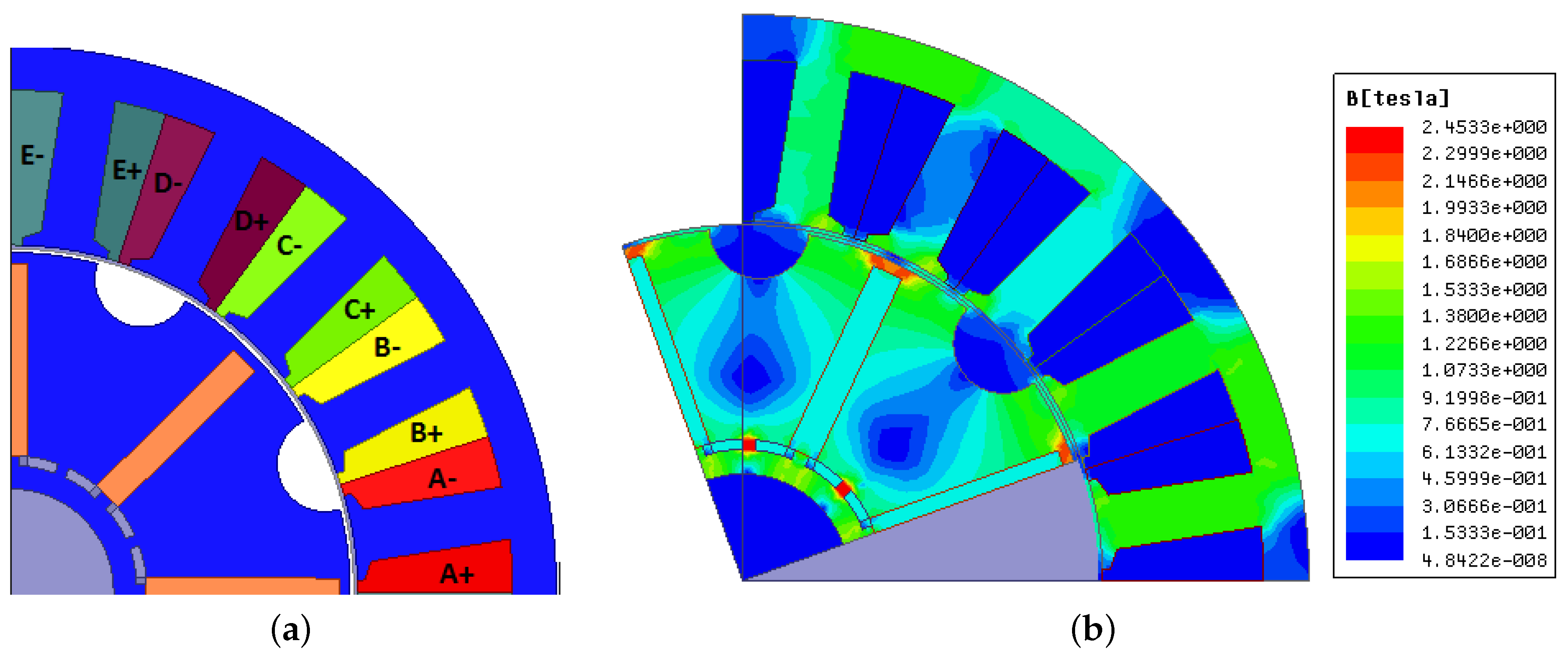
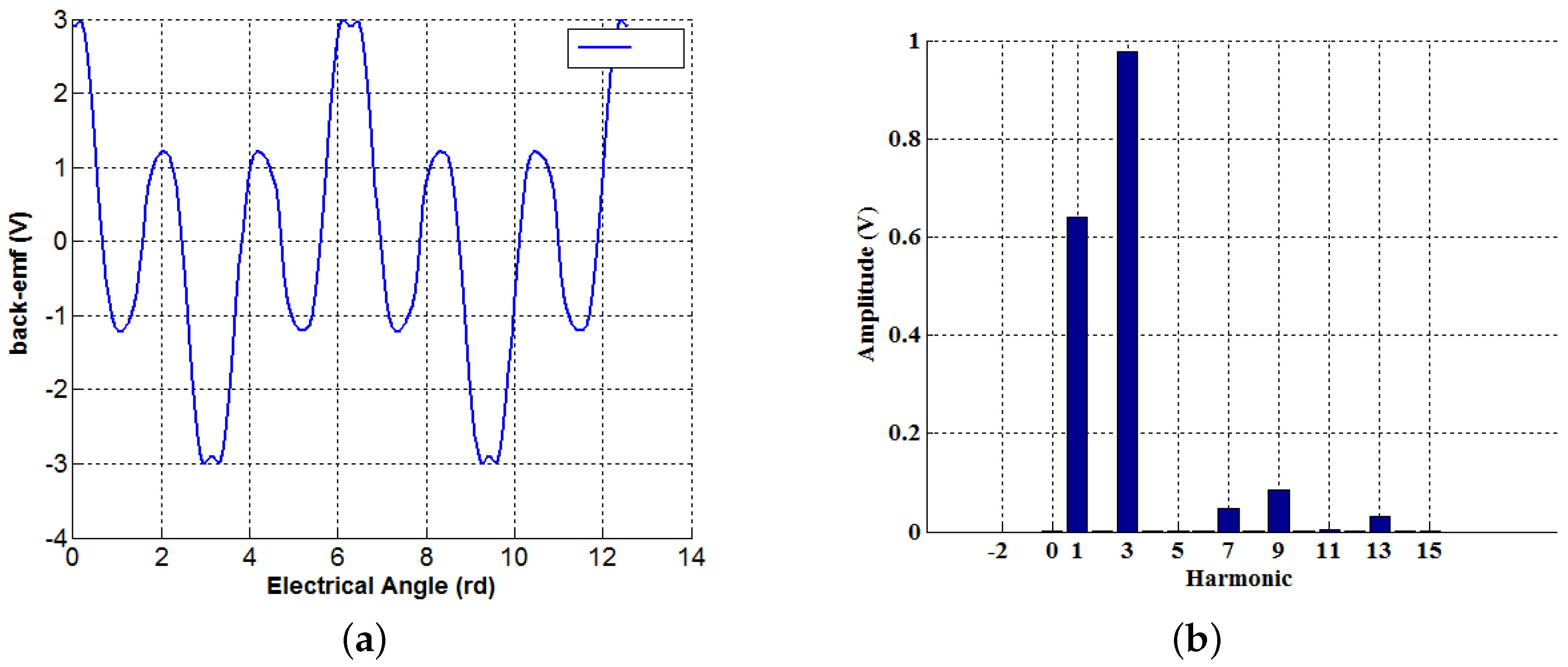
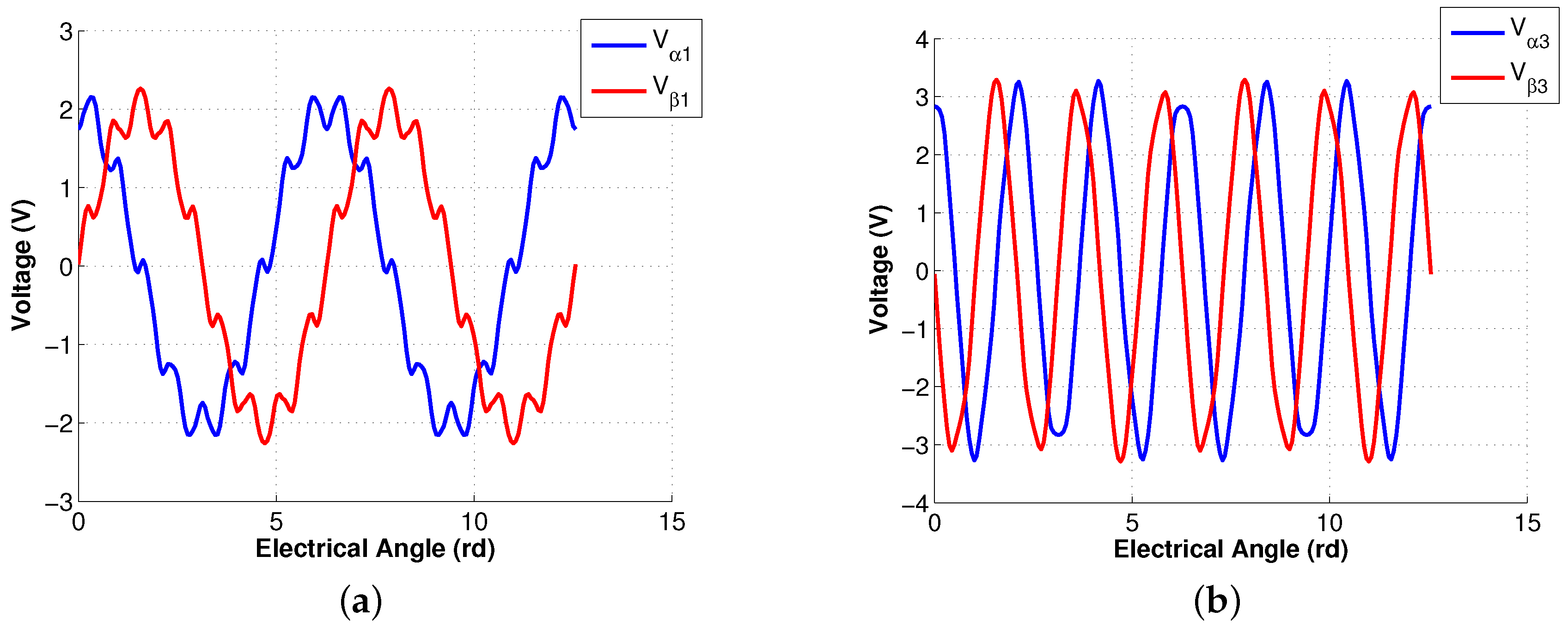
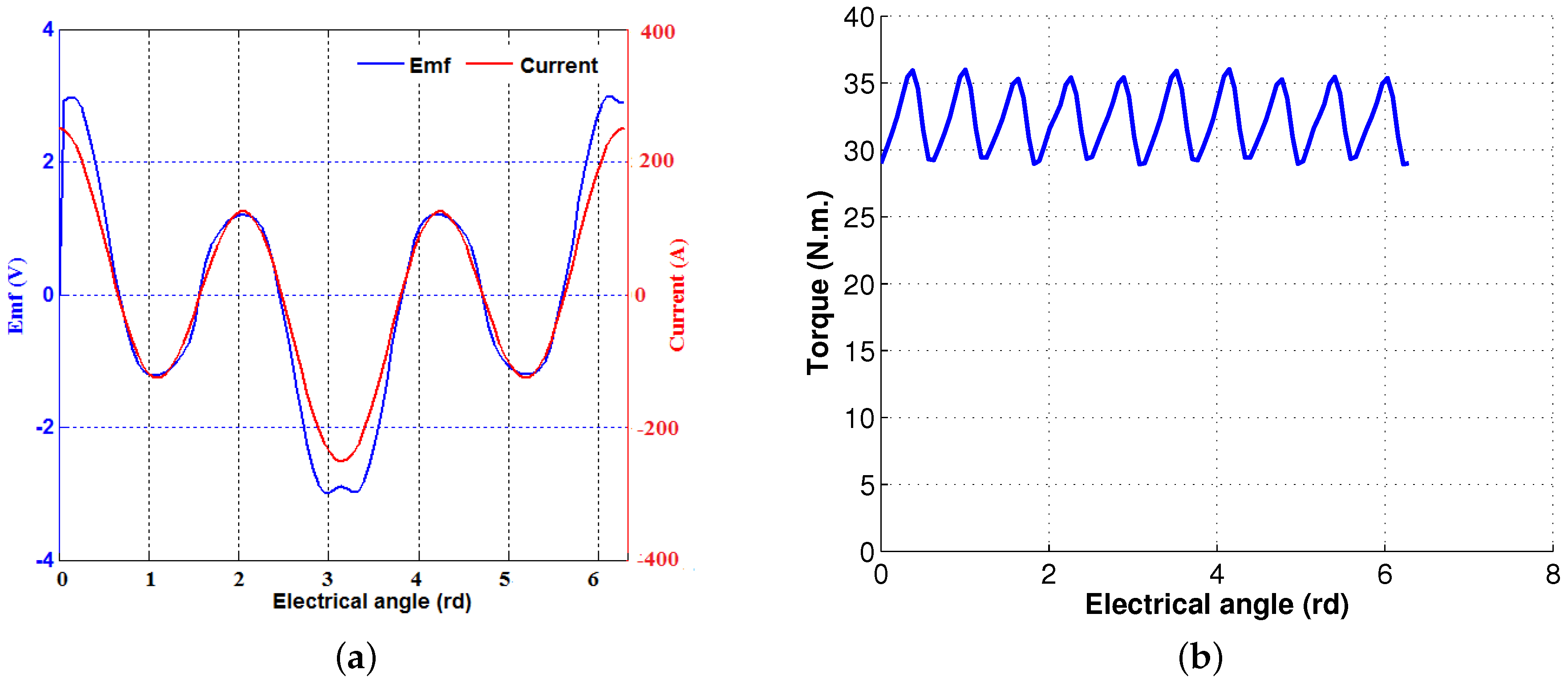
| Parameter | Value | Parameter | Value |
|---|---|---|---|
| Stator diameter | 130 mm | Air gap | 1 mm |
| Magnet width | 25.56 mm | Magnet height | 4 mm |
| Slot depth | 20.52 mm | Stator yoke | 5.8 mm |
| Hole width | 12.7 mm | Hole maximum depth | 6.34 mm |
| Magnet bridge | 1.25 mm | Length | 92.6 mm |
| Magnet type | NdFeB N40UH | Steel | Fe-Si M270-35A |
| Rated speed at 5 A/mm | 3700 rpm | Rated torque at 5 A/mm | 32.7 N.m. |
| Rated power at 5 A/mm | 12.7 kW | peak power at 5 A/mm | 19.6 kW |
| Maximum Torque for 10 A/mm at low speed | 44 N.m. | Maximum speed | 14,000 rpm |
| Peak power for 10 A/mm | 29.4 kW |
| Speed | First Harmonic | Third Harmonic | Voltage Peak | Torque | ||||
|---|---|---|---|---|---|---|---|---|
| (rpm) | Frequency (Hz) | Frequency | (V) | (N.m.) | ||||
| 500 | 33 | 100 | 176 | −0.04 | 330.8 | 0.15 | 12.5 | 43.8 |
| 1000 | 66 | 200 | 176 | −0.04 | 330.8 | 0.15 | 21.2 | 43.8 |
| 2000 | 133 | 400 | 176 | −0.04 | 330.8 | 0.15 | 42 | 43.8 |
| 2500 | 167 | 500 | 308.45 | 0.47 | 210.66 | 0.14 | 48 | 42.1 |
| 3000 | 200 | 600 | 310 | 0.51 | 208.3 | 0.09 | 47.5 | 41.9 |
| 4000 | 266 | 800 | 321.1 | 0.95 | 190.8 | 0.27 | 48 | 39.6 |
| 6000 | 400 | 1200 | 360 | 1.1 | 99.5 | 0.3 | 48 | 37 |
| 7000 | 467 | 1400 | 369.2 | 0.59 | 56.64 | 0.9 | 48 | 36.2 |
| 8000 | 533 | 1600 | 370 | 1.12 | 51 | 0.31 | 48 | 35.1 |
| 9000 | 600 | 1800 | 370.42 | 0.6 | 48.06 | 1.48 | 48 | 29.6 |
| 10,000 | 667 | 2000 | 372.1 | 1.21 | 37.1 | 0.45 | 48 | 25 |
| Speed (rpm) | J (A/mm) | Voltage Peak (V) | ||||
|---|---|---|---|---|---|---|
| 500 | 176 | −0.039 | 330.8 | 0.15 | 10 | 12.6 |
| 1000 | 167.8 | 0.026 | 325.4 | 0.22 | 9.8 | 25.2 |
| 2000 | 178 | 0.349 | 282.8 | 0.24 | 9 | 43.8 |
| Speed (rpm) | J (A/mm) | Voltage Peak (V) | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 3000 | 229.4 | 136.4 | 0.536 | 0.42 | 209.1 | 127.7 | 0.29 | 0.27 | 8.31 | 5 | 47.8 | 30.5 |
| 4000 | 250 | 169.9 | 0.53 | 0.55 | 150 | 35.7 | 0.16 | 0.54 | 7.8 | 4.64 | 47.5 | 19.8 |
| 6000 | 250 | 146.3 | 0.55 | 0.54 | 100 | 19 | 0.51 | 1 | 7.2 | 3.95 | 47.5 | 26.3 |
| 7000 | 245.85 | 137.14 | 0.48 | 0.62 | 75.5 | 32.5 | 0.41 | 1.31 | 6.89 | 3.7 | 47.27 | 24.97 |
| 8000 | 152.5 | 126.9 | 0.65 | 1 | 85 | 60.7 | 0.84 | 1.35 | 4.67 | 3.76 | 47.3 | 20.6 |
| 9000 | 109.47 | 101.39 | 0.52 | 0.92 | 56.25 | 45.25 | 0.66 | 1.26 | 5.32 | 2.97 | 46.72 | 27.83 |
| 10,000 | 146.6 | 104 | 0.489 | 0.986 | 58.9 | 38.2 | 1 | 1.28 | 4.23 | 2.69 | 47.4 | 32 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zahr, H.; Gong, J.; Semail, E.; Scuiller, F. Comparison of Optimized Control Strategies of a High-Speed Traction Machine with Five Phases and Bi-Harmonic Electromotive Force. Energies 2016, 9, 952. https://doi.org/10.3390/en9120952
Zahr H, Gong J, Semail E, Scuiller F. Comparison of Optimized Control Strategies of a High-Speed Traction Machine with Five Phases and Bi-Harmonic Electromotive Force. Energies. 2016; 9(12):952. https://doi.org/10.3390/en9120952
Chicago/Turabian StyleZahr, Hussein, Jinlin Gong, Eric Semail, and Franck Scuiller. 2016. "Comparison of Optimized Control Strategies of a High-Speed Traction Machine with Five Phases and Bi-Harmonic Electromotive Force" Energies 9, no. 12: 952. https://doi.org/10.3390/en9120952
APA StyleZahr, H., Gong, J., Semail, E., & Scuiller, F. (2016). Comparison of Optimized Control Strategies of a High-Speed Traction Machine with Five Phases and Bi-Harmonic Electromotive Force. Energies, 9(12), 952. https://doi.org/10.3390/en9120952






