Improving the Stability and Accuracy of Power Hardware-in-the-Loop Simulation Using Virtual Impedance Method
Abstract
:1. Introduction
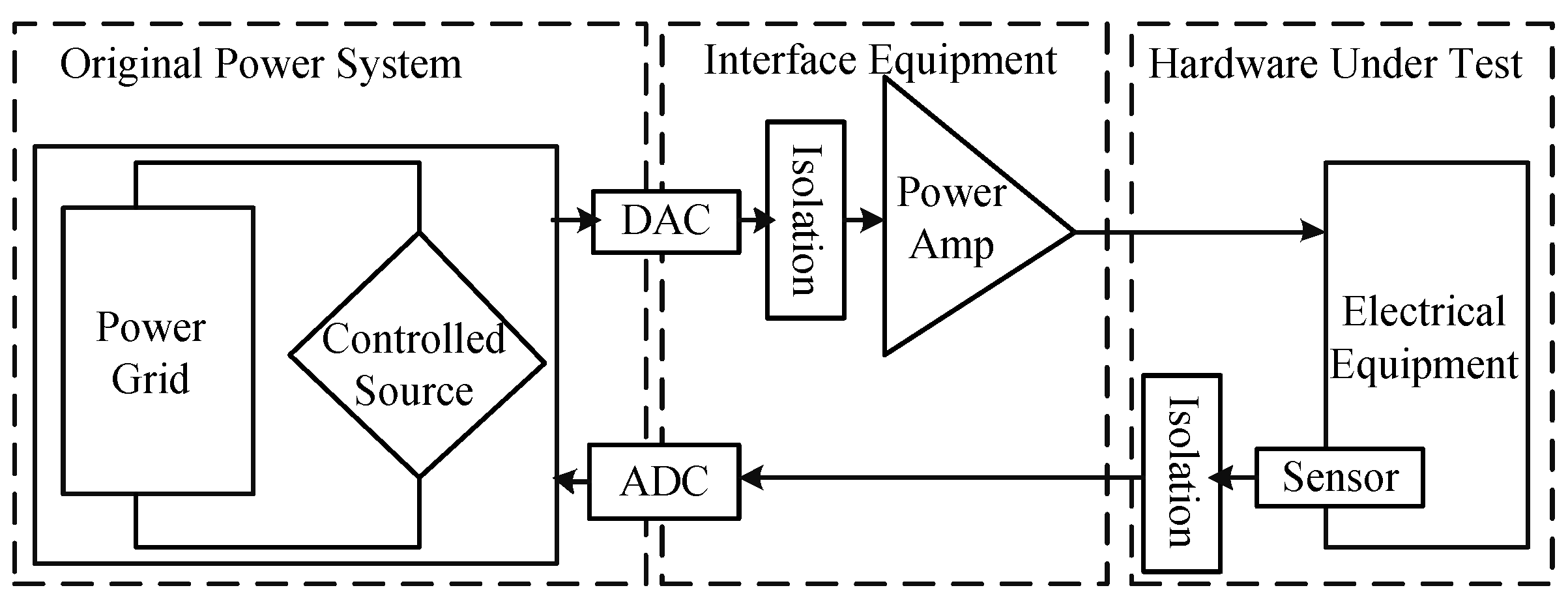
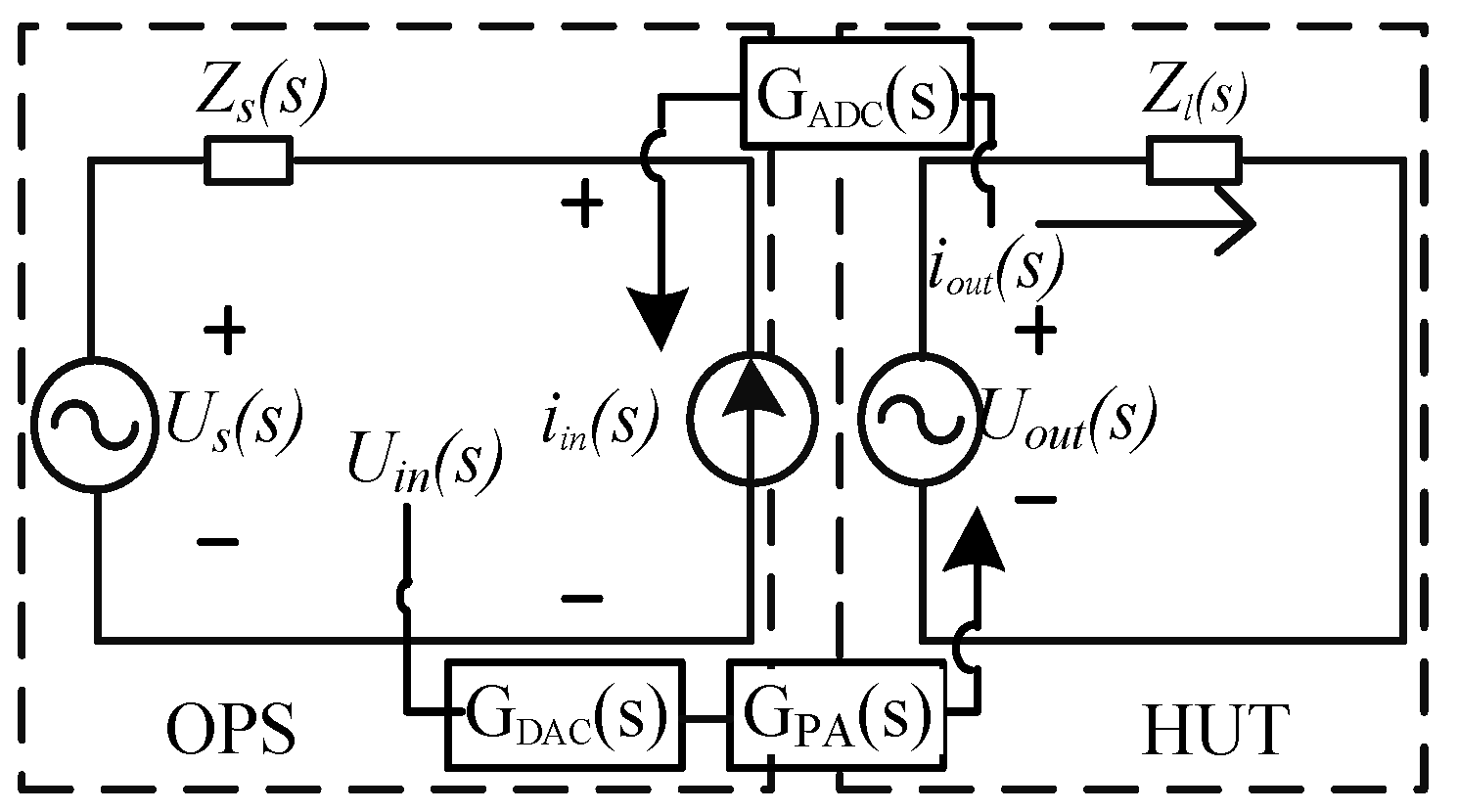
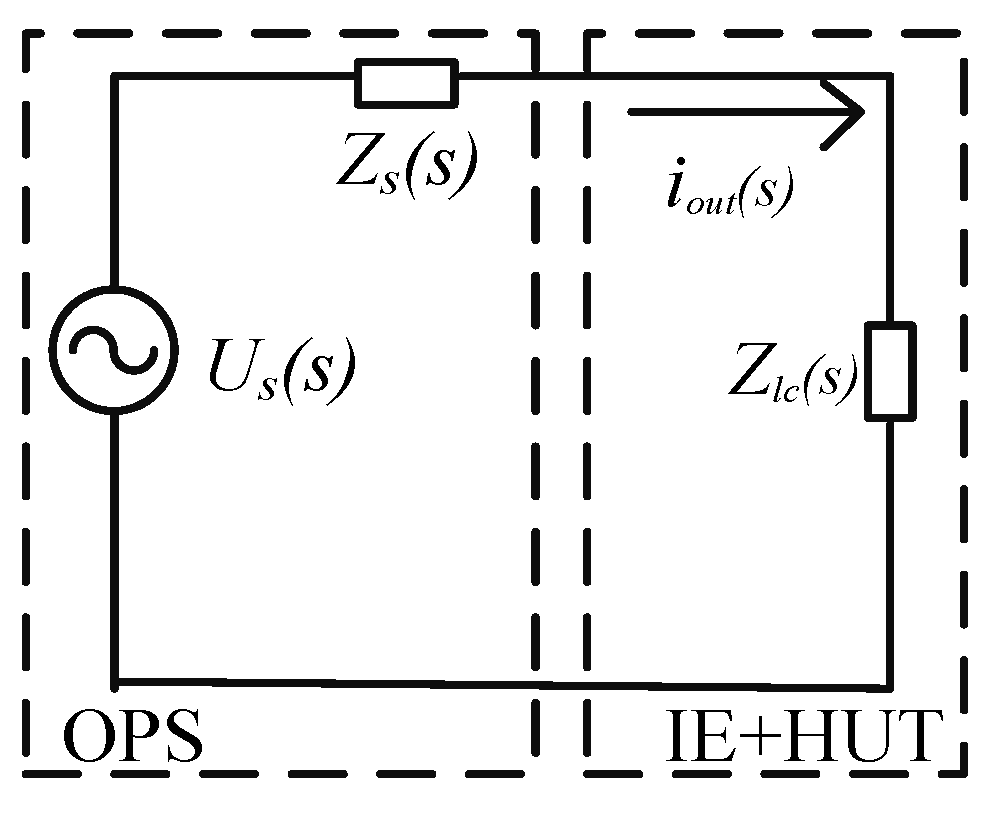
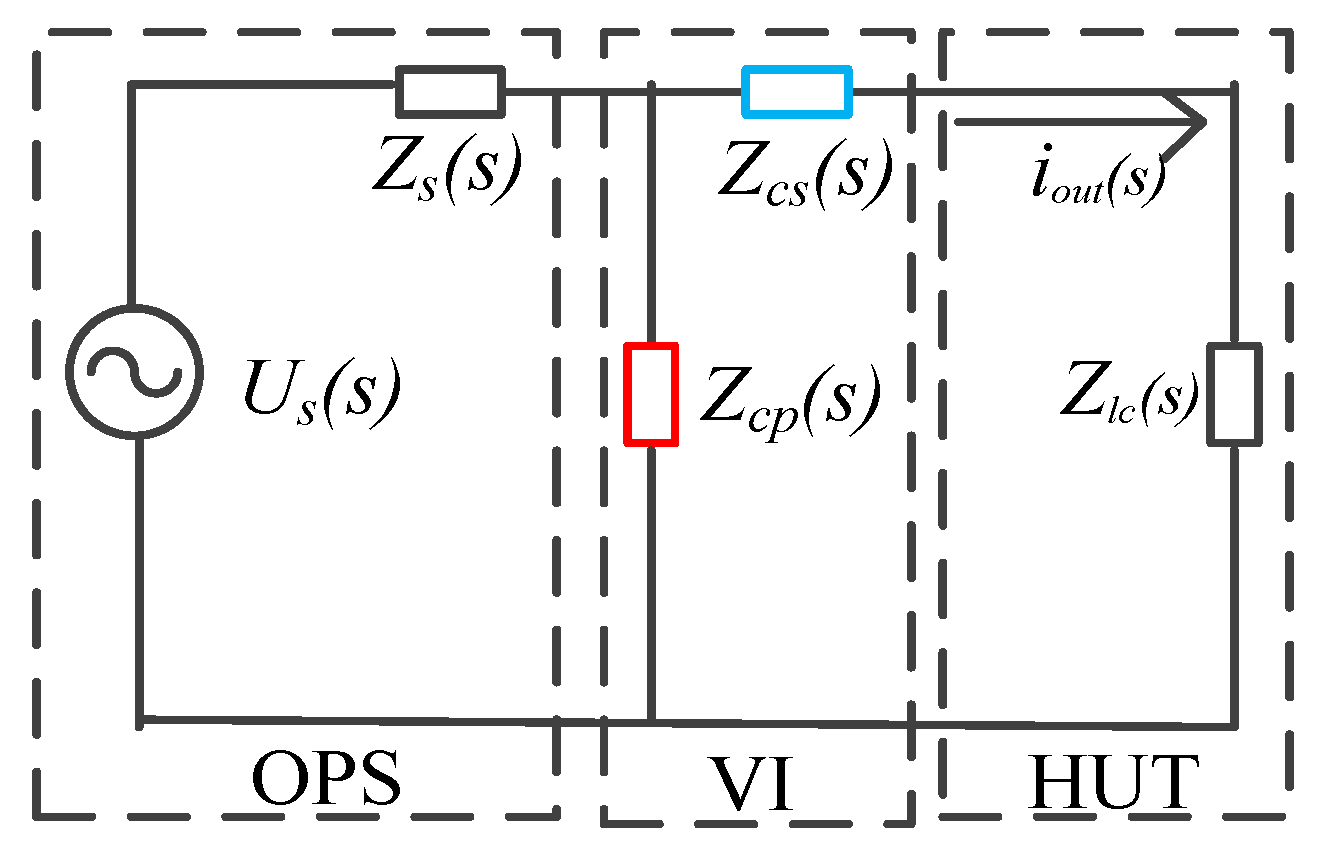
2. Modeling of a PHIL System
2.1. PHIL System Model
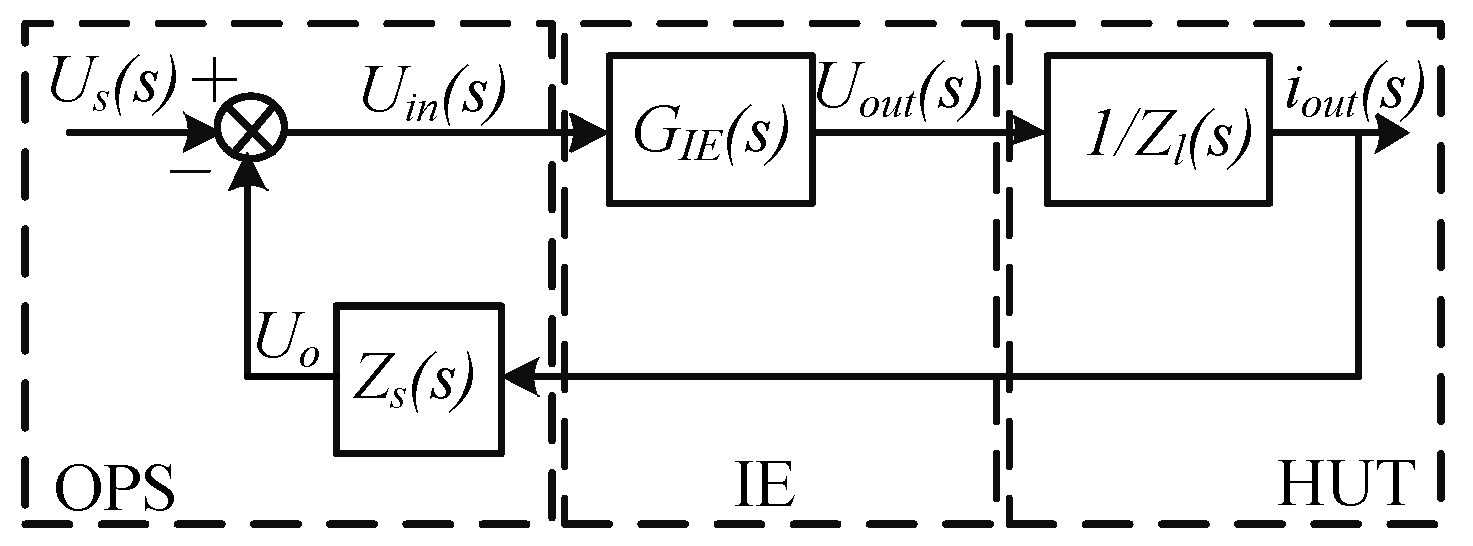
2.2. Stability Analysis
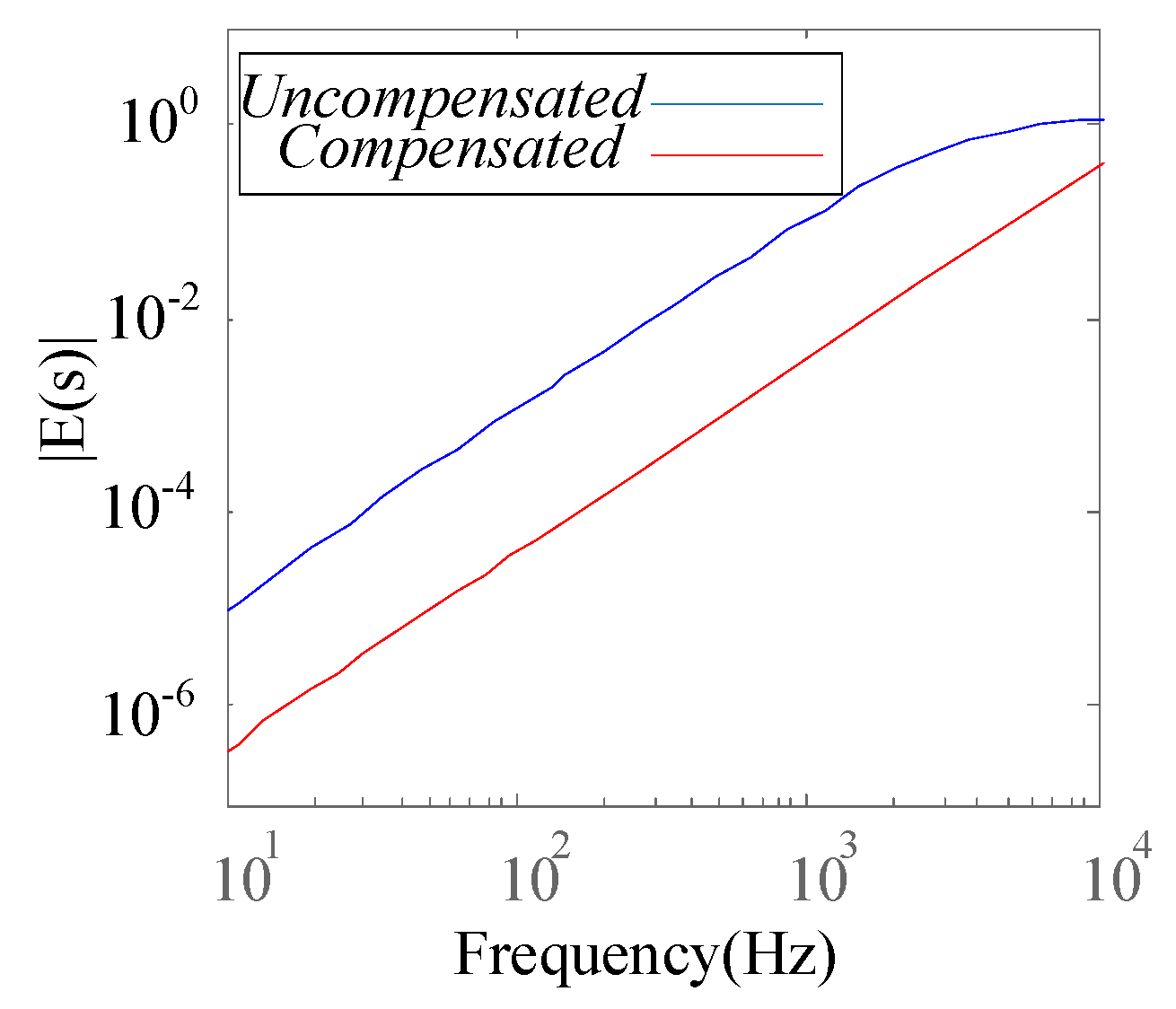
2.3. Accuracy Evaluation
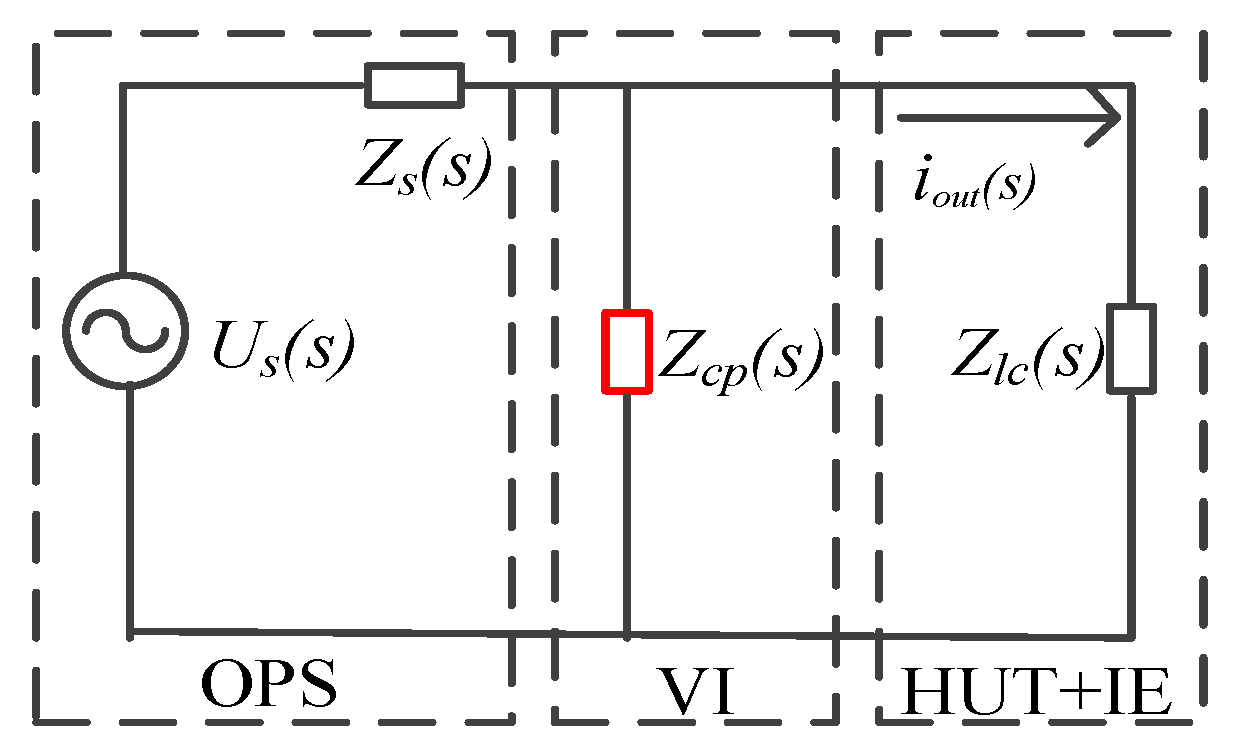
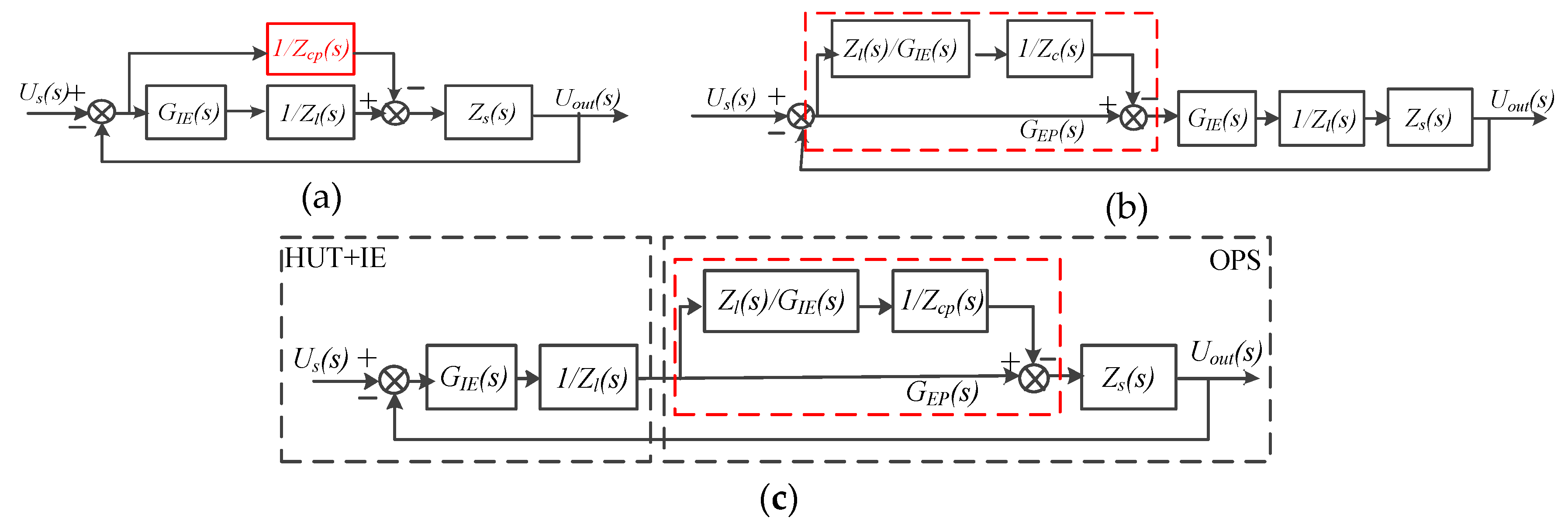
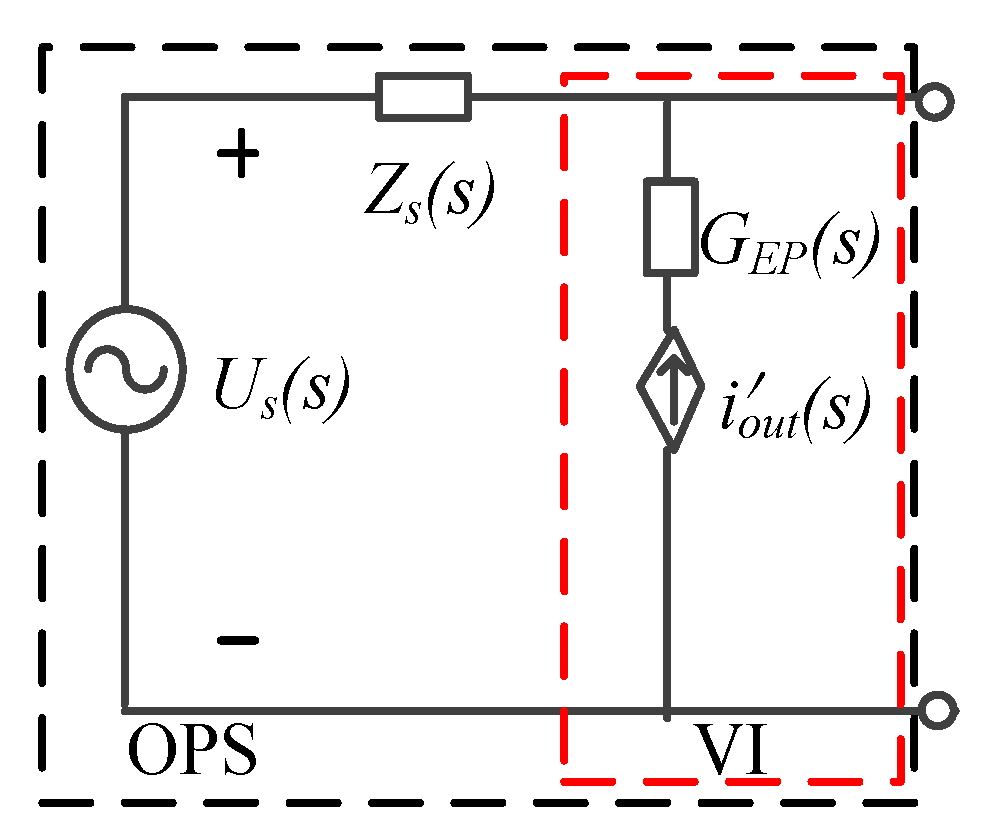
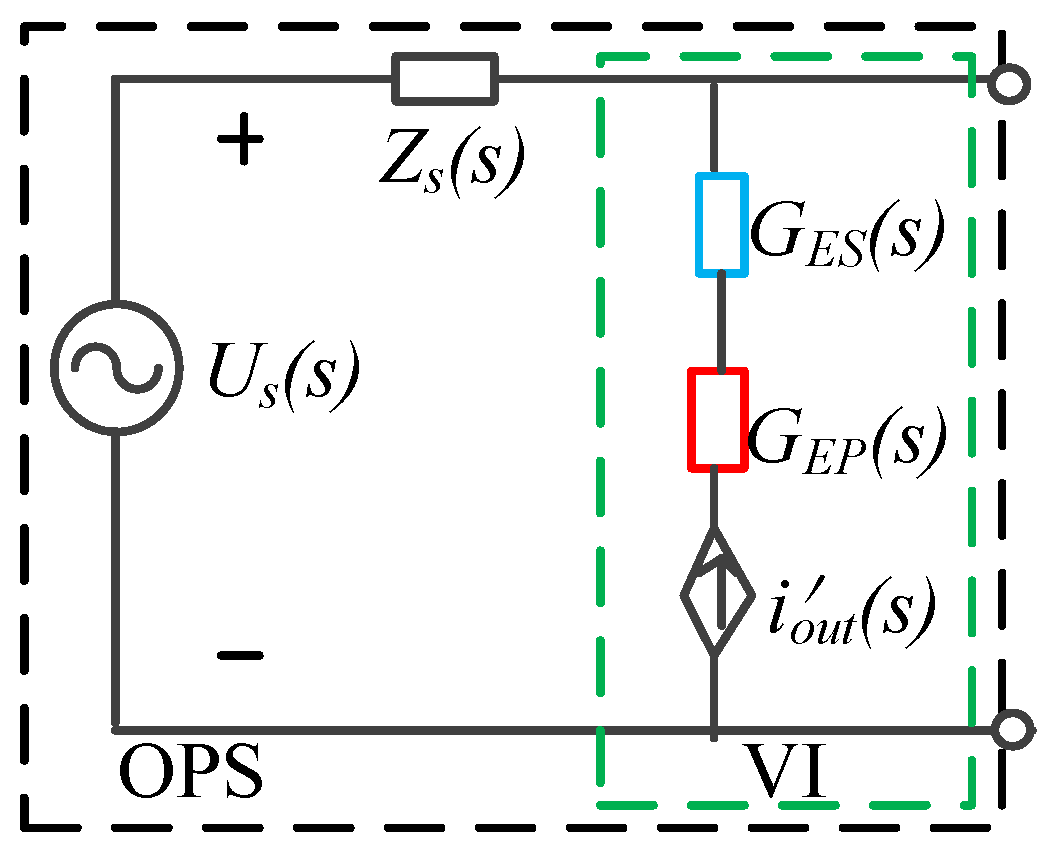
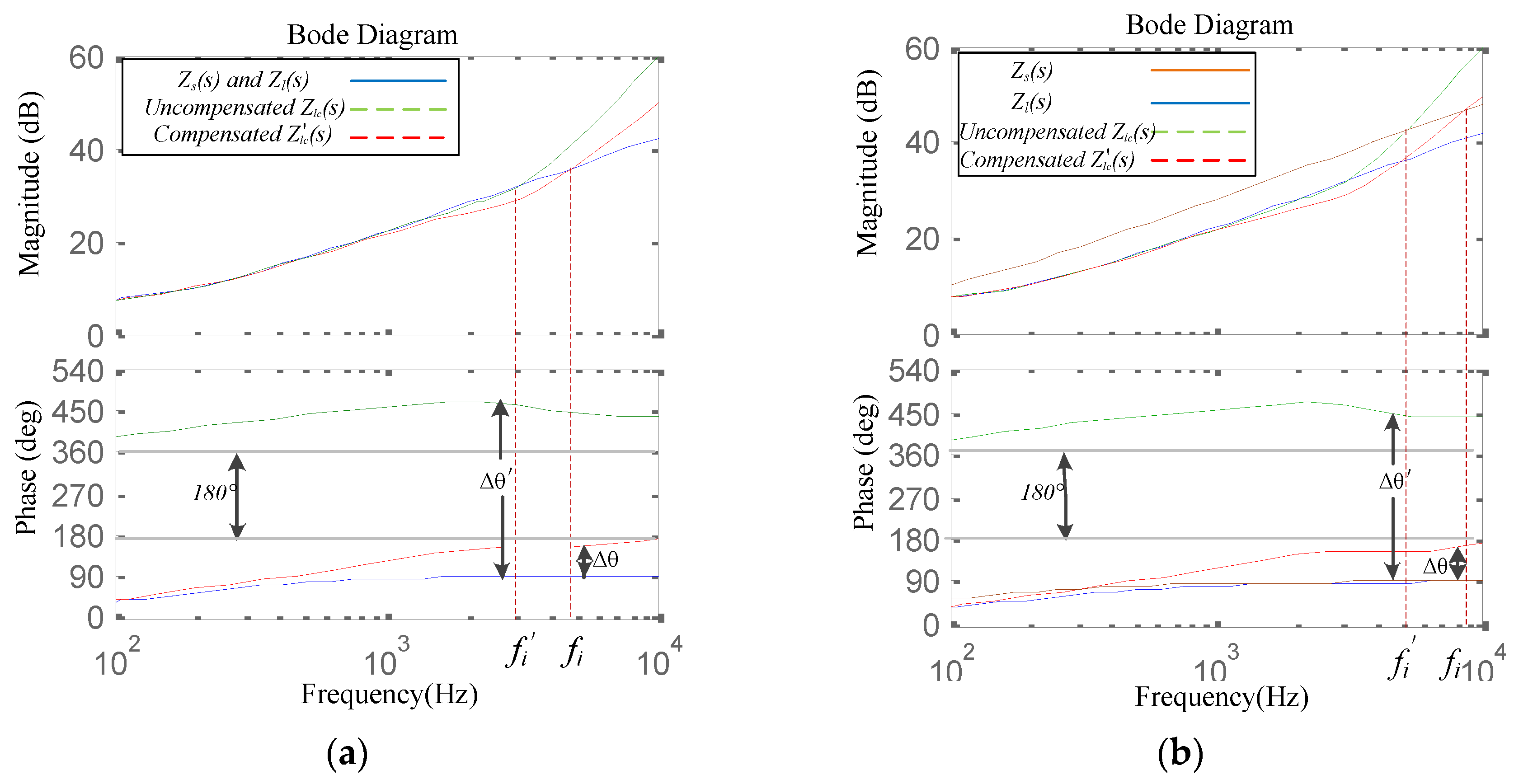
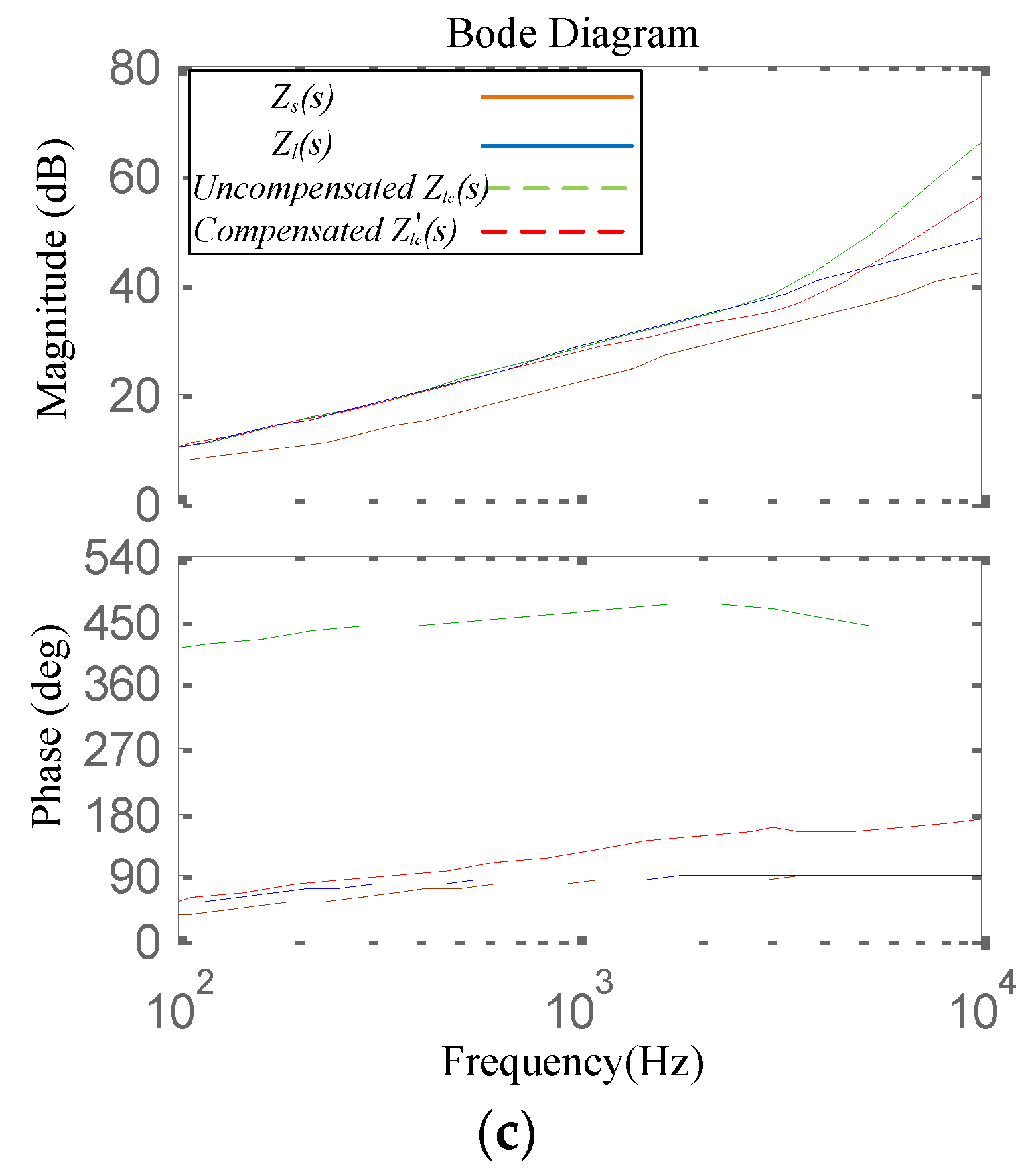
3. Proposal to Improve the Stability and Accuracy of PHIL Simulations
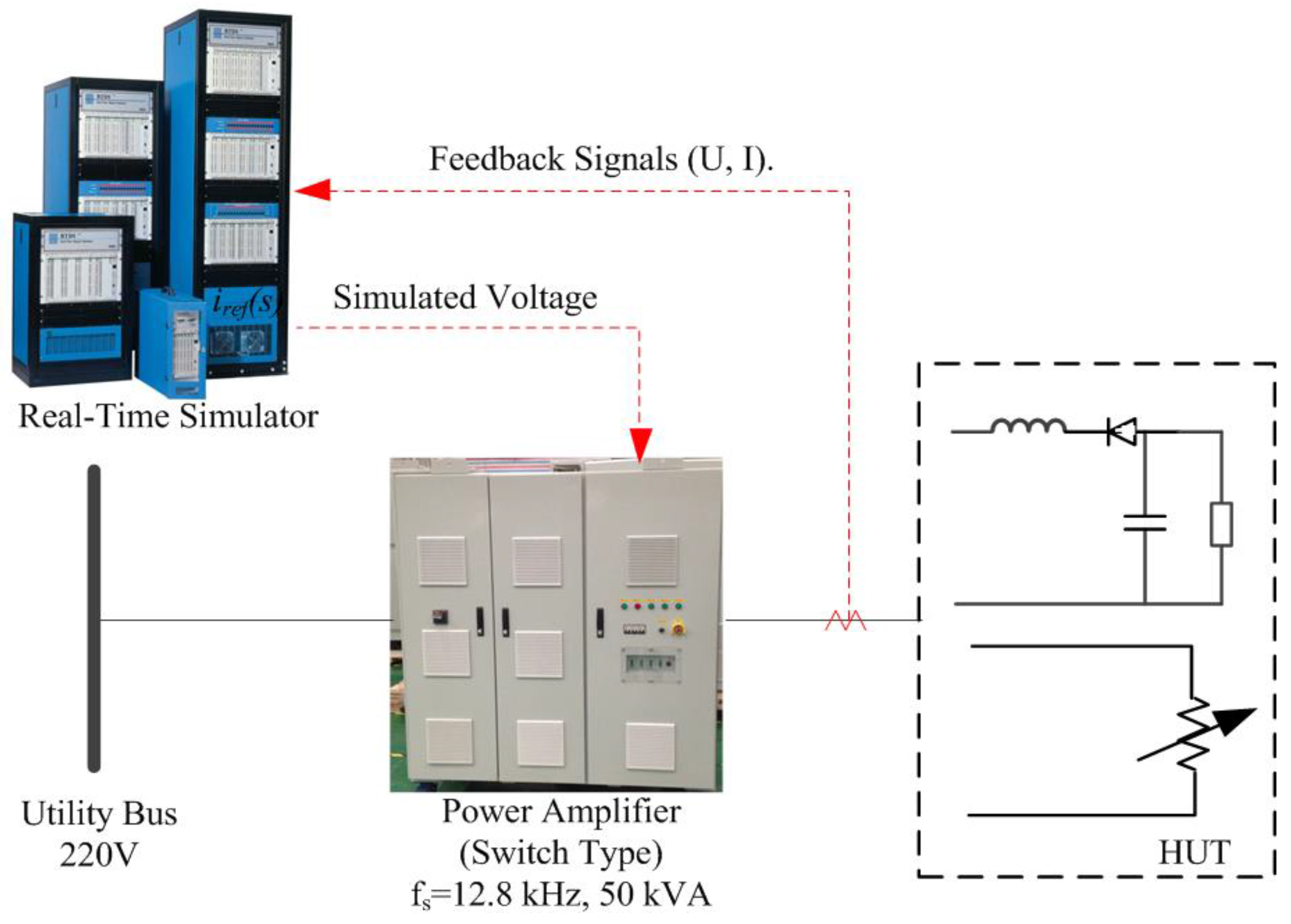
4. Experimental Verification
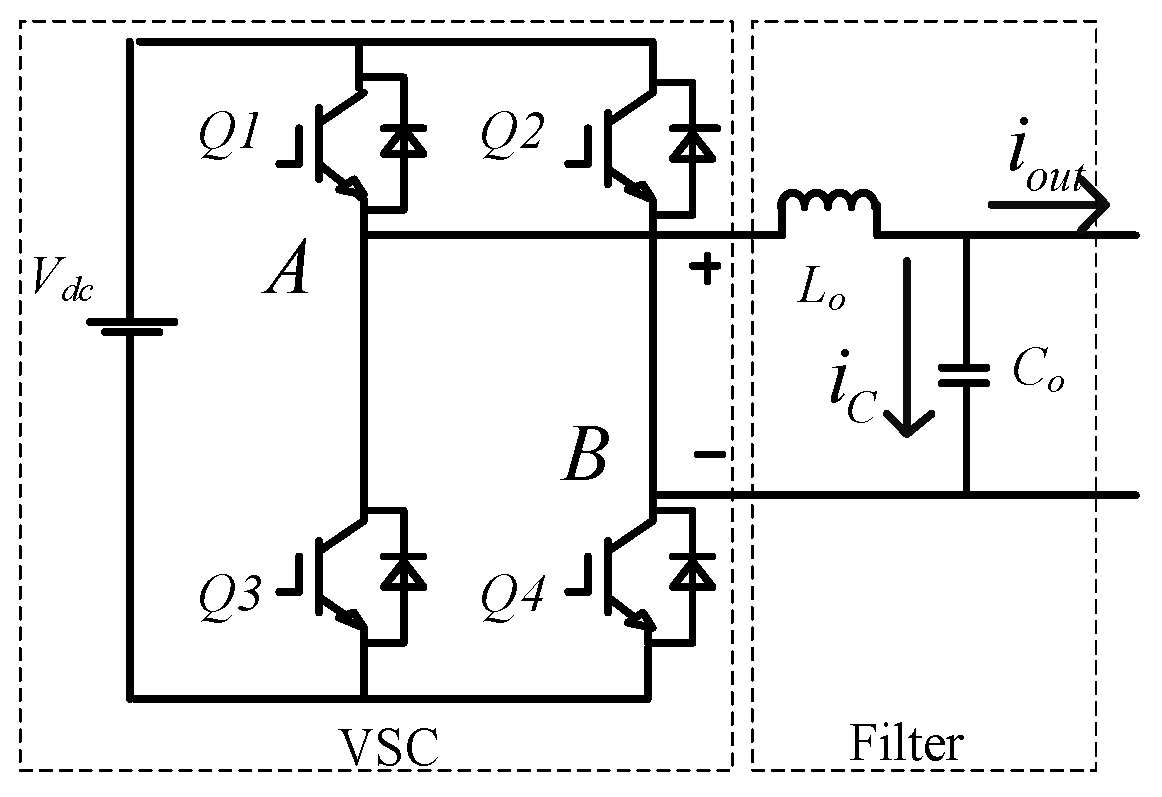
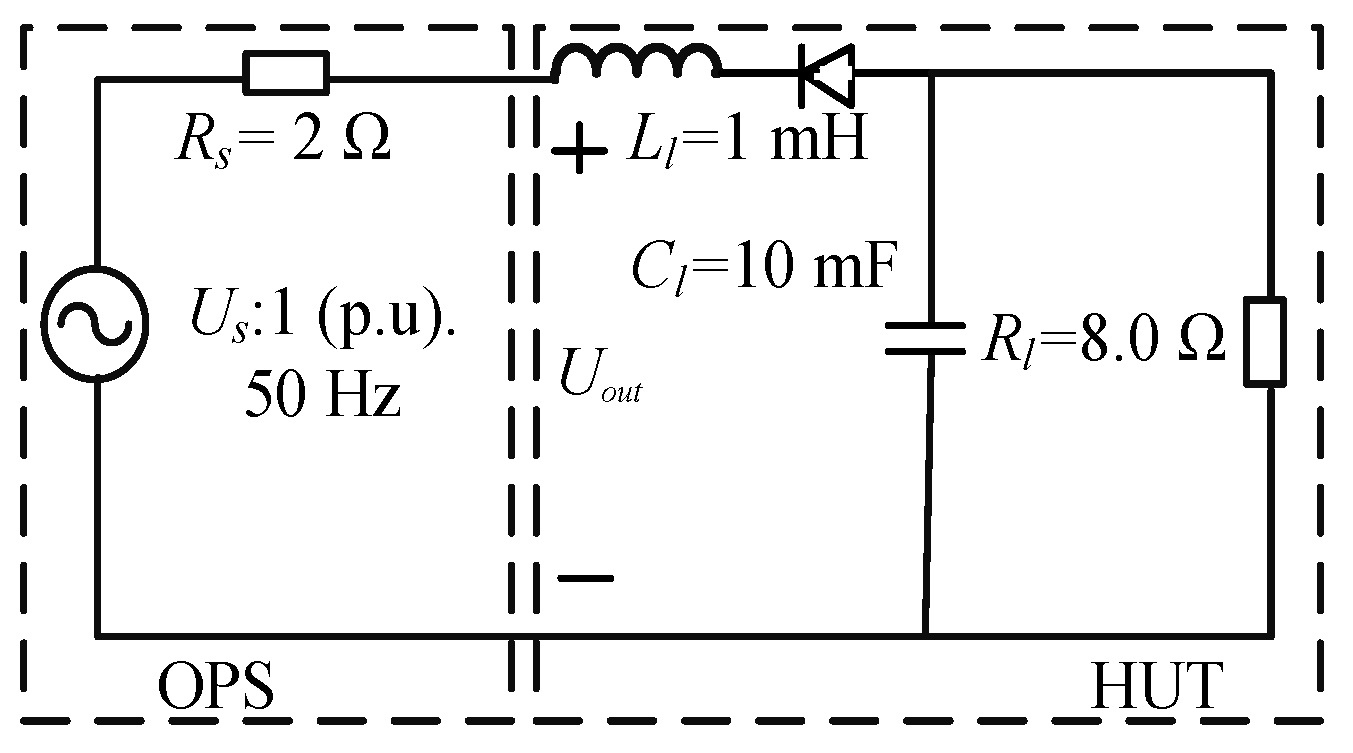
4.1. Description of the PHIL Platform
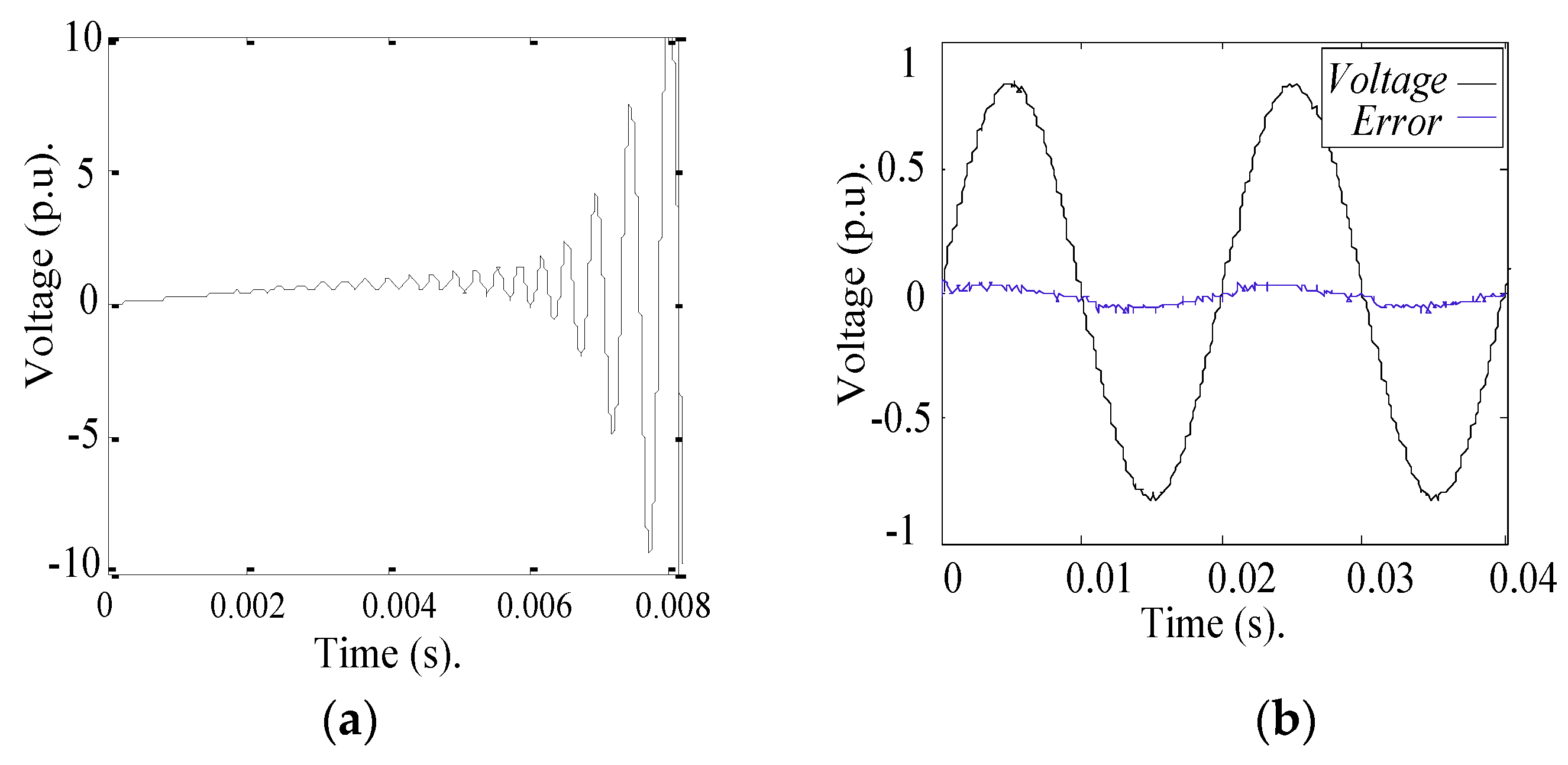
4.2. Experimental Results
Scenario 1: Hardware with Linear Behavior
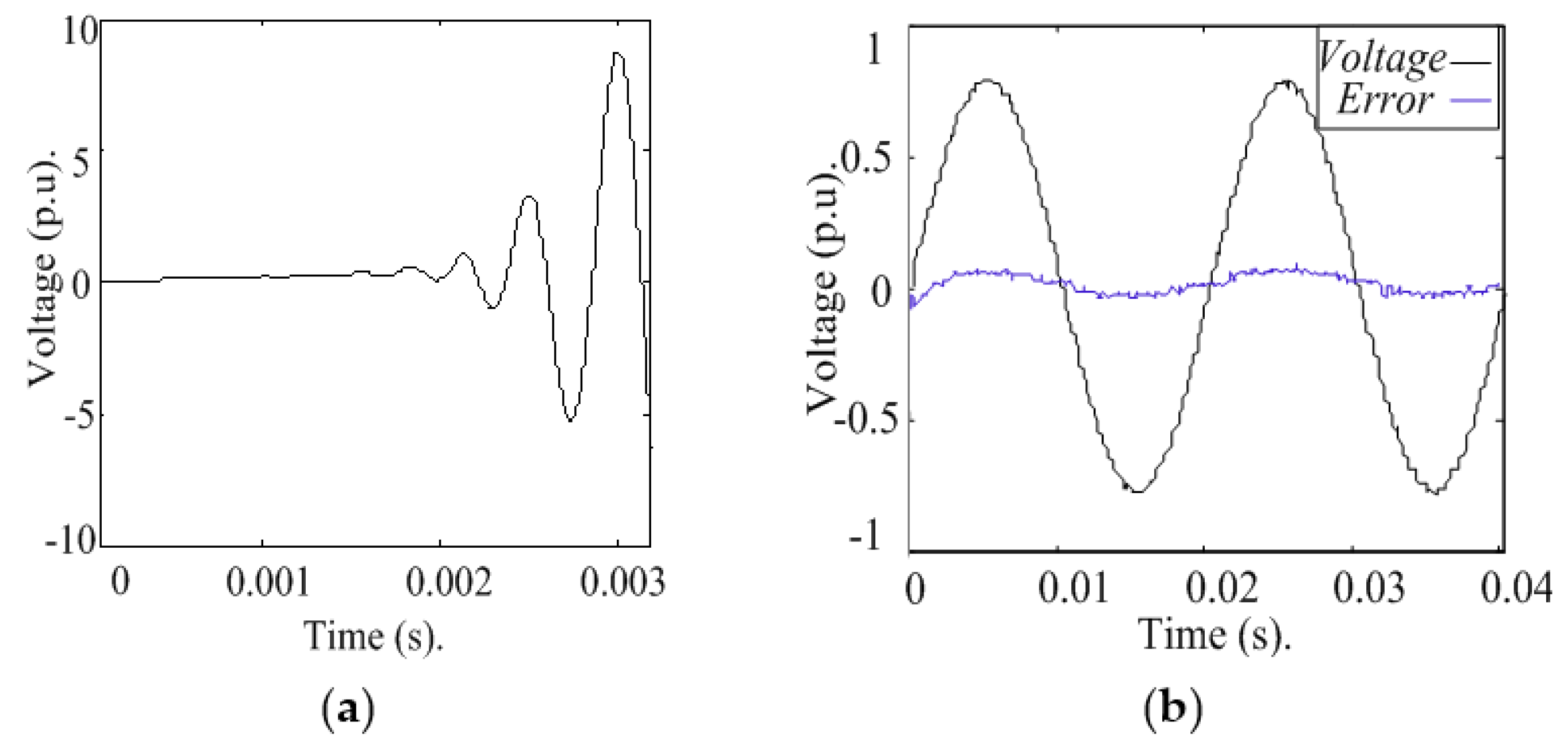
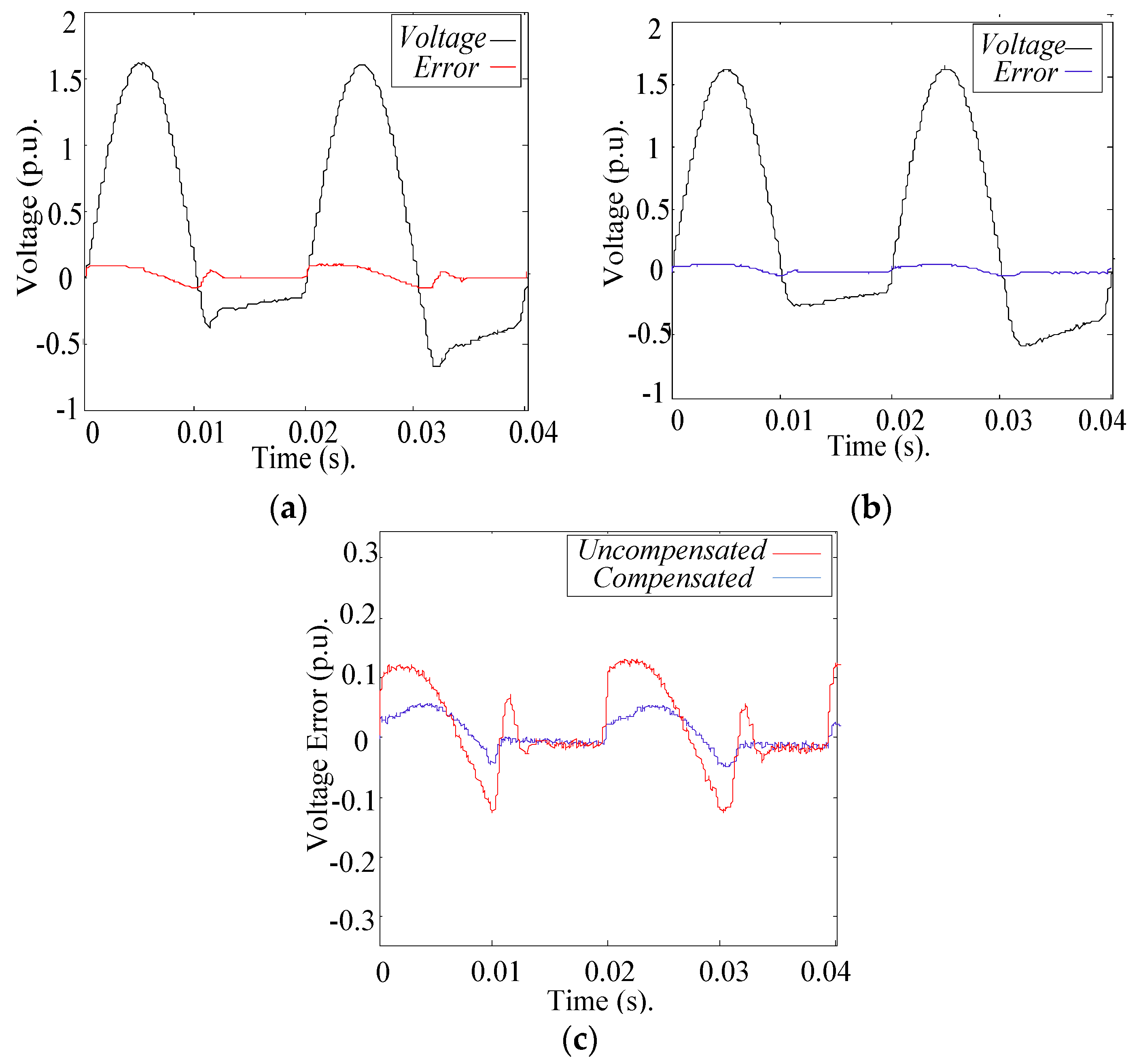
Scenario 2: Hardware with Nonlinear Behavior
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Ren, W.; Sloderbeck, M.; Steurer, M.; Dinavahi, V.; Noda, T.; Filizadeh, S.; Chevrefils, A.R.; Matar, M.; Iravani, R.; Dufour, C.; et al. Interfacing issues in real-time digital simulators. IEEE Trans. Power Deliv. 2011, 26, 1221–1230. [Google Scholar] [CrossRef]
- Steurer, M.; Edrington, C.S.; Sloderbeck, M.; Ren, W.; Langston, J. A megawatt-scale power hardware-in-the-loop simulation setup for motor drives. IEEE Trans. Ind. Electron. 2010, 57, 1254–1260. [Google Scholar] [CrossRef]
- Li, H.; Steurer, M.; Shi, K.L.; Woodruff, S.; Zhang, D. Development of a unified design, test, and research platform for wind energy systems based on hardware-in-the-loop real-time simulation. IEEE Trans. Ind. Electron. 2006, 53, 1144–1151. [Google Scholar] [CrossRef]
- Liu, Y.; Steurer, M.; Ribeiro, P. A novel approach to power quality assessment: Real time hardware-in-the-loop test bed. IEEE Trans. Power Deliv. 2005, 20, 1200–1201. [Google Scholar] [CrossRef]
- Tucker, J. Power-Hardware-In-the-Loop (PHIL) Considerations and Implementation Methods for Electrically Coupled Systems. Master’s Thesis, University of South Carolina, Columbia, SC, USA, 2011. [Google Scholar]
- Etemadi, A.H.; Iravani, R. Overcurrent and overload protection of directly voltage-controlled distributed resources in a microgrid. IEEE Trans. Ind. Electron. 2013, 60, 5629–5638. [Google Scholar] [CrossRef]
- Li, H.; Guo, F.; Yang, S.; Zhu, L.; Yao, C.; Wang, J. Usage profile optimization of the retired PHEV battery in residential microgrid. In Proceedings of the IEEE Transportation Electrification Conference and Expo, Asia-Pacific, Beijing, China, 31 August–3 September 2014; pp. 1–6.
- Guo, F.; Herrera, L.; Alsolami, M.; Li, H.; Xu, P.; Lu, X.; Lang, A.; Wang, J.; Long, Z. Design and development of a reconfigurable hybrid Microgrid test bed. In Proceedings of the IEEE Energy Conversion Congress and Exposition (ECCE), Denver, CO, USA, 15–19 Septemer 2013; pp. 1350–1356.
- Hwang, T.; Park, S. A seamless control strategy of a distributed generation inverter for the critical load safety under strict grid disturbances. IEEE Trans. Power Electron. 2013, 28, 4780–4790. [Google Scholar] [CrossRef]
- Dufour, C.; Bélanger, J. On the use of real-time simulation technology in smart grid research and development. IEEE Trans. Ind. Appl. 2014, 50, 3963–3970. [Google Scholar] [CrossRef]
- Ivanović, Z.R.; Adžić, E.M.; Vekić, M.S.; Grabić, S.U.; Čelanović, N.L.; Katić, V.A. HIL evaluation of power flow control strategies for energy storage connected to smart grid under unbalanced conditions. IEEE Trans. Power Electron. 2012, 27, 4699–4710. [Google Scholar] [CrossRef]
- Park, M.; Yu, I. A novel real-time simulation technique of photovoltaic generation systems using RTDS. IEEE Trans. Energy Convers. 2004, 19, 164–169. [Google Scholar] [CrossRef]
- Adzic, E.; Grabic, S.; Vekic, M.; Porobic, V.; Celanovic, N.F. Hardware-in-the-loop optimization of the 3-phase grid connected converter controller. In Proceedings of the 39th Annual Conference of the IEEE Industrial Electronics Society, Vienna, Austria, 10–13 November 2013; pp. 5392–5397.
- Knauff, M.; Schegan, C.; Chunko, J.; Fischl, R.; Miu, K. A preliminary modeling and simulation platform to investigate new shipboard power system prototyping techniques. In Proceedings of the Grand Challenges in Modeling and Simulation, Istabul, Turkey, 13–16 July 2009; pp. 198–204.
- Oh, S.; Yoo, C.; Chung, I.; Won, D. Hardware-in-the-loop simulation of distributed intelligent energy management system for Microgrids. Energies 2013, 6, 3263–3283. [Google Scholar] [CrossRef]
- Shiau, J.; Lee, M.; Wei, Y.; Chen, B. Circuit simulation for solar Power maximum Power Point tracking with different Buck-Boost converter topologies. Energies 2014, 7, 5027–5046. [Google Scholar] [CrossRef]
- Calise, F.; Capuano, D.; Vanoli, L. Dynamic simulation and Exergo-Economic optimization of a hybrid solar–geothermal cogeneration plant. Energies 2015, 8, 2606–2646. [Google Scholar] [CrossRef]
- Marco, J.; Kumari, N.; Widanage, W.D.; Jones, P. A cell-in-the-loop approach to systems modelling and simulation of energy storage systems. Energies 2015, 8, 8244–8262. [Google Scholar] [CrossRef]
- Locment, F.; Sechilariu, M. Modeling and simulation of DC Microgrids for electric vehicle charging stations. Energies 2015, 8, 4335–4356. [Google Scholar] [CrossRef]
- Lehfuss, F.; Lauss, G.; Kostampopoulos, P.; Hatziargyriou, N.; Crolla, P.; Roscoe, A. Comparison of multiple power amplification types for power hardware-in-the-loop applications. In Proceedings of the IEEE Workshop Complexity Engineering, Aachen, Germany, 11–13 June 2012; pp. 1–6.
- Lauss, G.; Faruque, M.O.; Schoder, K.; Dufour, C.; Viehweider, A.; Langston, J. Characteristics and design of Power hardware-in-the-loop simulations for electrical Power systems. IEEE Trans. Ind. Electron. 2016, 63, 406–417. [Google Scholar] [CrossRef]
- Viehweider, A.; Lauss, G.; Lehfuss, F. Interface and stability issues for SISO and MIMO power hardware in the loop simulation of distribution networks with photovoltaic generation. Int. J. Renew. Energy Res. 2012, 2, 632–639. [Google Scholar]
- Wu, X.; Lentijo, S.; Deshmuk, A.; Monti, A.; Ponci, F. Design and implementation of a power-hardware-in-the-loop interface: A nonlinear load case study. In Proceedings of the Twentieth Annual IEEE Applied Power Electronics Conference and Exposition, Urbana, IL, USA, 6–10 March 2005.
- Ayasun, S.; Fischl, R.; Chmielewski, T.; Vallieu, S.; Miu, K.; Nwankpa, C. Evaluation of static performance of simulation-stimulation interface for Power hardware in the loop. In Proceedings of the IEEE Power Tech Conference, Bologna, Italy, 23–26 June 2003.
- Jha, K.; Mishra, S.; Joshi, A. Boost-amplifier-based Power-hardware-in-the-loop simulator. IEEE Trans. Ind. Electron. 2015, 62, 7479–7488. [Google Scholar] [CrossRef]
- Lentijo, S.; D’Arco, S.; Monti, A. Comparing the dynamic performances of power hardware-in-the-loop interfaces. IEEE Trans. Ind. Electron. 2010, 57, 1195–1207. [Google Scholar] [CrossRef]
- Gan, C.; Todd, R.; Apsley, J.M. Drive system dynamics compensator for a mechanical system emulator. IEEE Trans. Ind. Electron. 2015, 62, 70–78. [Google Scholar] [CrossRef]
- Wu, X.; Lentijo, S.; Monti, A. A novel interface for power hardware-in-the-loop simulation. In Proceedings of the IEEE Workshop on Computers in Power Electronics (COMPEL 2004), Urbana, IL, USA, 15–18 August 2004; pp. 178–182.
- Ren, W.; Steurer, M.; Baldwin, T.L. Improve the stability and the accuracy of power hardware-in-the-loop simulation by selecting appropriate interface algorithms. IEEE Trans. Ind. Appl. 2008, 44, 1286–1294. [Google Scholar] [CrossRef]
- Feng, X.; Liu, J.; Lee, F.C. Impedance specifications for stable dc distributed power systems. IEEE Trans. Power Electron. 2002, 17, 157–162. [Google Scholar] [CrossRef]
- Paran, S.; Edrington, C.S. Improved power hardware in the loop interface methods via impedance matching. In Proceedings of the IEEE Electric Ship Technologies Symposium, Arlington, VA, USA, 22–24 April 2013; pp. 342–346.
- Siegers, J.; Santi, E. Improved power hardware-in-the-loop interface algorithm using wideband system identification. In Proceedings of the IEEE Applied Power Electronics Conference and Exposition, Fort Worth, TX, USA, 16–20 March 2014; pp. 1198–1204.
- Viehweider, A.; Lauss, G.; Felix, L. Stabilization of power hardware-in-the-loop simulations of electric energy systems. Simul. Model. Pract. Theory 2011, 19, 1699–1708. [Google Scholar] [CrossRef]
- Sun, J. Impedance-based stability criterion for grid-connected inverters. IEEE Trans. Power Electron. 2011, 26, 3075–3078. [Google Scholar] [CrossRef]
- He, J.; Li, Y.W.; Bosnjak, D.; Harris, B. Investigation and active damping of multiple resonances in a parallel-inverter-based microgrid. IEEE Trans. Power Electron. 2013, 28, 234–246. [Google Scholar] [CrossRef]
- Zhang, S.; Jiang, S.; Lu, X.; Ge, B.; Peng, F.Z. Resonance issues and damping techniques for grid-connected inverters with long transmission cable. IEEE Trans. Power Electron. 2014, 29, 110–120. [Google Scholar] [CrossRef]
- Wang, F.; Duarte, J.L.; Hendrix, M.A.M.; Ribeiro, P.F. Modeling and analysis of grid harmonic distortion impact of aggregated DG inverters. IEEE Trans. Power Electron. 2011, 26, 786–797. [Google Scholar] [CrossRef]
- Jia, Y.; Zhao, J.; Fu, X. Direct grid current control of LCL-filtered grid-connected inverter mitigating grid voltage disturbance. IEEE Trans. Power Electron. 2014, 29, 1532–1541. [Google Scholar]
- Lauss, G.; Lehfuss, F.; Viehweider, A.; Strasser, T. Power hardware in the loop simulation with feedback current filtering for electric systems. In Proceedings of the 37th Annual Conference on IEEE Industrial Electronics Society, Melbourne, Australia, 7–10 November 2011; pp. 3725–3730.
- Cespedes, M.; Sun, J. Impedance modeling and analysis of grid-connected voltage-source converters. IEEE Trans. Power Electron. 2014, 29, 1254–1261. [Google Scholar] [CrossRef]
- Ren, W.; Steurer, M.; Baldwin, T.L. An effective method for evaluating the accuracy of power hardware-in-the-loop simulations. IEEE Trans. Ind. Appl. 2009, 45, 1484–1490. [Google Scholar] [CrossRef]
- Yang, D.; Ruan, X.; Wu, H. Impedance shaping of the grid-connected inverter with LCL filter to improve its adaptability to the weak grid condition. IEEE Trans. Power Electron. 2014, 29, 5795–5806. [Google Scholar] [CrossRef]


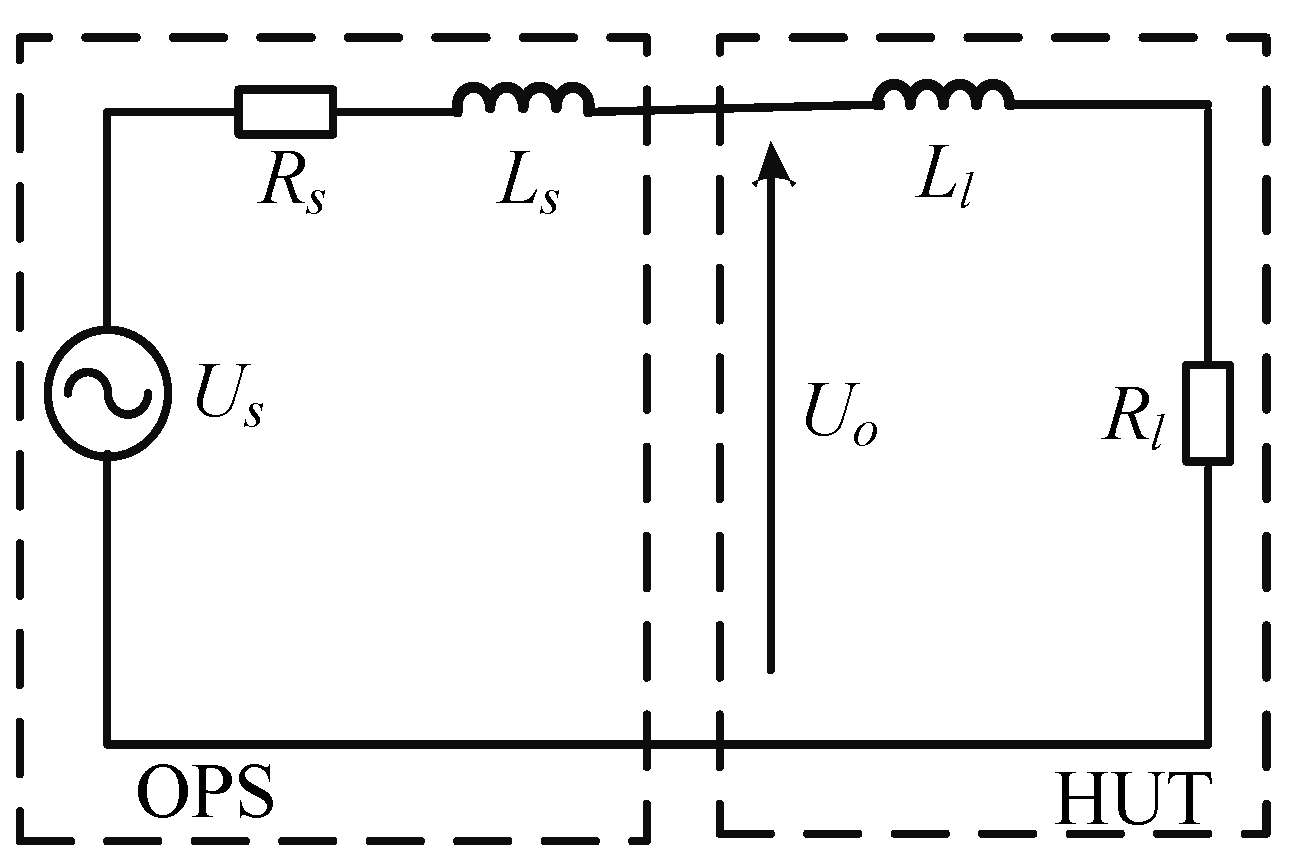

| Parameter | Value | Parameter | Value |
|---|---|---|---|
| Rs | 2 Ω | Rl | 2 Ω |
| Ls | Case (1): 2 mH | Ll | Case (1): 2 mH |
| Case (2): 4 mH | Case (2): 2 mH | ||
| Case (3): 2 mH | Case (3): 4 mH |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zha, X.; Yin, C.; Sun, J.; Huang, M.; Li, Q. Improving the Stability and Accuracy of Power Hardware-in-the-Loop Simulation Using Virtual Impedance Method. Energies 2016, 9, 974. https://doi.org/10.3390/en9110974
Zha X, Yin C, Sun J, Huang M, Li Q. Improving the Stability and Accuracy of Power Hardware-in-the-Loop Simulation Using Virtual Impedance Method. Energies. 2016; 9(11):974. https://doi.org/10.3390/en9110974
Chicago/Turabian StyleZha, Xiaoming, Chenxu Yin, Jianjun Sun, Meng Huang, and Qionglin Li. 2016. "Improving the Stability and Accuracy of Power Hardware-in-the-Loop Simulation Using Virtual Impedance Method" Energies 9, no. 11: 974. https://doi.org/10.3390/en9110974
APA StyleZha, X., Yin, C., Sun, J., Huang, M., & Li, Q. (2016). Improving the Stability and Accuracy of Power Hardware-in-the-Loop Simulation Using Virtual Impedance Method. Energies, 9(11), 974. https://doi.org/10.3390/en9110974





