Coil Design for High Misalignment Tolerant Inductive Power Transfer System for EV Charging
Abstract
:1. Introduction
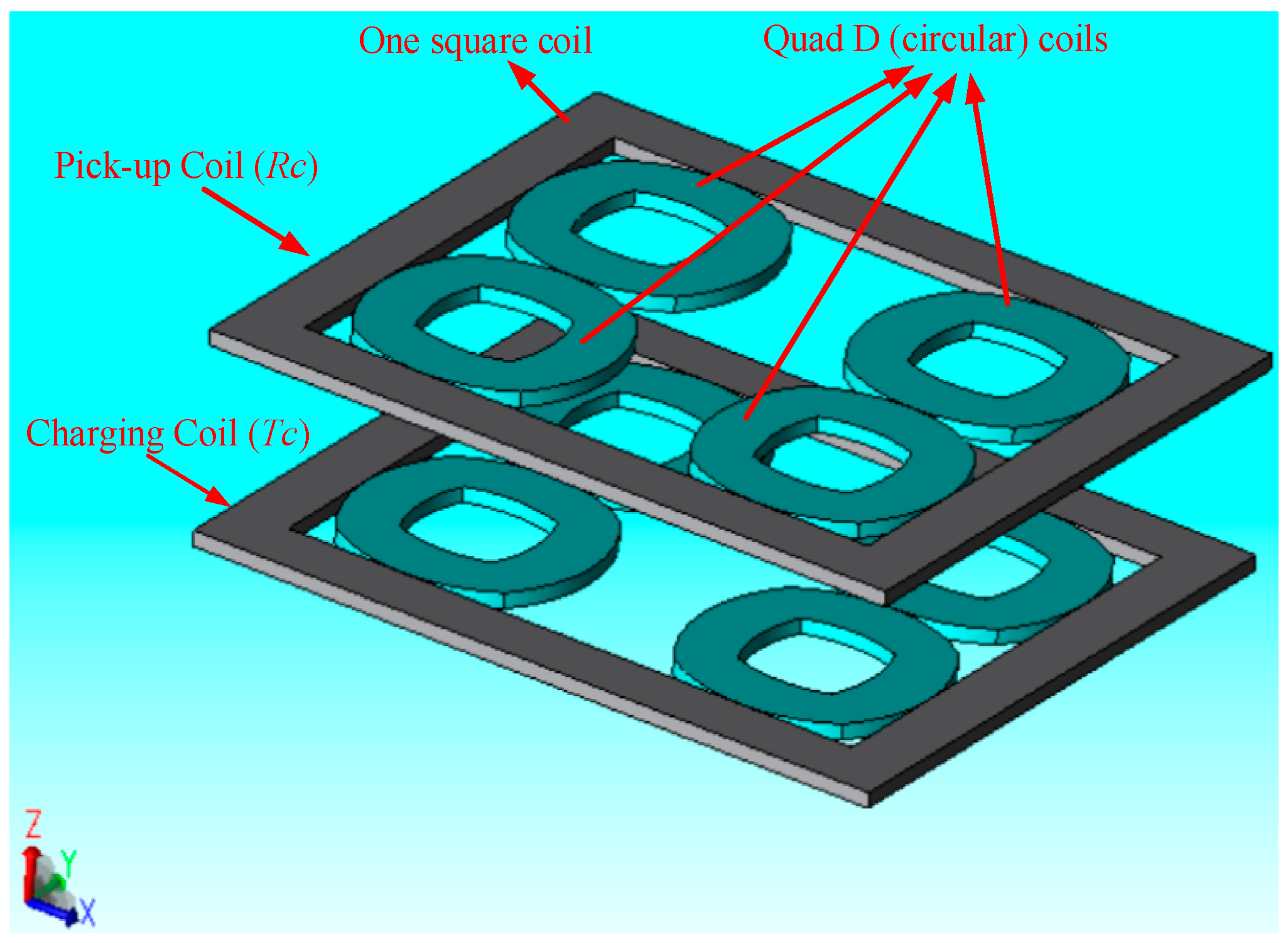
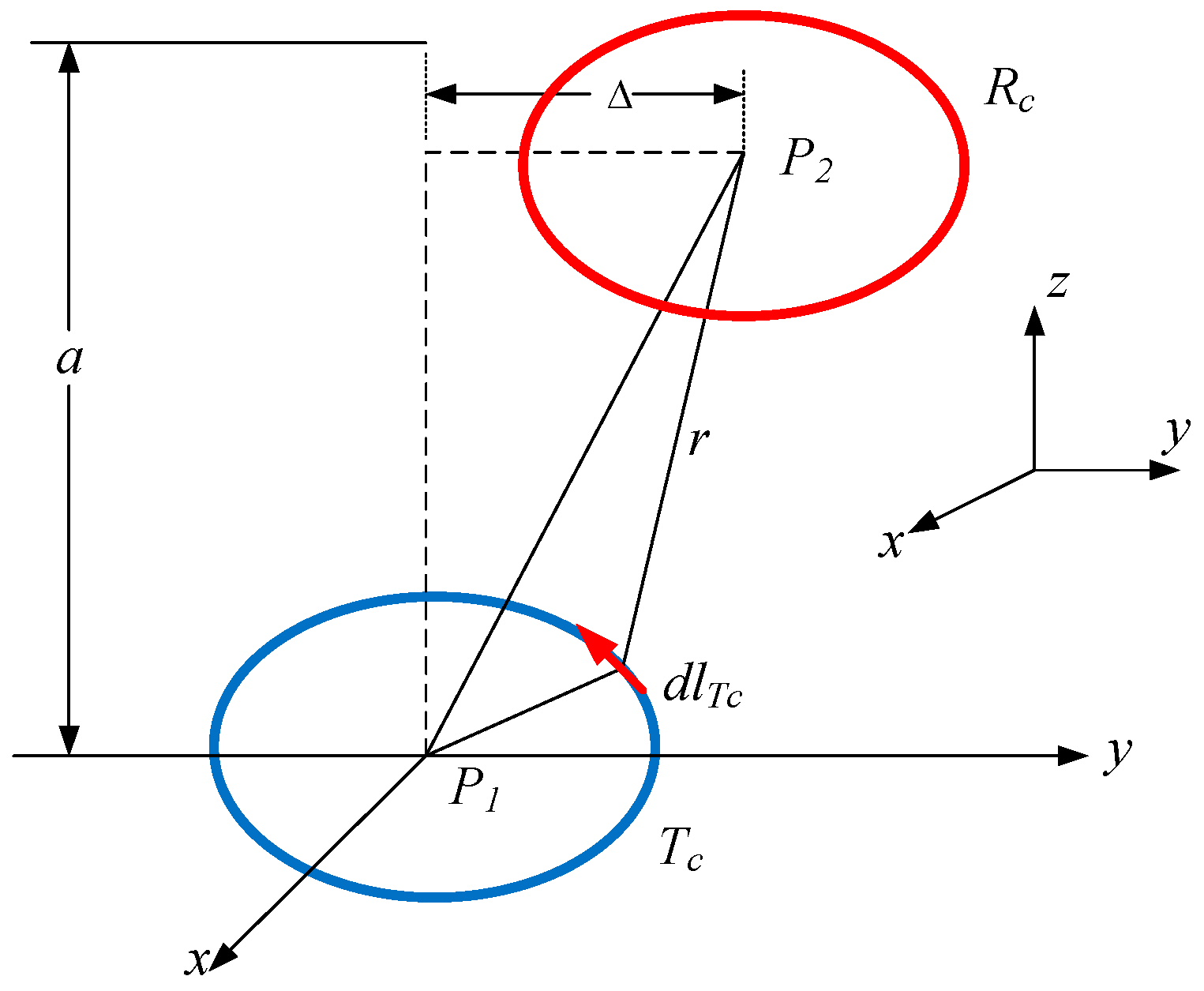
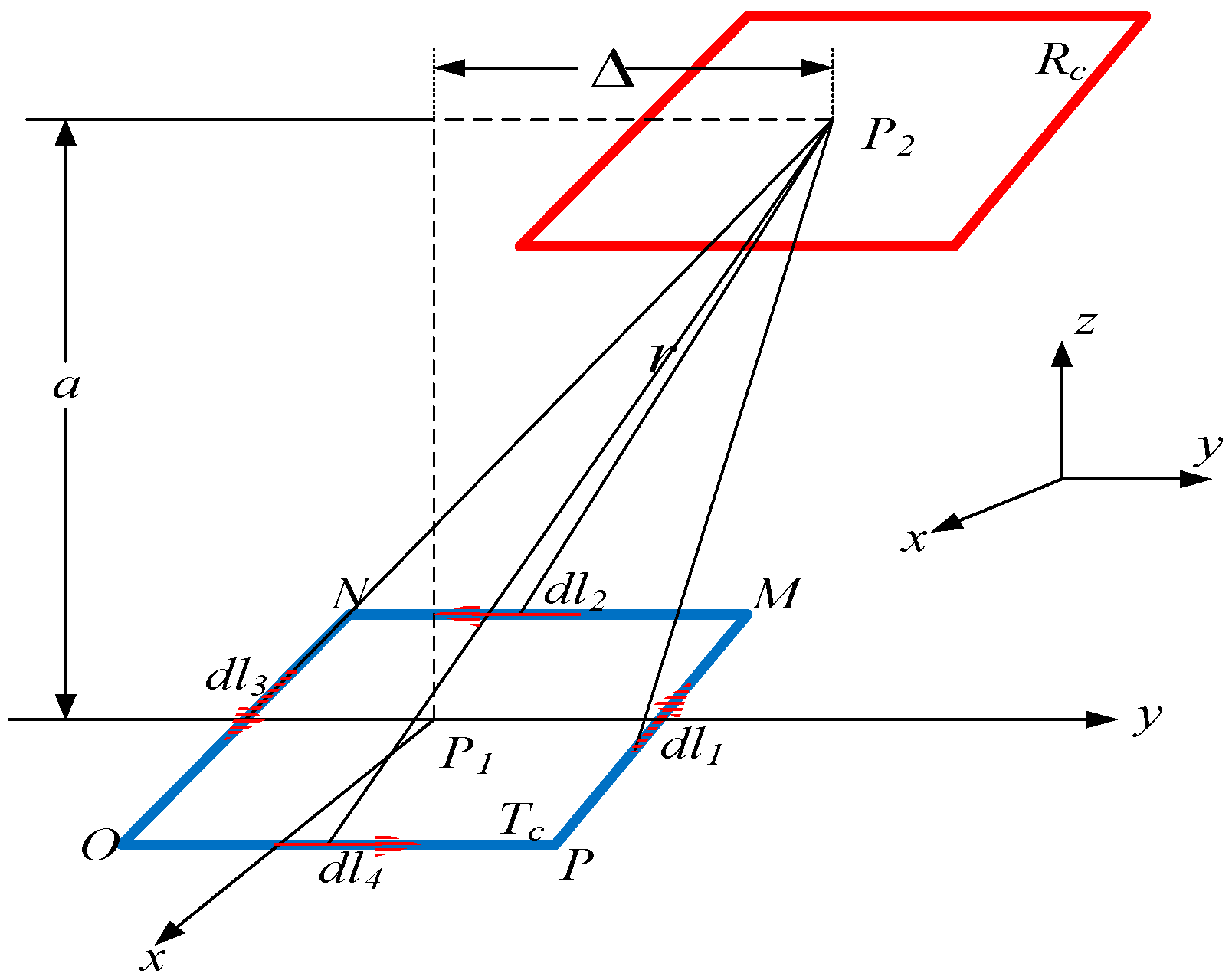
2. Proposed Coil Design
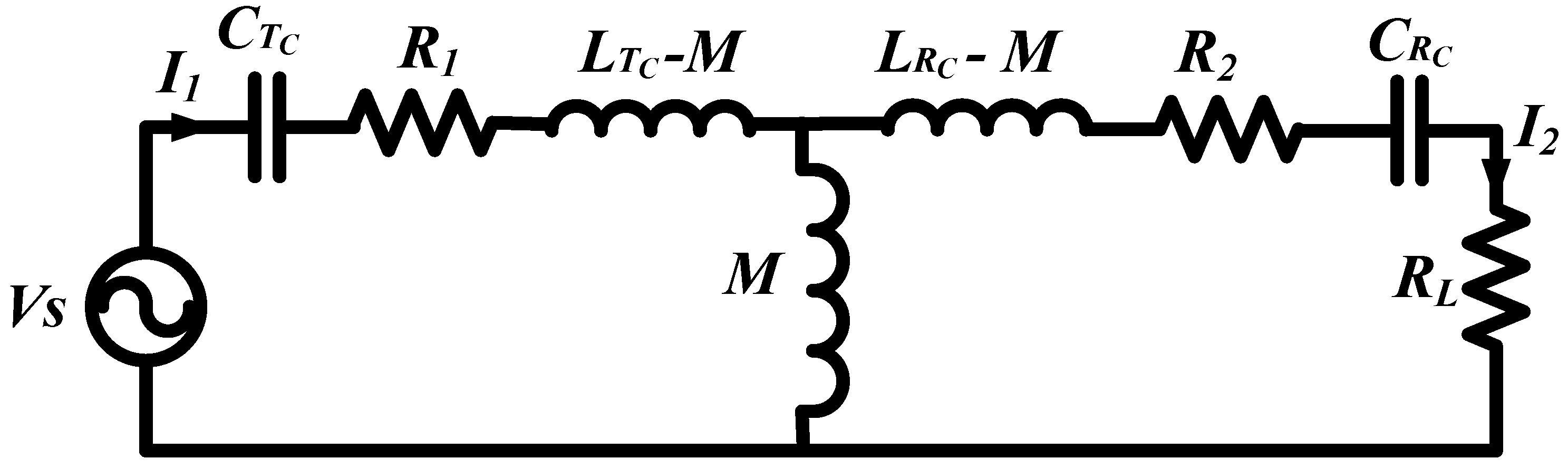
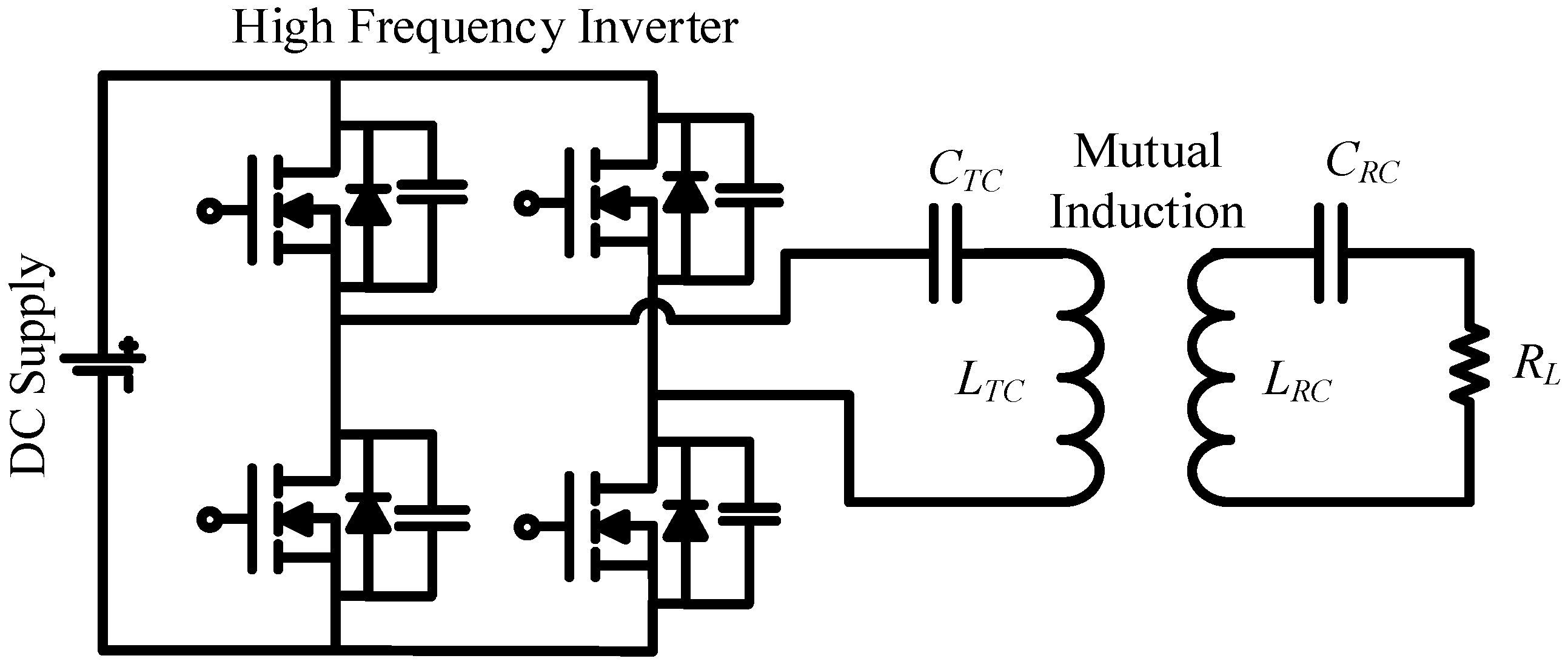
3. System Overview
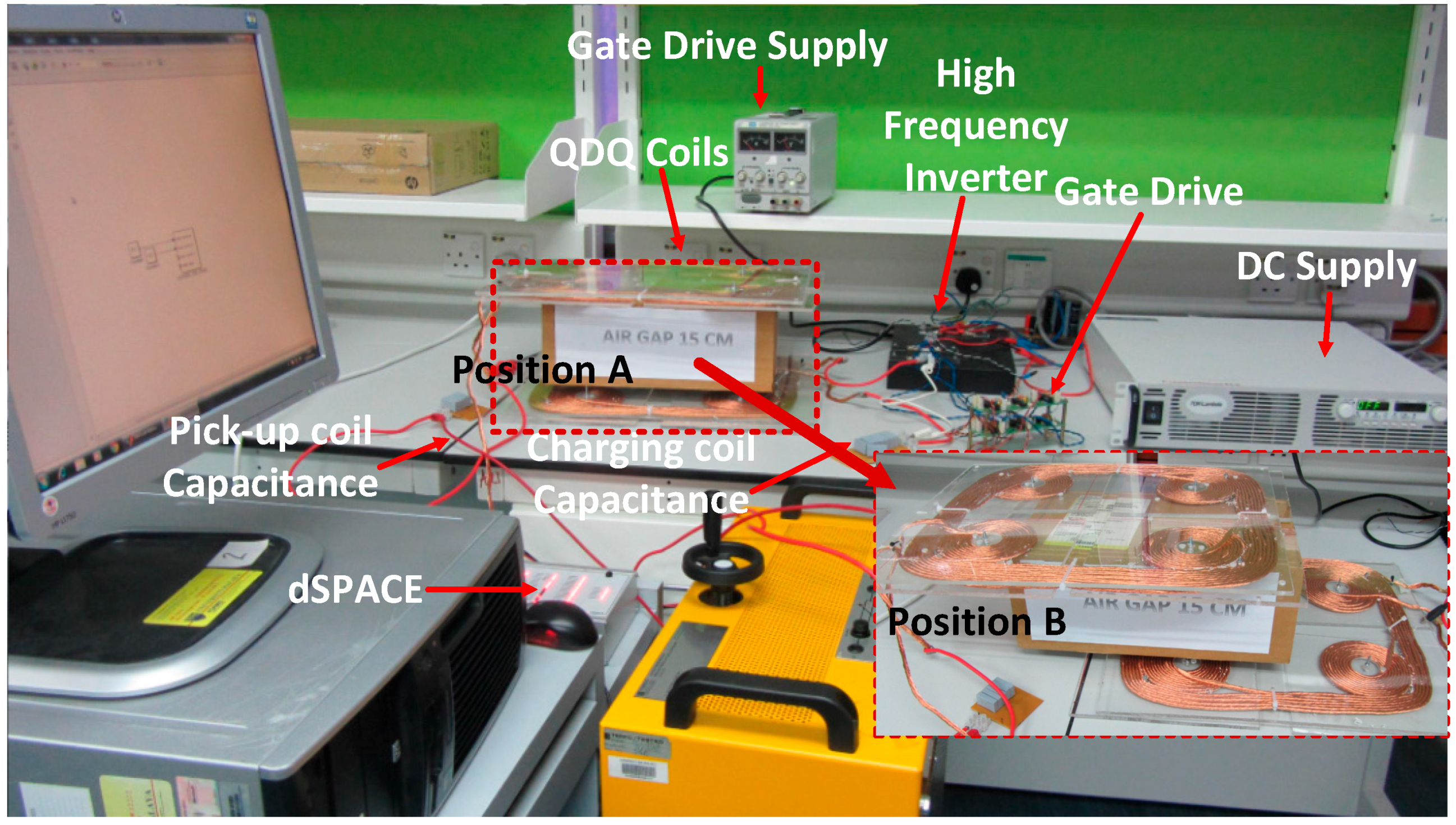
4. Experimental Results
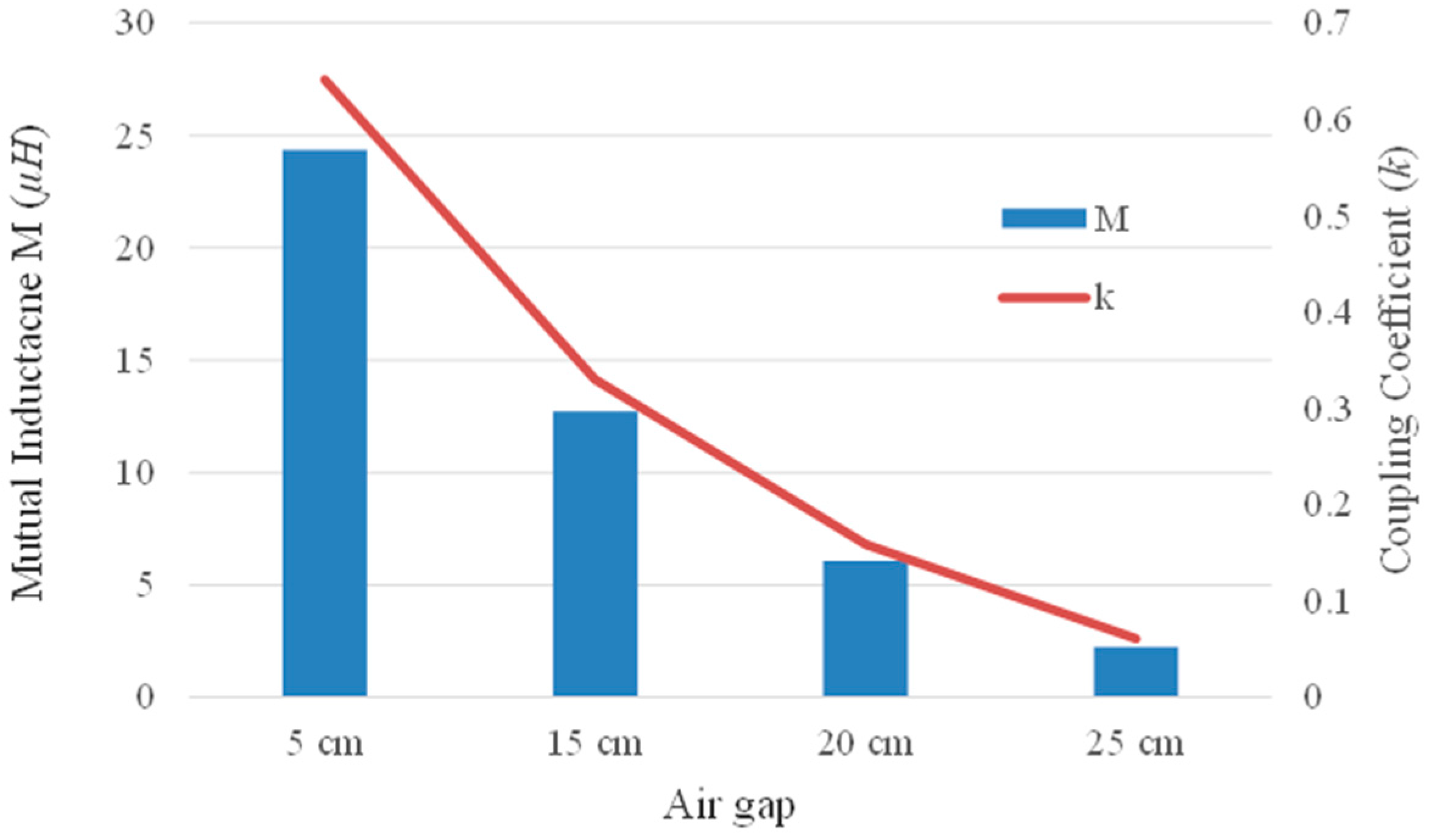
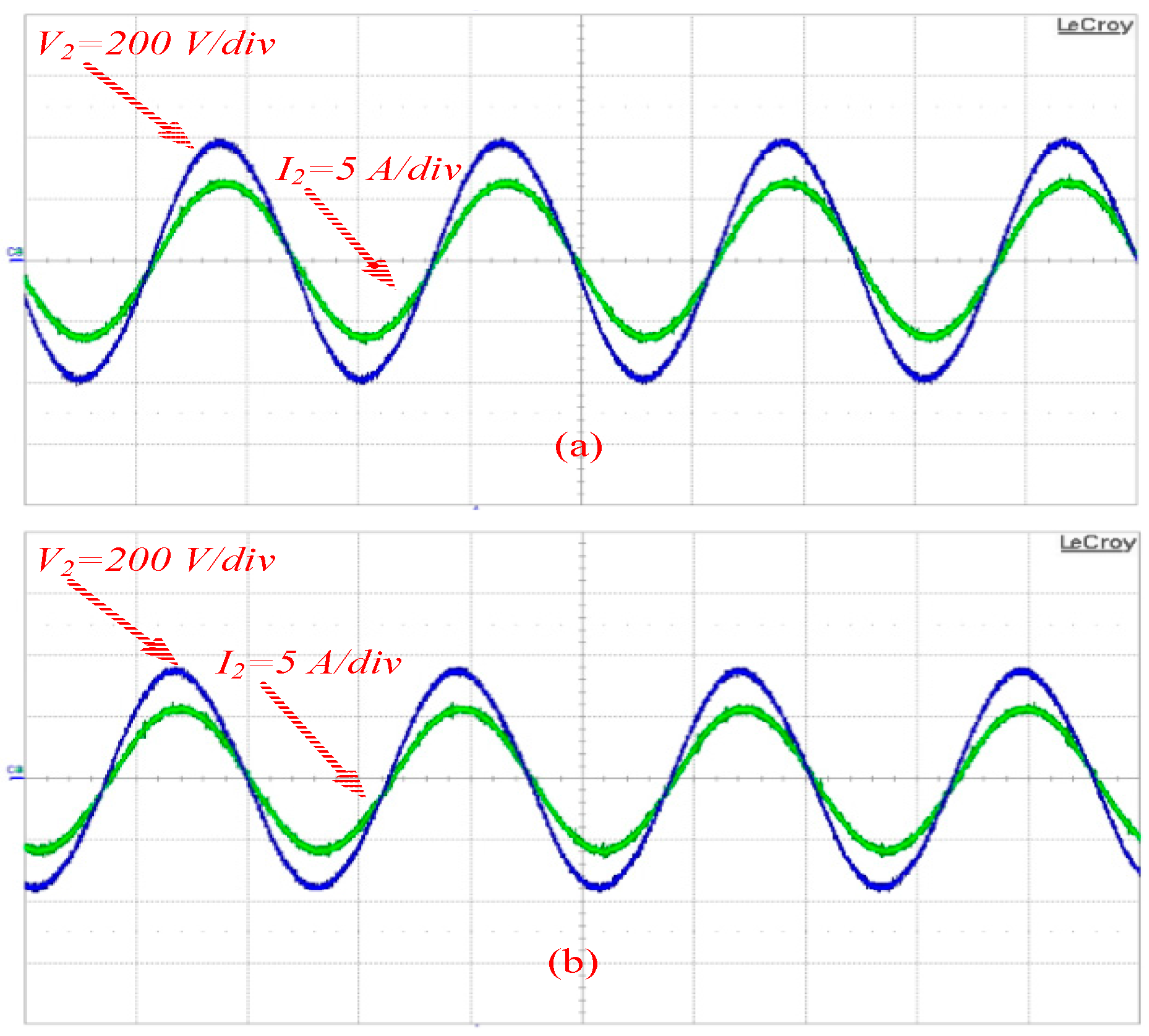
4.1. Coupling Coefficient
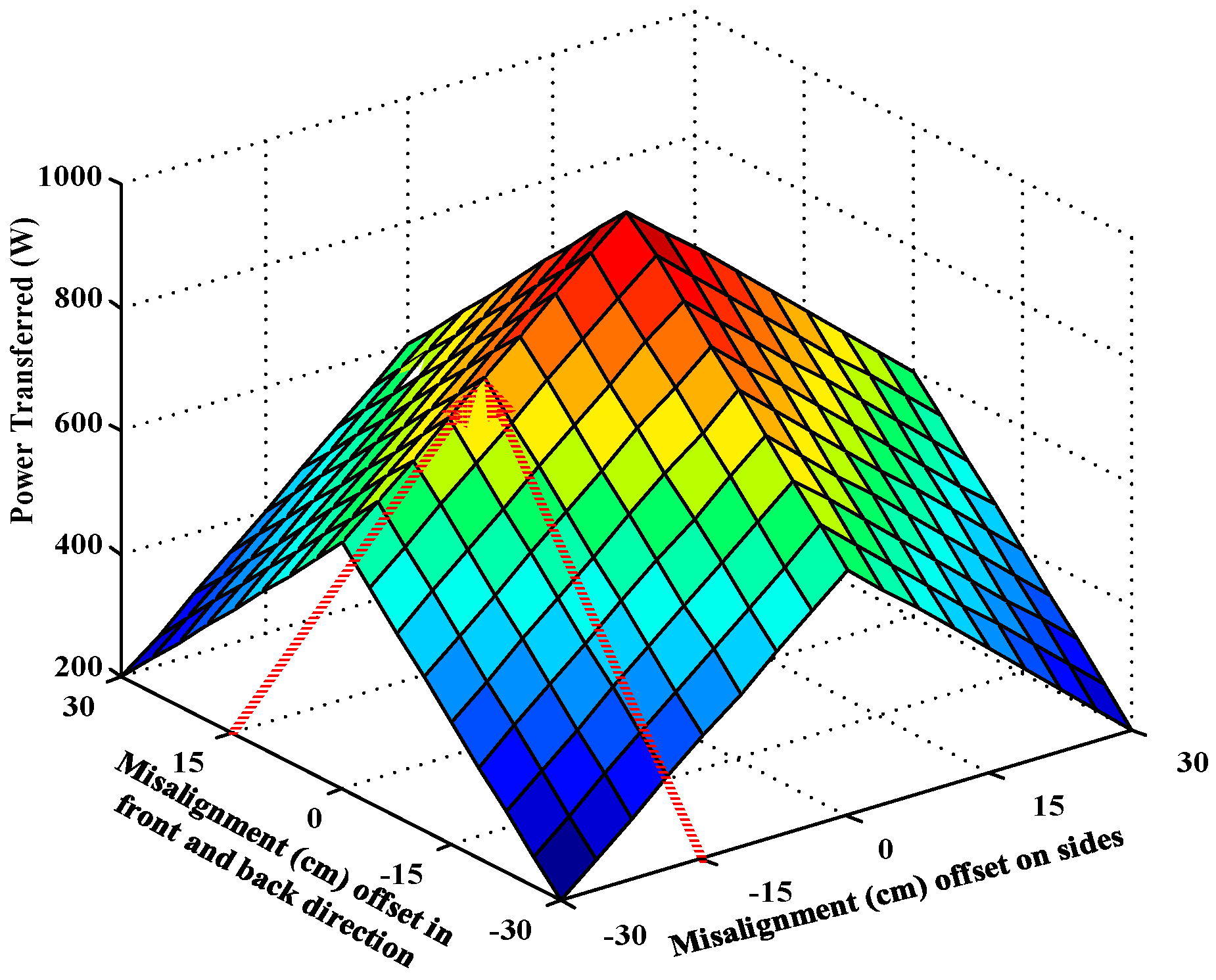
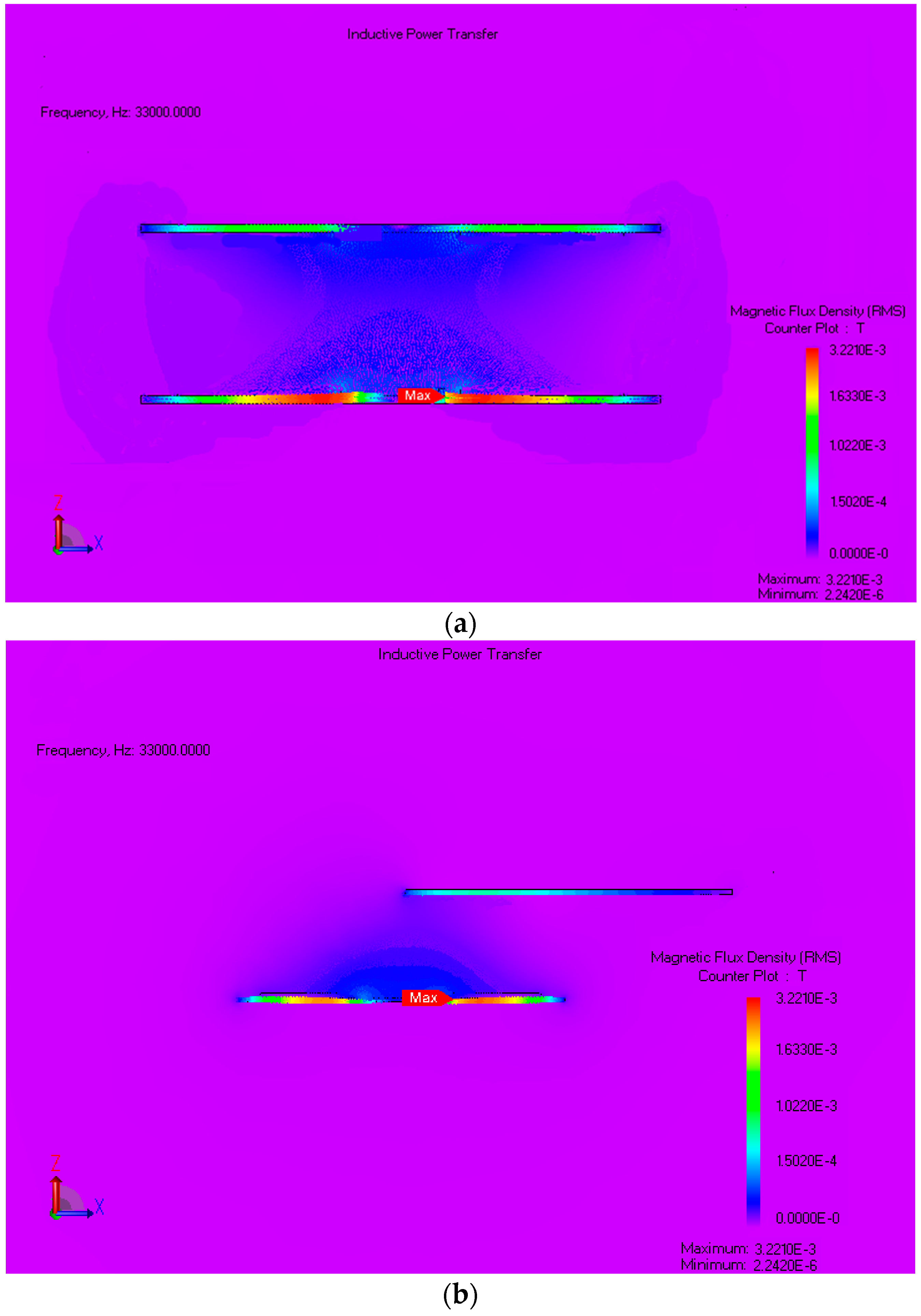
4.2. Misalignment Tolerance Analysis
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Boys, J.T.; Elliott, G.A.; Covic, G.A. An appropriate magnetic coupling coefficient for the design and comparison of icpt pick-ups. IEEE Trans. Power Electron. 2007, 22, 333–335. [Google Scholar] [CrossRef]
- Madawala, U.K.; Thrimawithana, D.J. A bidirectional inductive power interface for electric vehicles in V2G systems. IEEE Trans. Ind. Electron. 2011, 58, 4789–4796. [Google Scholar] [CrossRef]
- Del Toro García, X.; Vázquez, J.; Roncero-Sánchez, P. Design, implementation issues and performance of an inductive power transfer system for electric vehicle chargers with series-series compensation. IET Power Electron. 2015, 8, 1920–1930. [Google Scholar] [CrossRef]
- Keeling, N.A.; Covic, G.A.; Boys, J.T. A unity-power-factor IPT pick-up for high-power applications. IEEE Trans. Ind. Electron. 2010, 57, 744–751. [Google Scholar] [CrossRef]
- Sallan, J.; Villa, J.L.; Llombart, A.; Sanz, J.F. Optimal design of ICPT systems applied to electric vehicle battery charge. IEEE Trans. Ind. Electron. 2009, 56, 2140–2149. [Google Scholar] [CrossRef]
- Yuan, X.F.; Zhang, Y.L.; Wang, Y.; Li, Z.Q. Output voltage control of inductive power transfer system based on extremum seeking control. IET Power Electron. 2015, 8, 2290–2298. [Google Scholar] [CrossRef]
- Duan, C.; Jiang, C.; Taylor, A.; Bai, K. Design of a zero-voltage-switching large-air-gap wireless charger with low electric stress for electric vehicles. IET Power Electron. 2013, 6, 1742–1750. [Google Scholar] [CrossRef]
- Liao, Y.H.; Yuan, X.Q. Compensation topology for flat spiral coil inductive power transfer systems. IET Power Electron. 2015, 8, 1893–1901. [Google Scholar] [CrossRef]
- Zheng, C.; Ma, H.B.; Lai, J.S.; Zhang, L.H. Design considerations to reduce gap variation and misalignment effects for the inductive power transfer system. IEEE Trans. Power Electron. 2015, 30, 6108–6119. [Google Scholar] [CrossRef]
- Elliott, G.A.J.; Raabe, S.; Covic, G.A.; Boys, J.T. Multiphase pick-ups for large lateral tolerance contactless power-transfer systems. IEEE Trans. Ind. Electron. 2010, 57, 1590–1598. [Google Scholar] [CrossRef]
- Kurschner, D.; Rathge, C.; Jumar, U. Design methodology for high efficient inductive power transfer systems with high coil positioning flexibility. IEEE Trans. Ind. Electron. 2013, 60, 372–381. [Google Scholar] [CrossRef]
- Hsu, J.U.W.; Hu, A.P.; Swain, A. Fuzzy logic-based directional full-range tuning control of wireless power pick-ups. IET Power Electron. 2012, 5, 773–781. [Google Scholar] [CrossRef]
- Liu, X.C.; Wang, G.F.; Ding, W. Efficient circuit modelling of wireless power transfer to multiple devices. IET Power Electron. 2014, 7, 3017–3022. [Google Scholar] [CrossRef]
- Moradewicz, A.J.; Kazmierkowski, M.P. Contactless energy transfer system with FPGA-controlled resonant converter. IEEE Trans. Ind. Electron. 2010, 57, 3181–3190. [Google Scholar] [CrossRef]
- Liu, N.; Habetler, T. Design of a universal inductive charger for multiple electric vehicle models. IEEE Trans. Power Electron. 2015, 30, 6378–6390. [Google Scholar] [CrossRef]
- Wang, C.S.; Stielau, O.H.; Covic, G.A. Design considerations for a contactless electric vehicle battery charger. IEEE Trans. Ind. Electron. 2005, 52, 1308–1314. [Google Scholar] [CrossRef]
- Grover, F.W. Inductance Calculations: Working Formulas and Tables; Courier Corporation: North Chelmsford, MA, USA, 2004. [Google Scholar]
- Mecke, R.; Rathge, C. High Frequency Resonant Inverter for Contactless Energy Transmission over Large Air Gap. In Proceedings of the IEEE 35th Annual ower Electronics Specialists Conference (PESC), Aachen, Germany, 20–25 June 2004.
- Budhia, M.; Covic, G.A.; Boys, J.T. Design and optimization of circular magnetic structures for lumped inductive power transfer systems. IEEE Trans. Power Electron. 2011, 26, 3096–3108. [Google Scholar] [CrossRef]
- Budhia, M.; Boys, J.T.; Covic, G.A.; Huang, C.Y. Development of a single-sided flux magnetic coupler for electric vehicle IPT charging systems. IEEE Trans. Ind. Electron. 2013, 60, 318–328. [Google Scholar] [CrossRef]
- Urankar, L.K. Vector potential and magnetic field of current-carrying finite ARC segment in analytical form, part I: Filament approximation. IEEE Trans. Magn. 1980, 16, 1283–1288. [Google Scholar] [CrossRef]
- Kaneko, Y.; Abe, S. Technology trends of wireless power transfer systems for electric vehicle and plug-in hybrid electric vehicle. In Proceedings of the IEEE 10th International Conference on Power Electronics and Drive Systems, Kitakyushu, Japan, 22–25 April 2013.
- Villa, J.L.; Sallan, J.; Sanz Osorio, J.F.; Llombart, A. High-misalignment tolerant compensation topology for ICPT systems. IEEE Trans. Ind. Electron. 2012, 59, 945–951. [Google Scholar] [CrossRef]
- Throngnumchai, K.; Kai, T.; Minagawa, Y. A Study on Receiver Circuit Topology of a Cordless Battery Charger for Electric Vehicles. In Proceedings of the IEEE Energy Conversion Congress and Exposition (ECCE), Phoenix, AZ, USA, 17–22 September 2011.
- Yilmaz, M.; Krein, P.T. Review of battery charger topologies, charging power levels, and infrastructure for plug-in electric and hybrid vehicles. IEEE Trans. Power Electron. 2013, 28, 2151–2169. [Google Scholar] [CrossRef]
- Bhuyan, S.; Sivanand, K.; Panda, S.K.; Kumar, R.; Hu, J. Resonance-based wireless energizing of piezoelectric components. IEEE Magn. Lett. 2011, 2, 6000204. [Google Scholar] [CrossRef]
- Mohan, S.S.; Hershenson, M.D.; Boyd, S.P.; Lee, T.H. Simple accurate expressions for planar spiral inductances. IEEE J. Solid-State Circuits 1999, 34, 1419–1424. [Google Scholar] [CrossRef]
- Budhia, M.; Covic, G.A.; Boys, J.T. Design and optimisation of magnetic structures for lumped inductive power transfer systems. In Proceedings of the IEEE Energy Conversion Congress and Exposition, San Jose, CA, USA, 20–24 September 2009.
- Chigira, M.; Nagatsuka, Y.; Kaneko, Y.; Abe, S.; Yasuda, T.; Suzuki, A. Small-size light-weight transformer with new core structure for contactless electric vehicle power transfer system. In Proceedings of the IEEE Energy Conversion Congress and Exposition (ECCE), Phoenix, AZ, USA, 17–22 September 2011.
- Si, P.; Hu, A.P.; Malpas, S.; Budgett, D. A frequency control method for regulating wireless power to implantable devices. IEEE Trans. Biomed. Circuits Syst. 2008, 2, 22–29. [Google Scholar] [CrossRef] [PubMed]
- Madawala, U.K.; Neath, M.; Thrimawithana, D.J. A power-frequency controller for bidirectional inductive power transfer systems. IEEE Trans. Ind. Electron. 2013, 60, 310–317. [Google Scholar] [CrossRef]
- Kamineni, A.; Covic, G.; Boys, J.T. Analysis of co-planar intermediate coil structures in inductive power transfer systems. In Proceedings of the IEEE Energy Conversion Congress and Exposition (ECCE), Pittsburgh, PA, USA, 14–18 September 2014.
- Zhu, Q.W.; Guo, Y.J.; Wang, L.F.; Liao, C.L.; Li, F. Improving the misalignment tolerance of wireless charging system by optimizing the compensate capacitor. IEEE Trans. Ind. Electron. 2015, 62, 4832–4836. [Google Scholar] [CrossRef]
- Zhang, W.; White, J.C.; Abraham, A.M.; Mi, C.C. Loosely coupled transformer structure and interoperability study for EV wireless charging systems. IEEE Trans. Power Electron. 2015, 30, 6356–6367. [Google Scholar] [CrossRef]
- Boys, J.; Covic, G.; Green, A.W. Stability and control of inductively coupled power transfer systems. IEE Proc. Electr. Power Appl. 2000, 147, 37–43. [Google Scholar] [CrossRef]
- Gao, Y.; Farley, K.B.; Tse, Z.T.H. A uniform voltage gain control for alignment robustness in wireless EV charging. Energies 2015, 8, 8355–8370. [Google Scholar] [CrossRef]
- International Commission on Non-Ionizing Radiation Protection. Guidelines for limiting exposure to time-varying electric and magnetic fields (1 Hz to 100 kHz). Health Phys. 2010, 99, 818–836. [Google Scholar]
- Wen, F.; Huang, X. Optimal magnetic field shielding method by metallic sheets in wireless power transfer system. Energies 2016, 9, 733. [Google Scholar] [CrossRef]
| Topology | Power Factor at Longer Distance | Total Impedance at Resonant State | Suitability for Power Level | Sensitivity to Alignment |
|---|---|---|---|---|
| Series-Series (SS) | Significantly High | Low | High Power | Less Sensitive |
| Series-Parallel (SP) | High | Low | High Power | Less Sensitive |
| Parallel-Series (PS) | Medium | High | Low Power | Sensitive |
| Parallel-Parallel (PP) | Medium | High | Low Power | Highly Sensitive |
| Symbol | Quantity | Value |
|---|---|---|
| LTC | Charging coil inductance | 46.46 µH |
| LRC | Pick-up coil inductance | 30.99 µH |
| M | Mutual inductance | 12.27 µH |
| k | Coupling coefficient | 0.33 |
| f | Resonant frequency | 33 kHz |
| CTC | Charging coil compensating capacitance | 0.5 µF |
| CRC | Pick-up coil compensating capacitance | 0.75 µF |
| A | Physical dimensions of the coil | 30 cm × 30 cm |
| Component | Product Number | Specification | |||
|---|---|---|---|---|---|
| MOSFET | IPW60R041C6 | VDS | ID | fmax | RDS (ON) |
| 650 V | 44 A | 100 kHz | 0.041 Ω | ||
| Capacitors | 105PHC700KN | Type | C | fmax | VAC |
| Film | 1 µF | 100 kHz | 380 V | ||
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kalwar, K.A.; Mekhilef, S.; Seyedmahmoudian, M.; Horan, B. Coil Design for High Misalignment Tolerant Inductive Power Transfer System for EV Charging. Energies 2016, 9, 937. https://doi.org/10.3390/en9110937
Kalwar KA, Mekhilef S, Seyedmahmoudian M, Horan B. Coil Design for High Misalignment Tolerant Inductive Power Transfer System for EV Charging. Energies. 2016; 9(11):937. https://doi.org/10.3390/en9110937
Chicago/Turabian StyleKalwar, Kafeel Ahmed, Saad Mekhilef, Mehdi Seyedmahmoudian, and Ben Horan. 2016. "Coil Design for High Misalignment Tolerant Inductive Power Transfer System for EV Charging" Energies 9, no. 11: 937. https://doi.org/10.3390/en9110937
APA StyleKalwar, K. A., Mekhilef, S., Seyedmahmoudian, M., & Horan, B. (2016). Coil Design for High Misalignment Tolerant Inductive Power Transfer System for EV Charging. Energies, 9(11), 937. https://doi.org/10.3390/en9110937








