Forecasting Electricity Market Risk Using Empirical Mode Decomposition (EMD)—Based Multiscale Methodology
Abstract
:1. Introduction
2. Methodology
2.1. Value at Risk
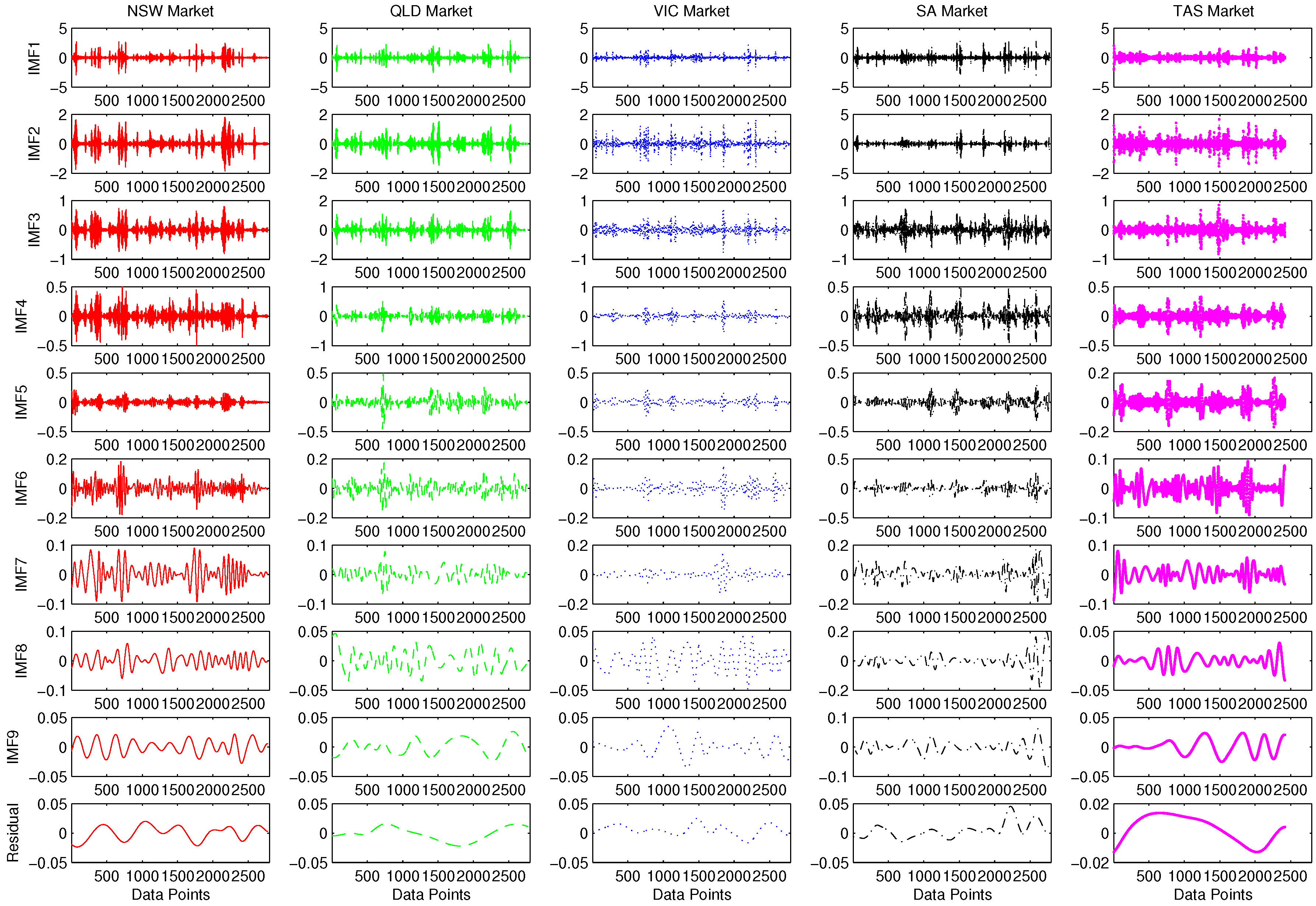
2.2. Empirical Mode Decomposition
- The number of extrema and zero-crossing should be the same, or differs at most by one;
- The functions are zero mean and symmetric, in terms of upper and lower envelope.
- Given time series data , identify the locations for local maxima and minima of .
- Generate the upper envelope (lower envelope ) of the local maxima (minima) using local spline interpolation. Calculate the local mean .
- Define the modulated oscillation .
- Repeat the previous steps until the residual satisfies the stopping criteria. Then, the original electricity data is represented as two parts; i.e., the IMFs and the residue.
2.3. Empirical Mode Decomposition (EMD)-Based Value at Risk Estimation
- Different investment strategies are stationary and mutually independent.
- Extreme or transient events would exhibit the biggest volatility.
3. Empirical Studies
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Deng, S.; Oren, S. Electricity derivatives and risk management. Energy 2006, 31, 940–953. [Google Scholar] [CrossRef]
- Liu, M.; Wu, F.F. Risk management in a competitive electricity market. Int. J. Electr. Power Energy Syst. 2007, 29, 690–697. [Google Scholar] [CrossRef]
- Pineda, S.; Conejo, A.J. Managing the financial risks of electricity producers using options. Energy Econ. 2012, 34, 2216–2227. [Google Scholar] [CrossRef]
- Shenoy, S.; Gorinevsky, D. Data-driven stochastic pricing and application to electricity market. IEEE J. Sel. Top. Signal Proces. 2016, 10, 1029–1039. [Google Scholar] [CrossRef]
- Kaye, R.; Outhred, H.; Bannister, C.H. Forward contracts for the operation of an electricity industry under spot pricing. IEEE Trans. Power Syst. 1990, 5, 46–52. [Google Scholar] [CrossRef]
- Tanlapco, E.; Lawarree, J.; Liu, C.C. Hedging with futures contracts in a deregulated electricity industry. IEEE Trans. Power Syst. 2002, 17, 577–582. [Google Scholar] [CrossRef]
- Dahlgren, R.; Liu, C.C.; Lawarree, J. Risk assessment in energy trading. IEEE Trans. Power Syst. 2003, 18, 503–511. [Google Scholar] [CrossRef]
- Walls, W.; Zhang, W. Using extreme value theory to model electricity price risk with an application to the alberta power market. Energy Explor. Exploit. 2005, 23, 375–403. [Google Scholar] [CrossRef]
- Chan, F.; Gray, P. Using extreme value theory to measure value-at-risk for daily electricity spot prices. Int. J. Forecast. 2006, 22, 283–300. [Google Scholar] [CrossRef]
- Peters, E.E. Chaos and Order in the Capital Markets: A New View of Cycles, Prices, and Market Volatility; John Wiley & Sons: New York, NY, USA, 1996; Volume 1. [Google Scholar]
- Lux, T.; Marchesi, M. Scaling and criticality in a stochastic multi-agent model of a financial market. Nature 1999, 397, 498–500. [Google Scholar] [CrossRef]
- Karandikar, R.G.; Deshpande, N.R.; Khaparde, S.A.; Kulkarni, S.V. Modelling volatility clustering in electricity price return series for forecasting value at risk. Eur. Trans. Electr. Power 2009, 19, 15–38. [Google Scholar] [CrossRef]
- Huang, N.E.; Wu, M.L.; Qu, W.; Long, S.R.; Shen, S.S. Applications of Hilbert–Huang transform to non-stationary financial time series analysis. Appl. Stoch. Model. Bus. Ind. 2003, 19, 245–268. [Google Scholar] [CrossRef]
- Yu, L.; Wang, S.; Lai, K.K. Forecasting crude oil price with an EMD-based neural network ensemble learning paradigm. Energy Econ. 2008, 30, 2623–2635. [Google Scholar] [CrossRef]
- Premanode, B.; Toumazou, C. Improving prediction of exchange rates using differential EMD. Expert Syst. Appl. 2012, 40, 377–384. [Google Scholar] [CrossRef]
- Premanode, B.; Vonprasert, J.; Toumazou, C. Prediction of exchange rates using averaging intrinsic mode function and multiclass support vector regression. Artif. Intell. Res. 2013, 2, 47. [Google Scholar] [CrossRef]
- Wu, M.C. Phase correlation of foreign exchange time series. Phys. A Stat. Mech. Appl. 2007, 375, 633–642. [Google Scholar] [CrossRef]
- Zhang, X.; Lai, K.; Wang, S.Y. A new approach for crude oil price analysis based on Empirical Mode Decomposition. Energy Econ. 2008, 30, 905–918. [Google Scholar] [CrossRef]
- An, N.; Zhao, W.; Wang, J.; Shang, D.; Zhao, E. Using multi-output feedforward neural network with empirical mode decomposition based signal filtering for electricity demand forecasting. Energy 2012, 49, 279–288. [Google Scholar] [CrossRef]
- Dong, Y.; Wang, J.; Jiang, H.; Wu, J. Short-term electricity price forecast based on the improved hybrid model. Energy Convers. Manag. 2011, 52, 2987–2995. [Google Scholar] [CrossRef]
- Dowd, K. Measuring Market Risk, 2nd ed.; John Wiley & Sons: West Sussex, UK, 2005. [Google Scholar]
- He, K.; Lai, K.K.; Xiang, G. Portfolio value at risk estimate for crude oil markets: A multivariate wavelet denoising approach. Energies 2012, 5, 1018–1043. [Google Scholar] [CrossRef]
- He, K.; Xie, C.; Chen, S.; Lai, K.K. Estimating VaR in crude oil market: A novel multi-scale non-linear ensemble approach incorporating wavelet analysis and neural network. Neurocomputing 2009, 72, 3428–3438. [Google Scholar] [CrossRef]
- He, K.; Lai, K.K.; Yen, J. Ensemble forecasting of value at risk via multi resolution analysis based methodology in metals markets. Expert Syst. Appl. 2012, 39, 4258–4267. [Google Scholar] [CrossRef]
- He, K.; Lai, K.K.; Yen, J. Value-at-risk estimation of crude oil price using MCA based transient risk modeling approach. Energy Econ. 2011, 33, 903–911. [Google Scholar] [CrossRef]
- Xu, G.; Wang, X.; Xu, X.; Zhou, L. Improved EMD for the analysis of FM signals. Mech. Syst. Signal Process. 2012, 33, 181–196. [Google Scholar]
- Yu, L.; Wang, S.; Lai, K.K. Credit risk assessment with a multistage neural network ensemble learning approach. Expert Syst. Appl. 2008, 34, 1434–1444. [Google Scholar] [CrossRef]
- Brooks, C. Introductory Econometrics for Finance, 2nd ed.; Cambridge University Press: Cambridge, UK, 2008. [Google Scholar]
- Brock, W.A.; Hsieh, D.A.; LeBaron, B.D. Nonlinear Dynamics, Chaos, and Instability: Statistical Theory and Economic Evidence; MIT Press: Cambridge, MA, USA, 1991. [Google Scholar]
- Panagiotidis, T. Testing the assumption of linearity. Econ. Bull. 2002, 3, 1–9. [Google Scholar]
- Spoehr, J. Power Politics: The Electricity Crisis and You; Wakefield Press: Kent Town, Australia, 2003. [Google Scholar]
- Lien, D.; Yang, X.B.; Ye, K.Y. Alternative approximations to value-at-risk: A comparison. Commun. Stat. Simul. Comput. 2014, 43, 2225–2240. [Google Scholar] [CrossRef]
- Andriosopoulos, K.; Nomikos, N. Risk management in the energy markets and Value-at-Risk modelling: A hybrid approach. Eur. J. Financ. 2015, 21, 548–574. [Google Scholar] [CrossRef]
- Gencer, H.G.; Demiralay, S. Volatility modeling and value-at-risk (var) forecasting of emerging stock markets in the presence of long memory, asymmetry, and skewed heavy tails. Emerg. Mark. Financ. Trade 2016, 52, 639–657. [Google Scholar] [CrossRef]
| Markets | Mean | Standard Deviation | Skewness | Kurtosis | ||
|---|---|---|---|---|---|---|
| 0 | 0.3929 | −0.4391 | 38.7708 | 0.001 | 0 | |
| 0 | 0.4341 | −0.1822 | 32.0143 | 0.001 | 0 | |
| 0 | 0.4824 | 0.4772 | 24.2047 | 0.001 | 0 | |
| 0 | 0.3305 | −0.5707 | 26.3124 | 0.001 | 0 | |
| 0 | 0.3401 | −0.1732 | 34.5017 | 0.001 | 0 |
| Model | Market | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| SA | 28 | 14 | 8 | 16.6667 | 0 | 0.0011 | 0.227 | 0.0760 | 52.9937 | 59.4396 | 67.9623 | 60.1319 | |
| TAS | 33 | 20 | 12 | 21.6667 | 0.0039 | 0.2145 | 0.6264 | 0.2816 | 17.7443 | 20.0184 | 22.8756 | 20.2128 | |
| EWMA | VIC | 33 | 16 | 9 | 19.3333 | 0.0001 | 0.0052 | 0.3773 | 0.1275 | 31.9751 | 34.9794 | 39.329 | 35.4278 |
| NSW | 34 | 22 | 10 | 22.0000 | 0.0002 | 0.1316 | 0.5692 | 0.2337 | 13.6768 | 15.0194 | 16.8504 | 15.1822 | |
| QLD | 31 | 18 | 10 | 19.6667 | 0 | 0.0187 | 0.5692 | 0.1960 | 41.4191 | 47.1902 | 54.4574 | 47.6889 | |
| SA | 65 | 42 | 25 | 44.0000 | 0.4707 | 0.032 | 0.0009 | 0.1679 | 46.3525 | 49.41 | 53.8644 | 49.8756 | |
| TAS | 54 | 45 | 32 | 43.6667 | 0.7773 | 0.0006 | 0 | 0.2593 | 15.8873 | 17.4368 | 19.4366 | 17.5869 | |
| EMD-EWMA | VIC | 79 | 42 | 21 | 47.3333 | 0.0133 | 0.032 | 0.0167 | 0.0207 | 32.5269 | 34.2162 | 36.7786 | 34.5072 |
| NSW | 74 | 49 | 32 | 51.6667 | 0.0627 | 0.0011 | 0 | 0.0213 | 14.354 | 15.652 | 17.3934 | 15.7998 | |
| QLD | 58 | 39 | 24 | 40.3333 | 0.8412 | 0.1009 | 0.0019 | 0.3147 | 38.9737 | 43.9293 | 50.2608 | 44.3879 |
| Model | Market | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| SA | 22 | 8 | 2 | 10.6667 | 0 | 0 | 0.0004 | 0.0001 | 56.3005 | 65.591 | 79.1048 | 66.9988 | |
| TAS | 26 | 14 | 4 | 14.6667 | 0 | 0.0091 | 0.0226 | 0.0106 | 18.9285 | 22.0918 | 26.4875 | 22.5026 | |
| EWMA | VIC | 20 | 13 | 2 | 11.6667 | 0 | 0.0005 | 0.0004 | 0.0003 | 33.4747 | 38.0882 | 45.37 | 38.9776 |
| NSW | 29 | 12 | 5 | 15.3333 | 0 | 0.0002 | 0.023 | 0.0077 | 14.3598 | 16.336 | 19.3053 | 16.6670 | |
| QLD | 23 | 11 | 6 | 13.3333 | 0 | 0.0001 | 0.0574 | 0.0192 | 44.4216 | 52.4633 | 63.643 | 53.5093 | |
| SA | 46 | 27 | 12 | 28.3333 | 0.0619 | 0.6041 | 0.9768 | 0.5476 | 48.0837 | 53.0234 | 61.0517 | 54.0529 | |
| TAS | 49 | 36 | 21 | 35.3333 | 0.6666 | 0.0603 | 0.0037 | 0.2435 | 16.7912 | 19.0735 | 22.3791 | 19.4146 | |
| EMD-EWMA | VIC | 59 | 24 | 13 | 32.0000 | 0.9469 | 0.2695 | 0.7522 | 0.6562 | 33.4739 | 36.2884 | 41.0526 | 36.9383 |
| NSW | 61 | 36 | 20 | 39.0000 | 0.8425 | 0.261 | 0.0315 | 0.3783 | 15.1041 | 17.0733 | 20.0307 | 17.4027 | |
| QLD | 46 | 27 | 12 | 28.3333 | 0.0619 | 0.6041 | 0.9768 | 0.5476 | 41.8694 | 49.1166 | 59.4536 | 50.1465 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
He, K.; Wang, H.; Du, J.; Zou, Y. Forecasting Electricity Market Risk Using Empirical Mode Decomposition (EMD)—Based Multiscale Methodology. Energies 2016, 9, 931. https://doi.org/10.3390/en9110931
He K, Wang H, Du J, Zou Y. Forecasting Electricity Market Risk Using Empirical Mode Decomposition (EMD)—Based Multiscale Methodology. Energies. 2016; 9(11):931. https://doi.org/10.3390/en9110931
Chicago/Turabian StyleHe, Kaijian, Hongqian Wang, Jiangze Du, and Yingchao Zou. 2016. "Forecasting Electricity Market Risk Using Empirical Mode Decomposition (EMD)—Based Multiscale Methodology" Energies 9, no. 11: 931. https://doi.org/10.3390/en9110931
APA StyleHe, K., Wang, H., Du, J., & Zou, Y. (2016). Forecasting Electricity Market Risk Using Empirical Mode Decomposition (EMD)—Based Multiscale Methodology. Energies, 9(11), 931. https://doi.org/10.3390/en9110931






