1. Introduction
The increasing concern over global climate changes and air pollution has motivated policy makers to promote renewable energy sources [
1]. Distributed generation (DG) based on renewable sources presents an opportunity to decrease this pollution impact considerably. The power industry represents a significant portion of the global carbon dioxide (CO
2) emissions corresponding to about 40% [
2] and regulations are currently in place for controlling the level of emissions in this sector [
1]. In Portugal the 2000s level of CO
2 emissions from electricity generation was 480 kgCO
2/MWh [
3]. In 2020 and 2050, it is expected that this level will drop to 190 kg CO
2/MWh and 20 kgCO
2/MWh, respectively [
3]. The emissions from power sector decline as more renewable based generation is integrated. This raises an interesting research issue which is discussed in this work: understanding the impact of considering CO
2 emissions in the energy management problem up to 2050 within smart grids operation context.
With the emergence of intelligent infrastructures it will be possible to deploy smart grid capabilities, such as optimizing energy resources scheduling and reducing the load demand, avoiding high peaks at high electricity prices, while enabling a smoothed demand profile and profit maximization [
4]. However, there may exist other challenges beyond maximizing the profit, such as minimizing CO
2 emissions due to environmental concerns [
5,
6]. For that reason it is necessary to find an optimal solution that considers two or more objectives. Hence, in most real-world circumstances system operators are faced with a multi-objective problem [
7,
8,
9,
10].
In the literature, several approaches have been reported concerning intelligent energy resources management (ERM) [
8,
9,
11,
12,
13,
14,
15,
16,
17]. Regarding ERM under different design goals, several multi-objective models have been investigated so far, to determine the optimal resource scheduling of a microgrid over a day-ahead period time. In [
16], the proposed ERM optimizes an aggregated multi-objective criterion taking into account both the energy cost and thermal comfort of the occupants. In most multi-objective ERM models developed in the literature, minimizing the emissions is considered as an additional objective [
8,
9,
11,
12,
13,
14,
15]. The multi-objective model published in [
15] does not include the power flow equations, electric vehicles (EVs), demand response (DR) and energy storage systems (ESS). The model proposed in [
11] considers a simple load balance (active power) and does not consider the presence of EVs neither any type of DR. EVs and DR resources can bring important benefits to the future smart grid [
14,
18]. A Benders’ decomposition approach to solve ERM is presented in [
8]. This work proposes a multi-objective operational scheduling for charging and discharging of EVs in a smart distribution network in the day-ahead context. The multi-objective optimization considers both costs and emissions but the work seems limited since it does not formulate or consider demand response, wind or photovoltaic (PV) generation and ESS, which are vital smart grids features . Moreover, uncertainties of the day-ahead decisions are not addressed. In [
17], a differential search algorithm (DSA) and quantum particle swarm optimization (QPSO) are used to solve a hard combinatorial scheduling problem. A comparison between the DSA and QPSO, with their hybrid versions is presented. However, that work considers only a single objective function to maximize the profits and not addressing DR, ESS, market bids (sell or buy), and CO
2 emissions. In [
19], the tradeoff between cost and environment emissions is presented using a regular and a binary particle swarm optimization (PSO). The computational intelligence-based scheduling seems promising to reduce cost and emissions, while maximizing the renewable energy sources use. The multi-objective problem is solved using a weighted sum approach with PSO, instead of a multi-objective evolutionary algorithm or multi-objective PSO (MOPSO) [
20]. Moreover, the network constraints are not considered in the mentioned approach. In [
15], a multi-objective energy management for a micro-grid using both intelligent techniques and linear programming is presented to minimize the operation costs and the environment impacts. However, the work proposes a linear formulation without power flow equations and not considering the possibility of vehicle-to-grid (V2G). A modified PSO methodology is developed in [
21,
22] to solve the problem of ERM with high penetration of DG and EVs with V2G, with the aim to improve the performance of PSO. However, the reported work considers a single objective function, i.e., the operation cost minimization. In [
18], a multi-objective model is presented, introducing the ERM model reliability concern through a multi-objective formulation. Pareto solutions provide multiple alternatives for the energy aggregator, namely by picking the most appropriate solution, taking into account the preference between minimum operation cost and the maximum available reserve. Weighted PSO (W-PSO) is proposed to solve the multi-objective problem, which uses a Pareto set scheme.
The problem handled in this paper concerns a profit seeking aggregator entity managing several distributed energy resources (DER). The aggregator needs to solve the ERM problem, which is a large-scale non-linear combinatorial DER scheduling problem including V2G resources, DR, sells/buys market and external suppliers. A multi-objective function is used to maximize the profit corresponding to the difference between the income and operating costs and a function to minimize the CO
2 emissions. Three metaheuristics are compared, namely, the W-PSO, MOPSO and non-dominated sorting genetic algorithm II (NSGA-II). Hence, the previous signaling method for PSO used in [
23] is adapted and used here to help W-PSO, MOPSO and NSGA-II to escape violations and improve fitness function. That way, this paper reviews the signaling method influence in the multi-objective problem. This validation has not been addressed before in the literature, so it constitutes its major contribution.
The work is validated with a case study concerning a real 233-bus distribution network from a region of northern Portugal, namely a part of the distribution grid from Vila Real city. Two scenarios are assessed and evaluated using the multi-objective approaches for years 2020 and 2050, respectively. In addition to the renewable generation increase from 2020 to 2050, EVs are expected to be increasingly adopted. The study presented here takes into account these changes, including different DG technologies EVs characteristics. The electricity grid is slightly updated, namely expanding the DG units’ capacity to supply approximately 14,000 consumers. The EVs scenarios reach 5080 EVs in 2050, enabled with V2G capability. The results obtained suggest that signaling method effectively improves Pareto front in the tested metaheuristics and finds profitable solutions with less CO2 impact and without constraint violations. Furthermore, W-PSO seems to present better results, but requiring more computational times. The robustness test and sensitivity analysis suggest that signaling method is robust and works well under variations of important parameters.
This paper is organized as follows: after this introductory part,
Section 2 presents the multi-objective ERM mathematical model,
Section 3 presents the technical solutions employed in this paper,
Section 4 discusses the case study, and finally
Section 5 presents our conclusions.
4. Case Study
The proposed methodology was tested using a case study implemented on a MV 30 kV distribution network with 233 buses. This is part of a real network from Vila Real in Portugal. A reconfiguration was performed to the original mostly meshed network using the software developed in [
41] to obtain the radial configuration presented in
Figure 1. This single-line diagram does not represent the actual geographical design.
The work was developed in MATLAB R2014a 64 bits (MathWorks, Natick, MA, USA) using a computer equipped with one Intel Xeon E5-1650 processor (Intel Corporation, Santa Clara, CA, USA) and 10 GB of RAM running Windows 8.1. The parallel platform is implemented in MATLAB distributed computing, i.e., a total of six computers with 42 cores. The single-core tests are done on the mentioned workstation.
4.1. Scenario Description
The regular demand (without EVs) was forecasted for 2020 and 2050, taking into account the published results [
3,
42,
43]. According to [
3], the consumption will rise by 4% and 29% for 2020 and 2050, respectively, in comparison with 2010. Hence, an updated consumption curve for 2020 and 2050 were obtained from the base consumption data available for this grid. Taken into account the actual population (21,000) in Vila Real city, the total number of regular vehicles was estimated using the expected growth/decay rate and the vehicle rate per person. According to the penetration rate of EVs provided by [
43], the total number of EVs was set to 1540 for 2020 and 5080 for 2050. The EVs’ scenarios were created using EVeSSi tool (GECAD, Porto, Portugal) [
44]. The charging and discharging efficiency considered was 80% for 2020 and 90% for 2050. According to [
3], the forecasted penetration of renewable generation in Portugal will amount to 49% and 77% in 2020 and 2050, respectively. Photovoltaic capacity installation is expected to be larger than wind installation in the future [
3]. Moreover, it was considered that the capacity of the combined heat and power (CHP) increased by two-fold in 2050.
Table 2 shows the data for the developed scenario, taken into account the mentioned forecasts. The considered prices took into account the levelized generation costs presented in [
42]. In reality the prices correspond to the cost that the VPP has to pay to buy energy from the respective DER’ owner, except from the charge of ESS and EVs, where the owners pay to the VPP instead, therefore contributing to the income in Equation (1) (see
Section 2.1). The loads also pay to the VPP and the price varies as can be seen in
Table 2 depending on the contract (consumer type).
It is assumed that the VPP is responsible to manage the distribution network and all the energy resources aiming to maximize profit and minimize CO
2. It is expected that solutions with higher profits are also those with higher CO
2 emissions. The 14,000 network consumers are aggregated by bus totaling 162 aggregated bus-loads. In addition, 89 of the 162 aggregated loads offer DR possibility. The DG units are also aggregated by bus and by type as can be seen in
Table 2. The external supplier located in the substation represents the energy imported from the main grid and is modeled with a 10 MW contract for 2020 and 15 MW for 2050. The EVs are considered individually, increasing 3.3 times in 2050 when compared with 2020. The maximum energy that VPP can export is depicted in the table as the “market” resource, i.e., a maximum of 4 MW.
Table 3 presents the energy supplier (main grid) and the CHP CO
2 emission rate taken into account the values presented in [
3,
45]. A considerable reduction of CHP emission rate in the 2050 scenario from 2020 is considered.
Table 4 presents the parameters founded by empirical testing. W-PSO is run independently using the weighted sum approach (see
Section 3), namely with a set of 100 weights randomly generated for the two objectives, profit and emissions. In the end, a Pareto front algorithm determines the Pareto front in W-PSO, while NSGA-II and MOPSO obtain the Pareto front in a single run. In fact, the results shown in the following sections for scenarios 2020 (
Section 4.2) and 2050 (
Section 4.3) have been obtained using a random trial. Previously, a robustness test was performed to understand the results variability for the implemented algorithms. In
Section 4.4 this test is described, which verified that the variation of the solutions between trials was quite small. Any random trial should fall within those depicted ranges with a high probability.
4.2. Results–Scenario Portugal 2020
This section presents the results that have been studied for the scenario 2020.
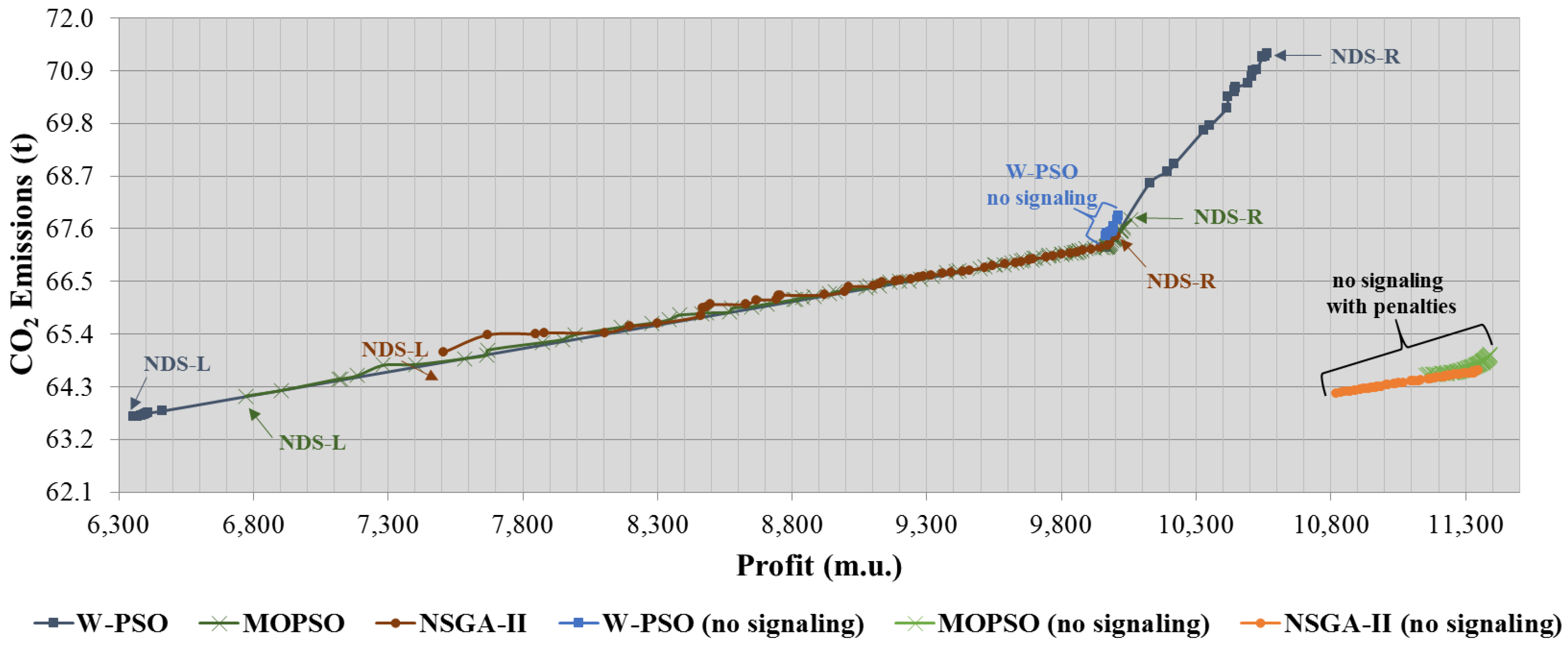
Figure 2 presents the Pareto front achieved in MOPSO, W-PSO and NSGA-II metaheuristics with and without signaling, respectively. The marker represents each obtained NDS. NDS-L (left) and NDS-R (right), represents the NDS with lower emissions and higher profit, respectively. There are some Pareto front regions with more markers representing higher density of NDS. Important to refer that without the use of the signaling method, the only metaheuristic that found solutions without violations was the W-PSO (8 NDS). In contrast, all the NDS found by MOPSO and NSGA-II, had violations, which was caused by the voltage and line limit violations and by insufficient generation. The range of the Pareto front results were greatly reduced when compared with the results obtained using the signaling method. Hence, it is possible to conclude that the signaling method use contributed to a better performance of the three metaheuristics addressed in this paper. In the results with the signaling method, the MOPSO profit ranged between 6771 m.u. and 10,058 m.u.; while in the W-PSO, the profit ranged between 6355 m.u. and 10,563 m.u. whereas in the NSGA-II, the profit ranged between 7506 m.u. and 10,006 m.u. In terms of CO
2 emissions, the range varies between 64.11 tCO
2 and 67.79 tCO
2 (tCO
2 is equivalent to 1000 kg CO
2 where t stands for tonne) in MOPSO; 63.67 tCO
2 and 71.26 tCO
2 in W-PSO; and 65.02 tCO
2 and 67.46 tCO
2 in NSGA-II.
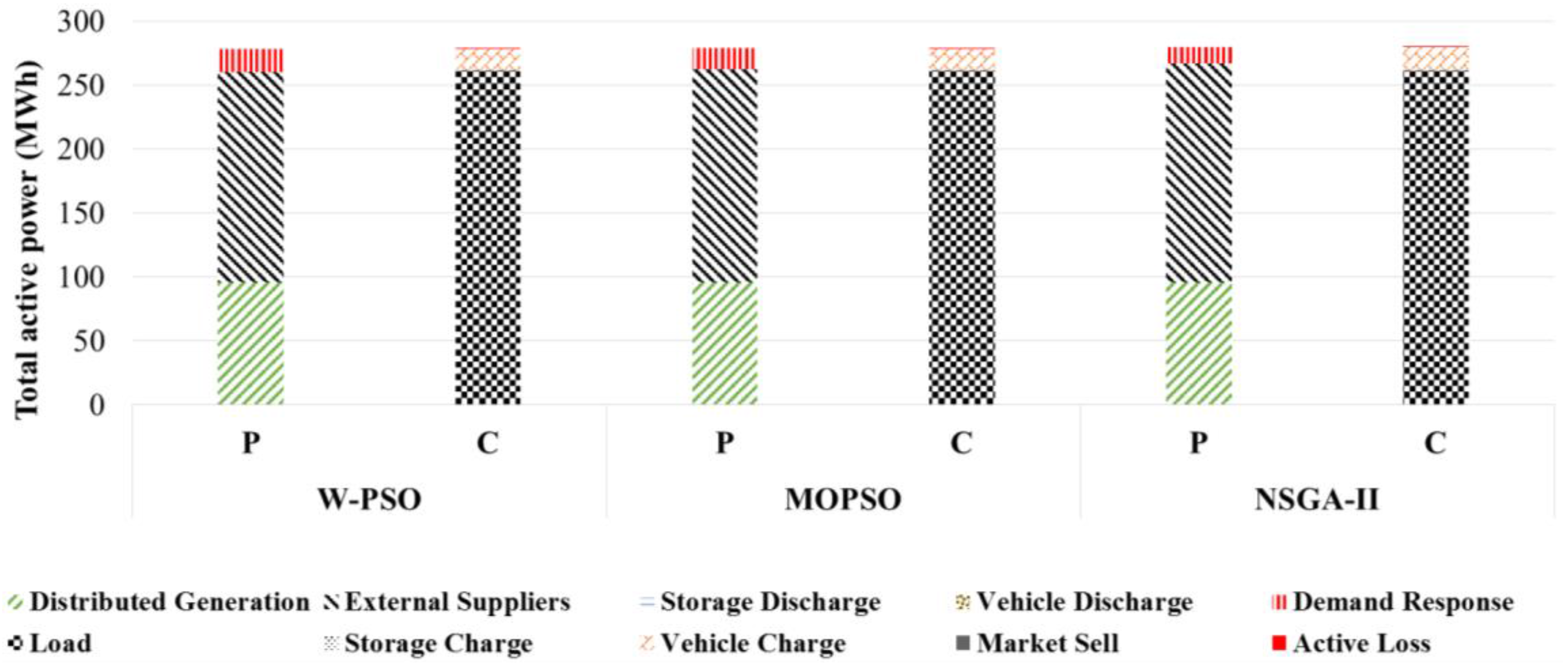
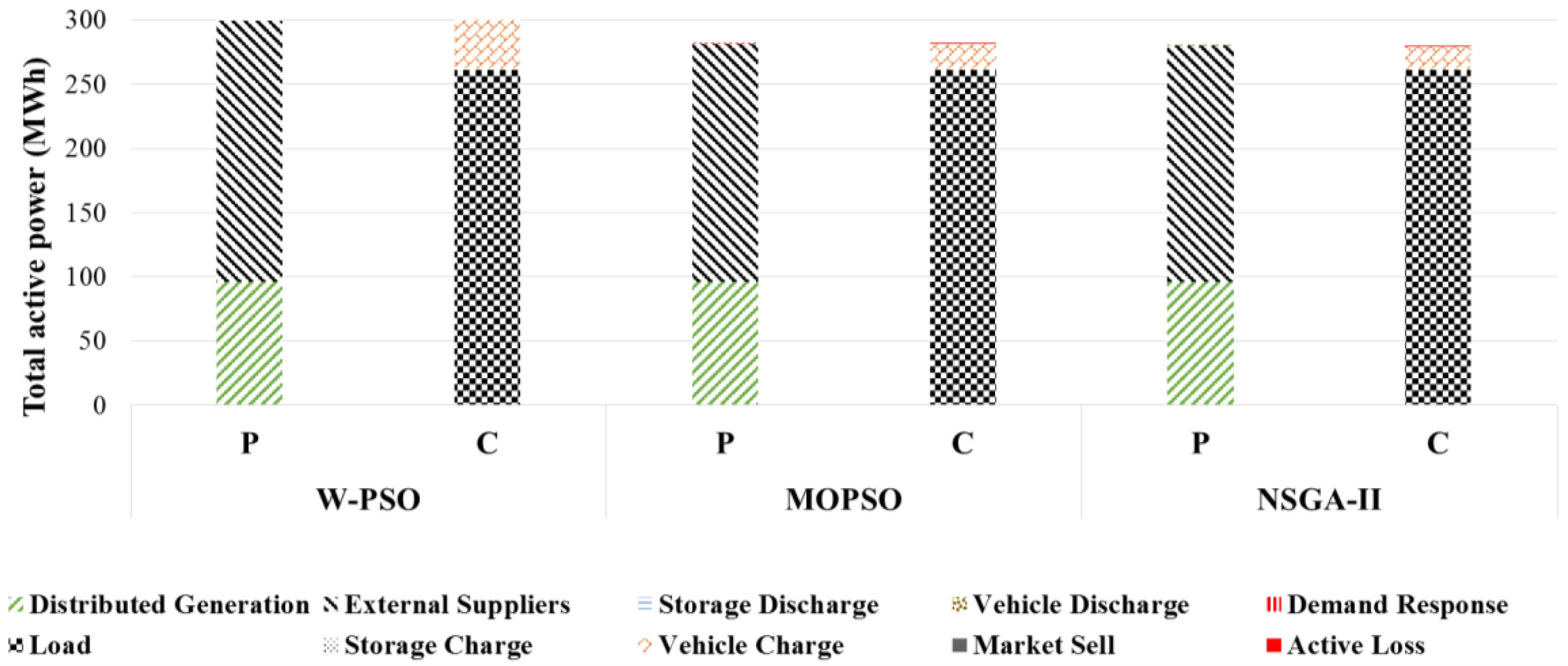
Figure 3 and
Figure 4 present the total generation and consumption for two solutions of the Pareto front, namely NDS-L and NDS-R for MOPSO, W-PSO, and NSGA-II method, with the utilization of signaling method. It can be seen that NDS-L uses DR. This enables a significant reduction in the use of power production sources that emit CO
2, but will lead to a lower profit due to the need to remunerate customers against the implementation of these measures.
Table 5 presents the obtained results for each method. The difference between NDS-L and NDS-R were analyzed. The highest profit was obtained in W-PSO (NDS-R solution), i.e., 10,564 m.u. The lowest CO
2 emissions was obtained in W-PSO, with 63.67 tCO
2. The highest difference between NDS-R and NDS-L in CO
2 emissions was achieved with W-PSO, i.e., 7.59 tCO
2, while the lowest difference was achieved in NSGA-II with 2.44 tCO
2. In MOPSO the difference was 3.68 tCO
2. Regarding profit, the highest difference was reported by W-PSO, with 4209 m.u., while NSGA-II presented the lowest difference of the tested methods, with 2500 m.u. Similarly to the previous scenario, this results indicated that W-PSO method performed better with a higher diversity and better convergence than NSGA-II and MOPSO when signaling method was used. Nevertheless, execution time in W-PSO was much higher than in those methods (65,100 s). However, in parallel mode the execution time was greatly improved (16×) to about 3973 s. In MOPSO this improvement is far less (3×) from 7020 s to 2021 s. In NSGA-II the execution time is 6096 s in single-core, while the parallel mode did not improved the performance.
4.3. Results–Scenario Portugal 2050
This section presents the obtained results regarding the scenario 2050.
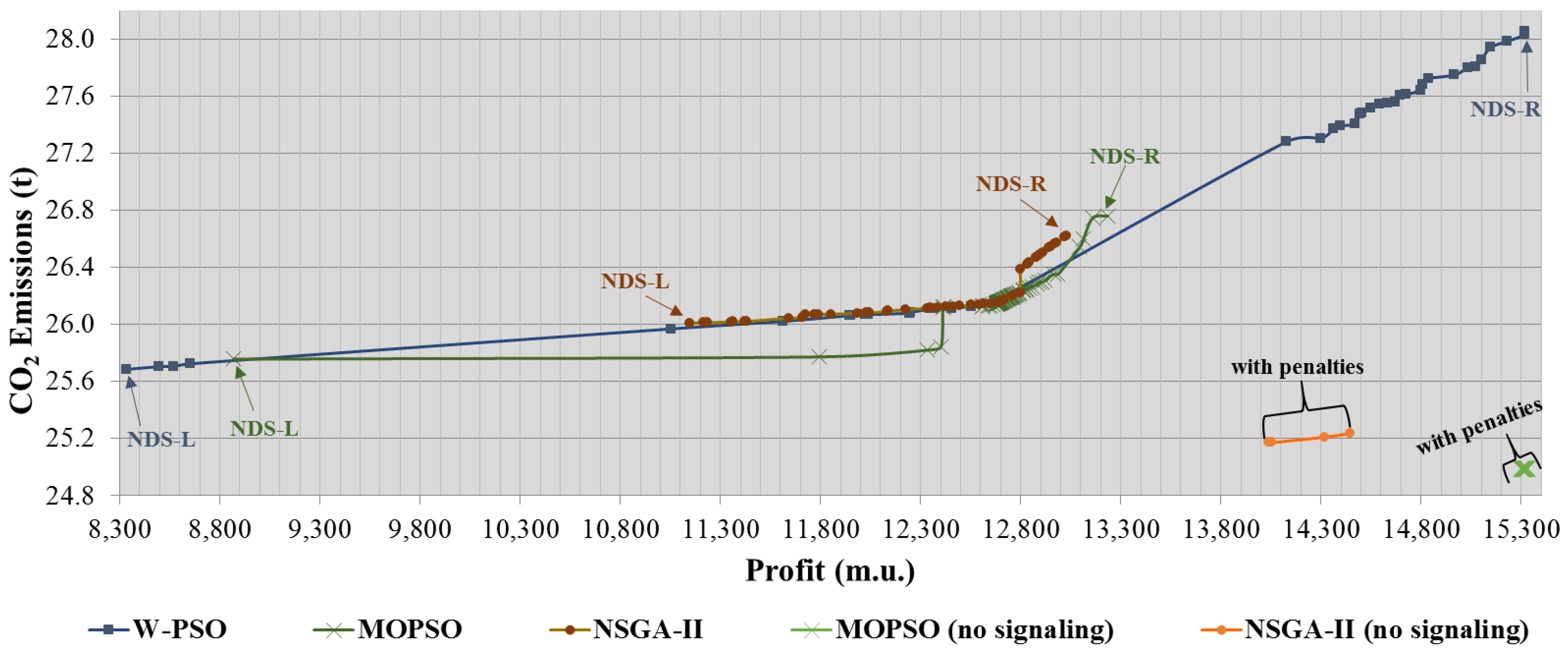
Figure 5 presents the Pareto front achieved in MOPSO, W-PSO, and NSGA-II metaheuristics with and without signaling, respectively.
The marker represents each obtained NDS. NDS-L and NDS-R, represent the NDS with lower emissions and higher profit, respectively. There are some regions of the Pareto front with more markers, representing higher density of NDS. Important to refer that without the use of the signaling method, all the NDS found by the three metaheuristics had violations, caused by voltage limit and line capacity violations and also by insufficient generation. Moreover, the range of the Pareto front was greatly reduced when compared with the results using signaling method. In the results with the signaling method, the MOPSO profit ranged between 8868 m.u. and 13,235 m.u., while in the W-PSO, the profit ranged between 8334 m.u. and 15,320 m.u. whereas in the NSGA-II, the profit ranged between 11,147 m.u. and 13,030 m.u. In terms of CO2 emissions, the range varies between 25.75 tCO2 and 26.76 tCO2 in MOPSO; 25.68 tCO2 and 28.05 tCO2 in W-PSO; and 26.01 tCO2 and 26.62 tCO2 in NSGA-II.
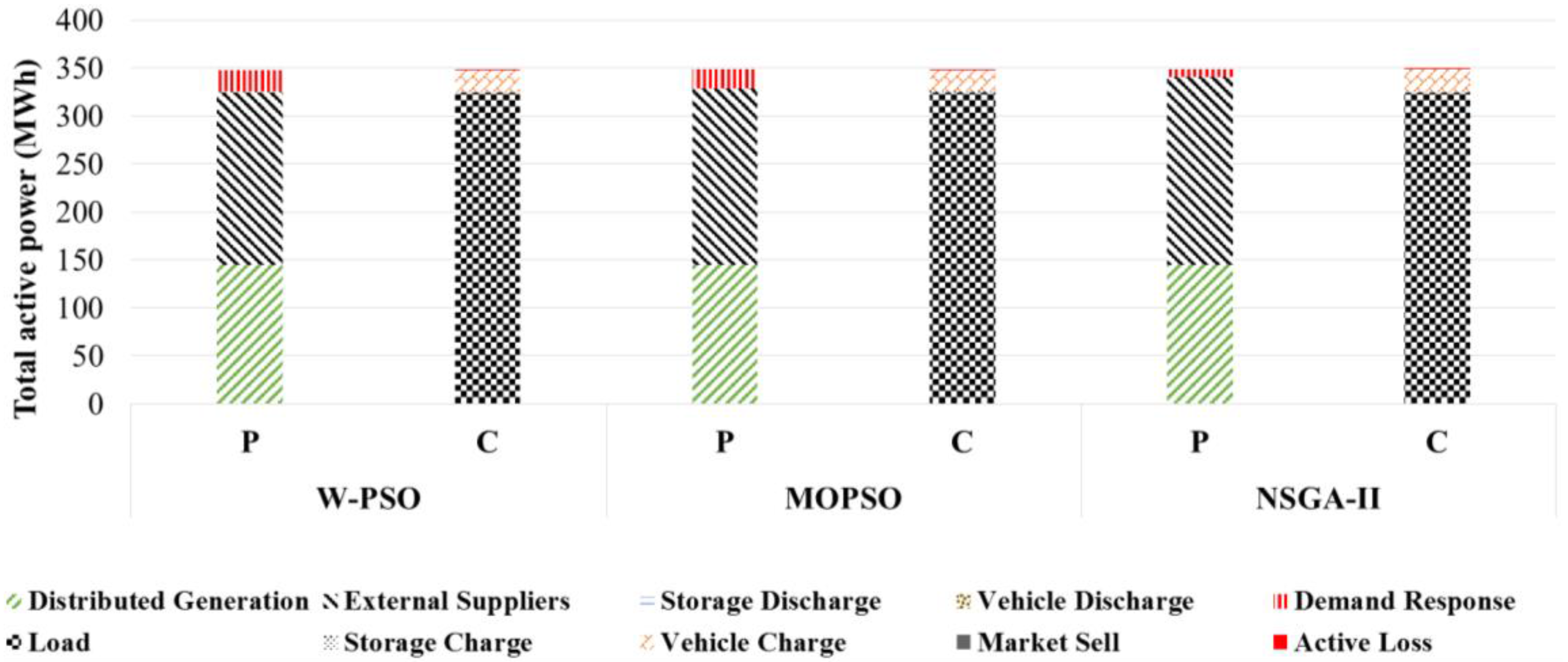
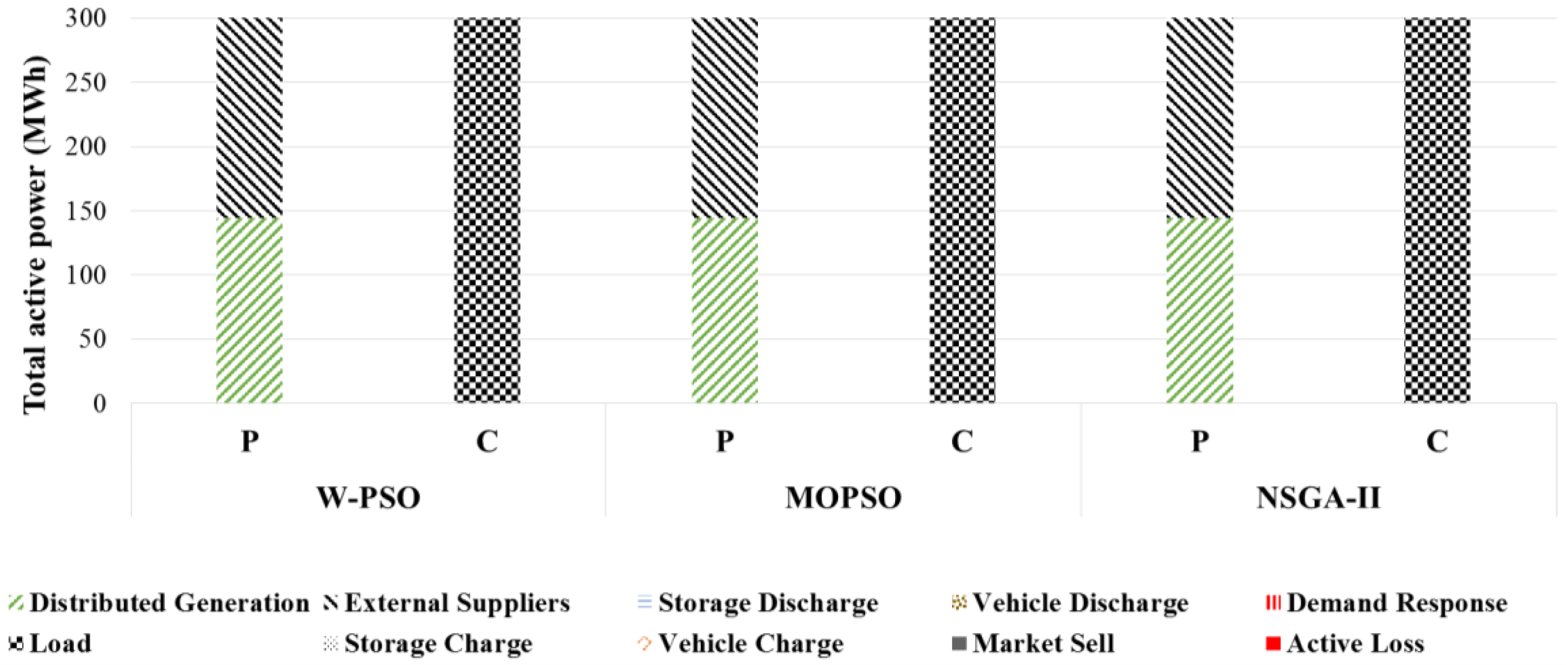
Figure 6 and
Figure 7 present the total generation and consumption for two solutions of the Pareto front, NDS-L and NDS-R, and each of compared methods MOPSO, W-PSO, and NSGA-II with signaling. It can be seen that NDS-L schedules DR whereas NDS-R do not in each method (higher in W-PSO). This use will mean a significant reduction in the generation sources that emit CO
2, but will lead to a lower profit due to the need to remunerate customers that use DR measures [
46].
Table 6 presents the results for each method. The difference between NDS-L and NDS-R can be seen. The highest profit was obtained in W-PSO (NDS-R). The lowest emissions were achieved with W-PSO, i.e., 25.68 tCO
2. The highest difference between NDS-R and NDS-L in CO
2 emissions was achieved with W-PSO, i.e., 2.37 tCO
2, while the least difference was achieved in NSGA-II, i.e., 0.61 tCO
2. In MOPSO the difference was 1.01 tCO
2. Regarding profit, the highest difference was reported by W-PSO, with 6985 m.u., while NSGA-II presented the least difference of the tested methods, with 1883 m.u. Similarly to the previous scenario, this results indicated that W-PSO method performed better with a higher diversity and better convergence than NSGA-II and MOPSO when signaling method was used. Nevertheless, execution time in W-PSO was much higher than those methods.
4.4. Robustness Test
To confirm the validity of the metaheuristics developed in this paper a robustness testing was computed. This test is necessary because for each run a slightly different Pareto front and solutions can be obtained with these metaheuristics, due to their stochastic nature. For this test each algorithm was run for 100 trials (100 Pareto fronts) in order to confirm that the variability of the obtained results are similar, i.e., robust.
Figure 8 presents the Pareto fronts, in two different perspectives: 3D and 2D, obtained in the W-PSO method with the use of signaling method for the 2020 scenario. The W-PSO was chosen here, since this was the method that yielded better solutions comparatively to the other methods, namely NSGA-II and MOPSO (see previous sections). The average standard deviation of the Pareto fronts are 37.25 m.u. (0.38%) and 0.039 m.u. (0.05%) for the profit and emissions, respectively. Despite the low variation, it can be seen that the front deviation tends to be higher (variability) for profitable solutions (
Figure 8b).
4.5. Parameter Sensitivy Analysis
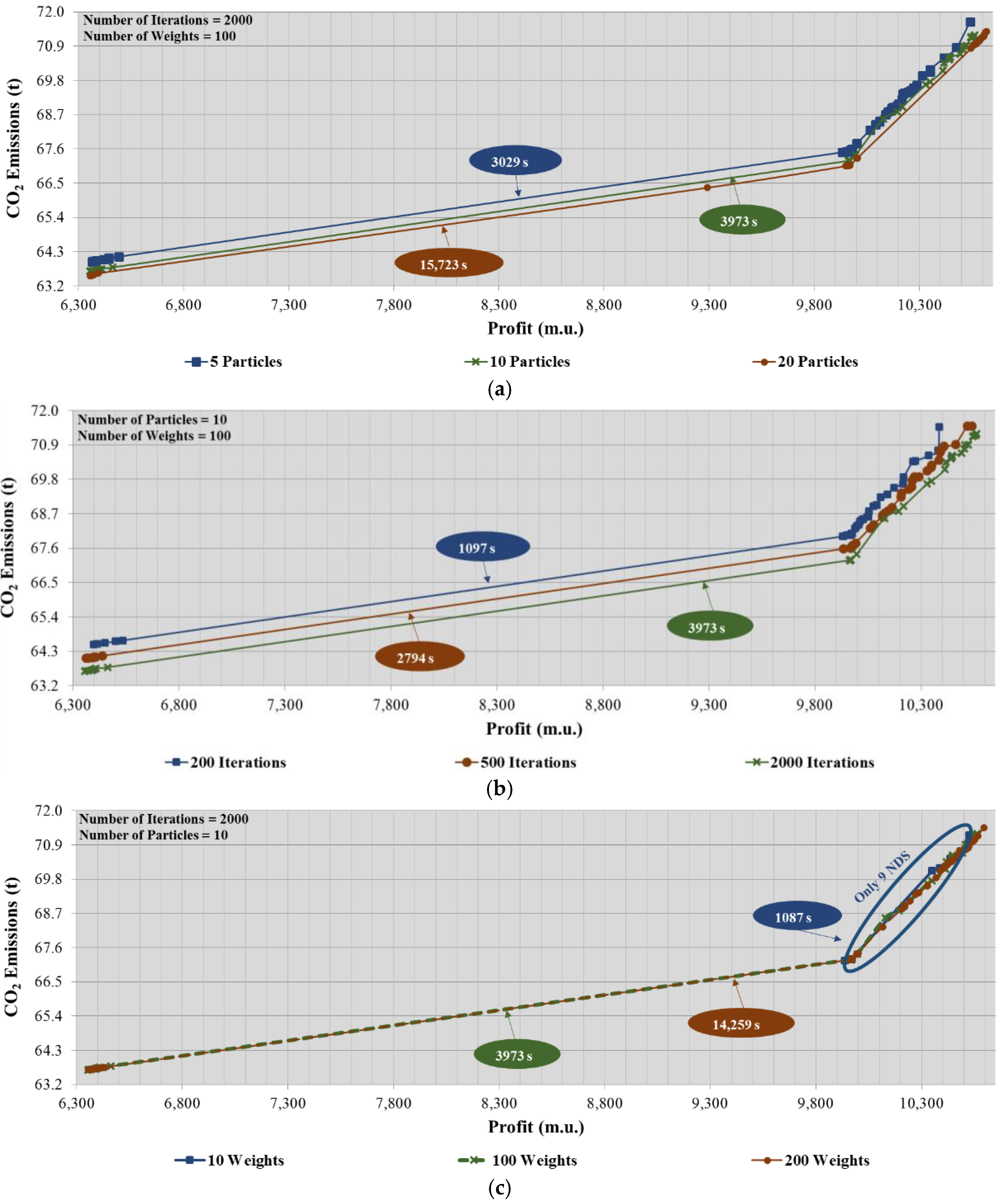
A sensitivity analysis experiment has been conducted to understand if W-PSO with signaling was robust enough to variation of essential parameters. The following parameters have been analyzed: number of particles, maximum number of iterations and the number of weight sets. Regarding the number of particles, the experiment has been made with 5, 10 and 20 particles. In what concerns the maximum number of iterations, it has been tested with 200, 500 and 2000 iterations. Finally, the weight sets with 10, 100 (default) and 200 weights. In each test, the remaining parameters of W-PSO have been left unchanged (
Table 4).
Figure 9 presents the tests made for each parameter as described.
The green line corresponds to the default parameters as tested in the case study (see
Table 4). The results suggest that increasing the number of particles and the number of iterations, can improve the Pareto front quality. However, this improvement cannot be deemed significant, except from the number of weight sets. This result suggest that signaling method contributes to W-PSO robustness if the number of weight sets is adequate. The execution times (parallel mode) for each tested case can be seen in the figure. Increasing any of the tested parameters can result in more computational burden. Reducing the number of iterations or the number of weight sets can reduce computational burden, but decrease the Pareto front quality. This degradation is more noticeable when changing the weight sets parameter, e.g., the case with 10 weight sets, the W-PSO obtained 9 NDS with a reduced range of choice regarding profit/CO
2. A trade-off between the Pareto front quality and the experimented parameters is recommend. Therefore, the recommended settings for W-PSO with signaling, based on this experiment are:
- -
10 or less particles (a higher number will exponentiallly increase execution times due to the Pareto front selection procedure);
- -
Between 500 and 2000 iterations (the execution time increases with a higher number of iterations, but it is more reasonable than increasing the number of particles and also more effective, particularly in parallel mode);
- -
At least 100 weight sets (more weight sets will mean more NDS but much higher computation times).
5. Conclusions
This paper presented a study regarding ERM in smart grid with multi-objective goals, namely the VPP profit and CO2 emissions. The metaheuristics implemented to tackle the ERM large-scale optimization are the weighted particle swarm optimization (W-PSO), multi-objective particle swarm optimization (MOPSO), and NSGA-II. A comparison between these methods was made using the signaling method adapted to the multi-objective problem. To validate the proposal, two realistic scenarios were developed using as basis a real distribution grid from Vila Real in Portugal. Several heterogeneous DERs managed by a VPP were considered in the grid. The considered characteristics of the cases studied took into account several research work and forecasts available in the literature for 2020 and 2050.
The findings achieved in this paper allowed to understand that the signaling method greatly improved the diversity and convergence of the Pareto front in the metaheuristics-based approaches. In addition, constraints violations were easily avoided with signaling when compared with the standard approaches counterpart, which presented a high number of infeasibilities in both scenarios. This enable to conclude that, the use signaling leverages the better performance of the addressed methods in the ERM as it was demonstrated previously in single-objective problem [
23]. In this case, the metaheuristic that featured better results was W-PSO, however, the execution time was higher, when compared with the NSGA-II and MOPSO, mainly in single-core. Therefore, a tradeoff between Pareto front quality and execution time seems to be important as well as considering parallel implementation, which demonstrated to be relevant in this work.
It was verified that CO2 emissions between 2020 and 2050 may drastically reduce if renewable share increases according to available projections. EVs will certainly contribute to increase the average load consumption, despite other loads consumption decrease with energy efficiency improvements. This study also reveals that pursuing CO2 goals reduction within next decades may lose its significance for electricity entities and other similar players. Indeed, the results showed that the profits are substantially affected in exchange for little emission in 2050.