Blade Fault Diagnosis in Small Wind Power Systems Using MPPT with Optimized Control Parameters
Abstract
:1. Introduction
2. System Circuit Architecture and Controller Design
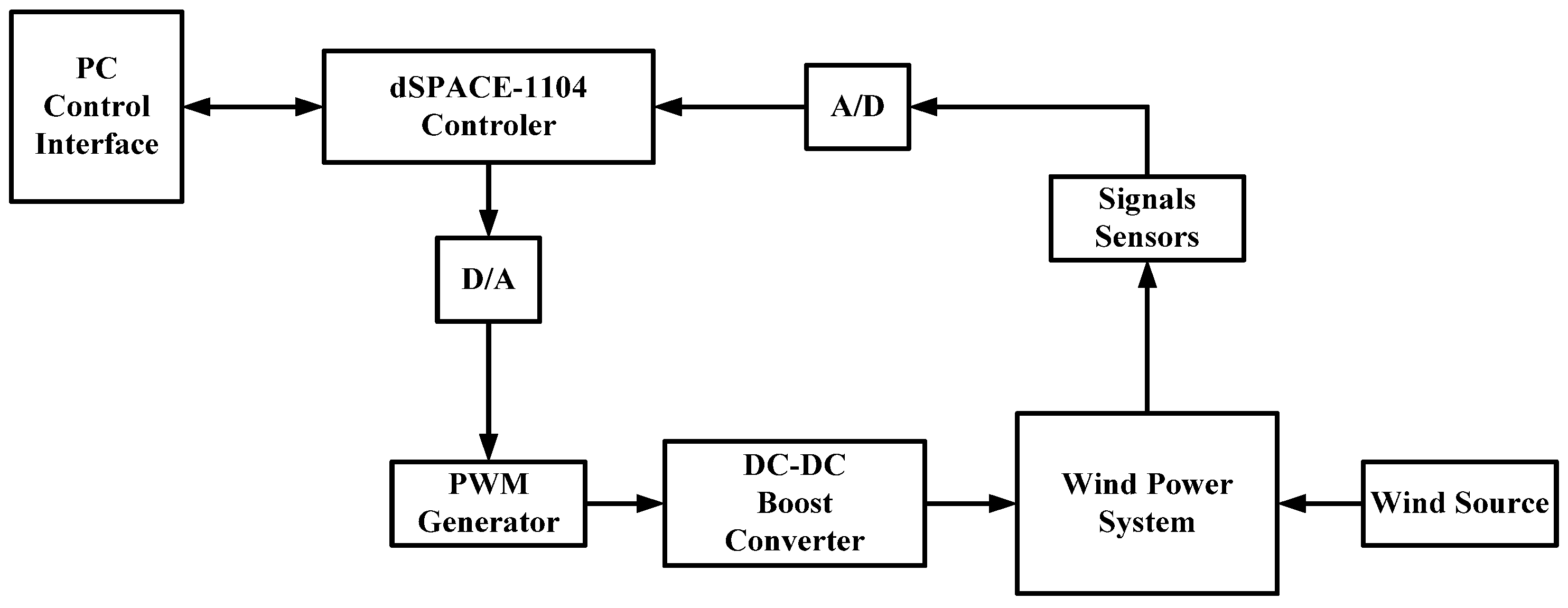
2.1. System Architecture


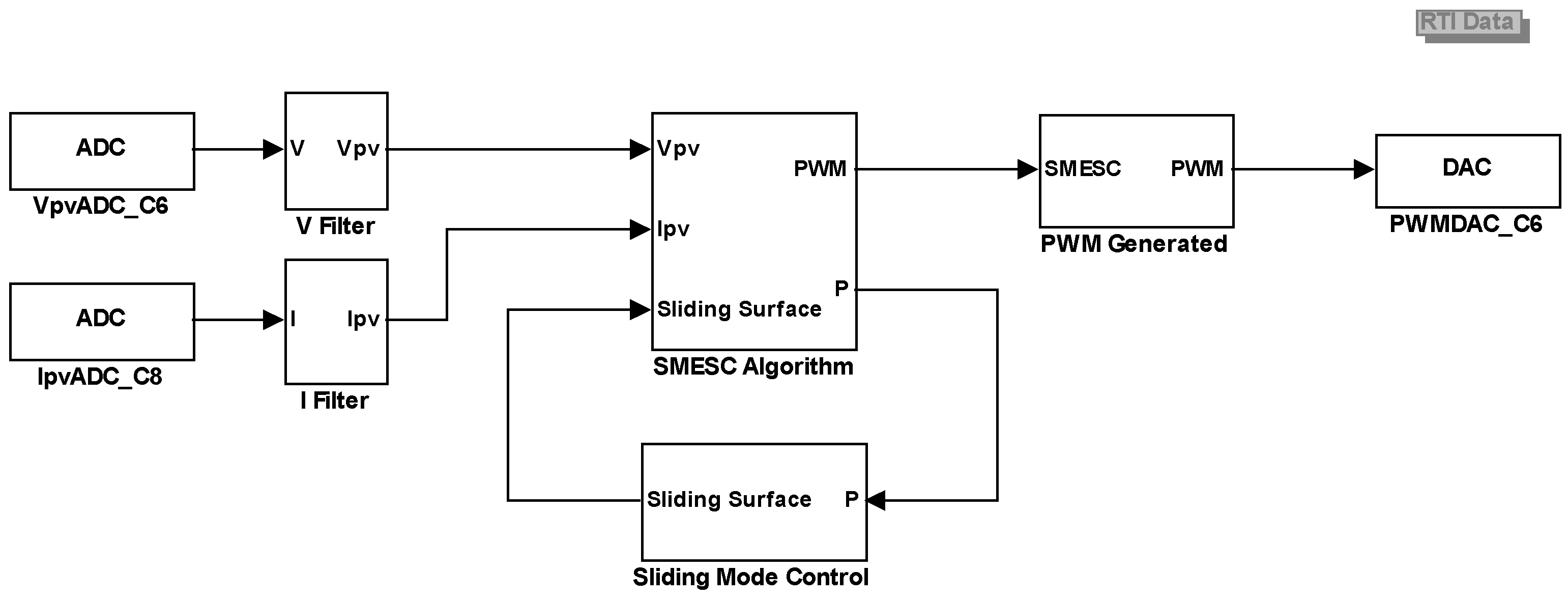
2.2. Control Parameter Optimization and Maximum Power Point Tracking Method
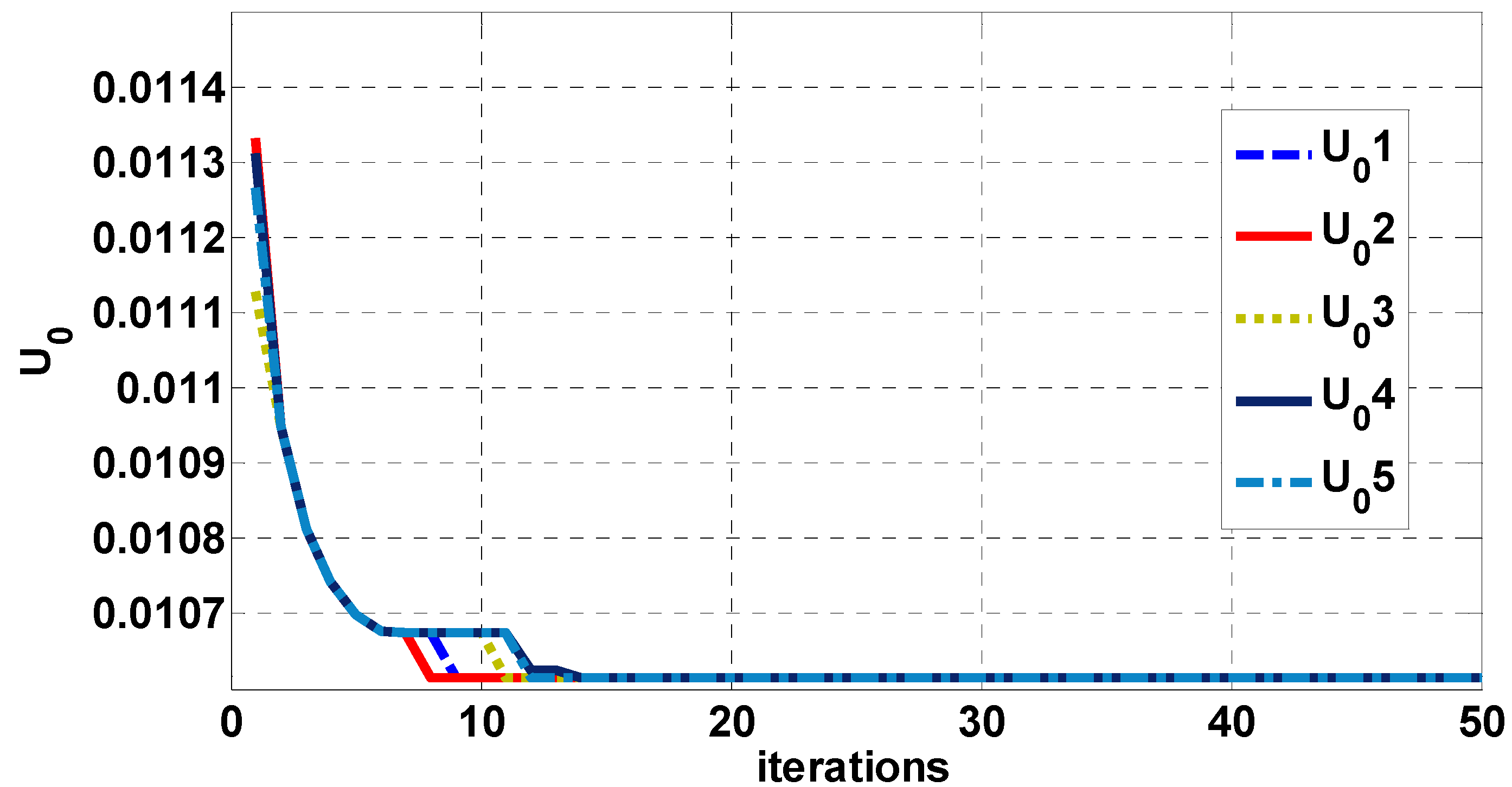
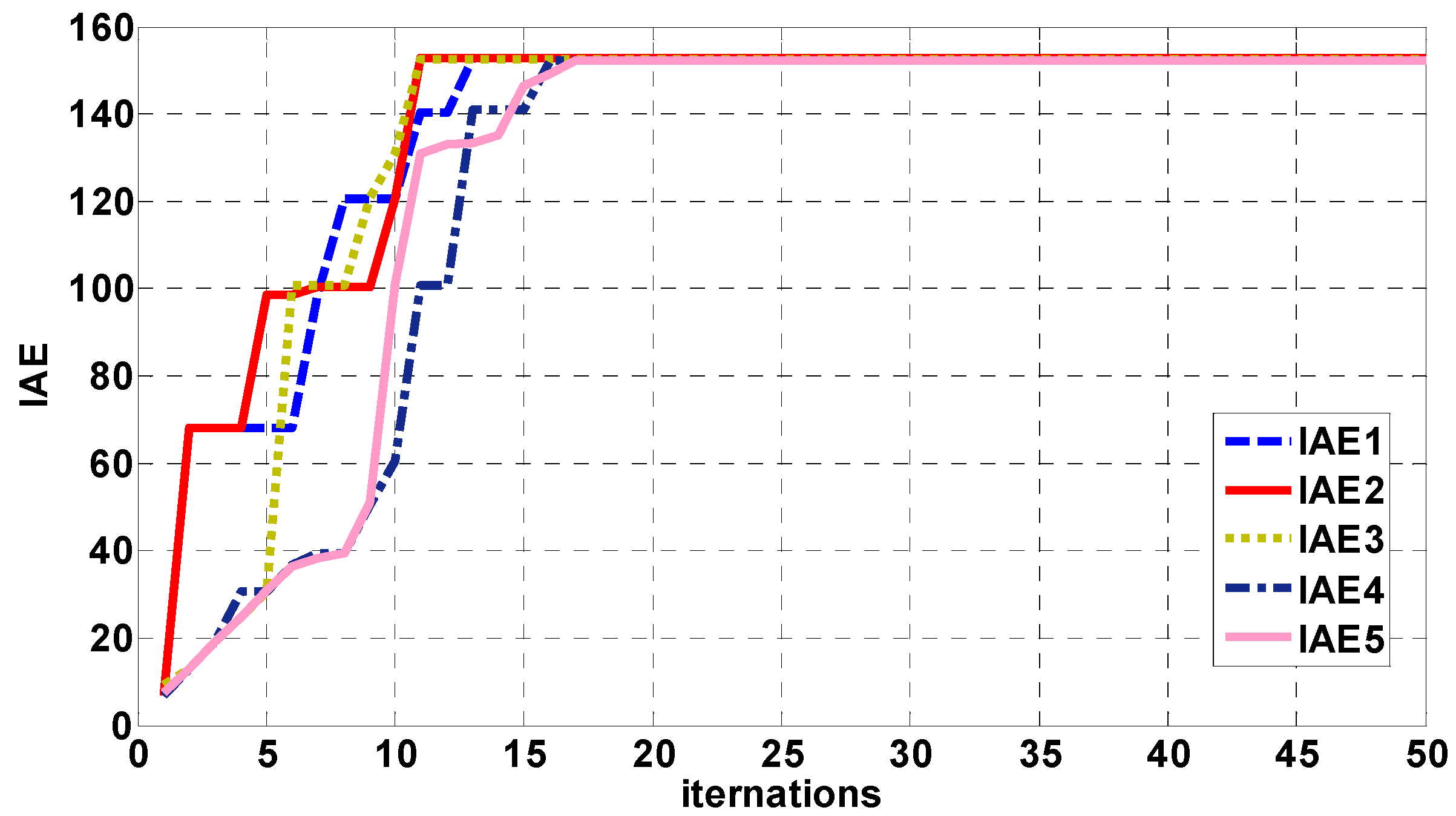
3. The System Status Signal Analysis and Fault Diagnosis Architecture
3.1. Master-Slave Chaos Dynamic Error System and Extenics Engineering Diagnosis
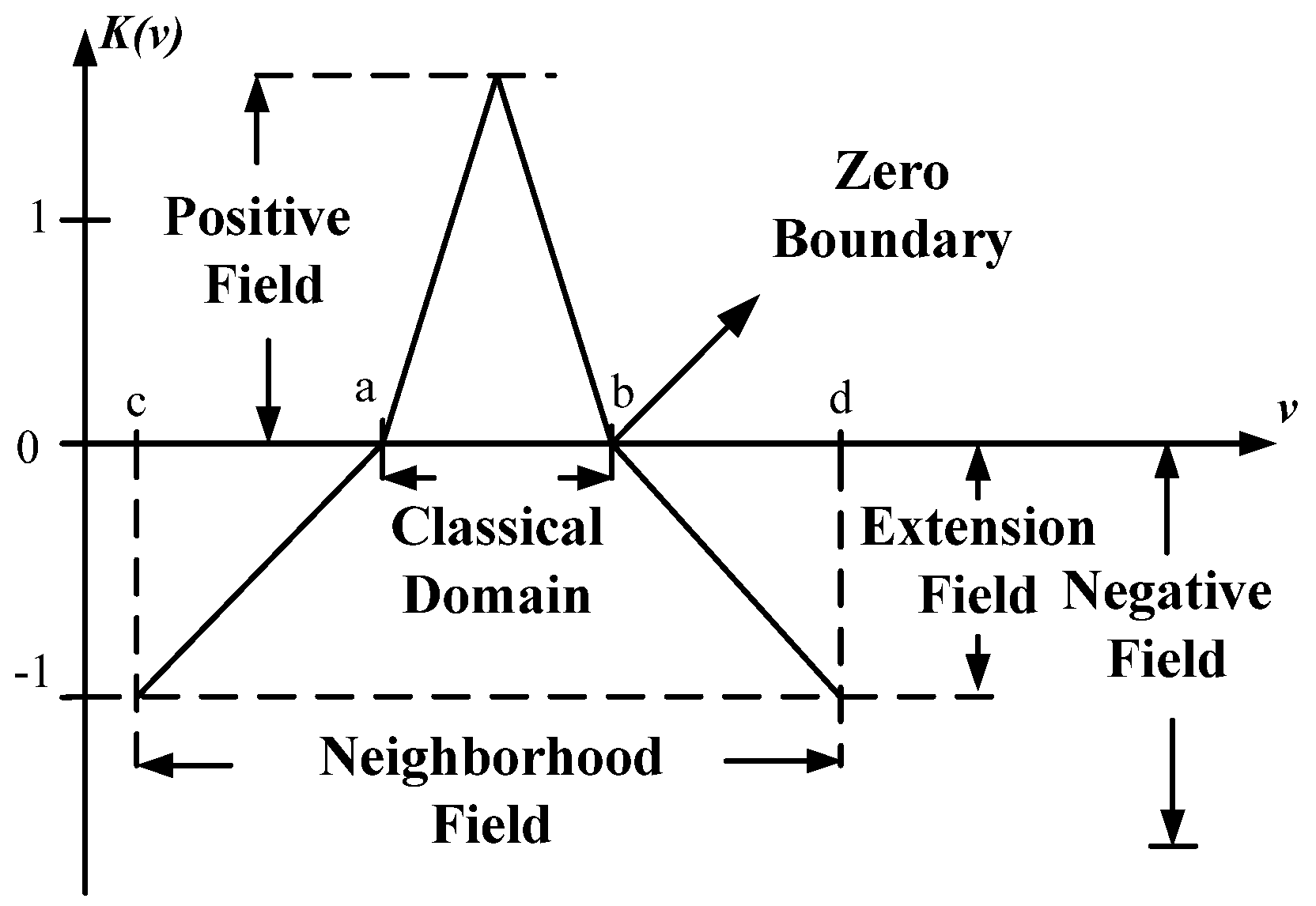
3.2. Extenics Engineering Diagnosis
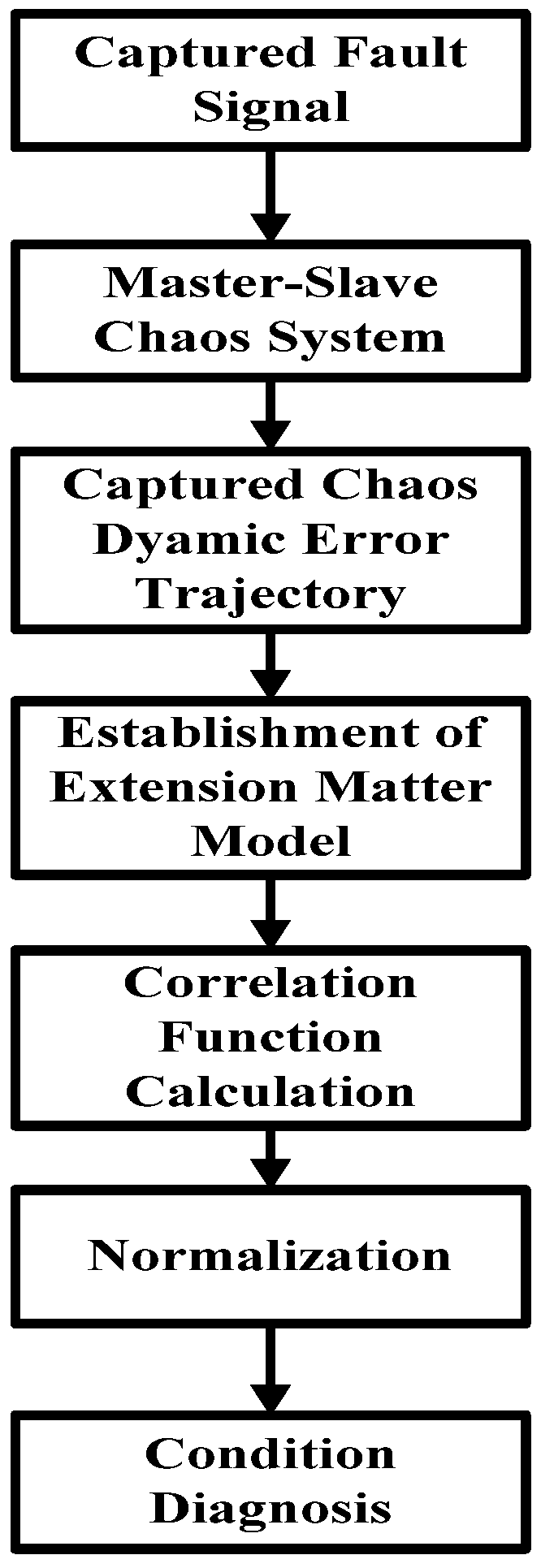
3.3. The Master-Slave Chaos Dynamic Error System Signal Integration Extenics Engineering Diagnosis Framework
4. The Maximum Power Point Tracking Simulation Analysis and Experimental Results
4.1. Maximum Power Point Tracking Algorithm Simulation
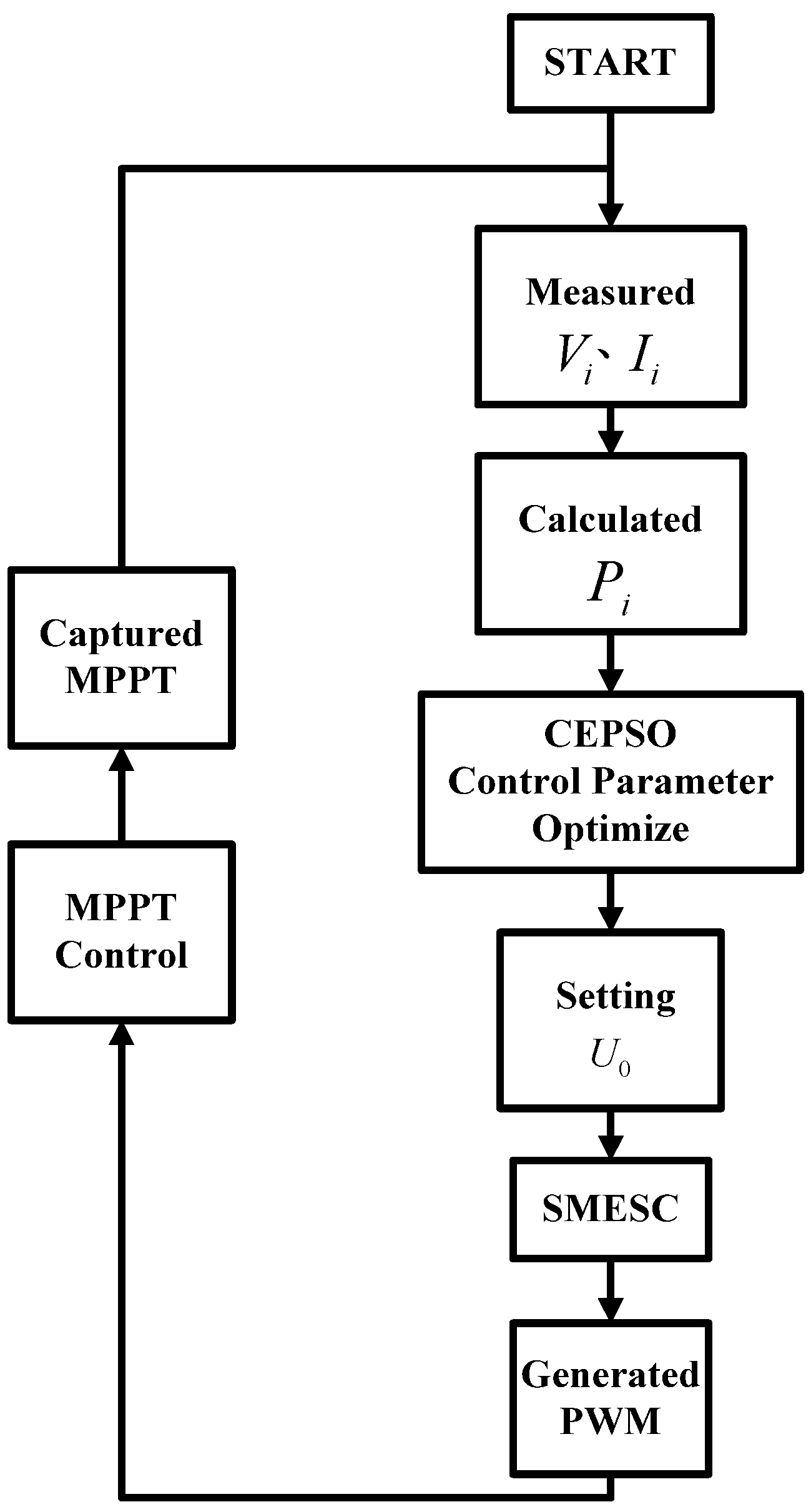
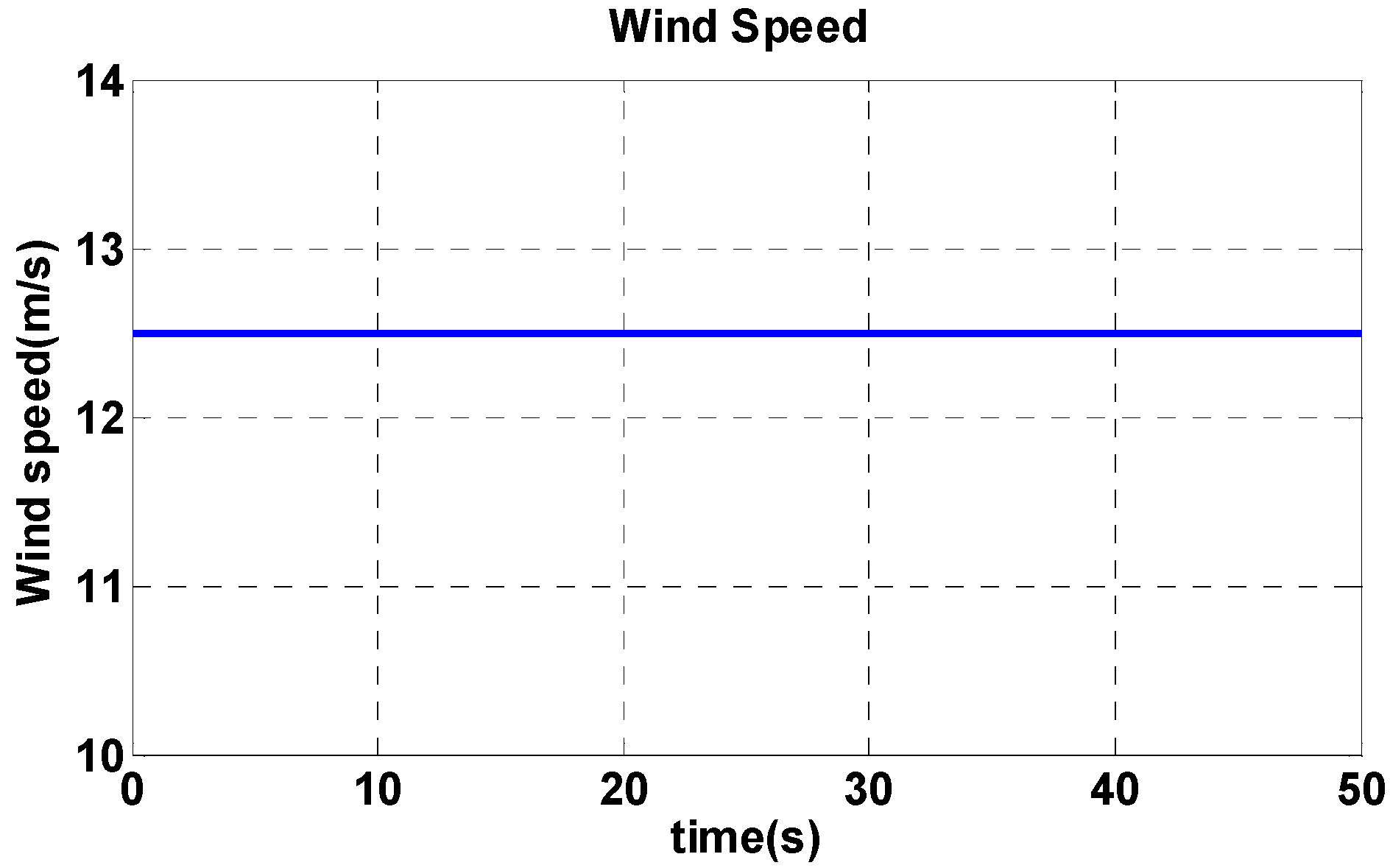
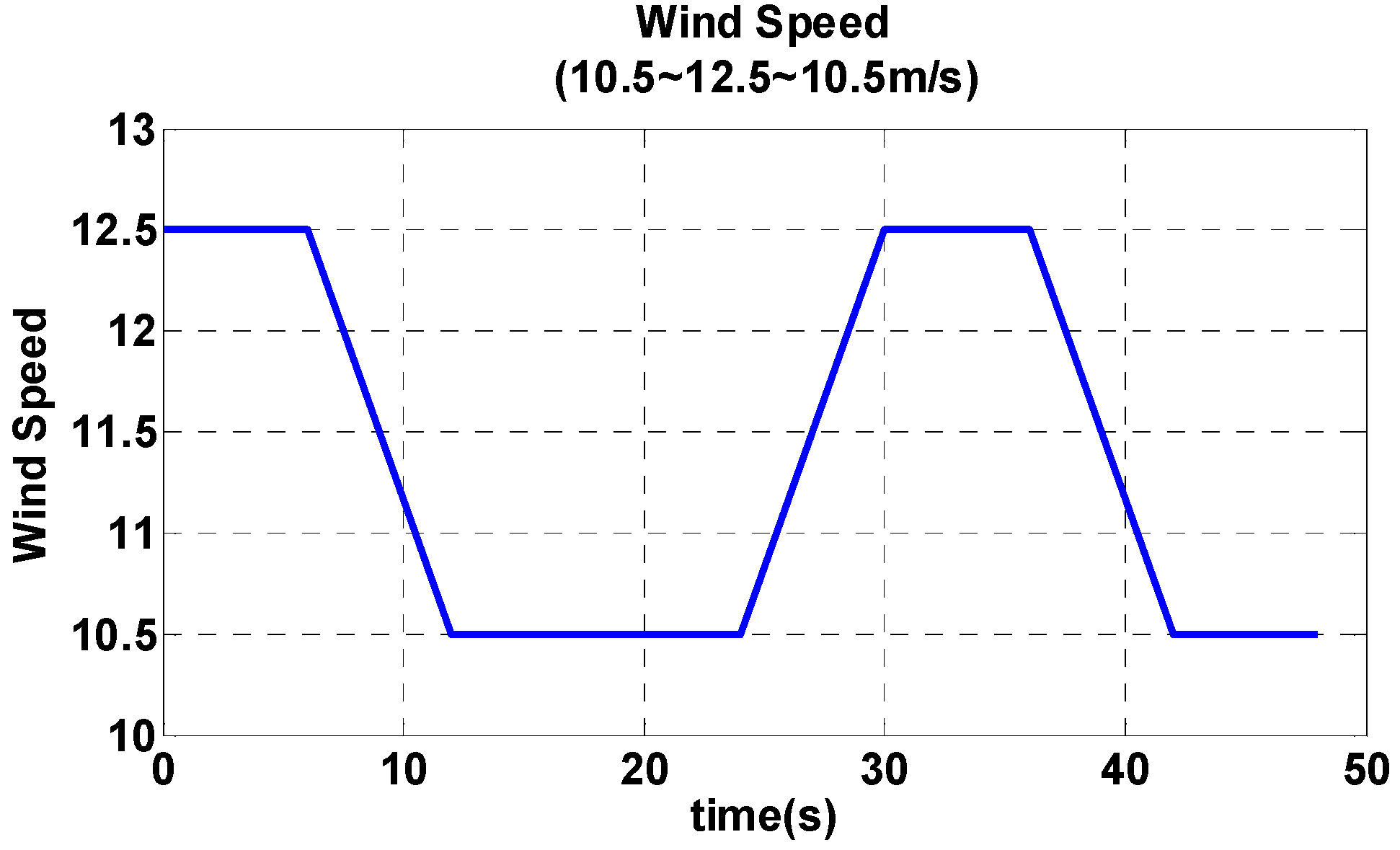
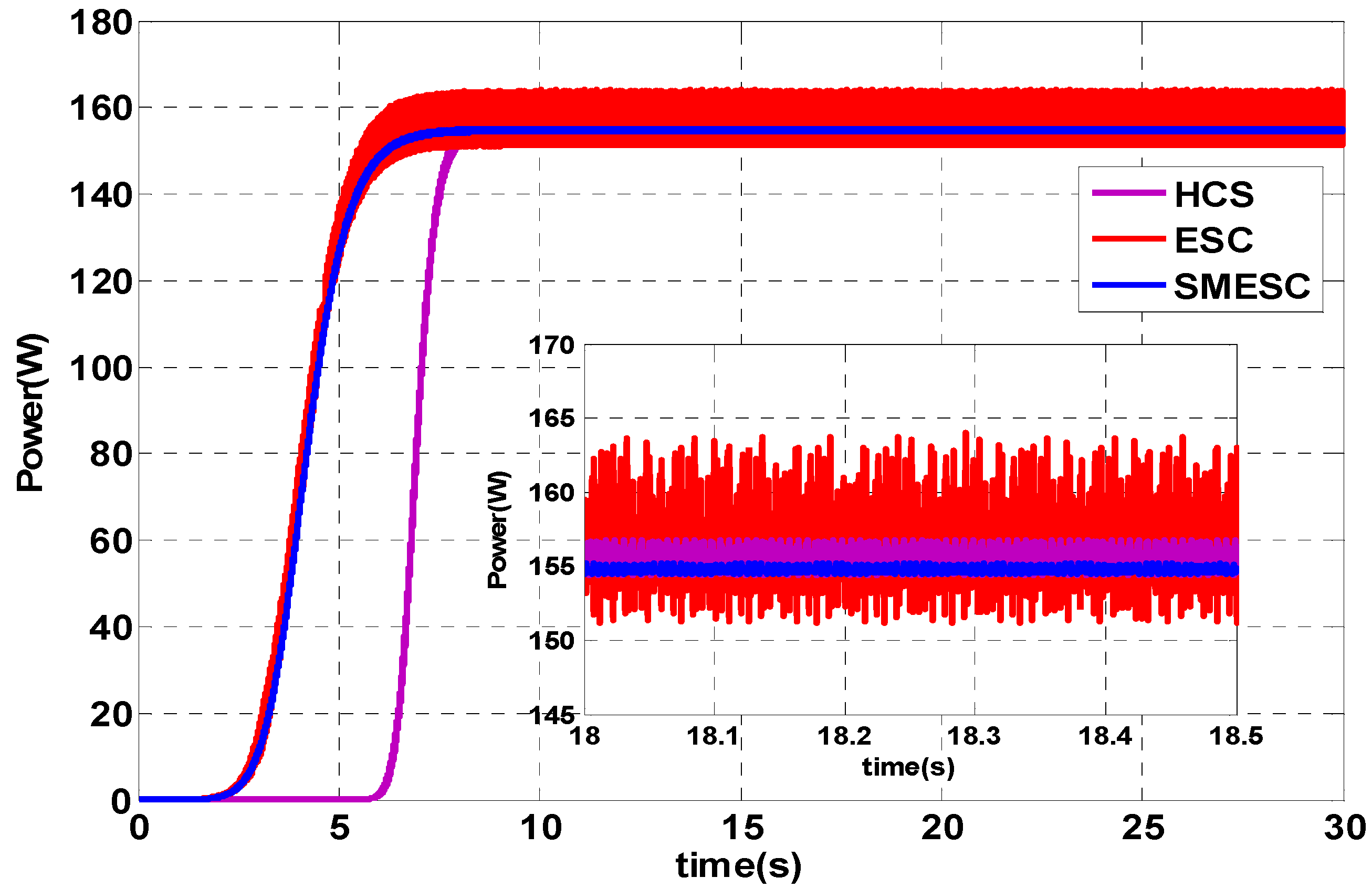
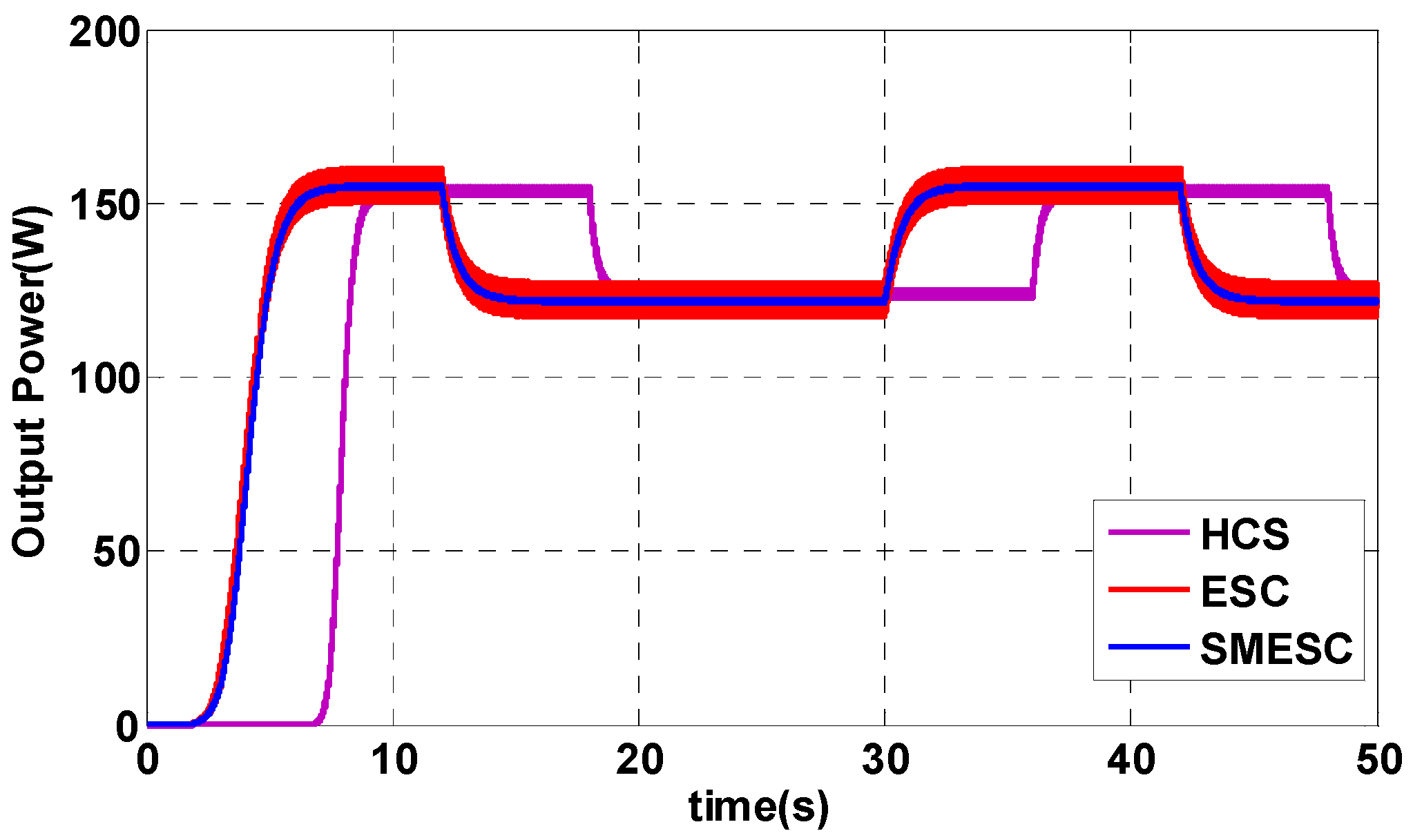
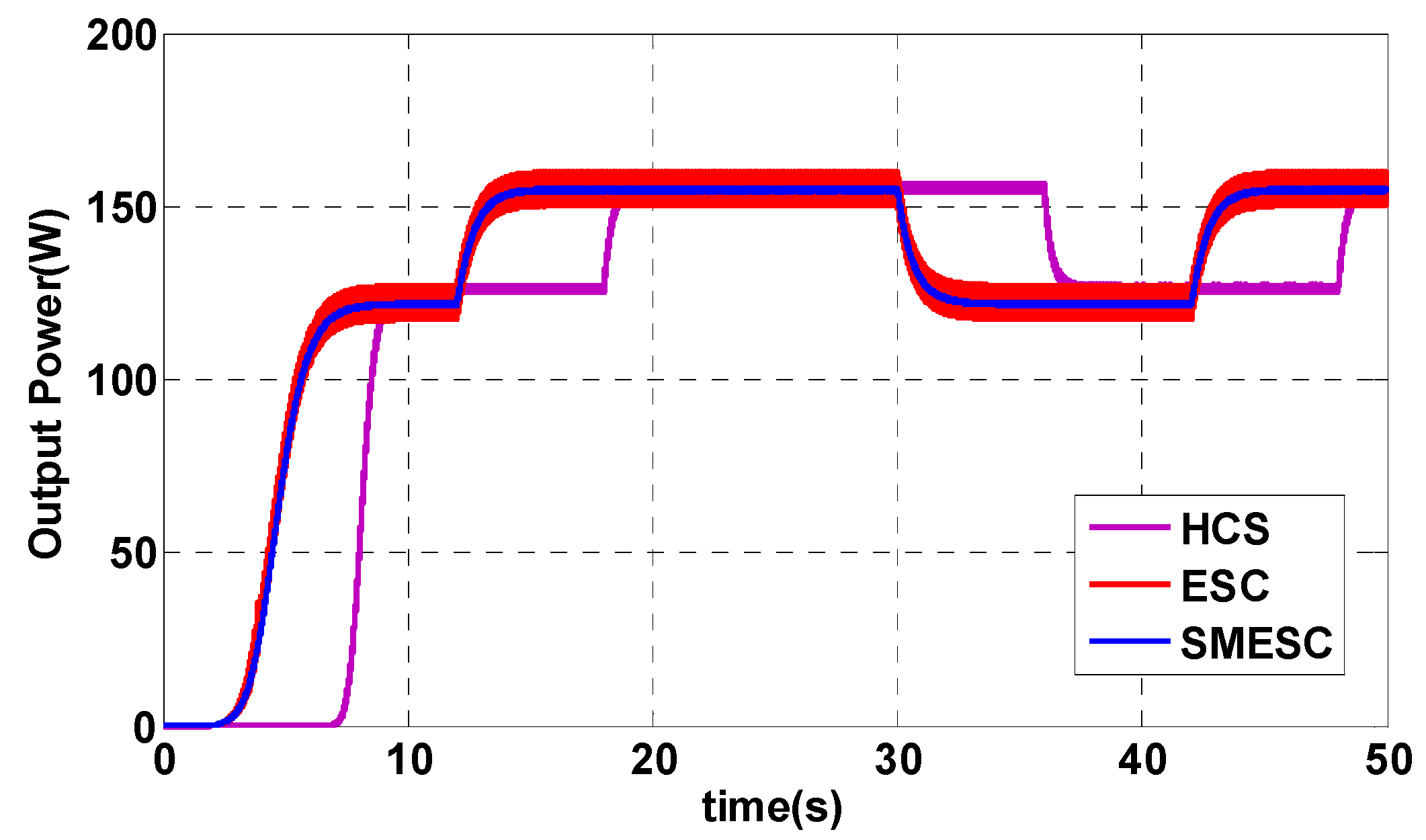
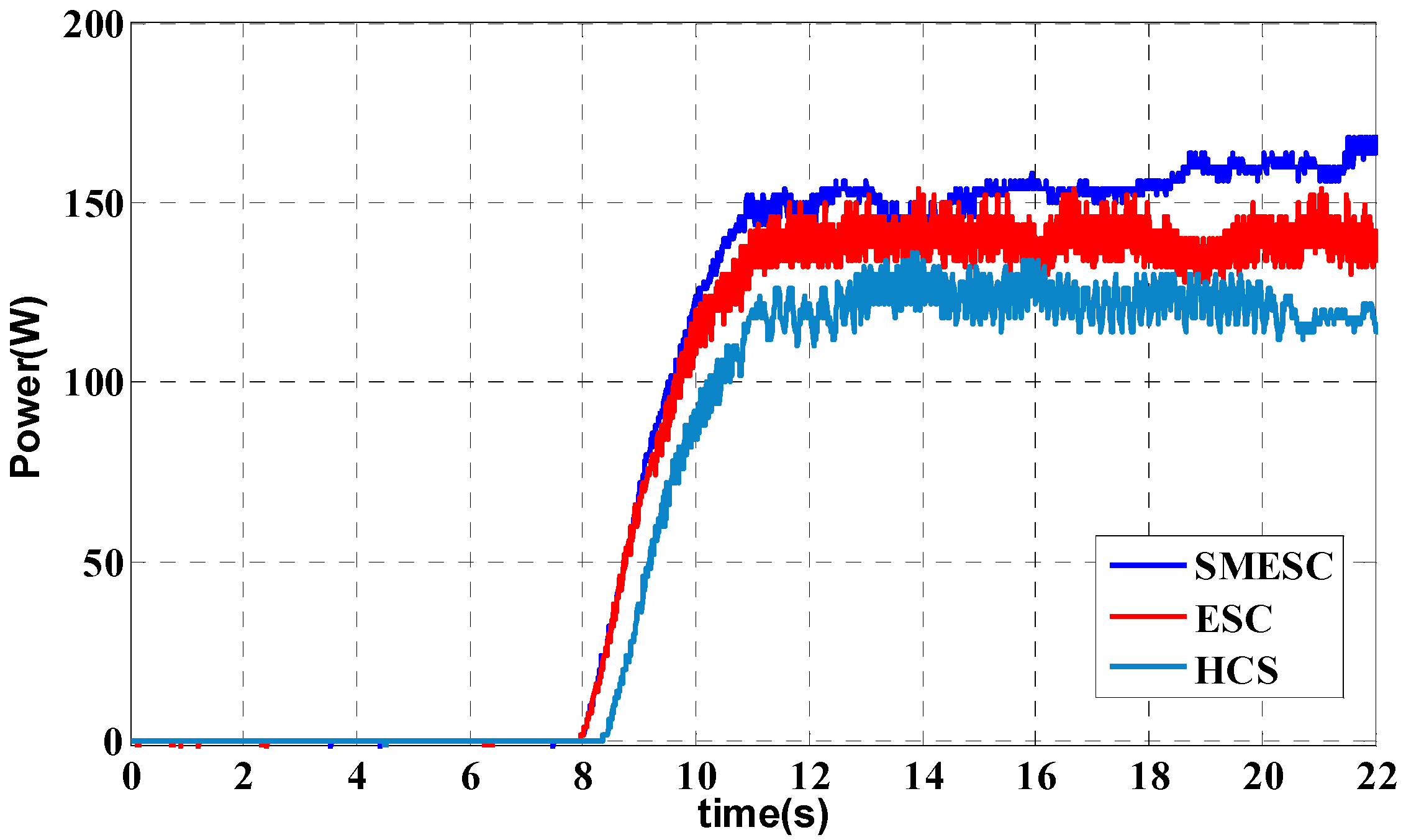
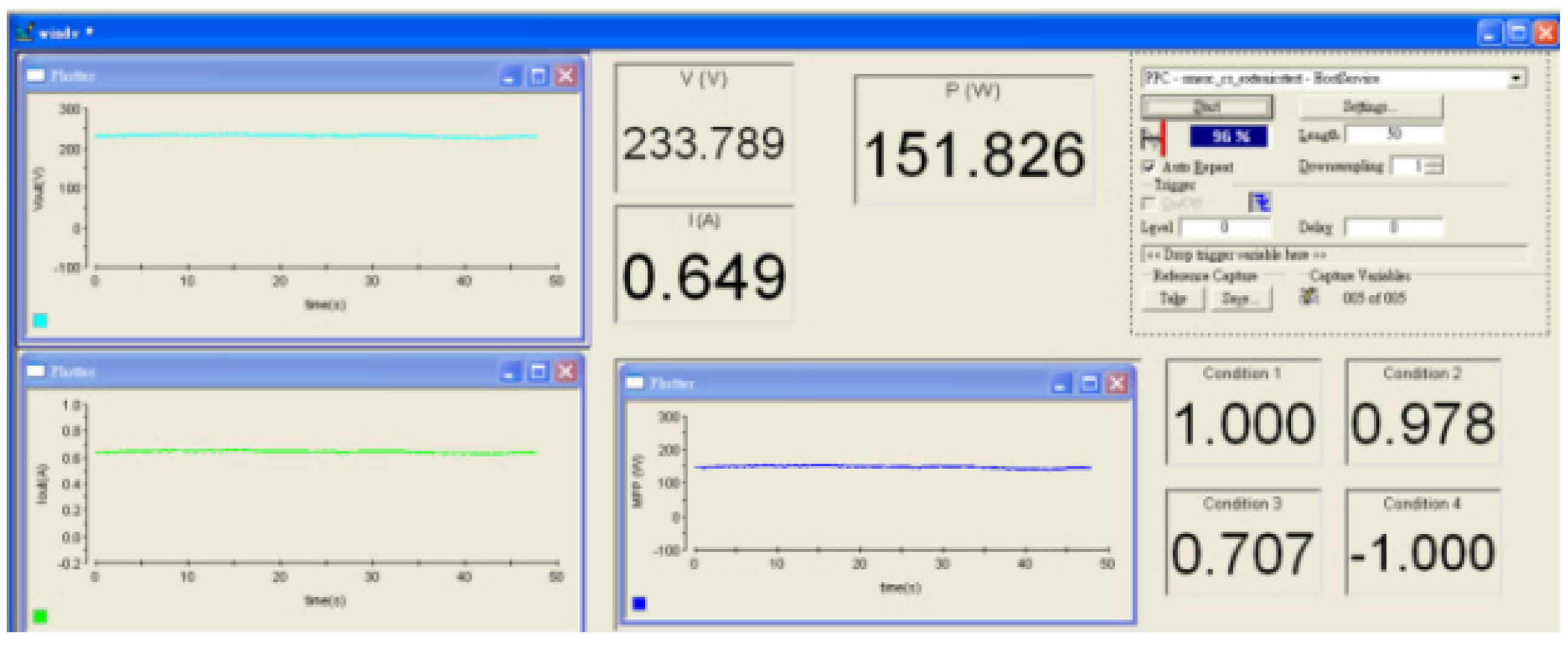
4.2. Maximum Power Point Tracking Algorithm Experimental Results
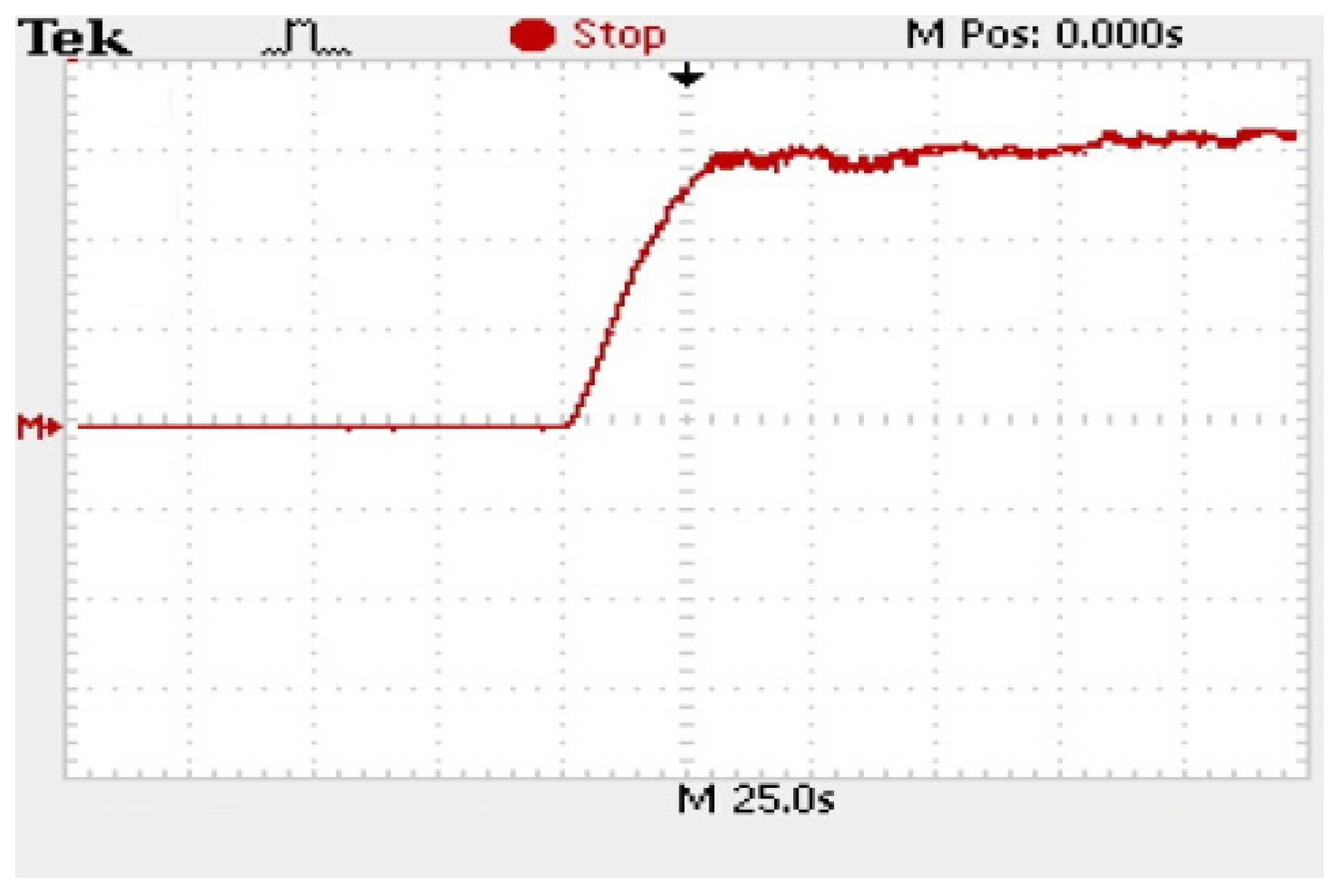
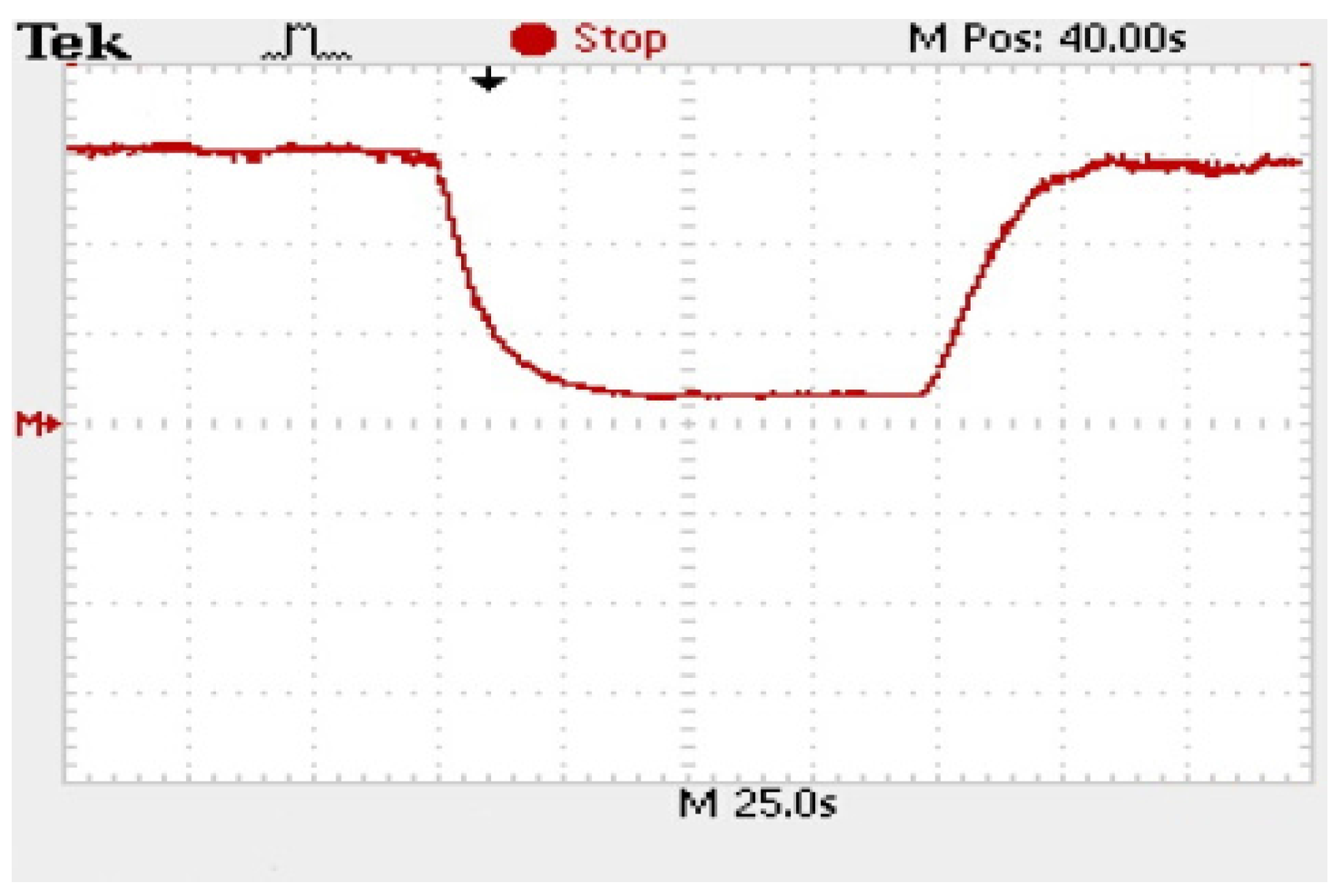
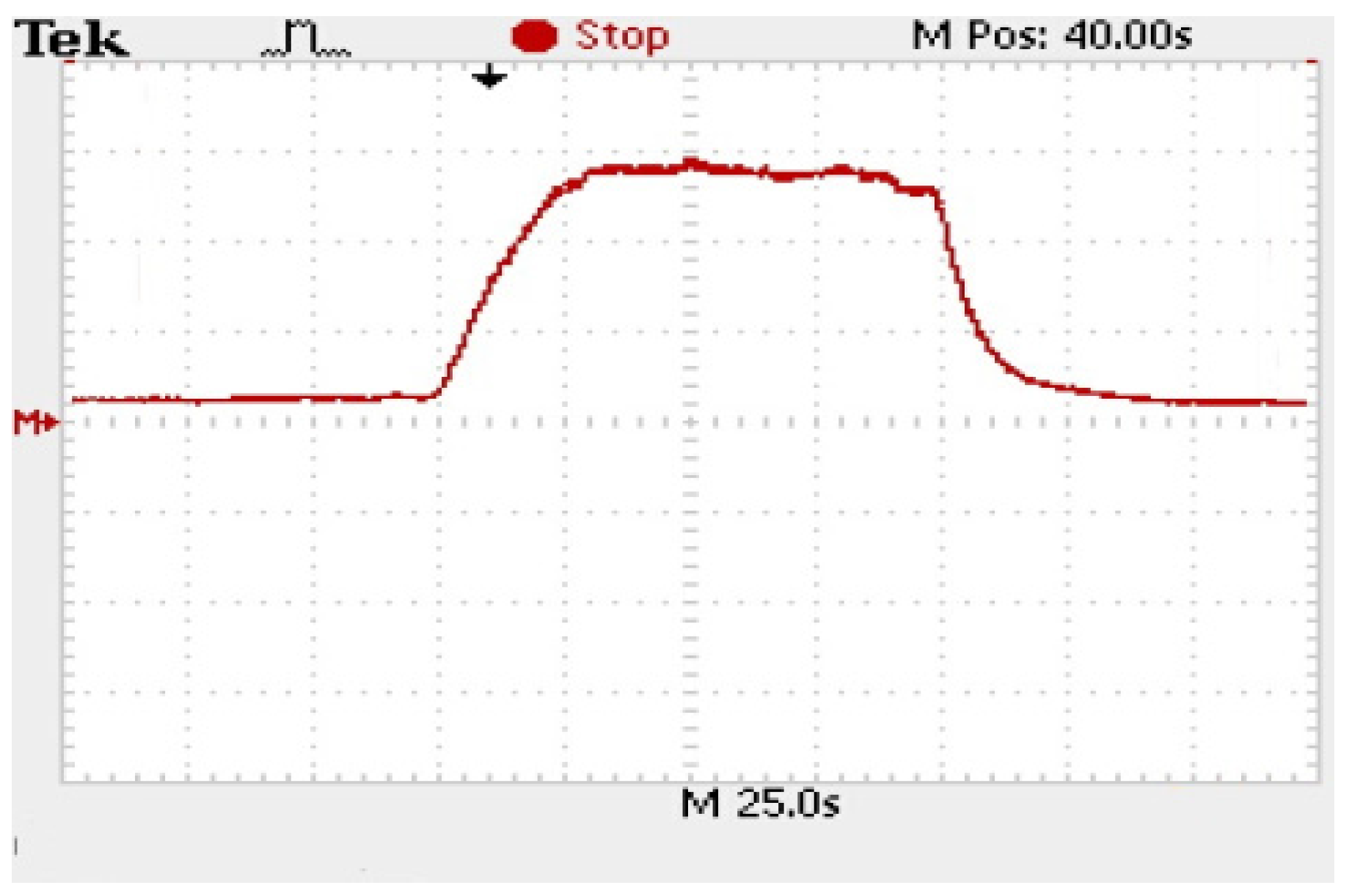
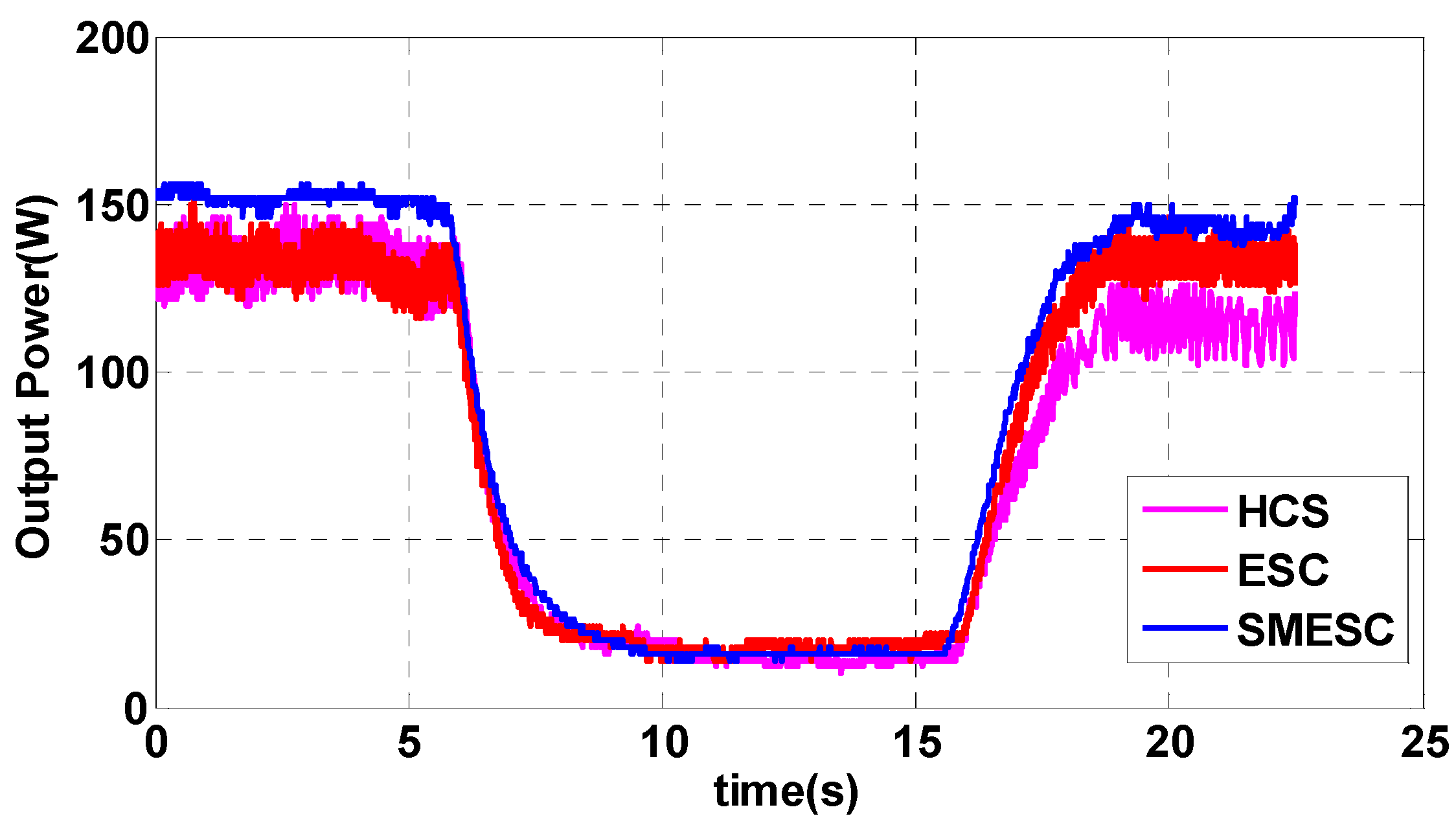
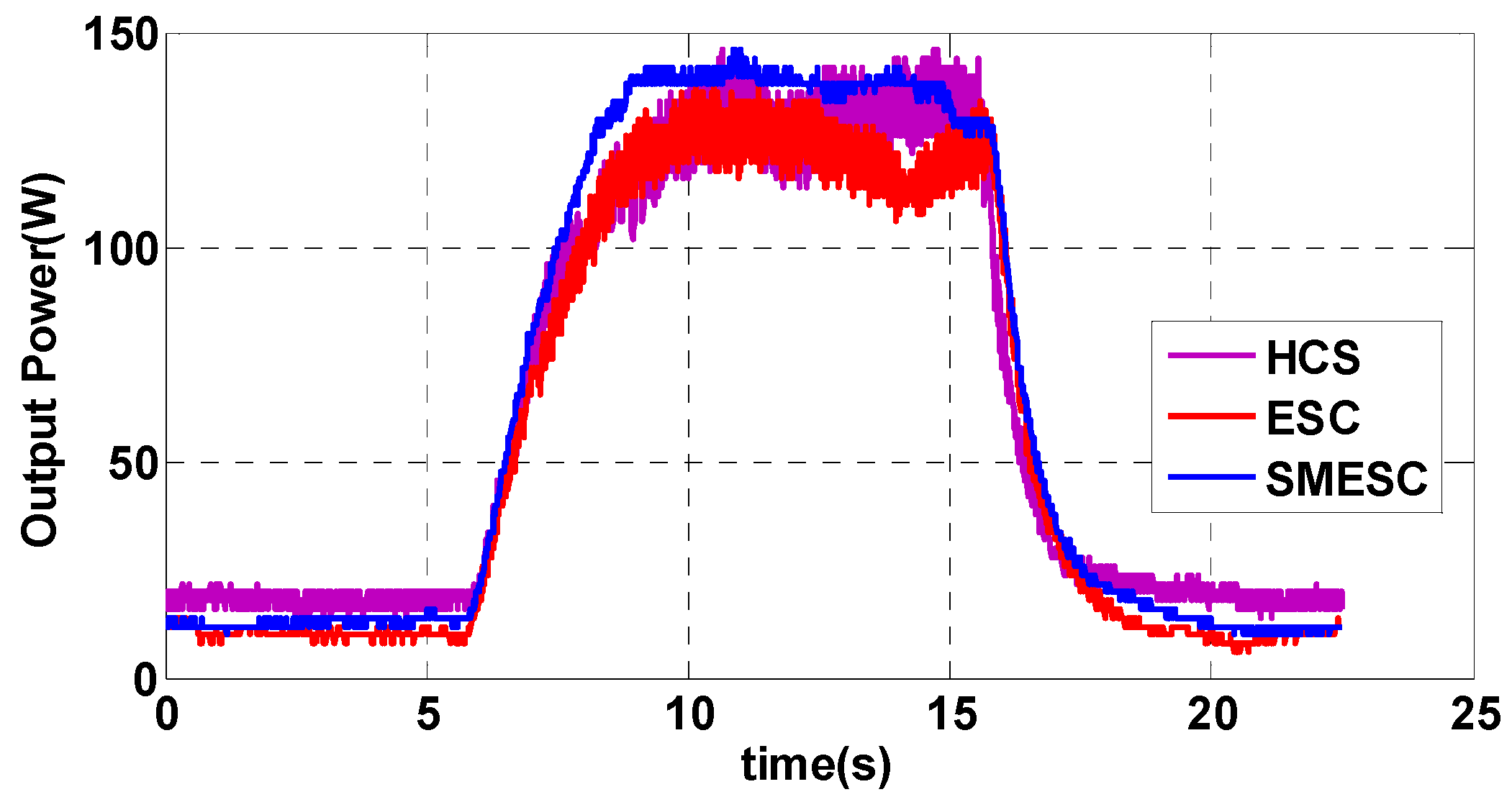
5. Results of Wind Turbine Blade Failure Diagnosis Experiments




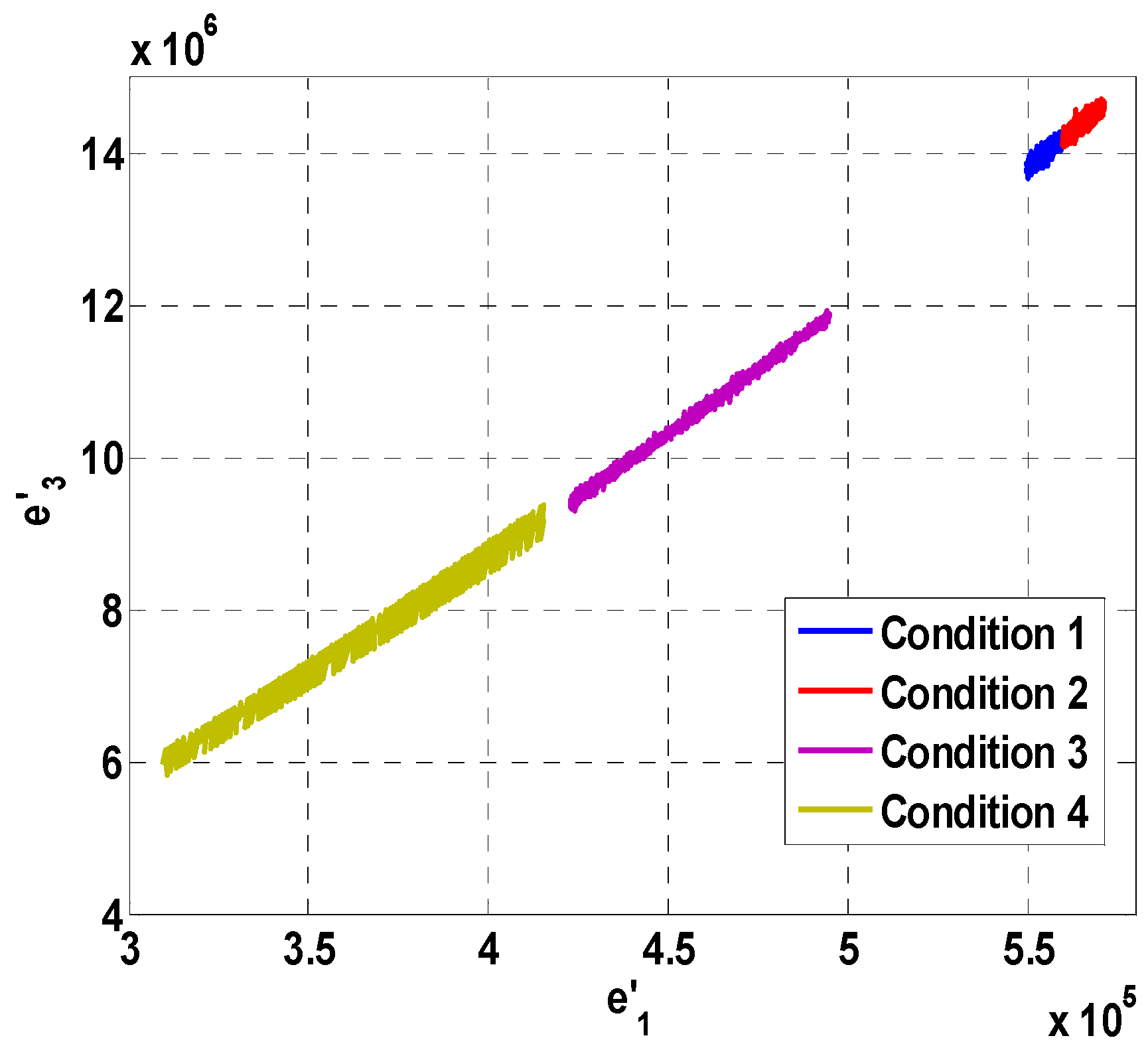
| Condition | C1 | C2 | C3 | C4 | |
|---|---|---|---|---|---|
| Signal numbers | |||||
| Condition1 | |||||
| 1 | 1 | 0.98676 | 0.59245 | −1 | |
| 2 | 1 | 0.985111 | 0.592729 | −1 | |
| 3 | 1 | 0.98372 | 0.592967 | −1 | |
| 4 | 1 | 0.984161 | 0.592891 | −1 | |
| 5 | 1 | 0.983625 | 0.592984 | −1 | |
| 6 | 1 | 0.982328 | 0.593209 | −1 | |
| 7 | 1 | 0.982904 | 0.593108 | −1 | |
| 8 | 1 | 0.980169 | 0.593588 | −1 | |
| 9 | 1 | 0.980077 | 0.593604 | −1 | |
| 10 | 1 | 0.977612 | 0.594046 | −1 | |
| Condition2 | |||||
| 1 | 0.900813 | 1 | 0.555983 | −1 | |
| 2 | 0.898779 | 1 | 0.555519 | −1 | |
| 3 | 0.90093 | 1 | 0.556009 | −1 | |
| 4 | 0.900092 | 1 | 0.555819 | −1 | |
| 5 | 0.900311 | 1 | 0.555868 | −1 | |
| 6 | 0.901339 | 1 | 0.556102 | −1 | |
| 7 | 0.899435 | 1 | 0.555669 | −1 | |
| 8 | 0.899246 | 1 | 0.555626 | −1 | |
| 9 | 0.90148 | 1 | 0.556135 | −1 | |
| 10 | 0.901216 | 1 | 0.556074 | −1 | |
| Condition 3 | |||||
| 1 | −0.96023 | −1 | 1 | 0.646727 | |
| 2 | −0.96028 | −1 | 1 | 0.713212 | |
| 3 | −0.96028 | −1 | 1 | 0.709737 | |
| 4 | −0.96022 | −1 | 1 | 0.670173 | |
| 5 | −0.96026 | −1 | 1 | 0.716586 | |
| 6 | −0.9602 | −1 | 1 | 0.663943 | |
| 7 | −0.96024 | −1 | 1 | 0.681759 | |
| 8 | −0.9602 | −1 | 1 | 0.650732 | |
| 9 | −0.96025 | −1 | 1 | 0.708213 | |
| 10 | −0.96019 | −1 | 1 | 0.668025 | |
| Condition 4 | |||||
| 1 | −0.96471 | −1 | 0.819589 | 1 | |
| 2 | −0.96471 | −1 | 0.819589 | 1 | |
| 3 | −0.96471 | −1 | 0.819589 | 1 | |
| 4 | −0.96471 | −1 | 0.819589 | 1 | |
| 5 | −0.96471 | −1 | 0.819589 | 1 | |
| 6 | −0.96471 | −1 | 0.819589 | 1 | |
| 7 | −0.96471 | −1 | 0.819589 | 1 | |
| 8 | −0.96471 | −1 | 0.819589 | 1 | |
| 9 | −0.96471 | −1 | 0.819589 | 1 | |
| 10 | −0.96471 | −1 | 0.819589 | 1 | |
| Signals | Non-real-time status diagnostic results | Status diagnosis rate |
|---|---|---|
| 500 500 | Normal | 100% 100% |
| 500 500 | Loose bolt on blade hub | 98.86% 98.86% |
| 500 500 | A block attached near the tip of the blade | 99.91% 99.91 |
| 500 500 | A mass hanging from the blade | 99.86% 99.86% |
| Signals | Real-time status diagnostic results | Status diagnosis rate |
| 500 500 | Normal | 100% 100% |
| 500 500 | Loose bolt on blade hub | 98.34% 98.34% |
| 500 500 | A block attached near the tip of the blade | 98.69% 98.69% |
| 500 500 | A mass hanging from the blade | 98.58% 98.58% |
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Femia, N.; Petrone, G.; Spagnuolo, G.; Vitelli, M. Optimizing duty-cycle perturbation of P&O MPPT technique. In Proceedings of the 35th IEEE Annual Power Electronics Specialists Conference (PESC), Aachen, Germany, 20–25 June 2004; pp. 1939–1944.
- Mahdi, A.J.; Tang, W.H.; Wu, Q.H. Estimation of tip speed ratio using an adaptive perturbation and observation method for wind turbine generator systems. In Proceedings of the IET Conference on Renewable Power Generation (RPG 2011), Edinburgh, UK, 6–8 September 2011; pp. 1–6.
- Mahdi, A.J.; Tang, W.H.; Wu, Q.H. Novel perturbation and observation algorithms for variable-speed wind turbine generator systems. In Proceedings of the IEEE Power and Energy Society General Meeting, San Diego, CA, USA, 22–26 July 2012; pp. 1–8.
- Raza Kazmi, S.M.; Goto, H.; Guo, H.J.; Ichinokura, O. A novel algorithm for fast and efficient speed-sensorless maximum power point tracking in wind energy conversion systems. IEEE Trans. Ind. Electron. 2010, 58, 29–36. [Google Scholar] [CrossRef]
- Yamakura, S.; Kesamaru, K. Dynamic simulation of PMSG small wind turbine generation system with HCS-MPPT control. In Proceedings of the 15th International Conference Electrical Machines and Systems (ICEMS), Sapporo, Japan, 21–24 October 2012; pp. 1–4.
- Tatsuta, F.; Suzuki, K.; Nishikata, S. A new control method to realize constant tip speed ratios of series connected wind turbine generators. In Proceedings of the 2013 International Conference Clean Electrical Power (ICCEP), Alghero, Italy, 11–13 June 2013; pp. 434–439.
- Yokoyama, H.; Tatsuta, F.; Nishikata, S. Tip speed ratio control of wind turbine generating system connected in series. In Proceedings of the 2011 International Conference Electrical Machines and Systems (ICEMS), Beijing, China, 20–23 August 2011; pp. 1–4.
- Zou, Y.; Elbuluk, M.; Sozer, Y. Stability analysis of maximum power point tracking (MPPT) method in wind power systems. In Proceedings of the 2011 IEEE Industry Applications Society Annual Meeting (IAS), Orlando, FL, USA, 9–13 October 2011; pp. 1–8.
- Koutroulis, E.; Kalaitzakis, K. Design of a maximum power tracking system for wind-energy-conversion applications. IEEE Trans. Ind. Electron. 2006, 53, 486–494. [Google Scholar] [CrossRef]
- Dalala, Z.M.; Zahid, Z.U.; Yu, W.; Cho, Y.; Lai, J.S. Design and analysis of an MPPT technique for small-scale wind energy conversion systems. IEEE Trans. Energy Convers. 2013, 28, 756–767. [Google Scholar] [CrossRef]
- Yau, H.T.; Lin, C.J.; Wu, C.H. Sliding Mode Extremum Seeking Control Scheme Based on PSO for Maximum Power Point Tracking in Photovoltaic Systems. Int. J. Photoenergy 2013, 2013, 1–10. [Google Scholar] [CrossRef]
- Li, X.; Chen, G.; Chen, Z.; Yuan, Z. Chaotifying linear Elman networks. IEEE Trans. Neural Netw. 2002, 13, 1193–1199. [Google Scholar] [PubMed]
- Chen, C.; Sun, C.; Zhang, Y.; Wang, N. Fault diagnosis for large-scale wind turbine rolling bearing using stress wave and wavelet analysis. In Proceedings of the Eighth International Conference Electrical Machines and Systems (ICEMS), Nanjing, China, 27–29 September 2005; pp. 2239–2244.
- Li, Y.; Li, G.; Yan, J. Fault diagnosis of wind turbine blades based on fuzzy theory. In Proceedings of the 2011 International Conference Control, Automation and Systems Engineering (CASE), Singapore, 30–31 July 2011; pp. 1–3.
- Wang, Z. Study on Condition Monitoring and Fault Diagnosis for Wind Turbine Blades; Department of Mechanical and Electronic Engineering, Tianjin University: Tianjin, China, 2010. [Google Scholar]
- Esteller, R.; Vachtsevanos, G.; Echauz, J.; Litt, B. A comparison of waveform fractal dimension algorithms. IEEE Trans. Circ. Syst. I Fundam. Theory Appl. 2001, 48, 177–183. [Google Scholar] [CrossRef]
- Mei, Y.; Xu, Y.; Wang, Z. Detection and damage diagnosis for wind turbine blades based on the theory of length fractal dimension on dynamic properties. In Proceedings of the 2010 International Conference Measuring Technology and Mechatronics Automation (ICMTMA), Changsha, China, 13–14 March 2010; pp. 1089–1092.
- Taso, T.F.; Kuo, C.C. Application of the Hilbert-Huang transform with fractal feature enhancement for failure types classification of wind turbines. In Proceedings of the 2012 International Conference Computer Distributed Control and Intelligent Environmental Monitoring (CDCIEM), Hunan, China, 5–6 March 2012; pp. 149–152.
- Pang, M.; Zhou, X.; Yang, C. Fault diagnosis of automobile main reducer based on correlation dimension. In Proceedings of the International Technology and Innovation Conference (ITIC), Hangzhou, China, 6–7 November 2006; pp. 1975–1979.
- Yang, G.; Liu, Y.; Zhao, L.; Cui, S. Typical power quality disturbance identification based on fractal box dimension. In Proceedings of the Chaos-Fractals Theories and Applications (IWCFTA) International Workshop, Shenyang, China, 6–8 November 2009; pp. 412–416.
- Chen, S.J.; Zhan, T.S.; Huang, C.H.; Chen, J.L.; Lin, C.H. Nontechnical loss and outage detection using fractional-order self-synchronization error-based fuzzy petri nets in micro-distribution systems. IEEE Trans. Smart Grid 2014, 6, 411–420. [Google Scholar] [CrossRef]
- Johnson, K.E.; Fleming, P.A. Development, implementation, and testing of fault detection strategies on the National Wind Technology Center’s controls advanced research turbines. Mechatronics 2011, 21, 728–736. [Google Scholar] [CrossRef]
- Odgaard, P.F.; Stoustrup, J.; Kinnaert, M. Fault-tolerant control of wind turbines: A benchmark model. IEEE Trans Control Syst. Technol. 2013, 21, 1168–1182. [Google Scholar] [CrossRef]
- Odgaard, P.F.; Stoustrup, J. Fault tolerant wind farm control—A benchmark model. In Proceedings of the 2013 IEEE International Conference on Control Applications (CCA), Hyderabad, India, 28–30 August 2013; pp. 412–417.
- Odgaard, P.F.; Johnson, K.E. Wind turbine fault detection and fault tolerant control—An enhanced benchmark challenge. In Proceedings of the American Control Conference (ACC), Washington, DC, USA, 17–19 June 2013; pp. 4447–4452.
- Johnson, K.E.; Pao, L.Y.; Balas, M.J.; Fingersh, L.J. Control of variable-speed wind turbines: Standard and adaptive techniques for maximizing energy capture. Control Syst. 2006, 26, 70–81. [Google Scholar] [CrossRef]
- Sloth, C.; Esbensen, T.; Stoustrup, J. Active and passive fault-tolerant LPV control of wind turbines. In Proceedings of the American Control Conference (ACC), Baltimore, MD, USA, 30 June–2 July 2010; pp. 4640–4646.
- Sami, M.P.; Ron, J. An FTC approach to wind turbine power maximisation via T–S fuzzy modelling and control. In Proceedings of the 8th IFAC Symposium on Fault Detection, Supervision and Safety of Technical Processes, National Autonomous University of Mexico, Mexico City, Mexico, 29–31 August 2012; pp. 349–354.
- Puig, V. Fault diagnosis and fault tolerant control using set-membership approaches: Application to real case studies. Int. J. Appl. Math. Comput. Sci. 2010, 20, 619–635. [Google Scholar] [CrossRef] [Green Version]
- Mickael, R.; Didier, T.; Samir, A.; Dominique, S. Fault Tolerant Control design for polytopic LPV systems. Int. J. Appl. Math. Comput. Sci. 2007, 17, 27–37. [Google Scholar]
- Niemann, H.; Stoustrup, J. An architecture for fault tolerant controllers. Int. J. Control 2005, 78, 1091–1110. [Google Scholar] [CrossRef]
- Chen, Z.; Patton, R.; Chen, J. Robust fault-tolerant system synthesis via LMI. In Proceedings of the 3rd IFAC Symposium on Fault Detection, Supervision and Safety for Technical Processes 1997 (SAFEPROCESS 97), Kingston-upon-Hull, UK, 26–28 August 1997; pp. 347–352.
- Chen, J.H.; Yau, H.T.; Hung, W. Design and study on sliding mode extremum seeking control of the chaos embedded particle swarm optimization for maximum power point tracking in wind power systems. Energies Wind Turbine 2014, 7, 1706–1720. [Google Scholar] [CrossRef]
- Chen, J.H.; Yau, H.T.; Hung, T.H. Design and implementation of FPGA-based intelligent sunlight tracking system. Mechatronics 2015, 25, 55–64. [Google Scholar] [CrossRef]
- Kuo, Y.-C.; Hsieh, C.-T.; Yau, H.-T.; Li, Y.-C. Research and development of a chaotic signal synchronization error dynamics-based ball bearing fault diagnostor. Entropy 2014, 16, 5358–5376. [Google Scholar] [CrossRef]
- Wang, M.H.; Ho, C.Y. Application of extension theory to the fault diagnosis of power transformers. In Proceeding of the 22nd Symposium on Electrical Power Engineering, Kaohsiung, Taiwan, 26 November 2001.
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, J.-H.; Hung, W. Blade Fault Diagnosis in Small Wind Power Systems Using MPPT with Optimized Control Parameters. Energies 2015, 8, 9191-9210. https://doi.org/10.3390/en8099191
Chen J-H, Hung W. Blade Fault Diagnosis in Small Wind Power Systems Using MPPT with Optimized Control Parameters. Energies. 2015; 8(9):9191-9210. https://doi.org/10.3390/en8099191
Chicago/Turabian StyleChen, Jui-Ho, and Weir Hung. 2015. "Blade Fault Diagnosis in Small Wind Power Systems Using MPPT with Optimized Control Parameters" Energies 8, no. 9: 9191-9210. https://doi.org/10.3390/en8099191
APA StyleChen, J.-H., & Hung, W. (2015). Blade Fault Diagnosis in Small Wind Power Systems Using MPPT with Optimized Control Parameters. Energies, 8(9), 9191-9210. https://doi.org/10.3390/en8099191





