Optimal Energy Reduction Schedules for Ice Storage Air-Conditioning Systems
Abstract
:1. Introduction
2. Problem Formulation
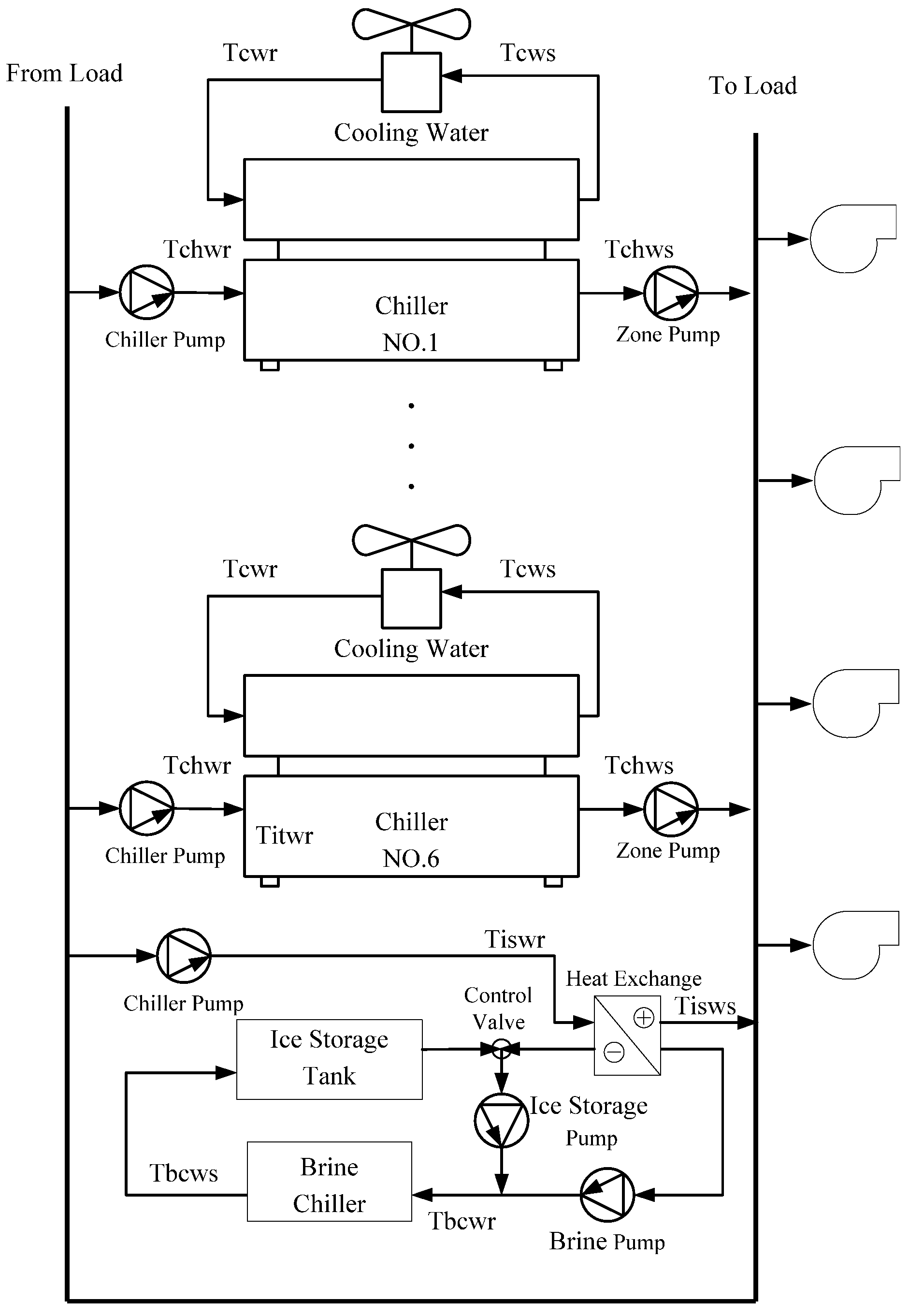
2.1. The Cooling Load Capacity of Chillers
- : the cooling load of chillers (kJ/hr);
- : the flow rate of chilled water (liter/hr);
- : the density of chilled water (1 kg/L);
- : the specific heat of water at average temperature (4.186kJ/kg-°C).
- is the temperature difference of chilled water (°C), which is defined as Equation (2):
- : the return temperature of chilled water (°C);
- : the supply temperature of chilled water (°C).
2.2. The Cooling Load Capacity of the Ice Storage Tank
- : the temperature difference of ice storage brine (°C);
- : the specific heat of ice storage brine at average temperature (3.6 kJ/kg-°C);
- : the return temperature of ice storage brine (°C);
- : the supply temperature of ice storage brine (°C);
- : the flow rate of ice storage brine (L/h);
- : cooling load capacity of the ice storage tank (kJ/h).
2.3. Power Consumption of Cooling Towers and Pumps
2.4. Power Consumption of Chillers and Ice Storage Tanks
2.5. Objective Function and Constraints
- : the power consumption of the i-th chiller at time t;
- : the power consumption of the i-th cooling tower at time t;
- : the power consumption of pump at time t;
- : the i-th unit on/off at time t, 1 is on and 0 is off;
- : power consumption of the ice storage at time t (kW);
- : the scheduling time;
- : the total number of chillers;
- : the total number of ice storage tanks.
3. The Proposed Methodology
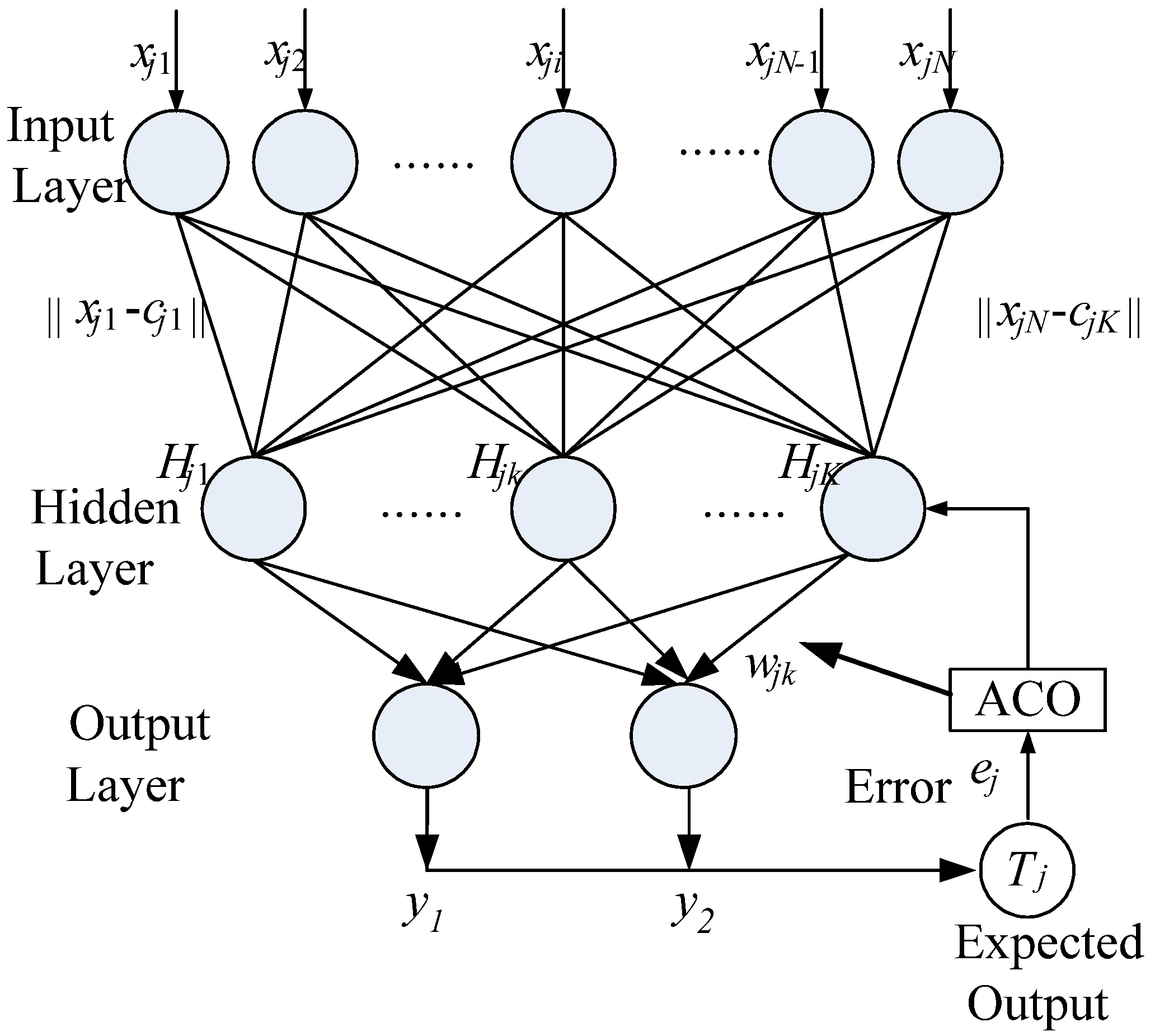
3.1. Input Layer
3.2. Hidden Layer
3.3. Output Layer
- 1)
- Calculate Euclidean distance ║xji ﹣cjk║;
- 2)
- Calculate hidden layer output Hjk by Equation (15);
- 3)
- Calculate output layer output by Equation (17);
- 4)
- Calculate the error between simulation output yj and its expected value Tj by error function. In this paper, the fitness function is set to an error function which is defined as Equation (18):
3.4. Ant Colony Optimization (ACO) Process

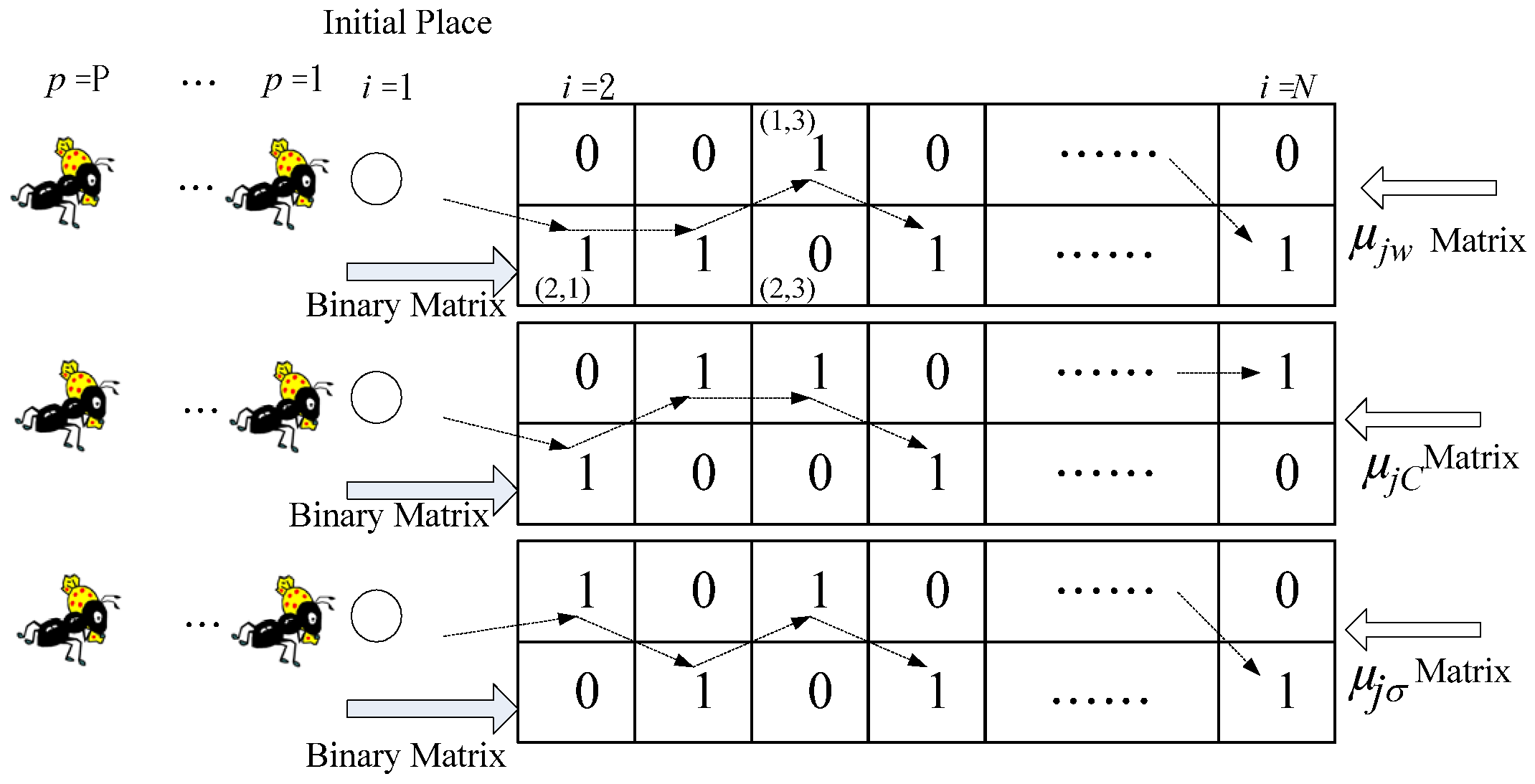
3.5. Implementation of ARBFN
4. Case Study
| Unit | a | b | c | d |
|---|---|---|---|---|
| 65.7772 | 0.1961 | 1.3707E-08 | 1.249E-09 | |
| 128.7969 | 0.0449 | 1.139E-04 | −2.628E-08 | |
| 68.2033 | 0.1418 | 4.13921E-05 | −7.599E-09 | |
| 107.7250 | 0.1181 | 1.87115E-05 | −1.467E-09 | |
| 623.2087 | −0.4555 | 0.000228205 | −2.660E-08 | |
| 101.5365 | 0.0851 | 6.87455E-05 | −1.141E-08 | |
| Charging Process Pice | 2204.5246 | −24.3534 | 9.252E-02 | −1.022E-04 |
| Discharging Process Pice | −21.7173 | 0.2206 | 5.533E-05 | −1.591E-08 |
| Chiller NO1 | Max. | Min. | Chiller NO2 | Max. | Min. |
|---|---|---|---|---|---|
| PLR(%) | 100 | 50 | PLR(%) | 100 | 50 |
| 5 | 2.5 | 5 | 2.5 | ||
| 5 | 3 | 5 | 3 | ||
| Chiller NO3 | Max. | Min. | Chiller NO4 | Max. | Min. |
| PLR(%) | 100 | 50 | PLR(%) | 100 | 50 |
| 5 | 2.5 | 5 | 2.5 | ||
| 5 | 2 | 5 | 3.5 | ||
| Chiller NO5 | Max. | Min. | Chiller NO6 | Max. | Min. |
| PLR(%) | 100 | 50 | PLR(%) | 100 | 50 |
| 5 | 2.5 | 5 | 2.5 | ||
| 5 | 3.5 | 5 | 2 | ||
| Charge Process | Max. | Min. | Discharge Process | Max. | Min. |
| 3.9 | 1.9 | 11 | 5.6 | ||
| 4.2 | 2.6 | Control Valve(LPM) | 5109.1 | 3627 |
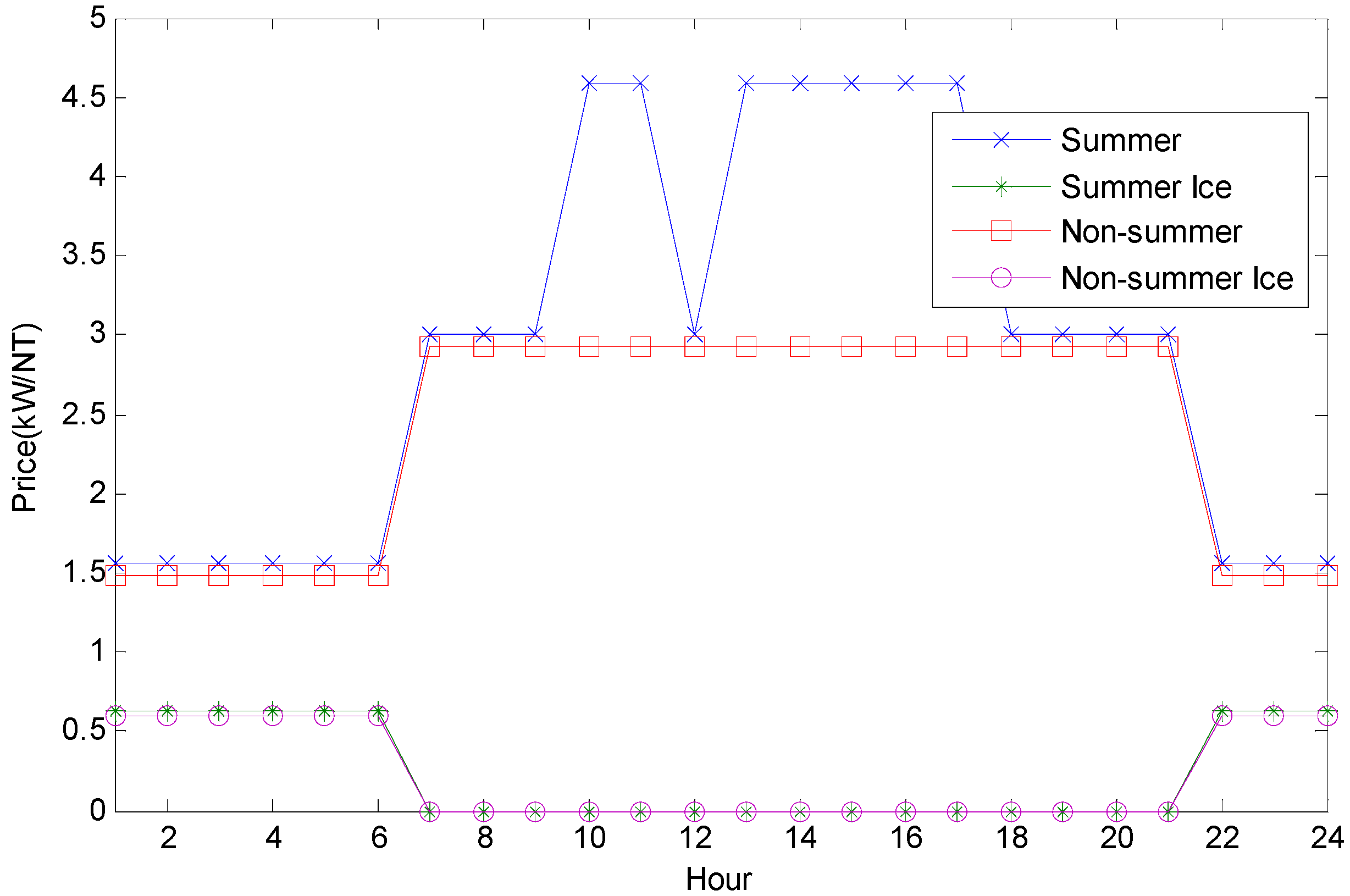
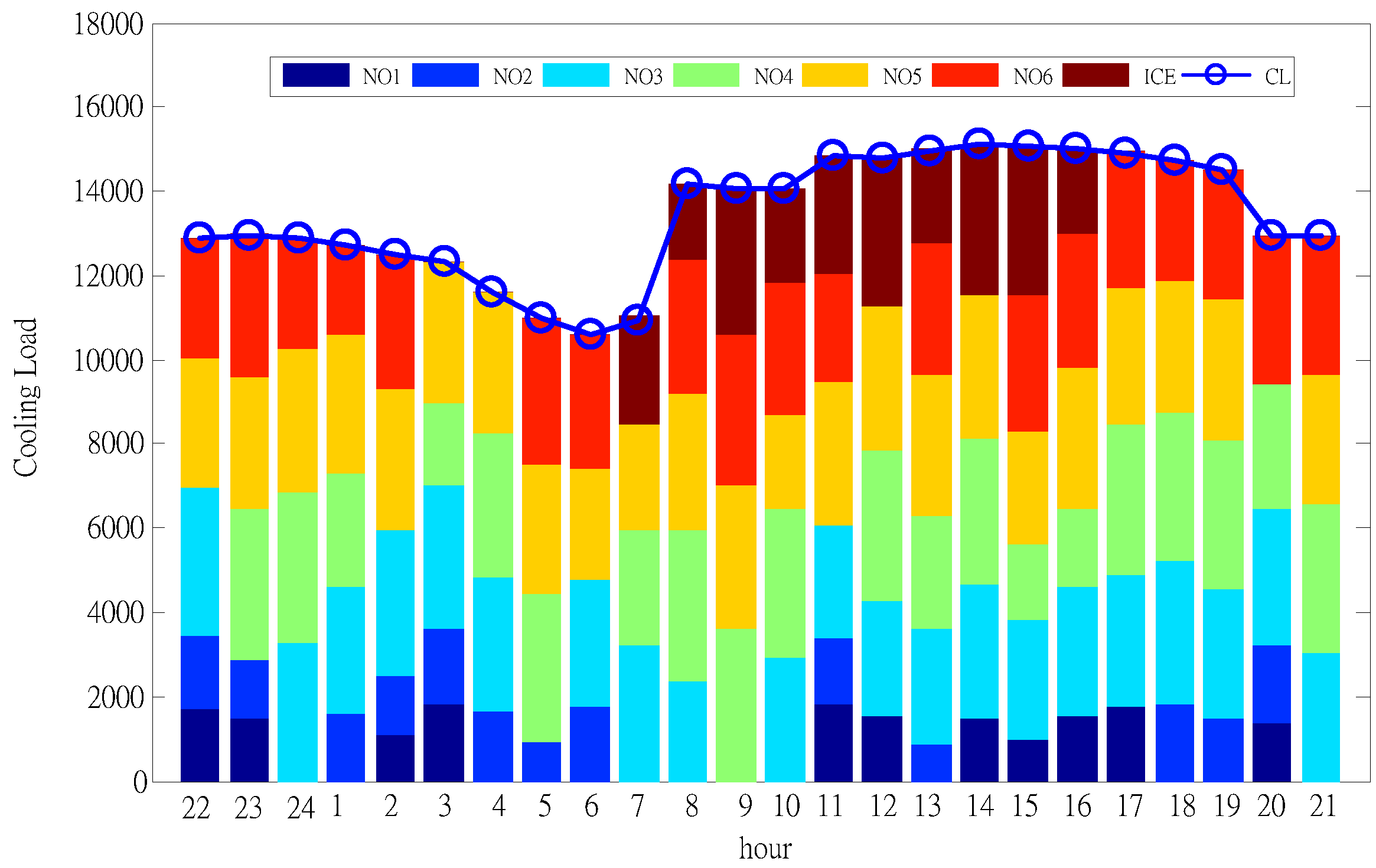
4.1. Results at Different TOU Intervals
| Hour | Chiller | ICE (%) | Power (kW) | Cost (NT$) | |||||
|---|---|---|---|---|---|---|---|---|---|
| NO1 | NO2 | NO3 | NO4 | NO5 | NO6 | ||||
| 22 | 1 | 1 | 1 | 0 | 1 | 1 | 7.10 | 3152.97 | 4620.07 |
| 23 | 1 | 1 | 0 | 1 | 1 | 1 | 14.64 | 3144.25 | 4593.52 |
| 24 | 0 | 0 | 1 | 1 | 1 | 1 | 22.78 | 3037.77 | 4409.24 |
| 1 | 0 | 1 | 1 | 1 | 1 | 1 | 31.42 | 3013.29 | 4353.75 |
| 2 | 1 | 1 | 1 | 0 | 1 | 1 | 40.64 | 3087.55 | 4452.04 |
| 3 | 1 | 1 | 1 | 1 | 1 | 0 | 49.18 | 3062.86 | 4424.93 |
| 4 | 0 | 1 | 1 | 1 | 1 | 0 | 58.17 | 2760.67 | 3948.25 |
| 5 | 0 | 1 | 0 | 1 | 1 | 1 | 65.85 | 2667.75 | 3836.68 |
| 6 | 0 | 1 | 1 | 0 | 1 | 1 | 73.39 | 2583.26 | 3716.21 |
| 7 | 0 | 0 | 1 | 1 | 1 | 0 | 65.87 | 1758.33 | 5292.58 |
| 8 | 0 | 0 | 1 | 1 | 1 | 1 | 60.12 | 2532.70 | 7623.44 |
| 9 | 0 | 0 | 0 | 1 | 1 | 1 | 51.25 | 2203.22 | 6631.69 |
| 10 | 0 | 0 | 1 | 1 | 1 | 1 | 44.73 | 2507.66 | 11510.18 |
| 11 | 1 | 1 | 1 | 0 | 1 | 1 | 37.33 | 2625.41 | 12050.61 |
| 12 | 1 | 0 | 1 | 1 | 1 | 0 | 27.98 | 2379.28 | 7161.63 |
| 13 | 0 | 1 | 1 | 1 | 1 | 1 | 20.87 | 2702.69 | 12405.37 |
| 14 | 1 | 0 | 1 | 1 | 1 | 0 | 11.50 | 2445.28 | 11223.84 |
| 15 | 1 | 0 | 1 | 1 | 1 | 1 | 1.94 | 2589.96 | 11887.91 |
| 16 | 1 | 0 | 1 | 1 | 1 | 1 | 0.00 | 2792.89 | 12819.35 |
| 17 | 1 | 0 | 1 | 1 | 1 | 1 | 0.00 | 3143.81 | 14430.08 |
| 18 | 0 | 1 | 1 | 1 | 1 | 1 | 0.00 | 3163.51 | 9522.18 |
| 19 | 0 | 1 | 1 | 1 | 1 | 1 | 0.00 | 3027.51 | 9112.82 |
| 20 | 1 | 1 | 1 | 1 | 0 | 1 | 0.00 | 2878.31 | 8663.70 |
| 21 | 0 | 0 | 1 | 1 | 1 | 1 | 0.00 | 2655.52 | 7993.12 |
| Total | 65916.46 | 186683.17 | |||||||
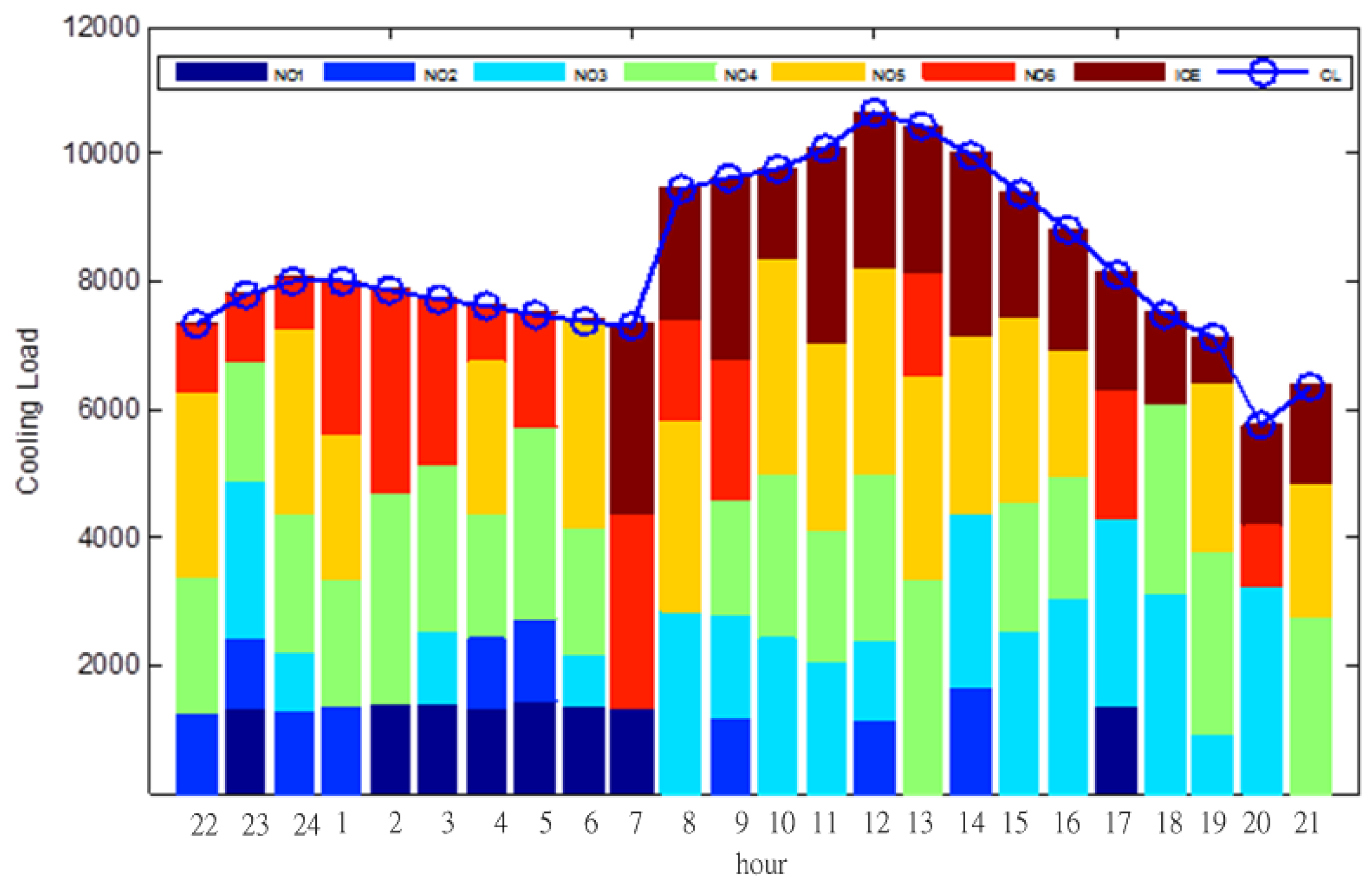
| Hour | Chiller | ICE (%) | Power (kW) | Cost (NT$) | |||||
|---|---|---|---|---|---|---|---|---|---|
| NO1 | NO2 | NO3 | NO4 | NO5 | NO6 | ||||
| 22 | 0 | 1 | 0 | 1 | 1 | 1 | 7.69 | 1885.10 | 2466.67 |
| 23 | 1 | 1 | 1 | 1 | 0 | 1 | 16.96 | 2139.77 | 2810.98 |
| 24 | 0 | 1 | 1 | 1 | 1 | 1 | 25.43 | 2098.53 | 2766.18 |
| 1 | 0 | 1 | 0 | 1 | 1 | 1 | 34.68 | 2103.68 | 2758.08 |
| 2 | 1 | 0 | 0 | 1 | 0 | 1 | 43.67 | 2042.69 | 2674.30 |
| 3 | 1 | 0 | 1 | 1 | 0 | 1 | 52.65 | 2057.44 | 2699.09 |
| 4 | 1 | 1 | 0 | 1 | 1 | 1 | 59.48 | 1995.04 | 2652.43 |
| 5 | 1 | 1 | 0 | 1 | 0 | 1 | 68.17 | 2015.33 | 2650.33 |
| 6 | 1 | 0 | 1 | 1 | 1 | 0 | 75.66 | 1895.39 | 2499.20 |
| 7 | 1 | 0 | 0 | 0 | 0 | 1 | 68.49 | 958.99 | 2809.83 |
| 8 | 0 | 0 | 1 | 0 | 1 | 1 | 63.45 | 1543.89 | 4523.59 |
| 9 | 0 | 1 | 1 | 1 | 0 | 1 | 56.55 | 1551.37 | 4545.51 |
| 10 | 0 | 0 | 1 | 1 | 1 | 0 | 51.93 | 1679.36 | 4920.53 |
| 11 | 0 | 0 | 1 | 1 | 1 | 0 | 44.31 | 1432.15 | 4196.20 |
| 12 | 0 | 1 | 1 | 1 | 1 | 0 | 38.00 | 1717.87 | 5033.35 |
| 13 | 0 | 0 | 0 | 1 | 1 | 1 | 32.19 | 1645.15 | 4820.30 |
| 14 | 0 | 1 | 1 | 0 | 1 | 0 | 24.92 | 1541.14 | 4515.53 |
| 15 | 0 | 0 | 1 | 1 | 1 | 0 | 19.39 | 1496.22 | 4383.93 |
| 16 | 0 | 0 | 1 | 1 | 1 | 0 | 14.88 | 1416.48 | 4150.27 |
| 17 | 1 | 0 | 1 | 0 | 0 | 1 | 10.52 | 1363.52 | 3995.11 |
| 18 | 0 | 0 | 1 | 1 | 0 | 0 | 7.12 | 1236.36 | 3622.52 |
| 19 | 0 | 0 | 1 | 1 | 1 | 0 | 5.66 | 1273.19 | 3730.45 |
| 20 | 0 | 0 | 1 | 0 | 0 | 1 | 1.96 | 926.44 | 2714.47 |
| 21 | 0 | 0 | 0 | 1 | 1 | 0 | 0.00 | 944.50 | 2767.38 |
| Total | 38959.58 | 84706.24 | |||||||
4.2. Energy Reduction Analysis
| Actual | ARBFN | Difference | Reduction (%) | LSR | Difference * | Reduction (%) | ||
|---|---|---|---|---|---|---|---|---|
| Summer day | Power consumption (KW) | 68,481.8 | 67,562.4 | 1232 | 1.34 | 73,054.8 | 30,548 | 6.68 |
| Total cost (NT$) | 194,726 | 192,310 | 2996 | 1.24 | 181,517 | 89,557 | 6.78 | |
| Non-summer day | Power Consumption (KW) | 41,456.9 | 41,739.9 | 192 | 0.68 | 39,079.1 | 13,648 | 5.74 |
| Total cost (NT$) | 91,457 | 92,249 | 689 | 0.87 | 98,605 | 51,823 | 7.25 |
4.3. Convergence Test
| Algorithms | Summer Day | Non-Summer Day | ||
|---|---|---|---|---|
| Power consumption (KW) | Total Cost (NT$) | Power Consumption (KW) | Total Cost (NT$) | |
| ARBFN | 65,916.46 | 186,683.17 | 38,959.58 | 84,706.24 |
| GA-RBFN | 66,148.61 | 187,309.84 | 39,287.41 | 85,371.62 |
| EP-RBFN | 66,431.83 | 188,131.15 | 39,514.37 | 85,984.38 |
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Bureau of Energy. Energy and Industrial Technology White Paper; Ministry of Economic Affairs: Taipei, Taiwan, 2014.
- Ashok, S.; Banerjee, R. An Optimization Model for Industrial Management. IEEE Trans. Power Syst. 2011, 16, 879–884. [Google Scholar] [CrossRef]
- Chang, Y.C.; Chen, W.H.; Lee, C.Y.; Huang, C.N. Simulated annealing based optimal chiller loading for saving energy. Energy Convers. Manag. 2006, 47, 2044–2058. [Google Scholar] [CrossRef]
- Chang, Y.C.; Lin, J.K.; Chuang, M.H. Optimal chiller loading by genetic algorithm for reducing energy consumption. Energy Build. 2005, 37, 147–155. [Google Scholar] [CrossRef]
- Chang, Y.C. Genetic algorithm based optimal chiller loading for energy conservation. Appl. Therm. Eng. 2005, 25, 2800–2815. [Google Scholar] [CrossRef]
- Chang, Y.C.; Chang, F.A.; Lin, C.H. Optimal chiller sequencing by branch and bound method for saving energy. Energy Convers. Manag. 2005, 46, 2158–2172. [Google Scholar] [CrossRef]
- Chang, Y.C.; Chen, W.H. Optimal chilled water temperature calculation of multiple chiller systems using Hopfield neural network for saving energy. Energy 2009, 34, 448–456. [Google Scholar] [CrossRef]
- Lee, W.S.; Chen, Y.T.; Kuo, Y. Optimal chiller loading by differential evolution algorithm for reducing energy consumption. Energy Build. 2011, 43, 599–604. [Google Scholar] [CrossRef]
- Coelho, S.L.D.; Klein, C.E.; Sabat, S.L.; Mariani, V.C. Optimal chiller loading for energy conservation using a new differential cuckoo search approach. Energy 2014, 75, 237–243. [Google Scholar] [CrossRef]
- Coelho, S.L.D.; Mariani, V.C. Improved firefly algorithm approach applied to chiller loading for energy conservation. Energy Build. 2013, 59, 273–278. [Google Scholar] [CrossRef]
- Chang, Y.C. An Outstanding Method for Saving Energy-Optimal Chiller Operation. IEEE Trans. Energy Convers. 2006, 21, 527–532. [Google Scholar] [CrossRef]
- Luo, X.; Wang, J.; Dooner, M.; Clarke, J. Overview of current development in electrical energy storage technologies and the application potential in power system operation. Appl. Energy 2015, 137, 511–536. [Google Scholar] [CrossRef]
- Shirazi, A.; Najafi, B.; Aminyavari, M.; Rinaldi, F.; Taylor, R.A. Thermal-economic-environmental analysis and multi-objective optimization of an ice thermal energy storage system for gas turbine cycle inlet air cooling. Energy 2014, 69, 212–226. [Google Scholar] [CrossRef]
- Powell, K.M.; Cole, W.J.; Ekarika, U.F.; Edgar, T.F. Optimal chiller loading in a district cooling system with thermal energy storage. Energy 2013, 50, 445–453. [Google Scholar] [CrossRef]
- Hajiah, A.; Krarti, M. Optimal Control of Building Storage Systems using both Ice Storage and Thermal Mass—Part I: Simulation Environment. Energy Convers. Manag. 2012, 64, 499–508. [Google Scholar] [CrossRef]
- Hajiah, A.; Krarti, M. Optimal Control of Building Storage Systems using both Ice Storage and Thermal Mass—Part II: Parametic Analysis. Energy Convers. Manag. 2012, 64, 509–515. [Google Scholar] [CrossRef]
- Sehar, F.; Rahman, S.; Pipattanasomporn, M. Impacts of ice storage on electrical energy consumptions in office buildings. Energy Build. 2012, 51, 255–262. [Google Scholar] [CrossRef]
- Campoccia, A.; Dusonchet, L.; Telaretti, E.; Zizzo, G. Economic Impact of Ice Thermal Energy Storage Systems in Residential Buildings in Presence of Double-Tariffs Contracts for Electricity. In Proceedings of the 6th International Conference on the European Energy Market, Leuven, The Netherlands, 27–29 May 2009; pp. 1–5.
- Sebzali, M.J.; Rubini, P.A. The impact of using chilled water storage systems on the performance of air cooled chillers in Kuwait. Energy Build. 2007, 39, 975–984. [Google Scholar] [CrossRef]
- Sebzali, M.J.; Rubini, P.A. Analysis of ice cool thermal storage for a clinic building in Kuwait. Energy Convers. Manag. 2006, 47, 3417–3434. [Google Scholar] [CrossRef]
- Chan, A.L.S.; Chow, T.T.; Fong, S.K.F.; Lin, J.Z. Performance evaluation of district cooling plant with ice storage. Energy 2006, 31, 2750–2762. [Google Scholar] [CrossRef]
- Lee, W.S.; Chen, Y.T.; Wu, T.H. Optimization for ice-storage air-conditioning system using swarm algorithm. Appl. Energy 2009, 86, 1589–1595. [Google Scholar] [CrossRef]
- Sanaye, S.; Shirazi, A. Thermo-economic optimization of an ice thermal energy storage system for air-conditioning applications. Energy Build. 2013, 60, 100–109. [Google Scholar] [CrossRef]
- Vetterli, J.; Benz, M. Cost-optimal design of an ice-storage cooling system using mixed-integer linear programming techniques under various electricity tariff schemes. Energy Build. 2012, 49, 226–234. [Google Scholar] [CrossRef]
- McCuen, R.H. Statistical Methods for Engineers; Prentice-Hall, Inc.: Englewood Cliffs, NJ, USA, 1985. [Google Scholar]
- TPC. Time-of-Use Rate for Cogenerator Plants; The Electricity Rate Structure for Taipower Company: Taipei, Taiwan, 2014. [Google Scholar]
- Dorigo, M.; Gambardella, L.M. Ant colony system: a cooperative learning approach to the traveling salesman problem. IEEE Trans. Evolut. Comput. 1997, 11, 53–66. [Google Scholar] [CrossRef]
- Lin, W.M.; Yan, C.D.; Lin, C.H.; Tsay, M.T. A Fault Classification Method by RBF Neural Network with OLS Learning Procedure. IEEE Trans. Power Deliv. 2001, 16, 473–477. [Google Scholar] [CrossRef]
- King, D.J.; Potter, R.A. Description of a steady-state cooling plant model developed for use in evaluating optimal control of ice thermal energy storage systems. ASHRAE Trans. 1998, 104, 42. [Google Scholar]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lin, W.-M.; Tu, C.-S.; Tsai, M.-T.; Lo, C.-C. Optimal Energy Reduction Schedules for Ice Storage Air-Conditioning Systems. Energies 2015, 8, 10504-10521. https://doi.org/10.3390/en80910504
Lin W-M, Tu C-S, Tsai M-T, Lo C-C. Optimal Energy Reduction Schedules for Ice Storage Air-Conditioning Systems. Energies. 2015; 8(9):10504-10521. https://doi.org/10.3390/en80910504
Chicago/Turabian StyleLin, Whei-Min, Chia-Sheng Tu, Ming-Tang Tsai, and Chi-Chun Lo. 2015. "Optimal Energy Reduction Schedules for Ice Storage Air-Conditioning Systems" Energies 8, no. 9: 10504-10521. https://doi.org/10.3390/en80910504
APA StyleLin, W.-M., Tu, C.-S., Tsai, M.-T., & Lo, C.-C. (2015). Optimal Energy Reduction Schedules for Ice Storage Air-Conditioning Systems. Energies, 8(9), 10504-10521. https://doi.org/10.3390/en80910504





