Exergetic Analysis of an Integrated Tri-Generation Organic Rankine Cycle
Abstract
:1. Introduction
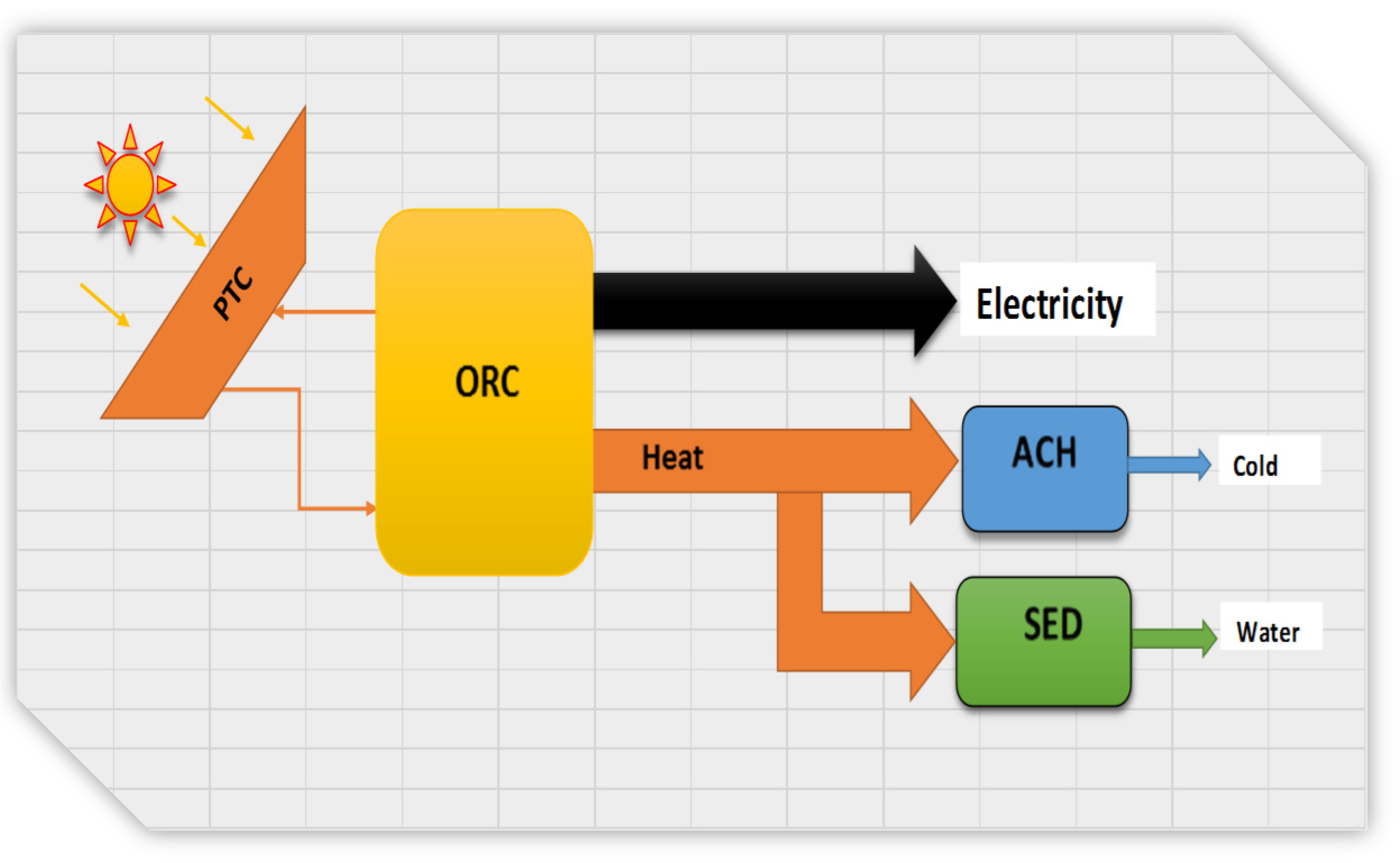
2. Background
3. System Description
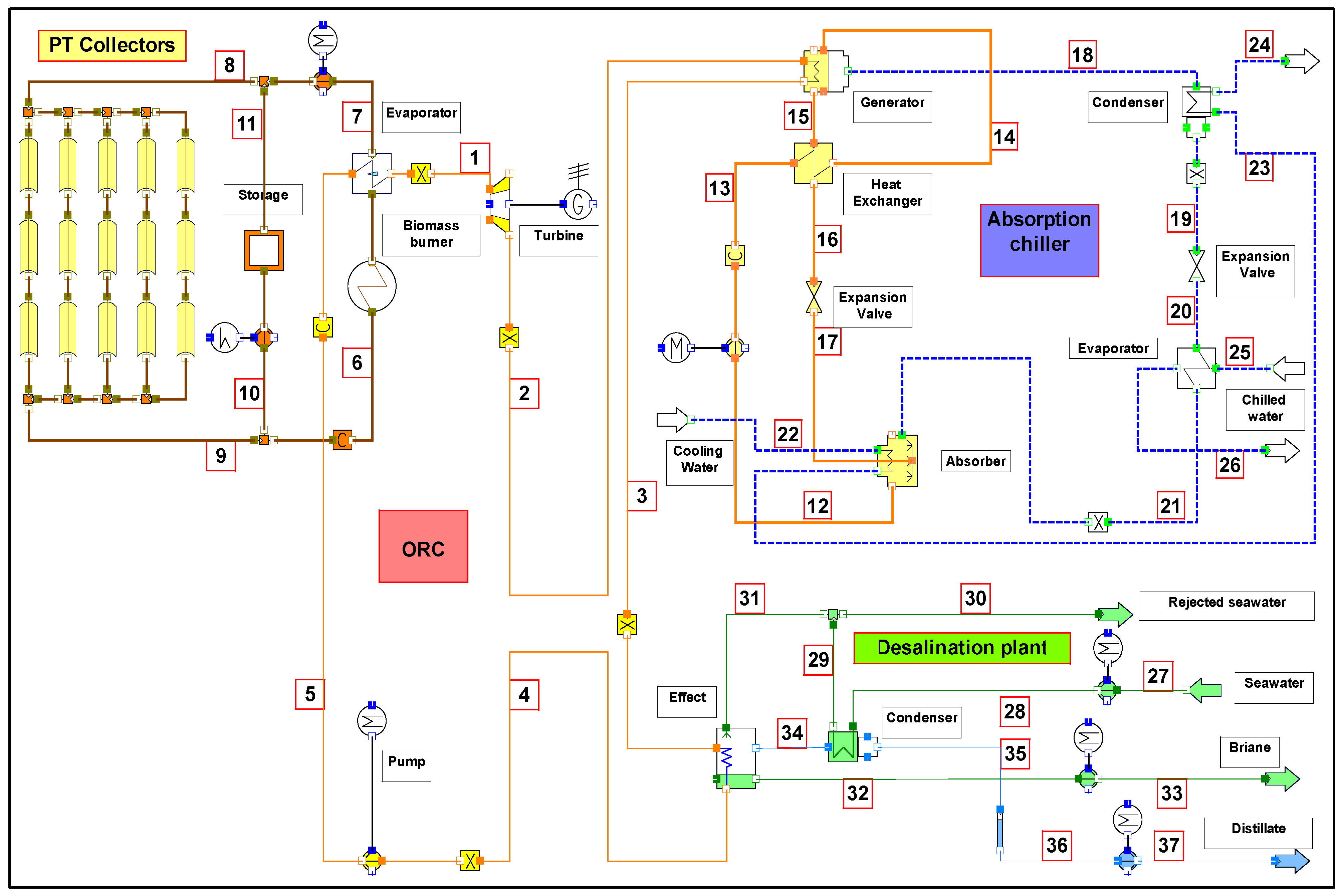
4. Thermal Analysis
4.1. Energy Analysis
4.2. Exergy Analysis
| Components | Fuel (MW) | Product (MW) |
|---|---|---|
| Turbine | ||
| Evaporator | ||
| Pump | ||
| PTC | ||
| Thermal storage | - | |
| Generator | ||
| Condenser | ||
| Evaporator | ||
| Absorber | ||
| Expansion valve | - | |
| Heat exchanger | ||
| Seawater pump | ||
| Effect | ||
| Condenser |
5. Modeling and Validation
5.1. Parabolic Trough Collector (PTC)
| Subsystem | Developed model | Experimental model [22] | The difference | |||
|---|---|---|---|---|---|---|
| Exergy delivered (MW) | Exergy loss (MW) | Exergy delivered (MW) | Exergy loss (MW) | Exergy delivered (%) | Exergy loss (%) | |
| Collector | 44.93 | 64.44 | 44.91 | 64.22 | 0.05 | 0.34 |
| Receiver | 29.41 | 15.51 | 29.87 | 15.04 | 1.56 | 3.03 |
| Collector-Receiver | 29.41 | 79.95 | 29.87 | 79.26 | 0.02 | 0.86 |
5.2. Organic Rankine Cycle (ORC)
| Parameter | Unit | Experimental result | Model result | Difference (%) |
|---|---|---|---|---|
| Gross power | kw | 250 | 254 | 1.60 |
| Net power | kw | 210 | 212 | 0.95 |
| Pump power consumption | kw | 40.0 | 41.7 | 4.07 |
| ORC efficiency | % | 8.20 | 8.08 | 1.46 |
| Cooling water flow | kg/s | 101.00 | 99.64 | 1.35 |
| Refrigerant flow | kg/s | 12.20 | 12.56 | 2.87 |
| Evaporator outlet temperature | 54.4 | 54.4 | 0.00 | |
| Evaporator heat transfer | kw | 2580 | 2633 | 2.01 |
| Condenser heat transfer | kw | 2360 | 2326 | 1.44 |
5.3. Single-Effect Desalination (SED)
| Th,in (°C) | Th,out (°C) | mh (kg/s) | Qe,1 (kw) | mc (kg/s) | Experimental (m3/d) | Model (m3/d) | Difference (%) |
|---|---|---|---|---|---|---|---|
| 65 | 54.3 | 1.38 | 62 | 2.18 | 2 | 2.0723 | 3.49 |
| 65 | 54.4 | 2.76 | 123 | 4.34 | 4 | 4.1032 | 2.52 |
| 65 | 57.7 | 5.00 | 153 | 6.24 | 5 | 5.0193 | 0.38 |
| 65 | 57.3 | 6.65 | 215 | 8.51 | 7 | 7.0602 | 0.85 |
| 65 | 57.2 | 9.37 | 307 | 10.21 | 10 | 10.143 | 1.41 |
| 65 | 57.1 | 13.86 | 460 | 15.88 | 15 | 15.180 | 1.19 |
5.4. Single Effect H2O/LiBr Absorption Chiller (ACH)
| Parameter | Unit | Exprimental | Model | Difference (%) |
|---|---|---|---|---|
| COP | - | 0.74 | 0.75 | 1.33 |
| Generator heat transfer | kw | 2987 | 3065 | 2.54 |
| Generator outlet temperature | °C | 85 | 81.1 | 4.58 |
| Generatore evaporator heat transfer | kw | 5200 | 5364 | 3.05 |
| Absorber and Condenser heat transfer | kw | 5193 | 5364 | 3.18 |
| Cooling water flow | kg/s | 211 | 214 | 1.40 |
| Chilled water flow | kg/s | 52.6 | 54.7 | 3.83 |
6. Results and Discussion
| Subsystem | Energy received (MW) | Energy delivered (MW) | Energy loss (MW) | Energy loss (%) | First law efficiency (%) |
|---|---|---|---|---|---|
| Collector | 26.59 | 20.21 | 06.38 | 24.00 | 76.00 |
| Receiver | 20.21 | 04.15 | 16.05 | 79.00 | 20.54 |
| Collector-receiver | 26.59 | 04.15 | 22.44 | 84.00 | 15.61 |
| Subsystem | Irreversibility (MW) | Exergy received (MW) | Energy loss (%) | Exergy loss (%) | First law efficiency (%) | Second law efficiency (%) |
|---|---|---|---|---|---|---|
| Collector | 15.61 | 25.27 | 24.00 | 61.77 | 76.00 | 38.22 |
| Receiver | 07.54 | 09.66 | 79.00 | 78.01 | 20.54 | 21.98 |
| Collector-receiver | 23.15 | 25.27 | 84.00 | 91.59 | 15.61 | 08.40 |
| State | Fluid | h0 (kj/kg) | so (kj/kg.k) | T0 (K) | m (kg/s) | T ( K ) | P bar | h (kj/kg) | s (kj/kg.k) | Salinity | x | Ex (kw) |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | Cyclo-pentane | −45.47 | −0.15 | 298.15 | - | 298.15 | 1.01 | −45.47 | −0.15 | - | - | - |
| 0 | Oil | 38.58 | 0.31 | 298.15 | - | 298.15 | 1.01 | 38.58 | 0.31 | - | - | - |
| 0 | LiBr | 68.83 | 0.15 | 298.15 | - | 298.15 | 1.01 | 68.83 | 0.15 | - | 0.57 | - |
| 0 | LiBr | 92.73 | 0.13 | 298.15 | - | 298.15 | 1.01 | 92.73 | 0.13 | - | 0.61 | - |
| 0 | Water | 104.93 | 0.37 | 298.15 | - | 298.15 | 1.01 | 104.93 | 0.37 | - | - | - |
| 0 | Water | 113.29 | 0.40 | 300.15 | - | 300.15 | 1.01 | 113.29 | 0.40 | - | - | - |
| 0 | Seawater | 107.44 | 0.37 | 300.15 | - | 300.15 | 1.01 | 99.48 | 0.37 | 0.04 | - | - |
| 1 | Cyclo-pentane | −45.47 | −0.15 | 298.15 | 21.25 | 461.83 | 22.30 | 562.30 | 1.34 | - | - | 3521.85 |
| 2 | Cyclo-pentane | −45.47 | −0.15 | 298.15 | 21.25 | 388.15 | 3.21 | 481.03 | 1.34 | - | - | 1795.04 |
| 3 | Cyclo-pentane | −45.47 | −0.15 | 298.15 | 21.25 | 362.43 | 3.20 | 438.78 | 1.22 | - | - | 1613.34 |
| 4 | Cyclo-pentane | −45.47 | −0.15 | 298.15 | 21.25 | 362.43 | 3.20 | 82.15 | 0.24 | - | - | 269.44 |
| 5 | Cyclo-pentane | −45.47 | −0.15 | 298.15 | 21.25 | 363.58 | 22.40 | 85.72 | 0.24 | - | - | 332.51 |
| 6 | Oil | 38.58 | 0.31 | 298.15 | 109.00 | 610.33 | 14.14 | 661.81 | 1.68 | - | - | 23377.27 |
| 7 | Oil | 38.58 | 0.31 | 298.15 | 109.00 | 571.07 | 14.04 | 568.91 | 1.55 | - | - | 17475.95 |
| 8 | Oil | 38.58 | 0.31 | 298.15 | 218.00 | 571.15 | 15.14 | 569.11 | 1.55 | - | - | 34993.98 |
| 9 | Oil | 38.58 | 0.31 | 298.15 | 218.00 | 610.33 | 14.14 | 661.81 | 1.68 | - | - | 46754.54 |
| 10 | Oil | 38.58 | 0.31 | 298.15 | 109.00 | 610.33 | 14.14 | 661.81 | 1.68 | - | - | 23377.27 |
| 11 | Oil | 38.58 | 0.31 | 298.15 | 109.00 | 571.15 | 16.00 | 569.11 | 1.55 | - | - | 17496.99 |
| 12 | LiBr | 68.83 | 0.15 | 298.15 | 4.02 | 317.65 | 0.01 | 108.34 | 0.28 | - | 0.57 | 9.46 |
| 13 | LiBr | 68.83 | 0.15 | 298.15 | 4.02 | 317.65 | 0.07 | 108.34 | 0.28 | - | 0.57 | 9.46 |
| 14 | LiBr | 68.83 | 0.15 | 298.15 | 4.02 | 344.45 | 0.07 | 162.71 | 0.44 | - | 0.57 | 34.39 |
| 15 | LiBr | 92.73 | 0.13 | 298.15 | 3.73 | 357.54 | 0.07 | 205.60 | 0.47 | - | 0.61 | 44.72 |
| 16 | LiBr | 92.73 | 0.13 | 298.15 | 3.73 | 326.66 | 0.07 | 146.89 | 0.30 | - | 0.61 | 14.42 |
| 17 | LiBr | 92.73 | 0.13 | 298.15 | 3.73 | 326.66 | 0.01 | 146.89 | 0.30 | - | 0.61 | 14.42 |
| 18 | Water | 104.93 | 0.37 | 298.15 | 0.30 | 352.64 | 0.07 | 2648.89 | 8.52 | - | - | 33.39 |
| 19 | Water | 104.93 | 0.37 | 298.15 | 0.30 | 311.53 | 0.07 | 160.70 | 0.55 | - | - | 0.32 |
| 20 | Water | 104.93 | 0.37 | 298.15 | 0.30 | 285.16 | 0.01 | 160.70 | 0.57 | - | - | −1.10 a |
| 21 | Water | 104.93 | 0.37 | 298.15 | 0.30 | 285.16 | 0.01 | 2461.10 | 8.63 | - | - | −32.22 a |
| 22 | Water | 104.93 | 0.37 | 298.15 | 39.82 | 300.15 | 1.60 | 113.35 | 0.40 | - | - | 9.23 |
| 23 | Water | 104.93 | 0.37 | 298.15 | 39.82 | 305.23 | 1.47 | 134.49 | 0.47 | - | - | 19.96 |
| 24 | Water | 104.93 | 0.37 | 298.15 | 39.82 | 309.65 | 1.34 | 153.03 | 0.53 | - | - | 34.09 |
| 25 | Water | 104.93 | 0.37 | 298.15 | 38.61 | 291.35 | 2.38 | 76.61 | 0.27 | - | - | 17.93 |
| 26 | Water | 104.93 | 0.37 | 298.15 | 38.61 | 287.15 | 1.40 | 58.93 | 0.21 | - | - | 37.47 |
| 27 | Seawater | 107.44 | 0.37 | 300.15 | 212.44 | 300.15 | 1.01 | 107.44 | 0.37 | 0.04 | - | 0.00 |
| 28 | Seawater | 107.44 | 0.37 | 300.15 | 212.44 | 300.16 | 1.50 | 107.51 | 0.37 | 0.04 | - | 10.08 |
| 29 | Seawater | 107.44 | 0.37 | 300.15 | 212.44 | 307.65 | 1.50 | 137.35 | 0.47 | 0.04 | - | 82.43 |
| 30 | Seawater | 107.44 | 0.37 | 300.15 | 202.97 | 307.65 | 1.50 | 137.35 | 0.47 | 0.04 | - | 78.76 |
| 31 | Seawater | 107.44 | 0.37 | 300.15 | 9.47 | 307.65 | 1.50 | 137.35 | 0.47 | 0.04 | - | 3.68 |
| 32 | Seawater | 107.44 | 0.37 | 300.15 | 6.77 | 340.56 | 0.27 | 263.64 | 0.86 | 0.05 | - | 77.01 |
| 33 | Seawater | 107.44 | 0.37 | 300.15 | 6.77 | 340.58 | 2.00 | 263.88 | 0.86 | 0.05 | - | 78.23 |
| 34 | Water | 113.29 | 0.40 | 300.15 | 2.71 | 340.56 | 0.27 | 2621.84 | 7.81 | - | - | 767.66 |
| 35 | Water | 113.29 | 0.40 | 300.15 | 2.71 | 339.83 | 0.27 | 279.13 | 0.91 | - | - | 26.09 |
| 36 | Water | 113.29 | 0.40 | 300.15 | 2.71 | 339.83 | 0.30 | 279.13 | 0.91 | - | - | 26.10 |
| 37 | Water | 113.29 | 0.40 | 300.15 | 2.71 | 339.86 | 2.00 | 279.38 | 0.92 | - | - | 26.61 |
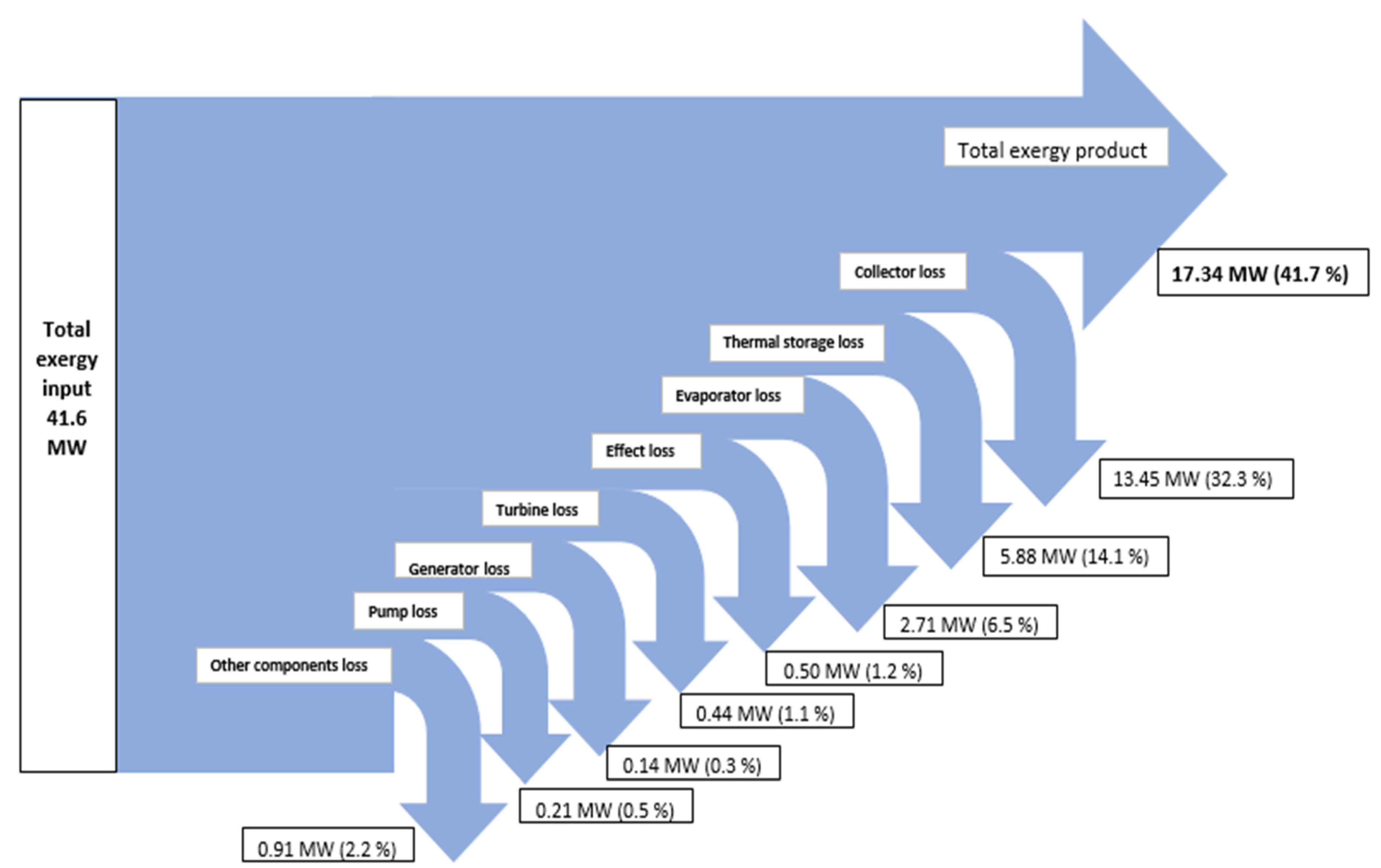
| Component | Exergy fuel ExF (kw) | Exergy production ExP (kw) | Exergy destruction ExD (kw) | Exergy loss ExL (kw) | Exergetic efficiency (%) |
|---|---|---|---|---|---|
| Turbine | 1,726.81 | 1,286.14 | 440.67 | 0.00 | 74.48 |
| Evaporator | 5,901.31 | 3,189.34 | 2,711.98 | 0.00 | 54.04 |
| Pump | 270.60 | 63.08 | 207.52 | 0.00 | 23.31 |
| PTC | 25,207.90 | 1,1760.56 | 5,910.75 | 7,536.60 | 46.65 |
| Thermal storage | 5,880.28 | 0.00 | 4,890.50 | 989.78 | 0.00 |
| Generator | 181.71 | 43.71 | 137.99 | 0.00 | 24.06 |
| Condenser | 33.07 | 14.13 | 18.94 | 0.00 | 42.73 |
| Evaporator | 31.12 | 19.54 | 11.58 | 0.00 | 62.79 |
| Absorber | 27.26 | 10.73 | 16.53 | 0.00 | 39.37 |
| Expansion valve | 1.42 | 0.00 | 1.42 | 0.00 | 0.00 |
| Heat exchanger | 30.30 | 24.93 | 5.37 | 0.00 | 82.28 |
| Seawater pump | 23.56 | 10.08 | 13.48 | 0.00 | 42.79 |
| Effect | 1,343.90 | 840.99 | 502.91 | 0.00 | 62.58 |
| Condenser | 741.57 | 72.35 | 669.21 | 0.00 | 9.76 |
| Cooling process | 78.76 | 0.00 | 78.76 | 0.00 | 0.00 |
| Brine disposal | 65.45 | 0.00 | 65.45 | 0.00 | 0.00 |
| System | 41,572.53 | 17,335.59 | 15,710.57 | 8,526.38 | 41.70 |
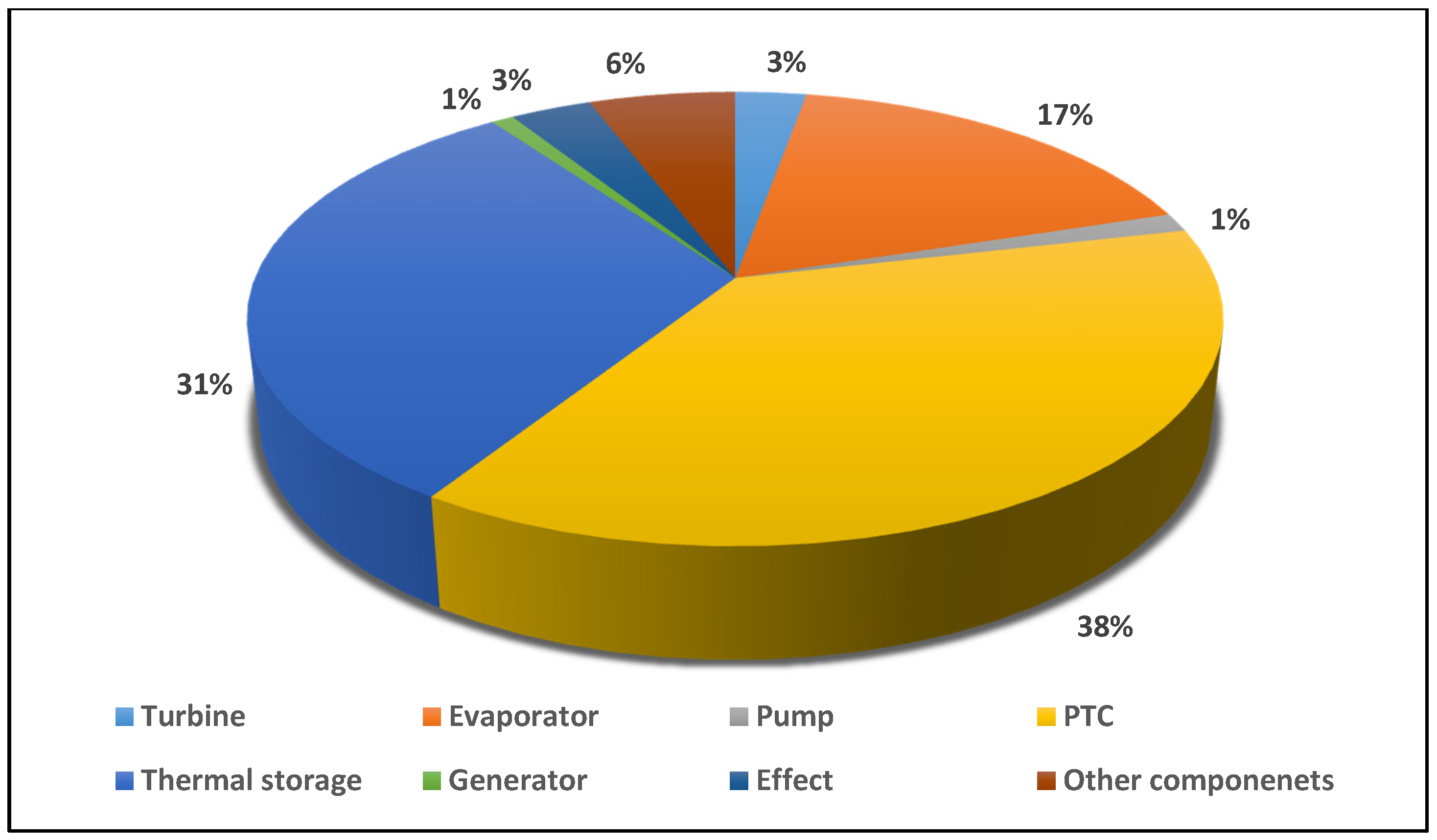
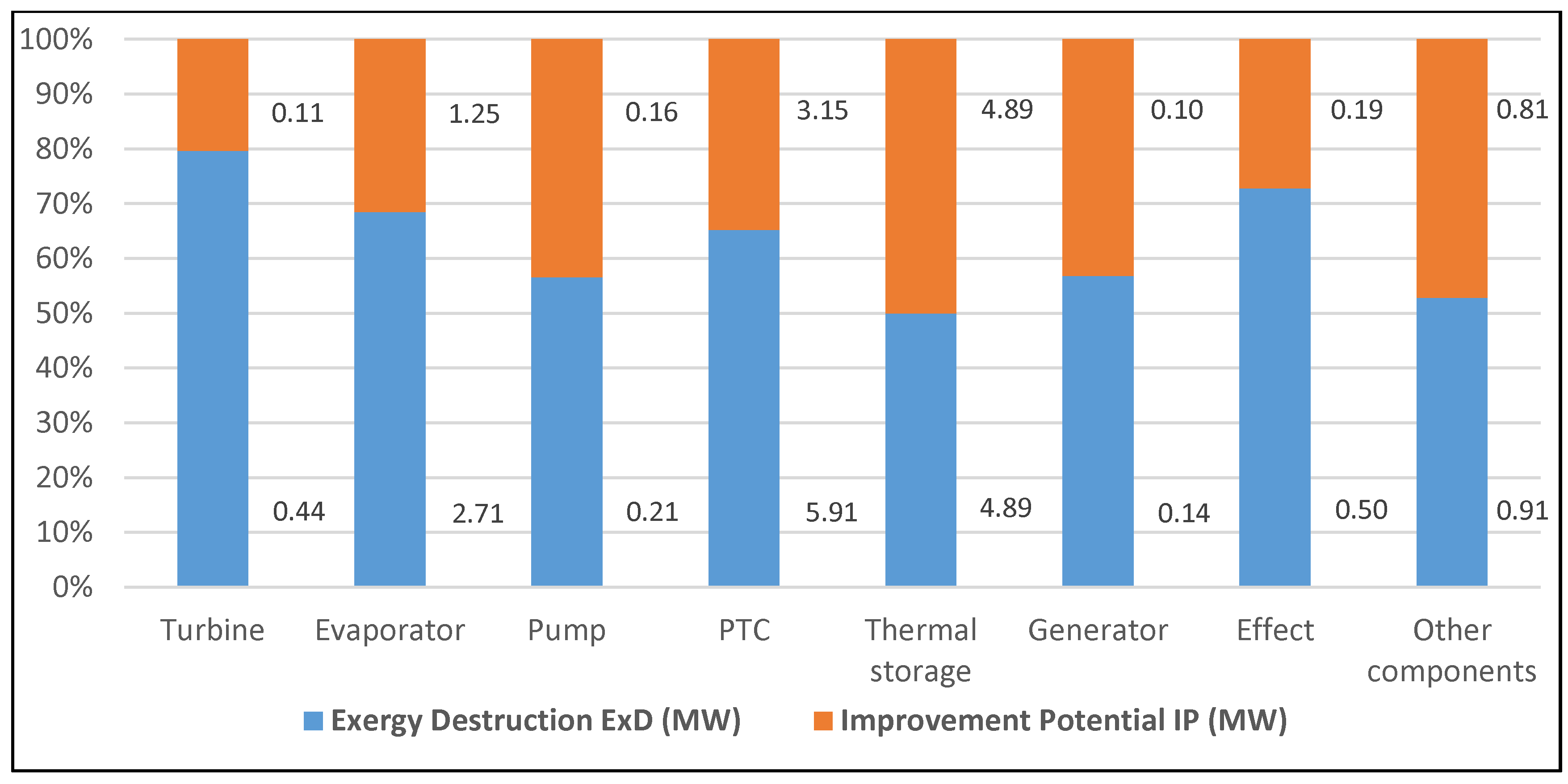
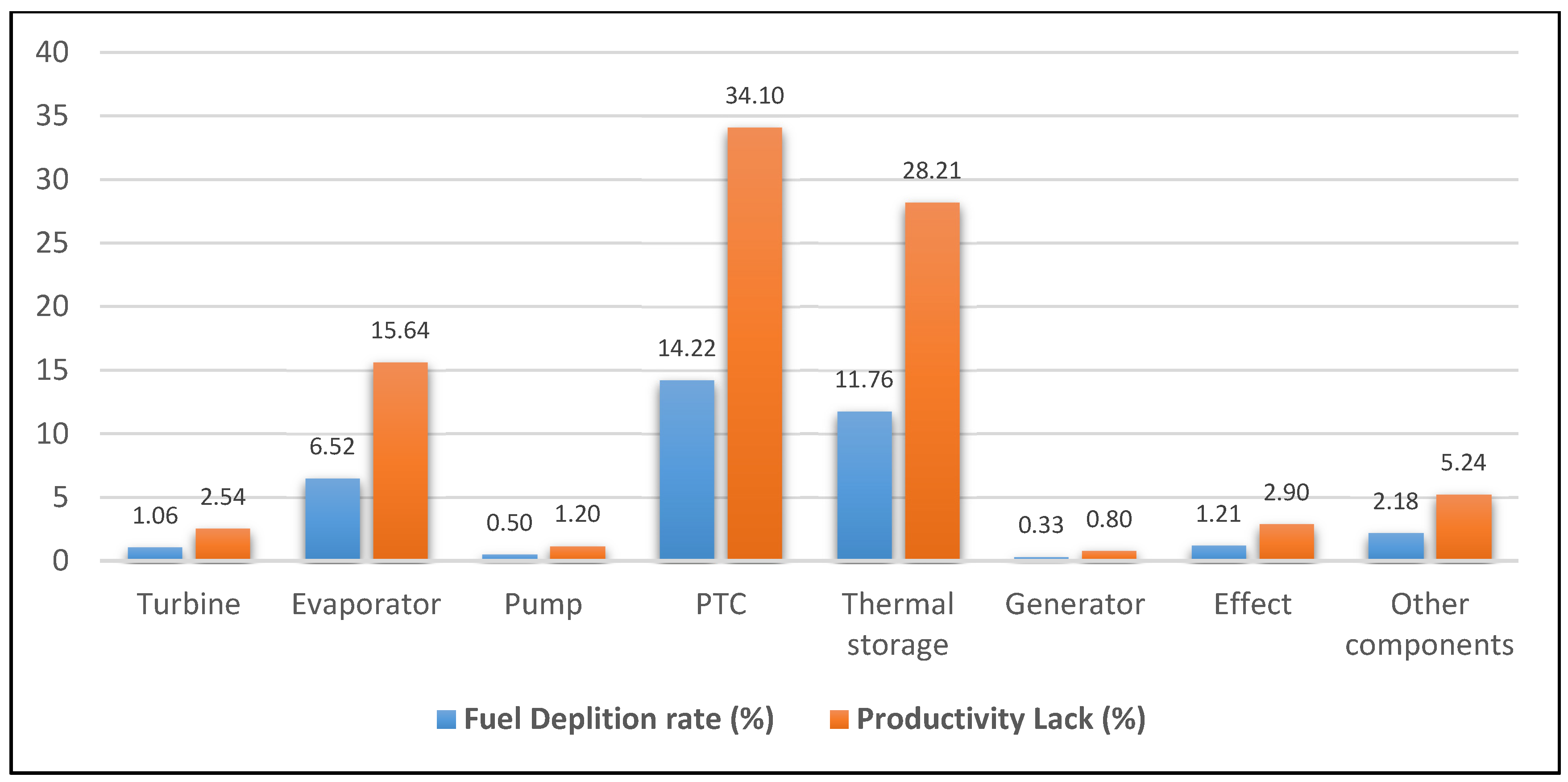
| Component | Fuel depletion rate (%) | Exergetic factor f (%) | Productivity lack (%) | Improvement potential IP (MW) | Relative irreversibility (%) |
|---|---|---|---|---|---|
| Turbine | 1.06 | 4.15 | 2.54 | 0.11 | 2.80 |
| Evaporator | 6.52 | 14.20 | 15.64 | 1.25 | 17.26 |
| Pump | 0.50 | 0.65 | 1.20 | 0.16 | 1.32 |
| PTC | 14.22 | 60.64 | 34.10 | 3.15 | 37.62 |
| Thermal storage | 11.76 | 14.14 | 28.21 | 4.89 | 31.13 |
| Generator | 0.33 | 0.44 | 0.80 | 0.10 | 0.88 |
| Condenser | 0.05 | 0.08 | 0.11 | 0.01 | 0.12 |
| Evaporator | 0.03 | 0.07 | 0.07 | 0.00 | 0.07 |
| Absorber | 0.04 | 0.07 | 0.10 | 0.01 | 0.11 |
| Expansion valve | 0.00 | 0.00 | 0.01 | 0.00 | 0.01 |
| Heat exchanger | 0.01 | 0.07 | 0.03 | 0.00 | 0.03 |
| Seawater pump | 0.03 | 0.06 | 0.08 | 0.01 | 0.09 |
| Effect | 1.21 | 3.23 | 2.90 | 0.19 | 3.20 |
| Condenser | 1.61 | 1.78 | 3.86 | 0.60 | 4.26 |
| Cooling process | 0.19 | 0.19 | 0.45 | 0.08 | 0.50 |
| Brine disposal | 0.16 | 0.16 | 0.38 | 0.07 | 0.42 |
7. Conclusions
- The highest exergy destruction value for the PTC leads to the improvement potential in terms of effectiveness. Moreover, PTC has the highest fuel depletion value, which is directly proportional to productivity lack.
- The highest exergy destruction values for the PTC, thermal storage, and evaporator in the solar tri-generation system mean that these components need to be improved.
- From the analysis of exergy destruction in the solar tri-generation system, as illustrated in Figure 3, the PTC is the main source of exergy destruction at 38% followed by the thermal storage, evaporator, other components, effect, turbine, generator, and pump at 31%, 17%, 6%, 3%, 3%, 1%, and 1% respectively.
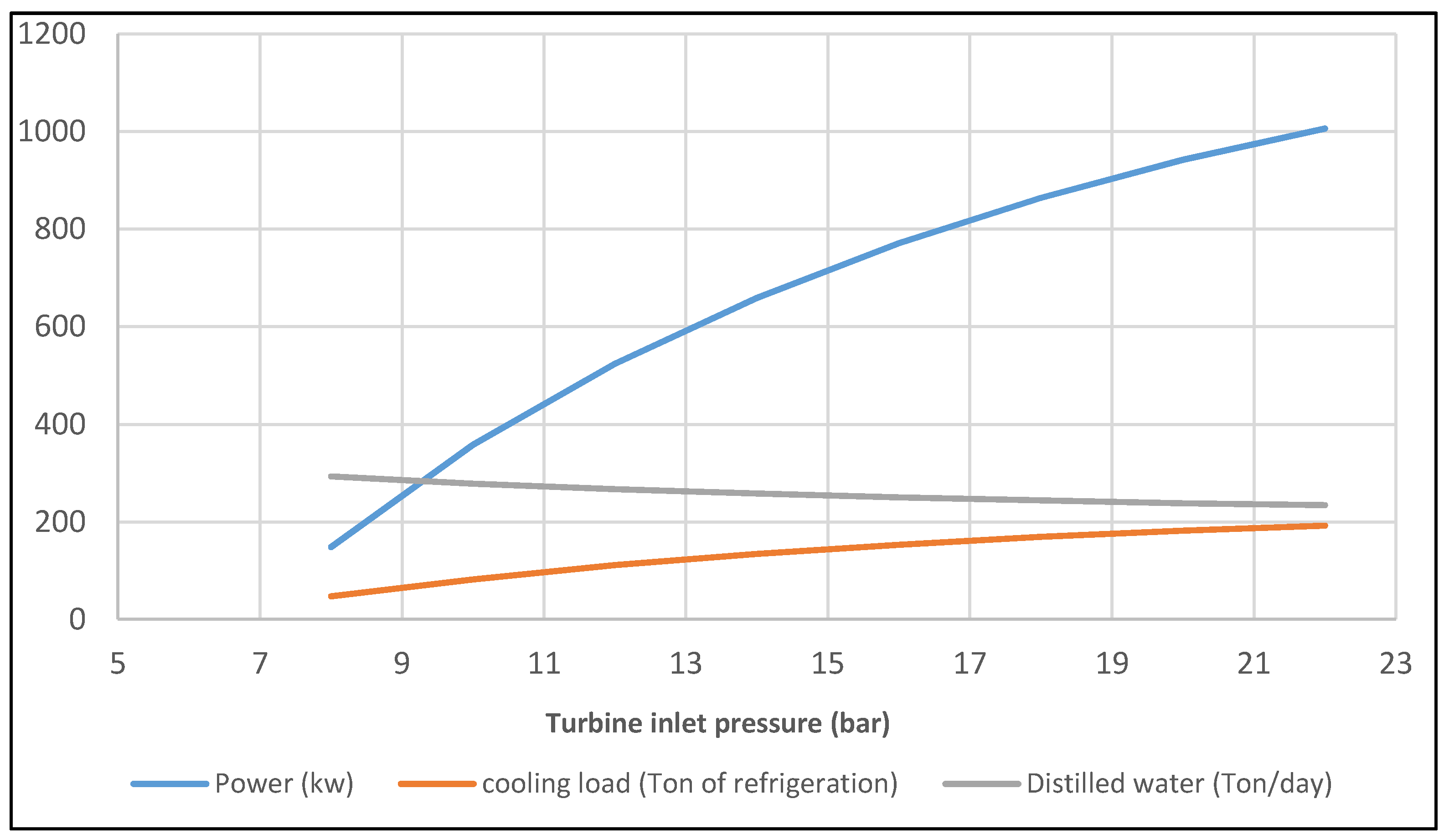
- The optimum value for inlet turbine pressure is 22.3 bar for this tri-generation case.
- The exergy efficiency of the solar tri-generation system is 41.7% and for this specific system, the ORC, single absorption chiller, and single effect desalination were able to produce about 1 MW of electrical power, 194 Ton of refrigeration cooling load, and 234 t/day distilled water.
Author Contributions
Conflicts of Interest
Nomenclature
area (m2) | |
Exergy (kw) | |
Specific enthalpy (kJ/kgK) | |
solar intensity(W/m2) | |
Irreiversibility (kw) | |
length (m) | |
mass flow rate (kg/s) | |
pressure (bar) | |
number of collector | |
heat transfer rate (kw) | |
Specific entropy (kJ/kgK) | |
temperature (°C) | |
aperture (m) | |
| W | Work input/work transfer rate (kw) |
| w | Salinity |
| Χ | Concentration |
| Z | Elevation(m) |
Abbreviations
| ACH | Absorption Chiller |
| COP | Coefficient of Performance |
| H2O | Water |
Heat Transfer Oil | |
| GWP | Global warming potential |
| LiBr | Lithium Bromide |
| LiBr/H2O | Lithium bromide water mixture |
Organic Rankine Cycle | |
| ODP | Ozone depletion potential |
Prabolic Trough Collector | |
| SED | Single Effect Desalination |
| TR | Ton of refrigeration |
Greek Symbols
thermal efficiency | |
exergy efficiency | |
| ΔT | Temperature difference |
Subscripts
ambient temperature | |
| Ab | Absorber |
| co | Condenser |
| c.v. | Control volume |
| cwp | Cooling water pump |
| ev | Evaporator |
| F | Fuel |
fluid | |
generator | |
| H | hot |
inlet | |
loss | |
| m | Mechanical |
outlet | |
pump | |
recieiver | |
solar | |
| ss | Strong solution |
| t | Thermal |
| w | Water |
| Wf | Working fluid |
| wfp | Working fluid pump |
| ws | Weak solution |
Appendix
| 0 | −945.8 | −0.3293 | 7.43 × 10−3 | −2.27 × 10−6 |
| 1 | 4.78 × 102 | 4.08 × 10−2 | −1.51 × 10−4 | - |
| 2 | −1.59235 | −1.36 × 10−5 | 1.36 × 10−6 | - |
| 3 | 2.09 × 10−2 | −7.14 × 10−6 | - | - |
| 4 | −7.69 × 10−5 | - | - | - |
| 0 | 0.5127558 | −0.01393954 | 2.92415 × 10−5 | 9.0357 × 10−7 |
| 1 | 0.01225678 | −9.15682 × 10−5 | 1.82045 × 10−8 | −7.99181 × 10−10 |
| 2 | −1.3649 × 10−5 | 1.0689 × 10−7 | −1.38111 × 10−9 | 1.52978 × 10−11 |
| 3 | 1.0215 × 10−8 | 0 | 0 | 0 |
| Correlations for equations (13) and (16) | |||
| Parabolic trough collector (PTC) | |||
| Length | 49 | m | [21] |
| Aperture | 5 | m | [21] |
| Optical efficiency | 0.76 | % | [21] |
| Direct normal irradiance | 810 | W/m2 | [20] |
| Number of collector | 134 | - | - |
| Organic rankine cycle (ORC) | |||
| Organic cycle turbine efficiency | 80 | % | [32] |
| Organic cycle pump efficiency | 85 | % | [32] |
| Turbine inlet pressure | 22.3 | bar | [36] |
| Electrical generator efficiency | 95 | % | [37] |
| Electrical motor efficiency | 95 | % | [37] |
| Single effect desalination (SED) | |||
| Seawater temperature | 27 | °C | [38] |
| Salinity | 0.038 | - | [39] |
| Absorption chiller (ACH) | |||
| Inlet evaporator temperature | 18.2 | °C | [40] |
| Outlet condenser temperature | 36.5 | °C | [41] |
| Cooling water temperature | 27 | °C | [29] |
| Mechanical efficiency | 75 | % | [29] |
| Pump efficiency | 90 | % | [29] |
References
- Rowe, D.M. Modules, Systems, and Applications in Thermoelectrics; CRC Press: Boca Raton, FL, USA, 2012. [Google Scholar]
- Liu, H.; Shao, Y.; Li, J. A biomass-fired micro-scale CHP system with organic Rankine cycle (ORC)—Thermodynamic modelling studies. Biomass Bioenerg. 2011, 35, 3985–3994. [Google Scholar] [CrossRef]
- Dincer, I. Renewable energy and sustainable development: A crucial review. Renew. Sustain. Energy Rev. 2000, 4, 157–175. [Google Scholar] [CrossRef]
- Carayannis, E.G. Planet Earth 2011—Global Warming Challenges and Opportunities for Policy and Practice; InTech: Rijeks, Croatia, 2011; p. 656. [Google Scholar]
- Nafey, A.S.; Sharaf, M.A. Combined solar organic Rankine cycle with reverse osmosis desalination process: Energy, exergy, and cost evaluations. Renew. Energy 2010, 35, 2571–2580. [Google Scholar] [CrossRef]
- Mathkor, R.Z.; Agnew, B.; Al-Weshahi, M.A.; Etaig, S. Thermal analysis of a solar powered ORC in Libya. Appl. Mech. Mater. 2015, 789–790, 389–395. [Google Scholar]
- Li, C.; Kosmadakis, G.; Manolakos, D.; Stefanakos, E. Performance investigation of concentrating solar collectors coupled with a transcritical organic Rankine cycle for power and seawater desalination co-generation. Desalination 2013, 318, 107–117. [Google Scholar] [CrossRef]
- Al-Sulaiman, F.A.; Dincer, I.; Hamdullahpur, F. Exergy modeling of a new solar driven trigeneration system. Sol. Energy 2011, 85, 2228–2243. [Google Scholar] [CrossRef]
- Al-Sulaiman, F.A. Thermodynamic Modeling and Thermoeconomic Optimization of Integrated Trigeneration Plants Using Organic Rankine Cycles. Ph.D. Thesis, Mechanical Engineering, University of Waterloo, Waterloo, ON, Canada, 2010. [Google Scholar]
- Dharmadhikari, S.; Principaud, F. Contribution of stratified thermal storage to cost-effective trigeneration project. ASHRAE Trans. 2000, 106, 912–919. [Google Scholar]
- Jradi, M.; Riffat, S. Tri-generation systems: Energy policies, prime movers, cooling technologies, configurations and operation strategies. Renew. Sustain. Energy Rev. 2014, 32, 396–415. [Google Scholar] [CrossRef]
- Drescher, U.; Brüggemann, D. Fluid selection for the Organic Rankine Cycle (ORC) in biomass power and heat plants. Appl. Therm. Eng. 2007, 27, 223–228. [Google Scholar] [CrossRef]
- Karellas, S.; Schuster, A. Supercritical fluid parameters in organic rankine cycle applications. Int. J. Thermodyn. 2008, 11, 101–108. [Google Scholar]
- Maraver, D.; Sin, A.; Royo, J.; Sebastian, F. Assessment of CCHP systems based on biomass combustion for small-scale applications through a review of the technology and analysis of energy efficiency parameters. Appl. Energy 2013, 102, 1303–1313. [Google Scholar] [CrossRef]
- Dudley, V.E.; Slon, M.; Kearney, D. Test Results SEGS LS-2 Solar Collector. Technical Report for Sandia National Laboratories: Washington, DC, USA, December 1994. [Google Scholar]
- Ginosar, D.M.; Petkovic, L.M.; Guillen, D.P. Thermal stability of cyclopentane as an organic Rankine cycle working fluid. Energy Fuels 2011, 25, 4138–4144. [Google Scholar] [CrossRef]
- Pierobon, L.; Nguyen, T.V.; Larsen, U.; Haglind, F. Multi-objective optimization of organic Rankine cycles for waste heat recovery: Application in an offshore platform. Energy 2013, 58, 538–549. [Google Scholar] [CrossRef]
- Pasetti, M.; Invernizzi, C.M.; Iora, P. Thermal stability of working fluids for organic Rankine cycles: An improved survey method and experimental results for cyclopentane, isopentane and n-butane. Appl. Therm. Eng. 2014, 73, 764–774. [Google Scholar] [CrossRef]
- De Falco, M.; Giaconia, A.; Marelli, L.; Tarquini, P. Enriched methane production using solar energy: An assessment of plant performance. Int. J. Hydrog. Energy 2009, 34, 98–109. [Google Scholar] [CrossRef]
- Aldali, Y.; Morad, K. Thermal performance improvement of Derna electric power station (unit5) using solar energy. J. Sustain. Dev. 2014, 7, 60–71. [Google Scholar] [CrossRef]
- Price, H.; Lupfert, E.; Kearney, D. Advances in parabolic trough solar power technology. J. Sol. Energy Eng. 2002, 124, 109–125. [Google Scholar] [CrossRef]
- Baghernejad, A.; Yaghoubi, M. Exergy analysis of an integrated solar combined cycle system. Renew. Energy 2010, 35, 2157–2164. [Google Scholar] [CrossRef]
- Al-Weshahi, M.A.; Anderson, A.; Tian, G. Organic Rankine Cycle recovering stage heat from MSF desalination distillate water. Appl. Energy 2014, 130, 738–747. [Google Scholar] [CrossRef]
- Feuercker, G.; Scharfe, J.; Greiter, I.; Frank, C.; Alefeld, G. Measurement of thermophysical properties of aqueous LiBr solution at high temperatures and concentrations. In Proceedings of the International Absorption Heat Pump Conference ASME, New Orleans, LA, USA, 1993; pp. 493–499.
- Kaita, Y. Thermodynamic properties of lithium bromide-water solutions at high temperatures. Int. J. Refrig. 2001, 24, 374–390. [Google Scholar] [CrossRef]
- Sharqawy, M.H.; Lienhard, V. On exergy calculations of seawater with applications in desalination systems. Int. J. Therm. Sci. 2011, 50, 187–196. [Google Scholar] [CrossRef]
- Sharqawy, M.H.; Lienhard, V.; Zubair, J.H.; Syed, M. The thermophysical properties of seawater: A review of existing correlations and data. Desalination Water Treat. 2010, 16, 354–380. [Google Scholar] [CrossRef]
- Bejan, A.; Tsatsaronis, G.; Moran, M. Thermal Design and Optimization, 1st ed.; Wiley: New York, NY, USA, 1996. [Google Scholar]
- Misra, R.D.; Sahoo, P.K.; Sahoo, S.; Gupta, A. Thermoeconomic optimization of a single effect water/LiBr vapour absorption refrigeration system. Int. J. Refrig. 2003, 26, 158–169. [Google Scholar] [CrossRef]
- Lozano, M.A.; Valero, A. Theory of the exergetic cost. Energy 1993, 18, 939–960. [Google Scholar] [CrossRef]
- Petela, R. Exergy analysis of the solar cylindrical-parabolic cooker. Sol. Energy 2005, 79, 221–233. [Google Scholar] [CrossRef]
- Holdmann, G. The Chena hot springs 400 KW geothermal power plant: Experience gained during the first year of operation. In Proceedings of the Geothermal Resources Council Annual Meeting, Sparks (Reno), NV, USA, 30 September–3 October 2007; pp. 515–519.
- Wang, X.; Christ, A.; Regenauer-Lieb, K.; Hooman, K. Low grade heat driven multi-effect distillation technology. Int. J. Heat Mass Transf. 2011, 54, 5497–5503. [Google Scholar] [CrossRef]
- Zabala, E. S. Technological and Economic Evaluation of District Cooling with Absorption Cooling Systems. Master’s Thesis, University of Gävle, Gävle, Sweden, 2009. [Google Scholar]
- Talbi, M.M.; Agnew, B. Exergy analysis: An absorption refrigerator using lithium bromide and water as the working fluids. Appl. Therm. Eng. 2000, 20, 619–630. [Google Scholar] [CrossRef]
- Price, H. Parabolic trough Organic Rankine Cycle solar power plant. In Proceedings of the 2004 DOE Solar Energy Technologies Program Review Meeting, Denver, CO, USA, 25–28 October 2004.
- Al-Sulaiman, F.A.; Hamdullahpur, F.; Dincer, I. Performance comparison of three trigeneration systems using Organic Rankine Cycles. Energy 2011, 36, 5741–5754. [Google Scholar] [CrossRef]
- Fath, H.E.S.; Ismail, M.A. Operational performance of 2 × 5000 m3/day MSF Sidi Krir desalination plant—Part I—enhancement of chemical cleaning and brine heater condensate process. In Proceedings of the 7th International Water Technology Conference, Cairo, Egypt, 1–3 April 2009; pp. 603–615.
- Hamza, A. Towards a Representative Network of Marine Protected Areas in Libya; Interim Report; IUCN: Gland, Switzerland; Málaga, Spain, 2011. [Google Scholar]
- Buru, M.M. A Geographical Study of the Eastern Jebel Akhdar, Cyrenaica. Ph.D. Thesis, Durham University, Durham, UK, 1960. [Google Scholar]
- Mehrabian, M.A.; Shahbeik, A.E. Thermodynamic modelling of a single-effect LiBr-H2O absorption refrigeration cycle. Proc. Inst. Mech. Eng. Part E: J. Process Mech. Eng. 2005, 219, 261–273. [Google Scholar] [CrossRef]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mathkor, R.Z.; Agnew, B.; Al-Weshahi, M.A.; Latrsh, F. Exergetic Analysis of an Integrated Tri-Generation Organic Rankine Cycle. Energies 2015, 8, 8835-8856. https://doi.org/10.3390/en8088835
Mathkor RZ, Agnew B, Al-Weshahi MA, Latrsh F. Exergetic Analysis of an Integrated Tri-Generation Organic Rankine Cycle. Energies. 2015; 8(8):8835-8856. https://doi.org/10.3390/en8088835
Chicago/Turabian StyleMathkor, Ratha Z., Brian Agnew, Mohammed A. Al-Weshahi, and Fathi Latrsh. 2015. "Exergetic Analysis of an Integrated Tri-Generation Organic Rankine Cycle" Energies 8, no. 8: 8835-8856. https://doi.org/10.3390/en8088835
APA StyleMathkor, R. Z., Agnew, B., Al-Weshahi, M. A., & Latrsh, F. (2015). Exergetic Analysis of an Integrated Tri-Generation Organic Rankine Cycle. Energies, 8(8), 8835-8856. https://doi.org/10.3390/en8088835






