Finite Time Analysis of a Tri-Generation Cycle
Abstract
:1. Introduction
2. Literature Review
3. Analysis
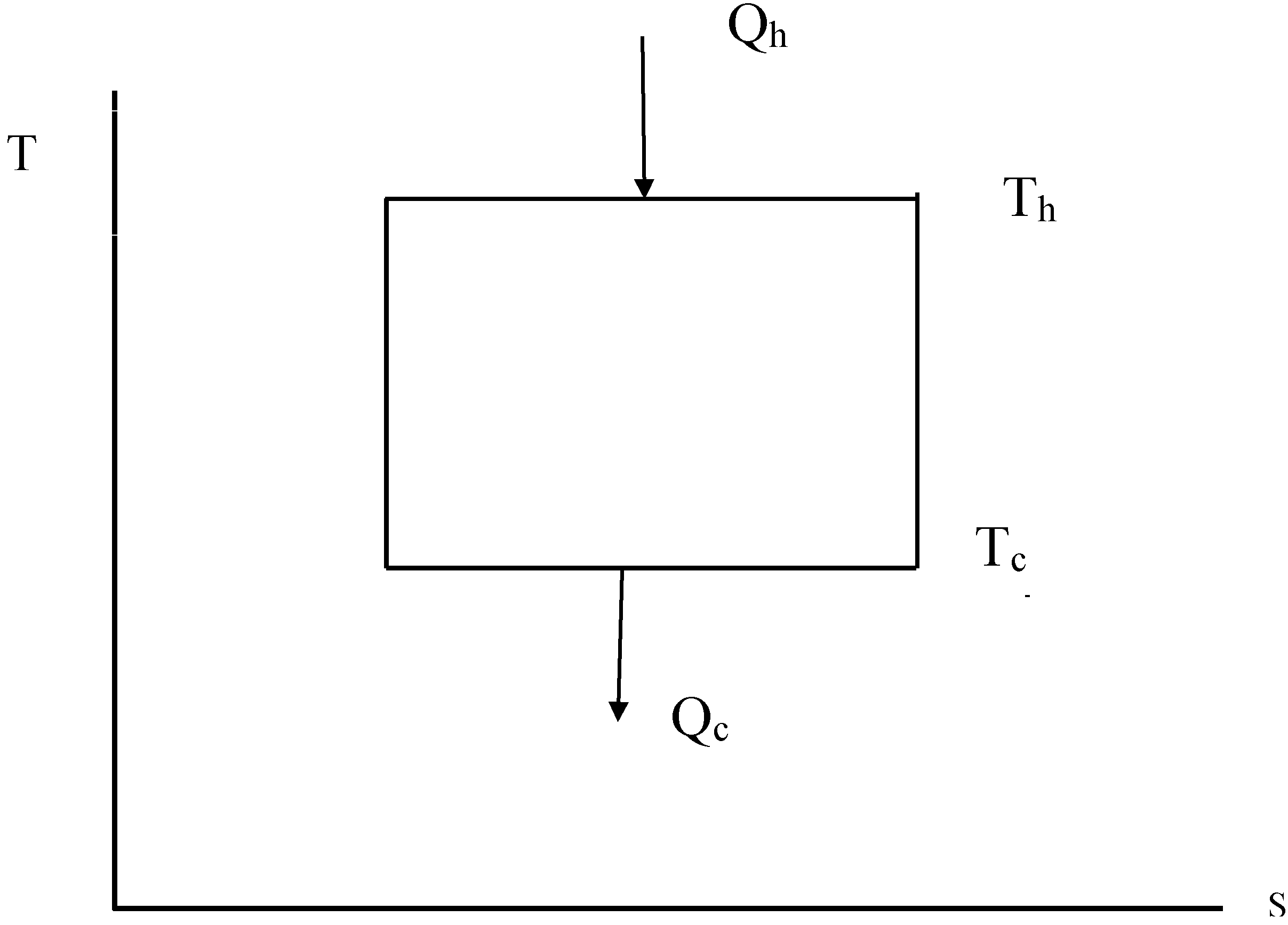
3.1. Finite Time Analysis

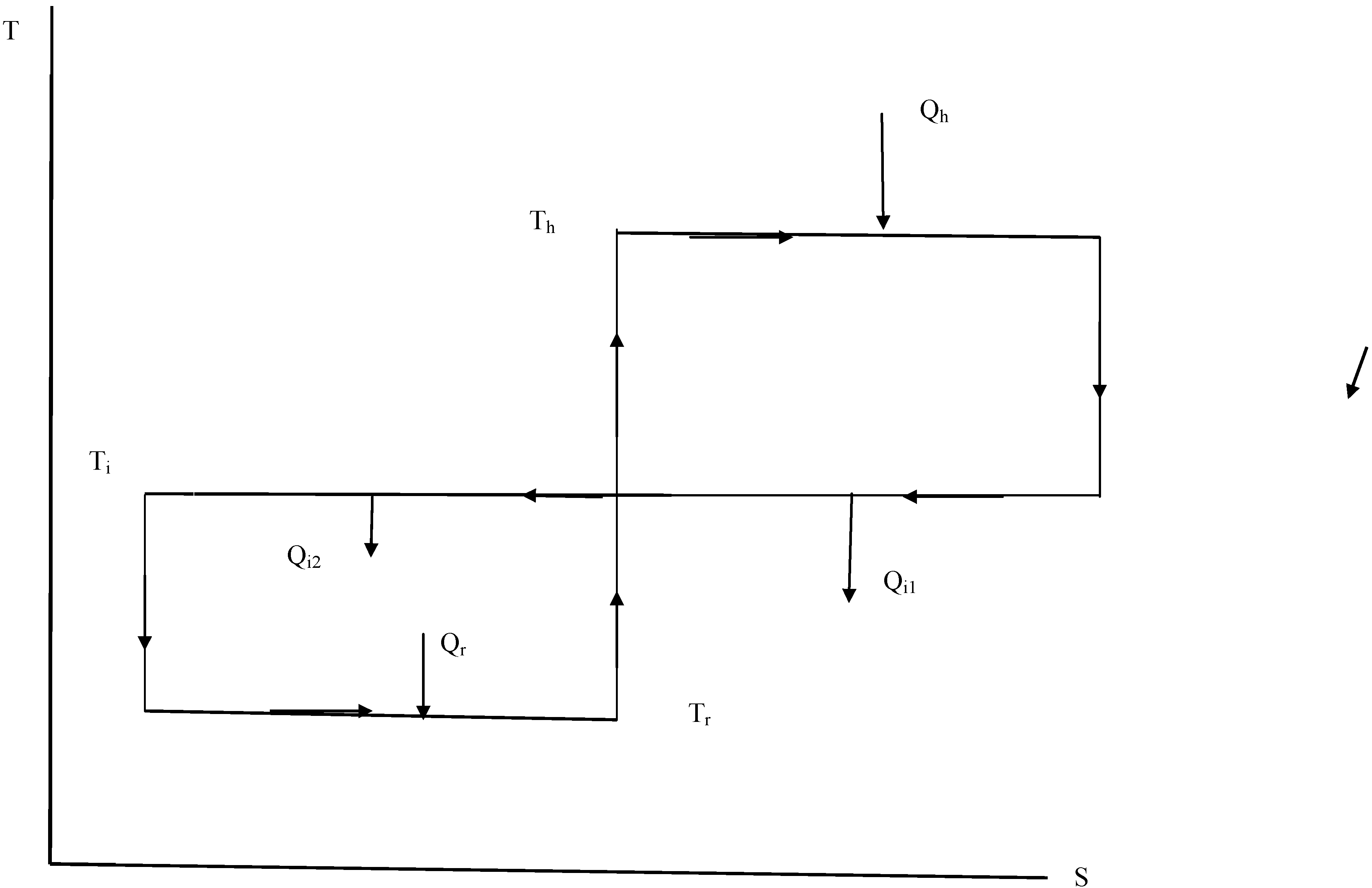
3.2. Tri-Generation Cycle
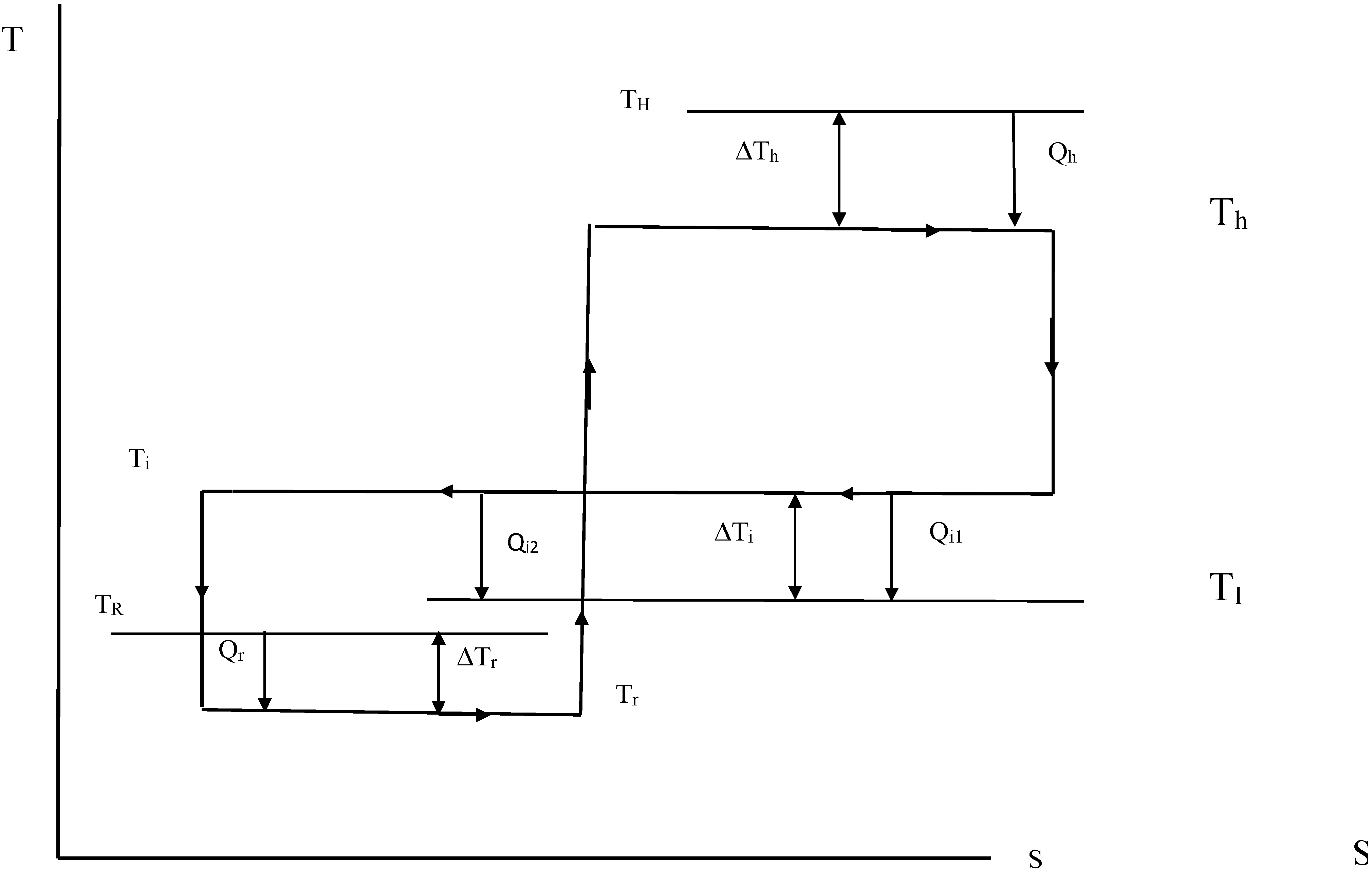
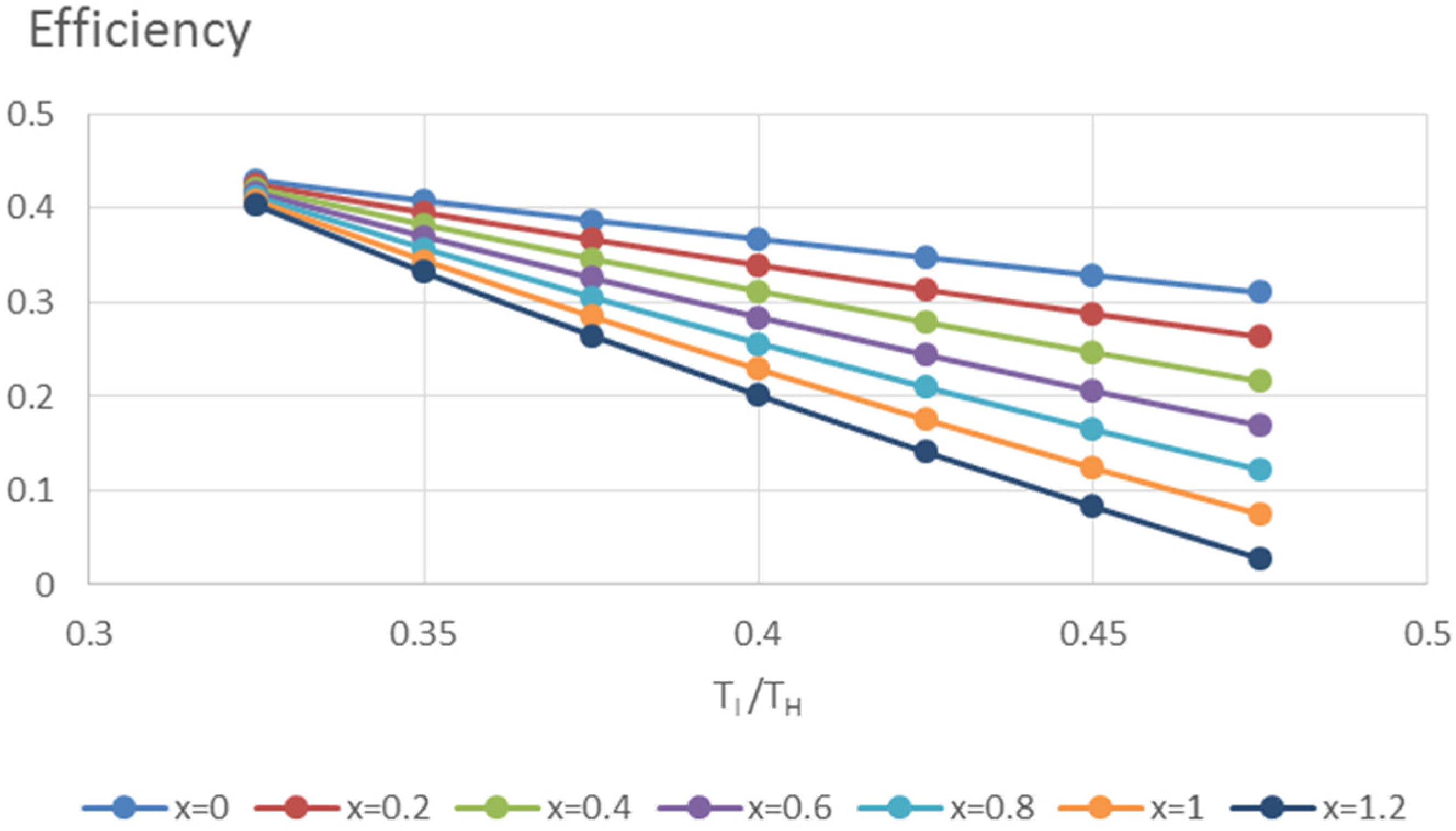
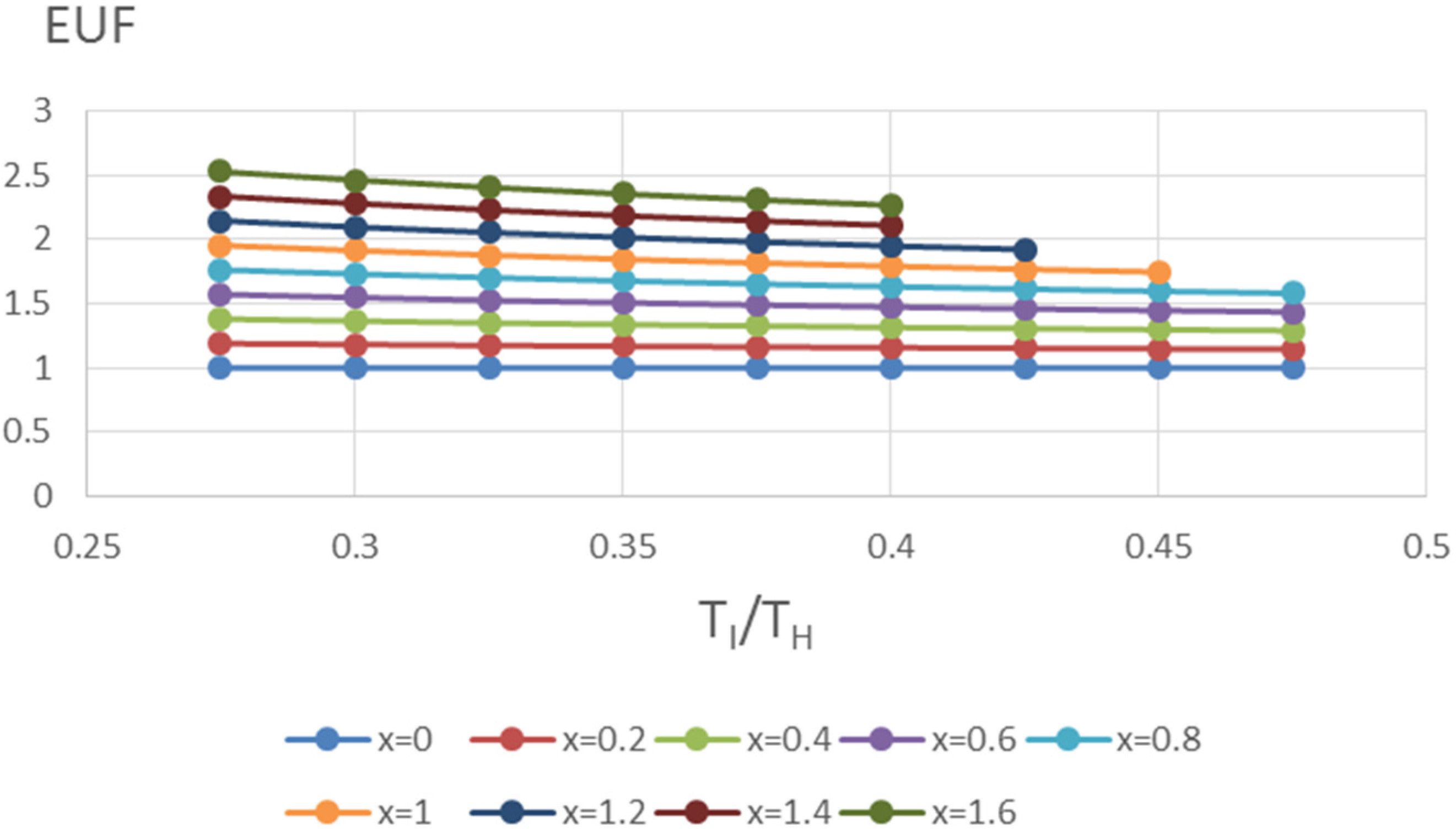
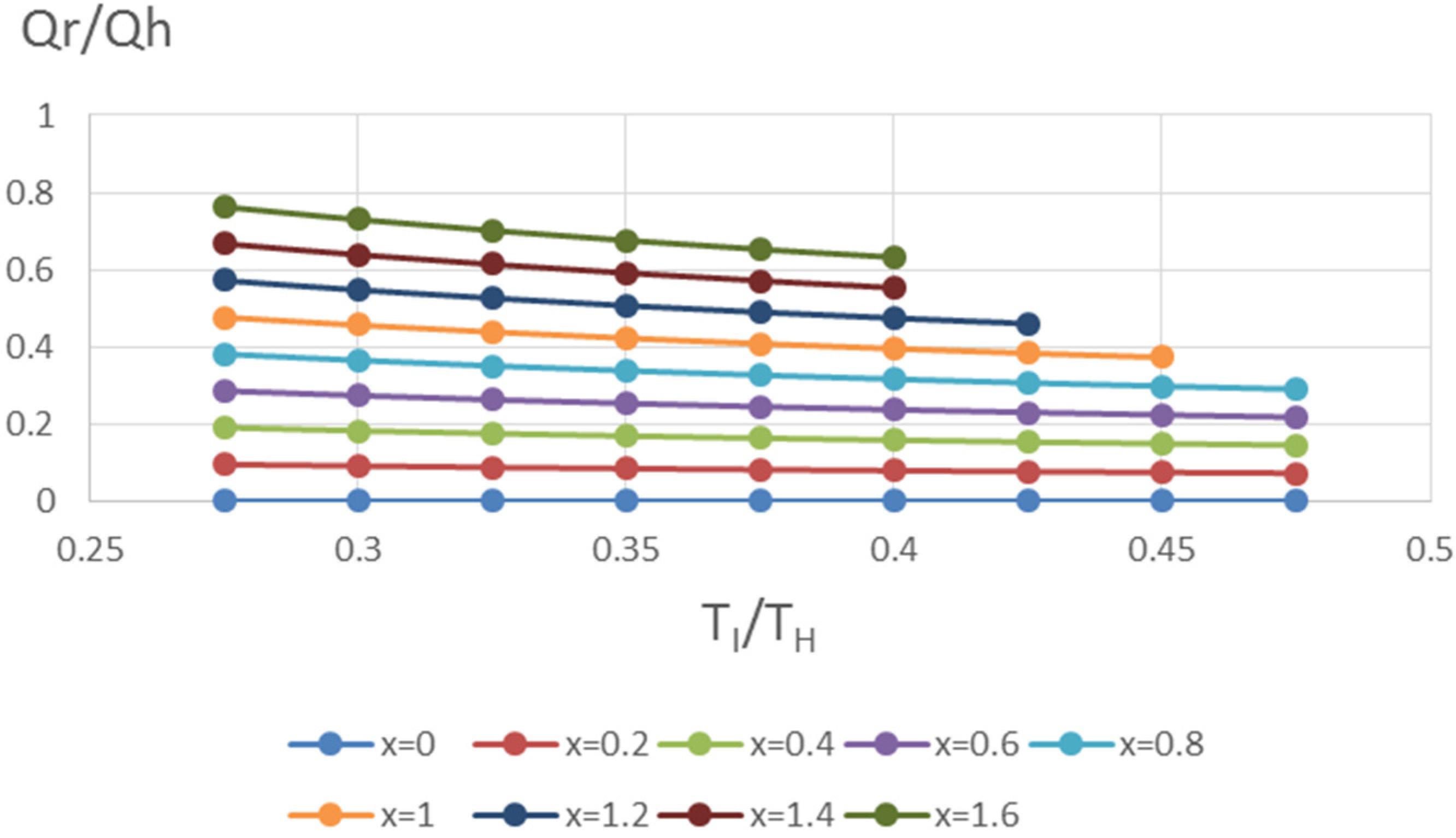

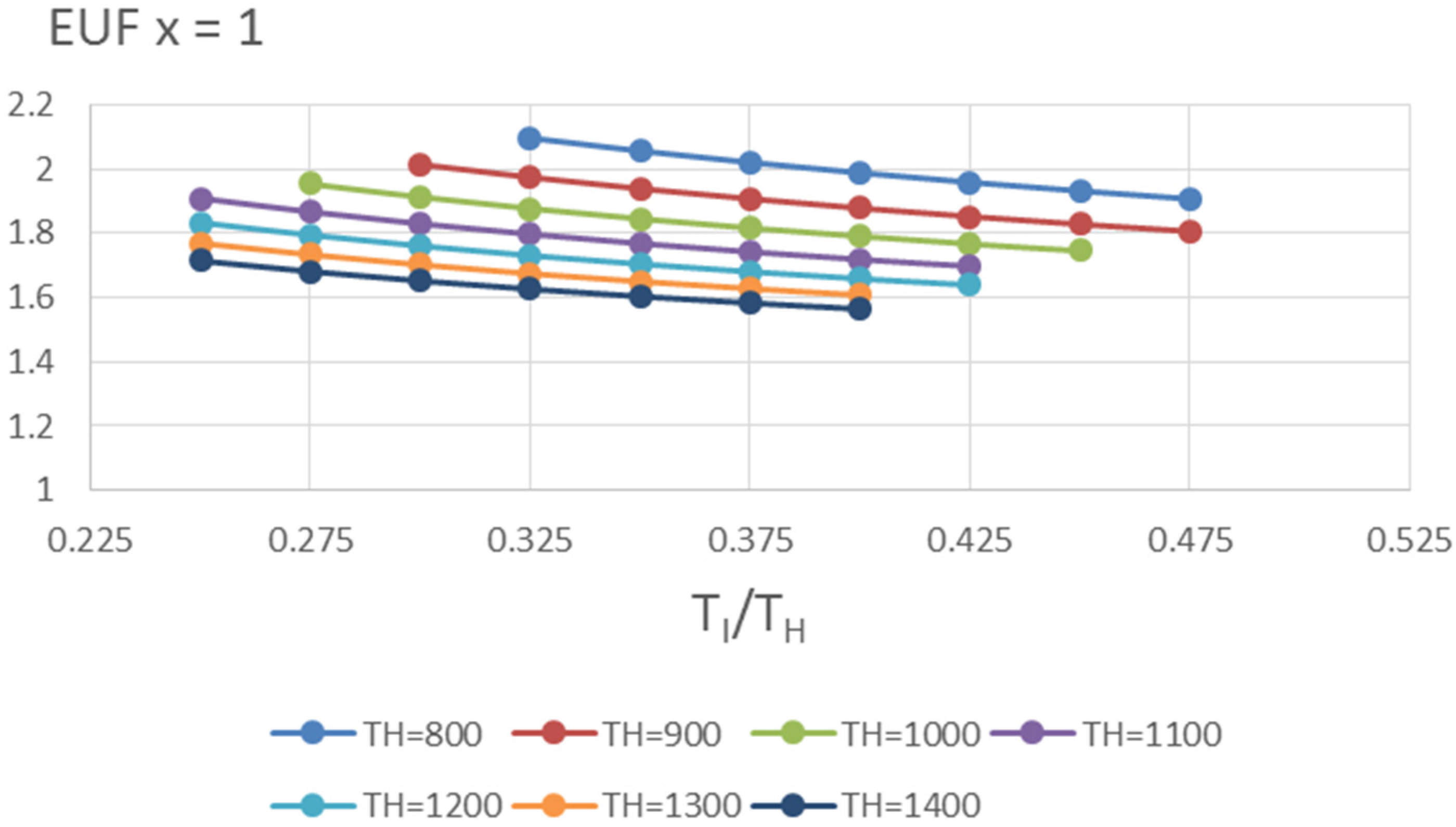
4. Discussion of Results
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Nomenclature
| A | Effective heat transfer area m2 |
| eff | Thermal Efficiency, Network/Primary heat input |
| effp | Efficiency at maximum power condition |
| EUF | Energy utilisation factor; Useful output/Primary input |
| h | Heat transfer coefficient W/m2K |
| P | Net power output W |
| Q | Heat transfer J; Heat transfer rate W |
| Qh | Primary Energy input i.e., that provided from an external source at a financial cost. |
| R | Specific gas constant J/kgK |
| S | Entropy J/kgK |
| T | Temperature K |
| T0 | Heat sink temperature |
| vr | Volume ratio |
| x | Ratio of volume ratios, cooling cycle vr/power cycle vr |
| ΔT | Temperature difference K |
| θ | hA W/K |
| Subscripts | |
| C, c | Low temperature isotherm of Stirling cycle |
| H, h | High temperature |
| I, i | Intermediate temperature |
| R, r | Refrigeration temperature |
| Upper case refers to external reservoir temperature; lower case refers to cycle isotherm | |
References
- Horlock, J.H. Approximate Analysis of Feed and District Heating Cycles for Steam Combined Heat and Power. Proc. Inst. Mech. Eng. Part A: J. Power Energy 1987, 201, 193–200. [Google Scholar] [CrossRef]
- Horlock, J.H.; Haywood, R.W. Thermodynamic Availability and its Application to Combined Heat and Power Plant. Proc. Inst. Mech. Eng. Part C: J. Mech. Eng. Sci. 1985, 199, 11–17. [Google Scholar] [CrossRef]
- Curzon, F.L.; Ahlborn, B. Efficiency of a Carnot Engine at Maximum Power Output. Am. J. Phys. 1975, 43, 22–24. [Google Scholar] [CrossRef]
- Leff, H.S. Thermal efficiency at Maximum Work Output; New Results for Old Engines. Am. J. Phys. 1987, 55, 602–610. [Google Scholar] [CrossRef]
- Salamon, P.; Nitzan, A. Finite Time Optimisation of a Newton’s law Carnot Cycle. J. Chem. Phys. 1981, 74, 3546–3560. [Google Scholar] [CrossRef]
- Gordon, J.M. Maximum Power Point Characteristics of Heat Engines as a General Thermodynamic Problem. Am. J. Phys. 1989, 57, 1136–1142. [Google Scholar] [CrossRef]
- Swanson, L.W. Thermodynamic Optimisation of Irreversible Power Cycles with Constant External Reservoir Temperatures. ASME J. Eng. Gas Turbine Power 1991, 113, 505–510. [Google Scholar] [CrossRef]
- Salamon, P.; Band, Y.B.; Kafri, O. Maximum Power from a Cycling Working Fluid. J. Appl. Phys. 1982, 53, 197–202. [Google Scholar] [CrossRef]
- Rozonoer, L.I.; Tsitlin, A.M. Optimal Control of Thermodynamic Processes. Autom. Remote Control 1983, 44, 314–321. [Google Scholar]
- Kaushik, S.C.; Tyagi, S.K.; Bose, S.K.; Singhal, M.K. Performance Evaluation of Irreversible Stirling and Ericsson Heat Pump cycles. Int. J. Therm. Sci. 2002, 41, 193–200. [Google Scholar] [CrossRef]
- Ondrechen, M.J.; Andersen, B.; Mozurkiewicz, M.; Berry, M.S. Maximum Work from a Finite Reservoir by Sequential Carnot Cycles. Am. J. Phys. 1981, 49, 681–685. [Google Scholar] [CrossRef]
- Pinho, C. The Curzon-Ahlborn Efficiency of Combined Cycles. In Proceedings of the 17th International Congress of Mechanical Engineering, Sao Paulo, Brazil, 10–14 November 2003.
- Sieniutycz, S. Optimal Work in Sequential Systems with Complex Heat Exchange. Int. J. Heat Mass Transf. 2001, 44, 897–918. [Google Scholar] [CrossRef]
- Agnew, B.; Alikitiwi, A.; Anderson, A.A.; Fisher, E.H.; Potts, I. A Finite Time Analysis of Combined Carnot Driving and Cooling Cycles Optimised for Maximum Refrigeration Effect with Applications to Absorption Refrigeration Systems. Exergy Int. J. 2002, 2, 186–191. [Google Scholar] [CrossRef]
- Bejan, A. Advanced Engineering Thermodynamics; Wiley: New York, NY, USA, 1988. [Google Scholar]
- Agnew, B.; Anderson, A.; Frost, T.H. Optimisation of a Steady Flow Carnot Cycle with External Irreversibility for Maximum Specific Output. Appl. Therm. Eng. 1997, 17, 3–15. [Google Scholar] [CrossRef]
- Maloney, J.D.; Robertson, R.C. Thermodynamic Study of Ammonia-Water Heat Power Cycles; Oak Ridge National Laboratory: Oak Ridge, TN, USA, 1953.
- Kalina, A.I.; Tribus, M. Advances in Kalina Cycle Technology (1980–1991): Part I Development of a Practical Cycle. In Proceedings of the Florence World Energy Research Symposium, Firenze, Italy, 7–12 June 1992.
- Xu, F.; Goswami, D.Y. Thermodynamic Properties of Ammonia-Water Mixtures for Power Cycle Applications. Energy 1999, 24, 525–536. [Google Scholar] [CrossRef]
- Tassou, S.A.; Chaer, I.; Suguartha, N.; Ge, T.; Marriott, D. Application of Tri-generation Systems to the Food Retail Industry. Energy Convers. Manag. 2007, 48, 2988–2995. [Google Scholar] [CrossRef]
- Ameri, M.; Behbahaninia, A.; Tanha, A.A. Thermodynamic Analysis of a Tri-generation System Based on Micro-gas Turbine with a Steam Ejector Refrigeration System. Energy 2010, 35, 2203–2209. [Google Scholar] [CrossRef]
- Meunier, F.; Chevalier, C. Environmental Assessment of Biogas Co- or Tri-generation Units by Life Cycle Analysis Methodology. Appl. Therm. Eng. 2005, 25, 3025–3041. [Google Scholar]
- Meunier, F. Co-and Tri-generation Contribution to Climate Change Control. Appl. Therm. Eng. 2002, 22, 703–718. [Google Scholar] [CrossRef]
- Godefroy, J.; Riffat, S.B.; Worall, M.; Boukhanouf, R. Design and Optimisation of a Small-scale Tri-generation System. Int. J. Low-Carbon Technol. 2008, 3, 32–43. [Google Scholar]
- Chen, X. Integration and Optimisation of Bio-fuel Micro Tri-generation with Energy Storage. Ph.D. Thesis, Newcastle University, Newcastle upon Tyne, UK, 2013. [Google Scholar]
- Glavan, I.; Prelec, Z. The Analysis of Trigeneration Energy Systems and Selection of the Best Option Based on Criteria of GHG Emission, Cost and Efficiency. Eng. Rev. 2012, 32, 131–139. [Google Scholar]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Agnew, B.; Walker, S.; Ng, B.; Tam, I.C.K. Finite Time Analysis of a Tri-Generation Cycle. Energies 2015, 8, 6215-6229. https://doi.org/10.3390/en8066215
Agnew B, Walker S, Ng B, Tam ICK. Finite Time Analysis of a Tri-Generation Cycle. Energies. 2015; 8(6):6215-6229. https://doi.org/10.3390/en8066215
Chicago/Turabian StyleAgnew, Brian, Sara Walker, Bobo Ng, and Ivan C. K. Tam. 2015. "Finite Time Analysis of a Tri-Generation Cycle" Energies 8, no. 6: 6215-6229. https://doi.org/10.3390/en8066215
APA StyleAgnew, B., Walker, S., Ng, B., & Tam, I. C. K. (2015). Finite Time Analysis of a Tri-Generation Cycle. Energies, 8(6), 6215-6229. https://doi.org/10.3390/en8066215







