Effects of Scavenging System Configuration on In-Cylinder Air Flow Organization of an Opposed-Piston Two-Stroke Engine
Abstract
:1. Introduction
2. OP2S Engine Scavenging System
2.1. Engine Configuration
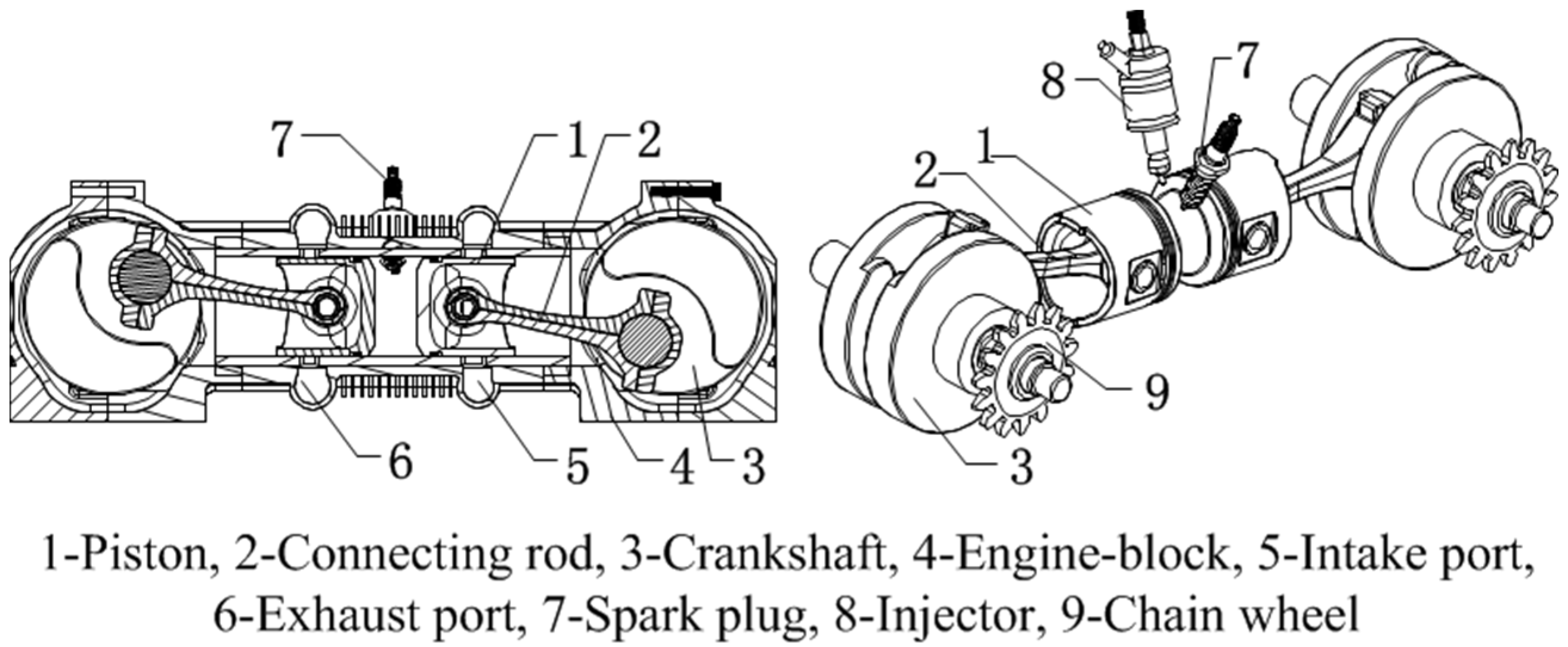
| Parameters | Unit | Value |
|---|---|---|
| Bore | mm | 56 |
| Stroke | mm | 49.5 (×2) |
| Connecting rod | mm | 82.5 |
| Effective compression Ratio | – | 10.5 |
| Engine speed | rpm | 6000 |
| Number of intake ports | – | 10 |
| Number of exhaust ports | – | 10 |
| Intake port height | mm | 12 |
| Exhaust port height | mm | 14 |
| Intake port circumference ratio | – | 0.75 |
| Exhaust port circumference ratio | – | 0.6 |
| Intake port radial angle | ° | 15 |
| Exhaust port radial angle | ° | 0 |
| Power | kW | 15 |
| Fuel consumption rate | g/kW·h | 276 |
2.2. In-Cylinder Air flow Organization

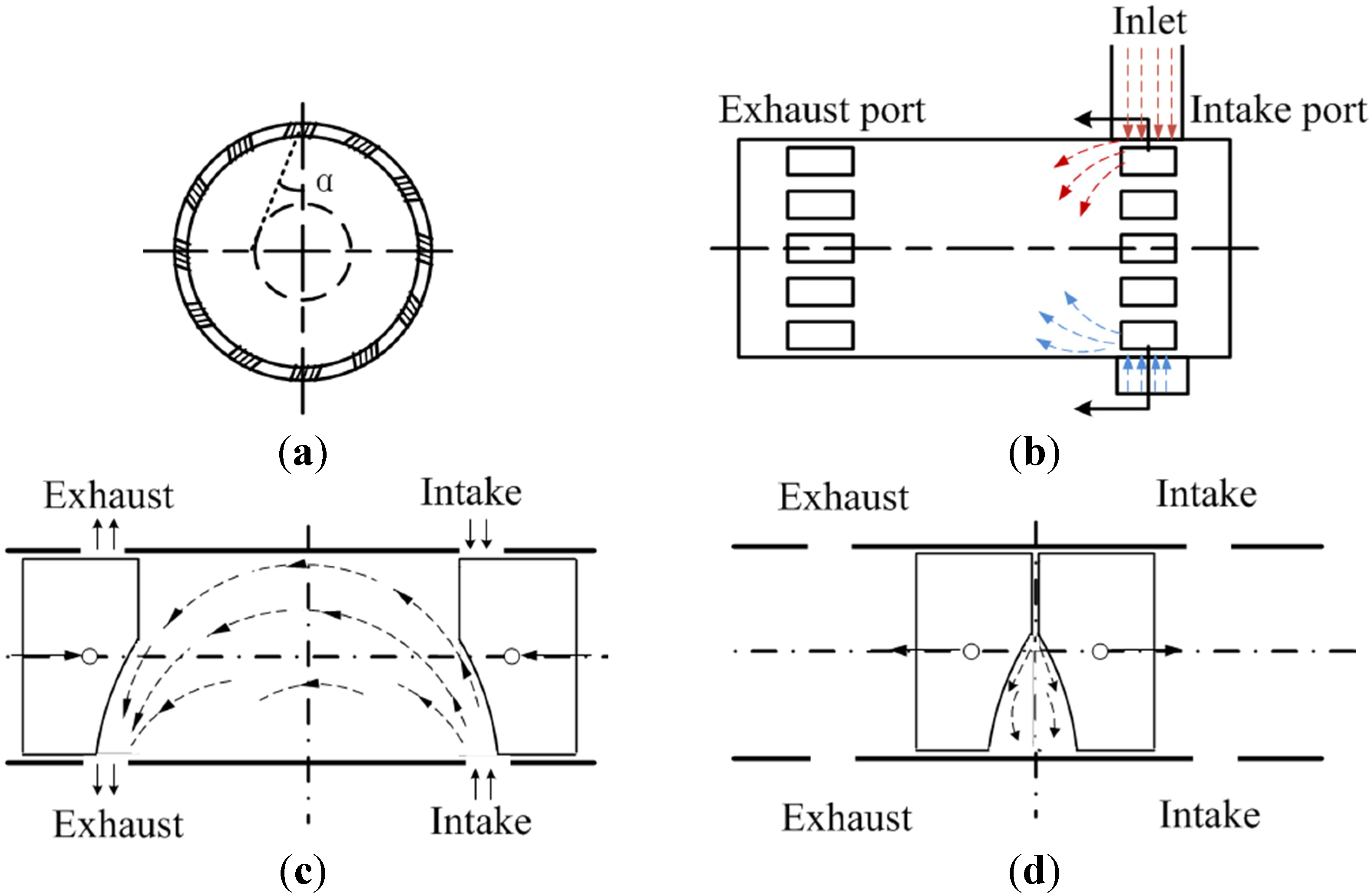
3. Theoretic-Interpretative 0D Model
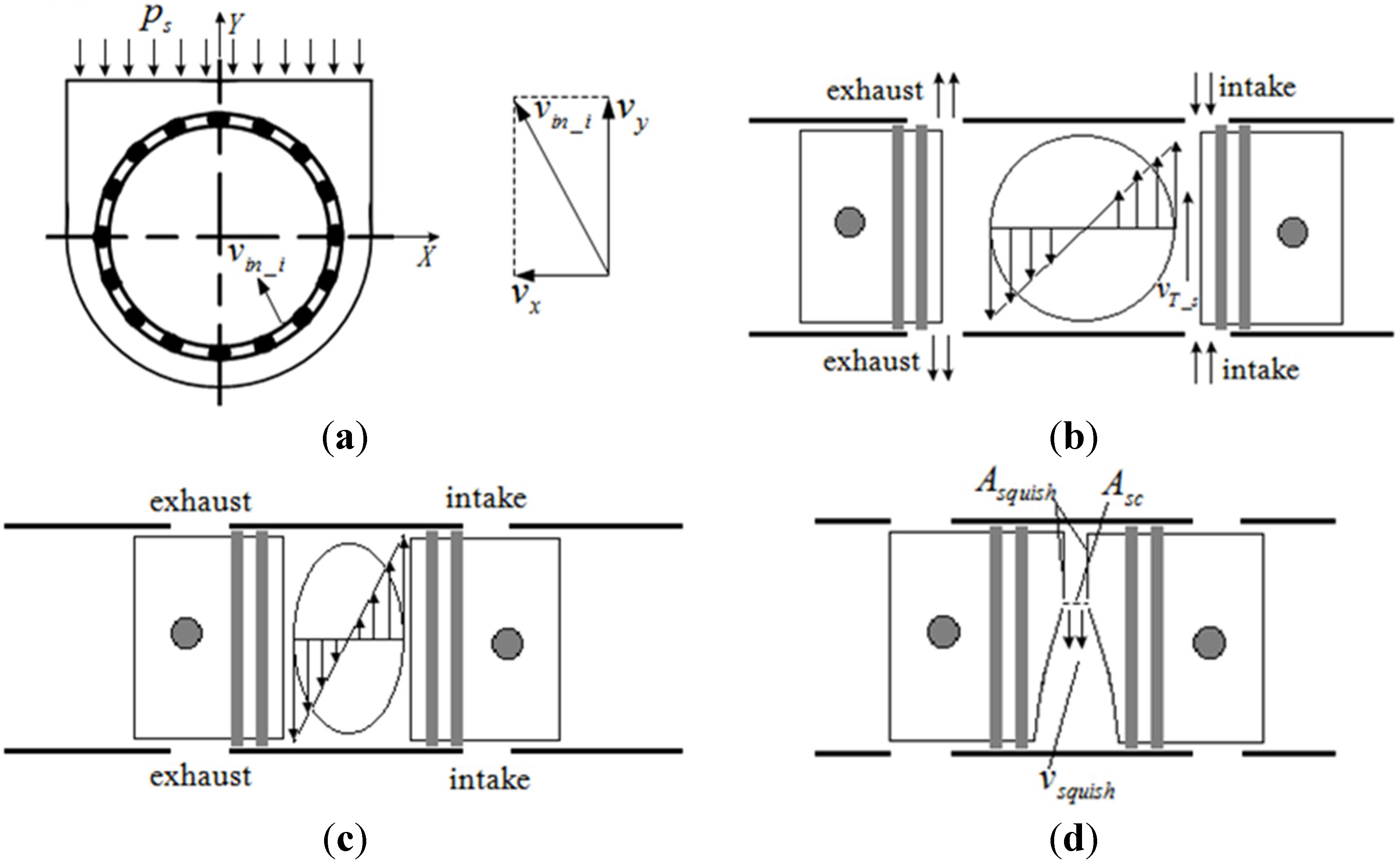
3.1. Tumble Velocity of Non-Uniform Scavenging Process
3.2. The Tumble Velocity in Compression Strokes
3.3. Squish Velocity around IDC
4. Engine Modeling
4.1. CFD Model and Setup

| Scheme | Arrangement | Comments |
|---|---|---|
| 1 |  | Flat piston and uniform scavenging chamber |
| 2 |  | Flat piston and non-uniform scavenging chamber |
| 3 |  | Pit piston and non-uniform scavenging chamber |
4.2. Boundary and Initial Conditions
4.3. Model Validation
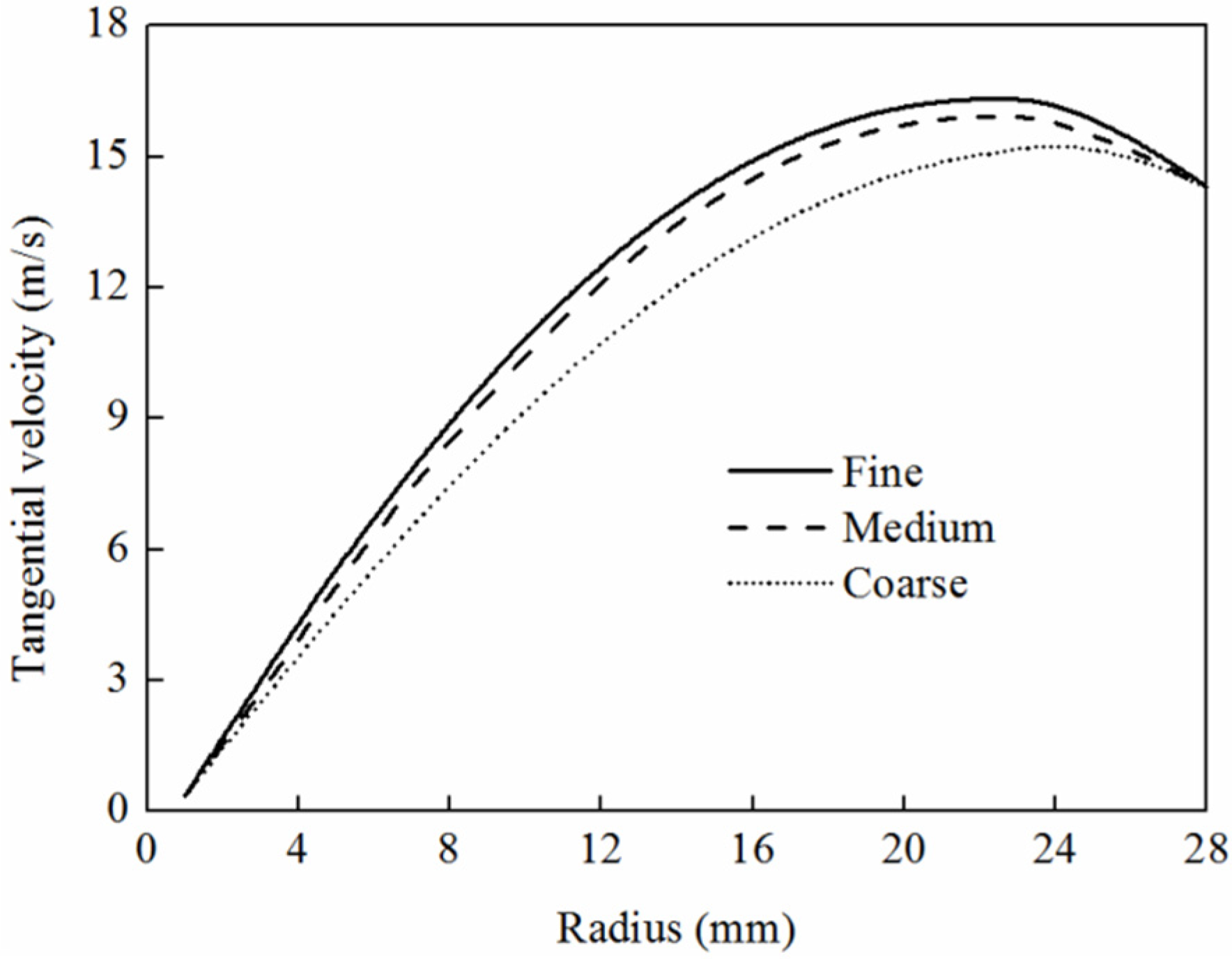
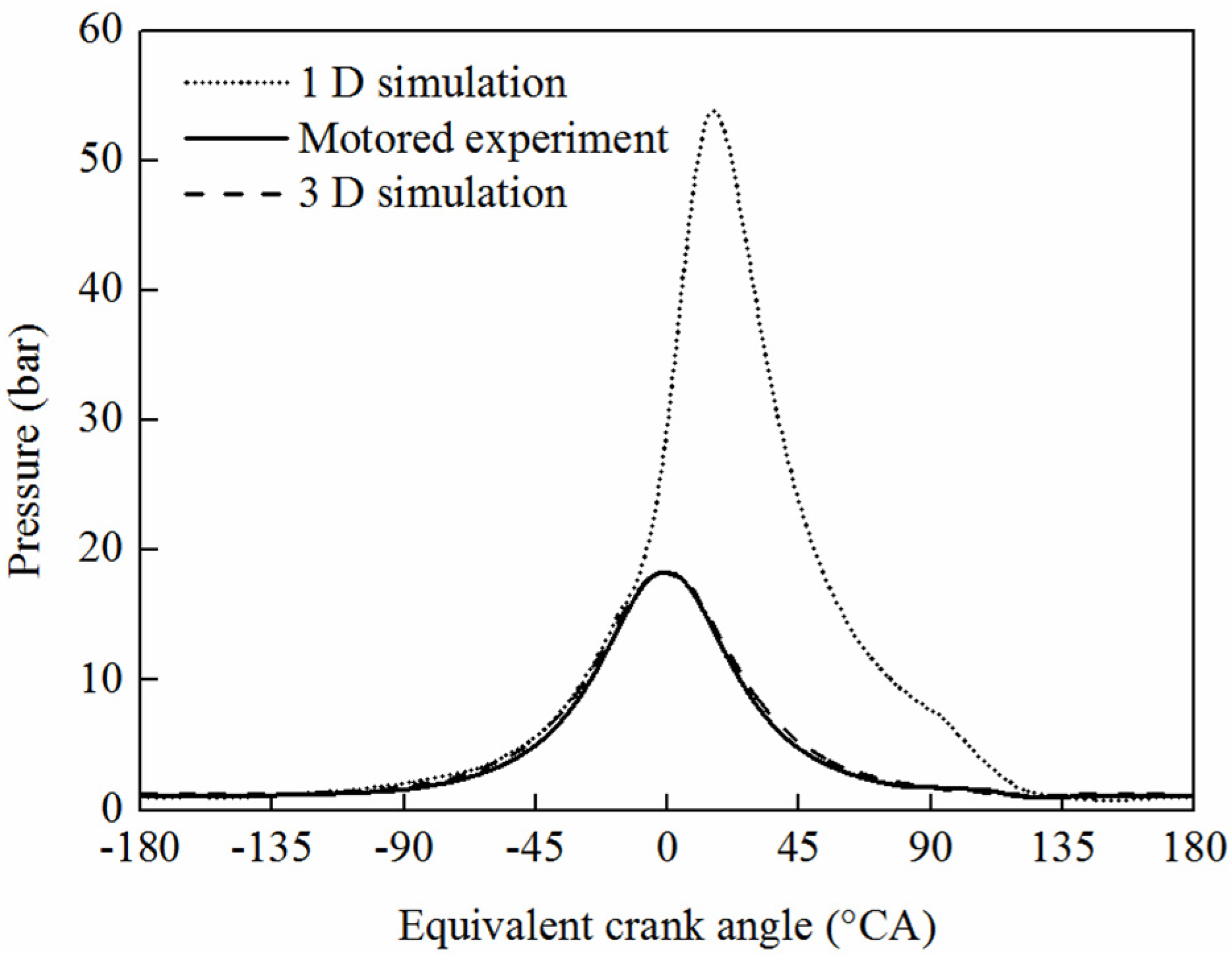
5. Simulation Results and Discussion
5.1. In-Cylinder Air Motion
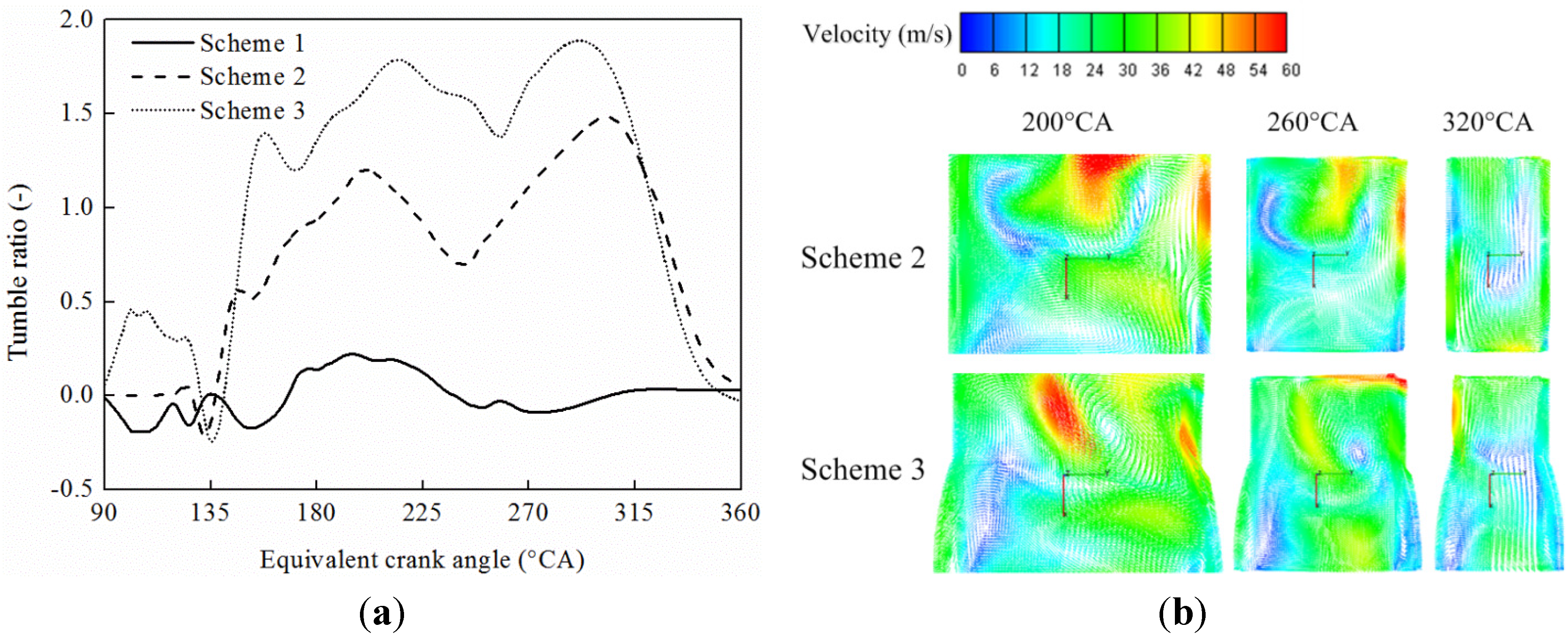
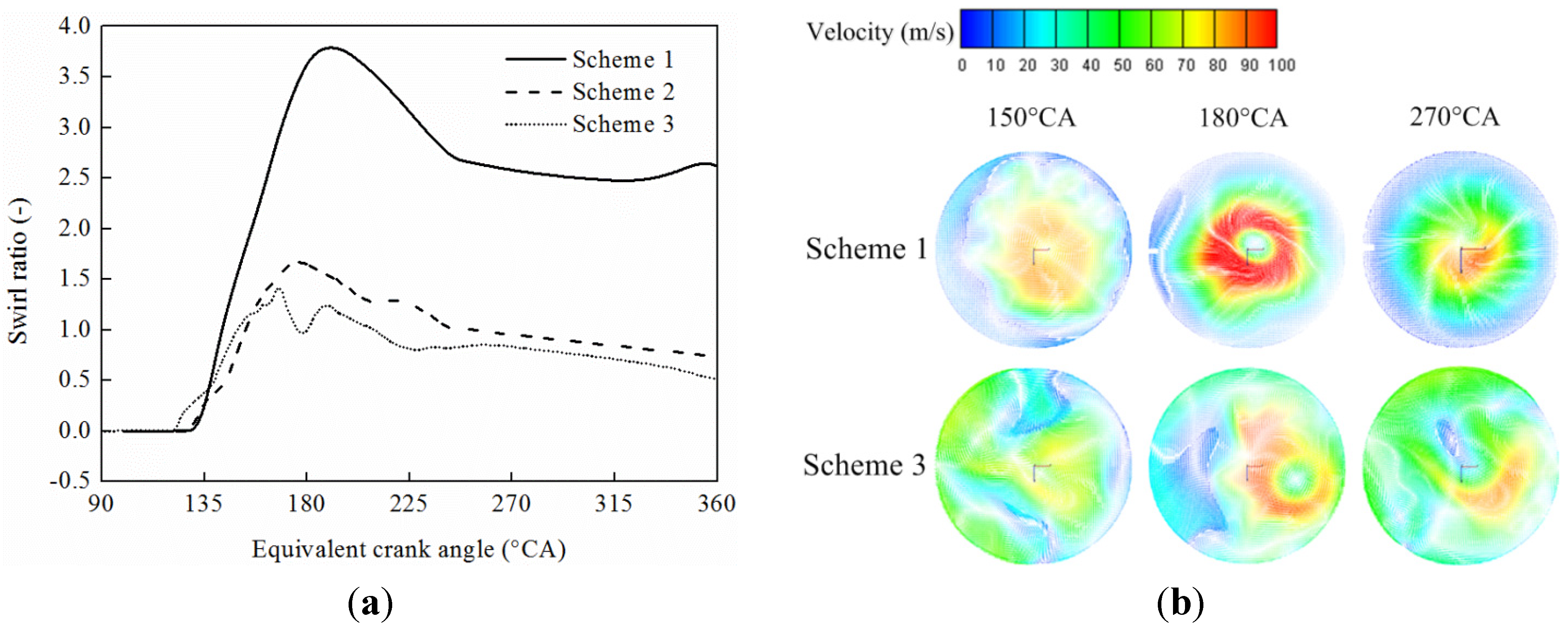
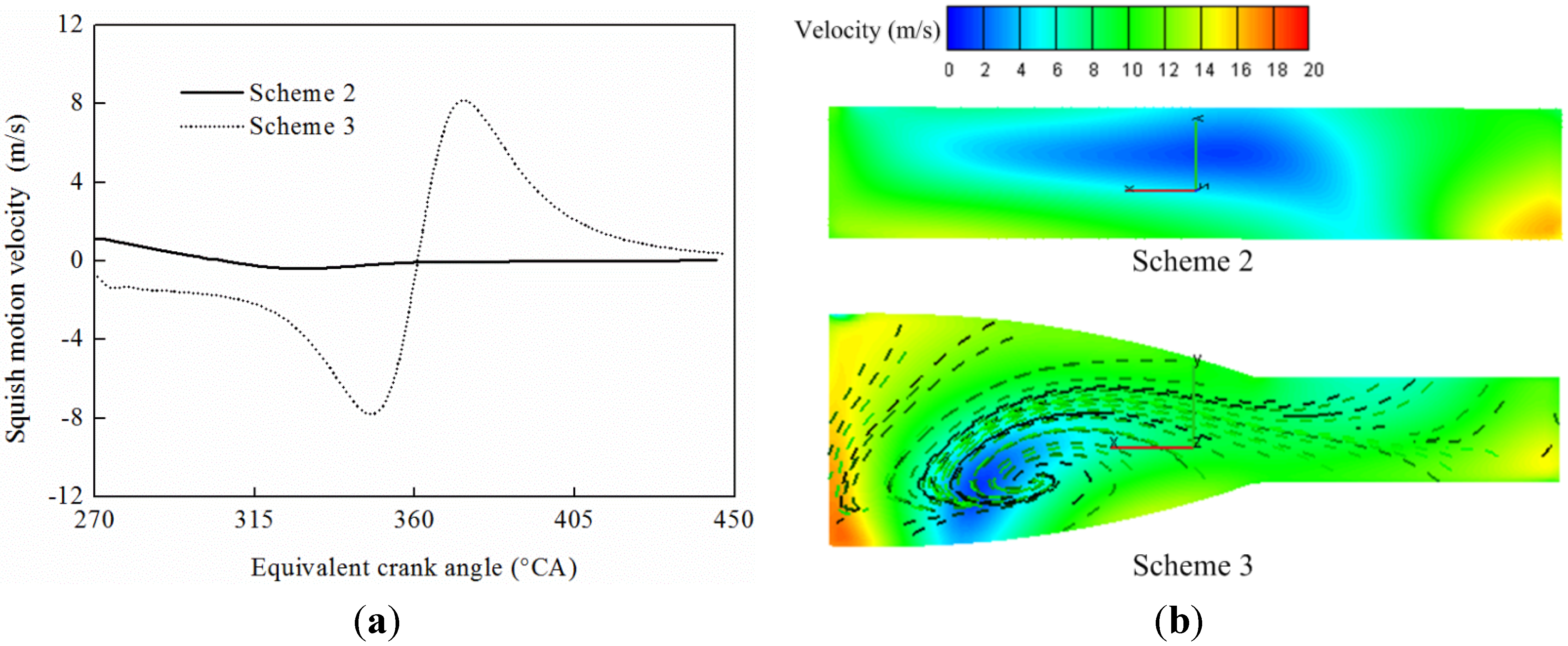
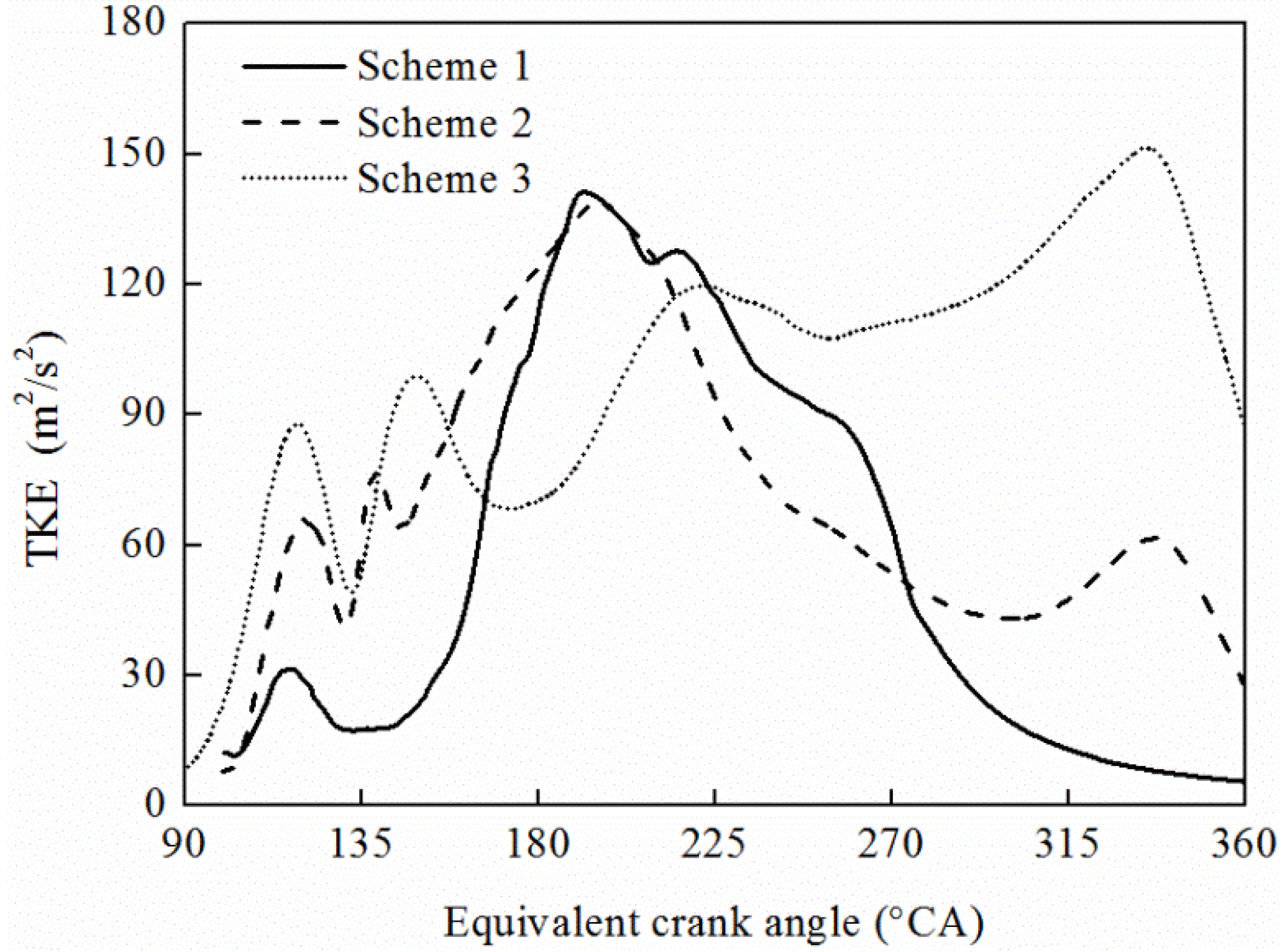
5.2. Turbulence Kinetic Energy
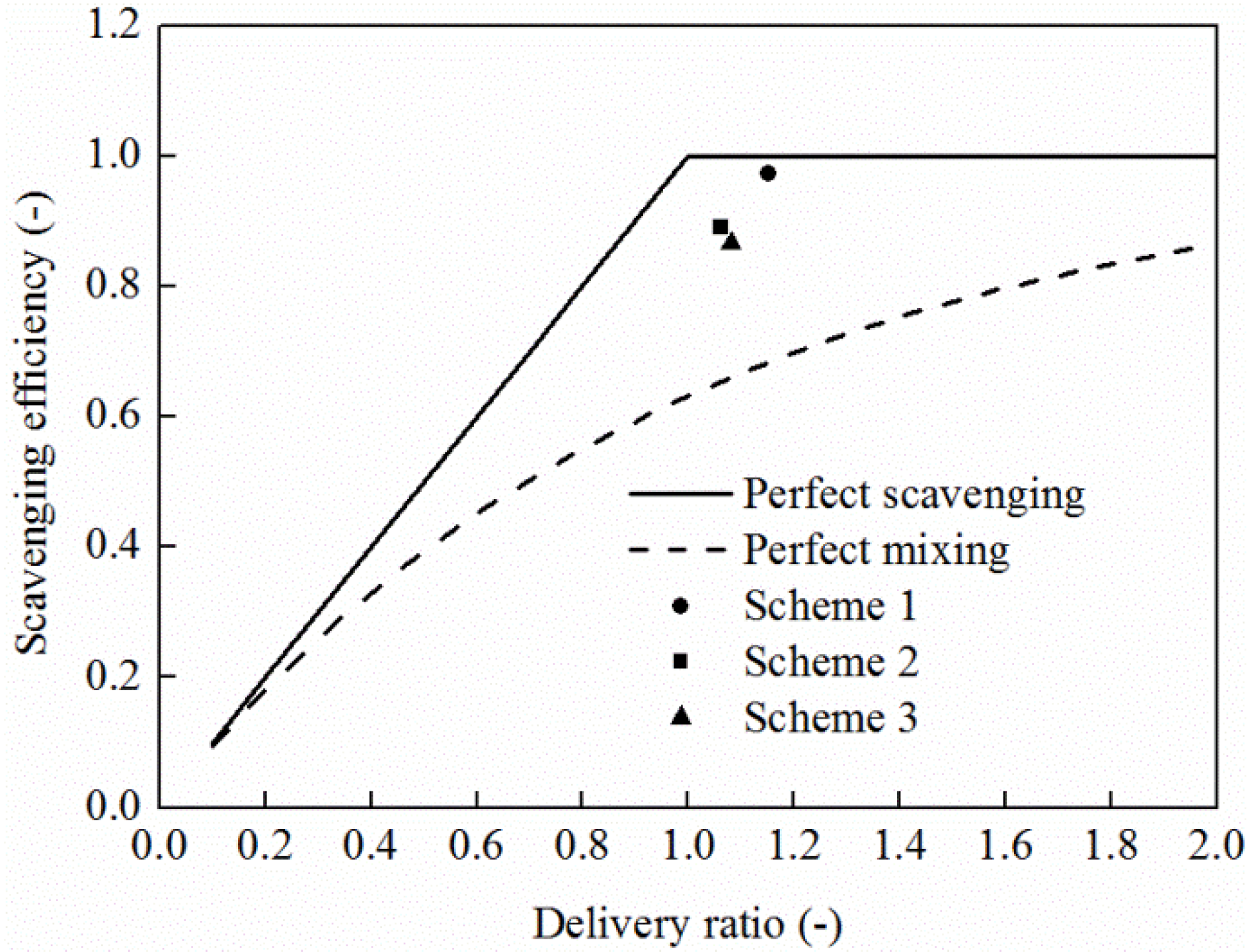
5.3. Scavenging Process

6. Conclusions
- (1)
- The coincidence of the 3D calculation results with the theoretical-interpretative results of the 0D model manifests the veracity of this approach.
- (2)
- The swirl ratio organized by uniform intake chamber is obviously higher than that obtained by a non-uniform intake chamber, while the non-uniform intake chamber can organize inclined-axis tumble, which increases TKE around IDC.
- (3)
- For the non-uniform intake chamber, the pit piston scheme is more beneficial to tumble vortex formation compared to all other scavenging schemes, with a maximum tumble ratio improvement of about 26% over the flat piston scheme.
- (4)
- At 340 °CA, CFD results show that there is an increase in TKE of about 150% for a pit piston compared to that of a flat piston, which is due to squish effect of the pit piston. The uniform intake chamber scheme is not beneficial to the tumble vortex formation and the TKE is minimum before IDC.
- (5)
- The scavenging efficiency and delivery ratio are higher for the uniform intake chamber scheme. It is concluded that a pit piston non-uniform scavenging chamber is a better choice to have good tumble ratio and TKE, but a flat piston uniform scavenging chamber is a better choice to have good swirl ratio, scavenging efficiency and delivery ratio.
Acknowledgments
Author Contributions
Conflicts of Interest
Nomenclature
| 0D | zero-dimensional | number of intake port | |
| 1D | mono-dimensional | engine speed | |
| 3D | three-dimensional | ODC | outer dead center |
| squish compression area | OP2S | opposed-piston two-stroke | |
| CFD | computational fluid dynamics | PIV | particle image velocimetry |
| relative velocity of the opposed pistons | in-cylinder gas pressure | ||
| EPO | exhaust port opening | gas constant | |
| area of intake port in different crank angle | radius of tumble vortex | ||
| GDI | gasoline direct injection | SOC | start of combustion |
| g | gravitational acceleration | gas temperature | |
| distance between the opposed pistons | TDC | top dead center | |
| half distance between the opposed pistons at IPC | relative velocity of the opposed pistons before IDC | ||
| half distance between the opposed pistons in compression process | squish velocity | ||
| instantaneous squish height | instantaneous flow velocity of intake ports | ||
| fluid vortex inertia | instantaneous flow velocity of every intake ports | ||
| fluid vortex inertia in compression process | vectorial sum of the X axial component | ||
| the fluid vortex inertia at IPC | vectorial sum of the Y axial component | ||
| IDC | inner dead center | tumble velocity in compression process | |
| IC | ignition combustion | the tumble velocity at IPC | |
| IPC | intake ports closing | the tumble velocity | |
| angular momentum | the X axial component | ||
| inertia angular momentum at IPC | the Y axial component | ||
| proportionality coefficient | angular velocity of the equivalent rotating solid body | ||
| ratio of squish compression area to cylinder cross section area | intake port flow coefficient | ||
| adiabatic exponent | ϕ | crank angle |
References
- Pirault, J.P.; Flint, M. Opposed Piston Engines: Evolution, Use, and Future Applications; SAE International: Warrendale, PA, USA, 2010. [Google Scholar]
- Naik, S.; Johnson, D.; Koszewnik, J. Practical Applications of Opposed-Piston Engine Technology to Reduce Fuel Consumption and Emissions; SAE Technical Paper 2013-01-2754; SAE International: Warrendale, PA, USA, 2013. [Google Scholar]
- Hofbauer, P. Opposed Piston Opposed Cylinder (OPOC) Engine for Military Ground Vehicles; SAE Technical Paper 2005-01-1548; SAE International: Warrendale, PA, USA, 2005. [Google Scholar]
- Hirsch, N.R.; Schwarz, E.E.; McGough, M.G. Advanced Opposed-Piston Two-Stroke Diesel Demonstrator; SAE Technical Paper 2006-01-0926; SAE International: Warrendale, PA, USA, 2006. [Google Scholar]
- Herold, R.E.; Wahl, M.H.; Regner, G. Thermodynamic Benefits of Opposed-Piston Two-Stroke Engines; SAE Technical Paper 2011-01-2216; SAE International: Warrendale, PA, USA, 2011. [Google Scholar]
- Regner, G.; Herold, R.E.; Wahl, M.H. The Achates Power Opposed-Piston Two-Stroke Engine: Performance and Emissions Results in a Medium-Duty Application; SAE Technical Paper 2011-01-2221; SAE International: Warrendale, PA, USA, 2011. [Google Scholar]
- Redon, F.; Kalebjian, C.; Kessler, J. Meeting Stringent 2025 Emissions and Fuel Efficiency Regulations with an Opposed-Piston, Light-Duty Diesel Engine; SAE Technical Paper 2014-01-1187; SAE International: Warrendale, PA, USA, 2014. [Google Scholar]
- Regner, G.; Johnson, D.; Koszewnik, J. Modernizing the Opposed Piston, Two-Stroke Engine for Clean, Efficient Transportation; SAE Technical Paper 2013-26-0114; SAE International: Warrendale, PA, USA, 2013. [Google Scholar]
- Zhao, F.; Lai, M.C.; Harrington, D.L. Automotive spark-ignited direct-injection gasoline engines. Prog. Energy Combust. Sci. 1999, 25, 437–562. [Google Scholar] [CrossRef]
- Arcoumanis, C.; Bae, C.S.; Hu, Z. Flow and Combustion in a Fourvalve, Spark-Ignition Optical Engines; SAE Paper 940475; SAE International: Warrendale, PA, USA, 1994. [Google Scholar]
- Fan, L.; Reitz, R.D.; Trigui, N. Intake Flow Simulation and Comparison with PTV Measurements; SAE Technical Paper 1999-01-0176; SAE International: Warrendale, PA, USA, 1999. [Google Scholar]
- Ismail, H.M.; Ng, H.K.; Gan, S. Evaluation of non-premixed combustion and fuel spray models for in-cylinder diesel engine simulation. Appl. Energy 2012, 90, 271–279. [Google Scholar] [CrossRef]
- Mikalsen, R.; Roskilly, A.P. A computational study of free-piston diesel engine combustion. Appl. Energy 2009, 86, 1136–1143. [Google Scholar] [CrossRef]
- Rakopoulos, C.D.; Kosmadakis, G.M.; Dimaratos, A.M. Investigating the effect of crevice flow on internal combustion engines using a new simple crevice model implemented in a CFD code. Appl. Energy 2011, 88, 111–126. [Google Scholar] [CrossRef]
- Jia, M.; Xie, M.Z.; Wang, T.Y. The effect of injection timing and intake valve close timing on performance and emissions of diesel PCCI engine with a full engine cycle simulation. Appl. Energy 2011, 88, 2967–2975. [Google Scholar] [CrossRef]
- Micklow, G.J.; Gong, W.D. Intake and in-cylinder flow field modeling of a four valve diesel engine. Proc. Mech. Int. J. Automob. Eng. 2007, 221, 1425–1440. [Google Scholar] [CrossRef]
- Nordgren, H.; Hildingsson, L.; Johansson, B. Comparison between In-Cylinder Measurements, CFD Simulations and Steady Flow Impulse Torque Swirl Meter Measurements; SAE Technical Paper 2003-01-3147; SAE International: Warrendale, PA, USA, 2003. [Google Scholar]
- Sweetland, P.; Reitz, R.D. Particle Image Velocimetry Measurements in the Piston Bowl of a DI Diesel Engine; SAE Technical Paper 940283; SAE International: Warrendale, PA, USA, 1994. [Google Scholar]
- Gunasekaran, E.J.; Ganesan, V. Simulation of Fuel-Air Interaction in a Four Stroke Four Valve Direct Injected Spark Ignition Engine; SAE Technical Paper 2007-01-0153; SAE International: Warrendale, PA, USA, 2007. [Google Scholar]
- Rakopoulos, C.D.; Kosmadakis, G.M.; Pariotis, E.G. Investigation of piston bowl geometry and speed effects in a motored HSDI diesel engine using a CFD against a quasi-dimensional model. Energy Convers Manag. 2010, 51, 470–484. [Google Scholar] [CrossRef]
- Lin, L.; Shulin, D.; Jin, X. Effects of Combustion Chamber Geometry on In-Cylinder Air Motion and Performance in DI Diesel Engine; SAE technical paper 2000-01-0510; SAE International: Warrendale, PA, USA, 2000. [Google Scholar]
- Shimoda, M.; Shigemori, M.; Tsuruoka, S. Effect of Combustion Chamber Configuration on In-Cylinder Air Motion and Combustion Characteristics of DI Diesel Engine; SAE Technical Paper 850070; SAE International: Warrendale, PA, USA, 1985. [Google Scholar]
- Dolak, J.G.; Shi, Y.; Reitz, R.D. A Computational Investigation of Stepped-Bowl Piston Geometry for a Light Duty Engine Operating at Low Load; SAE Technical Paper 2010-01-1263; SAE International: Warrendale, PA, USA, 2010. [Google Scholar]
- Falfari, S.; Brusiani, F.; Bianchi, G.M. Assessment of the Influence of Intake Duct Geometrical Parameters on the Tumble Motion Generation in a Small Gasoline Engine; SAE Technical Paper 2012-32-0095; SAE International: Warrendale, PA, USA, 2012. [Google Scholar]
- Falfari, S.; Brusiani, F.; Bianchi, G.M. Numerical analysis of in-cylinder tumble flow structures-parametric 0D model development. Energy Procedia 2014, 45, 987–996. [Google Scholar] [CrossRef]
- Ramajo, D.; Zanotti, A.; Nigro, N. Assessment of a zero-dimensional model of tumble in four-valve high performance engine. Int. J. Numer. Methods Heat Fluid Flow 2007, 17, 770–787. [Google Scholar] [CrossRef]
- Sigurdsson, E.; Ingvorsen, K.M.; Jensen, M.V. Numerical analysis of the scavenge flow and convective heat transfer in large two-stroke marine diesel engines. Appl. Energy 2014, 123, 37–46. [Google Scholar] [CrossRef]
- Taylor, C.F. The Internal-Combustion Engine in Theory and Practice: Thermodynamics, Fluid Flow, Performance, 2nd ed.; MIT Press: Cambridge, UK, 1985; Volume 1, p. 584. [Google Scholar]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ma, F.; Zhao, C.; Zhang, F.; Zhao, Z.; Zhang, S. Effects of Scavenging System Configuration on In-Cylinder Air Flow Organization of an Opposed-Piston Two-Stroke Engine. Energies 2015, 8, 5866-5884. https://doi.org/10.3390/en8065866
Ma F, Zhao C, Zhang F, Zhao Z, Zhang S. Effects of Scavenging System Configuration on In-Cylinder Air Flow Organization of an Opposed-Piston Two-Stroke Engine. Energies. 2015; 8(6):5866-5884. https://doi.org/10.3390/en8065866
Chicago/Turabian StyleMa, Fukang, Changlu Zhao, Fujun Zhang, Zhenfeng Zhao, and Shuanlu Zhang. 2015. "Effects of Scavenging System Configuration on In-Cylinder Air Flow Organization of an Opposed-Piston Two-Stroke Engine" Energies 8, no. 6: 5866-5884. https://doi.org/10.3390/en8065866
APA StyleMa, F., Zhao, C., Zhang, F., Zhao, Z., & Zhang, S. (2015). Effects of Scavenging System Configuration on In-Cylinder Air Flow Organization of an Opposed-Piston Two-Stroke Engine. Energies, 8(6), 5866-5884. https://doi.org/10.3390/en8065866







