Credibility Theory-Based Available Transfer Capability Assessment
Abstract
:1. Introduction
2. Credibility Theory
2.1. Basic Concept
2.2. Random Fuzzy Variable
3. Credibility Theory-Based ATC Assessment Approach
3.1. Modeling Uncertainties in ATC Calculation
3.2. ATC Calculation Model
3.3. ATC Assessment Indices
- (a)
- The expected value of random fuzzy ATC—EATC—it comprehensively reflects the ATC of a power system.
- (b)
- The variance of random fuzzy ATC—VATC—it expresses the fluctuation of ATC and reflects the impacts of uncertainties on ATC:
- (c)
- Calculation time t: it reflects the efficiency of different ATC calculation approaches under the same initial conditions.
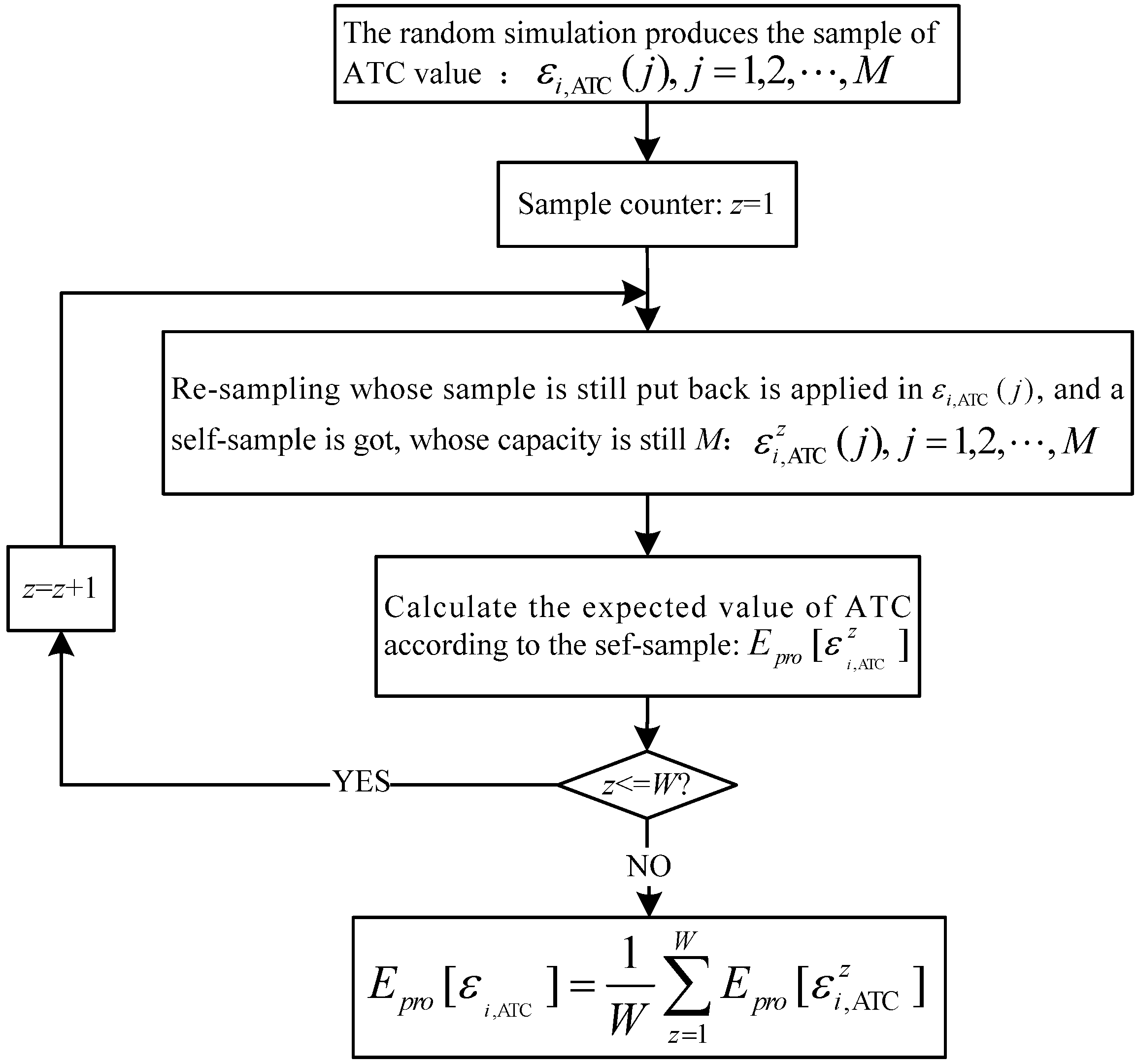
3.4. Parallel Algorithm with Bootstrap Method
3.5. Random Fuzzy Simulation Based ATC Assessment
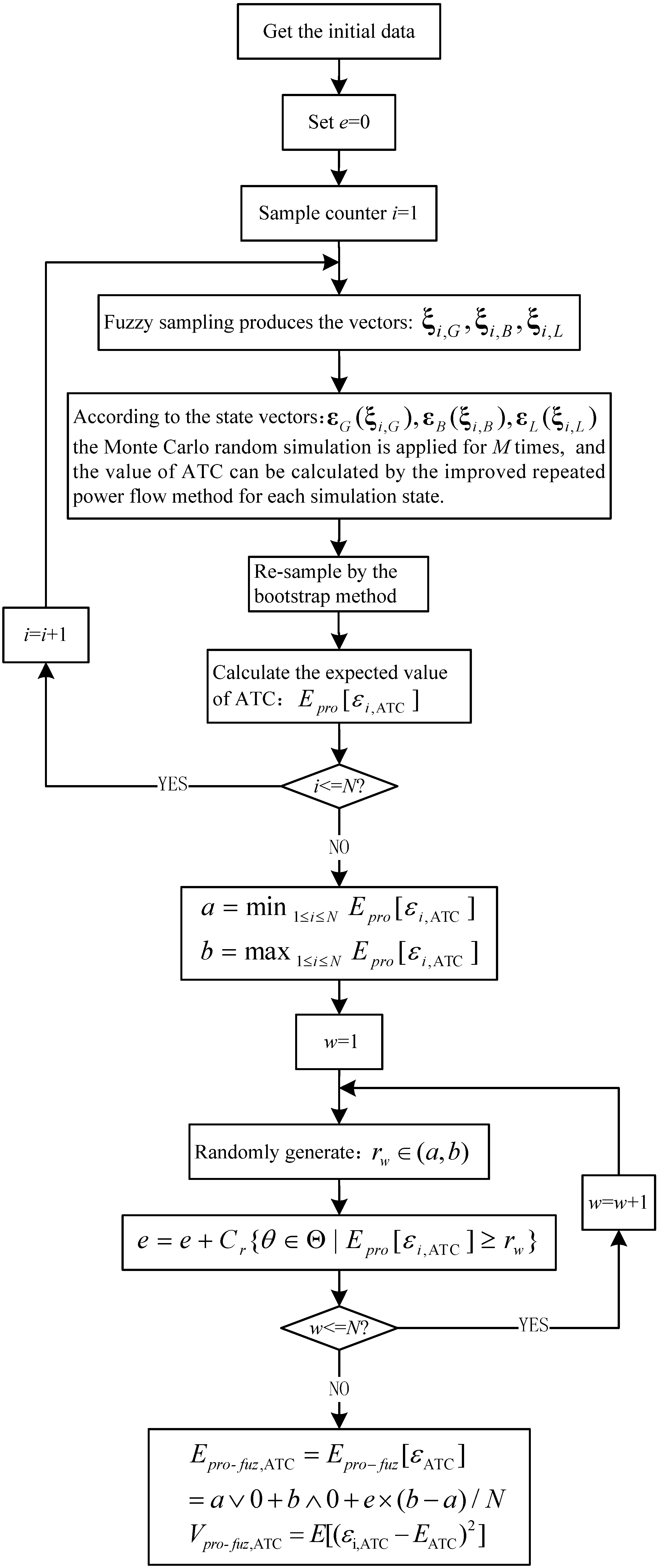
- (1)
- Read the initial parameters of generators, transmission lines and loads, build basic system information and set e = 0, i = 1.
- (2)
- From the set Θ extract a θk which meets POS{θk} ≥ ε (ε is a permissible small value making the sample space be bounded), get the variables of generators, transmission lines and loads, and produce a set of fuzzy sampling vectors: .
- (3)
- According to and the corresponding equipment random parameters, get the system state vectors: , change the random fuzzy models of generators, transmission lines and loads to the random ones, then the fuzziness is eliminated. Then the Monte Carlo random simulation is applied M times, and the value of ATC can be calculated by the improved repeated power flow method for each simulation state.
- (4)
- By the bootstrap method re-sample in the above obtained ATC values, and calculate their expected value of ATC. Figure 2 illustrates the bootstrap method procedure.
- (5)
- Set sample counter i = i + 1, and repeat (2) to (4) for N times.
- (6)
- Set a = min1≤i≤NEpro[εi,ATC], b = max1≤i≤NEpro[εi,ATC], and loop control variable w = 1.
- (7)
- From the interval [a, b] randomly generate rw and calculate .
- (8)
- Set w = w + 1, and repeat (7) for N times.
- (9)
- Lastly calculate the expected value and variance of ATC as follows:
4. Numerical Example
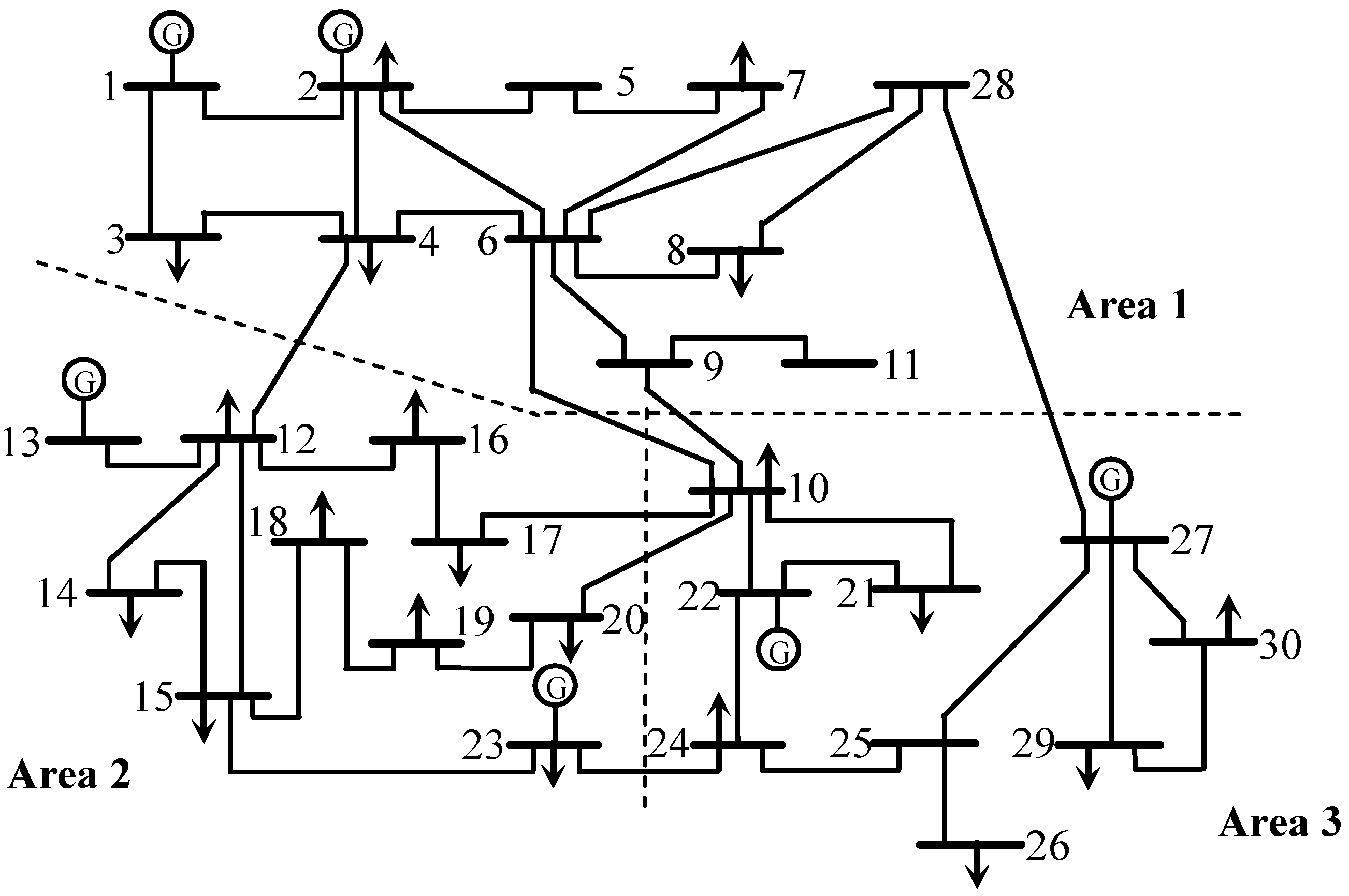
4.1. IEEE-30-bus System
Part 1: Compatibility analysis between the proposed approach and the conventional Monte Carlo random simulation.
| Method | Case | Generators | Transmission Lines | Loads | |
|---|---|---|---|---|---|
| λG | ξG | ξB | ξL | ||
| Monte Carlo random simulation (10,000 times) | A | 0.01 | 1 | None | None |
| B | None | None | 0.02 | None | |
| C | None | None | None | 0.02 | |
| Random fuzzy simulation | D | 0.01 | (0.9999, 1, 1.0001) | None | None |
| E | None | None | (0.0199, 0.0200, 0.0201) | None | |
| F | None | None | None | (0.0199, 0.0200, 0.02001) | |
| Case | Epro-fuzz,ATC (MW) | Vpro-fuzz,ATC (MW2) |
|---|---|---|
| A | 8.5883 | 3.8085 |
| D | 8.4657 | 3.6602 |
| Error (%) | −1.4275 | −3.8939 |
| Case | Epro-fuzz,ATC (MW) | Vpro-fuzz,ATC (MW2) |
|---|---|---|
| B | 9.7541 | 121.4598 |
| E | 10.8670 | 123.5610 |
| Error (%) | 11.4096 | 1.7300 |
| Case | Epro-fuzz,ATC (MW) | Vpro-fuzz,ATC (MW2) |
|---|---|---|
| C | 11.3496 | 117.2293 |
| F | 11.7530 | 117.3173 |
| Error (%) | 3.5543 | 0.0751 |
Part 2: The comparison between the proposed assessment method and the traditional Monte Carlo simulation approach.
| Case | Generators | Transmission Lines | Loads | |
|---|---|---|---|---|
| λG | ξG | ξB | ξL | |
| J | 0.01 | (0.700, 1.0000, 1.100) | None | None |
| H | None | None | (0.0100, 0.0200, 0.0600) | None |
| I | None | None | None | (0.0100, 0.0200, 0.0600) |
| Case | Epro-fuzz,ATC (MW) | Vpro-fuzz,ATC (MW2) |
|---|---|---|
| A | 8.5883 | 3.8085 |
| J | 8.4212 | 3.8310 |
| Error (%) | 1.9457 | 0.5908 |
| Case | Epro-fuzz,ATC (MW) | Vpro-fuzz,ATC (MW2) |
|---|---|---|
| B | 9.7541 | 121.4598 |
| H | 10.6504 | 168.7090 |
| Error (%) | 9.1890 | 38.9011 |
| Case | Epro-fuzz,ATC (MW) | Vpro-fuzz,ATC (MW2) |
|---|---|---|
| C | 11.3496 | 117.2293 |
| I | 14.3061 | 261.7169 |
| Error (%) | 26.0494 | 123.2521 |
Part 3: The sensitivity analysis to the fuzzy influencing factors of ATC.
| Case | Epro-fuzz,ATC (MW) | Vpro-fuzz,ATC (MW2) |
|---|---|---|
| H | 10.6504 | 168.709 |
| J | 10.5893 | 141.8906 |
| Case | Epro-fuzz,ATC (MW) | Vpro-fuzz,ATC (MW2) |
|---|---|---|
| I | 14.3061 | 261.7169 |
| K | 14.3047 | 261.6058 |
| L | 13.0457 | 170.9183 |
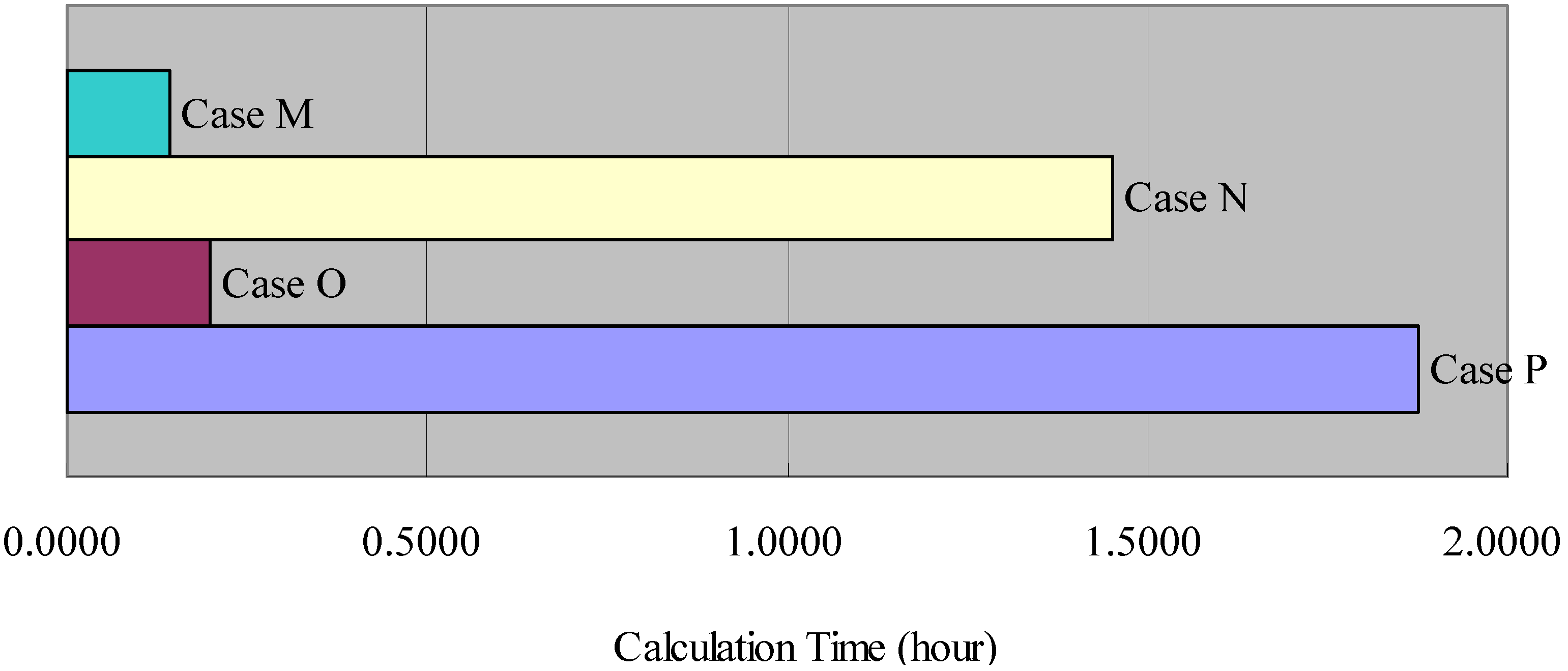
Part 4: The comparison about the processing efficiency.
| Case | Bootstrap Method | Dual-core Parallel Computing Technique |
|---|---|---|
| M | √ | √ |
| N | × | √ |
| O | √ | × |
| P | × | × |
4.2. An Actual Power System in Northwest China
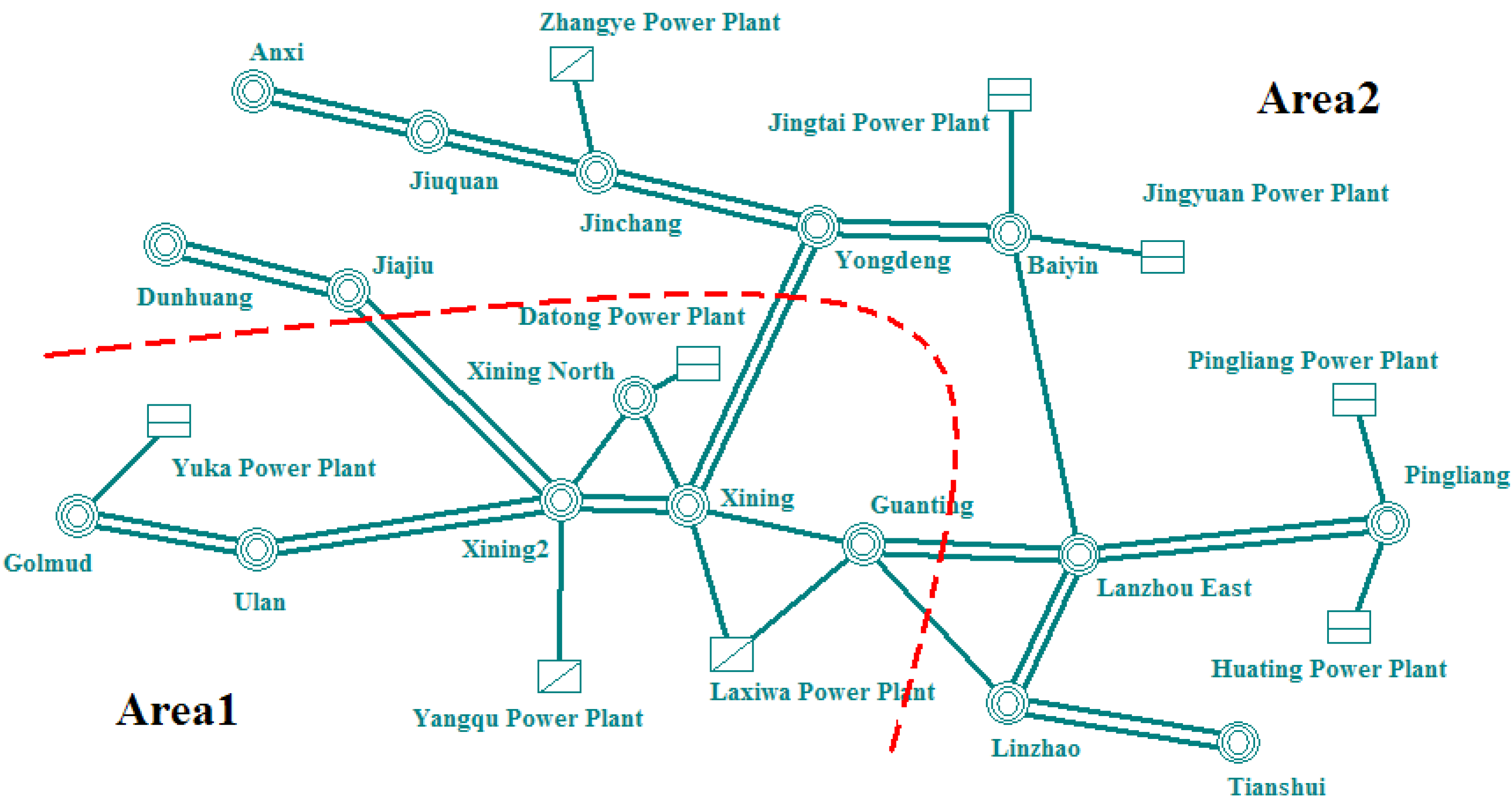
| Method | Case | Generators | Transmission Lines | Loads | |
|---|---|---|---|---|---|
| λG | ξG | ξB | ξL | ||
| Monte Carlo random simulation (10,000 times) | Q | 0.01 | 1 | 0.02 | 0.02 |
| Random fuzzy simulation | R | 0.01 | (0.9400, 1, 1.1400) | (0.0100, 0.0190, 0.0400) | (0.0100, 0.0190, 0.0400) |
| Case | Epro-fuzz,ATC (MW) | Vpro-fuzz,ATC (MW2) |
|---|---|---|
| Q | 4417 | 4,702,842 |
| R | 4145 | 5,241,506 |
| Error (%) | −6.1591 | 11.4540 |
5. Conclusions
Author Contributions
Conflicts of Interest
Nomenclature
| Θ | Nonempty set. |
| ϕ | Empty set. |
| P(Θ) | Power set of Θ. |
| ∧ | Minimum operator. |
| ∨ | Maximum operator. |
| Pos | Possibility measure of fuzzy event. |
| Nec | Necessity measure of fuzzy event. |
| Cr | Credibility measure of fuzzy event. |
| μ | Membership function of fuzzy variable. |
| B | Borel set. |
| sup | Supremum. |
| Efuz | Expected value of fuzzy variable. |
| Epro | Expected value of random variable. |
| Epro-fuz | Expected value of random fuzzy variable. |
| R | Set of real numbers. |
| (Θ,P(Θ),POS) | Possiblity space. |
| Ppro,G | State occurrence probability of generator. |
| Ppro,B | State occurrence probability of transmission line. |
| εG | Random fuzzy state of generator. |
| εB | Random fuzzy state of transmission line. |
| εL | Random fuzzy nodal load. |
| λG | Forced outage rate of generator. |
| ξG | Fuzzy available output of generator. |
| ξB | Fuzzy failure rate of transmission line. |
| ξL | Fuzzy variance of a nodal load. |
| Ffuz,G | Membership function of ξG. |
| Ffuz,B | Membership function of ξB. |
| Ffuz,L | Membership function of ξL. |
| a*,L | Minimum possible value. |
| a*,M | Most likely possible value. |
| a*,H | Maximum possible value. |
| βL | Load forecasting value. |
| f | Electricity purchase cost. |
| Pg | Active power output of the generator g. |
| Pgmax, Pgmin | Upper and lower limits of Pg. |
| Qg | Reactive power output of the generator g. |
| Qgmax, Qgmin | Upper and lower limits of Qg. |
| Pd | Active load of the node d. |
| Qd | Reactive load of the node d. |
| Vz | Voltage of the node z. |
| Vzmax, Vzmin | Upper and lower limits of Vz. |
| Sl | Apparent power of the transmission line l. |
| Slmax | Maximum value of Sl. |
| Gxy | Conductance of the branch from node x to y. |
| Bxy | Susceptance of the branch from node x to y. |
| δxy | Voltage phase angle difference of the branch from node x to y. |
| εATC | Random fuzzy value of ATC. |
| Epro-fuz,ATC | Expected value of random fuzzy ATC. |
| Vpro-fuz,ATC | Variance of random fuzzy ATC. |
| t | Calculation time. |
| N, M, W | Sampling times. |
References
- North American Electric Reliability Council (NERC). Available Transfer Capability Definitions and Determination; NERC: Swindon, UK, 1996. [Google Scholar]
- Power Systems Engineering Research Center (PSERC). Electric Power Transfer Capability: Concepts, Applications, Sensitivity and Uncertainty; PSERC Publication: Tempe, AZ, USA, 2001. [Google Scholar]
- Sauer, P.W. Alternatives for calculating transmission reliability margin (TRM) in available transfer capability. In Proceedings of the Thirty-First Hawaii International Conference, Kona, HI, USA, 6–9 January 1998; p. 89.
- Ou, Y.; Singh, C. Assessment of Available Transfer Capability and Margins. IEEE Trans. Power Syst. 2002, 17, 463–468. [Google Scholar]
- Shin, D.-J.; Kim, J.-O.; Kim, K.-H.; Singh, C. Probabilistic approach to available transfer capability calculation. Electr. Power Syst. Res. 2007, 77, 813–820. [Google Scholar] [CrossRef]
- Akbari, T.; Rahimikian, A.; Kazemi, A. A multi-stage stochastic transmission expansion planning method. Energy Convers. Manag. 2011, 52, 2844–2853. [Google Scholar] [CrossRef]
- Liu, B.; Liu, Y.-K. Expected value of fuzzy variable and fuzzy expected value models. IEEE Trans. Fuzzy Syst. 2002, 10, 445–450. [Google Scholar]
- Liu, B. Toward fuzzy optimization without mathematical ambiguity. Fuzzy Optim. Decis. Mak. 2002, 1, 43–63. [Google Scholar] [CrossRef]
- Liu, B. Uncertainty Theory: An Introduction to Its Axiomatic Foundations; Springer-Verlag: Berlin/Heidelberg, Germany, 2004. [Google Scholar]
- Liu, B. A survey of credibility theory. Fuzzy Optim. Decis. Mak. 2006, 5, 387–408. [Google Scholar] [CrossRef]
- Liu, B.; Liu, Y.-K. Expected value operatot of random fuzzy variable and random fuzzy expected value models. Int. J. Uncertain. Fuzziness Knowl.-Based Syst. 2003, 11, 195–215. [Google Scholar] [CrossRef]
- Feng, Y.; Wu, W.; Zhang, B.; Li, W. Power system operation risk assessment using credibility theory. IEEE Trans. Power Syst. 2008, 23, 1309–1318. [Google Scholar] [CrossRef]
- Feng, Y.; Wu, W.; Zhang, B.; Sun, H.; Wang, S. Hydro-thermal generator maintenance scheduling based on credibility theory. Proc. Chin. Soc. Electr. Eng. 2006, 26, 14–19. [Google Scholar]
- Ma, X.; Liu, J.; Wen, F. Random-fuzzy programming model for developing optimal bidding strategies in the uncertain environment. Proc. Chin. Soc. Electr. Eng. 2009, 29, 77–83. [Google Scholar]
- Wu, J.; Wu, Q.; Chen, G.; Liang, Y.; Zhou, J. Fuzzy random chance-constrained programming for quantifying the transmission reliability margin. Autom. Electr. Power Syst. 2007, 31, 23–28. [Google Scholar]
- Kwakernaak, H. Fuzzy random variables I. Inf. Sci. 1978, 15, 1–29. [Google Scholar] [CrossRef]
- Kwakernaak, H. Fuzzy random variables II. Inf. Sci. 1979, 17, 253–278. [Google Scholar] [CrossRef]
- Zhou, J.; Liu, B. Analysis and algorithms of bifuzzy systems. Int. J. Uncertain. Fuzziness Knowl.-Based Syst. 2004, 12, 357–376. [Google Scholar] [CrossRef]
- Liang, R.-H.; Liao, J.-H. A fuzzy optimization approach for generation scheduling with wind and solar energy systems. IEEE Trans. Power Syst. 2007, 22, 1665–1674. [Google Scholar] [CrossRef]
- Kaufmann, A. Introduction to the Theory of Fuzzy Subsets; Academic Press: Waltham, MA, USA, 1975. [Google Scholar]
- Zadeh, L.A. Fuzzy sets as a basis for a theory of possibility. Fuzzy Sets Syst. 1978, 1, 3–28. [Google Scholar] [CrossRef]
- IEEE Power & Energy Society. IEEE Standard Definitions for Use in Reporting Electric Generating Unit Reliability, Availability, and Productivity; ANSI/IEEE Std 762-1987; IEEE Power & Energy Society: Piscataway, MJ, USA, 1998. [Google Scholar]
- Feng, Y.; Wu, W.; Zhang, B.; Sun, H.; He, Y. Short-term transmission line maintenance scheduling based on credibility theory. Proc. Chin. Soc. Electr. Eng. 2007, 27, 65–71. [Google Scholar]
- Ding, M.; Dai, R.; Hong, M.; Xu, X. Simulation to the weather condition affecting the reliability of transmission network. Autom. Electr. Power Syst. 1997, 21, 18–20. [Google Scholar]
- Duman, S.; Güvenç, U.; Sönmez, Y.; Yörükeren, N. Optimal power flow using gravitational search algorithm. Energy Convers. Manag. 2012, 59, 86–95. [Google Scholar] [CrossRef]
- Mahdada, B.; Bouktir, T.; Srairi, K.; EL Benbouzidc, M. Dynamic strategy based fast decomposed GA coordinated with FACTS devices to enhance the optimal power flow. Energy Convers. Manag. 2010, 51, 1370–1380. [Google Scholar] [CrossRef]
- Efron, B.; Tibshirani, R.J. An Introduction to the Bootstrap; Chapman and Hall/CRC Press: London, UK; Boca Raton, FL, USA, 1993. [Google Scholar]
- Khosravi, A.; Nahavandi, S.; Creighton, D. A neural network-GARCH-based method for construction of prediction intervals. Electr. Power Syst. Res. 2012, 96, 185–193. [Google Scholar] [CrossRef]
- Zimmerman, R.D.; Murillo-Sánchez, C.E.; Thomas, R.J. MATPOWER’s extensible optimal power flow architecture. In Proceedings of the Power and Energy Society General Meeting, Calgary, AB, Canada, 26–30 July 2009; pp. 1–7.
- Shaaban, M.; Liu, H.; Li, W.; Yan, Z.; Ni, Y.; Wu, F. ATC calculation with static security constraints using benders decomposition. Proc. Chin. Soc. Electr. Eng. 2003, 23, 7–11. [Google Scholar]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zheng, Y.; Yang, J.; Hu, Z.; Zhou, M.; Li, G. Credibility Theory-Based Available Transfer Capability Assessment. Energies 2015, 8, 6059-6078. https://doi.org/10.3390/en8066059
Zheng Y, Yang J, Hu Z, Zhou M, Li G. Credibility Theory-Based Available Transfer Capability Assessment. Energies. 2015; 8(6):6059-6078. https://doi.org/10.3390/en8066059
Chicago/Turabian StyleZheng, Yanan, Jin Yang, Zhaoguang Hu, Ming Zhou, and Gengyin Li. 2015. "Credibility Theory-Based Available Transfer Capability Assessment" Energies 8, no. 6: 6059-6078. https://doi.org/10.3390/en8066059
APA StyleZheng, Y., Yang, J., Hu, Z., Zhou, M., & Li, G. (2015). Credibility Theory-Based Available Transfer Capability Assessment. Energies, 8(6), 6059-6078. https://doi.org/10.3390/en8066059






