Optimization and Analysis of a Hybrid Energy Storage System in a Small-Scale Standalone Microgrid for Remote Area Power Supply (RAPS)
Abstract
:1. Introduction
2. A Small-Scale Standalone Microgrid and ESSs
2.1. System Structure of a Standalone Microgrid for RAPS
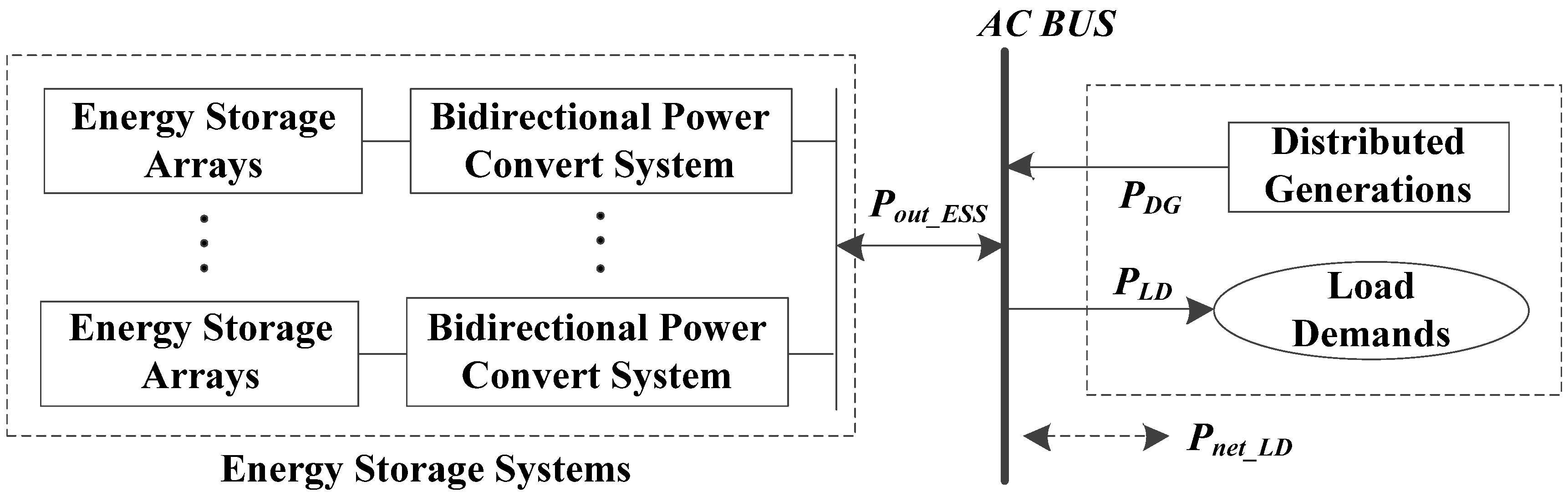
2.2. The Proposed Index Named ESS Effective Rate
2.3. General Mathematical Model of ESSs
3. Control Strategy of HESS
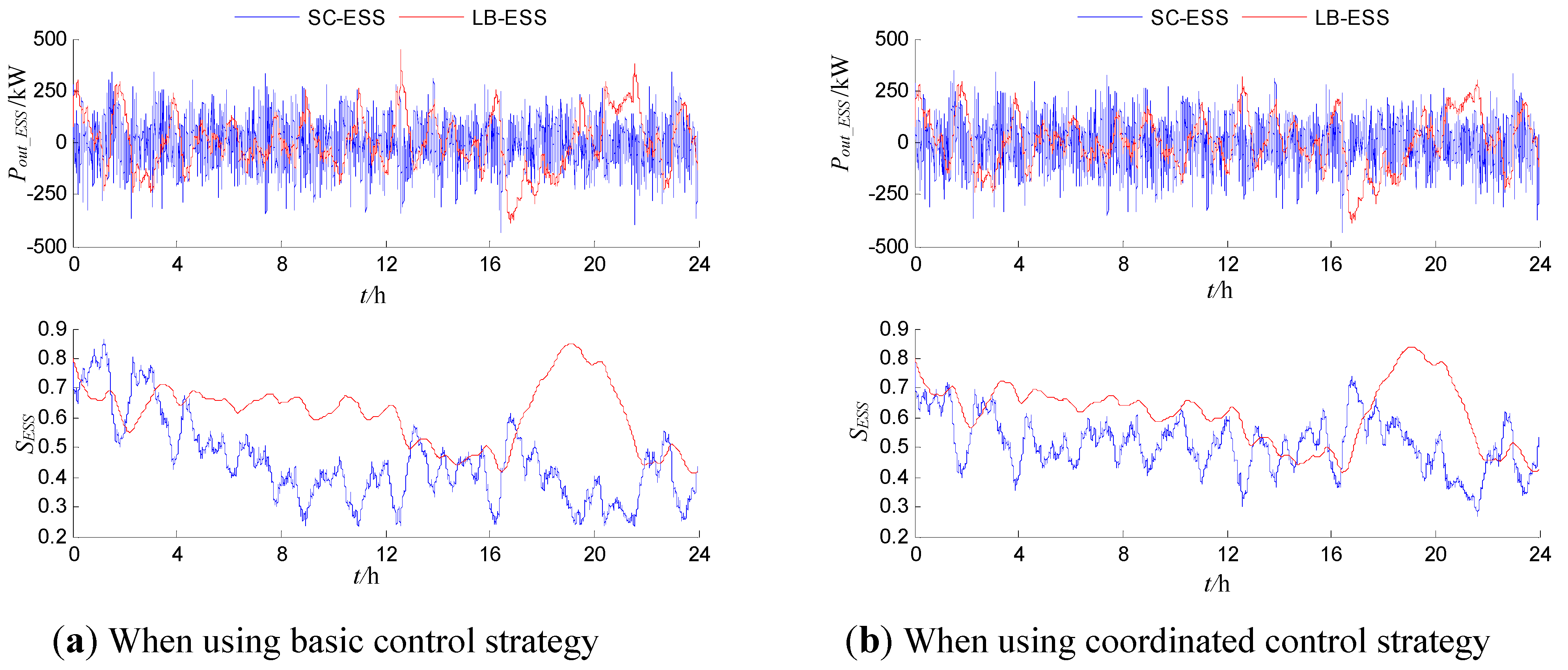
3.1. The Basic Control Strategy Considering Power Allocation Only
3.2. The Coordinated Control Strategy Based on State Cooperation
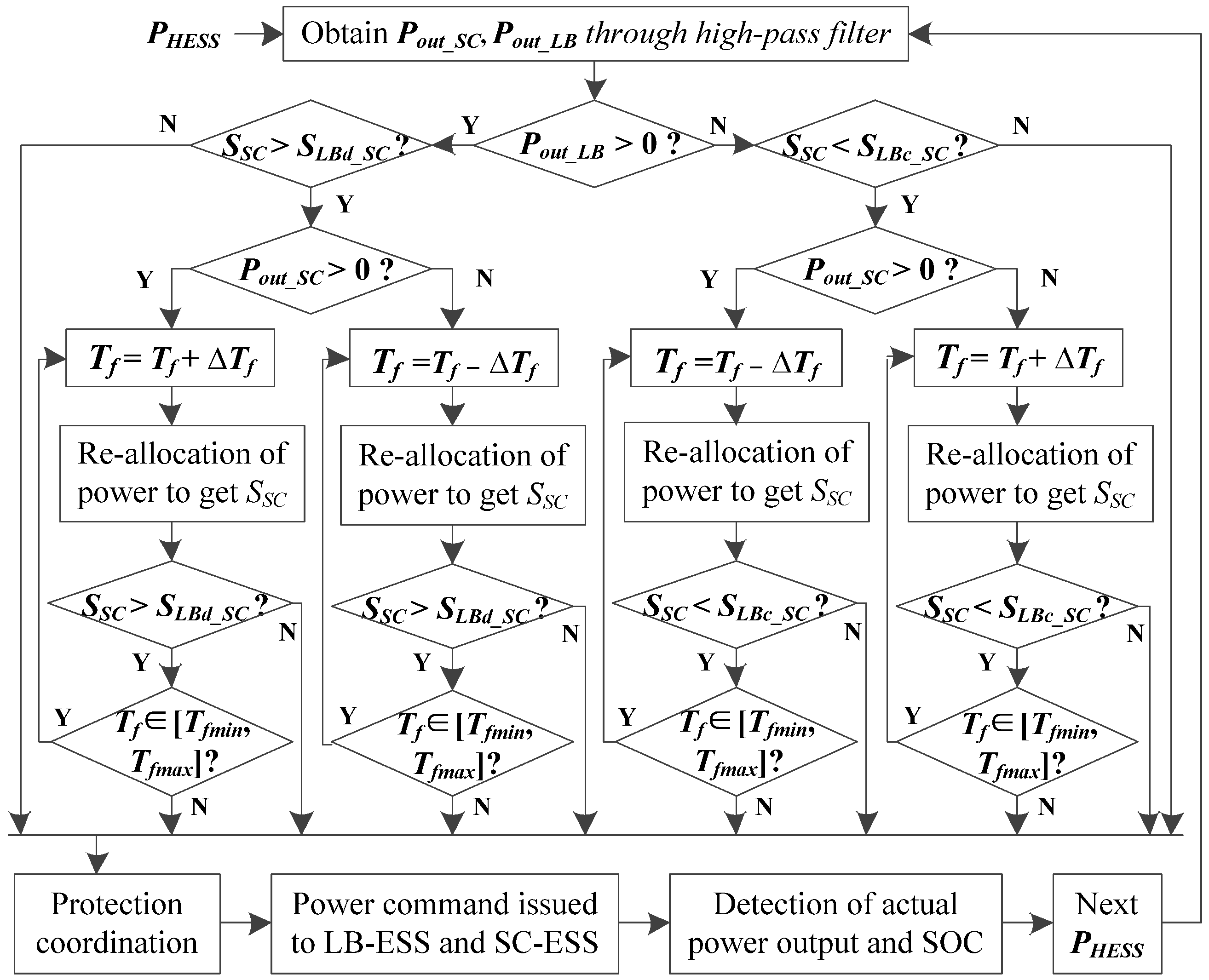
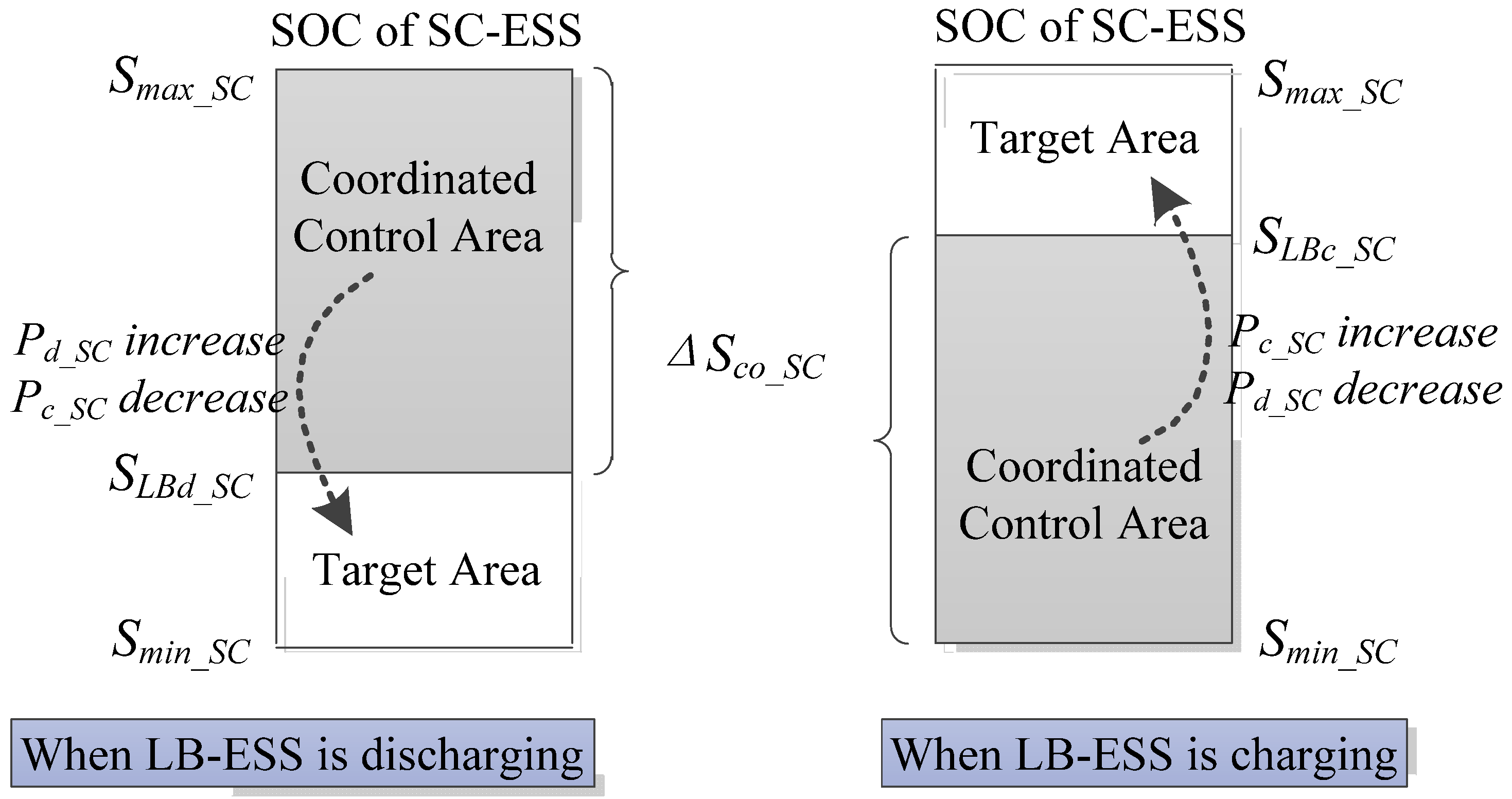
4. Cost Calculation and Life Quantification of HESS
4.1. Initial Investment Cost of HESS
4.2. Life Quantification and Loss Equivalent Cost of Storage Arrays in LB-ESS
4.3. Overall Life Quantification and Total Loss Equivalent Cost of HESS
4.4. Impact Analysis Models of Different Cost and Life Considerations

5. Comparative Analysis Models of ESSs under Different Application Schemes
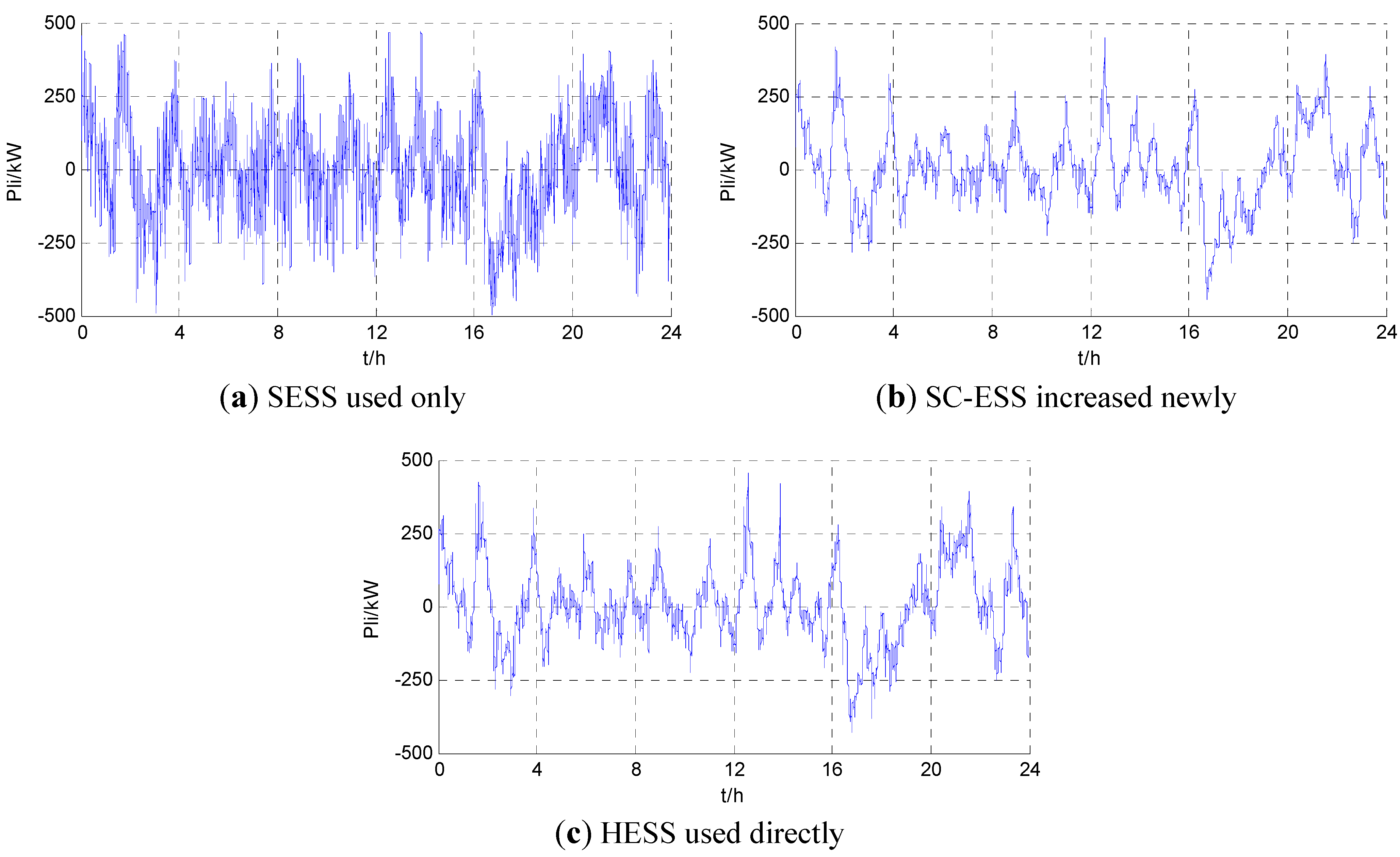
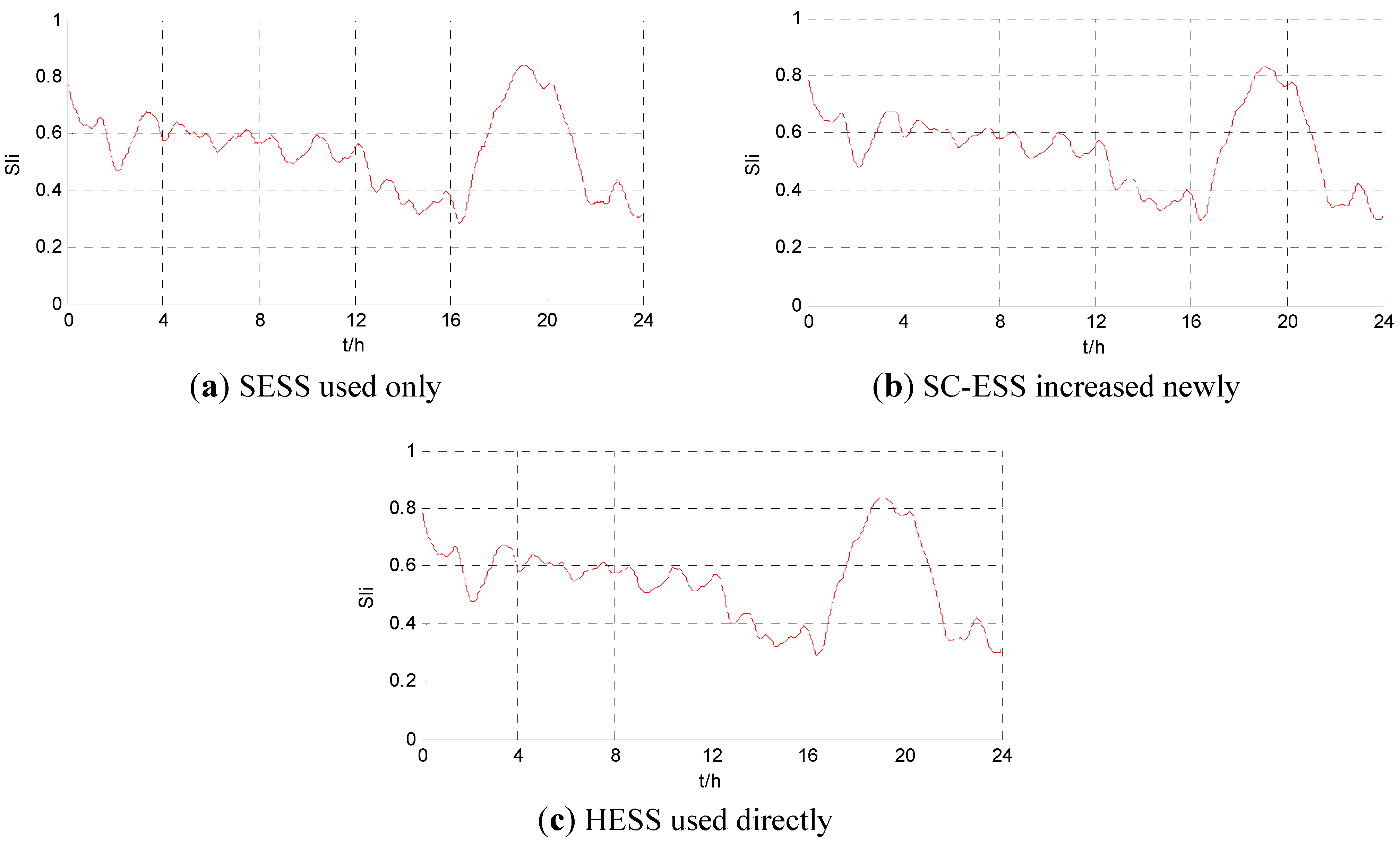
5.1. SESS Used Only
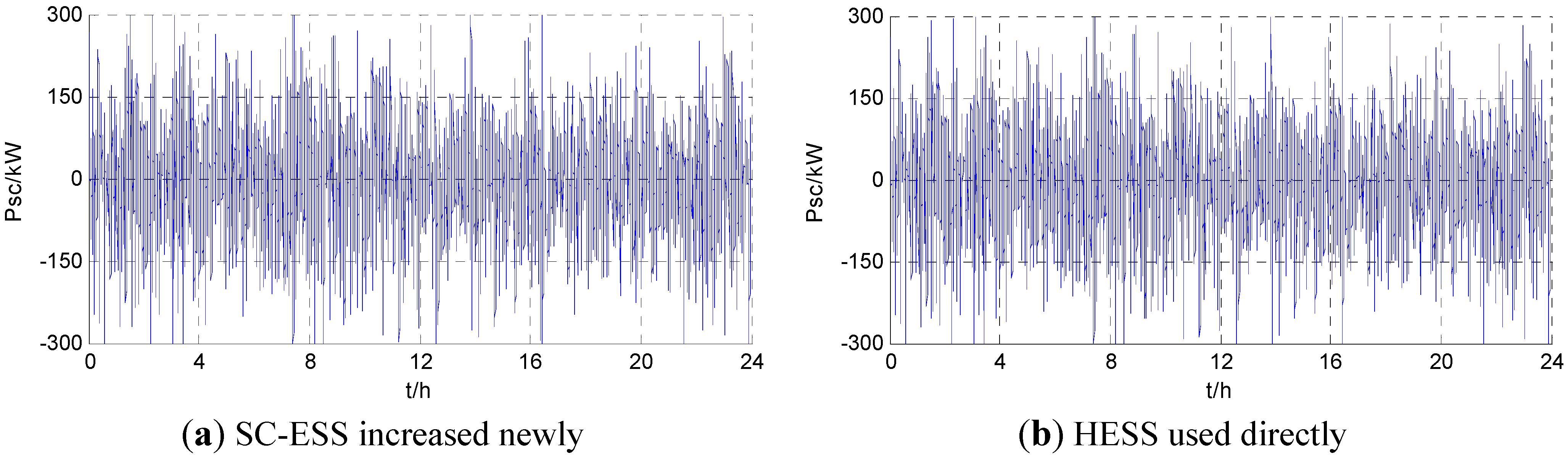
5.2. SC-ESS Increased Newly Based on the Existing SESS
5.3. HESS Used Directly
6. Case Studies
6.1. System Demand and ESS Parameters
| Parameter type | LB-ESS | SC-ESS |
|---|---|---|
| Operating range of SOC | 0.25~0.95 | 0.2~0.9 |
| SOC threshold of over-charge protection | 0.9 | 0.85 |
| SOC threshold of over-discharge protection | 0.3 | 0.25 |
| Initial value of SOC | 0.8 | 0.8 |
| Charge and discharge efficiency | 90% | 95% |
| Self-discharge rate (%·s−1) | 0 | 0.00017 |
| Unit capacity cost ($·kWh−1) | 655.7 | 157,377.0 |
| Pr_PCS (kW) | 50 | 100 | 200 | 250 | 300 | 400 | 500 |
|---|---|---|---|---|---|---|---|
| CPCS_LB (104·$) | 1.00 | 1.97 | 3.77 | 4.61 | 5.41 | 6.89 | 8.20 |
| CPCS_SC (104·$) | 1.21 | 2.36 | 4.52 | 5.54 | 6.49 | 8.26 | 9.84 |
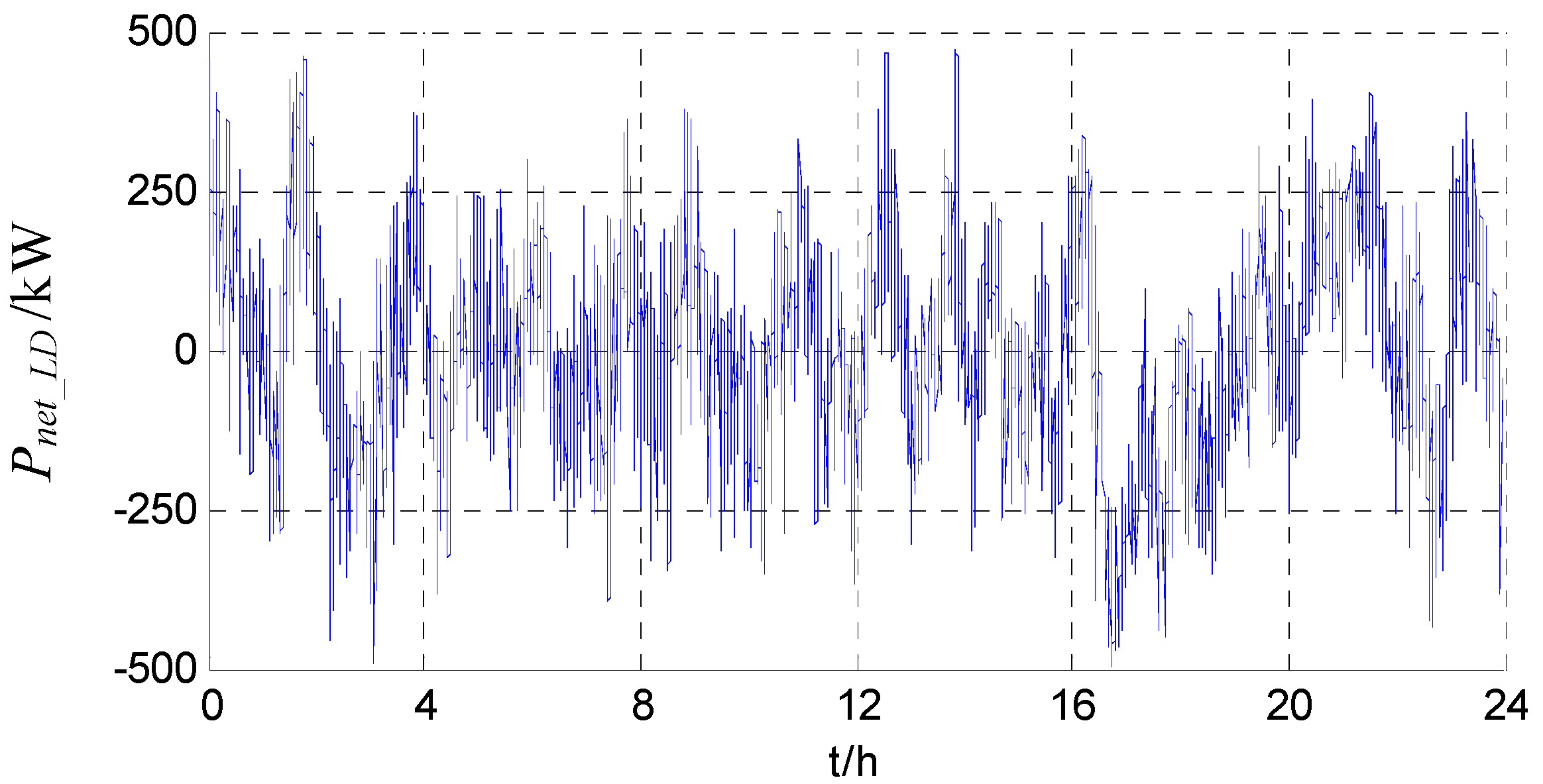
6.2. Comparison of HESS Operation under Different Control Strategies


6.3. Comparative Analysis Based on Different Cost and Life Considerations
| Optimal results | Optimized parameters | Optimized objectives | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Pr_LB (kW) | Er_LB (kWh) | Pr_SC (kW) | Er_SC (kWh) | Tf0 (s) | ΔSco_SC | Cinitial_HESSarr ($) | Cinitial_HESS ($) | Closs_LBarr ($) | Closs_HESS ($) | Cpen_ESS ($) | Copt_HESS ($) | |
| opt1 | 500 | 779.4 | 300 | 1.73 | 15 | 0.52 | 78.3 × 104 | —— | —— | —— | 0 | 78.3 × 104 |
| opt2 | 500 | 779.4 | 300 | 1.73 | 15 | 0.52 | —— | 93.0 × 104 | —— | —— | 0 | 93.0 × 104 |
| opt3 | 500 | 749.6 | 300 | 5.92 | 43 | 0.68 | —— | —— | 406.3 | —— | 0 | 406.3 |
| opt4 | 500 | 756.8 | 300 | 3.17 | 24 | 0.63 | —— | —— | —— | 467.9 | 0 | 467.9 |
| Optimalresults | Initial investment cost | Loss equivalent cost | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Carray_LB (104·$) | CPCS_LB (104·$) | Carray_SC (104·$) | CPCS_SC (104·$) | Cinitial_HESS (104·$) | Closs_LBarr ($) | Closs_LB ($) | Closs_SCarr ($) | Closs_SC ($) | Closs_HESS ($) | |
| opt1 | 51.1 | 8.2 | 27.2 | 6.5 | 93.0 | 443.2 | 465.7 | 25.2 | 27.0 | 492.7 |
| opt2 | 51.1 | 8.2 | 27.2 | 6.5 | 93.0 | 443.2 | 465.7 | 25.2 | 27.0 | 492.7 |
| opt3 | 49.2 | 8.2 | 93.2 | 6.5 | 157.0 | 406.3 | 428.7 | 44.8 | 46.6 | 475.3 |
| opt4 | 49.6 | 8.2 | 49.9 | 6.5 | 114.2 | 415.9 | 438.3 | 27.8 | 29.6 | 467.9 |
- The initial investment cost of HESS is optimized in both Objective 1 and Objective 2, and the difference is whether to consider the cost of matched PCS. The optimized results are the same for both objectives, because PCSs in practical engineering applications are usually standard equipment packages. The rated output power of PCS has only a few optional specification values. This characteristic of non-continuous changes makes the initial investment cost of matched PCS relatively fixed. However, if this part of the cost has not counted in the project budget, a poor decision will be made. For example, an additional expense of 0.147 million dollars will be produced in this case study. Therefore, to minimize the amount of capital in initial investment of HESS, optimization using Objective 2 is more reasonable.
- The data comparing optimization when using Objective 2, Objective 3 and Objective 4 is analyzed to obtain the differences between minimizing the initial investment cost and minimizing the loss equivalent cost. The initial investment cost of whole HESS when using Objective 2 is 0.930 million dollars, which is 0.640 million dollars lower than using Objective 3 with a decline of 40.75%, and 0.212 million dollars lower than using Objective 4 with a decline of 18.55%. At the same time, the total loss equivalent cost of HESS when using Objective 2 is 492.7 dollars, which is 17.4 dollars more than using Objective 3 with an increase of 3.67%, and 24.8 dollars more than using Objective 4 with an increase of 5.29%. Compared with the cost when optimizing the loss equivalent cost, although the initial investment cost of whole HESS when optimizing the initial investment cost is lower, the total loss equivalent cost of HESS per unit time is significantly higher. As a result, from the point of life cycle cost, the overall performance of HESS is better when optimizing the loss equivalent cost.
- The life loss and cost conversion of storage arrays in LB-ESS are considered in Objective 3, and the life loss and cost conversion of whole HESS are considered in Objective 4. The life of storage arrays in LB-ESS is much less than the life of other components in HESS, so it is the main factor in HESS performance. As shown in Table 4, the minimum total loss equivalent cost of HESS is 467.9 dollars, i.e., the result when using Objective 4. When using Objective 3, the total loss equivalent cost of HESS is 475.3 dollars, which is only 7.3 dollars more than the optimal value with a difference of 1.57%. That is to say that, an approximately optimal value is obtained when using Objective 3. Meanwhile, the loss equivalent cost of storage arrays in LB-ESS is lowest when using Objective 3, which is 9.6 dollars lower than when using Objective 4 with a decline of 2.32%. The initial investment cost of whole HESS when using Objective 3 is 0.428 million dollars more than when using Objective 4 with an increase of 37.48%. Hence, the economic cost when using Objective 3 is difficult to accept, although the loss equivalent cost of storage arrays in LB-ESS can be lowest and an approximate minimum of total loss equivalent cost of HESS can be obtained.
6.4. Comparative Analysis Based on Different ESS Application Schemes
| Optimal results | Optimized parameters | Loss equivalent cost | Initial investment cost | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Pr_LB (kW) | Er_LB (kWh) | Pr_SC (kW) | Er_SC (kWh) | Tf0 (s) | ΔSco_SC | Closs_LB ($) | Closs_SC ($) | Closs_HESS ($) | Cinitial_LB (104·$) | Cinitial_SC (104·$) | Cinitial_HESS (104·$) | |
| SESS used only | 500 | 781.5 | —— | —— | —— | —— | 577.7 | —— | 577.7 | 59.4 | —— | 59.4 |
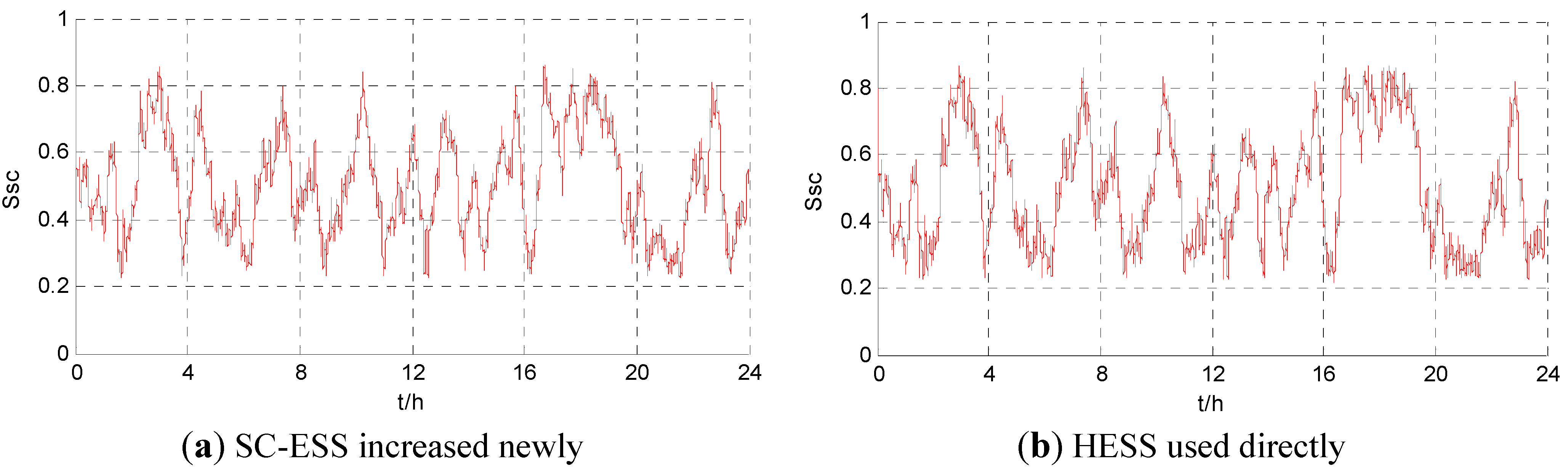
| SC-ESS increased newly | —— | —— | 300 | 3.58 | 28 | 0.54 | 456.7 | 30.6 | 487.4 | —— | 62.8 | 122.3 |
| HESS used directly | 500 | 756.8 | 300 | 3.17 | 24 | 0.63 | 438.3 | 29.6 | 467.9 | 57.8 | 56.4 | 114.2 |
- As shown in the optimal results of the three schemes, the loss equivalent cost of LB-ESS is 577.7, 456.7 and 438.3 dollars, respectively. Compared with the loss equivalent cost of LB-ESS when SESS is used alone, this cost is decreased by 20.9% when SC-ESS is newly increased, and decreased by 24.1% when HESS is used directly. The data analysis above shows that, compared with SESS used alone, the utilization of SC-ESS can effectively reduce the life loss equivalent cost of LB-ESS.
- Compared with SESS used alone, an additional initial investment cost of 0.628 million dollars is needed after SC-ESS is newly increased. However, the total loss equivalent cost of HESS in the simulation time is reduced from 577.7 dollars to 487.4 dollars, which is decreased by 15.6% based on the cost of SESS. This indicates that the initial investment cost is increased because of a newly increased SC-ESS, but the total loss of ESSs demanded by a standalone microgrid is effectively reduced in unit time, so the technical and economic characteristics are much better than SESS.
- After overall optimization of HESS used directly, the total loss equivalent cost has been decreased to 467.9 dollars, which represents a significant decreased amplitude of 19.0% compared with SESS used alone. In addition, compared with optimization of SC-ESS increased newly, the overall optimization of HESS used results in a decrease of the total initial investment cost from 1.223 to 1.142 million dollars, i.e., a savings 80.7 thousand dollars in the initial investment cost. Therefore, the technical and economic characteristics have a further enhance after overall optimization of HESS used directly.
7. Conclusions
Acknowledgments
Author Contributions
Nomenclature
| PDG | Output power of distributed generations |
| PLD | Power demand of loads |
| Pnet_LD | Power demand of net loads |
| Pout_ESS | Output power of ESS |
| RESS | Effective rate of ESS |
| ΔTcom | Time step of computation |
| NT | Number of discrete data points in time T with in interval △Tcom |
| Pref_ESS(n) | Output power reference of ESS at the nth time interval |
| Pout_ESS(n) | Actual output power of ESS at the nth time interval |
| Rset_ESS | Setting constraint of ESS effective rate |
| Cpen_ESS | Penalty cost without satisfying Rset_ESS |
| F | Fixed value much bigger than other cost |
| Pclmt_ESS(n) | Charging power limit of ESS within the nth time interval |
| Pdlmt_ESS(n) | Discharging power limit of ESS within the nth time interval |
| Pcmax_ESS | Maximum charging power of ESS |
| Pdmax_ESS | Maximum discharging power of ESS |
| Er_ESS | Rated storage capacity of ESS |
| Smax_ESS | Maximum SOC of ESS |
| Smin_ESS | Minimum SOC of ESS |
| SESS(n) | SOC of ESS at the nth time interval moment |
| SESS(n-1) | SOC of ESS at the n-1th time interval moment |
| σESS | Self-discharge rate of ESS |
| ηc_ESS | Charging efficiency of ESS |
| ηd_ESS | Discharging efficiency of ESS |
| PHESS | Power command of HESS |
| Pout_LB | Output power of LB-ESS |
| Pout_SC | Output power of SC-ESS |
| Tf | Filter time constant |
| Tf0 | Initial value of Tf in power allocation |
| ΔTf | Adjustment step of Tf |
| Tfmin | Minimum of Tf Adjustment |
| Tfmax | Maximum of Tf Adjustment |
| SSC | SOC of SC-ESS |
| Smin_SC | Minimum SOC of SC-ESS |
| Smax_SC | Maximum SOC of SC-ESS |
| SLBd_SC | SOC control objective of SC-ESS when LB-ESS discharges |
| SLBc_SC | SOC control objective of SC-ESS when LB-ESS charges |
| ΔSco_SC | SOC coordinated response margin of SC-ESS |
| Er_LB | Rated storage capacity of LB-ESS |
| Cunit_LB | Unit storage capacity cost of LB-ESS |
| Er_SC | Rated storage capacity of SC-ESS |
| Cunit_SC | Unit storage capacity cost of SC-ESS |
| Cinitial_HESSarr | Total initial investment cost of storage arrays in HESS |
| CPCS_LB | PCS cost of LB-ESS |
| Cinitial_LB | Initial investment cost of LB-ESS |
| CPCS_SC | PCS cost of SC-ESS |
| Cinitial_SC | Initial investment cost of SC-ESS |
| Cinitial_HESS | Initial investment cost of whole HESS |
| Larray_LB | Lifetime loss coefficient of LB-ESS storage arrays |
| M | Number of time interval in the life quantification of LB-ESS storage arrays |
| ΔDLB(m) | Degenerate increment of LB-ESS storage capacity within the mth time interval |
| Dlmt_LB | Degenerate limit of LB-ESS storage capacity |
| D1, D2 | Intermediate variable of ΔDLB |
| τ | Duration of the mth time interval |
| Savg_LB | SOC average value of LB-ESS |
| Sdev_LB | SOC normalized deviation of LB-ESS |
| NLB | Equivalent throughput cycle of LB-ESS |
| Tref | Reference temperature in degrees centigrade |
| TLB | Operation temperature of LB-ESS storage arrays in degrees centigrade |
| Ta_ref | Absolute temperature of Tref |
| Ta_LB | Absolute temperature of TLB |
| τlife_LB | Calendar lifetime estimate of LB-ESS storage arrays end of 80% initial capacity |
| KT, Kco, Kex, KSOC | Empirical constant of specific LB-ESS storage arrays |
| Closs_LBarr | Loss equivalent cost of LB-ESS storage arrays |
| Larray_SC | Lifetime loss coefficient of SC-ESS storage arrays |
| Ncycle_SC | Charge and discharge cycles of SC-ESS storage arrays |
| Ntotal_SC | Total charge and discharge cycles of SC-ESS storage arrays |
| Closs_SCarr | Loss equivalent cost of SC-ESS storage arrays |
| Lloss_PCS | Lifetime loss coefficient of PCS |
| T | Running time of PCS |
| Tlife_PCS | Service lifetime of PCS |
| Closs_LB | Loss equivalent cost of LB-ESS |
| Closs_SC | Loss equivalent cost of SC-ESS |
| Closs_HESS | Loss equivalent cost of HESS |
| Copt1_HESS | Considered cost of HESS under optimization objective 1 |
| Copt2_HESS | Considered cost of HESS under optimization objective 2 |
| Copt3_HESS | Considered cost of HESS under optimization objective 3 |
| Copt4_HESS | Considered cost of HESS under optimization objective 4 |
| Pr_LB | Rated output power of LB-ESS |
| Pr_SC | Rated output power of SC-ESS |
| Pcmax_LB | Maximum charging power of LB-ESS |
| Pdmax_LB | Maximum discharging power of LB-ESS |
| SLB | SOC of LB-ESS |
| Smin_LB | Minimum SOC of LB-ESS |
| Smax_LB | Maximum SOC of LB-ESS |
| Pcmax_SC | Maximum charging power of SC-ESS |
| Pdmax_SC | Maximum discharging power of SC-ESS |
| Copt_SESS | Loss equivalent cost of SESS used only |
| Copt_SAESS | Loss equivalent cost of SC-ESS increased newly |
| Copt_HESS | Loss equivalent cost of HESS used directly |
| Ctotal_SESS | Total initial investment cost of SESS used only |
| Ctotal_SAESS | Total initial investment cost of SC-ESS increased newly |
| Ctotal_HESS | Total initial investment cost of HESS used directly |
| Pr_PCS | Rated power of PCS |
Conflicts of Interest
References
- Mendis, N.; Muttaqi, K.M.; Perera, S. Management of low- and high-frequency power components in demand-generation fluctuations of a DFIG-based wind-dominated RAPS system using hybrid energy storage. IEEE Trans. Ind. Appl. 2014, 50, 2258–2268. [Google Scholar] [CrossRef]
- Moseley, P.T. Energy storage in remote area power supply (RAPS) systems. J. Power Sources 2006, 155, 83–87. [Google Scholar] [CrossRef]
- Dragicevic, T.; Guerrero, J.M.; Vasquez, J.C. A distributed control strategy for coordination of an autonomous LVDC microgrid based on power-line signalling. IEEE Trans. Ind. Electron. 2014, 61, 3313–3326. [Google Scholar] [CrossRef]
- Wu, D.; Tang, F.; Dragicevic, T.; Vasquez, J.C.; Guerrero, J.M. Autonomous active power control for islanded AC microgrids with photovoltaic generation and energy storage system. IEEE Trans. Energy Convers. 2014, 29, 882–892. [Google Scholar] [CrossRef]
- Dragicevic, T.; Pandzic, H.; Skrlec, D.; Kuzle, I.; Guerrero, J.M.; Kirschen, D.S. Capacity optimization of renewable energy sources and battery storage in an autonomous telecommunication facility. IEEE Trans. Sustain. Energy 2014, 5, 1367–1378. [Google Scholar] [CrossRef]
- Kim, J.Y.; Kim, H.M.; Kim, S.K.; Jeon, J.H.; Choi, H.K. Designing an energy storage system fuzzy PID controller for microgrid islanded operation. Energies 2011, 4, 1443–1460. [Google Scholar] [CrossRef]
- Li, J.; Wei, W.; Xiang, J. A simple sizing algorithm for stand-alone PV/Wind/Battery hybrid microgrids. Energies 2012, 5, 5307–5323. [Google Scholar] [CrossRef]
- Marzband, M.; Sumper, A.; Ruiz-Alvarez, A.; Dominguez-Garcia, J.L.; Tomoiaga, B. Experimental evaluation of a real time energy management system for stand-alone microgrids in day-ahead markets. Appl. Energy 2013, 106, 365–376. [Google Scholar] [CrossRef]
- Marzband, M.; Sumper, A.; Dominguez-Garcia, J.L.; Gumara-Ferret, R. Experimental Validation of a Real Time Energy Management System for Microgrids in Islanded Mode Using a Local Day-Ahead Electricity Market and MINLP. Energy Convers. Manag. 2013, 76, 314–322. [Google Scholar] [CrossRef]
- Marzband, M.; Ghadimi, M.; Sumper, A.; Dominguez-Garcia, J.L. Experimental validation of a real-time energy management system using multi-period gravitational search algorithm for microgrids in islanded mode. Appl. Energy 2014, 128, 164–174. [Google Scholar] [CrossRef]
- Gao, L.; Dougal, R.A.; Liu, S. Power enhancement of an actively controlled battery/ultracapacitor hybrid. IEEE Trans. Power Electron. 2005, 20, 236–243. [Google Scholar] [CrossRef]
- Dougal, R.A.; Liu, S.; White, R.E. Power and life extension of battery ultracapacitor hybrids. IEEE Trans. Components Packag. Technol. 2002, 25, 120–131. [Google Scholar] [CrossRef]
- Li, W.; Joos, G.; Belanger, J. Real-time simulation of a wind turbine generator coupled with a battery supercapacitor energy storage system. IEEE Trans. Ind. Electron. 2010, 57, 1137–1145. [Google Scholar] [CrossRef]
- Thounthong, P.; Rael, S.; Davat, B. Control strategy of fuel cell and supercapacitors association for a distributed generation system. IEEE Trans. Ind. Electron. 2007, 54, 3225–3233. [Google Scholar] [CrossRef]
- Gee, A.M.; Roninson, F.V.P.; Dunn, R.W. Analysis of battery lifetime extension in a small-scale wind-energy system using supercapacitors. IEEE Trans. Energy Convers. 2013, 28, 24–33. [Google Scholar] [CrossRef]
- Mendis, N.; Muttaqi, K.M.; Perera, S. Management of battery-supercapacitor hybrid energy storage and synchronous condenser for isolated operation of PMSM based variable-speed wind turbine generating systems. IEEE Trans. Smart Grid 2014, 5, 944–953. [Google Scholar] [CrossRef]
- Xue, F.; Gooi, H.B.; Chen, S. Hybrid energy storage with multimode fuzzy power allocator for PV systems. IEEE Trans. Sustain. Energy 2014, 5, 389–397. [Google Scholar] [CrossRef]
- Singo, T.A.; Martinez, A.; Saadate, S. Design and implementation of a photovoltaic system using hybrid energy storage. In Proceedings of the IEEE 11th International Conference on Optimization of Electrical and Electronic Equipment, Brasov, Romania, 22–24 May 2008.
- Li, C.; Yang, X.; Zhang, M.; Wang, H.; Ye, J.; Chen, J. Optimal configuration scheme for hybrid energy storage system of super-capacitors and batteries based on cost analysis. Autom. Electr. Power Syst. 2013, 37, 1–5. [Google Scholar]
- Tian, P.; Xiao, X.; Ding, R.; Huang, X. A capacity configuring method of composite energy storage system in autonomous multi-microgrid. Autom. Electr. Power Syst. 2013, 37, 168–173. [Google Scholar]
- Zhou, T.; Sun, W. Optimization of battery-supercapacitor hybrid energy storage station in wind/solar generation system. IEEE Trans. Sustain. Energy 2014, 5, 408–415. [Google Scholar] [CrossRef]
- Glavin, M.E.; Chan, P.K.W.; Hurley, W.G. Optimization of autonomous hybrid energy storage system for photovoltaic application. In Proceedings of the Energy Conversion Congress and Exposition, San Jose, CA, USA, 20–24 September 2009.
- Etinski, M.; Schulke, A. Optimal hybrid energy storage for wind energy integration. In Proceedings of the IEEE International Conference on Industrial Technology (ICIT), Cape Town, South Africa, 25–28 February 2013.
- Yu, W.; Liu, D.; Huang, Y. Operation optimization based on the power supply and storage capacity of an active distribution network. Energies 2013, 6, 6423–6438. [Google Scholar] [CrossRef]
- Wee, K.W.; Choi, S.S.; Vilathgamuwa, D.M. Design of a least-cost battery-supercapacitor energy storage system for realizing dispatchable wind power. IEEE Tans. Sustain. Energy 2013, 4, 786–796. [Google Scholar] [CrossRef]
- Sen, C.; Usama, Y.; Carciumaru, T.; Lu, X.; Kar, N.C. Design of a novel wavelet based transient detection unit for in-vehicle fault determination and hybrid energy storage utilization. IEEE Trans. Smart Grid 2012, 3, 422–433. [Google Scholar] [CrossRef]
- Jiang, Q.; Hong, H. Wavelet-based capacity configuration and coordinated control of hybrid energy storage system for smoothing out wind power fluctuations. IEEE Trans. Power Syst. 2013, 28, 1363–1372. [Google Scholar] [CrossRef]
- Kazempour, S.J.; Moghaddam, M.P.; Haghifam, M.R.; Yousefi, G.R. Electric energy storage systems in a market-based economy: Comparison of emerging and traditional technologies. Renew. Energy 2009, 34, 2630–2639. [Google Scholar] [CrossRef]
- Nguyen, M.Y.; Nguyen, D.H.; Yoon, Y.T. A new battery energy storage charging/discharging scheme for wind power producers in real-time markets. Energies 2012, 5, 5439–5452. [Google Scholar] [CrossRef]
- Yang, W.; Wang, X.; Li, X.; Liu, Z. An active power sharing method among distributed energy sources in an islanded series micro-grid. Energies 2014, 7, 7878–7892. [Google Scholar] [CrossRef]
- Li, F.; Xie, K.; Zhang, X.; Wang, K.; Zhou, D.; Zhao, B. Design of control strategy for hybrid energy storage system based on charge-discharge state of lithium battery. Autom. Electr. Power Syst. 2013, 37, 70–75. [Google Scholar]
- Li, F.; Xie, K.; Zhang, X.; Zhao, B.; Chen, J. Optimization of coordinated control parameters for hybrid energy storage system based on life quantization. Autom. Electr. Power Syst. 2014, 38, 1–5. [Google Scholar]
- Millner, A. Modeling lithium ion battery degradation in electric vehicles. In Proceedings of the IEEE Conference on Innovative Technologies for an Efficient and Reliable Electricity Supply (CITRES), Waltham, MA, USA, 27–29 September 2010.
- Xie, Q.; Lin, X.; Wang, Y.; Pedram, M.; Shin, D.; Chang, N. State of health aware charge management in hybrid electrical energy storage systems. In Proceedings of the Design, Automation & Test in Europe Conference & Exhibition (DATE), Dresden, Germany, 12–16 March 2012.
- Xie, Q.; Yue, S.; Pedram, M.; Shin, D.; Chang, N. Adaptive thermal management for portable system batteries by forced convection cooling. In Proceedings of the Design, Automation & Test in Europe Conference & Exhibition (DATE), 18–22 March 2013.
- Lam, L.; Bauer, P. Practical capacity fading model for Li-ion battery cells in electric vehicles. IEEE Trans. Power Electron. 2013, 28, 5910–5918. [Google Scholar] [CrossRef]
- Vergara, C.R. Parametric interface for battery energy storage systems providing ancillary services. In Proceedings of the 3rd IEEE PES International Conference and Exhibition on Innovative Smart Grid Technologies (ISGT Europe), 14–17 October 2012.
- Traube, J.; Lu, F.; Maksimovic, D.; Mossoba, J.; Kromer, M.; Faill, P.; Katz, S.; Borowy, B.; Nichols, S.; Casey, L. Mitigation of solar irradiance intermittency in photovoltaic power systems with integrated electric-vehicle charging functionality. IEEE Trans. Power Electron. 2013, 28, 3058–3067. [Google Scholar] [CrossRef]
- Grahn, P.; Munkhammar, J.; Widen, J.; Alvehag, K.; Soder, L. PHEV home-charging model based on residential activity patterns. IEEE Trans. Power Syst. 2013, 28, 2507–2515. [Google Scholar] [CrossRef]
- Xie, Q.; Wang, Y.; Kim, Y.; Pedram, M.; Chang, N. Charge allocation in hybrid electrical energy storage systems. IEEE Trans. Comput. Aided Des. Integr. Circuits Syst. 2013, 32, 1003–1016. [Google Scholar] [CrossRef]
- Onar, O.C.; Khaligh, A. A novel integrated magnetic structure based DC/DC converter for hybrid battery/ultracapacitor energy storage systems. IEEE Trans. Smart Grid 2012, 3, 296–307. [Google Scholar] [CrossRef]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, F.; Xie, K.; Yang, J. Optimization and Analysis of a Hybrid Energy Storage System in a Small-Scale Standalone Microgrid for Remote Area Power Supply (RAPS). Energies 2015, 8, 4802-4826. https://doi.org/10.3390/en8064802
Li F, Xie K, Yang J. Optimization and Analysis of a Hybrid Energy Storage System in a Small-Scale Standalone Microgrid for Remote Area Power Supply (RAPS). Energies. 2015; 8(6):4802-4826. https://doi.org/10.3390/en8064802
Chicago/Turabian StyleLi, Fengbing, Kaigui Xie, and Jiangping Yang. 2015. "Optimization and Analysis of a Hybrid Energy Storage System in a Small-Scale Standalone Microgrid for Remote Area Power Supply (RAPS)" Energies 8, no. 6: 4802-4826. https://doi.org/10.3390/en8064802
APA StyleLi, F., Xie, K., & Yang, J. (2015). Optimization and Analysis of a Hybrid Energy Storage System in a Small-Scale Standalone Microgrid for Remote Area Power Supply (RAPS). Energies, 8(6), 4802-4826. https://doi.org/10.3390/en8064802





