Multi-Period Optimization Model for Electricity Generation Planning Considering Plug-in Hybrid Electric Vehicle Penetration
Abstract
:1. Introduction
| Benefits | Challenges |
|---|---|
| Flexibility of fuel | Battery cost |
| GHGs emissions reduction | Shifted emissions to power plants |
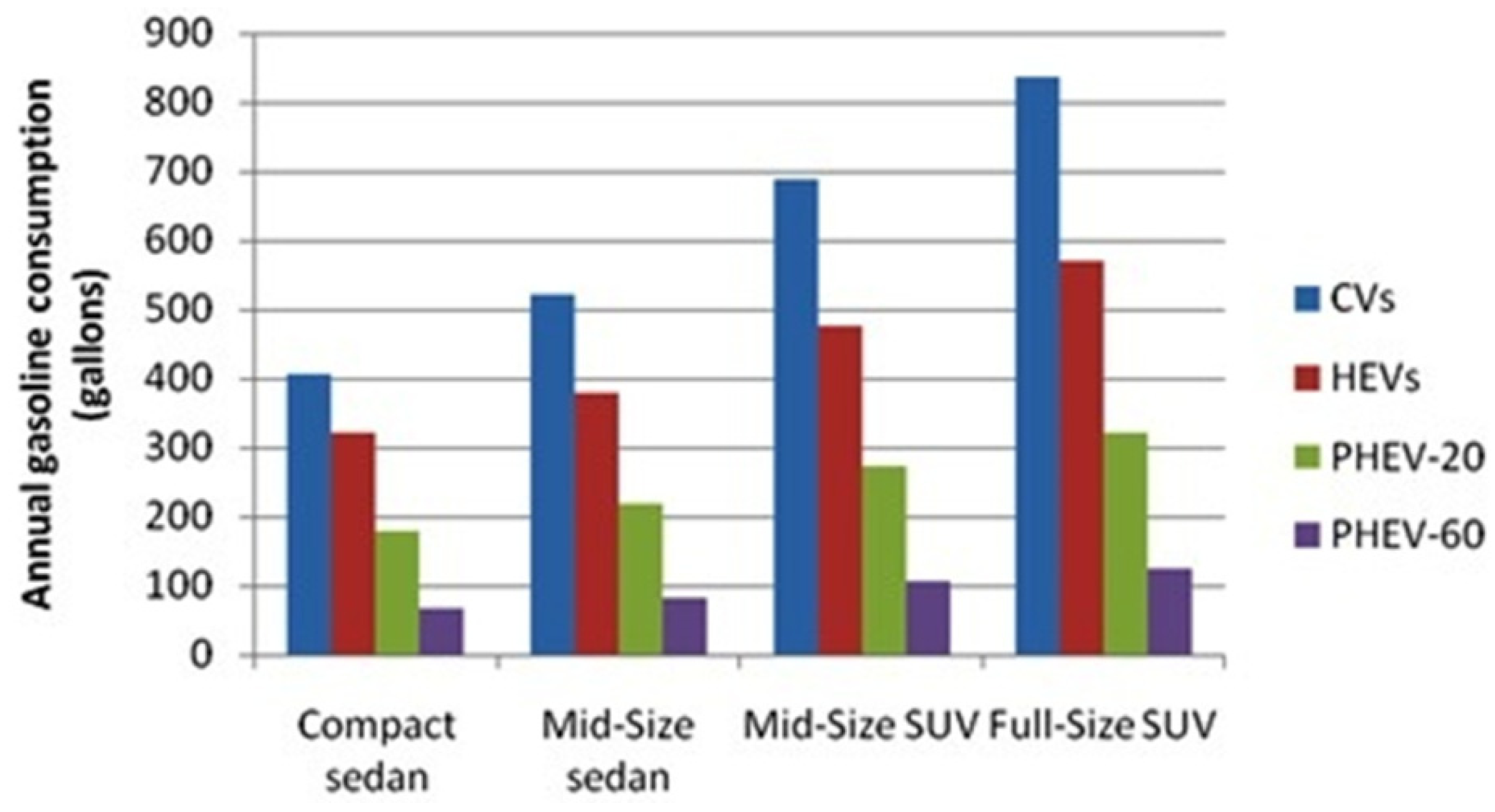
| Gasoline consumption reduction | Load demand increase |
| Improved fuel economy |
- Study the effect of PHEVs penetration on energy planning for long term (in the literature, most existing investigations considered only short periods of time such as 24 h).
- Employing more comprehensive data and modeling techniques for predicting PHEVs penetration and load demands.
- Developing a multi-period optimization model based on the current and projected infrastructure of Ontario encompassing all generating companies (in the literature, multi-period energy planning in Ontario has been done using OPG data only).
- Defining new and realistic charging scenarios on an hourly basis. The results can contribute significantly to the establishment of an Ontario government policy to encourage consumers to save energy.
- Developing an optimization model to address optimal planning of the Ontario power generating sector in consideration of different PHEV penetration levels.
- The developed optimization model can be used on a larger scale i.e., for all Canadian provinces and territories, as well as for other parts of the world.
2. Optimization Methodology for Multi-Period Energy Planning
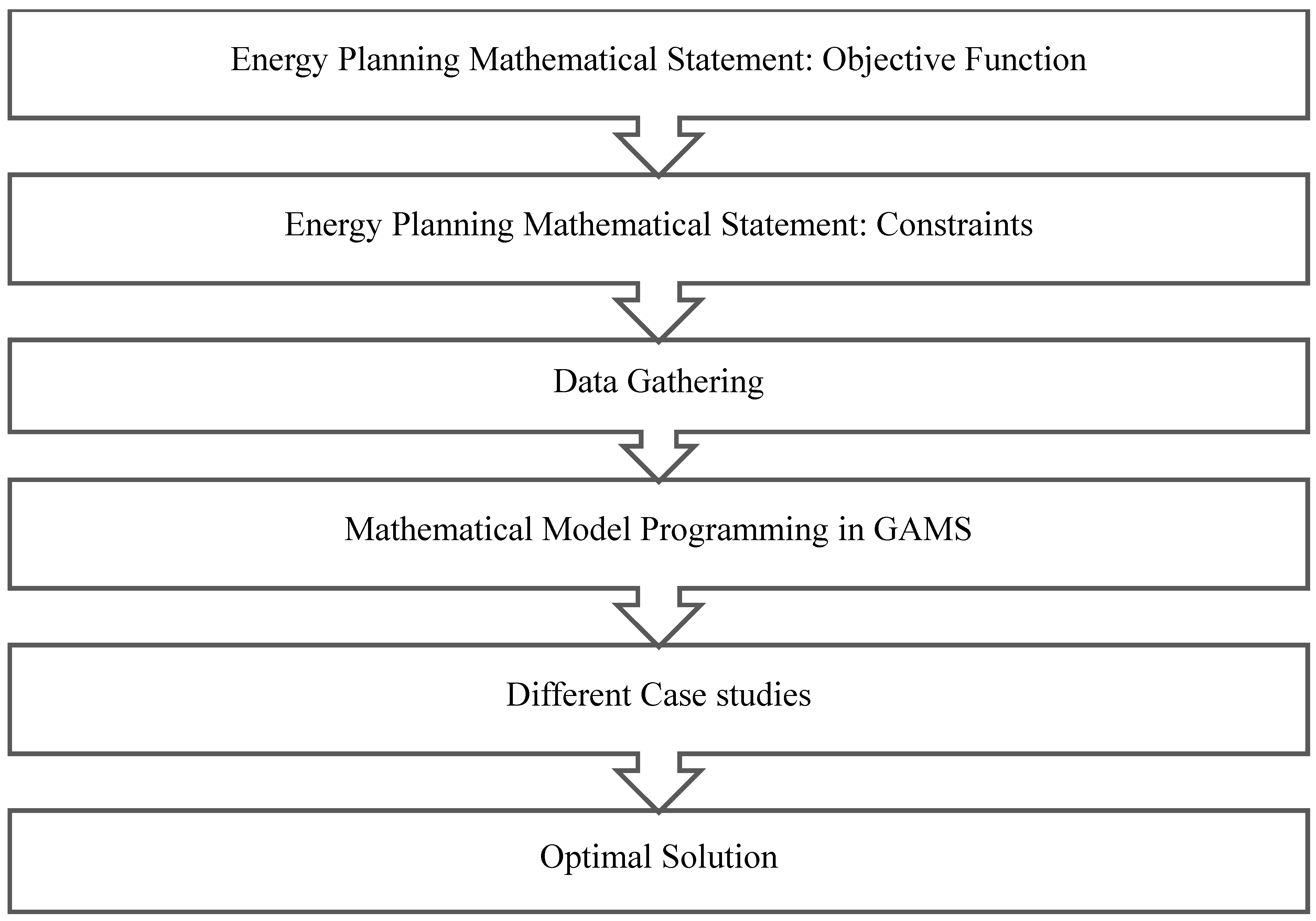
2.1. Objective Function
2.2. Constraints
2.3. Data Gathering
- Installed capacity of power plants
- Net electricity generation
- Capacity factor of power plants
- Operating cost
- Retrofit cost
- New power plants economic evaluation
2.4. Mathematical Model Programming in GAMS
3. Case Studies, Results and Discussion
| Case Study | PHEVs Adoption Rate | Type of Potential Power plants | CO2 Limit |
|---|---|---|---|
| A: Base Case | Medium Penetration | All type of power plants except Coal power stations | No |
| B: Base case with increased NG prices | Medium Penetration | All type of power plants including NG double price | No |
| C: Base case with Coal | Low Penetration | All type of Power plants | No |
| D: Base case with 6% reduction in year 2018 CO2 | High Penetration | All type of power plants except Nuclear power stations | Yes |
| E: Base case without considering current load deficit | Medium Penetration | All type of power plants except Coal power stations | No |
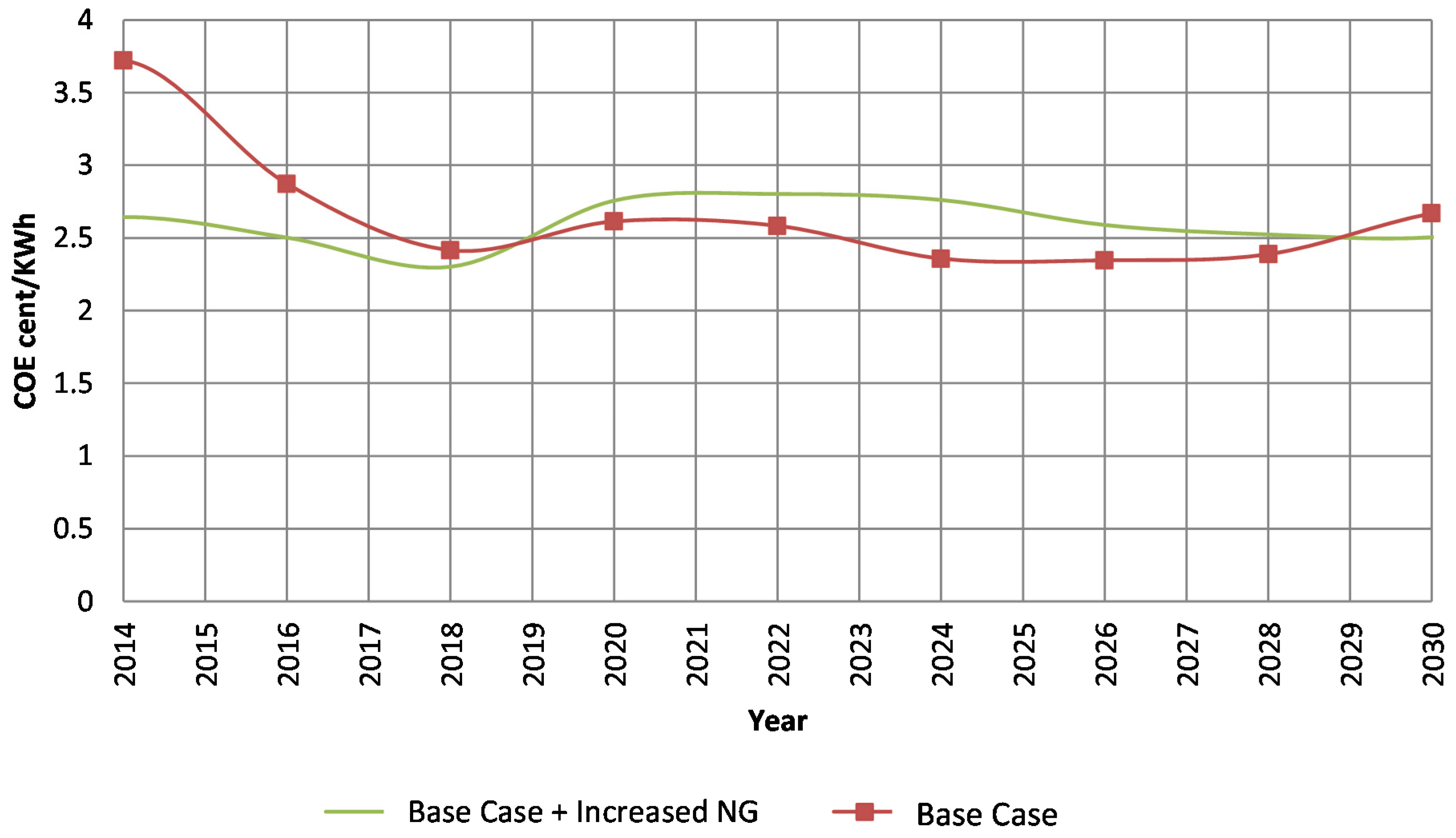
3.1. Case Study A (Base Case) & B (Base Case with Increased NG Prices)
3.1.1. New Power Generating Stations
| New Capacity (MW) | Years (20..) | |||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | ||
| NGCC | 1080 | |||||||||||||||||
| NGCC | 770 | |||||||||||||||||
| Wind | 1000 | |||||||||||||||||
| Wind | 1000 | |||||||||||||||||
| Nuclear | 1080 | |||||||||||||||||
| NGCC | 1040 | |||||||||||||||||
| Import | 1300 | |||||||||||||||||
| New Capacity (MW) | Years (20..) | |||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | ||
| PC | 420 | |||||||||||||||||
| PC | 410 | |||||||||||||||||
| PC | 410 | |||||||||||||||||
| PC | 420 | |||||||||||||||||
| IGCC | 440 | |||||||||||||||||
| NGCC | 430 | |||||||||||||||||
| NGCC | 500 | |||||||||||||||||
| Nuclear | 1010 | |||||||||||||||||
| Import | 1250 | |||||||||||||||||
| Wind | 1000 | |||||||||||||||||
| Wind | 1000 | |||||||||||||||||
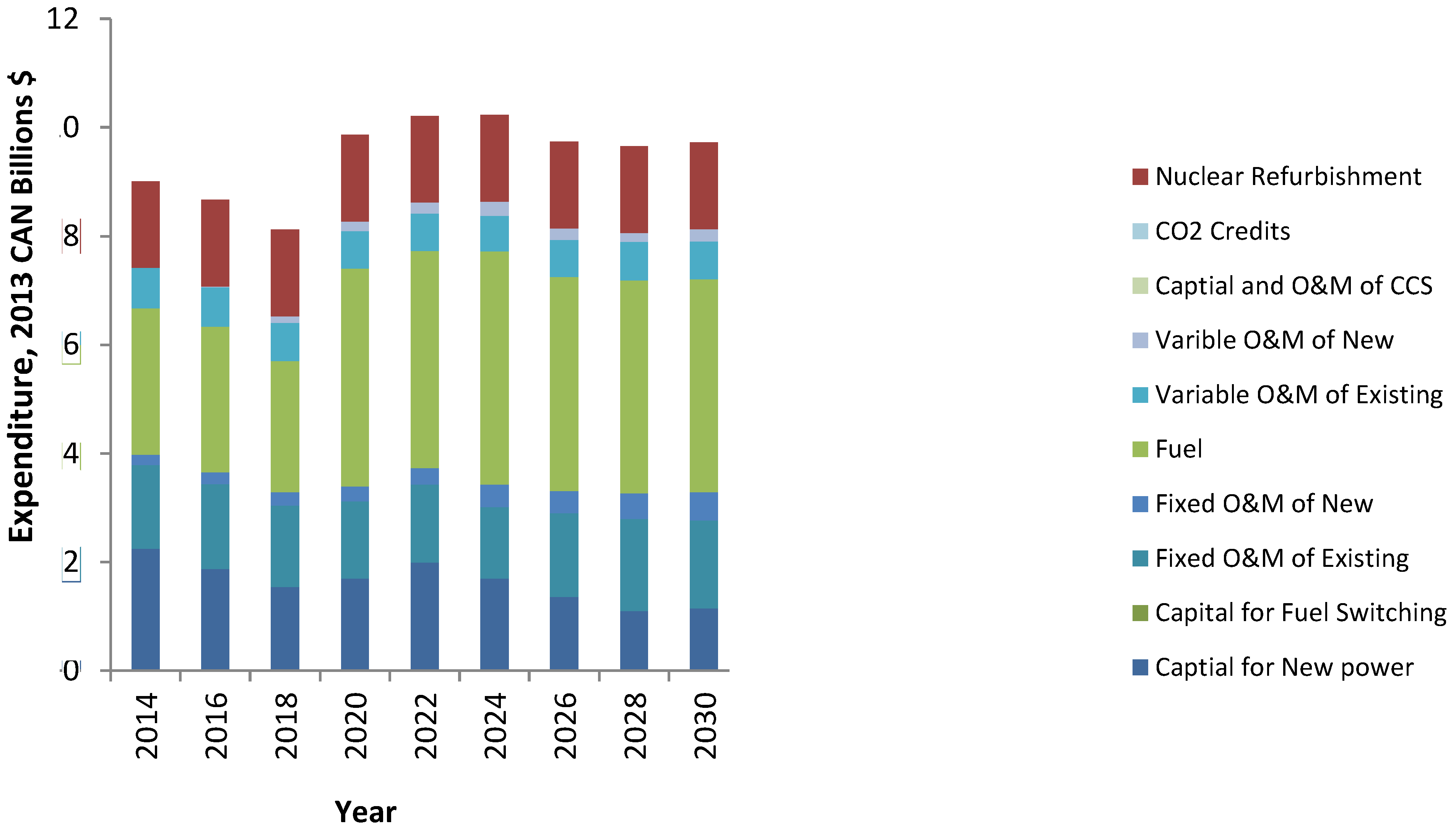
3.1.2. Economic and Emission Analysis
3.2. Case Study C: Base Case with Coal
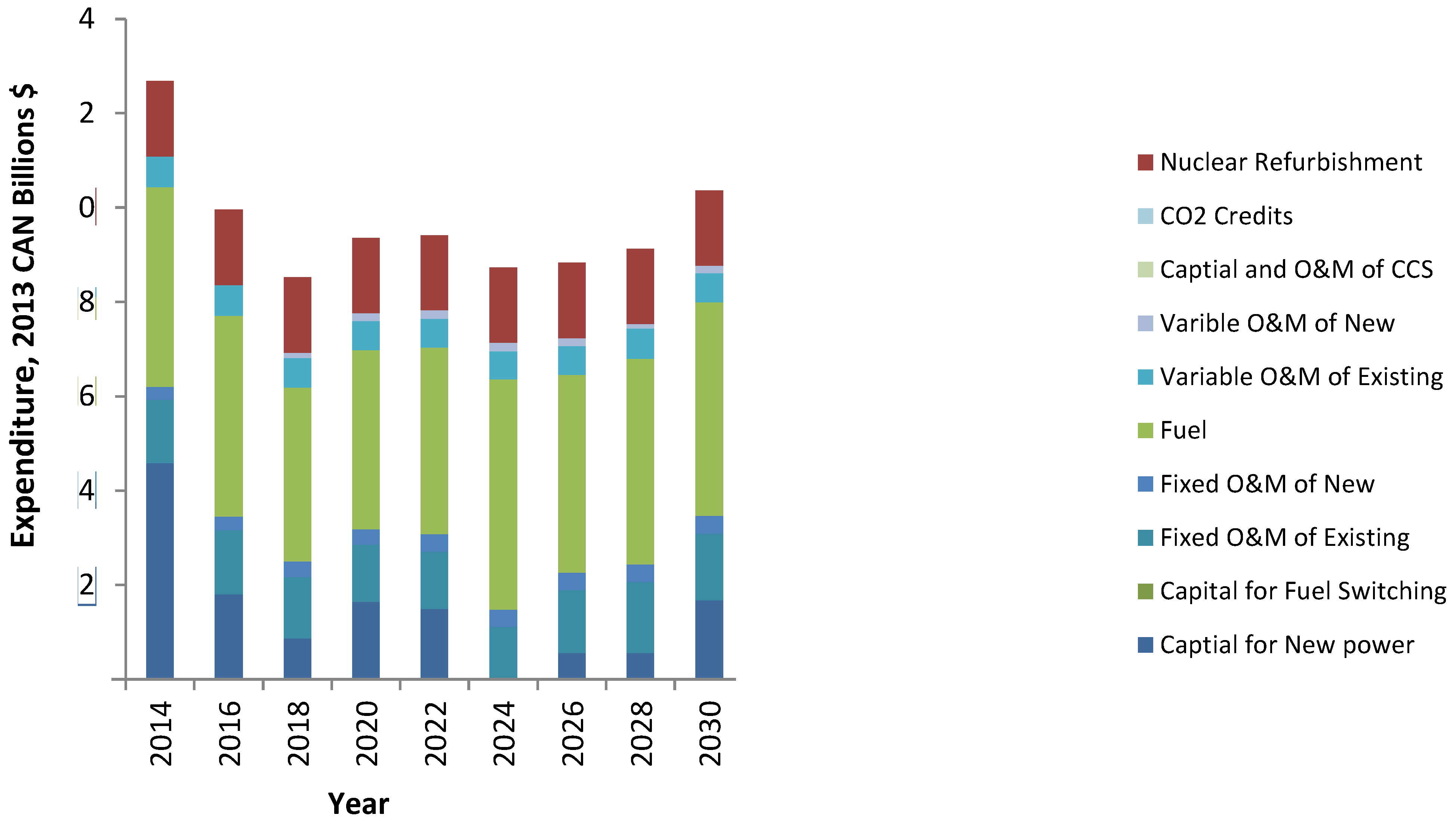
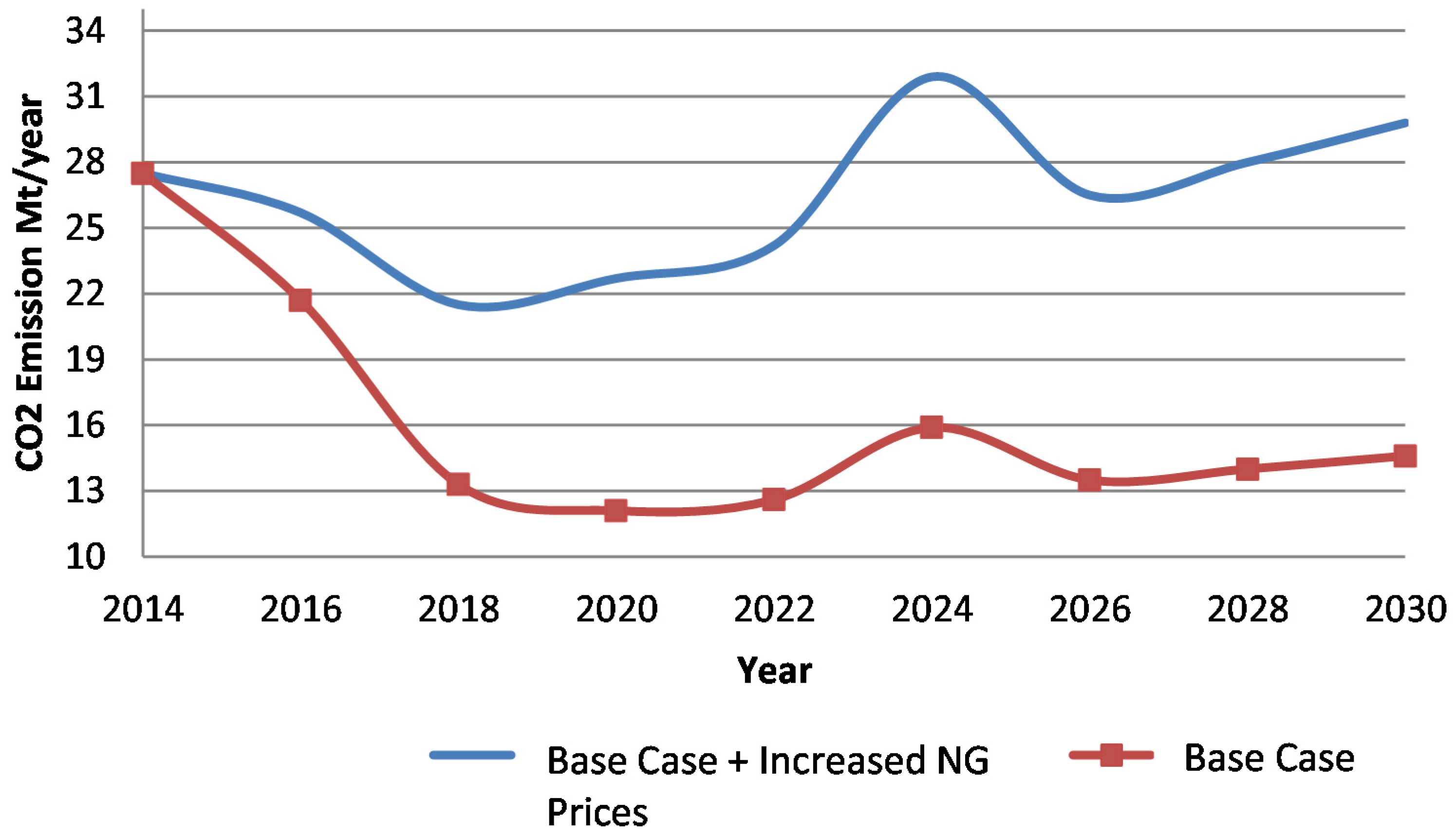
3.2.1. New Power Generating Stations
| New Capacity (MW) | Years (20..) | |||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | ||
| PC | 2119 | |||||||||||||||||
| NGCC | 1568 | |||||||||||||||||
| NGCC | 1568 | |||||||||||||||||
| PC | 1245 | |||||||||||||||||
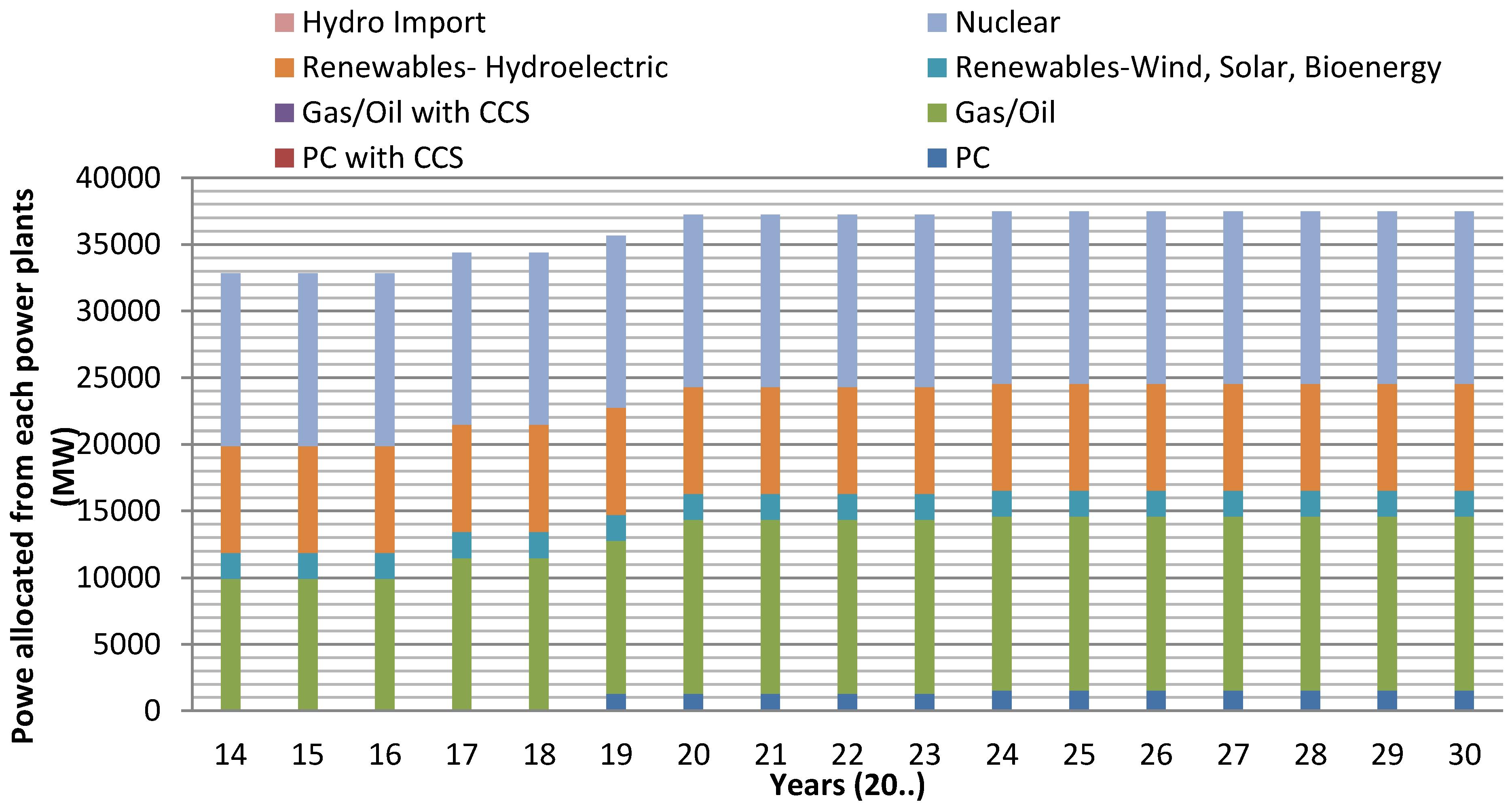
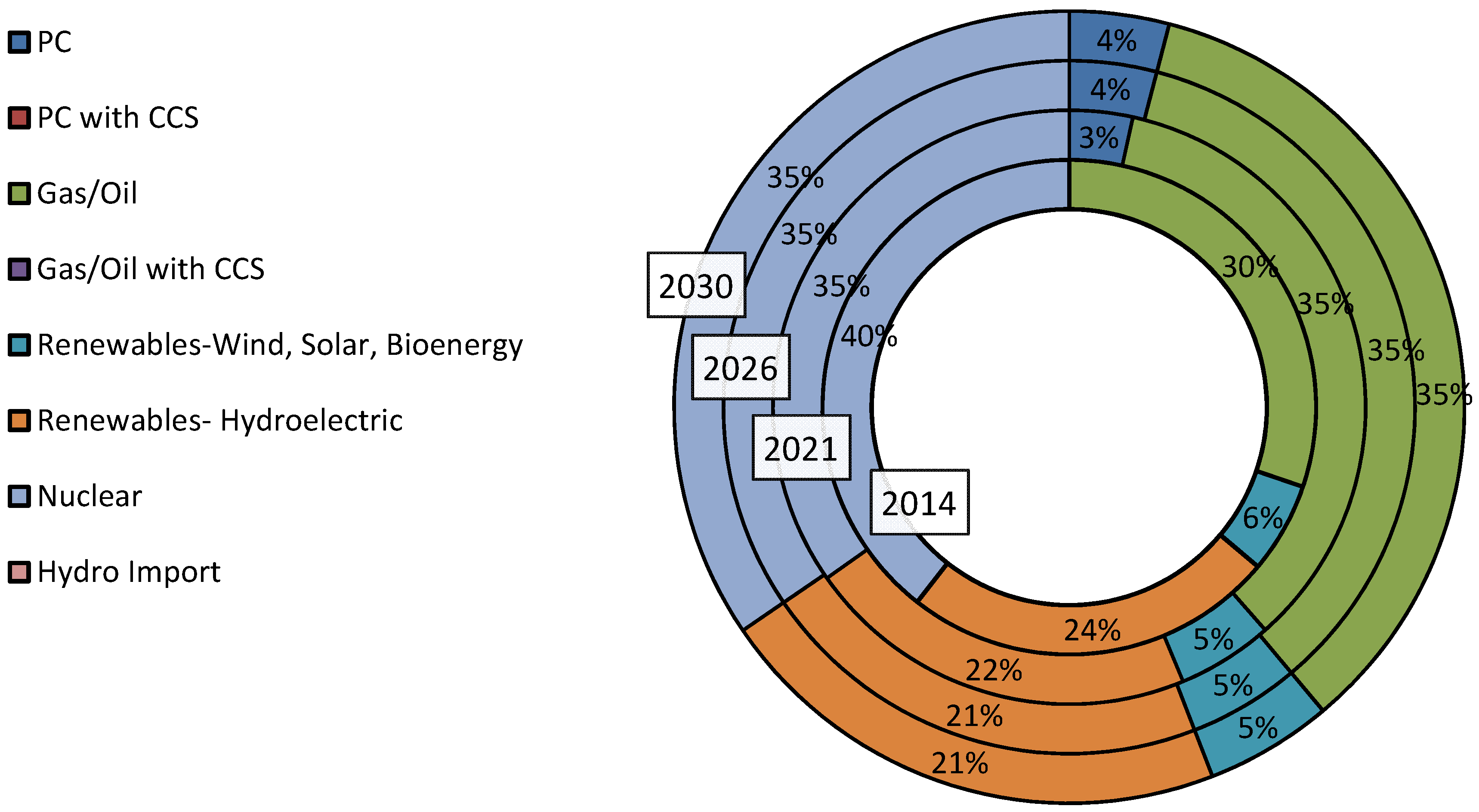
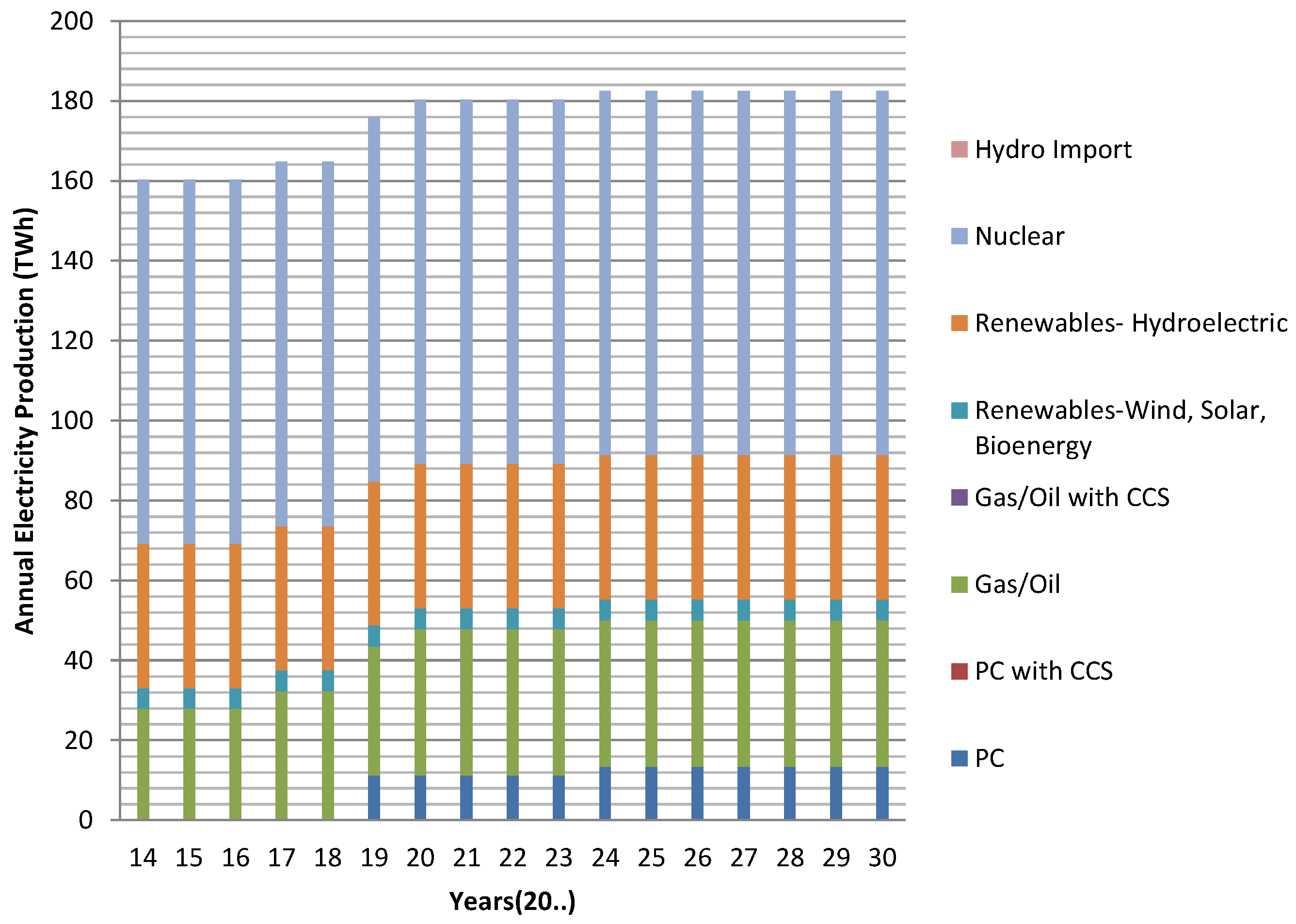
3.2.2. Economic and Emission Analysis
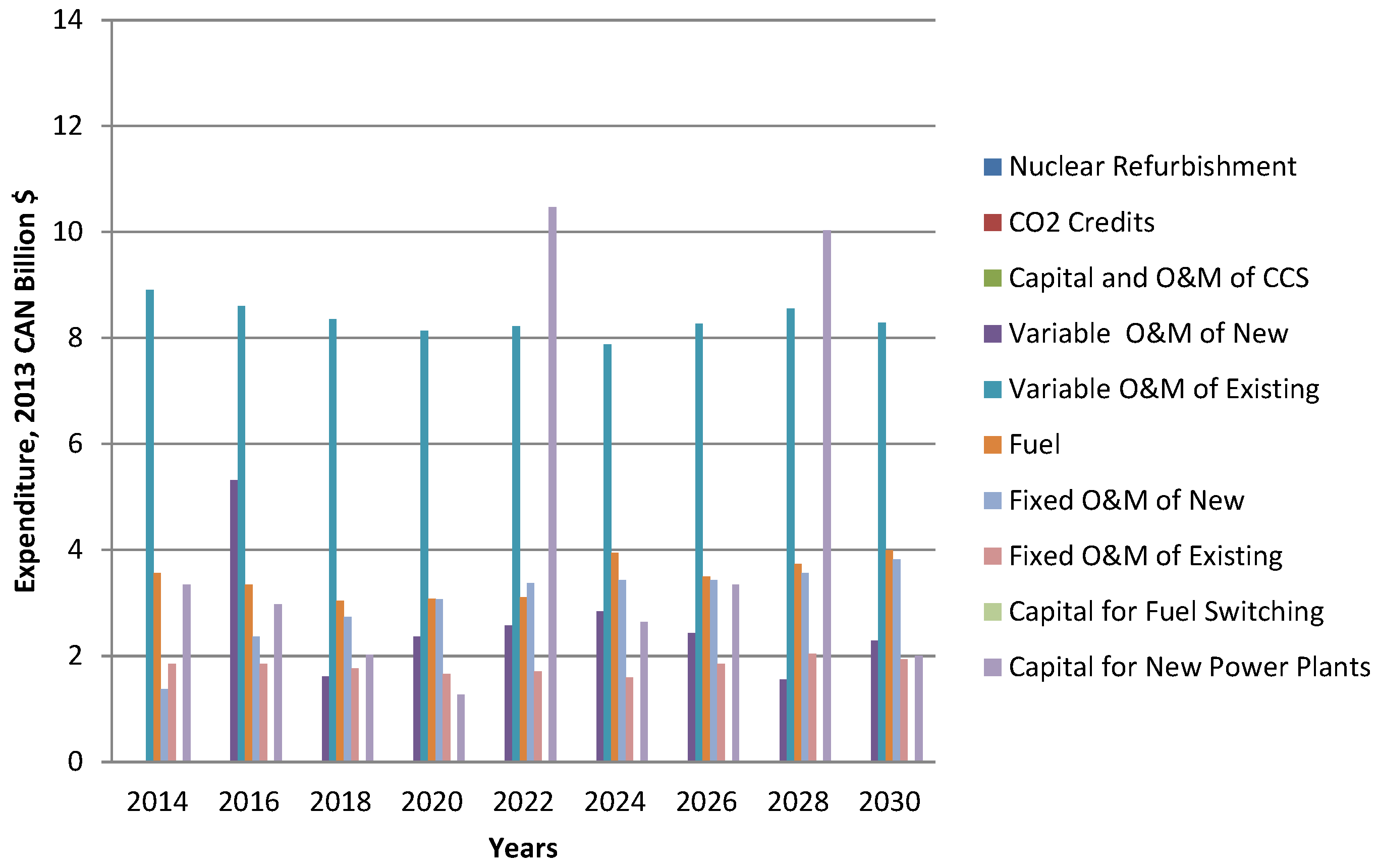
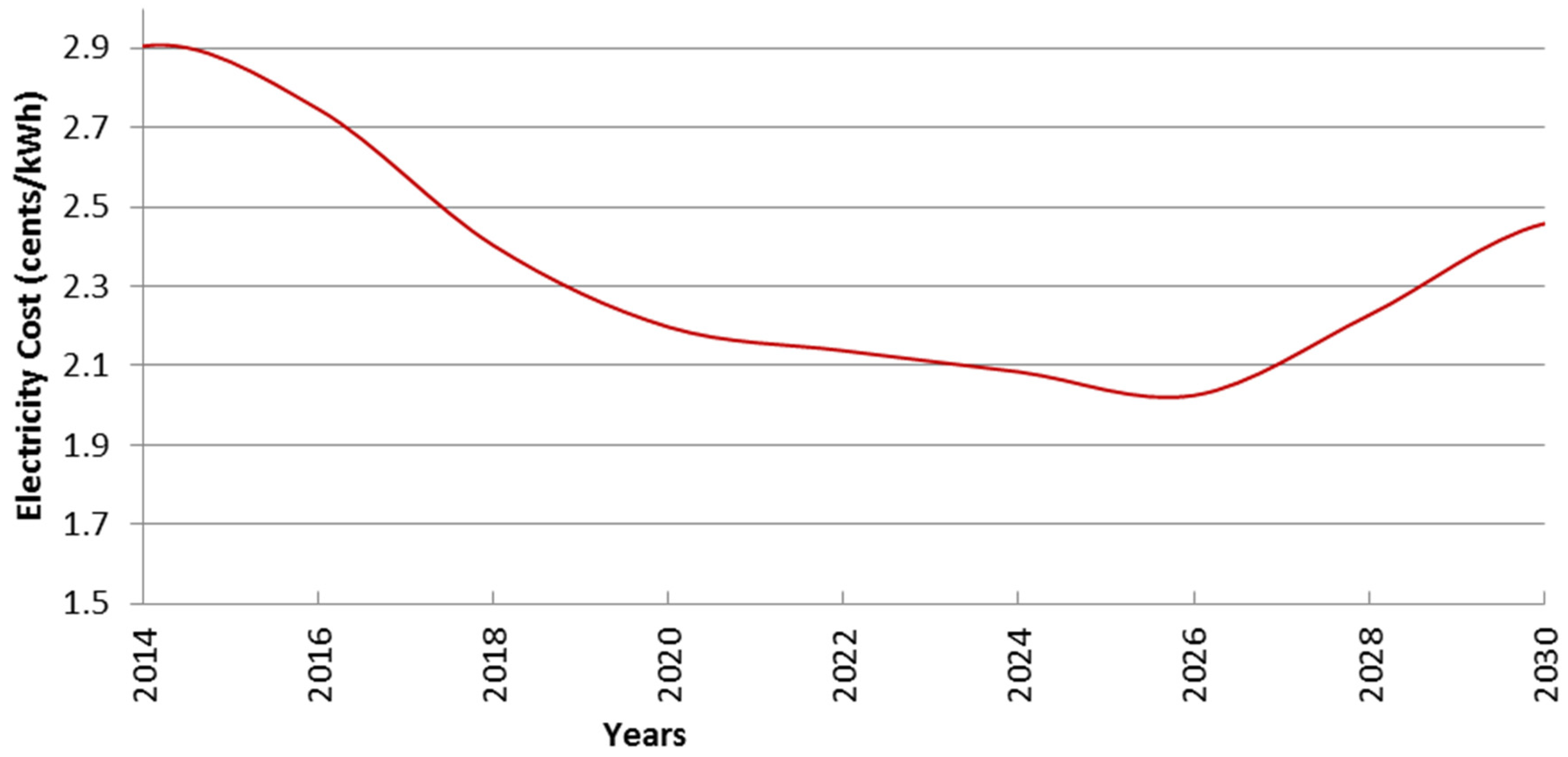
3.3. Case Study D: Base Case with 6% Reduction in CO2 by Year 2018
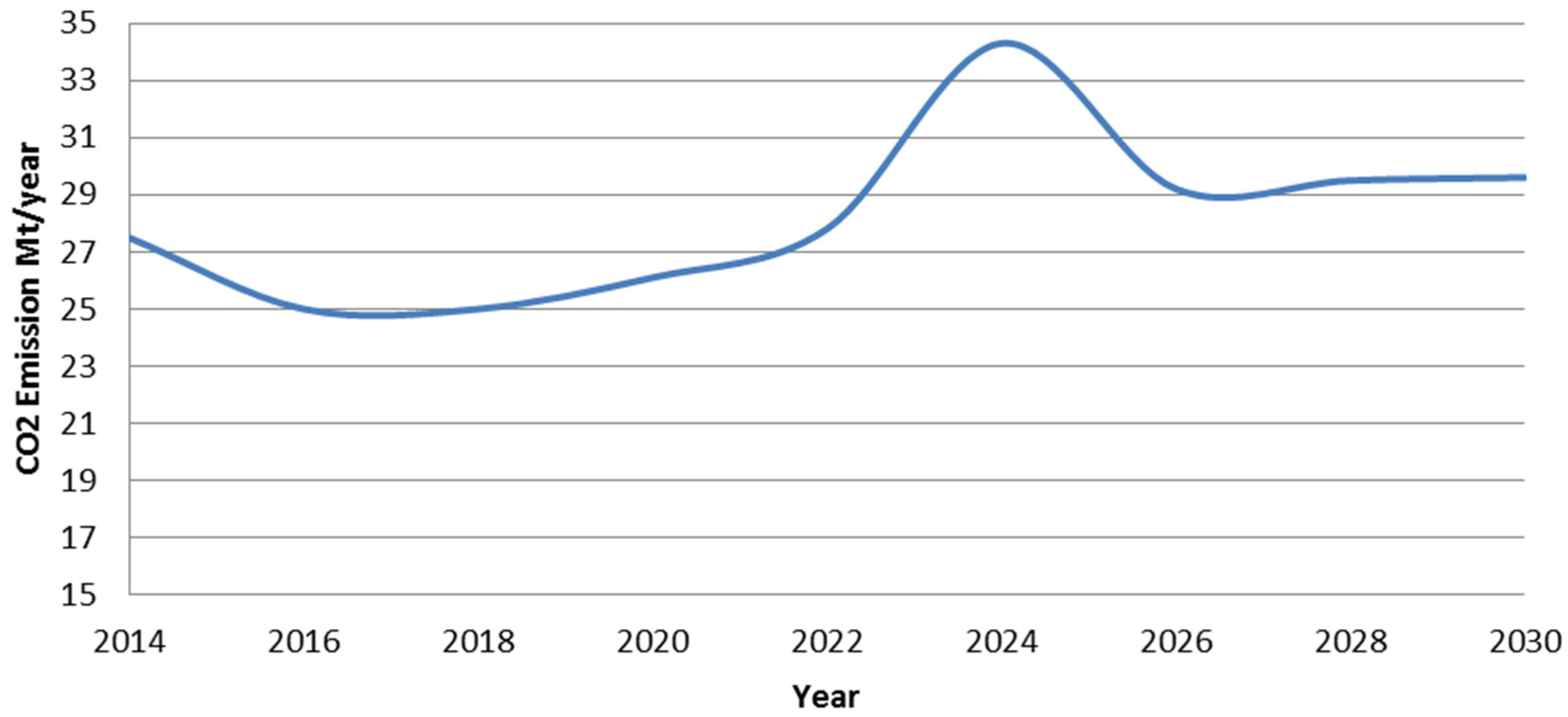
3.3.1. New Power Generation Stations
| New Capacity (MW) | Years (20..) | |||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | ||
| NGCC | 528 | |||||||||||||||||
| NGCC | 730 | |||||||||||||||||
| NGCC | 950 | |||||||||||||||||
| NGCC | 892 | |||||||||||||||||
| NGCC | 866 | |||||||||||||||||
| IGCC+CCS | 700 | |||||||||||||||||
| IGCC+CCS | 400 | |||||||||||||||||
| NGCC+CCS | 432 | |||||||||||||||||
| Import | 1250 | |||||||||||||||||
| Wind | 1000 | |||||||||||||||||
| Wind | 1000 | |||||||||||||||||
3.3.2. Economic and Emission Analysis
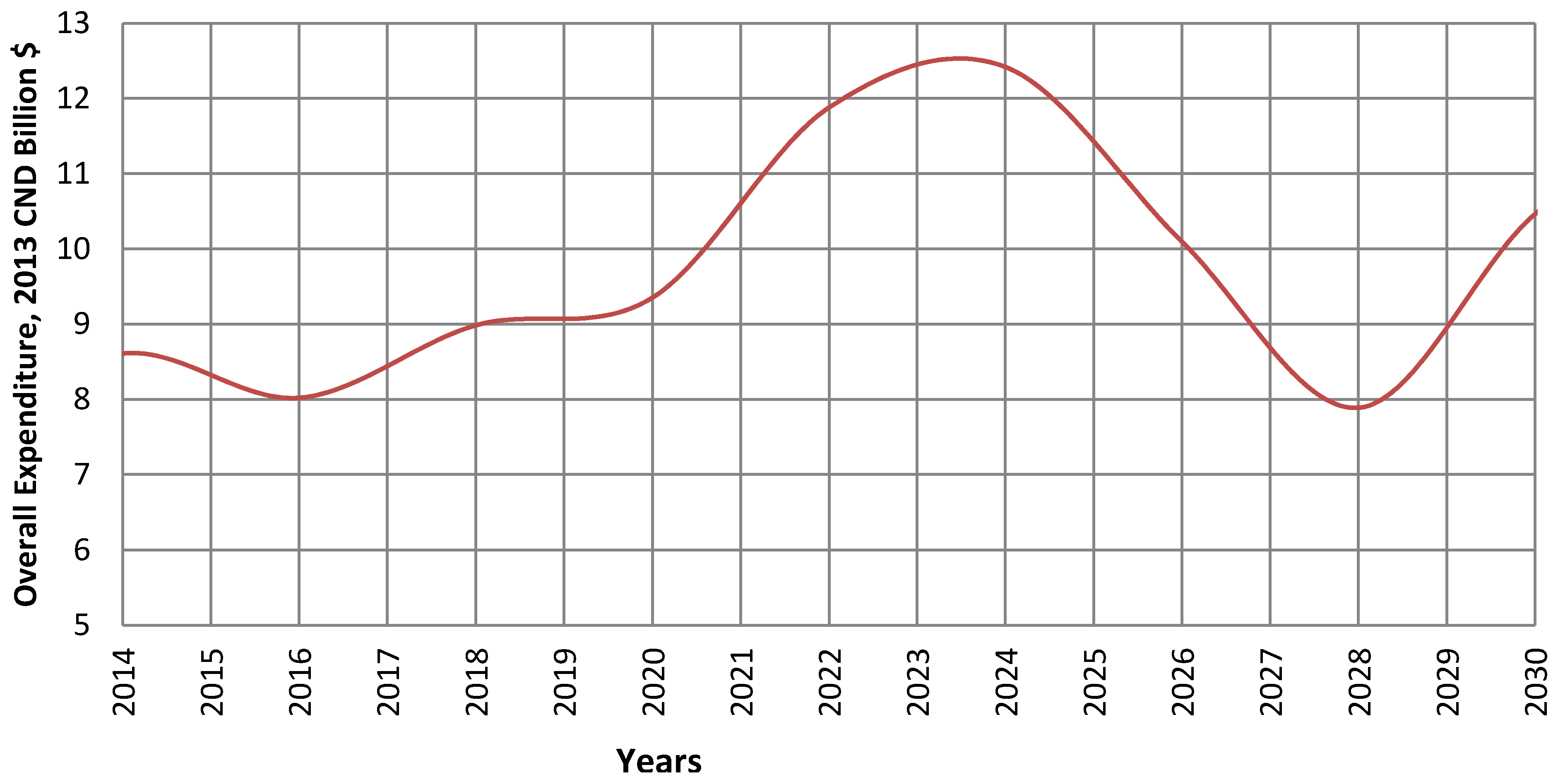
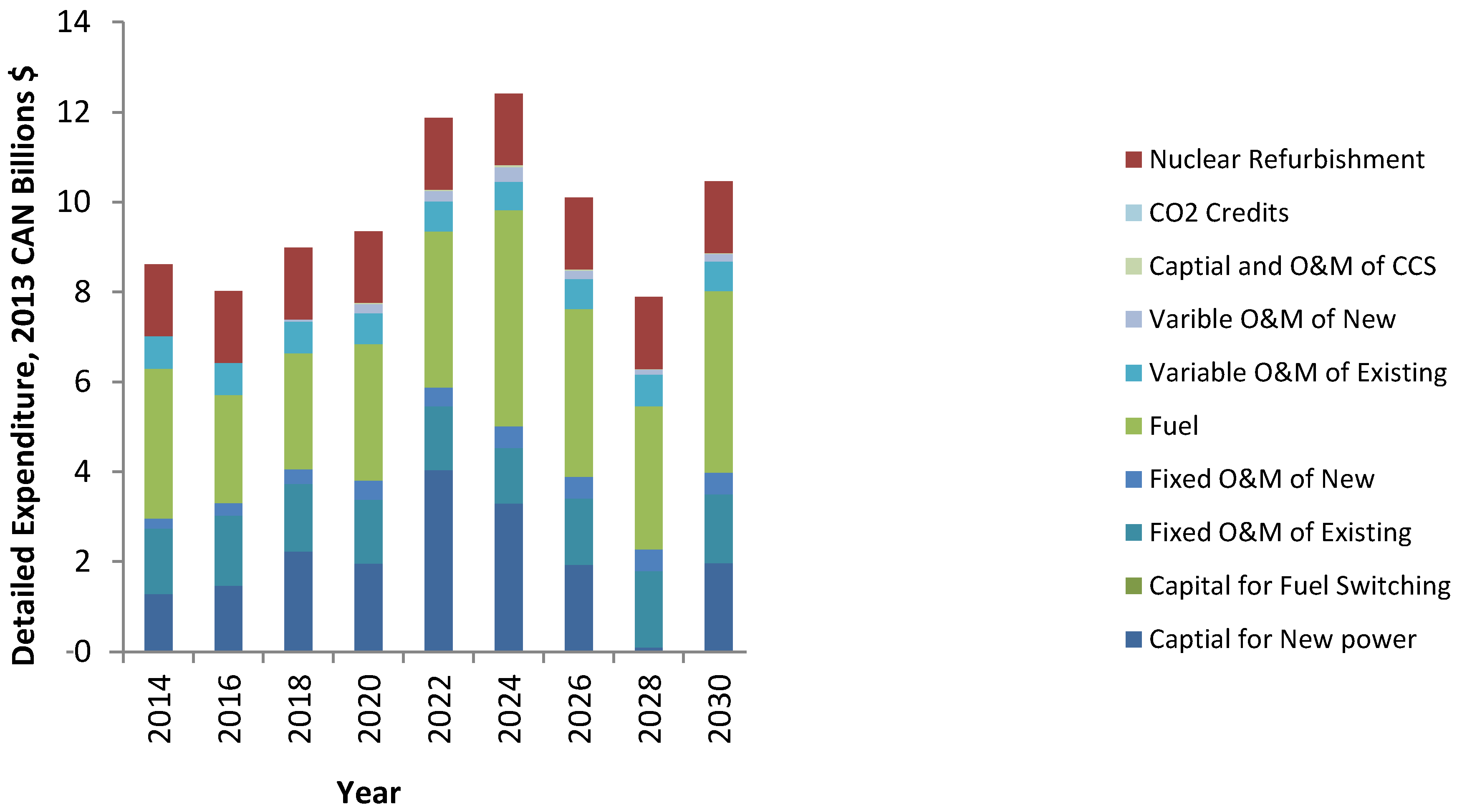
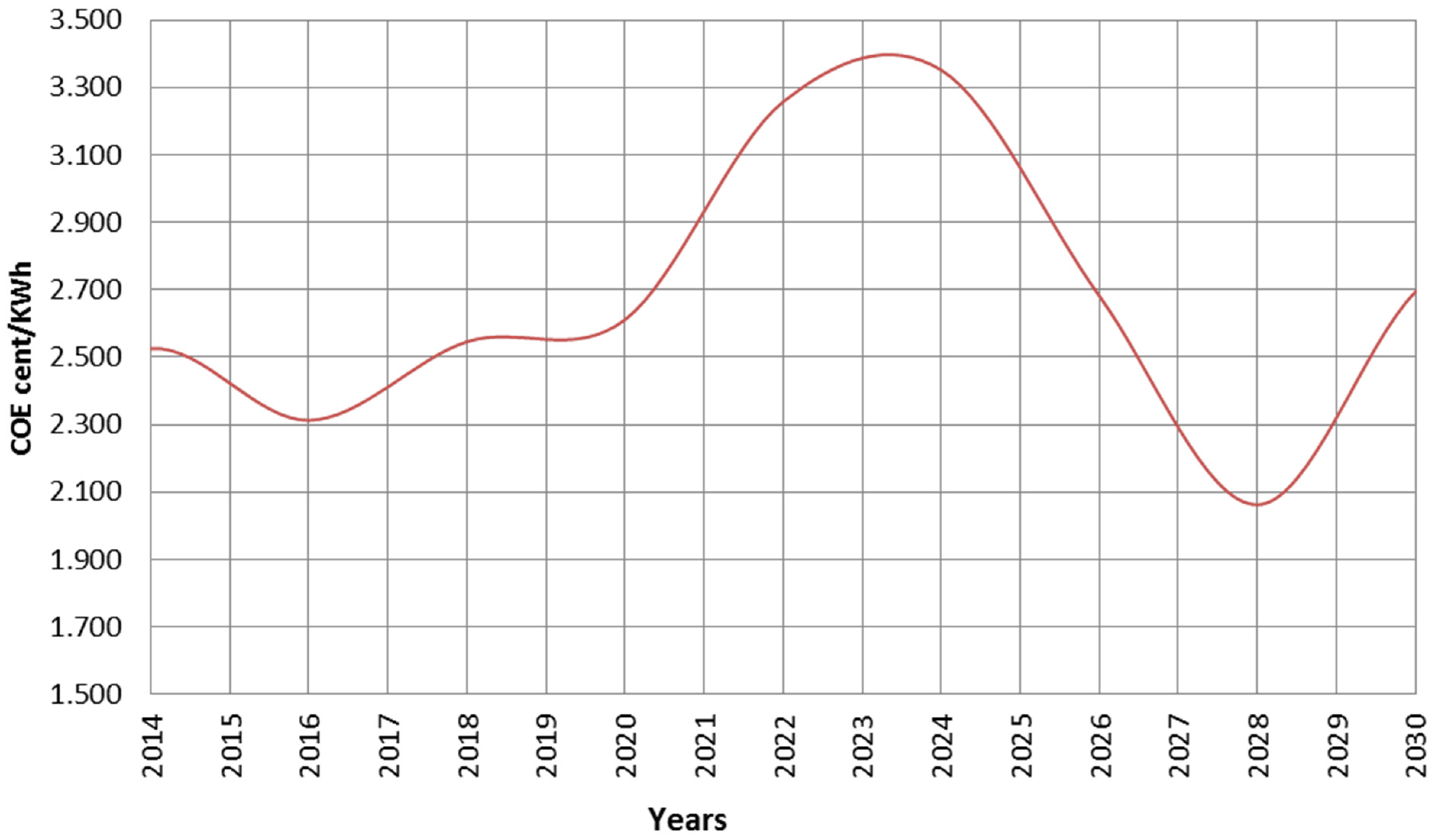
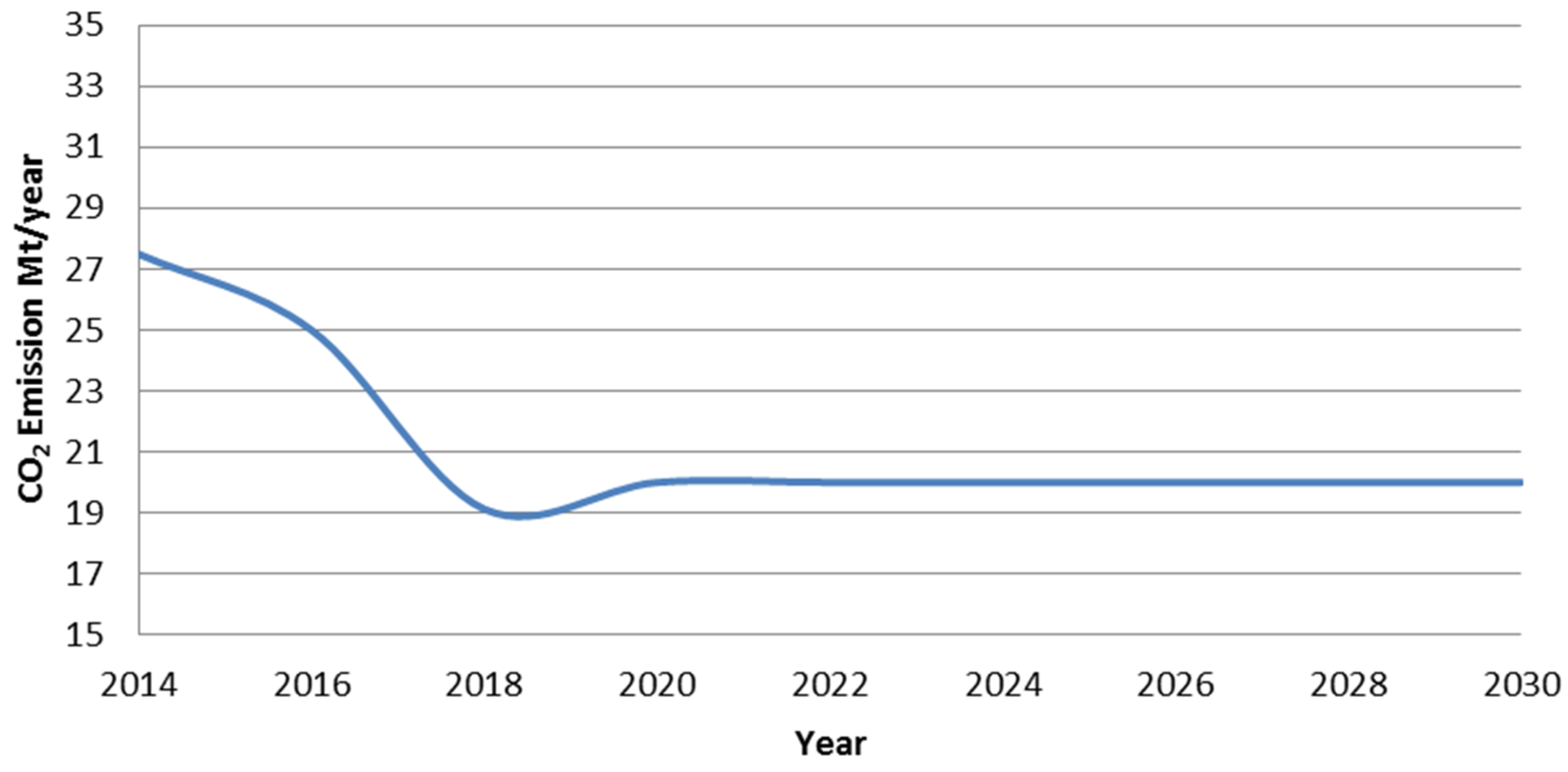
3.4. Case Study E: Base Case without Considering Current Load Deficit
3.4.1. New Power Generating Stations
| New Capacity (MW) | Years (20..) | |||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | ||
| NGCC | 210 | |||||||||||||||||
| NGCC | 320 | |||||||||||||||||
| NGCC | 375 | |||||||||||||||||
| Wind | 500 | |||||||||||||||||
| NGCC | 530 | |||||||||||||||||
| NGCC | 550 | |||||||||||||||||
3.4.2. Economic and Emission Analysis
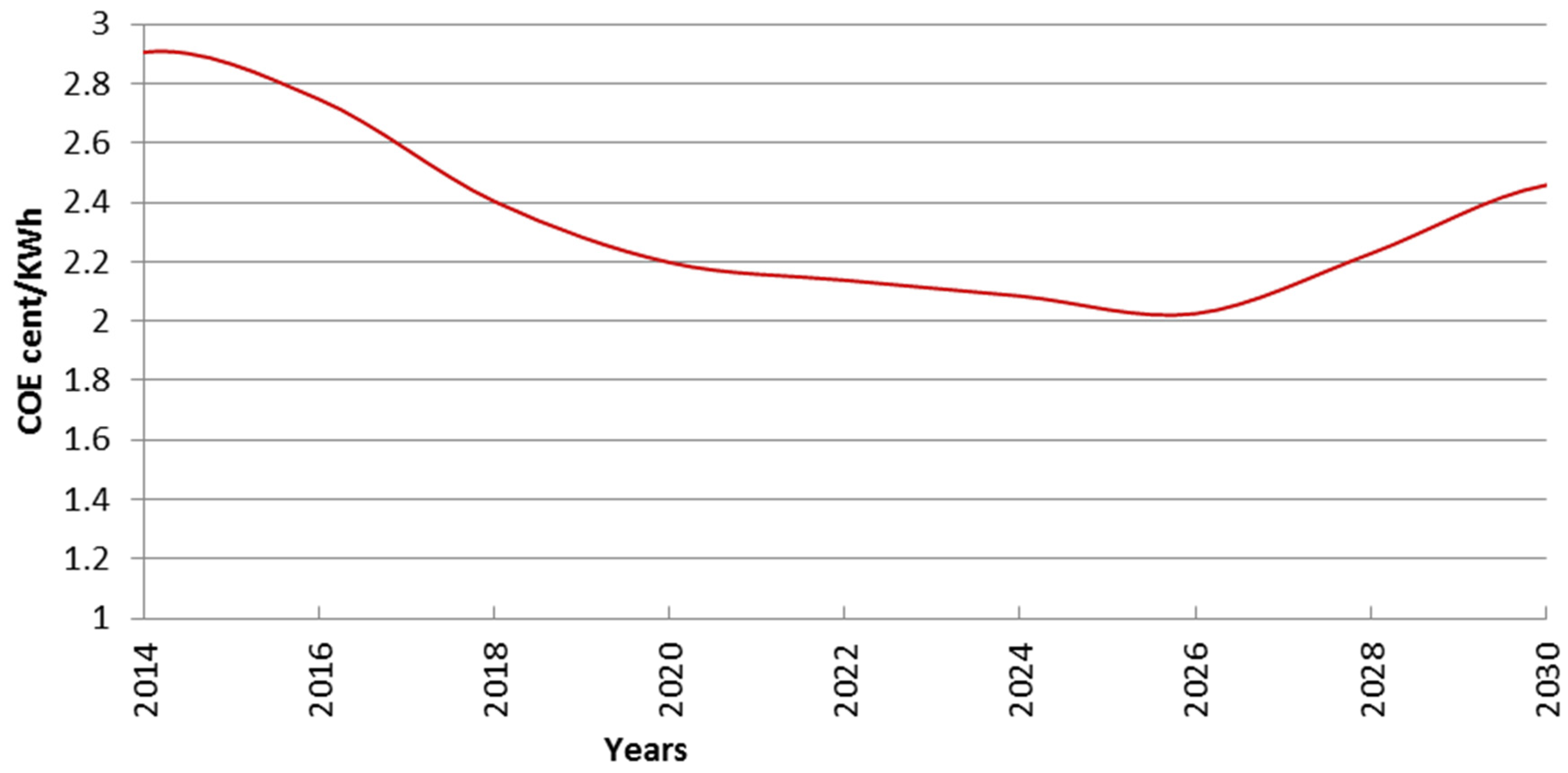

3.5. Summary
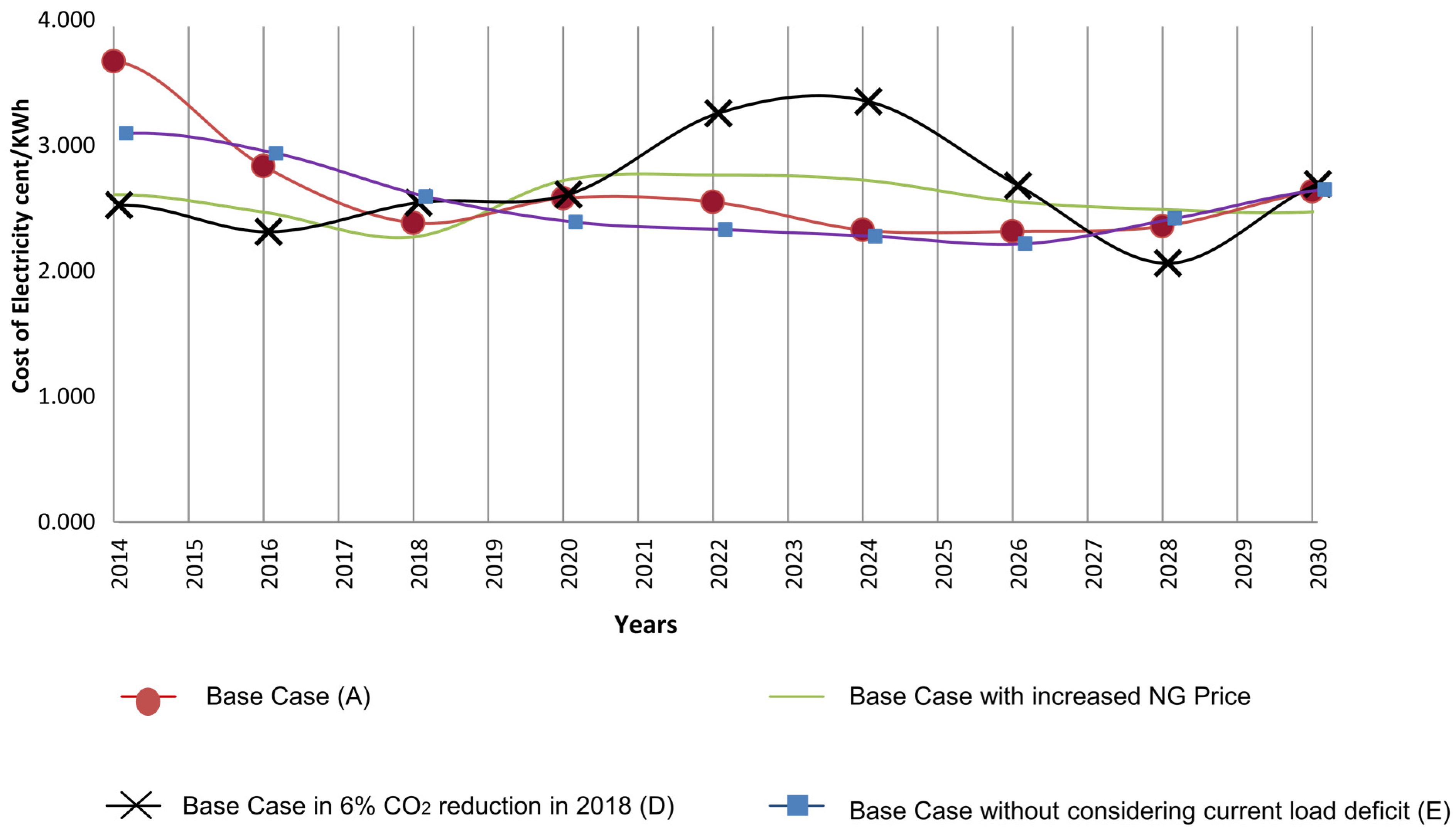
| Case | Total New Installed Cap (MW) | COE ¢/kwh | New Power (MW) | Installed Cap in 2030 Compared to 2013 | ||||
|---|---|---|---|---|---|---|---|---|
| Coal | NGCC | Wind | Hydro | Nuclear | ||||
| Case A | 7270 | 2.27 | NGCC: 2890 Wind: 2000 Nuclear: 1080 | 2%↓ | 4%↑ | 4%↑ | 0 | 3%↓ |
| Case B | 7270 | 2.34 | Coal: 1660 NGCC: 1370 Wind: 2000 Nuclear: 12010 | 2%↑ | 0 | 4%↑ | 3%↓ | 3%↓ |
| Case C | 6500 | 2.20 | Coal: 2792 NGCC: 3136 | 7%↑ | 4%↑ | 1%↓ | 4%↑ | 6%↓ |
| Case D | 8748 | 2.36 | IGCC: 1100 NGCC: 4398 Wind: 2000 | 1%↑ | 6%↑ | 4%↑ | 4%↑ | 7%↓ |
| Case E | 2400 | 2.19 | NGCC: 1985 Wind: 500 | 2%↓ | 5%↑ | 1%↑ | 1%↓ | 3%↓ |
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Graham, R. Comparing the Benefits and Impact of Hybrid Electric Vehicle Options; 1000349; Electric Power Research Institute (EPRI): Palo Alto, CA, USA, 2001; pp. 6–14. [Google Scholar]
- Duvall, M. Comparing the Benefits and Impacts of Hybrid Electric Vehicle Options for Compact Sedan and Sport Utility Vehicles; 1006892; Electric Power Research Institute (EPRI): Palo Alta, CA, USA, 2002. [Google Scholar]
- Yabe, K.; Shinoda, Y.; Seki, T.; Tanaka, H.; Akisawab, A. Market penetration speed and effects on CO2 reduction of electric vehicles and plug-in hybrid electric vehicles in Japan. Energy Policy 2012, 45, 529–540. [Google Scholar] [CrossRef]
- Wu, Y.; Yang, Z.; Lin, B.; Liu, H.; Wang, R.; Zhou, B.; Hao, J. Energy consumption and CO2 emission impacts of vehicle electrification in three developed regions of China. Energy Policy 2012, 48, 537–550. [Google Scholar] [CrossRef]
- Ahmadi, L.; Croiset, E.; Elkamel, A.; Douglas, P.L.; Unbangluang, W.; Entchev, E. Impact of PHEVs penetration on Ontario’s electricity grid and environmental considerations. Energies 2012, 5, 5019–5037. [Google Scholar] [CrossRef]
- Jansen, K.H.; Tim, M.; Brown, G.; Scott, S. Emissions impacts of plug-in hybrid electric vehicle deployment on the U.S. western grid. J. Power Sources 2010, 195, 5409–5416. [Google Scholar] [CrossRef]
- Srivastava, A.K.; Annabathina, B.; Kamalasadan, S. The challenges and policy options for integrating plug-in hybrid electric vehicle into the electric grid. Electr. J. 2010, 23, 83–91. [Google Scholar] [CrossRef]
- Waraich, R.A.; Galus, M.D.; Doblea, C.; Balmer, M.; Andersson, G.; Axhausena, K.W. Plug-in hybrid electric vehicles and smart grids: Investigations based on a microsimulation. Transp. Res. Part C: Emerg. Technol. 2013, 28, 74–86. [Google Scholar] [CrossRef]
- Richardson, D.B. Electric vehicles and the electric grid: A review of modeling approaches, Impacts, and renewable energy integration. Renew. Sustain. Energy Rev. 2013, 19, 247–254. [Google Scholar] [CrossRef]
- Hota, A.R.; Juvvanapudi, M.; Bajpai, P. Issues and solution approaches in PHEV integration to smart grid. Renew. Sustain. Energy Rev. 2014, 30, 217–229. [Google Scholar] [CrossRef]
- Valentine, K.; Acquaviva, J.; Foster, E.J.; Max Zhang, K. Transmission network-based energy and environmental assessment of plug-in hybrid electric vehicles. J. Power Sources 2011, 196, 3378–3386. [Google Scholar] [CrossRef]
- Falvo, M.C.; Lamedic, R.; Bartoni, R.; Maranzano, G. Energy management in metro-transit systems: An innovative proposal toward an integrated and sustainable urban mobility system including plug-in electric vehicles. Electr. Power Syst. Res. 2011, 81, 2127–2138. [Google Scholar] [CrossRef]
- Kempton, W.; Tomić, J. Vehicle-to-grid power implementation: From stabilizing the grid to supporting large-scale renewable energy. J. Power Sources 2005, 144, 280–294. [Google Scholar] [CrossRef]
- Mullan, J.; Harries, D.; Bräunl, T.; Whitely, S. The technical, economic and commercial viability of the vehicle-to-grid concept. Energy Policy 2012, 48, 394–406. [Google Scholar] [CrossRef]
- Göransson, L.; Karlsson, S.; Johnsson, F. Integration of plug-in hybrid electric vehicles in a regional wind-thermal power system. Energy Policy 2010, 38, 5482–5492. [Google Scholar] [CrossRef]
- Kiviluoma, J.; Meibom, P. Methodology for modelling plug-in electric vehicles in the power system and cost estimates for a system with either smart or dumb electric vehicles. Energy 2011, 36, 1758–1767. [Google Scholar] [CrossRef]
- Hedegaard, K.; Ravn, H.; Juul, N.; Meibom, P. Effects of electric vehicles on power systems in Northern Europe. Energy 2012, 48, 356–368. [Google Scholar] [CrossRef]
- Peng, M.; Liu, L.; Jiang, C. A review on the economic dispatch and risk management of the large-scale plug-in electric vehicles (PHEVs)-penetrated power systems. Renew. Sustain. Energy Rev. 2012, 16, 1508–1515. [Google Scholar] [CrossRef]
- Soares, B.; Borb, M.C.; Szklo, A.; Schaeffer, A. Plug-in hybrid electric vehicles as a way to maximize the integration of variable renewable energy in power systems: The case of wind generation in northeastern Brazil. Energy 2012, 37, 469–481. [Google Scholar] [CrossRef]
- Wu, D.; Aliprantis, D.C. Modeling light-duty plug-in electric vehicles for national energy and transportation planning. Energy Policy 2013, 63, 419–432. [Google Scholar] [CrossRef]
- Brouwer, A.S.; Kuramochi, T.; Broek, M.V.D.; Faaij, A. Fulfilling the electricity demand of electric vehicles in the long term future: An evaluation of centralized and decentralized power supply systems. Appl. Energy 2013, 107, 33–51. [Google Scholar] [CrossRef]
- Zhang, L.; Brown, T.; Samuelsen, S. Evaluation of charging infrastructure requirements and operating costs for plug-in electric vehicles. J. Power Sources 2013, 240, 515–524. [Google Scholar] [CrossRef]
- Weis, A.; Jaramillo, P.; Michalek, J. Estimating the potential of controlled plug-in hybrid electric vehicle charging to reduce operational and capacity expansion costs for electric power systems with high wind penetration. Appl. Energy 2014, 115, 190–204. [Google Scholar] [CrossRef]
- Mirzaesmaeeli, H.; Elkamela, A.; Douglas, P.L.; Croiset, E.; Gupta, M. A multi-period optimization model for energy planning with CO2 emission consideration. J. Environ. Manag. 2010, 91, 1063–1070. [Google Scholar] [CrossRef]
- Ontario Power Generation (OPG). 2009 Sustainable Development Report. Available online: http://192.75.131.106/pdf/Sustainable%20Development%20Reports/004%20Sustainable%20Development%20Report%202009.pdf (accessed on 28 April 2015).
- Independent Electricity System Operator (IESO). Generator Output and Capability. Available online: http://reports.ieso.ca/public/GenOutputCapability/ (accessed on 28 April 2015).
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ahmadi, L.; Elkamel, A.; Abdul-Wahab, S.A.; Pan, M.; Croiset, E.; Douglas, P.L.; Entchev, E. Multi-Period Optimization Model for Electricity Generation Planning Considering Plug-in Hybrid Electric Vehicle Penetration. Energies 2015, 8, 3978-4002. https://doi.org/10.3390/en8053978
Ahmadi L, Elkamel A, Abdul-Wahab SA, Pan M, Croiset E, Douglas PL, Entchev E. Multi-Period Optimization Model for Electricity Generation Planning Considering Plug-in Hybrid Electric Vehicle Penetration. Energies. 2015; 8(5):3978-4002. https://doi.org/10.3390/en8053978
Chicago/Turabian StyleAhmadi, Lena, Ali Elkamel, Sabah A. Abdul-Wahab, Michael Pan, Eric Croiset, Peter L. Douglas, and Evgueniy Entchev. 2015. "Multi-Period Optimization Model for Electricity Generation Planning Considering Plug-in Hybrid Electric Vehicle Penetration" Energies 8, no. 5: 3978-4002. https://doi.org/10.3390/en8053978
APA StyleAhmadi, L., Elkamel, A., Abdul-Wahab, S. A., Pan, M., Croiset, E., Douglas, P. L., & Entchev, E. (2015). Multi-Period Optimization Model for Electricity Generation Planning Considering Plug-in Hybrid Electric Vehicle Penetration. Energies, 8(5), 3978-4002. https://doi.org/10.3390/en8053978







