Comparison of Output Current Ripple in Single and Dual Three-Phase Inverters for Electric Vehicle Motor Drives
Abstract
:1. Introduction

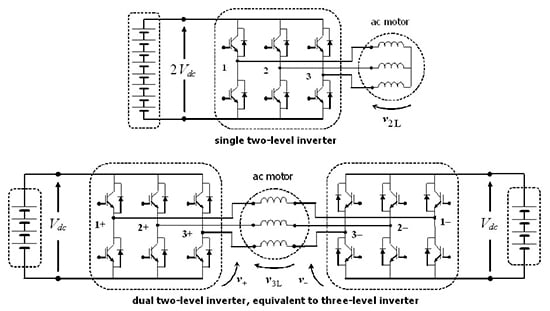
2. Space Vector Analysis of Single and Dual Inverters
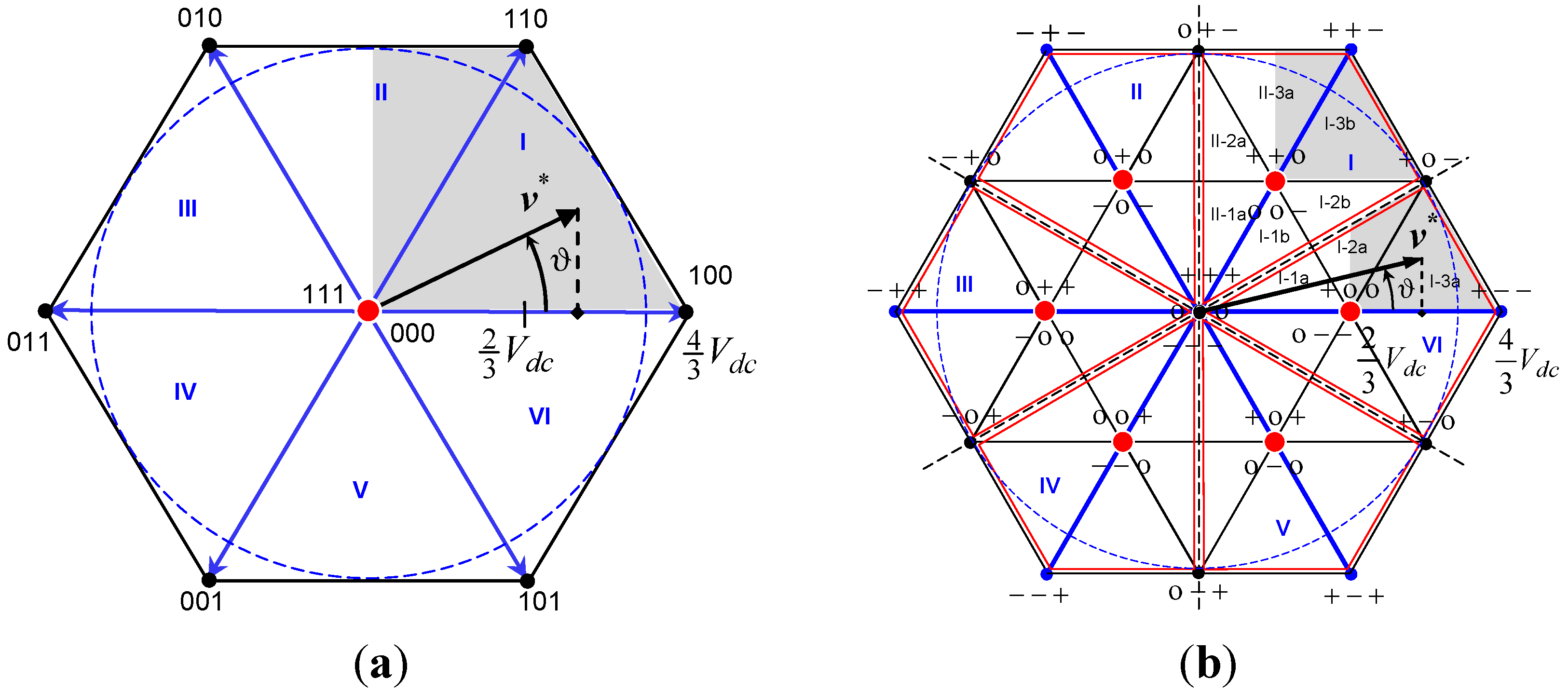
3. Inverter Modulation
3.1. Space Vector Modulation
3.2. Implementation of Centered (Optimized) Modulation in Carrier-Based PWM

4. Current Ripple Evaluation
4.1. Current Ripple Definitions
4.2. Current Ripple Evaluation in Single-2L Inverter
4.3. Current Ripple Evaluation in Dual-2L Inverter (3L)
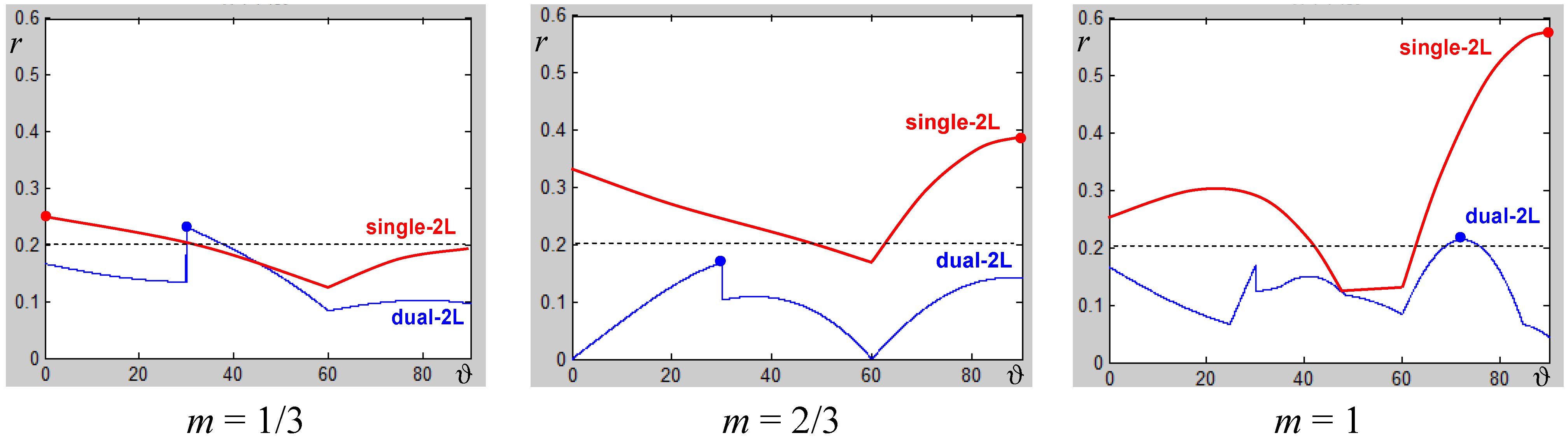
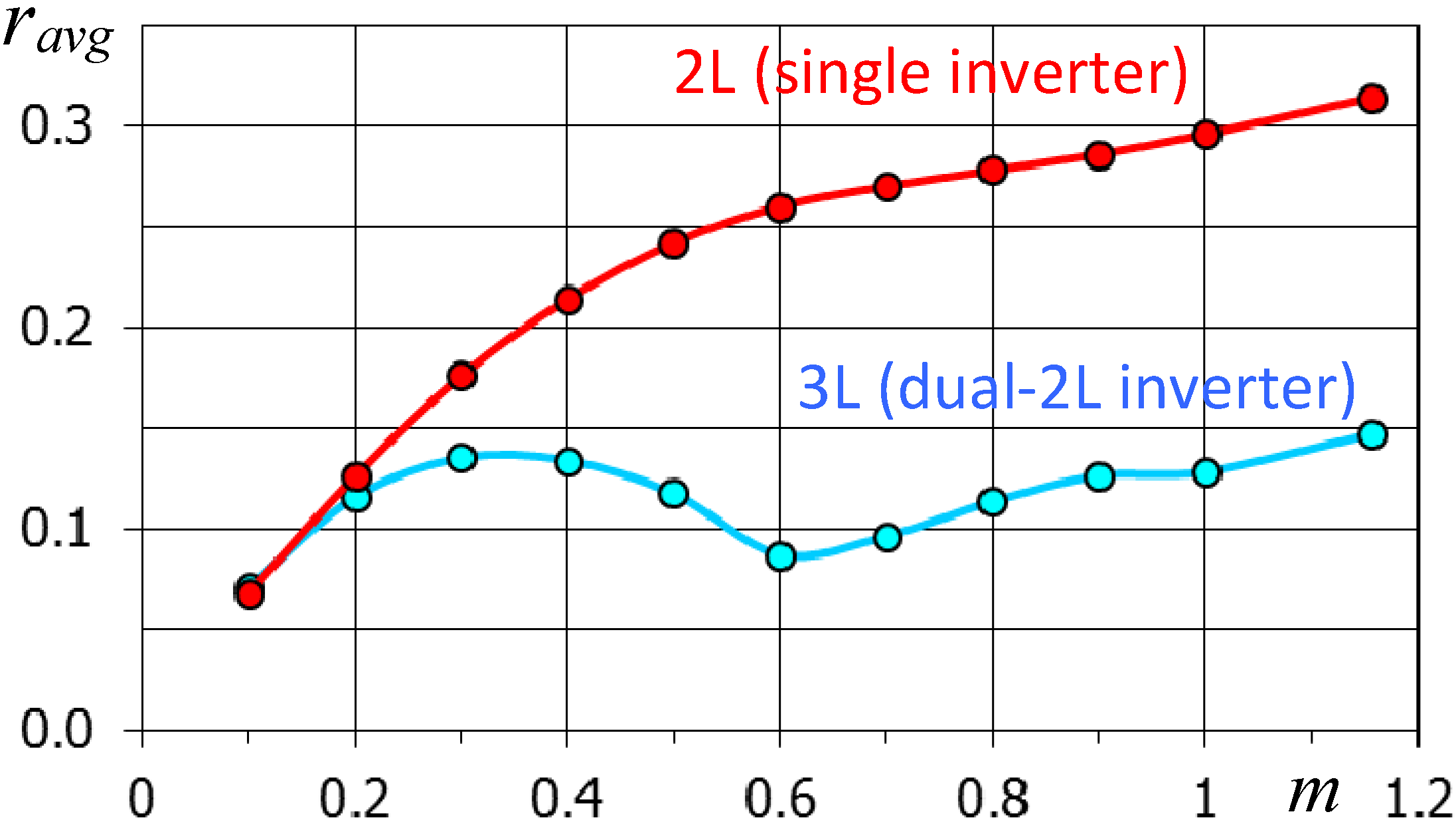
5. Results
5.1. Theoretical Results
5.2. Experimental Results

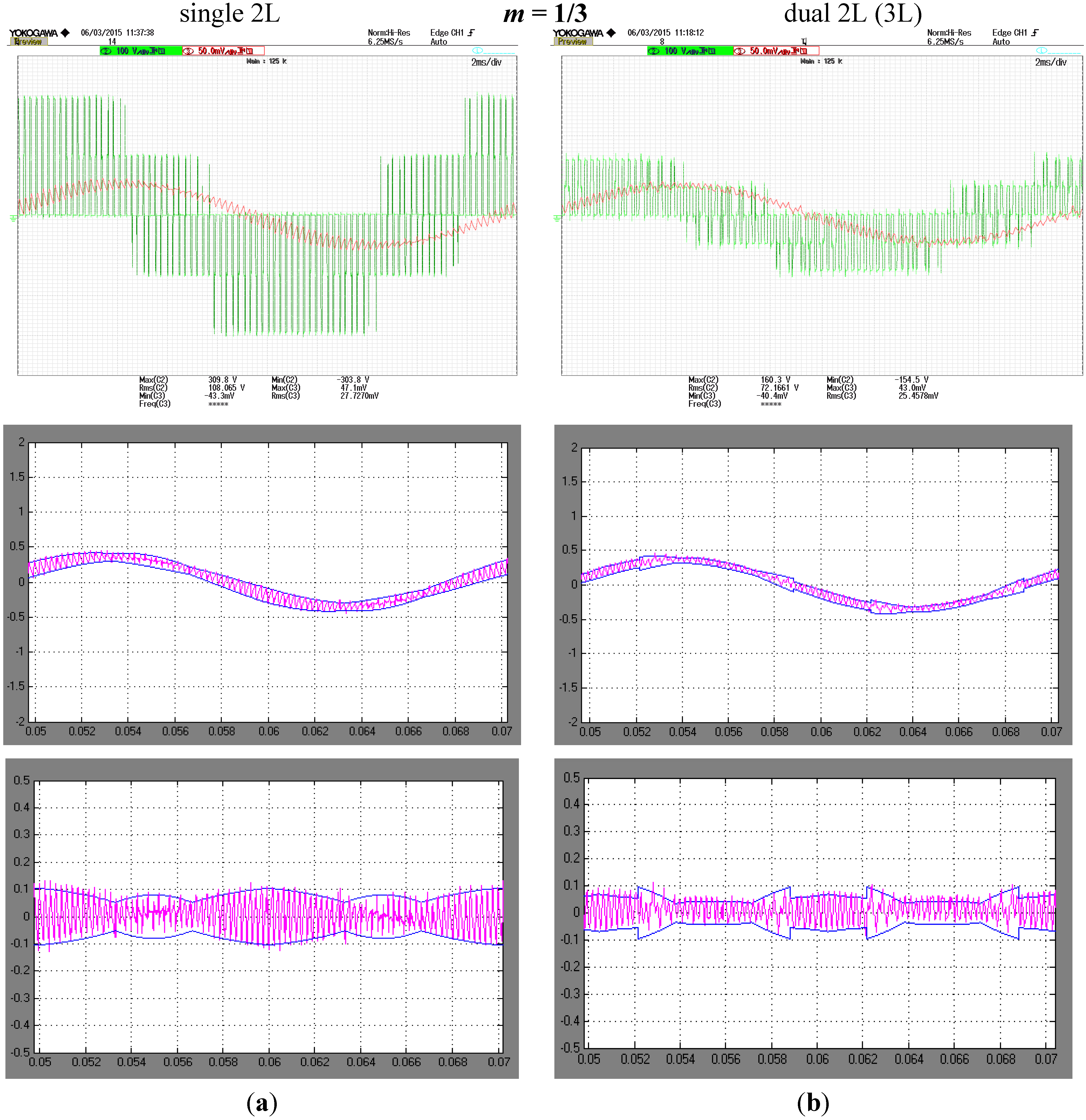
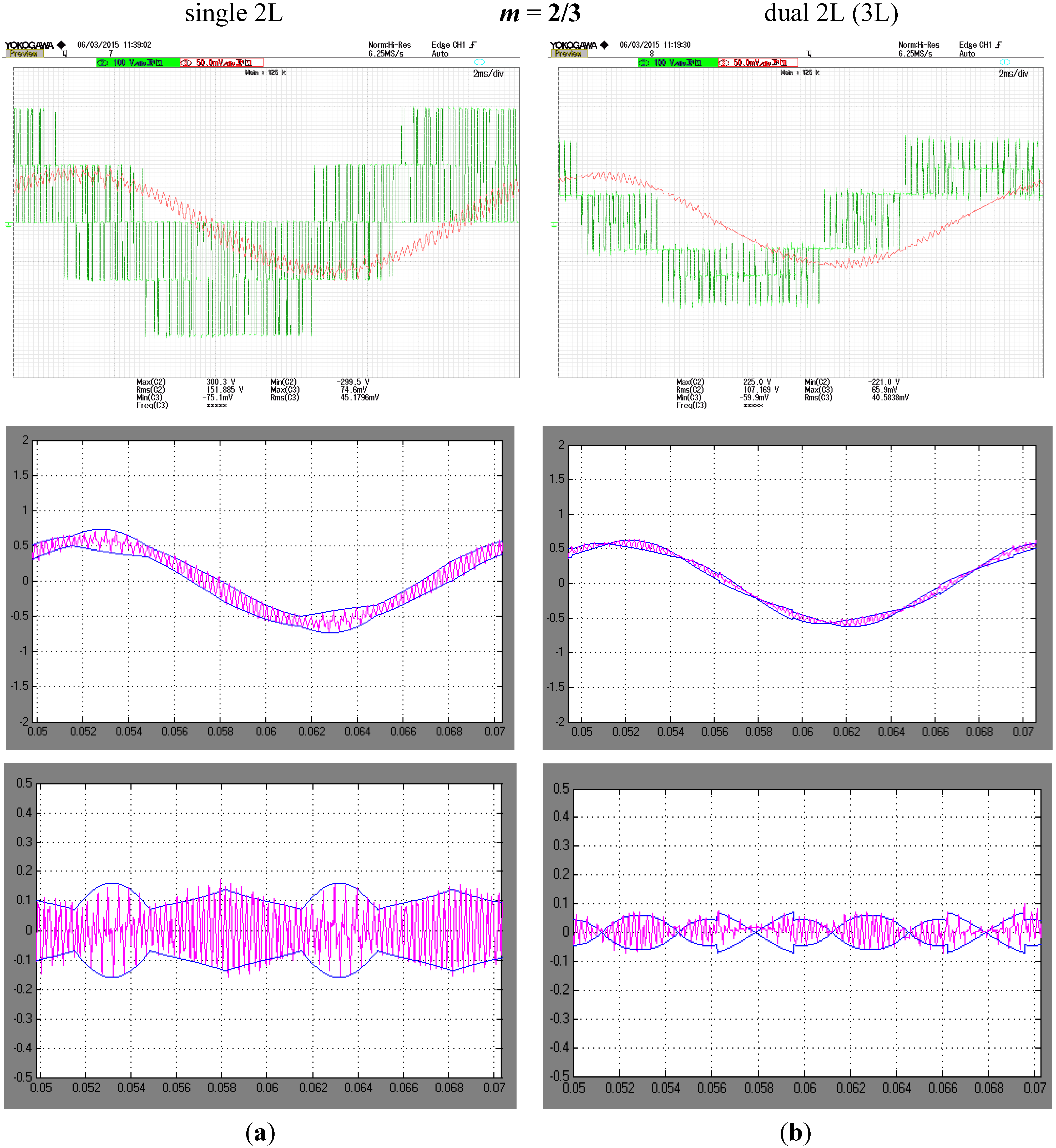
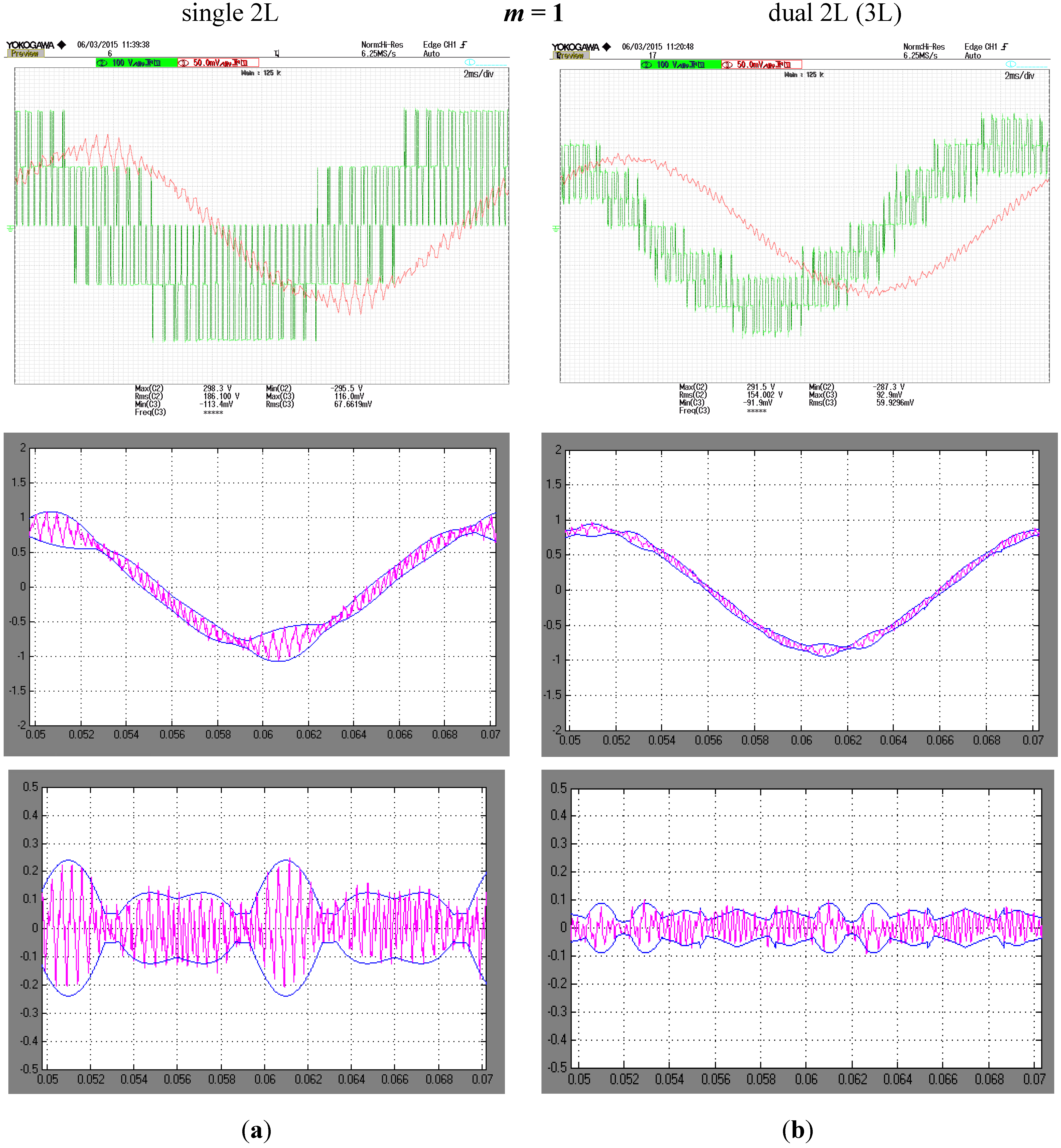
6. Conclusions
Author Contributions
Conflicts of Interest
References
- Rodríguez, J.; Lai, J.S.; Peng, F.Z. Multilevel inverters: A survey of topologies, controls, and applications. IEEE Trans. Ind. Electron. 2002, 49, 724–738. [Google Scholar] [CrossRef]
- Franquelo, L.G.; Rodriguez, J.; Leon, J.I.; Kouro, S.; Portillo, R.; Prats, M.M. The age of multilevel converters arrives. IEEE Trans. Ind. Electron. Mag. 2008, 2, 28–39. [Google Scholar] [CrossRef]
- Kawabata, Y.; Nasu, M.; Nomoto, T.; Ejiogu, E.C.; Kawabata, T. High-efficiency and low acoustic noise drive system using open-winding AC motor and two space-vector-modulated inverters. IEEE Trans. Ind. Electron. 2002, 49, 783–789. [Google Scholar] [CrossRef]
- Kim, J.; Jung, J.; Nam, K. Dual-inverter control strategy for high-speed operation of EV induction motors. IEEE Trans. Ind. Electron. 2004, 51, 312–320. [Google Scholar] [CrossRef]
- Rossi, C.; Casadei, D.; Grandi, G.; Lega, A. Multilevel operation and input power balancing for a dual two-level inverter with insulated DC sources. IEEE Trans. Ind. Appl. 2008, 44, 1815–1824. [Google Scholar] [CrossRef]
- Srinivas, S.; Sekhar, K.R. Theoretical and experimental analysis for current in a dual-inverter-fed open-end winding induction motor drive with reduced switching PWM. IEEE Trans. Ind. Electron. 2013, 60, 4318–4328. [Google Scholar] [CrossRef]
- Sekhar, K.R.; Srinivas, S. Discontinuous decoupled PWMs for reduced current ripple in a dual two-level inverter fed open-end winding induction motor drive. IEEE Trans. Power Electron. 2013, 28, 2493–2502. [Google Scholar] [CrossRef]
- Hong, J.; Lee, H.; Nam, K. Charging method for the secondary battery in dual inverter drive systems for electric vehicles. IEEE Trans. Power Electron. 2015, 30, 909–921. [Google Scholar] [CrossRef]
- Mutoh, N.; Kanesaki, M. A suitable method for ecovehicles to control surge voltage at motor terminals connected to PWM inverters and to control induced EMI noise. IEEE Trans. Veh. Technol. 2008, 57, 2089–2098. [Google Scholar] [CrossRef]
- Kanchan, R.; Tekwani, P.; Gopakumar, K. Three-level inverter scheme with common mode voltage elimination and dc link capacitor voltage balancing for an open-end winding induction motor drive. IEEE Trans. Power Electron. 2006, 21, 1676–1683. [Google Scholar] [CrossRef]
- Grandi, G.; Tani, A.; Sanjeevikumar, P.; Ostojic, D. Multi-phase multi-level AC motor drive based on four three-phase two-level inverters. In Proceedings of the 20th Symposium on Power Electronics, Electrical Drives and Advanced Electrical Motors (SPEEDAM), Pisa, Italy, 14–16 June 2010; pp. 1768–1775.
- Boller, T.; Holtz, J.; Rathore, A.K. Optimal pulsewidth modulation of a dual three-level inverter system operated from a single DC link. IEEE Trans. Ind. Appl. 2012, 48, 1610–1615. [Google Scholar] [CrossRef]
- Ruderman, A. Understanding PWM current ripple in star-connected AC motor drive. IEEE Power Electron. Soc. Newsl. 2009, 21, 14–17. [Google Scholar]
- Grandi, G.; Loncarski, J. Evaluation of current ripple amplitude in three-phase PWM voltage source inverters. In Proceedings of the 8th IEEE International Conference-Workshop on Compatibility and Power Electronics (CPE), Ljubljana, Slovenia, 5–7 June 2013; pp. 156–161.
- Jiang, D.; Wang, F. Current-ripple prediction for three-phase PWM converters. IEEE Trans. Ind. Appl. 2014, 50, 531–538. [Google Scholar] [CrossRef]
- Grandi, G.; Loncarski, J. Evaluation of current ripple amplitude in five-phase PWM voltage source inverters. In Proceedings of the IEEE Conference on ICT, Power Engineering, and Signal Processing (EUROCON), Zagreb, Croatia, 1–4 July 2013; pp. 1073–1080.
- Jiang, D.; Wang, F. A general current ripple prediction method for the multiphase voltage source converter. IEEE Trans. Power Electron. 2014, 29, 2643–2648. [Google Scholar] [CrossRef]
- Grandi, G.; Loncarski, J. Analysis of peak-to-peak current ripple amplitude in seven-phase PWM voltage source inverters. Energies 2013, 6, 4429–4447. [Google Scholar] [CrossRef]
- Grandi, G.; Loncarski, J.; Rossi, C. Comparison of peak-to-peak current ripple amplitude in multiphase PWM voltage source inverters. In Proceedings of the 15th IEEE Conference on Power Electronics and Applications (EPE'13 ECCE Europe), Lille, France, 3–5 September 2013.
- Grandi, G.; Loncarski, J.; Dordevic, O. Analytical evaluation of output current ripple amplitude in three-phase three-level inverters. IET Power Electron. 2014, 7, 2258–2268. [Google Scholar] [CrossRef]
- Grandi, G.; Loncarski, J.; Dordevic, O. Analysis and comparison of peak-to-peak current ripple in two-level and multilevel PWM inverters. IEEE Trans. Ind. Electron. 2014. [Google Scholar] [CrossRef]
- Schulz, S.E.; Kowalewski, D.L. Implementation of variable-delay random PWM for automotive applications. IEEE Trans. Veh. Technol. 2007, 56, 1427–1433. [Google Scholar] [CrossRef]
- Wang, F. Sine-triangle versus space-vector modulation for three-level PWM voltage-source inverters. IEEE Trans. Ind. Appl. 2002, 38, 500–506. [Google Scholar] [CrossRef]
- McGrath, B.P.; Holmes, D.G.; Lipo, T.A. Optimized space vector switching sequences for multilevel inverters. IEEE Trans. Power Electron. 2003, 18, 1293–1301. [Google Scholar] [CrossRef]
- Grandi, G.; Loncarski, J. Simplified implementation of optimised carrier-based PWM in three-level inverters. IET Electron. Lett. 2014, 50, 631–633. [Google Scholar] [CrossRef]
- Seo, J.H.; Choi, C.H.; Hyun, D.S. A new simplified space-vector PWM method for three-level inverters. IEEE Trans. Power Electron. 2001, 16, 545–550. [Google Scholar] [CrossRef]
- Holmes, D.; Lipo, T.A. Pulse Width Modulation for Power Converters—Principles and Practice; Wiley-IEEE Press: Piscataway, NJ, USA, 2003; pp. 215–257. [Google Scholar]
- Prats, M.M.; Carrasco, J.M.; Franquelo, L.G. Effective algorithm for multilevel converters with very low computational cost. IET Electron. Lett. 2002, 38, 1398–1400. [Google Scholar] [CrossRef]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Loncarski, J.; Leijon, M.; Srndovic, M.; Rossi, C.; Grandi, G. Comparison of Output Current Ripple in Single and Dual Three-Phase Inverters for Electric Vehicle Motor Drives. Energies 2015, 8, 3832-3848. https://doi.org/10.3390/en8053832
Loncarski J, Leijon M, Srndovic M, Rossi C, Grandi G. Comparison of Output Current Ripple in Single and Dual Three-Phase Inverters for Electric Vehicle Motor Drives. Energies. 2015; 8(5):3832-3848. https://doi.org/10.3390/en8053832
Chicago/Turabian StyleLoncarski, Jelena, Mats Leijon, Milan Srndovic, Claudio Rossi, and Gabriele Grandi. 2015. "Comparison of Output Current Ripple in Single and Dual Three-Phase Inverters for Electric Vehicle Motor Drives" Energies 8, no. 5: 3832-3848. https://doi.org/10.3390/en8053832
APA StyleLoncarski, J., Leijon, M., Srndovic, M., Rossi, C., & Grandi, G. (2015). Comparison of Output Current Ripple in Single and Dual Three-Phase Inverters for Electric Vehicle Motor Drives. Energies, 8(5), 3832-3848. https://doi.org/10.3390/en8053832