Enhanced Load Power Sharing Accuracy in Droop-Controlled DC Microgrids with Both Mesh and Radial Configurations
Abstract
:1. Introduction
2. Traditional Droop Control
2.1. State-of-the-Art of DC Microgrids
- Control [11,12]: DC microgrids have simpler models and control since there is no phase angle, frequency or reactive power, while synchronization, reactive power flow and harmonics have to be considered for AC systems which leads to more complicated control system. Moreover, DC is chosen over AC because it facilitates integrating most modern electronic loads, energy storage devices, and DG technologies—all of them inherently DC.
- Economical operation [13,14,15]: Economical operation in DC microgrids can be achieved without complex and computation-intensive optimization algorithms and as pointed out in the existing literature, the total cost of ownership, infrastructure, equipment, maintenance and operation are lower in DC microgrids.
- Efficiency [16,17,18]: The system efficiency becomes higher due to the reduction of conversion losses of inverters between DC output sources and loads. DC microgrids already have a fault-ride-through capability of their own due to the stored energy of the DC capacitor and the voltage control of the AC/DC converter.
2.2. Configuration of DC Microgrids
- Equipment costs become lower.
- Distribution capabilities are enhanced.
- Sustainability is improved due to reduced copper use.
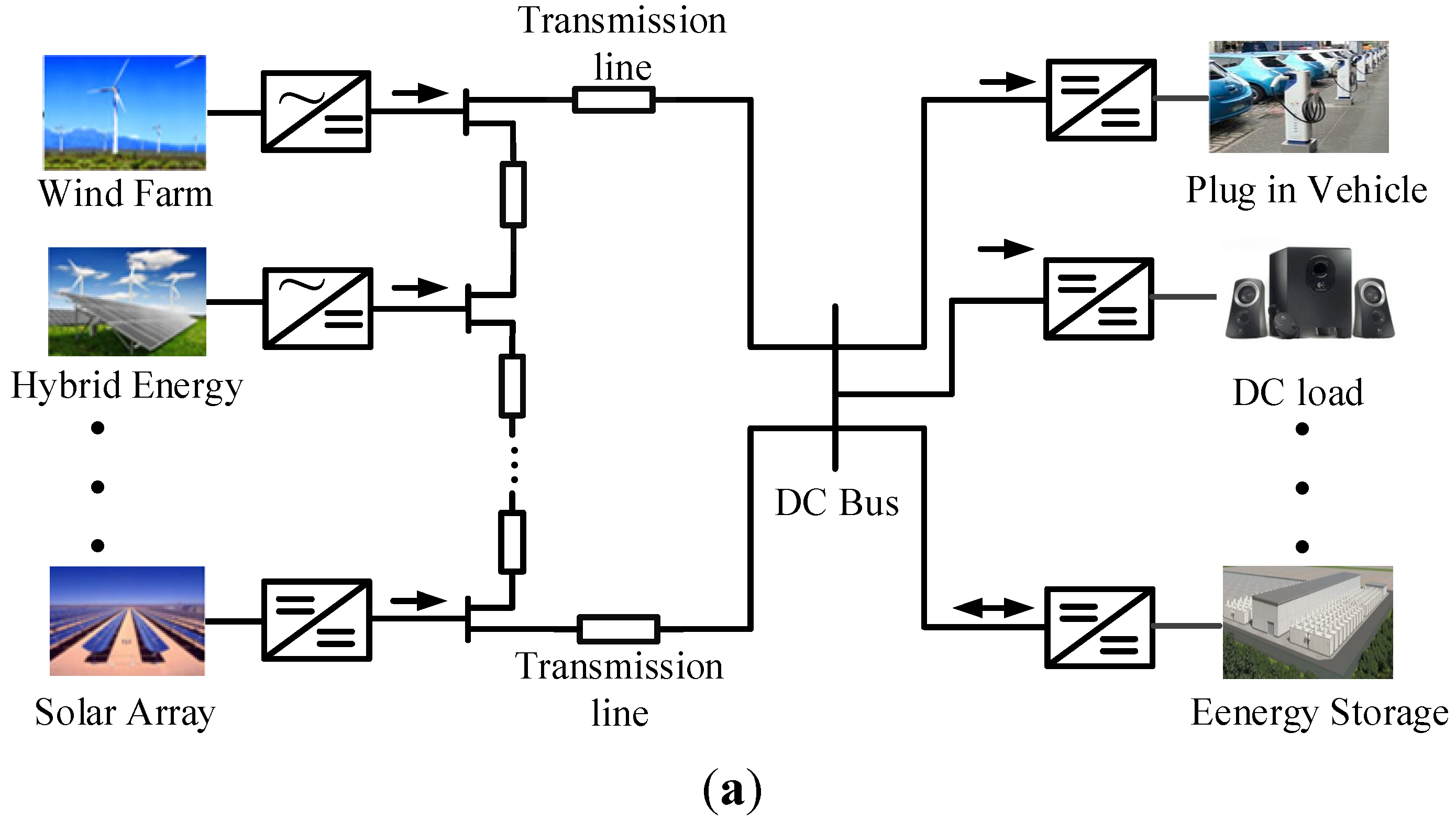

2.3. Drawbacks of Traditional Droop Control
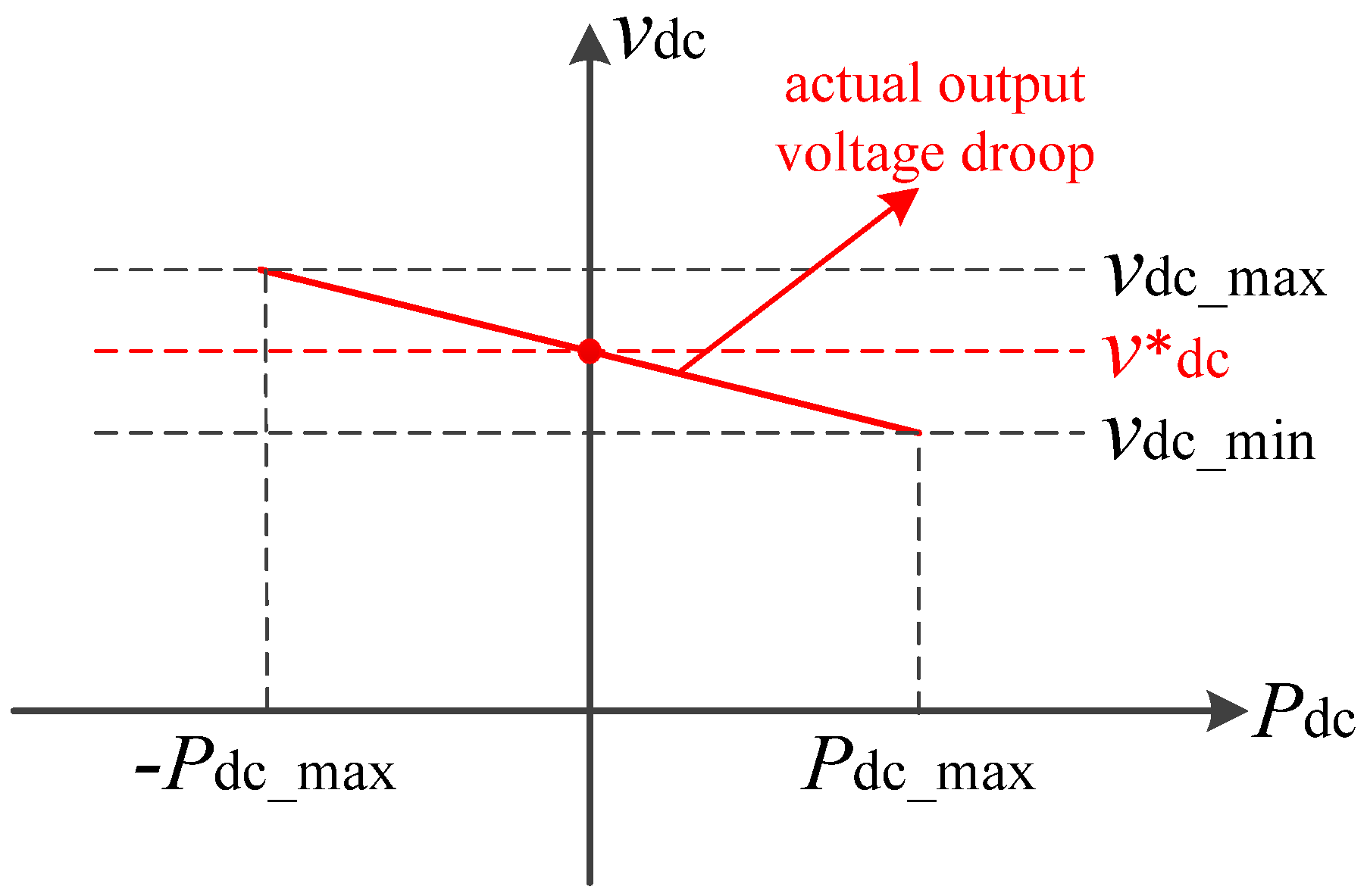
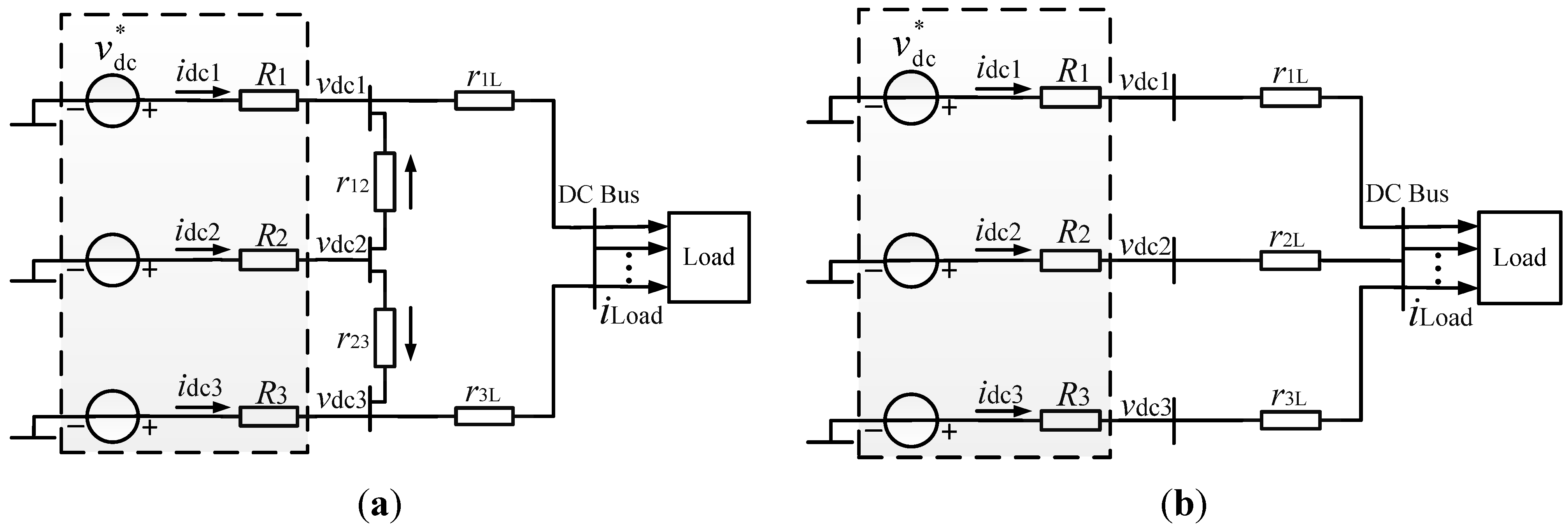
- Deviation of bus voltage is inevitable.
- There is trade-off between power-sharing accuracy and voltage deviation.
3. Analysis of Droop Control Issues
3.1. Mesh Configuration
3.2. Radial Configuration
4. Proposed Approach
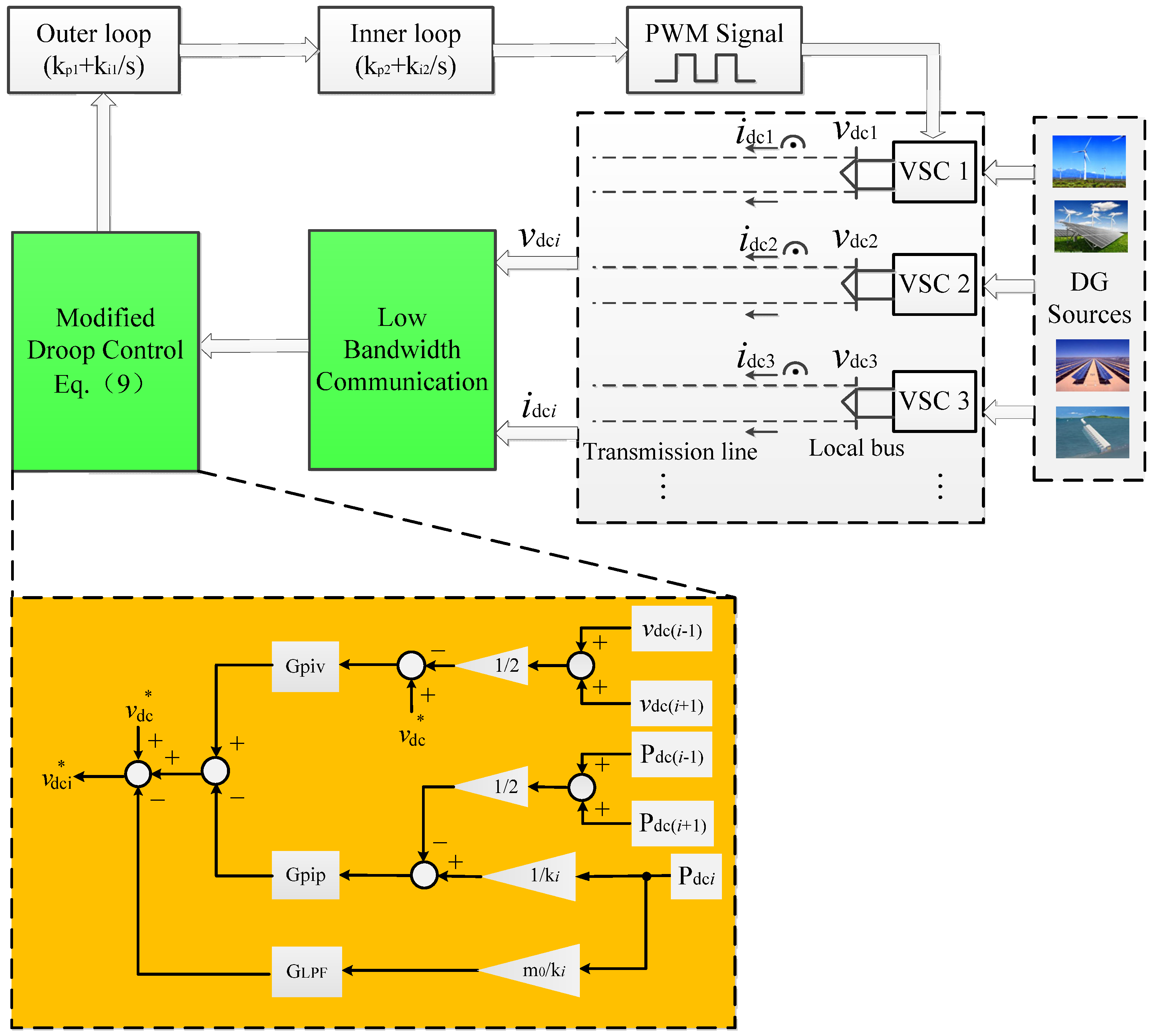
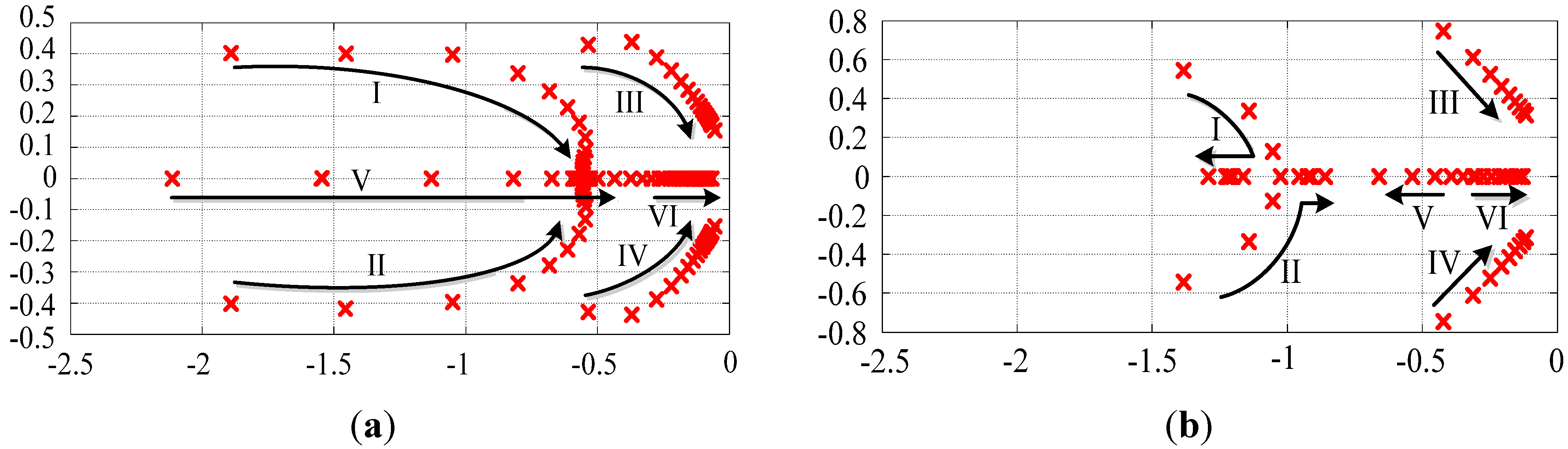
5. Simulations and Experimental Results
| Item | Symbol | Value | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Reference of DC output voltage | vdc | 380 V | ||||||||
| Load resistance | RL | 19 Ω | ||||||||
| Power sharing proportion (Converter #i=1,2,3) | ki | 1 | ||||||||
| LPF cutting frequency | fc | 20 Hz | ||||||||
| Communication delay | τ | 0.1 s or 1 s | ||||||||
| Droop coefficient | m0 | 0.0015 | ||||||||
| Averaging voltage controller proportion coefficient | kpv | 2 × 10−3 | ||||||||
| Averaging voltage controller integral coefficient | kiv | 4.5 × 10−2 | ||||||||
| Averaging power controller proportion coefficient | kpp | 2.3 × 10−3 | ||||||||
| Averaging power controller integral coefficient | kip | 5.5 × 103 | ||||||||
| Mesh configuration | Radial configuration | |||||||||
| Case No. | r1L | r12 | r23 | r3L | τ | Case No. | r1L | r2L | r3L | τ |
| 1 | 0.8 Ω | 1.0 Ω | 1.0 Ω | 1.2 Ω | 0.1 s | 4 | 0.8 Ω | 1.0 Ω | 1.2 Ω | 0.1 s |
| 2 | 0.8 Ω | 1.0 Ω | 1.0 Ω | 1.2 Ω | 1 s | 5 | 0.8 Ω | 1.0 Ω | 1.2 Ω | 1 s |
| 3 | 0.6 Ω | 1.2 Ω | 1.2 Ω | 1.8 Ω | 1 s | 6 | 0.6 Ω | 1.2 Ω | 1.8 Ω | 1 s |
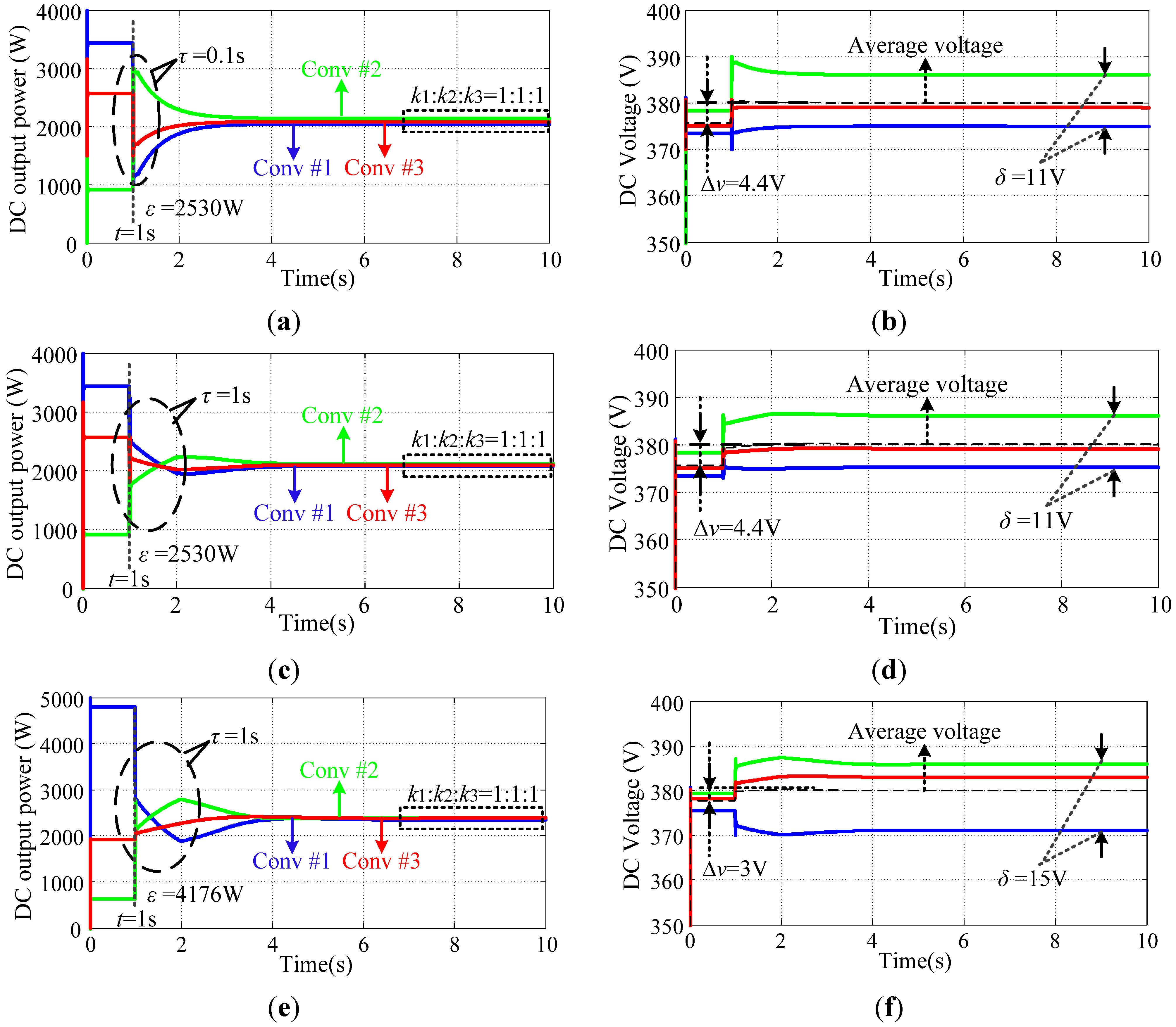
5.1. Simulation Results for Mesh Configuration
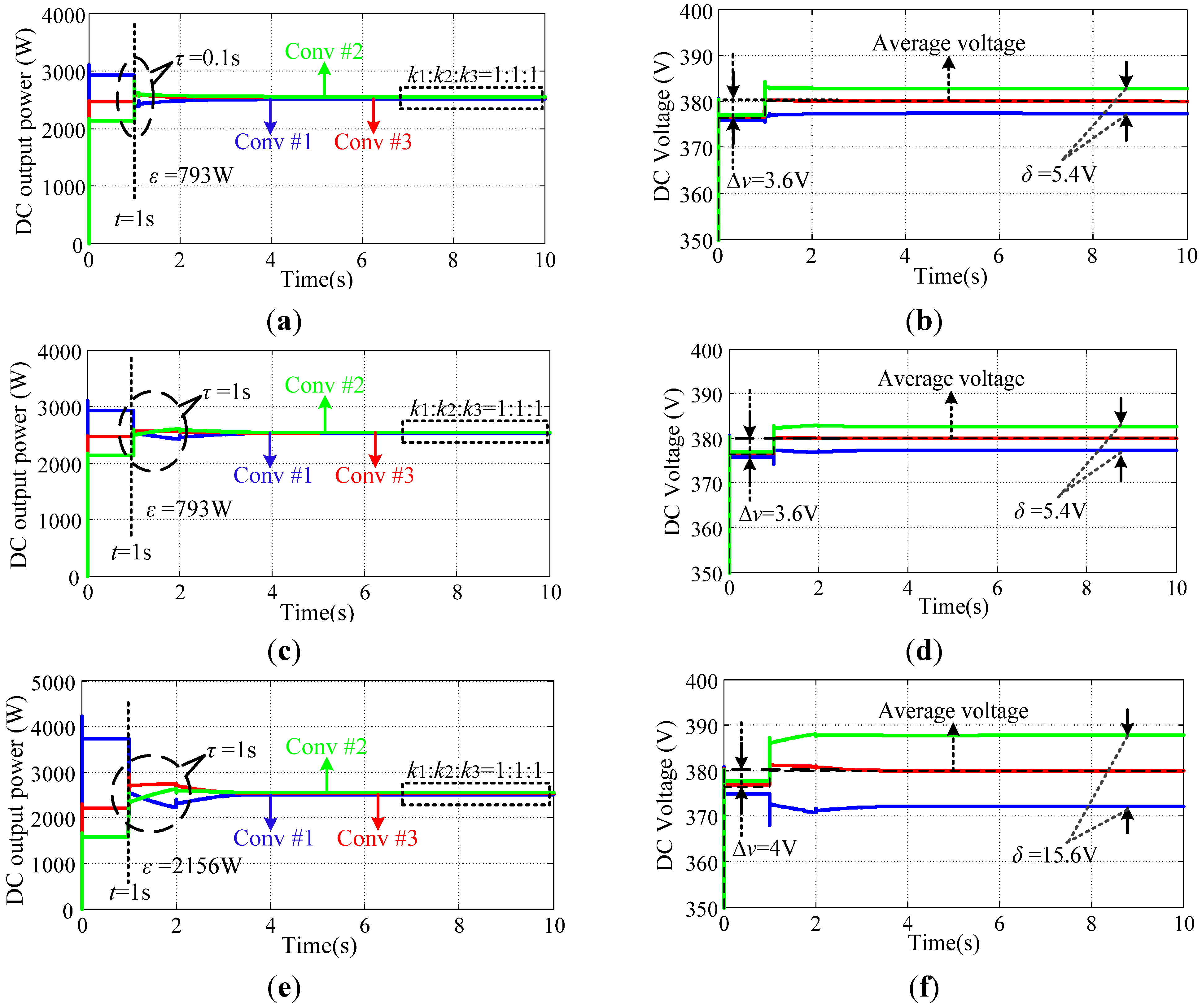
5.2. Simulation Results for Radial Configuration
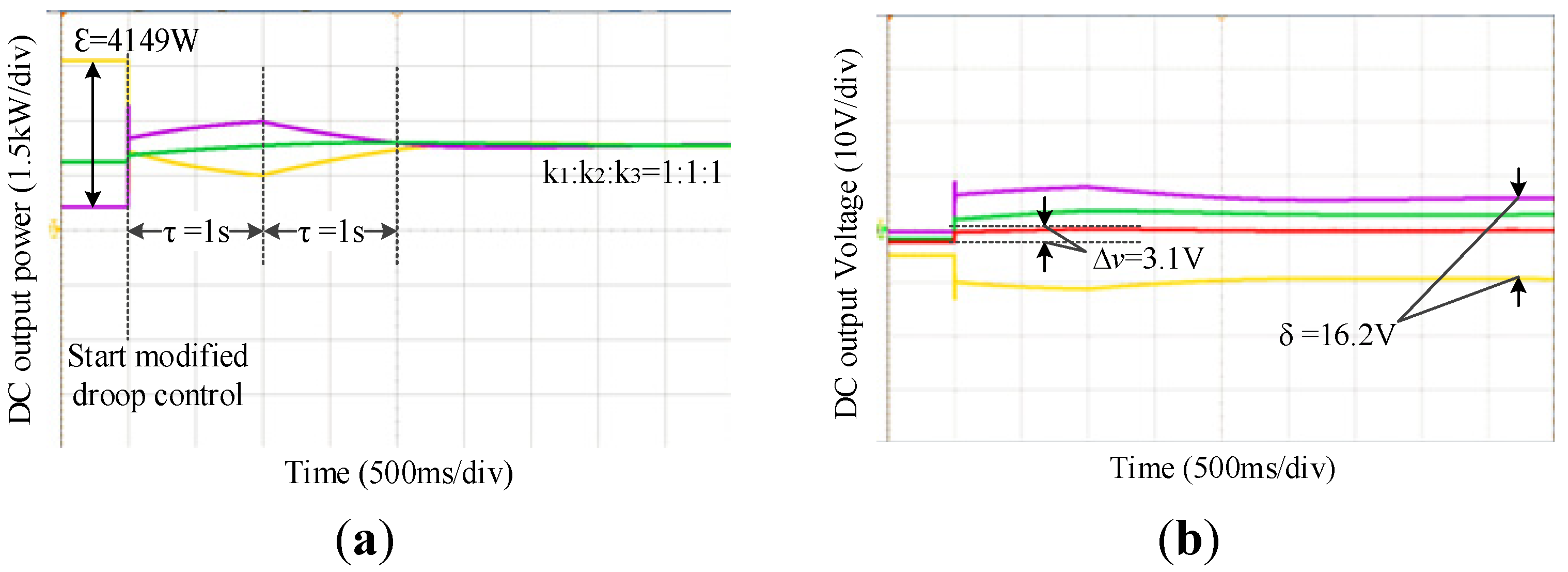
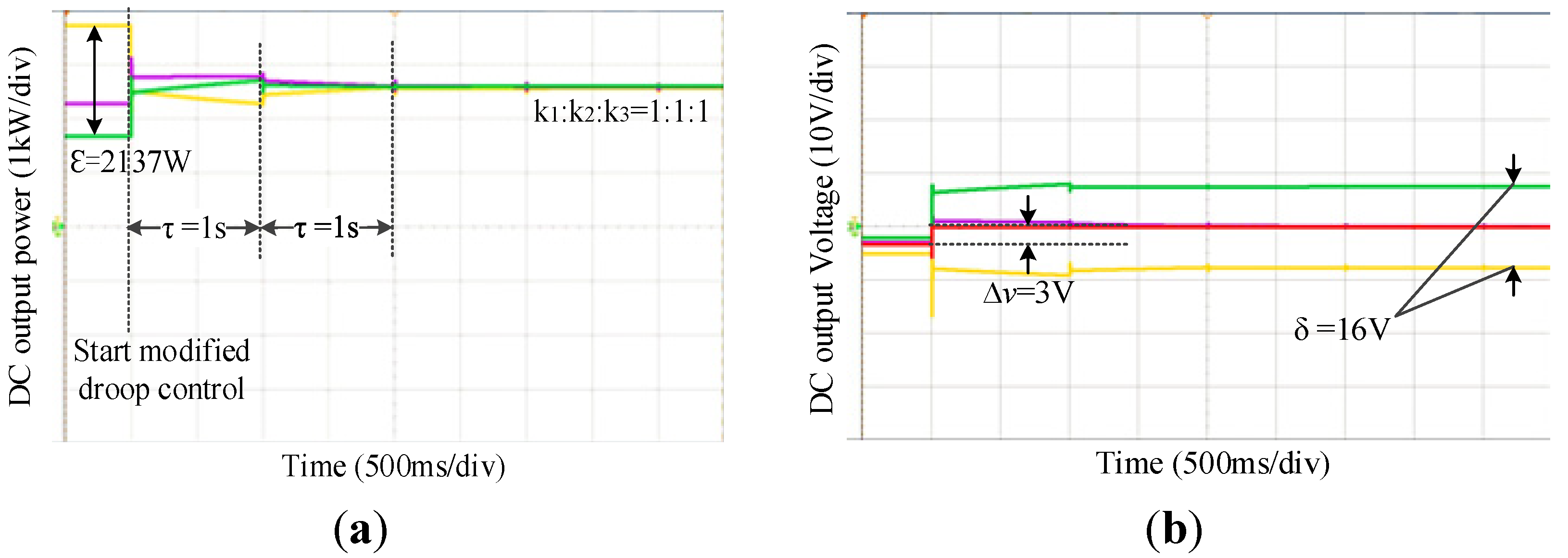
5.3. Experimental Verification
6. Conclusions
- (1)
- It was demonstrated that the feasibility and stability of the control system can be guaranteed with both mesh and radial configurations.
- (2)
- Local DC output voltage deviation can be eliminated and the load power sharing accuracy can be enhanced with the modified droop control method.
- (3)
- The proposed control method only relies on the data of voltage and current sampled from two adjacent converters, which reduces the stress on the communication system.
- (4)
- The control system is also stable considering the longer communication delay time and larger mismatch of line resistance.
Author Contributions
Conflicts of Interest
References
- Dasgupta, S.; Mohan, S.N.; Sahoo, S.K.; Panda, S.K. Application of four-switch-based three-phase grid-connected inverter to connect renewable energy source to a generalized unbalanced microgrid system. IEEE Trans. Ind. Electron. 2013, 60, 1204–1215. [Google Scholar] [CrossRef]
- Hakimi, S.M.; Moghaddas-Tafreshi, S.M. Optimal planning of a smart microgrid including demand response and intermittent renewable energy resources. IEEE Trans. Smart Grid 2014, 5, 2889–2900. [Google Scholar] [CrossRef]
- Eghtedarpour, N.; Farjah, E. Distributed charge/discharge control of energy storages in a renewable-energy-based DC micro-grid. IET Renew. Power Gener. 2014, 8, 45–57. [Google Scholar] [CrossRef]
- Vandoorn, T.L.; de Kooning, J.D.M.; Meersman, B.; Guerrero, J.M.; Vandevelde, L. Automatic power-sharing modification of P/V droop controllers in low-voltage resistive microgrids. IEEE Trans. Power Deliv. 2012, 27, 2318–2325. [Google Scholar] [CrossRef]
- Augustine, S.; Mishra, M.; Lakshminarasamma, N. Adaptive droop control strategy for load sharing and circulating current minimization in low-voltage standalone DC microgrid. IEEE Trans. Sustain. Energy 2015, 6, 132–141. [Google Scholar] [CrossRef]
- Guerrero, J.M.; Vasquez, J.C.; Matas, J.; de Vicuña, L.G.; Castilla, M. Hierarchical control of droop-controlled AC and DC microgrids—A general approach toward standardization. IEEE Trans. Ind. Electron. 2011, 58, 158–172. [Google Scholar] [CrossRef]
- Rouzbehi, K.; Miranian, A.; Candela, J.I.; Luna, A.; Rodriguez, P. A generalized voltage droop strategy for control of multiterminal DC grids. IEEE Trans. Ind. Appl. 2015, 51, 607–618. [Google Scholar] [CrossRef]
- Bevrani, H.; Shokoohi, S. An intelligent droop control for simultaneous voltage and frequency regulation in islanded microgrids. IEEE Trans. Smart Grid 2013, 4, 1505–1513. [Google Scholar] [CrossRef]
- Dou, X.; Quan, X.; Wu, Z. Improved control strategy for microgrid ultracapacitor energy storage systems. Energies 2014, 7, 8095–8115. [Google Scholar] [CrossRef]
- Lu, X.; Guerrero, J.M.; Sun, K.; Vasquez, J.C. An improved droop control method for DC microgrids based on low bandwidth communication with DC bus voltage restoration and enhanced current sharing accuracy. IEEE Trans. Power Electron. 2014, 29, 1800–1812. [Google Scholar] [CrossRef]
- Maknouninejad, A.; Qu, Z.; Lewis, F.L.; Davoudi, A. Optimal, nonlinear, and distributed designs of droop controls for dc microgrids. IEEE Trans. Smart Grid 2014, 5, 2508–2516. [Google Scholar] [CrossRef]
- Wang, B.; Sechilariu, M.; Locment, F. Intelligent DC microgrid with smart grid communications: Control strategy consideration and design. IEEE Trans. Smart Grid 2012, 3, 2148–2156. [Google Scholar] [CrossRef]
- Liang, C.; Shahidehpour, M. DC Microgrids: Economic operation and enhancement of resilience by hierarchical control. IEEE Trans. Smart Grid 2014, 5, 2517–2526. [Google Scholar] [CrossRef]
- Kanchev, H.; Colas, F.; Lazarov, V.; Francois, B. Emission reduction and economical optimization of an urban microgrid operation including dispatched pv-based active generators. IEEE Trans. Sustain. Energy 2014, 5, 1397–1405. [Google Scholar] [CrossRef]
- Nutkani, I.U.; Wang, P.; Poh, C.L.; Blaabjerg, F. Autonomous economic operation of grid connected DC microgrid. In Proceedings of the 2014 IEEE 5th International Symposium on Power Electronics for Distributed Generation Systems (PEDG), Galway, Ireland, 24–27 June 2014; pp. 1–5.
- Kwasinski, A. Quantitative evaluation of DC microgrids availability: Effects of system architecture and converter topology design choices. IEEE Trans. Power Electron. 2011, 26, 835–851. [Google Scholar] [CrossRef]
- Yukita, K.; Shimizu, Y.; Goto, Y.; Yoda, M.; Ueda, A.; Ichiyanagi, K.; Hirose, K.; Takeda, T.; Ota, T.; Okui, Y.; et al. Study of AC/DC power supply system with DGs using parallel processing method. In Proceedings of the International Power Electronics Conference (IPEC)-ECCE, Sapporo, Japan, 21–24 June 2010; pp. 722–725.
- Kakigano, H.; Miura, Y.; Ise, T. Low-voltage bipolar-type DC microgrid for super high quality distribution. IEEE Trans. Power Electron 2010, 25, 3066–3075. [Google Scholar] [CrossRef]
- Shadmand, M.B.; Balog, R.S. Multi-objective optimization and design of photovoltaic-wind hybrid system for community smart DC microgrid. IEEE Trans. Smart Grid 2014, 5, 2635–2643. [Google Scholar] [CrossRef]
- Mehrizi-Sani, A.; Iravani, R. Potential-function based control of a microgrid in islanded and grid-connected modes. IEEE Trans. Power Syst. 2010, 25, 1883–1891. [Google Scholar] [CrossRef]
- Prasai, A.; Du, Y.; Paquette, A.; Buck, E.; Harley, R.G.; Divan, D. Protection of meshed microgrids with communication overlay. In Proceedings of the 2010 IEEE Energy Conversion Congress and Exposition (ECCE), Atlanta, GA, USA, 12–16 September 2010; pp. 64–71.
- Shukla, S.; Deng, Y.; Shukla, S.; Mili, L. Construction of a microgrid communication network. In Proceedings of the 2014 IEEE PES Innovative Smart Grid Technologies Conference (ISGT), Washington, DC, USA, 19–22 February 2014; pp. 1–5.
- Luo, F.; Lai, Y.M.; Loo, K.H.; Tse, C.K.; Ruan, X. A generalized droop-control scheme for decentralized control of inverter-interfaced microgrids. In Proceedings of the 2013 IEEE International Symposium on Circuits and Systems (ISCAS), Beijing, China, 19–23 May 2013; pp. 1320–1323.
- Wang, W.; Zeng, X.; Tang, X.; Tang, C. Analysis of microgrid inverter droop controller with virtual output impedance under non-linear load condition. IET Power Electron. 2014, 7, 1547–1556. [Google Scholar] [CrossRef]
- Becker, D.J.; Sonnenberg, B.J. DC microgrids in buildings and data centers. In Proceedings of the 2011 IEEE 33rd International Telecommunications Energy Conference (INTELEC), Amsterdam, The Netherlands, 9–13 October 2011; pp. 1–7.
- Emerge Alliance. Available online: http://www.emergealliance.org/Standards/DataTelecom/Overview.aspx (accessed on 20 March 2015).
- Wu, T.-F.; Chang, C.-H.; Lin, L.-C.; Yu, G.-R.; Chang, Y.-R. DC-bus voltage control with a three-phase bidirectional inverter for DC distribution systems. IEEE Trans. Power Electron. 2013, 28, 1890–1899. [Google Scholar] [CrossRef]
- Olivares, D.E.; Mehrizi-Sani, A.; Etemadi, A.H.; Canizares, C.A.; Iravani, R.; Kazerani, M.; Hajimiragha, A.H.; Gomis-Bellmunt, O.; Saeedifard, M.; Palma-Behnke, R.; et al. Trends in microgrid control. IEEE Trans. Smart Grid 2014, 5, 1905–1919. [Google Scholar] [CrossRef]
- Choi, J.; Jeong, H.Y.; Choi, J.-Y. Voltage control scheme with distributed generation and grid connected converter in a DC microgrid. Energies 2014, 7, 6477–6491. [Google Scholar] [CrossRef]
- Kim, J.; Guerrero, J.M.; Rodriguez, P.; Teodorescu, R.; Nam, K. Mode adaptive droop control with virtual output impedances for an inverter-based flexible AC microgrid. IEEE Trans. Power Electron. 2011, 26, 689–701. [Google Scholar] [CrossRef]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Y.; Wang, J.; Li, N.; Fu, Y.; Ji, Y. Enhanced Load Power Sharing Accuracy in Droop-Controlled DC Microgrids with Both Mesh and Radial Configurations. Energies 2015, 8, 3591-3605. https://doi.org/10.3390/en8053591
Liu Y, Wang J, Li N, Fu Y, Ji Y. Enhanced Load Power Sharing Accuracy in Droop-Controlled DC Microgrids with Both Mesh and Radial Configurations. Energies. 2015; 8(5):3591-3605. https://doi.org/10.3390/en8053591
Chicago/Turabian StyleLiu, Yiqi, Jianze Wang, Ningning Li, Yu Fu, and Yanchao Ji. 2015. "Enhanced Load Power Sharing Accuracy in Droop-Controlled DC Microgrids with Both Mesh and Radial Configurations" Energies 8, no. 5: 3591-3605. https://doi.org/10.3390/en8053591
APA StyleLiu, Y., Wang, J., Li, N., Fu, Y., & Ji, Y. (2015). Enhanced Load Power Sharing Accuracy in Droop-Controlled DC Microgrids with Both Mesh and Radial Configurations. Energies, 8(5), 3591-3605. https://doi.org/10.3390/en8053591






