Recent Advances in the Characterization of Gaseous and Liquid Fuels by Vibrational Spectroscopy
Abstract
:1. Introduction
| Property | Iso-octane, C8H18 | Ethanol, C2H5OH |
|---|---|---|
| Density (@ 25 °C) in kg/m3 | 688 | 785 |
| Viscosity (@ 25 °C) in mPa s | 0.473 | 1.040 |
| Surface tension (@ 25 °C) in dyn/cm | 18.3 | 22.4 |
| Latent heat of vaporization in kJ/mol | 35.1 | 42.3 |
| Boiling temperature in °C | 99.3 | 78.5 |
| Energy content in MJ/kg | 44.3 | 26.8 |
| Research Octane Number RON | 100 | 108.6 |
2. Vibrational Spectroscopy
2.1. Infrared Spectroscopy
2.1.1. Fundamentals
2.1.2. Experimental Realization
2.1.3. Advantages and Disadvantages
- High sensitivity can be achieved. With conventional IR spectroscopy a limit of detection (LOD) in the order of 0.1% (depending on the species, it can be even better) can be obtained. Special arrangements, e.g., cavity enhancement, can improve the sensitivity further and an LOD at ppm-level is possible.
- When only one or a few species need to be detected (in other words, when the absorption measurement of one or a few selected wavelengths is sufficient), the experiment can be miniaturized and in principle be implemented as a kind of lab-on-chip technology. The absorption measurement at only a few selected wavelengths allows using simpler and cheaper light sources and detectors.
- Fiber-coupled ATR probes facilitate in situ measurements in liquid systems. Such probes can be installed in the same way as thermocouples or pressure transducers. Hence, there is no need for optical access to the sample.
- The technique allows fast measurements at high repetition rate. The measurement time can be as short as a few milliseconds. However, it must be kept in mind that the shorter the measurement/acquisition time, the lower the sensitivity and accuracy as the noise level increases.
- Homonuclear diatomic molecules (such as hydrogen, oxygen, and nitrogen) are not IR-active and hence cannot be detected. This may be a problem when gaseous fuels are analyzed.
- Background black-body radiation may be detected as an interference signal when the fluid or parts of the analytical device exhibit elevated temperature.
- Saturation of the absorbing transition and overlapping peaks may lead to nonlinearities and deviations from the Beer-Lambert law and hence represent a potential problem when the signal needs to be quantified.
- Strongly absorbing species may virtually completely absorb the wavelength of interest and hence the measurement is not sensitive to changes in concentration any longer.
- Fiber-coupled ATR probes are not suitable for gases due to the small penetration depth and with it a short absorption path length. To avoid confusion in this context, it should be mentioned that occasionally vapor peaks, for example from water, can be observed in ATR IR spectra. These peaks are not a result of absorption in the evanescent field at the IRE, but from vapor in the path of the radiation inside the instrument. Such interfering signals can be avoided using appropriate background correction and/or purging the instrument with nitrogen or using a vacuum model of the instrument.
- Water is a strong absorber in the infrared spectral range and may represent an interference making the evaluation of the signal difficult.
2.2. Raman Spectroscopy
2.2.1. Fundamentals
2.2.2. Experimental Realization
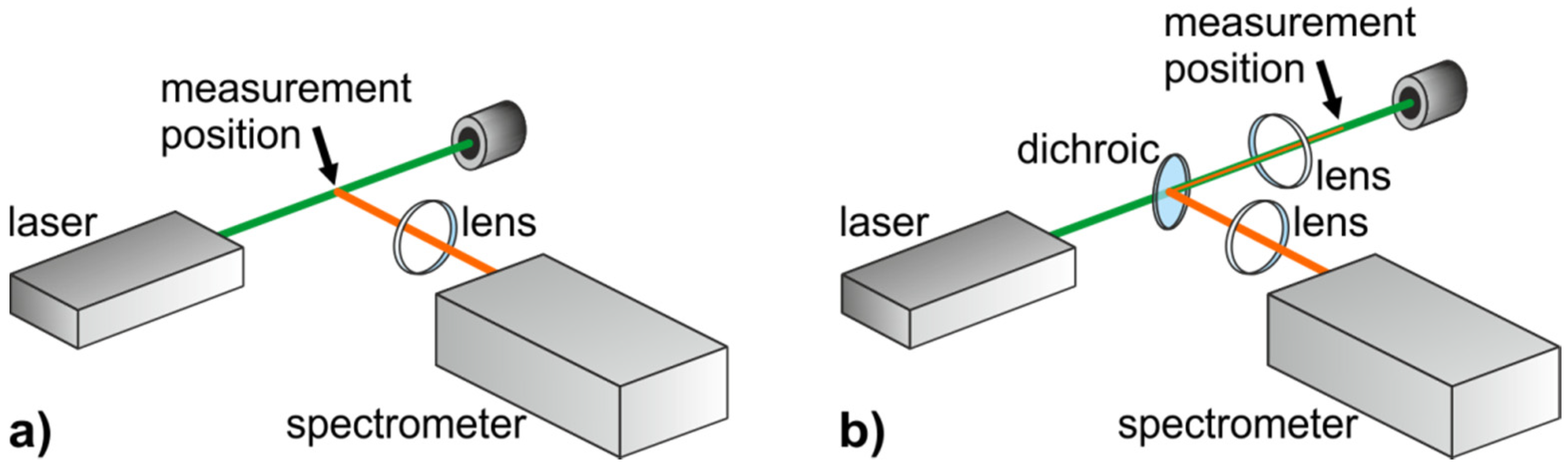
2.2.3. Advantages and Disadvantages
- The wavelength of the light source can, in principle, be chosen arbitrarily. Due to the non-resonant nature of the Raman scattering process, the incident light does not have to match a molecular transition in the species of interest. Consequently, all Raman-active species can be detected with a single laser source at the same time.
- Most molecules, in particular those in typical fuels, are Raman-active and hence can be detected simultaneously. This includes the homo-nuclear diatomics, which cannot be measured using IR spectroscopy.
- Good sensitivity can be obtained. Depending on the scattering cross-section it can be in the order of ~0.1%. Multi-pass arrangements, the use of cavities, resonant or near-resonant excitation, and the utilization of plasmonic enhancement (surface enhanced Raman scattering, SERS) allow a further significant improvement of the sensitivity for selected species. An LOD in the order of ppm and sub-ppm can be achieved.
- Fiber-coupled probes allow in situ measurements without the requirement of large optical accesses to the sample.
- The technique allows fast measurements at high repetition rate. The measurement time can be sub-second. However, it must be kept in mind that the shorter the measurement/acquisition time the lower the sensitivity and accuracy as the noise level increases. Pulsed laser sources are suitable to bring acquisition times down to nanoseconds should extremely high temporal resolution be required.
- Water has a weak Raman scattering cross section. Therefore, even in aqueous systems, Raman scattering does not suffer from water interference like in IR.
- Accurate gas-phase measurements often require high power laser sources in order to generate sufficient signal photons.
- Interference from laser-induced fluorescence may be a problem in some applications. In order to avoid such effects a number of approaches have been developed including near-infrared Raman [26], deep-UV Raman [27], polarization-resolved detection Raman [28], and shifted-excitation Raman difference spectroscopy (SERDS) [29,30,31,32]. An overview can be found in reference [23].
- The 90°-setup normally requires three optical accesses, which cannot always be arranged in a technical object.
- The presence of phase boundaries, e.g., when the sample contains small particles or droplets, can result in interference from elastically scattered light (Rayleigh scattering and Mie-Lorentz scattering). This scattering can be orders of magnitude stronger than the Raman signal. Therefore, suitable spectral filters may be required, for example holographic notch filters or long-pass filters, or a combination of the two.
2.3. Signal Evaluation
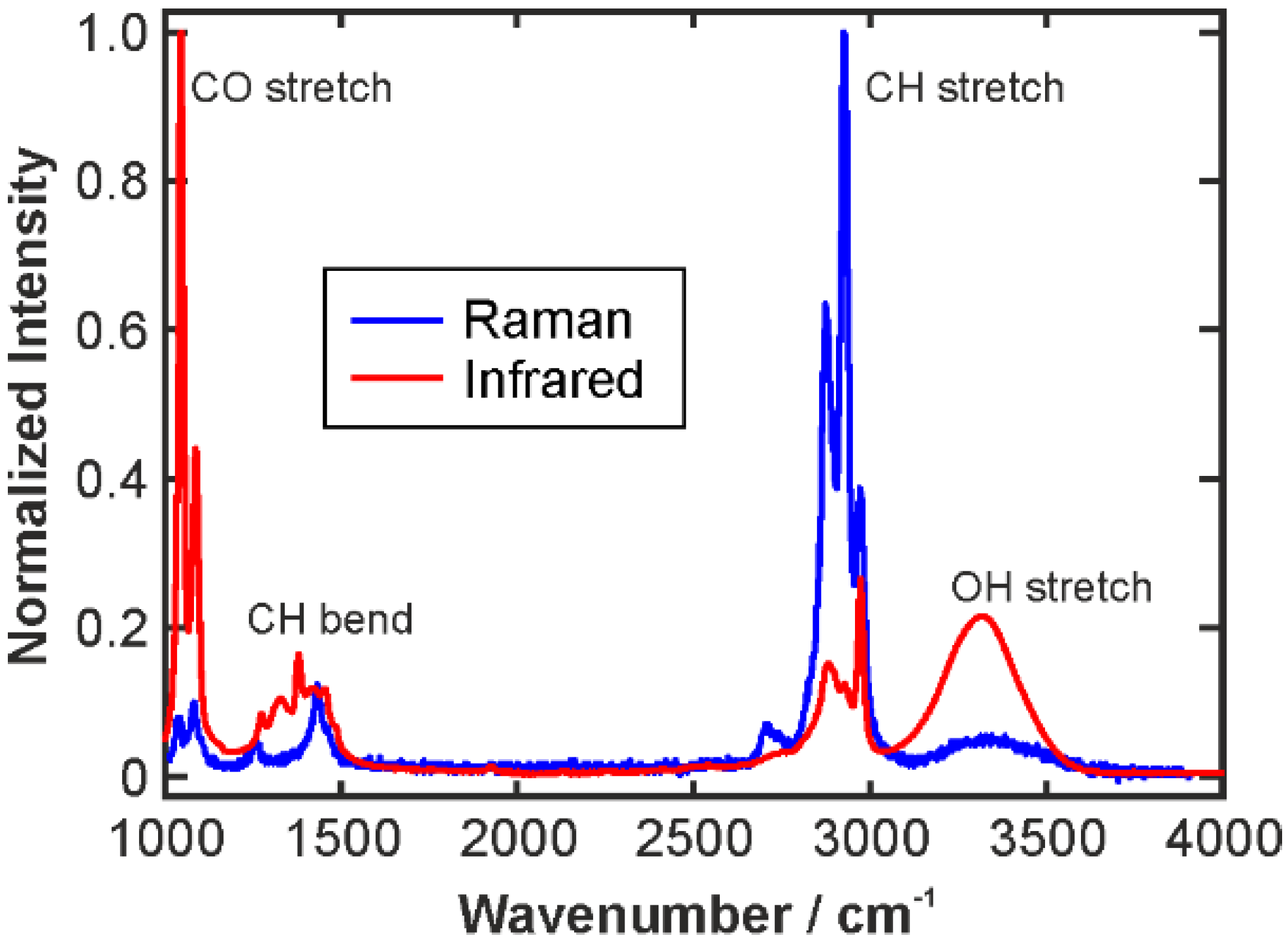
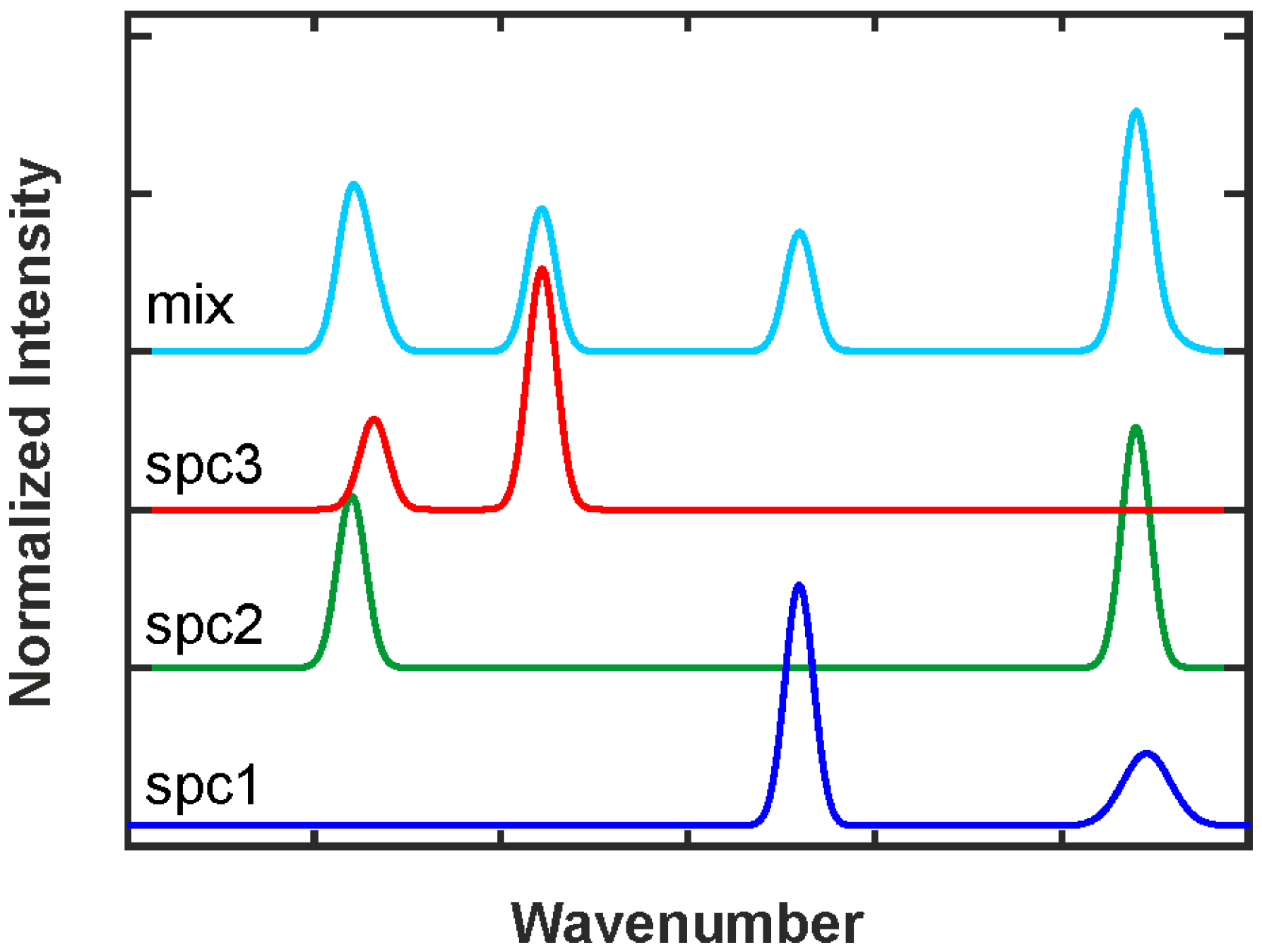
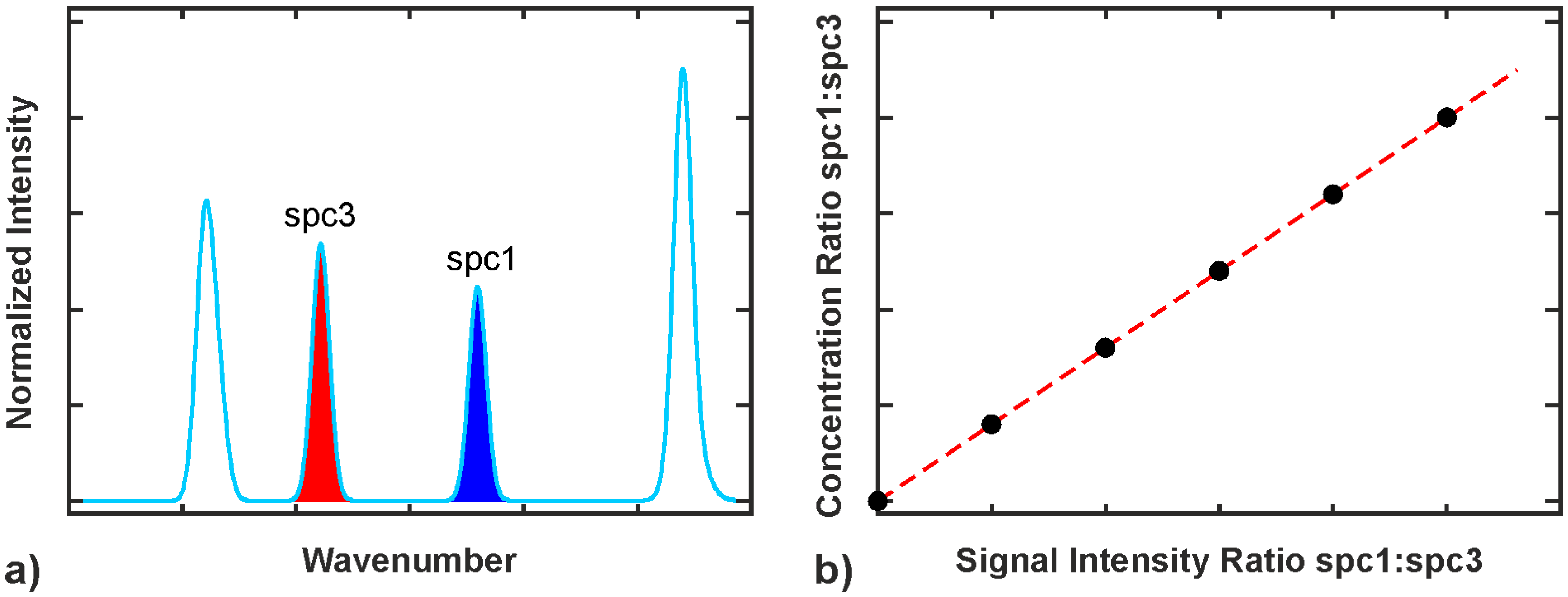
2.3.1. Intensity and Intensity Ratio Calibration
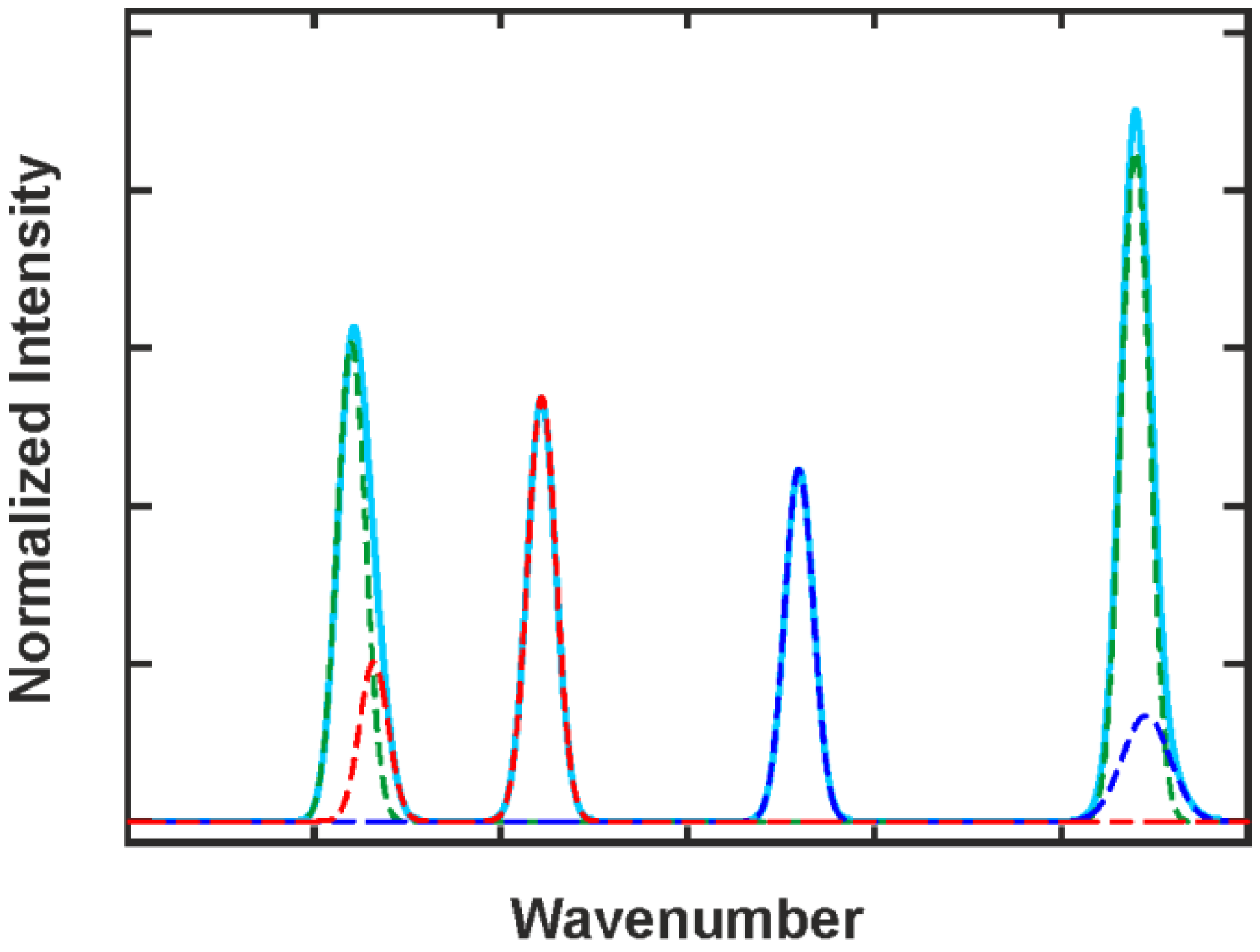
2.3.2. Spectral Soft Modeling
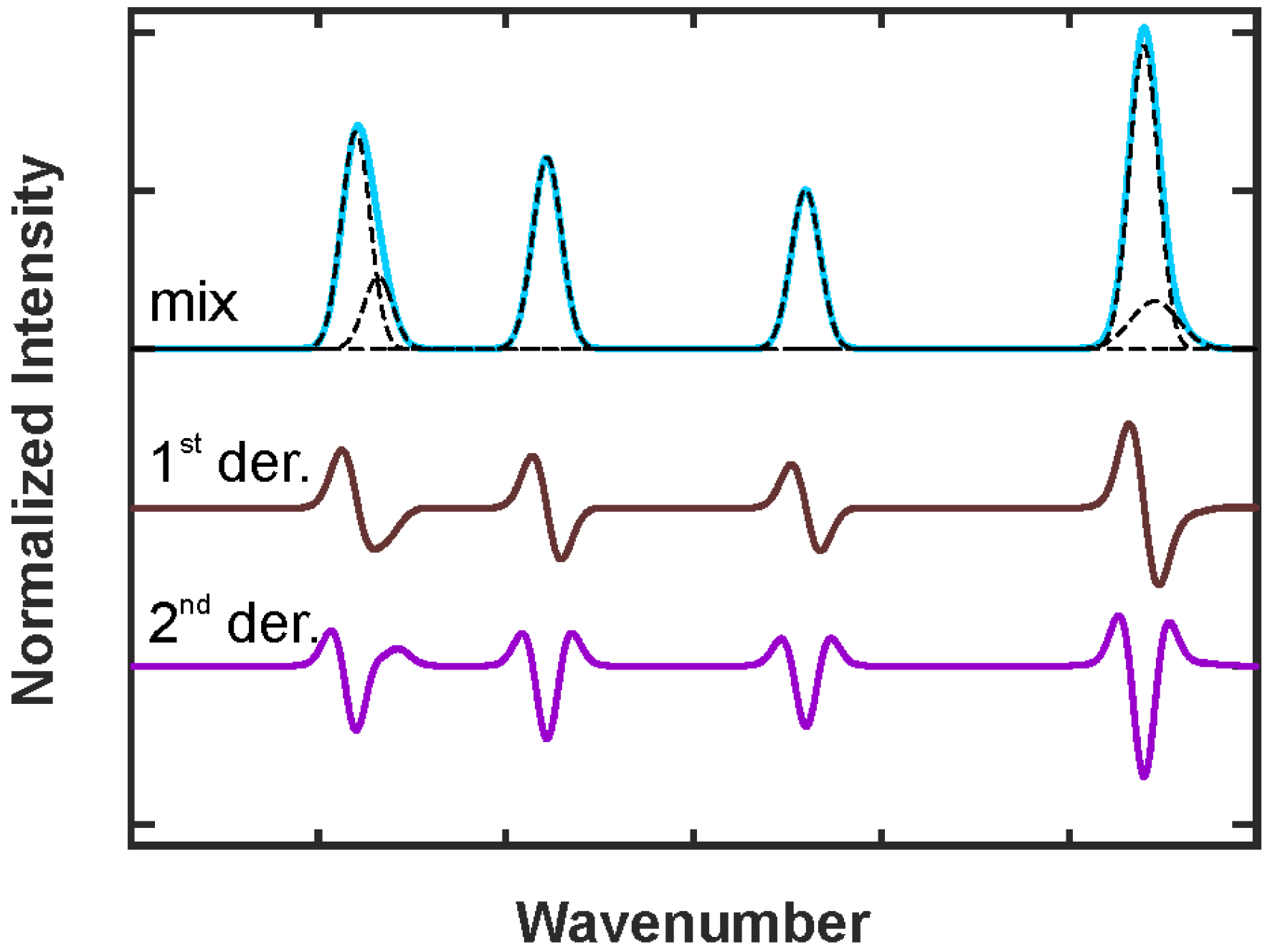
2.3.3. Deconvolution, Peak Fitting and Indirect Spectral Hard Modeling
2.3.4. Chemometrics
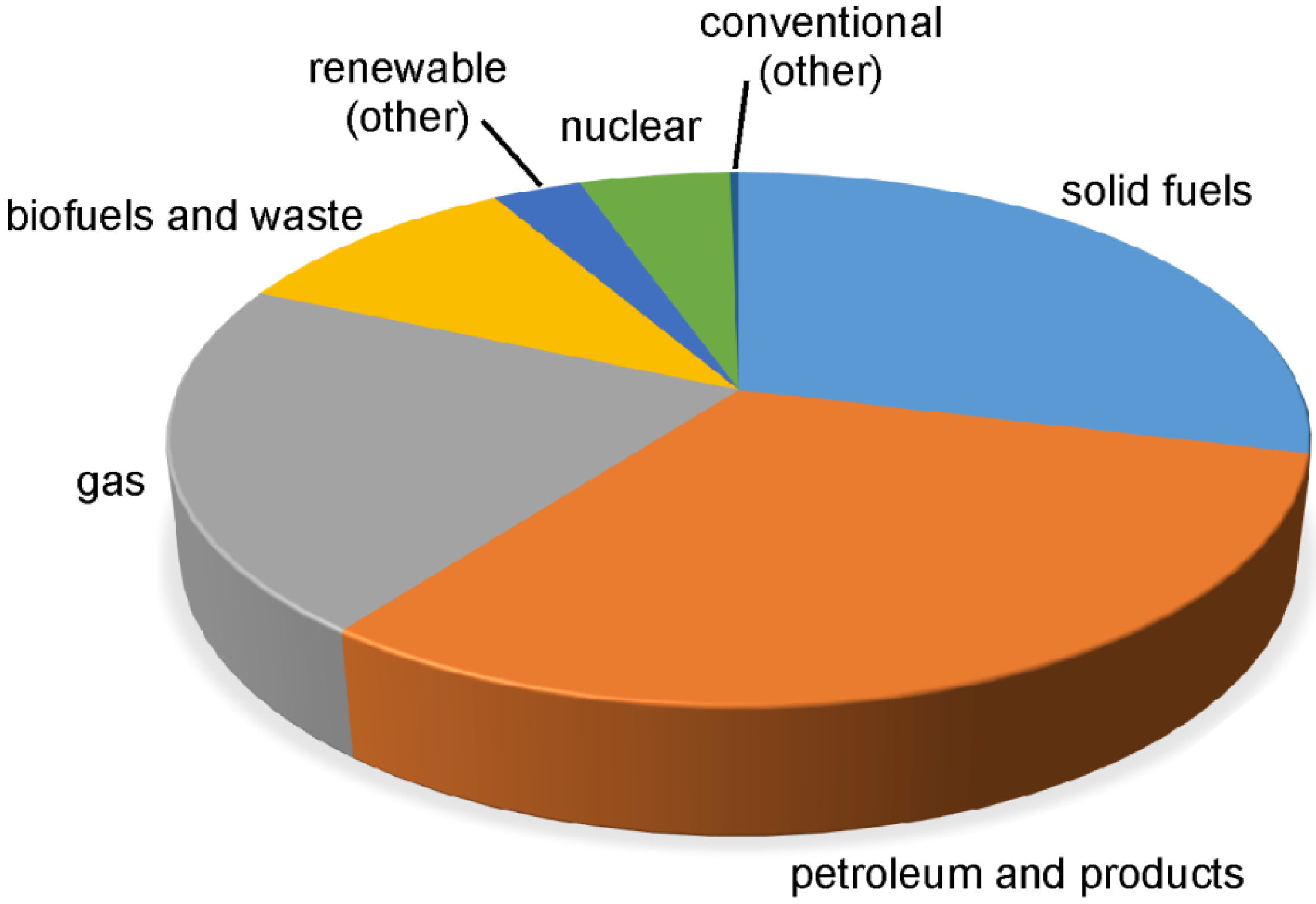
3. Characterization of Gaseous Fuels

3.1. Natural Gas
3.2. Biogas
3.3. Alternative Gaseous Fuels and Special Applications
4. Characterization of Liquid Fuels
4.1. Petrochemical Liquid Fuels
4.2. Blends with Biofuels
4.3. Alternative Liquid fuels and Special Applications
5. Summary and Outlook
- (1)
- Virtually all relevant species are Raman-active and can be detected simultaneously. This includes the homonuclear diatomic species hydrogen, nitrogen, and oxygen, all of which are not IR-active and hence cannot be detected using absorption methods.
- (2)
- Raman spectroscopy is relatively insensitive to water vapor due to the low scattering cross section. In contrast, IR spectra are difficult to interpret as the water signals are very strong and appear in wide ranges of the near- and mid-infrared spectrum.
- (3)
- The advances in the development of suitable light sources and detectors allow relatively small and fully automatic Raman gas analyzers to be built.
Acknowledgments
Conflicts of Interest
References
- World Energy Outlook 2014; International Energy Agency: Paris, France, 2014.
- EU Energy in Figures Pocketbook; Publications Office of the European Union: Luxembourg, 2014.
- Davis, S.C.; Diegel, S.W.; Boundy, R.G. Transportation Energy Data Book, 33rd ed.; Oak Ridge National Laboratory: Oak Ridge, TN, USA, 2014. [Google Scholar]
- Lehmann, S.; Lorenz, S.; Rivard, E.; Brüggemann, D. Experimental analysis and semicontinuous simulation of low-temperature droplet evaporation of multicomponent fuels. Exp. Fluids 2015, 56, 1–12. [Google Scholar]
- Lichty, L.C.; Phelps, C.W. Gasoline-alcohol blends in internal combustion engines. Ind. Eng. Chem. 1938, 30, 222–230. [Google Scholar]
- Turner, D.; Xu, H.; Cracknell, R.F.; Natarajan, V.; Chen, X. Combustion performance of bio-ethanol at various blend ratios in a gasoline direct injection engine. Fuel 2011, 90, 1999–2006. [Google Scholar]
- Sielghem, L.; Alekseev, V.A.; Vancoillie, J.; Nilsson, E.J.K.; Verhelst, S.; Konnov, A.A. Laminar burning velocities of primary reference fuels and simple alcohols. Fuel 2014, 115, 32–40. [Google Scholar]
- Kiefer, J.; Noack, K.; Kirchner, B. Hydrogen bonding in mixtures of dimethyl sulfoxide and cosolvents. Curr. Phys. Chem. 2011, 1, 340–351. [Google Scholar]
- Noack, K.; Kiefer, J.; Leipertz, A. Concentration dependent hydrogen bonding effects on the dimethyl sulfoxide vibrational structure in the presence of water, methanol and ethanol. ChemPhysChem 2010, 11, 630–637. [Google Scholar]
- Ulbig, P.; Hoburg, D. Determination of the calorific value of natural gas by different methods. Thermochim. Acta 2002, 382, 27–35. [Google Scholar]
- Philp, R.P. High-temperature gas-chromatography for the analysis of fossil fuels: A review. J. High Resolut. Chromatogr. 1994, 17, 398–406. [Google Scholar]
- Cross, R.A. Analysis of major constituents of fuel gases by gas chromatography. Nature 1966, 211, 409. [Google Scholar]
- Segudovic, N.; Tomic, T.; Skrobonja, L.; Kontic, L. Local round robin test for determination of aromatics in diesel fuels by HPLC. J. Sep. Sci. 2004, 27, 65–70. [Google Scholar]
- Haken, H.; Wolf, H.C. Molecular Physics and Elements of Quantum Chemistry; Springer: Heidelberg, Germany, 1995. [Google Scholar]
- Banwell, C.N.; McCash, E.M. Fundamentals of Molecular Spectroscopy, 4th ed.; McGraw Hill: London, UK, 1994. [Google Scholar]
- Schrader, B. Infrared and Raman Spectroscopy; VCH Verlagsgesellschaft: Weinheim, Germany, 1995. [Google Scholar]
- Griffiths, P.R.; De Haseth, J.A. Fourier Transform Infrared Spectrometry, 2nd ed.; Wiley: Weinheim, Germany, 2007. [Google Scholar]
- Rahinov, I.; Goldman, A.; Cheskis, S. Intracavity laser absorption spectroscopy and cavity ring-down spectroscopy in low-pressure flames. Appl. Phys. B 2005, 81, 143–149. [Google Scholar]
- Thorpe, M.J.; Moll, K.D.; Jones, R.J.; Safdi, B.; Ye, J. Broadband cavity ringdown spectroscopy for sensitive and rapid molecular detection. Science 2006, 311, 1595–1599. [Google Scholar]
- Kiefer, J.; Rasul, N.H.; Ghosh, P.K.; Von Lieres, E. Surface and bulk porosity mapping of polymer membranes using infrared spectroscopy. J. Membr. Sci. 2014, 452, 152–156. [Google Scholar]
- Averett, L.A.; Griffiths, P.R. Effective path length in attenuated total reflection spectroscopy. Anal. Chem. 2008, 80, 3045–3049. [Google Scholar]
- Harrick, N.J.; du Pre, F.K. Effective thickness of bulk materials and of thin films for internal reflection spectroscopy. Appl. Opt. 1966, 5, 1739–1743. [Google Scholar]
- Wei, D.; Chen, S.; Liu, Q. Review of fluorescence suppression techniques in Raman spectroscopy. Appl. Spectr. Rev. 2015. [Google Scholar] [CrossRef]
- Greer, J.S.; Petrov, G.I.; Yakovlev, V.V. Raman spectrocopy with LED excitation source. J. Raman Spectrosc. 2013, 44, 1058–1059. [Google Scholar]
- Schmidt, M.A.; Kiefer, J. Polarization-resolved high-resolution Raman spectroscopy with a light-emitting diode. J. Raman Spectrosc. 2013, 44, 1625–1627. [Google Scholar]
- Meyer, M.W.; Lupoi, J.S.; Smith, E.A. 1064 nm dispersive multichannel Raman spectroscopy for the analysis of plant lignin. Anal. Chim. Acta 2011, 706, 164–170. [Google Scholar]
- Liu, C.; Berg, R.W. Nonlinearity in intensity versus concentration dependence for the deep UV resonance Raman spectra of toluene and heptane. Appl. Spectr. Rev. 2013, 48, 425–437. [Google Scholar]
- Egermann, J.; Seeger, T.; Leipertz, A. Application of 266-nm and 355-nm Nd: YAG laser radiation for the investigation of fuel-rich sooting hydrocarbon flames by Raman scattering. Appl. Opt. 2004, 43, 5564–5574. [Google Scholar] [CrossRef] [PubMed]
- Shreve, A.P.; Cherepy, N.J.; Mathies, R.A. Effective rejection of fluorescence interference in Raman spectroscopy using a shifted excitation difference technique. Appl. Spectrosc. 1992, 46, 707–711. [Google Scholar] [CrossRef]
- Zhao, J.; Carrabba, M.M.; Allen, F.S. Automated flurescence rejection using shifted-excitation Raman difference spectroscopy. Appl. Spectrosc. 2002, 56, 834–845. [Google Scholar] [CrossRef]
- Maiwald, M.; Erbert, G.; Klehr, A.; Kronfeldt, H.D.; Schmidt, H.; Sumpf, B.; Trankle, G. Rapid shifted excitation Raman difference spectroscopy with a distributed feedback laser emitting at 785 nm. Appl. Phys. B 2006, 85, 509–512. [Google Scholar] [CrossRef]
- Noack, K.; Eskofier, B.; Kiefer, J.; Dilk, C.; Bilow, G.; Schirmer, M.; Buchholz, R.; Leipertz, A. Combined shifted-excitation Raman difference spectroscopy and support vector regression for monitoring the algal production of complex polysaccharides. Analyst 2013, 138, 5639–5646. [Google Scholar] [CrossRef] [PubMed]
- Joseph, J.; Jemmis, E.D. Red-, blue-, or no-shift in hydrogen bonds: A unified explanation. J. Am. Chem. Soc. 2007, 129, 4620–4632. [Google Scholar] [CrossRef] [PubMed]
- Kiefer, J.; Molina Martinez, M.; Noack, K. The peculiar nature of molecular interactions between an imidazolium ionic liquid and acetone. ChemPhysChem 2012, 13, 1213–1220. [Google Scholar] [CrossRef] [PubMed]
- Kiefer, J.; Kozlov, D.N.; Seeger, T.; Leipertz, A. Local fuel concentration measurements for mixture formation diagnostics using diffraction by laser-induced gratings in comparison to spontaneous Raman scattering. J. Raman Spectrosc. 2008, 39, 711–721. [Google Scholar] [CrossRef]
- Zehentbauer, F.M.; Kiefer, J. Detection of unexpected species in soft modelling of vibrational spectra. Chimica Oggi-Chemistry Today 2012, 30, 54–56. [Google Scholar]
- Kiefer, J.; Seeger, T.; Steuer, S.; Schorsch, S.; Weikl, M.C.; Leipertz, A. Design and characterization of a Raman-scattering-based sensor system for temporally resolved gas analysis and its application in a gas turbine power plant. Meas. Sci. Technol. 2008, 19. [Google Scholar] [CrossRef]
- Struthers, H.C.; Zehentbauer, F.M.; Ono-Sorhue, E.; Kiefer, J. Chemical composition monitoring in a batch distillation process using Raman spectroscopy. Ind. Eng. Chem. Res. 2011, 50, 12824–12830. [Google Scholar] [CrossRef]
- Alsmeyer, F.; Koß, H.-J.; Marquardt, W. Indirect spectral hard modeling for the analysis of reactive and interacting mixtures. Appl. Spectrosc. 2004, 58, 975–985. [Google Scholar]
- Viell, J.; Marquardt, W. Concentration measurements in ionic liquid-water mixtures by mid-infrared spectroscopy and indirect hard modeling. Appl. Spectrosc. 2012, 66, 208–217. [Google Scholar] [CrossRef] [PubMed]
- Wold, S.; Esbensen, K.; Geladi, P. Principal Component Analysis. Chemom. Intell. Lab. Syst. 1987, 2, 37–52. [Google Scholar] [CrossRef]
- Bakeev, K.A. Process Analytical Technology, 2nd ed.; Wiley-Blackwell: Hoboken, NJ, USA, 2010. [Google Scholar]
- Mark, H.; Workman, J., Jr. Chemometrics in Spectroscopy; Academic Press: New York, NY, USA, 2007. [Google Scholar]
- ISO 6976: Natural Gas—Calculation of Calorific Values, Density, Relative Density and Wobbe Index from Composition; International Organization for Standardization: Geneva, Switzerland, 1996.
- Denys, F.; de Vries, W. Gas Composition Transition Agency Report 2013; Gas Composition Transition Agency: Assen, The Netherlands, 2013. [Google Scholar]
- Haus, R.; Wilkinson, R.; Heland, J.; Schäfer, K. Remote sensing of gas emissions on natural gas flares. Pure Appl. Opt. 1998, 7, 853–862. [Google Scholar] [CrossRef]
- Makhoukhi, N.; Pere, E.; Creff, R.; Pouchan, C. Determination of the composition of a mixture of gases by infrared analysis and chemometric methods. J. Mol. Struct. 2005, 744–747, 855–859. [Google Scholar] [CrossRef]
- Dantas, H.V.; Barbosa, M.F.; Nascimento, E.C.L.; Moreira, P.N.T.; Calvao, R.K.H.; Aroujo, M.C.U. Screening analysis of natural gas with respect to methane content by near-infrared spectrometry. Microchem. J. 2014, 114, 210–215. [Google Scholar] [CrossRef]
- Mullins, O.C.; Daigle, T.; Crowell, C.; Groenzin, H.; Joshi, N.B. Gas-oil ratio of live crude oils determined by near-infrared spectroscopy. Appl. Spectrosc. 2001, 55, 197–201. [Google Scholar] [CrossRef]
- Fujisawa, G.; van Agthoven, M.A.; Jenet, F.; Rabbito, P.A.; Mullins, O.C. Near-infrared compositional analysis of gas and condensate reservoir fluids at elevated pressures and temperatures. Appl. Spectrosc. 2002, 56, 1615–1620. [Google Scholar] [CrossRef]
- Diller, D.E.; Chang, R.F. Composition of mixtures of natural gas components determined by Raman spectroscopy. Appl. Spectrosc. 1980, 34, 411–414. [Google Scholar] [CrossRef]
- Brunsgaard Hansen, S.; Berg, R.W.; Stenby, E.H. High-pressure measuring cell for Raman spectroscopic studies of natural gas. Appl. Spectrosc. 2001, 55, 55–60. [Google Scholar]
- Buric, M.P.; Chen, K.P.; Falk, J.; Woodruff, S.D. Enhanced spontaneous Raman scattering and gas composition analysis using a photonic crystal fiber. Appl. Opt. 2008, 47, 4255–4261. [Google Scholar] [CrossRef] [PubMed]
- Salter, R.; Chu, J.; Hippler, M. Cavity-enhanced Raman spectroscopy with optical feedback cw diode lasers for gas phase analysis and spectroscopy. Analyst 2012, 137, 4669–4676. [Google Scholar] [CrossRef] [PubMed]
- Kaiser Optical Systems Inc. Available online: http://www.kosi.com (accessed on 8 February 2015).
- Egermann, J.; Jonuscheit, J.; Seeger, T.; Leipertz, A. Untersuchung von diodenlaserbasierten Mehrkomponenten-Konzentrationsmesssystemen zur Gasanalyse. Tech. Messen 2001, 68, 400–405. (In German) [Google Scholar]
- Seeger, T.; Kiefer, J.; Leipertz, A. A. Sensor system for accurate, quantitative analysis of natural gas in gas turbine. In Proceedings of the International Gas Union Research Conference (IGRC), Paris, France, 8–10 October 2008; pp. 1–11.
- Seeger, T.; Kiefer, J.; Leipertz, A. Entwicklung eines laserbasierten Sensorsystems zur schnellen Gasanalyse. GWF Gas/Erdgas 2007, 148, 548–552. (In German) [Google Scholar]
- Schorsch, S.; Kiefer, J.; Steuer, S.; Seeger, T.; Leipertz, A.; Gonschorek, S.; Abröll, B.; Käß, M. Entwicklung eines Echtzeitanalyse-Systems zur Charakterisierung von Brenngasgemischen in Gasturbinenkraftwerken. Chem. Ing. Tech. 2011, 83, 247–253. (In German) [Google Scholar] [CrossRef]
- Buldakov, M.A.; Korolev, B.V.; Matrosov, I.I.; Petrov, D.V.; Tikhomirov, A.A. Raman gas analyzer for determining the composition of natural gas. J. Appl. Spectroscopy 2013, 80, 124–128. [Google Scholar] [CrossRef]
- Buldakov, M.A.; Korolkov, V.A.; Matrosov, I.I.; Petrov, D.V.; Tikhomirov, A.A.; Korolev, B.V. Analyzing natural gas by spontaneous Raman scattering spectroscopy. J. Opt. Technol. 2013, 80, 426–430. [Google Scholar] [CrossRef]
- Seitz, J.C.; Pasteris, J.D.; Chou, I.M. Raman spectroscopic characterization of gas mixtures. 2. Quantitative composition and pressure detrmination of the CO2-CH4 system. Am. J. Sci. 1996, 296, 577–600. [Google Scholar] [CrossRef]
- Buric, M.P.; Chen, K.P.; Falk, J.; Woodruff, S.D. Improved sensitivity gas detection by spontaneous Raman scattering. Appl. Opt. 2009, 48, 4424–4429. [Google Scholar] [CrossRef] [PubMed]
- Pearman, W.F.; Carter, J.C.; Angel, M.; Chan, J.W.J. Quantitative measurements of CO2 and CH4 using a multipass Raman capillary cell. Appl. Opt. 2008, 47, 4627–4632. [Google Scholar] [CrossRef] [PubMed]
- Numata, Y.; Shinohara, Y.; Kitayama, T.; Tanaka, H. Rapid and accurate quantitative analysis of fermentation gases by Raman spectroscopy. Process Biochem. 2013, 48, 569–574. [Google Scholar] [CrossRef]
- Schlüter, S.; Seeger, T.; Popovska-Leipertz, N.; Leipertz, A. Laserbasierte On-line-Analyse von Biogasen mit einer Raman-Sonde. Tech. Messen 2014, 81, 546–553. [Google Scholar]
- Eichmann, S.C.; Kiefer, J.; Benz, J.; Kempf, T.; Leipertz, A.; Seeger, T. Determination of gas composition in a biogas plant using a Raman-based sensor system. Meas. Sci. Technol. 2014, 25. [Google Scholar] [CrossRef]
- Eichmann, S.C.; Weschta, M.; Kiefer, J.; Seeger, T.; Leipertz, A. Characterization of a fast gas analyzer based on Raman scattering for the analysis of synthesis gas. Rev. Sci. Instrum. 2010, 81. [Google Scholar] [CrossRef]
- Ernst, A.; Zibrak, J.D. Carbon monoxide poisoning. N. Engl. J. Med. 1998, 339, 1603–1608. [Google Scholar] [CrossRef] [PubMed]
- Rae, S.I.; Khan, I. Surface anhanced Raman spectroscopy (SERS) sensors for gas analysis. Analyst 2010, 135, 1365–1369. [Google Scholar] [CrossRef] [PubMed]
- Li, X.; Xia, Y.; Zhan, L.; Huang, J. Near-confocal cavity-enhanced Raman spectroscopy for multitrace-gas detection. Opt. Lett. 2008, 33, 2143–2145. [Google Scholar] [CrossRef] [PubMed]
- Li, X.; Xia, Y.; Huang, J.; Zhan, L. Diagnosis of multiple gases separated from transformer oil using cavity-enhanced Raman spectroscopy. Chin. Phys. Lett. 2008, 25, 3326–3329. [Google Scholar] [CrossRef]
- Li, X.Y.; Xia, Y.X.; Huang, J.M.; Zhan, L. A Raman system for multi-gas-species analysis in power transformer. Appl. Phys. B 2008, 93, 665–669. [Google Scholar] [CrossRef]
- Buffett, B.; Archer, D. Global inventory of methane clathrate: Sensitivity to changes in the deep ocean. Earth Planet. Sci. Lett. 2004, 227, 185–199. [Google Scholar] [CrossRef]
- Uchida, T.; Hirano, T.; Ebinuma, T.; Narita, H.; Gohara, K.; Mae, S.; Matsumoto, R. Raman spectroscopic determination of hydration number of methane hydrates. Environ. Energy Eng. 1999, 45, 2641–2645. [Google Scholar]
- Hester, K.C.; Dunk, R.M.; White, S.N.; Brewer, P.G.; Peltzer, E.T.; Sloan, E.D. Gas hydrate measurements at Hydrate Ridge using Raman spectroscopy. Geochim. Cosmochim. Acta 2007, 71, 2947–2959. [Google Scholar] [CrossRef]
- Hester, K.C.; White, S.N.; Peltzer, E.T.; Brewer, P.G.; Sloan, E.D. Raman spectroscopic measurements of synthetic gas hydrates in the ocean. Marine Chem. 2006, 98, 304–314. [Google Scholar] [CrossRef]
- Hester, K.C.; Dunk, R.M.; Walz, P.M.; Peltzer, E.T.; Sloan, E.D.; Brewer, P.G. Direct measurements of multi-component hydrates on the seafloor: Pathways to growth. Fluid Phase Equilibria 2007, 261, 396–406. [Google Scholar] [CrossRef]
- Uchida, T.; Takeya, S.; Kamata, Y.; Ohmura, R.; Narita, H. Spectroscopic measurements of binary, ternary, and quaternery mixed-gas molecules in clathrate structures. Ind. Eng. Chem. Res. 2007, 46, 5080–5087. [Google Scholar] [CrossRef]
- Dabelstein, W.; Reglitzky, A.; Schütze, A.; Reders, K. Automotive fuels. In Ullmann’s Encyclopedia of Industrial Chemistry; Wiley-VCH: Weinheim, Germany, 2007. [Google Scholar]
- Venkataramanan, L.; Fujisawa, G.; Mullins, O.C.; Vasques, R.R.; Valero, H.P. Uncertainty analysis of visible and near-infrared data of hydrocarbons. Appl. Spectrosc. 2006, 60, 653–662. [Google Scholar] [CrossRef] [PubMed]
- Diniz, P.S.R.; da Silva, E.A.B.; Netto, S.L. Digital Signal Processing: System Analysis and Design, 2nd ed.; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar]
- Jingyan, L.; Xiaoli, C.; Songbai, T.; Wanhen, L. The identification of highly similar crude oils by infrared spectroscopy combined with pattern recognition method. Spectrochim. Acta A 2013, 112, 457–462. [Google Scholar] [CrossRef]
- Wilt, B.K.; Welch, W.T.; Rankin, J.G. Determination of asphaltenes in petroleum crude oils by Fourier transform infrared spectroscopy. Energy Fuels 1998, 12, 1008–1012. [Google Scholar] [CrossRef]
- Aske, N.; Kallevik, H.; Sjöblom, J. Determination of saturate, aromatic, resin, and asphaltenic components in crude oils by means of infrared and near-infrared spectroscopy. Energy Fuels 2001, 15, 1304–1312. [Google Scholar] [CrossRef]
- Gawel, B.; Eftekhardadkhah, M.; Oye, G. Elemental composition and Fourier transform infrared spectroscopy analysis of crude oils and their fractions. Energy Fuels 2014, 28, 997–1003. [Google Scholar] [CrossRef]
- Rest, A.J.; Warren, R.; Murray, S.C. Near-infrared study of the light liquid alkanes. Appl. Spectrosc. 1996, 50, 517–520. [Google Scholar] [CrossRef]
- Pasadakis, N.; Kardamakis, A.A. Idenfying constituents in commercial gasoline using Fourier transform-infrared spectroscopy and independent component analysis. Anal. Chim. Acta 2006, 578, 250–255. [Google Scholar] [CrossRef] [PubMed]
- Kardamakis, A.A.; Mouchtaris, A.; Pasadakis, N. Linear predictive spectral coding and independent component analysis in identifying gasoline constituents using infrared spectroscopy. Chemom. Intell. Lab. Syst. 2007, 89, 51–58. [Google Scholar] [CrossRef]
- Balabin, R.M.; Safieva, R.Z.; Lomakina, E.I. Gasoline classification using near inrared (MI) spectroscopy data: Comparison of mulitvariate techniques. Anal. Chim. Acta 2010, 671, 27–35. [Google Scholar] [CrossRef] [PubMed]
- Balabin, R.M.; Safieva, R.Z. Gasoline classification by source and type based on near infrared (NIR) spectroscopy data. Fuel 2008, 87, 1096–1101. [Google Scholar] [CrossRef]
- Li, S.; Dai, L.K. Classification of gasoline brand and origin by Raman spectroscopy and a novel R-weighted LSSVM algorithm. Fuel 2012, 96, 146–152. [Google Scholar] [CrossRef]
- da Silva, M.P.F.; Rodrigues e Brito, L.; Honorato, F.A.; Paim, A.P.S.; Pasquini, C.; Pimentel, M.F. Classification of gasoline as with or without dispersant and detergent additives using infrared spectroscopy and multivariate classification. Fuel 2014, 116, 151–157. [Google Scholar]
- Tan, K.M.; Barman, I.; Dingari, N.C.; Singh, G.P.; Chia, T.F.; Tok, W.L. Toward the development of Raman spectroscopy as a nonperturbative online monitoring tool for gasoline adulteration. Anal. Chem. 2013, 85, 1846–1851. [Google Scholar] [CrossRef] [PubMed]
- Johnston, R.W.B.; Appleby, W.G.; Baker, M.O. Determination of olefins in gasoline—Application of infrared spectroscopy. Anal. Chem. 1948, 20, 805–812. [Google Scholar] [CrossRef]
- Diehl, J.W.; Finkbeiner, J.W.; DiSanzo, F.P. Determination of aromatic hydrocarbons in gasoline by gas chromatography/Fourier transform infrared spectroscopy. Anal. Chem. 1995, 67, 2015–2019. [Google Scholar] [CrossRef]
- Reboucas, M.V.; Santos, J.B.; Pimentel, M.F.; Teixeira, L.S.G. A novel approach for development of a multivariate calibration model using a Doehlert experimental design: Application for prediction of key gasoline properties by near-infrared spectroscopy. Chemom. Intell. Lab. Syst. 2011, 107, 185–193. [Google Scholar] [CrossRef]
- Pinto, L.A.; Galvao, R.K.H.; Araujo, M.C.U. Ensemble wavelet modelling for detrmination of wheat and gasoline properties by near and middle infrared spectroscopy. Anal. Chim. Acta 2010, 682, 37–47. [Google Scholar] [CrossRef] [PubMed]
- Özdemir, D. Determination of octane number of gasoline using near infrared spectroscopy and genetic multivariate calibration methods. Pet. Sci. Technol. 2005, 23, 1139–1152. [Google Scholar] [CrossRef]
- Flecher, P.E.; Welch, W.T.; Albin, S.; Cooper, J.B. Determination of octane numbers and Reid vapor pressure in commercial gasoline using dispersive fiber-optic Raman spectroscopy. Spectrochim. Acta A 1997, 53, 199–206. [Google Scholar]
- Al-Degs, Y.S.; Al-Ghouti, M.; Walker, G. Determination of higher heating value of petro-diesels using mid-infrared spectroscopy and chemometry. J. Therm. Anal. Calorim. 2012, 107, 853–862. [Google Scholar] [CrossRef]
- Santos, V.O., Jr.; Oliveira, F.C.C.; Lima, D.G.; Petry, A.C.; Carcia, E.; Suarez, P.A.Z.; Rubim, J.C. A comparative study of diesel analysis by FTIR, FTNIR and FT-Raman spectroscopy using PLS and artificial neural network analysis. Anal. Chim. Acta 2005, 547, 188–196. [Google Scholar] [CrossRef]
- Alves, J.C.L.; Henriques, C.B.; Poppi, R.J. Determination of diesel quality parameters using support vector regression and near infrared spectroscopy for an in-line blending optimizer system. Fuel 2012, 97, 710–717. [Google Scholar] [CrossRef]
- Cooper, J.B.; Wise, K.L.; Welch, W.T.; Bledsoe, R.R.; Sumner, M.B. Determination of weight percent oxygen in commercial gasoline: A comparison between FT-Raman, FT-IR and dispersive near-IR spectroscopies. Appl. Spectrosc. 1996, 50, 917–921. [Google Scholar] [CrossRef]
- Li, J.; Dai, L. A hard modeling approach to determine methanol concentration in methanol gasoline by Raman spectroscopy. Sens. Actuators B 2012, 173, 385–390. [Google Scholar] [CrossRef]
- Van Ness, H.C.; van Winkle, J.; Richtol, H.H.; Hollinger, H.B. Infrared spectra and the thermodynamics of alcohol-hydrocarbon systems. J. Phys. Chem. 1967, 71, 1483–1494. [Google Scholar] [CrossRef]
- Corsetti, S.; Zehentbauer, F.M.; McGloin, D.; Kiefer, J. Characterization of gasoline/ethanol blends by infrared and excess infrared spectroscopy. Fuel 2015, 141, 136–142. [Google Scholar] [CrossRef]
- Pitz, W.J.; Mueller, C.J. Recent progress in the development of diesel surrogate fuels. Prog. Energy Combust. Sci. 2011, 37, 330–350. [Google Scholar] [CrossRef]
- Sileghem, L.; Alekseev, V.A.; Vancoillie, J.; van Geem, K.M.; Nilsson, E.J.K.; Verhelst, S.; Konnov, A.A. Laminar burning velocity of gasoline and the gasoline surrogate components iso-octane, n-heptane and toluene. Fuel 2013, 112, 355–365. [Google Scholar] [CrossRef]
- Ye, Q.; Xu, Q.; Yu, Y.; Qu, R.; Fang, Z. Rapid and quantitative detection of ethanol proportion in ethanol-gasoline mixtures by Raman spectroscopy. Opt. Commun. 2009, 282, 3785–3788. [Google Scholar] [CrossRef]
- Battiste, D.R.; Fry, S.E.; White, F.T.; Scoggins, M.W.; McWilliams, T.B. Determination of ethanol in gasohol by infrared spectrometry. Anal. Chem. 1981, 53, 1096–1099. [Google Scholar] [CrossRef]
- Balabin, R.M.; Syunyaev, R.Z.; Karpov, S.A. Quantitative measurement of ethanol distribution over fractions of ethanol-gasoline fuel. Energy Fuels 2007, 21, 2460–2465. [Google Scholar] [CrossRef]
- Ravi Prasad, P.; Rama Rao, K.S.; Bhuvaneswari, K.; Praveena, N.; Srikanth, Y.V.V. Determination of ethanol in blend petrol by gas chromatography and Fourier transform infrared spectroscopy. Energy Sources A 2008, 30, 1534–1539. [Google Scholar] [CrossRef]
- Ahmed, M.K.; Levenson, J. Application of near-infrared spectroscopy to the quality assurance of ethanol and butanol blended gasoline. Petroleum Sci. Technol. 2012, 30, 115–121. [Google Scholar] [CrossRef]
- Zhang, W.B. Review on analysis of biodiesel with infrared spectroscopy. Renew. Sustain. Energy Rev. 2012, 16, 6048–6058. [Google Scholar] [CrossRef]
- Mazivila, S.J.; De Santana, F.B.; Mitsutake, H.; Gontijo, L.C.; Santos, D.Q.; Neto, W.B. Discrimination of the type of biodiesel/diesel blend (B5) using mid-infrared spectroscopy and PLS-DA. Fuel 2015, 142, 222–226. [Google Scholar] [CrossRef]
- De Lira, L.F.B.; De Vasconcelos, F.V.C.; Pereira, C.F.; Paim, A.P.S.; Stragevitch, L.; Pimentel, M.F. Prediction of properties of diesel/biodiesel blends by infrared spectroscopy and multivariate calibration. Fuel 2010, 89, 405–409. [Google Scholar] [CrossRef]
- Oliveira, F.C.C.; Brandao, C.R.R.; Ramalho, H.F.; Da Costa, L.A.F.; Suarez, P.A.Z.; Rubim, J.C. Adulteration of diesel/biodiesel blends by vegetable oil as determined by Fourier transform (FT) near infrared spectrometry and FT-Raman spectroscopy. Anal. Chim. Acta 2007, 587, 194–199. [Google Scholar] [CrossRef] [PubMed]
- Soares, I.P.; Rezende, T.F.; Fortes, I.C.P. Study of the behavior changes in physical-chemistry properties of diesel/biodiesel (B2) mixtures with residual oil and its quantification by partial least-squares attenuated total reflection-Fourier transformed infrared spectroscopy (PLS/ATR-FTIR). Energy Fuels 2009, 23, 4143–4148. [Google Scholar] [CrossRef]
- Guarieiro, L.L.N.; Pinto, A.C.; De Aguiar, P.F.; Ribeiro, N.M. Metodologia analitica para quantificar o teor de biodiesel na mistura biodiesel: Diesel utilizando espectroscopia na regiao do infravermelho. Quimica Nova 2008, 31, 421–426. (In Portuguese) [Google Scholar] [CrossRef]
- Oliveira, J.S.; Montalvao, R.; Daher, L.; Suarez, P.A.Z.; Rubim, J.C. Determination of methyl ester contents in biodiesel blends by FTIR-ATR and FTNIR spectroscopies. Talanta 2006, 69, 1278–1284. [Google Scholar] [CrossRef] [PubMed]
- De Carvalho Rocha, W.F.; Nogueira, R.; Vaz, B.G. Validation of model of multivariate calibration: An aplication to the determination of biodiesel blend levels in diesel by near-infrared spectroscopy. J. Chemom. 2012, 26, 456–461. [Google Scholar] [CrossRef]
- Gontijo, L.C.; Guimaraes, E.; Mitsutake, H.; De Santana, F.B.; Santos, D.Q.; Neto, W.B. Quantification of soybean biodiesels in diesel blends according to ASTM E1655 using mid-infrared spectroscopy and multivariate calibration. Fuel 2014, 117, 1111–1114. [Google Scholar] [CrossRef]
- Pimentel, M.F.; Ribeiro, G.M.G.S.; Da Cruz, R.S.; Stragevitch, L.; Pacheco Filho, J.G.A.; Teixeira, L.S.G. Determination of biodiesel content when blended with mineral diesel fuel using infrared spectroscopy and multivariate calibration. Microchem. J. 2006, 82, 201–206. [Google Scholar] [CrossRef]
- Song, S.Q.; Maragou, V.; Tsiakaras, P. How far are direct alcohol fuel cells from our energy future? J. Fuel Cell Sci. Technol. 2007, 4, 203–209. [Google Scholar] [CrossRef]
- Yu, E.H.; Krewer, U.; Scott, K. Principles and materials aspects of direct alkaline alcohol fuel cells. Energies 2010, 3, 1499–1528. [Google Scholar] [CrossRef]
- Leo, T.J.; Raso, M.A.; Navarro, E.; Mora, E. Long term performance study of a direct methanol fuel cell fed with alcohol blends. Energies 2013, 6, 282–293. [Google Scholar] [CrossRef]
- Burikov, S.; Dolenko, T.; Patsaeva, S.; Starokurov, Y.; Yuzhakov, V. Raman and IR spectroscopy research on hydrogen bonding in water-ethanol systems. Mol. Phys. 2010, 108, 2427–2436. [Google Scholar] [CrossRef]
- Nedic, M.; Wassermann, T.N.; Wugt Larsen, R.; Suhm, M.A. A combined Raman- and infrared jet study of mixed methanol-water and ethanol-water clusters. Phys. Chem. Chem. Phys. 2011, 13, 14050–14063. [Google Scholar] [CrossRef] [PubMed]
- Zehentbauer, F.M.; Bain, E.J.; Kiefer, J. Multiple parameter monitoring in a direct methanol fuel cell. Meas. Sci. Technol. 2012, 23. [Google Scholar] [CrossRef]
- Mendes, L.S.; Oliveira, F.C.C.; Suarez, P.A.Z.; Rubim, J.C. Determination of ethanol in fuel ethanol and beverages by Fourier transform (FT)-near infrared and FT-Raman spectrometries. Anal. Chim. Acta 2003, 493, 219–231. [Google Scholar] [CrossRef]
- Arita, Y.; Ewart, P. Infra-red multi-mode absorption spectroscopy of acetylene using an Er/Yb: Glass micro-laser. Opt. Express 2008, 16, 4437–4442. [Google Scholar] [CrossRef] [PubMed]
- Northern, J.H.; Thompson, A.W.J.; Hamilton, M.L.; Ewart, P. Multi-species detection using multi-mode absorption spectroscopy (MUMAS). Appl. Phys. B 2013, 111, 627–635. [Google Scholar] [CrossRef]
- Kiefer, J. Instantaneous shifted-excitation Raman difference spectroscopy (iSERDS). J. Raman Spectrosc. 2014, 45, 980–983. [Google Scholar] [CrossRef]
- Kaminski, C.F.; Watt, R.S.; Elder, A.D.; Frank, J.H.; Hult, J. Supercontinuum radiation for applications in chemical sensing and microscopy. Appl. Phys. B 2008, 92, 367–378. [Google Scholar] [CrossRef]
- Werblinski, T.; Engel, S.R.; Engelbrecht, R.; Zigan, L.; Will, S. Temperature and multi-species measurements by supercontinuum absorption spectroscopy for IC engine applications. Opt. Express 2013, 21, 13656–13667. [Google Scholar] [CrossRef] [PubMed]
- Hult, J.; Watt, R.S.; Kaminski, C.F. High bandwidth absorption spectroscopy with a dispersed supercontinuum source. Opt. Express 2007, 15, 11385–11395. [Google Scholar] [CrossRef] [PubMed]
- Sych, Y.; Engelbrecht, R.; Schmauss, B.; Kozlov, D.N.; Seeger, T.; Leipertz, A. Broadband time-domain absorption spectroscopy with a ns-pulse supercontinuum source. Opt. Express 2010, 18, 22762–22771. [Google Scholar] [CrossRef] [PubMed]
- Walewski, J.; Sanders, S.T. High-resolution wavelength-agile laser source based on pulsed super-continua. Appl. Phys. B 2004, 79, 415–418. [Google Scholar] [CrossRef]
- Kiefer, J.; Ewart, P. Laser diagnostics and minor species detection in combustion using resonant four-wave mixing. Prog. Energy Combust. Sci. 2011, 37, 525–564. [Google Scholar] [CrossRef]
- Roy, S.; Gord, J.R.; Patnaik, A.K. Recent advances in coherent anti-Stokes Raman scattering spectroscopy: Fundamental developments and applications in reacting flows. Prog. Energy Combust. Sci. 2010, 36, 280–306. [Google Scholar] [CrossRef]
- Beyrau, F.; Seeger, T.; Malarski, A.; Leipertz, A. Determination of temperatures and fuel/air ratios in an ethene-air flame by dual-pump CARS. J. Raman Spectrosc. 2003, 34, 946–951. [Google Scholar] [CrossRef]
- Li, Z.S.; Linvin, M.; Zetterberg, J.; Kiefer, J.; Aldén, M. Mid-infrared polarization spectroscopy of C2H2: Non-intrusive spatial-resolved measurements of polyatomic hydrocarbon molecules for combustion diagnostics. Proc. Combust. Inst. 2007, 31, 817–824. [Google Scholar] [CrossRef]
- Li, Z.S.; Rupinski, M.; Zetterberg, J.; Aldén, M. Mid-infrared PS and LIF detection of CH4 and C2H6 in cold flows and flames at atmospheric pressure. Proc. Combust. Inst. 2005, 30, 1629–1636. [Google Scholar] [CrossRef]
- Germann, G.J.; Farrow, R.L.; Rakestraw, D.J. Infrared degenerate four-wave mixing spectrsocopy of polyatomic molecules: CH4 and C2H2. JOSA B 1995, 12, 25–32. [Google Scholar] [CrossRef]
- Sun, Z.W.; Li, Z.S.; Li, B.; Alden, M.; Ewart, P. Detection of C2H2 and HCl using mid-infrared degenerate four-wave mixing with stable beam alignment: Towards practical in situ sensing of trace molecular species. Appl. Phys. B 2010, 98, 593–600. [Google Scholar] [CrossRef]
- Roshani, B.; Flügel, A.; Schmitz, I.; Kozlov, D.N.; Seeger, T.; Zigan, L.; Kiefer, J.; Leipertz, A. Simultaneous measurements of fuel vapor concentration and temperature in a flash-boiling propane jet using laser-induced gratings. J. Raman Spectrosc. 2013, 44, 1356–1362. [Google Scholar] [CrossRef]
- Seeger, T.; Kiefer, J.; Weikl, M.C.; Leipertz, A.; Kozlov, D.N. Time-resolved measurement of the local equivalence ratio in a gaseous propane injection process using laser-induced gratings. Opt. Express 2006, 14, 12994–13000. [Google Scholar] [CrossRef] [PubMed]
- Bohlin, A.; Kliewer, C.J. Single-shot hyperspectral coherent Raman planar imaging in the range 0–4200 cm−1. Appl. Phys. Lett. 2014, 105. [Google Scholar] [CrossRef]
- Bohlin, A.; Kliewer, C.J. Two-beam ultrabroadband coherent anti-Stokes Raman spectroscopy for high resolution gas-phase multiplex imaging. Appl. Phys. Lett. 2014, 104. [Google Scholar] [CrossRef]
- Tedder, S.A.; Wheeler, J.L.; Cutler, A.D.; Danehy, P.M. Width-increased dual-pump enhanced coherent anti-Stokes Raman spectroscopy. Appl. Opt. 2010, 49, 1305–1313. [Google Scholar] [CrossRef] [PubMed]
- Roy, S.; Meyer, T.R.; Brown, M.S.; Velur, V.N.; Lucht, R.P.; Gord, J.R. Triple-pump coherent anti-Stokes Raman scattering (CARS): Temperature and multiple-species concentration measurements in reacting flows. Opt. Commun. 2003, 224, 131–137. [Google Scholar] [CrossRef]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kiefer, J. Recent Advances in the Characterization of Gaseous and Liquid Fuels by Vibrational Spectroscopy. Energies 2015, 8, 3165-3197. https://doi.org/10.3390/en8043165
Kiefer J. Recent Advances in the Characterization of Gaseous and Liquid Fuels by Vibrational Spectroscopy. Energies. 2015; 8(4):3165-3197. https://doi.org/10.3390/en8043165
Chicago/Turabian StyleKiefer, Johannes. 2015. "Recent Advances in the Characterization of Gaseous and Liquid Fuels by Vibrational Spectroscopy" Energies 8, no. 4: 3165-3197. https://doi.org/10.3390/en8043165
APA StyleKiefer, J. (2015). Recent Advances in the Characterization of Gaseous and Liquid Fuels by Vibrational Spectroscopy. Energies, 8(4), 3165-3197. https://doi.org/10.3390/en8043165