Predictive Densities for Day-Ahead Electricity Prices Using Time-Adaptive Quantile Regression
Abstract
: A large part of the decision-making problems actors of the power system are facing on a daily basis requires scenarios for day-ahead electricity market prices. These scenarios are most likely to be generated based on marginal predictive densities for such prices, then enhanced with a temporal dependence structure. A semi-parametric methodology for generating such densities is presented: it includes: (i) a time-adaptive quantile regression model for the 5%–95% quantiles; and (ii) a description of the distribution tails with exponential distributions. The forecasting skill of the proposed model is compared to that of four benchmark approaches and the well-known the generalist autoregressive conditional heteroskedasticity (GARCH) model over a three-year evaluation period. While all benchmarks are outperformed in terms of forecasting skill overall, the superiority of the semi-parametric model over the GARCH model lies in the former’s ability to generate reliable quantile estimates.1. Introduction
Probabilistic forecasts of the day-ahead wholesale price in the form of predictive densities are required to solve many of the challenges faced by participants in today’s electricity markets. For instance, optimal bidding strategies for wind power producers, like the ones described in [1,2], require such forecasts for scenario generation. Similarly, scenarios for day-ahead prices are used in the pricing of hydropower in [3,4] and for the optimal bidding of other types of generation units in [5]. This aside, foreseeable developments in the electricity sector, such as continuing growth of renewable energy technologies and the emergence of flexible demand, are likely to further boost the demand for such forecasts.
The aim of this paper is to present a methodology for the density forecasting of day-ahead electricity prices that permits the generation of operational scenarios. First and foremost, such a model should produce reliable density forecasts of the untransformed prices. For the purpose of scenario generation, it is important that the forecasts properly describe the full density of the prices (instead of a set of quantiles only, as is sometimes the case for applications in risk management concerned with a single variable). Once a proper description of the density is obtained, scenarios respecting the prices’ correlation structure are easily obtainable using a scenario generation framework similar to that presented in [6].
The unique features of electricity as a commodity explain the distinct characteristics of its price. This is mostly since supply and demand must be matched constantly and instantaneously. In addition, since electricity cannot be stored directly in an efficient and cost-effective manner, production must take place synchronous with consumption. Together, this makes arbitrage over time and space close to impossible [7,8]. Electricity consumption, however, is highly inelastic in the short-term and exhibits multiple strong seasonal patterns [9]. The supply function, on the other hand, is discontinuous, convex and steeply increasing in the high production end [10,11]. Altogether, this results in electricity prices that in most markets exhibit most or all of the following features: strong multiple periodicities, intra- and inter-day correlation, non-stationarity, positive skewness, high kurtosis, mean reverting spikes and general excessive volatility [11–13].
Density forecasting of day-ahead electricity prices has received increased attention over recent years. The most popular approach in the existing literature on the matter is to describe conditional price densities by some variant of the generalist autoregressive conditional heteroskedasticity model (GARCH), uni- or multi-variate ([14–16] and the references therein), often with the aid of a jump-diffusion model [17,18]. Disappointingly, though, rigorous measures of the forecasting skill for such conditional density models are, in most cases, not reported. Alternative approaches are quite rare in the literature. As a first example, [11] presented a novel approach for Bayesian density forecasting based on a vector autoregressive model with skew-t noise, while assessing the overall fit of the predictive densities obtained. All inference is, however, performed on logarithmic transformed data, and no scheme for conversion to the original scale is discussed. This is while such a scheme is paramount for a proper transformation of the forecast for a non-linear and non-stationary process, like electricity prices. It is therefore hard to pinpoint how their model would perform on the real scale and compared to other types of models. Besides, [19,20] present interesting methods for modeling the first four moments of conditional price densities with alternative probability density functions. More recently, novel nonparametric approaches were proposed based on quantile regression averaging, therefore allowing one to issue probabilistic forecasts in a forecast combination framework, e.g., [21,22].
In the broadest sense, there are two different methodological lines to model conditional densities: adopting parametric assumptions and non/semi-parametric modeling. The parametric approaches have the appeal that the full density of the modeled process is characterized by very few parameters. This, in turn, makes a single model sufficient for obtaining a description of the whole density. This very same feature is, however, also the main drawback of parametric approaches, since it constrains density shape. In contrast, non- or semi-parametric approaches do not suffer from this shape inflexibility, since assumptions about the distributional shape are either none or conditioned to a certain domain. These approaches, however, involve either severely increased model complexity, or a substantial growth in the number of models to be estimated, or even both.
Using data from the Western Danish price area for Nord Pool’s Elspot, models for conditional price densities from both categories will be derived, analyzed and compared in the following. As a parametric approach and as a form of baseline approach, modeling the standard deviation of a Gaussian distribution is attempted through a series of formulations of the well-known ARCH/GARCH models [23,24] and similar regression models. Alternatively, a non-parametric quantile regression (QR) [25–27] model is derived for quantiles ranging from 0.05 to 0.95. In order to overcome the shortcomings of QR regarding the modeling of distribution tails, it is coupled with a model for the tails based on an exponential assumption. All models have time-varying parameters and describe the conditional densities of electricity prices given an already existing point forecast, here generated with the model described in [28]. Generally, any well-tuned model for point forecasting of electricity prices could be applied. These point forecasts enter the models as an explanatory variable, potentially supplemented by load forecasts. Therefore, a particularity of our approach is that it builds on point forecasts that may already be routinely provided to forecast users. These forecasts are to be “dressed” with conditional distributions of potential forecast errors, then allowing one to inform of forecast uncertainty in a methodologically sound and pragmatic manner.
In addition to comparing the models with each other, their performance is compared to that of four benchmark approaches. These are the (i) empirical marginal density of electricity prices, often referred to as climatology forecasts in meteorology; (ii) a Gaussian unconditional density; (iii) a conditional Gaussian density whose mean and standard deviation are estimated by exponential smoothing; and (iv) a kernel density estimation model. The continuous ranked probability score ( ) [29,30] and the related continuous ranked probability skill score (CRPSS) are used for a comparison of forecasting skill. In terms of these measures, both models are shown to outperform the benchmarks. It is also demonstrated based on reliability diagrams that even though the CRPSS of these two models types is quite compatible, it is only the QR-exponential model that produces reliable density forecasts.
The remainder of this paper is structured as follows: Section 2 describes the functions of Nord Pool and the data, then developing into an empirical analysis in order to highlight the main data features to be modeled subsequently. The models and related parameter estimation are described in Section 3, while further analysis and genuine comparison of their forecasting skill are the focus of Section 4. Finally, concluding remarks are given in Section 5.
2. The Data
2.1. Nord Pool’s Elspot
Nord Pool’s Elspot is a day-ahead market for the physical delivery of electricity, which covers 5 different countries. By default, the day-ahead price should be the same in the entire market region unless prevented by transmission bottlenecks. Gate-closure is every day at noon for exchange during the upcoming day. The prices are set with hourly resolution as the intersection between the aggregated supply and demand curves. At first, curves for the whole region are constructed, and their intersection constitutes the system price—the price at which trades are settled if transmission capacity is sufficient. If, however, the resulting production and consumption schedules prompt congestion in the transmission network, two or more area prices are calculated. The area prices are found in the same manner as the system price. The supply and demand curves, however, only comprise the bids within the area where transmission capacity is sufficient along with full utilization of congested lines. Further information can be found in [31].
The empirical work of this paper is based on data from the Western Danish price area (DK-1). The data covers a period of almost exactly three years from 21 December 2008, through December 2011. The data set comprises hourly forecast and observed day-ahead prices for the area, forecast system load and the area’s forecast wind power production. The point forecasts for the prices are found by the model described in [28], while the load forecasts were obtained from Nord Pool’s website [32]. Finally, the wind power forecasts originate from a statistically-based wind power prediction software (see [33]).
2.2. Data Analysis
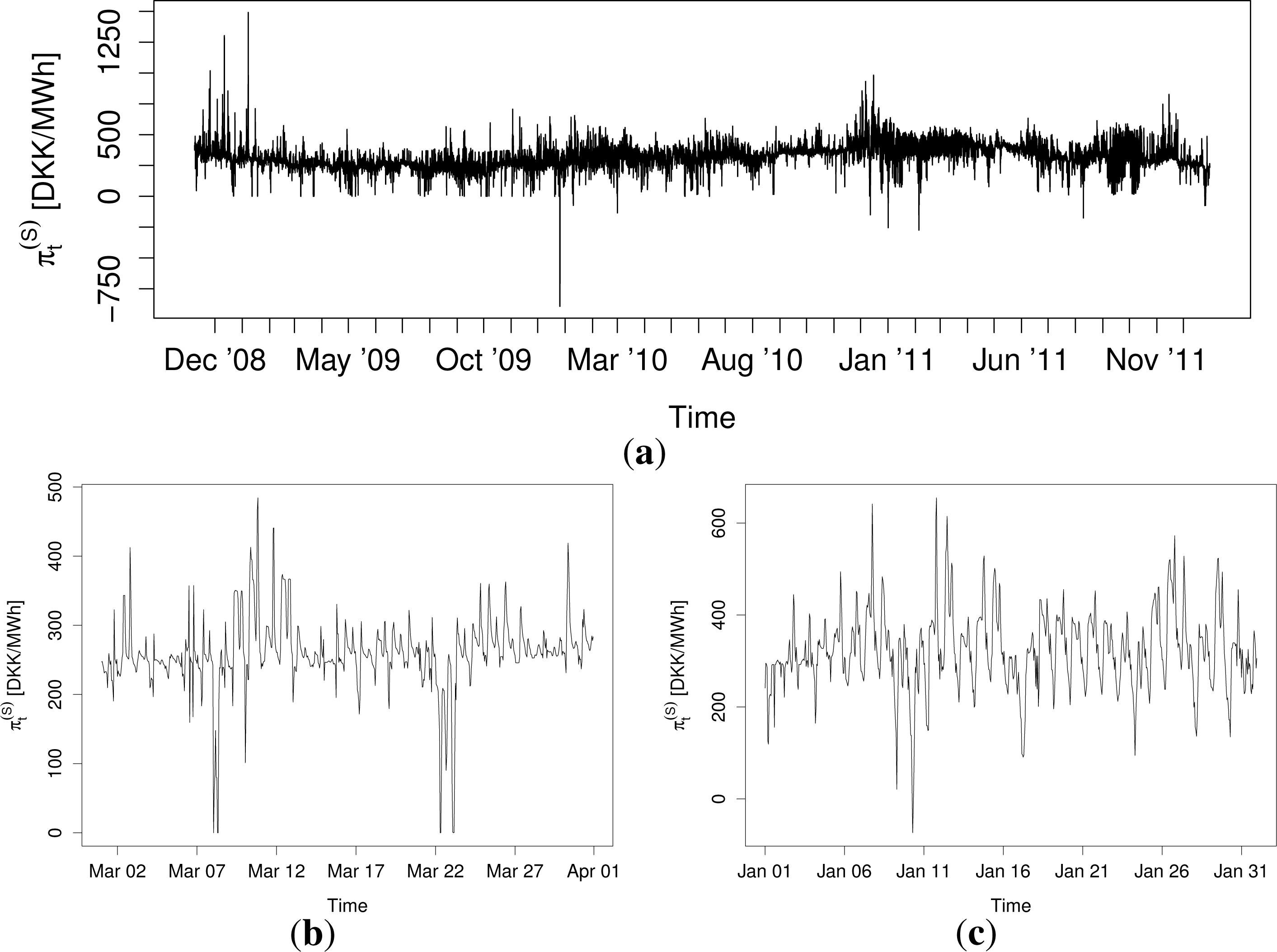
In order to demonstrate the previously described characteristics of the prices and to establish the necessary properties of a model for their density, a brief empirical data analysis is presented. Let denote the day-ahead electricity price for hour t. The top plot in Figure 1 shows a time series plot of for the whole data period. From the plot, some of the features mentioned in the previous section are apparent. The prices’ mean and volatility varies constantly throughout the series, and price spikes are quite frequent. From the bottom two plots in Figure 1, which show time series plots of for March, 2009, and January, 2010, the daily and weekly seasonal cycles of the prices are apparent, as well as some of the other features previously mentioned.
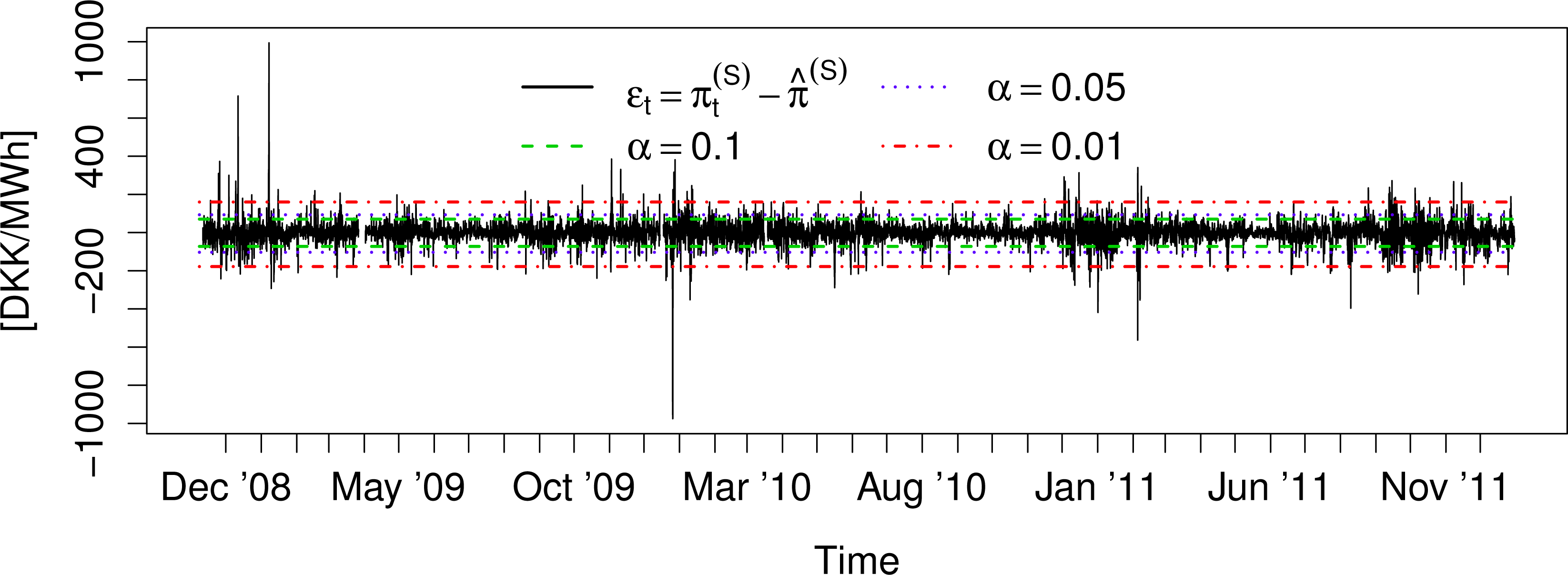
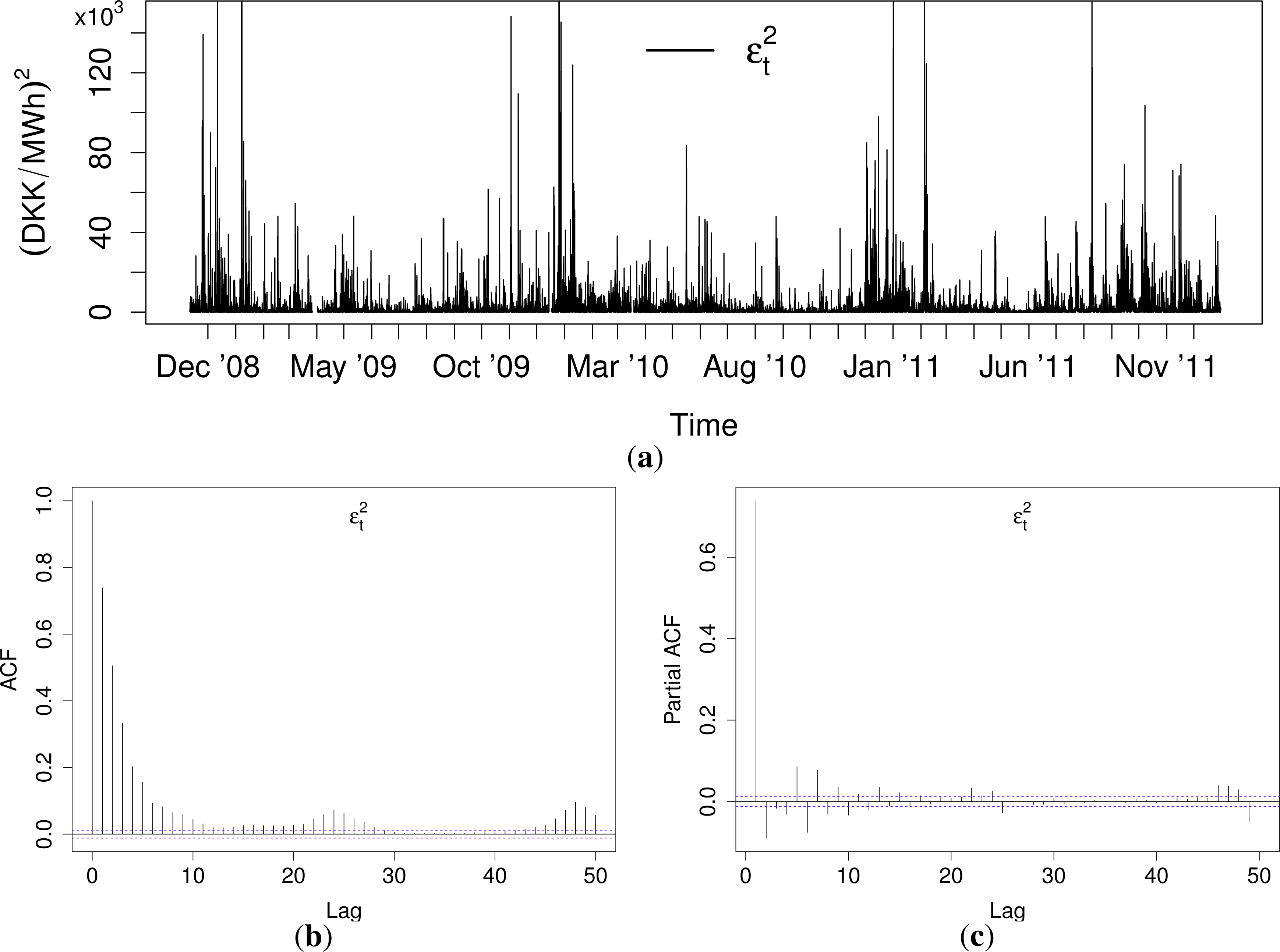
Figure 2 shows the residual series:
The variation of the mean and volatility is far less severe for ɛt series than for . Furthermore, the magnitude of the spikes in the residual series is severely reduced compared to the unfiltered prices. The reduction of these features makes ɛt better suited for parametric modeling than and will yield more stable parameters over time for any type of model.
Another appeal of modeling the density of ɛt is that it does not exhibit nearly as much diurnal variation as that of . Furthermore, the dependence of the mean on exogenous variables vanishes. This can be seen from the plots in Figures 3 and 4.
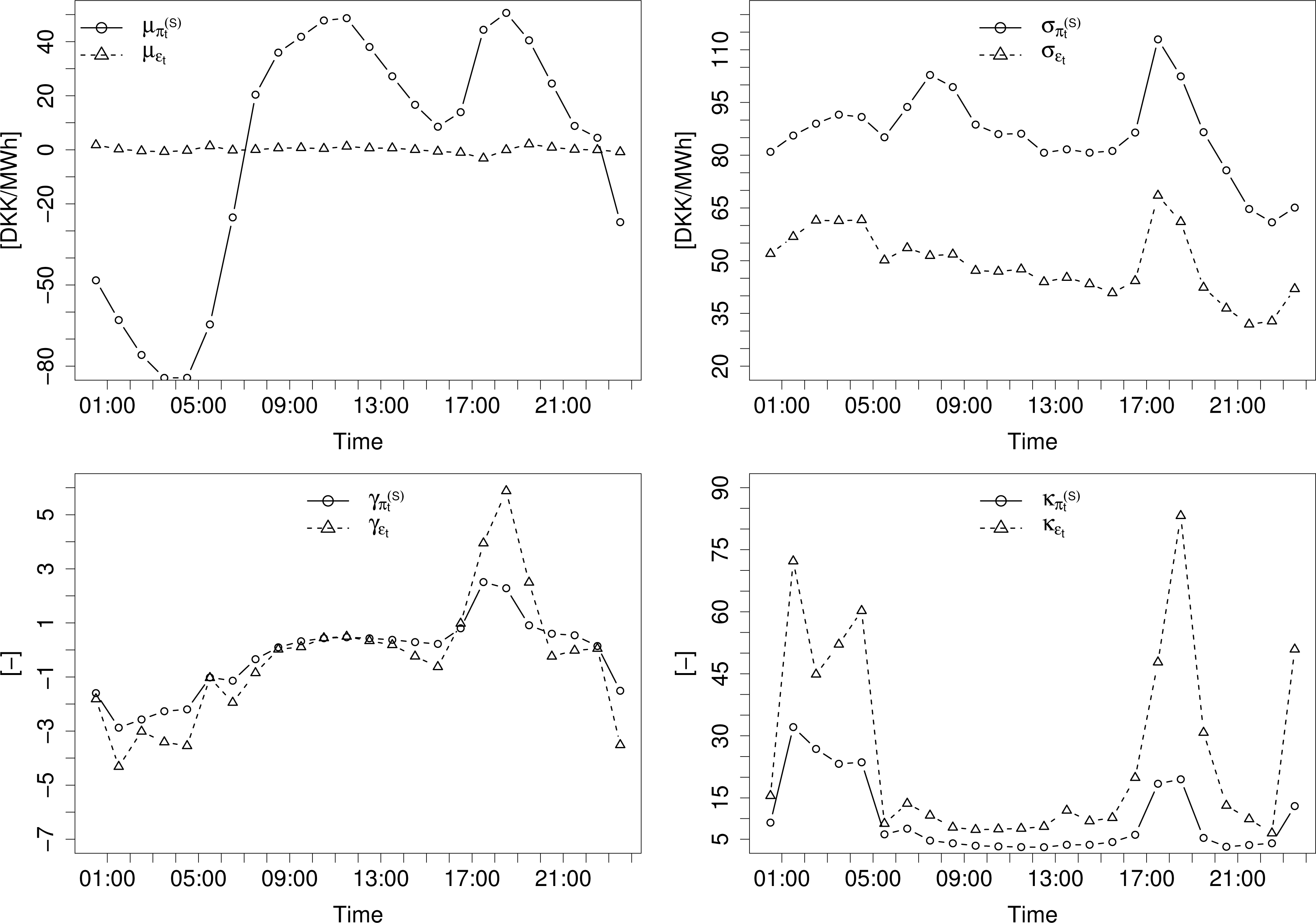
Figure 3 shows the mean (μ), standard deviation (σ), skewness (γ) and Pearson’s kurtosis (κ) of ɛt and conditional to different explanatory variables. Three variables are considered here and a fourth one derived from the others. These are the price forecast , the forecast system load L̂t, the forecast wind power production Ŵt and the forecast wind power penetration . In order to ease the comparison between ɛt and , the empirical mean of has been subtracted from the corresponding conditional means.
The plots in Figure 3 reveal that the impact of the explanatory variables on the mean becomes negligible for ɛt, while it is quite strong for . Apart from the lower standard deviation and somewhat elevated kurtosis, the relationship patterns between ɛt and appear consistent for higher order moments. An explanation for the higher kurtosis of ɛt is to be found in excessive price spikes, which, due to the lowered σ, yield an increase of κ. The strongest relation seems to be with the expected price, and since the other variables have already been taken into account in the derivation of , it seems reasonable to start out with a density model depending on expected price (i.e., given by point forecasts) and subsequently add other variables and examine whether the predictive skill is improved or not. In addition to the analysis based on moments presented here, dependencies with other potential explanatory variables were also verified visually. The probabilistic calibration assessment presented later on will permit one to verify the suitability of distributional assumptions.
Figure 4 shows hourly values of μ, σ, γ and κ for the two series. A comparison of the two lines in each plot reveals that by subtracting , much of the diurnal variation in residual densities is mitigated. The daily seasonality that remains is consistent with the relationship between and the density of ɛt. Hence, a model relying on to explain conditional densities of through ɛt will not require an explicit daily seasonality term, while the direct modeling of densities of would. Overall, in a parametric probabilistic forecasting framework, the observed behavior of γ and κ should favor distributions with higher flexibility than Gaussian ones, e.g., generalized Gaussian and Student’s t distributions. Here, instead of dealing with more complex probability distributions, our proposal below is to concentrate on a semi-parametric approach that gives more flexibility in describing conditional distributions of forecast errors. For simplicity, our parametric benchmark is based on a Gaussian assumption. It should be upgraded if one was truly interested in benchmarking parametric vs. nonparametric approaches to probabilistic electricity price forecasting.
3. Models for Density Forecasts
3.1. Benchmarks
Four relatively simple benchmark models are constructed, which the more elaborate models will be evaluated against. These models include:
The empirical unconditional distribution of electricity prices (climatology, defined by a set of quantiles);
A time-invariant Gaussian density, i.e., a density defined by the empirical mean and standard deviation of electricity prices;
A simple exponential smoothing for the mean and standard deviation of the prices, yielding time-varying Gaussian densities;
A kernel density model estimated using all past data, the last week worth of data, the last 500 and the last 1000 observations available;
For Model I, the predictions are obviously constant. The sample quantile Qπ(S) (τ) with nominal level τ is found as:
The prediction intervals obtained from Model II are also constant. They are taken from a Gaussian distribution with standard deviation: σπ(S):
Model III relies on a two-stage exponential smoothing of the mean (μπ(S),t) and the standard deviation (σπ(S),t) of , i.e.:
Finally, Model IV is a kernel density estimation of the probability density function (pdf) of ɛt:
3.2. Gaussian Models
The parametric assumption formulated here is that the residuals from the electricity price point forecasts can be seen as Gaussian. The relationship between spot prices and the point forecast from [28] can be written as:
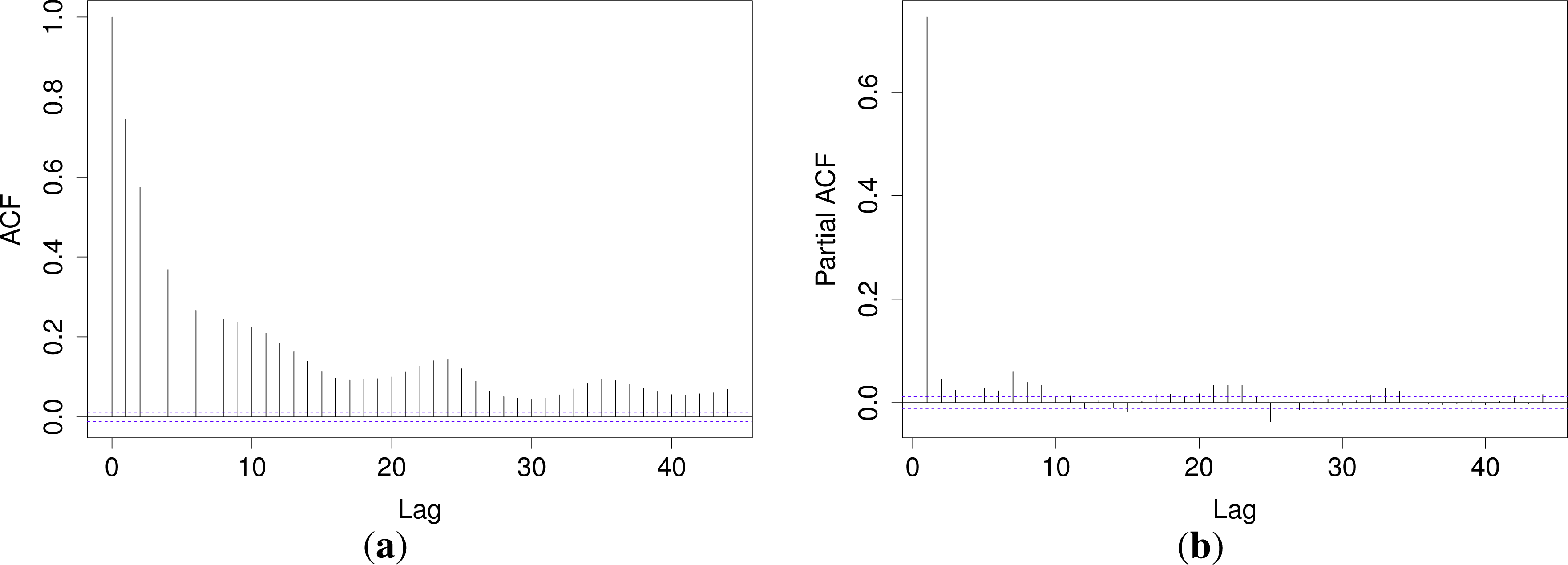
All of the models for Gaussian density forecasts derived in this section involve modeling of , which is plotted in the top panel of Figure 5. Relative to the scale of the plot, seems to have a level close to zero, though with frequent spikes. Autocorrelation and partial autocorrelation functions (ACF and PACF, respectively) for are shown in the bottom panel of Figure 5. The ACF and the PACF suggest that a low order ARCH or GARCH model is sufficient.
A GARCH model of order (q, p) (see, e.g., [24]), describing σɛ,t, is formulated as:
For p = 0, the model in Equation (12) becomes an ARCH(q) model, and M exogenous variables can be introduced in the model by adding an extra term, such that:
Based the preceding data analysis and the ACF and PACF for in Figure 5, 10 different model formulations are chosen for analysis. Experiments with the models revealed that only the predicted price and load contributed to improving forecasting skill. Thus, the formulations are given here explicitly in terms of these variables:
The parameters, α, β, γ and θ, are estimated recursively (as described in [28] and [35]) with the forgetting factor λ chosen as:
The regression parameters, α, β and γ, are estimated separately for each lead-time. This translates to estimating hourly-specific parameters. A prediction formula can be written generally for models (I)–(X) as:
The alternative approach of estimating a single set of parameters for one-step ahead prediction and to generate prediction for further lead times iteratively was found to perform worse than this direct prediction approach.
3.3. Time Adaptive Quantile Regression
The QR model is based on the time adaptive QR-framework described in [27]. The QR model is used to describe the conditional densities of ɛt for nominal levels between 5% and the 95%. Afterwards, this model is supplemented with a description of the distributions’ tails. The readers interested in topics ranging from fundamental properties to the latest developments in the field of quantile regression are referred to [25].
The most basic form of a QR model [26] for ɛt, given a nominal level τ, is:
The non-linear relationship between ɛt and the explanatory variables is accounted for by representing xt by B-splines. Furthermore, the estimation dataset is updated as new observations become available, while the oldest observations are discarded. Then, a new estimate of the regression parameters is obtained by solving Equation (18). Estimating the parameters on relatively recent values only has the drawback that deviations from the average behavior are quickly discarded. In order to ensure a broader coverage of the explanatory variables’ previous values in the estimation set, its updating is done on a number of partitions or bins. Each bin contains observations falling within a pre-specified range, and every time a new observation becomes available, it replaces the oldest observation in the corresponding bin. Meanwhile, other bins containing data for different values of the variable remain intact. Afterwards, the data bins are combined into a single estimation set, which then contains a broader range of observations than it otherwise would. The updating procedure is described more thoroughly in [27].
In light of the analysis presented earlier on, we start out with a QR-model of the form:
Since the optimal memory of the model is likely to vary for different values of τ, a best model setup is found for each individual value of τ. This calls for a skill score that can rate a single quantile forecast and not the entire cdf. Following the suggestions of ([36] and the references therein), such a score is defined from Equation (18) as:
The number and placement of bins and knots is chosen as the setup yielding the highest value of , for the estimation period, out of six setups. For Setups I–III, bin edges are placed at Fπ̂(S)(τ), τ ∈ {0, 0.25, 0.75, 1}, where Fπ̂(S) denotes the empirical cdf of π̂(S) for the same period. The bin edges for Setups IV–VI, however, are chosen as τ ∈ {0, 1}. The knots are placed at τ ∈ {0, 0.25, 0.5, 0.75, 1} for Setups I and IV, at τ ∈ {0, 0.125, 0.25, 0.5, 0.75, 0.875, 1} for Setups II and V and at τ ∈ {0, 0.25, 0.75, 1} for Setups III and VI.
For deciding on the appropriate bin size, NB, for each of the aforementioned setups, the following scheme is adopted for each value of τ:
- (1)
For Setups I–III: Estimate for NB ∈ {200, 400, . . . , 1200}
For setups IV–VI: Estimate for NB ∈ {200, 400, . . . , 3200}.
- (2)
Find the bin size , .
- (3)
Estimate SSc(NB) for .
- (4)
Again, find out of the new set of NB’s.
- (5)
Estimate SSc(NB) for .
- (6)
Decide on out of the third set of NB’s as the bin size for that particular value of τ.
3.4. Estimating the Distribution Tail for QR Predictions
One of the drawbacks of quantile regression is that it only provides a description of particular quantiles. Thus, one has to assume a distributional shape for the τ value for which a model has not been estimated. This becomes especially problematic when a description of the distribution tails is desired, since they are unlikely to be well approximated by inter- or extra-polation. For any risk management, however, a proper description of the tails is paramount. Likewise, such a description is also important to have for scenario generation. Without it, the scenarios will not reflect properly the full range of possible outcomes.
Therefore, a quantile regression model for an unbounded process, like the one just described, must be accompanied by a model for the tails. In order to obtain such a model, we now define two new variables, and , as:
Indeed, the choice of defining the coverage of the tail models as the data exceeding or not the 95% and 5% quantiles, respectively, is somewhat arbitrary. Here, we will not go into detail in this discussion, but these values seem to be a reasonable choice, since the quantile regression seems to perform well up to these values. On the other hand, estimating quantiles further out in the tails would dilute the estimation data for the tail models severely. Furthermore, for this reason, we restrict ourselves to models with parametric assumptions, as obtaining a description of the full density will always end up in a parametric assumption for the extremes.
Based on our analysis of the data, it appears that exponential tails could be seen as a relevant and simple choice for such modeling of the tails of conditional densities of residuals. Alternatives, such as Pareto and Weibull, could also be considered if deemed more appropriate. The probabilistic calibration results shown in a further part of the paper will actually show that, for our test case and dataset, this exponential assumption is acceptable.
For an exponentially distributed variable x, the pdf f(x; λ) and the cdf F(x; λ) are defined as:
The estimate of λ at time t, λ̂t, is obtained by maximum likelihood estimation using all data available until time t. It is easily shown that such an estimate of the rate-parameter is found as:
4. Numerical Results
4.1. Evaluation of Forecasting Skill
For a comparison of the forecast quality, the average continuous ranked probability score ( ) [29] and the related continuous ranked probability skill score (CRPSS) are used. For a single observation, xo, and a corresponding predicted cdf, F̂(x), the CRPS is defined as:
Subsequently, is found as:
The CRPSS for a certain model is defined as:
In order to allow for a fair comparison of the performance of all of the derived models, two sets of values are reported. One is estimated using a set of quantiles, τ1, ranging from zero to one in steps of 0.05. For the other one, τ2, the set of quantiles used includes additional quantiles in the tails of the distribution. The sets τ1 and τ2 are defined as:
In both cases, the empirical minimum and maximum for the whole data set are used for the zero and one quantiles, respectively.
4.2. Estimation Results
For all models, parameter estimation is done using data from 21 December 2008, until 31 December 2009. The remaining two years are used as an independent test set. These data sets will be referred to as the training set and the test set, respectively. Part of the training data (the last 20%) is used for cross-validation, i.e., to avoid overfitting of the models that would affect their generalization ability when being used to predict based on new data over the evaluation set. Scores are then reported in the following for the training and test data, separately. Implemented in R and run on a Lenovo X230 laptop with an Intel Core i5-3320M (2.60 GHz) processor, estimation of all quantiles models and tails based on this one year of data takes less than one hour. Then, issuing predictions is extremely cheap, since one is only feeding the models with new data and not having to perform any optimization.
Table 1 lists values for the best performing models along with the corresponding parameter estimates for the benchmark and the parametric models. The model parameters for the QR-E model are collated in Table 2. It is to be noted that, to be completely rigorous, one would associate statistical significance test results with the various verification metrics, in order to asses whether the differences in score values may be seen as significant or not. This was not done here, since, in our experience, when using such long evaluation sets (two years), such differences in CRPS values may be deemed of practical magnitude.
Among the benchmarks, the kernel density estimation model outperforms the other ones. This was the case for all values of Nest tried, although Nest = 168 was the one for which the difference was largest. The exponential smoothing model was also found to outperform the time-invariant benchmarks, although it performs poorer than the kernel model.
The best performing parametric models are the GARCH-X model with as the explanatory variable (III) and the GARCH-X and ARCH-X models with both and L̂t as exogenous variables (V and VI, respectively). Although the ARCH-X model outperforms the other two, the difference in is small. Furthermore, the forgetting factor λ is suspiciously low for the ARCH-X model, as it can not rely on the moving average term to accommodate the short-term dynamics of σɛt. Thus, the forgetting factor of the two GARCH models is of a more desirable magnitude in terms of parameter stability.
The τ-specific bin sizes, NB, for the QR-E model are listed in Table 2 along with the placement of the spline knots and the bin edges. According to expectations, the largest amount of data is used to estimate quantiles close to the tails. Then, on both sides of the median, there are quantiles for which the model has a relatively short memory, indicating more rapidly varying dynamics. Closer to the median, memory increases again, since point forecasts have already accommodated most dynamic changes there. All in all, the merits of the model’s flexibility, compared to the parametric models, is illustrated by the longer memory of the QR-E model, thus allowing for more stable regression parameters.
The rate parameters for and are, like for the other models, updated daily using all available data at the estimation time. The corresponding values are listed in Table 3, along with that of climatology forecasts for the tails.
Table 3 shows that a slightly better description of the lower tail is obtained with the exponential model, if compared to climatology. Disappointingly, however, the opposite is the case for the upper tail. It should be remembered that this climatology benchmark does not yield genuine forecasts, since it is based on all available data on electricity prices. Indeed, if issuing a forecast at a given time t, it relies on information for future times t + k, k > 0. In contrast, the forecasts issued based on the exponential model are genuine and only rely on information up to time t.
4.3. Model Comparison
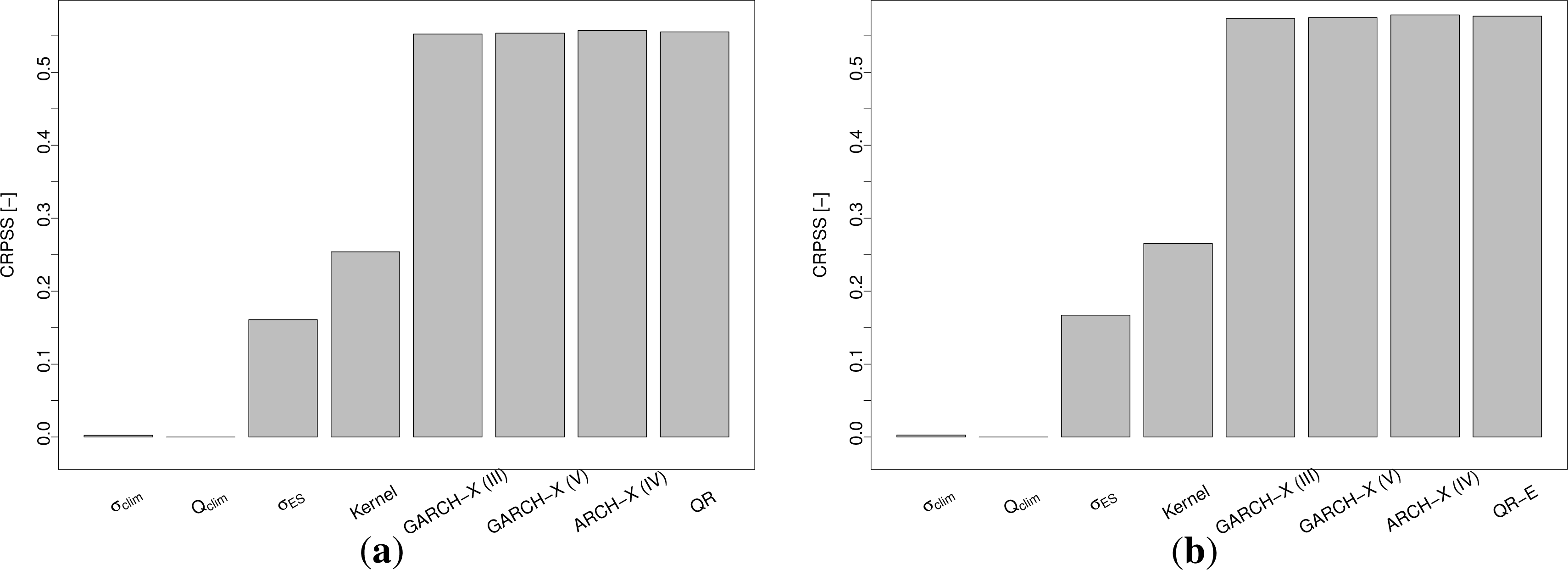
Bar-plots of the CRPSSs for the test period are presented in Figure 6, using τ ∈ τ1 and τ ∈ τ2 as earlier defined.
Overall, the more elaborate models seem to outperform the benchmarks by a significant margin. The difference between the Gaussian and the QR-E models may appear negligible, in comparison.
For any type of risk management or scenario generation, the reliability of the density forecasts is essential. Most risk management models, such as value-at-risk (VaR) or conditional value-at-risk (CVaR), aim at minimizing losses at or beyond a certain quantile of the loss probability distribution. Thus, an unreliable density estimate will severely affect all risk assessment. Similarly for scenario generation that often is used for generating inputs to models, such as VaR and CVaR, an unreliable density forecasts will yield scenarios that do not cover the full spectrum of possible outcomes. Moreover, since uncertainty generally tends to be underestimated in density forecasts ([37]), unreliable density forecast will generally prompt risk to be underestimated. For this reason, the reliability of the probabilistic forecasts generated by the various models is examined.
A thorough discussion of the concept of reliability is given in [38,39], so only a brief introduction will be given here. Ideally, a series of N forecasts (with N large) for the quantile with a nominal level τ of the density of ɛt, Q̂ɛt,t(τ), should satisfy:
The reliability level is usually assessed in terms of a probabilistic bias, i.e., τ − τ̃. For a finite data set, a deviation of τ̃ from the nominal level τ is natural, due to sampling effects. Both [38,39] present estimation procedures for the range of likely deviations. These intervals are commonly referred to as consistency intervals, and correspondingly, they are illustrated as consistency bars on reliability diagrams.
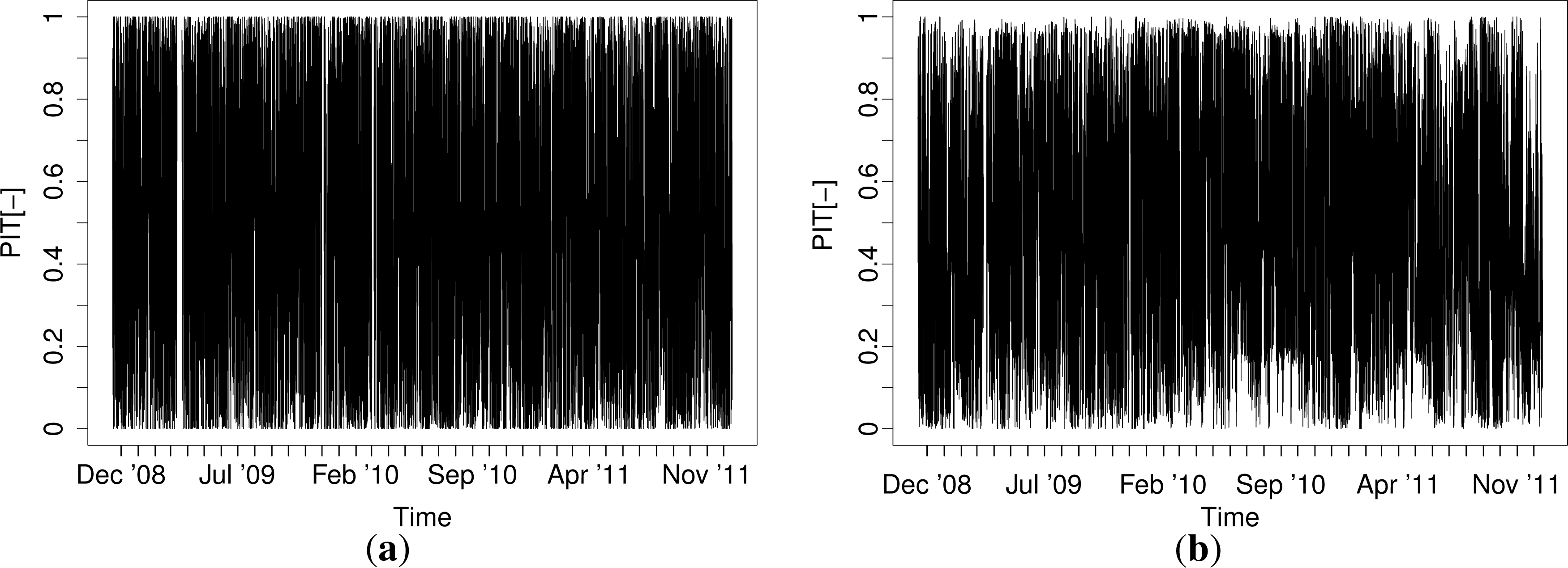
In [39], it was suggested that the autocorrelation of the probability integral transform (PIT) [40] should be accounted for in the estimation of consistency intervals for reliability diagrams. Using the predictive densities obtained by the models described here, the PIT of ɛt is found as:
Figure 8 shows the rank ACFs for the QR-E model. The non-negligible autocorrelation in the PIT needs to be accounted for when the reliability of the forecasts is evaluated. The ACFs for the other models look similar.
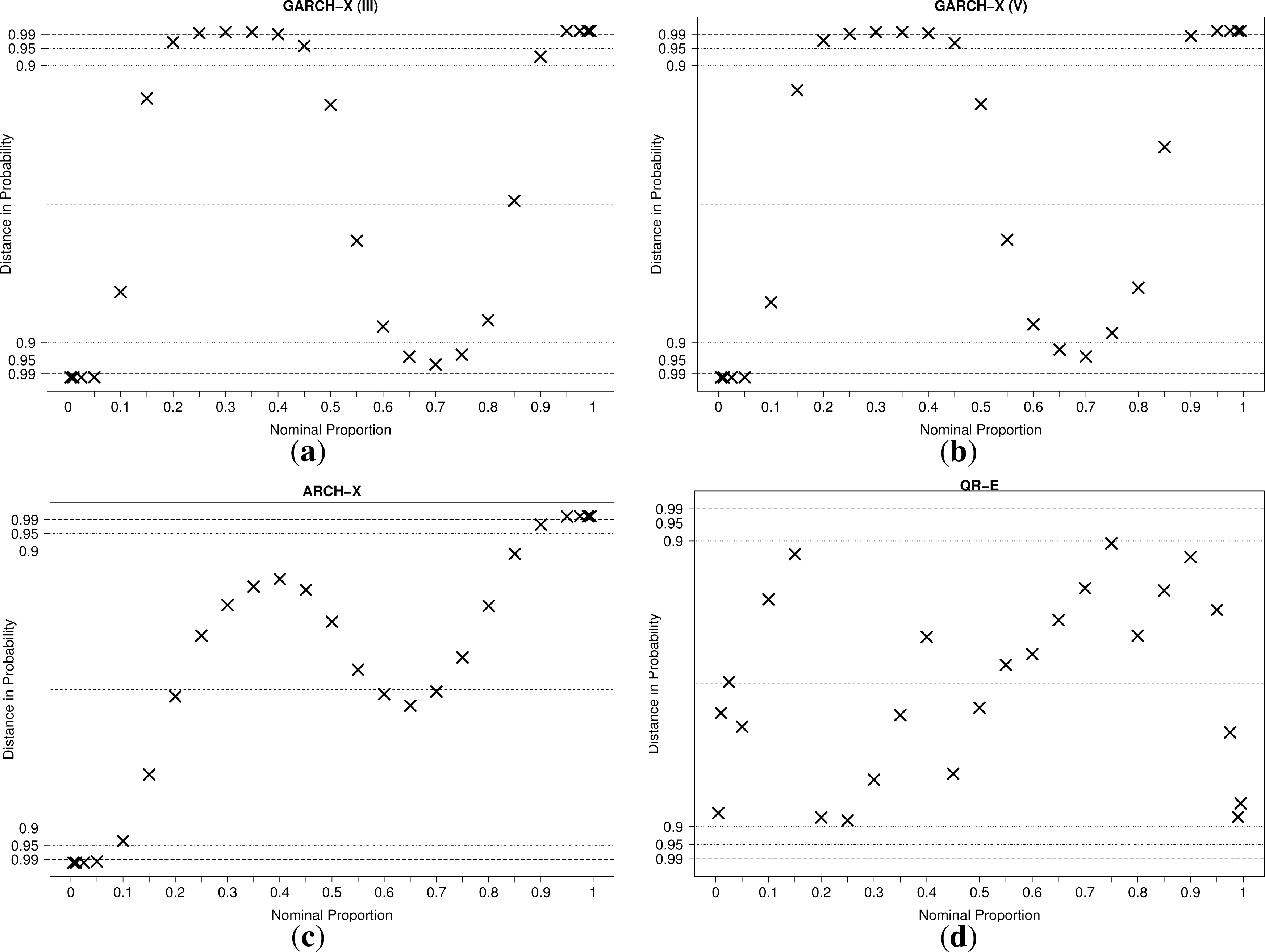
Therefore, the methodology presented in [39] for constructing consistency intervals for the reliability diagrams is adopted. Reliability diagrams, plotted on probability paper (see [38]), are shown for the four models in Figure 9.
For the QR-E model, the reliability hypothesis can not be rejected at the 10% significance level for all quantiles. For the ARCH-X model, however, the hypothesis is rejected for nine out of the 25 quantiles at the 5% significance level. Furthermore, going to the 1% significance level only reduces this number to eight. For the two GARCH models, the results are even worse. Thus, one must conclude that even though the two models score similarly in terms of CRPSS, the Gaussian models fail to produce reliable probabilistic forecasts. The reliability diagrams are a clear testimony of the shortcomings of the Gaussian assumption. The assumed shape of the density causes center quantiles to be generally overestimated, while the tail quantiles are underestimated. This indicates that ɛt has, in fact, a sharper density with higher kurtosis than a standard normal distribution, even conditionally. If aiming to produce parametric probabilistic forecasts of day-ahead prices that would be better calibrated, better assumptions on the shape of predictive densities should be formulated. This was not done here, since we are aiming to further analyze the quality and properties of the semi-parametric approach based on the QR-E model.
4.4. Properties of the QR-E Model
Based on the previous results, we aim here at going into a further level of detail in analyzing the characteristics of the forecasts issued based on the QR-E model, e.g., based on various price levels or on the time of the day.
Firstly, Table 4 lists the CRPSS for the QR-E forecasts and the for both that model and the climatology one within each estimation bin for of the training and the test set. That is, the quantile forecasts have been segmented by the first and the third sample quartiles and the CRPSS estimated for each bin.
As one would expect from any advanced forecasting approach, the QR-E model consistently outperforms the climatology benchmark regardless of the expected price (CRPSS > 0). Besides, the superiority of the QR-E model is greater in situations where the prices are expected to be high or low. The fact that the difference in between the intermediate bin and the bins outside the inter-quartile range is at least 70% larger for the benchmark model than for the QR-E model is a testimony of this. These results are not surprising, since a static reference model is generally expected to give the best result under ordinary circumstances at the cost of less frequent events. Thus, greater improvements should be expected for above and below average by using a more elaborate model.
The varying performance of the QR-E model in the outer bins is partly due to their varying update frequency between the two periods. During the training period, the average spot price is lower than during the test period. The segmentation, on the other hand, is done according to the empirical quantiles of the whole data set. Thus, the bin containing the high expected prices is updated less frequently than the low price bin during the training period. On the contrary, the low price bin represents expected prices further from the mean during the test period than during the training period. This prompts the question of whether time-varying bin edges would be appropriate. No effort for obtaining such a model was made, though.
Figure 10 depicts the CRPSS and the for each hour of the day, which in this case, is also for each lead-time. Again, the instability of the CRPSS seems to be mainly driven by the varying skill of the climatology quantiles. In the context of [28], it is interesting to see the peak (poorest performance) of the climatology model in the early evening hours. These were observed in the forecast quality of the model presented in [28], and since the CRPS is closely related to the mean absolute error (MAE) for point forecasts, the appearance of these is natural for the climatology model. Interestingly, however, this peak is by far less severe in the curves representing the QR-E model.
It was shown in [28] that this poor performance during these hours was due to more volatile prices. Thus, it is pleasant to see that the combination of the model from [28] and the QR-E model is able to capture this increased volatility to some extent.
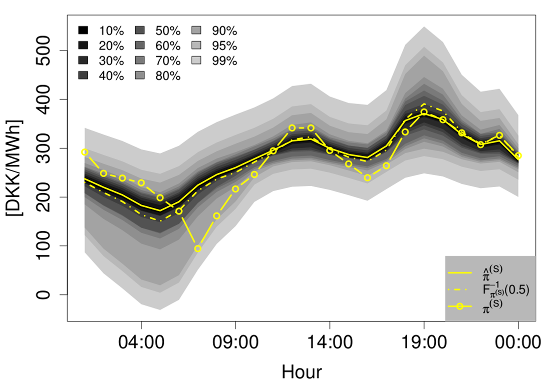
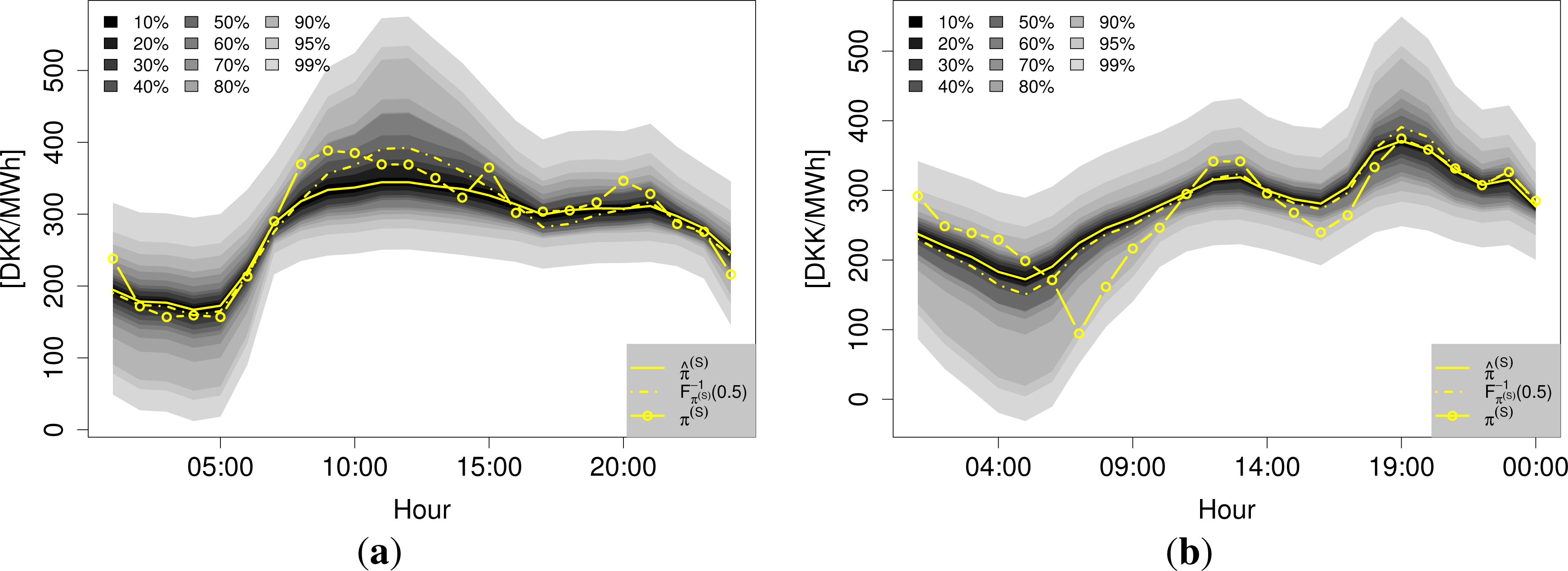
Two examples of the density forecasts from the QR-E model are shown in Figure 11. They illustrate well how the density of varies with the expected price.
5. Concluding Remarks and Discussion
A model able to generate reliable density forecasts for the day-ahead electricity prices at Nord Pool’s Elspot has been presented. Time-adaptive quantile regression is used to describe the density between the 5% and the 95% quantiles. The distribution tails are then approximated with an exponential function. The proposed methodology is shown to consistently outperform four different benchmark approaches for every hour of the day and regardless of the level of the prices. Compared to the parametric Gaussian models also presented in this paper, the QR-E model has the advantage that it produces reliable quantile forecasts.
The density model is built as an independent extension of the point forecasts presented in [28], which simplifies the modeling process considerably. The expected price could, however, be obtained by any other well-tuned model serving the same purpose. Unlike the majority of procedures in the existing literature, the modeling is done on untransformed data, allowing for directly deriving density forecasts on the actual scale of the prices. Furthermore, as the results presented in this paper are derived by mimicking practical data availability, the model can be applied as presented for online density forecasting of the prices.
The type of forecasts here presented are valuable for various applications. For one, the model’s predictions can be used directly for determining the optimal structure of block bids ([31], see for the definition) in markets where such bids are accepted. Secondly, the model can be used for generating the scenarios necessary to solve the decision problems described in [1–5]. In the scenario generation process, the auto-correlation of the PIT needs to be accounted for, e.g., by applying the scenario generation framework from [6]. The sequential clearing of many liberalized electricity markets, e.g., the Scandinavian and the Spanish ones, makes density forecasts of the day-ahead prices vital for any generation of market scenarios, even though the day-ahead prices themselves are not explicitly required in the scenarios. This is since other market variables are either strongly influenced or even directly dependent upon the day-ahead prices. Accounting for the whole range of potential outcomes on the day-ahead market is vital for obtaining a set of scenarios spanning the whole density of possible realizations on other markets.
Our probabilistic forecasting methodology could be improved in many different ways. First of all, from Figure 7, a relatively slow drift in the realized PIT can be detected. For a time-varying process like electricity prices, such effects will never be fully prevented; although, it would be interesting to see whether an auto-regressive or a moving average term could mitigate this behavior of the PIT. This could either be done in the quantile autoregression framework discussed in Koenker [25] (Section 8.3, pp. 260–265) or as an exponential smoothing model like the one described in Taylor [41] (and the references therein). Secondly, an alternative definition of the bin edges, e.g., in terms of sample quantiles over a given period, could be interesting to pursue. Thirdly, even though the parametric models yielded unreliable forecasts, there are several extensions to the models that might successfully mitigate that problem. For instance, some of a mixture model might help in this regard. The mixture model could be either a discrete one, e.g., a Hidden Markov model, or a continuous latent model could be applied. Another interesting possibility would be a double stochastic (G)ARCH-X model [35]. This would serve the purpose of accommodating the shifts between periods of excessive volatility and periods of relative tranquility better than the exponential smoothing does. Furthermore, other parametric distributions could be considered (e.g., generalized Gaussian and Student’s t). For such models, one should bear in mind that some form of adaptivity in the parameter estimation would be of core importance.
Finally, given a larger data set, revisiting the exponential tail models would be worthwhile. For one, even though the center part of the density of ɛt does not exhibit any apparent diurnal variation, it seems plausible that the tail quantiles would do so due to the higher demand during the day. For the data set at hand, however, hourly estimation dilutes the data set so severely that the estimation of a seasonal model for the tail would be meaningless. A larger data set would also allow for investigation of whether a limited memory is appropriate for estimation of the tail.
Acknowledgments
Pierre Pinson is partly supported by the Danish Council for Strategic Research through the project “5s—Future Electricity Markets”, No. 12-132636/DSF. Three reviewers are acknowledged for their comments and suggestions on an earlier version of this manuscript.
Author Contributions
Henrik Madsen is the head of the group at the Technical University of Denmark, where a part of the research and empirical investigation was carried out. Henrik Aalborg Nielsen is a principal scientist at ENFOR A/S, a company that also contributed to the work by providing data, background knowledge and feedback on the proposal development. Tryggvi Jónsson is the lead contributor, both in terms of the modeling and forecasting proposals, empirical investigation and writing of the paper. This was done in direct collaboration with Pierre Pinson, his supervisor at the Technical University of Denmark, who contributed to all aspects of this work.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Morales, J.M.; Conejo, A.J.; Pérez-Ruiz, J. Short-term trading for a wind power producer. IEEE Trans. Power Syst 2010, 25, 554–564. [Google Scholar]
- Jónsson, T. Mean-CVaR Bidding Strategy for Both Price Taking and Price Making Wind Power Producer, Technical Report. Technical University of Denmark, Department of Informatics and Mathematical Modelling, Kgs. Lyngby, Denmark. 2011.
- Fleten, S.-E.; Kristoffersen, T.K. Short-term hydropower production planning by stochastic programming. Comput. Oper. Res 2008, 35, 2656–2671. [Google Scholar]
- Fleten, S.-E.; Kristoffersen, T.K. Stochastic programming for optimizing bidding strategies of a Nordic hydropower producer. Eur. J. Oper. Res 2007, 181, 916–928. [Google Scholar]
- Heredia, F.-J.; Rider, M.J.; Corchero, C. Optimal bidding strategies for thermal and generic programming units in the day-ahead electricity market. IEEE Trans. Power Syst 2010, 25, 1504–1518. [Google Scholar]
- Pinson, P.; Papaefthymiou, G.; Klockl, B.; Nielsen, H.A.; Madsen, H. From probabilistic forecasts to statistical scenarios of short-term wind power production. Wind Energy 2009, 12, 51–62. [Google Scholar]
- Boogert, A.; Dupont, D. On the effectiveness of the anti-gaming policy between the day-ahead and real-time electricity markets in the Netherlands. Energy Econ 2005, 27, 752–770. [Google Scholar]
- Sewalt, M.; de Jong, C. Negative prices in electricity markets. Commodities Now. Available online: http://www.erasmusenergy.com/articles/91/1/Negative-prices-in-electricity-markets/Page1.html (accessed on 20 August 2014).
- Taylor, J.W.; McSharry, P.E. Short-term load forecasting methods: An evaluation based on european data. IEEE Trans. Power Syst 2007, 22, 2213–2219. [Google Scholar]
- Karakatsani, N.V.; Bunn, D.W. Forecasting electricity prices: The impact of fundamentals and time-varying coefficients. Int. J. Forecast 2008, 24, 764–785. [Google Scholar]
- Panagiotelis, A.; Smith, M. Bayesian density forecasting of intraday electricity prices using multivariate skew t distributions. Int. J. Forecast 2008, 24, 710–727. [Google Scholar]
- Conejo, A.J.; Contreras, J.; Espínola, R.; Plazas, M.A. Forecasting electricity prices for a day-ahead pool-based electric energy market. Int. J. Forecast 2005, 21, 435–462. [Google Scholar]
- Jónsson, T.; Pinson, P.; Madsen, H. On the market impact of wind energy forecasts. Energy Econ 2010, 32, 313–320. [Google Scholar]
- Diongue, A.K.; Guegan, D.; Vignal, B. Forecasting electricity spot market prices with a k-factor GIGARCH process. Appl. Energy 2009, 86, 505–510. [Google Scholar]
- García-Martos, C.; Rodríguez, J.; Sánchez, M.J. Forecasting electricity prices and their volatility using unobserved components. Energy Econ 2011, 33, 1227–1239. [Google Scholar]
- Higgs, H. Modelling price and volatility inter-relationships in the Australian wholesale spot electricity markets. Energy Econ 2009, 31, 748–756. [Google Scholar]
- Chan, K.F.; Gray, P.; van Campen, B. A new approach to characterizing and forecasting electricity price volatility. Int. J. Forecast 2008, 24, 728–743. [Google Scholar]
- Haugom, E.; Westgaard, S.; Solibakke, P.B.; Lien, G. Realized volatility and the influence of market measures on predictability: Analysis of Nord Pool forward electricity data. Energy Econ 2011, 33, 1206–1215. [Google Scholar]
- Deng, S.-J.; Jiang, W. Modelling Prices in Competitive Electricty Markets. Ch. 7—Quantile-Based Probabilistic Models for Electricity Prices; John Wiley & Sons: Hoboken, NJ, USA, 2004; pp. 161–176. [Google Scholar]
- Serinaldi, F. Distributional modeling and short-term forecasting of electricity prices by generalized additive models for location, scale and shape. Energy Econ 2011, 33, 1216–1226. [Google Scholar]
- Maciejowska, K.; Nowotarski, J.; Weron, R. Probabilistic Forecasting of Electricity Spot Prices Using Factor Quantile Regression Averaging. Avalaible online: http://prac.im.pwr.wroc.pl/~hugo/RePEc/wuu/wpaper/HSC_14_09.pdf (accessed on 20 August 2014).
- Nowotarski, J.; Weron, R. Computing Electricity Spot Price Prediction Intervals Using Quantile Regression and Forecast Averaging. Avalaible online: http://prac.im.pwr.wroc.pl/~hugo/RePEc/wuu/wpaper/HSC_13_12.pdf (accessed on 20 August 2014).
- Engle, R.F. Autoregressive conditional heteroscedasticity with estimates of the variance of United Kingdom inflation. Econometrica 1982, 50, 987–1007. [Google Scholar]
- Bollerslev, T. Generalized autoregressive conditional heteroskedasticity. J. Econ 1986, 31, 307–327. [Google Scholar]
- Koenker, R. Quantile Regression; Cambridge University Press: New York, NY, USA, 2005. [Google Scholar]
- Koenker, R.; Basset, G. Regression quantiles. Econometrica 1978, 46, 33–50. [Google Scholar]
- Møller, J.K.; Nielsen, H.A.; Madsen, H. Time-adaptive quantile regression. Comput. Statist. Data Anal 2008, 51, 1292–1303. [Google Scholar]
- Jónsson, T.; Pinson, P.; Nielsen, H.A.; Madsen, H.; Nielsen, T.S. Forecasting electricity spot prices accounting for wind power predictions. IEEE Trans. Sustain. Energy 2013, 4, 210–218. [Google Scholar]
- Matheson, J.E.; Winkler, R.L. Scoring rules for continuous probability distributions. Manag. Sci 1976, 22, 1087–1095. [Google Scholar]
- Gneiting, T.; Raftery, A.E. Strictly proper scoring rules, prediction and estimation. J. Am. Statist. Assoc 2007, 102, 369–378. [Google Scholar]
- Nord Pool Spot AS, The Power Market. Avaliable online: http://www.nordpoolspot.com/How-does-it-work/ (accessed on 15 August 2011).
- Nord Pool. Avaliable online: http://www.nordpoolspot.com (accessed on 20 August 2014).
- Nielsen, T.S.; Nielsen, H.A.; Madsen, H. Prediction of wind power using time-varying coefficient functions. In Proceedings of the 15th IFAC World Congress, Barcelona, Spain, 21–26 July 2002.
- Sheather, S.J.; Jones, M.C. A reliable data-based bandwidth selection method for kernel density estimation. J. R. Statist. Soc. Ser. B 1991, 53, 683–690. [Google Scholar]
- Madsen, H. Time Series Analysis; Chapman & Hall/CRC: London, UK, 2008. [Google Scholar]
- Gneiting, T.; Ranjan, R. Comparing density forecasts using threshold and quantile weighted prober scoring rules. J. Bus. Econ. Stat 2011, 29, 411–422. [Google Scholar]
- Chatfield, C. Time Series Forecasting; Chapman & Hall/CRC: London, UK, 2000. [Google Scholar]
- Bröcker, J.; Smith, L.A. Increasing the reliability of reliability diagrams. Weather Forecast 2007, 22, 651–661. [Google Scholar]
- Pinson, P.; McSharry, P.; Madsen, H. Reliability diagrams for nonparametric density forecasts of continuous variables: Accounting for serial correlation. Q. J. R. Meteorol. Soc. Soc. Ser. B Stat. Methodol 2010, 136, 77–90. [Google Scholar]
- Gneiting, T.; Balabdaoui, F.; Raftery, A.E. Probabilistic forecasts, calibration and sharpness. J. R. Statis 2007, 69, 243–268. [Google Scholar]
- Taylor, J.W. Using exponentially weighted quantile regression to estimate value at risk and expected shortfall. J. Financ. Econ 2008, 6, 382–406. [Google Scholar]


| Model | Parameters | Training Period | Test Period | |||
|---|---|---|---|---|---|---|
| τ ∈ τ1 | τ ∈ τ2 | τ ∈ τ1 | τ ∈ τ2 | |||
| Benchmark | I | — | 50.76 | 48.62 | 56.64 | 54.52 |
| II | — | 51.97 | 49.82 | 56.50 | 54.37 | |
| III | α = 0.0119 | 48.96 | 47.03 | 47.53 | 45.41 | |
| IV | Nest = 168 | 46.17 | 44.32 | 42.26 | 40.04 | |
| Gaussian | III | λ = 0.9954 | 23.50 | 21.39 | 25.35 | 23.24 |
| V | λ = 0.9956 | 23.43 | 21.33 | 25.28 | 23.16 | |
| VI | λ = 0.9039 | 23.18 | 21.08 | 25.07 | 22.97 | |
| QR-E | I | See Table 2 | 22.71 | 21.26 | 25.18 | 23.06 |
| τ | NB | τ | NB | τ | NB | τ | NB | τ | NB |
|---|---|---|---|---|---|---|---|---|---|
| 0.05 | 1,710 | 0.25 | 210 | 0.45 | 810 | 0.65 | 790 | 0.85 | 550 |
| 0.10 | 1,790 | 0.30 | 230 | 0.50 | 760 | 0.70 | 820 | 0.90 | 1,090 |
| 0.15 | 2,000 | 0.35 | 210 | 0.55 | 800 | 0.75 | 840 | 0.95 | 1,280 |
| 0.20 | 200 | 0.40 | 300 | 0.60 | 740 | 0.80 | 550 | ||
| Knots: | ∈ {−158.85, 240.25, 275.61, 311.64, 675.07} | ||||||||
| Bin Edges: | ∈ {−∞, 240.25, 311.64, ∞} | ||||||||
| Period: | Qclim | Exp (λ̂) | ||
|---|---|---|---|---|
| Lower Tail | Upper Tail | Lower Tail | Upper Tail | |
| Training | 22.93 | 27.65 | 22.93 | 27.59 |
| Test | 22.51 | 12.15 | 22.09 | 12.90 |
| Range | CRPSS | |||||
|---|---|---|---|---|---|---|
| QR-E | Qclim | QR-E vs. Qclim | ||||
| Training | Test | Training | Test | Training | Test | |
| −295.43 ≤ ≤ 266.87 | 21.48 | 36.63 | 51.03 | 67.20 | 0.5790 | 0.4549 |
| 266.87 ≤ ≤ 381.27 | 18.07 | 19.97 | 27.74 | 35.08 | 0.3487 | 0.4307 |
| 381.27 ≤ ≤ 867.74 | 47.89 | 24.23 | 76.61 | 90.93 | 0.3749 | 0.7335 |
© 2014 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Jónsson, T.; Pinson, P.; Madsen, H.; Nielsen, H.A. Predictive Densities for Day-Ahead Electricity Prices Using Time-Adaptive Quantile Regression. Energies 2014, 7, 5523-5547. https://doi.org/10.3390/en7095523
Jónsson T, Pinson P, Madsen H, Nielsen HA. Predictive Densities for Day-Ahead Electricity Prices Using Time-Adaptive Quantile Regression. Energies. 2014; 7(9):5523-5547. https://doi.org/10.3390/en7095523
Chicago/Turabian StyleJónsson, Tryggvi, Pierre Pinson, Henrik Madsen, and Henrik Aalborg Nielsen. 2014. "Predictive Densities for Day-Ahead Electricity Prices Using Time-Adaptive Quantile Regression" Energies 7, no. 9: 5523-5547. https://doi.org/10.3390/en7095523
APA StyleJónsson, T., Pinson, P., Madsen, H., & Nielsen, H. A. (2014). Predictive Densities for Day-Ahead Electricity Prices Using Time-Adaptive Quantile Regression. Energies, 7(9), 5523-5547. https://doi.org/10.3390/en7095523