1. Introduction
The use of zeotropic mixtures in Organic Rankine Cycle (ORC) applications has been widely investigated during the last years. The focus of this research is mainly on low temperature applications like geothermal systems [
1,
2,
3,
4]. In these cases an efficiency increase of up to 20% is possible by using mixtures compared to the most efficient pure component due to a better glide matching during condensation and evaporation caused by non-isothermal phase change of zeotropic mixtures. Recent investigations also figure the combination of zeotropic mixtures and a transcritical mode of operation due to a better matching of temperature profiles [
5,
6]. Next to the non-isothermal phase change during condensation resulting from the use of zeotropic mixtures, the evaporation phase change also occurs non-isothermally, due to the supercritical mode of operation. This results in an increase in second law efficiency of up to 60% [
5]. Beside geothermal power generation, the benefit of using zeotropic mixtures is also investigated for other specific applications, like for example in the field of heat recovery from engines [
7,
8]. Furthermore, the first studies that focus on zeotropic mixtures for high temperature ORC have been published. Along with Angelino and Colonna [
9,
10], who investigated multi-component mixtures of linear siloxanes, Dong
et al. [
11] show results of the performance of hexamethyldisiloxane (MM)/octamethyltrisiloxane (MDM)-mixtures at a heat source temperature of 280 °C. Compared to low temperature applications, the efficiency increase achieved with mixtures in high temperature ORCs is less. Chys
et al. [
12] describe a benefit of nearly 16% for a heat source temperature of 150 °C, whereas at 250 °C the increase is less than 6%.
Next to this advantage of zeotropic mixtures with respect to cycle efficiency, there is also an inherent drawback of using them in ORC-applications caused by their generally reduced heat transfer characteristics compared to pure fluids [
13,
14]. This fact is often neglected when analysing mixtures in ORC-systems, but regarding sizing of heat exchangers the knowledge of this degradation in heat transfer coefficient is important. Looking at common refrigerants, measurements of heat transfer coefficients of those as well as their mixtures are already available in literature as their long-serving use in refrigeration-systems has driven this research [
15,
16,
17,
18,
19,
20]. However, in case of siloxane mixtures as well as pure siloxanes up to now there has been a lack of data.
The present study shows a thermodynamic analysis of a high temperature ORC using the linear siloxanes hexamethyldisiloxane (MM) and octamethyltrisiloxane (MDM) as well as their mixtures. Moreover, the results of measurements of heat transfer coefficients of these fluids and their mixtures in steps of 20 wt % MM are presented. Kandlikar’s correlation is adapted to the experimental values and is then used for calculating the required heat exchanger area for preheating and evaporation.
2. Thermodynamic Process Analysis
In this study the recovery of waste heat from biogas plants is chosen exemplarily as one application of the ORC. The specifications of the exhaust gas from the biogas-engine (MAN E 2842 LE 322, MAN Truck & Bus AG, Nuremberg, Germany) of the selected biogas plant are summarized in
Table 1.
Table 1.
Parameters of heat source (EG).
Table 1.
Parameters of heat source (EG).
| TEG-IN (K) | ṁEG (kg/s) | pEG (bar) | Composition (mol %) |
|---|
| 733.15 | 0.48 | 1 | N2 | H2O | CO2 | O2 | Ar |
| 64.55 | 18.15 | 9.74 | 6.63 | 0.93 |
Siloxanes were chosen as a working fluid due to their good performance in high temperature applications [
9,
21,
22]. In particular, the two linear siloxanes hexamethyldisiloxane (MM) and octamethyltrisiloxane (MDM) as well as their mixtures are investigated. First degradation measurements of MM show its thermal stability up to a temperature of 300 °C [
23]. Therefore, with regard to the high heat source temperature, an additional intermediate circuit is considered in the simulations in order to prevent the working fluid from decomposition. Dowtherm G is chosen as thermal oil due to its high thermal stability [
24].
2.1. Methodology
Simulations have been performed using the simulation tool Aspen Plus [
25]. As property method the PENG-ROB (Peng-Robinson equation of state) model is used for the exhaust gas, air, and Dowtherm G as well as the ORC-fluid. In the case of water, STEAM-NBS (NBS/NRC Steam Tables) is applied [
26].
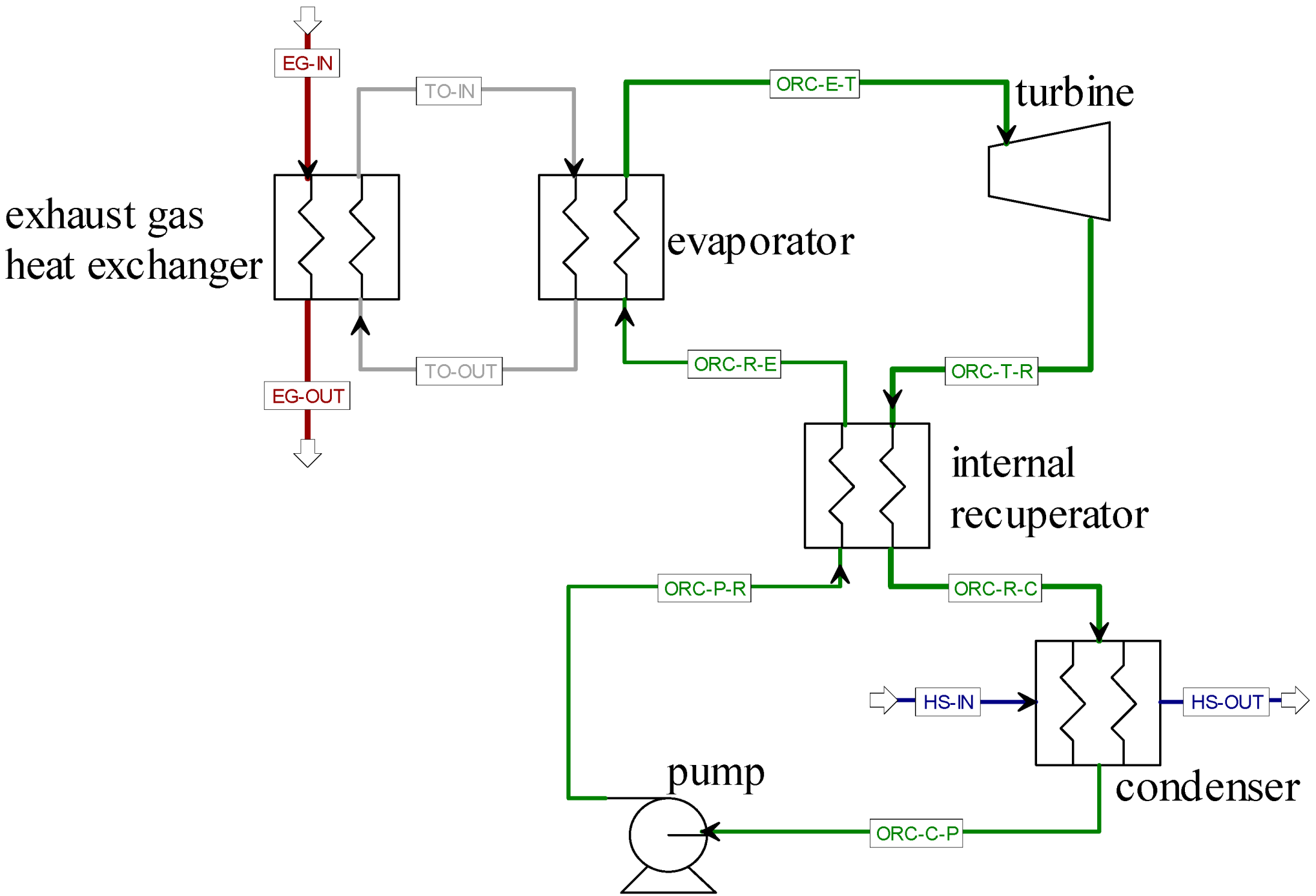
Figure 1 shows the flowsheet of the process. It consists of the ORC, in which an internal recuperator is applied for the purpose of efficiency improvement, and the additional thermal oil loop. All heat exchangers are operating in counter flow mode and pressure drops are neglected.
Figure 1.
Aspen Plus flowsheet.
Figure 1.
Aspen Plus flowsheet.
For the heat sink, two different scenarios are analysed. The first one represents pure electricity generation out of waste heat assuming direct air cooled condensation, whereas the second one considers an additional use of the condenser duty in a heating network using water.
Table 2 lists the general parameters of the heat sink for those two cases.
Table 2.
Heat sink (HS) parameters.
Table 2.
Heat sink (HS) parameters.
| Case | Fluid | THS-IN (K) | THS-OUT (K) | ṁHS (kg/s) | pHS (bar) |
|---|
| heat sink (electricity) | air | 288.15 | 303.15 | variable | 1 |
| heat sink (CHP) | water | 323.15 | 343.15 | variable | 2 |
As boundary conditions, the pinch point differences in the heat exchangers are kept constant (
Table 3). Only the pinch point differences in the condenser and internal recuperator can reach values higher than those given in
Table 3. In the condenser this occurs due to the limitation of the lower working pressure to a minimum value of 0.1 bar. Regarding fluid mixtures, partial condensation can take place in the internal recuperator. If this occurs, the boundary condition is switched. Instead of the fixed pinch point temperature difference a vapour fraction of one is set for the hot outlet stream of the recuperator (ORC-R-C). As a result, pinch point differences can reach higher values. Due to the heat source parameters, the investigated systems are small-scale ORCs with an electrical power output in the kilowatt range. Therefore, the isentropic efficiency of the turbine is set to the relatively small value of 60%.
Table 3.
Boundary conditions.
Table 3.
Boundary conditions.
| PPEG heat exchanger (K) | PPevaporator (K) | PPcondenser (K) (min) | PPinternal recuoerator (K) (min) | ηturbine (%) | ηgenerator (%) | ηpump (%) | ηdriver (%) |
|---|
| 20 | 30 | 10 | 10 | 60 | 90 | 70 | 90 |
To compare the simulation results of the different fluids, the exergetic efficiency is chosen as a criterion. For pure generation of electric energy, the exergetic efficiency is defined by the net power
Pnet (power of turbine
Pel,turb minus power of pump
Ppump) divided by the exergy of heat source
ĖEG:
For calculating
ĖEG, mass flow rate
ṁEG, enthalpy
hEG,in as well as entropy of heat source
sEG,in are used. The index 0 corresponds to the reference state (288.15 K, 1 bar). In the case of combined heat and power generation the exergy content of the condenser duty
Ėcond has to be taken into account:
It is calculated by using inlet and outlet enthalpies (hHS,in/out) and entropies (sHS,in/out) of the cooling water as well as its mass flow rate ṁHS.
For evaluating the performance during evaporation and condensation, the irreversibilities of the evaporator and condenser are calculated by using respective inlet and outlet enthalpies and entropies:
The logarithmic mean temperatures are defined as follows:
In case of the condenser Tin and Tout describe the inlet and outlet temperatures of the heat sink. For the irreversibilities of the evaporator the temperatures of Dowtherm G have to be used.
2.2. Results of Process Simulation
Due to the available heat source, the applied ORC shows power outputs in the low power range (
Pnet < 30 kW). The results of the process simulation are displayed in
Figure 2. On the left hand side the exergetic efficiency against the mass fraction of MM in case of pure electricity generation is presented, whereas the results for the combined heat and power case are shown on the right hand side. Next to the efficiency, the corresponding upper working pressure, that yields the highest efficiency in each case, is added in the diagrams.
Figure 2.
Exergetic efficiencies and respective maximum working pressures against mass fraction of MM ((a): pure electricity generation, (b): combined heat and power generation).
Figure 2.
Exergetic efficiencies and respective maximum working pressures against mass fraction of MM ((a): pure electricity generation, (b): combined heat and power generation).
Regarding the case of pure electricity generation and using steps of mass fraction of MM of 10%, it seems that there is a nearly linear behaviour of exergetic efficiency with respect to mass fraction of MM. A closer look reveals that at high mass fractions of MM there might be a deviation from this trend. Therefore, additional steps of 95%, 97% and 98% MM are added and an efficiency increase of nearly 1.3% compared to the most efficient pure component, MM, occurs for 97% MM. A similar effect between mass fractions of 10% and 20% occur, but efficiencies do not exceed that of MM.
A quite different trend with respect to mass fraction of MM can be seen for the combined heat and power production. Compared to the pure fluid with the best exergetic efficiency (MM: η
ex = 31.73%) an efficiency increase of 2.9% is possible when using mixtures (60 wt % MM: η
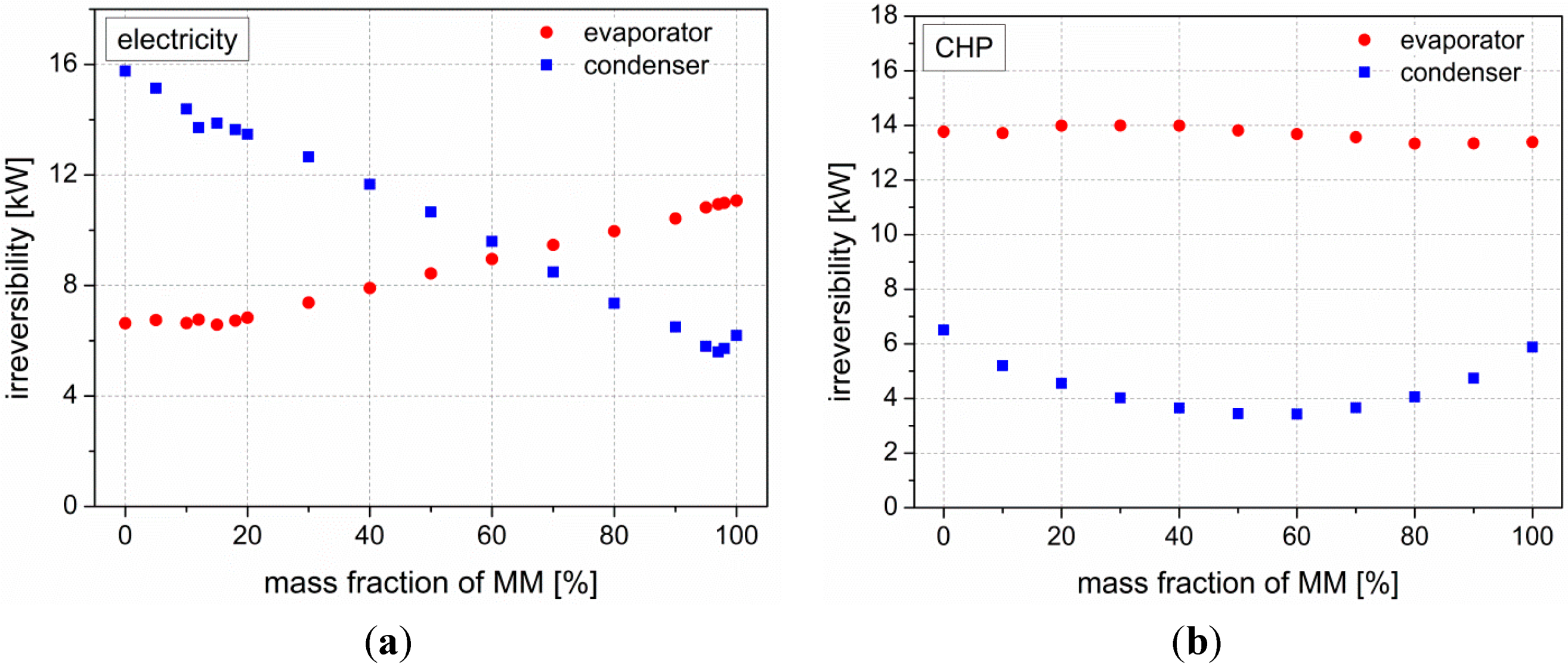
ex = 32.65%). Next to this improved cycle efficiency, lower working pressures are needed compared to pure MM. As shown in
Figure 3, this increase in second law efficiency derives from an irreversibility minimum in the condenser. Regarding the irreversibilities in the evaporator, smaller differences between the fluids can be observed. Therefore, they do not affect the overall cycle efficiency.
Figure 3.
Irreversibilities in evaporator and condenser in case of (a) pure electricity generation and (b) combined heat and power generation.
Figure 3.
Irreversibilities in evaporator and condenser in case of (a) pure electricity generation and (b) combined heat and power generation.
The reason for this behaviour can be revealed by regarding the temperature profiles during evaporation and condensation (
Figure 4). It can be seen that the temperature glide during evaporation is negligible compared to that during condensation. Therefore, as also published by other authors [
3], a good glide matching during condensation, which results in a lower average heat rejection temperature of the cycle, is decisive for cycle efficiency.
Figure 4b fairly shows the accordance in the slope of the temperature profile of heat sink and the most efficient mixture.
All in all, the results show that an increase in efficiency of nearly 1.3% (electricity) or 3% (CHP) is possible by using mixtures of MM and MDM, but, whether a use of mixtures is really advantageous or not depends, next to the pure thermodynamic performance, on several additional aspects. In this regard, the effect of an eventual composition shift on the cycle efficiency has to be considered. Moreover, the influence of mixtures on the performance of cycle components (e.g., the respective turbine efficiency) has to be evaluated. As heat transfer coefficients of mixtures are said to be lower than those of the pure components, it is crucial to investigate the required size of heat exchangers. In order to estimate this heat transfer area, proper correlations to describe the heat transfer characteristics are necessary. To identify them, measurements of heat transfer coefficients have to be conducted. The main parameter for a waste heat recovery system is the coupling with the heat source and, therefore, the evaporation process. Hence, this study focuses in a first step on evaporation heat transfer.
Figure 4.
Temperature profiles during (a) evaporation and (b) condensation for the pure fluids as well as for the most efficient mixture (60 wt % MM) in case of CHP.
Figure 4.
Temperature profiles during (a) evaporation and (b) condensation for the pure fluids as well as for the most efficient mixture (60 wt % MM) in case of CHP.
4. Estimation of Required Heat Exchanger Area
In order to reveal, whether the reduced heat transfer characteristics of fluid mixtures compensate their slight predominance in case of system efficiency, required heat exchange areas are investigated. For that purpose, a shell-and-tube heat exchanger with one shell pass and two tube passes is used as preheater and evaporator.
Table 4 lists the main specifications and assumptions.
Table 4.
Specifications and assumptions for the shell and tube heat exchanger.
Table 4.
Specifications and assumptions for the shell and tube heat exchanger.
| Geometry Data | Maximum Velocities (m/s) [30,31] |
|---|
| outer tube radius ra (mm) | wall thickness Δd (mm) | thermal conductivity λsteel (W/mK) | ORC liquid | ORC vapour | Dowtherm |
| 9.5 | 2.1 | 15 | 4 | 20 | 4 |
The general approach for calculating the heat exchanger area is derived from Roetzel and Spang [
32]. It is based on the Number of Transfer Units (NTU)-method. The NTU of the real shell and tube heat exchanger is obtained by applying a correction factor to the NTU of an ideal counterflow heat exchanger. For calculating the heat transfer coefficients at the inner and outer tube different models are applied. For Dowtherm G as well as for the ORC-fluid in the preheater, the correlation for turbulent flow by Gnielinski [
33] is chosen, whereas for the evaporation of the ORC-fluid Kandlikar’s correlation, as presented in
Section 3, is used. The whole calculation is performed in Matlab [
34]. Fluid properties are derived from REFPROP [
27].
The calculations of required heat transfer area are performed for the pure fluids as well as for one more efficient mixture for the case of pure electricity and combined heat and power generation, respectively.
Table 5 and
Table 6 list the respective process parameters that derived from the thermodynamic analysis in
Section 2. These values represent the input parameters of the heat exchanger calculations.
Table 5.
Process parameters for pure electric energy generation.
Table 5.
Process parameters for pure electric energy generation.
| Fluid | ṁTO (kg/s) | TTO-IN (K) | TTO-OUT (K) | ṁORC (kg/s) | TORC-R-E (K) | TORC-E-T (K) | pORC (bar) |
|---|
| MM | 0.35 | 645.94 | 449.68 | 0.50 | 419.68 | 511.59 | 17.23 |
| MDM | 0.35 | 645.41 | 502.74 | 0.51 | 472.74 | 541.93 | 10.30 |
| MM/MDM 95/05 | 0.35 | 646.32 | 452.51 | 0.50 | 422.51 | 513.32 | 16.92 |
Table 6.
Process parameters for combined heat and power generation.
Table 6.
Process parameters for combined heat and power generation.
| Fluid | ṁTO (kg/s) | TTO-IN (K) | TTO-OUT (K) | ṁORC (kg/s) | TORC-R-E (K) | TORC-E-T (K) | pORC (bar) |
|---|
| MM | 0.35 | 646.32 | 452.58 | 0.57 | 422.56 | 480.22 | 10.46 |
| MDM | 0.35 | 647.04 | 457.78 | 0.65 | 427.78 | 472.37 | 3.00 |
| MM/MDM 60/40 | 0.35 | 645.99 | 450.09 | 0.57 | 420.30 | 480.90 | 6.77 |
The results of the heat exchanger analysis are summarised in
Table 7 and
Table 8. In both cases MM requires the smallest heat transfer area. For pure electricity generation MDM shows the biggest heat exchanger areas. Regarding the evaporator (
EVAP), 19% more heat compared to MM has to be transferred, but the heat transfer coefficient of evaporation exceeds that of MM by 53%. Due to that, an additional aspect has to contribute to the increased heat transfer area of 56%.
Table 5 shows that mass flow rates of all three fluids are in the same range, but MDM shows the lowest pressure as well as temperature differences. Therefore, process parameters like temperatures and the respective fluid properties affect the required area just as well as pure heat transfer characteristics of fluids.
Table 7.
Results of heat exchanger calculations for the case of pure electric power generation.
Table 7.
Results of heat exchanger calculations for the case of pure electric power generation.
| Pure Electricity | Heat Exchange Area (m2) | Number of Tubes | Heat Transfer Coefficient (kW/m2·K) ORC/Dowtherm | Heat Duty (kW) |
|---|
| | PH | EVAP | PH | EVAP | PH | EVAP | PH | EVAP |
| MM | 0.725 | 0.120 | 2 | 2 | 5.761/7.202 | 26.414/8.343 | 113.35 | 30.725 |
| MDM | 0.741 | 0.187 | 2 | 2 | 5.141/7.450 | 40.502/8.256 | 86.901 | 36.500 |
| MM/MDM 95/05 | 0.728 | 0.125 | 2 | 2 | 5.699/7.201 | 32.575/8.336 | 111.6 | 32.135 |
Table 8.
Results of heat exchanger calculations for the case of combined heat and power generation.
Table 8.
Results of heat exchanger calculations for the case of combined heat and power generation.
| CHP | Heat Exchange Area (m2) | Number of Tubes | Heat Transfer Coefficient (kW/m2·K) ORC/Dowtherm | Heat Duty (kW) |
|---|
| | PH | EVAP | PH | EVAP | PH | EVAP | PH | EVAP |
| MM | 0.583 | 0.270 | 2 | 3 | 5.756/6.942 | 34.394/8.660 | 77.76 | 65.276 |
| MDM | 0.536 | 0.379 | 2 | 9 | 4.869/6.806 | 60.753/10.312 | 63.873 | 83.795 |
| MM/MDM 60/40 | 0.602 | 0.373 | 2 | 4 | 5.245/6.762 | 37.859/8.914 | 64.009 | 80.192 |
In case of the mixture the evaporator needs a 4.2% enlarged area compared to that of MM. Process parameters are quite similar. The heat transfer coefficient of the mixture lies 23.3% above that of MM, whereas a higher heat duty of 4.6% is transferred. Together with slightly reduced temperature differences a higher area is required. Regarding the whole process of heat input using the mixture, 0.9% higher heat transfer areas result compared to MM.
For the case of the combined heat and power generation similar trends occur. Regarding the evaporator, MDM requires a 40.4% higher area than MM. Heat transfer coefficient is 76.6%, heat duty 28.4% above the values of MM. A 14% higher mass flow rate as well as again lower pressure and temperature differences affect the required area, too. As the number of tubes is set according to the maximum velocity in the tubes, more tubes are required in the evaporator for MDM due to higher mass flow rates. As the system pressure in case of combined heat and power generation is lower than in the case of pure electricity generation, a higher part of the area is omitted to the evaporator due to increased heat of vaporisation.
The process parameters in case of the mixture again correspond more to those of MM. The heat duty in the evaporator exceeds that of MM by 22.9%. Heat transfer coefficients are 10.1% higher. An increase in heat transfer area of 38.15% is required. Again, compared to MM, slightly lower temperature differences and pressures are present. The total heat transfer area of preheater (PH) and evaporator exceeds that of MM by 14%.
Summing up it has to be stated that the pure heat transfer characteristics of fluids do not necessarily determine the size of the heat exchanger area. Process parameters play an even comparable role. For the investigated cases, the most efficient mixtures require an increase in heat transfer area for the heat input compared to the most efficient pure component of 0.9% and 14%, respectively. This corresponds to an increase in second law efficiency of 0.8% and 2.9%, respectively. As stated in the introduction, the potential of efficiency increase in high temperature ORC is low compared to low temperature applications. Heberle [
35] reports an efficiency increase of almost 16% for a geothermal application using mixtures of R245fa and R365mfc. But the required heat transfer area (evaporator + preheater) for the most efficient mixture composition exceeds that of the most efficient pure fluid by 83% [
35]. This effect is strongly influenced by the highly reduced heat transfer coefficients of R245fa/R365mfc-mixture compared to their pure components. Reductions compared to the pure fluids of up to nearly 50% are observed [
36], whereas for the here investigated siloxane mixtures maximum deviations from the pure component with the lowest heat transfer coefficient are −21.5%. Therefore, it can be concluded, that even though comparably low efficiency increases are possible in high temperature applications, the required additional heat transfer area for mixtures is reduced compared to low temperature systems.
As the present investigations use an additional thermal oil loop, liquid heat transfer coefficients of heat source and ORC-fluid are quite similar. Therefore, the heat transfer coefficient of the ORC-fluid during evaporation can have a strong effect on the required heat transfer area. Regarding applications with direct use of exhaust gas, this effect is diminished or even negligible due to the generally low heat transfer characteristics of the exhaust gas. In these cases, already slight increases in efficiency by using mixtures can justify their application.
Next to the evaporation process, it is necessary to investigate the heat transfer areas of internal heat exchanger and condenser as well. As during internal heat exchange no phase change occurs, degradation of heat transfer coefficients of mixtures are not expected and, therefore, there should be no additional increase in heat transfer area. In contrary, during condensation, reduced heat transfer coefficients in case of mixtures are obvious. Thus, the heat transfer area of the condenser has to be calculated, too. In case of directly air cooled processes, the effect of heat transfer degradation of mixtures is again negligible due to the worse heat transfer characteristics of air. But, regarding the case of combined heat and power generation, where water is used as a cooling medium, the effect of the lower heat transfer coefficients of mixtures can again result in larger heat exchange areas.
5. Conclusions
The performance of the two linear siloxanes MM and MDM as well as their mixtures in a high temperature ORC are analysed using the example of waste heat from biogas plant. In case of pure electricity generation only slight improvements (1.3%) in second law efficiency can be achieved by using a mixture of 97 wt % MM. An efficiency increase of nearly 3% is obtained for the combined heat and power generation with the mixture 60/40-wt % MM/MDM. As the potential of efficiency increase drops with rising heat source temperature, these results seem reasonable compared to those given in literature.
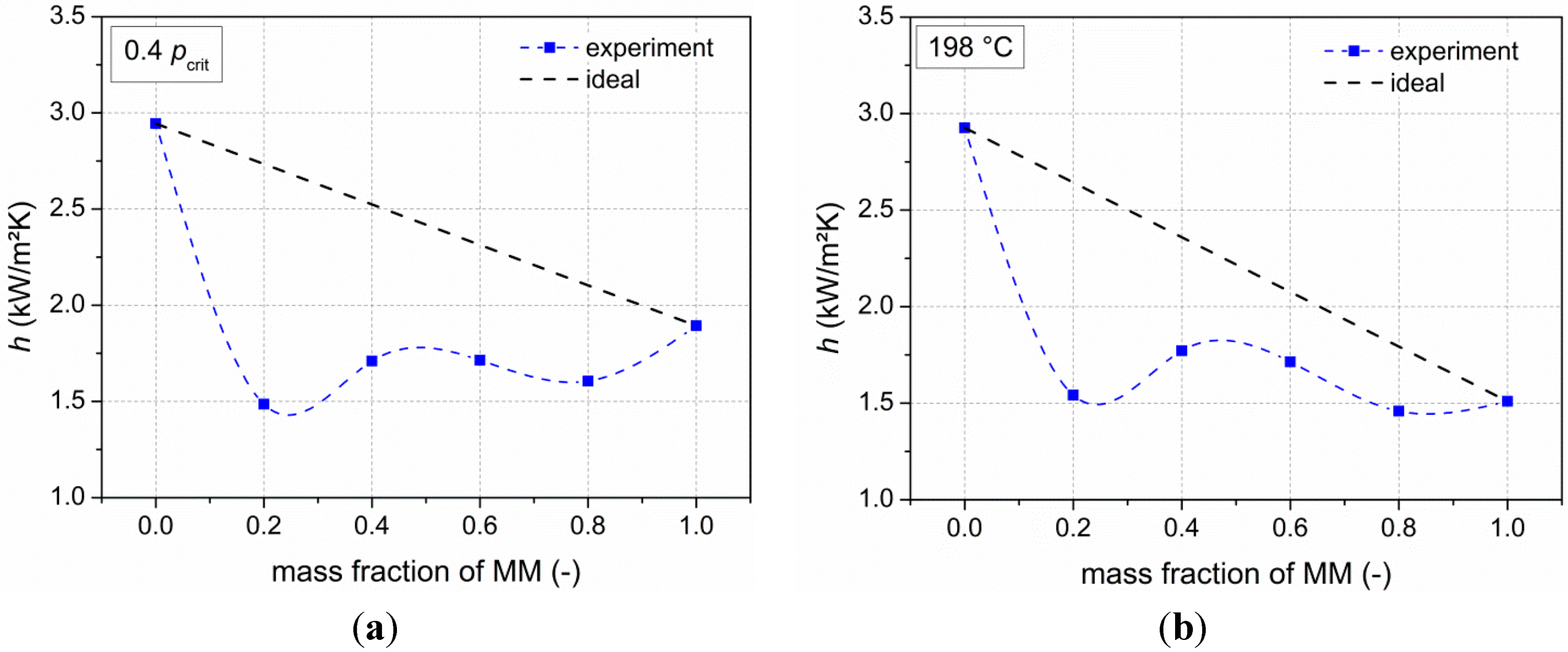
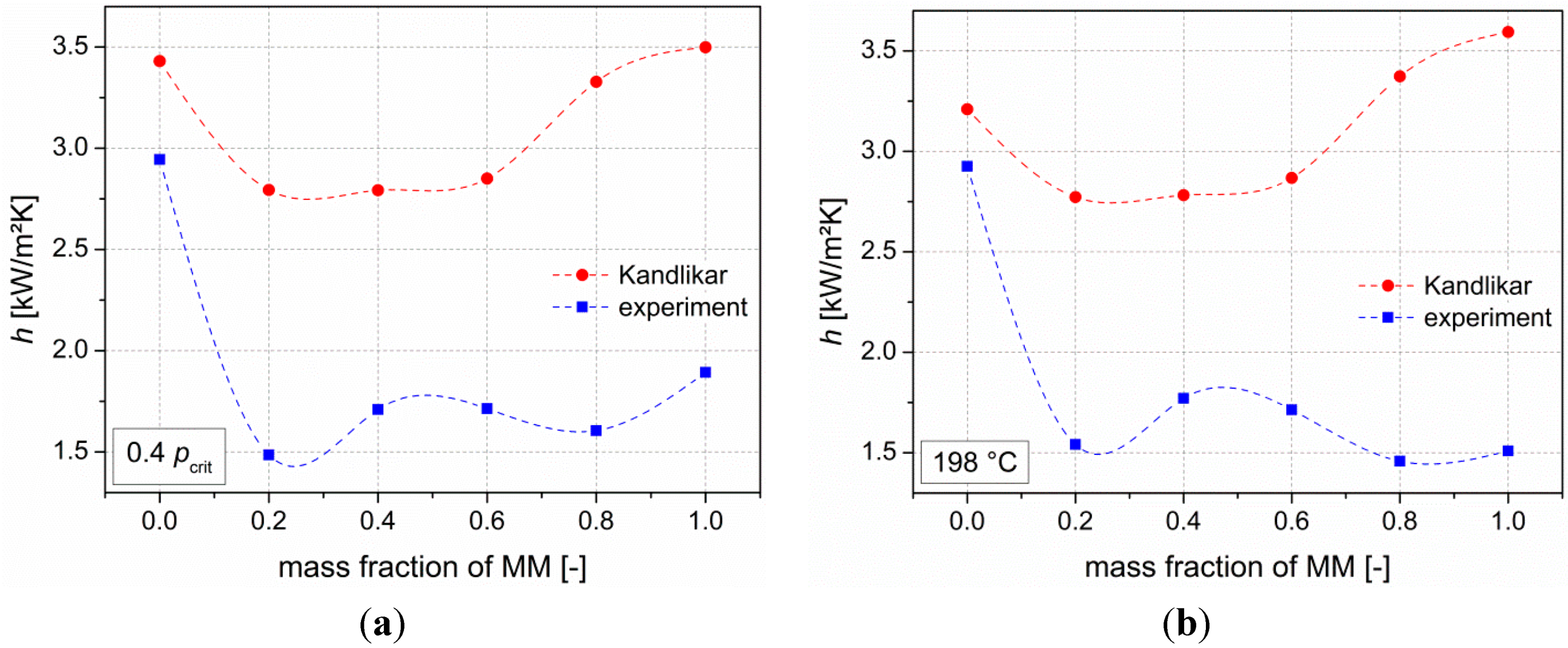
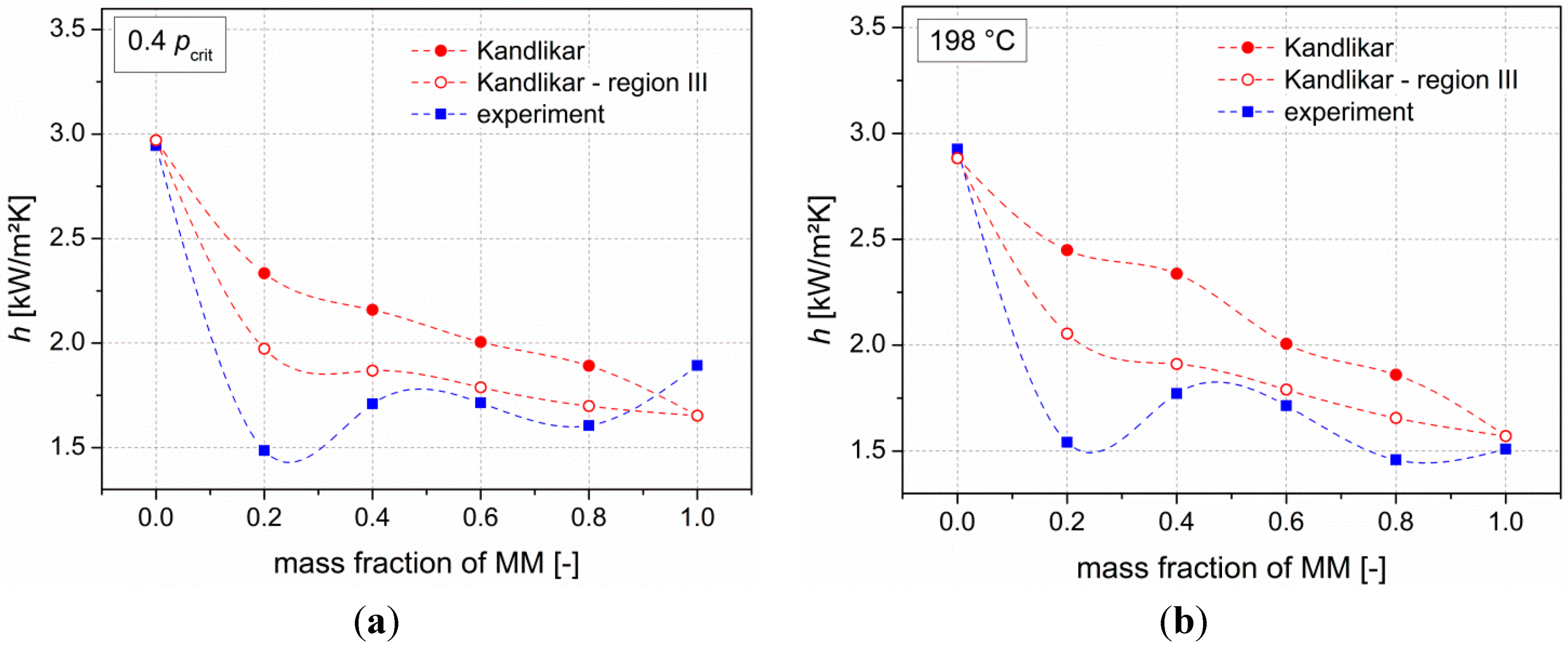
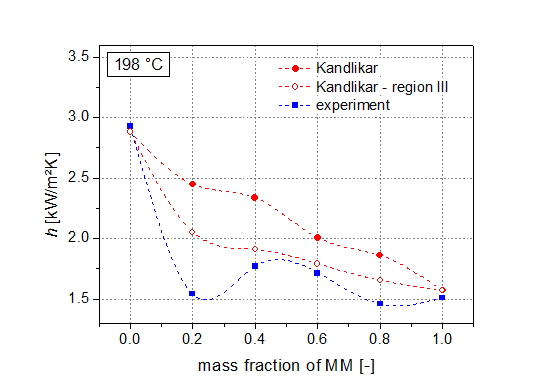
Next to the thermodynamic analysis, measurements of heat transfer coefficients of the pure siloxanes as well as their mixtures (steps of 20 wt % MM) have been performed. Results show degradations of heat transfer coefficients compared to the ideal values of up to 46%. Kandlikar’s correlation is used to describe the experimental data. In order to achieve a good agreement with the real values, the fluid-surface parameter was used to adjust the correlation. Moreover, the severe-diffusion induced region was chosen. By using this adapted correlation, mean deviations of less than 10% between the experimental data and the correlation are present.
Based on all these results, required heat transfer areas of evaporator and preheater are estimated assuming shell-and-tube heat exchangers. Calculations are performed for the case of pure electricity generation as well as combined heat and power generation for the pure components and one mixture. Results show an increased heat transfer area in case of the mixtures of around 1% (pure electricity, 95 wt % MM, efficiency increase: ≈ 1%) and 14% (combined heat and power, 60 wt % MM, efficiency increase: ≈ 3%). Moreover, it is obvious that next to the heat transfer coefficients, process parameters do have a strong influence on the required heat exchange area. Therefore, it cannot be stated that lower heat transfer coefficients lead to higher heat transfer areas than comparing a certain application. It is always necessary to calculate the respective areas under consideration of the (sometimes even just slightly) different operating conditions. However, it can be concluded that siloxanes, as working fluids for high temperature applications, exhibit reduced heat transfer degradation compared to low temperature fluids like for example R245fa/R365mfc. As a result, heat transfer areas are not as additionally increased as in case of geothermal applications and, therefore, the use of mixtures can be beneficial, even though efficiency increases are comparably small.
In order to definitely decide whether the use of mixtures is economically feasible in a certain application, it is certainly necessary to analyse the heat transfer areas of internal heat exchanger and condenser as well. In addition, the performance of turbine and pump has to be investigated, too. Finally, specific problems that can occur by using mixtures, as for example compositions shifts during the process, have to be analysed in detail. Therefore, in future work, analogous investigations (measurements of heat transfer coefficients, identifying of appropriate correlations as well as estimation of required heat transfer areas) will be performed with respect to the condenser. Then, a holistic evaluation of using mixtures in ORC-applications is possible.