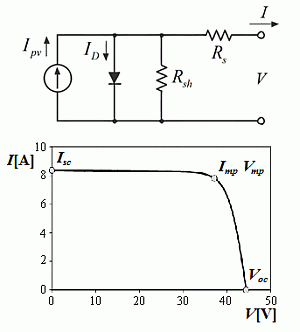
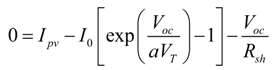Explicit Expressions for Solar Panel Equivalent Circuit Parameters Based on Analytical Formulation and the Lambert W-Function †
Abstract
:1. Introduction
2. Methods
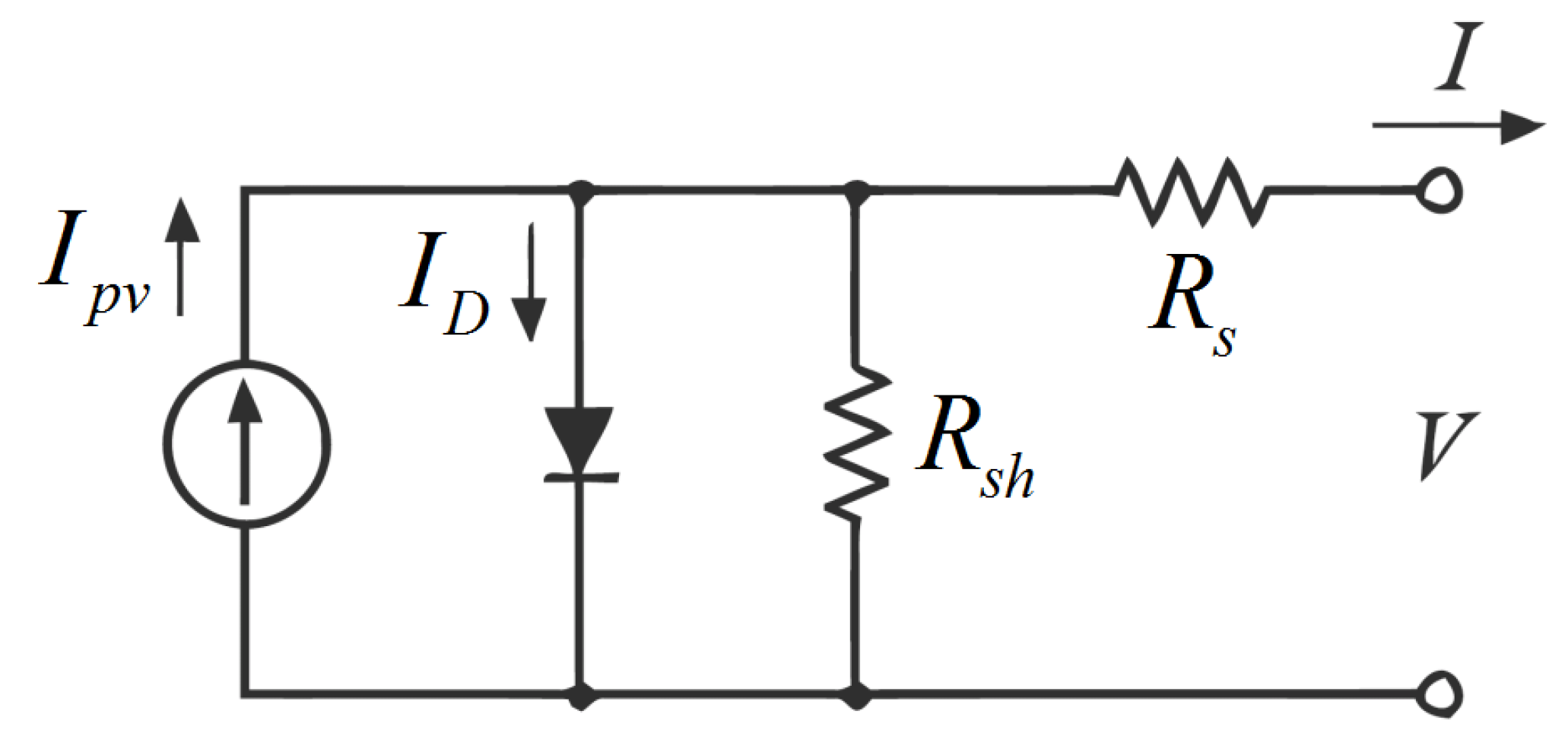
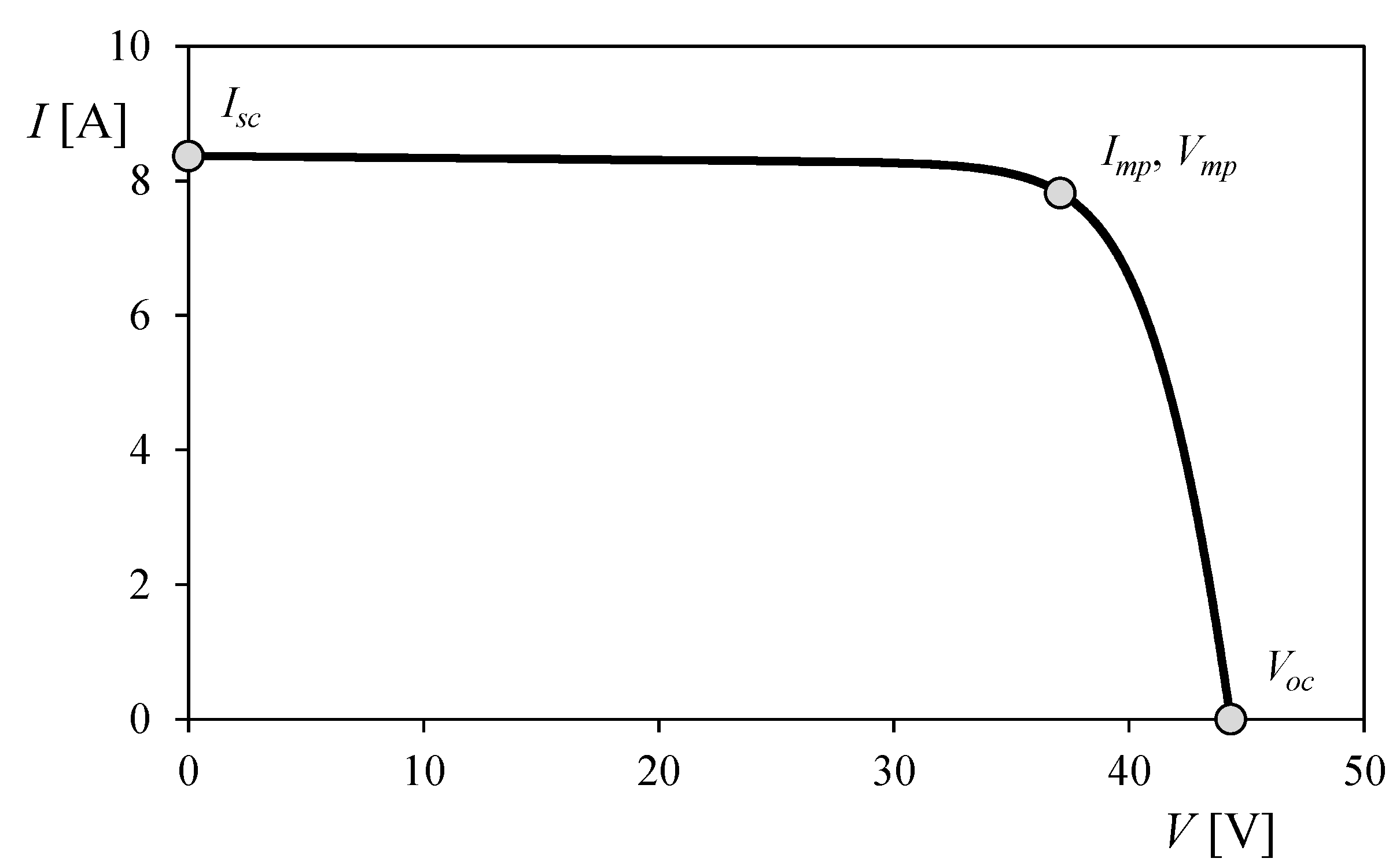
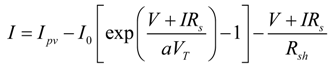
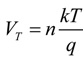
2.1. Parameter Calculation
- Short circuit equation:
- Open circuit equation:
- Maximum power point circuit equation:
- Zero derivative for the power at maximum power point circuit equation:
- Equation for Rs:
- Equation for Rsh:
- Equation for I0:
- Equation for Ipv:
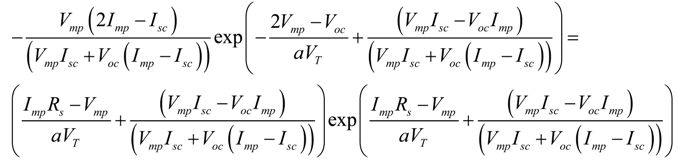
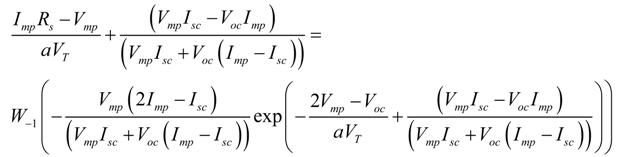
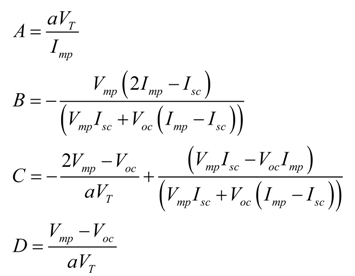
| Blue Solar Cell | Grey Solar Cell | ||
|---|---|---|---|
| a | 1.51 ± 0.07 | a | 1.72 ± 0.08 |
| Imp (A) | 0.0934 | Imp (A) | 0.485 |
| Vmp (V) | 0.433 | Vmp (V) | 0.387 |
| Isc (A) | 0.1023 | Isc (A) | 0.561 |
| Voc (V) | 0.536 | Voc (V) | 0.524 |
| Tr (K) | 300 | Tr (K) | 307 |
| Blue Solar Cell | Grey Solar Cell | ||||||
|---|---|---|---|---|---|---|---|
| Equivalent Circuit Parameters | Benchmark [17] | Iterative Method [50] | Present Method | Equivalent Circuit Parameters | Benchmark [17] | Iterative Method [50] | Present Method |
| Rs (Ω) | 0.07 ± 0.009 | 0.0671 | 0.0652 | Rs (Ω) | 0.08 ± 0.01 | 0.0784 | 0.0781 |
| Rsh (Ω) | 1000 ± 50 | 977 | 1093 | Rsh (Ω) | 26 ± 1 | 26.09 | 26.25 |
| Ipv (A) | 0.1023 ± 0.0005 | 0.1023 | 0.1023 | Ipv (A) | 0.5625 ± 0.0005 | 0.561 | 0.5627 |
| I0 (A) | 110 ± 50 × 10−9 | 111 × 10−9 | 111 × 10−9 | I0 (A) | 6 ± 3 × 10−6 | 5.6 × 10−6 | 5.4 × 10−6 |
2.2. Parameter Dependence on Environmental Conditions
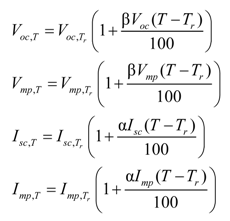
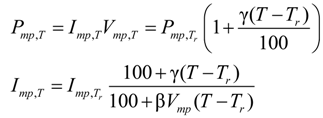
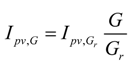
3. Results and Discussion
- Estimate the value of the parameter a. In this method this parameter is considered as a constant, independent of the temperature and the irradiation. In this case the chosen value is a = 1.1.
- Calculate Vt for the panel at that temperature level with Equation (2).
- Determine the boundary conditions at that temperature and irradiation level using manufacturer’s data and Equations (17) and/or (18).
- Calculate Rs with Equation (15).
- Calculate Rsh with Equation (8).
- Calculate I0 with Equation (9).
- Calculate Ipv with Equation (10).
| MSP290AS-36.EU (Multicrystalline) | MSMD290AS-36.EU (Monocrystalline) | ||||||
|---|---|---|---|---|---|---|---|
| n | 72 | Tr (°C) | 25 | n | 72 | Tr (°C) | 25 |
| Pmp (W) | 290 | γ (%/°C) | −0.45 | Pmp (W) | 290 | γ (%/°C) | −0.44 |
| Imp (A) | 7.82 | αImp (%/°C) | - | Imp (A) | 7.70 | αImp (%/°C) | - |
| Vmp (V) | 37.08 | βVmp (%/°C) | −0.35 | Vmp (V) | 37.66 | βVmp (%/°C) | −0.35 |
| Isc (A) | 8.37 | αIsc (%/°C) | +0.04 | Isc (A) | 8.24 | αIsc (%/°C) | +0.04 |
| Voc (V) | 44.32 | βVoc (mV/°C) | −0.33 | Voc (V) | 44.68 | βVoc (mV/°C) | −0.31 |
| MSP290AS-36.EU (Multicrystalline) | MSMD290AS-36.EU (Monocrystalline) | ||
|---|---|---|---|
| a | 1.10 | a | 1.10 |
| Ipv (A) | 8.37 | Ipv (A) | 8.24 |
| I0 (A) | 2.86 × 10−9 | I0 (A) | 2.36 × 10−9 |
| Rs (Ω) | 0.162 | Rs (Ω) | 0.130 |
| Rsh (Ω) | 331 | Rsh (Ω) | 316 |
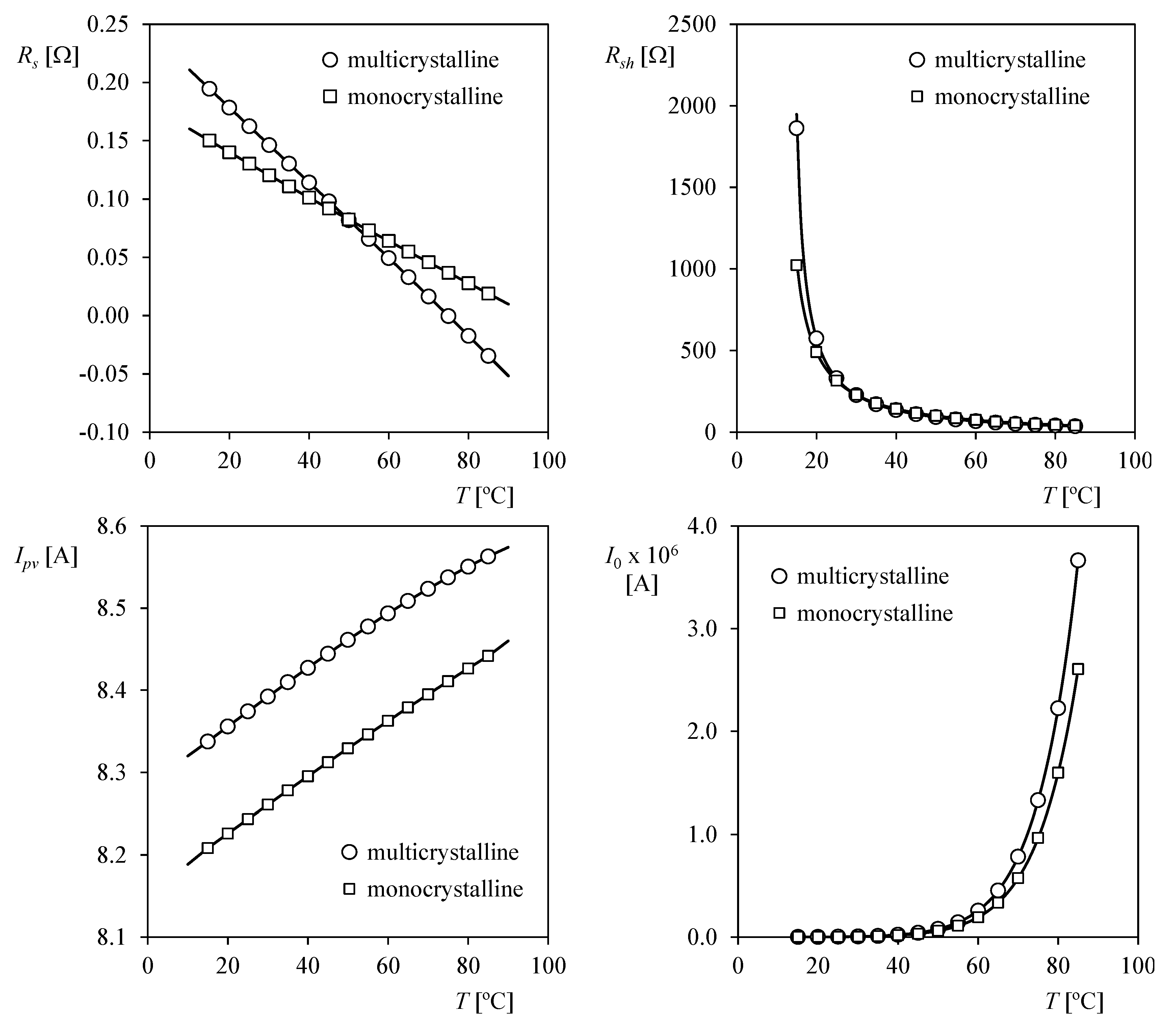
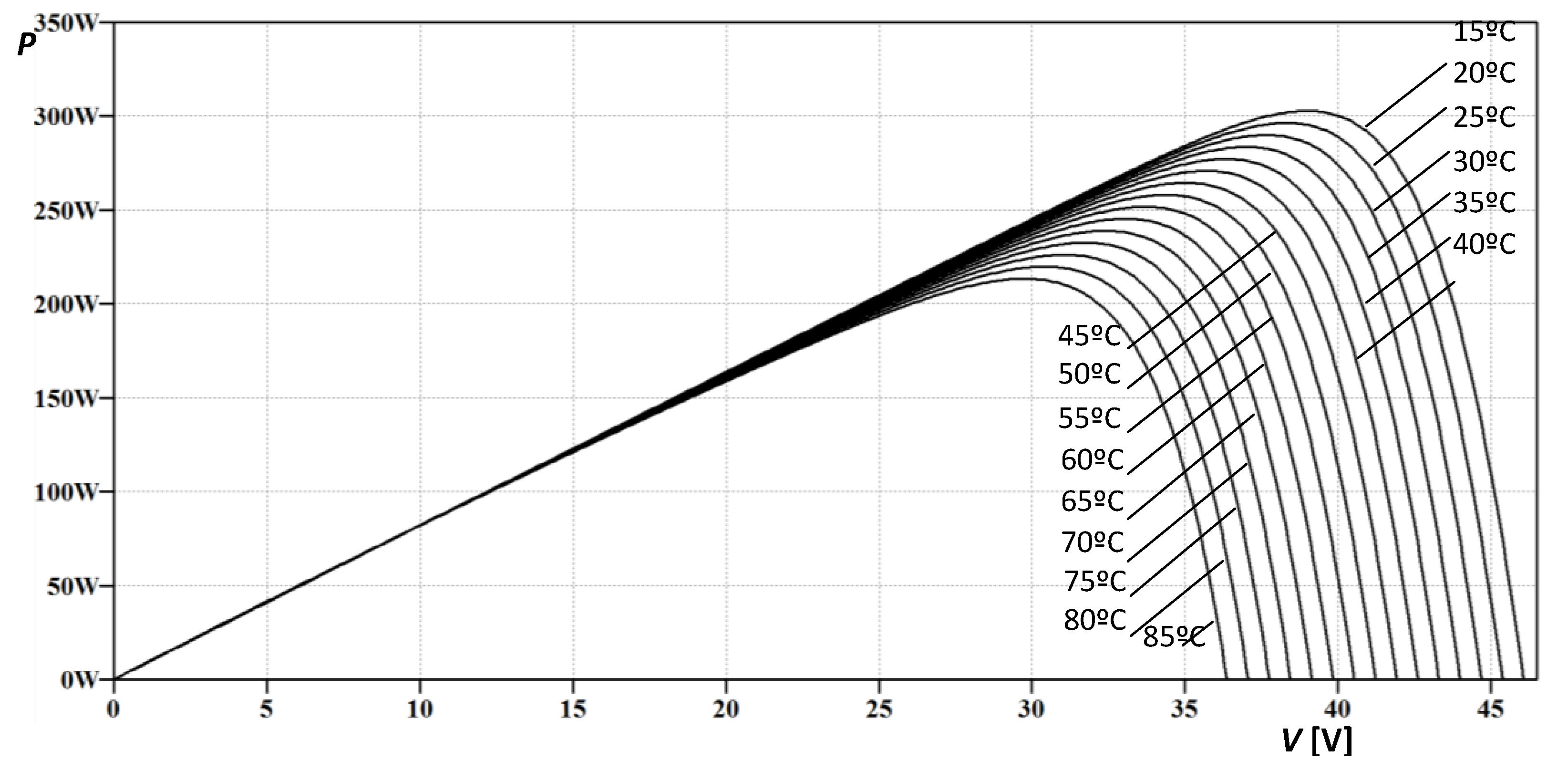
- For MSP290AS-36.EU:Ipv (T) = 8.37 + 3.62·10−3 ∆T − 3.38·10−6 ∆T2 − 7.58·10−8 ∆T3
Rs (T) = 1.62·10−1 − 3.21·10−3 ∆T + 7.05·10−7 ∆T2 − 3.01·10−8 ∆T3
Rsh (T) = 1/(3.03·10−3 + 2.65·10−4 ∆T + 1.50·10−6 ∆T2 + 1.56·10−8 ∆T3)
I0 (T) = exp(−1.97·101 + 1.44·10−1 ∆T − 4.80·10−4 ∆T2 + 1.15·10−6 ∆T3) - For MSMD290AS-36.EU:Ipv (T) = 8.24 + 3.49·10−3 ∆T − 1.68·10−6 ∆T2 − 2.41·10−8 ∆T3
Rs (T) = 1.30·10−1 − 1.97·10−3 ∆T + 2.53·10−6 ∆T2 − 1.07·10−8 ∆T3
Rsh (T) = 1/(3.18·10−3 + 2.33·10−4 ∆T + 1.27·10−6 ∆T2 + 1.33·10−8 ∆T3)
I0 (T) = exp(−1.98·101 + 1.41·10−1 ∆T − 4.69·10−4 ∆T2 + 1.13·10−6 ∆T3)
- For MSP290AS-36.EU:
- For MSMD290AS-36.EU:
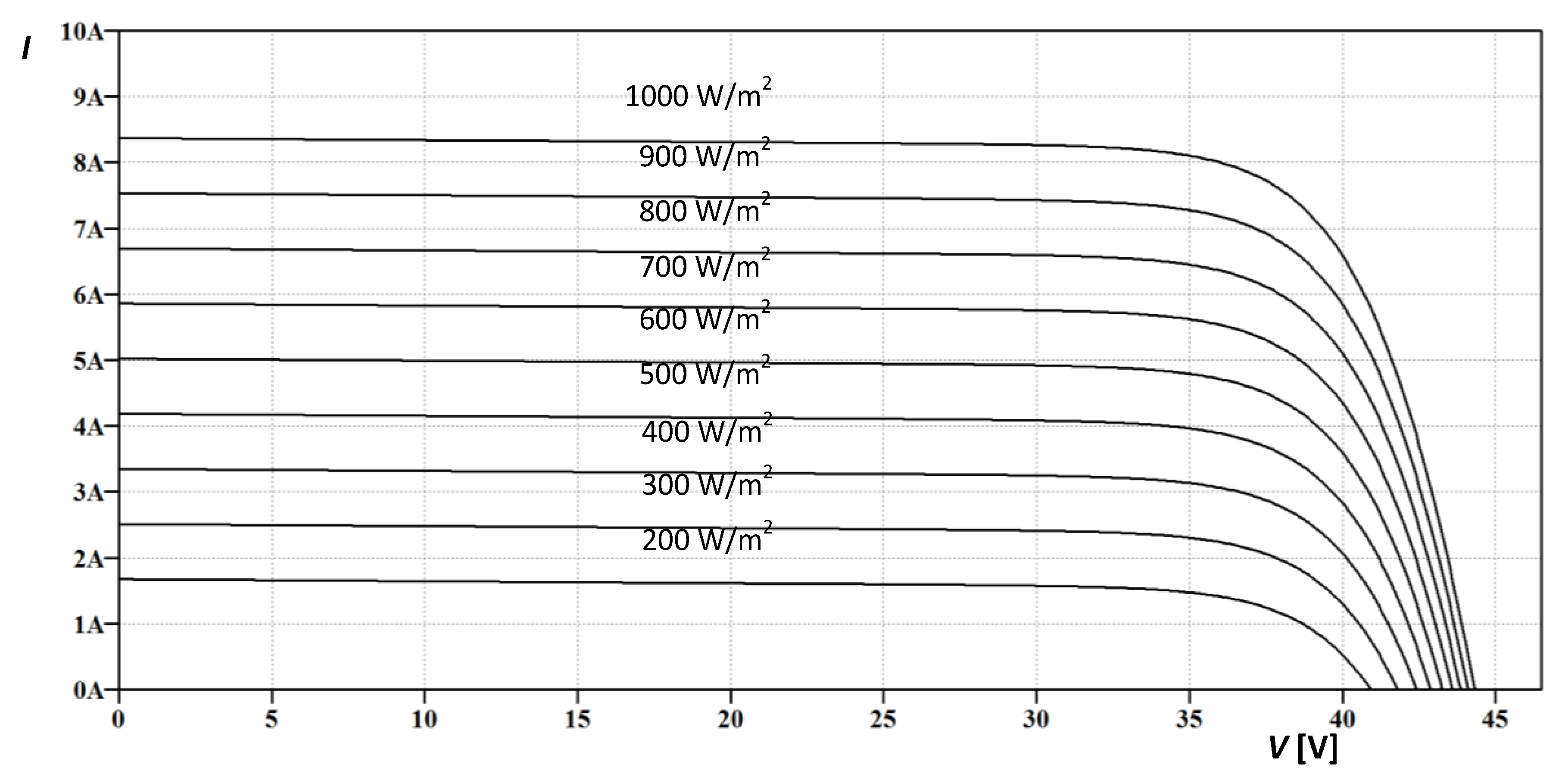
4. Experimental Section


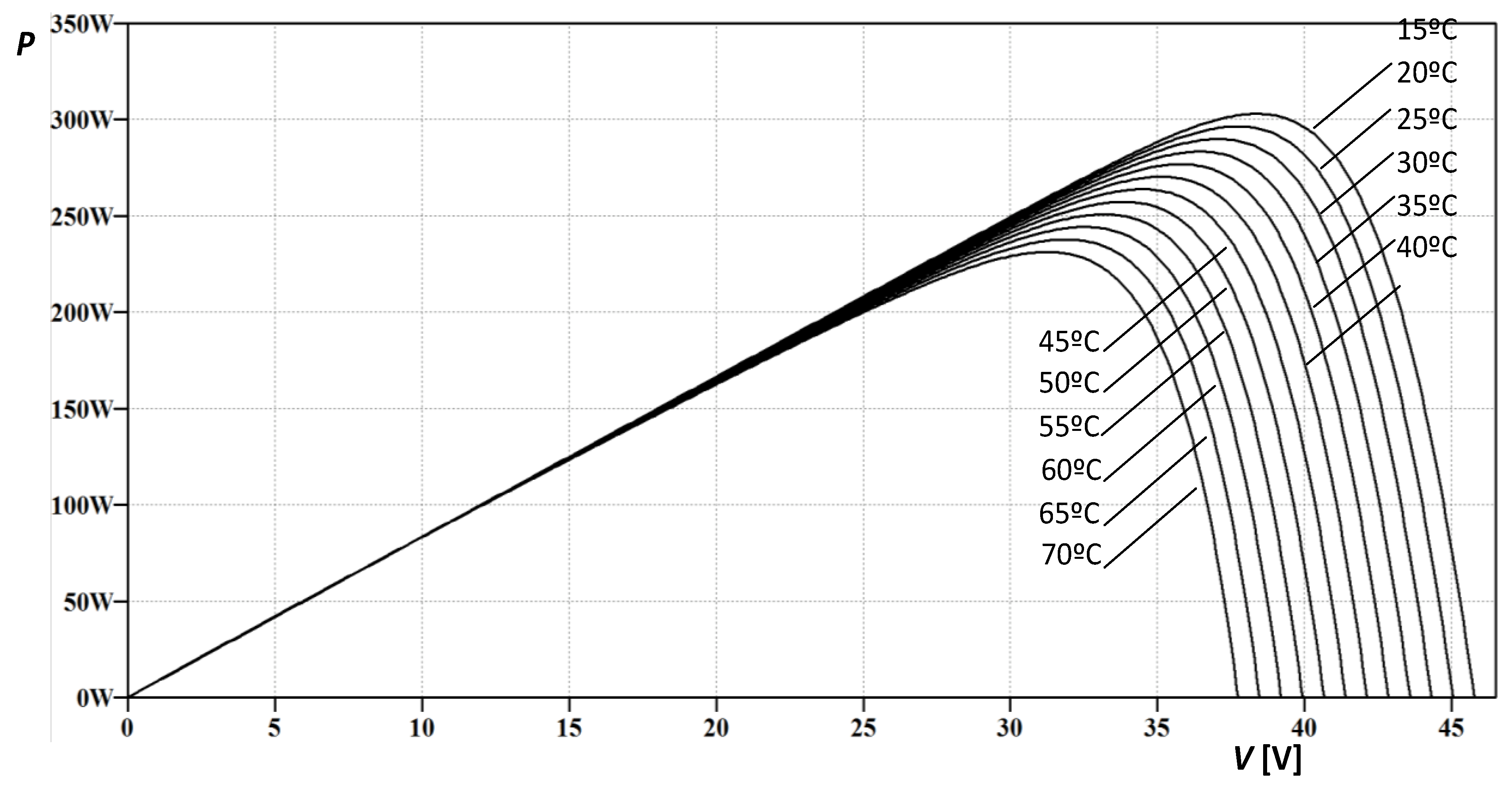
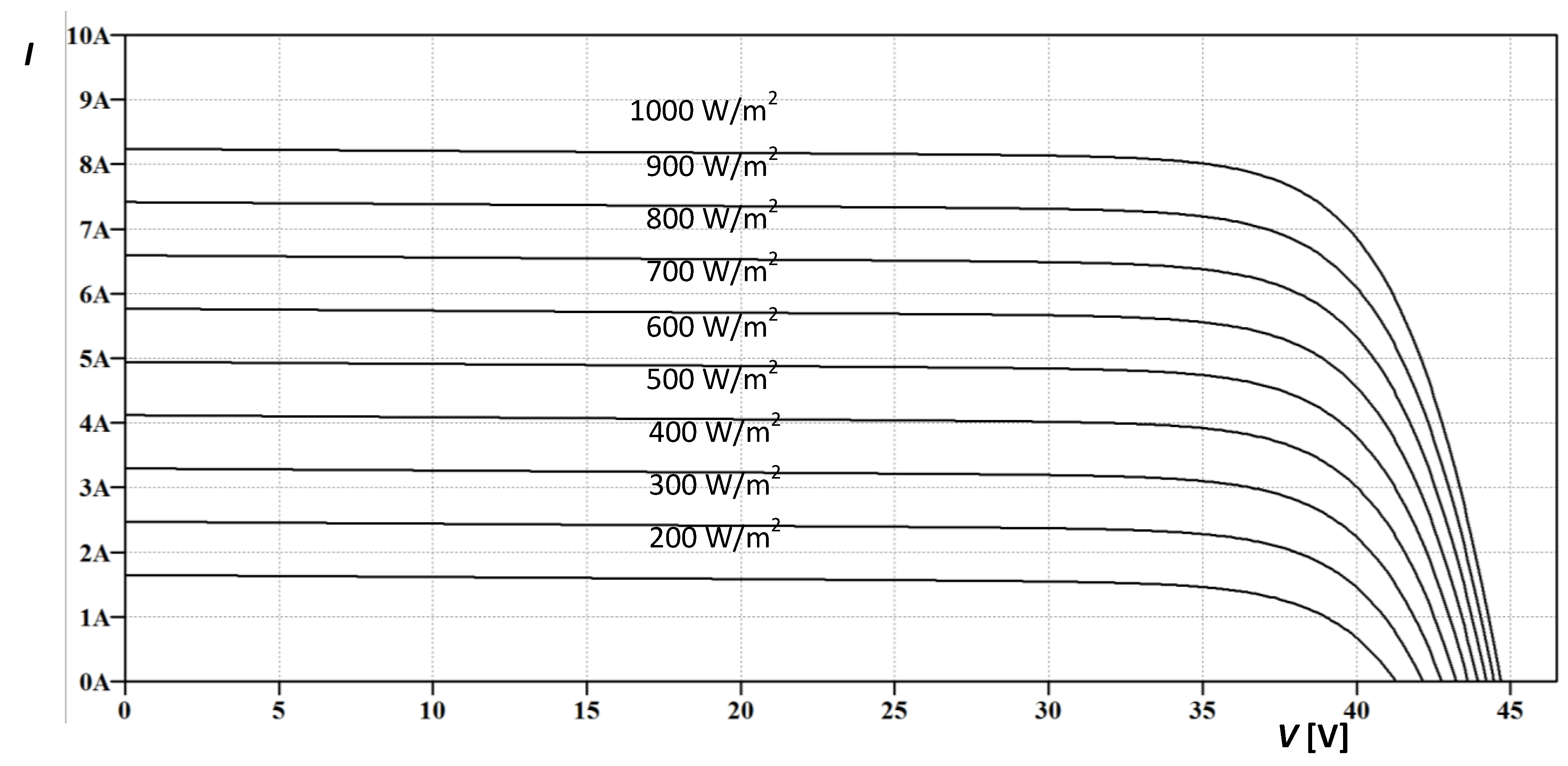
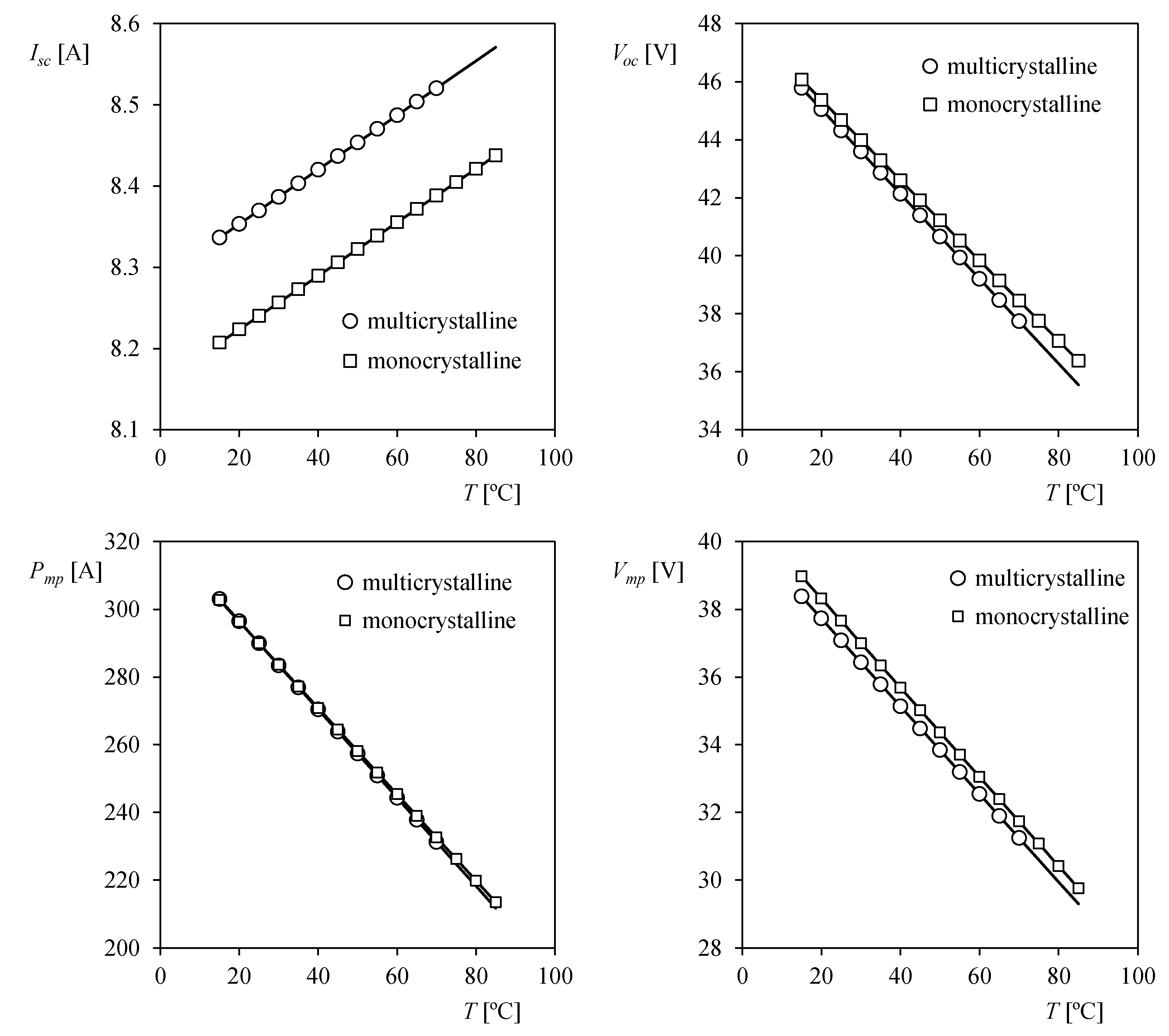
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Aminzadeh, F.; Pindado, S. How has Spain become a leader in thewind energy industry during the last decade? (An analysis of influential factors on the development of wind energy in Spain). In Proceedings of the EWEA Annual Event, Brussels, Belgium, 14–17 March 2011.
- Vázquez, C.T. Energía Solar Fotovoltaica; Ediciones Ceysa: Madrid, Spain, 2008. (In Spanish) [Google Scholar]
- Razykov, T.M.; Ferekides, C.S.; Morel, D.; Stefanakos, E.; Ullal, H.S.; Upadhyaya, H.M. Solar photovoltaic electricity: Current status and future prospects. Sol. Energy 2011, 85, 1580–1608. [Google Scholar] [CrossRef]
- Hernandez, V.R. Solar Thermal Power. History of a Research Success; Protermosolar: Sevilla, Spain, 2010. [Google Scholar]
- Valluri, S.R.; Jeffrey, D.J.; Corless, R.M. Some applications of the Lambert W function to physics. Can. J. Phys. 2000, 78, 823–831. [Google Scholar]
- Caillol, J. Some applications of the Lambert W function to classical statistical mechanics. J. Phys. A Math. Gen. 2003, 36. [Google Scholar] [CrossRef]
- Sze, S.M. Physics of Semiconductor Devices; Wiley-Interscience: New York, NY, USA, 1969. [Google Scholar]
- Pfann, W.G.; van Roosbroeck, W. Radioactive and Photoelectric p-n Junction Power Sources. J. Appl. Phys. 1954, 25. [Google Scholar] [CrossRef]
- Prince, M.B. Silicon solar energy converters. J. Appl. Phys. 1955, 26, 534–540. [Google Scholar]
- Wolf, M.; Rauschenbach, H. Series resistance effects on solar cell measurements. Adv. Energy Convers. 1963, 3, 455–479. [Google Scholar] [CrossRef]
- Van Dyk, E.E.; Meyer, E.L. Analysis of the effect of parasitic resistances on the performance of photovoltaic modules. Renew. Energy 2004, 29, 333–344. [Google Scholar] [CrossRef]
- De Blas, M.; Torres, J.; Prieto, E.; Garcı́a, A. Selecting a suitable model for characterizing photovoltaic devices. Renew. Energy 2002, 25, 371–380. [Google Scholar] [CrossRef]
- Carrero, C.; Rodríguez, J.; Ramírez, D.; Platero, C. Simple estimation of PV modules loss resistances for low error modelling. Renew. Energy 2010, 35, 1103–1108. [Google Scholar] [CrossRef]
- Zhu, X.-G.; Fu, Z.-H.; Long, X.-M. Sensitivity analysis and more accurate solution of photovoltaic solar cell parameters. Sol. Energy 2011, 85, 393–403. [Google Scholar] [CrossRef]
- Bätzner, D.L.; Romeo, A.; Zogg, H.; Tiwari, A.N. CdTe/CdS Solar Cell Performance under Low Irradiance. In Proceedings of the 17th European Photovoltaic Solar Energy Conference and Exhibition, Munich, Germany, 22–26 October 2001; pp. 1–4.
- Kennerud, K.L. Analysis of Performance Degradation in CdS Solar Cells. IEEE Trans. Aerosp. Electron. Syst. 1969, AES-5, 912–917. [Google Scholar] [CrossRef]
- Charles, J.; Abdelkrim, M.; Muoy, Y.; Mialhe, P. A practical method of analysis of the current-voltage characteristics of solar cells. Sol. Cells 1981, 4, 169–178. [Google Scholar] [CrossRef]
- De Soto, W.; Klein, S.A.; Beckman, W.A. Improvement and validation of a model for photovoltaic array performance. Sol. Energy 2006, 80, 78–88. [Google Scholar]
- Carrero, C.; Amador, J.; Arnaltes, S. A single procedure for helping PV designers to select silicon PV modules and evaluate the loss resistances. Renew. Energy 2007, 32, 2579–2589. [Google Scholar] [CrossRef]
- Shockley, W. The Theory of p-n Junctions in Semiconductors and p-n Junction Transistors. Bell Syst. Tech. J. 1949, 28, 435–489. [Google Scholar] [CrossRef]
- Cubas, J.; Pindado, S.; Victoria, M. On the analytical approach for modeling photovoltaic systems behavior. J. Power Sources 2014, 247, 467–474. [Google Scholar] [CrossRef]
- Lineykin, S. Five-Parameter Model of Photovoltaic Cell Based on STC Data and Dimensionless. In Proceedings of the 2012 IEEE 27th Convention of Electronical and Electronics Engineers in Israel, Eilat, Israel, 14–17 November 2012; pp. 1–5.
- Peng, L.; Sun, Y.; Meng, Z.; Wang, Y.; Xu, Y. A new method for determining the characteristics of solar cells. J. Power Sources 2013, 227, 131–136. [Google Scholar]
- Peng, L.; Sun, Y.; Meng, Z. An improved model and parameters extraction for photovoltaic cells using only three state points at standard test condition. J. Power Sources 2014, 248, 621–631. [Google Scholar] [CrossRef]
- Orioli, A.; Di Gangi, A. A procedure to calculate the five-parameter model of crystalline silicon photovoltaic modules on the basis of the tabular performance data. Appl. Energy 2013, 102, 1160–1177. [Google Scholar] [CrossRef] [Green Version]
- Ma, J.; Man, K.L.; Ting, T.O.; Zhang, N.; Guan, S.-U.; Wong, P.W.H. Approximate single-diode photovoltaic model for efficient I-V characteristics estimation. Sci. World J. 2013, 2013, 230471:1–230471:7. [Google Scholar]
- Ma, J.; Ting, T.O.; Man, K.L.; Zhang, N.; Guan, S.-U.; Wong, P.W.H. Parameter Estimation of Photovoltaic Models via Cuckoo Search. J. Appl. Math. 2013, 2013, 362619:1–362619:8. [Google Scholar]
- Li, Y.; Huang, W.; Huang, H.; Hewitt, C.; Chen, Y.; Fang, G.; Carroll, D.L. Evaluation of methods to extract parameters from current–voltage characteristics of solar cells. Sol. Energy 2013, 90, 51–57. [Google Scholar] [CrossRef]
- Dongue, S.B.; Njomo, D.; Tamba, J.G.; Ebengai, L. Modeling of Electrical Response of Illuminated Crystalline Photovoltaic Modules Using Four- and Five-Parameter Models. Int. J. Emerg. Technol. Adv. Eng. 2012, 2, 612–619. [Google Scholar]
- Ishibashi, K.; Kimura, Y.; Niwano, M. An extensively valid and stable method for derivation of all parameters of a solar cell from a single current-voltage characteristic. J. Appl. Phys. 2008, 103. [Google Scholar] [CrossRef]
- Lineykin, S.; Averbukh, M.; Kuperman, A. An improved approach to extract the single-diode equivalent circuit parameters of a photovoltaic cell/panel. Renew. Sustain. Energy Rev. 2014, 30, 282–289. [Google Scholar] [CrossRef]
- Cotfas, D.T.; Cotfas, P.A.; Kaplanis, S. Methods to determine the DC parameters of solar cells: A critical review. Renew. Sustain. Energy Rev. 2013, 28, 588–596. [Google Scholar] [CrossRef]
- Cotfas, D.T.; Cotfas, P.A.; Ursutiu, D.; Samoila, C. The methods to determine the series resistance and the ideality factor of diode for solar cells-review. In Proceedings of the 2012 13th International Conference on Optimization of Electrical and Electronic Equipment (OPTIM), Brasso, Romania, 24–26 May 2012; pp. 966–972.
- Easwarakhanthan, T.; Bottin, J.; Bouhouch, I.; Boutrit, C. Nonlinear Minimization Algorithm for Determining the Solar Cell Parameters with Microcomputers. Int. J. Sol. Energy 1986, 4, 1–12. [Google Scholar] [CrossRef]
- Gow, J.A.; Manning, C.D. Development of a photovoltaic array model for use in power-electronics simulation studies. IEEE Proc. Electr. Power Appl. 1999, 146, 193–200. [Google Scholar] [CrossRef]
- Eikelboom, J.A.; Reinders, A.H.M.E. Determination of the Irradiation Dependent Efficiency of Multicrystalline Si PV Modules on Basis of IV Curve Fitting and Its Influence on the Annual Performance; Netherlands Energy Research Foundation: Petten, The Netherlands, 1997; pp. 2–5. [Google Scholar]
- Kuo, Y.; Liang, T.; Chen, J. Novel maximum-power-point-tracking controller for photovoltaic energy conversion system. IEEE Trans. Ind. Electron. 2001, 48, 594–601. [Google Scholar]
- Walker, G. Evaluating MPPT Converter Topologies Using a Matlab PV Model. J. Electr. Electron. Eng. Aust. 2001, 21, 49–55. [Google Scholar]
- Alqahtani, A.H. A Simplified and Accurate Photovoltaic Module Parameters Extraction Approach using Matlab. In Proceedings of the 2012 IEEE International Symposium on Industrial Electronics (ISIE), Hangzhou, China, 28–31 May 2012; pp. 1748–1753.
- Chan, D.S.H.; Phang, J.C.H. Analytical methods for the extraction of solar-cell single- and double-diode model parameters from I-V characteristics. IEEE Trans. Electron Devices 1987, 34, 286–293. [Google Scholar] [CrossRef]
- Lo Brano, V.; Orioli, A.; Ciulla, G.; di Gangi, A. An improved five-parameter model for photovoltaic modules. Sol. Energy Mater. Sol. Cells 2010, 94, 1358–1370. [Google Scholar] [CrossRef]
- Das, A.K. Analytical derivation of explicit J–V model of a solar cell from physics based implicit model. Sol. Energy 2012, 86, 26–30. [Google Scholar] [CrossRef]
- Laudani, A.; Riganti Fulginei, F.; Salvini, A. High performing extraction procedure for the one-diode model of a photovoltaic panel from experimental I–V curves by using reduced forms. Sol. Energy 2014, 103, 316–326. [Google Scholar] [CrossRef]
- Villalva, M.G.; Gazoli, J.R.; Filho, E.R. Comprehensive Approach to Modeling and Simulation of Photovoltaic Arrays. IEEE Trans. Power Electron. 2009, 24, 1198–1208. [Google Scholar] [CrossRef]
- Villalva, M.G.; Gazoli, J.R.; Filho, E.R. Modeling and circuit-based simulation of photovoltaic arrays. In Proceedings of the 2009 Brazilian Power Electronics Conference, Bonito-Mato Grosso do Sul, Brazil, 27 September–1 October 2009; pp. 1244–1254.
- Cubas, J.; Pindado, S.; Farrahi, A. New Method for Analytical Photovoltaic Parameter Extraction. In Proceedings of the 2nd International Conference on Renewable Energy Research and Applications, ICRERA, Madrid, Spain, 20–23 October 2013; pp. 873–877.
- Banwell, T.C.; Jayakumar, A. Exact analytical solution for current flow through diode with series resistance. Electron. Lett. 2000, 36, 291–292. [Google Scholar] [CrossRef]
- Jain, A.; Kapoor, A. A new approach to study organic solar cell using Lambert W-function. Sol. Energy Mater. Sol. Cells 2005, 86, 197–205. [Google Scholar] [CrossRef]
- Jain, A.; Kapoor, A. Exact analytical solutions of the parameters of real solar cells using Lambert W-function. Sol. Energy Mater. Sol. Cells 2004, 81, 269–277. [Google Scholar] [CrossRef]
- Ghani, F.; Duke, M. Numerical determination of parasitic resistances of a solar cell using the Lambert W-function. Sol. Energy 2011, 85, 2386–2394. [Google Scholar] [CrossRef]
- Rauschenbach, H.S. Solar Cell Array Design Handbook, The Principles and Technology of Photovoltaic Energy Conversion; Van Nostrand Reinhold Co.: New York, NY, USA, 1980. [Google Scholar]
- München Solarenergie GmbH Multicrystalline MSPxxxAS-36.EU. Available online: http://www.munchensolar.de/download/M%C3%BCnchen%20Solar%20%C3%9C%20MSPxxxAS-36.EU%20EN.pdf (accessed on 5 February 2014).
- München Solarenergie GmbH Monocrystalline MSMDxxxAS-36.EU. Available online: http://www.munchensolar.de/download/München%20Solar%20M%20MSMDxxxAS-36.EU%20EN.pdf (accessed on 5 February 2014).
- Cuce, P.M.; Cuce, E. A novel model of photovoltaic modules for parameter estimation and thermodynamic assessment. Int. J. Low-Carbon Technol. 2011, 7, 159–165. [Google Scholar] [CrossRef]
- Xiao, W.; Dunford, W.G.; Capel, A. A novel modeling method for photovoltaic cells. In Proceedings of the 2004 IEEE 35th Annual Power Electronics Specialists Conference (IEEE Cat. No.04CH37551), Aachen, Germany, 20–25 June 2004; pp. 1950–1956.
© 2014 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Cubas, J.; Pindado, S.; De Manuel, C. Explicit Expressions for Solar Panel Equivalent Circuit Parameters Based on Analytical Formulation and the Lambert W-Function. Energies 2014, 7, 4098-4115. https://doi.org/10.3390/en7074098
Cubas J, Pindado S, De Manuel C. Explicit Expressions for Solar Panel Equivalent Circuit Parameters Based on Analytical Formulation and the Lambert W-Function. Energies. 2014; 7(7):4098-4115. https://doi.org/10.3390/en7074098
Chicago/Turabian StyleCubas, Javier, Santiago Pindado, and Carlos De Manuel. 2014. "Explicit Expressions for Solar Panel Equivalent Circuit Parameters Based on Analytical Formulation and the Lambert W-Function" Energies 7, no. 7: 4098-4115. https://doi.org/10.3390/en7074098