Evaluation of the Wave Energy Conversion Efficiency in Various Coastal Environments †
Abstract
:1. Introduction
| Device | Power per Unit (kW) | Movement | Depth (m) | Size |
|---|---|---|---|---|
| Oceantec | 500 | heave | 30–50 | medium |
| Pelamis | 750 | surge & heave | 50–70 | medium |
| P P Converter | 3620 | heave | deep | large |
| Seabased | 15 | heave | 30–50 | small |
| Wave Dragon | 7000 | overtopping | 30–50 | large |
| Aqua Buoy | 250 | heave | >50 | small |
| AWS (Archimedes Wave Swing) | 2320 | heave | 40–100 | medium |
| Langlee | 1665 | oscillating flaps | deep | medium |
| OE Buoy | 2800 | oscillating column | deep | medium |
| Wavebob | 1000 | heave | deep | medium |
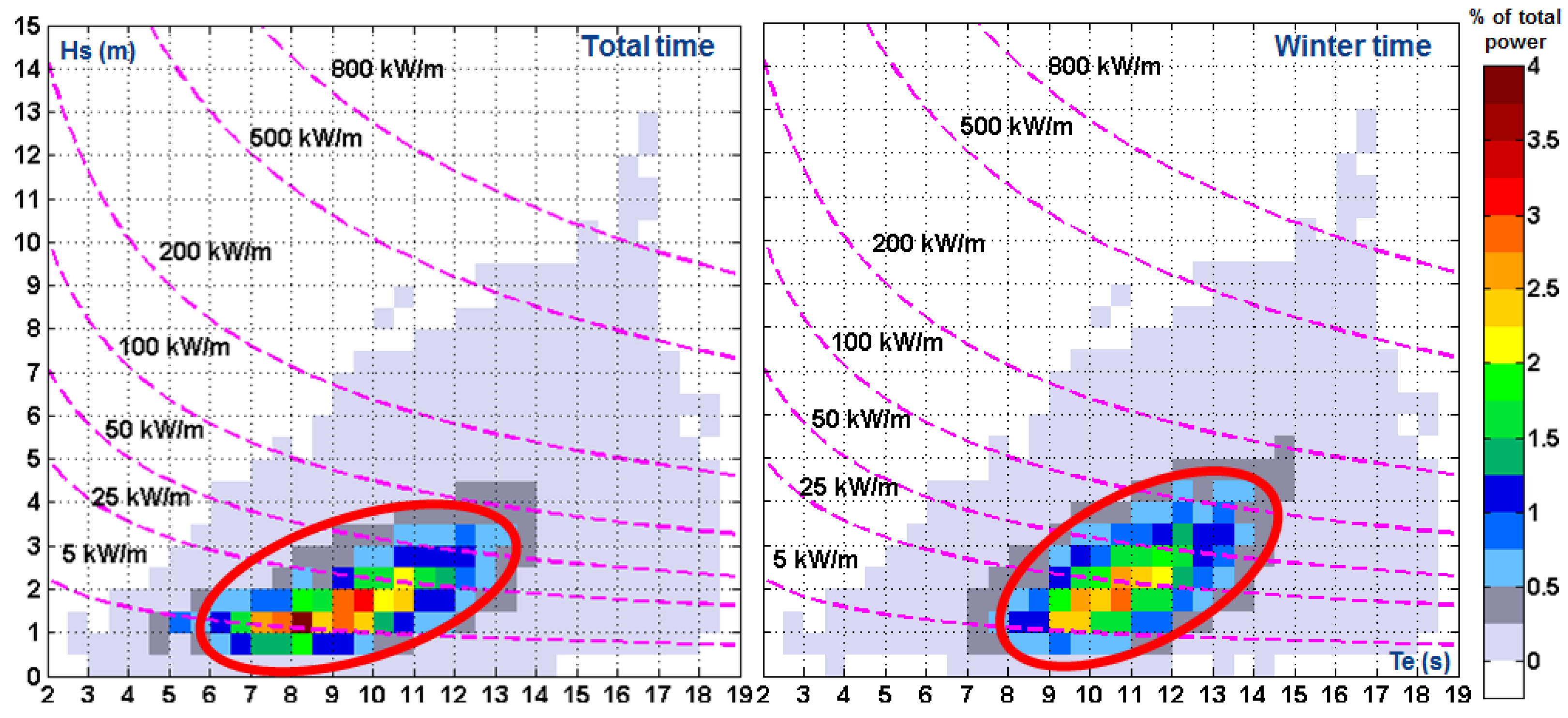




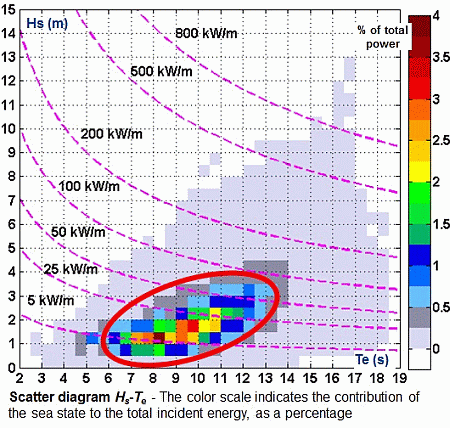
2. Results and Discussion
2.1. Transformation of the Wave Energy in Western Iberian Nearshore
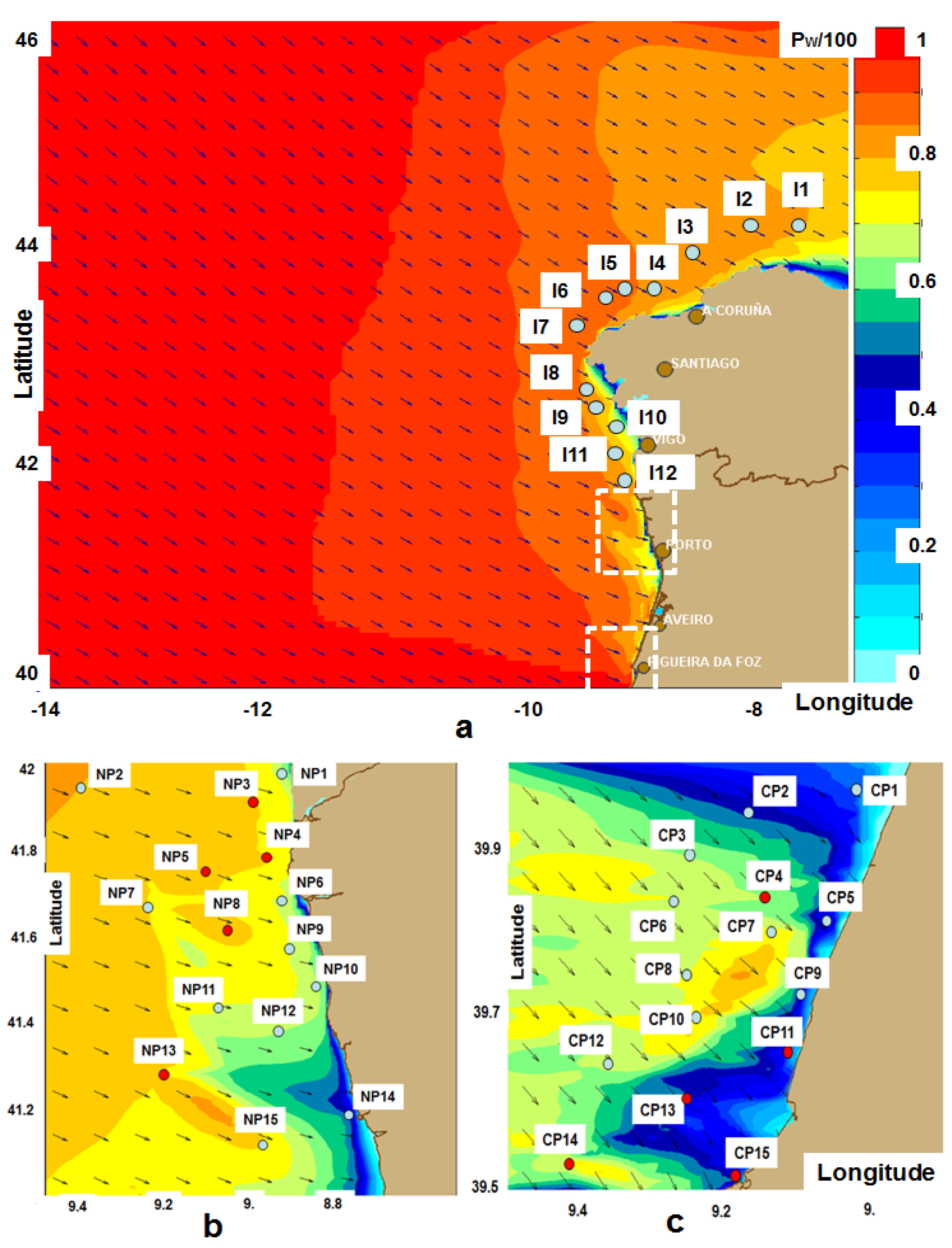

| Points | I1 | I2 | I3 | I4 | I5 | I6 | I7 | I8 | I9 | I10 | I11 | I12 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| PWmed (kW/m) | TT | 28.7 | 29.7 | 29.2 | 25.5 | 28.7 | 31.7 | 30.2 | 20.4 | 23.8 | 12.8 | 15.7 | 19.4 |
| WT | 51.9 | 53.6 | 52.3 | 44.6 | 50.9 | 56.2 | 53.3 | 36.8 | 42.3 | 25.0 | 30.1 | 34.2 | |
| PE (kW) Point/Period | Oceantec | Pelamis | Pontoon Power C | Seabased AB | Wave Dragon | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| TT | WT | TT | WT | TT | WT | TT | WT | TT | WT | |
| I1 | 96.5 | 102.8 | 114.2 | 145.4 | 221.5 | 252.1 | 2.6 | 3.2 | 2037.2 | 2667.6 |
| I2 | 99.9 | 105.4 | 118.1 | 150.2 | 227.2 | 258.5 | 2.7 | 3.3 | 2083.8 | 2730.9 |
| I3 | 97.2 | 100.4 | 118.4 | 150.0 | 224.8 | 253.1 | 2.7 | 3.2 | 2112.6 | 2768.6 |
| I5 | 94.4 | 94.4 | 115.6 | 144.8 | 219.7 | 244.4 | 2.6 | 3.2 | 2095.2 | 2736.4 |
| I6 | 107.1 | 106.5 | 126.6 | 158.6 | 239.4 | 239.4 | 2.8 | 3.4 | 2197.8 | 2875.0 |
| I7 | 105.0 | 103.6 | 124.5 | 155.9 | 236.3 | 263.7 | 2.8 | 3.3 | 2172.4 | 2839.5 |
| NP-Points Pw (kW/m) | NP1 | NP2 | NP3 | NP4 | NP5 | NP6 | NP7 | NP8 | NP9 | NP10 | NP11 | NP12 | NP13 | NP14 | NP15 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| TT | 17.3 | 27.8 | 26.2 | 22.9 | 25.2 | 19.8 | 25.2 | 27.4 | 23.7 | 17.9 | 24.6 | 22.8 | 26.5 | 17.1 | 24.9 |
| WT | 26.8 | 43.1 | 40.7 | 35.4 | 38.9 | 30.5 | 38.9 | 42.7 | 36.5 | 27.9 | 37.9 | 34.9 | 41.3 | 26.6 | 38.6 |
| CP-points Pw (kW/m) | CP1 | CP2 | CP3 | CP4 | CP5 | CP6 | CP7 | CP8 | CP9 | CP10 | CP11 | CP12 | CP13 | CP14 | CP15 |
| TT | 20.3 | 24.7 | 23.2 | 24.9 | 21.7 | 24.1 | 23.4 | 23.5 | 21.2 | 24.9 | 24.8 | 25.3 | 24.5 | 24.8 | 24.8 |
| WT | 31.5 | 38.4 | 35.9 | 38.9 | 33.7 | 37.5 | 36.3 | 36.4 | 32.8 | 36.1 | 38.9 | 39.1 | 37.8 | 38.5 | 38.5 |
| PE (kW) Point/Period | Pelamis | AWS | Aqua Buoy | Wave Dragon | ||||
|---|---|---|---|---|---|---|---|---|
| TT | WT | TT | WT | TT | WT | TT | WT | |
| NP3 | 95.1 | 130 | 282.7 | 446 | 34.4 | 48.9 | 907.5 | 1359 |
| NP4 | 78.7 | 109 | 246.9 | 396 | 28.8 | 41.5 | 766.7 | 1153 |
| NP5 | 98.0 | 134 | 286.8 | 451 | 35.7 | 50.6 | 927.9 | 1388 |
| NP8 | 101.1 | 139 | 302.8 | 476 | 36.3 | 51.4 | 979.2 | 1475 |
| NP13 | 100.2 | 138 | 295.9 | 467 | 36.1 | 51.4 | 957.1 | 1440 |
| CP4 | 95.8 | 132 | 274.5 | 436 | 34.1 | 48.6 | 895.8 | 1339 |
| CP11 | 85.4 | 121 | 275.1 | 447 | 30.3 | 44.2 | 859.2 | 1317 |
| CP13 | 102.3 | 142 | 286.9 | 455 | 36.2 | 51.8 | 955.9 | 1436 |
| CP14 | 97.5 | 136 | 274.0 | 433 | 33.9 | 48.3 | 905.2 | 1354 |
| CP15 | 83.1 | 115 | 262.7 | 421 | 30.0 | 43.0 | 820.8 | 1232 |
2.2. Transformation of the Wave Energy in the Nearshore of Canary Islands and Madeira Archipelago
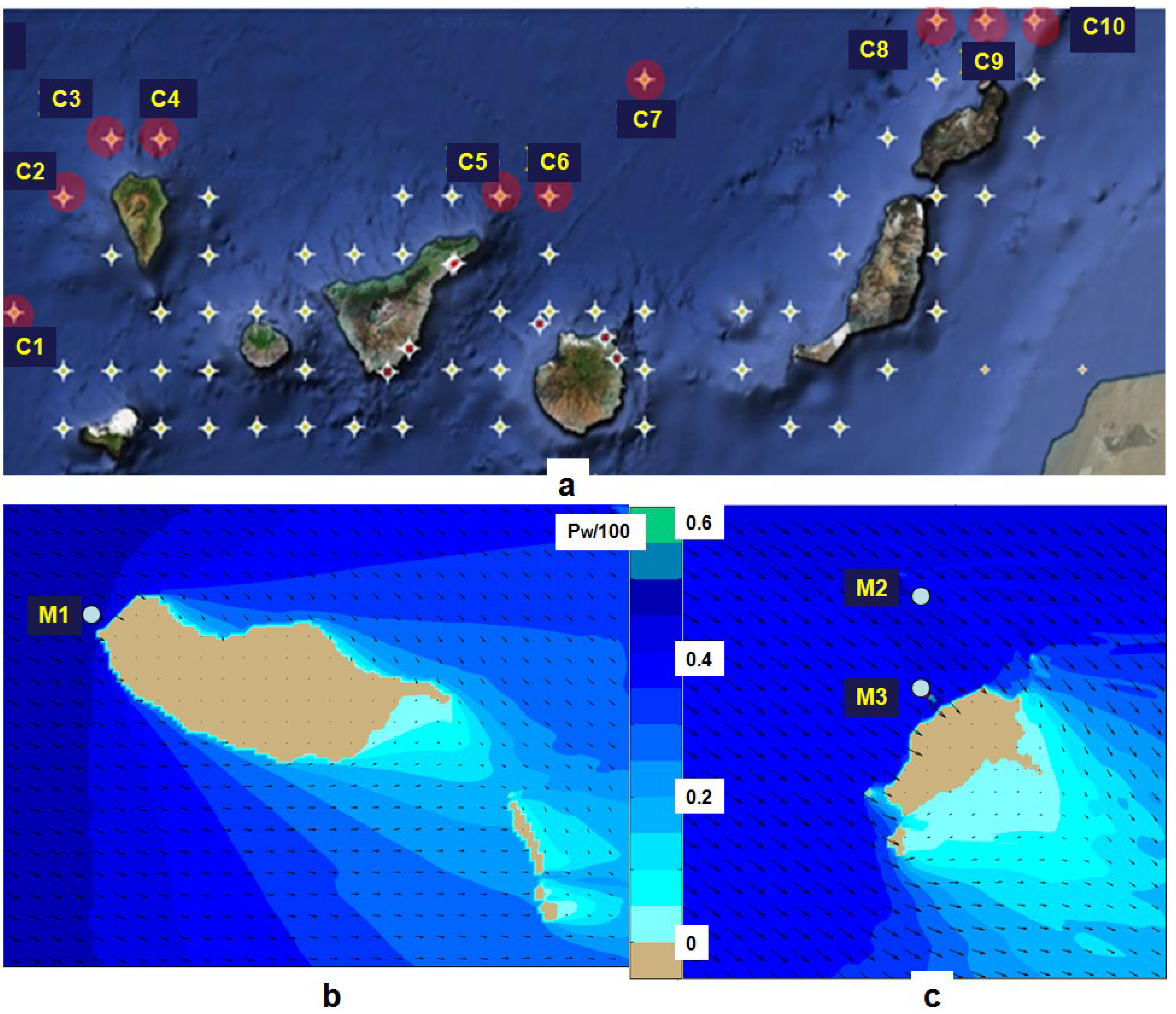
| C-points Pw (kW/m) | C1 | C2 | C3 | C4 | C5 | C6 | C7 | C8 | C9 | C10 |
|---|---|---|---|---|---|---|---|---|---|---|
| TT | 16.3 | 16.2 | 17.3 | 17.3 | 16.8 | 16.9 | 17.4 | 19.1 | 19.1 | 19.3 |
| WT | 18.2 | 18.4 | 19.2 | 19.0 | 18.3 | 18.5 | 19.2 | 20.6 | 20.6 | 20.7 |
| M-points | M1 | M2 | M3 | – | – | – | – | – | – | – |
| WT | 51.5 | 65.4 | 57.4 | – | – | – | – | – | – | – |
| PE (kW) Point/Period | Pelamis | AWS | Aqua Buoy | OE Buoy | Langlee | Wave Bob | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| TT | WT | TT | WT | TT | TT | WT | WT | TT | WT | TT | WT | |
| C1 | 65.4 | 78.8 | 260.1 | 403.2 | 24.3 | 52.2 | 52.9 | 32.3 | 126.9 | 168.8 | 86.9 | 112.8 |
| C2 | 66.2 | 79.5 | 260.2 | 403.0 | 24.6 | 52.1 | 53.0 | 32.5 | 128.2 | 171.2 | 87.4 | 113.4 |
| C3 | 76.0 | 90.0 | 273.5 | 421.0 | 27.6 | 61.5 | 62.0 | 36.0 | 143.1 | 188.5 | 95.5 | 123.0 |
| C4 | 74.8 | 88.3 | 271.8 | 418.5 | 27.2 | 60.5 | 60.6 | 35.4 | 141.1 | 185.5 | 94.4 | 121.3 |
| C5 | 72.5 | 80.8 | 255.3 | 391.1 | 25.8 | 61.5 | 57.2 | 32.3 | 134.4 | 169.2 | 89.7 | 111.5 |
| C6 | 74.1 | 82.1 | 257.7 | 394.0 | 32.3 | 63.1 | 58.2 | 32.7 | 137.1 | 171.8 | 91.3 | 112.9 |
| C7 | 81.3 | 90.4 | 270.0 | 412.6 | 28.7 | 69.2 | 64.2 | 35.8 | 149.5 | 187.9 | 98.3 | 121.9 |
| C8 | 87.8 | 93.4 | 275.6 | 417.1 | 30.7 | 75.6 | 66.3 | 37.0 | 159.6 | 193.7 | 103.7 | 124.9 |
| C9 | 88.5 | 93.2 | 275.8 | 416.6 | 31.0 | 76.3 | 66.1 | 37.0 | 160.7 | 193.4 | 104.2 | 124.7 |
| C10 | 90.3 | 94.2 | 277.4 | 418.1 | 31.5 | 78.3 | 67.1 | 37.3 | 163.6 | 195.5 | 105.7 | 125.7 |
| PE (kW) Point/Period | Pelamis | Aqua Buoy | Wave Dragon | |||
|---|---|---|---|---|---|---|
| TT | WT | TT | WT | TT | WT | |
| M1 | - | 134.9 | - | 40.2 | - | 1147.4 |
| M3 | - | 105.3 | - | 50.4 | - | 1644.2 |
| B | 60.0 | 89.0 | 15.9 | 24.0 | 391.2 | 578.1 |
| F | 69.7 | 98.0 | 12.1 | 25.5 | 735.4 | 895.1 |
2.3. Transformation of the Wave Energy in Enclosed Environments with Sea Waves
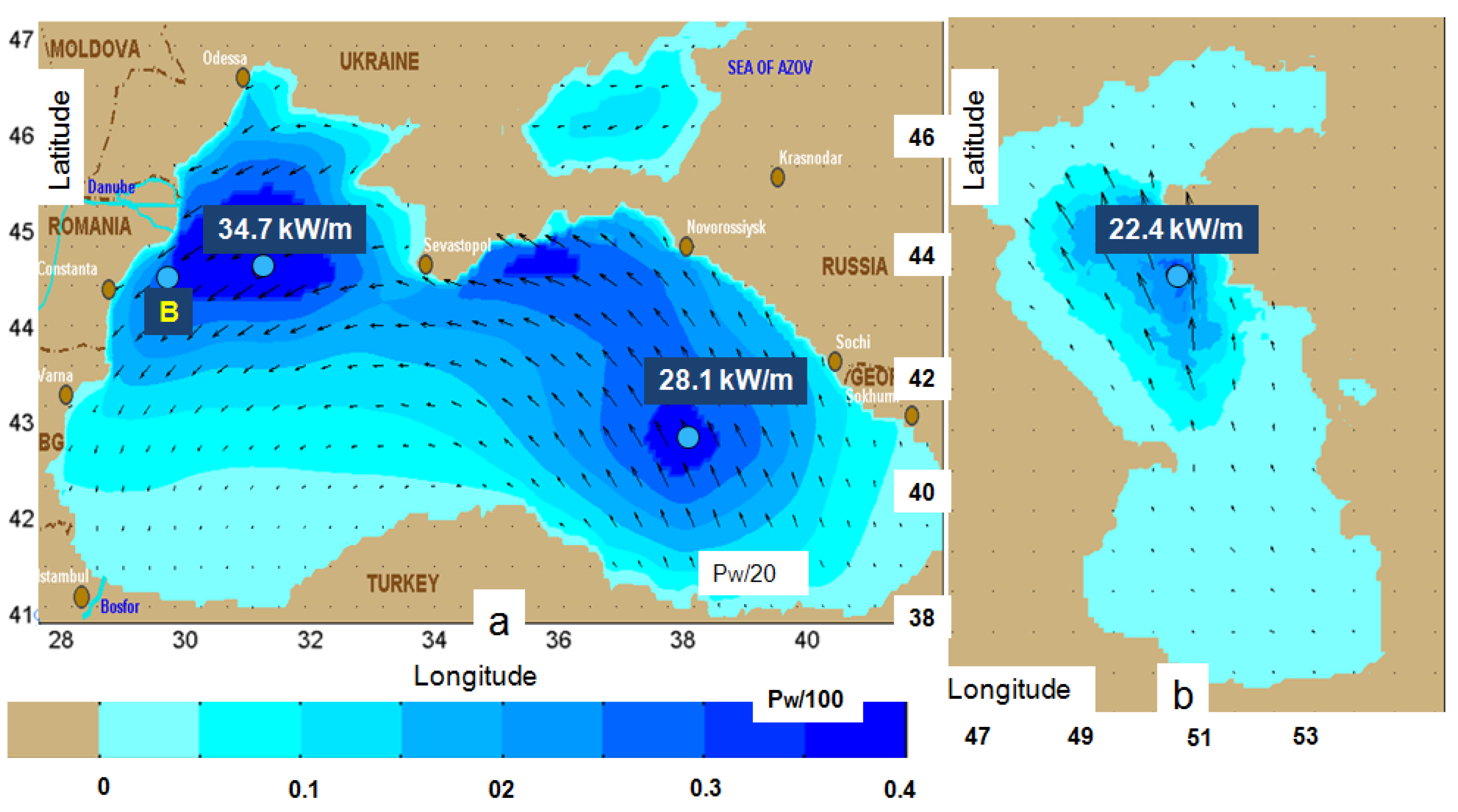
2.4. Discussion
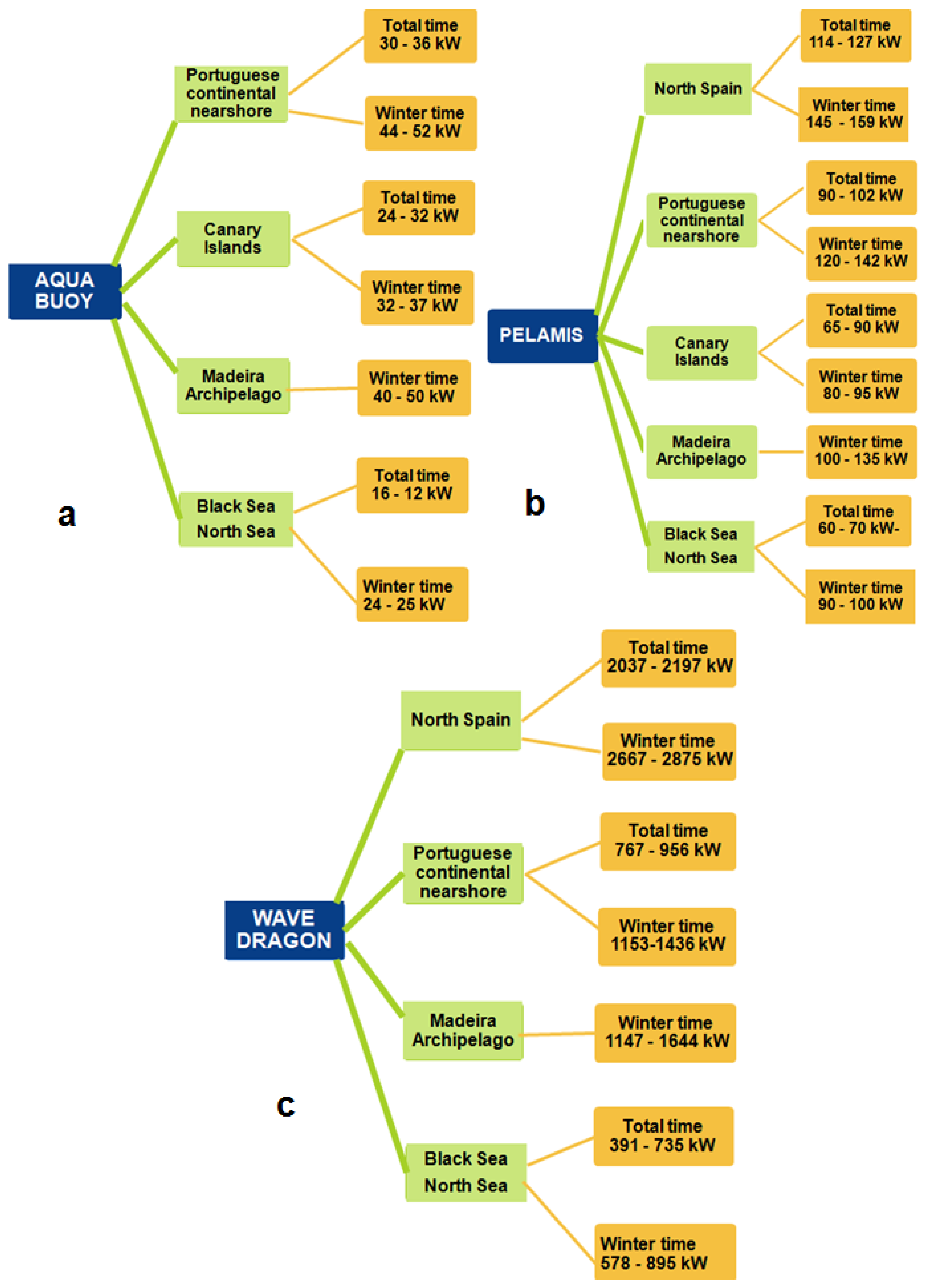
| IL (%) Location/Period | Pelamis | Aqua Buoy | Wave Dragon | |||
|---|---|---|---|---|---|---|
| TT | WT | TT | WT | TT | WT | |
| Spanish Nearshore | 15.2–16.9 | 19.3–21.1 | - | - | 34.5–37.3 | 45.2–48.7 |
| Sea Environment | - | 11.9–13.07 | - | 8.4–9.5 | - | 8.2–2.78 |
| Cw (m) Location/Period | Pelamis | Aqua Buoy | Wave Dragon | |||
|---|---|---|---|---|---|---|
| TT | WT | TT | WT | TT | WT | |
| Spanish Nearshore | 3.98–4.13 | 2.80–2.93 | - | - | 69.42–73.05 | 51.0–53.77 |
| Portuguese Nearshore | 3.3–4.2 | 3.0–3.7 | 1.2–1.5 | 1.1–1.4 | 33.1–39.2 | 32.0–38.0 |
| Madeira Archipelago | - | 1.61–2.62 | - | 0.77–0.78 | - | 22.28–25.14 |
3. Conclusions
Acknowledgments
Conflicts of Interest
References
- Nielsen, K. Ocean Energy Technology Study; Technical Report No.1 for the Alliance for Offshore Renewables; Danish Wave Energy Center: Hanstholm, Danmark, 2012. [Google Scholar]
- European Commission. Energy Roadmap 2050; European Commission: Brussels, Belgium, 2011; p. 885. [Google Scholar]
- European Commission. Technology Map of the SET-Plan; European Commission: Brussels, Belgium, 2011; p. 24979. [Google Scholar]
- OCEANTEC—Desarrollo Tecnologico de un Sistema de Aprovechamiento de la Energia de las olas. Available online: http://www.bizkaia.net/Home2/Archivos/DPTO8/Temas/Pdf/Ekin_Eus_2005/16-2005.pdf (accessed on 18 June 2014).
- Henderson, R. Design, simulation, and testing of a novel hydraulic power take-off system for the Pelamis wave energy converter. Energy 2006, 31, 271–283. [Google Scholar]
- Babarit, A.; Hals, J.; Muliawan, M.J.; Kurniawan, A.; Moan, T.; Krokstad, J. Numerical benchmarking study of a selection of wave energy converters. Renew. Energy 2012, 41, 44–63. [Google Scholar]
- Kofoed, J.P.; Frigaard, P.; Friis-Madsen, E.; Sørensen, H.C. Prototype testing of the wave energy converter Wave Dragon. Energy 2006, 31, 181–189. [Google Scholar]
- Weinstein, A.; Fredrikson, G.; Parks, M.J.; Neislen, K. AquaBuOY—The offshore wave energy converter: Numerical modeling and optimization. In Proceedings of the Oceans ’04 MTS/IEEE Techno-Ocean’04, Kobe, Japan, 9–12 November 2004.
- Variability of UK Marine Resources; Environmental Change Institute: Oxford, UK, 2005.
- LaBonte, A.; O’Connor, P.; Fitzpatrick, C.; Hallett, K.; Li, Y. Standardized cost and performance reporting for marine and hydrokinetic technologies. In Proceedings of the 1st Marine Energy Technology Symposium (METS13), Washington, DC, USA, 10–11 April 2013.
- EMEC. The European Marine Energy Centre 2009. In Assessment of Wave Energy Resource; The European Marine Energy Centre Ltd.: Stromness, Orkney, UK, 2009; Volume 36. [Google Scholar]
- Waters, R.; Engstrom, J.; Isberg, J.; Leijon, M. Wave climate off the Swedish west coast. Renew. Energy 2009, 34, 1600–1606. [Google Scholar] [CrossRef]
- Carballo, R.; Iglesias, G. A methodology to determine the power performance of wave energy converters at a particular coastal location. Energy Convers. Manag. 2012, 61, 8–18. [Google Scholar] [CrossRef]
- Silva, D.; Rusu, E.; Guedes Soares, C. Evaluation of various technologies for wave energy conversion in the portuguese nearshore. Energies 2013, 6, 1344–1364. [Google Scholar] [CrossRef]
- Rusu, E.; Guedes Soares, C. Wave energy pattern around the Madeira islands. Energy 2012, 5, 771–785. [Google Scholar] [CrossRef]
- Iglesias, G.; Carballo, R. Wave farm impact: The role of farm-to-coast distance. Renew. Energy 2014, 69, 375–385. [Google Scholar] [CrossRef]
- Iglesias, G.; Carballo, R. Offshore and inshore wave energy assessment: Asturias (N Spain). Energy 2010, 35, 1964–1972. [Google Scholar] [CrossRef]
- Iglesias, G.; Carballo, R. Wave energy potential along the death coast (Spain). Energy 2009, 34, 1963–1975. [Google Scholar] [CrossRef]
- Iglesias, G.; Carballo, R. Wave energy resource in the Estaca de Bares area (Spain). Renew. Energy 2010, 35, 1574–8154. [Google Scholar] [CrossRef]
- Carballo, R.; Sánchez, M.; Ramos, V.; Taveira-Pinto, F.; Iglesias, G. A high resolution geospatial database for wave energy exploitation. Energy 2014, 68, 572–583. [Google Scholar] [CrossRef]
- WAMDI Group. The WAM model—A third generation ocean wave prediction model. J. Phys. Oceanogr. 1988, 18, 1775–1810. [Google Scholar] [CrossRef]
- Booij, N.; Ris, R.C.; Holthuijsen, L.H. A third-generation wave model for coastal regions. I—Model description and validation. J. Geophys. Res. 1999, 104, 7649–7666. [Google Scholar] [CrossRef]
- Rusu, E.; Ventura Soares, C.; Rusu, L. Computational strategies and visualization techniques for the waves modeling in the portuguese nearshore. In Maritime Transportation and Exploitation of Ocean and Coastal Resources; Taylor & Francis Publications: London, UK, 2006; pp. 1129–1136. [Google Scholar]
- Morales Vaquero, A.; Castro Ruiz, F.; Rusu, E. Evaluation of the wave power potential in the northwestern side of the Iberian nearshore. In Developments in Maritime Transportation and Exploitation of Sea Resources—Guedes Soares & López Peña; Taylor & Francis Group: London, UK, 2014; pp. 1012–1019. [Google Scholar]
- Rusu, E.; Guedes Soares, C. Numerical modeling to estimate the spatial distribution of the wave energy in the Portuguese nearshore. Renew. Energy 2009, 34, 1501–1516. [Google Scholar] [CrossRef]
- Tolman, H.L. A third-generation model for wind waves on slowly varying, unsteady and inhomogeneous depths and currents. J. Phys. Oceanogr. 1991, 21, 782–797. [Google Scholar] [CrossRef]
- Molina Andres, O.; Castro Ruiz, F.; Rusu, L. Efficiency assessments for different WEC types in the Canary Islands. In Developments in Maritime Transportation and Exploitation of Sea Resources—Guedes Soares & López Peña; Taylor & Francis Group: London, UK, 2014; pp. 879–887. [Google Scholar]
- Rusu, L.; Guedes Soares, C. Wave energy assessments in the Azores islands. Renew. Energy 2012, 45, 183–196. [Google Scholar] [CrossRef]
- Veigas, M.; Iglesias, G. ave and offshore wind potential for the island of Tenerife. Energy Convers. Manag. 2013, 76, 738–745. [Google Scholar] [CrossRef]
- Iglesias, G.; Carballo, R. Wave resource in El Hierro-an island towards energy self-sufficiency. Renew. Energy 2011, 36, 689–698. [Google Scholar] [CrossRef]
- Rusu, E. Wave energy assessments in the Black Sea. J. Mar. Sci. Technol. 2009, 14, 359–372. [Google Scholar] [CrossRef]
- Rusu, E.; Onea, F. Evaluation of the wind and wave energy along the Caspian Sea. Energy 2013, 50, 1–14. [Google Scholar] [CrossRef]
- Onea, F. Study Concerning the Opportunity of the Renewable Energy Extraction in Marine Environment with Application to the Black Sea Basin. Ph.D. Thesis, Dunarea de Jos University of Galati, Galaţi, Romania, 2013; p. 223. [Google Scholar]
- Vicinanza, D.; Margheritini, L.; Kofoed, J.P.; Buccino, M. The SSG wave energy converter: Performance, status and recent developments. Energies 2012, 5, 193–226. [Google Scholar] [CrossRef]
- Buccino, M.; Banfi, D.; Vicinanza, D.; Calabrese, M.; del Giudice, G.; Carravetta, A. Non breaking wave forces at the front face of seawave slotcone generators. Energies 2012, 5, 4779–4803. [Google Scholar] [CrossRef]
© 2014 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Rusu, E. Evaluation of the Wave Energy Conversion Efficiency in Various Coastal Environments. Energies 2014, 7, 4002-4018. https://doi.org/10.3390/en7064002
Rusu E. Evaluation of the Wave Energy Conversion Efficiency in Various Coastal Environments. Energies. 2014; 7(6):4002-4018. https://doi.org/10.3390/en7064002
Chicago/Turabian StyleRusu, Eugen. 2014. "Evaluation of the Wave Energy Conversion Efficiency in Various Coastal Environments" Energies 7, no. 6: 4002-4018. https://doi.org/10.3390/en7064002
APA StyleRusu, E. (2014). Evaluation of the Wave Energy Conversion Efficiency in Various Coastal Environments. Energies, 7(6), 4002-4018. https://doi.org/10.3390/en7064002