Study on the Optimal Charging Strategy for Lithium-Ion Batteries Used in Electric Vehicles
Abstract
:1. Introduction
2. Lumped Parameter Battery Model
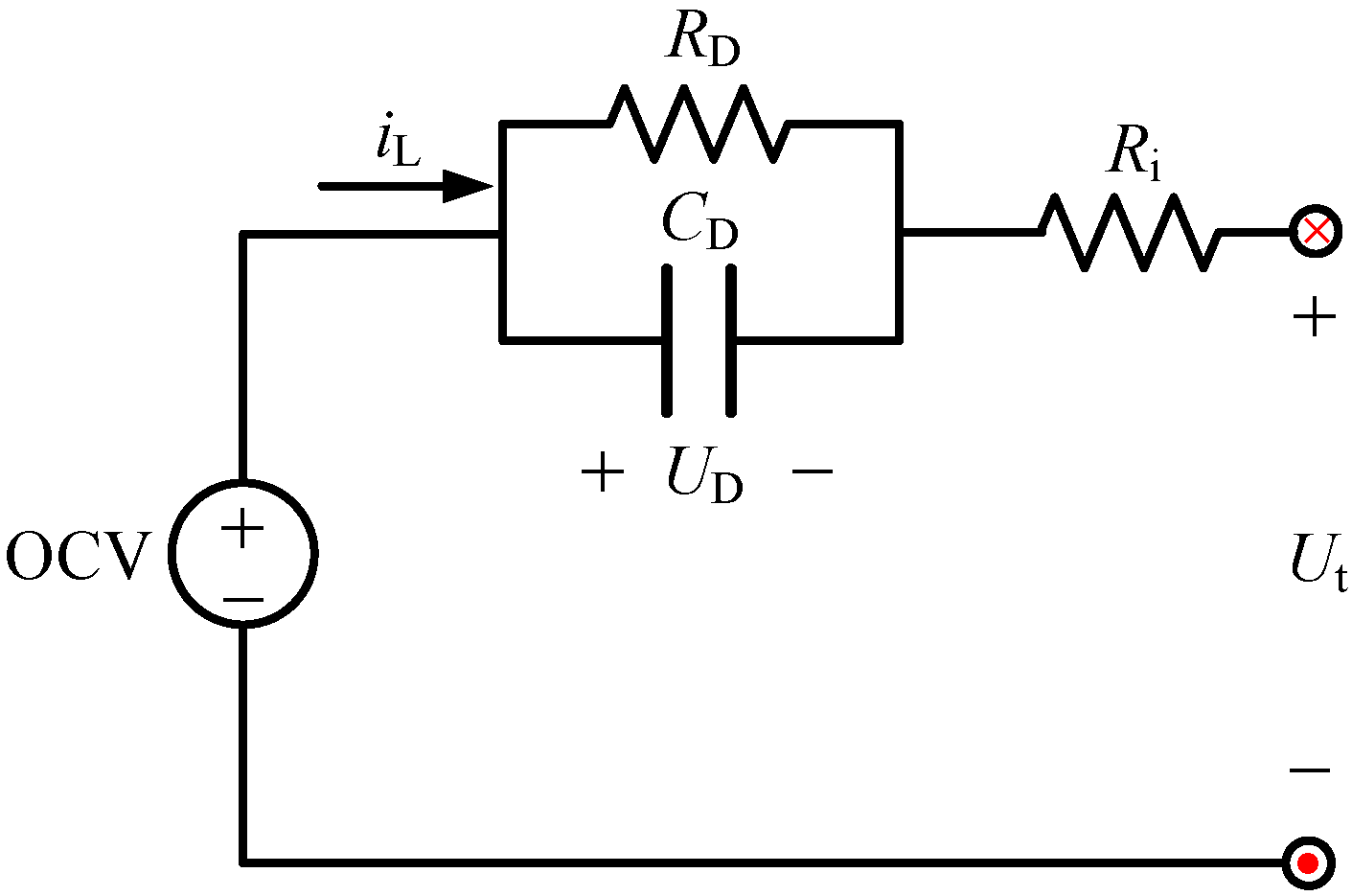
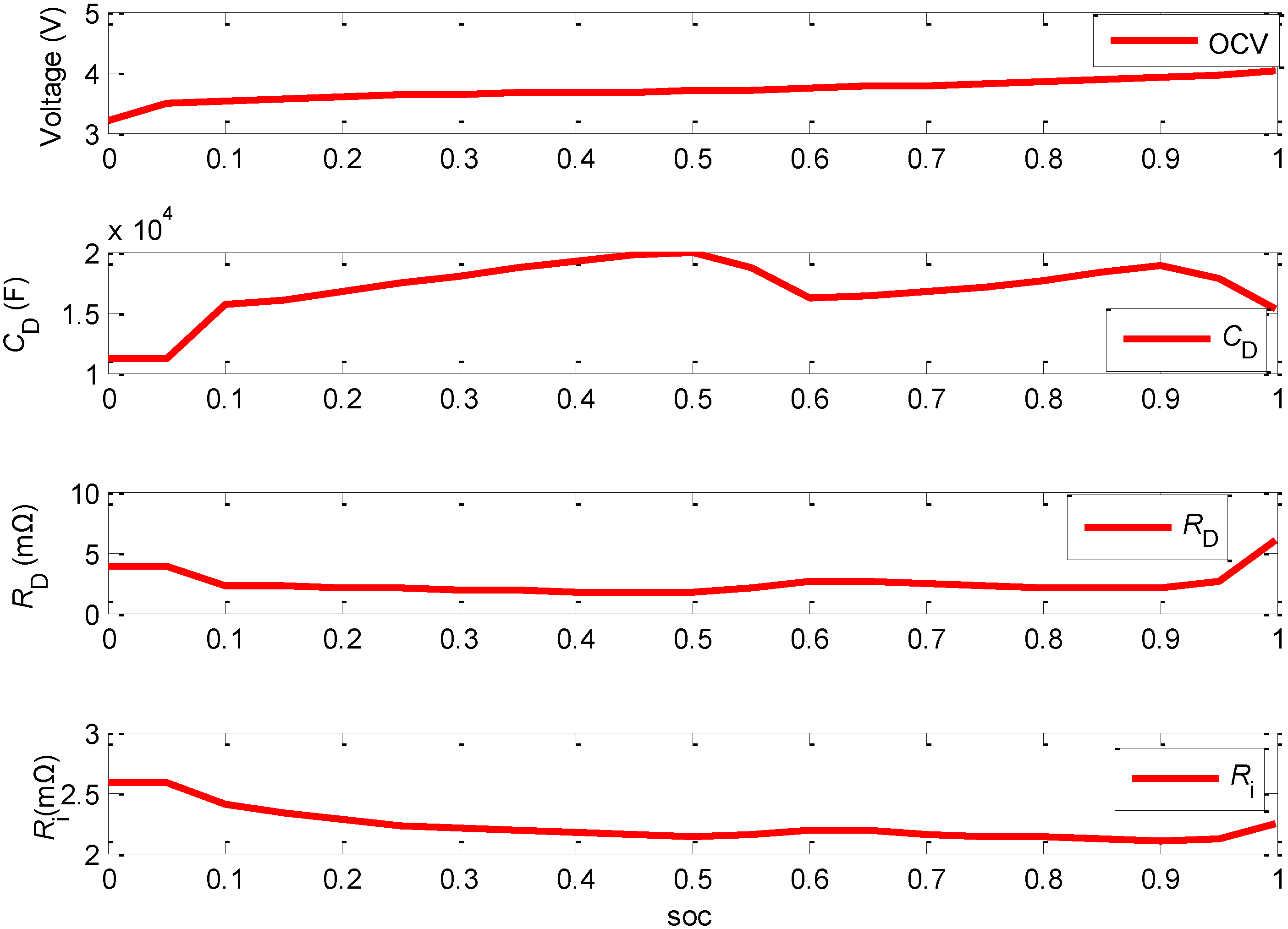
3. Dynamic Optimization Problem
3.1. Problem Definition
| Bound | Value | Bound | Value |
|---|---|---|---|
| Imin (A) | −96 | UD_min (V) | −0.2 |
| Imax (A) | 0 | UD_max (V) | 0 |
| Ut_min (V) | 3.0 | SOCmin | 0.2 |
| Ut_max (V) | 4.05 | SOCmax | 1 |
| Tmin (s) | 1000 | Tmax (s) | 2700 |
| Parameter | SOC | UD | I |
|---|---|---|---|
| Range | [0.2, 1] | [−0.2, 0.2] | [−96, 96] |
| Discretization | 0.0142 | 0.004 V | 0.8 A |
3.2. The Simulation Results
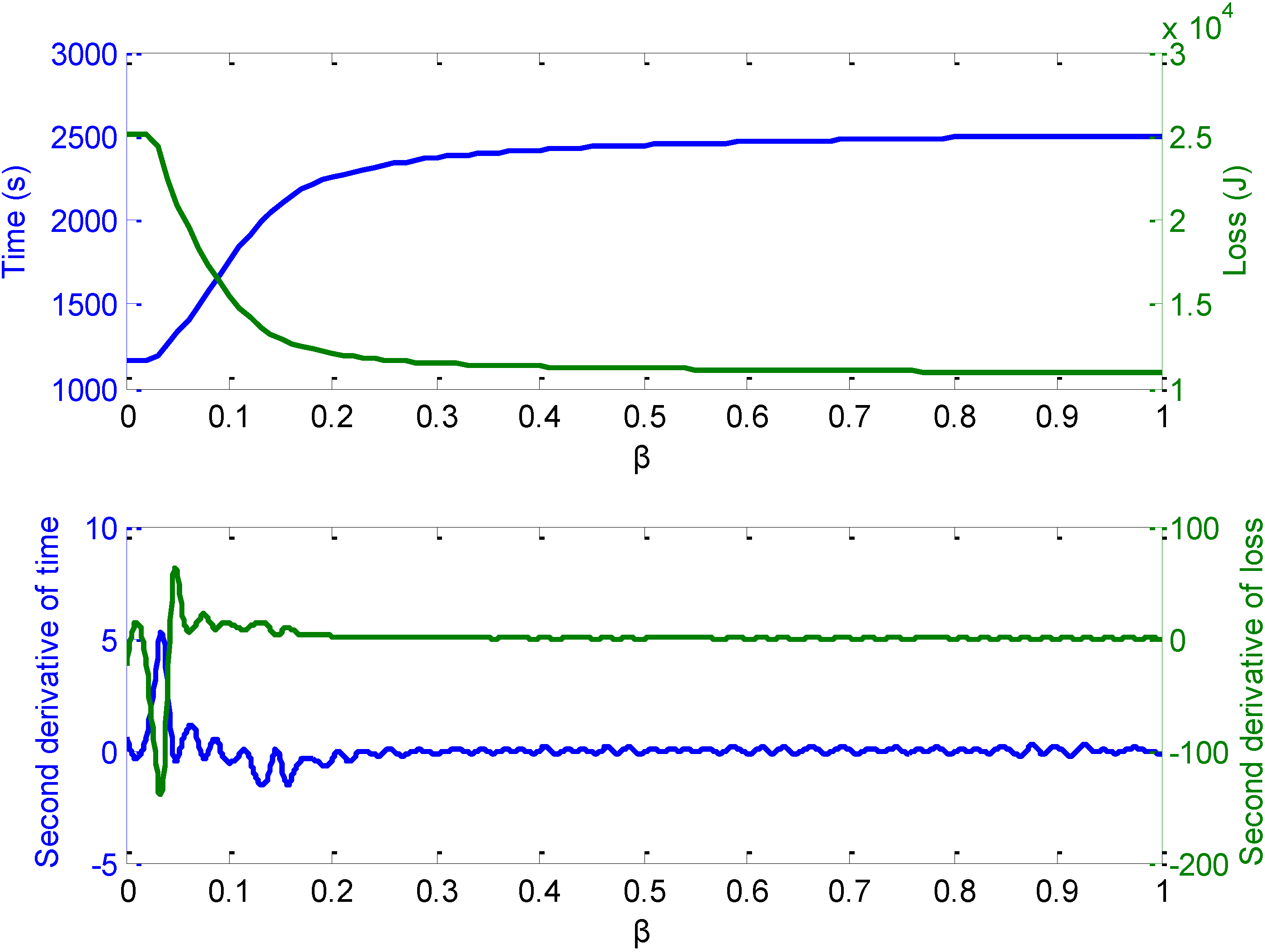
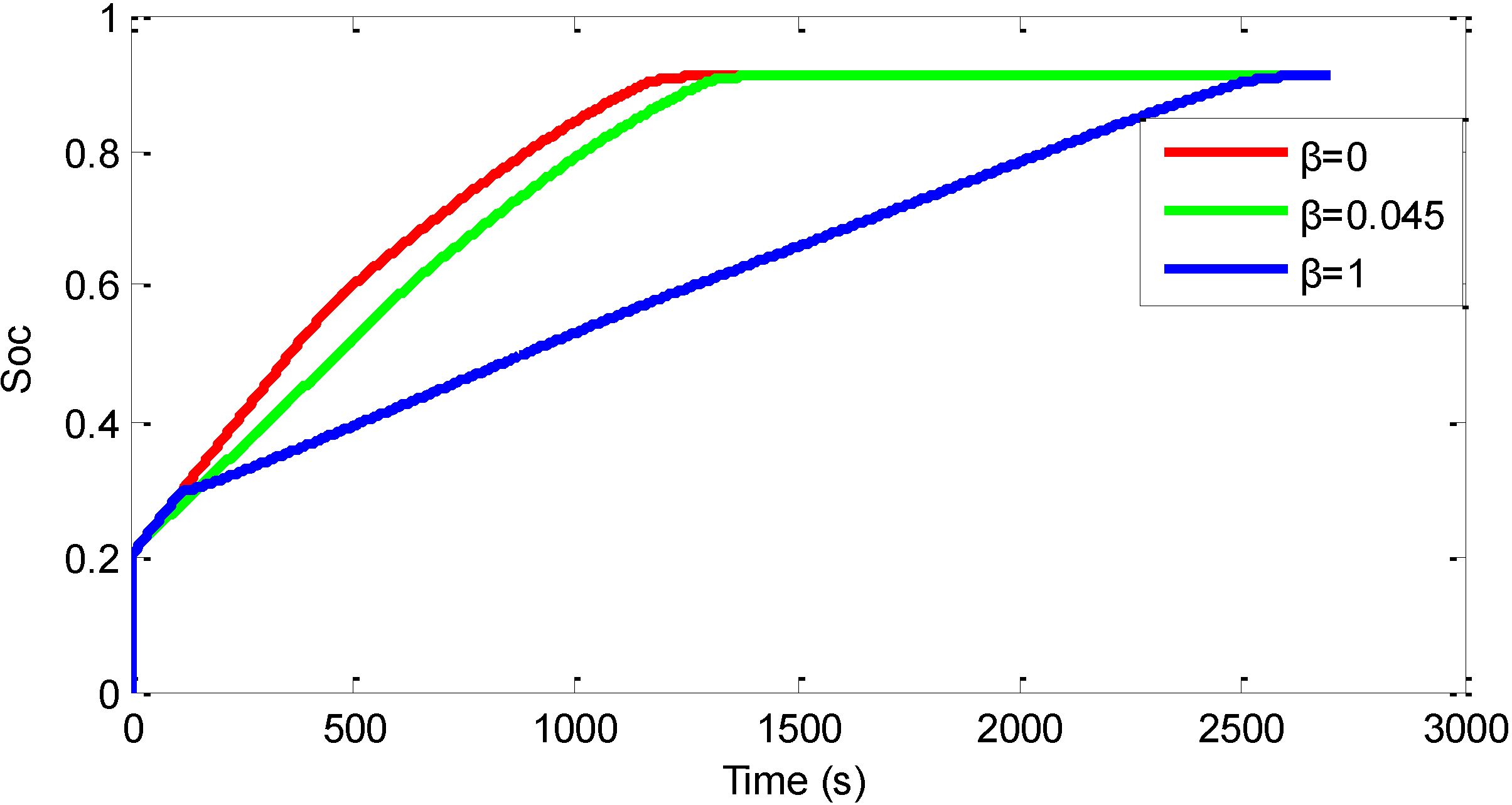
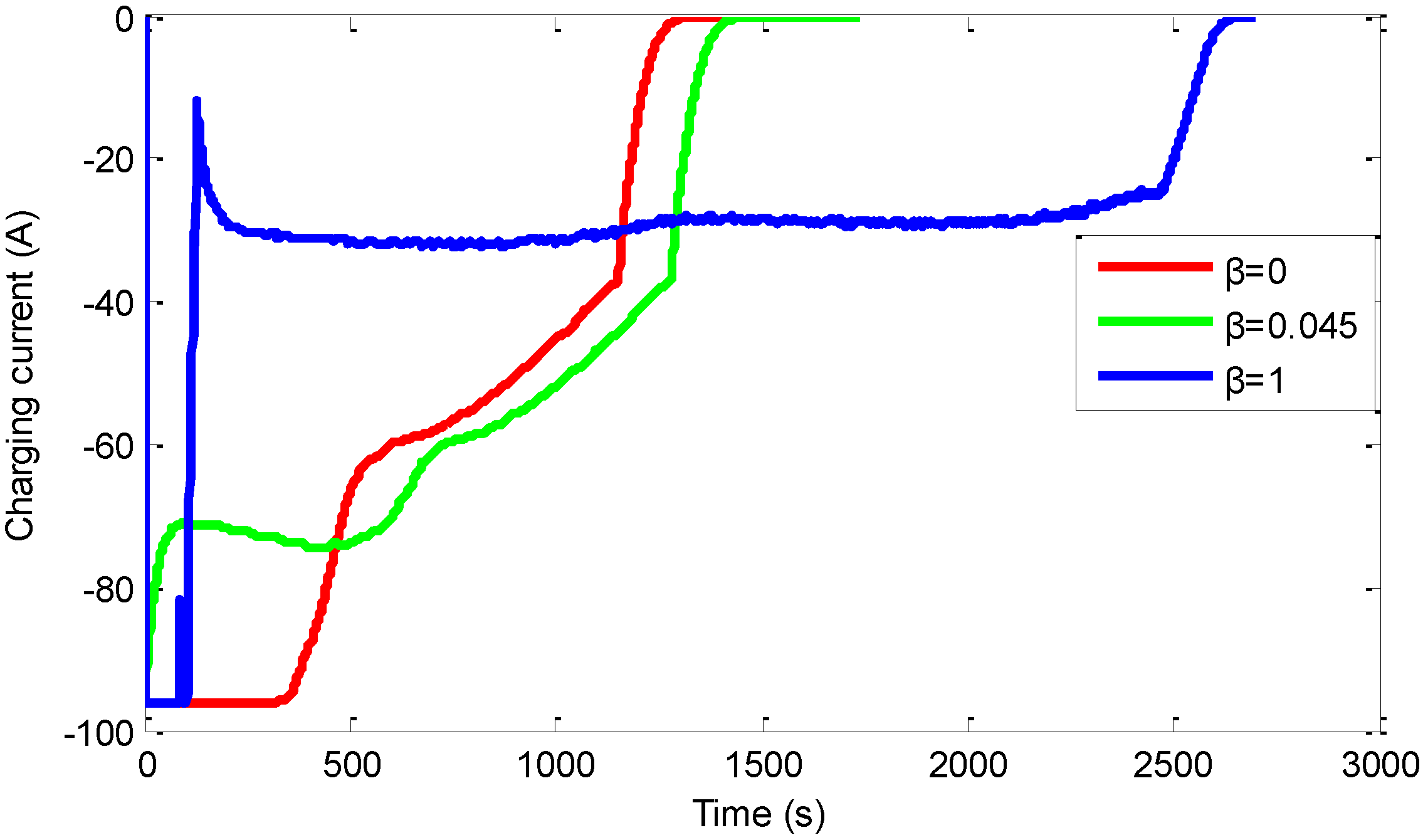
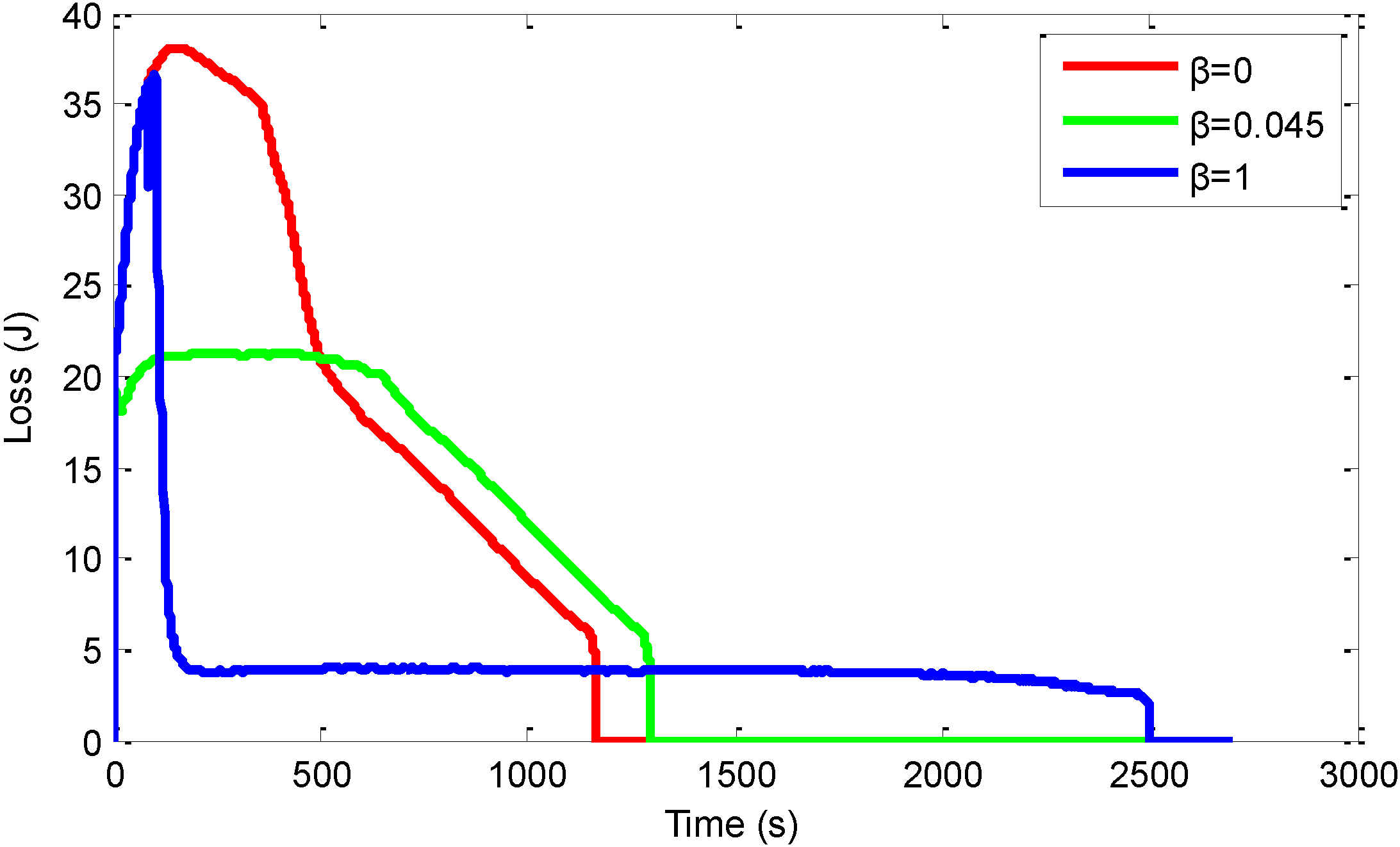
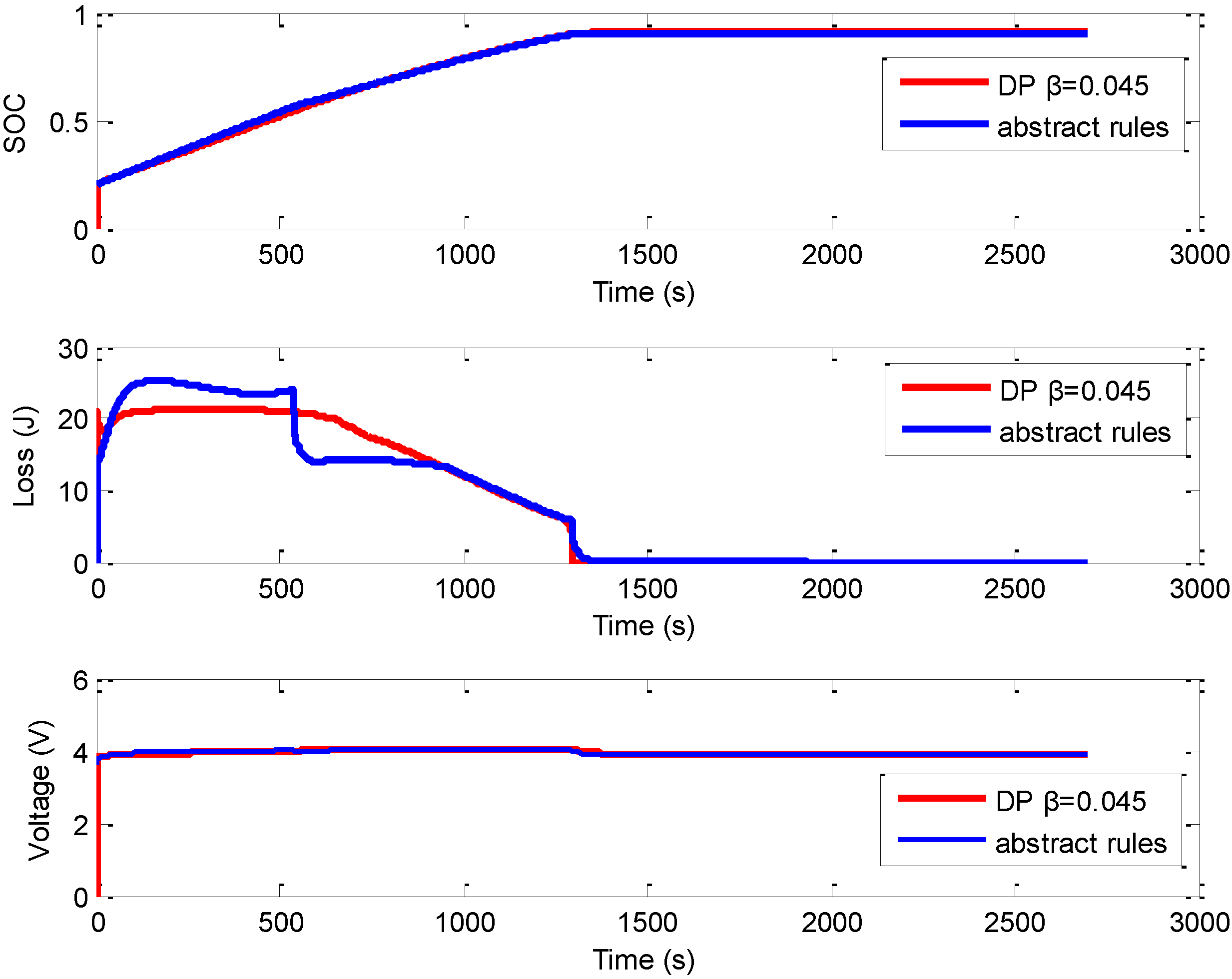
3.3. The Abstracted Control Strategy and Simulation Results

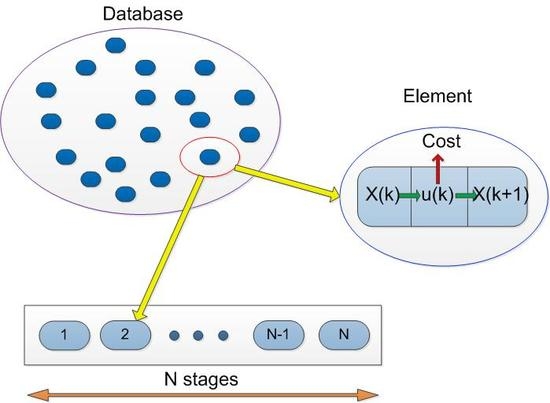
4. The Database Based Dynamic Programing Optimal Method
4.1. The Operation Principle of the Database
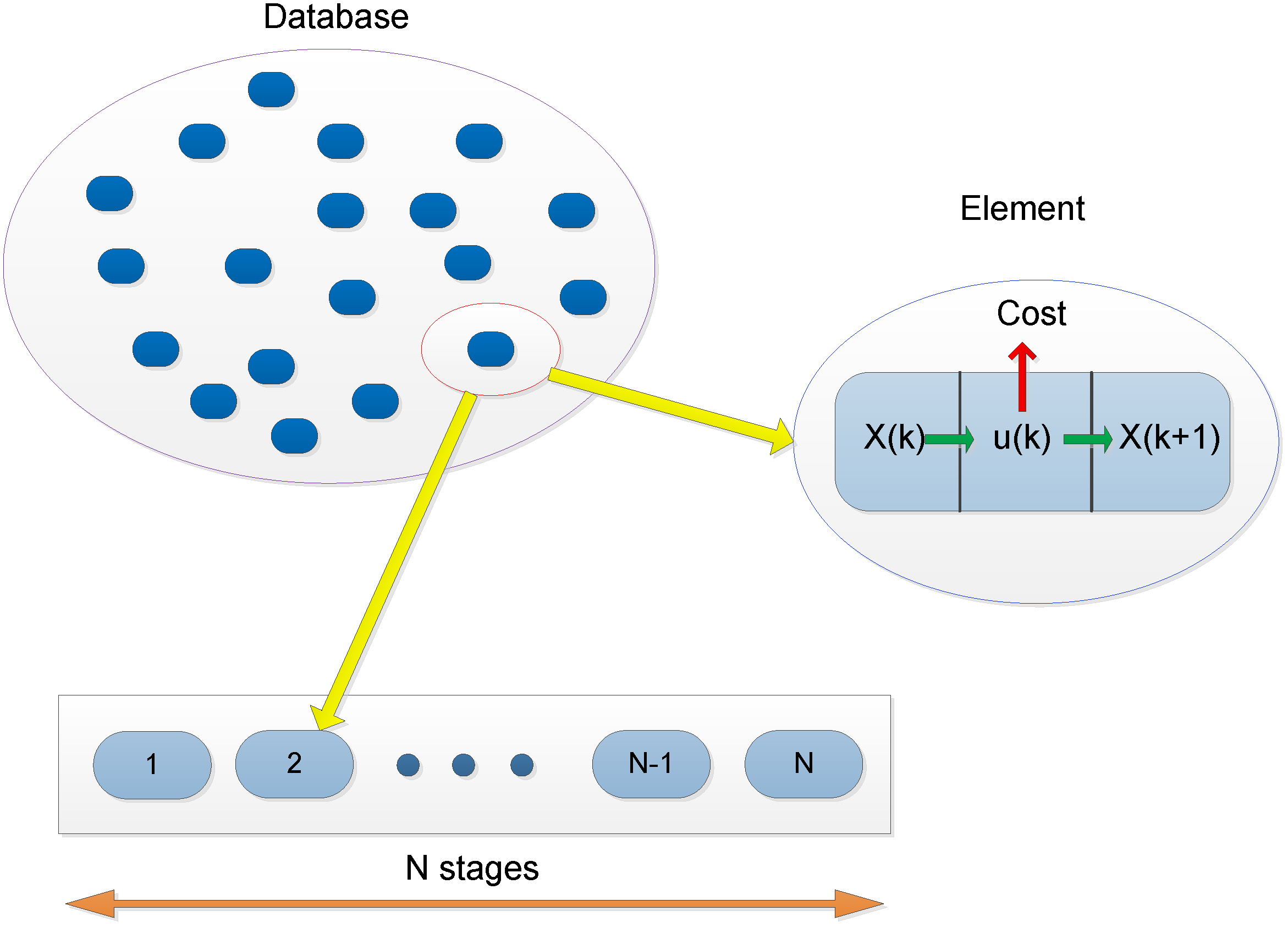
4.2. The Construction of Database
4.3. The Simulation Results for the Databased Dynamic Programing Method
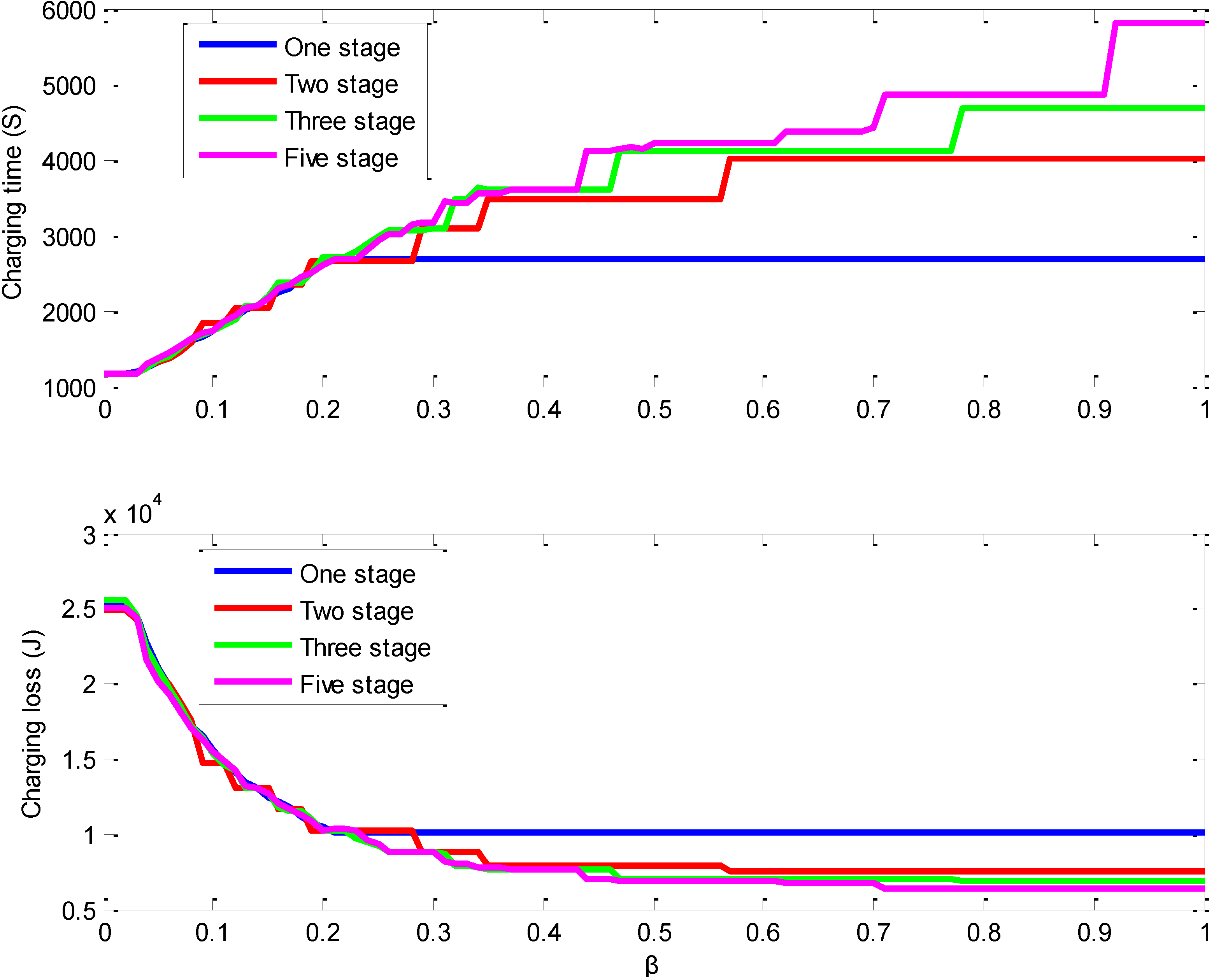

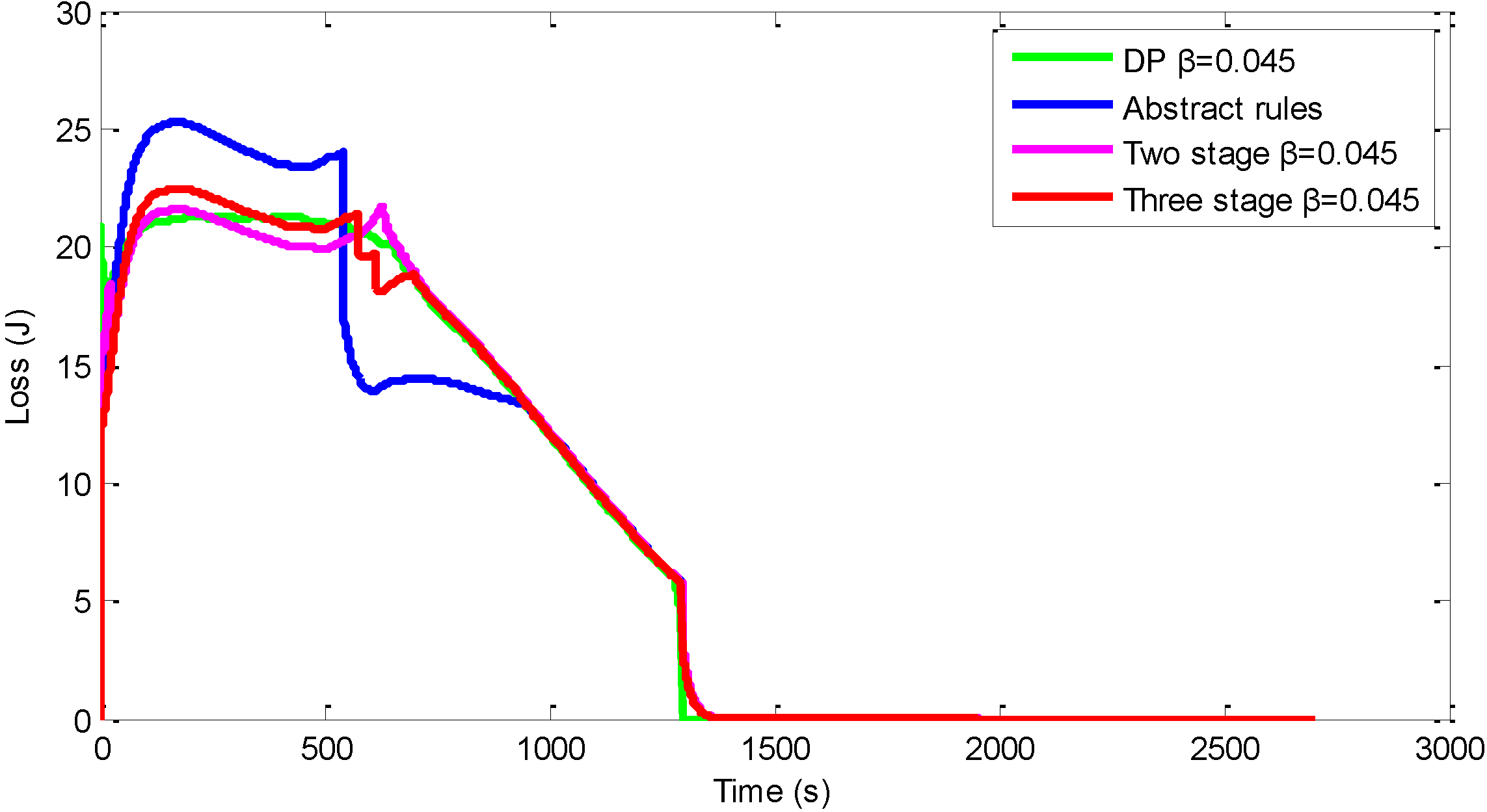
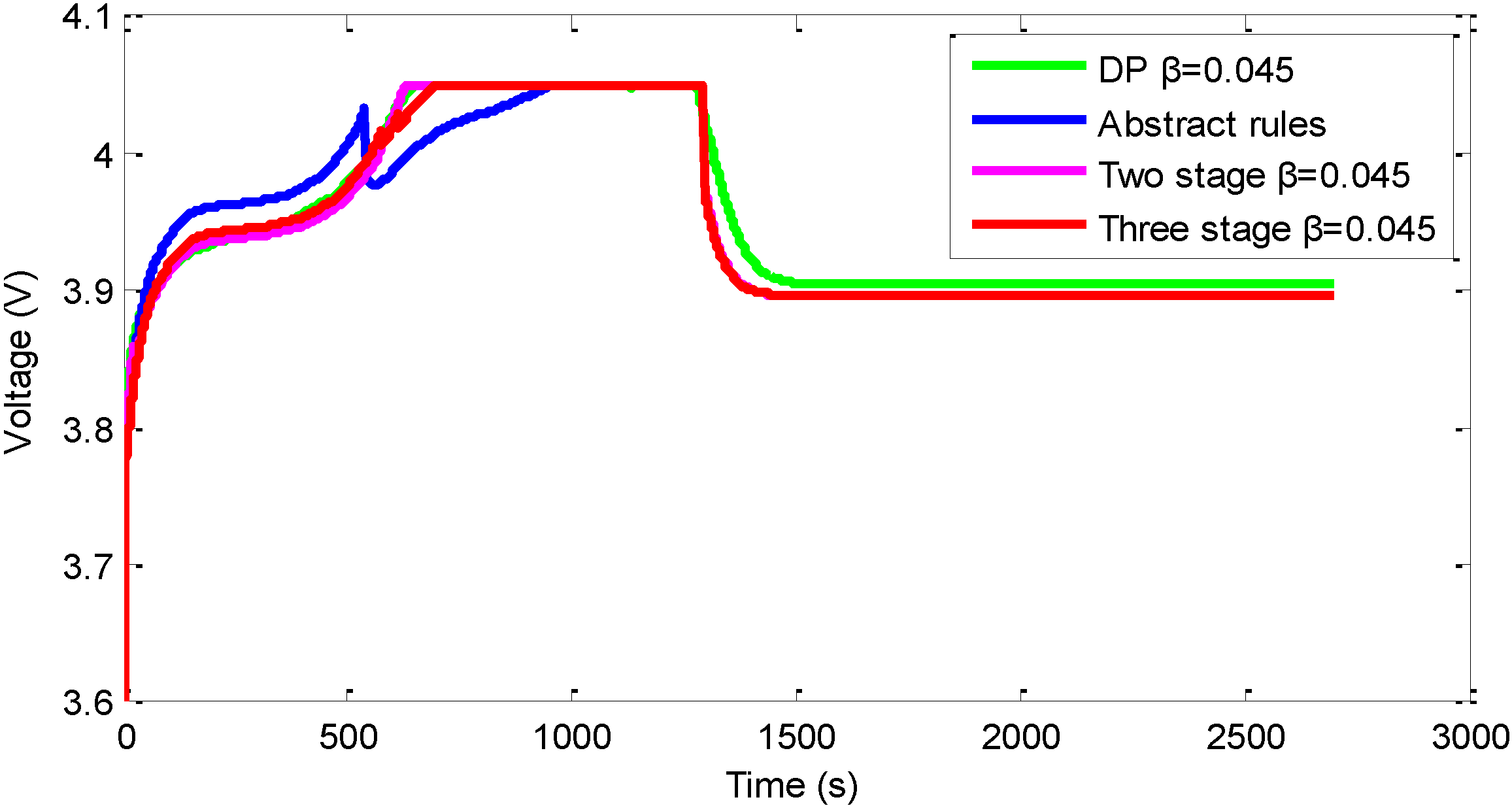
| Method | Charging time (s) | Charging loss (kJ) |
|---|---|---|
| DP β = 0.045 | 1294 | 21.65 |
| Abstract rules | 1298 | 21.82 |
| Database (two stage) β = 0.045 | 1298 | 21.57 |
| Database (three stage) β = 0.045 | 1294 | 21.67 |
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Chen, L.-R.; Wu, S.-L.; Chen, T.-R.; Yang, W.-R.; Wang, C.-S.; Chen, P.-C. Detecting of Optimal Li-Ion Battery Charging Frequency by Using AC Impedance Technique. In Proceedings of the 4th IEEE Conference on Industrial Electronics and Applications (ICIEA 2009), Xi’an, Shaanxi, China, 25–27 May 2009; pp. 3378–3381.
- Xiong, R.; Sun, F.; Chen, Z.; He, H. A data-driven multi-scale extended Kalman filtering based parameter and state estimation approach of lithium-ion polymer battery in electric vehicles. Appl. Energy 2014, 113, 463–476. [Google Scholar] [CrossRef]
- Xiong, R.; Sun, F.; Gong, X.; Gao, C. A data-driven based adaptive state of charge estimator of lithium-ion polymer battery used in electric vehicles. Appl. Energy 2014, 113, 1421–1433. [Google Scholar] [CrossRef]
- Xiong, R.; Sun, F.; Gong, X.; He, H. Adaptive state of charge estimator for lithium-ion cells series battery pack in electric vehicles. J. Power Sources 2013, 242, 699–713. [Google Scholar] [CrossRef]
- Xiong, R.; Sun, F.; He, H.; Nguyen, T. A data-driven adaptive state of charge and power capability joint estimator of lithium-ion polymer battery used in electric vehicles. Energy 2013, 63, 295–308. [Google Scholar] [CrossRef]
- Yilmaz, M.; Krein, P.T. Review of battery charger topologies, charging power levels, and infrastructure for plug-in electric and hybrid vehicles. IEEE Trans. Power Electron. 2013, 28, 2151–2169. [Google Scholar] [CrossRef]
- Ahn, C.S.; Li, C.-T.; Peng, H. Optimal decentralized charging control algorithm for electrified vehicles connected to smart grid. J. Power Sources 2011, 196, 10369–10379. [Google Scholar] [CrossRef]
- Bashash, S.; Moura, S.J.; Forman, J.C.; Fathy, H.K. Plug-in hybrid electric vehicle charge pattern optimization for energy cost and battery longevity. J. Power Sources 2011, 196, 541–549. [Google Scholar] [CrossRef]
- Bashash, S.; Moura, S.J.; Fathy, H.K. On the aggregate grid load imposed by battery health-conscious charging of plug-in hybrid electric vehicles. J. Power Sources 2011, 196, 8747–8754. [Google Scholar] [CrossRef]
- Carcone, J.A. Performance of lithium-ion battery systems. In Proceedings of the WESCON/94. Idea/Microelectronics. Conference Record, Anaheim, CA, USA, 27–29 September 1994; pp. 242–248.
- Tseng, S.-Y.; Shih, T.-C.; Fan, S.-Y.; Chang, G.-K. Design and implementation of lithium-ion/lithium-polymer battery charger with impedance compensation. In Proceedings of the International Conference on Power Electronics and Drive Systems (PEDS 2009), Taipei, Taiwan, 2–5 November 2009; pp. 866–870.
- Dearborn, S. Charging Li-ion batteries for maximum run times. Power Electron. Technol. 2005, 31, 40–49. [Google Scholar]
- Zhang, S.S.; Xu, K.; Jow, T.R. Study of the charging process of a LiCoO2-based Li-ion battery. J. Power Sources 2006, 160, 1349–1354. [Google Scholar] [CrossRef]
- Liu, Y.-H.; Teng, J.-H.; Lin, Y.-C. Search for an optimal rapid charging pattern for lithium-ion batteries using ant colony system algorithm. IEEE Trans. Ind. Electron. 2005, 52, 1328–1336. [Google Scholar] [CrossRef]
- Hsieh, G.-C.; Chen, L.-R.; Huang, K.-S. Fuzzy-controlled Li-ion battery charge system with active state-of-charge controller. IEEE Trans. Ind. Electron. 2001, 48, 585–593. [Google Scholar] [CrossRef]
- Surmann, H. Genetic optimization of a fuzzy system for charging batteries. IEEE Trans. Ind. Electron. 1996, 43, 541–548. [Google Scholar] [CrossRef]
- Ullah, Z.; Burford, B.; Dillip, S. Fast intelligent battery charging: Neural-fuzzy approach. IEEE Aerosp. Electron. Syst. Mag. 1996, 11, 26–34. [Google Scholar] [CrossRef]
- Chen, L.-R.; Hsu, R.C.; Liu, C.-S. A design of a grey-predicted Li-ion battery charge system. IEEE Trans. Ind. Electron. 2008, 55, 3692–3701. [Google Scholar] [CrossRef]
- Hu, X.; Li, S.; Pen, H.; Sun, F. Charging time and loss optimization for LiNMC and LiFePO4 batteries based on equivalent circuit models. J. Power. Sources 2013, 239, 449–457. [Google Scholar] [CrossRef]
- Lin, C.C.; Peng, H.; Grizzle, J.W.; Kang, J.M. Power management strategy for a parallel hybrid electric truck. IEEE Trans. Control Syst. Technol. 2003, 11, 839–849. [Google Scholar] [CrossRef]
- Brahma, A.; Guezennec, Y.; Rizzoni, G. Dynamic optimization of mechanical/electrical power flow in parallel hybrid electric vehicles. In Proceedings of the 5th International Symposium Advanced Vehicle Control, Ann Arbor, MI, USA, 22–24 August 2000.
- He, H.; Tang, H.; Wang, X. Global optimal energy management strategy research for a plug-in series-parallel hybrid electric bus by using dynamic programming. Math. Probl. Eng. 2013, 2013. [Google Scholar] [CrossRef]
- Wang, W.; Lukic, S.M. Dynamic programming technique in hybrid electric vehicle optimization. In Proceedings of the 2012 IEEE International Electric Vehicle Conference (IEVC), Greenville, SC, USA, 4–8 March 2012; pp. 1–8.
- Bertsekas, D.P. Dynamic Programming and Optimal Control; Athena Scientific: Belmont, MA, USA, 1995. [Google Scholar]
- Zou, Y.; Hou, S.J.; Han, E.L. Dynamic programming-based energy management strategy optimization for hybrid electric commercial vehicle. Automot. Eng. 2012, 34, 663–668. [Google Scholar]
- Zou, Y.; Hou, S.; Li, D.; Gao, W.; Hu, X. Optimal energy control strategy design for a hybrid electric vehicle. Discret. Dyn. Nat. Soc. 2013, 2013. [Google Scholar] [CrossRef]
- Zhang, S.; Zhang, C.; Han, G.; Wang, Q. Optimal control strategy design based on dynamic programming for a dual-motor coupling-propulsion system. Sci. World J. 2014, 2014. [Google Scholar] [CrossRef]
© 2014 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, S.; Zhang, C.; Xiong, R.; Zhou, W. Study on the Optimal Charging Strategy for Lithium-Ion Batteries Used in Electric Vehicles. Energies 2014, 7, 6783-6797. https://doi.org/10.3390/en7106783
Zhang S, Zhang C, Xiong R, Zhou W. Study on the Optimal Charging Strategy for Lithium-Ion Batteries Used in Electric Vehicles. Energies. 2014; 7(10):6783-6797. https://doi.org/10.3390/en7106783
Chicago/Turabian StyleZhang, Shuo, Chengning Zhang, Rui Xiong, and Wei Zhou. 2014. "Study on the Optimal Charging Strategy for Lithium-Ion Batteries Used in Electric Vehicles" Energies 7, no. 10: 6783-6797. https://doi.org/10.3390/en7106783
APA StyleZhang, S., Zhang, C., Xiong, R., & Zhou, W. (2014). Study on the Optimal Charging Strategy for Lithium-Ion Batteries Used in Electric Vehicles. Energies, 7(10), 6783-6797. https://doi.org/10.3390/en7106783