Numerical Investigation of the Thermal Management Performance of MEPCM Modules for PV Applications

Abstract

The efficiency of photovoltaic modules decreases as the cell temperature increases. It is necessary to have an adequate thermal management mechanism for a photovoltaic module, especially when combined with a building construction system. This study aims to investigate via computational fluid dynamics simulations the heat transfer characteristics and thermal management performance of microencapsulated phase change material modules for photovoltaic applications under temporal variations of daily solar irradiation. The results show that the aspect ratio of the microencapsulated phase change material layer has significant effects on the heat transfer characteristics and the overall thermal performance of the two cases examined with different melting points (26 °C and 34 °C) are approximately the same.

1. Introduction

The photovoltaic (PV) cell temperature is associated with the generation efficiency of the solar irradiation energy that is converted into electricity. The nominal power of a PV module is tested under standardized testing conditions (AM 1.5, 25 °C, 1000 W/m²). However, in a normal environment, it is difficult to maintain a PV cell temperature of 25 °C because the cell is affected by the ambient climate and heat transfer conditions. The efficiencies in a PV module decrease as the module temperature increases [1], therefore, whenever possible, it is necessary to enhance the heat dissipation of a PV module.

During the processes of melting or solidification, a phase change material (PCM) can effectively release or store a great amount of latent heat. The temperature of the PCM can also be stably maintained during the latent heat transfer process. Therefore, in the energy storage and thermal environmental control application, a PCM is a very promising material choice.

The applications of PCM include systems for thermal storage [2], integration with building materials, usage in fireproof engineering, etc. Integrating building materials with PCM for environmental control has been achieved by two PCM treatment methods: adding PCM particles during material production processing (especially microencapsulated PCM, MEPCM) or laminating PCM onto construction panels [3,4,5]. Comprehensive literature reviews on PCMs, thermophysical properties, long term stability, impregnation methods, current building applications and their thermal performance analyses, as well as numerical simulation of buildings with PCMs can be found in the cited review articles [6,7,8,9].

PV/PCM systems that use internal fins to limit the temperature increase in the PV cell are discussed in Huang et al. [10]. The results show that smaller width spacing lowers the constant temperature and shortens the melting process. Another way to improve the low thermal conductivity of PCMs is to combine the PCM with other materials such as metal. An experiment using a metal-embedded wax matrix showed that the PV temperature can be maintained at approximately 60–65 °C for some time interval and that the overall power gain was approximately 1.7 times when used on sunny days [11].

The existing literature on heat transfer investigations of MEPCM is still limited. Thus, in this study, the thermal performance of MEPCM layers for PV uses was investigated via engineering considerations and computational fluid dynamics (CFD) simulations.

2. Mathematical Treatment of the Simulation and Numerical Methods

2.1. Test Cell

Figure 1 shows a building facade integrated with a MEPCM (in grey color), where a building integrated PV (BIPV) panel was used as the investigated building façade in this study. G_s(t) represents the incident solar irradiation that penetrates a PV cell of thickness δ_pv. The top and bottom surfaces of the PV/MEPCM layer are assumed to be thermally insulated. The MEPCM layer has thickness W and length H.

The PV cell energy balance consists of a convection term, as well as terms for the solar irradiation and heat flux through the backside. Two cases are presented: one without MEPCM integration and the other with PV/MEPCM integration. In the case without the MEPCM, the amount of heat flux that exits the PV cell is equal to the heat transfer convection term on the back side, whereas in the case with PV/MEPCM, the heat flux exiting the PV cell is equal to the heat flux entering the MEPCM. We define x⁺ = 0 to be the position of the left wall of the MEPCM container and x⁺ = W to be the position of the right wall of the MEPCM.

Figure 1. Schematics of heat transfer in an MEPCM layer.

Figure 1. Schematics of heat transfer in an MEPCM layer.

PV without MEPCM:

$$q_{pv,out}^{″}=U_{\infty ,i}(T_{pv}-T_{\infty ,i})$$

(1)

PV/MEPCM integration:

$$x^{+}=0; q_{pv,out}^{″}=-k_m\frac{\partial T_m}{\partial x^{+}}$$

(2)

$$x^{+}=W; -k_m\frac{\partial T_m}{\partial x^{+}}=U_{\infty ,i}(T_m-T_{\infty ,i})$$

(3)

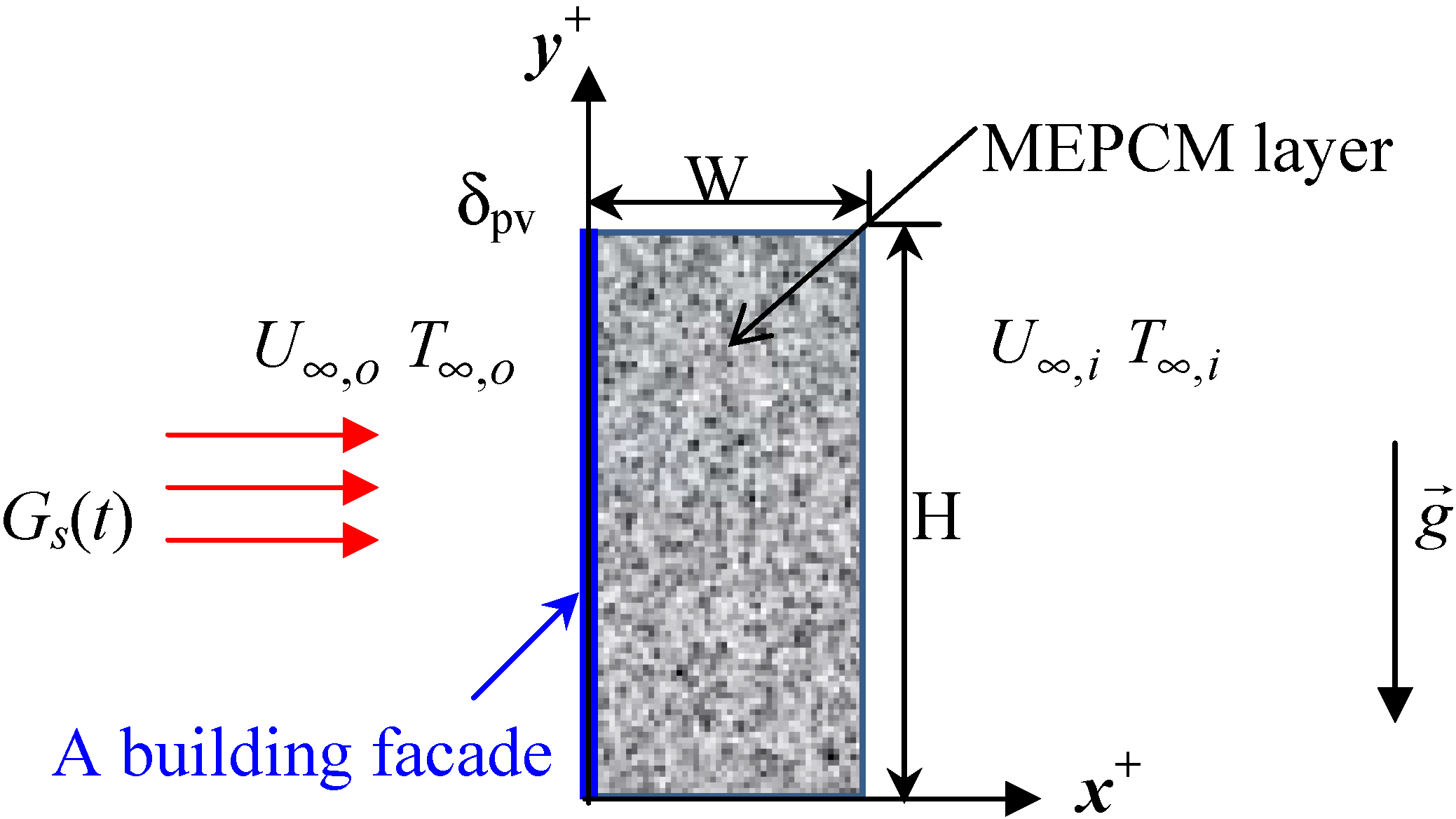
2.2. PV/MEPCM Model

The resulting transient conjugate heat transfer processes of conduction across the PV layer, as well as buoyancy-driven convection in the porous layer packed with MEPCM particles, can then be modeled by invoking the following assumptions:

(1)

Because the temperature gradient along the thickness δ_pv of the PV cell is negligibly small, the conduction is one-dimensional and takes place along its length L_pv (>>δ_pv);

(2)

The thermal properties of the PV cell are isotropic and constant;

(3)

The ohmic losses in the PV cell are negligible, and the photovoltaic efficiency is a function of temperature;

(4)

The time-dependent solar irradiation onto the outer surface of the PV cell is uniform at G_s(t);

(5)

The outer surface of the PV cell has an effective absorptivity of α_r,pv;

(6)

The rectangular MEPCM layer is treated as an air-filled isotropic and homogenous porous medium with a porosity of ϕ_f;

(7)

The MEPCM particles are spheres of uniform diameter $d_p^{+}$ in local thermal equilibrium with the fluid, except during the solid-liquid phase change process;

(8)

The thermophysical properties of the fluid and the MEPCM particles are constant except for the density variation for the buoyancy force, which is treated using the Boussinesq approximation.

2.3. Dimensional Mathematical Model

2.3.1. Photovoltaic Cell Energy Balance

The energy balance from the first to the fifth assumption (in Section 2.2) can be written as the following:

$${\rho }_{pv}{c}_{p,pv}{\delta }_{pv}\frac{\partial T_{pv}}{\partial t}=k_{pv}{\delta }_{pv}\frac{{\partial }^2{T}_{pv}}{\partial y^{+2}}+{\alpha }_{r,pv}{G}_s-{\dot{E}}_{pv}-U_{\infty ,o}(T_{pv}-T_{\infty ,o})-q_{pv,out}^{″}$$

(4)

The electric power output ${\dot{E}}_{pv}$ per unit cell area is calculated according to the following:

$${\dot{E}}_{pv}=G_s{\eta }_{pv}$$

(5)

The electrical efficiency depends on the PV temperature according to the following function:

$${\eta }_{pv}={\eta }_{pv,ref}\left[1-{\beta }_{pv}\left(T_{pv}-T_{pv,ref}\right)\right]$$

(6)

Where $T_{pv,ref}$ is the solar cell reference temperature; ${\beta }_{pv}$ is the material and temperature dependent coefficient for the solar cell.

2.3.2. MEPCM Mathematical Equation

The MEPCM model consists of a momentum equation, stream function-vorticity equations, energy balance, melting fraction equation, and initial/boundary conditions.

2.3.2.1. Momentum Equation

Assuming there is only 2-D heat transfer inside the MEPCM, the continuity equation is the following:

$$\frac{\partial u^{+}}{\partial x^{+}}+\frac{\partial v^{+}}{\partial y^{+}}=0$$

(7)

The momentum equation uses the Darcy-Brinkman-Forcheimer integrated model [12]. If the Boussinesq approximation ( $\Delta {\rho }_f<<\Delta {\rho }_{f,0}\text{ and }{\rho }_{\mathrm{f}}\approx {\rho }_{\text{f},0}$ ) is used, then the x-axis and y-axis momentum equations can be expressed as follows:

$$\begin{gathered} {\rho }_f\left[{{\varphi }_f}^{-1}\frac{\partial v^{+}}{\partial t^{+}}+{{\varphi }_f}^{-2}\left(v^{+}\cdot \nabla \right)v^{+}\right]=-\frac{\partial P^{+}}{\partial y^{+}}+\frac{\partial }{\partial x^{+}}\left({\mu }_e\frac{\partial v^{+}}{\partial x^{+}}\right)+\frac{\partial }{\partial y^{+}}\left({\mu }_e\frac{\partial v^{+}}{\partial y^{+}}\right) \\ -g{\beta }_{T,f}(T-T_{ref})-\frac{{\mu }_f}{K}{v}^{+}-C_F{K}^{-0.5}\left|{\overrightarrow{V}}^{+}\right|v^{+} \end{gathered}$$

(8)

$$\begin{gathered} {\rho }_f\left[{{\varphi }_f}^{-1}\frac{\partial u^{+}}{\partial t^{+}}+{{\varphi }_f}^{-2}\left(u^{+}\cdot \nabla \right)u^{+}\right]=-\frac{\partial P^{+}}{\partial x^{+}}+\frac{\partial }{\partial x^{+}}\left({\mu }_e\frac{\partial u^{+}}{\partial x^{+}}\right)+\frac{\partial }{\partial y^{+}}\left({\mu }_e\frac{\partial u^{+}}{\partial y^{+}}\right) \\ -\frac{{\mu }_f}{K}{u}^{+}-C_F{K}^{-0.5}\left|{\overrightarrow{V}}^{+}\right|u^{+} \end{gathered}$$

(9)

K is the Ergun Equation coefficient, which can be calculated from:

$$K=\frac{d_p^2{\varphi }_f^3}{150{\left(1-{\varphi }_f\right)}^2}$$

(10)

where C_F is the Forcheimer Equation coefficient, which is set to 0.55. This value can be assumed to be constant as long as the porosity is between 0.4 and 0.6. ${\mu }_e$ is the viscosity in the porous medium; for non-Darcy flow, ${\mu }_e={\mu }_f$ [12]. $|{\overrightarrow{V}}^{+}|=\sqrt{u^{+2}+v^{+2}}$ usually. The fluid density can be assumed to be temperature dependent:

$$\mathrm{\Delta }{\rho }_f={\rho }_f(T,{\varphi }_f)-{\rho }_{f,0}=-{\rho }_{f,0}{\beta }_{T,f}(T-T_c)-{{\rho }^{*}}_{pf}{\beta }_s({\varphi }_f-{\varphi }_{fi})$$

(11)

Then, assuming the porosity different is very small and uniform, the thermal expansion coefficient can be described as:

$${\beta }_{T,f}=-\frac{1}{{\rho }_{f,0}}{\left(\frac{\partial {\rho }_f}{\partial T}\right)}_{T_c}$$

(12)

2.3.2.2. Stream Function—Vorticity Equations

The stream function equation is expressed as follows:

$$\frac{{\partial }^2{\psi }^{+}}{\partial x^{+2}}+\frac{{\partial }^2{\psi }^{+}}{\partial y^{+2}}=-{\omega }^{+}$$

(13)

Combining Equations (8) and (13), the vorticity Equation can be described as the following:

$$\frac{1}{{\phi }_f}\frac{\partial {\omega }^{+}}{\partial t}+\frac{1}{{{\phi }^2}_f}(\frac{\partial (u^{+}{\omega }^{+})}{\partial x^{+}}+\frac{\partial (v^{+}{\omega }^{+})}{\partial y^{+}})=(\frac{\tilde{\mu }}{{\mu }_f})\frac{{\nu }_f}{{\phi }_f}{\nabla }^2{\omega }^{+}+g{\beta }_f\frac{\partial T_m}{\partial x^{+}}-\frac{{\nu }_f}{K}{\omega }^{+}-\frac{C_F}{\sqrt{K}}|\overrightarrow{u}|{\omega }^{+}$$

(14)

2.3.2.3. Energy Balance

The energy balance uses the heat transfer model for a rectangular container [13], including the phase change melting rate and melting rate Equations listed below:

$${\rho }_m{c}_{p,m}\frac{\partial T_m}{\partial t}+{\rho }_f{c}_{p,f}\left(u^{+}\frac{\partial T_m}{\partial x^{+}}+v^{+}\frac{\partial T_m}{\partial y^{+}}\right)=\left(k_m\frac{{\partial }^2{T}_m}{\partial x^{+2}}+k_m\frac{{\partial }^2{T}_m}{\partial y^{+2}}\right)-\left(1-{\varphi }_f\right){\rho }_p{h}_{LS}\left(\frac{\partial \xi }{\partial t}\right)$$

(15)

The mixed density and mixed specific heat capacity can be calculated as the following:

$${\rho }_m={\varphi }_f{\rho }_f+(1-{\varphi }_f){\rho }_p$$

(16)

$$c_{p,m}=\frac{{\varphi }_f{\rho }_f{c}_{p,f}+\left(1-{\varphi }_f\right){\rho }_p{c}_{p,p}}{{\varphi }_f{\rho }_f+\left(1-{\varphi }_f\right){\rho }_p}$$

(17)

2.3.2.4. Melting Fraction Equation

The relationship between the MEPCM temperature and melting fraction can be described using the following equation:

$$\frac{\partial \xi }{\partial t}=\frac{A_p{h}_p}{{\rho }_p{\forall }_p{h}_{LS}}\left[(T_m-T_M)-{\tau }_t\frac{\partial T_m}{\partial t}\right]$$

(18)

The delay entry can be expressed as follows:

$${\tau }_t=\left[\frac{{\left({\forall }_p/A_p\right)}^2}{{\alpha }_p}\right]\left(\frac{c_{p,m}}{c_{p,p}}\right)$$

(19)

2.3.3. Initial and Boundary Conditions

2.3.3.1. PV Layer Initial and Boundary Condition

At the initial time, we assume all temperatures in the PV cell and MEPCM are same. There is no heat transfer through the top and bottom wall for the entire time. The initial and boundary conditions for the considered problem can be expressed as follows:

At t = 0,

$$T_{pv}(y^{+},t=0)=T_{\infty ,i}for,-{\delta }_{pv}\le x^{+}\le 0,0\le y^{+}\le H$$

(20)

$$T_m(x^{+},y^{+},t=0)=T_{\infty ,i}; {\omega }^{+}={\psi }^{+}(x^{+},y^{+},t=0)=0; \text{for} 0\le y^{+}\le H,0\le x^{+}\le W$$

(21)

For t > 0,

$$\text{and} y^{+}=0 or H; \frac{\partial T_{pv}}{\partial y^{+}}=0$$

(22)

2.3.3.2. MEPCM Layer Initial and Boundary Condition

At the left wall (x⁺ = 0), we assume that the stream function equals zero, the MEPCM temperature equals the PV cell temperature, and that all heat released from the PV cell’s right wall is absorbed by the left wall of the MEPCM with no losses. At the right wall (x⁺ = W), the total heat transfer from the MEPCM right wall equals the convection heat transfer of the inside. The interior ambient temperature is constant, and the small convection heat transfer coefficient is applied to simulate the natural convection process. Because the top and bottom walls are insulated, the process is assumed to be adiabatic:

$$\text{at} x^{+}=0; {\psi }^{+}=0,T_m=T_{pv}, q_{pv,out}^{″}=-k_m\frac{\partial T_m}{\partial x^{+}}$$

(23)

$$\text{at} x^{+}=W; {\psi }^{+}=0,-k_m\frac{\partial T_m}{\partial x^{+}}=U_{\infty ,i}(T_m-T_{\infty ,i})$$

(24)

$$\text{at} y^{+}=0 or H; {\psi }^{+}=0, \frac{\partial T_m}{\partial y^{+}}=0$$

(25)

2.3.4. Formulation for PV/MEPCM Composite Layer under Temporal Variations of Solar Irradiation and Exterior Ambient Temperature

To simulate a real time application, the daily solar irradiation uses a time dependent function. There is no solar irradiation before sunrise or after sunset. At sunrise, the solar irradiation starts to increase until it reaches its maximum, after which it decreases. Daily variation of the solar irradiation onto the PV cell may be expressed as a sinusoidal function in terms of the instants for the sunrise, t_rise, and the sunset, t_set, as follows:

$$G_s(t)=\{\begin{array}{ll}0,& 0\le t\le t_{rise}\\ G_{s,o} sin\left[\frac{\pi (t-t_{rise})}{2(t_{max}-t_{rise})}\right],& t_{rise}\le t\le t_{max}\\ G_{s,o} cos\left[\frac{\pi (t-t_{max})}{2(t_{set}-t_{max})}\right],& t_{max}\le t\le t_{set}\\ 0,& t_{set}\le t\le 24\end{array}$$

(26)

t_max represents the instant of occurrence of maximum solar irradiation. Meanwhile, the exterior ambient temperature may be simulated as sinusoidal variation of the form:

$$T_{\infty ,o}(t)={\overline{T}}_{\infty ,o}+\Delta T_{\infty ,o} sin(\frac{2\pi t}{24}), 0\le t\le 24$$

(27)

where ${\overline{T}}_{\infty ,o}$ and $\mathrm{\Delta }{T}_{\infty ,o}$ denote, respectively, the mean value and the oscillation amplitude of the exterior ambient temperature over a time period (one day = 24 h). All of the equations in dimensional form are converted to dimensionless form to simplify the numerical modeling.

2.4. Properties and used parameters

Numerical simulations have been undertaken to compare the case without the MEPCM layer with the case with integrated MEPCM for different melting temperatures (T_M = 26 and 34 °C, respectively) and different aspect ratios. The remaining geometric parameters pertinent to the test cells are held constant as follows: H = 18 cm, W = 5 cm, ${\delta }_{PV}$ = 1.8 mm, and $d_P^{+}$ = 18 μm. The relevant physical properties used are: K = 1.56 × 10⁻¹² m², $c_{p,f}$ = 1007 J kg⁻¹ K⁻¹, $k_f$ = 0.03 W m⁻¹ K⁻¹, ${\beta }_{T,f}$ = −3.25×10⁻³, ${\alpha }_f$ = 2.625×10⁻⁵, ${\nu }_f$ = 1.57 × 10⁻⁵ m²/s, $k_m$ = 0.07 W m⁻¹ K⁻¹, $h_{ls}$ = 172 kJ/kg, ${\beta }_{PV}$ = −4.5×10⁻³ %/K, $T_{PV,ref}$ = 25 °C, and $T_M$ = 26 °C or 34 °C. The investigated weather conditions have been taken as: $T_{\infty ,o}$ = 26 °C, ${\overline{T}}_{\infty ,i}$ = 25 °C, $\Delta T_{\infty ,o}$ = 3 °C, $G_{s,o}$ = 600 W/m², $U_{\infty ,o}$ = 10 W m⁻² K⁻¹, $U_{\infty ,i}$ = 2 W m⁻² K⁻¹, $t_{rise}$ = 4, $t_{max}$ = 10, and $t_{set}$ = 16.

2.5. Numerical Method

A variable density grid system is used to improve the resolution of the numerical method. The time, space, convection, and vorticity wall boundary terms are treated by the first order, second order, QUICK scheme, and Thom formula discretizations, respectively. There are two loops in the numerical simulation calculation process: the time loop and the space loop. The iterative calculation continued until a prescribed relative convergence of 2 × 10⁻⁵ was satisfied for all the field variables in this problem.

2.6. Quantities of Technical Interest

(1) Surface-averaged temperature over the PV cell:

$$T_{pv,avg}=\frac{1}{H}{\displaystyle {\int }_0^H{T}_{pv}d{y}^{+}}$$

(28)

(2) Surface averaged electrical efficiency of PV cell:

$${\eta }_{pv,avg}=\frac{1}{H}{\displaystyle {\int }_0^H{\eta }_{pv}d{y}^{+}}$$

(29)

(3) Total electrical energy generated by the MEPV cell over a time interval of solar irradiation:

$$Q_{pv,E}(\Delta t)={\displaystyle {\int }_{t_{rise}}^{t_{rise}+\Delta t}}{\displaystyle {\int }_0^H{\dot{E}}_{pv}d{y}^{+}dt}={\displaystyle {\int }_{t_{rise}}^{t_{rise}+\Delta t}}{\displaystyle {\int }_0^H{G}_s{\eta }_{pv}d{y}^{+}dt}$$

(30)

(4) Total energy into the PCM layer over a time interval:

$$Q_{m,o}(\Delta t)=H{\displaystyle {\int }_t^{t+\Delta t}{q}_{pv,in,avg}^{″}dt}$$

(31)

(5) Surface averaged heat transfer rate into the outer ambient:

$$q_{pv,out,avg}^{″}=\frac{1}{H}{\displaystyle {\int }_0^H{q}_{pv,out}^{″}d{y}^{+}}$$

(32)

(6) Total energy dissipated into the interior ambient over a time interval:

$$Q_{m,i}(\Delta t)={\displaystyle {\int }_t^{t+\Delta t}}{\displaystyle {\int }_0^H{q}_{m,i}^{″}d{y}^{+}dt}$$

(33)

3. Results and Discussion

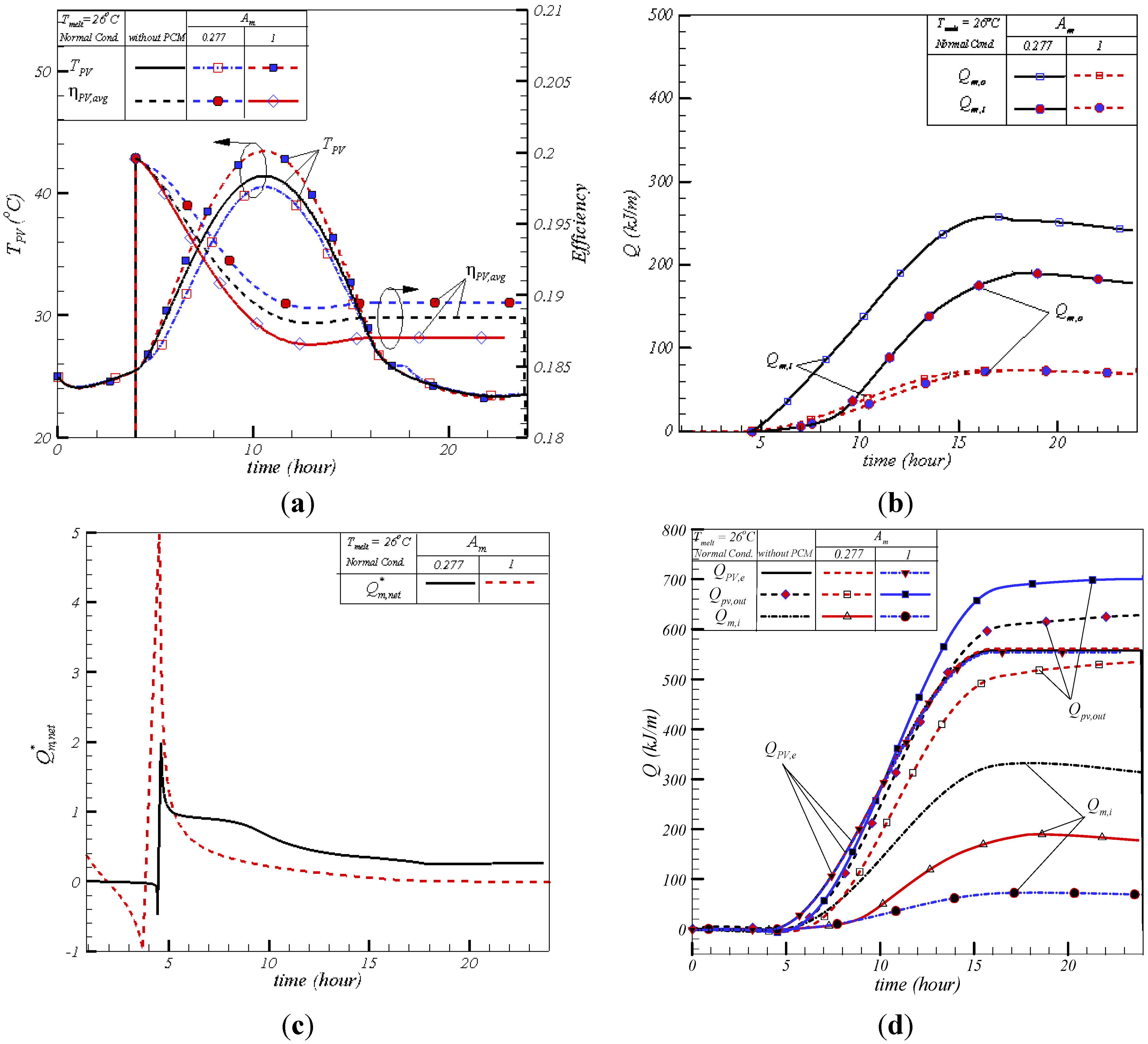
3.1. Aspect Ratio Effect

Figure 2a shows the streamlines (red dashed lines) and isotherms (black solid lines) for the case with a PCM melting point of 26 °C and aspect ratio (A_m) of 0.277 for practical weather conditions. The melted region has a fast temperature increase compared to the part that has not yet melted because the solid phase still has to go through the melting process, which keeps the MEPCM temperature almost constant. Figure 2b shows the case with A_m = 1, where the temperature gradient slowly increases to a maximum and decreases afterwards.

Figure 3a shows that the minimum average efficiencies of the PV cell without the MEPCM layer and with A_m = 0.277 and A_m = 1 MEPCM layers are 18.80%, 18.91%, and 18.65%, respectively. The stable average efficiencies for the PV cell without the MEPCM layer and with A_m = 0.277 and A_m = 1 MEPCM layers are 18.84%, 18.94%, and 18.7%, respectively. Use of the MEPCM layer with A_m = 0.277 increases the stable average efficiency by approximately 0.1%. Use of the MEPCM layer with A_m = 1 decreases the stable average efficiency by approximately 0.14%. Figure 3b shows that at both the left (Q_m,o) and right walls (Q_m,i), the heat transfer quantities for the case of A_m = 0.277 are higher than those for A_m = 1. The maximum heat transfer on the left and right for A_m = 0.277 is 241.2 kJ/m and 177.72 kJ/m, respectively. The maximum heat transfer on the left and right for A_m = 1 is 68.56 kJ/m and 68.93 kJ/m, respectively. For A_m = 0.277, the heat transfer on the left is much higher than that on the right, but for A_m = 1, it is the same on both sides.

Figure 2. Streamlines (red) and isotherms (black) in the MEPCM layer. (a) A_m = 0.277 (T_M = 26 ^oC) and (b) A_m = 1 (T_M = 26 ^oC).

Figure 2. Streamlines (red) and isotherms (black) in the MEPCM layer. (a) A_m = 0.277 (T_M = 26 ^oC) and (b) A_m = 1 (T_M = 26 ^oC).

Figure 3c has an initial displacement curve, which occurs because the increasing rate of heat input from the left side is much higher than the heat transfer on the right side. When these two heat transfer amounts are approximately equal, the energy fraction becomes zero (the A_m = 1 results); however, for A_m = 0.277, the heat transfer quantities are never equal, and the energy fraction is approximately 0.26. Figure 3d shows that the amount of heat transferred to the interior of the cell (Q_m,i) with the MEPCM (for both A_m = 0.277 and A_m = 1) is less than that of the PV cell without the MEPCM. The amount of heat transferred to the exterior of the cell with the A_m = 1 MEPCM layer is larger than that of the PV cell without the MEPCM layer, but the cell with the A_m = 0.277 MEPCM layer has a smaller amount of heat transferred than the PV cell without the MEPCM. The total electrical gain, heat transfer to the exterior, and heat transfer to the interior of the PV cell without the MEPCM layer are 559.94 kJ/m, 628.06 kJ/m, and 313.53 kJ/m, respectively. The total electrical gain, heat transfer to the exterior, and heat transfer to the interior of the PV cell with the A_m = 0.277 MEPCM layer are 562.98 kJ/m, 534.71 kJ/m, and 177.72 kJ/m, respectively. The total electrical gain, heat transfer to the exterior, and heat transfer to the interior of the PV cell with the A_m = 1 MEPCM layer are 555.67 kJ/m, 700.45 kJ/m, and 68.93 kJ/m, respectively.

Figure 3. Thermal and electrical performance of PV module with and without MEPCM layer of different aspect ratios of A_m = 0.277 and 1. (a) Average temperature and efficiency of PV cell; (b) Total heat transfer rate across the MEPCM layer; (c) Fraction of energy stored inside the MEPCM layer; and (d) Total heat transfer rate across the PV cell.

Figure 3. Thermal and electrical performance of PV module with and without MEPCM layer of different aspect ratios of A_m = 0.277 and 1. (a) Average temperature and efficiency of PV cell; (b) Total heat transfer rate across the MEPCM layer; (c) Fraction of energy stored inside the MEPCM layer; and (d) Total heat transfer rate across the PV cell.

The aspect ratio seems to affect whether the MEPCM layer is advantageous or disadvantageous for the electrical energy gain or electrical efficiency. For example, A_m = 0.277 gives a better electrical energy gain and better PV cell efficiency, but A_m = 1 reduces the electrical energy gain and electrical efficiency. The results in Figure 3b imply that the interior wall temperature for A_m = 1 is lower than that for A_m = 0.277, but the A_m = 1 layer cannot maintain the outer temperature, i.e., the PV cell temperature below the outer temperature of the A_m = 0.277 layer. Thus, we can conclude that A_m = 1 reduces the heat transferred through the interior wall but is not good for improving the electrical efficiency of the PV cell, while A_m = 0.277 can somewhat improve the efficiency because the temperature, compared to that of only the PV cell, is too small.

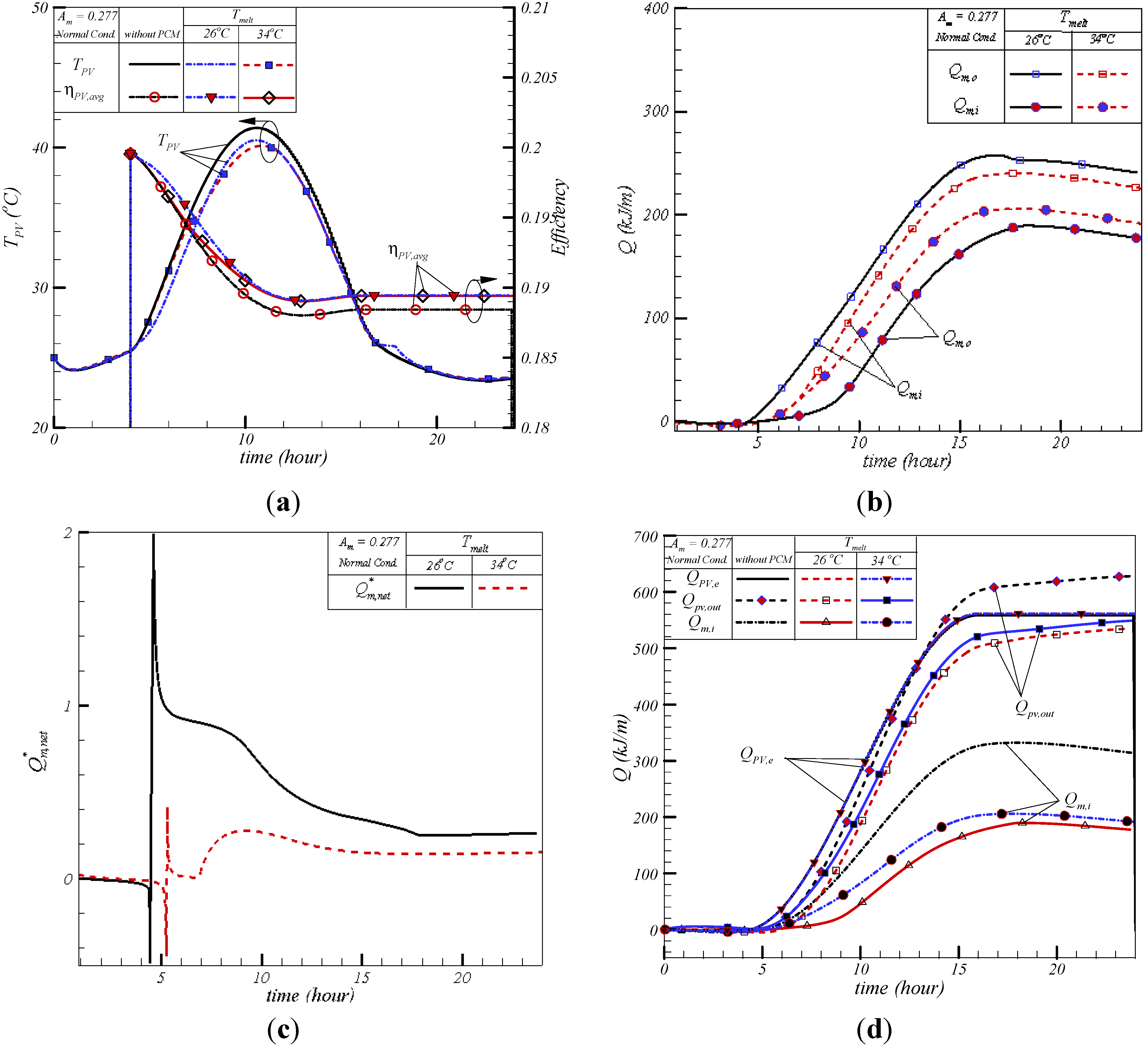
3.2. Melting Temperature Effect

Figure 4a shows that the minimum average efficiencies for the PV cell without the MEPCM layer and with the T_M = 26 °C and T_M = 34 °C MEPCM layers are 18.80%, 18.91%, and 18.9%, respectively. The stable average efficiencies for the PV cell without the MEPCM layer and with the T_M = 26 °C and T_M = 34 °C MEPCM layers are 18.84%, 18.94%, and 18.94%, respectively. Use of the T_M = 26 °C MEPCM layer increases the minimum average efficiency by approximately 0.11%. Inclusion of the T_M = 34 °C MEPCM layer decreases the minimum average efficiency by approximately 0.1%. Figure 4b shows that the maximum heat transfers on the left (Q_m,o) and right walls (Q_m,i) for T_M = 26 °C are 241.2 kJ/m and 177.72 kJ/m, respectively. The maximum heat transfers on the left and right for T_M = 34 °C are 225.8 kJ/m and 191.45 kJ/m, respectively. For T_M = 26 °C, the heat transfer on the left is much higher than that for T_M = 34 °C, but the heat transfer on the right wall for T_M = 34 °C is higher than that for T_M = 26 °C.

Figure 4c shows an initial displacement curve, which occurs because the increasing rate of heat input from the left side is much higher than the heat transfer on the right side due to increasing solar irradiation. The energy fraction for T_M = 34 °C starts to increase later than when T_M = 26 °C because its melting point is higher. Neither of these stored energy fractions reaches zero. In the end, the T_M = 26 °C and T_M = 34 °C layers have a stored energy fraction of approximately 0.26 and 0.152, respectively.

Figure 4d shows that the heat transferred to the interior and exterior using the MEPCM (both T_M = 26 °C and T_M = 34 °C) is less than that of the PV cell without the MEPCM layer. The total electrical gain, heat transfer to the exterior, and heat transfer to the interior of the PV cell without the MEPCM layer are 559.94 kJ/m, 628.06 kJ/m, and 313.53 kJ/m, respectively. The total electrical gain, heat transfer to the exterior, and heat transfer to the interior for the PV cell with the T_M = 34 °C MEPCM layer are 562.98 kJ/m, 534.71 kJ/m, and 177.72 kJ/m, respectively. The total electrical gain, heat transfer to the exterior, and heat transfer to the interior for the PV cell with the T_M = 26 °C MEPCM layer are 562.86 kJ/m, 549.12 kJ/m, and 191.45 kJ/m, respectively.

Figure 4. Thermal and electrical performance of PV module with and without MEPCM layer (A_m = 0.277) with different melting points of T_M = 26 and 34 °C. (a) Average temperature and efficiency of PV cell; (b) Total heat transfer rate across the MEPCM layer; (c) Fraction of energy stored inside the MEPCM layer; and (d) Total heat transfer rate across the PV cell.

Figure 4. Thermal and electrical performance of PV module with and without MEPCM layer (A_m = 0.277) with different melting points of T_M = 26 and 34 °C. (a) Average temperature and efficiency of PV cell; (b) Total heat transfer rate across the MEPCM layer; (c) Fraction of energy stored inside the MEPCM layer; and (d) Total heat transfer rate across the PV cell.

4. Conclusions

The conclusions are the following: (1) The aspect ratio seems to affect whether the MEPCM layer is advantageous or disadvantageous for the electricity generation. Use of the MEPCM layer with aspect ratio (A_m = 0.277) and A_m = 1 increases and decreases the stable average PV cell efficiency by approximately 0.1% and 0.14%; (2) The overall performances of the two cases with different melting points are approximately the same. The MEPCM layer with the melting point 26 °C (T_M = 26 °C) initially maintains a lower PV temperature than the T_M = 34 °C layer, but when the T_M = 34 °C layer begins to melt, it exhibits a lower PV temperature than the T_M = 26 °C layer.

The modeling and simulation results are limited to the used MEPCM and the chosen specific location. To explore the practical aspect and applications at other locations, MEPCM with different melting point could be tested. The focus of this study is to explore a new computational modeling. The model validation works are very important. This is not what we are exploring in this study, but worthy of further consideration.