Cost and CO2 Emission Optimization of Steel Reinforced Concrete Columns in High-Rise Buildings
Abstract
:1. Introduction
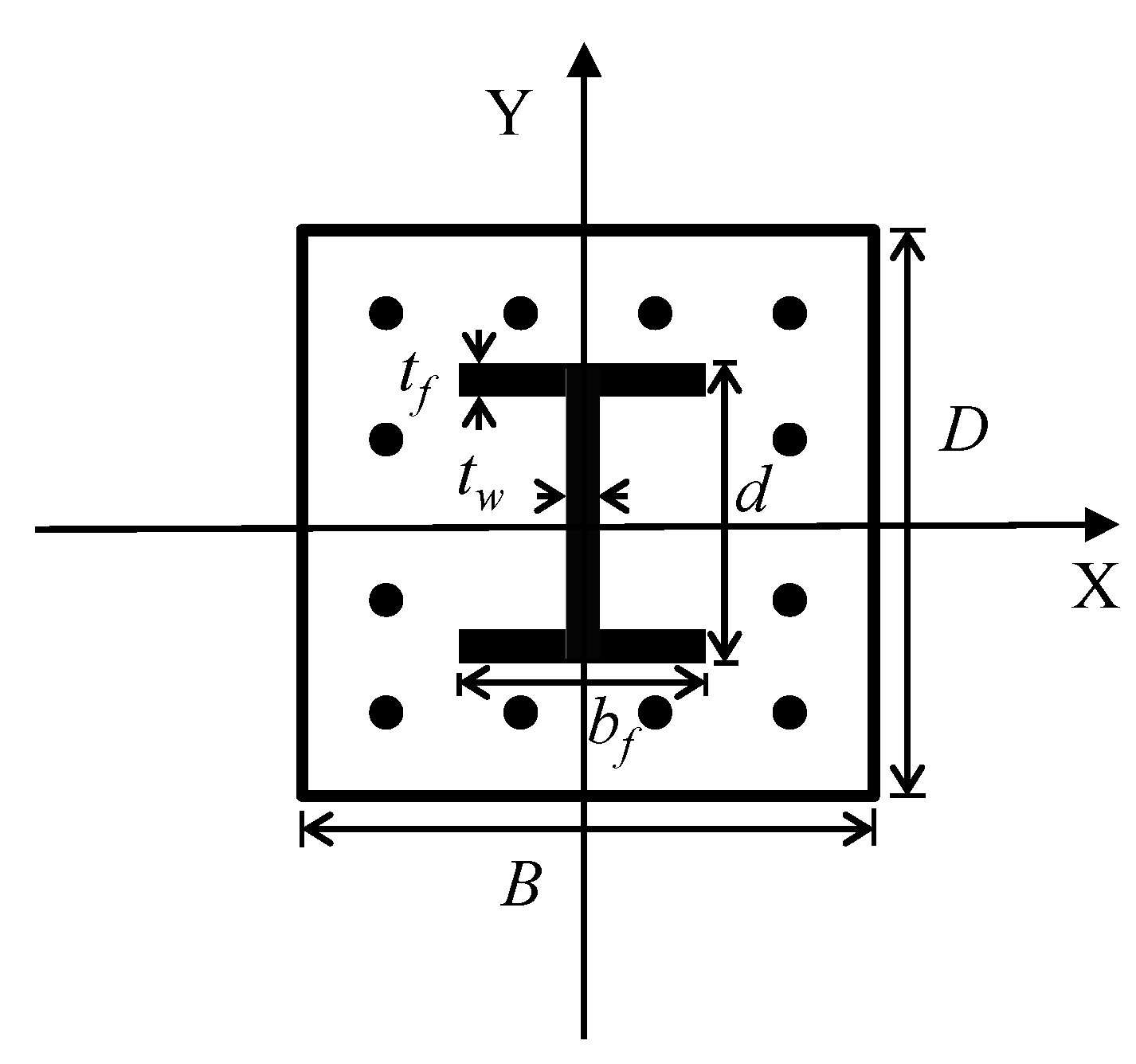
2. Steel Reinforced Concrete (SRC) Columns in a Building Frame System
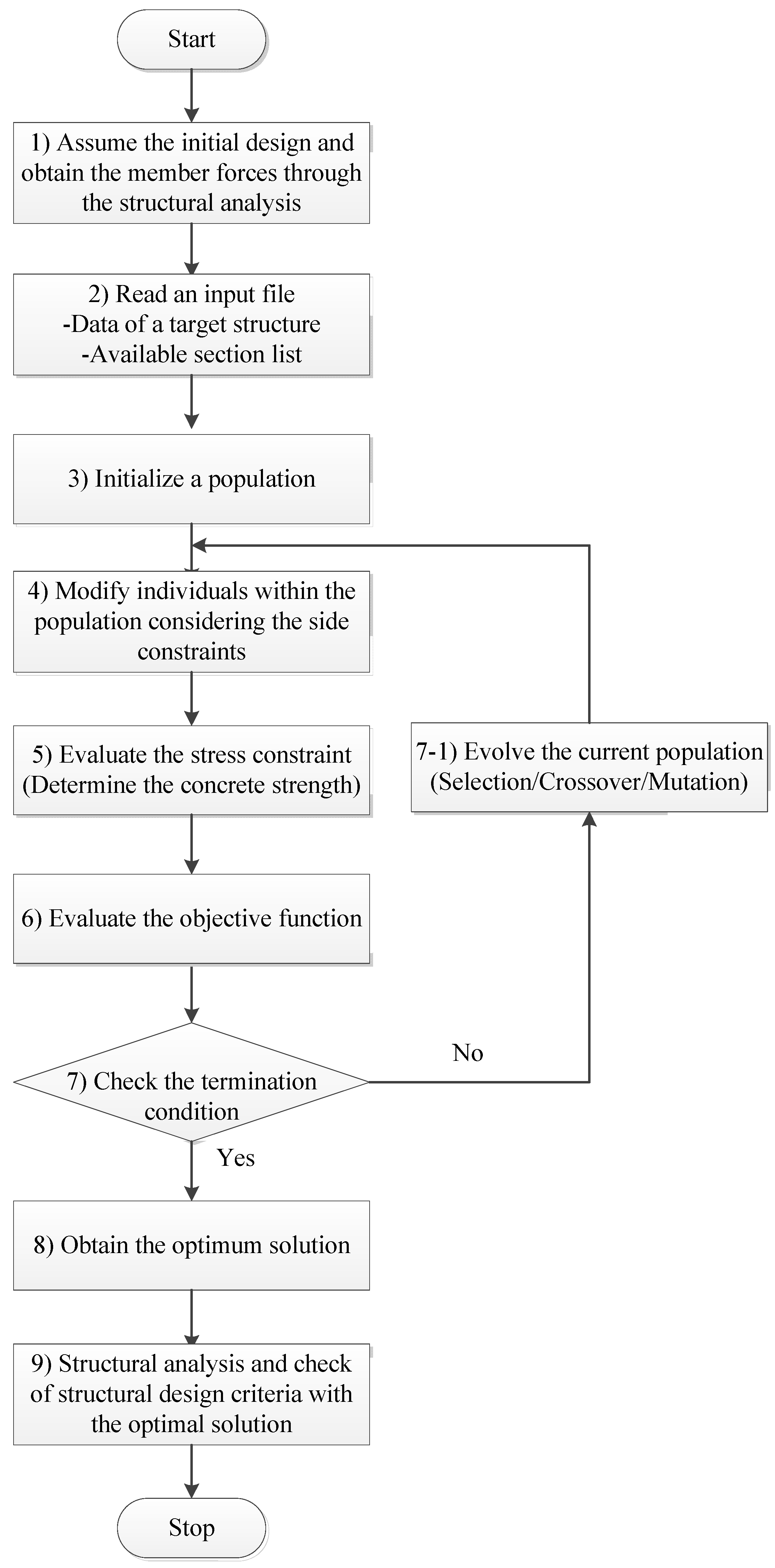
3. Optimization Methodology
3.1. Formulation of the Optimization Problem
3.2. Proposed Optimization Technique
| No. | Member size | Type of steel section | Cost (USD/m) | CO2 (kg-CO2/m) | |||||
|---|---|---|---|---|---|---|---|---|---|
| D (mm) | B (mm) | d (mm) | bf (mm) | tw (mm) | tf (mm) | ||||
| 1 | 450 | 450 | 200 | 200 | 8 | 12 | SM490 rolled | 33.02 | 251.15 |
| … | … | … | … | … | … | … | … | … | … |
| 23 | 700 | 700 | 428 | 407 | 20 | 35 | SM490 rolled | 191.42 | 1456.02 |
| 24 | 600 | 600 | 300 | 300 | 10 | 15 | SM490 built-up | 76.78 | 583.99 |
| … | … | … | … | … | … | … | … | … | … |
| 40 | 650 | 650 | 350 | 350 | 30 | 30 | SM490 built-up | 196.79 | 1496.82 |
| … | … | … | … | … | … | … | … | … | … |
| 54 | 800 | 800 | 440 | 400 | 35 | 35 | SM490 built-up | 271.33 | 2063.80 |
| 55 | 800 | 800 | 450 | 400 | 20 | 40 | SM490 TMCP | 268.95 | 2045.71 |
| … | … | … | … | … | … | … | … | … | … |
| 110 | 900 | 900 | 530 | 400 | 70 | 80 | SM490 TMCP | 621.91 | 4,730.36 |
| … | … | … | … | … | … | … | … | … | … |
| 186 | 1100 | 1100 | 730 | 600 | 80 | 80 | SM490 TMCP | 979.55 | 7450.72 |
| 187 | 600 | 600 | 300 | 300 | 10 | 15 | SM520 TMCP | 79.46 | 604.37 |
| … | … | … | … | … | … | … | … | … | … |
| 280 | 950 | 950 | 590 | 500 | 50 | 60 | SM520 TMCP | 581.10 | 4,419.98 |
| … | … | … | … | … | … | … | … | … | … |
| 349 | 1100 | 1100 | 730 | 600 | 80 | 80 | SM520 TMCP | 987.74 | 7,512.96 |
| 350 | 600 | 600 | 300 | 300 | 10 | 15 | SM570 TMCP | 88.80 | 675.46 |
| … | … | … | … | … | … | … | … | … | … |
| 420 | 850 | 850 | 510 | 400 | 60 | 70 | SM570 TMCP | 598.06 | 4548.96 |
| … | … | … | … | … | … | … | … | … | … |
| 512 | 1100 | 1100 | 730 | 600 | 80 | 80 | SM570 TMCP | 1082.93 | 8236.99 |
| Structural materials | Unit price | Unit CO2 emission | ||
|---|---|---|---|---|
| Concrete | Strength | 21 MPa | 48.23 USD/m3 | 472.61 kg-CO2/m3 |
| 24 MPa | 50.55 USD/m3 | 495.42 kg-CO2/m3 | ||
| 27 MPa | 52.88 USD/m3 | 518.23 kg-CO2/m3 | ||
| 30 MPa | 55.58 USD/m3 | 544.69 kg-CO2/m3 | ||
| 35 MPa | 57.54 USD/m3 | 563.85 kg-CO2/m3 | ||
| 40 MPa | 68.24 USD/m3 | 668.78 kg-CO2/m3 | ||
| 50 MPa | 48.23 USD/m3 | 793.77 kg-CO2/m3 | ||
| Steel section | SM490 rolled | 0 < thickness ≤ 25 | 0.68 USD/kg | 5.15 kg-CO2/kg |
| 25 < thickness ≤ 38 | 0.69 USD/kg | 5.21 kg-CO2/kg | ||
| 38 < thickness ≤ 50 | 0.69 USD/kg | 5.27 kg-CO2/kg | ||
| 50 < thickness ≤ 100 | 0.70 USD/kg | 5.33 kg-CO2/kg | ||
| SM490 built-up | 0 < thickness ≤ 25 | 0.84 USD/kg | 6.35 kg-CO2/kg | |
| 25 < thickness ≤ 38 | 0.84 USD/kg | 6.41 kg-CO2/kg | ||
| 38 < thickness ≤ 50 | 0.85 USD/kg | 6.47 kg-CO2/kg | ||
| 0 < thickness ≤ 25 | 0.86 USD/kg | 6.54 kg-CO2/kg | ||
| SM490 TMCP | 0 < thickness ≤ 25 | 0.86 USD/kg | 6.51 kg-CO2/kg | |
| 25 < thickness ≤ 38 | 0.86 USD/kg | 6.57 kg-CO2/kg | ||
| 38 < thickness ≤ 50 | 0.87 USD/kg | 6.63 kg-CO2/kg | ||
| 50 < thickness ≤ 100 | 0.88 USD/kg | 6.70 kg-CO2/kg | ||
| SM520 TMCP | 0 < thickness ≤ 25 | 0.86 USD/kg | 6.57 kg-CO2/kg | |
| 25 < thickness ≤ 38 | 0.87 USD/kg | 6.64 kg-CO2/kg | ||
| 38 < thickness ≤ 50 | 0.88 USD/kg | 6.70 kg-CO2/kg | ||
| 50 < thickness ≤ 100 | 0.89 USD/kg | 6.75 kg-CO2/kg | ||
| SM570 TMCP | 0 < thickness ≤ 50 | 0.97 USD/kg | 7.35 kg-CO2/kg | |
| 50 < thickness ≤ 100 | 0.97 USD/kg | 7.40 kg-CO2/kg | ||
4. Application
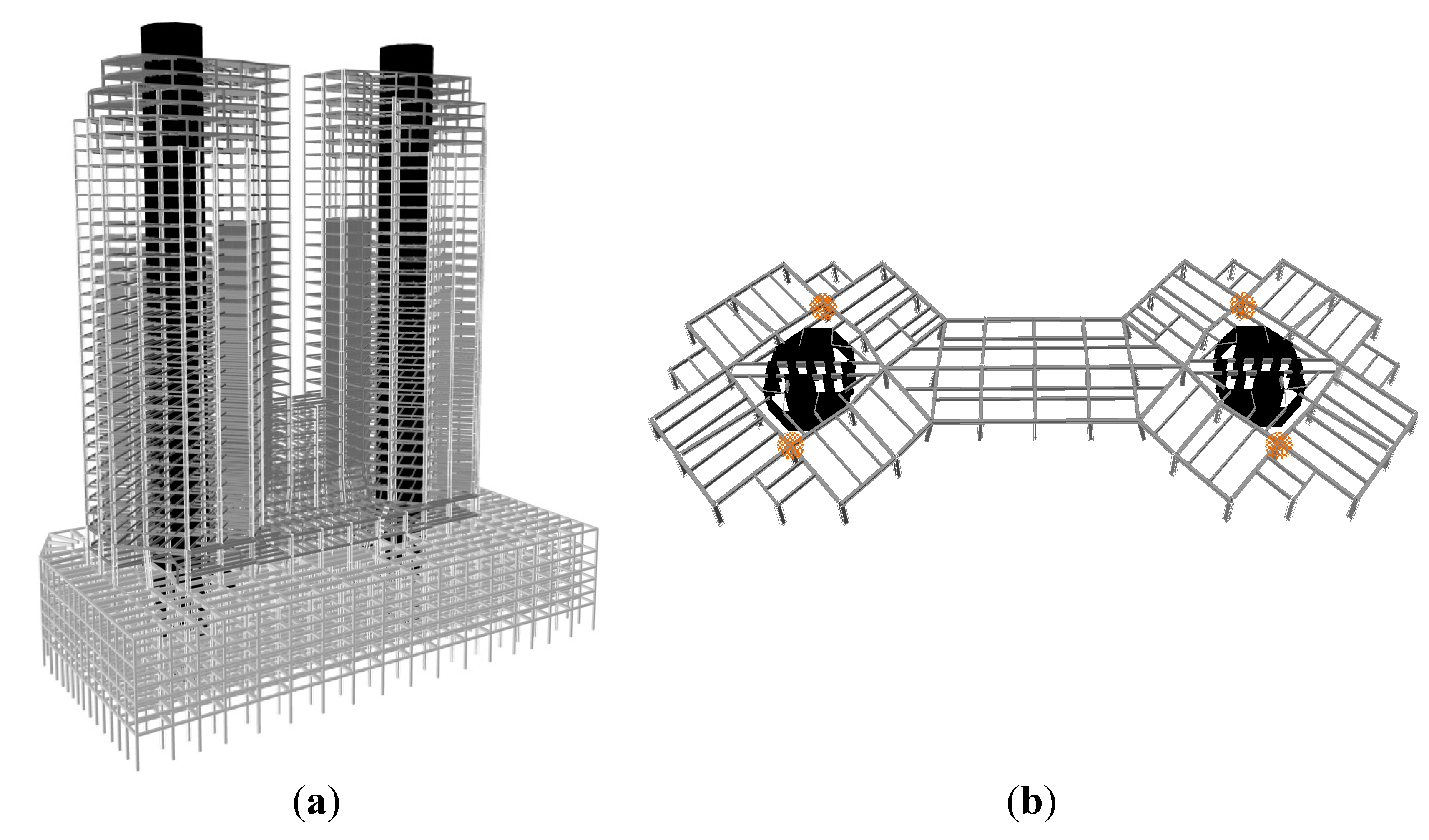
4.1. Introduction of the Example Structure
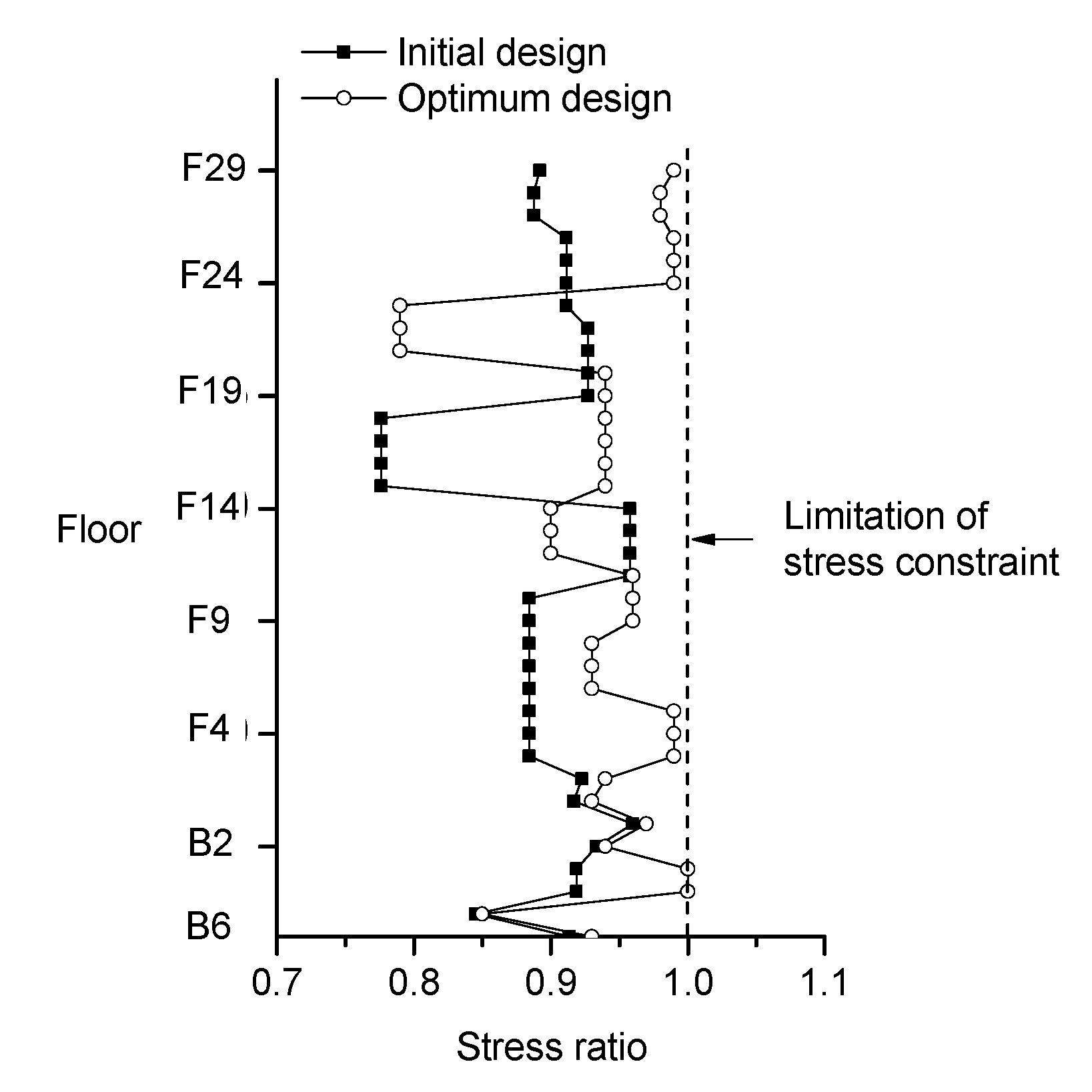
4.2. Results
| Design type | Cost (USD) | Additional cost by CO2 (USD) | Total cost (USD) | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Rebar | Steel section | Concrete | Sum | Rebar | Steel section | Concrete | Sum | Rebar | Steel section | Concrete | Sum | |
| Initial design | 1,405 | 59,702 | 3,246 | 64,353 | 149 | 6,342 | 444 | 6,935 | 1,554 | 66,044 | 3,690 | 71,288 |
| (1.97%) | (83.75%) | (4.55%) | (90.27%) | (0.21%) | (8.90%) | (0.62%) | (9.73%) | (2.18%) | (92.64%) | (5.18%) | (100.00%) | |
| Optimum design | 1,428 | 37,670 | 4,975 | 44,074 | 152 | 4,001 | 681 | 4,834 | 1,580 | 41,672 | 5,656 | 48,908 |
| (2.92%) | (77.02%) | (10.17%) | (90.12%) | (0.31%) | (8.18%) | (1.39%) | (9.88%) | (3.23%) | (85.20%) | (11.57%) | (100.00%) | |
| Design type | Weight (kN) | ||
|---|---|---|---|
| Steel section | Concrete | Sum | |
| Initial design | 670.40 | 1398.29 | 2068.69 |
| (32.41%) | (67.59%) | (100.00%) | |
| Optimum design | 408.03 | 1499.38 | 1907.51 |
| (21.39%) | (78.60%) | (100.00%) | |

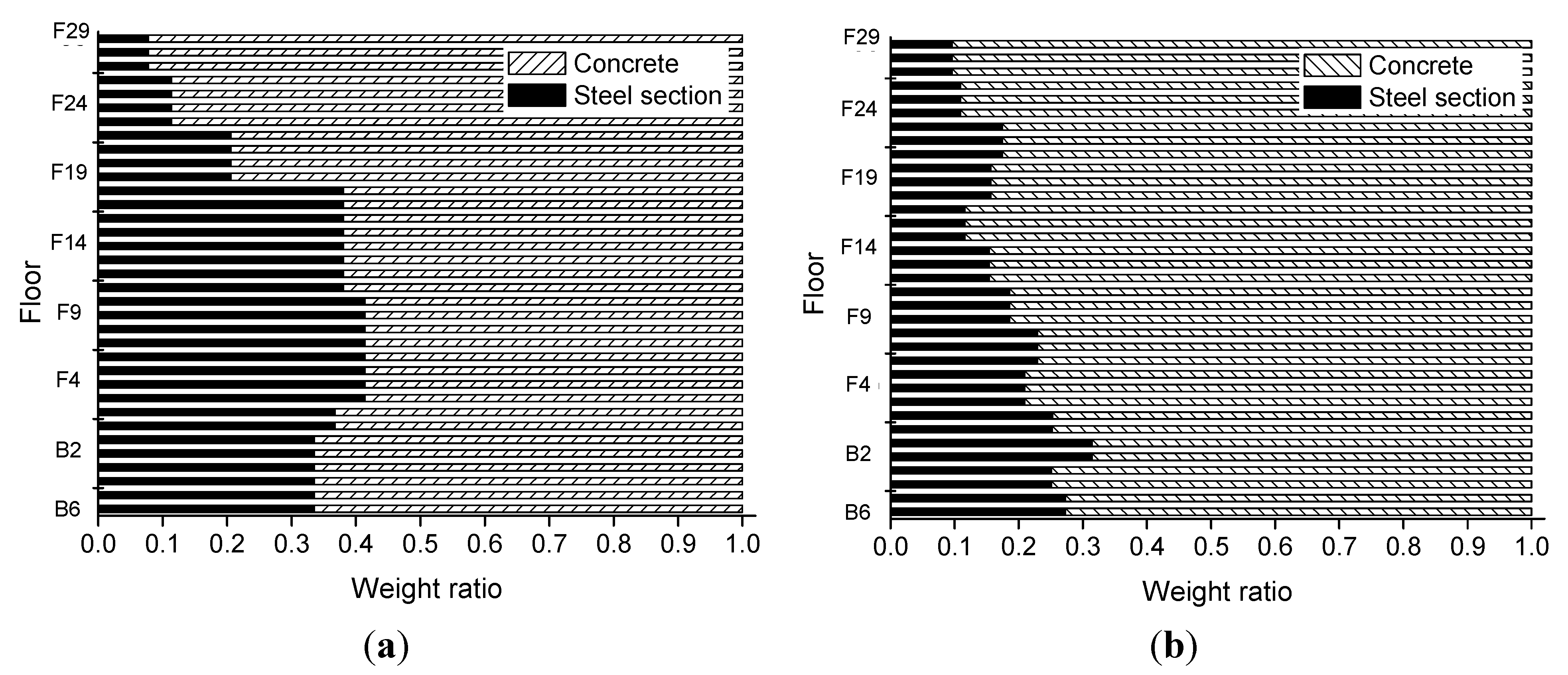
| Floor | Initial design | Optimum design | ||
|---|---|---|---|---|
| Strength of concrete (MPa) | Type of steel section | Strength of concrete (MPa) | Type of steel section | |
| F29 | 24 | SM490 rolled | 40 | SM490 rolled |
| F28 | 24 | SM490 rolled | 40 | SM490 rolled |
| F27 | 24 | SM490 rolled | 40 | SM490 rolled |
| F26 | 24 | SM490 rolled | 40 | SM490 rolled |
| F25 | 24 | SM490 rolled | 40 | SM490 rolled |
| F24 | 24 | SM490 rolled | 40 | SM490 rolled |
| F23 | 24 | SM490 rolled | 40 | SM490 built-up |
| F22 | 24 | SM490 rolled | 40 | SM490 built-up |
| F21 | 24 | SM490 rolled | 40 | SM490 built-up |
| F20 | 24 | SM490 rolled | 50 | SM490 built-up |
| F19 | 24 | SM490 rolled | 50 | SM490 built-up |
| F18 | 24 | SM490 rolled | 50 | SM490 built-up |
| F17 | 24 | SM490 rolled | 50 | SM490 built-up |
| F16 | 24 | SM490 rolled | 50 | SM490 built-up |
| F15 | 24 | SM490 rolled | 50 | SM490 built-up |
| F14 | 24 | SM490 rolled | 50 | SM490 built-up |
| F13 | 24 | SM490 rolled | 50 | SM490 built-up |
| F12 | 24 | SM490 rolled | 50 | SM490 built-up |
| F11 | 24 | SM490 rolled | 50 | SM490 built-up |
| F10 | 24 | SM570 TMCP | 50 | SM490 built-up |
| F9 | 24 | SM570 TMCP | 50 | SM490 built-up |
| F8 | 24 | SM570 TMCP | 50 | SM520 TMCP |
| F7 | 24 | SM570 TMCP | 50 | SM520 TMCP |
| F6 | 24 | SM570 TMCP | 50 | SM520 TMCP |
| F5 | 24 | SM570 TMCP | 50 | SM570 TMCP |
| F4 | 24 | SM570 TMCP | 50 | SM570 TMCP |
| F3 | 24 | SM570 TMCP | 50 | SM570 TMCP |
| F2 | 27 | SM570 TMCP | 50 | SM570 TMCP |
| F1 | 27 | SM570 TMCP | 50 | SM570 TMCP |
| B1 | 27 | SM570 TMCP | 50 | SM570 TMCP |
| B2 | 27 | SM570 TMCP | 50 | SM570 TMCP |
| B3 | 27 | SM570 TMCP | 50 | SM570 TMCP |
| B4 | 27 | SM570 TMCP | 50 | SM570 TMCP |
| B5 | 27 | SM570 TMCP | 50 | SM570 TMCP |
| B6 | 27 | SM570 TMCP | 50 | SM570 TMCP |
| Type of steel section | Initial design | Optimum design | ||
|---|---|---|---|---|
| Weight (kN) | Ratio (%) | Weight (kN) | Ratio (%) | |
| SM490 rolled | 207.55 | 30.96 | 12.36 | 3.03 |
| SM490 built-up | - | - | 104.02 | 25.49 |
| SM490 TMCP | - | - | - | 0.00 |
| SM520 TMCP | - | - | 38.26 | 9.38 |
| SM570 TMCP | 462.85 | 69.04 | 253.38 | 62.10 |
| Total | 670.40 | 100.00 | 408.03 | 100.00% |
5. Conclusions
Acknowledgments
Conflicts of Interest
References
- T’Serclaes, P. Financing Energy Efficient Homes: Existing Policy Responses to Financial Barriers; International Energy Agency: Paris, France, 2007. [Google Scholar]
- Guggemos, A.A.; Horvath, A. Comparison of environmental effects of steel- and concrete-framed buildings. J. Infrastruct. Syst. 2008, 11, 93–101. [Google Scholar] [CrossRef]
- Zhang, Z.; Wu, X.; Yang, X.; Zhu, Y. BEPAS—A life cycle building environmental performance assessment model. Build. Environ. 2006, 51, 669–675. [Google Scholar] [CrossRef]
- Yang, L.; Zmeureanu, R.; Rivard, H. Comparison of environmental impacts of two residential heating systems. Build. Environ. 2008, 43, 1072–1081. [Google Scholar] [CrossRef]
- Radhi, H. On the optimal selection of wall cladding system to reduce direct and indirect CO2 emissions. Energy 2010, 35, 1412–1424. [Google Scholar] [CrossRef]
- Gartner, E. Industrially interesting approaches to “low-CO2” cements. Cem. Concr. Res. 2004, 34, 1489–1498. [Google Scholar] [CrossRef]
- Wang, W.; Zmeureanu, R.; Rivard, H. Applying multi-objective genetic algorithms in green building design optimization. Build. Environ. 2005, 40, 1512–1525. [Google Scholar] [CrossRef]
- Sartori, I.; Hestnes, A.G. Energy use in the life cycle of conventional and low-energy buildings: A review article. Energy Build. 2007, 39, 249–257. [Google Scholar] [CrossRef]
- Pachauari, R.K.; Reisinger, A. Climate Change 2007: Synthesis Report. Contribution of Working Groups I, II and III to the Fourth Assessment Report on Intergovernmental Panel on Climate Change; Intergovernmental Panel on Climate Change (IPCC): Geneva, Switzerland, 2007. [Google Scholar]
- Thiel, C.L.; Campion, N.; Landis, A.E.; Jones, A.K.; Schaefer, L.A.; Bilec, M.M. A materials life cycle assessment of a net-zero energy building. Energies 2013, 6, 1125–1141. [Google Scholar] [CrossRef]
- Airaksinen, M.; Matilainen, P. A carbon footprint of an office building. Energies 2011, 4, 1197–1210. [Google Scholar] [CrossRef]
- Dixit, M.K.; Fernández-Solís, J.L.; Lavy, S.; Culp, C.H. Identification of parameters for embodied energy measurement: A literature review. Energy Build. 2010, 42, 1238–1247. [Google Scholar] [CrossRef]
- Thormark, C. A low energy building in a life cycle—Its embodied energy, energy need for operation and recycling potential. Build. Environ. 2002, 37, 429–435. [Google Scholar] [CrossRef]
- Reddy, B.V.V.; Jagadish, K.S. Embodied energy of common and alternative building materials and technologies. Energy Build. 2003, 35, 129–137. [Google Scholar] [CrossRef]
- Liu, K.S.; Hsueh, S.L.; Wu, W.C.; Chen, Y.L. A DFuzzy-DAHP decision-making model for evaluating energy-saving design strategies for residential buildings. Energies 2012, 5, 4462–4480. [Google Scholar] [CrossRef]
- Moon, K.S. Sustainable structural engineering strategies for tall building. Struct. Des. Tall Spec. Build. 2008, 17, 895–914. [Google Scholar] [CrossRef]
- Yeo, D.; Gabbai, R.D. Sustainable design of reinforced concrete structures through embodied energy optimization. Energy Build. 2011, 43, 2028–2033. [Google Scholar] [CrossRef]
- Yeo, D.; Potra, F.A. Sustainable design of reinforced concrete structures through CO2 emission optimization. J. Struct. Eng. 2013. [Google Scholar] [CrossRef]
- Paya-Zaforteza, I.; Yepes, V.; Hospitaler, A.; González-Vidosa, F. CO2-Optimization of reinforced concrete frames by simulated annealing. Eng. Struct. 2009, 31, 1501–1508. [Google Scholar] [CrossRef]
- Paya, I.; Yepes, V.; González-Vidosa, F.; Hospitaler, A. Multiobjective optimization of concrete frames by simulated annealing. Comput.-Aided Civ. Infrastruct. Eng. 2008, 23, 596–610. [Google Scholar] [CrossRef]
- Saw, H.S.; Liew, J.Y.R. Assessment of current methods for the design of composite columns in buildings. J. Constr. Steel Res. 2000, 53, 121–147. [Google Scholar] [CrossRef]
- Lu, Y.; Zhu, X.; Cui, Q. Effectiveness and equity implications of carbon policies in the United States construction industry. Build. Environ. 2012, 49, 259–269. [Google Scholar] [CrossRef]
- Architectural Institute of Korea (AIK). Korean Building Code and Commentary (in Korean); Architectural Institute of Korea: Seoul, Korea, 2009. [Google Scholar]
- Cheng, L.; Chan, C.M. Optimal lateral stiffness design of composite steel and concrete tall frameworks. Eng. Struct. 2009, 31, 523–533. [Google Scholar] [CrossRef]
- Structural Stability Research Council. A specification for the design of steel-concrete composite columns. Eng. J. 1979, 4, 101–115. [Google Scholar]
- Goldberg, D.E. Genetic Algorithms in Optimization, Search and Machine Learning; Addison Wesley: New York, NY, USA, 1989. [Google Scholar]
- Zhu, B. A novel multiscale ensemble carbon price prediction model integrating empirical mode decomposition, genetic algorithm and artificial neural network. Energies 2012, 5, 355–370. [Google Scholar] [CrossRef]
- Tomoiagă, B.; Chindriş, M.; Sumper, A.; Sudria-Andreu, A.; Villafafila-Robles, R. Pareto optimal reconfiguration of power distribution systems using a genetic algorithm based on NSGA-II. Energies 2013, 6, 1439–1455. [Google Scholar] [CrossRef]
- Fang, L.; Qin, S.; Xu, G.; Li, T.; Zhu, K. Simultaneous optimization for hybrid electric vehicle parameters based on multi-objective genetic algorithms. Energies 2011, 4, 532–544. [Google Scholar] [CrossRef]
- Choi, S.W.; Park, H.S. Multi-objective seismic design method for ensuring beam-hinging mechanism in steel frames. J. Constr. Steel Res. 2012, 74, 17–25. [Google Scholar] [CrossRef]
- Choi, S.W.; Kim, Y.; Lee, J.; Hong, K.; Park, H.S. Minimum column-to-beam strength ratios for beam-hinge mechanisms based on multi-objective seismic design. J. Constr. Steel Res. 2013, 88, 53–62. [Google Scholar] [CrossRef]
- Cha, Y.J.; Agrawal, A.K.; Kim, Y.; Raich, A.M. Multi-objective genetic algorithms for cost-effective distributions of actuators and sensors in large structures. Expert Syst. Appl. 2012, 39, 7822–7833. [Google Scholar] [CrossRef]
- Cha, Y.J.; Kim, Y.; Raich, A.M.; Agrawal, A.K. Multi-objective optimization for actuator and sensor layouts of actively controlled 3D buildings. J. Vib. Control 2013, 19, 942–960. [Google Scholar] [CrossRef]
- Goggins, J.; Keane, T.; Kelly, A. The assessment of embodied energy in typical reinforced concrete building structures in Ireland. Energy Build. 2010, 42, 735–744. [Google Scholar] [CrossRef]
- Korea LCI Database Information Network (in Korean). Available online: http://www.edp.or.kr/lcidb/english/main/main.asp (accessed on 16 August 2013).
- Hong, T.; Ji, C.; Jang, M. An analysis on CO2 emission of structural steel materials by strength using input-output LCA. Korea J. Constr. Eng. Manag. 2012, 13, 132–140. (in Korean). [Google Scholar] [CrossRef]
- De Jong, K.A. Analysis of the Behavior of a Class of Genetic Adaptive Systems. Ph.D. Thesis, University of Michigan, Ann Arbor, MI, USA, 1975. [Google Scholar]
- Tae, S.; Baek, C.; Shin, S. Life cycle CO2 evaluation on reinforced concrete structures with high-strength concrete. Environ. Impact Assess. Rev. 2011, 31, 253–260. [Google Scholar] [CrossRef]
© 2013 by the authors licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license ( http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Park, H.S.; Kwon, B.; Shin, Y.; Kim, Y.; Hong, T.; Choi, S.W. Cost and CO2 Emission Optimization of Steel Reinforced Concrete Columns in High-Rise Buildings. Energies 2013, 6, 5609-5624. https://doi.org/10.3390/en6115609
Park HS, Kwon B, Shin Y, Kim Y, Hong T, Choi SW. Cost and CO2 Emission Optimization of Steel Reinforced Concrete Columns in High-Rise Buildings. Energies. 2013; 6(11):5609-5624. https://doi.org/10.3390/en6115609
Chicago/Turabian StylePark, Hyo Seon, Bongkeun Kwon, Yunah Shin, Yousok Kim, Taehoon Hong, and Se Woon Choi. 2013. "Cost and CO2 Emission Optimization of Steel Reinforced Concrete Columns in High-Rise Buildings" Energies 6, no. 11: 5609-5624. https://doi.org/10.3390/en6115609
APA StylePark, H. S., Kwon, B., Shin, Y., Kim, Y., Hong, T., & Choi, S. W. (2013). Cost and CO2 Emission Optimization of Steel Reinforced Concrete Columns in High-Rise Buildings. Energies, 6(11), 5609-5624. https://doi.org/10.3390/en6115609






