1. Introduction
DC-to-DC switching converters are frequently used to adapt the voltage and current levels provided by power generators, such as fuel cells or photovoltaic modules, to the ones required by electrical loads. Large switching ripples at the converters’ input current reduce the efficiency of the photovoltaic generation and shorten the life expectancy of fuel cells. Adding input filters to the switching stages [
1] or using conventionally interleaved converters [
2] are some well known procedures to reduce the detrimental ripple amplitudes of the currents requested by switching converters from power generators. Conventional interleaving is the parallel connection of N identical switching stages whose control signals and subsequent current ripple waveforms are uniformly phase-shifted over the switching period. The resultant harmonic cancellation lowers ripple amplitudes by raising the effective switching frequency without increasing switching losses or device stresses [
2]. In addition to these interleaving benefits, since the aggregated current is evenly shared among the parallelled stages, high amounts of power can be processed. However, specific current control strategies are required in conventional interleaving to ensure an even sharing of the current among the parallelled power modules [
3,
4,
5]. Without these sharing control strategies [
6], small inequalities between converter parameters in addition to a bidirectional current implementation of the switches result in large circulating currents associated with high losses and stresses in power inductors and semiconductor devices. The use of unidirectional current switches without current sharing control strategies could also have severe drawbacks such as the appearance of discontinuous conduction modes (DCM) [
1]. In this case, one of the modules frequently operates in continuous conduction mode (CCM) and processes the largest amount of power, while the rest of the paralleled modules, being in DCM, transfer very small amounts of power from the generator to the load.
The asymmetrical interleaved converters (AIC) presented in [
7] are a particular case of interleaving in which the inputs of two non-identical unidirectional converters are connected in parallel and an open-loop straightforward control strategy consisting in the complementary activation of the converter’s switches is enforced. The breaking of the symmetry results in one of the stages to operate in CCM and the other in DCM but the specific form in which the non-identical converter’s outputs are connected causes that a significant fraction of the input current is processed by the DCM phase. The simplicity of the open-loop control strategy required to obtain a partial input current sharing in addition with a significant reduction in the amplitudes of input and output current ripples are some of the advantages of the recently reported new high-order family of converters. Since discontinuous conduction modes are inherent to the AIC family, closing a regulation loop requires using specific modeling techniques that are reviewed in
Section 2 from which the revised averaging method [
8] has been selected as the most suitable one. The application of the revised averaging method to the boost derived asymmetrical interleaved dual boost (AIDB) converter is detailed in
Section 3. However, as it will be seen in
Section 4, the high-order of the converter and the simultaneous coexistence of continuous and discontinuous conduction have required an improved modeling approach that provides better agreement between the frequency responses of the model and the simulated switching converter. The results of applying the new modeling approach to the remaining members of the AIC family [asymmetrical interleaved dual buck-boost (AIDBB) and asymmetrical interleaved dual flyback (AIDF)] are provided in
Section 5.
Section 6 shows an example of multivariable control design that uses the model previously obtained in
Section 4. Finally, conclusions and some proposals for future studies are discussed in
Section 7.
3. Modeling the AIDB Converter Using the Revised Averaging Method
The discontinuous conduction mode, in which the AIDB converter works, limits the modeling possibilities of methods that are traditionally applied to CCM. Among the DCM modeling methods, the one that offers the best approximation is
the revised averaging method (RAM) proposed in [
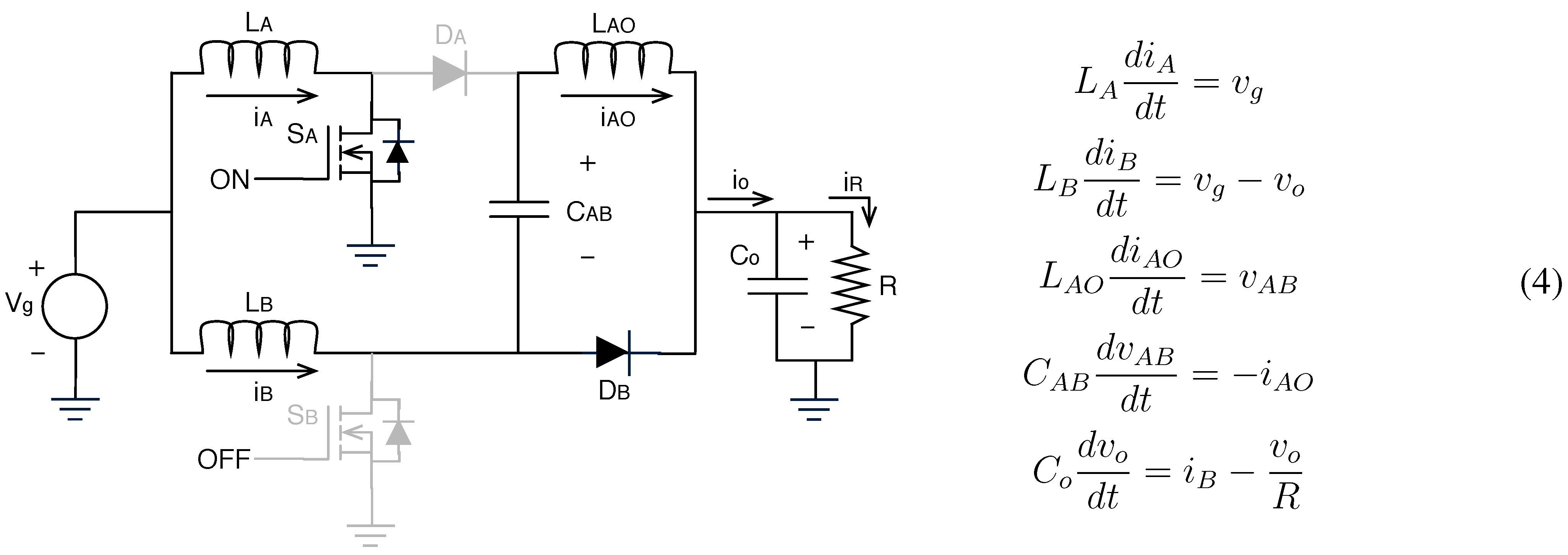
8] due to its improved approximation of the high-frequency poles. This section presents the modeling of the AIDB converter using the RAM to illustrate its limitations in the reproduction of the converter dynamic behavior. The electrical circuit of the AIDB converter is depicted in
Figure 1a, where the asymmetrical interleaved structure is observed. Moreover,
Figure 1b shows the inductor current waveforms where the DCM condition is put in evidence at
. In addition, such a figure shows the three operation intervals that define the switching period:
,
and
, which duty cycles are related as in Equations (
1) and (
2). It must be pointed out that the modeling procedures presented in this section are based on the circuital analyses given in [
7] for the AIDB converter:
The RAM consists of three steps: averaging, correction, and duty-cycle constraint definition [
8]. The first step consist in the conventional state variables averaging as given in [
1], while the second one consists of dividing all the inductor currents in the converter by the factor
since these are the two duty ratios in which the inductors are conducting. Such a correction must be made because, in DCM, the inductor currents (or the discontinuous variables) have three intervals instead of the two intervals present in CCM.
Figure 1b shows that such a DCM condition exists in the inductor currents
and
of the AIDB converter.
Figure 1.
Asymmetrical interleaved dual boost (AIDB) converter circuit and waveforms: (a) electrical scheme; and (b) discontinuous currents.
Figure 1.
Asymmetrical interleaved dual boost (AIDB) converter circuit and waveforms: (a) electrical scheme; and (b) discontinuous currents.
To perform the averaging procedure, the AIDB topologies an equations obtained in [
7] must be analyzed. In addition, reference [
7] was demonstrated that the AIC converters must be operated at duty cycles within
, in which low ripple conditions are ensured. Therefore, the modeling approaches consider the three topologies exhibited by the AIDB for the duty cycles of interest:
Topology 1 ( and ON, and OFF): it is active in the first interval , during , it begins when is turned ON and is turned OFF, and it ends when is turned OFF and is turned ON (Topology 2). In this topology increases while and decrease;
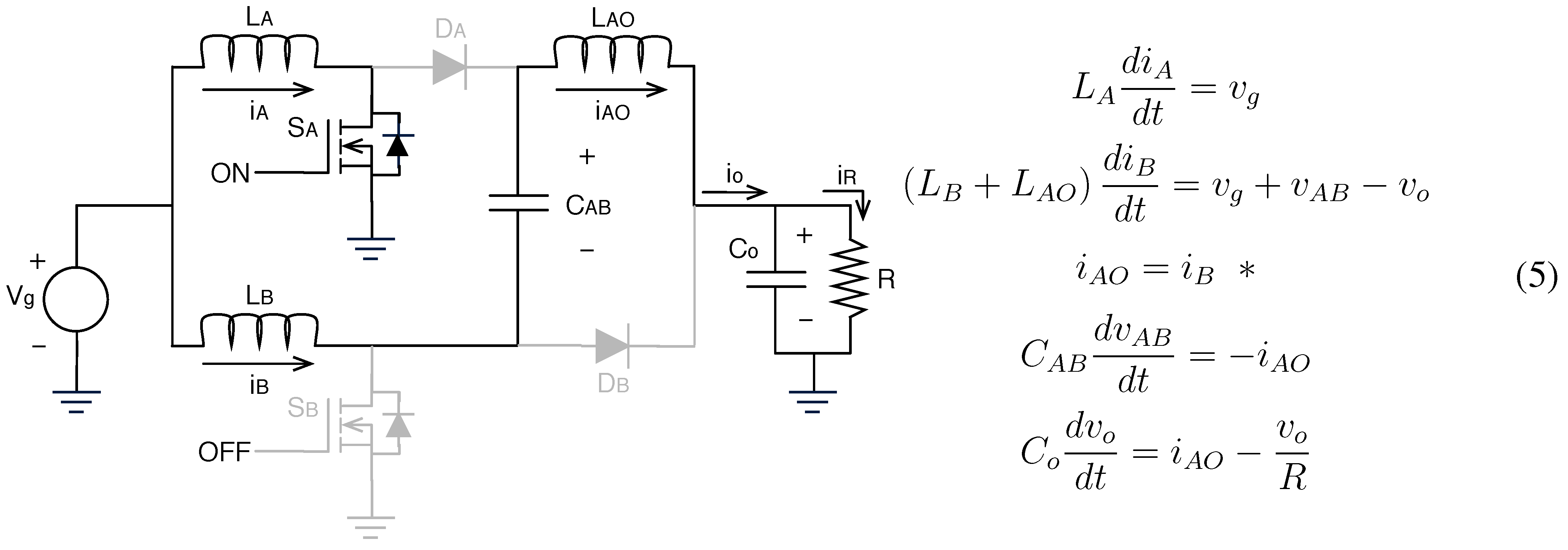
Topology 2 ( and ON, and OFF): it is active in the second interval during , it begins when is turned OFF and is turned ON, and it ends when is automatically turned OFF (Topology 3). In this topology decreases while and increase;
Topology 3 ( ON, , and OFF): it is active in the third interval during , it begins when is automatically turned OFF by the DCM condition generated when (null current in ), and it ends when is turned ON and is turned OFF (Topology 1). In this topology and are constant and equal while still increases.
Figure 2,
Figure 3 and
Figure 4 show the topologies and their equations, where
and
are the voltages of capacitors
and
, respectively. In Topology 3, the equation marked with an asterisk (*) reflects the reduction of order that occurs in DCM, which makes difficult to perform the averaging calculations.
The averaged equations are obtained using the conventional method of multiplying each equation by the corresponding intervals and dividing it by the period [
1]. Then, the state space averaged system (for
) is:
In the correction step proposed in [
8], all the equations are affected. But from the equations on
Figure 2,
Figure 3 and
Figure 4, it is noted that
is always continuous in the AIDB, while
and
are discontinuous in Topology 3. Therefore, in the AIDB it is only necessary to apply the correction to the equations in which
and
appear since the CCM averaging in
is correct. Consequently, the averaged equations of
and
must be divided by the factor
, as described in [
8], to obtain the corrected expressions:
To obtain the dynamic model, the duty cycle
must be replaced in Equation (
7) by an expression depending on other variables. Equation (
8) gives the expression obtained in [
8] for
, where
is the average value of the discontinuous current and
is the voltage across the inductor when the switch is ON:
Since there are two discontinuous currents in the AIDB, it is possible to define
from
as in Equation (
9) or from
as in Equation (
10):
But replacing Equation (
9) in Equation (
7) produces an operating point that does not match the simulation results of [
7], predicting a
value close to zero and predicting RHP poles that make this model unstable, it behaving totally differently from the converter. Similarly, by replacing Equation (
10) in Equation (
7), the prediction is worst since the variable
does not appear in the equations, which makes impossible to obtain a solution for the system. Therefore, it became necessary to explore another way to calculate
to apply the RAM approach described in [
8].
3.1. New Calculation Procedure for Duty Cycle
The average converter currents are calculated using the areas of the triangles in the waveforms of
Figure 1b, where the average value of
and
currents are given in Equations (
11) and (
12), respectively. In such expressions, the peak currents
and
are calculated from Equation (5),
i.e., Topology 3, as in Equation (
13). Then, the expression for
given in Equation (
14) is obtained by subtracting Equations (
11) and (
12):
3.2. RAM Applied to the AIDB Using the New Value
Replacing Equations (
1) and (
14) in Equation (
7) leads to the dynamic model of the AIDB (for
) based on the approach proposed in [
8]:
where:
The input and state variables of the model are represented in terms of steady-state and small signal components as in Equations (
17) and (
18), where
. Moreover,
are the averaged states,
X,
and
are the steady-state values while
,
and
are small-signal quantities:
Then, the steady-state condition given in Equation (
19) is obtained by solving Equation (
15) with all the derivatives equal to zero, where the capital letters indicate steady-state values for the states in
X:
The prediction provided by such steady-state expressions has been contrasted with numerical values obtained from electrical simulations (using PSIM software) of the AIDB converter with
H,
H,
H,
F,
F,
, and
s (switching period) and duty cycles from
to
each
. In such conditions, expressions from Equation (
19) exhibit a Root Mean Squared Error (RMSE) equal to 0.3%.
Similarly, the small-signal model, given in Equation (
20), of the state space averaged system,
i.e., Equation (
15), is obtained by linearizing, around the operating point, the states and inputs Jacobians
A and
B as in Equations (
21) and (
22), respectively:
To test the model accuracy in the reproduction of the converter dynamic behavior, a numerical small-signal model was obtained for the converter parameters previously described. Moreover, the AIDB converter was simulated in PSIM to obtain the circuit frequency response, which was contrasted with the small-signal model predictions.
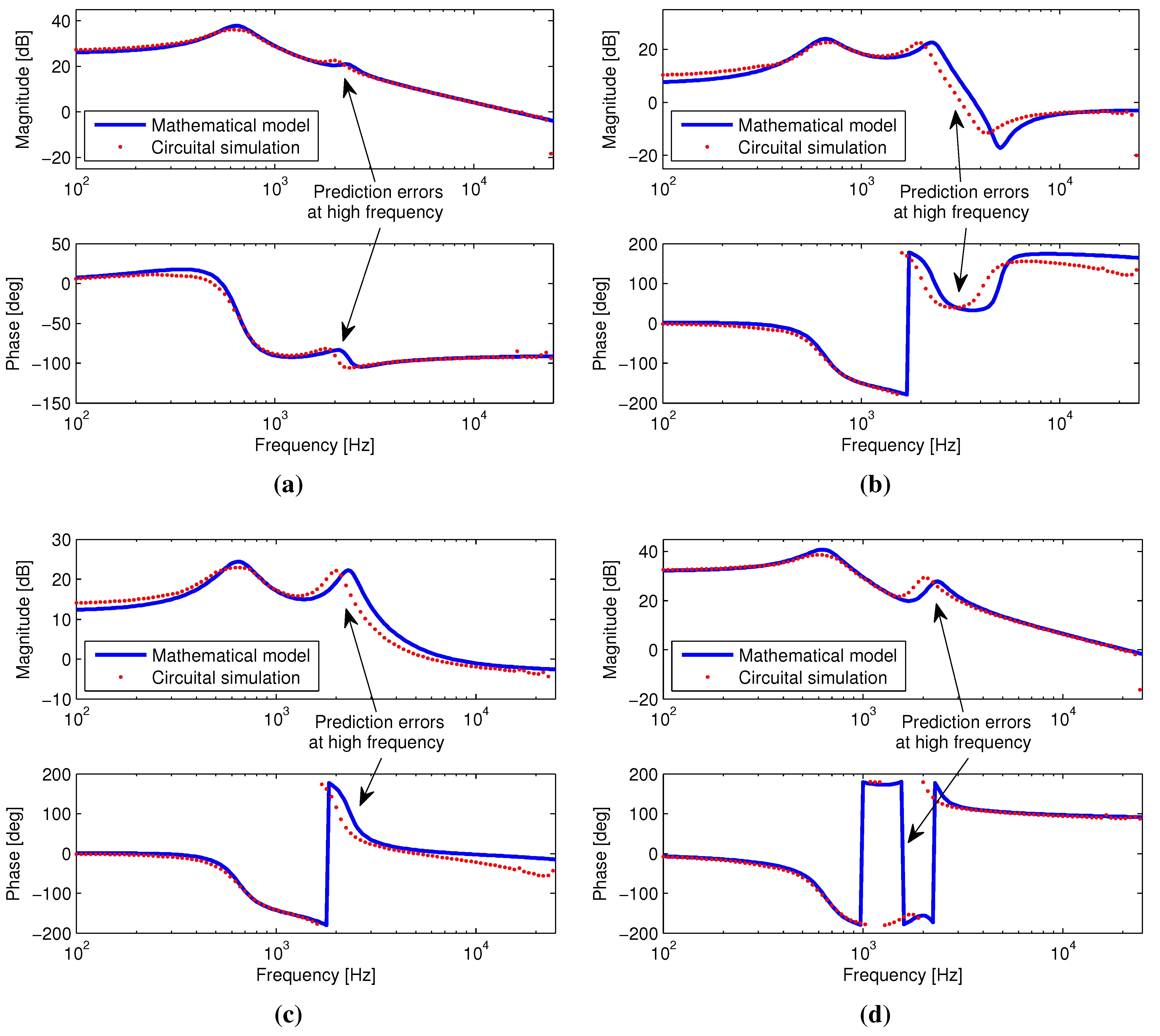
Figure 5 and
Figure 6 show the Bode diagrams of the states
obtained with both the model and the circuit, where the model approximation is not accurate enough: at low frequencies the model reproduces with very small differences the circuit behavior, but at high frequencies the model exhibits large errors. Hence, the model obtained following the approach given in [
8] is not suitable for control purposes, or even for dynamic analyses, due to its large errors. Therefore, a new approach must be adopted to find a more accurate dynamic model suitable for control design.
Figure 5.
AIDB Bode diagrams from circuital simulation and revised averaging method (RAM) simulation: (a) ; (b) ; (c) and (d) .
Figure 5.
AIDB Bode diagrams from circuital simulation and revised averaging method (RAM) simulation: (a) ; (b) ; (c) and (d) .
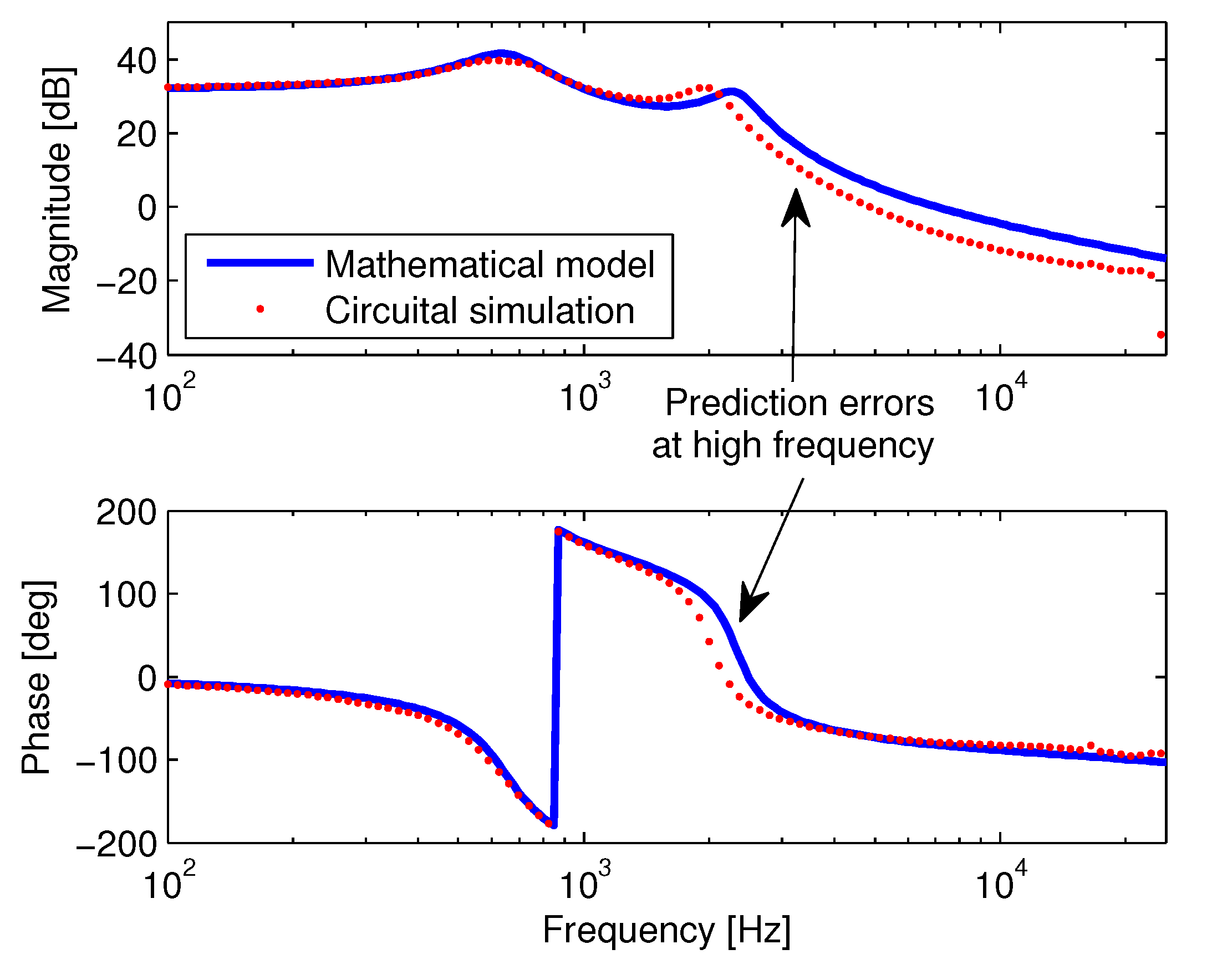
Figure 6.
AIDB Bode diagrams from circuital simulation and RAM simulation: output voltage .
Figure 6.
AIDB Bode diagrams from circuital simulation and RAM simulation: output voltage .
4. Improved Method for Modeling High-Order Converters in DCM
This method has the aim of improving the prediction of dynamical behaviors in converters operating in DCM, it focused in the AIC family despite it is applicable to any converter. The design of this method was necessary due to the simultaneous appearance of discontinuous currents (with three intervals) and continuous currents (with two intervals) in the AIDB converter, as in the AIC family also. In theory, if both continuous and discontinuous currents were not concurrent, the RAM would provide an accurate approach. In such a way, this new method averages the state variables of the converter in a conventional way but includes two changes to improve the approximation of the model: the definition of an additional variable to describe the behavior of discontinuous variables and a novel procedure to calculate the duty cycle .
The steps of the new
improved averaging method, named IAM, are the following:
Identify new variables that affect the converter dynamics using circuital analyses;
Include in the topologies equations the new variable;
Obtain the averaged equations from the modified topologies equations;
Calculate the correct expression for the duty cycle ;
Calculate the new variable in terms of the circuit states and inputs;
Replace both the new variable and in the averaged equations;
Calculate the steady-state and small-signal expressions.
In the following subsections, the IAM is illustrated by modeling the AIDB converter. In addition, such a model is contrasted with circuital simulations and experimentally tested to validate the IAM.
4.1. Modeling the AIDB Using the IAM
To illustrate the IAM technique, each step is described considering an AIDB converter:
Step 1: From the AIDB scheme in
Figure 1a, it is noted that the output current
is obtained by adding two currents: the current in the inductor
and the current in the diode
. Therefore, to provide an accurate prediction of the AIDB output current, it is necessary to include the current in diode
in the analytical model as the new variable
. In this way, the error generated in RAM [
8] by neglecting this current is avoided.
Step 2: From the circuital topologies (
Figure 3) it is noted that diode
conducts in Topology 2. Therefore, the expressions in Equation (4) describing this topology are modified to include the current
as follows:
Step 3: The new state space averaged system (
) including the new variable
is given in Equation (
24), where
represents the averaged value of
:
Step 4: The procedure to calculate the correct duty cycle
, for the AIDB converter, was described in
Subsection 3.1 leading to Equation (
14). Moreover, the duty cycle
is calculated from the fundamental relation given in Equation (
1).
Step 5: Taking into account that diode
only conducts in Topology 2 with
, it describes a triangular waveform in
with a peak current equal to
: since
and
in Topology 2, the maximum current in
(peak current) is achieved at the beginning of the interval
when both
and
exhibit their peak currents,
i.e.,
and
, respectively. Then,
is calculated as in Equation (
25), where substituting the expressions for
and
obtained in Equation (
13) and the expression of
given in Equation (
14), the
expression given in Equation (
26) is obtained:
Step 6: Replacing Equations (
1), (
14) and (
26) in Equation (
24), the new averaged equations in terms of the duty cycle
are:
where:
Step 7: The calculation of the expressions for both the steady-state and small-signal model are performed following the procedures given in
Subsection 3.2, where the states vector is defined as
. Again, the input and state variables of the model are represented in terms of steady-state and small signal components as in Equations (
17) and (
18).
The small-signal model,
i.e.,
, of the state space averaged system,
i.e., Equation (
27), is obtained by linearizing, around the steady-state operating point, the states and inputs Jacobians
A and
B as in Equations (
21) and (
22), respectively.
Then, the steady-state condition given in Equation (
29) is obtained by solving Equation (
27) with all the derivatives equal to zero, where the capital letters indicate steady-state values. Expressions in Equation (
29) include modifications in the equations of the three currents (
,
and
), with respect to Equation (
19), which are the result of the correction introduced by
current. Such modifications improve the prediction of the steady-state conditions: the prediction of those steady-state expressions exhibit a RMSE equal to 0.01% with respect to the electrical simulations performed with the same circuit parameters reported in
Subsection 3.2. Therefore, the proposed model improves the accuracy of the steady-state calculations in one order of magnitude. But the most important improvement of the new model concerns its high accuracy in dynamic conditions, which will be illustrated in the following subsection by means of simulation and experimental results:
4.2. Simulation and Experimental Validation
To verify the accuracy of the dynamic model for the AIDB converter obtained with IAM,
i.e., Equation (
27), the IAM model was parameterized with the values reported in
Subsection 3.2. Both the IAM model and PSIM circuit (from
Subsection 3.2) were simulated to obtain the IAM and circuital frequency responses presented in
Figure 7 and
Figure 8: the high accuracy of IAM over RAM at high frequency is observed for all the states, but also improvements at low frequency are obtained with this new modeling technique for the prediction of the currents. Such simulation results put in evidence the satisfactory prediction of the AIDB dynamics provided by the IAM, which makes such a model useful for control purposes.
In addition to the simulations, an experimental prototype with the same circuit parameters was used to obtain the frequency response of a practical AIDB converter:
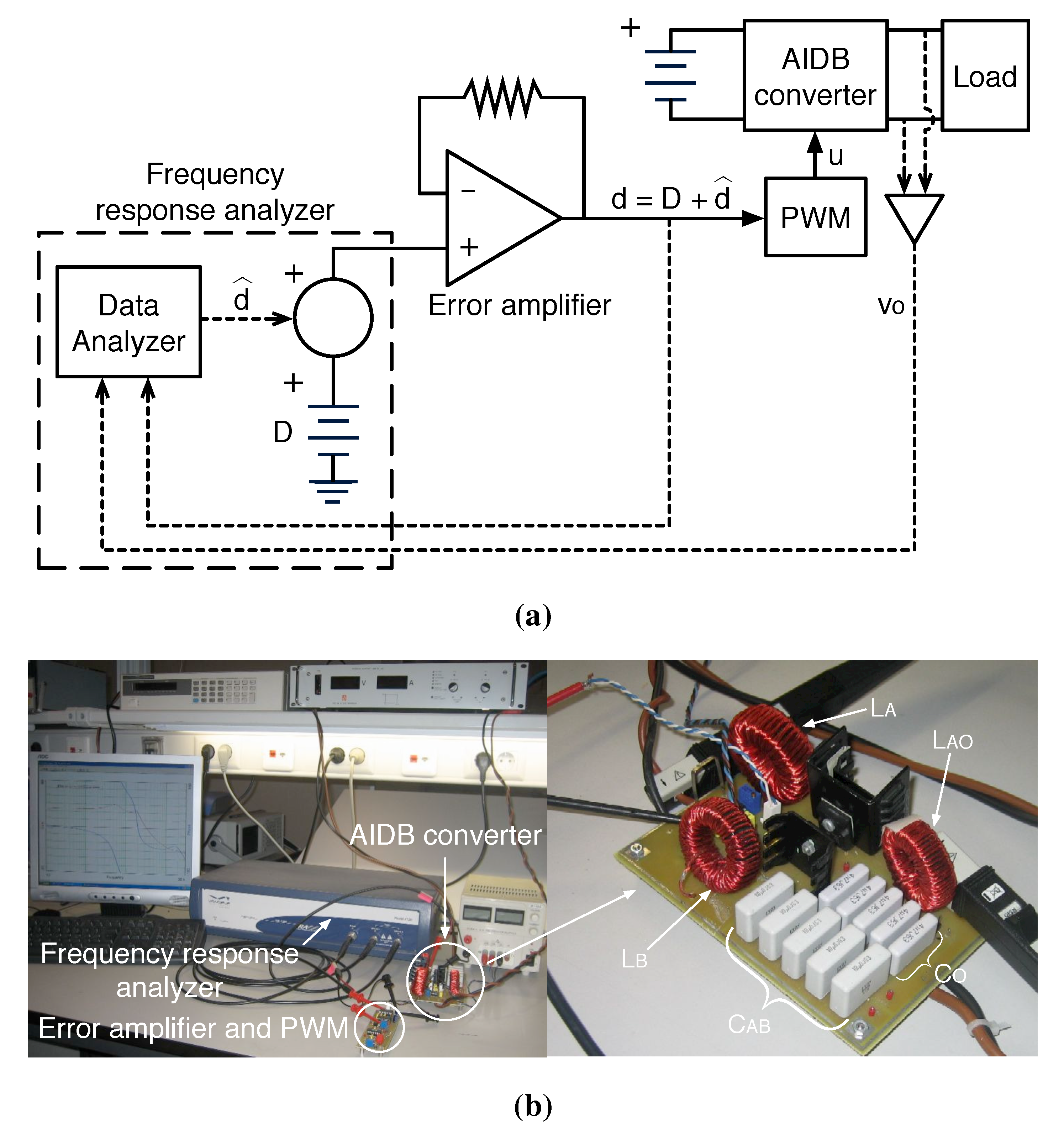
Figure 9a shows the block diagram of the experimental setup, where a frequency response analyzer (FRA) excites the converter by means of an error amplifier (for isolation) and a PWM (to drive the switches) with multiple frequencies. Then, the signals at the PWM input and converter output are measured to calculate the experimental frequency response of the output voltage.
Figure 9b shows the test bench, where the FRA and electrical circuits used in the experiments are observed.
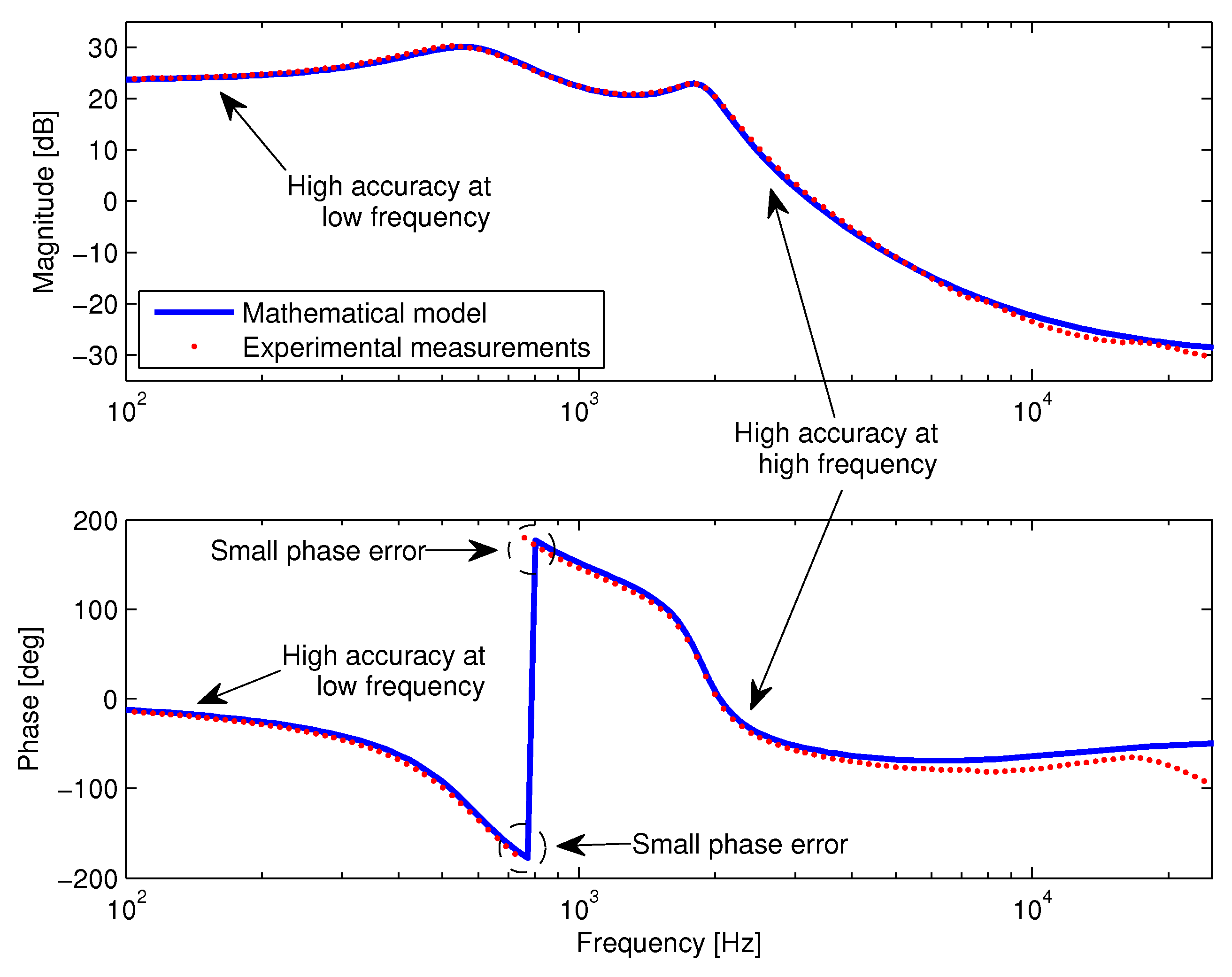
Figure 10 shows the Bode diagrams obtained by means of the new model (IAM) and the one measured experimentally (FRA) for the output voltage. The figure shows the satisfactory prediction provided by the model at both high and low frequency conditions with some small errors in the phase. This result validates the IAM approach, demonstrating its accurate prediction of the converter dynamic behavior, which in turn is useful for control purposes.
Figure 7.
AIDB Bode diagrams from circuital simulation and improved averaging method (IAM) simulation: (a) ; (b) ; (c) ; and (d) .
Figure 7.
AIDB Bode diagrams from circuital simulation and improved averaging method (IAM) simulation: (a) ; (b) ; (c) ; and (d) .
Figure 8.
AIDB Bode diagrams from circuital simulation and IAM simulation: output voltage .
Figure 8.
AIDB Bode diagrams from circuital simulation and IAM simulation: output voltage .
Figure 9.
Experimental setup used to obtain the AIDB frequency response: (a) block diagram; and (b) test bench.
Figure 9.
Experimental setup used to obtain the AIDB frequency response: (a) block diagram; and (b) test bench.
Figure 10.
AIDB Bode diagrams from experiments and IAM simulation.
Figure 10.
AIDB Bode diagrams from experiments and IAM simulation.
6. Application Example: AIDB Control Design
This section illustrates the usefulness of the proposed IAM technique in practical applications: the AIDB converter is controlled to supply a regulated voltage to a resistive load, where the electrical power is provided by a fuel cell. As clearly described in [
7], the AIC family provides the useful conditions to interface fuel cells: low current ripple and high voltage conversion ratio. But, since the fuel cell voltage changes with the requested power, the AIDB output voltage must be regulated to compensate both load and fuel cell perturbations.
This example considers the AIDB parameters given in
Subsection 3.2 operating with a fuel cell stack from Pragma Industries (named FCPc) composed by 2 parallel strings of 18 cells in series each. The polarization and power curves of such a FCPs stack are depicted in
Figure 13a and
Figure 13b, respectively. Moreover, the application considers a load with a nominal impedance of
that requires a fixed voltage of 30 V to operate. In such a condition the fuel cell must to provide 90 W, disregarding losses, which imposes stack current and voltage near to 9 A and 10 V, respectively. Such an operating point is highlighted in
Figure 13a and
Figure 13b. Moreover, taking into account that the load voltage must be regulated, such figures put in evidence that changes on the load impedance generate changes in the fuel cell voltage, which imposes the voltage at the input of the AIDB converter. Therefore, a suitable controller must be designed to compensate both input and output perturbations in the converter.
Figure 13.
Fuel cell electrical characteristics: (a) polarization curve; and (b) power curve.
Figure 13.
Fuel cell electrical characteristics: (a) polarization curve; and (b) power curve.
Then, the improved model based on the IAM approach, and presented in
Subsection 4.1, is used to design a linear-quadratic regulator (LQR) to provide the required compensation. Such a control technique was adopted since it is based on the states feedback and not only on the output feedback as Proportional-Integral (PI) or Proportional-Integral-Derivative (PID) controllers. Therefore, the design of a LQR controller helps to illustrate, in a better way, the usefulness of the modeling approach proposed in this paper.
6.1. The LQR Controller
The quadratic optimal control theory is used to design stable control systems by choosing the control vector
such that a given performance index is minimized. Therefore, considering the system representation given in Equation (
38), the designing problem is reduced to determine the matrix
K of the optimal control vector [
32], as in Equation (
39), to minimize the complex quadratic performance index given in Equation (
40):
In Equation (
40),
Q is a positive-definite (or positive-semidefinite) Hermitian or real symmetric matrix and
R is a positive-definite Hermitian or real symmetric matrix. The matrices
Q and
R determine the relative importance of the error and the expenditure of the energy in the system.
The procedure followed to find the matrix
K beings with the definition of the parameter-optimizing problem, then using the second method of Liapunov the performance index
J is evaluated and minimized, and the result is the reduced-matrix Riccati equation which solution provides the optimal matrix
K. The details of such a procedures are given in [
32].
Moreover, to ensure null steady-state error, a sixth state variable was introduced to the system: the integral of the error between the output voltage and the reference. Such additional state equation is given in Equation (
41), where
V is the reference voltage:
The feedback vector gains
K Equation (
39) can be obtained using the MATLAB command
, which provides the solution to the Riccati equation in continuous time (matrix
S), determines the optimal feedback matrix gains (vector
K) and the closed loop poles location (vector
e). The matrices
Q and
R are usually selected by the designer and adjusted by trial and error. In this example, such matrices have been defined taking into account energy considerations and the relative weight of the output voltage and its error: considering the energy stored in the capacitors (
) and inductors (
) given in Equation (
42), and taking into account that
Q matrix is related to energy expenditure, the coefficients of such a matrix were defined as in Equation (
43). In such a matrix, the coefficients related to the currents have the same weight since in the adopted converter all the inductors have very similar values (see circuit parameters given in
Subsection 3.2); but the coefficients related to the voltages are weighted in agreement with the capacitor values since they are very different. In addition, the coefficient related to the error was selected large enough to give priority to the null steady-state error condition. Finally, the
Q matrix was normalizer with respect to the output voltage coefficient to avoid numerical values too small:
Then, matrix
R must be small enough to provide a fast correction of the perturbations as given in Equation (
44). Finally, using
Q and
R matrices given in Equations (
43) and (
44), the IAM model parameterized as in
Subsection 3.2, and both the FCPc fuel cell stack and load characteristics previously described, the numerical
K vector given in Equation (
45) was calculated:
6.2. Simulation Results
The designed LQR controller was tested by means of circuital simulations in PSIM. The simulation considers the fuel cell modeled by a Thevenin equivalent, while the load perturbations were introduced by changing the load current. In such a way, 20% step-up and step-down load perturbations were introduced to evaluate the controller performance.
Figure 14 shows the simulation results: the controller compensates both step-up and step-down load perturbations by providing settling times equal to 1.8 ms in both cases.
Figure 14.
Dynamic simulation in PSIM.
Figure 14.
Dynamic simulation in PSIM.
The figure also shows the change on the stack voltage caused by the increment in the load power. In any case, both perturbations are satisfactorily attenuated. Moreover, the operating point defined by the interaction between the converter and the fuel cell slightly diverges from the theoretical values (10 V, 9 A) due to the stack electrical characteristic (
Figure 13a and
Figure 13b), but such a difference is compensated by the controller to provide the desired conditions to the load.
Finally, this example put in evidence the usefulness of the proposed IAM modeling approach in the design of control strategies for practical applications.
7. Conclusions
The challenge of accurately modeling the members of the AIC family has been initially addressed by selecting the revised averaging method [
8], which consists of three steps: averaging, correction and duty-cycle constraint definition. Being the AIC family a particular case of high-order dc/dc switching converters operating in discontinuous conduction mode in which two of the inductor currents are in discontinuous conduction while another one is not, the application of the revised averaging method is not straightforward. A new calculation procedure for the duty cycle
in the duty-cycle constraint definition step has been illustrated in the modeling of the AIDB converter. However, the resulting full-order continuous non-linear model of the AIDB converter is not suitable for advanced control design because it exhibits large errors at high frequencies.
An improved averaging method that overcomes the high frequency modeling deficiencies of the previous revised averaging method has been carefully detailed and validated by means of both PSIM simulations and experimental measurements of an AIDB stage operating at duty cycles above . The key factor in the improved modeling is the explicit inclusion in the equations of the current flowing though the diode that operates in discontinuous conduction mode.
The improved method has also been successfully applied to the remaining members of the AIC family. Examples of modeling the AIDBB and the I-NI-AIF converters are provided in the paper. The modeling of other high-order converters operating in DCM such as Cuk, sepic or zeta will be addressed in future works. Similarly, a simplified version of the proposed technique, aimed for field engineers, is an open problem to be addressed.
Finally, the excellent accuracy in the frequency response provided by the improved averaging method has allowed to design a voltage regulator for a fuel cell application in which an AIDB converter is successfully controlled by means of a linear quadratic regulation technique.