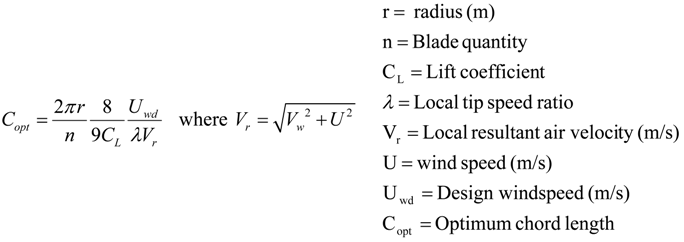1. Introduction
Power has been extracted from the wind over hundreds of years with historic designs, known as windmills, constructed from wood, cloth and stone for the purpose of pumping water or grinding corn. Historic designs, typically large, heavy and inefficient, were replaced in the 19th century by fossil fuel engines and the implementation of a nationally distributed power network. A greater understanding of aerodynamics and advances in materials, particularly polymers, has led to the return of wind energy extraction in the latter half of the 20th century. Wind power devices are now used to produce electricity, and commonly termed wind turbines.
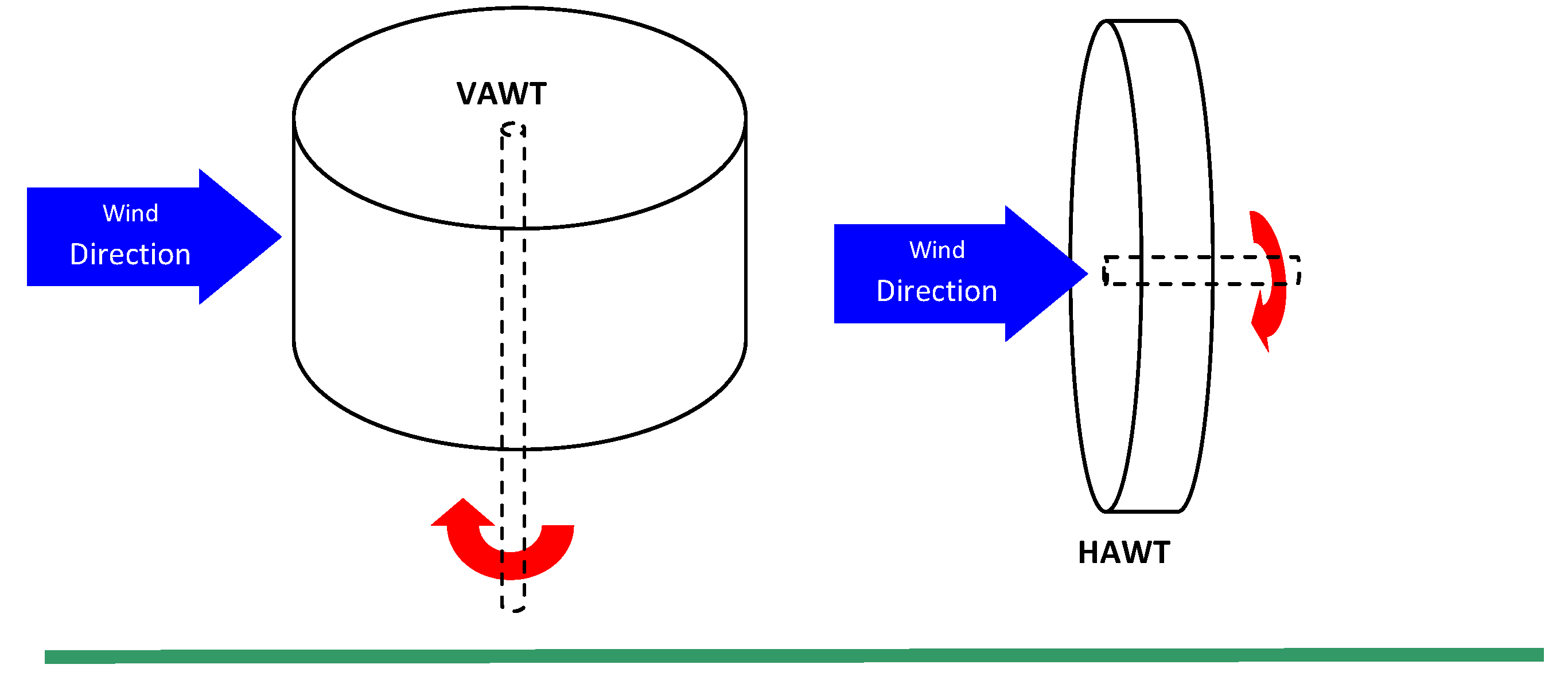
The orientation of the shaft and rotational axis determines the first classification of the wind turbine. A turbine with a shaft mounted horizontally parallel to the ground is known as a horizontal axis wind turbine or (HAWT). A vertical axis wind turbine (VAWT) has its shaft normal to the ground (
Figure 1).
Figure 1.
Alternative configurations for shaft and rotor orientation.
Figure 1.
Alternative configurations for shaft and rotor orientation.
The two configurations have instantly distinguishable rotor designs, each with its own favourable characteristics [
1]. The discontinued mainstream development of the VAWT can be attributed to a low tip speed ratio and difficulty in controlling rotor speed. Difficulties in the starting of vertical turbines have also hampered development, believed until recently to be incapable of self-starting [
2]. However, the VAWT requires no additional mechanism to face the wind and heavy generator equipment can be mounted on the ground, thus reducing tower loads. Therefore, the VAWT is not completely disregarded for future development. A novel V-shaped VAWT rotor design is currently under investigation which exploits these favourable attributes [
3]. This design is currently unproven on a megawatt scale, requiring several years of development before it can be considered competitive. In addition to the problems associated with alternative designs, the popularity of the HAWT can be attributed to increased rotor control through pitch and yaw control. The HAWT has therefore emerged as the dominant design configuration, capitalised by all of today’s leading large scale turbine manufacturers.
2. Theoretical Maximum Efficiency
High rotor efficiency is desirable for increased wind energy extraction and should be maximised within the limits of affordable production. Energy (
P) carried by moving air is expressed as a sum of its kinetic energy [Equation (1)]:
A physical limit exists to the quantity of energy that can be extracted, which is independent of design. The energy extraction is maintained in a flow process through the reduction of kinetic energy and subsequent velocity of the wind. The magnitude of energy harnessed is a function of the reduction in air speed over the turbine. 100% extraction would imply zero final velocity and therefore zero flow. The zero flow scenario cannot be achieved hence all the winds kinetic energy may not be utilised. This principle is widely accepted [
4,
5] and indicates that wind turbine efficiency cannot exceed 59.3%. This parameter is commonly known as the power coefficient
Cp, where max
Cp = 0.593 referred to as the Betz limit [
6]. The Betz theory assumes constant linear velocity. Therefore, any rotational forces such as wake rotation, turbulence caused by drag or vortex shedding (tip losses) will further reduce the maximum efficiency. Efficiency losses are generally reduced by:
Avoiding low tip speed ratios which increase wake rotation
Selecting aerofoils which have a high lift to drag ratio
Specialised tip geometries
In depth explanation and analysis can be found in the literature [
4,
6].
3. Propulsion
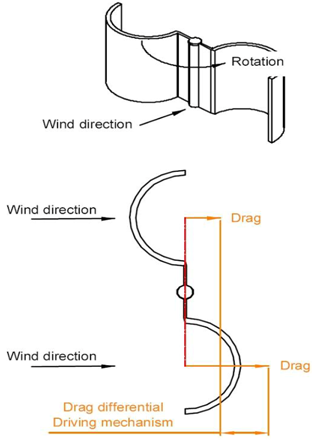
The method of propulsion critically affects the maximum achievable efficiency of the rotor. Historically, the most commonly utilised method was drag, by utilising a sail faced normal to the wind, relying on the drag factor (
Cd) to produce a force in the direction of the prevailing wind. This method proved inefficient as the force and rotation of the sail correspond to the wind direction; therefore, the relative velocity of the wind is reduced as rotor speed increases (
Table 1).
Table 1.
The two mechanisms of propulsion compared.
Table 1.
The two mechanisms of propulsion compared.
| Propulsion | Drag | Lift |
|---|
| Diagram | ![]() | ![]() |
| Relative Wind Velocity | | |
| Maximum Theoretical Efficiency | 16% [4] | 50% [6] |
Reducing efficiency further is the drag of the returning sail into the wind, which was often shielded from the oncoming wind. Unshielded designs rely on curved blade shapes which have a lower drag coefficient when returning into the wind and are advantageous as they work in any wind direction. These differential drag rotors can be seen in use today on cup anemometers and ventilation cowls. However, they are inefficient power producers as their tip speed ratio cannot exceed one [
4].
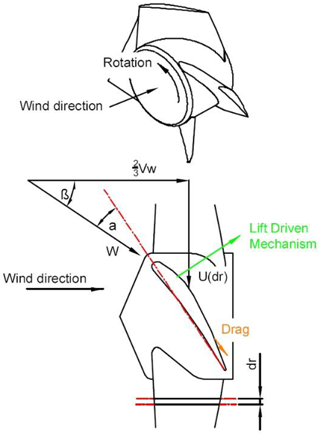
An alternative method of propulsion is the use of aerodynamic lift (
Table 1), which was utilised without precise theoretical explanation for over 700 years in windmills then later in vintage aircraft. Today, due to its difficult mathematical analysis, aerodynamics has become a subject of its own. Multiple theories have emerged of increasing complexity explaining how lift force is generated and predicted. Aerodynamic force is the integrated effect of the pressure and skin friction caused by the flow of air over the aerofoil surface [
7]. Attributed to the resultant force caused by the redirection of air over the aerofoil known as downwash [
8]. Most importantly for wind turbine rotors, aerodynamic lift can be generated at a narrow corridor of varying angles normal to the wind direction. This indicates no decrease in relative wind velocity at any rotor speed (
Table 1).
For a lift driven rotor (
Table 1) the relative velocity at which air strikes the blade (W) is a function of the blade velocity at the radius under consideration and approximately two thirds of the wind velocity (Betz theory
Sections 2) [
4]. The relative airflow arrives at the blade with an angle of incidence (
β) dependant on these velocities. The angle between the blade and the incidence angle is known as the angle of attack (α).
4. Practical Efficiency
In practice rotor designs suffer from the accumulation of minor losses resulting from:
Therefore, the maximum theoretical efficiency has yet to be achieved [
9]. Over the centuries many types of design have emerged, and some of the more distinguishable are listed in
Table 2. The earliest designs, Persian windmills, utilised drag by means of sails made from wood and cloth. These Persian windmills were principally similar to their modern counterpart the Savonius rotor (No. 1) which can be seen in use today in ventilation cowls and rotating advertising signs. Similar in principle is the cup type differential drag rotor (No. 2), utilised today by anemometers for calculating airspeed due to their ease of calibration and multidirectional operation. The American farm windmill (No. 3) is an early example of a high torque lift driven rotor with a high degree of solidity, still in use today for water pumping applications. The Dutch windmill (No. 4) is another example of an early lift type device utilised for grinding corn which has now disappeared from mainstream use, yet a small number still survive as tourist attractions. The Darrieus VAWT (No. 5) is a modern aerodynamic aerofoil blade design which despite extensive research and development has so far been unable to compete with the modern HAWT design, although recent developments [
2,
3] could see a resurgence of this rotor type. Due to its efficiency and ease of control, the aerofoil three bladed HAWT (No. 6) has become the wind turbine industry benchmark, with a fully established international supply chain securing its dominance for the foreseeable future.
Table 2.
Modern and historical rotor designs.
5. HAWT Blade Design
A focus is now being made on the HAWT due to its dominance in the wind turbine industry. HAWT are very sensitive to changes in blade profile and design. This section briefly discusses the major parameters that influence the performance of HAWT blades.
5.1. Tip Speed Ratio
The tip speed ratio defined as the relationship between rotor blade velocity and relative wind velocity [Equation (2)] is the foremost design parameter around which all other optimum rotor dimensions are calculated:
Aspects such as efficiency, torque, mechanical stress, aerodynamics and noise should be considered in selecting the appropriate tip speed (
Table 3). The efficiency of a turbine can be increased with higher tip speeds [
4], although the increase is not significant when considering some penalties such as increased noise, aerodynamic and centrifugal stress (
Table 3).
Table 3.
Tip speed ratio design considerations.
Table 3.
Tip speed ratio design considerations.
| Tip Speed Ratio | ![]() | ![]() |
|---|
| Value | Tip speeds of one to two are considered low | Tip Speeds higher than 10 are considered high |
| Utilisation | traditional wind mills and water pumps | Mainly single or two bladed prototypes |
| Torque | Increases | Decreases |
| Efficiency | Decreases significantly below five due to rotational wake created by high torque [4] | Insignificant increases after eight |
| Centrifugal Stress | Decreases | Increases as a square of rotational velocity [4] |
| Aerodynamic Stress | Decreases | Increases proportionally with rotational velocity [4] |
| Area of Solidity | Increases, multiple 20+ blades required | Decreases significantly |
| Blade Profile | Large | Significantly Narrow |
| Aerodynamics | Simple | Critical |
| Noise | Increases to the 6th power approximately [4] |
A higher tip speed demands reduced chord widths leading to narrow blade profiles. This can lead to reduced material usage and lower production costs. Although an increase in centrifugal and aerodynamic forces is associated with higher tip speeds. The increased forces signify that difficulties exist with maintaining structural integrity and preventing blade failure. As the tip speed increases the aerodynamics of the blade design become increasingly critical. A blade which is designed for high relative wind speeds develops minimal torque at lower speeds. This results in a higher cut in speed [
10] and difficulty self-starting. A noise increase is also associated with increasing tip speeds as noise increases approximately proportionately to the sixth power [
4,
11]. Modern HAWT generally utilise a tip speed ratio of nine to ten for two bladed rotors and six to nine for three blades [
1]. This has been found to produce efficient conversion of the winds kinetic energy into electrical power [
1,
6].
5.2. Blade Plan Shape and Quantity
The ideal plan form of a HAWT rotor blade is defined using the BEM method by calculating the chord length according to Betz limit, local air velocities and aerofoil lift. Several theories exist for calculating the optimum chord length which range in complexity [
1,
4,
10,
12], with the simplest theory based on the Betz optimisation [Equation (3)] [
1]. For blades with tip speed ratios of six to nine utilising aerofoil sections with negligible drag and tip losses, Betz’s momentum theory gives a good approximation [
1]. In instances of low tip speeds, high drag aerofoil sections and blade sections around the hub, this method could be considered inaccurate. In such cases, wake and drag losses should be accounted for [
4,
12]. The Betz method gives the basic shape of the modern wind turbine blade (
Figure 2). However, in practice more advanced methods of optimization are often used [
12,
13,
14].
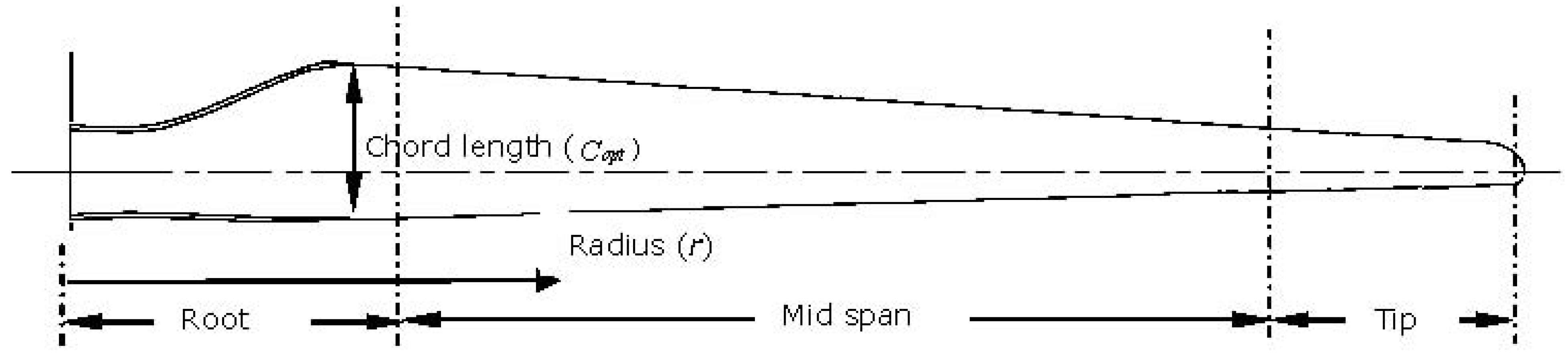
Figure 2.
A typical blade plan and region classification.
Figure 2.
A typical blade plan and region classification.
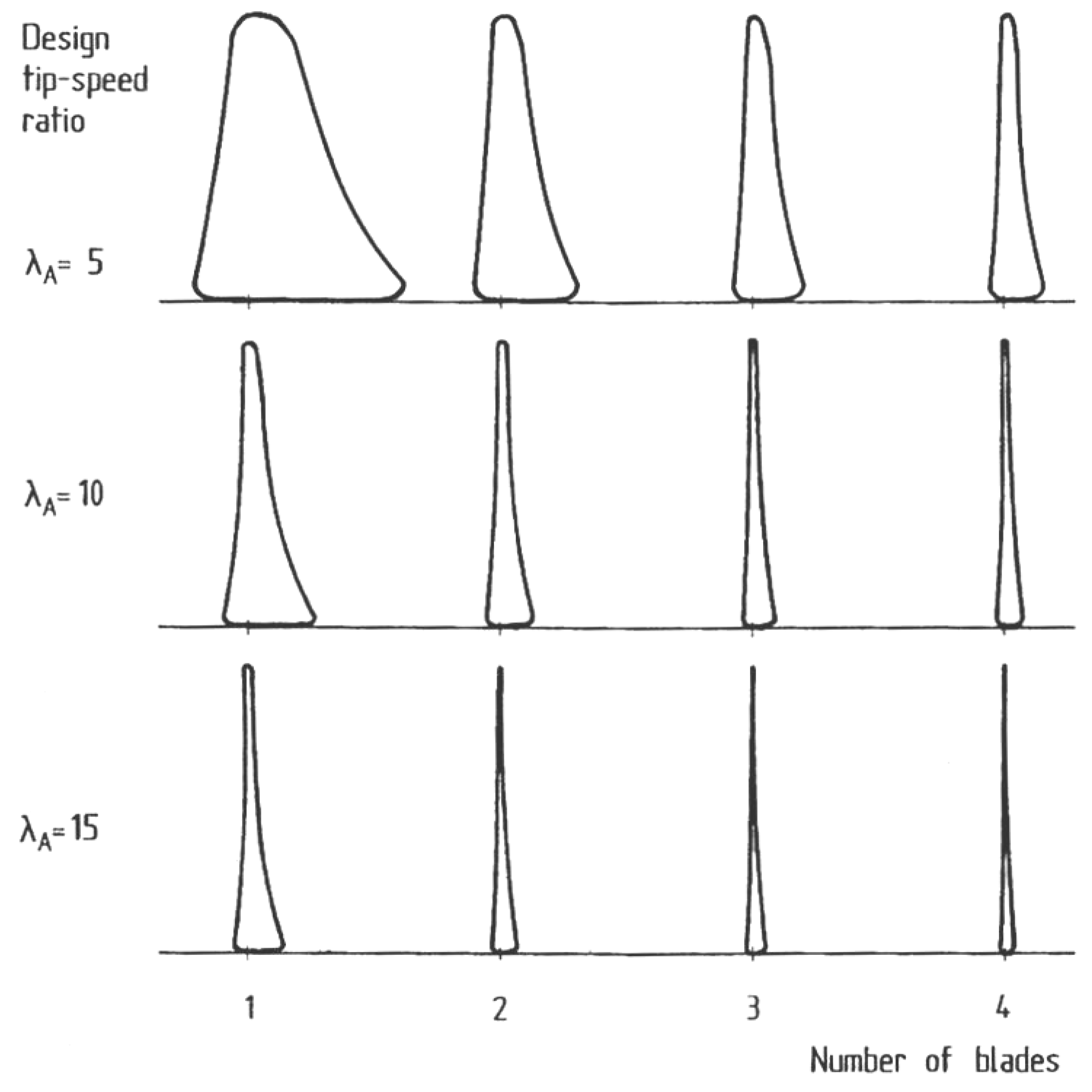
Assuming that a reasonable lift coefficient is maintained, utilising a blade optimisation method produces blade plans principally dependant on design tip speed ratio and number of blades (
Figure 3). Low tip speed ratios produce a rotor with a high ratio of solidity, which is the ratio of blade area to the area of the swept rotor. It is useful to reduce the area of solidity as it leads to a decrease in material usage and therefore production costs. However, problems are associated with high tip speeds (
Section 5.1).
Figure 3.
Optimal blade plan shape for alternate design tip speed ratios and number of blades [
1].
Figure 3.
Optimal blade plan shape for alternate design tip speed ratios and number of blades [
1].
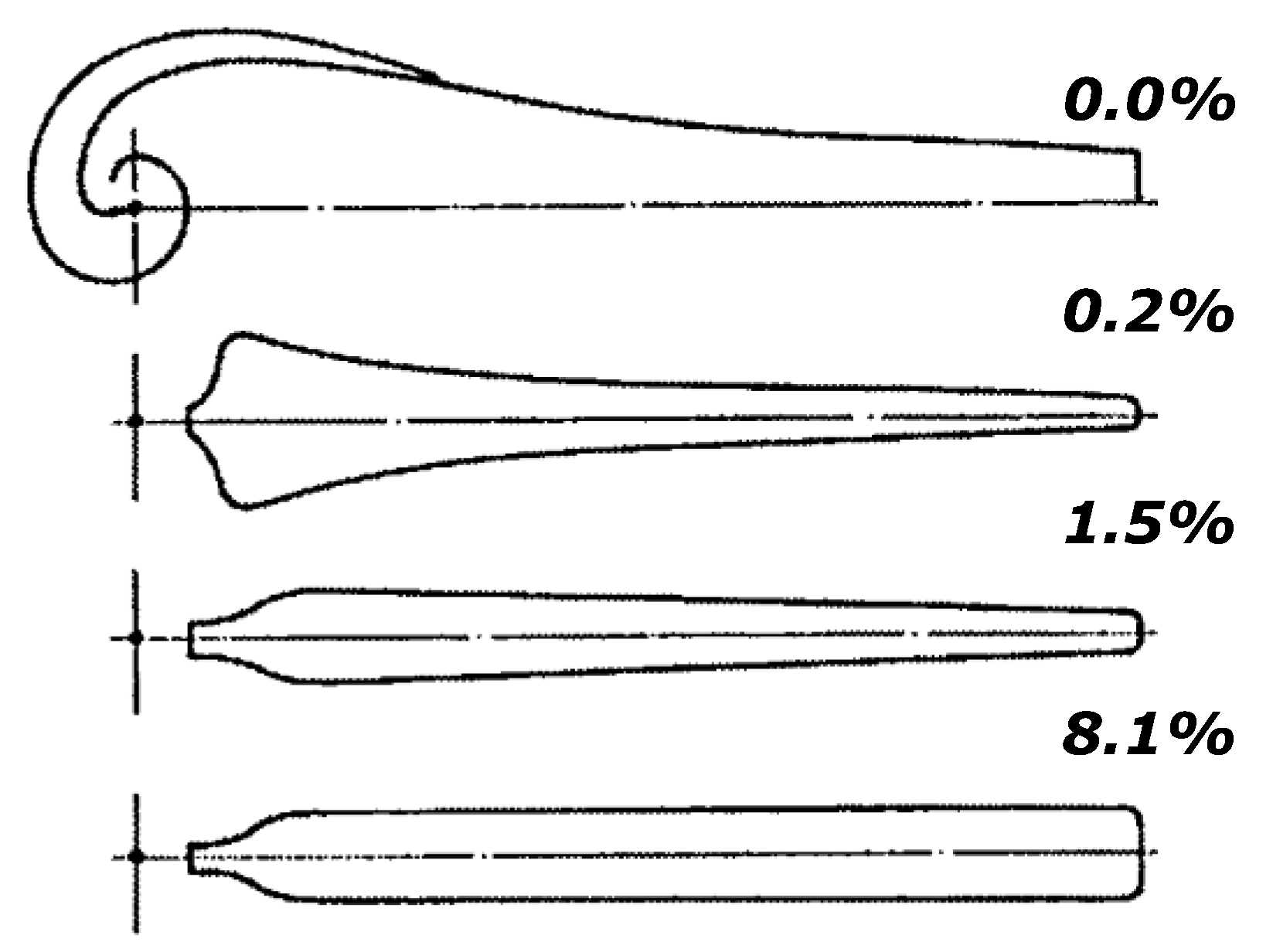
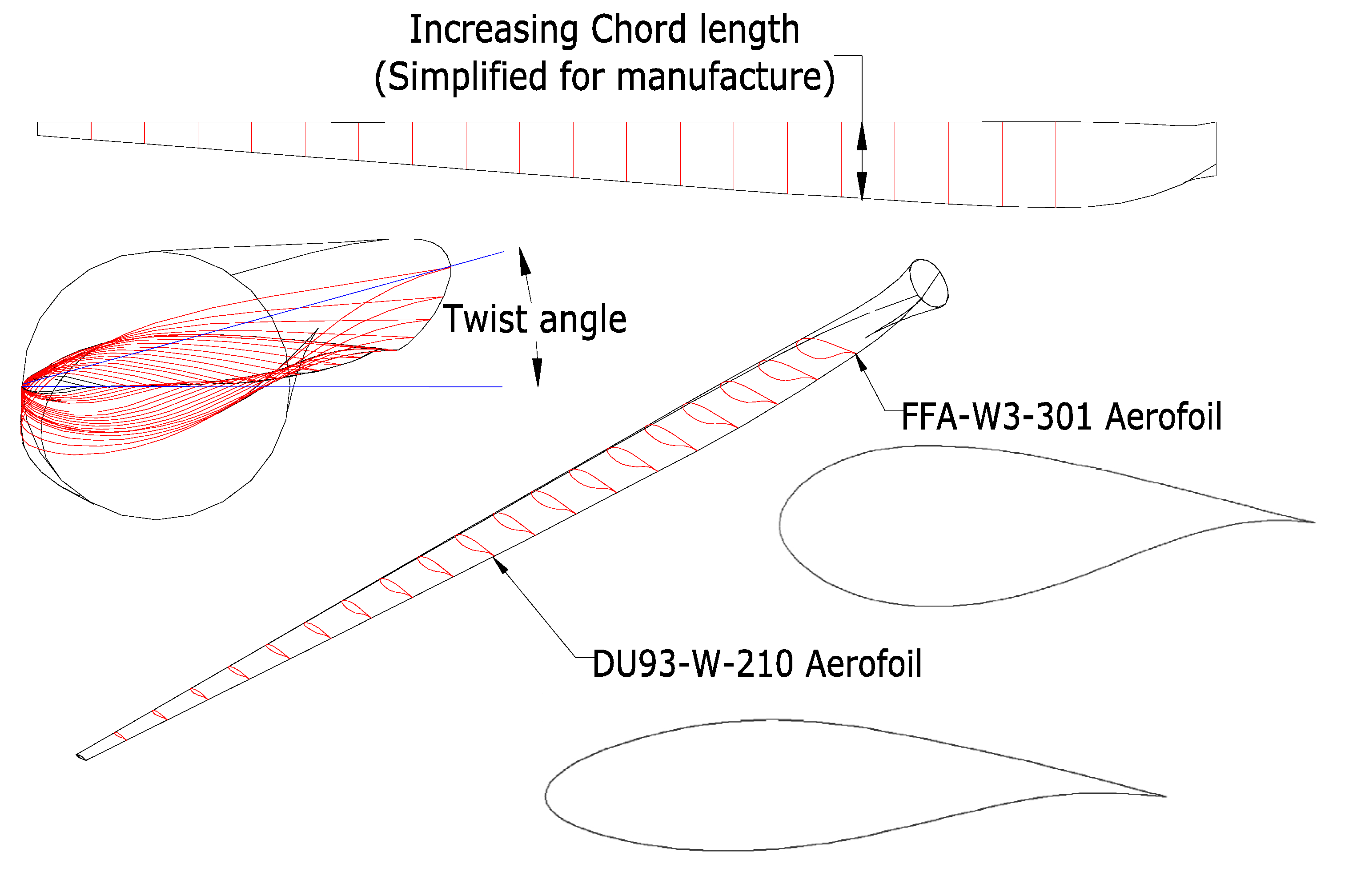
Generally, in practice the chord length is simplified to facilitate manufacture and which involves some linearization of the increasing chord length (
Figure 4). The associated losses signify that simplification can be justified by a significant production cost saving.
Figure 4.
Efficiency losses as a result of simplification to ideal chord length [
15].
Figure 4.
Efficiency losses as a result of simplification to ideal chord length [
15].
For optimum chord dimensioning (Equation 3) the quantity of blades is considered negligible in terms of efficiency. However, in practice when blade losses are considered a 3% loss is incurred for two bladed designs [
1] and a 7%–13% loss for one bladed design [
6] when compared to three blades. A four bladed design offers marginal efficiency increases which do not justify the manufacturing cost of an extra blade. Tower loading must also be considered when choosing the appropriate blade quantity [
6]. Four, three, two and one bladed designs lead to increased dynamic loads, respectively [
16].
The imposing size and location of wind turbines signify that the visual impact must be considered. Three bladed designs are said to appear smoother in rotation therefore more aesthetically pleasing. Faster one and two bladed designs have an apparent jerky motion [
1]. Three bladed rotors are also thought to appear more orderly when in the stationary position [
17].
5.3. Configuration
A favourable reduction in rotor nacelle weight and manufacturing costs occur with the use of fewer blades [
16]. However, dynamic structural and balancing difficulties of the polar asymmetrical rotor are apparent [
16]. Increased wear, inferior aesthetic qualities and bird conservation problems are also associated with one and two bladed rotors [
17,
18]. The three blade turbine (
Figure 5) has been widely adopted (
Table 4) as the most efficient design to meet environmental, commercial and economic constraints and therefore dominates today’s large scale wind turbine industry. Modern commercially available wind turbines include complex control and safety systems, remote monitoring and maintenance with provision for the survival of lightning strike (
Table 5).
Table 4.
A selection of turbine size and weight configurations.
Table 4.
A selection of turbine size and weight configurations.
| Turbine Name | Pitch or Stall | Rotor Dia (m) | No. of Blades | Nacelle and Rotor Weight (kg) | Weight per Swept Area (kg/m²) |
|---|
| Mitsubishi MWT-1000 (1 MW) | P | 57 | 3 | unspecified |
| Nordex N90 (2.3 MW) | P | 90 | 3 | 84,500 | 13.3 |
| Nordex N80 (2.5 MW) | P | 80 | 3 | 80,500 | 16 |
| Repower 5M (5 MW) | P | 126 | 3 | Unspecified |
| Siemens SWT-3.6-107 (3.6 MW) | P | 107 | 3 | 220,000 | 24.5 |
| Siemens SWT-2.3-93 (2.3 MW) | P | 93 | 3 | 142,000 | 20.9 |
| Gamesa G90-2MW (2 MW) | P | 90 | 3 | 106,000 | 16.7 |
| Gamesa G58-850 (850 kW) | P | 58 | 3 | 35,000 | 13.3 |
| Enercon E82 (2 MW) | P | 82 | 3 | Unspecified |
| GE wind 3.6sl (3.6 MW) | P | 111 | 3 | Unspecified |
| Vestas V164 (7.0 MW) | P | 164 | 3 | Unspecified |
| Vestas V90 (2 MW) | P | 90 | 3 | 106,000 | 16.7 |
| Vestas V82 (1.65 MW) | P | 82 | 3 | 95,000 | 18 |
Table 5.
A Typical modern 2MW wind turbine specification.
Table 5.
A Typical modern 2MW wind turbine specification.
| Rotor |
|---|
| Diameter | 90 m |
| Swept Area | 6362 m² |
| Rotational Speed | 9–19 rpm |
| Direction of Rotation | Clockwise from front |
| Weight (including hub) | 36 T |
| Top Head Weight | 106 T |
| Blades |
| Quantity | 3 |
| Length | 44 m |
| Aerofoils | Delft University and FFA-W3 |
| Material | Pre impregnated epoxy glass fibre + carbon fibre |
| Mass | 5800 kg |
| Tower |
| Tubular modular design | Height | Weight |
| 3 Section | 67 m | 153 T |
| 4 Section | 78 m | 203 T |
| 5 Section | 100 m | 255 T |
| Gearbox |
| Type | 1 planetary stage, 2 helical stages |
| Ratio | 1:100 |
| Cooling | Oil pump with oil cooler |
| Oil heater | 2.2 kW |
| 2.0 MW Generator |
| Type | Doubly fed machine |
| Voltage | 690 V ac |
| Frequency | 50 Hz |
| Rotational speed | 900–1900 |
| Stator current | 1500A @ 690v |
| Mechanical Design |
| Drive train with main shaft supported by two spherical bearings that transmit the side loads directly onto the frame by means of the bearing housing. This prevents the gearbox from receiving additional loads. Reducing and facilitating its service. |
| Brake |
| Full feathering aerodynamic braking with a secondary hydraulic disc brake for emergency use. |
| Lightening Protection |
| In accordance with IEC 61024-1. Conductors direct lightening from both sides of the blade tip down to the root joint and from there across the nacelle and tower structure to the grounding system located in the foundations. As a result, the blade and sensitive electrical components are protected. |
| Control System |
| The generator is a doubly fed machine (DFM), whose speed and power is controlled through IGBT converters and pulse width modulation (PWM) electronic control. Real time operation and remote control of turbines, meteorological mast and substation is facilitated via satellite-terrestrial network. TCP/IP architecture with a web interface. A predictive maintenance system is in place for the early detection of potential deterioration or malfunctions in the wind turbines main components. |
5.4. Aerodynamics
Aerodynamic performance is fundamental for efficient rotor design [
19]. Aerodynamic lift is the force responsible for the power yield generated by the turbine and it is therefore essential to maximise this force using appropriate design. A resistant drag force which opposes the motion of the blade is also generated by friction which must be minimised. It is then apparent that an aerofoil section with a high lift to drag ratio [Equation (4)], typically greater than 30 [
20], be chosen for rotor blade design [
19]:
The co-efficient for the lift and drag of aerofoils is difficult to predict mathematically, although freely available software, such as XFOIL [
21] model results accurately with the exception of post stall, excessive angles of attack and aerofoil thickness conditions [
22,
23]. Traditionally aerofoils are tested experimentally with tables correlating lift and drag at given angles of attack and Reynolds numbers [
24]. Historically wind turbine aerofoil designs have been borrowed from aircraft technologies with similar Reynolds numbers and section thicknesses suitable for conditions at the blade tip. However, special considerations should be made for the design of wind turbine specific aerofoil profiles due to the differences in operating conditions and mechanical loads.
The effects of soiling have not been considered by aircraft aerofoils as they generally fly at altitudes where insects and other particulates are negligible. Turbines operate for long periods at ground level where insect and dust particulate build up is problematic. This build up known as fouling can have detrimental effects on the lift generated. Provision is therefore made for the reduced sensitivity to fouling of wind turbine specific aerofoil designs [
25].
The structural requirements of turbine blades signify that aerofoils with a high thickness to chord ratio be used in the root region. Such aerofoils are rarely used in the aerospace industry. Thick aerofoil sections generally have a lower lift to drag ratio. Special consideration is therefore made for increasing the lift of thick aerofoil sections for use in wind turbine blade designs [
25,
26].
National Advisory Committee for Aeronautics (NACA) four and five digit designs have been used for early modern wind turbines [
1]. The classification shows the geometric profile of a NACA aerofoil where the 1st digit refers to maximum chamber to chord ratio, 2nd digit is the camber position in tenths of the chord and the 3rd & 4th digits are the maximum thickness to chord ratio in percent [
24]. The emergence of wind turbine specific aerofoils such as the Delft University [
23], LS, SERI-NREL and FFA [
6] and RISO [
26] now provide alternatives specifically tailored to the needs of the wind turbine industry.
The angle of attack is the angle of the oncoming flow relative to the chord line, and all figures for
CL and
CD are quoted relative to this angle. The use of a single aerofoil for the entire blade length would result in inefficient design [
19]. Each section of the blade has a differing relative air velocity and structural requirement and therefore should have its aerofoil section tailored accordingly. At the root, the blade sections have large minimum thickness which is essential for the intensive loads carried resulting in thick profiles. Approaching the tip blades blend into thinner sections with reduced load, higher linear velocity and increasingly critical aerodynamic performance. The differing aerofoil requirements relative to the blade region are apparent when considering airflow velocities and structural loads (
Table 6).
Table 6.
The aerofoil requirements for blade regions [
26].
Table 6.
The aerofoil requirements for blade regions [26].
| Parameter | Blade Position (Figure 2) |
|---|
| Root | Mid Span | Tip |
|---|
| Thickness to chord ratio (%) ( Figure 2) | >27 | 27–21 | 21–15 |
| Structural load bearing requirement | High | Med | Low |
| Geometrical compatibility | Med | Med | Med |
| Maximum lift insensitive to leading edge roughness | | | High |
| Design lift close to maximum lift off-design | | Low | Med |
| Maximum CL and post stall behaviour | | Low | High |
| Low Aerofoil Noise | | | High |
An aerodynamic phenomenon known as stall should be considered carefully in turbine blade design. Stall typically occurs at large angles of attack depending on the aerofoil design. The boundary layer separates at the tip rather than further down the aerofoil causing a wake to flow over the upper surface drastically reducing lift and increasing drag forces [
6]. This condition is considered dangerous in aviation and is generally avoided. However, for wind turbines, it can be utilised to limit the maximum power output to prevent generator overload and excessive forces in the blades during extreme wind speeds and could also occur unintentionally during gusts. It is therefore preferable that the onset of the stall condition is not instantaneous for wind turbine aerofoils as this would create excessive dynamic forces and vibrations [
1].
The sensitivity of blades to soiling, off design conditions including stall and thick cross sections for structural purposes are the main driving forces for the development of wind turbine specific aerofoil profiles [
1,
26]. The use of modern materials with superior mechanical properties may allow for thinner structural sections with increased lift to drag ratios at root sections. Thinner sections also offer a chance to increase efficiency through reducing drag. Higher lift coefficients of thinner aerofoil sections will in turn lead to reduced chord lengths reducing material usage [Equation (3)].
5.5. Angle of Twist
The lift generated by an aerofoil section is a function of the angle of attack to the inflowing air stream (
Section 5.4). The inflow angle of the air stream is dependent on the rotational speed and wind speed velocity at a specified radius. The angle of twist required is dependent upon tip speed ratio and desired aerofoil angle of attack. Generally the aerofoil section at the hub is angled into the wind due to the high ratio of wind speed to blade radial velocity. In contrast the blade tip is likely to be almost normal to the wind.
The total angle of twist in a blade maybe reduced simplifying the blade shape to cut manufacturing costs. However, this may force aerofoils to operate at less than optimum angles of attack where lift to drag ratio is reduced. Such simplifications must be well justified considering the overall loss in turbine performance.
5.6. Off-Design Conditions and Power Regulation
Early wind turbine generator and gearbox technology required that blades rotate at a fixed rotational velocity therefore running at non design tip speed ratios incurring efficiency penalties in all but the rated wind conditions [
1]. For larger modern turbines this is no longer applicable and it is suggested that the gearbox maybe obsolete in future turbines [
27]. Today the use of fixed speed turbines is limited to smaller designs therefore the associated off-design difficulties are omitted.
The design wind speed is used for optimum dimensioning of the wind turbine blade which is dependent upon site wind measurements. However, the wind conditions are variable for any site and the turbine must operate at off-design conditions, which include wind velocities higher than rated. Hence a method of limiting the rotational speed must be implemented to prevent excessive loading of the blade, hub, gearbox and generator. The turbine is also required to maintain a reasonably high efficiency at below rated wind speeds.
As the oncoming wind velocity directly affects the angle of incidence of the resultant airflow onto the blade, the blade pitch angle must be altered accordingly. This is known as pitching, which maintains the lift force of the aerofoil section. Generally the full length of the blade is twisted mechanically through the hub to alter the blade angle. This method is effective at increasing lift in lower than rated conditions and is also used to prevent over speed of the rotor which may lead to generator overload or catastrophic failure of the blade under excessive load [
1].
Two methods of blade pitching are used to reduce the lift force and therefore the rotational velocity of the rotor during excessive wind speeds. Firstly decreasing the pitch angle reduces the angle of attack which therefore reduces the lift generated. This method is known as feathering. The alternative method is to increase the pitch angle which increases the angle of attack to a critical limit inducing the stall condition and reducing lift. The feathering requires the maximum amount of mechanical movement in pitching the blade. However, it is still favoured as stalling can result in excessive dynamic loads. These loads are a result of the unpredictable transition from attached to detached airflow around the blade which may lead to undesirable fluttering [
1].
Utilising the stall condition a limiting speed can be designed into the rotor blade known as passive stall control [
1]. Increased wind velocity and rotor speed produce an angle at which stall is initiated therefore automatically limiting the rotor speed. In practice accurately ensuring stall occurs is difficult and usually leads to a safety margin. The use of a safety margin indicates that normal operation occurs at below optimum performance, consequently this method is utilised only by smaller turbines [
28].
Full blade feathered pitching at the hub is used by the majority of today’s wind turbine market leaders (
Table 4). Feathered pitching offers increased performance, flexibility and the capability of fully pitching the blades to a parked configuration. Manufacturers are reported as using collective pitch [
29], in that all the blades are pitched at identical angles. However, further load reductions can be found by pitching blades individually [
30]. This requires no extra mechanism in most designs and it is expected to be widely adopted [
29,
30].
5.7. Smart Blade Design
The current research trend in blade design is the so called “Smart Blades”, which alter their shape depending on the wind conditions. Within this category of blade design are numerous approaches which are either aerodynamic control surfaces or smart actuator materials. An extensive review of this subject is given by Barlas [
31]. The driver behind this research is to limit ultimate (extreme) loads and fatigue loads or to increase dynamic energy capture. Research is mainly initiated based on similar concepts from helicopter control and is being investigated by various wind energy research institutes. The work package “Smart rotor blades and rotor control” in the Upwind EU framework programme, the project “Smart dynamic control of large offshore wind turbines” and the Danish project “ADAPWING” all deal with the subject of Smart rotor control. In the framework of the International Energy Agency, two expert meetings were held on “The application of smart structures for large wind turbine rotors”, by Delft University and Sandia National Labs, respectively. The proceedings show a variety of topics, methods and solutions, which reflects the on-going research [
32,
33].
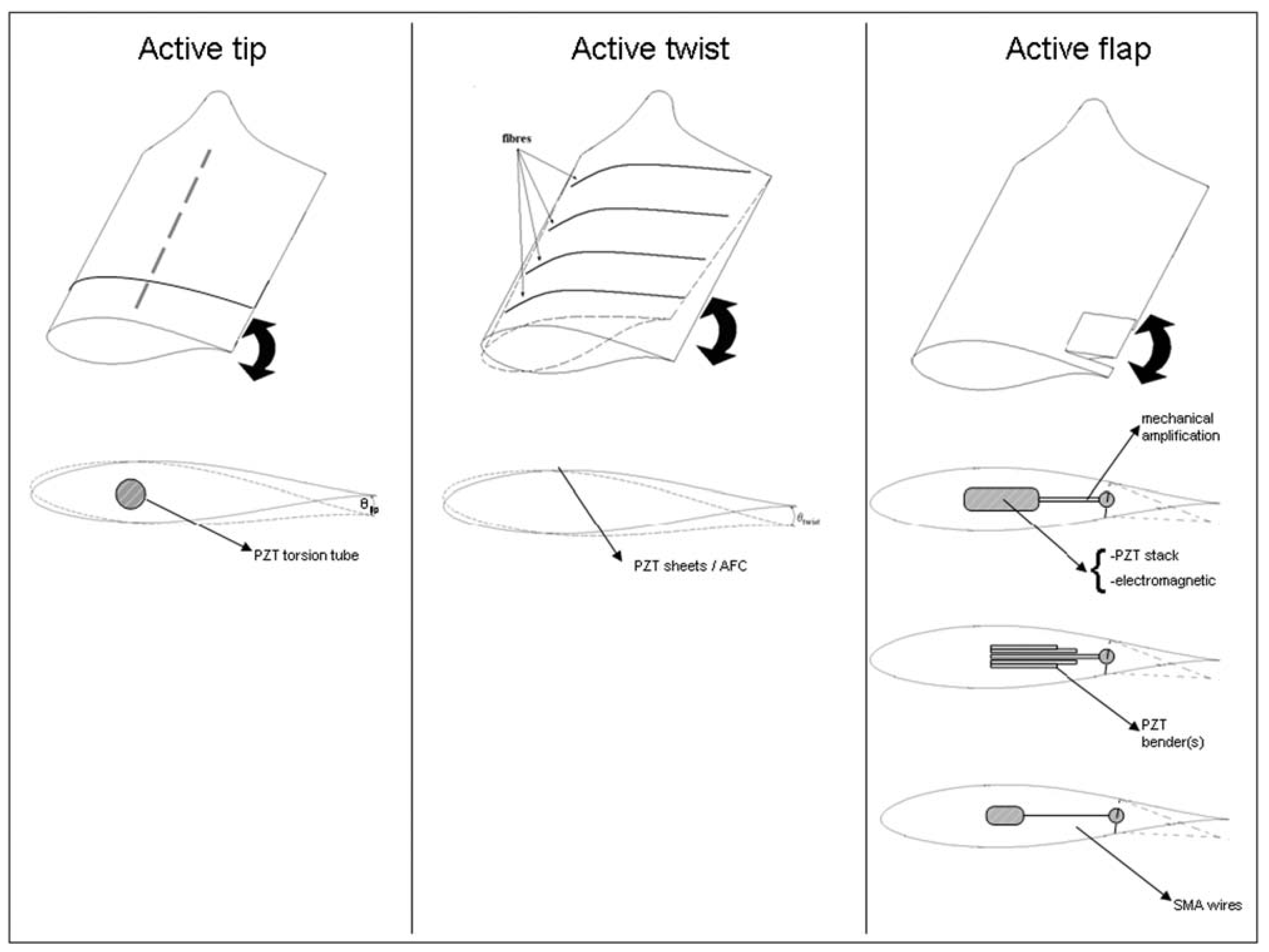
The use of aerodynamic control surfaces includes aileron style flaps, camber control, active twist and boundary layer control.
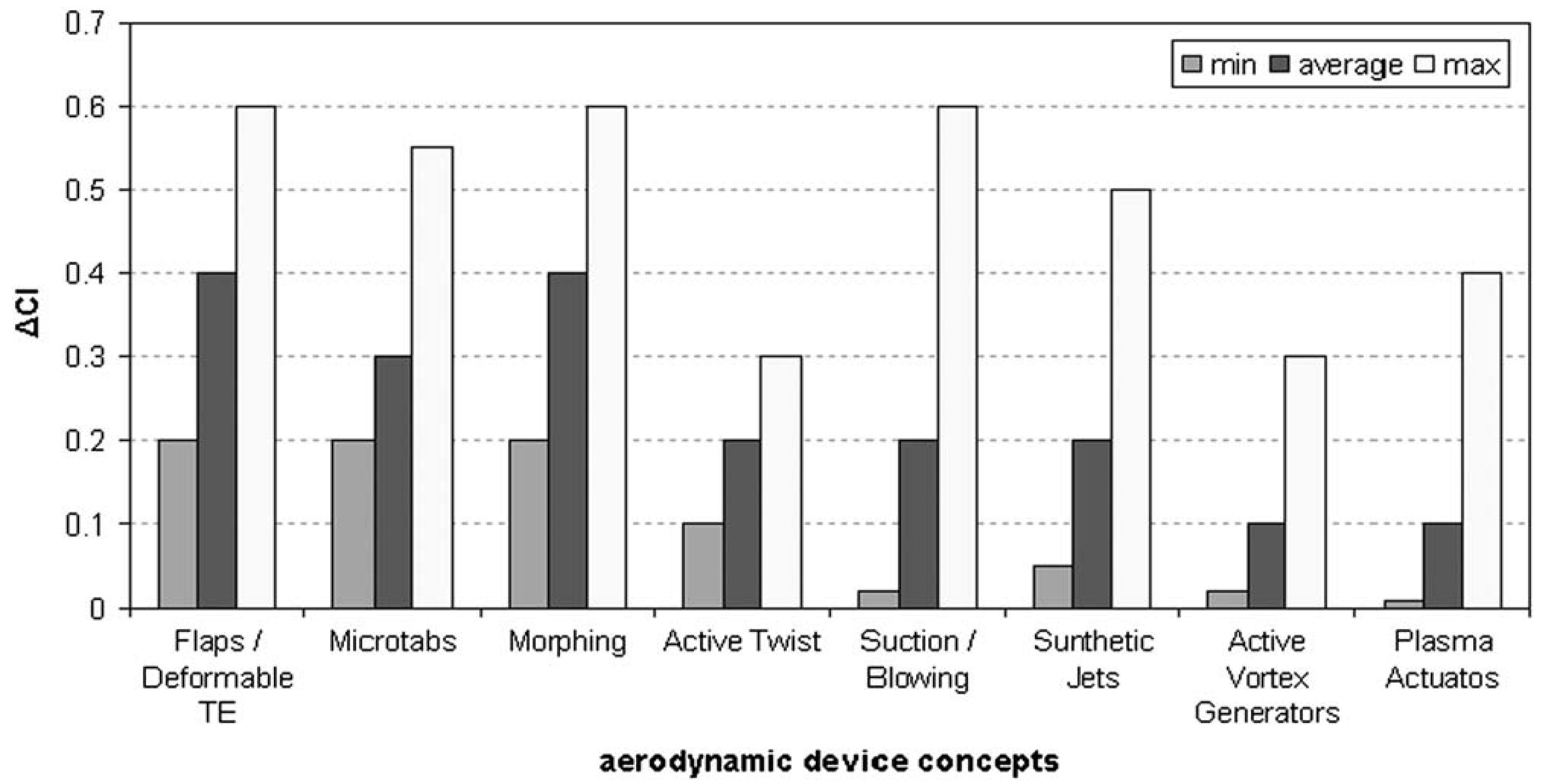
Figure 6 and
Figure 7 show a comparison graph of aerodynamic performance (lift control capability) of a variety of aerodynamic control surface based concepts
Figure 6.
Schematics of smart structure concepts.
Figure 6.
Schematics of smart structure concepts.
Figure 7.
Comparison of aerodynamic device concepts in terms of lift control capability [
31].
Figure 7.
Comparison of aerodynamic device concepts in terms of lift control capability [
31].
Smart actuator materials include conventional actuators, smart material actuators, piezoelectric and shape memory alloys. Traditional actuators probably do not meet minimum requirements for such concepts. Furthermore, proposed concepts of aerodynamic control surfaces (distributed along the blade span) require fast actuation without complex mechanical systems and large energy to weight ratios. Promising solution for this purpose is the use of smart material actuator systems. By definition, smart materials are materials which possess the capability to sense and actuate in a controlled way in response to variable ambient stimuli. Generally known types of smart materials are ferroelectric materials (piezoelectric, electrostrictive, magnetostrictive), variable rheology materials (electrorheological, magnetorheological) and shape memory alloys. Piezoelectric materials and shape memory alloys are generally the most famous smart materials used in actuators in various applications. The development of their technology has reached a quite high level and commercial solutions are available and widely used [
31].
5.8. Blade Shape Summary
An efficient rotor blade consists of several aerofoil profiles blended at an angle of twist terminating at a circular flange (
Figure 8) [
4,
34]. It may also include tip geometries for reducing losses. To facilitate production, several simplifications maybe made:
Reducing the angle of twist.
Linearization of the chord width.
Reducing the number of differing aerofoil profiles.
All manufacturing simplifications are detrimental to rotor efficiency and should be well justified. The introduction of new moulding techniques and materials has allowed the manufacture of increasingly complex blade shapes. However, the economics of production coupled with difficulty of design analysis still dictate final geometry. Leading wind turbine suppliers now include most optimisation features such as angle of twist, variable chord length and multiple aerofoil geometries.
Figure 8.
A typical modern HAWT blade with multiple aerofoil profiles, twist and linear chord length increase.
Figure 8.
A typical modern HAWT blade with multiple aerofoil profiles, twist and linear chord length increase.
6. Blade Loads
Multiple aerofoil sections and chord lengths, 22 specified stochastic load cases and an angle of twist with numerous blade pitching angles results in a complex engineering scenario. Therefore, the use of computer analysis software such as fluid dynamics (CFD) and finite element (FEA) is now commonplace within the wind turbine industry [
35]. Dedicated commercially available software such as LOADS, YawDyn, MOSTAB, GH Bladed, SEACC and AERODYN are utilised to perform calculations based upon blade geometry, tip speed and site conditions [
15].
To simplify calculations, it has been suggested that a worst case loading condition be identified for consideration, on which all other loads may be tolerated [
4]. The worst case loading scenario is dependent on blade size and method of control. For small turbines without blade pitching, a 50 year storm condition would be considered the limiting case. For larger turbines (
D > 70 m), loads resulting from the mass of the blade become critical and should be considered [
4]. In practice several load cases are considered with published methods detailing mathematical analysis for each of the IEC load cases [
6].
For modern large scale turbine blades the analysis of a single governing load case is not sufficient for certification. Therefore multiple load cases are analysed. The most important load cases are dependent on individual designs. Typically priority is given to the following loading conditions:
emergency stop scenario [
36]
extreme loading during operation [
6]
parked 50 year storm conditions [
34]
Under these operational scenarios the main sources of blade loading are listed below [
6]:
Aerodynamic
Gravitational
Centrifugal
Gyroscopic
Operational
The load magnitude will depend on the operational scenario under analysis. If the optimum rotor shape is maintained, then aerodynamic loads are unavoidable and vital to the function of the turbine, considered in greater detail (
Section 6.1). As turbines increase in size, the mass of the blade is said to increase proportionately at a cubic rate. The gravitational and centrifugal forces become critical due to blade mass and are also elaborated (
Section 6.2). Gyroscopic loads result from yawing during operation. They are system dependant and generally less intensive than gravitational loads. Operational loads are also system dependant, resulting from pitching, yawing, breaking and generator connection and can be intensive during emergency stop or grid loss scenarios. Gyroscopic and operational loads can be reduced by adjusting system parameters. Blades which can withstand aerodynamic, gravitational and centrifugal loads are generally capable of withstanding these reduced loads. Therefore, gyroscopic and operational loads are not considered within this work.
6.1. Aerodynamic Load
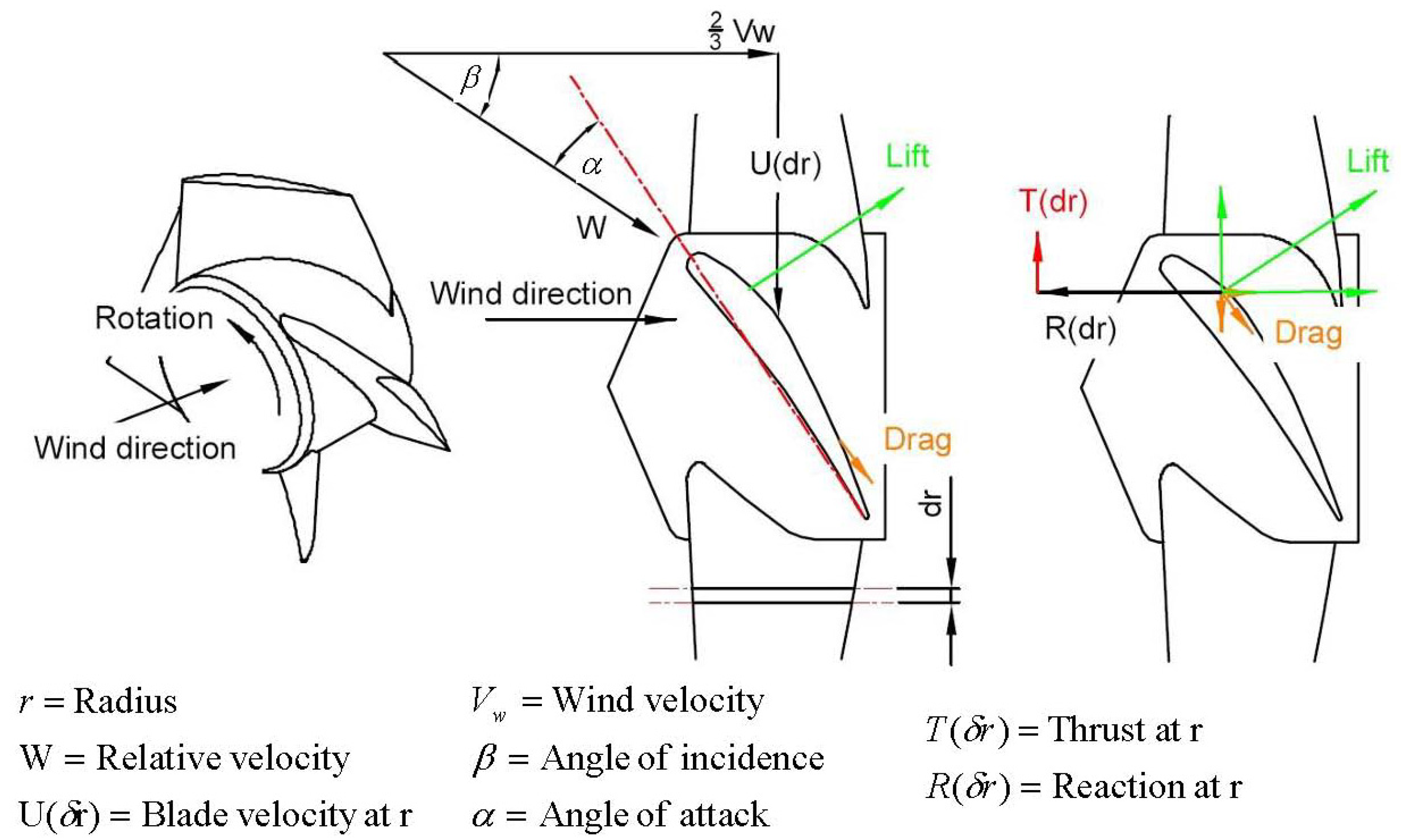
Aerodynamic load is generated by lift and drag of the blades aerofoil section (
Figure 9), which is dependent on wind velocity (
VW), blade velocity (
U), surface finish, angle of attack (
α) and yaw. The angle of attack is dependent on blade twist and pitch. The aerodynamic lift and drag produced (
Figure 9) are resolved into useful thrust (
T) in the direction of rotation absorbed by the generator and reaction forces (
R). It can be seen that the reaction forces are substantial acting in the flatwise bending plane, and must be tolerated by the blade with limited deformation.
Figure 9.
Aerodynamic forces generated at a blade element.
Figure 9.
Aerodynamic forces generated at a blade element.
For calculation of the blade aerodynamic forces the widely publicised blade element momentum (BEM) theory is applied [
4,
6,
37]. Working along the blade radius taking small elements (
δr), the sum of the aerodynamic forces can be calculated to give the overall blade reaction and thrust loads (
Figure 9).
6.2. Gravitational and Centrifugal Loads
Gravitational centrifugal forces are mass dependant which is generally thought to increase cubically with increasing turbine diameter [
38]. Therefore, turbines under ten meters diameter have negligible inertial loads, which are marginal for 20 meters upward, and critical for 70 meter rotors and above [
4]. The gravitational force is defined simply as mass multiplied by the gravitational constant, although its direction remains constant acting towards the centre of the earth which causes an alternating cyclic load case.
The centrifugal force is a product of rotational velocity squared and mass and always acts radial outward, hence the increased load demands of higher tip speeds. Centrifugal and gravitational loads are superimposed to give a positively displaced alternating condition with a wavelength equal to one blade revolution.
6.3. Structural Load Analysis
Modern load analysis of a wind turbine blade would typically consist of a three dimensional CAD model analysed using the Finite Element Method [
39]. Certification bodies support this method and conclude that there is a range of commercial software available with accurate results [
40]. These standards also allow the blade stress condition to be modelled conservatively using classical stress analysis methods.
Traditionally the blade would be modelled as a simple cantilever beam with equivalent point or uniformly distributed loads used to calculate the flap wise and edgewise bending moment. The direct stresses for root sections and bolt inserts would also be calculated. The following simple analysis (
Section 6.4,
Section 6.5 and
Section 6.6) offers basic insight into the global structural loading of a wind turbine blade. In practice a more detailed computational analysis would be completed including local analysis of individual features, bonds and material laminates.
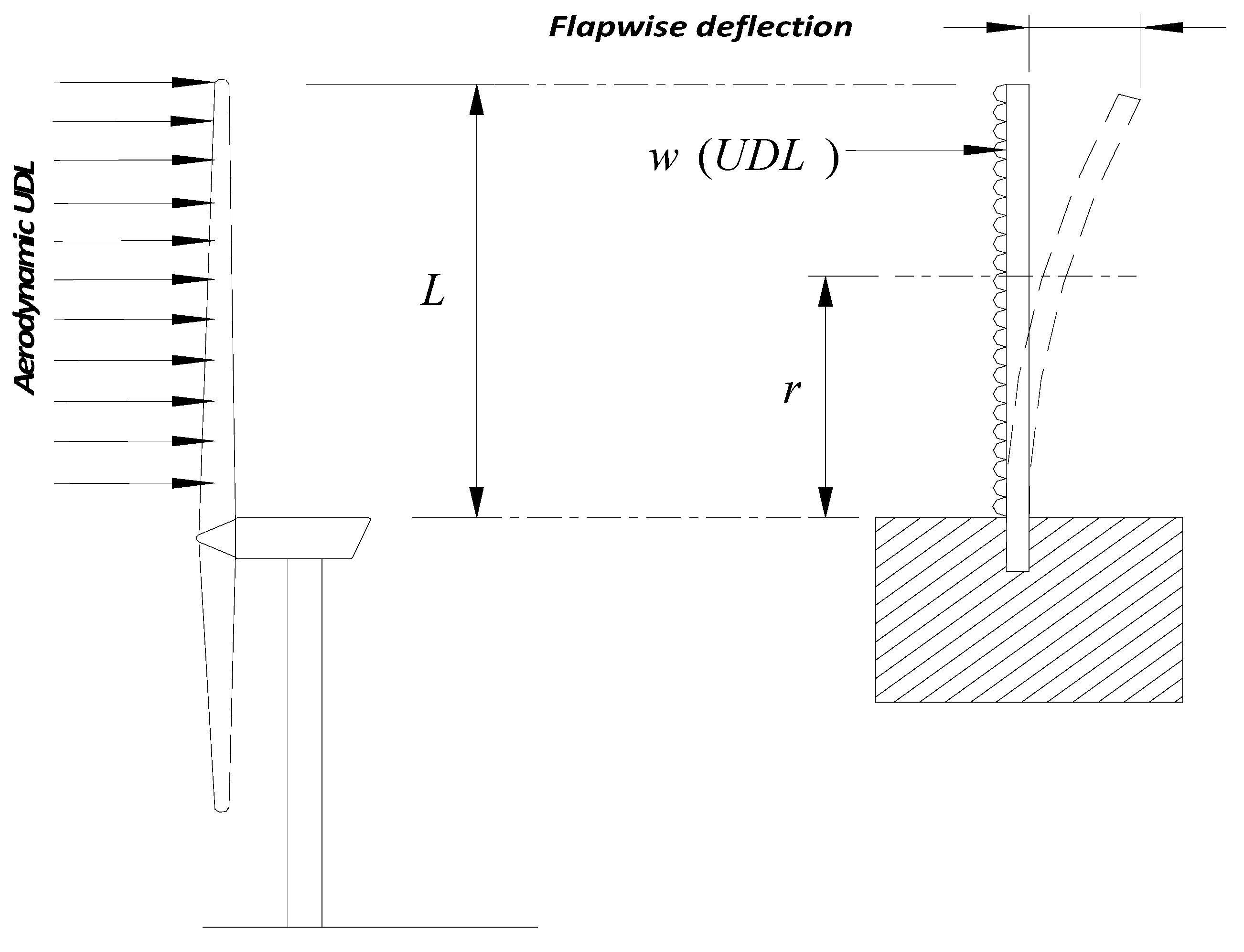
6.4. Flapwise Bending
The flap wise bending moment is a result of the aerodynamic loads (
Figure 9), which can be calculated using BEM theory (Section 6.1). Aerodynamic loads are suggested as a critical design load during 50 year storm and extreme operational conditions [
6]. Once calculated, it is apparent that load case can be modelled as a cantilever beam with a uniformly distributed load (
Figure 10) [
4]. This analysis shows how bending occurs about the chord axis creating compressive and tensile stresses in the blade cross section (
Figure 11). To calculate these stresses the second moment of area of the load bearing material must be calculated [Equation (6)]. Using classical beam bending analysis bending moments can be calculated at any section along the blade [
41]. Local deflections and material stresses can then be calculated at any point along the beam using the fundamental beam bending equation [Equation (7)].
Figure 10.
The blade modelled as a cantilever beam with uniformly distributed aerodynamic load.
Figure 10.
The blade modelled as a cantilever beam with uniformly distributed aerodynamic load.
Figure 11.
Flapwise bending about the axis xx.
Figure 11.
Flapwise bending about the axis xx.
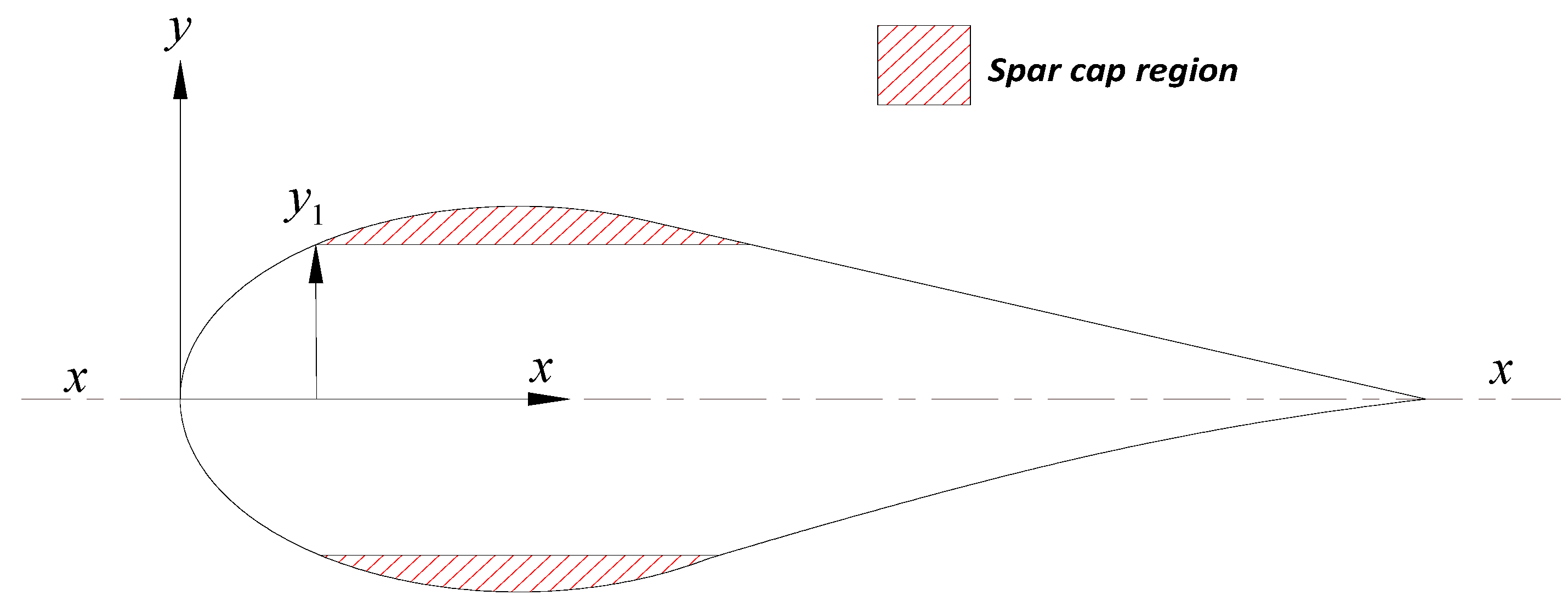
When calculating the second moment of area [Equation (5)] it is apparent that increasing the distance from the central axis of bending gives a cubic increase. When substituted into the beam bending equation [Equation (7)], it can be seen that a squared decrease in material stress can be obtained by simply moving load bearing material away from the central plane of bending. It is therefore efficient to place load bearing material in the spar cap region of the blade at extreme positions from the central plane of bending (
x) (
Figure 11). This signifies why thick section aerofoils are structurally preferred, despite their aerodynamic deficiencies. This increase in structural efficiency can be used to minimise the use of structural materials and allow significant weight reductions [
42]. The conflict between slender aerofoils for aerodynamic efficiency and thicker aerofoils for structural integrity is therefore apparent. Bending moments [Equation (6)] and therefore stress [Equation (7)] can be seen to increase towards the rotor hub. This signifies why aerofoil sections tend to increase in thickness towards the hub to maintain structural integrity.
6.5. Edgewise Bending
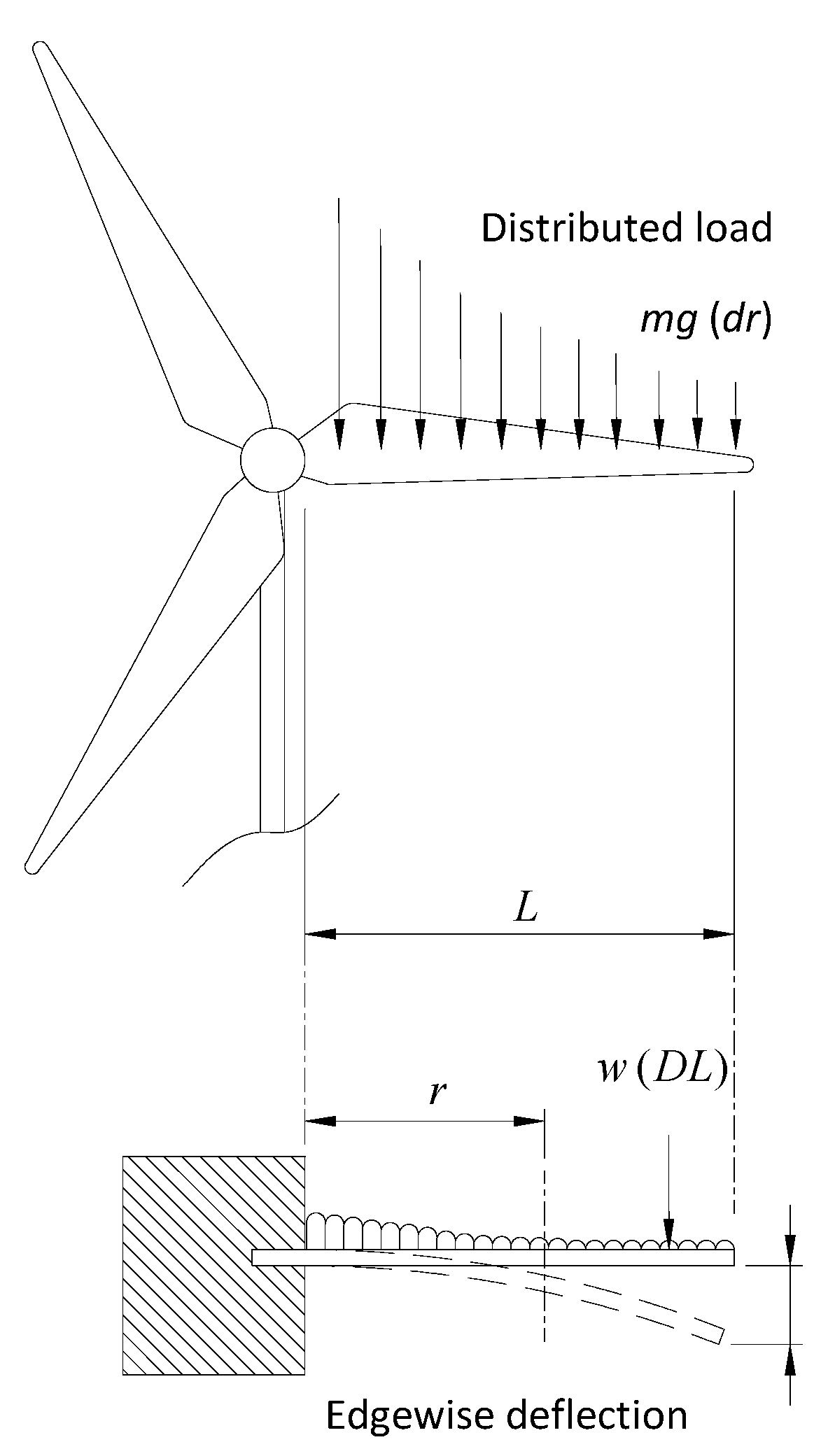
The edgewise bending moment is a result of blade mass and gravity. Therefore this loading condition can be considered negligible for smaller blades with negligible blade mass [
4]. Simple scaling laws dictate a cubic rise in blade mass with increasing turbine size. Therefore for increasing turbine sizes in excess of 70 m diameter, this loading case is said to be increasingly critical [
4].
The bending moment is at its maximum when the blade reaches the horizontal position. In this case the blade may once again be modelled as a cantilever beam (
Figure 12 and
Figure 13). The beam now has a distributed load which increases in intensity towards the hub as the blade and material thicknesses increase. The actual values for second moment of area, bending moments, material stress and deflections can be calculated in a similar procedure to flapwise bending (
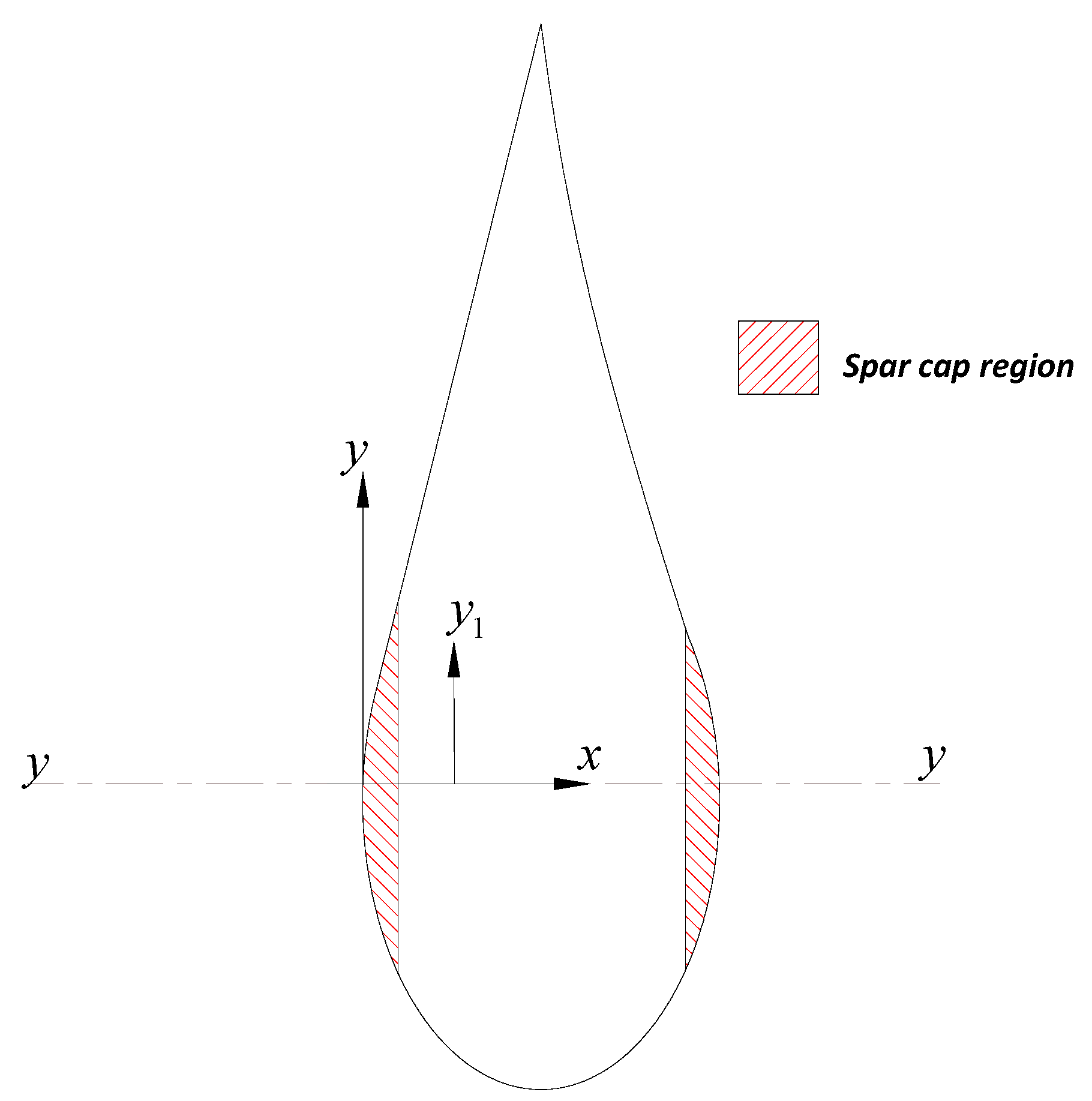
Sections 6.4). It should be noted that in the edgewise loading condition, the plane of central bending is now normal to the chord line. For flapwise bending it is beneficial to concentrate load bearing material centrally in the spar cap region at extreme positions on the aerofoil profile, away from flapwise plane of bending (
xx). This positioning is inefficient for edgewise bending as the centre of the spar cap is increasingly close to the central plane of bending (
yy). Careful consideration is therefore giving to position structural material efficiently for both the flapwise and edgewise bending conditions [
42].
6.6. Fatigue Loads
The major loading conditions applied to the blade are not static. Fatigue loading can occur when a material is subjected to a repeated non continuous load which causes the fatigue limit of the material to be exceeded. It is possible to produce a wind turbine blade capable of operating within the fatigue limit of its materials. However, such a design would require excessive amounts of structural material resulting in a heavy, large, expensive and inefficient blade. Fatigue loading conditions are therefore unavoidable in efficient rotor blade design.
Fatigue loading is a result of gravitational cyclic loads (
Sections 6.5) which are equal to the number of rotations throughout the lifetime of the turbine, typically 20 years. In addition smaller stochastic loads are created by the gusting wind contributing up to 1 × 10
9 cyclic loadings during the turbine lifetime [
43]. Therefore the design of many wind turbine components maybe governed by fatigue rather than ultimate load [
6]. Fatigue analysis and testing is required for both IEC [
44] and DNV [
40] certification [
45].
Figure 12.
Gravitational load modelled as a cantilever beam.
Figure 12.
Gravitational load modelled as a cantilever beam.
Figure 13.
Edgewise bending about yy.
Figure 13.
Edgewise bending about yy.
6.7. Structural Blade Regions
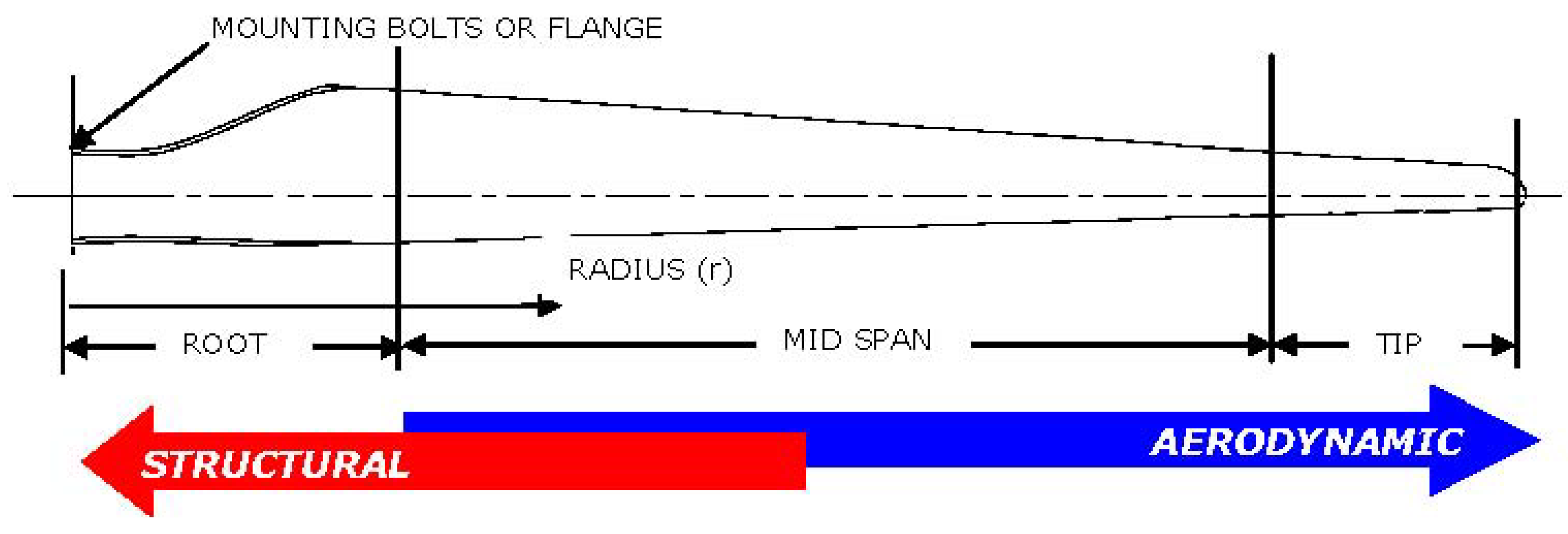
The modern blade can be divided into three main areas classified by aerodynamic and structural function (
Figure 14):
The blade root. The transition between the circular mount and the first aerofoil profile—this section carries the highest loads. Its low relative wind velocity is due to the relatively small rotor radius. The low wind velocity leads to reduced aerodynamic lift leading to large chord lengths. Therefore the blade profile becomes excessively large at the rotor hub. The problem of low lift is compounded by the need to use excessively thick aerofoil sections to improve structural integrity at this load intensive region. Therefore the root region of the blade will typically consist of thick aerofoil profiles with low aerodynamic efficiency.
The mid span. Aerodynamically significant—the lift to drag ratio will be maximised. Therefore utilising the thinnest possible aerofoil section that structural considerations will allow.
The tip. Aerodynamically critical—the lift to drag ratio will be maximised. Therefore using slender aerofoils and specially designed tip geometries to reduce noise and losses. Such tip geometries are as yet unproven in the field [
1], in any case they are still used by some manufacturers.
Figure 14.
The three blade regions.
Figure 14.
The three blade regions.
7. Conclusions
For reasons of efficiency, control, noise and aesthetics the modern wind turbine market is dominated by the horizontally mounted three blade design, with the use of yaw and pitch, for its ability to survive and operate under varying wind conditions. An international supply chain has evolved around this design, which is now the industry leader and will remain so for the immediate foreseeable future. During the evolution of this design many alternatives have been explored and have eventually declined in popularity. Manufacturers seeking greater cost efficiency have exploited the ability to scale the design, with the latest models reaching 164 m in diameter. The scale of investment in creating alternative designs of comparative size now ensures that new challengers to the current configuration are unlikely.
A comprehensive look at blade design has shown that an efficient blade shape is defined by aerodynamic calculations based on chosen parameters and the performance of the selected aerofoils. Aesthetics plays only a minor role. The optimum efficient shape is complex consisting of aerofoil sections of increasing width, thickness and twist angle towards the hub. This general shape is constrained by physical laws and is unlikely to change. However, aerofoil lift and drag performance will determine exact angles of twist and chord lengths for optimum aerodynamic performance.
A basic load analysis reveals that the blade can be modelled as a simple beam with a built in support at the hub end. A uniformly distributed load can be used to represent aerodynamic lift during operation. The increasing bending moment towards the support indicate that structural requirements will also determine blade shape especially in areas around the hub which require increased thickness.
Currently manufacturers are seeking greater cost effectiveness through increased turbine size rather than minor increases through improved blade efficiency. This is likely to change as larger models become problematic through construction, transport and assembly issues. Therefore, it is likely that the general shape will remain fixed and will increase in size until a plateau is reached. Minor changes to blade shape may then occur as manufacturers incorporate new aerofoils, tip designs and structural materials. A conflict of increased aerodynamic performance in slender aerofoils versus structural performance of thicker aerofoils is also evident.