Dynamic Modeling of Anode Function in Enzyme-Based Biofuel Cells Using High Mediator Concentration
Abstract
:1. Introduction
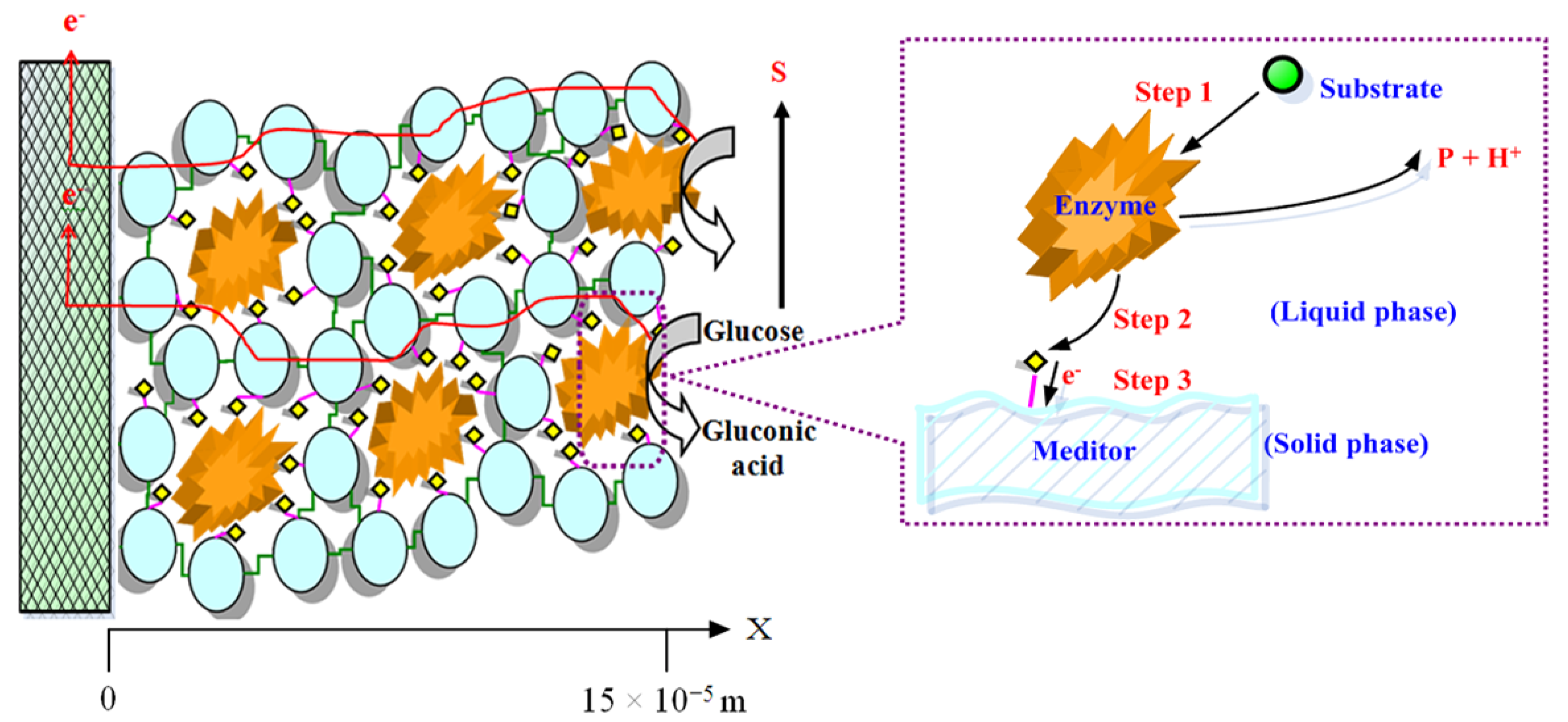
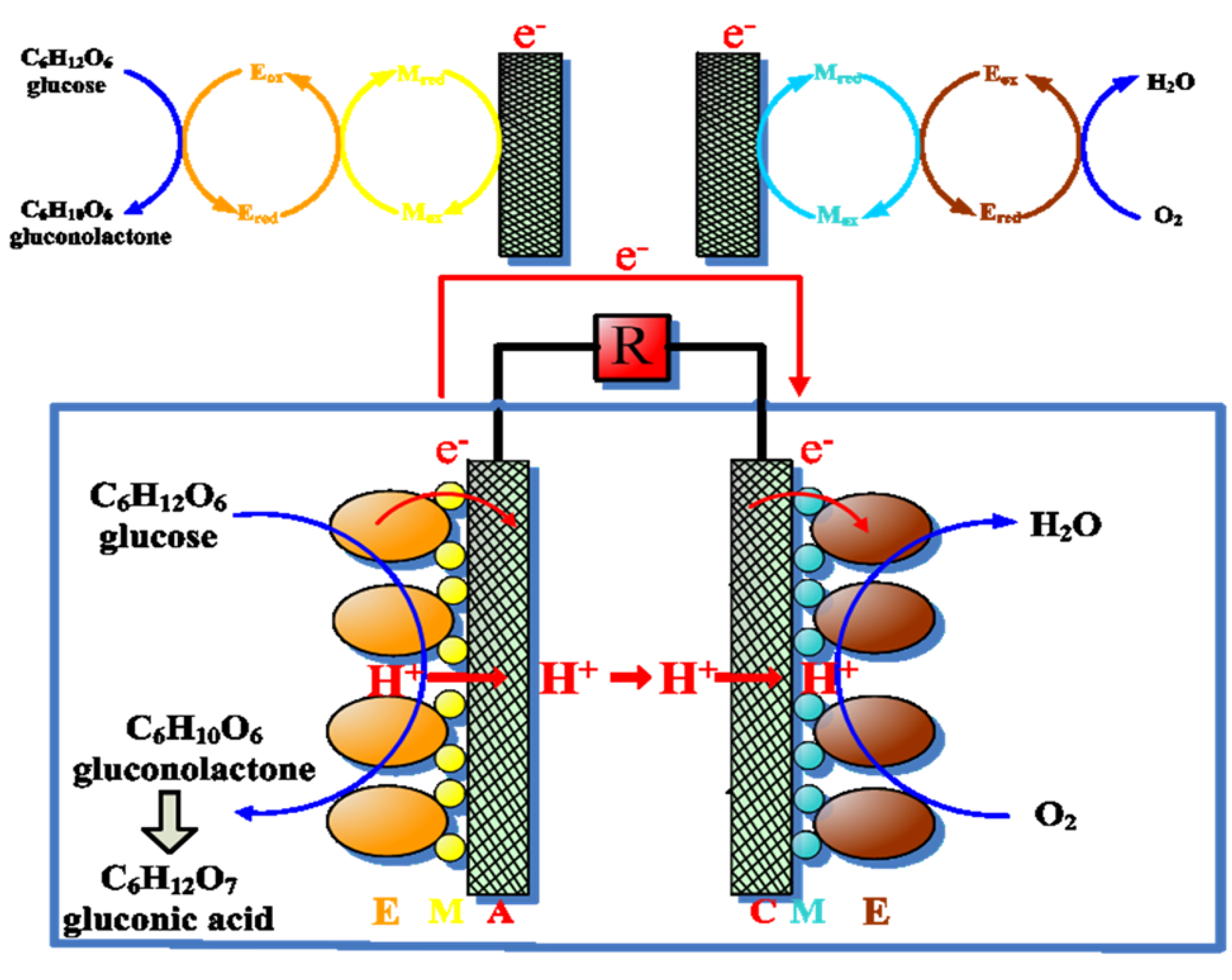
| Electrode | Species kinetic model | System | Immobilization | Electronic conductivity | Description | Ref. |
|---|---|---|---|---|---|---|
| Anode | S/E/M M-M | S-S/diffusion/- | E-bound/M-free | - | Redox mediator entrapped with a hydrogen film | [30] |
| Anode | S/E/M M-M | S-S/diffusion/- | E-bound/M-free | - | Practical application of the biosensors, bioreactors and biofuel cell | [26] |
| Anode | S/E/M M-M | S-S/diffusion/- | E-bound/M-free | - | Current is function of mediator concentration and electrode potential | [39] |
| Cathode | S/E/M M-M | S-S/diffusion/flow | E-bound/M-free | - | Oxygen transport in CME with macrohomogenous/thin-film model | [31] |
| Anode | S/E/- - | S-S/diffusion/- | E-free /- | - | Electroenzymes at the electrode/solution interface | [40] |
| Anode | S/E/- - | S-S/-/- | E-free/- | - | Amperometric bioanalytical system for lipase activity assay | [41] |
| Anode | S/E/- - | U-S/-/- | E-bound/- | - | Electrochemical system of lipase activity detection | [42] |
| Cathode | S/E/M M-M | S-S/diffusion/- | E-bound/M-free | - | Redox polymer-mediated enzyme electrode | [35] |
| Anode | S/E/M M-M | S-S/diffusion/- | E-bound/M-free | - | High-surface-area electrode of redox polymer-grafted carbon | [17] |
| Anode | S/E/M M-M | S-S/diffusion/- | E-bound/M-free | - | Redox enzyme CME biosensor | [43] |
| Anode | S/E/- M-M | U-S/diffusion/-U- | E-bound/- | - | Action of biosensor possessing pH and temperature parameters | [44] |
| Anode | S/E/- M-M | S/diffusion/- | E-bound/- | - | Conducting polymer modified electrode | [45] |
| Anode | S/E/M | U-S/diffusion/- | E-bound/M-bound | kl/ks | Enzyme-based biofuel cell using high mediator concentration | This study |
2. Experimental and Modeling
2.1. Chemicals and Materials
2.2. Enzyme Electrode Preparation
2.3. Electrochemical Measurements
2.4. Mathematical Formulation
| Species j | Source terms | |||
|---|---|---|---|---|
| Rj | ICj | BC1j | BC2j | |
| S | [S]b | 0 | [S]b | |
| H+ | 0 | 0 | ||
| P | 0 | 0 | ||
| ES | 0 | a | a | |
| Eox | a | a | ||
| Ered | a | a | ||
| Mox | a | a | ||
| Mred | a | a | ||
| Symbol | Simulated parameter | Ref. value | References |
|---|---|---|---|
| θ | 0.5 | given | |
| a | 2.3 × 104 [L/m] | Measured | |
| F | 96,500 [C/mol] | 96,485 to 96,487 [C/mol] | [17,33] |
| DH | 1.0 × 10−9 [m2/s] | 0.9 × 10−10[mol·m−3] | [44] |
| Dp | 5.0 × 10−10 [m2/s] | ||
| Ds | 5.0 × 10−10 [m2/s] | 4.9 × 10−6[cm2·s−1] | [17] |
| EA | −0.15 ~ 0.4 [V] | ||
| [Eox]i | 0.05 [mM] | 0.05 [mM] | [25] |
| [Ered]i | 0 [mM] | Initial value | |
| [ES]i | 0 [mM] | Initial value | |
| [H+]i | 0 [mM] | Initial value | |
| i0 | 1.5 × 10,4 [mA/cm2] | given | |
| k1b | 1.0 [1/s] | 0.41 to 1.17 × 10−6[mol·cm−2·s−1] | [42] |
| k1f | 1.0 × 103 [m3/(mol.s)] | 10 [s−1] | [42] |
| k2f | 1.0 × 102 [1/s] | 75 [s−1] | [42] |
| k3b | 1.0 [m3/(mol.s)] | 0.025 [s−1] | [42] |
| k3f | 1.0 × 102 [m3/(mol.s)] | 100 [cm·s−1] | [42] |
| kl | 5.5 × 10−1 [S/m] | Measured | |
| ks | 3.99 × 10−1 [S/m] | Measured | |
| L | 15 × 10−5 [m] | Measured | |
| Mt | 10 [mM] | 10 [mM] | [25] |
| [Mox]i | 5 [mM ] | Initial value | |
| [Mred]i | 5 [mM ] | Initial value | |
| n | 1 | 1 | [17,26] |
| [P]i | 0 [mM] | Initial value | |
| R | 8.314 [J/(mol.K)] | 8.314 [J/(mol.K)] | [17,33] |
| [S]i | 2.0 [mM] | 2.4 to 0.6 [mM] | Initial value |
| T | 310 [K] | 310 [K] | [5,25] |
3. Results and Discussion
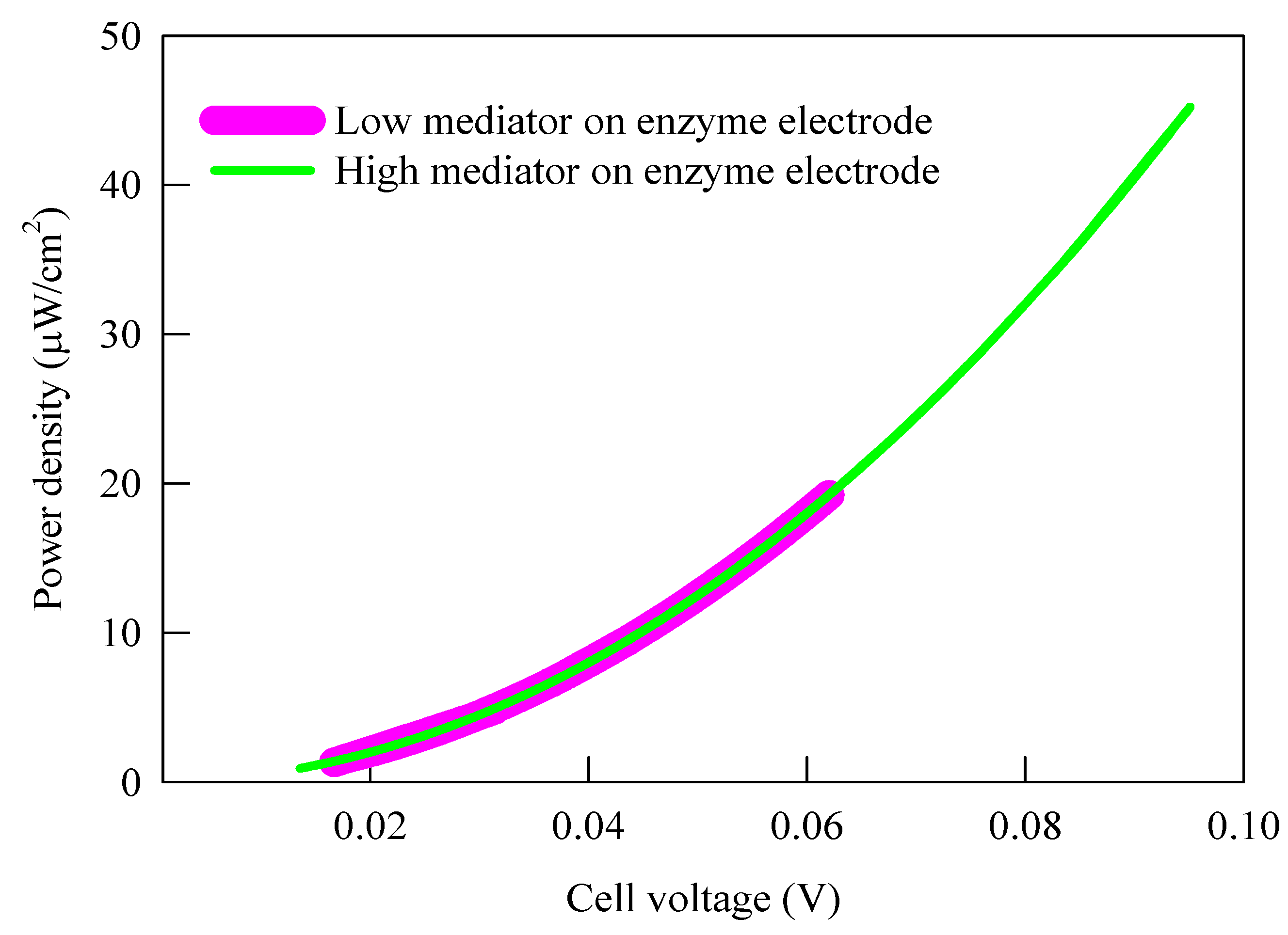
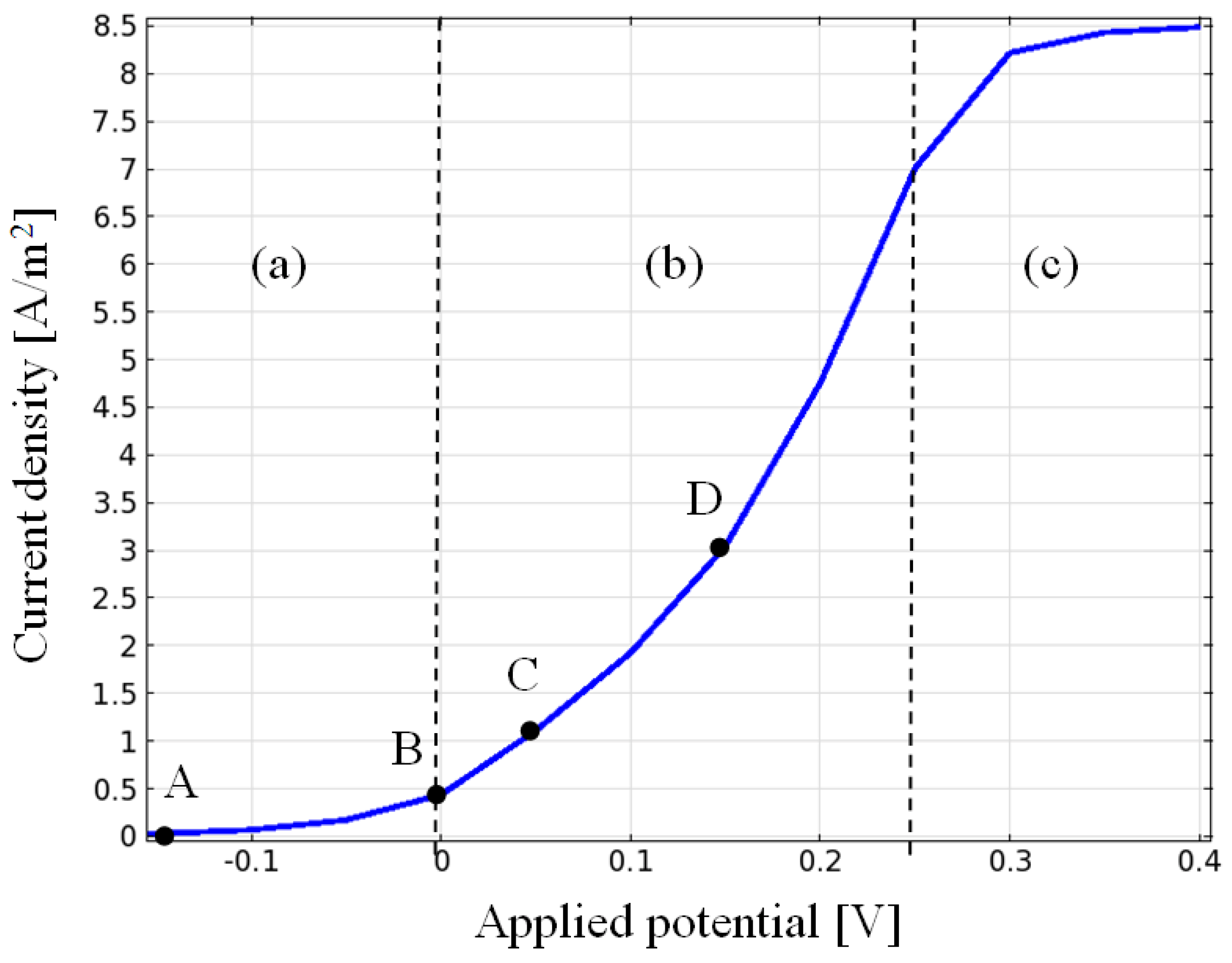
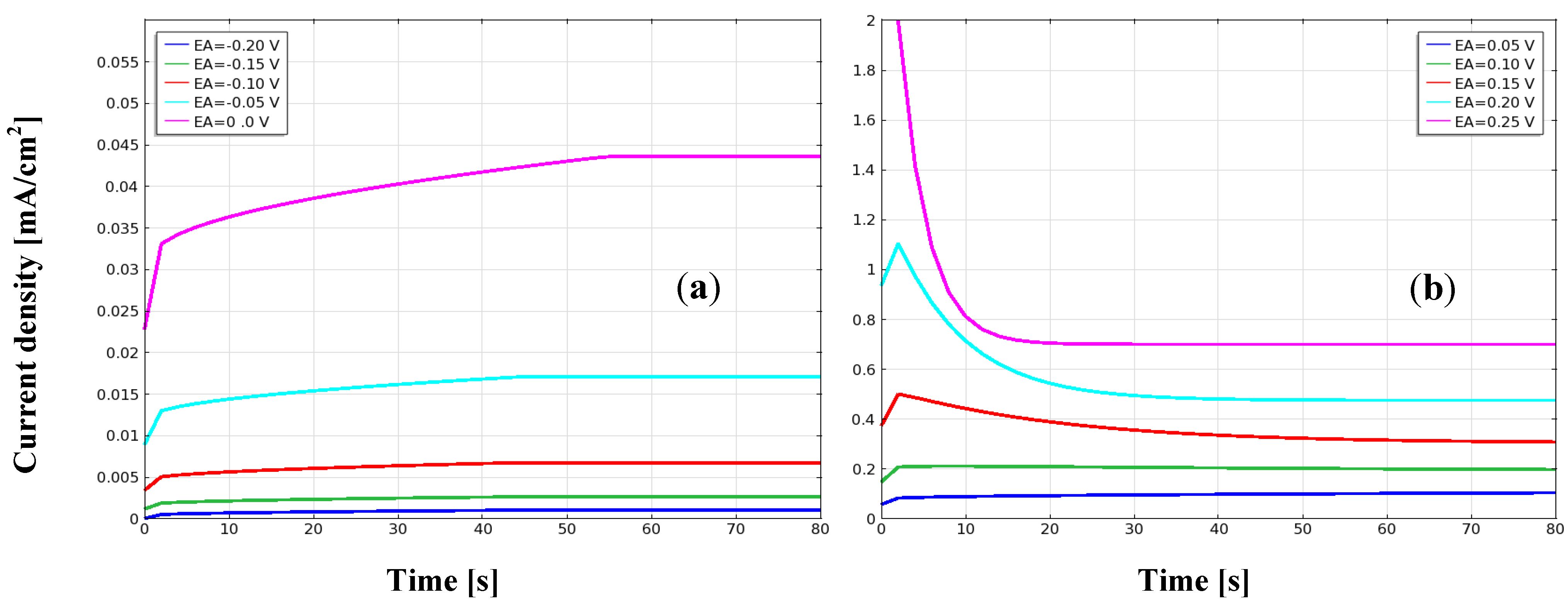
3.1. Current Density, Potential and Polarization Loss
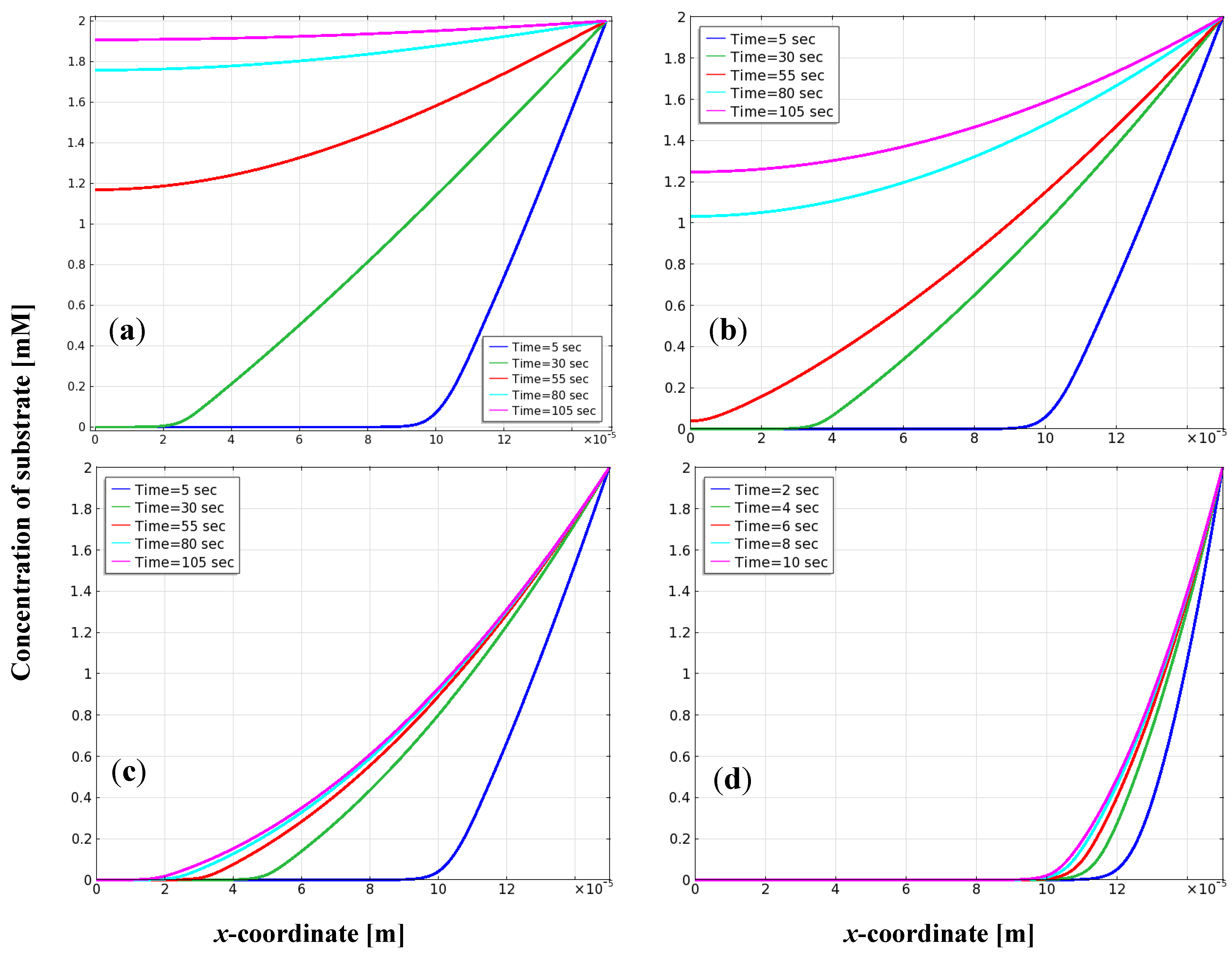
3.2. Distribution of Substrate on the Electrode
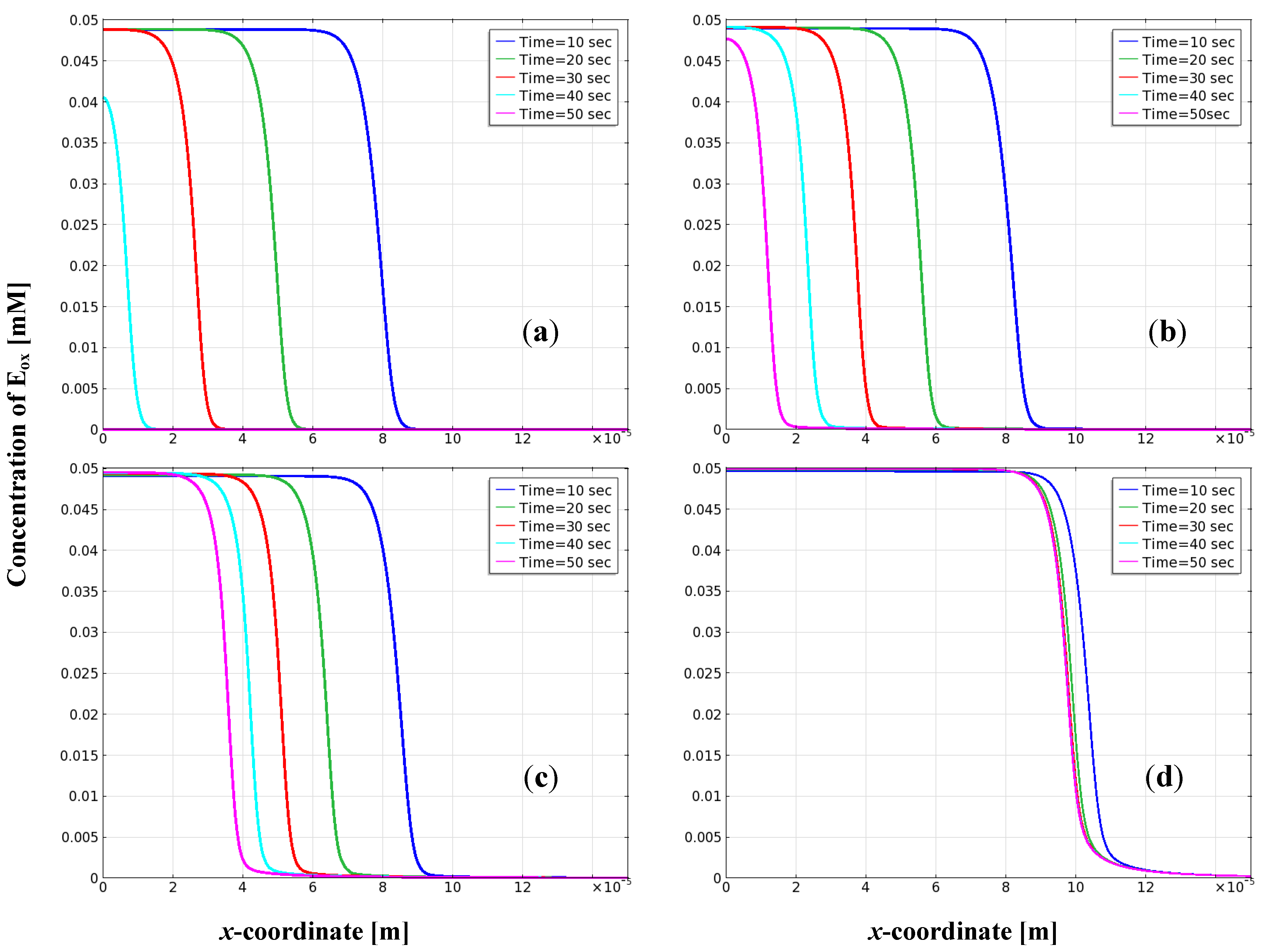
3.3. Distribution of Oxidized Enzyme on the Electrode
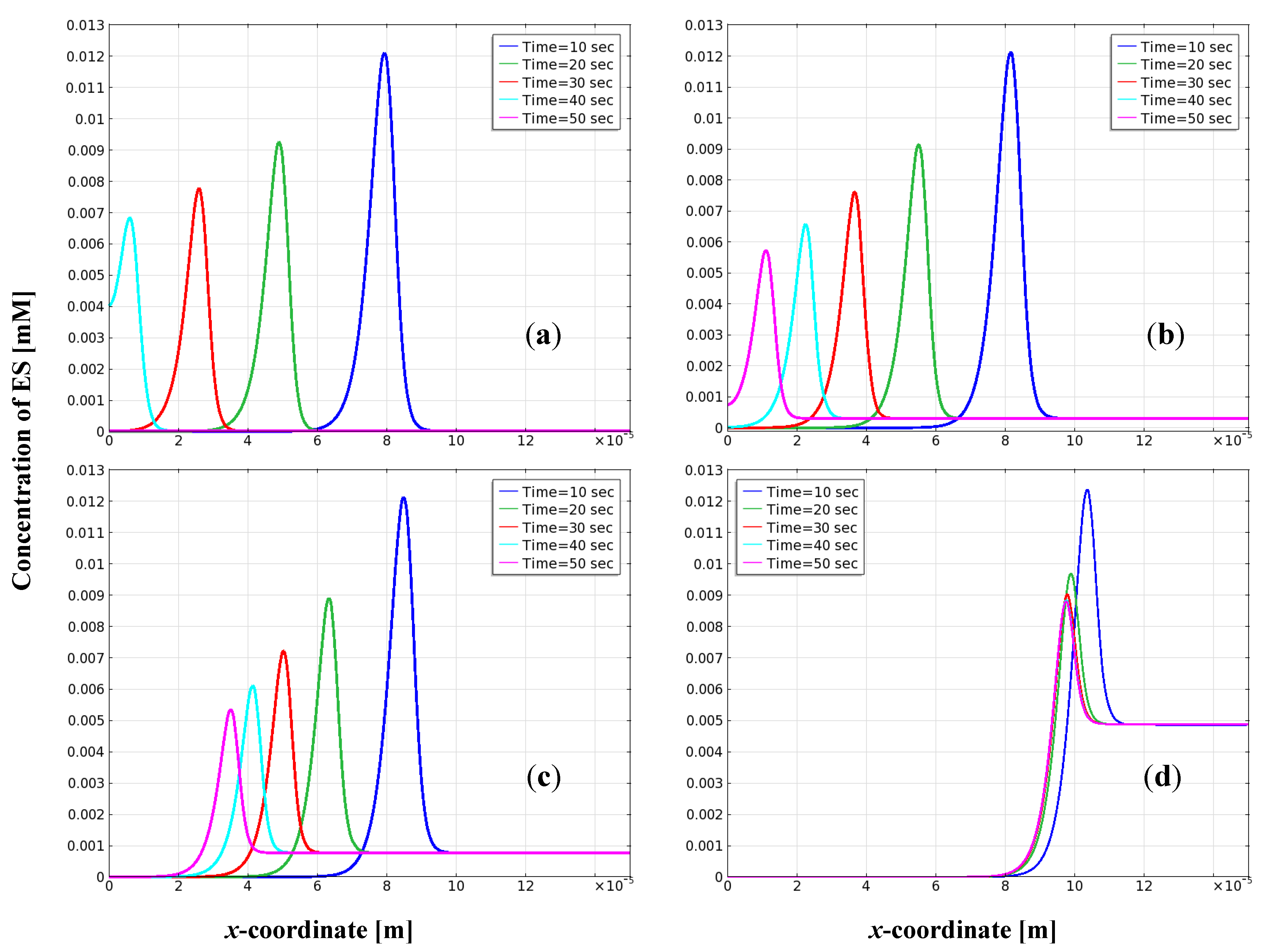
3.4. Distribution of Enzyme-Substrate Complex on the Electrode
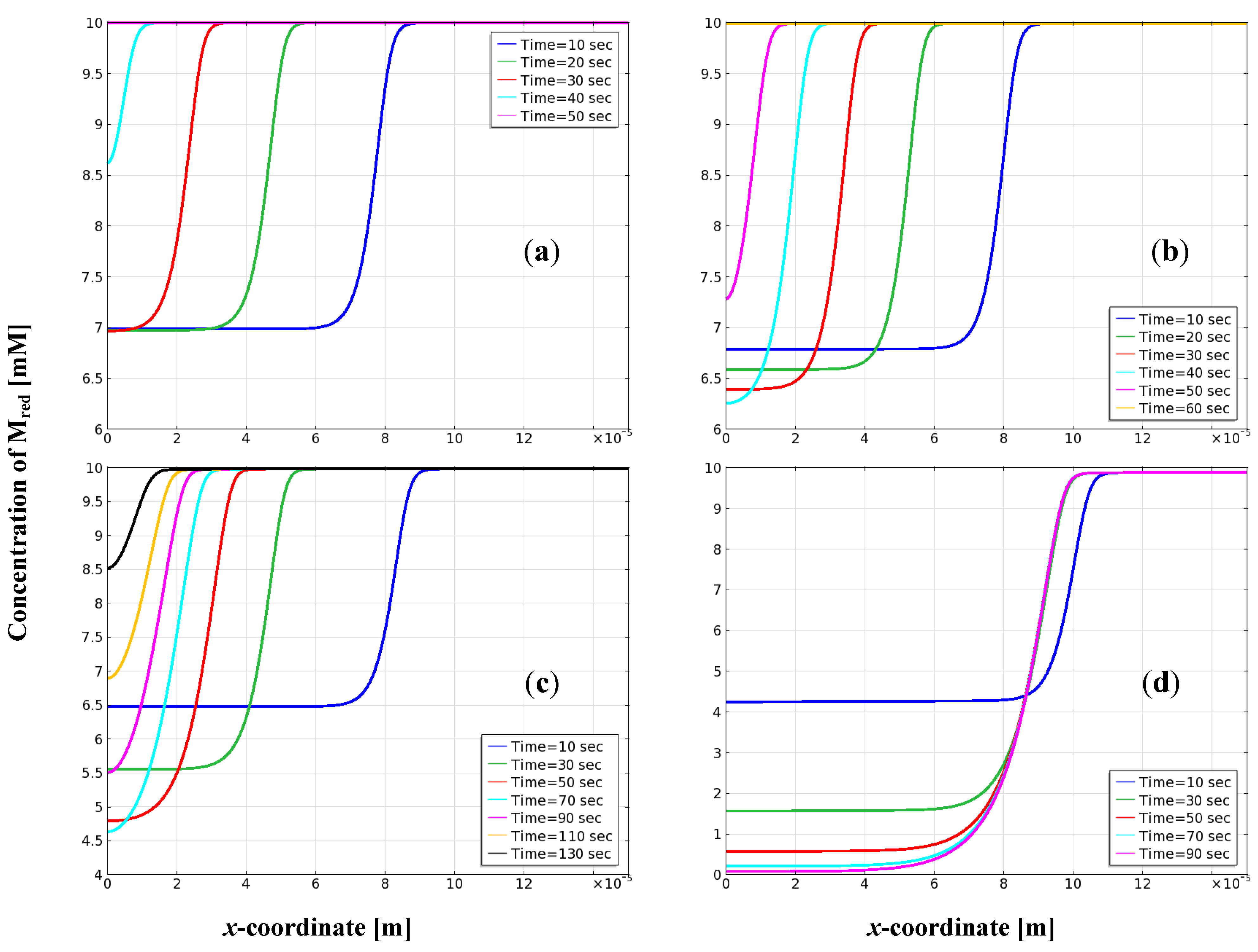
3.5. Distribution of Mediator on the Electrode
4. Conclusions
Notations
| [ ] | concentration in the system [mM] |
| a | surface area of the electrode per electrode volume [L/m] |
| DH | diffusion coefficient for free hydrogen [m2/s] |
| Dp | diffusion coefficient for free product [m2/s] |
| Ds | diffusion coefficient for free substrate [m2/s] |
| e− | electron |
| E | enzyme [mM] |
| EA | applied potential [V] |
| Ee | equilibrium potential |
| ES | enzyme-substrate complex [mM] |
| F | Faraday’s constant [C/mol] |
| H+ | hydrogen ion [mM] |
| i0 | exchange current density [mA/cm2] |
| it | local current density [mA/cm2] |
| It | total current density [mA/cm2] |
| k1b | back rate constant [1/s] |
| k1f | forward rate constant [mol.s] |
| k2f | product formation rate constant [1/s] |
| k3b | backward rate constant [1/(mM.s)] |
| k3f | forward rate constant [1/(mM.s)] |
| kl | conductivity of liquid phase [S/m] |
| ks | conductivity of solid phase [S/m] |
| L | length of the electrode film [m] |
| Mt | total concentration of mediator [mM] |
| M | mediator [mM] |
| n | number of electrons (in this case, n = 1) |
| P | product of enzyme reaction [mM] |
| R | gas constant [J/(mol.K)] |
| S | substrate [mM] |
| T | temperature [K] |
| Greek Letters | |
| β | anode transfer coefficient |
| potential in liquid phase | |
| potential in solid phase | |
| θ | volume fraction of liquid in the bioelectrode |
| Subscripts | |
| i | initial value |
| l | liquid phase |
| ox | oxidized state |
| red | reduced state |
| s | solid phase |
| t | time |
Acknowledgments
References
- Katz, E.; Shipway, A.N.; Willner, I. Handbook of Fuel Cells—Fundamentals, Technology and Applications; Vielstich, W., Lamm, A., Gasteiger, H.A., Eds.; Wiley: London, UK, 2003; pp. 355–381. [Google Scholar]
- Ikeda, T.; Kano, K. Bioelectrocatalysis-based application of quinoproteins and quinoprotein-containing bacterial cells in biosensors and biofuel cells. Biochim. Biophys. Acta 2003, 1647, 121–126. [Google Scholar] [CrossRef]
- Barton, S.C.; Gallaway, J.; Atanassov, P. Enzymatic biofuel cells for implantable and microscale devices. Chem. Rev. 2004, 104, 4867–4886. [Google Scholar] [CrossRef] [PubMed]
- Heller, A. Miniature biofuel cells. Phys. Chem. Chem. Phys. 2004, 6, 209–216. [Google Scholar] [CrossRef]
- Bullen, R.A.; Arnot, T.C.; Lakeman, J.B.; Walsh, F.C. Biofuel cells and their development. Biosens. Bioelectron. 2006, 21, 2015–2045. [Google Scholar] [CrossRef] [PubMed]
- Kim, J.; Jia, H.F.; Wang, P. Challenges in biocatalysis for enzyme-based biofuel cells. Biotechnol. Adv. 2006, 24, 296–308. [Google Scholar] [CrossRef] [PubMed]
- Minteer, S.D.; Liaw, B.Y.; Cooney, M.J. Enzyme-based biofuel cells. Curr. Opin. Biotechnol. 2007, 18, 228–234. [Google Scholar] [CrossRef] [PubMed]
- Ghindilis, A.L.; Atanassov, P.; Wilkins, E. Enzyme-catalyzed direct electron transfer: Fundamentals and analytical applications. Electroanalysis 1997, 9, 661–674. [Google Scholar] [CrossRef]
- Gorton, L.; Lindgren, A.; Larsson, T.; Munteanu, F.D.; Ruzgas, T.; Gazaryan, I. Direct electron transfer between heme-containing enzymes and electrodes as basis for third generation biosensors. Anal. Chim. Acta 1999, 400, 91–108. [Google Scholar] [CrossRef]
- Vincent, K.A.; Cracknell, J.A.; Lenz, O.; Zebger, I.; Friedrich, B.; Armstrong, F.A. Electrocatalytic hydrogen oxidation by an enzyme at high carbon monoxide or oxygen levels. Proc. Natl. Acad. Sci. USA 2005, 102, 16951–16954. [Google Scholar] [CrossRef] [PubMed]
- Tsujimura, S.; Nakagawa, T.; Kano, K.; Ikeda, T. Kinetic study of direct bioelectrocatalysis of dioxygen reduction with bilirubin oxidase at carbon electrodes. Electrochemistry 2004, 72, 437–439. [Google Scholar]
- Kamitaka, Y.; Tsujimura, S.; Setoyama, N.; Kajino, T.; Kano, K. Fructose/dioxygen biofuel cell based on direct electron transfer-type bioelectrocatalysis. Phys. Chem. Chem. Phys. 2007, 9, 1793–1801. [Google Scholar] [CrossRef] [PubMed]
- Tarasevich, M.R.; Bogdanovskaya, V.A.; Kapustin, A.V. Nanocomposite material laccase/dispersed carbon carrier for oxygen electrode. Electrochem. Commun. 2003, 5, 491–496. [Google Scholar] [CrossRef]
- Tominaga, M.; Otani, M.; Kishikawa, M.; Taniguchi, I. UV-ozone treatments improved carbon black surface for direct electron-transfer reactions with bilirubin oxidase under aerobic conditions. Chem. Lett. 2006, 35, 1174–1175. [Google Scholar] [CrossRef]
- Ivanov, I.; Vidaković-Koch, T.; Sundmacher, K. Recent advances in enzymatic fuel cells: Experiments and modeling. Energies 2010, 3, 803–846. [Google Scholar] [CrossRef]
- Chaubey, A.; Malhotra, B.D. Mediated biosensors. Biosens. Bioelectron. 2002, 17, 441–456. [Google Scholar] [CrossRef]
- Tamaki, T.; Ito, T.; Yamaguchi, T. Modelling of reaction and diffusion processes in a high-surface-area biofuel cell electrode made of redox polymer-grafted carbon. Fuel Cells 2009, 9, 37–43. [Google Scholar] [CrossRef]
- Sato, F.; Togo, M.; Islam, M.K.; Matsue, T.; Kosuge, J.; Fukasaku, N.; Kurosawa, S.; Nishizawa, M. Enzyme-based glucose fuel cell using vitamin K3-immobilized polymer as an electron mediator. Electrochem. Commun. 2005, 7, 643–647. [Google Scholar] [CrossRef]
- Togo, M.; Takamura, A.; Asai, T.; Kaji, H.; Nishizawa, M. An enzyme-based microfluidic biofuel cell using vitamin K3-mediated glucose oxidation. Electrochim. Acta 2007, 52, 4669–4674. [Google Scholar] [CrossRef]
- Fischback, M.B.; Youn, J.K.; Zhao, X.Y.; Wang, P.; Park, H.G.; Chang, H.N.; Kim, J.; Ha, S. Miniature biofuel cells with improved stability under continuous operation. Electroanalysis 2006, 18, 2016–2022. [Google Scholar] [CrossRef]
- Barton, S.C.; Sun, Y.H.; Chandra, B.; White, S.; Hone, J. Mediated enzyme electrodes with combined micro-and nanoscale supports. Electrochem. Solid-State Lett. 2007, 10, B96–B100. [Google Scholar] [CrossRef]
- Yan, Y.; Zheng, W.; Su, L.; Mao, L. Carbon-nanotube-based glucose-O2 biofuel cells. Adv. Mater. 2006, 18, 2639–2643. [Google Scholar] [CrossRef]
- Komaba, S.; Mitsuhashi, T.; Shiraishi, S. Polyion complex nanocomposite electrode incorporating enzyme and carbon nanotube for biofuel cells. Electrochemistry 2008, 76, 55–58. [Google Scholar] [CrossRef]
- Narushima, K.; Yamashita, N.; Fukuoka, M.; Inagaki, N.; Isono, Y.; Islam, M.R. Surface modification of polymer films by pulsed oxygen plasma. Jpn. J. Appl. Phys. 2007, 46, 4238–4245. [Google Scholar] [CrossRef]
- Dai, D.J.; Chan, D.S.; Wu, H.S. Modified carbon nanoball on electrode surface using plasma in enzyme-based biofuel cells. Energy Procedia 2012, 14, 1804–1810. [Google Scholar] [CrossRef]
- Kano, K.; Ikeda, T. Fundamentals and practices of mediated bioelectrocatalysis. Anal. Sci. 2000, 16, 1013–1021. [Google Scholar] [CrossRef]
- Yu, E.H.; Scott, K. Enzymatic biofuel cells-fabrication of enzyme electrodes. Energies 2010, 3, 23–42. [Google Scholar] [CrossRef]
- Svoboda, V.; Cooney, M.; Bor, Y.L.; Minteer, S.; Piles, E.; Lehnert, D.; Barton, S.C.; Atanassov, P. Standardized characterization of electrocatalytic electrodes. Electroanalysis 2008, 10, 1099–1109. [Google Scholar] [CrossRef]
- Ikeda, T.; Kano, K. An electrochemical approach to the studies of biological redox reactions and their applications to biosensors, bioreactors, and biofuel cells. J. Biosci. Bioeng. 2001, 92, 9–18. [Google Scholar] [CrossRef]
- Bartlett, P.N.; Pratt, K.F.E. Theoretical treatment of diffusion and kinetics in amperometric immobilized enzyme electrodes Part I: Redox mediator entrapped within the film. J. Electroanal. Chem. Interfacial Electrochem. 1995, 397, 61–78. [Google Scholar] [CrossRef]
- Barton, S.C. Oxygen transport in composite mediated biocathodes. Electrochim. Acta 2005, 50, 2145–2153. [Google Scholar] [CrossRef]
- Bartlett, P.N.; Toh, C.S.; Calvo, E.J.; Flexer, V. Modelling biosensor responses. In Bioelectrochemistry: Fundamentals, Experimental Techniques and Applications; Bartlett, P.N., Ed.; Wiley: Chichester, UK, 2008; pp. 267–325. [Google Scholar]
- Weber, A.Z.; Newman, J. Modeling transport in polymer-electrolyte fuel cells. Chem. Rev. 2004, 104, 4679–4726. [Google Scholar] [CrossRef] [PubMed]
- Verger, R.; Mieras, M.C.E.; Haas, G.H.D. Action of phospholipase A at interfase. J. Biol. Chem. 1973, 248, 4023–4034. [Google Scholar] [PubMed]
- Gallaway, J.W.; Barton, S.C. Kinetics of redox polymer-mediated enzyme electrodes. J. Am. Chem. Soc. 2008, 130, 8527–8536. [Google Scholar] [CrossRef] [PubMed]
- Bard, A.J.; Faulkner, L.R. Electrochemical methods. In Fundamentals and Applications, 2nd ed.; Wiley: New York, NY, USA, 2001. [Google Scholar]
- Flexer, V.; Ielmini, M.V.; Calvo, E.J.; Bartlett, P.N. Extracting kinetic parameters for homogeneous [Os(bpy)2ClPyCOOH]+ mediated enzyme reactions from cyclic voltammetry and simulations. Bioelectrochemistry 2008, 74, 201–209. [Google Scholar] [CrossRef] [PubMed]
- Deng, L.; Wang, F.; Chen, H.; Shang, L.; Wang, L.; Wang, T.; Dong, S. A biofuel cell with enhanced performance by multilayer biocatalyst immobilized on highly ordered macroporous electrode. Biosens. Bioelectron. 2008, 24, 329–333. [Google Scholar] [CrossRef] [PubMed]
- Matsumoto, R.; Kano, K.; Ikeda, T. Theory of steady-state catalytic current of mediated bioelectrocatalysis. J. Electroanal. Chem. 2002, 535, 37–40. [Google Scholar] [CrossRef]
- Lyons, M.E.G. Modelling the transport and kinetics of electroenzymes at the electrode/solution interface. Sensors 2006, 6, 1765–1790. [Google Scholar] [CrossRef]
- Puida, M.; Ivanauskas, F.; Ignatjev, I.; Valinčius, G.; Razumas, V. Computational modeling of the amperomet bioanalytical system for lipase activity assay: A time-dependent response. Nonlinear Anal. Model. Control 2007, 12, 245–251. [Google Scholar]
- Puida, M.; Ivanauskas, F.; Ignatjev, I.; Valinčius, G.; Razumas, V. Computational modeling of the electrochemical system of lipase activity detection. Sensors 2008, 8, 3873–3879. [Google Scholar] [CrossRef]
- Lyons, M.E.G. Transport and kinetics at carbon nanotube-redox enzyme composite modified electrode biosensors part 2: Redox enzyme dispersed in nanotube mesh of finite thickness. Int. J. Electrochem. Sci. 2009, 4, 1196–1236. [Google Scholar]
- Puida, M.; Ivanauskas, F. Mathematical modeling of the action of biosensor possessing variable parameters. J. Math. Chem. 2010, 47, 191–200. [Google Scholar] [CrossRef]
- Puida, M.; Malinauskas, A.; Ivanauskas, F. Modeling of electrocatalysis at conducting polymer modified electrodes: Nonlinear current-concentration profiles. J. Math. Chem. 2011, 49, 1151–1162. [Google Scholar] [CrossRef]
- Bedekar, A.S.; Feng, J.J.; Krishnamoorthy, S.; Lim, K.G.; Palmore, G.T.R.; Sundaram, S. Oxygen limitation in microfluidic biofuel cells. Chem. Eng. Commun. 2008, 195, 256–266. [Google Scholar] [CrossRef]
- Glykys, D.J.; Banta, S. Metabolic control analysis of an enzymatic biofuel cell. Biotechnol. Bioeng. 2009, 102, 1624–1635. [Google Scholar] [CrossRef] [PubMed]
- Jeon, S.W.; Lee, J.Y.; Lee, J.H.; Kang, S.W.; Park, C.H.; Kim, S.W. Optimization of cell conditions for enzymatic fuel cell using statistical analysis. J. Ind. Eng. Chem. 2008, 14, 338–343. [Google Scholar] [CrossRef]
- Kjeang, E.; Sinton, D.; Harrington, D.A. Strategic enzyme patterning for microfluidic biofuel cells. J. Power Sources 2006, 158, 1–12. [Google Scholar] [CrossRef]
- Albery, W.J.; Kalia, Y.N.; Magner, E. Amperometric enzyme electrodes part VI: Enzyme electrodes for sucrose and lactose. J. Electroanal. Chem. Interfacial Electrochem. 1992, 325, 83–93. [Google Scholar] [CrossRef]
© 2012 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Chan, D.-S.; Dai, D.-J.; Wu, H.-S. Dynamic Modeling of Anode Function in Enzyme-Based Biofuel Cells Using High Mediator Concentration. Energies 2012, 5, 2524-2544. https://doi.org/10.3390/en5072524
Chan D-S, Dai D-J, Wu H-S. Dynamic Modeling of Anode Function in Enzyme-Based Biofuel Cells Using High Mediator Concentration. Energies. 2012; 5(7):2524-2544. https://doi.org/10.3390/en5072524
Chicago/Turabian StyleChan, Der-Sheng, Der-Jong Dai, and Ho-Shing Wu. 2012. "Dynamic Modeling of Anode Function in Enzyme-Based Biofuel Cells Using High Mediator Concentration" Energies 5, no. 7: 2524-2544. https://doi.org/10.3390/en5072524
APA StyleChan, D.-S., Dai, D.-J., & Wu, H.-S. (2012). Dynamic Modeling of Anode Function in Enzyme-Based Biofuel Cells Using High Mediator Concentration. Energies, 5(7), 2524-2544. https://doi.org/10.3390/en5072524






