Abstract
A 2D unsteady computational fluid dynamics (CFD) model is employed to simulate buoyancy-driven turbulent ventilation in attics with different pitch values and ceiling insulation levels under summer conditions. The impacts of roof pitch and ceiling insulation on the cooling load of gable-roof residential buildings are investigated based on the simulation of turbulent air flow and natural convection heat transfer in attic spaces with roof pitches from 3/12 to 18/12 combined with ceiling insulation levels from R-1.2 to R-40. The modeling results show that the air flows in the attics are steady and exhibit a general streamline pattern that is qualitatively insensitive to the investigated variations of roof pitch and ceiling insulation. Furthermore, it is predicted that the ceiling insulation plays a control role on the attic cooling load and that an increase of roof pitch from 3/12 to 8/12 results in a decrease in the cooling load by around 9% in the investigated cases. The results suggest that the increase of roof pitch alone, without changing other design parameters, has limited impact on attics cooling load and airflow pattern. The research results also suggest both the predicted ventilating mass flow rate and attic cooling load can be satisfactorily correlated by simple relationships in terms of appropriately defined Rayleigh and Nusselt numbers.
1. Introduction
Ventilated attic has been a long-established practice in residential building construction [1], but how different attic designs affecting building energy performance has not been thoroughly investigated. The majority of the existing literature on attic energy performance concerned with sealed attics, as reviewed by Kamiyo et al. [2] and by Saha and Khan [3], while only a few publications reported studies involving attic ventilation. For example, Medina et al. [4,5] proposed a correlation-based mathematical model for vented residential attics and compared model predictions with experimental data, and Moujaes and Alsaiegh [6] employed a finite element model to simulate the thermal effects of placing a radiant barrier system inside a vented residential attic for a case study under summer weather conditions. However, very limited literature was found on investigating ventilated attics using turbulence CFD models. Due to relatively large size of attics, turbulence phenomenon in the vented attics is warranted in both summer and winter conditions [7]. Therefore, more accurate results are expected from using appropriate turbulence flow models. The improved results can provide better scientific evidence and guidance for building practitioners to improve energy performance of residential buildings and design ventilation enhancement devices, such as the wind driven rooftop ventilators [8,9,10,11].
Two major parameters are of particular interest in this paper: Roof pitch and ceiling insulation. There are many considerations behind the roof pitch designs, which range from discharging rainwater and snow to increasing aesthetic appearances. However, very limited research investigated its impact on attic energy performance. So, in this paper, the effects of roof pitch and ceiling insulation on the cooling load are parametrically investigated for gable-roof residential buildings, which are represented by two-dimensional CFD models. Since wind effects are not included in this study, the air flow and heat transfer in the attic spaces are purely driven by stack effects. Such buoyancy-driven cases are corresponding to a worst-case scenario, because real attic ventilation is generally enhanced by winds. In order to account for a wide range of roof pitch and ceiling insulation, involving several orders of magnitude variation of Rayleigh number, the buoyancy-driven air flow and natural convection heat transfer are modeled by the k-kl-ω model [12], which is a physics-based transitional turbulence model capable of modeling turbulent flows from laminar-turbulence transitional regime to fully turbulence regime. An unsteady numerical formulation is adopted in the study, as the steady solutions could not always converge, even after carefully adjusting the various under-relaxation factors. Unsteady Reynolds-averaged Navier-Stokes (URANS) modeling has been shown to be an effective approach to overcome numerical stiffness and improve solution convergence in previous studies for natural convection flows in enclosures [13,14,15,16,17]. The URANS approach is also a recommended strategy in commercial CFD manuals [18] for solving natural convection problems. In the following sections, the numerical model will be introduced first, followed by detailed presentation and discussion of the modeling results.
2. Numerical Model
A schematic diagram of a cross-section plan of the physical model is shown in Figure 1. In the direction perpendicular to the cross-section shown in Figure 1, it is assumed that the building is long enough to ignore the effects of the gable-end walls, and thus the problem is simplified to two dimensional.
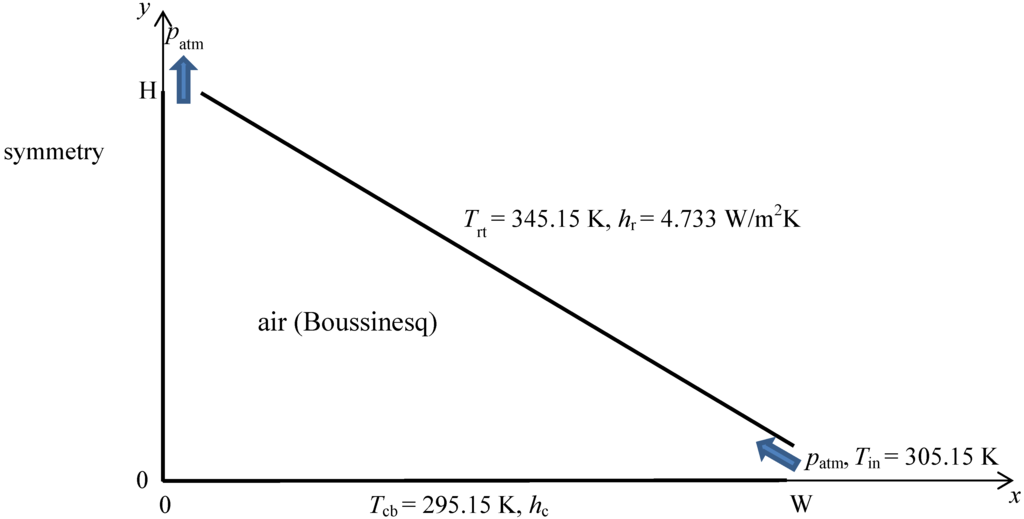
Figure 1.
Schematic of the computational domain and boundary conditions.
The modeled attic space is in a shape of an isosceles triangle, with a ceiling width of 2W and a height of H, resulting in a pitch of H/W. Due to the buoyancy stableness of the summertime attic ventilation as well as the symmetry in both geometry and boundary conditions, only the right half of the attic is included in the computational domain. In this study, the modeled attic is assumed to have a fixed ceiling half-width of W = 4 m and a height varying between 1 m and 6 m, corresponding to a roof pitch varying from 3/12 to 18/12. For simplicity, neither roofs nor ceiling trusses are included in the model, and the computational domain is only occupied by air, which is assumed to be a Boussinesq fluid with a reference temperature T0 specified to the outside ambient air temperature to correctly calculate the buoyancy effects. In all the cases reported in this study, T0 = 305.15 K is assumed.
In order to correctly account for the thermal resistances of the ceiling and roof, which are excluded from the computational domain, convection-type boundary conditions are applied to both the ceiling and roof boundaries. For example, energy balance across the ceiling thickness gives:
where Tcb and Tct are the temperatures at the ceiling-bottom and ceiling-top, respectively, and the heat transfer coefficient hc is determined by the thermal conductivity of ceiling material divided by ceiling thickness . It should be note that hc is the reciprocal of the ceiling thermal resistance Rc, which may be expressed in R-value, i.e., R-1 = 1 h·ft2·°F/Btu = 0.176110 Km2/W.
In this study, a ceiling-bottom temperature is specified to Tcb = 295.15 K, while a heat transfer coefficient of hc varying between 4.733 W/m2K to 0.142 W/m2K is adopted to approximate a ceiling insulation level between R-1.2 (Rc = 1.2 × 0.176110 Km2/W = 0.211 Km2/W) and R-40 (Rc = 7.044 Km2/W). Similarly, a roof-top temperature of Trt = 345.15 K and a heat transfer coefficient of hr = 4.733 W/m2K (equivalent to an insulation level of R-1.2) are specified to the roof boundary to simulate a condition of a 3 cm plywood roof.
For all the cases investigated in this study, balanced vent areas are assumed. Both the soffit and ridge vents are assumed to be 1 cm wide, resulting in a ventilation ratio of 1/200, which is a representative attic ventilation rate in construction practice. Typically, the net free vent area (unobstructed area where air can freely flow from outside to inside to outside) is required by the building codes to be 1/150 of the floor area of the attic space being ventilated, and a reduction of the ventilation ratio from 1/150 to 1/300 is allowed if at least 50% of the ventilating area is in the upper portion of the space and a continuous vapor retarder is installed on the warm side of the ceiling. In this study, pressures at the soffit and ridge vents are both specified to be zero gauge pressure. Therefore, the obtained air flow is purely driven by the thermally induced buoyancy forces, i.e., the stack effect. At the soffit vent, the inlet air is assumed to enter at an ambient temperature of 305.15 K and a turbulent intensity of 1%.
Following the URANS approach to turbulence, the time-averaged air velocity (), pressure (p), and temperature (T) distributions in the attic space shown in Figure 1 are governed by the following continuity, momentum, and energy equations:
where density ρ, kinetic viscosity ν, thermal expansion coefficient β, and thermal diffusivity α are air properties, while fluctuation kinetic energy k, eddy viscosity , and eddy thermal diffusivity are determined by the employed turbulence model. In Equations (3) and (4), the substantial derivative terms include unsteady terms (partial derivative with respective to time) that account for all unsteadiness that does not belong to the turbulence, i.e., the unsteadiness that is not represented by the turbulence model [14].
The turbulence model employed in this study is the k-kl-ω transition model [12], which is an eddy-viscosity turbulence model based on the k-ω framework and includes laminar kinetic energy to represent the pretransitional fluctuations in boundary layers. Additional information about the k-kl-ω transition model can be found in [12].
The governing equations formulated above are solved by the commercial CFD software Ansys Fluent 13.0 [18], with the space variables being discretized by the finite volume method and time domain discretized by the fully implicit scheme. The coupled algorithm is employed for solving the pressure and velocity coupling. The discretization of pressure is based on the second order scheme, while the third-order MUSCL scheme is adopted for all the other variables. Non-uniform triangular grids are employed, and the boundaries are inflated with nodes tightly clustered near the walls to ensure that the y+ value for the first grid close to the walls is everywhere less than 1.
The modeling results presented in this paper are based on grids consisting of about 25,000–50,000 nodes and a time step size of 1 s. All the calculations start from initial conditions of zero velocity and uniform temperature. Within each time step, 20 iterations are executed. Three cases for grid and time-step dependence tests are compared in Table 1 and Figure 2. All the three cases are corresponding to 5/12 attic and R-20 ceiling insulation. It is clear that decreasing the time step to 0.5 s and requiring 40 iterations in each time step generate negligible difference in solutions. In addition, refinement of the grid by doubling the node numbers results in noticeable differences in velocity and temperature profiles, as shown in Figure 2, but the overall differences in the total mass flow rate () as well as ceiling cooling load (Qc) and roof heat gain (Qr) results are less than 2% (Table 1).
Since there is no comparable experimental data found in the literature for this kind of attic ventilation, the present numerical model is validated through a benchmark problem of mixed turbulent convection in a square cavity, which has been studied both experimentally [19] and numerically [19,20,21]. The mixed turbulent convective air flow within a 1.04 m × 1.04 m cavity is created by a horizontal plane wall jet entering from an inlet slot at the ceiling level together with a heated floor.

Table 1.
Summary of grid and time-step dependence tests for a 5/12 attic with R-20 ceiling insulation.
| Case | A | B | C |
|---|---|---|---|
| Total nodes | 26,508 | 26,508 | 53,430 |
| Total elements | 46,835 | 46,835 | 88,715 |
| Time step (s) | 1 | 0.5 | 1 |
| Iterations per time step | 20 | 40 | 20 |
| Qc (W/m) | 13.85555 | 13.85551 | 13.58413 |
| Qr (W/m) | 216.5511 | 216.5506 | 215.6445 |
| (kg/s m) | 0.00923552 | 0.00923555 | 0.00908235 |
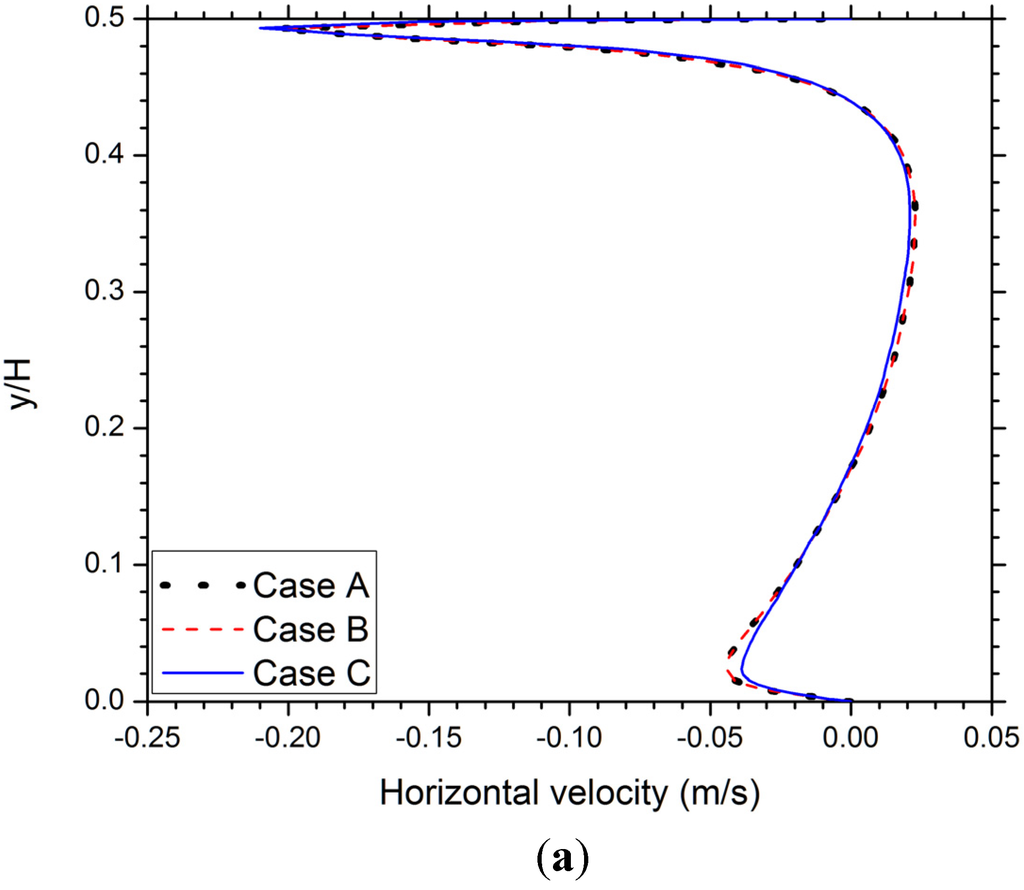
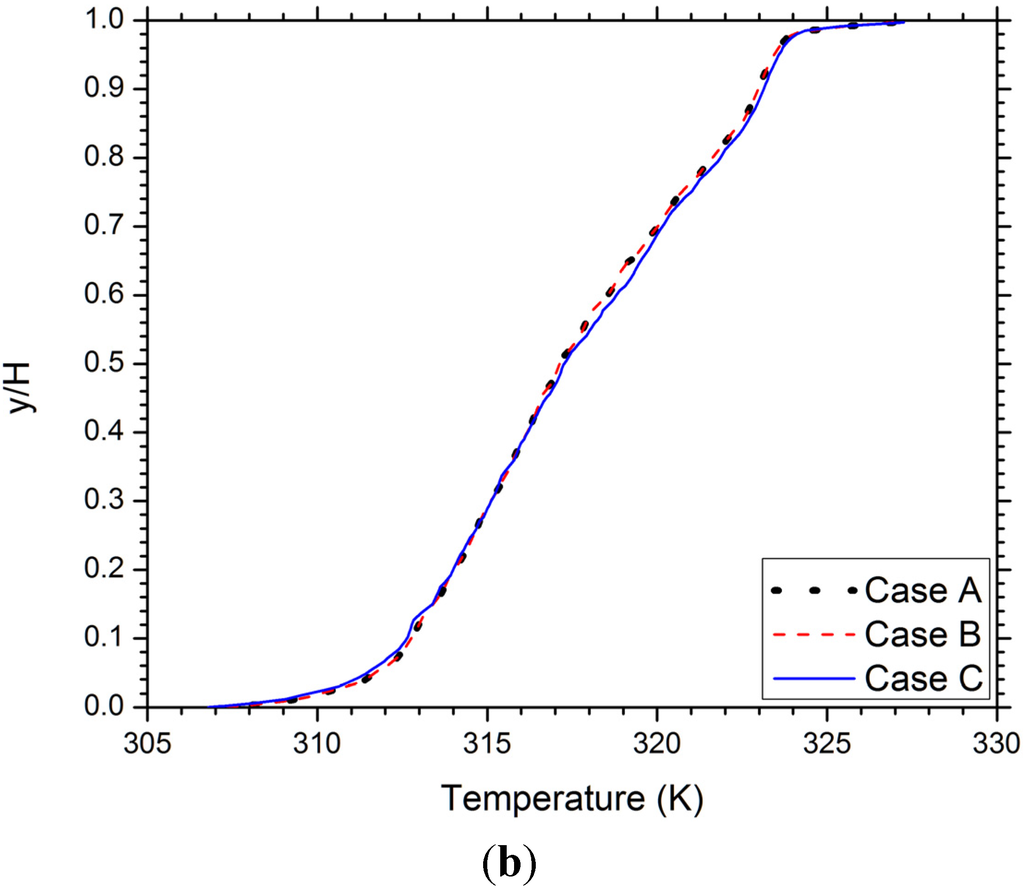
Figure 2.
Predicted profiles of (a) horizontal velocity along the vertical line x = 2 m and (b) temperature along the symmetric line x = 0 for gird and time-step dependence test cases defined in Table 1.
Subject to the experimentally measured boundary conditions [19], the predictions of the present model are shown in Figure 3 and Figure 4. The predicted mean velocity pattern shown in Figure 3c is very similar to that measured from the experiment (Figure 3a) [19] and that averaged from large eddy simulation (Figure 3b) [20], while the predicted profiles of velocity and temperature agree well with the experimental data, as shown in Figure 4.

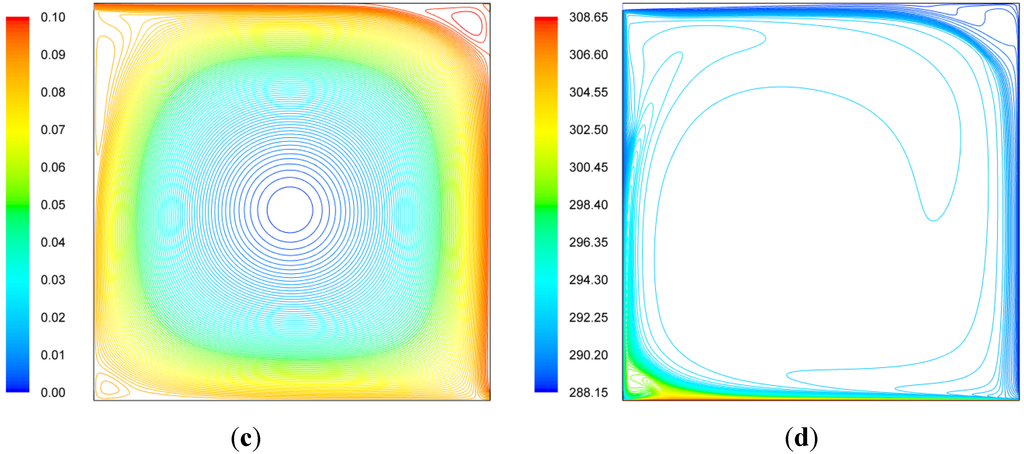
Figure 3.
Comparison of velocity distribution between (a) experimental measurement [19]; (b) large-eddy prediction [20]; and (c) present study (streamlines in kg/m·s), together with (d) the isotherms (in K) predicted by the present study, for the validation case of turbulent mixed convection in a square cavity.
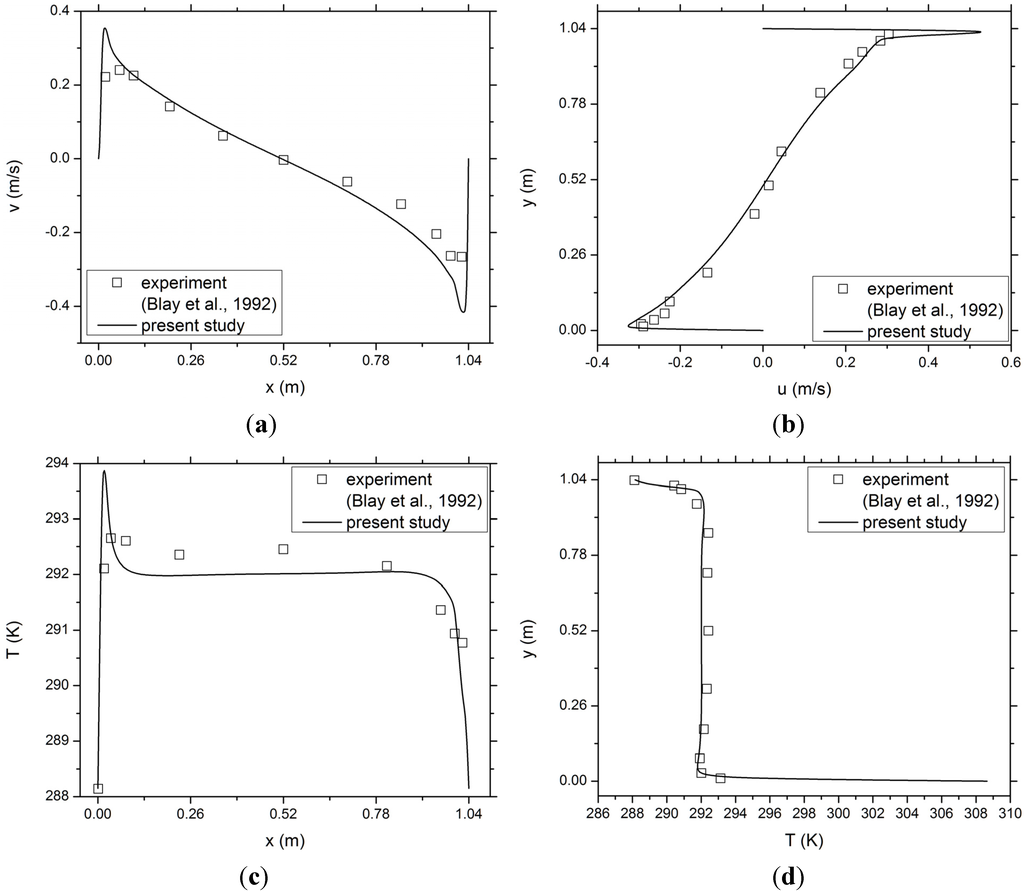
Figure 4.
Comparison of modeling predictions with experimental data for the validation case: (a) vertical velocity along the section of y = 0.502 m; (b) horizontal velocity along the section of x = 0.502 m; (c) temperature along the section of y = 0.502 m; (d) temperature along the section of x = 0.502 m.
3. Results and Discussion
In order to facilitate a parametric study of the effects of roof pitch and ceiling insulation on the cooling load, a total of 20 cases are calculated with five typical pitch values (3/12, 5/12, 8/12, 12/12, and 18/12), combined with four ceiling insulation levels (R-40, R-20, R-10, and R-1.2). The selected pitch values are typical in residential construction practice. Therefore, the results can be used to provide practical reference in attic and roof designs. For each case, the simulation converges to a steady solution after about 3500 time steps.
The predicted velocity and temperature distributions for the R-40, R-20, and R-10 cases exhibit quite similar patterns, thus only the results of the R-20 cases are presented in Figure 5 and Figure 6. The streamlines in Figure 5 show that the general patterns of the flow and temperature fields are essentially independent of the roof pitch variation. For all the roof pitch cases, the outside air enters from the soffit vent, travels along the roof bottom for a distance about 1/5 of the roof length, then follows two different paths. The mainstream of the ventilating air continues traveling along the roof bottom and leaves the attic from the ridge vent, while a portion of the ventilating air travels a “detoured” zigzag path bounded by three convection cells: A counterclockwise swirling cell near the soffit, a clockwise one occupying more than half of the attic space, and another counterclockwise one under the top portion of the roof. The temperature distributions shown in Figure 5 indicate that for all the pitch value cases, the thermal boundary layers develop along the roof and ceiling walls, and the attic space is dominated by thermal stratification, except for the soffit region.
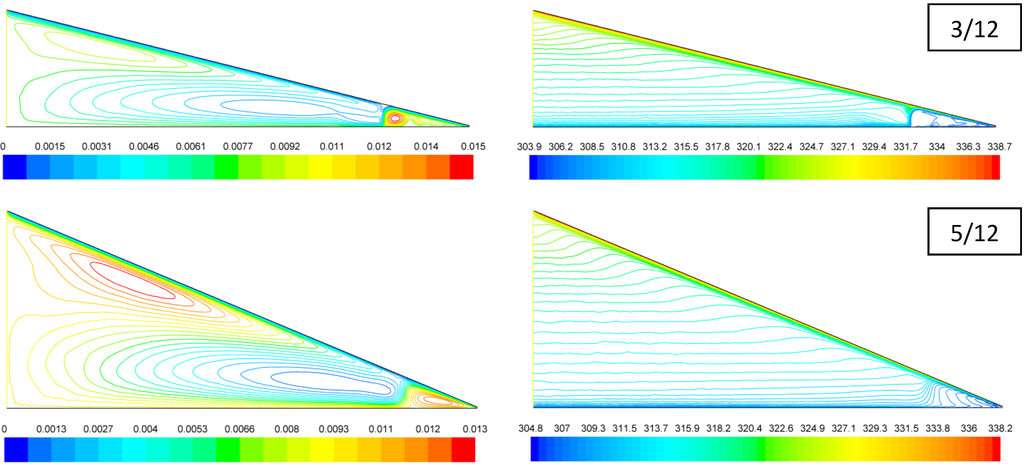
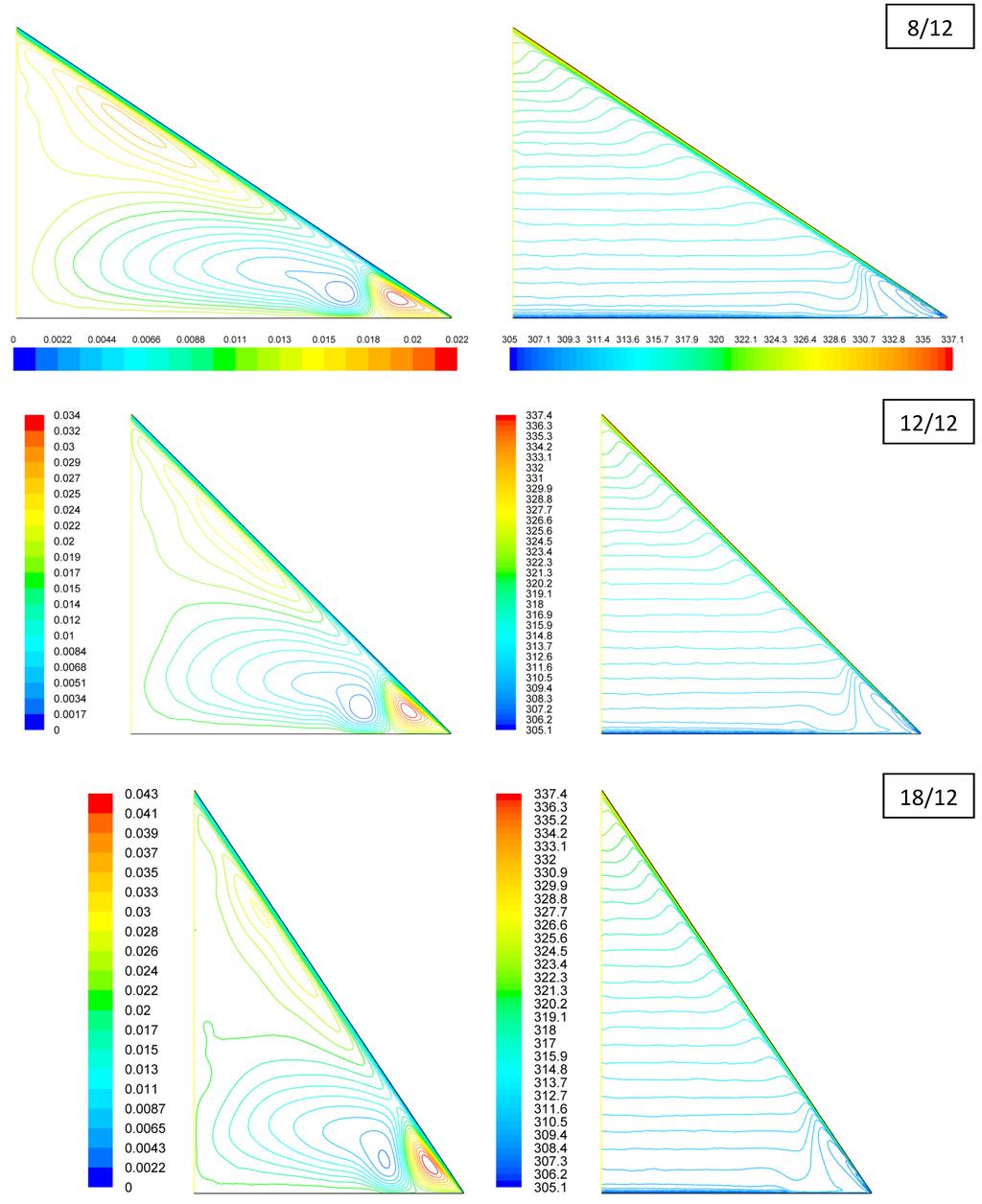
Figure 5.
Predicted (left) streamlines (in kg/m·s) and (right) isotherms (in K) for attics with R-20 ceiling insulation.
The predicted horizontal velocity profiles along the vertical line x = 2 m for the R-20 cases are shown in Figure 6(a). For each roof pitch case, since the vertical line cuts through two convection cells, the horizontal velocity changes directions at corresponding heights accordingly. The velocity peak under the roof is associated with the mainstream ventilating air flow, which has a much higher velocity than the air circulating within the two convection cells.
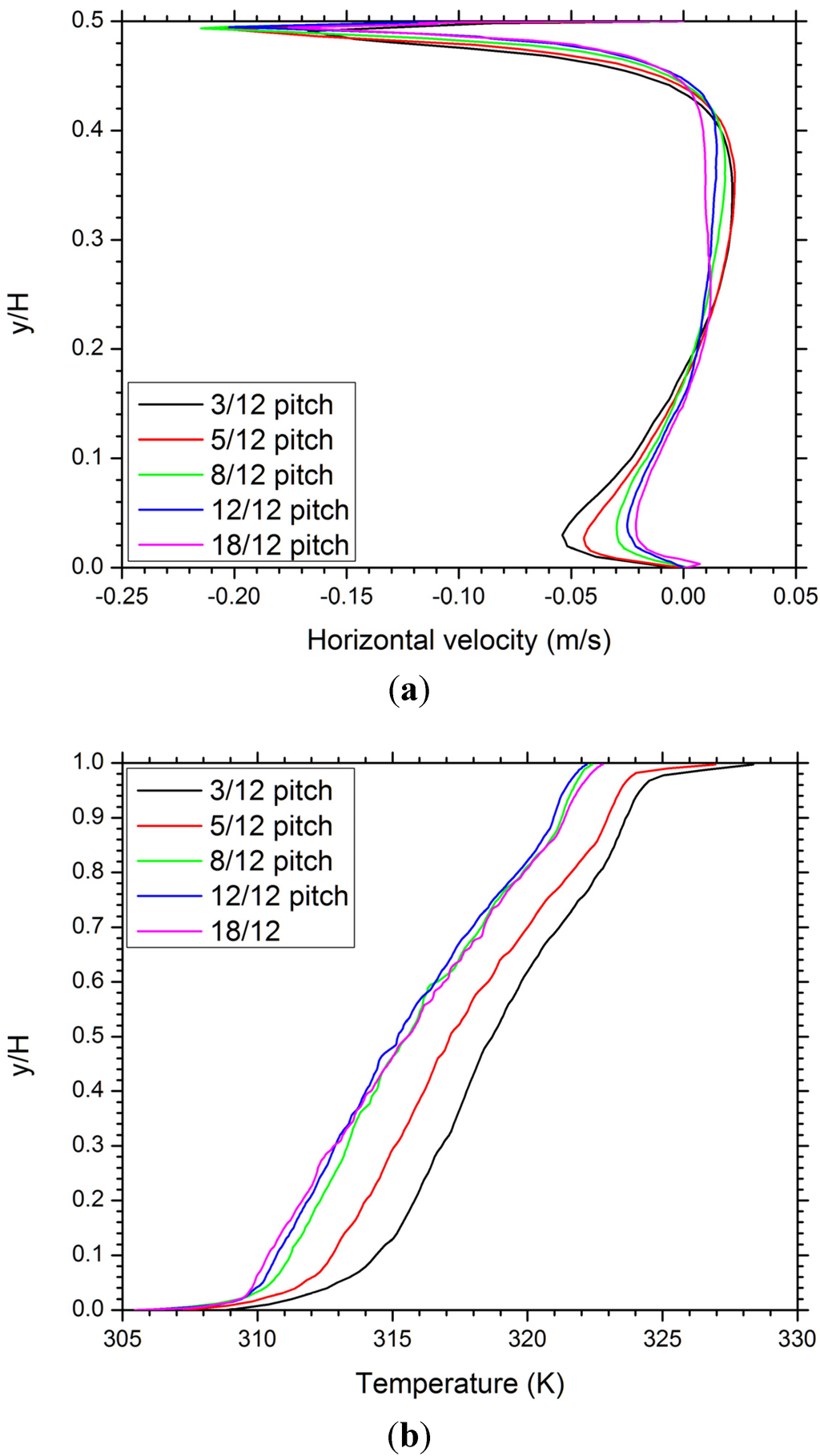
Figure 6.
Predicted profiles of (a) horizontal velocity along the vertical line x = 2 m and (b) temperature along the symmetric line x = 0 for attics with R-20 ceiling insulation.
The predicted temperature profiles along the symmetric line x = 0 for the R-20 cases are shown in Figure 6(b). For all the roof pitch cases, the temperature increases almost linearly with y/H, except in the regions near the soffit vent and ridge vent, where much greater temperature gradients indicate the effects of the ceiling and roof thermal boundary layers. It is also clear from the figure that the average attic temperature decreases with the increase of roof pitch from 3/12 to 8/12, but keeps essentially unchanged with roof pitch further increasing from 8/12 to 18/12. This result suggests that the overall cooling effect of the ventilating air (entering at 305.15 K) can be enhanced by increasing the roof pitch as long as it is less than 8/12. For pitches higher than 8/12, the attic ventilation seems reached a “saturated” state that further increasing the attic height gains very marginal cooling benefits. This finding is very useful in terms of providing quantitative guidance for roof and attic design and construction practitioner.
The predicted velocity and temperature distributions for R-1.2 cases are presented in Figure 7 and Figure 8. Although the basic patterns of the streamlines and isotherms shown in Figure 7 appear similar to those shown in Figure 5, some important differences exist. First, the ceiling-top temperatures are below the ambient temperature for all the R-1.2 cases but above the ambient temperature for all the R-20 cases, showing a direct consequence of the difference in ceiling insulation. At the R-1.2 insulation level, the ventilating air above the ceiling is cooled from below to a temperature lower than the ambient, as a result of the poor ceiling insulation. Second, the flow and temperature distributions in the soffit convection cell shown in Figure 7 are significant different from those in Figure 5. This may be explained by the most profound effect of the ceiling temperature and heat flux in the soffit region, as compared to other regions. Finally, from the streamline results of the 12/12 and 18/12 cases in Figure 7, an additional counterclockwise convection cell can be observed right above the ceiling wall. The horizontal velocity profiles along x = 2 m shown in Figure 8(a) indicate that such a cell also exists for the 8/12 case, although it is not captured by any streamlines in Figure 7. The temperature profiles along x = 0 in Figure 8(b) exhibit similar trends, as compared to Figure 6(b), except that the curves in Figure 8(b) all start from ceiling top temperatures lower than the ambient temperature.
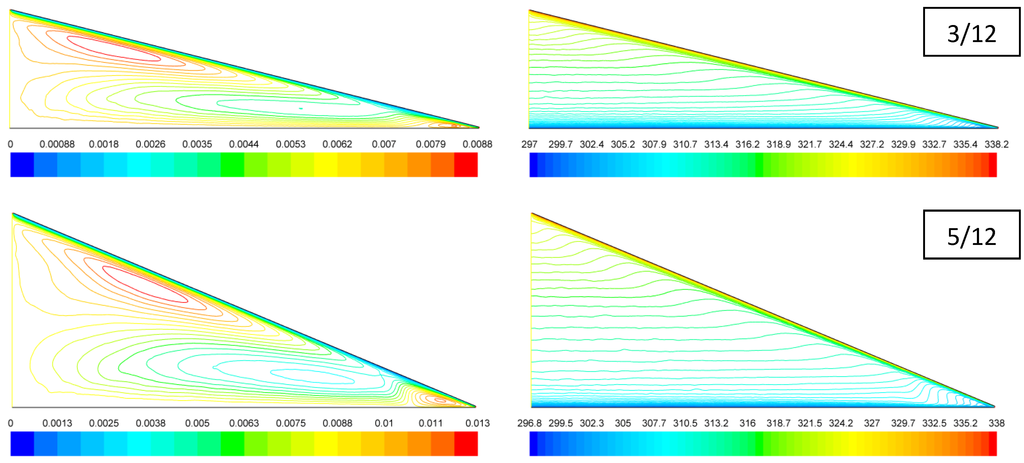
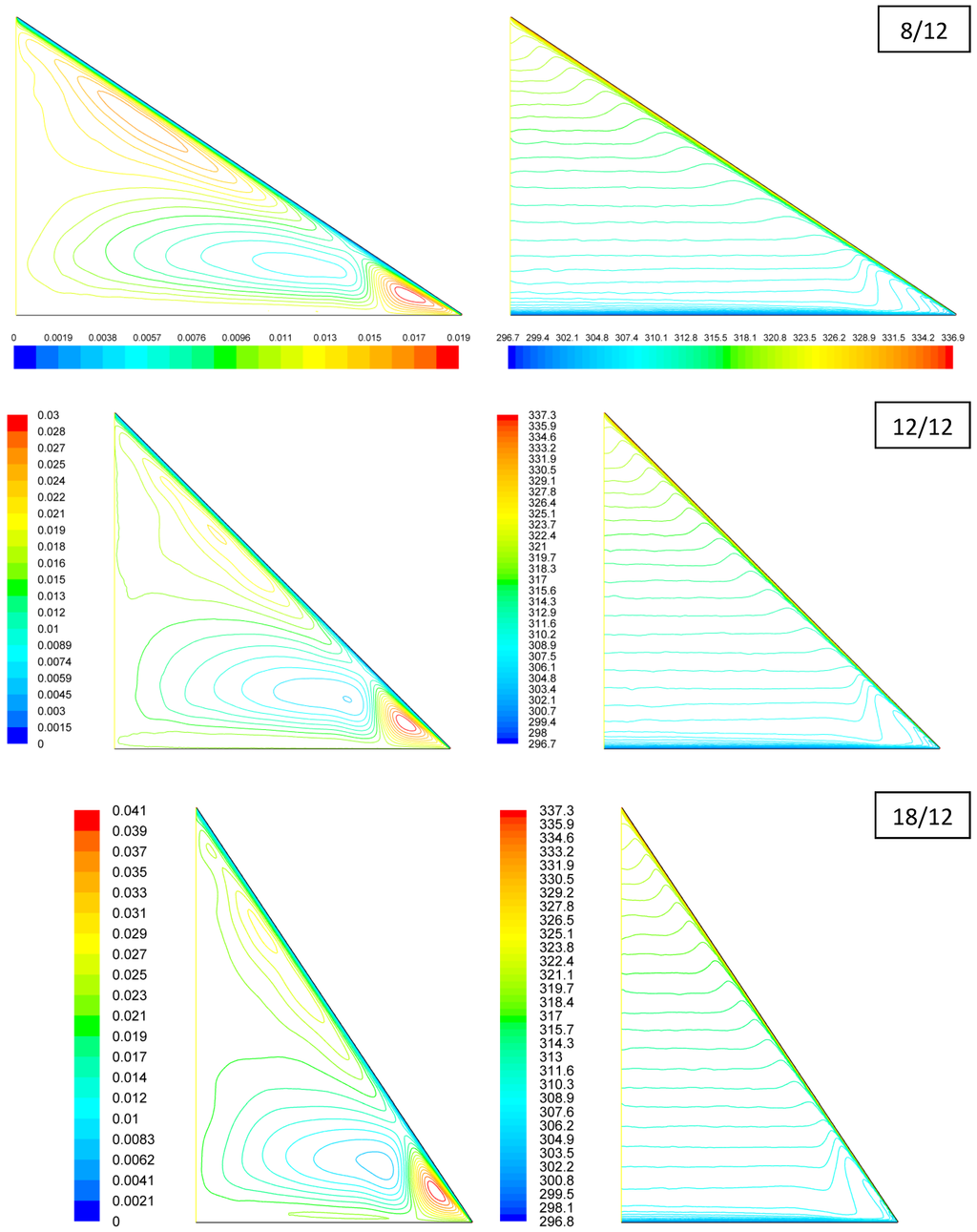
Figure 7.
Predicted (left) streamlines (in kg/m·s) and (right) isotherms (in K) for attics 3/12 with R-1.2 ceiling insulation.
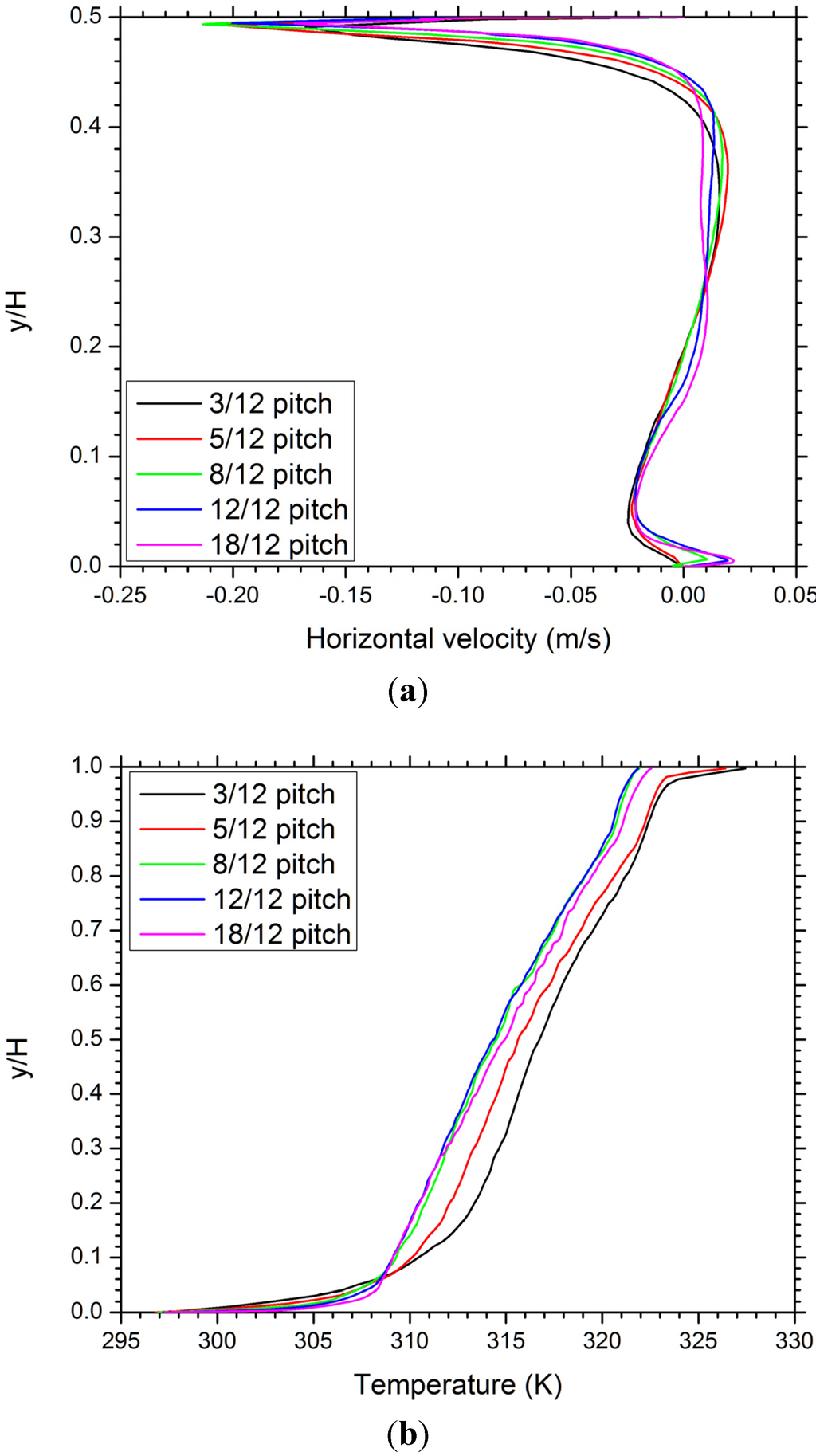
Figure 8.
Predicted profiles of (a) horizontal velocity along the vertical line x = 2 m and (b) temperature along the symmetric line x = 0 for attics with R-1.2 ceiling insulation.
The numerical results are summarized in Table 2, Table 3, Table 4 and Table 5 for the cases corresponding to R-40, R-20, R-10, and R-1.2, respectively. In these tables, the values for the heat loss to the ceiling (Qc), the heat gain from roof (Qr), and the ventilating mass flow rate () are direct modeling outputs.
The ceiling heat loss measures the attic cooling load and is directly related to the building energy performance. As evident in each of the tables, regardless of the ceiling insulation, the dependence of the roof heat gain and the ventilating flow rate on the roof pitch is remarkably different from that of the attic cooling load. As the roof pitch increases from 3/12 to 18/12, both the heat gain from the roof and the mass flow rate of the ventilating air increase by over 100%. On the other hand, the attic cooling load decreases by around 9% when the roof pitch increases from 3/12 to 8/12, and keeps essentially unchanged for roof pitches higher than 8/12. Such a dependence of the cooling load on the roof pitch shown in Table 2, Table 3, Table 4 and Table 5 is consistent with the average attic temperature results shown in Figure 6(b) and Figure 8(b), since a higher cooling load is a natural consequence of a higher attic air temperature.

Table 2.
Summary of numerical results for R-40 cases.
| Roof Pitch | 3/12 | 5/12 | 8/12 | 12/12 | 18/12 |
|---|---|---|---|---|---|
| Qc (W/m) | 8.14 | 7.92 | 7.61 | 7.57 | 7.39 |
| Qr (W/m) | 182.4 | 214.3 | 260.4 | 307.1 | 391.4 |
| (kg/s·m) | 0.0074 | 0.0094 | 0.0127 | 0.0154 | 0.0193 |
| Tct (K) | 309.5 | 309.1 | 308.6 | 308.5 | 308.2 |
| Tav (K) | 316.8 | 316.1 | 315.1 | 314.8 | 315.0 |
| Trb (K) | 335.5 | 333.8 | 331.4 | 328.9 | 324.5 |

Table 3.
Summary of numerical results for R-20 cases.
| Roof Pitch | 3/12 | 5/12 | 8/12 | 12/12 | 18/12 |
|---|---|---|---|---|---|
| Qc (W/m) | 14.22 | 13.86 | 13.18 | 13.11 | 12.75 |
| Qr (W/m) | 184.6 | 216.6 | 262.2 | 308.9 | 393.2 |
| (kg/s·m) | 0.0073 | 0.0092 | 0.0125 | 0.0153 | 0.0192 |
| Tct (K) | 307.7 | 307.4 | 306.8 | 306.7 | 306.4 |
| Tav (K) | 316.8 | 316.1 | 315.0 | 314.8 | 315.0 |
| Trb (K) | 335.4 | 333.7 | 331.3 | 328.8 | 324.4 |

Table 4.
Summary of numerical results for R-10 cases.
| Roof Pitch | 3/12 | 5/12 | 8/12 | 12/12 | 18/12 |
|---|---|---|---|---|---|
| Qc (W/m) | 22.46 | 21.69 | 20.49 | 20.30 | 19.62 |
| Qr (W/m) | 188.14 | 219.5 | 264.6 | 311.2 | 395.5 |
| (kg/s·m) | 0.0071 | 0.0091 | 0.0124 | 0.0151 | 0.0190 |
| Tct (K) | 305.0 | 304.7 | 304.2 | 304.1 | 303.8 |
| Tav (K) | 316.7 | 316.0 | 315.0 | 314.7 | 315.0 |
| Trb (K) | 335.2 | 333.6 | 331.2 | 328.7 | 324.3 |

Table 5.
Summary of numerical results for R-1.2 cases.
| Roof Pitch | 3/12 | 5/12 | 8/12 | 12/12 | 18/12 |
|---|---|---|---|---|---|
| Qc (W/m) | 45.11 | 43.04 | 40.85 | 40.77 | 40.21 |
| Qr (W/m) | 199.0 | 227.6 | 271.4 | 318.2 | 402.6 |
| (kg/s·m) | 0.0069 | 0.0086 | 0.0119 | 0.0145 | 0.0185 |
| Tct (K) | 297.5 | 297.4 | 297.3 | 297.3 | 297.3 |
| Tav (K) | 316.3 | 315.8 | 314.8 | 314.6 | 314.9 |
| Trb (K) | 334.6 | 333.1 | 330.8 | 328.3 | 323.9 |
A comparison between Table 2, Table 3, Table 4 and Table 5 indicates that the attic cooling load increases remarkably with the decrease of ceiling insulation. For the 5/12 pitch, for example, the cooling load increases by 75%, 170%, and 440%, respectively, as the ceiling insulation drops from R-40 to R20, R10, and R-1.2. In contrast to its control role on the cooling load, the ceiling insulation has a relatively weak influence on the roof heat gain and the ventilating flow rate. As the ceiling insulation decreases from R-40 to R-1.2, both the increase in the heat gain from the roof and the decrease in the mass flow rate of the ventilating air are less than 10%, regardless of the roof pitch. The general trend of the roof heat gain and the air flow rate depending on the ceiling insulation shown in the tables can be explained as follows. As the ceiling insulation decreases, the total thermal resistance of the roof-attic air-ceiling system decreases as well, this explains the predicted increase in the roof heat gain, since the total temperature difference across the roof-attic air-ceiling system is fixed to 50 K. However, since the decrease in the total thermal resistance is at a much lower percentage than that in the ceiling insulation decrease, the increased roof heat gain cannot compensate the increased ceiling heat loss, resulting in a decrease in the net heating to the ventilating air. This decreased heating effect explains the predicted decrease in the ventilating air flow rate along with the ceiling insulation decrease.
The average ceiling-top temperature (Tct) and the average roof-bottom temperature (Trb) listed in Table 2, Table 3, Table 4 and Table 5 are determined in terms of the ceiling thermal resistance (Rc) and the roof thermal resistance (Rr), respectively, i.e.:
whereas the average air temperature (Tav) is determined based on the overall energy balance of the attic air, i.e.:
Based on the temperature difference across the attic air, the Rayleigh number is defined by:
and used to characterize the ventilating mass flow. A log-log plot for the (, ) data is shown in Figure 9, which indicates that the - data points for the R-40, R-20, and R-10 cases can be approximately correlated by:
This empirical correlation, if corrected by a factor of about 0.88, may also provide an approximate estimate for the mass flow rates for the R-1.2 cases. In order to characterize the ceiling side heat transfer, the temperature difference between the attic air and the ceiling-top is used to define both the Rayleigh number and the Nusselt number , i.e.:
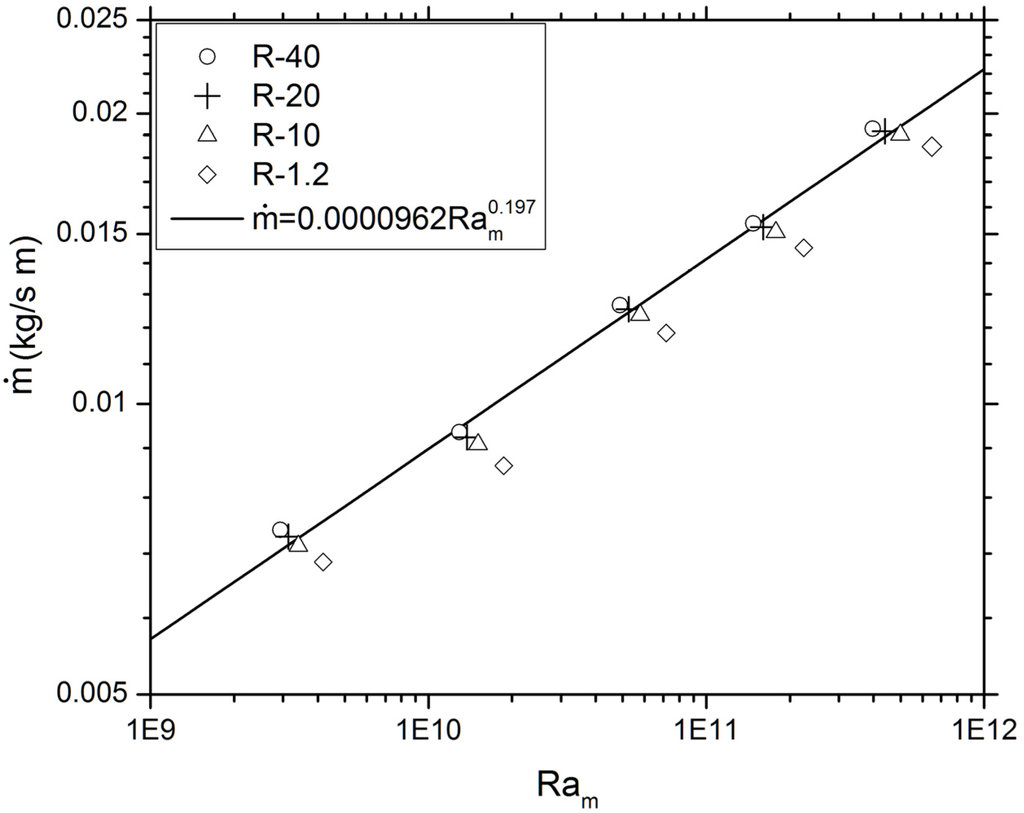
Figure 9.
Correlation for ventilating mass flow rate compared with numerical data.
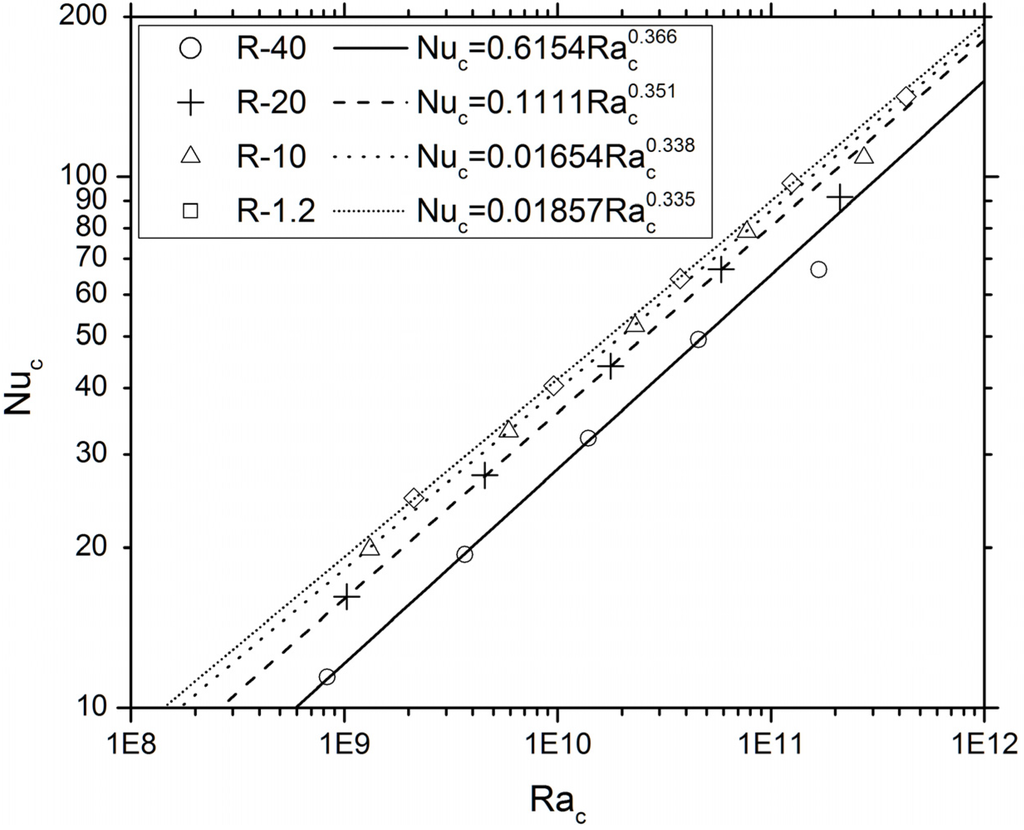
Figure 10.
Correlations for attic cooling load compared with numerical data.
A log-log plot for thus obtained (, ) data is shown in Figure 10. For each of ceiling insulation level, the − data points for the roof pitches between 3/12 and 12/12 distribute linearly on the plot, resulting in the following empirical correlations:
It is also implied that these empirical correlations need to be corrected for roof pitches higher than 12/12, since they systematically over predict the cooling loads for the 18/12 pitch cases.
4. Conclusions
In this study, the k-kl-ω transition model [12] is employed to simulate summer-time buoyancy-driven turbulent ventilation in triangular attics with coupled ridge and soffit vents. In particular, the impacts of roof pitch and ceiling insulation on the cooling load are investigated. The findings from the numerical results are summarized as follows:
- (1)
- Air flows in the attics are steady and exhibit a general streamline pattern that is qualitatively insensitive to the investigated variations of roof pitch and ceiling insulation.
- (2)
- For all the ceiling insulation levels investigated, the attic cooling load decreases by around 9% when the roof pitch increases from 3/12 to 8/12, and keeps essentially unchanged for roof pitches between 8/12 and 18/12. At the same time, along with the pitch increase, both the heat gain from the roof and the mass flow rate of the ventilating air increase by over 100%.
- (3)
- The attic cooling load increases remarkably with the decrease of ceiling insulation. For the 5/12 pitch, for example, the cooling load increases by 75%, 170%, and 440%, respectively, as the ceiling insulation drops from R-40 to R20, R10, and R-1.2. In the meantime, the heat gain from the roof increases by less than 10%, while the mass flow rate of the ventilating air decreases by less than 10%, regardless of the roof pitch. Therefore it is clear that ceiling insulation plays a dominant role in controlling cooling load of attic spaces in summer time, compared to ventilating factors.
- (4)
- Both the mass flow rate of the ventilating air and the cooling load of the attic can be satisfactorily correlated by simple relationships in terms of appropriately defined Rayleigh and Nusselt numbers.
In summary, these findings can provide practical scientific guidance for not only new residential roof and attic construction, but also energy retrofitting of existing residential buildings. For example, in residential construction practice, increasing roof pitch will lead to cost increase of roofs due to both roof material and labor cost increases. These cost increases can be significant with high pitch. At the same time, decreasing roof pitch to lower than 3/12 may lead to leakage issues and increased cooling load. So an optimal pitch design needs to consider many factors including attic airflow and cooling load as well as the dependence of solar radiation on roof pitch. For long time, construction practitioners have very little knowledge on how the roof pitches affect attic airflows and cooling loads. Therefore, the authors expect the findings, especially the identified correlations, will be of particular interest to building practitioners for optimizing roof/attic design using low-cost natural ventilation.
This research can be furthered by employing 3D numerical models to investigate the effects of gable walls for gable-roof buildings as well as roof-vent configurations other than continuous ridge and soffit vents.
Acknowledgments
This study was partially supported by the Faculty Seed Grants from the Durham School of Architectural Engineering and Construction at the University of Nebraska-Lincoln (2010–2011).
References
- Federal Housing Administration. Property Standards and Minimum Construction Requirements for Dwellings; Federal Housing Administration: Washington, DC, USA, 1942.
- Kamiyo, O.M.; Angeli, D.; Barozzi, G.S.; Collins, M.W.; Olunloyo, V.O.S.; Talabi, S.O. A comprehensive review of natural convection in triangular enclosures. Appl. Mech. Rev. 2010, 63, 1–13. [Google Scholar] [CrossRef]
- Saha, S.C.; Khan, M.M.K. A review of natural convection and heat transfer in attic-shaped space. Energy Build. 2011, 43, 2564–2571. [Google Scholar] [CrossRef]
- Medina, M.A.; O’Neal, D.L.; Turner, W.D. A transient heat and mass transfer model of residential attics used to simulate radiant barrier retrofits, Part I: Development. J. Sol. Energy Eng. 1998, 120, 32–38. [Google Scholar] [CrossRef]
- Medina, M.A.; O’Neal, D.L.; Turner, W.D. A transient heat and mass transfer model of residential attics used to simulate radiant barrier retrofits, Part II: Validation and simulations. J. Sol. Energy Eng. 1998, 120, 39–44. [Google Scholar] [CrossRef]
- Moujaes, S.F.; Alsaiegh, N.T. Numerical heat transfer attic model using a radiant barrier system. J. Sol. Energy Eng. 2000, 126, 32–51. [Google Scholar] [CrossRef]
- Wang, S.; Shen, Z.; Gu, L. Numerical simulation of buoyancy-driven turbulent ventilation in attic space under winter conditions. Energy Build. 2012, 47, 360–368. [Google Scholar] [CrossRef]
- Lien, S.J.; Ahmed, N.A. Numerical simulation of rooftop ventilator flow. Build. Environ. 2010, 45, 1808–1815. [Google Scholar] [CrossRef]
- Ahmed, N.A. Wind-Solar Driven Natural Electric Hybrid Ventilators. In Wind Power; Muyeen, S.M., Ed.; InTech: Rijeka, Croatia, 2010; pp. 537–558. [Google Scholar]
- Lien, J.; Ahmed, N.A. Wind Driven Ventilation for Enhanced Indoor Air Quality. In Chemistry, Emission Control, Radioactive Pollution and Indoor Air Quality; Mazzeo, N., Ed.; InTech: Rijeka, Croatia, 2011; pp. 539–562. [Google Scholar]
- Lien, S.J.; Ahmed, N.A. Effect of inclined roof on the airflow associated with a wind driven turbine ventilator. Energy Build. 2011, 43, 358–365. [Google Scholar] [CrossRef]
- Walters, D.K.; Cokljat, D. A three-equation eddy-viscosity model for Reynolds-averaged Navier-Stokes simulations of transitional flow. J. Fluid Eng. 2008, 130, 1–14. [Google Scholar] [CrossRef]
- Ozoe, H.; Mouri, A.; Ohmuro, M.; Churchill, S.W.; Lior, N. Numerical calculations of laminar and turbulent natural convection in water in rectangular channels heated and cooled isothermally on the opposing vertical walls. Int. J. Heat Mass Transf. 1985, 28, 125–138. [Google Scholar] [CrossRef]
- Henkes, R.A.W.M.; Van der Vlugt, F.F.; Hoogendoorn, C.J. Natural-convection flow in a square cavity calculated with low-Reynolds-number turbulence models. Int. J. Heat Mass Transf. 1991, 34, 377–388. [Google Scholar] [CrossRef]
- Henkes, R.A.W.M.; Hoogendoorn, C.J. Scaling of the turbulent natural convection flow in a heated square cavity. J. Heat Transf. 1994, 116, 400–408. [Google Scholar] [CrossRef]
- Hsieh, K.J.; Lien, F.S. Numerical modeling of buoyancy-driven turbulent flows in enclosures. Int. J. Heat Fluid Flow 2004, 25, 659–670. [Google Scholar] [CrossRef]
- Talabi, S.O.; Olunloyo, V.O.S.; Kamiyo, O.M.; Collins, M.W.; Karayiannis, T.G. Flow Field and Reynolds Stress Distribution in Low Turbulence Natural Convection in A Triangular Cavity. In Proceedings of Fifth International Symposium on Turbulence, Heat and Mass Transfer, Dubrovnik, Croatia, 2006; pp. 511–514.
- ANSYS FLUENT 13.0. ANSYS, Inc.: Canonsburg, PA, USA, 2011.
- Blay, D.; Mergui, S.; Niculae, C. Confined turbulence mixed convection in the presence of a horizontal buoyant wall jet. ASME Heat Trans. Division 1992, 213, 65–72. [Google Scholar]
- Zhang, W.; Chen, Q. Large eddy simulation of natural and mixed convection airflow indoors with two simple filtered dynamic subgrid scale models. Numer. Heat Transf. A 2000, 37, 447–463. [Google Scholar] [CrossRef]
- Zhang, Z.; Zhang, W.; Zhai, Z.; Chen, Q. Evaluation of various turbulence models in predicting airflow and turbulence in enclosed environments by CFD: Part 2—Comparison with experimental data from literature. HVAC R Res. 2007, 13, 871–886. [Google Scholar] [CrossRef]
© 2012 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license ( http://creativecommons.org/licenses/by/3.0/).