Abstract
In this paper, a high step-down interleaved buck coupled-inductor converter (IBCC) with active-clamp circuits for wind energy conversion has been studied. In high step-down voltage applications, an IBCC can extend duty ratio and reduce voltage stresses on active switches. In order to reduce switching losses of active switches to improve conversion efficiency, a IBCC with soft-switching techniques is usually required. Compared with passive-clamp circuits, the IBCC with active-clamp circuits have lower switching losses and minimum ringing voltage of the active switches. Thus, the proposed IBCC with active-clamp circuits for wind energy conversion can significantly increase conversion efficiency. Finally, a 240 W prototype of the proposed IBCC with active-clamp circuits was built and implemented. Experimental results have shown that efficiency can reach as high as 91%. The proposed IBCC with active-clamp circuits is presented in high step-down voltage applications to verify the performance and the feasibility for energy conversion of wind turbines.
1. Introduction
Limited fossil energy and serious greenhouse effect have forced most engineers to research renewable energy sources. The typical renewable energy sources include solar, wind and geothermal energy, which have the features of cleanliness, freedom from maintenance and abundance []. Therefore, the development of renewable and clean energy sources to substitute for fossil fuels has been an important topic. Currently, wind is one of most widely utilized renewable energies. The wind turbine technology has been undergoing a dramatic development and now is the world’s fastest growing energy form []. However, due to the instability and intermittent characteristics of wind energy, it cannot provide a constant or stable power output. Thus, the power processor usually adopts a dc/dc converter as its energy processing system [,,].
In wind energy conversion, most dc/dc converters are usually provided a low output voltage (24 Vdc or 12 Vdc) and high output current to load. Therefore, a conventional interleaved buck converter (IBC) as shown in Figure 1 is widely adopted, because it has a simple structure, high output current density and low output current ripple. However, in high step-down voltage applications, it suffers from extremely short duty ratio and high component stresses, resulting in low conversion efficiency [,,,]. To alleviate these limitations, the IBCC is proposed, as shown in Figure 2 (where n1 and n11 are primary and secondary winding turns of coupled inductor L1, n2 and n22 are primary and secondary winding turns of coupled inductor L2). A coupled inductor has a simple winding structure, and it can extend duty ratio and reduce peak primary winding current. Thus, a coupled inductor based on converter is relatively attractive. Although the IBCC can yield high step-down voltage ratios, its leakage inductance (Lk1 and Lk2) of coupled inductors not only increases voltage stresses on the active switches but induces significant switching losses too. To overcome these problems, the IBCC with passive-clamp circuits, as shown in Figure 3, it can recover the leakage energy and reduce voltage stresses of active switches, but the active switches are still operated in a hard-switching manner during turn-on transition [,,,].
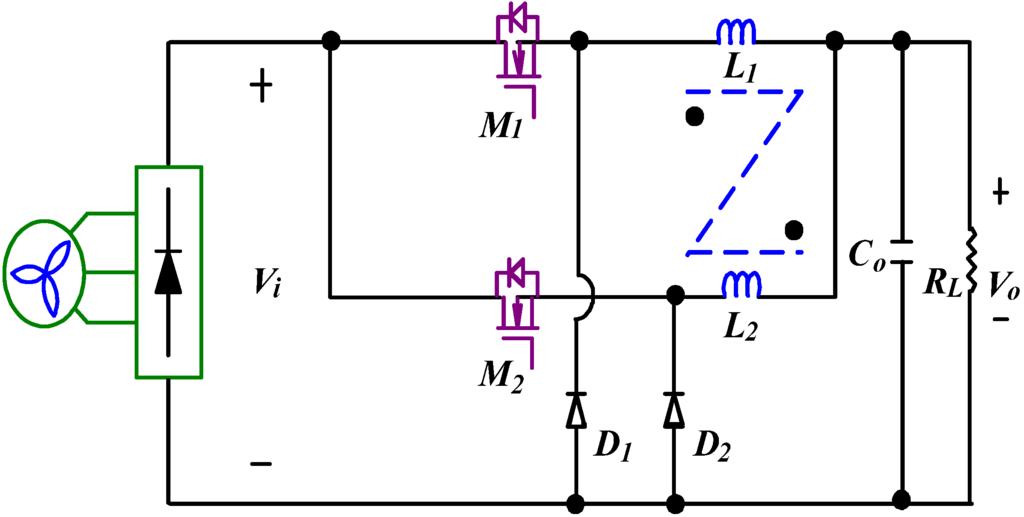
Figure 1.
Topology of conventional IBC for wind turbine applications.
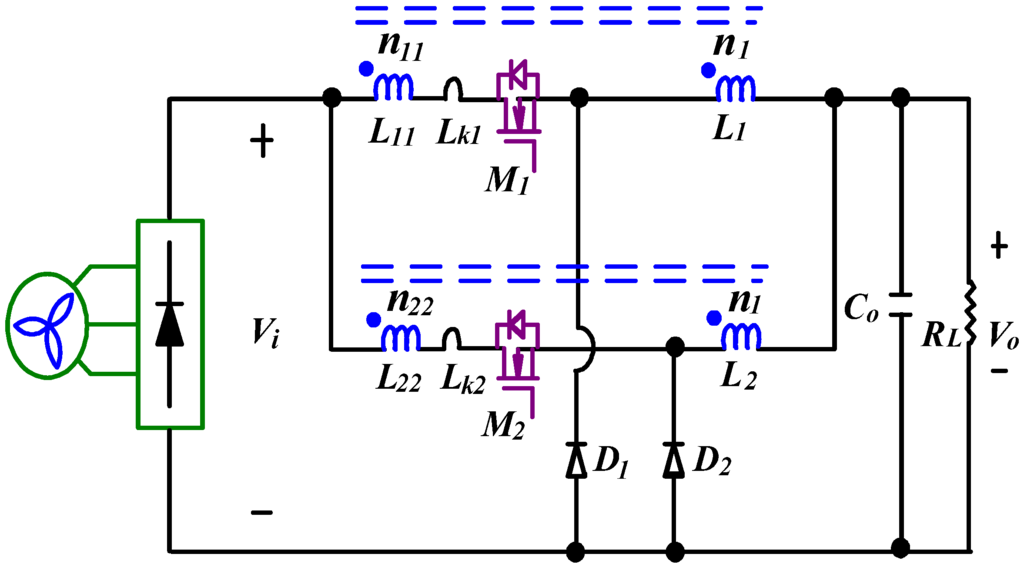
Figure 2.
Topology of the IBCC for wind turbine applications.
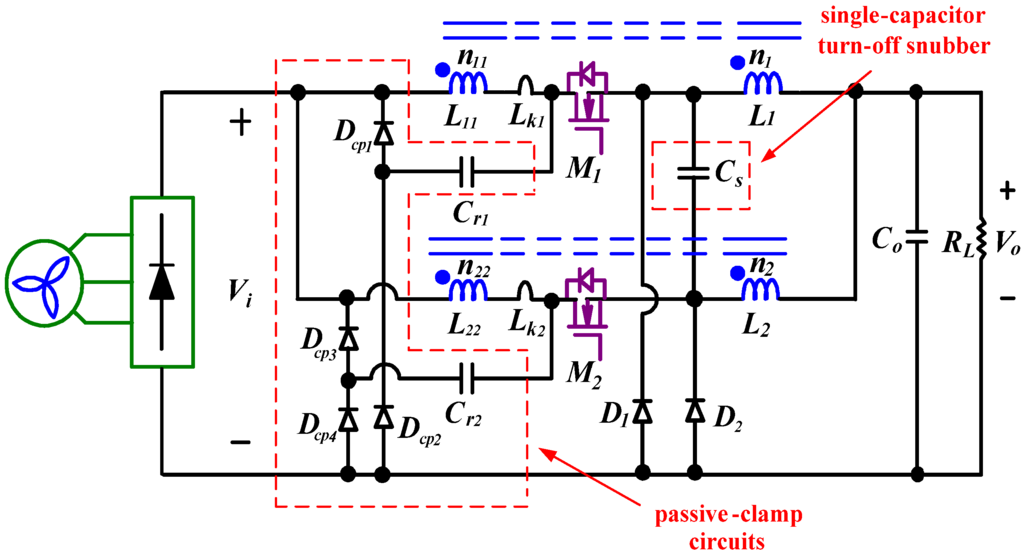
Figure 3.
Topology of IBCC with passive-clamp circuits for wind turbine applications.
In this paper, the IBCC with active-clamp circuits is proposed, as shown in Figure 4. The active-clamp circuits can implement zero-voltage switching (ZVS) of active switches during turn-on transition and recycle the energy trapped in leakage inductance of coupled inductors.
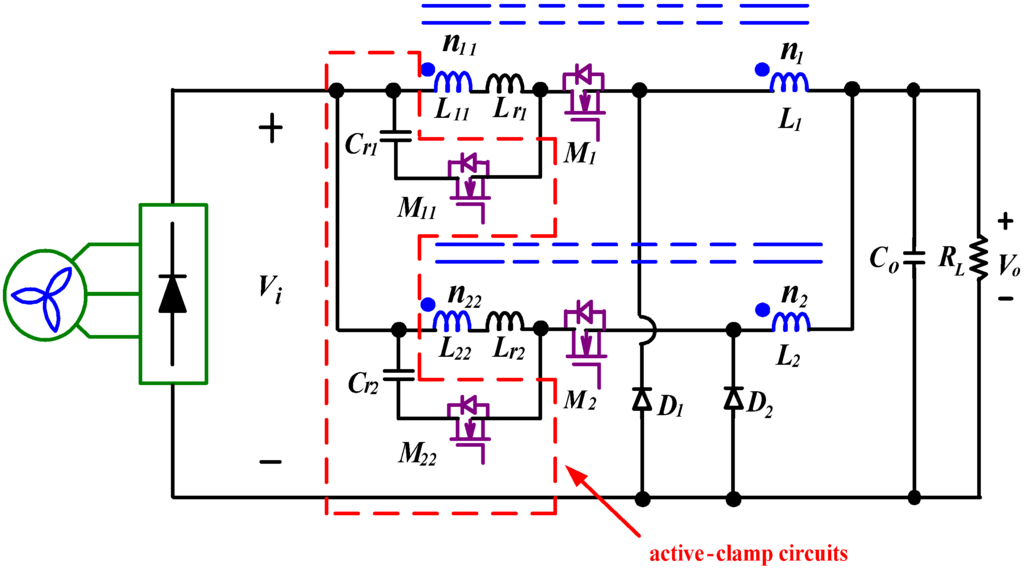
Figure 4.
Topology of IBCC with active-clamp circuits for wind turbine applications.
Therefore, the conversion efficiency can be improved significantly. In Figure 4, to achieve a zero-voltage switching (ZVS) feature at turn-on transition for both main switches (M1 and M2) and auxiliary switches (M11 and M22), the extra resonant inductors (Lr1 and Lr2) are usually required. In particular, the resonant inductors can also limit the rate of decrease of the free-wheeling diode currents at turn-off transition, reducing reverse-recovery losses a lot and further improving conversion efficiency [,,,,,].
2. Selection of Active-Clamp Circuit
The active-clamp circuits discussed in this study can be selected as two circuits, in which one is a flyback-type clamp circuit, as shown in Figure 5, and the other is a boost-type clamp circuit, as shown in Figure 6.
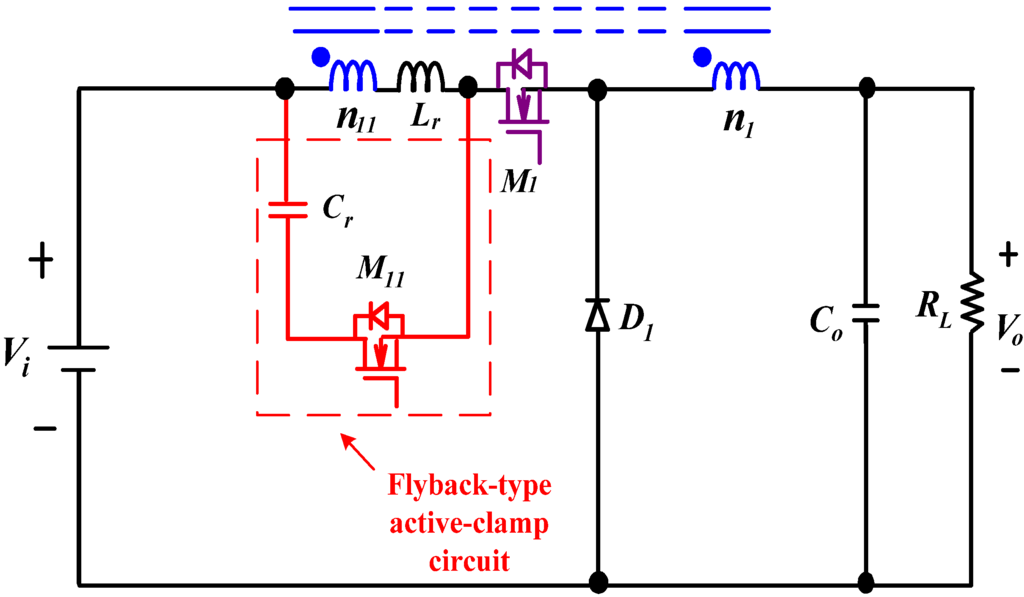
Figure 5.
Topology of IBCC with flyback-type active-clamp circuit.
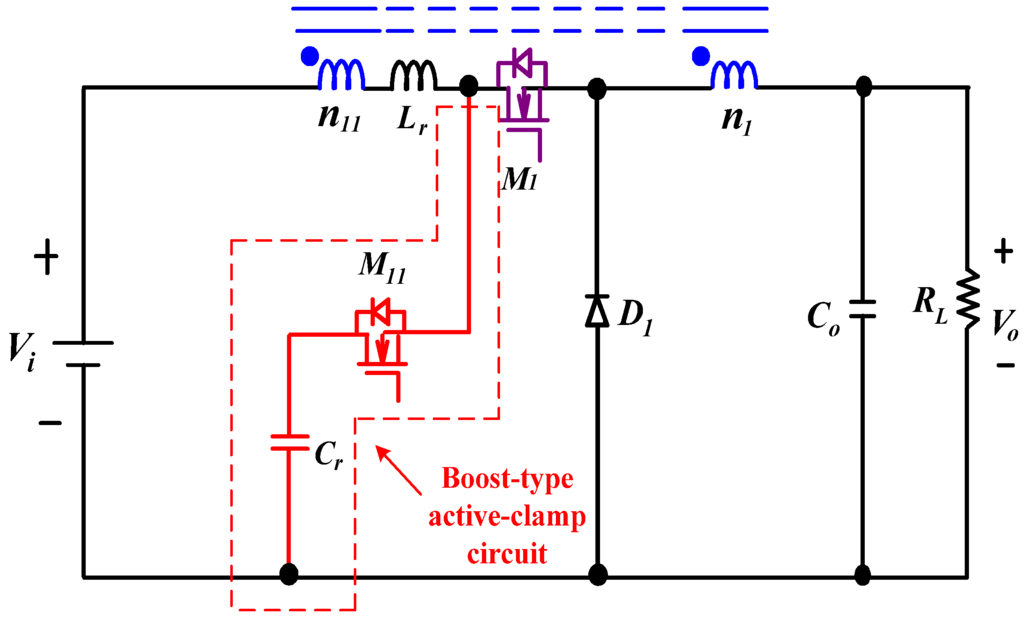
Figure 6.
Topology of IBCC with boost-type active-clamp circuit.
In Figure 5, by volt-second balance law, the voltage of the clamp capacitor Vcr(flyback) can be expressed as:
where Vi is input voltage and D is duty ratio of main switch M1. Similarly, In Figure 6, the voltage of the clamp capacitor Vcr(boost) can be expressed as:
From Equations (1) and (2), we can see that voltage stress of the flyback-type clamp circuit is less than that of the boost-type one, making the flyback-type clamp circuit more attractive. In this study, only the flyback-type clamp is considered due to its obvious advantages. Thus, the IBCC with flyback-type clamp circuits, as shown in Figure 4, is proposed.
3. Operational Principle
The proposed IBCC (Figure 4) mainly includes two sets of coupled inductors L1, L2, main switches M1, M2, auxiliary switches M11, M22, resonant inductors Lr1, Lr2, clamp capacitors Cr1, Cr2 and free-wheeling diodes D1, D2. In order to analyze the ZVS feature of the main and auxiliary switches (M1, M2, M11 and M22), their stray capacitors (CM1, CM2, CM11 and CM22) will be considered at the steady-state operation of the circuit, as shown in Figure 7. In Figure 7, each set of the coupled inductors can be treated as a transformer with two magnetizing inductors. Its turns ratio is defined as:
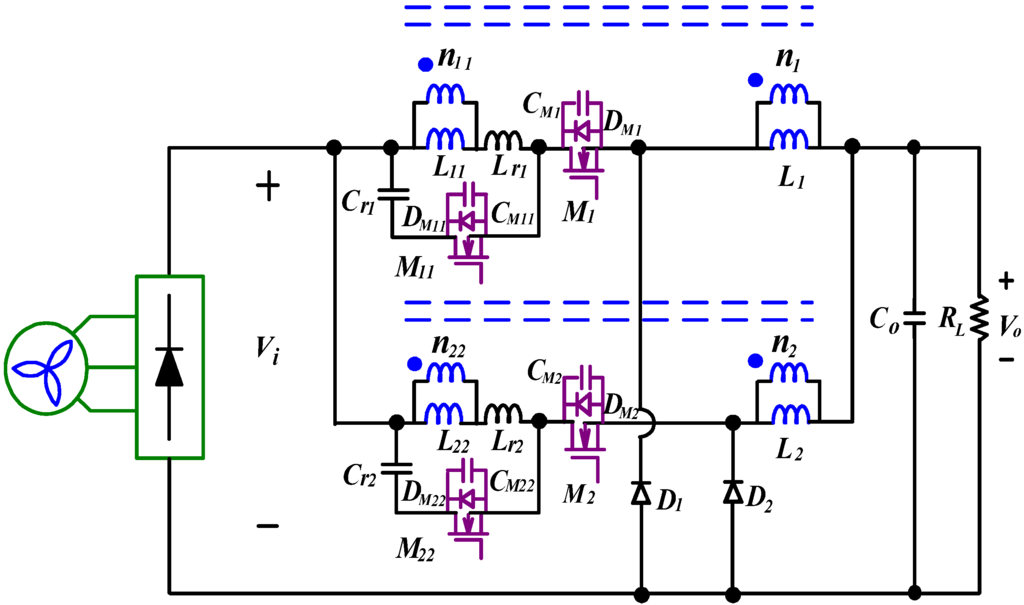
Figure 7.
The proposed IBCC with active-clamp circuits for wind turbine applications.
The following assumptions are made over one switching cycle:
- (1)
- clamp capacitors Cr1, Cr2 and output filter capacitor Co are large enough so that the voltages across them are constant over a switching period,
- (2)
- winding and turns of coupled inductors (L1 and L2) are identical, and
- (3)
- all semiconductor components are ideal, except the MOSFETs (M1, M2, M11 and M22).
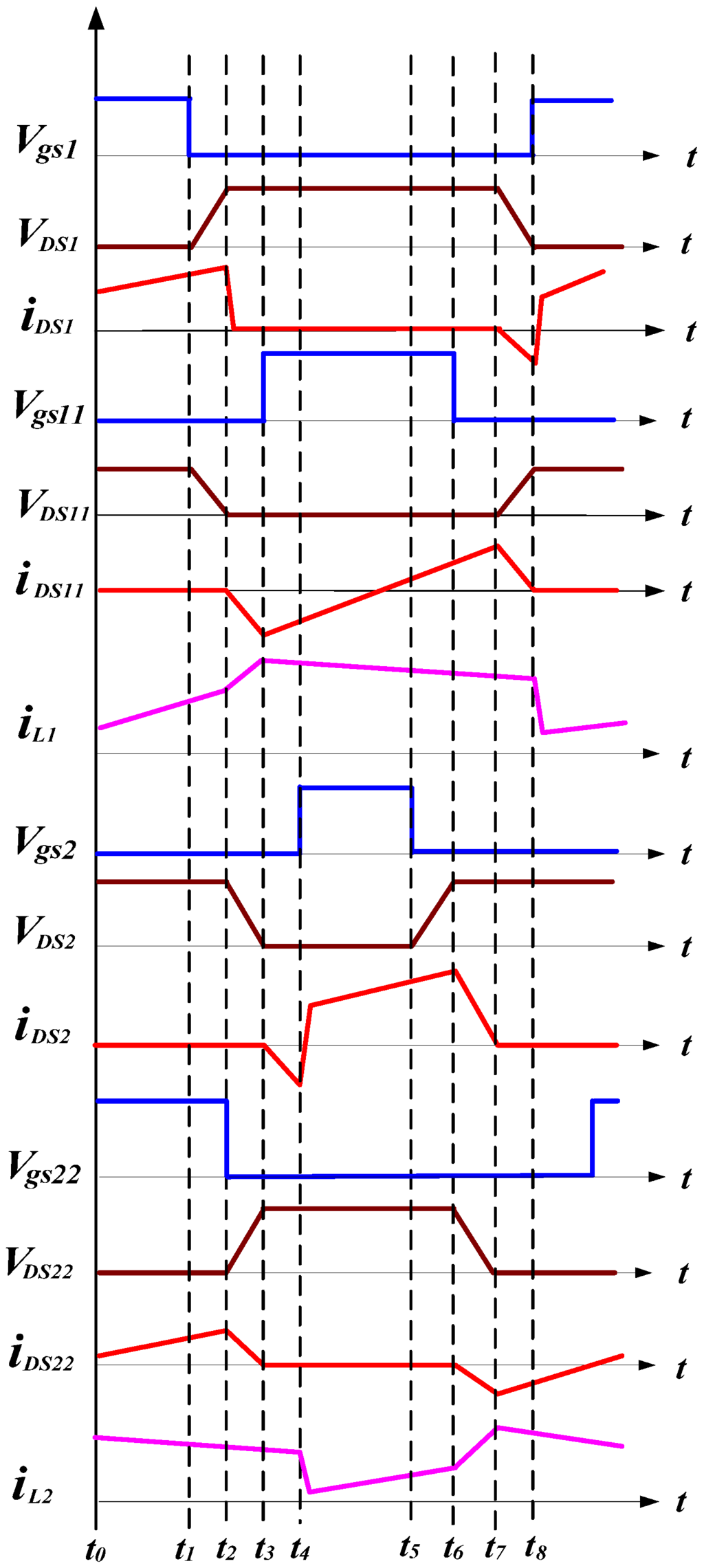
Figure 8.
Key waveforms of the IBCC with active-clamp circuits.
Under continuous inductor current operation, eight major operating modes are identified over one switching cycle. Figure 8 shows conceptual voltage and current waveforms of its key components and Figure 9 shows equivalent circuits of its operational modes:
In this mode, main switch M1 and auxiliary switch M22 are turned on. Inductor current iL1 flowing through the path Vi-L11-Lr1-M1-L1 to the load is linearly increased. Clamping capacitor Cr2 begins releasing its stored energy by coupled-inductor L2 and L22 transferring to the load.
At time t = t1, main switch M1 is turned off, resonant inductor Lr1 releases energy to stray capacitance CM1 of M1 and stray capacitance CM11 of M11 with a resonant manner. When time t = t2, stray capacitance CM1 of M1 will be charged toward to (Vi + nVo) while stray capacitance CM11 of M11 will be discharged down to zero. To achieve a ZVS feature for auxiliary switch M11, the energy stored in resonant inductor Lr1 should satisfy the following inequality:
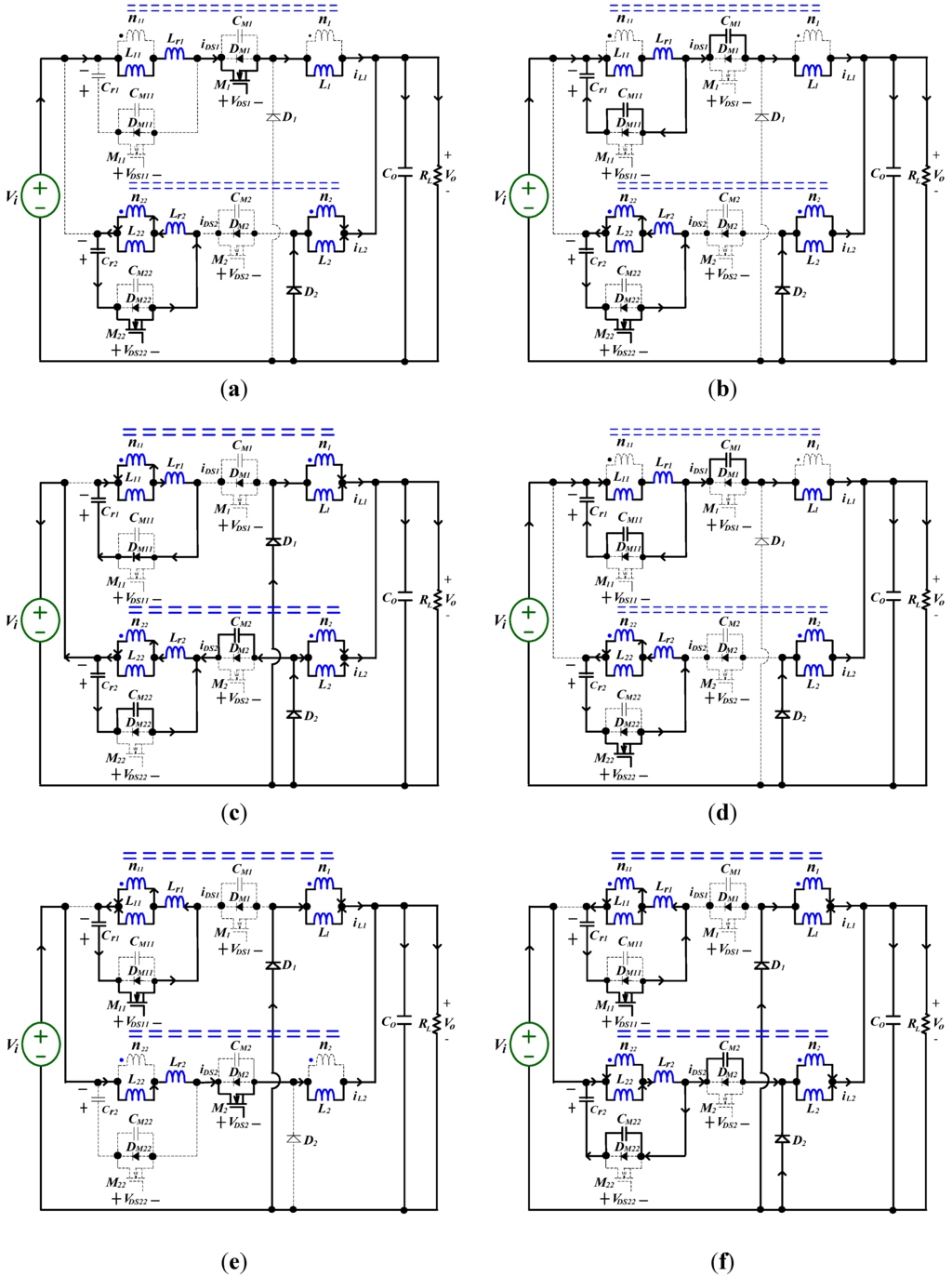
Figure 9.
Equivalent circuit modes of the IBCC with active-clamp circuits operating over one switching cycle. (a) Mode 1 [t0 ≤ t < t1]; (b) Mode 2 [t1 ≤ t < t2]; (c) Mode 3 [t2≤ t < t3]; (d) Mode 4 [t3 ≤ t < t4]; (e) Mode 5 [t4 ≤ t < t5]; (f) Mode 6 [t5 ≤ t < t6]; (g) Mode 7 [t6 ≤ t < t7]; (h) Mode 7 [t7 ≤ t < t8].
At time t = t2, voltage VDS11 of M11 is dropped to zero and VDS1 of M1 is reached to Vi + nVo. Main switch M1 is turned off and free-wheeling diode D1 is turned on. Current iDS11 forces the body diode DM11 of M11 conducting to create a ZVS operation for M11. In this mode, inductor current iL1 begins decreased through free-wheeling diode D1 to the load. The inductor currents iL1 and iL2 can be expressed as follows:
and :
During this interval, the energy trapped in the resonant inductor Lr1 is recycled to clamp capacitor Cr1. Due to the clamp capacitance of Cr1 being large enough, voltage VCr1 will keep constant.
When auxiliary switch M22 is turned off at time t2, resonant inductor Lr2 resonates with CM2 and CM22. Stray capacitance CM22 of M22 will be charged toward to VCr2 + [n/(1 + n)](Vi − Vo), while stray capacitance CM2 of M2 will be discharged down to zero. To achieve a ZVS feature for main switch M2, the energy trapped in resonant inductor Lr2 should satisfy the following inequality:
At time t = t3, auxiliary switch M11 is turned on under ZVS condition. When voltage VDS2 of M2 is dropped to zero and VDS22 of M22 is reached to VCr2 + [n/(1 + n)](Vi − Vo) , auxiliary switch M22 is turned off and current iDS2 forces the body diode DM2 of M2 conducting to create a ZVS operation for M2. In this mode, inductor current iL1 and iL2 are continuously decreased through free-wheeling diode D1 and D2 to the load.
At time t = t4, main switch M2 is turned on under ZVS condition and free-wheeling diode D2 is turned off. Inductor current iL2 flowing through the path of Vi-L22-Lr2-M2-L2 to the load is linearly increased, and inductor current iL1 continuously flowing through the path of Vo-D1-L1 is linearly decreases, which can be expressed as follows:
and:
At time t = t5, main switch M2 is turned off, resonant inductor Lr2 releases energy to stray capacitance CM2 of M2 and stray capacitance CM22 of M22 with a resonant manner. When time t = t6, the stray capacitance CM2 will be charged toward to (Vi + nVo), while stray capacitance CM22 will be discharged to zero. To achieve a ZVS feature for main switch M22, the energy stored in resonant inductor Lr2 should satisfy the following inequality:
At time t = t6, voltage VDS22 of M22 is dropped to zero and voltage VDS2 of M2 is reached to (Vi + nVo), main switch M2 is turned off and free-wheeling diode D2 is conducted. Current iDS22 forces the body diode DM22 of M22 conducting and to create a ZVS operation for auxiliary switch M22. In this mode, inductor current iL2 begins decreased through free-wheeling diode D2 to the load. The inductor currents iL1 and iL2 can be expressed as follows:
and:
The energy trapped in the resonant inductor Lr2 is recycled to clamp capacitor Cr2. Since the clamping capacitor of Cr2 is large enough, voltage Vcr2 will keep constant.
At time t = t7, voltage VDS1 of M1 is dropped to zero and voltage VDS11 of M1 is reached to (Vi + nVo), main switch M11 is turned off. Current iDS1 forces the body diode DM1 of M1 conducting and to create a ZVS operation for main switch M1. When main switch M1 starts conducting again at the end of mode 8, the converter operation over one switching cycle is completed.
4. Feature Analysis
The proposed IBCC with active-clamp circuits can extend duty ratio of the active switches and reduce component stress. This section describes the feature analysis and efficiency estimation for the proposed IBCC. The feature analysis includes voltage gain, duty ratio, and voltage stress of free-wheeling diode:
4.1. Voltage Gain and Duty Ratio
From the key waveforms of the converter shown in Figure 8 and by applying the volt-second balance law, the voltage gain and duty ratio can be derived as:
and:
where D is the duty ratio of the main switch (M1 or M2), respectively.
For example, input voltage Vi = 150–250 Vdc and output voltage Vo = 12 Vdc are considered. From Equations (13) and (14), we can sketch a set of curves showing the relationship between duty ratio D and voltage gain of Vo/Vi for different values of turns ratio n, as illustrated in Figure 10.
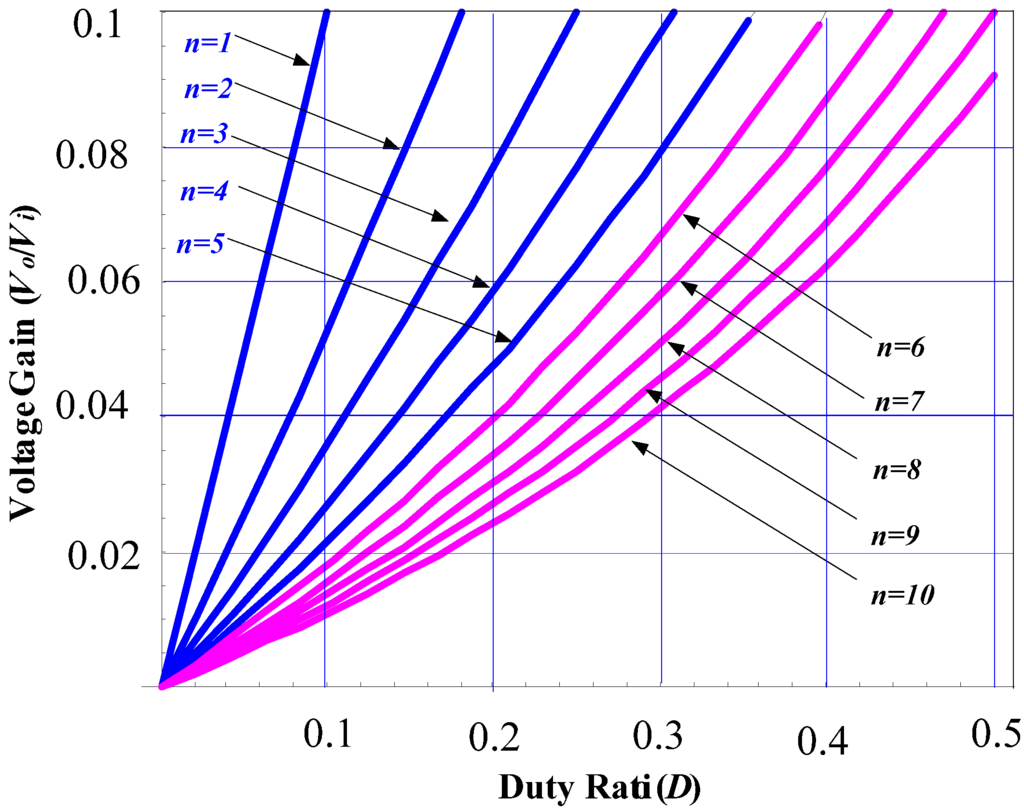
Figure 10.
Plots of Vo/Vi versus duty ratio D.
4.2. Voltage Stress of Free-Wheeling Diode and Active Switch
According to description of Mode 2, the voltage stress of the free-wheeling diodes (D1 and D2) and active switches (M1 and M2) can be derived as:
and
From Equations (15) and (16), we can sketch a set of curves showing the free-wheeling diode voltage stress versus turns ratio n under different input voltages, as shown in Figure 11.
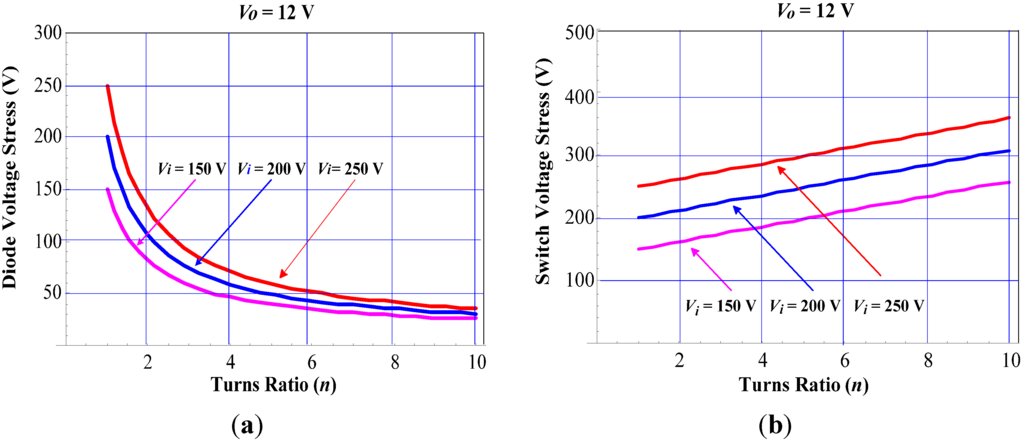
Figure 11.
Plots of voltage stress versus turns ratio n of the coupled inductor. (a) free-wheeling diodes (D1 and D2); (b) active switches (M1 and M2).
To objectively judge the merits of the proposed converter, performance comparison between the proposed converter and the IBC is shown in Figure 12. From these plots, it can be seen that the proposed IBCC yields higher duty ratio and lower diode voltage stress over the IBC.
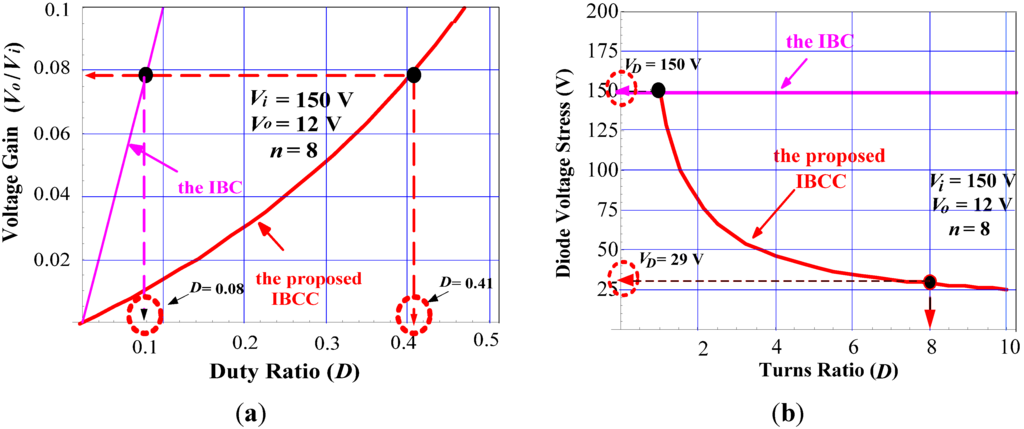
Figure 12.
Performance comparison between the IBCC and the IBC. (a) Duty ratio; (b) voltage stress of the free-wheeling diode.
5. Power Losses Estimation and Experimental Results
To verify the performance of the proposed IBCC with active-clamp circuits is higher than that of the IBCC with passive-clamp circuits, a 240 W prototype of the proposed converter was designed and built, as shown in Figure 7. Its specifications are listed as follows:
- Input voltage: 150–200 Vdc;
- Output voltage: 12 Vdc;
- Maximum output current:20 A;
- Switching frequency: 75 kHz.
As followed are the design considerations, power losses estimation and experimental results for the proposed IBCC with active-clamp circuits.
5.1. Design Considerations of Key Components
A larger duty ratio D corresponds to a larger coupled-inductor turns ratio n, which results in a lower voltage stress on free-wheeling diodes D1 and D2. In order to accommodate variations of loads, a proper turns ratio n of the coupled inductors is needed. From Figure 10, we can obtain a proper coupled-inductor turns ratio n = 8. Its maximum duty ratio is Dmax ≈ 0.41 under input voltage Vi = 150 Vdc and minimum duty ratio is Dmin ≈ 0.34 under input voltage Vi = 200 Vdc.
5.1.1. Design of the Coupled Inductors
Once the coupled-inductor turns ratio n = 8 is selected, the maximum duty ratio can be determined as Dmax ≈ 0.41. The maximum current ripple of the coupled inductors is designed with iL(ripple) = iL1(ripple) = iL2(ripple) = 10 A, and coupled inductance L = L1 = L2 can be determined as:
where fs is the switching frequency of the active switches. Coupled inductance L = 3 μH is selected in the design. When the turns ratio n = (n1 + n2)/n1 is equal to 8, the coupled inductance L11 = L22 can be determined as:
From TDK datasheets, we choose an optimum ferrite material PC40 and maximum flux Bmax = 200 mT, maximum winding factor Kw(max) = 0.4 and maximum current density Jmax = 400 A/cm2. Thus, the area product of the core can be determined as:
where Wa is the window area of the core, Ae is the effective cross-section area of the core, Po is the output power of the converter and η denotes the efficiency. From TDK datasheets, we select a proper size of core ETD-39 (Ae = 1.25 cm2, Wa = 2.57 cm2, Ve = 11.5 cm3 and AL = 3150 nH/N2) to reduce winding current density and core temperature.
By applying Faraday’s law, turns (n11 or n22) of the coupled inductor (L11 or L22) can be determined as:
In this design, n11 is chosen as 35 turns. From turns ratio of the coupled inductors, n = (n1 + n11)/n1, the turns (n1 or n2) of the coupled inductance (L1 or L2) can be correspondingly determined as:
5.1.2. Selection of Power Switches and Diodes
According to Equations (15) and (16), the maximum voltage stresses imposed on both free-wheeling diodes D1 and D2 is:
and both active switches M1 and M2 are:
When active switch M1 or M2 is turned on, the maximum switch current iDS(max) can be given as:
when free-wheeling diode D1 or D2 is conducting, the maximum diode current iD(max) can be given as
Selection of switching devices M1 and M2 involves a trade-off between conduction loss and switching loss. The selection of MOSFETs with low Rds(on) will reduce conduction loss, but it will result in high parasitic capacitance. Switches with lower Rds(on) also imply larger die size and higher cost. For this application, we can select the proper MOSFETs as the IRFP460, which provide high enough safety margins with a drain-source breakdown voltage of 500 V. Several important parameters of the IRFP460 are listed as follows:
VDSS = 500 V, Rds(on) = 0.27 Ω, Coss = 870 pF and ID = 20 A
According to (22)~(25), with the selection of free-wheeling diodes D1 and D2, a 40 A/60 V Schottky diode which has the lowest forward voltage drop can be employed. The Schottky diode manufactured by International Rectifier is 40CPQ60 with a maximum dc reverse voltage VRRM = 60 V and a forward voltage drop VF(max) = 0.47 V, which is a good choice for D1 and D2, was chosen.
5.1.3. Consideration of ZVS Condition
To achieve the ZVS feature for all of the active switches (M1, M2, M11 and M22) at turn-on transition, the IBCC is necessary to store enough energy in resonant inductor (Lr1 or Lr2). Because the voltage across main switch (M1 or M2) is larger than that across auxiliary switch (M11 or M22). Thus, the ZVS condition for all of the active switches is determined as follows:
where Δi is the peak current of the coupled inductors, and it can be expressed as:
(Note: In the analysis of ZVS condition for the proposed converter, the resonant inductor is expressed as Lr = Lr1 = Lr2, the clamp voltage of clamp capacitor Vcr = Vcr1 = Vcr2 and the stray capacitor of the active switch is expressed as CM1 = CM2 and CM11 = CM22).
According to (26), we can plot the curves showing the relationships between resonant inductor Lr and output current Io for different values of input voltage Vi, as illustrated in Figure 13. From Figure 13, a proper value of resonant inductor Lr should be selected for achieving ZVS feature.
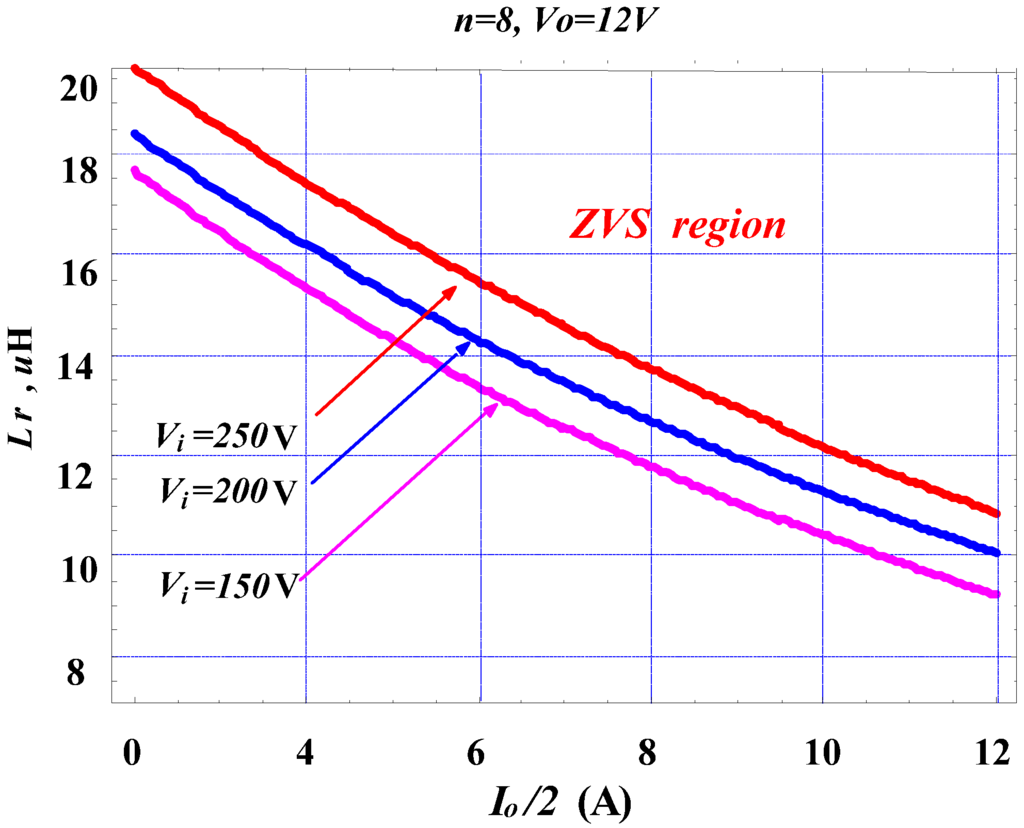
Figure 13.
Plots of resonant inductor Lr versus output current Io for different values of input voltage Vi.
5.2. Power Losses Estimation
Power losses of the proposed converter are estimated to verify the measured efficiency. The key component values of the experimental converter are shown in Figure 14, from which power losses are evaluated as follows:
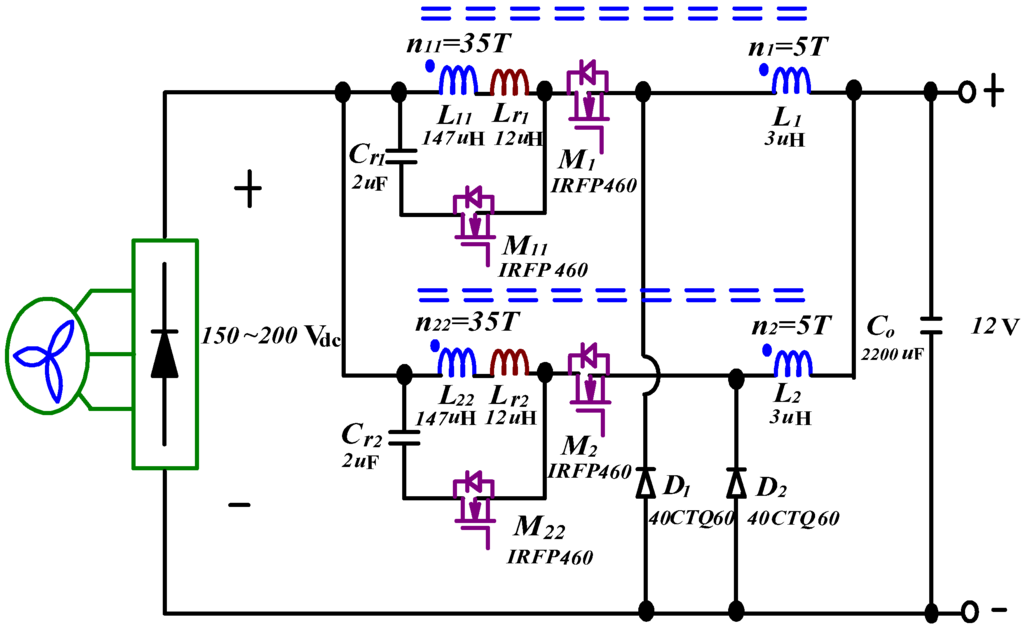
Figure 14.
Experimental circuit of the IBCC with active-clamp circuits.
5.2.1. Main Switches (M1 and M2)
The main switches of the proposed converter are designed to achieve ZVS during turn-on transition, so that their switching losses can be negligible. Only the conduction losses are taken into account in the estimation. Conduction losses of the main switches can be determined from their switch current iDS and channel resistance Rds(on). In the proposed converter, the MOSFETs used are IRFP460, and their channel resistance Rds(on) = 0.27 Ω. In the proposed converter, the maximum duty ratio Dmax = 0.41 and switch current iDS(max) = 9.1 A. Thus, total power losses of the main switches can be determined as:
5.2.2. Auxiliary Switches (M11 and M22)
The auxiliary switches of the proposed converter are also designed to achieve ZVS at turn-on transitions, so that their switching losses can also be neglected. Thus, total power losses of the auxiliary switches is determined as:
5.2.3. Free-Wheeling Diodes (D1 and D2)
The free-wheeling diodes are selected as 40CPQ60 Schottky diodes, and their forward voltage drop VF = 0.47 V. Thus, total conduction losses of the free-wheeling diodes can be determined as:
5.2.4. Coupled Inductors (L1 and L2)
According to the datasheets of the TDK Company, the cores of the coupled inductors are designed as PC-40 ETD-39 and maximum flux Bmax = 200 mT. Their total winding turns are ntotal = (n1 + n11) = 40, primary winding turns are np = n1 = 5, and the turns ratio is n = ntotal/np = 8. Thus, from Figure 15, we can obtain the core losses per volume, PCoup(cv) = 0.2 W/cm3 at 60 °C. The core loss will be:
According to measurement, the winding resistance of the coupled inductors is RCoup = 28 mΩ, and the copper losses can be estimated as:
Total power loss of the coupled inductors is therefore:
Power losses under full load condition on the key components are summarized in Table 1. The estimated efficiency of the proposed converter with the active-clamp circuits at input voltage Vi = 150 Vdc, and full-load condition is:
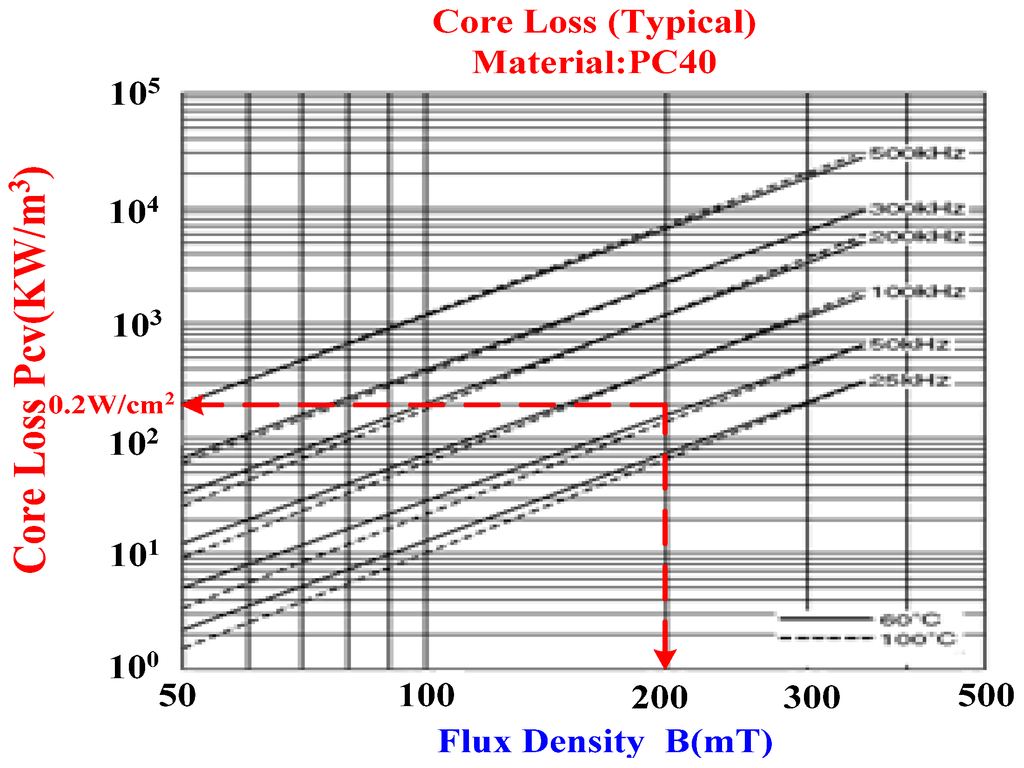
Figure 15.
Typical core loss data of the TDK PC-40.

Table 1.
Efficiency estimation of the proposed IBCC with active-clamp circuits.
| Components | Power Loss Calculation | Power Losses |
|---|---|---|
| Main switch (M1 and M2) | 6 W | |
| Auxiliary switch (M11 and M22) | 8.8 W | |
| Freewheel diode (D1 and D2) | 4.8 W | |
| Coupled inductor (L1 and L2) | 10.2 W | |
| Total power losses | 29.8 W | |
| Efficiency estimation | 89% |
5.3. Experimental Results
Figure 16 shows simulated and experimental voltage and current waveforms of the main switch (M1 or M2), from which it can be seen that the main switch has ZVS features during the turn-on transition. Figure 17 shows simulated and experimental voltage and current waveforms of the auxiliary switch (M11 or M22). It can be also seen that the auxiliary switch has ZVS feature during turn-on transition. Figure 18 shows simulated and experimental inductor current waveforms of coupled inductor (iL1 and iL2). Figure 19 shows measured current and voltage waveforms of the free-wheeling diode (D1 or D2), from which it can be seen that the proposed IBCC with active-clamp circuits can limit the rate of decrease of the free-wheeling diode current, reducing reverse-recovery losses a lot. Figure 20 shows measured output voltage and current waveforms. Figure 21 shows efficiency measurements of the IBCC with active-clamp circuits, from which it can be seen that the maximum efficiency can reach as high as 91%. It can increase efficiency about 2% over the IBCC with passive-clamp circuits (as shown in Figure 3). The reason behind is that the active switches of IBCC with passive-clamp circuits are still operated in a hard-switching manner during turn-on transition.
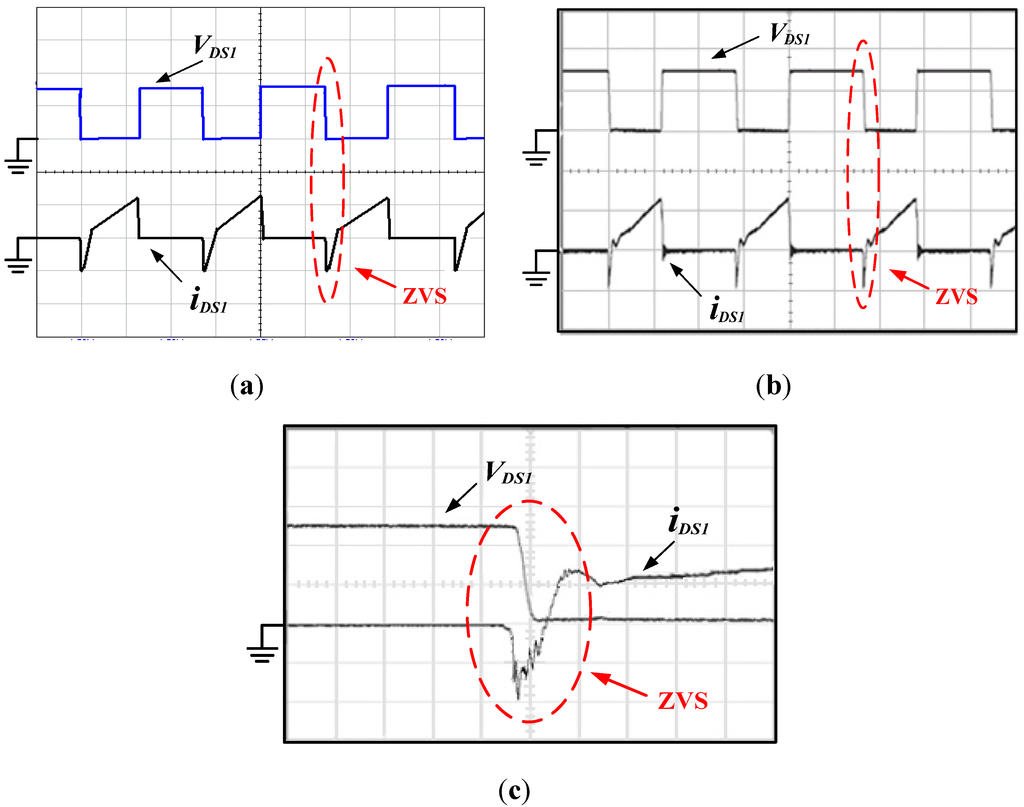
Figure 16.
Voltage and current waveforms of main switches (M1 or M2). (a) simulated results (VDS1: 200 V/div; iDS1: 10 A/div; Time: 5 μs/div); (b) experimental results (VDS1: 200 V/div; iDS1: 10 A/div; Time: 5 μs/div); (c) its expanded waveforms (VDS1: 100 V/div; iDS1: 5 A/div; Time: 0.5 μs/div).
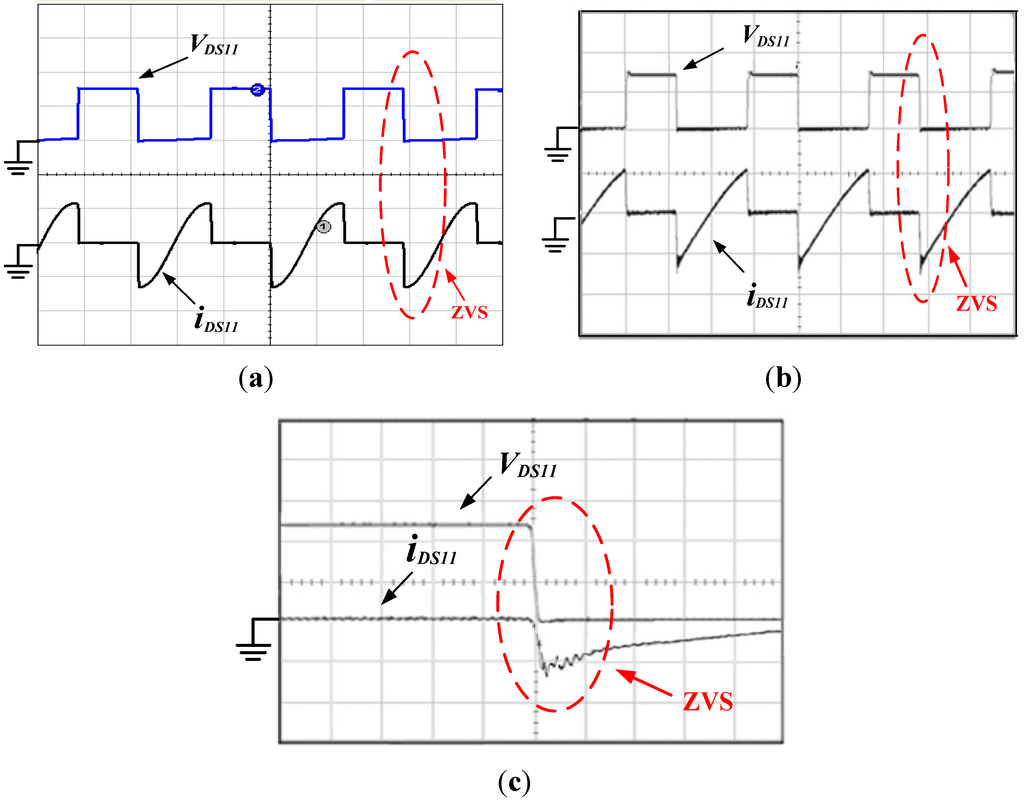
Figure 17.
Voltage and current waveforms of auxiliary switch (M11 or M22). (a) simulated results (VDS11: 200 V/div; iDS11: 10 A/div; Time: 5 μs/div); (b) experimental results (VDS11: 200 V/div; iDS11: 10 A/div; Time: 5 μs/div); (c) its expanded waveforms (VDS11: 100 V/div; iDS11: 10 A/div; Time: 0.5 μs/div).
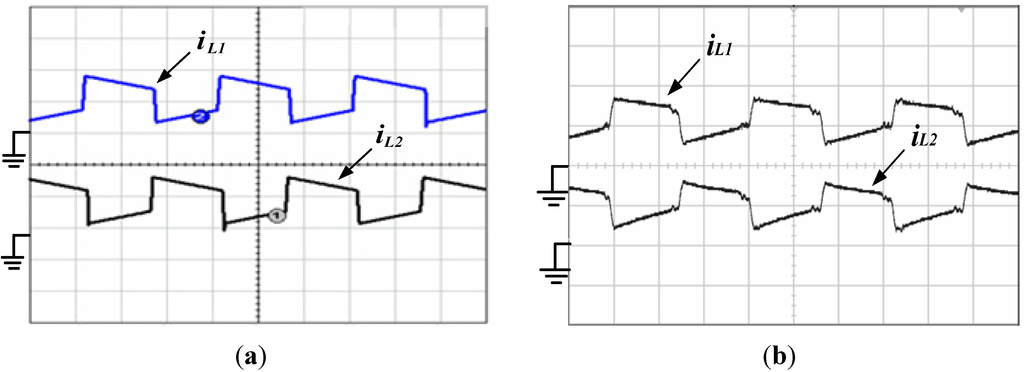
Figure 18.
Waveforms of inductor current (L1 and L2). (a) simulated results (iL1: 10 A/div; iL2: 10 A/div; Time: 5 μs/div); (b) experimental results (iL1: 10 A/div; iL2: 10 A/div; Time: 5 μs/div).
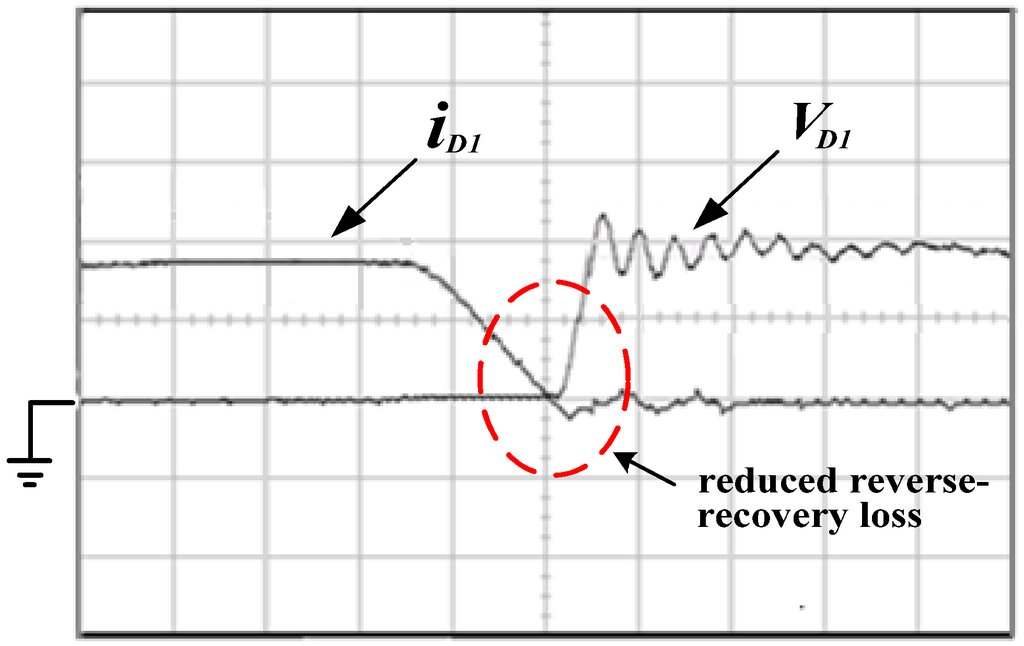
Figure 19.
Measured voltage and current waveforms of free-wheeling diode (D1 or D2; VD1: 20 V/div; iD1: 10 A/div; Time: 200 ns/div).
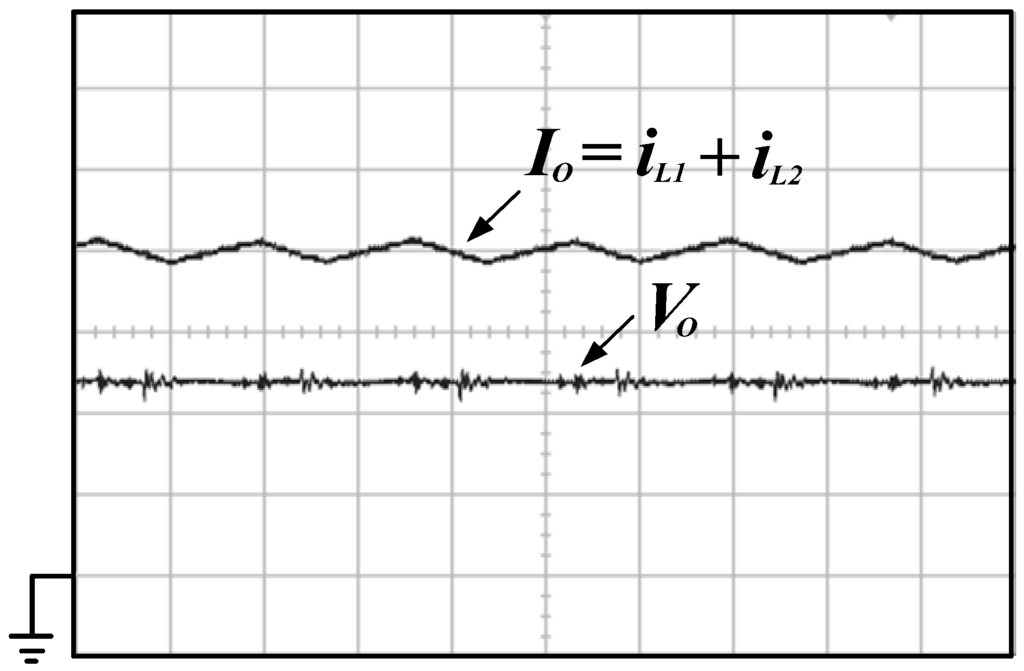
Figure 20.
Measured output voltage and current waveforms (Vo: 5 V/div; Io: 5 A/div; time: 500 ms/div).
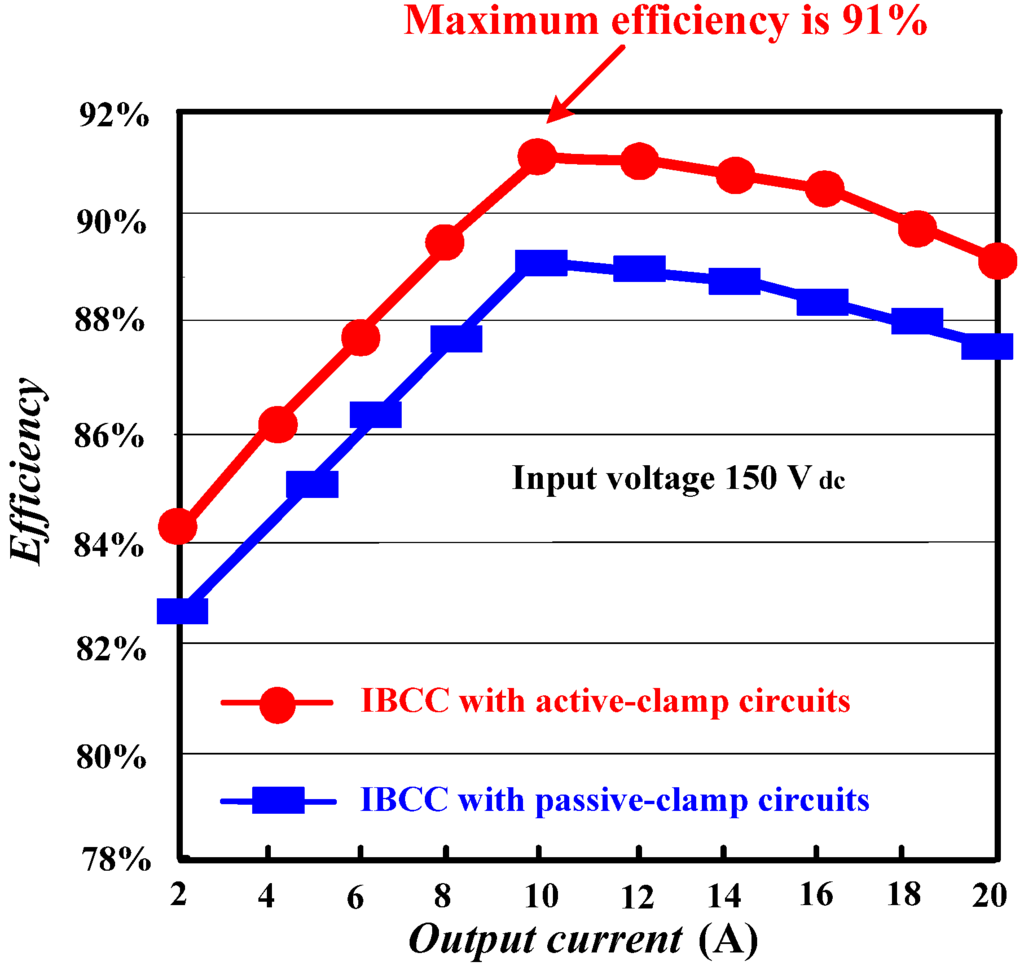
Figure 21.
Plots of efficiency versus output current for the IBCC with active-clamp circuits and without active-clamp circuits at input voltage 150 Vdc.
6. Conclusions
In this paper, an IBCC with active-clamp circuits for wind turbine conversion is proposed. The proposed converter can provide a proper duty ratio for high step-down voltage applications, resulting in low component stresses on active switches. By adopting active-clamp circuits, energy trapped in the leakage inductance of the coupled inductors can be recovered, ZVS features can be achieved and voltage spikes can be suppressed effectively for active switches. Therefore, the conversion efficiency of the proposed IBCC with active-clamp circuits can be increased significantly. In the study, analysis of the proposed IBCC with active-clamp circuits has been presented in detail, including operational principles, feature characteristics and power losses estimation. A 240 W model of the proposed IBCC with active-clamp circuits has been built and implemented. In Figure 21, experimental results can be seen showing that the maximum efficiency can reach as high as 91%. In high step-down voltage applications, the proposed IBCC with active-clamp circuits is relatively attractive for wind energy conversion.
References
- World Wind Energy Report 2008; World Wind Energy Association: Bonn, Germany, 2009.
- Rahimi, M.; Parniani, M. Efficient control scheme of wind turbines with doubly fed induction generators for low-voltage ride-through capability enhancement. Renew. Power Gener. IET 2010, 4, 242–252. [Google Scholar] [CrossRef]
- Tsai, C.T. Energy storage system with voltage equalization strategy for wind conversion. Energies 2012, 5, 2331–2350. [Google Scholar] [CrossRef]
- Shen, C.L.; Tsai, C.T. Double-linear approximation algorithm to achieve maximum-power-point tracking for photovoltaic arrays. Energies 2012, 5, 1982–1997. [Google Scholar] [CrossRef]
- Agarwal, V.; Aggarwal, R.K.; Patidar, P.; Patki, C. A novel scheme for rapid tracking of maximum power point in wind energy generation systems. IEEE Trans. Power Electron. 2010, 25, 228–236. [Google Scholar] [CrossRef]
- Wong, P.; Xu, P.; Lee, F.C. Performance improvements of interleaving VRMs with coupling inductors. IEEE Trans. Power Electron. 2001, 16, 499–507. [Google Scholar] [CrossRef]
- Chen, Y.M.; Tseng, S.Y.; Tsai, C.T.; Wu, T.F. Interleaved buck converters with a single-capacitor turn-off snubber. IEEE Trans. Aerosp. Electron. Syst. 2004, 40, 954–967. [Google Scholar] [CrossRef]
- Munoze, C. Study of a New Passive Lossless Turn-Off Snubber. In Proceedings of the International Power Electronics Congress, Seoul, Korea, 26–31 October 1998; pp. 147–152.
- Smith, K.M., Jr.; Smedley, K.M. Lossless Passive Soft Switching Methods for Inverters and Amplifiers. In Proceedings of the Power Electronics Specialists Conference, Saint Louis, MO, USA, 22–27 June 1997; pp. 1431–1439.
- Ilic, M.; Maksimovic, D. Interleaved zero-current-transition buck converter. IEEE Trans. Ind. Appl. 2007, 43, 1619–1627. [Google Scholar] [CrossRef]
- Tseng, C.J.; Chen, C.L. Passive Lossless Snubbers for DC/DC Converters. IEE Proc. Circuits Device Syst. 1998, 145, 396–401. [Google Scholar] [CrossRef]
- Gallo, C.A.; Tofoli, F.L.; Pinto, J.A.C. A passive lossless snubber applied to the AC-DC interleaved boost converter. IEEE Trans. Power Electron. 2010, 25, 775–785. [Google Scholar] [CrossRef]
- Tsai, C.T.; Shen, C.L. Interleaved soft-switching buck converter with coupled inductors. WSEAS Trans. Circuits Syst. 2011, 10, 99–103. [Google Scholar]
- Yao, K.; Ye, M.; Xu, M.; Lee, F.C. Tapped-inductor buck converter for high-step-down DC-DC converter. IEEE Trans. Power Electron. 2005, 20, 775–780. [Google Scholar] [CrossRef]
- Shoyama, M.; Li, G.; Ninomiya, T. Application of Common-Source Active-Clamp Circuit to Various DC-DC Converter Topologies. In Proceedings of the Power Electronics Specialists Conference, Acapulco, Mexico, 15–19 June 2003; pp. 1321–1326.
- Xu, D.H.; Chen, M.; Lou, J.; Luo, M. Transformer secondary leakage inductance based ZVS dual bridge DC/DC converter. IEEE Trans. Power Electron. 2004, 19, 1408–1416. [Google Scholar] [CrossRef]
- Jin, K.; Ruan, X. Zero-voltage-switched multi-resonant three-level converters. IEEE Trans. Ind. Electron. 2007, 54, 1705–1715. [Google Scholar] [CrossRef]
- Lo, Y.K.; Kao, T.S.; Lin, J.K. Analysis and design of an interleaved active-clamp forward converter. IEEE Trans. Ind. Electron. 2007, 54, 2323–2332. [Google Scholar] [CrossRef]
© 2012 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).