CFD in Wind Energy: The Virtual, Multiscale Wind Tunnel
Abstract
:1. Introduction
2. CFD at Small Scales: Aerodynamic Analysis of Wind Turbines
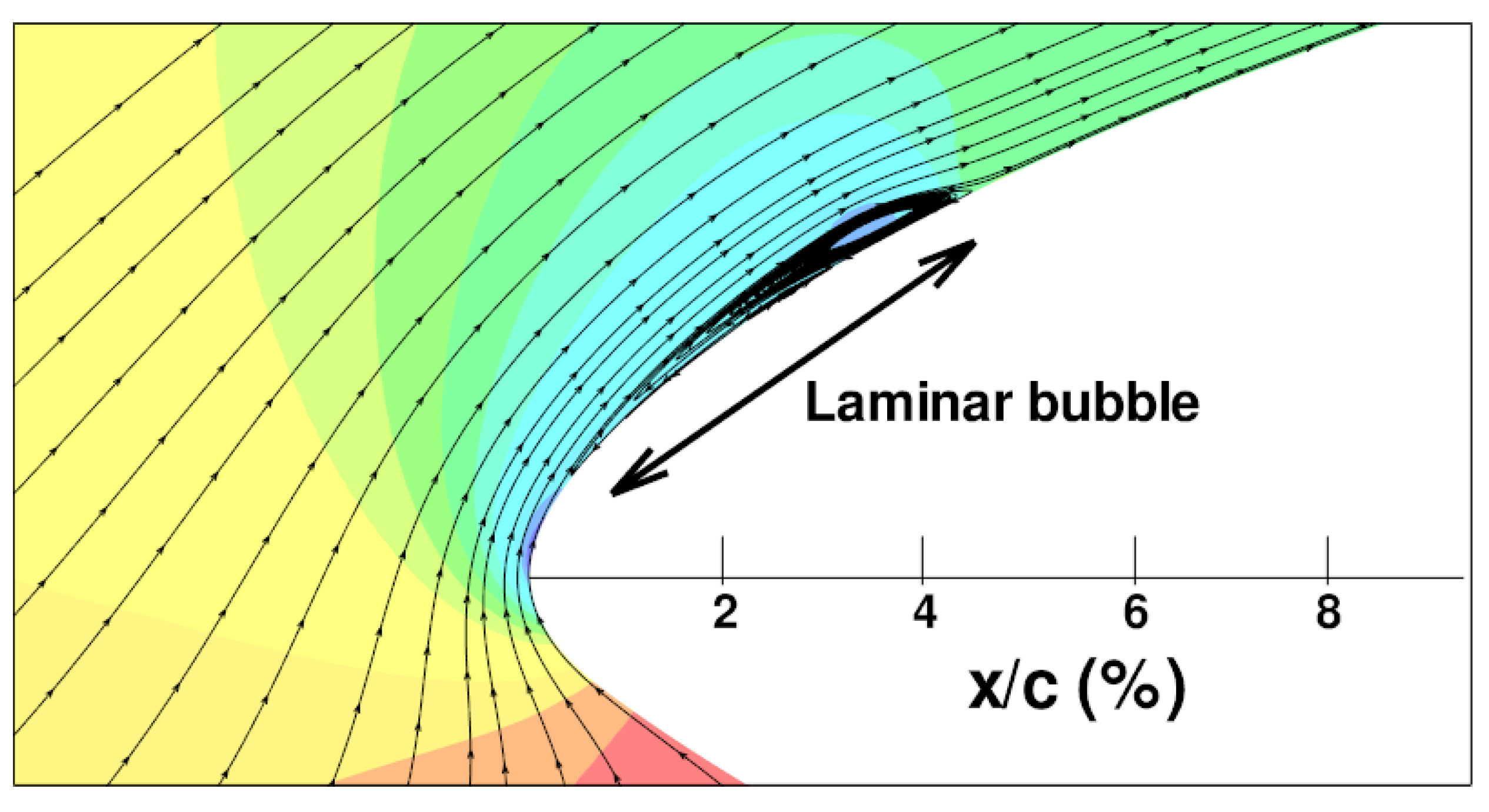
2.1. Prediction of two-dimensional airfoil aerodynamics
2.2. Prediction of three-dimensional rotor aerodynamics
2.3. Simplified approaches to three-dimensional rotor aerodynamics

3. CFD at Large Scales: Simulations in the Atmospheric Boundary Layer
3.1. Simulation of the homogeneous neutral surface layer
| Authors | κ | |||||
|---|---|---|---|---|---|---|
| Jones and Launder (1972) | 0.09 | 1.55 | 2.0 | 1.0 | 1.3 | 0.42 |
| Launder et al. (1972) | 0.09 | 1.44 | 1.92 | 1.0 | 1.3 | 0.42 |
| Crespo et al. (1985) | 0.0333 | 1.176 | 1.92 | 1.0 | 1.3 | 0.42 |
| Richards and Hoxey (1993) | 0.013 | 1.44 | 1.92 | 1.0 | 3.22 | 0.42 |
| Apsley and Castro (1997) | 0.09 | 1.44 | 1.92 | 1.0 | 1.11 | 0.40 |
| Bechmann and Sørensen (2009) | 0.03 | 1.21 | 1.92 | 1.0 | 1.3 | 0.40 |
3.2. Prediction of the flowfield over real terrain
3.3. Analysis of wind turbine wakes
4. Conclusions
Acknowledgements
References
- Pope, S.B. Turbulent Flows; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Hansen, M.; Sørensen, J.; Voutsinas, S.; Sørensen, N.; Madsen, H. State of the Art in Wind Turbine Aerodynamics and Aeroelasticity. Progr. Aerosp. Sci. 2006, 42, 285–330. [Google Scholar] [CrossRef]
- Hansen, A.; Butterfield, C. Aerodynamics of Horizontal-Axis Wind Turbines. Ann. Rev. Fluid Mechan. 2000, 25, 115–149. [Google Scholar] [CrossRef]
- Leishman, J.G. Challenges in Modeling the Unsteady Aerodynamics of Wind Turbines. In Proceedings of the ASME Wind Energy Symposium; AIAA: Reno, NV, USA, 2002. [Google Scholar]
- Snel, H. Review of Aerodynamics for Wind Turbines. Wind Energy 2003, 6, 203–211. [Google Scholar] [CrossRef]
- Advisory Group for Aerospace Research and Development. A Selection of Experimental Test Cases for the Validation of CFD Codes; Technical Report AGARD-AR-303; AGARD: Neuilly-sur-Seine, France, 1994. [Google Scholar]
- Hand, M.; Simms, D.; Fingersh, L.; Jager, D.; Cotrell, J.; Schreck, S.; Larwood, S. Unsteady Aerodynamics Experiment Phase VI: Wind Tunnel Test Configurations and Available Data Campaigns; Technical Report TP-500-29955; NREL: Golden, CO, USA, 2001. [Google Scholar]
- Simms, D.; Schreck, S.; Hand, M.; Fingersh, L. Unsteady Aerodynamics Experiment in the NASA-Ames Wind Tunnel: A Comparison of Predictions to Measurements; Technical Report NREL/TP-500-29494; NREL: Golden, CO, USA, 2001. [Google Scholar]
- Snel, H.; Schepers, J.; Montgomerie, B. The MEXICO project (Model EXperiments In Controlled cOnditions): The Database and First Results of Data Processing and Interpretation. In Proceedings of The Science of Making Torque from Wind (2nd conference) J. Phys.: Conf. Ser. 75; Danish Technical University: Copenhagen Denmark, 2007. [Google Scholar]
- Yang, S.; Chang, Y.; Arici, O. Navier-Stokes Computations of the NREL Airfoil Using a k-ω Turbulent Model at High Angles of Attack. J. Sol. Energ. – T. ASME 1995, 117, 304–310. [Google Scholar] [CrossRef]
- Wolfe, W.; Ochs, S. Predicting Aerodynamic Characteristics of Typical Wind Turbine Airfoils Using CFD; Technical Report SAND96-2345; Sandia National Laboratories: Albuquerque, NM, USA, 1997. [Google Scholar]
- Fuglsang, P.; Bak, C.; Gaunaa, M.; Antoniu, I. Design and Verification of the Risø-B1 Airfoil Family for Wind Turbines. J. Sol. Energ. – T. ASME 2006, 126, 1002–1010. [Google Scholar] [CrossRef]
- Bertagnolio, F.; Sørensen, N.; Johansen, J. Profile Catalogue for Airfoil Sections Based on 3D Computations; Technical Report R-1581(EN); Risø: Roskilde, Denmark, 2006. [Google Scholar]
- Rumsey, C.; Ying, S. Prediction of High Lift: Review of Present CFD Capability. Progr. Aerosp. Sci. 2006, 38, 145–180. [Google Scholar] [CrossRef]
- Mayda, E.; van Dam, C. Bubble-Induced Unsteadiness on a Wind Turbine Airfoil. J. Sol. Energ. – T. ASME 2002, 124, 335–344. [Google Scholar] [CrossRef]
- Brodeur, R.; van Dam, C. Transition Prediction for a Two-Dimensional Reynolds-Averaged Navier-Stokes Method Applied to Wind Turbine Airfoils. Wind Energy 2001, 4, 61–75. [Google Scholar] [CrossRef]
- Johansen, J.; Sørensen, J. Prediction of Laminar/Turbulent Transition in Airfoil Flows. In 36th Aerospace Sciences Meeting and Exhibit; AIAA: Reno, Nevada, 1998; pp. 679–688. [Google Scholar]
- Sørensen, N. Transition Prediction on the NORDTANK 500/41 Turbine Rotor; Technical Report R-1365(EN); Risø: Roskilde, Denmark, 2002. [Google Scholar]
- Johansen, J. Unsteady Airfoil Flows with Application ot Aeroelastic Stability . PhD thesis, Risø, Roskilde, Denmark, 1999. [Google Scholar]
- Windte, J.; Radespiel, R.; Scholz, U.; Eisfeld, B. RANS Simulation of the Transitional Flow Around Airfoils at Low Reynolds Numbers for Steady and Unsteady Onset Conditions; Technical Report RTO-MP-AVT-111; NATO, 2004. [Google Scholar]
- Freudenreich, K.; Kaiser, K.; Schaffarczyk, A.K.; Winkler, H.; Stahl, B. Reynolds Number and Roughness Effects on Thick Airfoils for Wind Turbines. Wind Eng. 2004, 28, 529–546. [Google Scholar] [CrossRef]
- Menter, F.; Langtry, R.; Likki, S.; Suzen, Y.; Huang, P.; Volker, S. A Correlation-Based Transition Model Using Local Variables – Part I: Model Formulation. J. Turbomach. 2006, 128, 413–422. [Google Scholar] [CrossRef]
- Sørensen, N. CFD Modelling of Laminar-turbulent Transition for Airfoils and Rotors Using the γ- Model. Wind Energy 2009, 12, 715–733. [Google Scholar] [CrossRef]
- Wilcox, D. Turbulence Modeling for CFD; DWC Industries: La Canada, CA, USA, 1998. [Google Scholar]
- Duque, E.; Johnson, W.; van Dam, C.; Cortes, R.; Yee, K. Numerical Predictions of Wind Turbine Power and Aerodynamic Loads for the NREL Phase II Combined Experiment Rotor. In Proceedings of the ASME Wind Energy Symposium; AIAA: Reno, Nevada, 2000. [Google Scholar]
- Sørensen, N.; Hansen, M. Rotor Performance Predictions using a Navier-Stokes Method. In Proceedings of the ASME Wind Energy Symposium; AIAA: Reno, Nevada, 1998. [Google Scholar]
- Varela, J.; Bercebal, D. CFD Calculations of the Flow Around a Wind Turbine Nacelle; Technical Report 910; Ciemat: Madrid, Spain, 1999. [Google Scholar]
- Duque, E.; Burklund, M.; Johnson, W. Navier-Stokes and Comprehensive Analysis Performance Predictions of the NREL Phase VI Experiment. J. Sol. Energ. – T. ASME 2003, 125, 457–467. [Google Scholar] [CrossRef]
- Sørensen, N.; Johansen, J.; Conway, S. CFD Computations of Wind Turbine Blade Loads During Standstill Operation KNOW-BLADE TASK 3.1 Report; Technical Report R-1465(EN); Risø: Roskilde, Denmark, 2004. [Google Scholar]
- Spalart, P. Detached Eddy Simulation. Ann. Rev. Fluid Mechan. 2009, 41, 181–202. [Google Scholar] [CrossRef]
- Le Pape, A.; Lecanu, J. 3D Navier-Stokes Computations of a Stall-regulated Wind Turbine. Wind Energy 2004, 7, 309–324. [Google Scholar] [CrossRef]
- Tachos, N.; Zioutis, C.; Filios, A.; Margaris, D. Aerodynamic Computational Analysis for a HAWT Rotor. In Proceedings of EWEC 2006; EWEA: Athens, Greece, 2006. [Google Scholar]
- Mandas, N.; Cambuli, F.; Carcangiu, C. Numerical Prediction of Horizontal Axis Wind Turbine Flow. In Proceedings of EWEC 2006; EWEA: Athens, Greece, 2006. [Google Scholar]
- Hartwanger, D.; Horvat, A. 3D Modelling of a Wind Turbine Using CFD. In Proceedings of NAFEMS Conference; NAFEMS: Cheltenham, UK, 2008. [Google Scholar]
- Gómez-Iradi, S.; Steijl, R.; Barakos, G. Development and Validation of a CFD Technique for the Aerodynamic Analysis of HAWT. J. Sol. Energ. – T. ASME 2009, 131. [Google Scholar] [CrossRef]
- Bechmann, A.; Sørensen, N. CFD Simulation of the MEXICO Rotor Wake. In Proceedings of EWEC 2009; EWEA: Marseille, France, 2009. [Google Scholar]
- Schreck, S.; Robinson, M. Rotational Augmentation of Horizontal Axis Wind Turbine Blade Aerodynamic Response. Wind Energy 2002, 5, 133–150. [Google Scholar] [CrossRef]
- Chaviaropoulos, P.; Hansen, M. Investigating Three-Dimensional and Rotational Effects on Wind Turbine Blades by Means of a Quasi-3D Navier-Stokes Solver. J. Fluid Eng. – T. ASME 2000, 122, 330–336. [Google Scholar] [CrossRef]
- Johansen, J.; Sørensen, N. Aerofoil Characteristics from 3D CFD Rotor Computations. Wind Energy 2004, 7, 283–294. [Google Scholar] [CrossRef]
- Ferrer, E.; Munduate, X. Wind Turbine Blade Tip Comparison Using CFD. In Proceedings of the Science of Making Torque from Wind (2nd conference) J. Phys.: Conf. Ser. 75; Danish Technical University: Copenhagen Denmark, 2007. [Google Scholar]
- Mac, G.; Johansen, J. Determination of the Maximum Aerodynamic Efficiency of Wind Turbine Rotors with Winglets. In Proceedings of the Science of Making Torque from Wind (2nd conference) J. Phys.: Conf. Ser. 75; Danish Technical University: Copenhagen Denmark, 2007. [Google Scholar]
- Gómez-Iradi, S.; Barakos, G. Computational Fluid Dynamics Investigation of Some Wind Turbine Rotor Design Parameters. Proc. Instit. Mechan. Eng. A: J. Power Energy 2008, 222, 455–470. [Google Scholar] [CrossRef]
- Chao, D.; van Dam, C. CFD Analysis of Rotating Two-Bladed Flatback Wind Turbine Rotor; Technical Report SAND2008-1688; Sandia National Laboratories: Albuquerque, NM, USA, 2008. [Google Scholar]
- Vermeer, L.; Sørensen, J.; Crespo, A. Wind Turbine Wake Aerodynamics. Progr. Aerosp. Sci. 2003, 39, 467–510. [Google Scholar] [CrossRef]
- Xu, G.; Sankar, L. Developement of Engineering Aerodynamic Models Using a Viscous Flow Methodology on the NREL Phase VI Rotor. Wind Energy 2002, 5, 171–183. [Google Scholar] [CrossRef]
- Schmitz, S.; Chattot, J.J. Parallelized Coupled Navier-Stokes/Vortex-Panel Solver. J. Sol. Energ. – T. ASME 2003, 127, 475–487. [Google Scholar] [CrossRef]
- Rajagopalan, R.; Fanucci, J. Finite Difference Model of Vertical Axis Wind Turbines. J. Propul. Power 1985, 1, 432–436. [Google Scholar] [CrossRef]
- Madsen, H. The Actuator Cylinder: A Flow Model for Vertical Axis Wind Turbines . PhD thesis, Aalborg University Centre,, Aalborg, Denmark, 1992. [Google Scholar]
- Chaffin, M.S.; Berry, J.D. Navier-Stokes Simulation of a Rotor Using a Distributed Pressure Disk Method. In Proceedings of the American Helicopter Society, 51st Annual Forum; AHS International: Fort Worth, TX, USA, 1995; pp. 112–136. [Google Scholar]
- Sørensen, J.; Myken, A. Unsteady Actuator Disk Model for Horizontal Axis Wind Turbines. J. Wind Eng. Ind. Aerod. 1992, 39, 139–149. [Google Scholar] [CrossRef]
- Masson, C.; Ammara, I.; Paraschivoiu, I. An Aerodynamic Method for the Analysis of Isolated Horizontal-Axis Wind Turbines. Int. J. Rotat. Machin. 1997, 3, 21–32. [Google Scholar] [CrossRef]
- Madsen, H. A CFD Analysis of the Actuator Disk Flow Compared with Momentum Theory Results. In Proceedings of the 10th IEA Symposium on the Aerodynamics of Wind Turbines; IEA: Edinburgh, UK, 1996; pp. 109–124. [Google Scholar]
- Mikkelsen, R. Actuator Disc Methods Applied to Wind Turbines . PhD thesis, Technical University of Denmark, Lyngby, Denmark, 2003. [Google Scholar]
- Sibuet Watters, C.; Breton, S.; Masson, C. Application of the Actuator Surface Concept to Wind Turbine Rotor Anerodynamics. Wind Energy 2009. Early View. [Google Scholar] [CrossRef]
- Sørensen, J.; Shen, W. Numerical Modeling of Wind Turbine Wakes. J. Fluid Eng. – T. ASME 2002, 124, 393–399. [Google Scholar] [CrossRef]
- Ivanell, S.; Sørensen, J.; Mikkelsen, R.; Henningson, D. Analysis of Numerically Generated Wake Structures. Wind Energy 2009, 12, 63–80. [Google Scholar] [CrossRef]
- Troldborg, N.; Sørensen, J.; Mikkelsen, R. Numerical Simulations of Wake Characteristics of a Wind Turbine in Uniform Flow. Wind Energy 2010, 13, 86–99. [Google Scholar] [CrossRef]
- Sibuet Watters, C.; Masson, C. Modelling of Lifting-Device Aerodynamics Using the Actuator Surface Concept. Int. J. Numer. Meth. Fl. 2009, (in press). [Google Scholar] [CrossRef]
- Dobrev, I.; Massouh, F.; Rapin, M. Actuator Surface Hybrid Model. In Proceedings of the Science of Making Torque from Wind (2nd conference) J. Phys.: Conf. Ser. 75; Danish Technical University: Copenhagen Denmark, 2007. [Google Scholar]
- Shen, W.; Zhang, J.; Sørensen, J. The Actuator Surface Model: A New Navier-Stokes Based Model for Rotor Computations. J. Sol. Energ. – T. ASME 2009, 131. 011002–1:011002–9. [Google Scholar] [CrossRef]
- Leclerc, C.; Masson, C. Wind Turbine Performance Predictions Using a Differential Actuator-Lifting Disk Model. J. Sol. Energ. – T. ASME 2005, 127, 200–208. [Google Scholar] [CrossRef]
- Prospathopoulos, J.; Voutsinas, S.G. Implementation Issues in 3D Wind Flow Predictions Over Complex Terrain. J. Sol. Energ. – T. ASME 2006, 128, 539–553. [Google Scholar] [CrossRef]
- Jones, W.; Launder, B. The Prediction of Laminarization with a Two-Equation Model of Turbulence. Int. J. Heat Mass Tran. 1972, 15, 301–314. [Google Scholar] [CrossRef]
- Launder, B.; Morse, A.; Rodi, W.; Spalding, D. The Prediction of Free Shear Flows—A Comparison of the Performance of Six Turbulence Models. In NASA Conference on Free Shear Flows; NASA: Langley, US, 1972. [Google Scholar]
- Detering, H.; Etling, D. Application of the E-ε turbulence model to the atmospheric boundary layer. Bound.–Lay. Meteorol. 1985, 33, 113–133. [Google Scholar] [CrossRef]
- Apsley, D.; Castro, I. A limited-length-scale k-ε model for the neutral and stably-stratified atmospheric boundary layer. Bound.–Lay. Meteorol. 1997, 83, 75–98. [Google Scholar] [CrossRef]
- Crespo, A.; Manuel, F.; Moreno, D.; Fraga, E.; Hernandez, J. Numerical Analysis of Wind Turbine Wakes. In Proceedings of Delphi Workshop on Wind Energy Applications; Bergeles, G., Chadjivassiliadis, J., Eds.; Delphi: Greece, 1985; pp. 15–25. [Google Scholar]
- Panofsky, H.; Dutton, J. Atmospheric Turbulence; Wiley: New York, NY, USA, 1984; p. 397. [Google Scholar]
- Richards, P.; Hoxey, R. Appropriate Boundary Conditions for Computational Wind Engineering Models Using the k-ε Turbulence Model. J. Wind Eng. Ind. Aerod. 1993, 46&47, 145–153. [Google Scholar] [CrossRef]
- El Kasmi, A.; Masson, C. Turbulence Modeling of Atmospheric Boundary Layer Flow Over Complex Terrain: A Comparison of Models at Wind Tunnel and Full Scale. Wind Energy 2010, (in press). [Google Scholar] [CrossRef]
- Richards, P.; Younis, B. Comments on ‘Prediction of wind generated pressure distribution around buildings’. J. Wind Eng. Ind. Aerod. 1990, 34, 107–110. [Google Scholar] [CrossRef]
- Blocken, B.; Stathopoulos, T.; Carmeliet, J. CFD Simulation of the Atmospheric Boundary Layer: Wall Function Problems. Atmos. Environ. 2007, 41, 238–252. [Google Scholar] [CrossRef]
- Hargreaves, D.; Wright, N. On the Use of the k-ε Model in Commercial CFD Software to Model the Neutral Atmospheric Boundary Layer. J. Wind Eng. Ind. Aerod. 2007, 95, 355–369. [Google Scholar] [CrossRef]
- Sumner, J.; Masson, C. k-ε Simulations of the Neutral ABL: Achieving Horizontal Homogeneity on Practical Grids. In Proceedings of 48th AIAA Aerospace Sciences Meeting; AIAA: Orlando, FL, US, 2010. [Google Scholar]
- Yang, Y.; Gu, M.; Chen, S.; Jin, X. New Inflow Boundary Conditions for Modelling the Neutral Equilibrium Atmospheric Boundary Layer in Computational Wind Engineering. J. Wind Eng. Ind. Aerod. 2009, 97, 88–95. [Google Scholar] [CrossRef]
- Gorlé, C.; van Beeck, J.; Rambaud, P.; Van Tendeloo, G. CFD Modelling of Small Particle Dispersion: The Influence of Turbulence Kinetic Energy in the Atmospheric Boundary Layer. Atmos. Environ. 2009, 43, 673–681. [Google Scholar] [CrossRef]
- Nielsen, M.; Landberg, L.; Mortensen, N.; Barthelmie, R.; Joensen, A. Application of the Measure-Correlate-Predict Approach for Wind Resource Assessment. In Proceedings of EWEC 2001; EWEA: Copenhagen, Denmark, 2001; pp. 773–776. [Google Scholar]
- Troen, I.; Petersen, E. The European Wind Atlas; Risø: Roskilde, Denmark, 1989. [Google Scholar]
- Taylor, P.; Walmsley, J.; Salmon, J. A Simple Model of Neutrally-stratified Boundary-layer Flow Over Real Terrain Incorporating Wavenumber-dependent Scaling. Bound.–Lay. Meteorol. 1983, 26, 169–189. [Google Scholar] [CrossRef]
- Ayotte, K.W. Computational Modelling for Wind Energy Assessment. J. Wind Eng. Ind. Aerod. 2008, 96, 1571–1590. [Google Scholar] [CrossRef]
- Landberg, L.; Myllerup, L.; Rathmann, O.; Petersen, E.L.; Jørgensen, B.H.; Badger, J.; Mortensen, N.G. Wind Resource Estimation - An Overview. Wind Energy 2003, 6, 261–271. [Google Scholar] [CrossRef]
- Bitsuamlak, G.; Stathopoulos, T.; Bedard, C. Numerical Evaluation of Wind Flow Over Complex Terrain: Review. J. Aerospace Eng. 1999, 17, 135–145. [Google Scholar] [CrossRef]
- Hashimoto, T.; Yoshida, S.; Iso, O. Wind Farm Layout Optimization in Complex Terrains. In Proceedings of EWEC 2007; EWEA: Milan, Italy, 2007. [Google Scholar]
- Bechmann, A.; Johansen, J.; Sørensen, N. The Bolund Experiment—Design of Measurement Campaign Using CFD; Technical Report R-1623(EN); Risø: Roskilde, Denmark, 2007. [Google Scholar]
- Brodeur, P.; Masson, C. Numerical Site Calibration Over Complex Terrain. J. Sol. Energ. – T. ASME 2008, 139, 1–12. [Google Scholar] [CrossRef]
- Palma, J.; Castro, F.; Ribeiro, L.; Rodrigues, A.; Pinto, A. Linear and Nonlinear Models in Wind Resource Assessment and Wind Turbine Micro-siting in Complex Terrain. J. Wind Eng. Ind. Aerod. 2008, 96, 2308–2326. [Google Scholar] [CrossRef]
- Chen, Y.; Kim, S. Computation of Turbulent Flows Using an Extended k-ϵ Turbulence Closure Model; Technical Report CR-179204; NASA-Marshall Space Flight Center: Huntsville, AL, USA, 1987. [Google Scholar]
- Yakhot, V.; Orszag, S.A. Renormalization Group Analysis of Turbulence. I. Basic Theory. J. Sci. Comput. 1986, 1, 3–51. [Google Scholar] [CrossRef]
- Yakhot, V.; Smith, L. The Renormalization Group, the ε-expansion and Derivation of Turbulence Models. J. Sci. Comput. 1992, 7, 35–61. [Google Scholar] [CrossRef]
- Maurizi, A. Numerical Simulation of Turbulent Flows Over 2-D Valleys Using Three Versions of the k-ε Closure Model. J. Wind Eng. Ind. Aerod. 2000, 85, 59–73. [Google Scholar] [CrossRef]
- Ying, R.; Canuto, V.; Ypma, R. Numerical Simulation of Flow Data Over Two-dimensional Hills. Bound.–Lay. Meteorol. 1994, 70, 401–427. [Google Scholar] [CrossRef]
- Durbin, P. Technical note: On the k-ε Stagnation Point Anomaly. Int. J. Heat Fluid Fl. 1996, 17, 89–90. [Google Scholar] [CrossRef]
- Nagano, Y.; Hattori, H.; Irikado, T. Prediction of Flow Over Complex Terrain using Turbulence Model. In Proceedings of the TED-Conference ’01; JSME: Kobe, Japan, 2001. (In Japanese) [Google Scholar]
- Nagano, Y.; Hattori, H. A New Low-Reynolds-number Turbulence Model with Hybrid Time-scales of Mean Flow and Turbulence for Complex Wall Flows. In Proceedings of the Fourth International Symposium on Turbulence, Heat and Mass Transfer; ICHMT: Antalya, Turkey, 2003. [Google Scholar]
- Shih, T.; Zhu, J.; Lumley, J. A New Reynolds Stress Algebraic Equation Model. Comput. Method Appl. M. 1995, 125, 287–302. [Google Scholar] [CrossRef]
- Lun, Y.; Mochida, A.; Murakami, S.; Yoshino, H.; Shirashawa, T. Numerical Simulation of Flow Over Topographic Features by Revised k-ε Models. J. Wind Eng. Ind. Aerod. 2003, 91, 231–245. [Google Scholar] [CrossRef]
- Lun, Y.F.; Mochida, A.; Yoshino, H.; Murakami, S. Applicability of Linear Type Revised k-ε Models to Flow Over Topographic Features. J. Wind Eng. Ind. Aerod. 2007, 95, 371–384. [Google Scholar] [CrossRef]
- Muramaki, S.; Mochida, A.; Kato, S. Development of Local Area Wind Prediction System for Selecting Suitable Site for Windmill. J. Wind Eng. Ind. Aerod. 2003, 91, 1759–1776. [Google Scholar]
- Kim, H.; Patel, V. Test of Turbulence Models for Wind Flow Over Complex Terrain with Separation and Recirculation. Bound.–Lay. Meteorol. 2000, 94, 5–21. [Google Scholar] [CrossRef]
- Kim, H.; Patel, V.; Lee, C. Numerical Simulation of Wind Flow Over Hilly Terrain. J. Wind Eng. Ind. Aerod. 2000, 87, 45–60. [Google Scholar] [CrossRef]
- Raithby, G.; Stubley, G.; Taylor, P. The Askervein Hill Project: A Finite Control Volume Prediction of Three-dimensional Flows Over the Hill. Bound.–Lay. Meteorol. 1987, 39, 247–267. [Google Scholar] [CrossRef]
- Castro, F.; Palma, J.; Silva Lopes, A. Simulation of the Askervein Flow. Part I: Reynolds Averaged Navier-Stokes Equations (k-ε Turbulence Model). Bound.–Lay. Meteorol. 2003, 107, 501–530. [Google Scholar] [CrossRef]
- Eidsvik, K.J. A System for Wind Power Estimation in Mountainous Terrain. Prediction of Askervein Hill Data. Wind Energy 2005, 8, 237–249. [Google Scholar] [CrossRef]
- Undheim, O.; Andersson, H.; Berge, E. Non-linear, Microscale Modelling of the Flow Over Askervein Hill. Bound.–Lay. Meteorol. 2006, 120, 477–495. [Google Scholar] [CrossRef]
- Laporte, L. Application d’un code CFD atmosphérique à l’estimation du productible éolien en terrain complexe . PhD thesis, Université Paris-Est, Champs-sur-Marne, France, 2008. [Google Scholar]
- Taylor, P.; Teunissen, H. The Askervein Hill Project: Overview and Background Data. Bound.–Lay. Meteorol. 1987, 39, 15–39. [Google Scholar] [CrossRef]
- Mickle, R.; Cook, N.; Hoff, A.; Jensen, N.; Salmon, J.; Taylor, P.; Tetzla, G.; Teunissen, H. The Askervein Hill Project: Vertical Profiles of Wind and Turbulence. Bound.–Lay. Meteorol. 1988, 43, 143–169. [Google Scholar] [CrossRef]
- Gatski, T.; Speziale, C. On Explicit Algebraic Stress Models for Complex Turbulent Flows. J. Fluid Mech. 1993, 254, 59–78. [Google Scholar] [CrossRef]
- Bechmann, A.; Berg, J.; Courtney, M.; Jørgensen, H.; Mann, J.; Sørensen, N. The Bolund Experiment: Overview and Background; Technical Report R-1658(EN); Risø DTU: Roskilde, Denmark, 2009. [Google Scholar]
- Risø DTU. The Bolund experiment: Blind comparison of codes – Wind in complex terrain. Avilable online: http://www.risoe.dk/da/Research/sustainable_energy/wind_energy/projects/VEA_Bolund/Bolund_Blind_Comparison.aspx?sc_lang=en (accessed on 5 May 2010).
- Lopes da Costa, J.; Castro, F.; Palma, J.; Stuart, P. Computer Simulation of Atmospheric Flows Over Real Forests for Wind Energy Resource Evaluation. J. Wind Eng. Ind. Aerod. 2006, 94, 603–620. [Google Scholar] [CrossRef]
- Svensson, U.; Häggkvist, K. A Two-equation Turbulence Model for Canopy Flows. J. Wind Eng. Ind. Aerod. 1990, 35, 201–211. [Google Scholar] [CrossRef]
- Dalpé, B.; Masson, C. Numerical Study of Fully Developed Turbulent Flow Within and Above a Dense Forest. Wind Energy 2008, 11, 503–515. [Google Scholar] [CrossRef]
- Katul, G.; Mahrt, L.; Poggi, D.; Sanz, C. One- and Two-equation Models for Canopy Turbulence. Bound.–Lay. Meteorol. 2004, 113, 81–109. [Google Scholar] [CrossRef]
- Alinot, C.; Masson, C. k-ε Model for the Atmospheric Boundary Layer Under Various Thermal Stratifications. J. Sol. Energ. – T. ASME 2005, 127, 438–443. [Google Scholar] [CrossRef]
- Sagaut, P. Large Eddy Simulation for Incompressible Flow, 3rd ed.; Springer: Berlin, Germany, 2006. [Google Scholar]
- Wood, N. Wind Flow Over Complex Terrain: A Historical Perspective and the Prospect for Large-eddy Modelling. Bound.–Lay. Meteorol. 2000, 96, 11–32. [Google Scholar] [CrossRef]
- Chow, F.; Street, R. Evaluation of Turbulence Models for Large-eddy Simulations of Flow Over Askervein Hill. In 16th Symposium on Boundary Layers and Turbulence; AMS: Portland, OR, USA, 2004; pp. 381–388. [Google Scholar]
- Chow, F.; Street, R. Evalution of Turbulence Closure Models for Large-eddy Simulation Over Complex Terrain: Flow over Askervein Hill. J. Appl. Meteorol. Clim. 2009, 48, 1050–1065. [Google Scholar] [CrossRef]
- Chow, F.; Weigel, A.; Street, R.; Rotach, M.; Xue, M. High-resolution Large-eddy Simulations of Flow in a Steep Alpine Valley. I. Methodology, Verification, and Sensitivity Experiments. J. Appl. Meteorol. 2006, 45, 63–86. [Google Scholar] [CrossRef]
- Uchida, T.; Ohya, Y. Numerical Simulation of Atmospheric Flow Over Complex Terrain. J. Wind Eng. Ind. Aerod. 1999, 81, 283–293. [Google Scholar] [CrossRef]
- Uchida, T.; Ohya, Y. Large-eddy Simulation of Turbulent Airflow Over Complex Terrain. J. Wind Eng. Ind. Aerod. 2003, 91, 219–229. [Google Scholar] [CrossRef]
- Uchida, T.; Ohya, Y. Application of LES Technique to Diagnosis of Wind Farm by Using High Resolution Elevation Data. JSME Int. J. B–Fluid T. 2006, 49, 567–575. [Google Scholar] [CrossRef]
- Uchida, T.; Ohya, Y. Micro-siting Technique for Wind Turbine Generators by Using Large-eddy Simulation. J. Wind Eng. Ind. Aerod. 2008, 96, 2121–2138. [Google Scholar] [CrossRef]
- Piomelli, U.; Balaras, E. Wall-layer Models for Large-eddy Simulations. Annu. Rev. Fluid Mech. 2002, 34, 349–374. [Google Scholar] [CrossRef]
- Piomelli, U. Wall-layer Models for Large-eddy Simulations. Progr. Aerosp. Sci. 2008, 44, 437–446. [Google Scholar] [CrossRef]
- Silva Lopes, A.; Palma, J. Large Eddy Simulation of Flow Around the Askervein Hill. In Proceedings of 3rd Theoretical Fluid Mechanics Meeting; AIAA: St. Louis, MO, USA, 2002. [Google Scholar]
- Silva Lopes, A.; Palma, J.; Castro, F. Simulation of the Askervein Flow. Part 2: Large-eddy Simulations. Bound.–Lay. Meteorol. 2007, 125, 85–108. [Google Scholar] [CrossRef]
- Bechmann, A.; Sørensen, N. Hybrid RANS/LES Method for Wind Flow Over Complex Terrain. Wind Energy 2009. [Google Scholar] [CrossRef]
- Crespo, A.; Hernandez, J.; Frandsen, S. Survey of Modelling Methods for Wind Turbine Wakes and Wind Farms. Wind Energy 1999, 2, 1–24. [Google Scholar] [CrossRef]
- El Kasmi, A.; Masson, C. An Extended k-ε Model for Turbulent Flow Through Horizontal-axis Wind Turbines. J. Wind Eng. Ind. Aerod. 2008, 96, 103–122. [Google Scholar] [CrossRef]
- Sørensen, J.; Shen, W.; Munduate, X. Analysis of Wake States by a Full-field Actuator Disc Model. Wind Energy 1998, 1, 73–88. [Google Scholar] [CrossRef]
- Cabezón, D.; Sanz, J.; Martí, I.; Crespo, A. CFD Modelling of the Interaction Between the Surface Boundary Layer and Rotor Wake: Comparison of Results Obtained with Different Turbulence Models and Mesh Strategies. In Proceedings of EWEC 2009; EWEA: Marseilles, France, 2009. [Google Scholar]
- Gómez-Elvira, R.; Crespo, A.; Migoya, E.; Manuel, F.; Hernández, J. Anisotropy of Turbulence in Wind Turbine Wakes. J. Wind Eng. Ind. Aerod. 2005, 93, 797–814. [Google Scholar] [CrossRef]
- Prospathopoulos, J.; Politis, E.; Rados, K.; Chaviaropoulos, P. Enhanced CFD Modelling of Wind Turbine Wakes. In Extended Abstracts for Euromech Colloquium 508 on Wind Turbine Wakes; European Mechanics Society: Madrid, Spain, 2009. [Google Scholar]
- Réthoré, P.E. Wind Turbine Wake in Atmospheric Turbulence . PhD thesis, Aalborg University, Aalborg, Denmark, 2009. [Google Scholar]
- Jimenez, A.; Crespo, A.; Migoya, E.; Garcia, J. Advances in Large-eddy Simulation of a Wind Turbine Wake. In Proceedings of The Science of Making Torque from Wind (2nd conference) J. Phys.: Conf. Ser. 75; Danish Technical University: Copenhagen Denmark, 2007. [Google Scholar]
- Patel, M. Wind and Power Solar Systems; CRC Press: Boca Raton, 1999. [Google Scholar]
- Ammara, I.; Leclerc, C.; Masson, C. A Viscous Three-dimensional Differential/Actuator-disk Method for the Aerodynamic Analysis of Wind Farms. J. Sol. Energ. – T. ASME 2002, 124, 345–356. [Google Scholar] [CrossRef]
- Barthelmie, R.; Hansen, K.; Frandsen, S.; Rathmann, O.; Schepers, J.; Schlez, W.; Philips, J.; Rados, K.; Zervos, A.; Politis, E.; Chaviaropoulos, P. Modelling and Measuring Flow and Wind Turbine Wakes in Large Wind Farms Offshore. Wind Energy 2009, 12, 431–444. [Google Scholar] [CrossRef]
- Barthelmie, R.; Schepers, J.; van der, Pijl.; Rathman, O.; Frandsen, S.; Cabezón, D.; Politis, E.; Prospathopoulos, J.; Rados, K.; Hansen, K.; Schlez, W.; Phillips, J.; Neubert, A. Flow and Wakes in Complex Terrain and Offshore: Model Development and Verification in UpWind. In Proceedings of EWEC 2007; EWEA: Milan, Italy, 2007. [Google Scholar]
- Ivanell, S.; Mikkelsen, R.; Sørensen, J.; Henningson, D. ACD Modelling of Wake Interaction in Horns Rev Wind Farm. In Extended Abstracts for Euromech Colloquium 508 on Wind Turbine Wakes; European Mechanics Society: Madrid, Spain, 2009. [Google Scholar]
- Meyers, J.; Meneveau, C. Large Eddy Simulations of Large Wind-turbine Arrays in the Atmospheric Boundary Layer. In Proceedings of 48th AIAA Aerospace Sciences Meeting; AIAA: Orlando, FL, USA, 2010. [Google Scholar]
© 2010 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license http://creativecommons.org/licenses/by/3.0/.
Share and Cite
Sumner, J.; Watters, C.S.; Masson, C. CFD in Wind Energy: The Virtual, Multiscale Wind Tunnel. Energies 2010, 3, 989-1013. https://doi.org/10.3390/en3050989
Sumner J, Watters CS, Masson C. CFD in Wind Energy: The Virtual, Multiscale Wind Tunnel. Energies. 2010; 3(5):989-1013. https://doi.org/10.3390/en3050989
Chicago/Turabian StyleSumner, Jonathon, Christophe Sibuet Watters, and Christian Masson. 2010. "CFD in Wind Energy: The Virtual, Multiscale Wind Tunnel" Energies 3, no. 5: 989-1013. https://doi.org/10.3390/en3050989
APA StyleSumner, J., Watters, C. S., & Masson, C. (2010). CFD in Wind Energy: The Virtual, Multiscale Wind Tunnel. Energies, 3(5), 989-1013. https://doi.org/10.3390/en3050989




