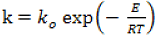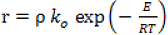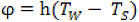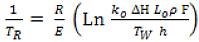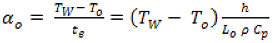1. Introduction
Biomass is one of the most often suggested source of renewable energy. It’s upgrading can be performed by biochemical and thermochemical routes [
1]. High temperature transformations have many advantages. Among them, the possibility to upgrade the whole feedstock (cellulose, lignin, hemicellulose, …) of any type of biomass. In addition, the products can be used for a great number of chemical and energy applications. Biomass thermochemical conversion routes are usually classified into combustion, gasification and pyrolysis processes.
In combustion, biomass is burned under an excess of O2 for the production of heat and electricity. In gasification, biomass is transformed in the presence of lower fractions of O2 or steam, into a gas mixture (mainly H2, CO) that must be further treated in order to meet the various specifications of a high quality syngas. This gas can be used for different possible applications: heat generation (motors, turbines, …), H2 or CH4 preparation and production of biofuels through Fisher-Tropsch synthesis.
Pyrolysis processes are conducted under an inert atmosphere for the production of solids (charcoal), liquids (bio-oils) or high heating values gases. Their relative fractions depend on the operating conditions (the extreme situations are usually referred to slow and fast pyrolysis).
In all these processes, the chemical phenomena begin with primary steps of biomass thermal degradation. These elementary pyrolysis processes give rise to several types of primary chemical species that can undergo further reactions, depending on the operating conditions of the reactor. These secondary reactions include gas phase (thermal cracking) and heterogeneous reactions (catalytic cracking, gas/char interactions, …). The scaling up to pilot and industrial levels of the knowledge obtained at the laboratory scale requires the establishment of models [
2]. These models must be written at two levels: primary pyrolysis of biomass particles (couplings between chemistry of biomass thermal decomposition, external and internal heat and mass transfers efficiencies inside the sample) and secondary phenomena (couplings between secondary chemical reactions, residence times distributions of solid and gas phases, heat and mass transfer resistances at the gas-solid interface inside the reactor). Actually, it is difficult to establish robust models because biomass is a very heterogeneous feedstock, each of its component having different physicochemical properties (chemical kinetics, enthalpies, thermal conductivities, heat capacities, optical properties, ...). Most of these parameters are still badly known from the literature. For example, the available chemical data often differ according to the type of laboratory facility in which they have been measured. In addition, these data are often used for the modelling of reactors inside which the thermal conditions are quite different from those prevailing in the laboratory device where they have been obtained. Such problems result from the difficulty to characterize the operating conditions on reliable basis.
Temperature and heating rate are the two main parameters which are usually considered by the authors. They are unfortunately never clearly defined [
3,
4]. For example, the temperature and heating rate values are often chosen as those of the external heat source, or of an undefined zone of the reactor. The definitions depend on the authors and/or on the type of experimental facility. The purpose of the present paper is to point out the significant mistakes that can be made when wrong assumptions are made in the values of temperature and heating rate defined at a reacting biomass particle level.
2. Temperature and Heating Rate of A Pyrolysing Biomass Particle
2.1. General modelling
Modelling of the competing phenomena occurring at the level of a reacting biomass particle has given rise to a great number of papers. The models rely on the solving the basic mass and energy balances under various experimental conditions. The purpose of the present paper is not to exhaustively review all related papers. However, and as examples, the References [
2,
5,
6,
7,
8,
9] can be considered. Many other references can be found as citations in these papers, notably in the recent review of Di Blasi [
8].
In order to simplify the problem and to highlight the problems connected with the definitions of temperature and heating rate, several simplifying assumptions will be made in the present paper.
Biomass pyrolysis gives usually rise to three phases: gases, condensable vapours and charcoal. Many types of related kinetic pathways have been published, from very simple to very complex ones. They usually include several elementary processes occurring in series or in competition. Several authors also include the formation of short life time intermediate species. They may be also different for cellulose, lignin and hemicelluloses (biomass main basic components) and also for usual biomasses according to their origins, inorganic contents, …etc. In order to simplify the problem, and in a first approximation, we shall suppose that the overall reaction can be represented by a simple elementary process of the type: Solid (biomass) gives Products. We shall also assume that mass transfer resistances are not limiting and that gaseous products escape freely out of the sample. Charcoal is expected to be rapidly eliminated (for example by attrition, as in a fluidized bed reactor), as well as primary intermediate liquids (for example by fast evaporation or by mechanical elimination, as in ablative reactors). It is also assumed that the superficial thicknesses of charcoal is small and does not influence heat transfer mechanisms.
The physical properties of biomass and main products do not change either with temperature, nor during the reaction. Biomass initial anisotropy is not taken into account.
The paper relies on the case of cellulose. Actually many works have been already published with this relatively well described material. In addition, and in order to compare the results presented in Subsections 2.2 and 2.3, it appears advisable to consider the material with which the authors cited in Subsection 2.3 have worked (see Reference [
12] reported in this section).
Several reported results have been obtained in the case of slab shaped particles. It can be shown that the conclusions would be quite similar with other shapes (such as a sphere, for example).
The reaction is assumed to be endothermic (constant enthalpy ΔH). The reaction is first order and the kinetic constant obeys an Arrhenius type law:
The rate of the chemical reaction is defined as:
where ρ is the biomass sample mass density.
The heat flux density transferred to the particle is defined as:
where h is the heat transfer coefficient. The heat exchange may occur by natural and free convection and/or by interaction with a hot surface (radiation and/or direct contact); T
S is the true biomass surface temperature; T
W is the heat source temperature. The paper will consider two cases: constant and time dependent values of T
W.
The heat transfer conditions are characterized by the Biot number Bi defined as:
where L
o is a characteristic initial size of the sample, and λ its heat conductivity.
Heat is assumed to be transferred by conduction inside the sample. The relative importances of internal transfer and chemical reaction is represented by the thermal Thiele modulus:
where C
p is the sample heat capacity.
The values of several parameters can be varied for sensitivity calculations. The chosen standard case corresponds to the values already used in reference [
6] and recalled below:
h = 103 W m−2 K−1 (this value is observed in ablative pyrolysis; in the case of gaseous convective heat transfer, h is about 50 times lower).
TW = 1200 K; λ = 0.2 W m−1 K−1; Cp = 2800 J kg−1 K−1; ρ = 700 kg m−3; ΔH = 40,000 J kg−1; ko = 2.83 × 1019 s−1; E/R = 29,000 K.
These values have been obtained from experimental measurements for cellulose properties, as well as the estimation of heat transfer coefficient.
2.2. First case of a fixed external heat source temperature TW
This situation is usually observed in the case of pilot plants, industrial facilities and in most of reactors operating under steady state conditions. It corresponds to the case where a biomass particle initially at room temperature is suddenly immersed into a fixed high temperature medium.
2.2.1. Chemical and ablation regimes [6,10].
Modelling of the phenomena occurring at the particle level shows that its overall behaviour may be represented according to the respective values of Bi and M numbers. Two limiting cases can be considered.
For small Bi and M values, the temperature and chemical rate are uniform inside the whole volume of the particle. The overall reaction is controlled by elementary chemical processes and the reaction occurs in the whole volume. It is the chemical regime which is, for example, observed in the case of small sized particles.
For large Bi and M values, a steep temperature gradient exists in the sample. The reaction occurs inside a thin (a few tens of microns) external layer moving towards the still cold heart of the solid. The overall reaction is controlled by close couplings between heat transfer and chemistry. It is the ablation regime which is mainly observed in the case of large sized particles.
2.2.2. Chemical regime
Actual biomass temperature
The results [
5,
6,
7] of the modelling show that after a certain time of heat up (without any reaction), the particle suddenly begins to react (pyrolysis reaction). Then, and after a fraction of a second (depending on the physical parameters and heating conditions), the uniform particle temperature stabilizes as long as the reaction proceeds. For example, in the case of our standard case, the variations of T
S between 10 and 90% conversion is only 74 K. To be noticed that the actual value of reacting biomass temperature at 50% conversion is of the order of 767 K,
i.e., 433 K lower than that of the heat source temperature (T
W = 1200 K for our standard case).
The model shows that this difference TW – TS increases when E decreases, E being the most sensible parameter. This temperature stabilization effect (referred on the basis of time) is more important for high ΔH values. However the influence of ΔH is low: multiplying ΔH by a factor of 100 induces a decrease of only 50 K for TS. It can be shown that decreasing h leads to a decrease of TS (a decrease of about 40 K for a h value divided by a factor of 10) and hence to an increase of the stabilization effect. For h = 100 Wm−2K−1, the TS value is about 727 K. Finally, the influence of TW is also small: varying TW from 900 to 1500 K induces a change of TS of only 30 K at 50% conversion. It is hence useless to significantly increase the heat source temperature in the hope of increasing the actual biomass pyrolysis temperature. Obviously, assuming TS = TW may lead to considerable errors in reactor modelling and/or kinetic constants measurements.
The “fusion like” model reported by several authors [
11,
12] during biomass pyrolysis is a consequence of these results. In a previous paper [
13] the thermal decomposition of a solid particle has been modelled. The results show that the phenomenon of reaction temperature stabilization at values which are much lower than that of the heat source exists for any kind of reaction of the type: Solid gives Products. An empirical relationship has been proposed for calculating an estimate of the actual reaction temperature (T
R):
This relationship is quite general and valid for most of conditions (kinetic constants, enthalpies, …) encountered in any type of solid particles reactions.
F, usually close to 1, has been introduced in order to take into account second order deviations (less than 5%) revealed in the modelling (see Reference [
13]).
The relationship (6) shows that the important parameter is E (T
R is proportional to E). The other ones situated inside a Logarithm have relatively less importance. Relationships (6) and (7) have been validated in the case of NaHCO
3 decarbonation reaction. It is also valid in the present case of biomass pyrolysis. Let us choose a small Lo value of 10
−5 m (in order to ensure the conditions required for a chemical regime (Bi ≅ 0.05)). On the basis of the numerical values of our standard case, it is possible to calculate a reaction temperature of 774 K, in quite good agreement with the value derived from the complete modelling (767 K, see above). It is also quite consistent with the well known “fusion temperature” of biomass estimated at around 740 K [
11,
14,
15]. Once again, these results show the very large differences that can exist between actual biomass and heat source temperatures (more than 400 K), even for very small particles. Such a simplified assumption often made in the literature is thus quite inconsistent.
These effects can be explained by the results of a competition between the heat flux demand for the endothermal pyrolysis reaction and the available external heat flux density
. Equation (3) shows, however, that after the onset of the process the value of
decreases regularly as T
S increases (mainly during preheating and the beginning of the reaction). Such a phenomenon is an additional reason that can explain the temperature stabilization phenomenon. It can be very important in the case of pyrolysis reactors operating under a prescribed external temperature T
W which is only slightly higher than that of pyrolysis. It is, of course, less important in the case of facilities operating under prescribed heat flux densities. This is, for example, the case when biomass samples are submitted to a controlled radiant flux density as in an image furnace [
2,
16] or a solar concentrator [
17].
Actual biomass heating rate
The complete numerical integration of energy and mass balances at the level of a small (chemical regime, i.e. small Bi and M numbers) reacting particle provides the time evolution of the sample temperature T
S [
5,
7]. As mentioned above, the temperature increases regularly before slowing down and stabilizing as soon as the reaction begins. In other words, the biomass actual heating rate (dT
S/dt) is a continuously decreasing function of time t. To be noticed that α is maximum at t = 0, with the corresponding value:
where T
o is the initial (ambient) temperature of the particle and t
e the heat transfer time constant.
Under the present standard conditions (and for To = 300 K and Lo = 10−5 m), we can calculate αo = 4.6 × 104 K s−1. It can be shown that for a conversion of 50%, the heating rate is about 10 times lower, due to the temperature stabilization effect. The α values are even lower for higher conversions.
It thus appears difficult to define an accurate and representative value of biomass heating rate. The value αo at t = 0 could be a priori recommended. Indeed αo is proportional to h and hence representative to the available external heat flux density imposed by the reactor properties. It is also independent of the chemical characteristics of the pyrolysis reaction. However Equation (8) shows that for a given solid, αo depends on its initial size (Lo) and requires a knowledge of ρ and Cp.
Other definitions of α could be considered, for example on the basis of the mean temperature increase between two given times or biomass conversion yields. However, such calculations require the definition of a conversion interval and can be only made on the basis of the complete modelling of the particle pyrolysis. Unfortunately, the model relies on values of several pyrolysis chemical data (kinetics, enthalpy, …) which are usually badly known. The mean heating rate could be also defined over the total time of complete conversion. However the final time of reaction is difficult to accurately estimate in most of usual facilities and also difficult to mathematically define for conversions which are close to 100%.
2.2.3. Ablation regime and comparison with chemical regime [6]
Solving the model in the case of high Bi and M numbers (ablation regime, often associated to large Lo values of thick samples) shows that the reaction occurs inside a thin peripherical layer moving at a given velocity towards the heart of the sample.
Actual biomass temperature
It is now very difficult to define a temperature of the biomass sample because of the existence of steep internal temperature gradients. Indeed, in ablation regime, the heart of the sample may be at a temperature close to the ambient, with no reaction, while the peripherical layer is hot and reacts. However, it can be shown that inside this thin layer the temperature gradients do not exceed about 70 K. As in the chemical regime, this temperature is also much lower than that of the heat source.
For given TW and h values, the mean temperature of the reacting layer is even lower than in the case of the chemical regime. The difference may reach about 100 K. Actually, in the case of the chemical regime, the external available heat flux is first only used for the heating up, followed by the pyrolysis of the whole sample. In the case of ablation, only a fraction of the flux is transferred by conduction towards the heart of the solid for preheating, the other fraction being used for peripheral pyrolysis. Compared with the case of the chemical regime, the dependence of pyrolysis temperature with experimental and chemical parameters are qualitatively the sames. However, the influence of ΔH is less important, while the influences of h and TW are more significant.
These results are important because they show that for a given external temperature (TW) and transfer conditions (h), the temperature at which biomass reacts is not the same, depending on its size. A consequence is the possibility of different final selectivities. For example, if more complex kinetic pathways (such as competitive processes having different activation energies) are considered. Of course, this conclusion does not apply in conditions of pure chemical regime (studied in Subsection 2.2.2) where the sample temperature does not depend significantly on Lo.
Actual biomass heating rate
We have seen that in the case of the chemical regime, the heating rate is difficult to define. However, for a given particle, it is the same at any point of the isothermal sample and it depends only on the conversion extent. In the case of the ablation regime, the definition of heating rate is much more complicated. Actually, it depends on the time t but also on the location inside the thick sample. It is maximum only at the beginning of the process (t = 0) and at the sample surface when it is initially submitted to the external heat flux. As the reaction begins, the heating rate inside the thin hot layer considerably decreases (as in the case of the chemical regime). At that time, the biomass zones located just behind the ablation layer begin to be heated. The corresponding heating rate is lower than in the case t = 0 because less flux density is locally available. During these processes, the heating rate of the central parts of the sample is 0 because they are still at To. The heating rate of this sample heart will only increase when reached by the moving hot reacting front.
It should be noted that for given external heat transfer conditions, the heating rate arbitrarily defined at the level of the ablation layer is much lower than the heating rate defined over the reaction period in chemical regime.
Defining mean values of the heating rate (for example on the basis of the time for total conversion) in the ablation regime is also difficult, because, as in the case of the chemical regime, it would be necessary to solve complete modelling relying on badly known chemical data. This time is experimentally also very hard to define. In addition, for a given outside temperature and heat transfer conditions, such values of mean heating rates would depend on the initial size of the sample.
In conclusion, both steep and time dependent temperature and heating rate gradients exist inside a thick pyrolysing biomass sample (ablation regime). It is thus even more difficult than in the chemical regime to define an accurate, representative and universal value of biomass thick sample heating rate.
2.3. Second case of a biomass sample exposed to a heat source whose temperature increases with time
In order to simplify the problem, T
W is expected to increase linearly with time t:
where β
e is the external heating rate.
This case is encountered in several laboratory scale facilities and mainly in thermogravimetric analysis (TGA). In most of the usual TGA devices, the values of βe vary approximately inside the range 0.1–100 K min−1 (1.67 × 10−3–1.67 K s−1). These low external heating rates associated to relatively low final TW values are usually associated to slow pyrolysis studies.
In other devices, sometimes used to simulate fast pyrolysis conditions, the biomass sample heating occurs through more or less direct contact with a metallic wire which is rapidly electrically heated [
18,
19]. Very high heat source temperatures T
W (much higher than 1000 K) and heating rates β
e of several thousand K s
−1 are claimed.
The aim of this section is to study the biomass behaviour in the cases of very slow and very fast external heating rates. Only the case corresponding to small Bi numbers will be considered since these laboratory devices usually operate with small biomass sample sizes and masses. The same model presented in the previous sections can be solved with the only new assumption given by Equation (9).
2.3.1. Biomass temperature
Under the usual conditions of TGA (low β
e values) the modelling results show [
20] that the actual temperature T
S of the biomass sample is roughly the same as that of the heat source. For example, for β
e = 0.1 K s
−1, the maximum difference (T
W – T
S) does not exceed 10 K. However, it rapidly increases with β
e. In their paper, Narayan and Antal [
12] report the results of an extensive modelling study of the phenomena. The variations of the thermal lag T
W – T
S and sample heating rate are studied as a function of several parameters. Their model accounts for thermocouple thermal lag and thermal lag due to heat demand by the chemical pyrolysis reaction. Their results clearly confirm that the difference T
W – T
S rapidly increases with β
e. A strong stabilization of sample temperature T
S is also observed as in the case of fixed T
W value (see previous section). The authors show that the thermal lag T
W – T
S decreases when h decreases and increases with ΔH. They confirm that it significantly increases with the external heating rate β
e and may theoretically exceed several hundred K. For example for β
e = 100 K s
−1, T
W – T
S may reach about 1200 K. To be noticed that this thermal lag is not constant and varies during the sample conversion, sometimes passing through a maximum value. The authors have not extended their calculations to conditions of very high values of β
e (see above), but we can expect the existence of considerable T
W – T
S differences. It can be concluded that biomass temperature may be very different from that of the heat source, except in the case of usual TGA operating under small heating rate conditions.
Narayan and Antal [
12] also show that inside their large range of parameter values, the roughly stabilized pyrolysis temperature is situated between about 600 and 700 K. These values are quite similar as those calculated in the previous section in the case of ablation regime and constant T
W. They are, thus, lower than in the case of chemical regime under constant T
W. This means that for a given small biomass mass sample (small Bi) and same external heat transfer efficiency (h), biomass does not pyrolyse at the same temperature when submitted to a fixed or to an increasing value of heat source temperature T
W. In the case of complex pyrolysis kinetics pathways, it could hence be illicit to use results obtained in laboratory scale devices (increasing T
W) for the modelling of pilot plant reactors (constant T
W).
2.3.2. Actual Biomass sample heating rate βs
It should be noted that the actual biomass heating rate β
s considered in the present
Section 2.3 (see Reference [
12]) should not be confused with the values of biomass heating rates α and α
e defined in
Section 2.2 in the case of a fixed external heat source temperature. Under the conditions of small external heating rates encountered in usual TGA, the calculations of Narayan and Antal [
12] show that the actual sample heating rate β
s is close to β
e at any moment during the conversion. This is in agreement with the observations made in the previous section for T
S.
However, above about 1 K s
−1, β
s may considerably differ from β
e, with the differences increasing rapidly with β
e (and as the heat transfer coefficient h decreases). In these conditions, β
s usually passes through a minimum (value always lower than β
e)
vs. biomass conversion before a sharp increase above about 80–90% conversion. On the basis of these minimum values of β
s, it is possible to calculate the β
s/ β
e ratio. For given physical, chemical and heat transfer parameters, this ratio decreases as β
e increases. For the maximum value of β
e (100 K s
−1) considered by Narayan and Antal [
12], the ratio value is 0.11 (and hence β
s = 11 K s
−1). A very rough extrapolation of the authors results to a very high β
e value of 10
4 K s
−1 (values claimed in the case of hot wire experiments) show that the β
s/ β
e ratio would be of the order of 0.02 corresponding to an actual biomass heating rate β
s of only 200 K s
−1.
3. Discussions and Conclusions
Biomass pyrolysis conditions and severity are often characterized in the literature by two parameters: temperature and heating rate. On the basis of a simplified model, the present paper has dealt with the influence of the reactor thermal conditions on the actual biomass temperature and heating rate. For the sake of simplification, only the case of cellulose has been considered. The main results are:
Biomass reacts inside a narrow range of temperatures in both cases of external fixed and linear increase values of temperature.
The actual biomass temperature may be much lower than that of the heat source. In the chemical regime and with high external temperatures, the differences may reach several hundred K. Thus, even for small particles, it is quite inconsistent to suppose that the reaction occurs at the external heat source temperature.
The narrow domains of reaction temperatures are different depending on whether the particle is submitted to a low external heating rate or to an external fixed heat source temperature. Thus, kinetic results derived in TGA experiments should not be used for modelling a fast pyrolysis reactor (for example a fluidized bed).
Sensitivity calculations show that the conclusions do not significantly depend on the parameters used in our standard case [
6,
13].
The temperature stabilization phenomenon results from a competition between available heat flux density and heat flux density demand for pyrolysis.
The consequences of the thermal lag existing between heat source and actual pyrolysis temperatures may be important at two levels:
For kinetic measurements. An overestimation of T
S resulting from the simple assumption that biomass reacts at the same temperature as that of the heat source, leads to a strong increase of the calculated kinetic constant value. For example, with the kinetic parameters chosen in our standard case (and with fixed T
W value and assumption of chemical regime), a T
S overestimation of only 100 K results in an increase of the kinetic constant value by a factor close to 100. To be noticed that Narayan and Antal [
12] have clearly suggested that thermal lag is the underlying cause of the compensation effect in kinetic values reported in the literature.
For reactor behavior. The present paper deals with the only primary process of biomass pyrolysis. Actually, the primary pyrolysis products may undergo further secondary reactions as soon as they leave the reacting particle. They include for example thermal cracking inside the gas phase. It appears that any modelling of the reactor should take into account the fact that primary pyrolysis and secondary cracking reactions do not occur at the same temperature.
The range of actual pyrolysis temperature is lower in ablation (thick samples of biomass) than in chemical (small particles) regime, for the same external heat transfer conditions. This result would be very important if more complex primary kinetic schemes (including several elementary processes of different activation energies) would be considered. In such cases we could expect different selectivities in the charcoal, vapour and gas fractions in the cases of small and thick samples. However, this conclusion does not theoretically apply inside the pure chemical regime domain where the sample temperature does not significantly depend on the size L
o [
6].
All these problems result from competitive basic phenomena (chemistry, transfers, …) and hence cannot be avoided by technological solutions. For example, biomass size reduction does not lead to a better knowledge of biomass pyrolysis temperature since we have shown that similar phenomena exist for thick and also small samples. They are also valid in any type of continuous reactor operating under conditions of fixed heat source temperature (TW). Hence, our conclusions apply whatever the reactor design.
In usual experiments performed in TGA, the actual biomass sample heating rate is close to that of the external heating rate of the TGA facility. However, for values higher than about 1 K s−1, the differences may be very high. It is, for example, the case where small biomass particles are heated by more or less contact with a heated metallic wire. It is interesting to notice that in such cases, the sample heating rate can be higher if heated under the influence of a high external fixed heat source temperature.
In any case, it is difficult, in practice, to define an accurate sample heating rate. For small particles, it regularly decreases as a function of time: it is maximum as soon as the biomass is submitted to the hot external medium. It is much lower during the reaction (stabilization effect). For bigger particles, the heating rate is still more difficult to define as it depends of time and of the location inside the sample.
The actual biomass temperature and heating rate can be obtained only from the modelling of the phenomena occurring at the particle level. This is a difficult task as the physicochemical parameters that are needed for modelling are often badly known. Apart from the usual case of TGA experiments, the concept of heating rate should be avoided for the characterization of biomass pyrolysis phenomena.
All the conclusions of this paper are derived on the basis of a very simple first order pyrolysis kinetics scheme where biomass thermally decomposes for giving products which are expected to be immediately eliminated from the sample. However, in the case of big pieces of biomass, charcoal can accumulate on the biomass surface under the form of a thick layer on the biomass surface through which heat is now transferred by conduction. In that case, we can expect that the temperature difference between reacting biomass and heat source is still increased. Anyway, the conclusion of this paper would have to be further validated in the case of more complex modellings. In a recent paper, Authier
et al. [
2] report the theoretical results of a more complex modelling comparing Lagrangian and Eulerian approaches of thick wood samples pyrolysis. The results clearly confirm the temperature stabilization effect at the biomass/char interface.
Actually, the direct experimental measurements of biomass temperature and heating rate are very difficult because often related to small moving particles undergoing fast reaction, under the influence of high external heat flux densities. New methods of temperature measurements adapted to these severe conditions should be imagined.
The pyrolysis processes are usually differentiated into fast and slow pyrolysis, depending on operating conditions. Such a classification usually relies on temperatures and heating rates [
21]. These parameters are never clearly defined by the authors, each one having his own references. Because of the practical difficulties in measuring these parameters, other criteria would have to be imagined. Among them, the heat flux density under which is submitted the sample could be a new basis for a first differentiation between fast and slow pyrolysis conditions. Actually, if this parameter is difficult to measure, it can be well estimated in the case of many usual gas solid reactors, mainly in the case of convective and/or conductive exchanges. In the case of radiative exchange, other difficulties arise from the bad knowledge of solid optical properties (however this drawback disappears as soon as biomass is covered with a thin black char layer). For laboratory scale studies, facilities such as the image furnace [
16] bring the advantage to provide prescribed and controlled heat flux densities at the sample surface. However, a drawback of using the heat flux density criterium in process reactors, is that it may decrease as the process occurs, mainly during the heating up where T
s sharply increases (see Equation (3)). However, this drawback vanishes as soon as pyrolysis begins because of the temperature stabilization effect. In the case of convective exchange the heat transfer coefficient would be, hence, a more advisable criterium.
All the conclusions of this paper also apply in the cases of any other types of solids undergoing thermal decomposition reactions.