Crowbar System in Doubly Fed Induction Wind Generators
Abstract
:Nomenclature
| DFIG | Doubly Fed Induction Generator |
| VRRIG | Variable Rotor Resistance Induction Generator |
| SCIG | Squirrel Cage Induction Generator |
| EESG | Electrical Excited Synchronous Generator |
| PMSG | Permanent Magnet Synchronous Generator |
| IGBT | Insulated Gate Bipolar Transistor |
| TSO | Transmission System Operator |
| RSC | Rotor Side Converter |
| GSC | Grid Side Converter |
| DC | Direct Current |
| CB | Circuit Breaker |
1. Introduction
| Rank | Country | MW | % |
|---|---|---|---|
| 1 | USA | 25.170 | 20.8 |
| 2 | Germany | 23.903 | 19.8 |
| 3 | Spain | 16.754 | 13.9 |
| 4 | China | 12.210 | 10.1 |
| 5 | India | 9.645 | 8.0 |
| 6 | Italy | 3.736 | 3.1 |
| 7 | France | 3.404 | 2.8 |
| 8 | UK | 3.241 | 2.7 |
| 9 | Denmark | 3.180 | 2.6 |
| 10 | Portugal | 2.862 | 2.4 |
| Rest of the world | 16.693 | 13.8 | |
| Total of the 10 first | 104.104 | 86.2 | |
| Total | 120.798 | 100.0 |
| Manufacture | Country | negotiated MW in 2008 | % | Electrical Generator |
|---|---|---|---|---|
| Vestas | Denmark | 5.647 | 19.0 | DFIG |
| GE Energy | USA | 5.350 | 18.0 | DFIG |
| Gamesa | Spain | 3.270 | 11.0 | DFIG |
| Enercon | Germany | 2.675 | 9.0 | EESG |
| Suzlon | India | 2.080 | 7.0 | VRRIG |
| Siemens | Germany | 2.080 | 7.0 | DFIG |
| Sinovel | China | 1.486 | 5.0 | DFIG |
| Goldwind | China | 1.189 | 4.0 | PMSG |
| Acciona WP | Spain | 1.189 | 4.0 | DFIG |
| Nordex | Germany | 1.189 | 4.0 | DFIG |
| Total by others manufacturers | 3.569 | 12.0 | ||
| Total | 29.724 | 100.0 | ||
2. Dynamic Model of Wind Turbines Based on the Doubly Fed Induction Generator (DFIG)
2.1. Aerodynamic Model
- Tm = Mechanical torque (N.m)
- Pm = Mechanical power (W)
- A = Swept area by the turbine rotor (m2)
- R = Turbine rotor radius (m)
- ρ = Air density (kg/m3)
- V = Wind speed (m/s)
- Cp = Power coefficient (or performance coefficient)
- λ = Tip speed ratio (ωm.R/V)
- ωm = Angular speed of the wind turbine (rad/s)
- β = Blade pitch angle (degree)
| c1 | c2 | c3 | c4 | c5 | c6 | c7 | c8 | c9 |
|---|---|---|---|---|---|---|---|---|
| 0.73 | 151 | 0.58 | 0.002 | 2.14 | 13.2 | 18.4 | –0.02 | –0.003 |
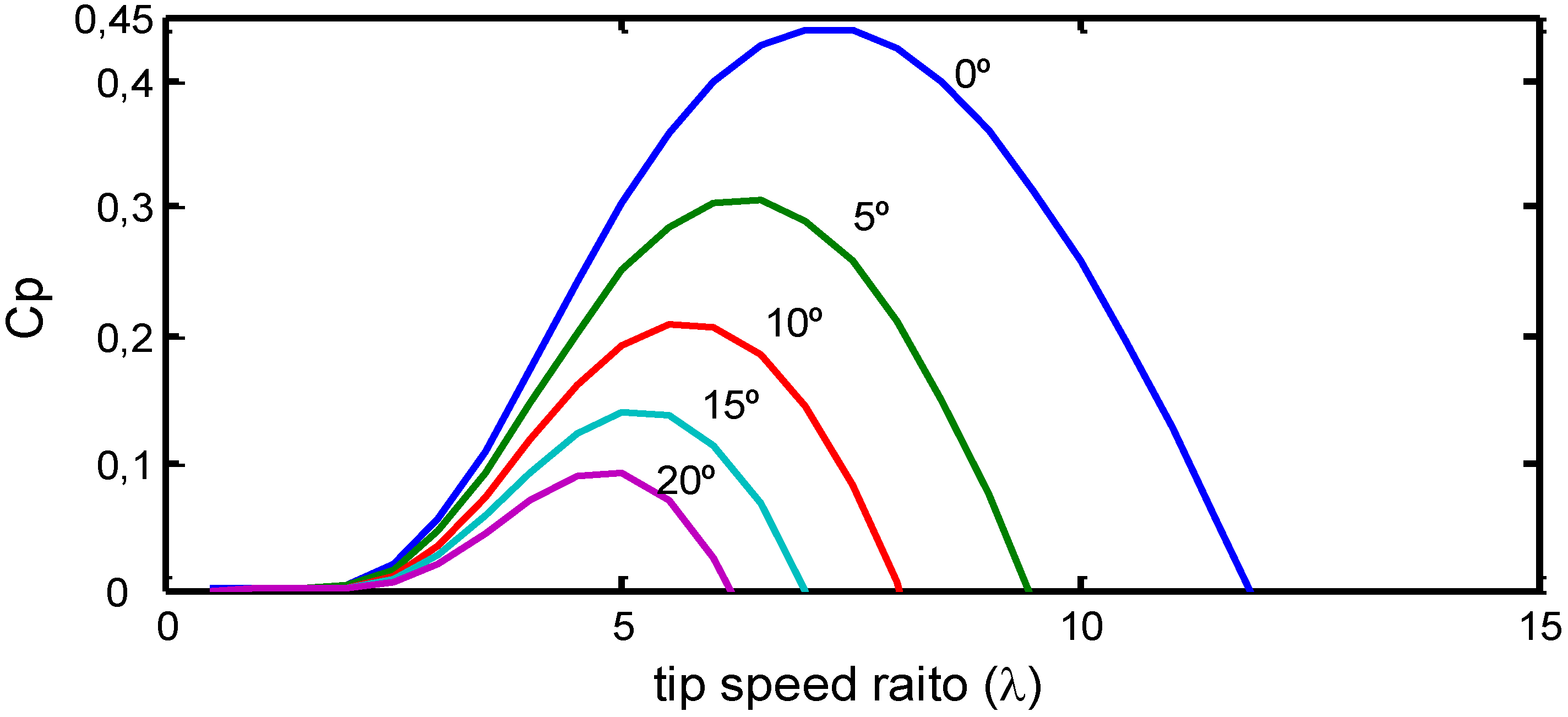
2.2. Electrical Model

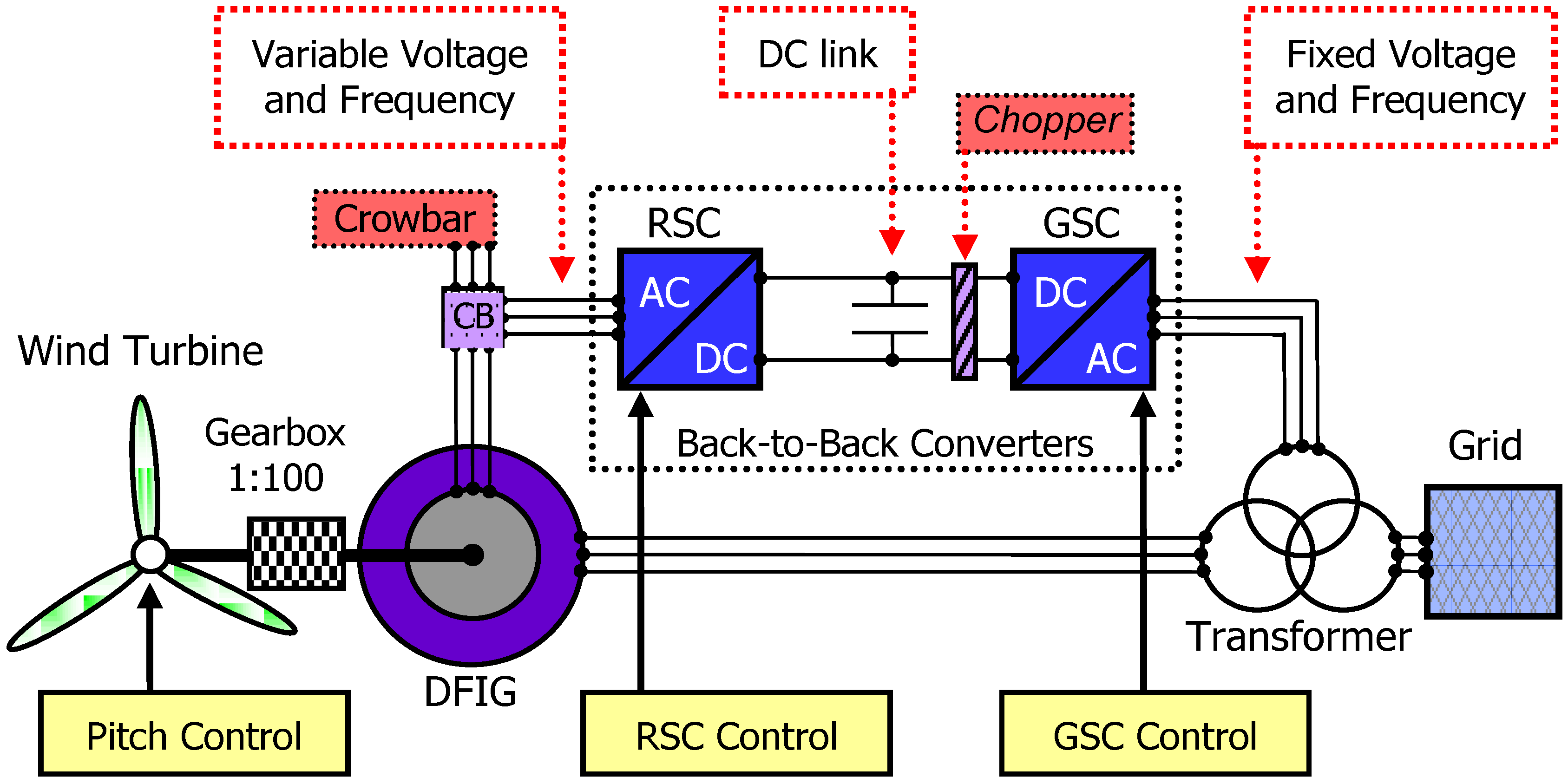
- Disconnection of the rotor windings from the RSC.
- Insertion of the three-phase resistance in series to the rotor windings (crowbar system).
- Disconnection of the crowbar system from the rotor windings.
- Reconnection of the RSC to the rotor windings.
3. The Induction Generators Stability and the Critical Rotor Speed


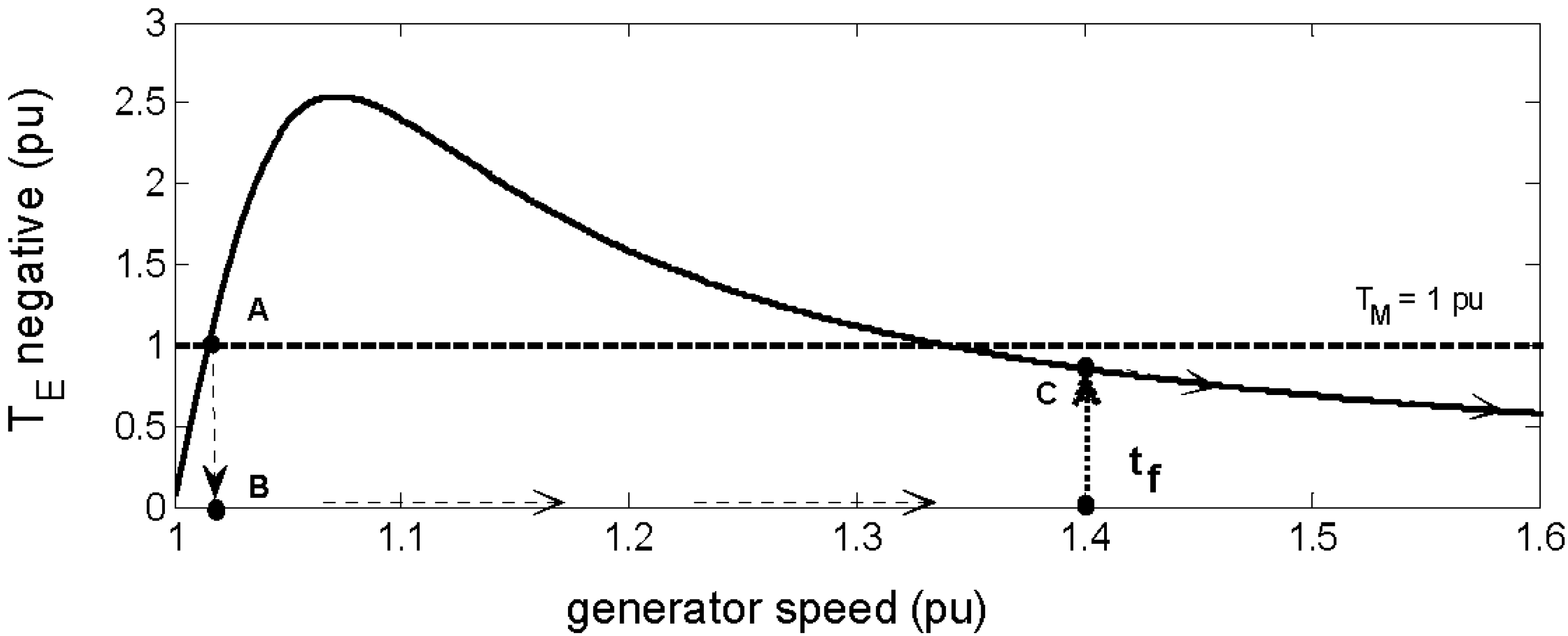
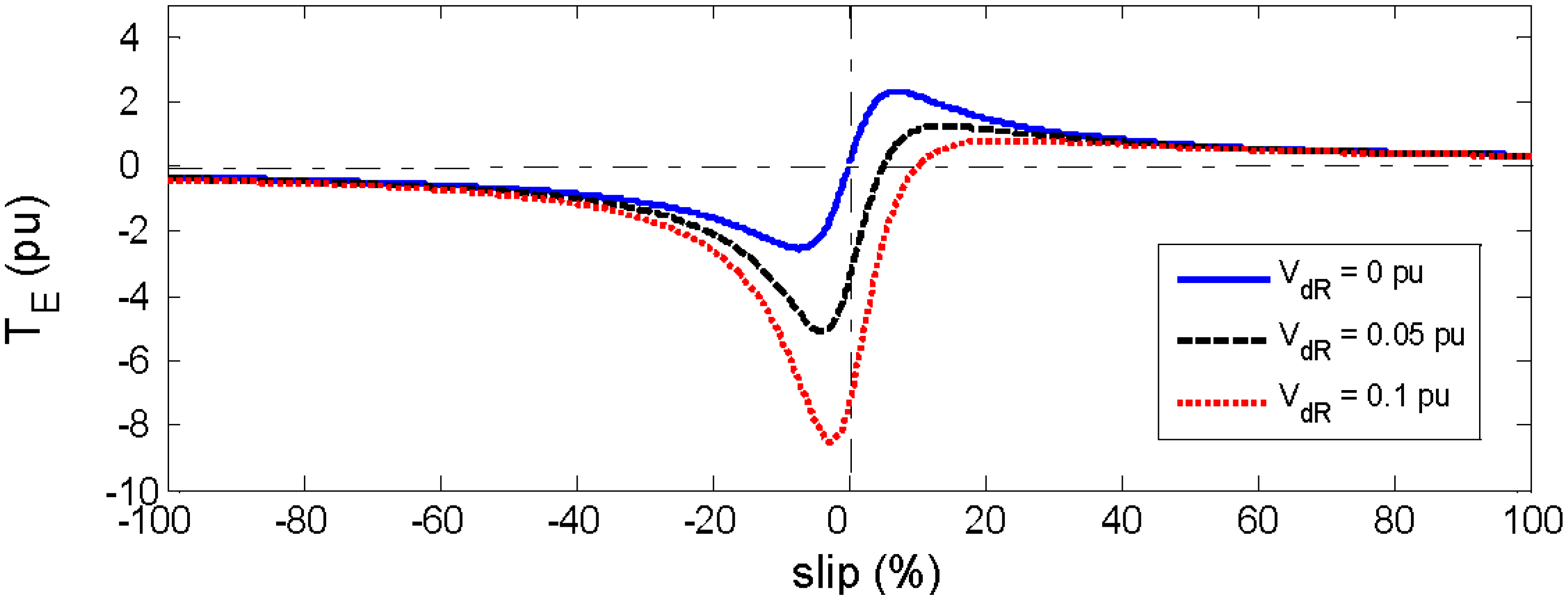
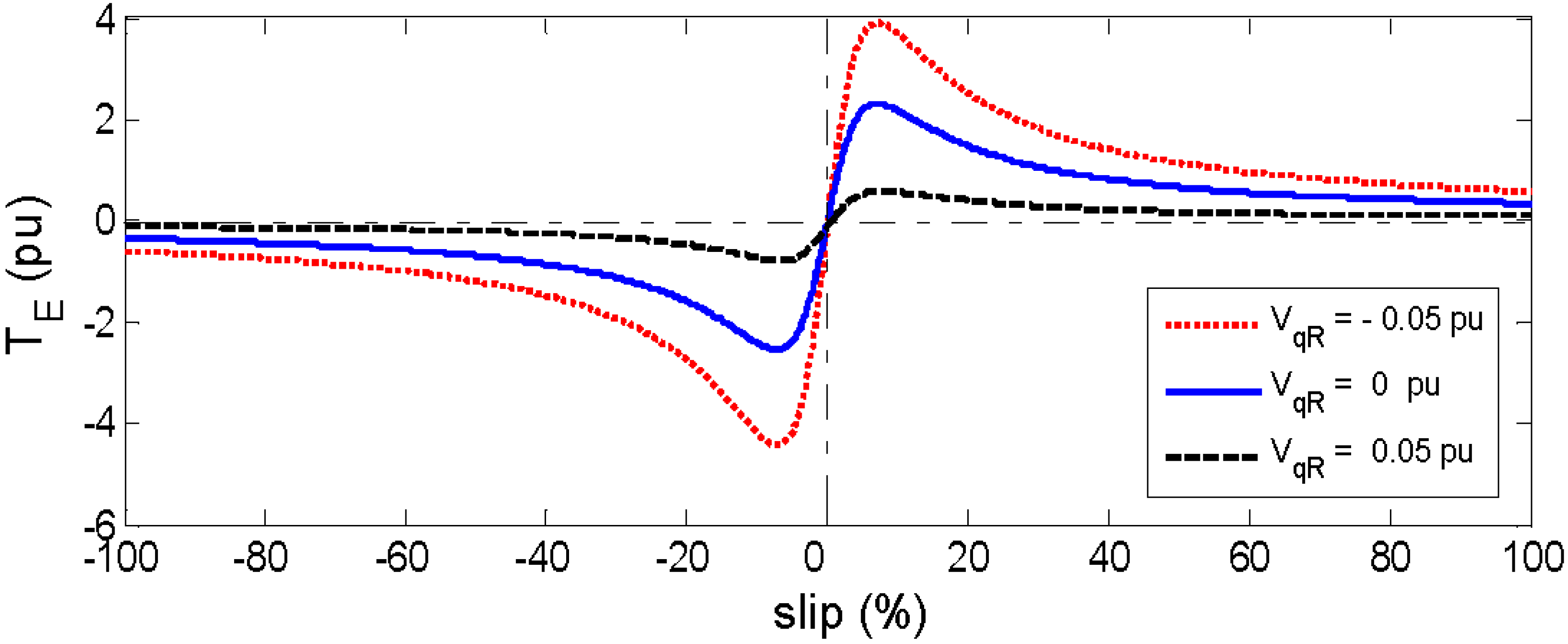
4. The Dynamic Analysis of the Crowbar System Actuation during Grid Faults
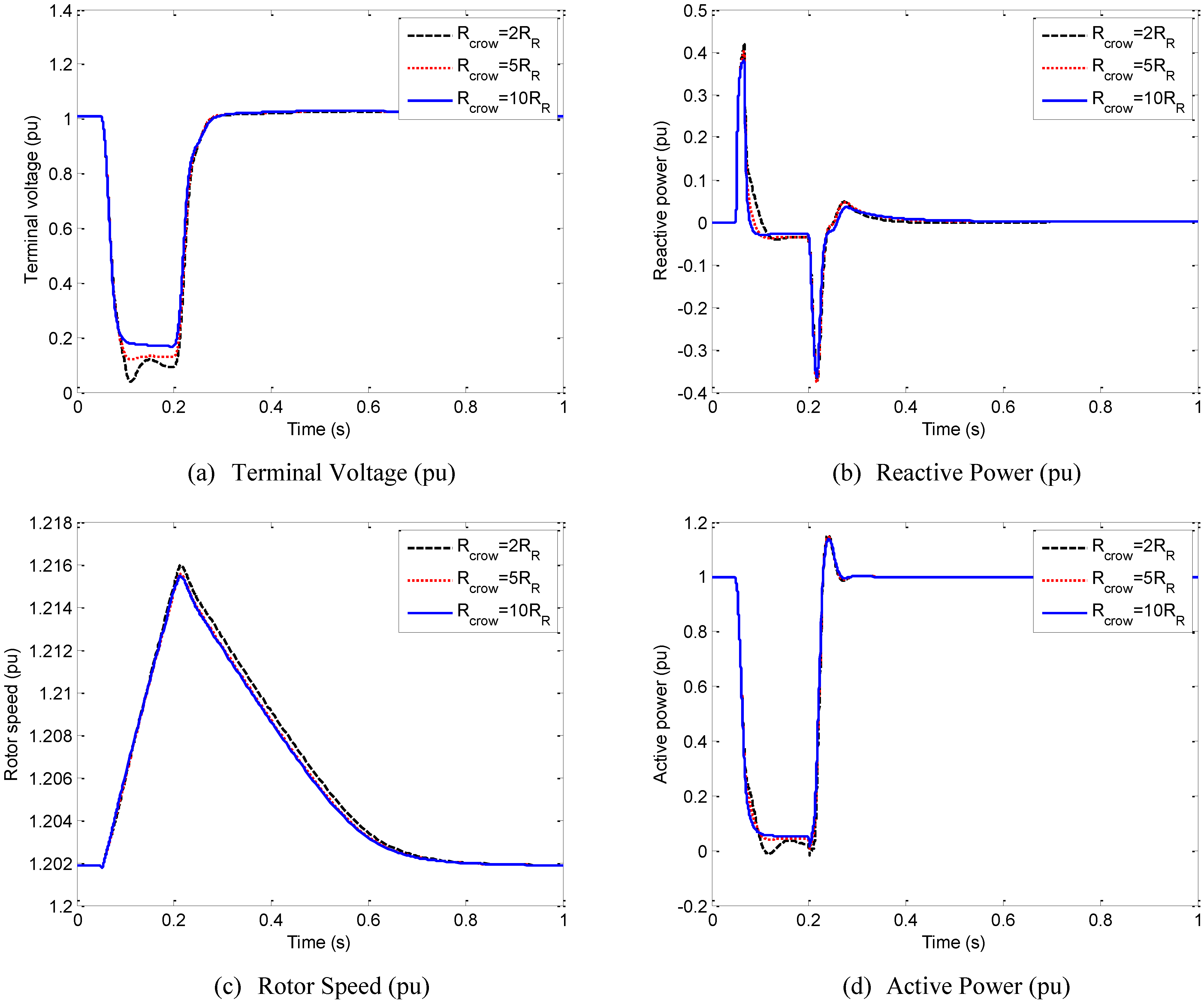
4.1. Influence of the Crowbar Resistance Value (Rcrow)

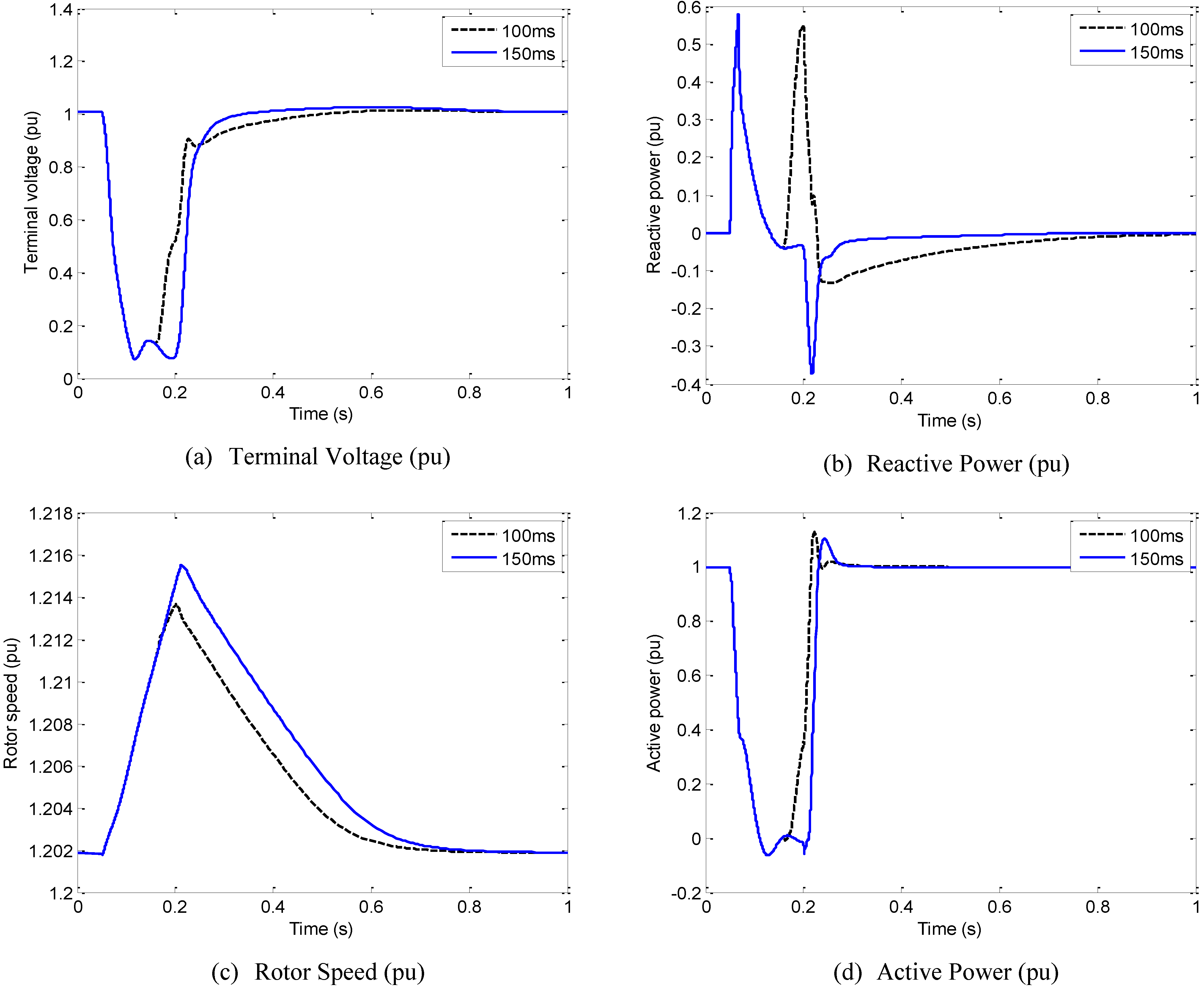
4.2. Influence of the Crowbar System Operation Time
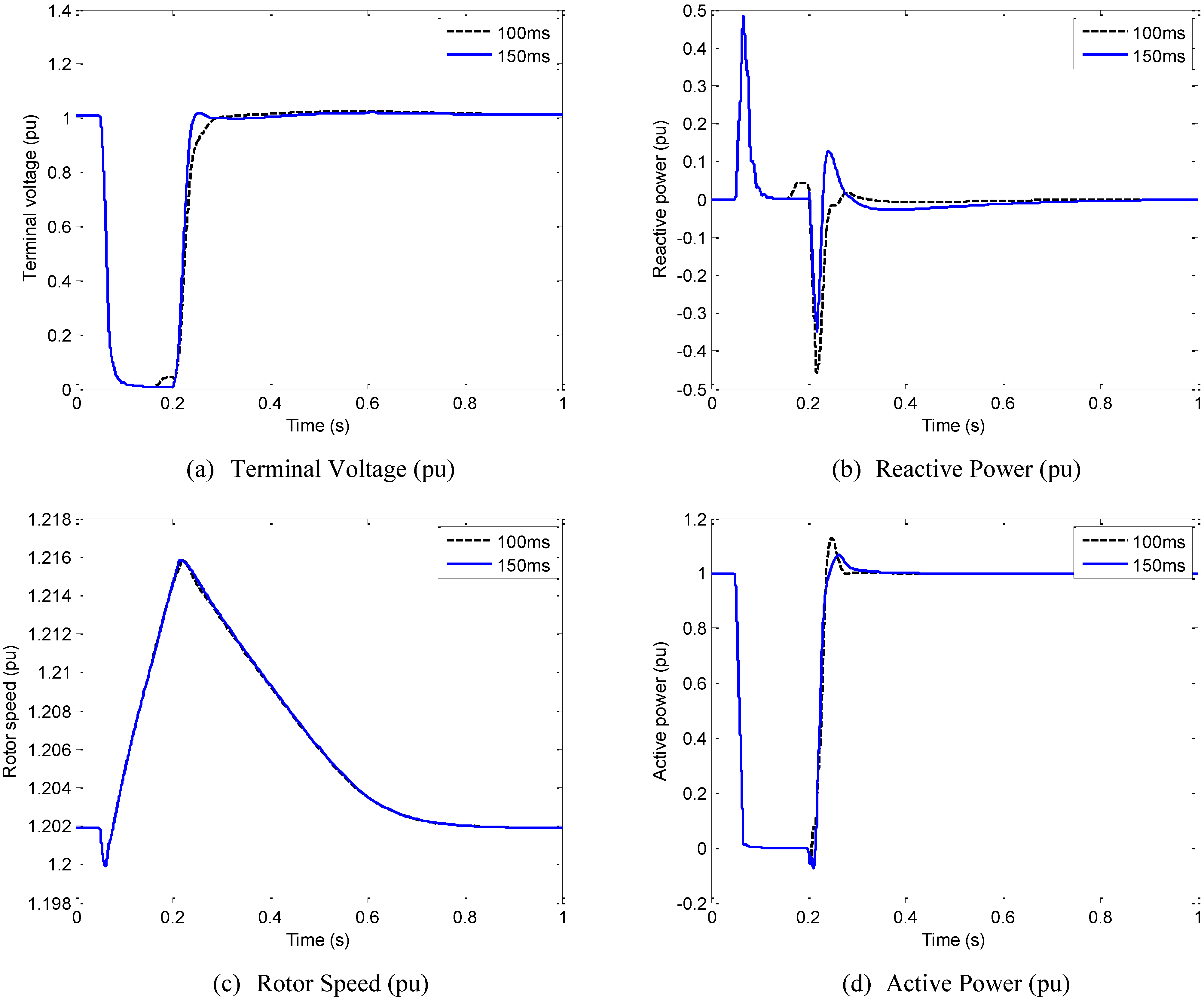
5. Conclusions
Acknowledgements
References
- European Wind Energy Association. Wind Energy—The Facts: A Guide To The Technology, Economics And Future Of Wind Power; Earthscan Publications: London, UK, March 2009. [Google Scholar]
- Global Wind Energy Council. Global Wind 2008 Report. Available online: http://www.gwec.net/fileadmin/documents/Global%20Wind%202008%20Report.pdf (accessed on 10 December 2009).
- ANEEL. Brazilian Information Data of Power Generation. Available online: http://www.aneel.gov.br/aplicacoes/capacidadebrasil/capacidadebrasil.asp (accessed on 10 December 2009).
- Emerging Energy Research. Global Wind Turbine Supply Market Share Update. Available online: http://www.environmentalleader.com/wp-content/uploads/2009/03/wind-turbine-market-share.jpg (accessed on 10 December 2009).
- Molly, J.P. Status der Windenergienutzung in Deutschland—Stand 31.12.2008 (in German). DEWI GmbH. Available online: http://www.wind-energie.de (accessed on 10 December 2009).
- Li, H.; Chen, Z. Overview of Different Wind Generator Systems and their Comparisons. IET Renew. Power Generat. 2008, 2, 123–138. [Google Scholar] [CrossRef]
- Morren, J.; de Haan, S.W.H. Ridethrough of Wind Turbines with Doubly-fed Induction Generator during a Voltage Dip. IEEE Trans. Energy Convers. 2005, 20, 435–441. [Google Scholar] [CrossRef]
- Ullah, N.R.; Thiringer, T.; Karlsson, D. Voltage and Transient Stability Support by Wind Farms Complying With the E.ON Netz Grid Code. IEEE Trans. Power System 2007, 22, 1647–1656. [Google Scholar] [CrossRef]
- Grid Code: High and Extra High Voltage. E.ON Netz GmbH Tech. Rep., Status: 1. Available online: http://www.eon-netz.com (accessed on 10 December 2009).
- Requisitos de Respuesta frente a Huecos de Tensión de las Instalaciones Eólicas. BOE no. 254. 2006, pp. 37017–37019. (in Spanish). Available online: http://www.ree.es/operacion/pdf/po/PO_resol_12.3_Respuesta_huecos_eolica.pdf (accessed on 10 December 2009).
- Grilo, A.P.; Mota, A.A.; Mota, L.T.M.; Freitas, W. An Analytical Method for Analysis of Large-Disturbance Stability of Induction Generators. IEEE Trans. Power Syst. 2007, 22, 1861–1869. [Google Scholar] [CrossRef]
- Akhmatov, V. Analysis of Dynamic Behaviour of Electric Power Systems with Large Amount of Wind Power. Ph.D. Thesis, Technical University of Denmark, Denmark, 2003. Available online: http://www.dtu.dk/upload/institutter/_oersted/eltek/research/00-05/05-va-thesis.pdf (accessed on 10 December 2009). [Google Scholar]
- Slootweg, J.G.; Polinder, H.; Kling, W.L. Representing Wind Turbine Electrical Generating Systems in Fundamental Frequency Simulations. IEEE Trans. Energy Conv. 2003, 18, 516–524. [Google Scholar] [CrossRef]
- Kundur, P. Power System Stability and Control; McGraw-Hill: New York, NY, USA, 1994. [Google Scholar]
- SimPower Systems—User's Guide: Version 5. Math Works. Available online: http://www.mathworks.com/access/helpdesk_r13/help/pdf_doc/physmod/powersys/powersys.pdf (accessed on 10 December 2009).
- Sauer, P.W.; Pai, M.A. Power System Dynamics and Stability; Prentice Hall: Upper Saddle River, NJ, USA, 1998. [Google Scholar]
- Salles, M.B.C.; Cardoso, J.R.; Grilo, A.P.; Rahmann, C.; Hameyer, K. Control Strategies of Doubly Fed Induction Generators to Support Grid Voltage. In Proceedings of IEEE International Electric Machines and Drives Conference—IEMDC'09, Miami, FL, USA, May 2009.
- Seman, S.; Niiranen, J.; Arkkio, A. Ride-Through Analysis of Doubly Fed Induction Wind-Power Generator Under Unsymmetrical Network Disturbance. IEEE Trans. Power Syst. 2006, 21, 1782–1789. [Google Scholar] [CrossRef]
- Samuelsson, O.; Lindahl, S. On Speed Stability. IEEE Trans. Power Syst. 2005, 20, 1179–1180. [Google Scholar] [CrossRef]
- Kundur, P.; Paserba, J.; Ajjarapu, V.; Andersson, G.; Bose, A.; Canizares, C.; Hatziargyriou, N.; Hill, D.; Stankovic, A.; Taylor, C.; Van Cutsem, T.; Vittal, V. Definition and Classification of Power System Stability IEEE/CIGRE Joint Task Force on Stability Terms and Definitions. IEEE Trans. Power Syst. 2004, 19, 1387–1401. [Google Scholar] [CrossRef]
- Storer, N.W. Three-Wire System for Variable Speed Motor Work. Transactions of the AIEE 1902, 20, 127–133. [Google Scholar]
- Submódulo 3.6 – Requisitos Técnicos Mínimos para a Conexão à Rede Básica. Operador Nacional do Sistema (ONS), Resolução Normativa 372/09. Agosto 2009. (in Portuguese)
© 2010 by the authors; licensee Molecular Diversity Preservation International, Basel, Switzerland. This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Salles, M.B.C.; Hameyer, K.; Cardoso, J.R.; Grilo, A.P.; Rahmann, C. Crowbar System in Doubly Fed Induction Wind Generators. Energies 2010, 3, 738-753. https://doi.org/10.3390/en3040738
Salles MBC, Hameyer K, Cardoso JR, Grilo AP, Rahmann C. Crowbar System in Doubly Fed Induction Wind Generators. Energies. 2010; 3(4):738-753. https://doi.org/10.3390/en3040738
Chicago/Turabian StyleSalles, Maurício B. C., Kay Hameyer, José R. Cardoso, Ahda. P. Grilo, and Claudia Rahmann. 2010. "Crowbar System in Doubly Fed Induction Wind Generators" Energies 3, no. 4: 738-753. https://doi.org/10.3390/en3040738
APA StyleSalles, M. B. C., Hameyer, K., Cardoso, J. R., Grilo, A. P., & Rahmann, C. (2010). Crowbar System in Doubly Fed Induction Wind Generators. Energies, 3(4), 738-753. https://doi.org/10.3390/en3040738




