Numerical Experiments Providing New Insights into Plasma Focus Fusion Devices
Abstract
:1. Introduction
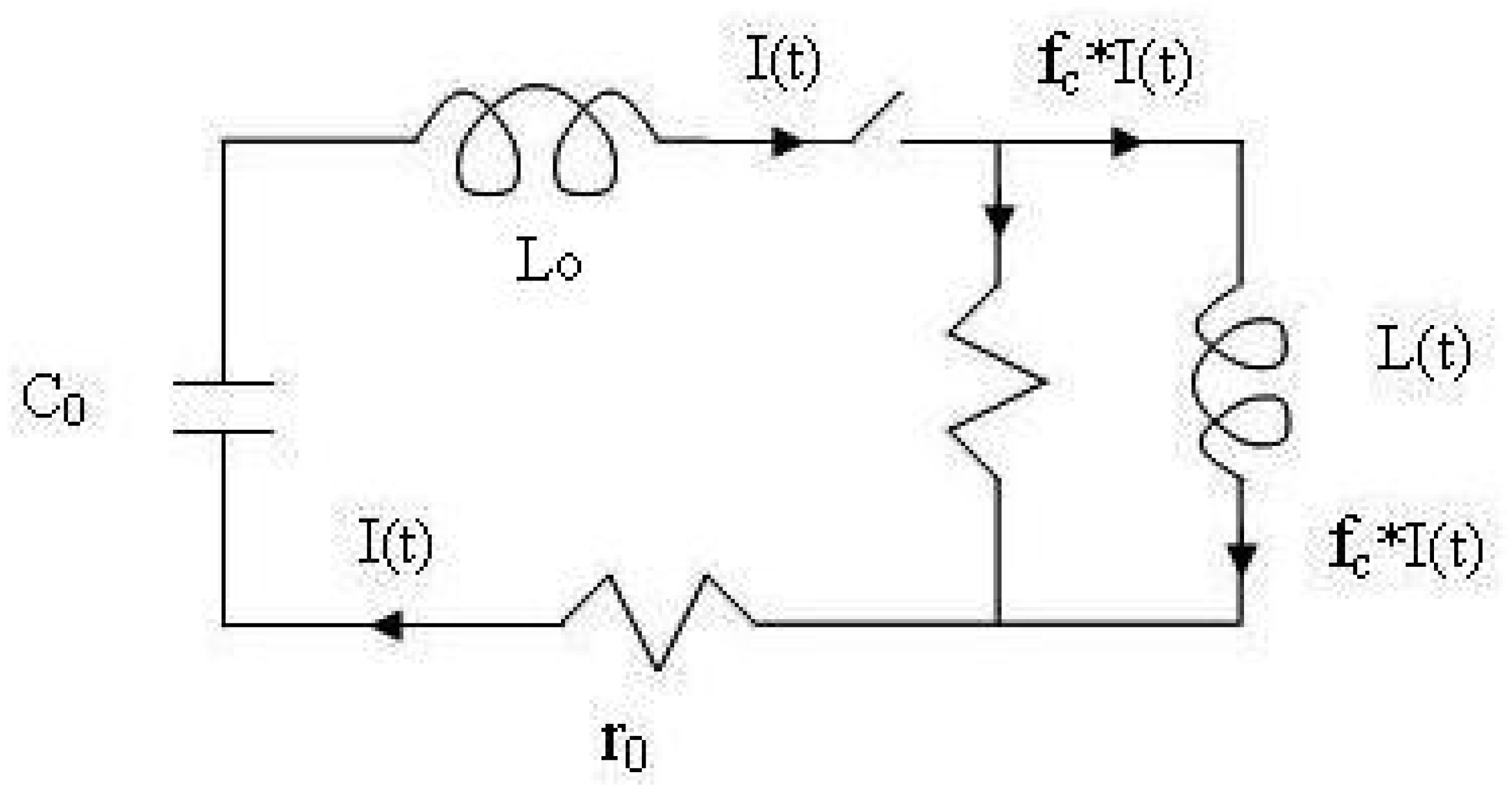
2. The 5-Phase Lee Model Code
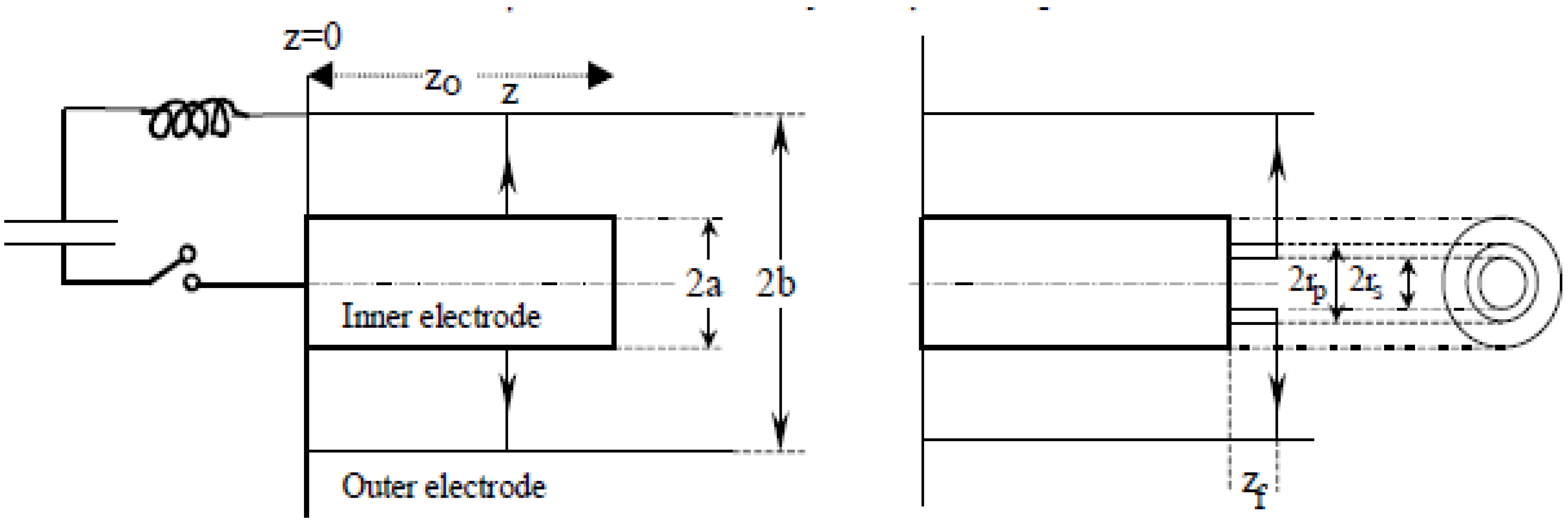
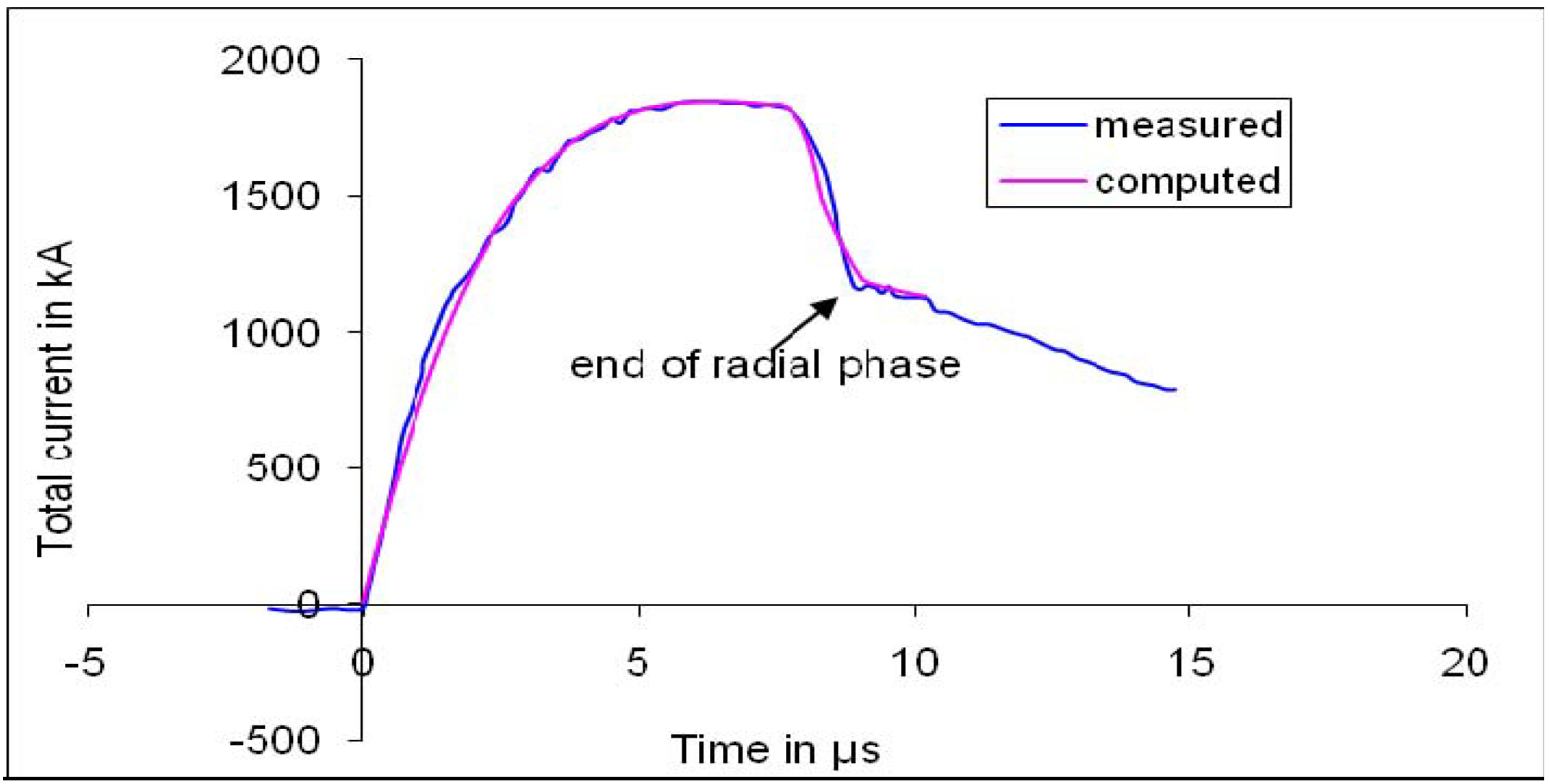
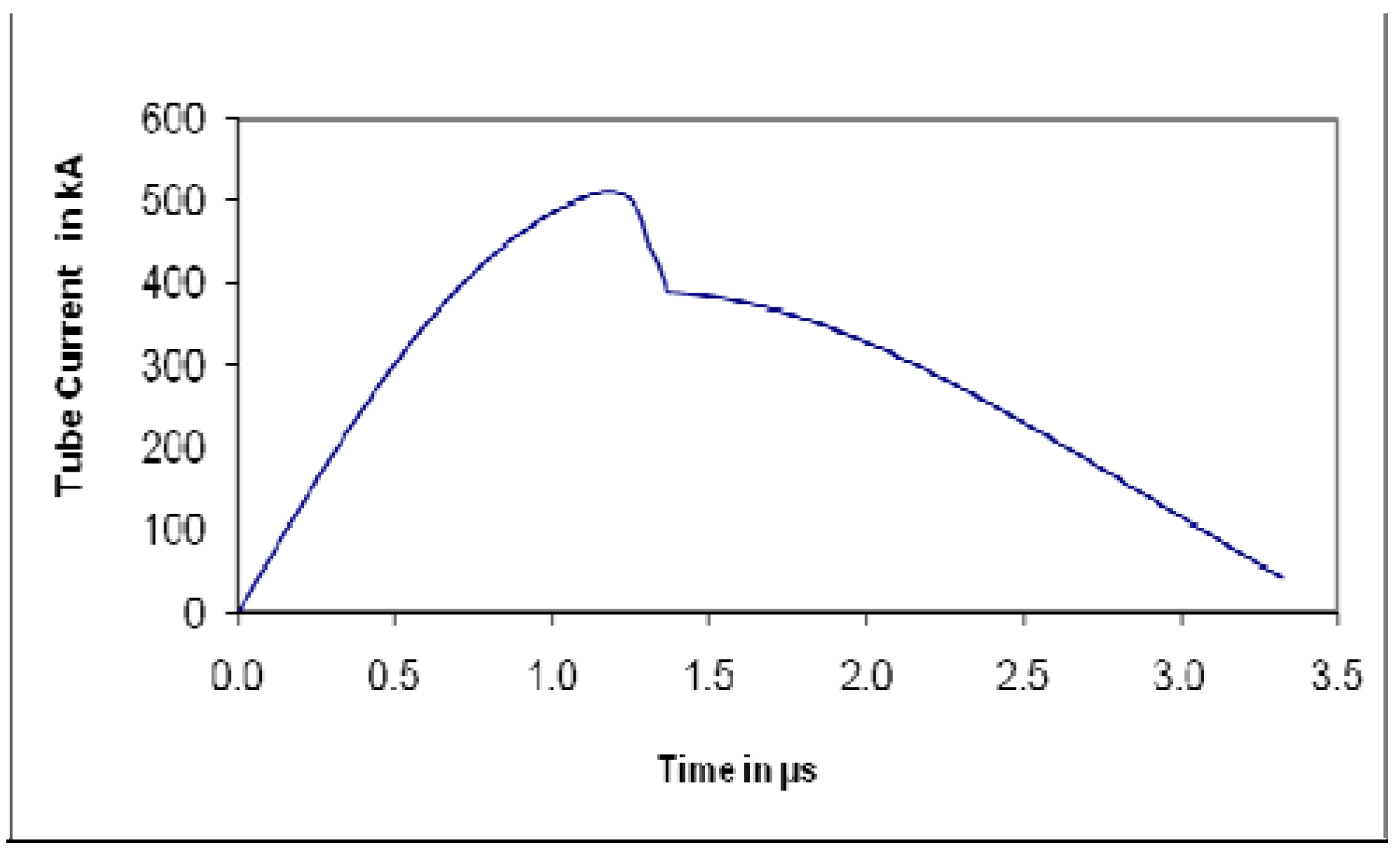
2.1. From Measured Current Waveform to Modeling for Diagnostics
- Bank parameters, L0, C0 and stray circuit resistance r0;
- Tube parameters b, a and z0 and
- Operational parameters V0 and P0 and the fill gas.

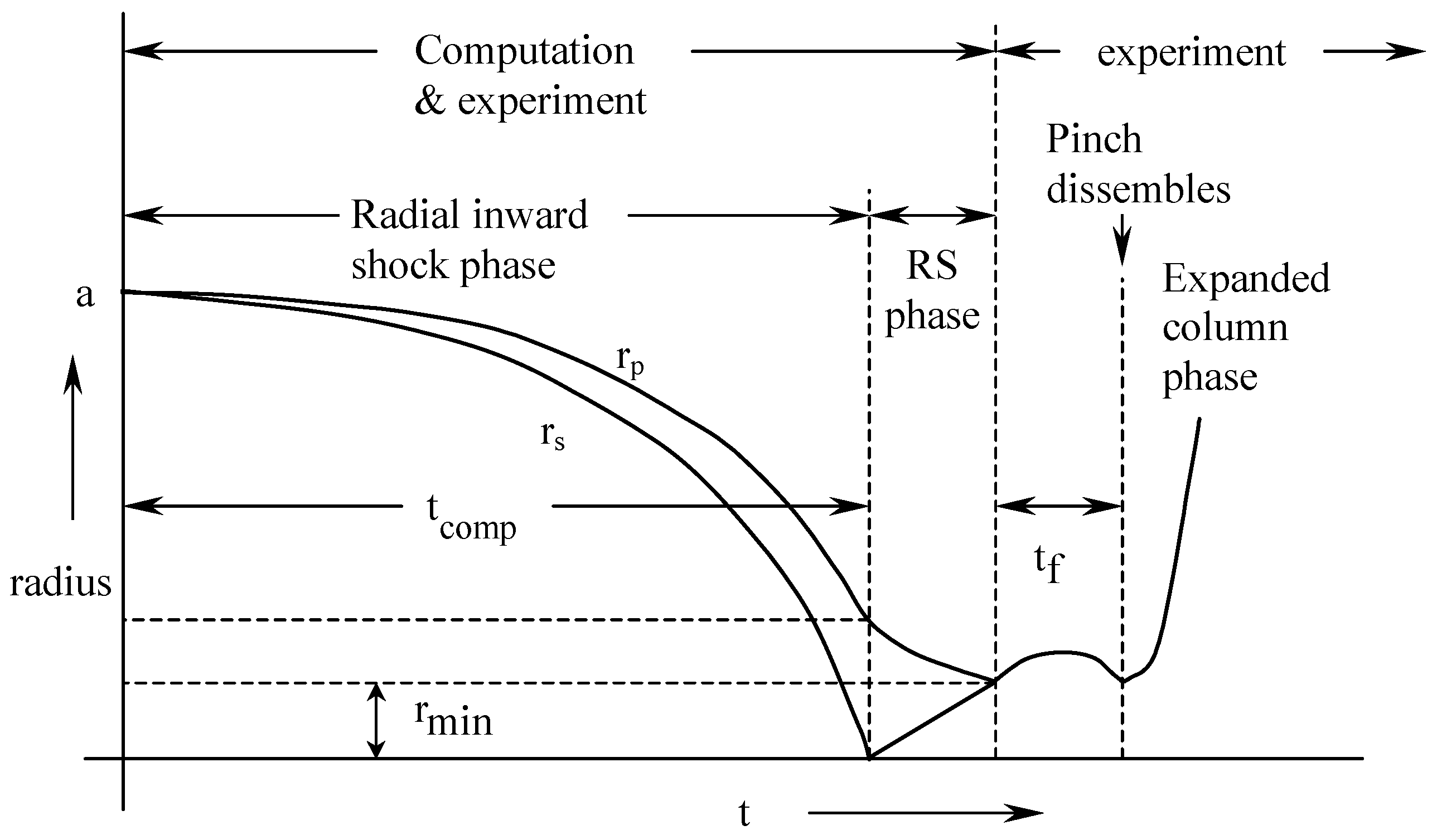
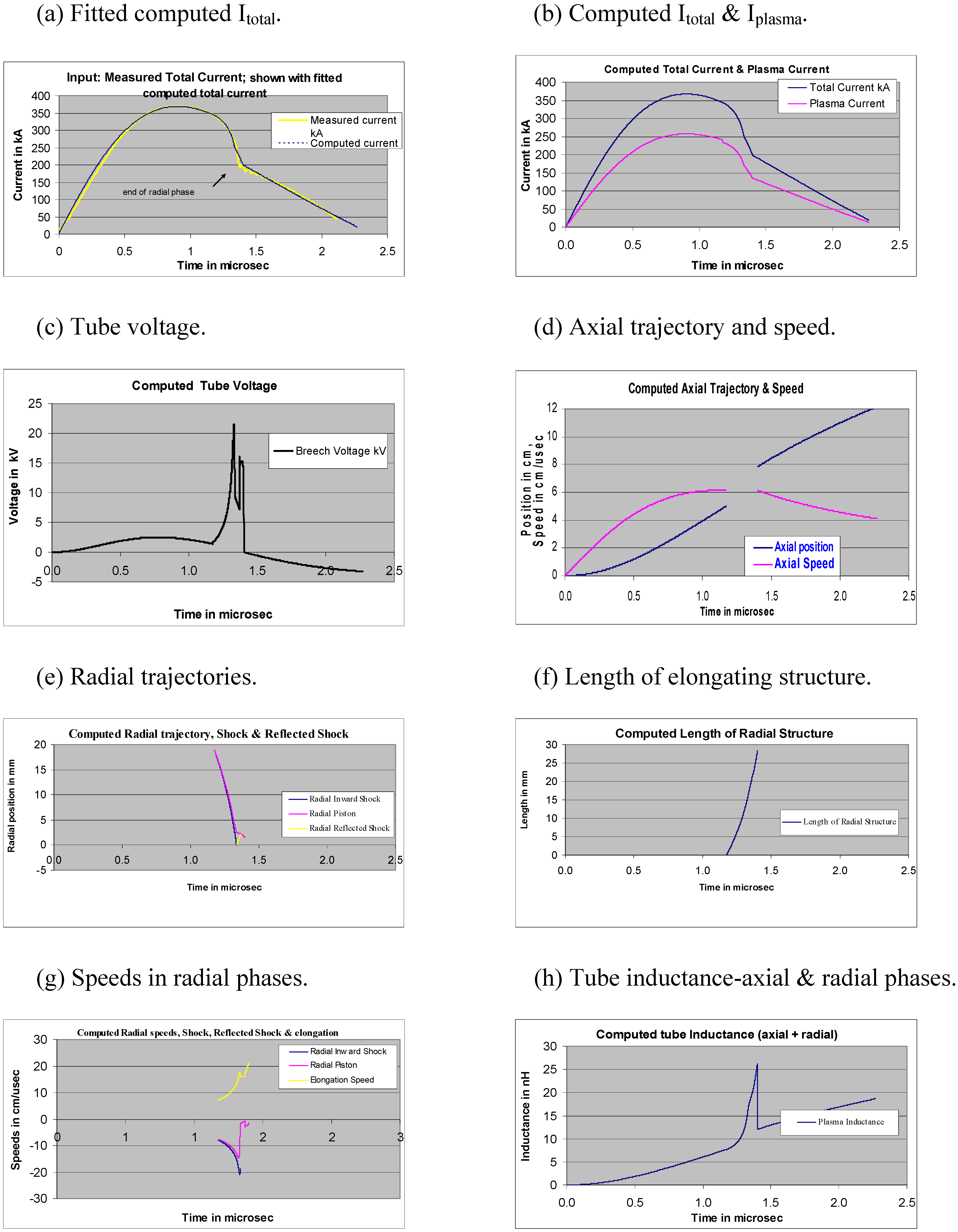
2.2. Diagnostics-Time Histories of Dynamics, Energies and Plasma Properties Computed from the Measured Total Current Waveform by the Code
2.3. Comments on Computed Quantities
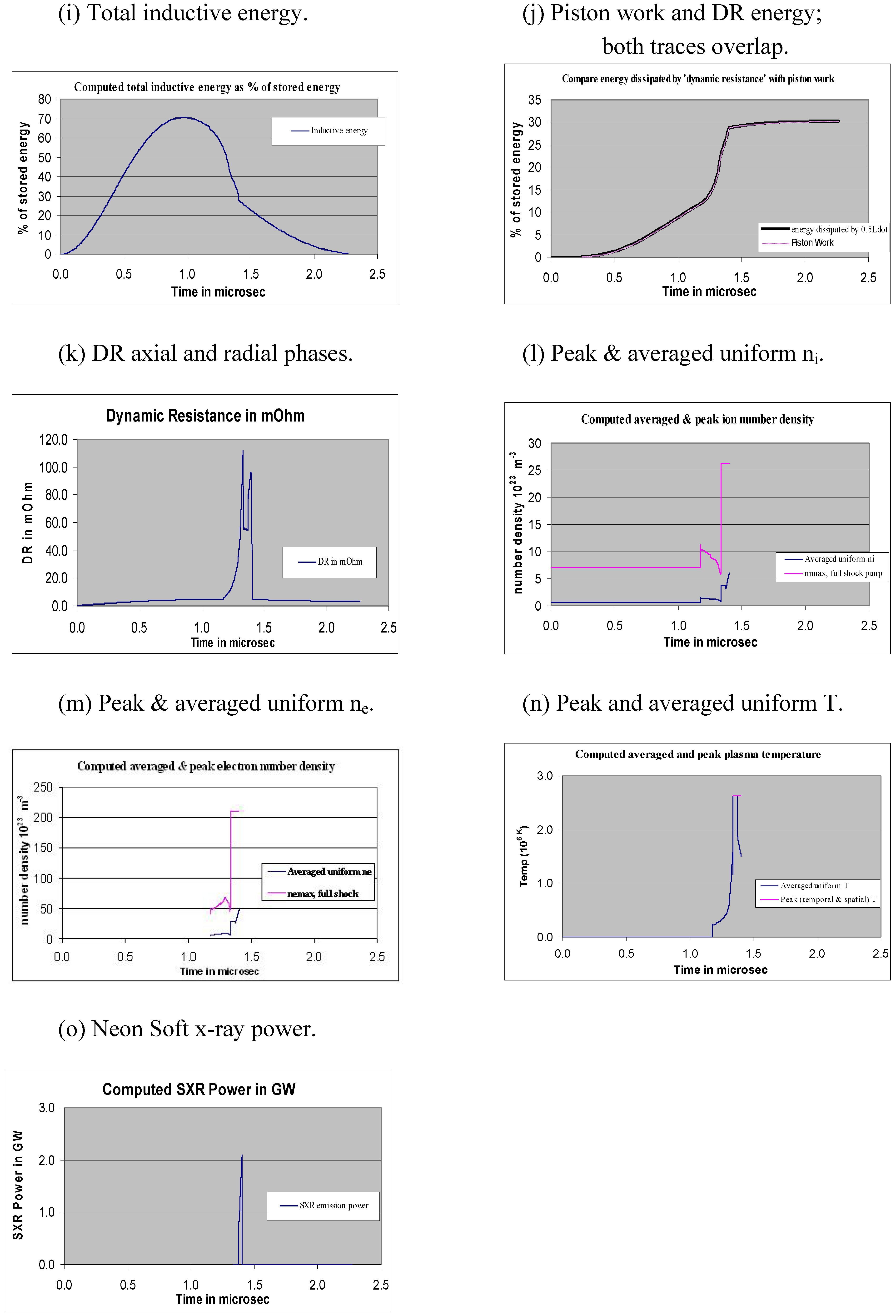
3. Insight 1-Pinch Current Limitation Effect as Static Inductance Is Reduced towards Zero
3.1. Optimum L0 for Maximum Pinch Current and Neutron Yield
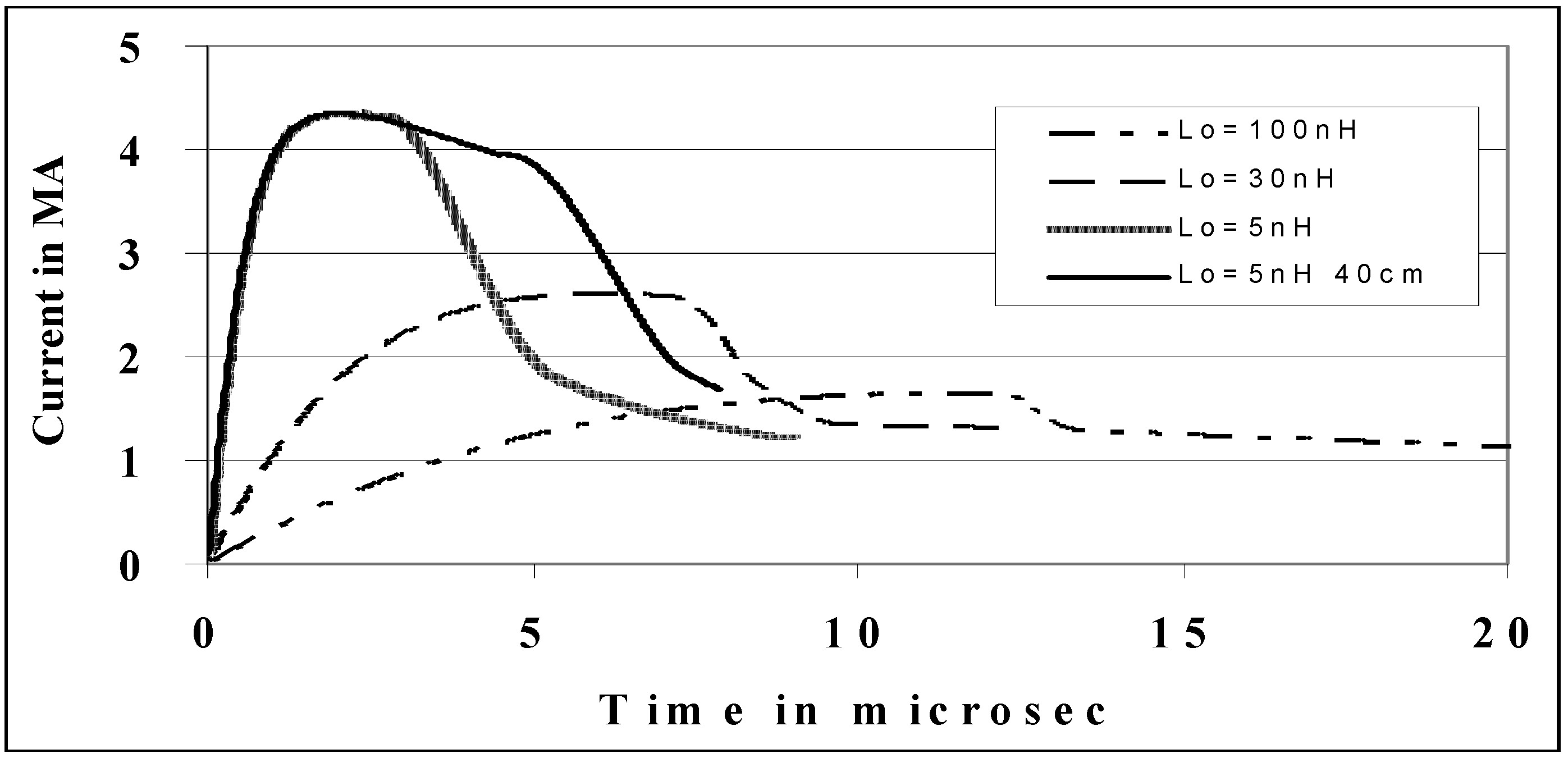
| L0(nH) | b(cm) | a(cm) | z0(cm) | Ipeak(MA) | Ipinch(M) | Yn(1011) | Ipinch/ Ipeak |
|---|---|---|---|---|---|---|---|
| 100 | 15.0 | 10.8 | 80 | 1.66 | 0.96 | 2.44 | 0.58 |
| 80 | 16.0 | 11.6 | 80 | 1.81 | 1.00 | 2.71 | 0.55 |
| 60 | 18.0 | 13.0 | 70 | 2.02 | 1.03 | 3.01 | 0.51 |
| 40 | 21.5 | 15.5 | 55 | 2.36 | 1.05 | 3.20 | 0.44 |
| 35 | 22.5 | 16.3 | 53 | 2.47 | 1.05 | 3.20 | 0.43 |
| 30 | 23.8 | 17.2 | 50 | 2.61 | 1.05 | 3.10 | 0.40 |
| 20 | 28.0 | 21.1 | 32 | 3.13 | 1.03 | 3.00 | 0.33 |
| 10 | 33.0 | 23.8 | 28 | 3.65 | 1.00 | 2.45 | 0.27 |
| 5 | 40.0 | 28.8 | 20 | 4.37 | 0.97 | 2.00 | 0.22 |

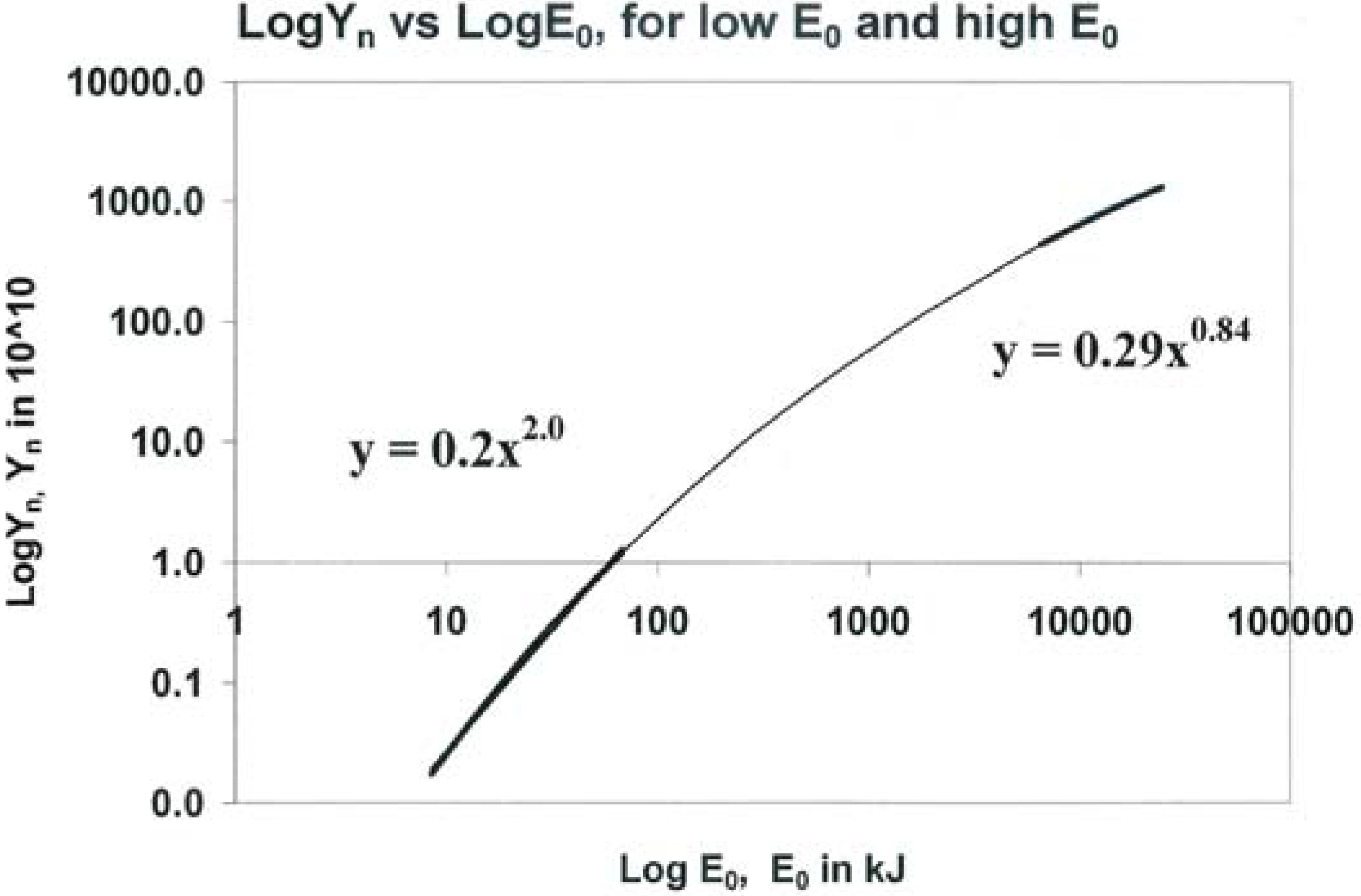
4. Insight 2-Scaling Laws for Neutron
4.1. Computation of Neutron Yield-describing the Beam-target Mechanism
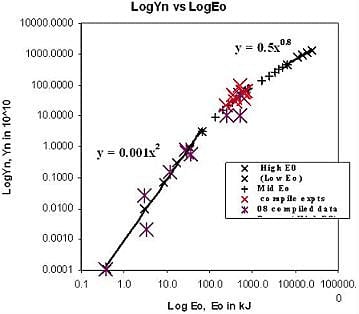
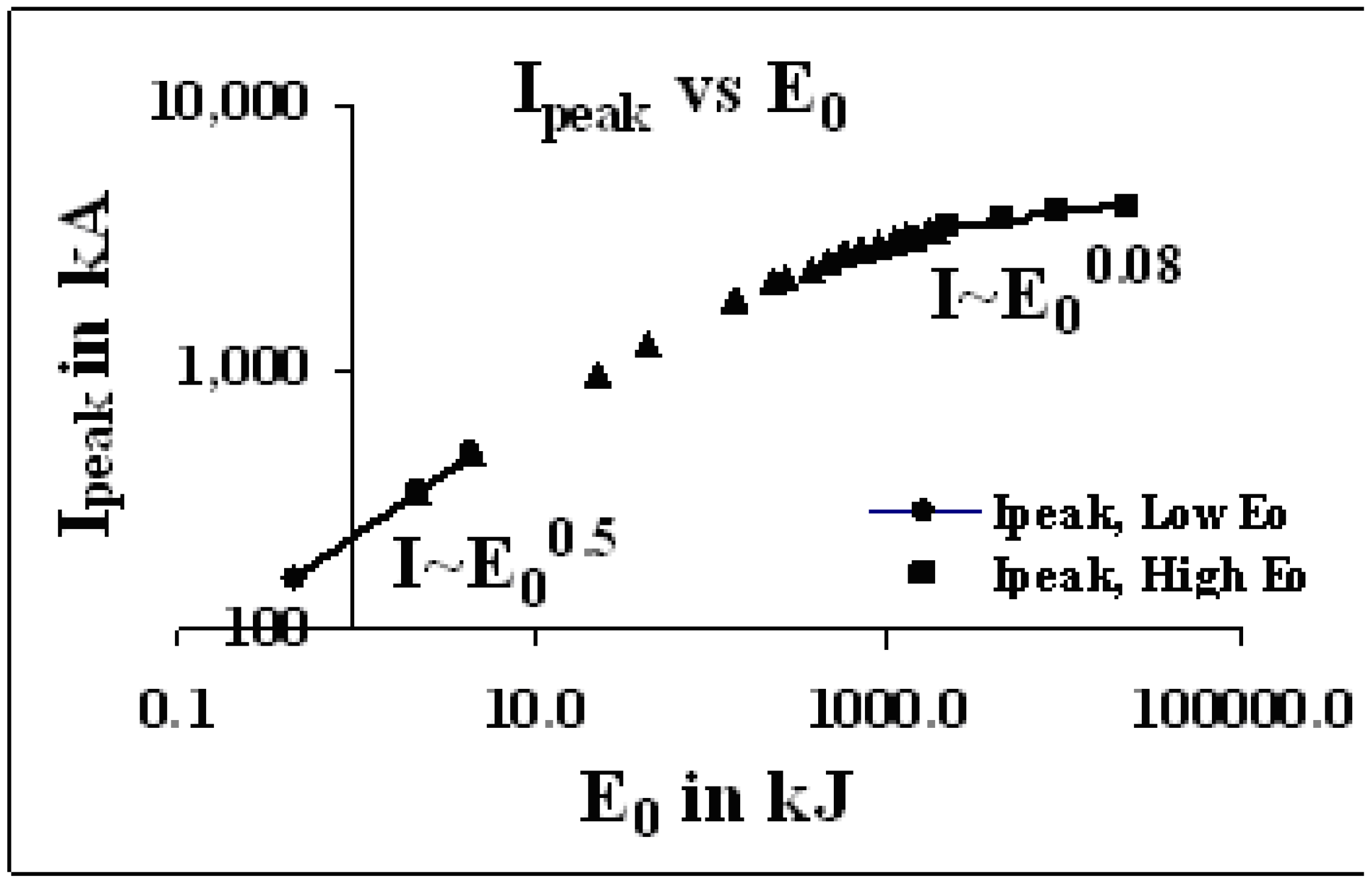
4.2. Scaling Laws for Neutrons from Numerical Experiments over a Range of Energies from 10 kJ to 25 MJ
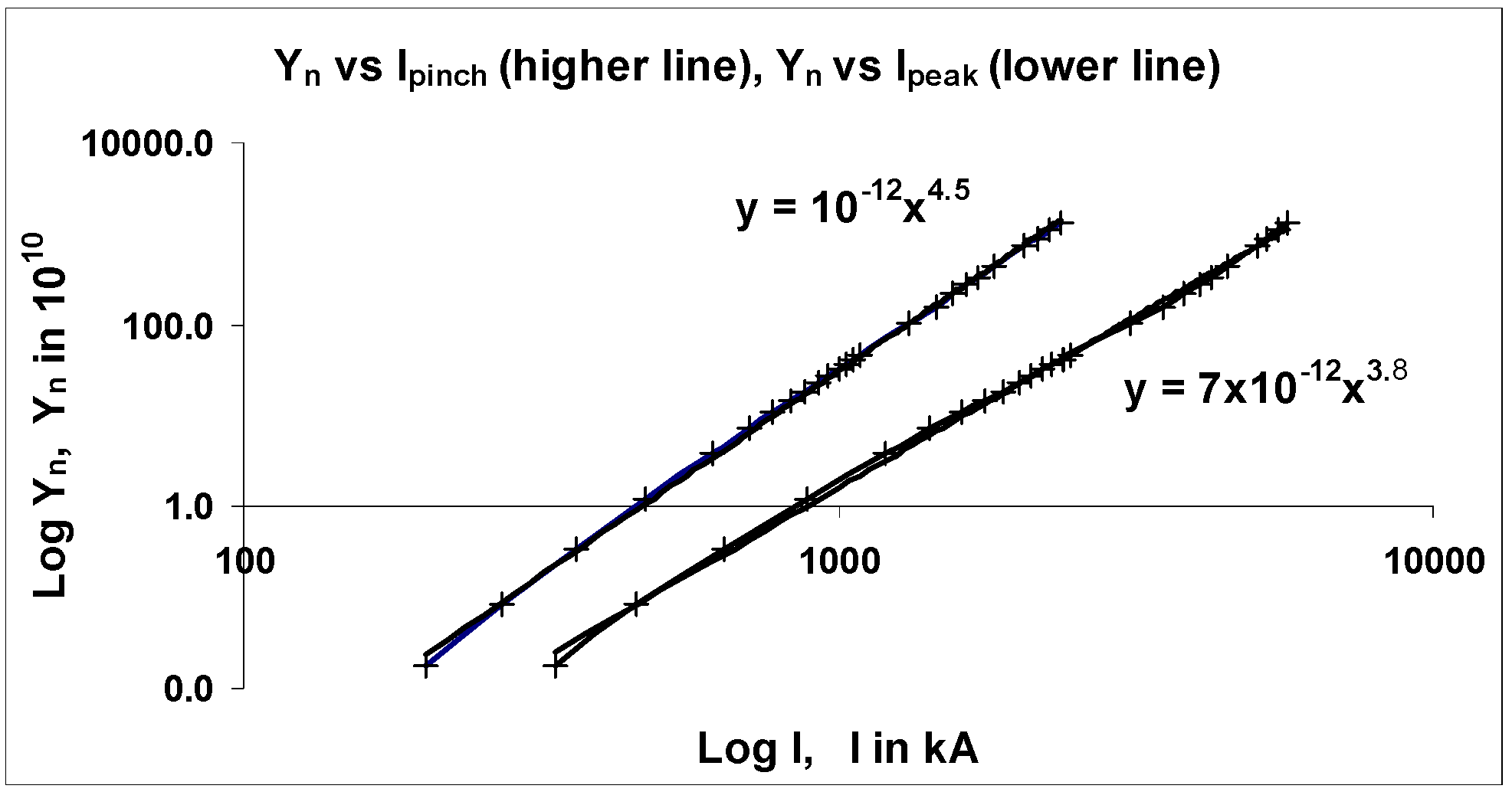
5. Insight 3-Scaling Laws for Soft X-ray Yield
5.1. Computation of Neon SXR Yield- the Equations Used in the Computation
5.2. Scaling Laws for Neon Sxr from Numerical Experiments over A Range of Energies from 0.2 kJ to 1 MJ
| E0 (kJ) | C0 (μF) | a (cm) | z0 (cm) | P0 (Torr) | Ipeak (kA) | Ipinch (kA) | va (cm/μs) | vs (cm/μs) | vp (cm/μs) | Ysxr (J) |
|---|---|---|---|---|---|---|---|---|---|---|
| 0.2 | 1 | 0.58 | 0.5 | 4.0 | 100 | 68 | 5.6 | 22.5 | 14.9 | 0.44 |
| 1 | 5 | 1.18 | 1.5 | 4.0 | 224 | 143 | 6.6 | 23.3 | 15.1 | 7.5 |
| 2 | 10 | 1.52 | 2.1 | 4.0 | 300 | 186 | 6.8 | 23.6 | 15.2 | 20 |
| 6 | 30 | 2.29 | 5.2 | 4.2 | 512 | 294 | 8.1 | 24.5 | 15.6 | 98 |
| 10 | 50 | 2.79 | 7.5 | 4.0 | 642 | 356 | 8.7 | 24.6 | 15.7 | 190 |
| 20 | 100 | 3.50 | 13 | 4.0 | 861 | 456 | 9.6 | 24.6 | 16.0 | 470 |
| 40 | 200 | 4.55 | 20 | 3.5 | 1109 | 565 | 10.3 | 24.7 | 16.2 | 1000 |
| 100 | 500 | 6.21 | 42 | 3.0 | 1477 | 727 | 11.2 | 24.8 | 16.4 | 2700 |
| 200 | 1000 | 7.42 | 63 | 3.0 | 1778 | 876 | 11.4 | 24.8 | 16.5 | 5300 |
| 400 | 2000 | 8.70 | 98 | 3.0 | 2079 | 1036 | 11.4 | 24.9 | 16.5 | 9400 |
| 500 | 2500 | 9.10 | 105 | 2.9 | 2157 | 1086 | 11.5 | 25.1 | 16.7 | 11,000 |
| 1000 | 5000 | 10.2 | 160 | 3.0 | 2428 | 1261 | 11.4 | 25.2 | 16.7 | 18,000 |
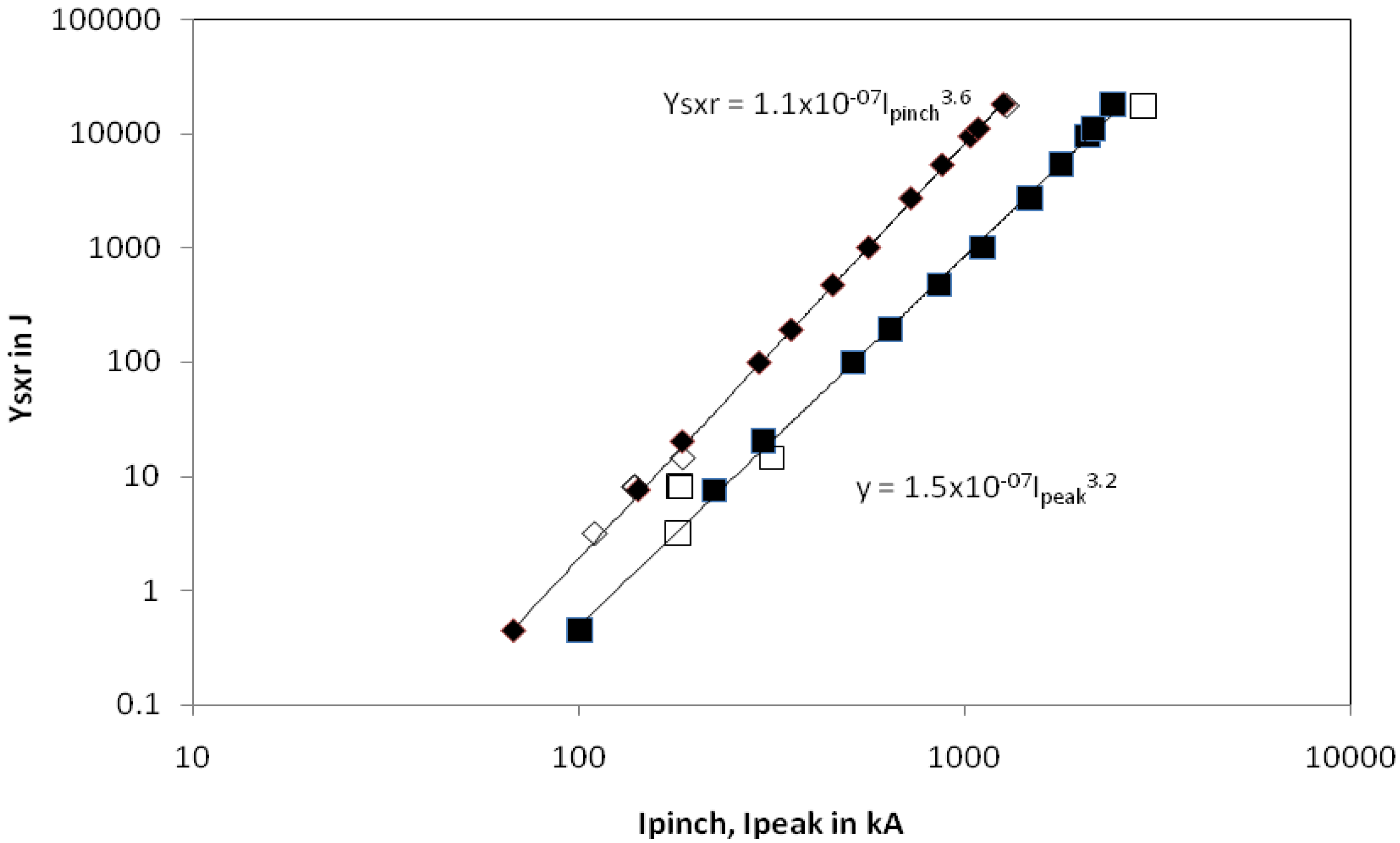
6. Insight 4-Neutron Saturation
6.1. The Global Neutron Scaling Law
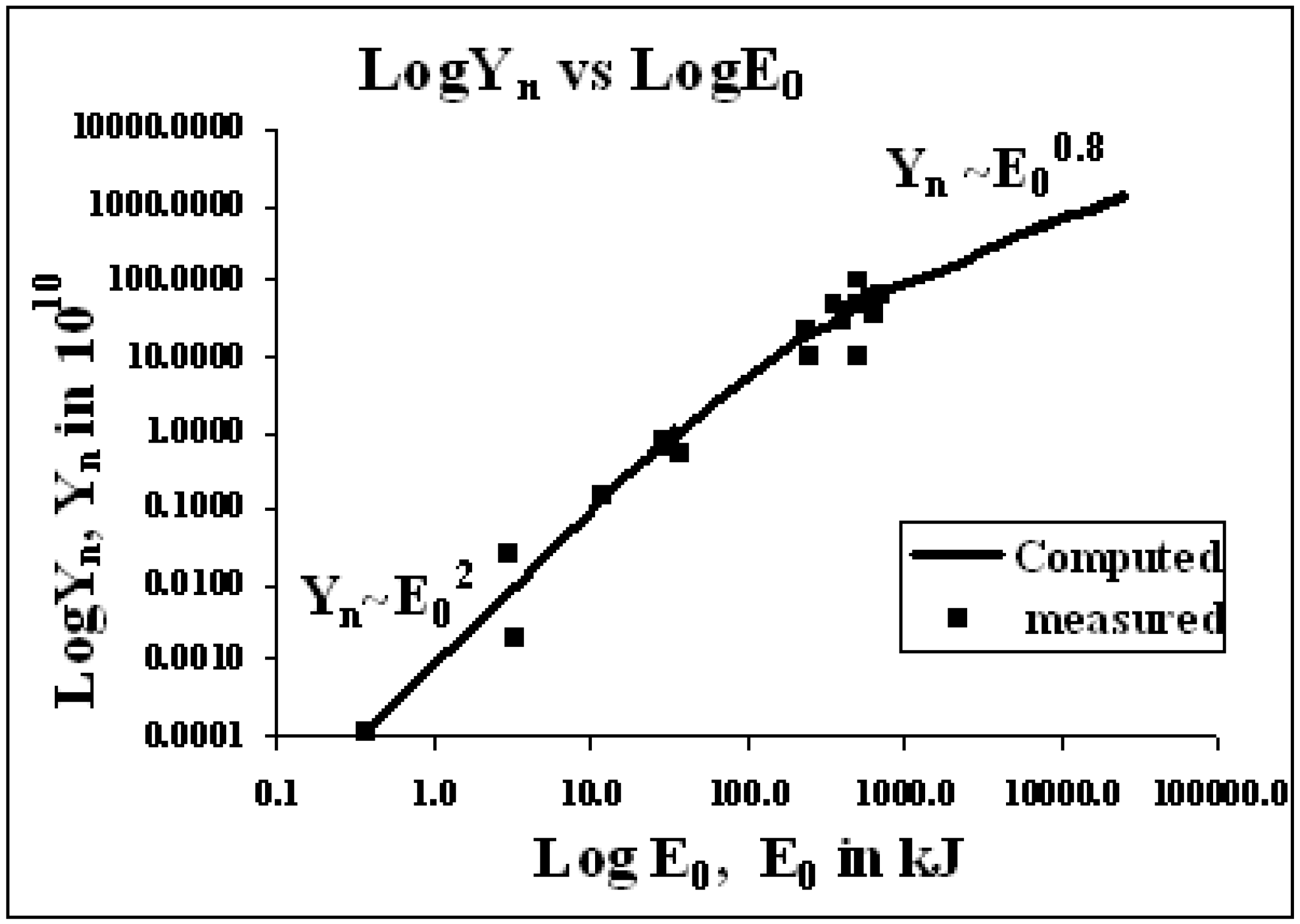
6.2. The Cause of Neutron ‘Saturation’ is the Dynamic Resistance
| E0 (kJ) | C0 (μF) | Z0 (mΩ) | DR0 (mΩ) | Ztotal (mΩ) | Ipeak = V0/Ztotal (kA) | Ipeak, L-C-R (kA) |
|---|---|---|---|---|---|---|
| 0.45 | 1 | 173 | 7 | 197 | 152 | 156 |
| 4.5 | 10 | 55 | 7 | 67 | 447 | 464 |
| 45 | 100 | 17 | 7 | 26 | 1156 | 1234 |
| 135 | 300 | 10 | 7 | 18 | 1676 | 1819 |
| 450 | 1000 | 5.5 | 7 | 12.9 | 2321 | 2554 |
| 1080 | 2400 | 3.5 | 7 | 10.8 | 2781 | 3070 |
| 4500 | 10,000 | 1.7 | 7 | 8.8 | 3407 | 3722 |
| 45,000 | 100,000 | 0.55 | 7 | 7.6 | 4209 | 4250 |
6.3. Beyond Presently Observed Neutron Saturation Regimes
7. Conclusions
References
- Lee, S. Plasma focus model yielding trajectory and structure. In Radiations in Plasmas; McNamara, B., Ed.; World Scientific: Singapore, 1984; Volume II, pp. 978–987. [Google Scholar]
- Lee, S.; Tou, T.Y.; Moo, S.P.; Eissa, M.A.; Gholap, A.V.; Kwek, K.H.; Mulyodrono, S.; Smith, A.J.; Suryadi, S.; Usada, W.; Zakaullah, M. A simple facility for the teaching of plasma dynamics and plasma nuclear fusion. Amer. J. Phys. 1988, 56, 62–68. [Google Scholar] [CrossRef]
- Tou, T.Y.; Lee, S.; Kwek, K.H. Non perturbing plasma focus measurements in the run-down phase. IEEE Trans. Plasma Sci. 1989, 17, 311–315. [Google Scholar] [CrossRef]
- Lee, S. A sequential plasma focus. IEEE Trans. Plasma Sci. 1991, 19, 912–919. [Google Scholar] [CrossRef]
- Jalil, A. Development and studies of a small plasma focus. Ph.D. Dissertation, Universiti Teknologi Malaysia, Kuala Lumpur, Malaysia, 1990. [Google Scholar]
- Potter, D.E. The formation of high-density z-pinches. Nucl. Fusion. 1978, 18, 813–823. [Google Scholar] [CrossRef]
- Lee, S.; Serban, A. Dimensions and lifetime of the plasma focus pinch. IEEE Trans. Plasma Sci. 1996, 24, 1101–1105. [Google Scholar] [CrossRef]
- Liu, M. Soft X-rays from compact plasma focus. Ph.D. dissertation, NIE, Nanyang Technological Univ., Singapore, 2006. Available online: http://eprints.ictp.it/327/ (accessed on 25 March 2010). [Google Scholar]
- Bing, S. Plasma dynamics and X-ray emission of the plasma focus. Ph.D. Dissertation, NIE, Nanyang Technological Univ., Singapore, 2000. Available online: http://eprints.ictp.it/99/ (accessed on 25 March 2010). [Google Scholar]
- Serban, A.; Lee, S. Experiments on speed-enhanced neutron yield from a small plasma focus. J. Plasma Phys. 1998, 60, 3–15. [Google Scholar] [CrossRef]
- Liu, M.H.; Feng, X.P.; Springham, S.V.; Lee, S. Soft X-ray measurement in a small plasma focus operated in neon. IEEE Trans. Plasma Sci. 1998, 26, 135–140. [Google Scholar] [CrossRef]
- Wong, D.; Lee, P.; Zhang, T.; Patran, A.; Tan, T.L.; Rawat, R.S.; Lee, S. An improved radiative plasma focus model calibrated for neon filled NX2 using a tapered anode. Plasma Sources Sci. Technol. 2007, 16, 116–123. [Google Scholar] [CrossRef]
- Lee, S. Plasma radiation source lab-computer package 2000–2007. Available online: http://ckplee.myplace.nie.edu.sg/plasmaphysics/ (accessed on 12 March 2010).
- Lee, S. Radiative dense plasma focus model computation package RADPFV5.008 (November 2005). ICTP Open Access Archive, 2005. Available online: http://eprints.ictp.it/85/ (accessed on 12 March 2010).
- Lee, S. Twelve Years of UNU/ICTP PFF—A Review; Abdus Salam ICTP: Trieste, Italy, 1998; pp. 5–34. Available online: http://eprints.ictp.it/31/ (accessed on 12 March 2010).
- Springham, S.V.; Lee, S.; Rafique, M.S. Correlated deuteron energy spectra and neutron yield for a 3 kJ plasma focus. Plasma Phys. Control. Fusion 2000, 42, 1023–1032. [Google Scholar] [CrossRef]
- Mohammadi, M.A.; Sobhanian, S.; Wong, C.S.; Lee, S.; Lee, P.; Rawat, R.S. The effect of anode shape on neon soft X-ray emissions and current sheath configuration in plasma focus device. J. Phys. D, Appl. Phys. 2009, 42, 045 203 (10pp). [Google Scholar] [CrossRef]
- Lee, S.; Lee, P.; Zhang, G.; Feng, X.; Gribkov, V.A.; Liu, M.; Serban, A.; Wong, T. High rep rate high performance plasma focus as a powerful radiation source. IEEE Trans. Plasma Sci. 1998, 26, 1119–1126. [Google Scholar] [CrossRef]
- Bogolyubov, E.P.; Bochkov, V.D.; Veretennikov, V.A.; Vekhoreva, L.T.; Gribkov, V.A.; Dubrovskii, A.V.; Ivanov, Y.P.; Isakov, A.I.; Krokhin, O.N.; Lee, P.; Lee, S.; Nikulin, V.Y.; Serban, A.; Silin, P.V.; Feng, X.; Zhang, G.X. A powerful soft X-ray source for X-ray lithography based on plasma focusing. Phys. Scr. 1998, 57, 488–494. [Google Scholar] [CrossRef]
- Siahpoush, V.; Tafreshi, M.A.; Sobhanian, S.; Khorram, S. Adaptation of Sing Lee’s model to the Filippov type plasma focus geometry. Plasma Phys. Control. Fusion 2005, 47, 1065–1075. [Google Scholar] [CrossRef]
- Lee, S.; Saw, S.H. Neutron scaling laws from numerical experiments. J. Fusion Energy 2008, 27, 292–295. [Google Scholar] [CrossRef]
- Lee, S. Current and neutron scaling for megajoule plasma focus machines. Plasma Phys. Control. Fusion 2008, 50, 105 005 (14pp). [Google Scholar]
- Lee, S.; Saw, S.H. Pinch current limitation effect in plasma focus. Appl. Phys. Lett. 2008, 92, 021 503. [Google Scholar]
- Lee, S.; Lee, P.; Saw, S.H.; Rawat, R.S. Numerical experiments on plasma focus pinch current limitation. Plasma Phys. Control. Fusion 2008, 50, 065 012 (8pp). [Google Scholar]
- Gribkov, V.A.; Banaszak, A.; Bienkowska, B.; Dubrovsky, A.V.; Ivanova-Stanik, I.; Jakubowski, L.; Karpinski, L.; Miklaszewski, R.A.; Paduch, M.; Sadowski, M.J.; Scholz, M.; Szydlowski, A.; Tomaszewski, K. Plasma dynamics in the PF-1000 device under fullscale energy storage: II. Fast electron and ion characteristics versus neutron emission parameters and gun optimization perspectives. J. Phys. D, Appl. Phys. 2007, 40, 3592–3607. [Google Scholar] [CrossRef]
- Lee, S. Institute for Plasma Focus Studies-Radiative Dense Plasma Focus Computation Package: RADPF. Available online: http://www.plasmafocus.net/IPFS/modelpackage/File1RADPF.htm (accessed on 12 March 2010).
- Internet Workshop on Plasma Focus Numerical Experiments (IPFS-IBC1). Available online: http://www.plasmafocus.net/IPFS/Papers/IWPCAkeynote2ResultsofInternet- basedWorkshop.doc (accessed on 12 March 2010).
- Lee, S.; Saw, S.H.; Lee, P.C.K.; Rawat, R.S.; Schmidt, H. Computing plasma focus pinch current from total current measurement. Appl. Phys. Lett. 2008, 92, 111 501. [Google Scholar]
- Akel, M.; Al-Hawat, Sh.; Lee, S. Pinch current and soft X-ray yield limitation by numerical experiments on nitrogen plasma focus. J. Fusion Energy. [CrossRef]
- Saw, S.H.; Lee, S. Scaling laws for plasma focus machines from numerical experiments. In Proceedings of IWPDA 2009, Singapore, July 2009.
- Lee, S. Diagnostics and insights from current waveform and modelling of plasma focus. In Proceedings of IWPDA 2009, Singapore, July 2009.
- Saw, S.H.; Lee, S. Scaling the plasma focus for fusion energy considerations. In Tubav Conferences: Nuclear & Renewable Energy Sources, Ankara, Turkey, September 2009; pp. 61–70.
- Lee, S. Nuclear fusion and the Plasma Focus. In Invited paper Tubav Conferences: Nuclear & Renewable Energy Sources, Ankara, Turkey, 28 & 29 September 2009; pp. 9–18.
- Lee, S.; Saw, S.H.; Lee, P.; Rawat, R.S. Numerical experiments on neon plasma focus soft X-rays scaling. Plasma Phys. Contr. Fusion 2009, 51, 105013 (8pp). [Google Scholar] [CrossRef]
- Akel, M.; Al-Hawat, Sh.; Lee, S. Numerical experiments on soft X-ray emission optimization of nitrogen plasma in 3 kJ plasma focus SY-1 using modified lee model. J Fusion Energy. [CrossRef]
- Saw, S.H.; Lee, P.C.K.; Rawat, R.S.; Lee, S. Optimizing UNU/ICTP PFF plasma focus for neon soft X-ray operation. IEEE Trans. Plasma Sci. 2009, 37, 1276–1282. [Google Scholar] [CrossRef]
- Lee, S.; Rawat, R.S.; Lee, P.; Saw, S.H. Soft X-ray yield from NX2 plasma focus. J App Phys. 2009, 106, 023309. [Google Scholar]
- Lee, S. Neutron yield saturation in plasma focus-A fundamental cause. App. Phys Letts. 2009, 95, 151503. [Google Scholar] [CrossRef]
- Lee, S.; Saw, S.H.; Soto, L.; Moo, S.P.; Springham, S.V. Numerical experiments on plasma focus neutron yield versus pressure compared with laboratory experiments. Plasma Phys. Control. Fusion 2009, 51, 075006 (11pp). [Google Scholar]
- Huba, J.D. Plasma Formulary. Available online: http://wwwppd.nrl.navy.mil/nrlformulary/NRL_FORMULARY_07.pdf (accessed on 12 March 2010).
- Gates, D.C. X-ray Yield Scaling. In 1978 Proceedings of the IInd Int Conference on Energy Storage, Compression and Switching; Venice, 2, 3239. Plenum Press: New York, 1983. [Google Scholar]
- Filippov, N.V.; Filippova, T.I.; Khutoretskaia, I.V.; Mialton, V.V.; Vinogradov, V.P. Megajoule scale plasma focus as efficient X-ray source. Phys. Lett. A 1996, 211, 168–171. [Google Scholar] [CrossRef]
- Rapp, H. Measurements referring to plasma focus scaling laws. Phys Lett A 1973, 43A, 420–422. [Google Scholar] [CrossRef]
- Herold, H.; Jerzykiewicz, A.; Sadowski, M.H. Comparative analysis of large plasma focus experiments performed at IPF, Stuttgart, and at IPJ, Swierk. Nucl Fusion 1989, 29, 1255–1260. [Google Scholar] [CrossRef]
- Bernard, A.; Bruzzone, H.; Choi, P.; Chuaqui, H.; Gribkov, V.; Herrera, J.; Hirano, K.; Krejci, A.; Lee, S.; Luo, C. Scientific status of plasma focus research. Moscow J Physical Society 1998, 8, 93–170. [Google Scholar]
- Kraus, V.I. Progress in plasma focus research and applications. In Proceedings of the 33rd EPS Conference on Plasma Physics, Rome, Italy, June, 2006. Plasma Phys. Control. Fusion 2006, 48, B221-B229.
- Scholz, M. Report at the ICDMP Meeting, ICDMP, Warsaw, Poland, November 2007.
- Schmidt, H. The role of beam target processes in extrapolating the plasma focus to reactor conditions. In Proceedings of the Fifth International Workshop on Plasma Focus and Z-pinch Research, Toledo, OH, USA, June 1987; p. 65.
- Kies, W. Laser and Plasma Technology, Proceedings of Second Tropical College; Lee, S., Tan, B.C., Wong, C.S., Chew, A.C., Low, K.S., Harith, A., Chen, Y.H., Eds.; World Scientific: Singapore, 1988; pp. 86–137. [Google Scholar]
- Herold, H. Laser and Plasma Technology, Proceedings of Third Tropical College; Wong, C.S., Lee, S., Tan, B.C., Chew, A.C., Low, K.S., Moo, S.P., Eds.; World Scientific: Singapore, 1990; pp. 21–45. [Google Scholar]
- Soto, L.; Silva, P.; Moreno, J.; Silvester, G.; Zambra, M.; Pavez, C.; Altamirano, L.; Bruzzone, H.; Barbaglia, M.; Sidelnikov, Y.; Kies, W. Research on pinch plasma focus devices of hundred of kilojoules to tens of joules. Brazil. J. Phys. 2004, 34, 1814. [Google Scholar] [CrossRef]
- Patran, A.; Rawat, R.S.; Koh, J.M.; Springham, S.V.; Tan, T.L.; Lee, P.; Lee, S. A High Efficiency Soft X-ray Source For Scientific and Industrial Applications. 30th EPS Conference on Plasma Phys. London 2004, ECA Vol.28G, 4.213. [Google Scholar]
- Chow, S.P.; Lee, S.; Tan, B.C. Current sheath studies in co-axial plasma focus gun. J. Plasma Phys 1972, 8, 21. [Google Scholar] [CrossRef]
- Decker, G.; Kies, W.; Nadolny, R.; Röwekamp, P.; Schmitz, F.; Ziethen, G.; Koshelev, K.N.; Sidelnikov, V. Micropinch actuation in the SPEED 2 plasma focus. Plasma Sources Sci. Technol. 1996, 5, 112. [Google Scholar] [CrossRef]
- Rishi, V.; Lee, P.; Lee, S.; Springham, S.V.; Tan, T.L.; Rawat, R.S.; Krishnan, M. order of magnitude enhancement in neutron emission with deuterium-krypton admixture operation in miniature plasma focus device. Appl. Phys. Lett. 2008, 93, 101501. [Google Scholar] [CrossRef]
- Saw, S.H. Experimental studies of a current-stepped pinch. PhD Thesis, Universiti Malaya, Kuala Lumpur, Malaysia, 1991. [Google Scholar]
- Lee, S. A current-stepping technique to enhance pinch compression. J. Phys. D: Appl. Phys. 1984, 17, 733–741. [Google Scholar] [CrossRef]
© 2010 by the authors; licensee Molecular Diversity Preservation International, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Lee, S.; Saw, S.H. Numerical Experiments Providing New Insights into Plasma Focus Fusion Devices. Energies 2010, 3, 711-737. https://doi.org/10.3390/en3040711
Lee S, Saw SH. Numerical Experiments Providing New Insights into Plasma Focus Fusion Devices. Energies. 2010; 3(4):711-737. https://doi.org/10.3390/en3040711
Chicago/Turabian StyleLee, Sing, and Sor Heoh Saw. 2010. "Numerical Experiments Providing New Insights into Plasma Focus Fusion Devices" Energies 3, no. 4: 711-737. https://doi.org/10.3390/en3040711
APA StyleLee, S., & Saw, S. H. (2010). Numerical Experiments Providing New Insights into Plasma Focus Fusion Devices. Energies, 3(4), 711-737. https://doi.org/10.3390/en3040711