1. Introduction
With increasing fuel prices and environmental pollution, it has become apparent that wind energy should be considered a good alternative to thermal energy power generation. However, unlike conventional generation, the wind power output depends on the wind speed, which is related to climatological and micrometeorological parameters. Due to the limited predictability and intermittency of wind speed, wind power is commonly regarded as problematic for power system operation. It will significantly influence the normal operation of power systems because the actual output of wind power usually deviates from the scheduled value [
1]. If the actual output is smaller than the scheduled one, the energy shortage will increase the risk of load shedding in power systems. On the contrary, an energy surplus will increase the risk of wind energy waste. Therefore, it is necessary to allocate additional spinning reserve in the ED issue for any possible unexpected generation deficit and surplus. In [
2,
3,
4], the authors used some efficient optimization algorithms to investigate the relationships between operation cost, spinning reserve requirements and wind power penetration level. The additional spinning reserve due to wind power generation was taken into consideration in the constraint and the spinning reserve requirement was treated as a simple fraction of the total wind power generation which was assumed from experimental results. The amount of spinning reserve equal to wind power capacity is absolutely safe for system operation, but it is a waste because the wind power output doesn’t operate at the rated value all the time. Moreover, a redundant reserve will also increase the operational cost, so this kind of deterministic generation scheduling is conservative at high wind penetration levels. Summing up the above, investigating the relationship between risk, cost, wind power penetration and reserve level is an urgent issue for the sake of safe and economic operation.
The uncertainty of wind power has been considered in several ED optimization models. Some are based on the fuzzy-set theory [
5,
6,
7], while others are based on the stochastic method [
8,
9,
10,
11,
12,
13,
14]. In the proposed ED model of [
5] and [
6], a fuzzy membership function was defined to describe the relationship between system security level and wind power penetration/operation cost. The dispatcher’s attitude toward the risk and cost was involved in the dispatch model of [
5]. Reference [
6] formulated a bi-objective ED problem and its optimization was achieved in a compromise between risk and cost. However, the spinning reserve, which is very indispensable for safe operation, is not considered in the model. Besides, Hong and Li [
7] pointed out that the fuzzy-set theory could be used to model uncertainties of wind power involving climate for the short-term active power scheduling. When the ED issue is investigated with stochastic model of wind power, different probability density functions have been involved. Reference [
8] developed a model with wind energy conversion system generators, in which a Weibull probability density function was used to characterize the stochastic wind speed [
9]. Both risk of overestimation and cost of underestimation of available wind power have been considered by introducing reserve cost and penalty cost into the objective function. It is worth noting that reserve requirement constraints were not mentioned in the model. Since the Weibull distribution indicates the average wind speed in one year, it can be easily found that this ED model is based on the long-term schedule. However, different from long-term schedule, forecasting techniques should be utilized when considering the actual short-term conditions. In order to describe the uncertainty of wind power, a corresponding stochastic model of wind speed/wind power forecast error should be formulated. Reference [
10] considered an optimal power flow wind-thermal coordination model similar to that reported in [
8], but different approaches were utilized to estimate the probability density function of wind power forecast error. In [
11], the wind power is subject to a normal distribution with available forecasted wind power as its expected value, and then the Monte Carlo simulation based on the Latin hypercube sampling technique was employed to generate possible wind power volatility scenarios. Bouffard and Galiana [
12] proposed a stochastic security planning methods which can better cope with the nature of wind generation while maintaining or even improving the current reliability and economic performance of power systems. Soder [
13] proposed a methodology to analyze the operation planning with an emphasis on maintaining the reserves, which has considered wind speed forecast uncertainties, system load forecast uncertainties, ramp rates of thermal units and spinning reserves,
etc. Siahkali and Vakilian [
14] described the uncertainties of the wind speed by a Gaussian distribution and simulated it by a sampling approach. As a reasonable distribution of wind speed forecast error for short-term ED issue, the normal distribution function is also applied in our paper. Besides, an effective treatment method is adopted in which the required reserve is determined by satisfying a given risk threshold [
15].
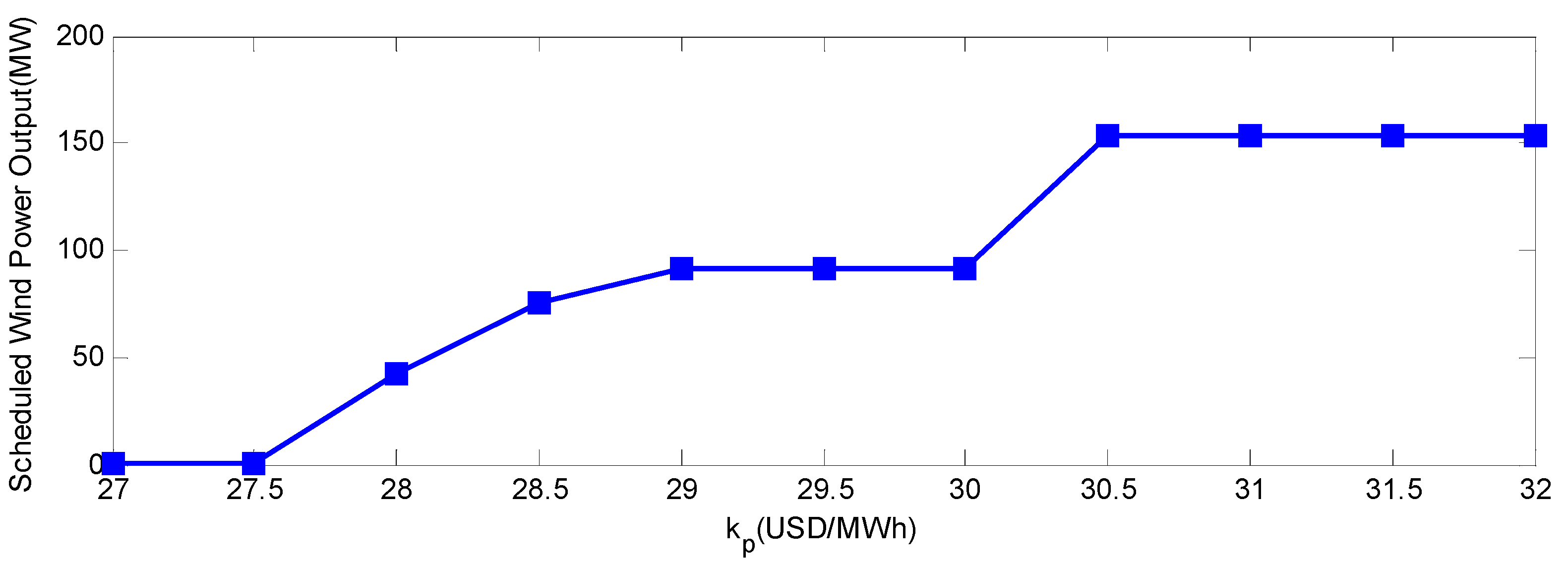
Based on the stochastic distribution of wind speed, a modified ED model including wind power penetration is presented. The overestimation and underestimation of the wind power generation are considered in the form of a reserve cost penalty, while satisfying the risk reserve constraints. According to the proposed model, all the available wind power will be utilized within a given risk level. The paper is structured as follows: in
Section 1, an introduction is given. In
Section 2, the proposed ED model is introduced. In
Section 3, stochastic characterizations of wind power and load demand are described. In order to quantify the effect of random variables on system risk, the normal distributions of wind speed and load forecast errors are assumed.
Section 4 points out the method for solving the proposed ED model. In
Section 5, the results of a ten-generator system containing a wind farm are analyzed. Finally, conclusions are drawn and discussed.
2. Risk Reserve Constrained Optimization Model
Because of the uncertainty of the wind energy available at any given time, this paper considers the costs associated with overestimation and underestimation of wind power generation. The shortage and surplus of wind power can be compensated by the up and down spinning reserves. Furthermore, indispensable spinning reserves are also used due to the generator outages and load forecast error.
The objective function is expressed as follows:
In the above function, the first term is the total fuel cost of conventional generators. Generally, the fuel cost will be a second order polynomial function as follows:
where
Pn is the power from
n th conventional generator;
N is the number of conventional generators;
an,
bn,
cn are constants of fuel cost function of
n th conventional generator.
The second term is the cost for wind-powered generators. In market-oriented liberalized power systems, the wind power is privately owned by a non-utility, so the incremental costs brought about by wind power generation cannot be neglected in the ED model. It is based on the special contractual agreements and can be given by:
where
Wn is the scheduled output of the
n th wind-powered generator;
Nw is the number of wind turbine generator;
dn is the direct cost coefficient for the
n th wind-powered generator. In order to simplify the problem, both the output and direct cost coefficient for each wind turbine generator are assumed to be identical in the wind farm. So the total amount of wind power generation in a wind farm is
.
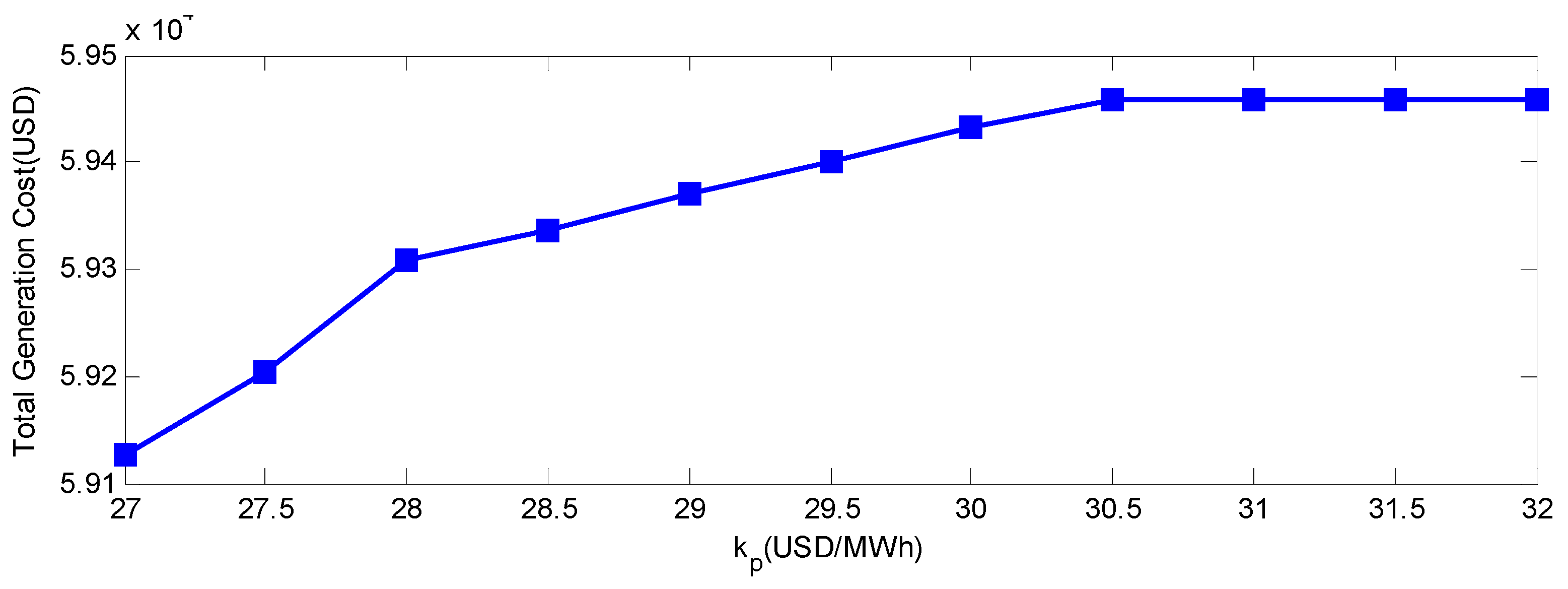
The third term indicates the cost of down spinning reserve required. It is a penalty cost for the case where not all the available wind power is used and load demand forecast is an overestimate of the active value. The expression is as follows:
where
Rd,n is the required down spinning reserve of the
n th generator;
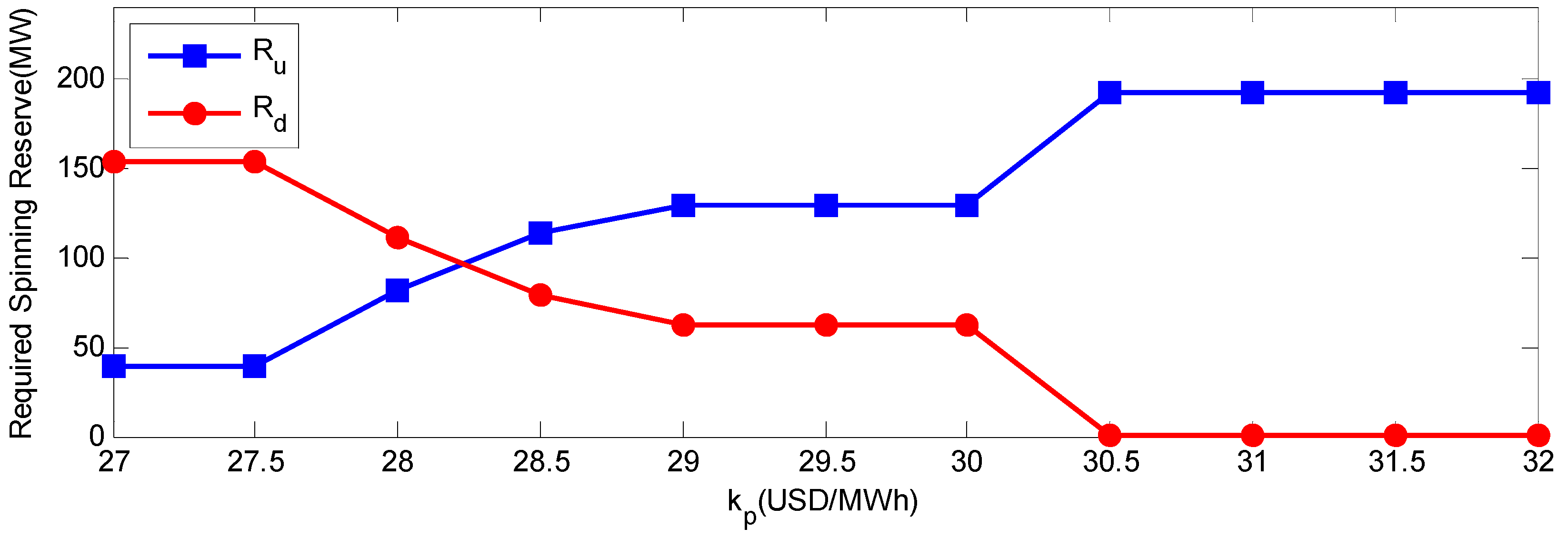
kp is the down reserve cost coefficient.
The last term in the objective function is the cost of the up spinning reserve required, which denotes a risk cost caused by the overestimate of available wind power, the underestimate of load demand and the generator outages:
where
Ru,n is the required up spinning reserve of the
n th generator;
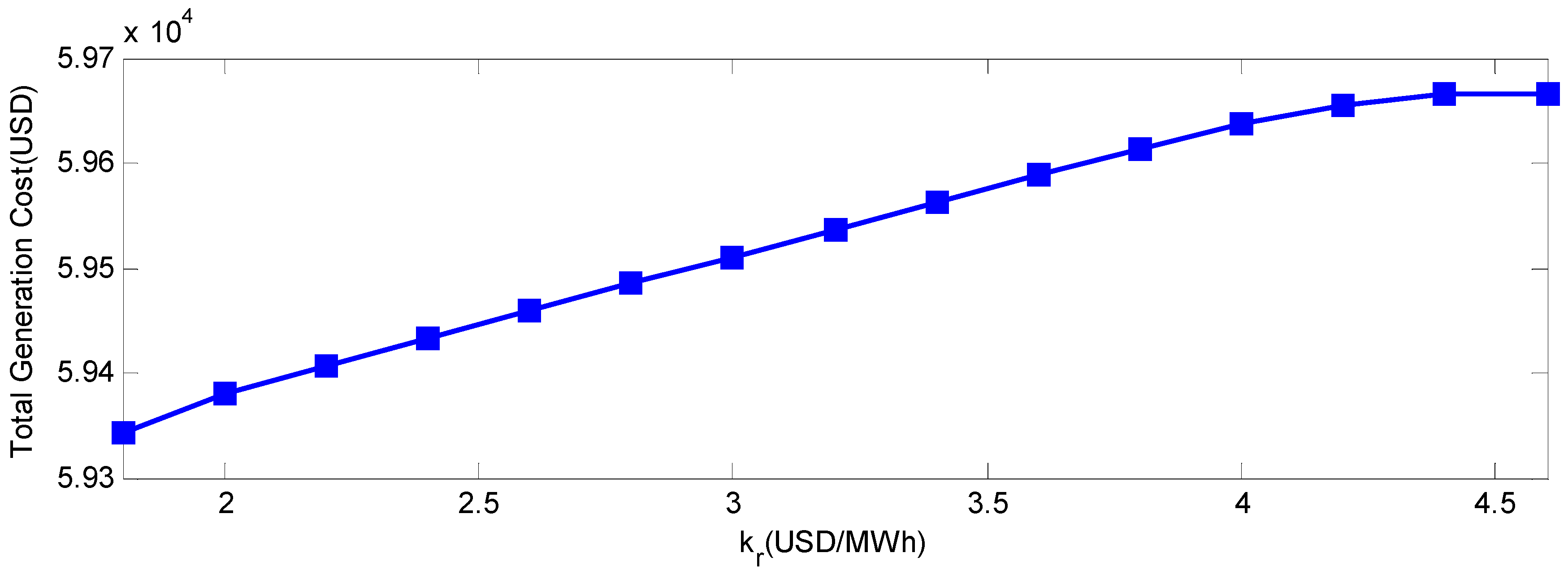
kr is the up reserve cost coefficient.
Compared to the model in [
8], there are two modifications in this paper: (1) the required up and down reserves in the objective function are introduced to substitute the expected surplus wind power and the expected deficit wind power; (2) the required up and down reserves are determined by the risk reserve constraints which will be explain in the following sections.
It should be noted that the up and down spinning reserve cost coefficient are identical for all the conventional generators. That is because the focus of the model in this paper is not on the economic dispatch of the spinning reserve, but on the relationship among the total reserve and generator outputs, so only the total required up spinning reserve Ru and down spinning reserve Rd will be calculated in this model.
Before listing all the constraints, it must be noted that this paper doesn’t consider transmission losses and transmission constraints in the formulation for the sake of simplicity and to avoid losing the key message of risk constraints. However, we are aware of the importance of including them and have started to incorporate them in the next phase of this research.
The system constraints are shown as follows:
(1) Power balance constraint:
(2) Power operating limit of
n th conventional generator:
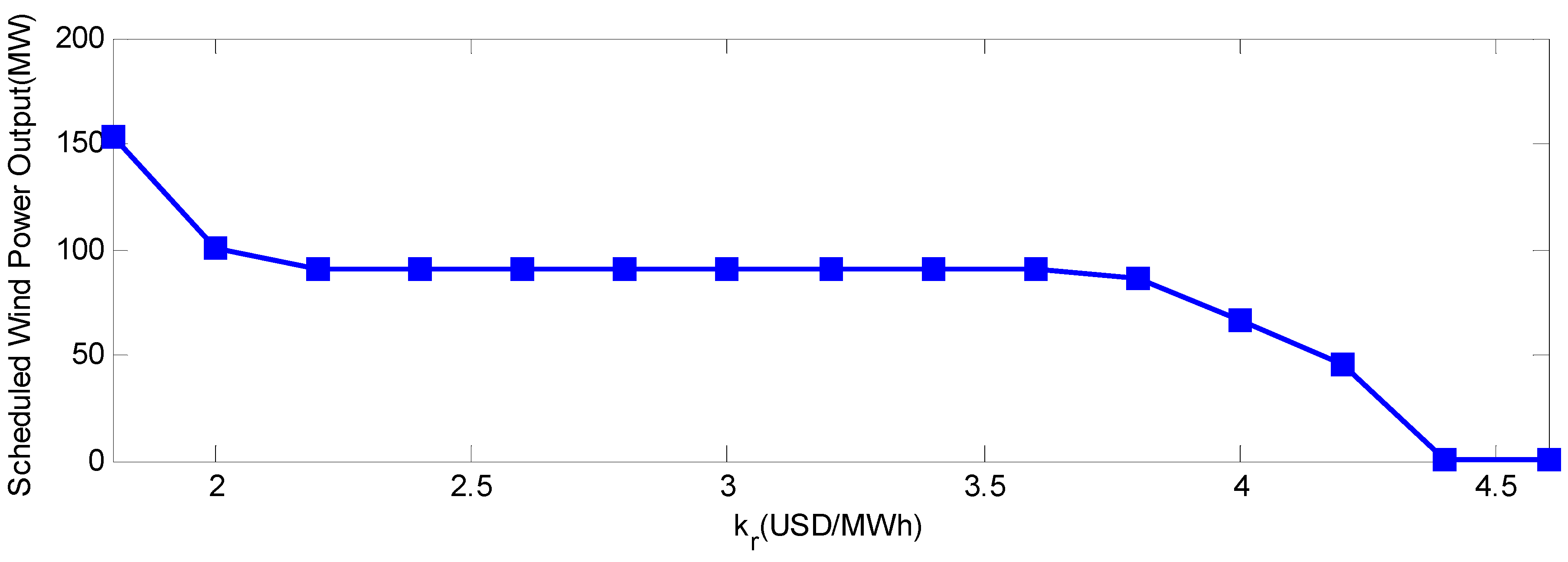
(3) Wind power output constraint:
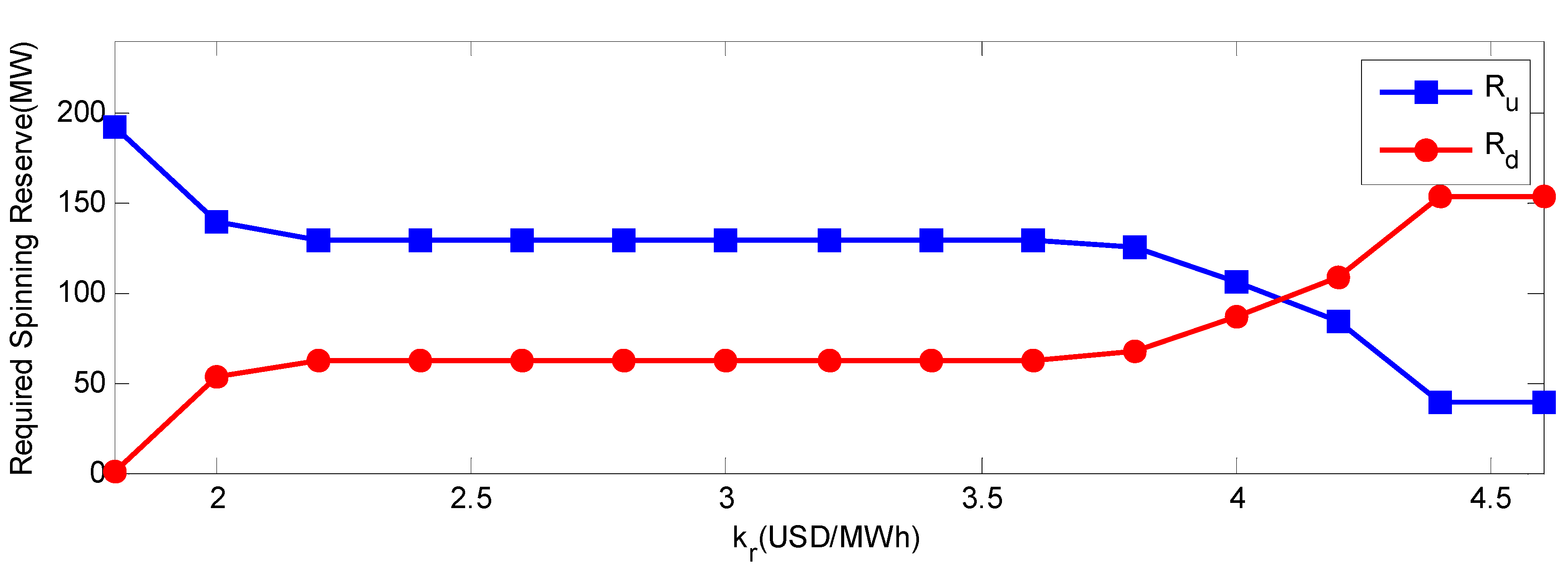
(4) Risk based up and down spinning reserve constraint:
For the sake of safe and reliable operation, system risk should be limited within an acceptable level. There are two kinds of risk constraints modeled in our paper, including the risk constraint of load shedding based on up spinning reserve and the risk constraint of wind energy waste based on down spinning reserve. The former can be expressed as follows:
If the total up spinning reserve supplied by all the conventional generators can be calculated by
then the total required up spinning reserve
Ru must be not more than
SRsu:
For the N-1 condition, the total up spinning reserve supplied by conventional generators can be calculated as:
then the total required up spinning reserve must also be not more than
:
Similar to inequality (9), the risk of wind energy waste based on down spinning reserve should be limited within a risk threshold:
If the following formula indicates the total down spinning reserve supplied by all the conventional generators:
then the total required down spinning reserve
Rd must be not more than
SRsd:
For the N-1 condition, the total down spinning reserve supplied by conventional generators can be calculated as:
then the total required down spinning reserve must also be not more than
:
where
PL is the forecast value of load demand;
and
are the maximum and minimum power from
n th conventional generator, respectively;
is the wind power capacity;
α and
β are the risk thresholds;
is the total up spinning reserve supplied by all the conventional generators;
is the total up spinning reserve supplied by all the conventional generators except
m th conventional generator;
is the total down spinning reserve supplied by all the conventional generators;
is the total down spinning reserve supplied by all the conventional generators except
m th conventional generator.
This model refers to two risks in formulae (9) and (14). Both of them consider the random distributions of available wind power generation, load demand forecast error and the probability of generation forced outage. The former describes the level of system reliability using the probability of shedding load. That means the probability of the total amount of required up spinning reserve being smaller than the power generation shortfall. It is expressed in terms of total probability formula:
where
is the probability of
n th conventional generator trip;
is the load forecast error, it is a random variable.
In the above formula, it is assumed that wind-powered generator does not provide a spinning reserve and the generation forced outage of wind-powered generator is not considered. The first term stands for the case of having no conventional generator trip, and the second term indicates the case of having only one conventional generator trip. The probability of two or more conventional generators trip is ignored in this model.
Similarly, the latter risk form denotes the probability of the required down spinning reserve being smaller than surplus power generation. Using the down spinning reserve constraint based on system risk, the waste of available wind power will be avoided within a given risk threshold:
Seen from formula (19) and (20), exists in both of them. The correlative probability distributions will be derived in the following section.