Valuation of Long-Term Investments in Energy Assets under Uncertainty
Abstract
:1. Introduction
2. Development of the NPV for Valuing Stochastic Cash Flows
2.1. The discount rate
2.2. Optionality
3. Relevant Issues for an Economic Assessment
3.1. Deterministic cash flows
3.2. Stochastic cash flows
4. Stochastic Models and Valuation of Incomes
4.1. The Inhomogeneous Geometric Brownian Motion and the Geometric Brownian Motion
4.2. Other models
5. Long-Term Valuation vs. Short-Term Valuation
5.1. Seasonality and valuation of annuities
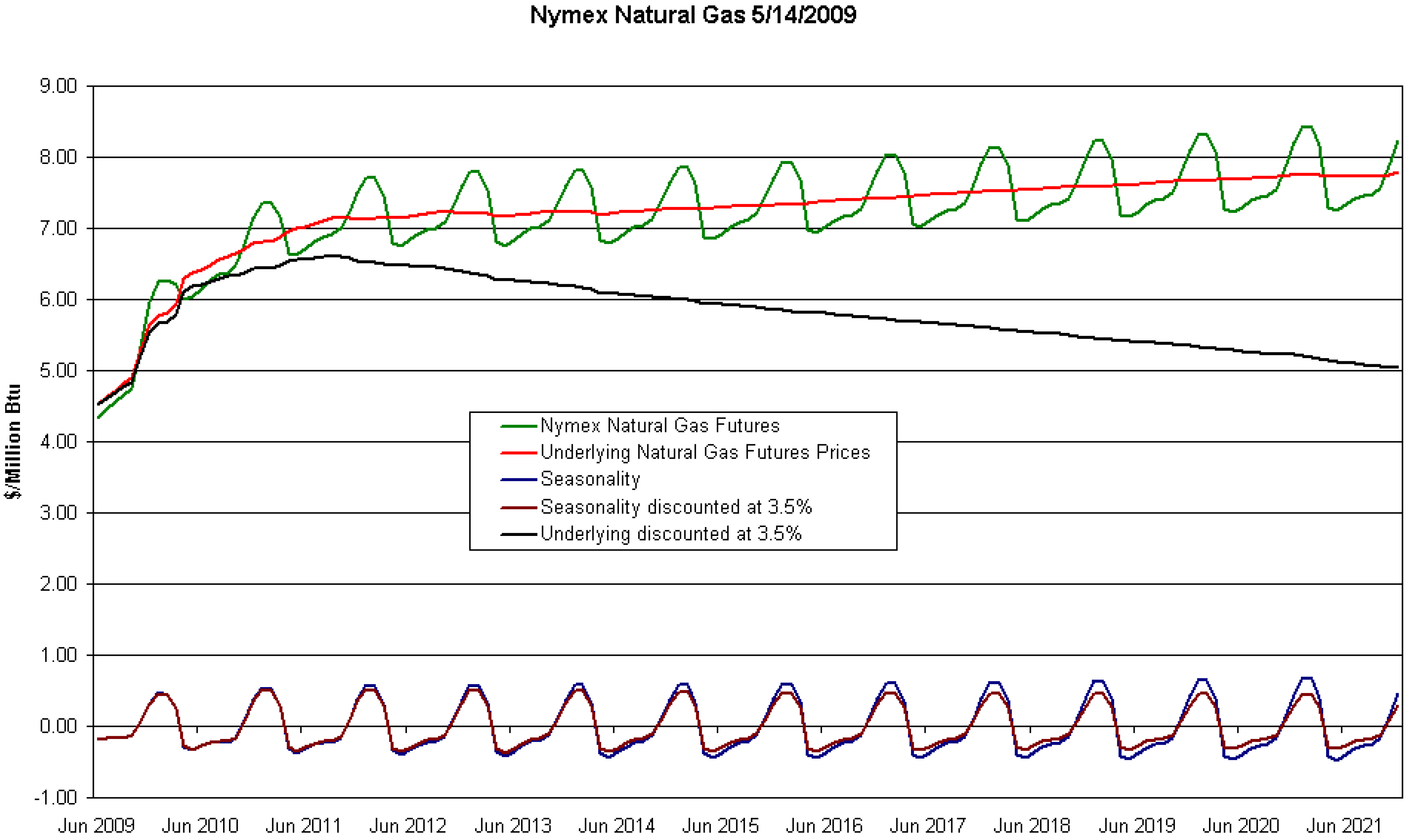
| without discounting | discounted at |
| 0.021 | 0.008 |
5.2. Jumps and valuation of annuities
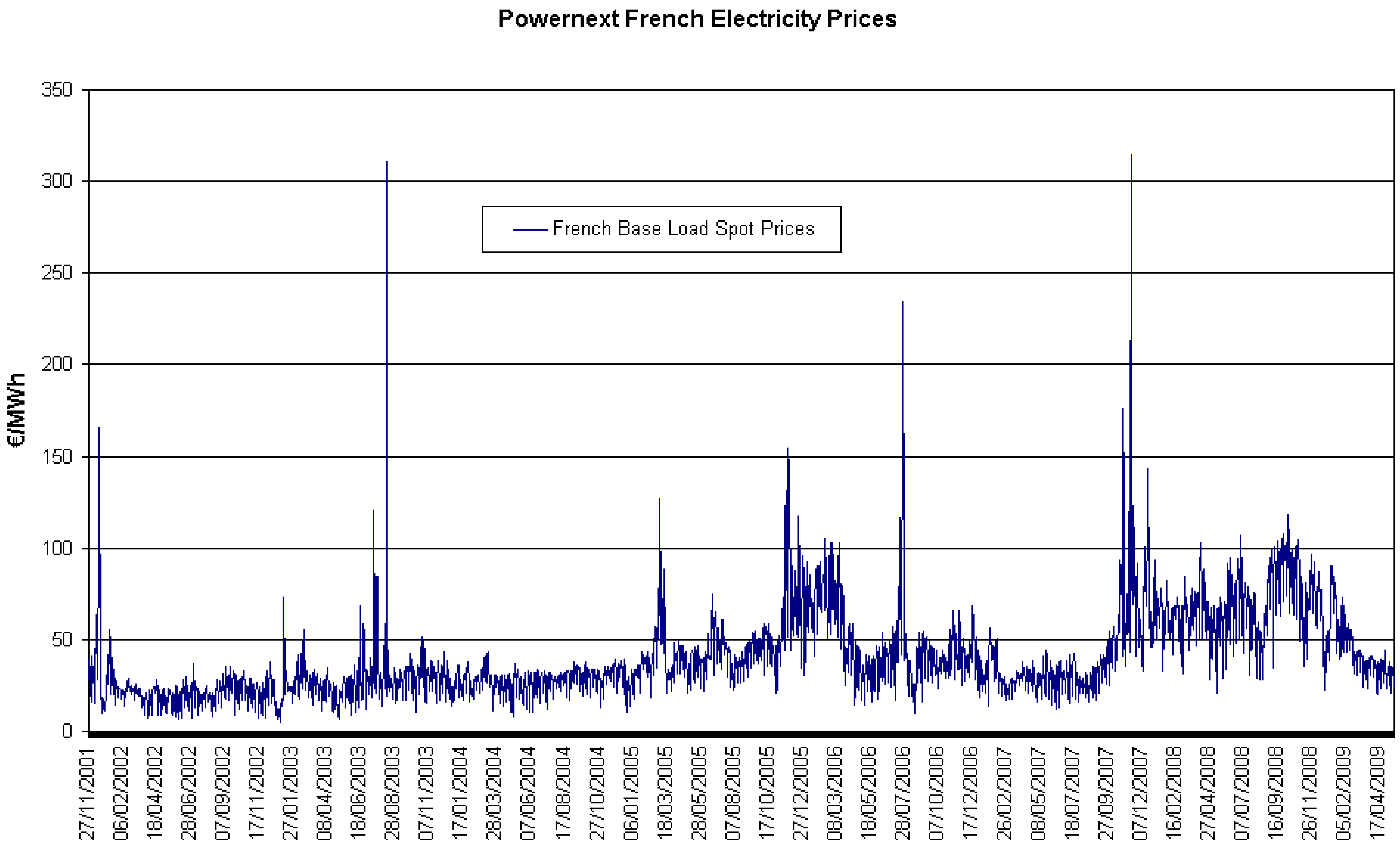
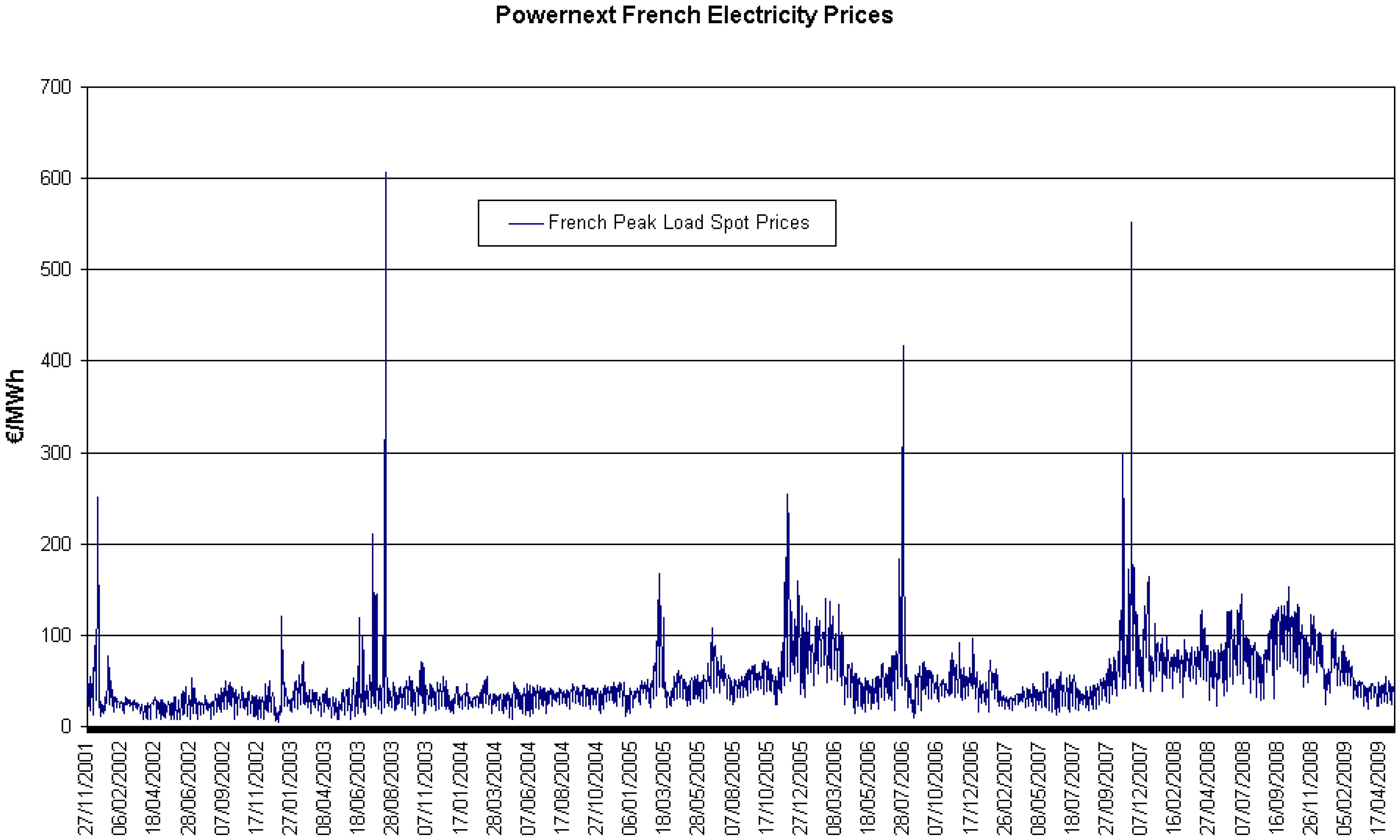
5.3. Stochastic volatility and valuation of annuities
| year | Base | Peak |
| 2002 | 21.19 | 25.82 |
| 2003 | 29.22 | 37.82 |
| 2004 | 28.13 | 33.71 |
| 2005 | 46.67 | 56.88 |
| 2006 | 49.29 | 61.07 |
| 2007 | 40.87 | 51.49 |
| 2008 | 69.15 | 82.91 |
| a | b | ||
| 0.5 | 0.5 | 1,904 | 1,900 |
| 0.5 | 1.0 | 1,904 | 1,921 |
| 1.0 | 0.5 | 1,904 | 1,899 |
| 1.0 | 1.0 | 1,904 | 1,905 |
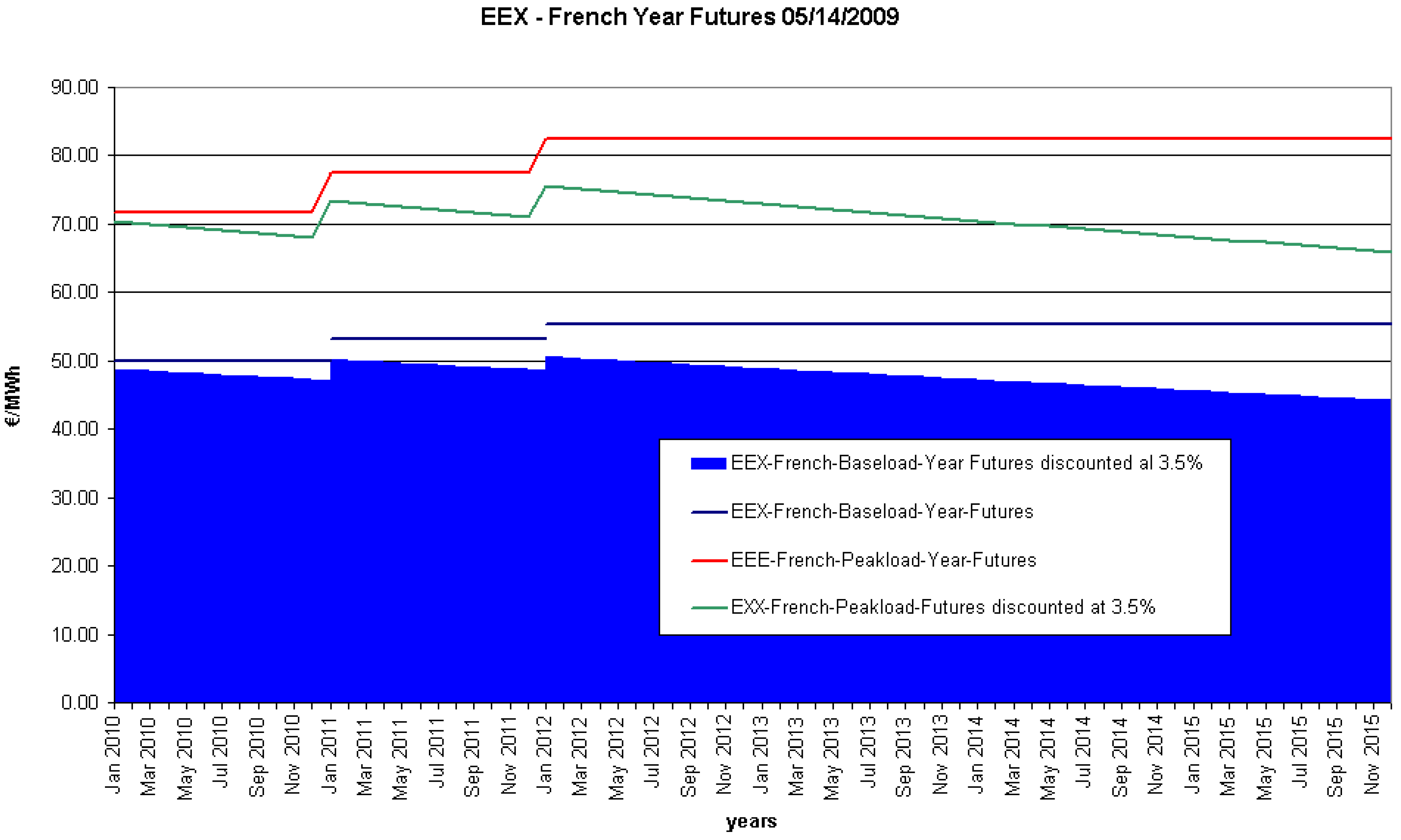
5.4. Stochastic dynamics in the long-term level and valuation of annuities
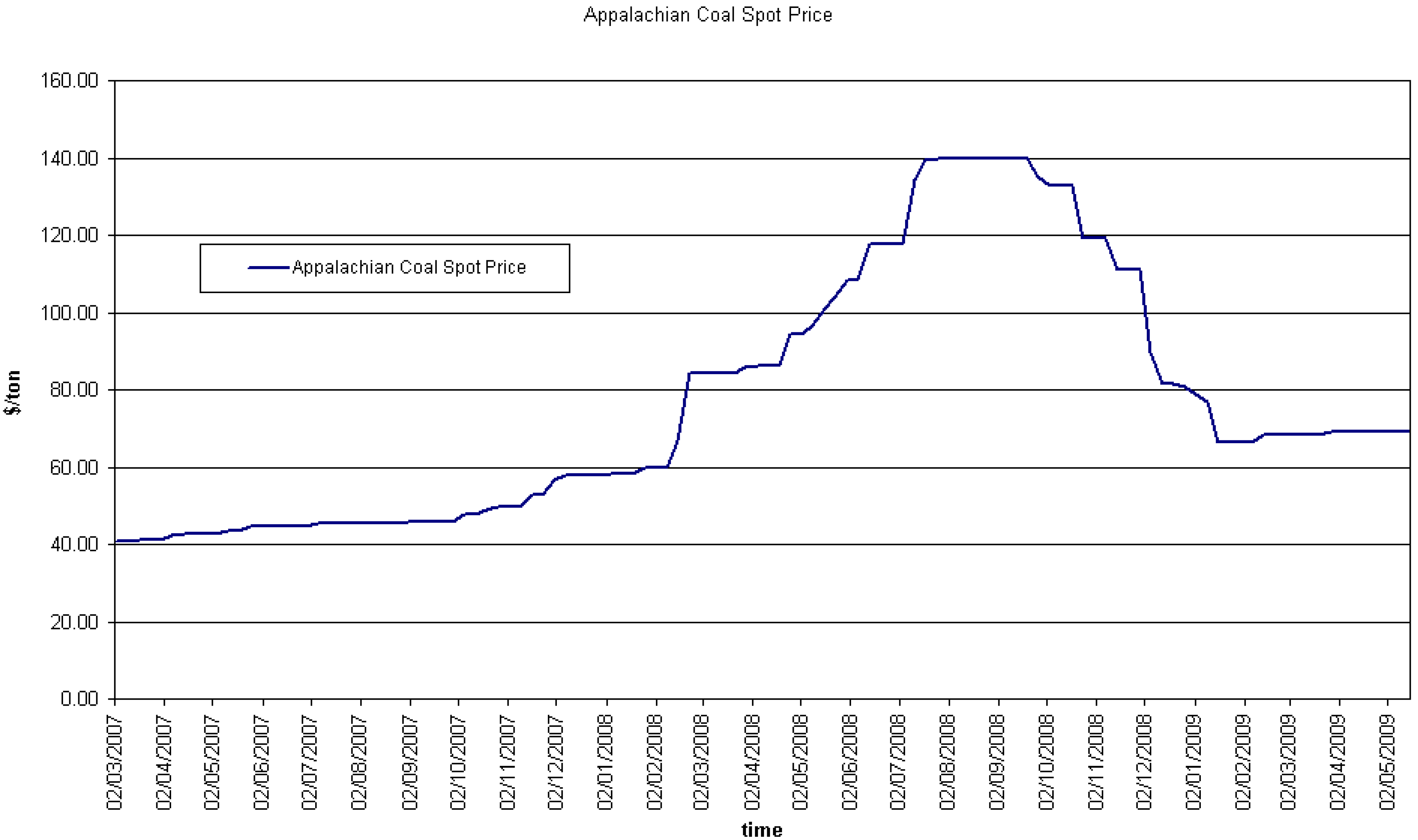
6. Case Study: Improvement in Coal Consumption
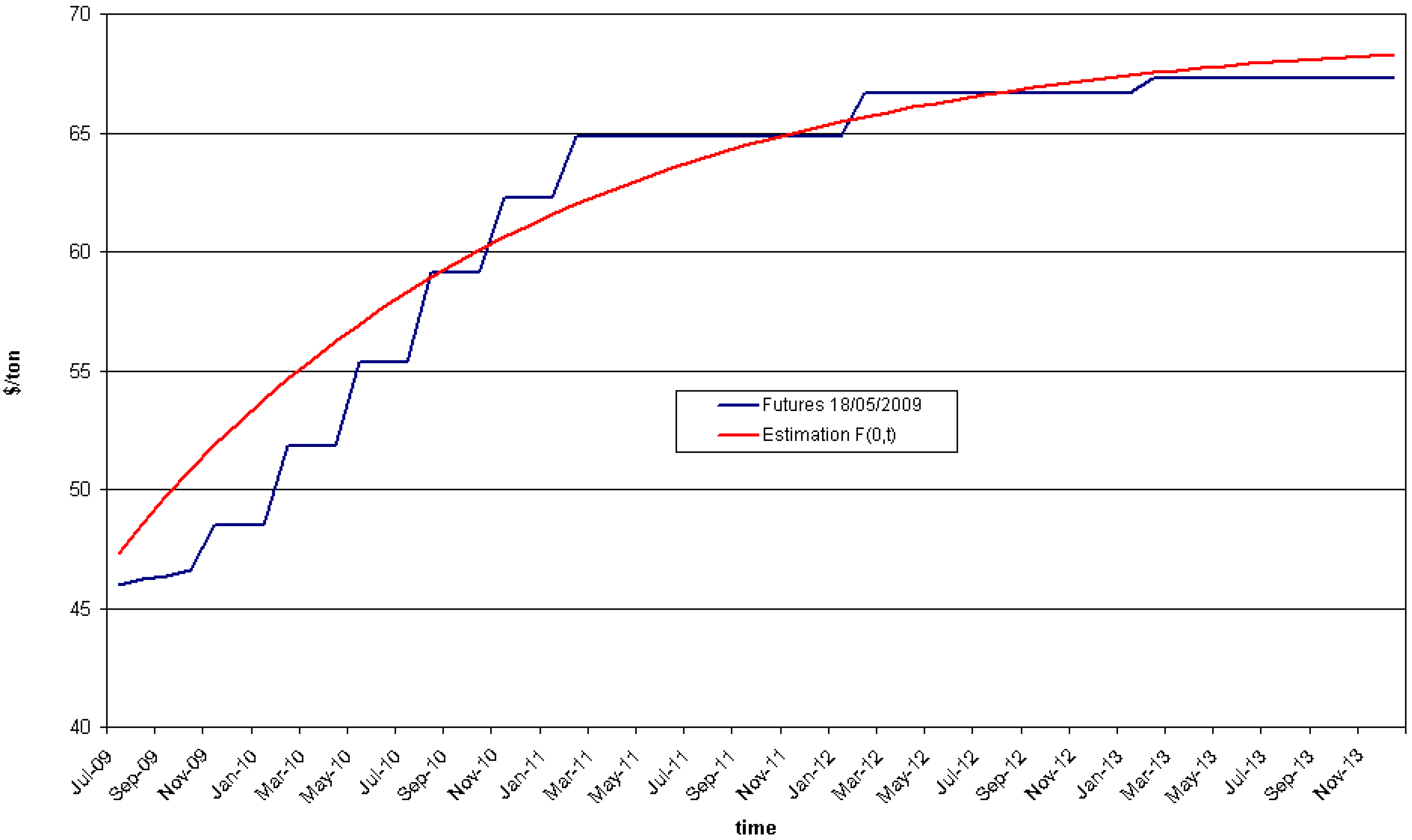
6.1. Case study under uncertainty
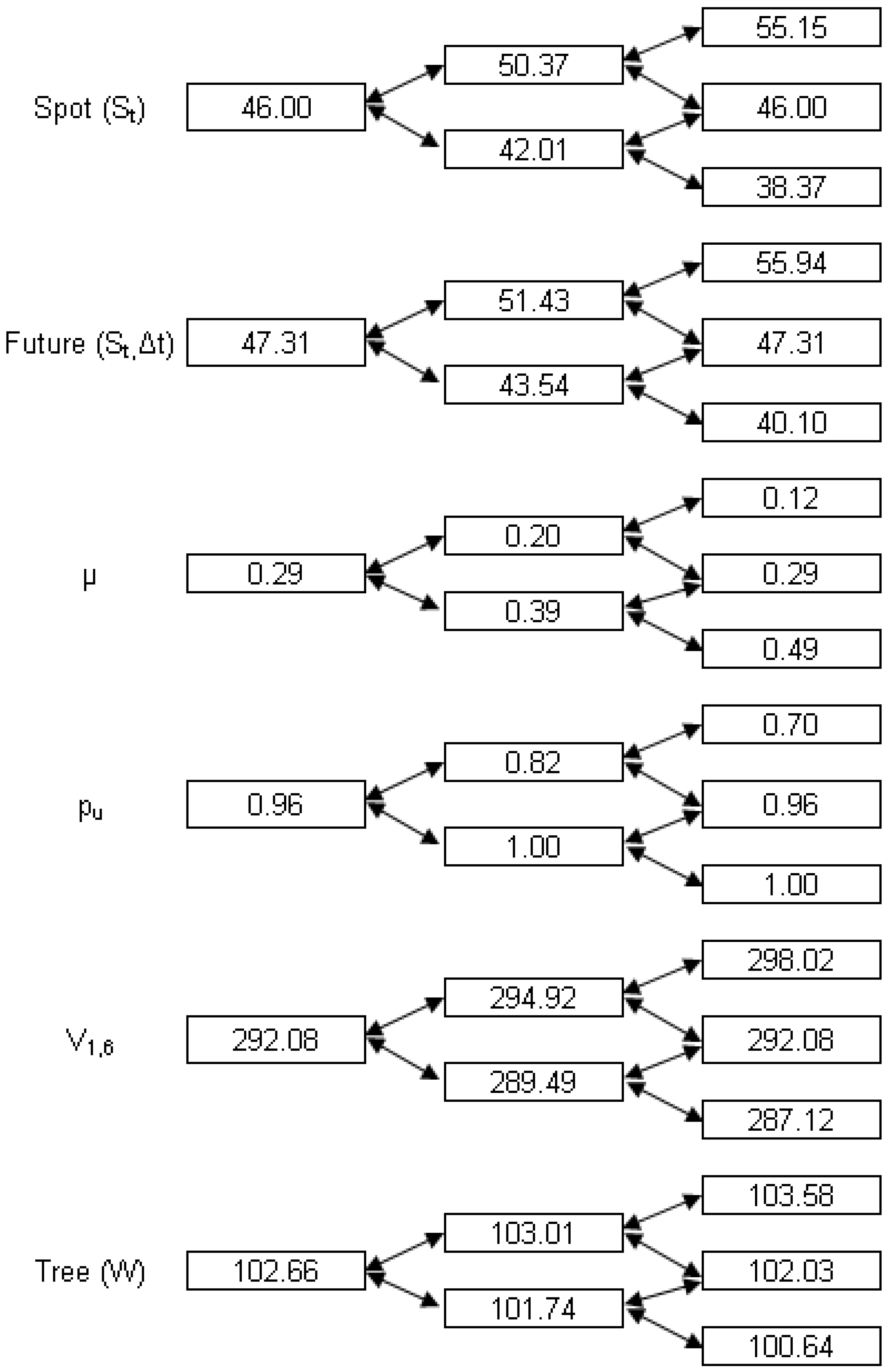
- (a) .
- (b) . The aim is to equate the first moment of the binomial lattice () to the first moment of the risk-neutral underlying variable ().
- (c) . In this case the equality refers to the second moments. For small values of , we have .
| 40.00 | 288.18 |
| 46.00 | 292.08 |
| 50.00 | 294.68 |
| 55.00 | 297.92 |
| 57.69 | 299.67 |
| 60.00 | 301.17 |
6.2. Case study: NPV and IRR
| -0.10 | 329.80 |
| -0.067 | 292.08 |
| -0.05 | 274.70 |
| 0.00 | 230.00 |
| 0.05 | 193.58 |
| 0.10 | 163.77 |
6.3. Case study:
7. Conclusions
Acknowledgements
References
- McCardell, S.B. Life Cycle Costing: Energy Projects. In Encyclopedia of Energy Engineering and Technology; Capehart, B.L., Ed.; CRC Press: Gainesville, Florida, USA, 2007; pp. 967–976. [Google Scholar]
- Bhattacharjee, U. Life Cycle Costing: Electric Power Projects. In Encyclopedia of Energy Engineering and Technology; Capehart, B.L., Ed.; CRC Press: Gainesville, Florida, USA, 2007; pp. 953–966. [Google Scholar]
- McDonald, R.L. Real options and rules of thumb in capital budgeting. In Innovation, Infrastructure and Strategic Options; Brenan, M.J., Trigeorgis, L., Eds.; Oxford University Press: London, UK, 1998. [Google Scholar]
- Graham, J.R.; Harvey, C.R. The theory and practice of corporate finance: evidence from the field. J. Finan. Econ. 2001, 60, 187–243. [Google Scholar] [CrossRef]
- Wilmott, P. Paul Wilmott on Quantitative Finance; John Wiley & Sons: West Sussex, UK, 2006. [Google Scholar]
- Dixit, A.K.; Pindyck, R.S. Investment under Uncertainty; Princeton University Press: Princeton, NJ, USA, 1994. [Google Scholar]
- Trigeorgis, L. Real Options - Managerial Flexibility and Strategy in Resource Allocation; The MIT Press: Cambridge, MA, USA, 1996. [Google Scholar]
- Ronn, E.I. Real Options and Energy Management Using Options Methodology to Enhance Capital Budgeting Decision; Risk Books: London, UK, 2002. [Google Scholar]
- Rocha, K.; Moreira, A.; Divid, P. Thermopower generation investment in Brazil-economics conditions. Energ. Policy 2004, 32, 91–100. [Google Scholar]
- Gollier, C.; Proult, D.; Thais, F.; Walgenwitz, G. Choice of electric power investment under uncertainty: the vaue of modularity. Energ. Econ. 2005, 27, 667–685. [Google Scholar] [CrossRef]
- Näsäkkälä, E.; Fleten, S.-E. Flexibility and technology choice in gas-fired power plant investments. Rev. Finan. Econ. 2005, 14, 371–393. [Google Scholar] [CrossRef]
- Abadie, L.M.; Chamorro, J.M. Valuing flexibility: The case of an Integrated Gasification Combined Cycle power plant. Energ. Econ. 2008, 30, 1850–1881. [Google Scholar] [CrossRef]
- Abadie, L.M.; Chamorro, J.M. Monte Carlo valuation of natural gas investments. Rev. Finan. Econ. 2009, 18, 10–22. [Google Scholar] [CrossRef]
- Deng, S.-J. Valuation of investment and oportunity-to-invest in power generation assets with spikes in electricity price. Manage. Finan. 2005, 31, 95–115. [Google Scholar]
- Deng, S.-J.; Johnson, B.; Sogomonian, A. Exotic electricity options and the valuations of electricity generation and transmision assets. Decis. Support Syst. 2001, 30, 383–392. [Google Scholar] [CrossRef]
- Gourieroux, C.; Jasiak, J. Financial Econometrics; Princeton University Press: Princeton, NJ, USA, 2001. [Google Scholar]
- Cortazar, G.; Milla, C.; Severino, F. A multicommodity model of futures prices: Using futures prices of one commodity to estimate the stochastic process of another. J. Futures Markets 2008, 28, 537–560. [Google Scholar] [CrossRef]
- Schwartz, E.S. The stochastic behavior of commodity prices: Implications for valuation and hedging. J. Finan. 1997, 52, 923–973. [Google Scholar] [CrossRef]
- Pilipović, D. Energy Risk; McGraw-Hill: New York, NY, USA, 1997. [Google Scholar]
- Dean, J.W. Investment Analysis Techniques. In Encyclopedia of Energy Engineering and Technology; Capehart, B.L., Ed.; CRC Press: Gainesville, FL, USA, 2007; pp. 930–936. [Google Scholar]
- Salahor, G. Implications of output price risk and operating leverage for the valuations of petroleum development projects. The Energy Journal 1998, 19, 13–46. [Google Scholar] [CrossRef]
- Laughton, D.G.; Sagi, J.S.; Samis, M.R. Modern assets pricing and project evaluation in the energy industry. J. Energ. Lit. 2000, 6, 3–46. [Google Scholar]
- Lucia, J.J.; Schwartz, E.S. Electricity prices and power derivatives: Evidence from the nordic power exchange. Rev. Derivatives Res. 2002, 5, 5–50. [Google Scholar] [CrossRef]
- Geman, H. Commodities and Commodity Derivatives. Modeling and Pricing for Agricultural, Metals and Energy; Wiley Finance: West Sussex, England, 2005. [Google Scholar]
Notes
- 1.Consider, for example, the time to build a nuclear power plant, which has shown a strong volatility in the last years because of risks that sometimes had not been taken into account initially.
- 2.The NPV and IRR methods are explained in Dean [20]. But, as the author admits (though it is not developed in his paper), the hardest issue to assess is risk. In real applications it must be included in the valuation together with the options embedded in the project. The NPV would be the starting point.
- 4.Though it is possible to compute it if one wants so. See Salahor [21].
- 5.A method of this type, though with a different approach, is analyzed in Laughton et al. [22].
- 6.The value is the riskless interest rate on a 365-days basis; it is slightly different from the continuous rate r. For a flat zero-coupon curve holds, so discounting can be equivalently accomplished either by multiplying by or by .
- 7.If construction costs are high and the construction period is several years long then investments will need funding presumably at a high rate. Also, it will take some time until revenues allow to service the debt and pay the principal back.
- 8.Some additional reasons are: (a) This model satisfies the following condition (which seems reasonable): if the price of one unit of the asset reverts to some mean value, then the price of two units reverts to twice that same mean value. (b) The term precludes, almost surely, the possibility of negative values. (c) The expected value in the long run is: ; this is not so in Schwartz [18] model, where .
- 9.If it is specified as a fixed amount independent of , the risk premium would only be λ, and the formulas derived would be slightly different.
- 10.The value of λ can be negative in certain cases.
- 11.δ reflects the profits enjoyed by the owner of the physical commodity, as opposed to the holder of a futures contract. It is equivalent to the dividends received by the holder of a firm’s stock (as opposed to the holder of a stock option).
- 12.In case the model for a given commodity is not mean reverting but GBM, the existence of a convenience yield should be considered.
- 13.Note that under very fast mean reversion the model in the end behaves as if it stayed constant at this equilibrium value.
- 14.Lucia and Schwartz [23] analyze the different forms of modeling seasonality and develop an estimation for the Nordic Power Exchange.
- 15.The term “base load” refers to the type of load for the delivery of electricity or the procurement of electricity with a constant output over 24 hours of each day of the delivery period. The term “peak load”, instead, refers to the load type for the delivery or procurement of electricity at a constant load over 12 hours from 08:00 am until 08:00 pm on every working day (Monday to Friday) during a delivery period.
- 16.See Geman [24], particularly chapter 11, which deals with Spot and Forward Electricity Markets.
- 17.We consider m years of useful life.
- 18.For simplicity we assume that is an integer number of years.
- 19.In this model , which implies .
- 20.For a particular number of tons saved per year, the results would be proportional to those in this example.
- 21.Though in this case the estimation has been done for just one day, it is possible to do it also with the futures prices on several days to test for the stability of the parameters and when the initial spot price changes, or even to calibrate a more complex model (this is beyond the scope of this paper).
- 22.Where and are measured from time t.
© 2009 by the author; licensee Molecular Diversity Preservation International, Basel, Switzerland. This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Abadie, L.M. Valuation of Long-Term Investments in Energy Assets under Uncertainty. Energies 2009, 2, 738-768. https://doi.org/10.3390/en20300738
Abadie LM. Valuation of Long-Term Investments in Energy Assets under Uncertainty. Energies. 2009; 2(3):738-768. https://doi.org/10.3390/en20300738
Chicago/Turabian StyleAbadie, Luis M. 2009. "Valuation of Long-Term Investments in Energy Assets under Uncertainty" Energies 2, no. 3: 738-768. https://doi.org/10.3390/en20300738
APA StyleAbadie, L. M. (2009). Valuation of Long-Term Investments in Energy Assets under Uncertainty. Energies, 2(3), 738-768. https://doi.org/10.3390/en20300738




