Modulization and Simulation of Thermal Management System Based on Pumped Two-Phase Loop for Hybrid-Electric Aircraft

Abstract

An efficient thermal management system (TMS) is essential for ensuring hybrid-electric aircraft (HEA) can handle the significant heat rejection required by electrified propulsion. This paper presents a system-level analysis of a compact P2PL TMS for a 1.4 MW battery generating a 70 kW heat load. A modular modeling method was used to size the key components, and then dynamic simulations were conducted under varying environmental conditions. The results indicate that a compact TMS weighing 22 kg can be developed, with a condenser heat transfer area of 26.20 m² and operating with a refrigerant mass flow rate of 0.56 kg/s while maintaining low pump power consumption at 22 W. This system can successfully regulate a battery’s temperature so that it remains below 40 °C in both standard (15 °C) and cold (−20 °C) environments. Pressure analysis confirmed the system’s flexibility and its ability to control battery temperature between 27 °C and 38 °C by adjusting the working pressure (6–8 bar). Furthermore, under hot day conditions (40 °C), battery temperature can be maintained at 47.6 °C. Even under extreme conditions (50 °C), the TMS limits the temperature to 57.45 °C, ensuring it stays within the safe operating range.

1. Introduction

Air transport is among the most rapidly growing transport sectors, with 9.3 million flights in 2019 from European Union airports [1], which reflects the importance of this dynamic industry. Aviation is responsible for approximately 2.4% of total global CO₂ emissions and contributes about 4% to the total global warming generated by human activities [2,3,4], thus creating an urgent need for research on more sustainable and greener solutions. Through Onward, the European Green Deal and the Civil Aviation Organization are targeting net-zero emissions by 2050 or a 55% cut in greenhouse gas emissions by 2030 [2].

A possible solution that would allow us to reach this target is to electrify propulsion systems. Fully electric aircraft (FEA) can radically solve the emission problem; however, hybrid-electric aircraft, requiring a smaller technological step, can be built within the timeframe imposed by the European project objectives. However, there are still limitations and challenges pertaining to this type of aircraft that make their integration into air transportation premature [5], such as the low energy density of power sources (i.e., batteries), which reduces the operating range [6].

Transforming traditional aircraft into FEA or HEA poses challenges related to developing subsystems that are better adapted to these models. One such subsystem is the thermal management system (TMS), which is crucial in electric and hybrid-electric aircraft [2].

For conventional aircraft, the TMS is less critical due to the self-cooling action of the propulsion system [7]. The main heat sources come from the propulsion system, which is located outside the aircraft fuselage and benefits from direct cooling by the outside air, and the generated heat is expelled with the exhaust gas [8]. In electric and fully electric aircraft, there are multiple heat sources from components such as batteries, fuel cells, and power electronics [9,10]; these parts generate a significant heat load, and almost all are installed inside the aircraft body [11], making them more difficult to cool and necessitating the design of a complex, larger, and more efficient TMS compared to TMSs used in traditional aircraft.

One challenge in designing a new TMS lies in weight and volume reduction [10]. Cooling a high heat load, like the one produced by the propulsion system, requires a bulky TMS and additional installation space, creating significant design challenges and driving the need for innovative solutions to minimize weight and total volume [12]. Several innovative TMS architectures can be found in the literature, such as the one for NASA’s ULI Program that uses an oil cooling loop and PCM for the TMS [13]. Other, more complex systems, such as absorption refrigeration systems (ARSs) and cryogenic cooling, are still under development and face challenges regarding high volume and weight [14].

Researchers are already developing less complex TMS using the most common cooling technologies, such as air-to-liquid cooling systems and vapor cycle systems [15]. These cooling systems are widely used in disciplines such as automotive [16], conventional aircraft [15], and industrial equipment [17]. Its functionality relies on convection and conduction principles, where a working fluid (e.g., water) absorbs heat and dissipates it via a heat sink. While efficient and reliable, scaling this system for large heat loads requires reaching a significant size [18].

These two cooling systems are widely investigated in the literature as they are well-matured technologies. VCSs for large heat loads tend to be bulky and increase energy consumption, as mentioned in [19]. The simple liquid-to-air system has been studied by several researchers, who have focused more on the design method and characteristics of the components. The design method mainly focuses on the heat exchanger (HX), which accounts for 80% of the system. However, the results show reduced performance in high-temperature conditions and large heat loads [20,21]. This lack of performance has been confirmed by another study investigating five different TMS configurations, which suggests that other innovative concepts and architectures must be explored for future aircraft [22].

Other cooling systems similar to VCS, called two-phase, became much more widely adopted in electric vehicles [23]. This system was used for spacecrafts as it has very high efficiency and is characterized by compactness [24]. Recently, several studies investigated the use of this system as TMS in electric vehicles, while its use in aviation focuses on power electronics and electric-motor cooling in hybrid aircraft [23,25,26]. However, when implementing this system as a TMS for the power systems of FEA and HEA [27], few studies are available. An example is research focused on large-scale, fuel-cell-powered aircraft. This scarcity makes the study of this TMS particularly interesting due to its characteristics, which are applicable to other kinds of power systems, including those utilizing large battery capacities.

This study presents the first system-level, modular investigation of a P2PL TMS designed specifically for the battery pack of a hybrid-electric aircraft. This work aims to (1) develop an integrated modeling framework combining Python-based component sizing and Siemens Amesim dynamic simulation for this application; (2) apply the framework to a case study of a 1.4 MW aircraft battery with a 70 kW heat load, comprising a complete system mass budget and performance envelope; and (3) validate a pressure-based control strategy capable of maintaining battery temperature within safe limits across the full aircraft operational range, from −20 °C to +50 °C ambient conditions.

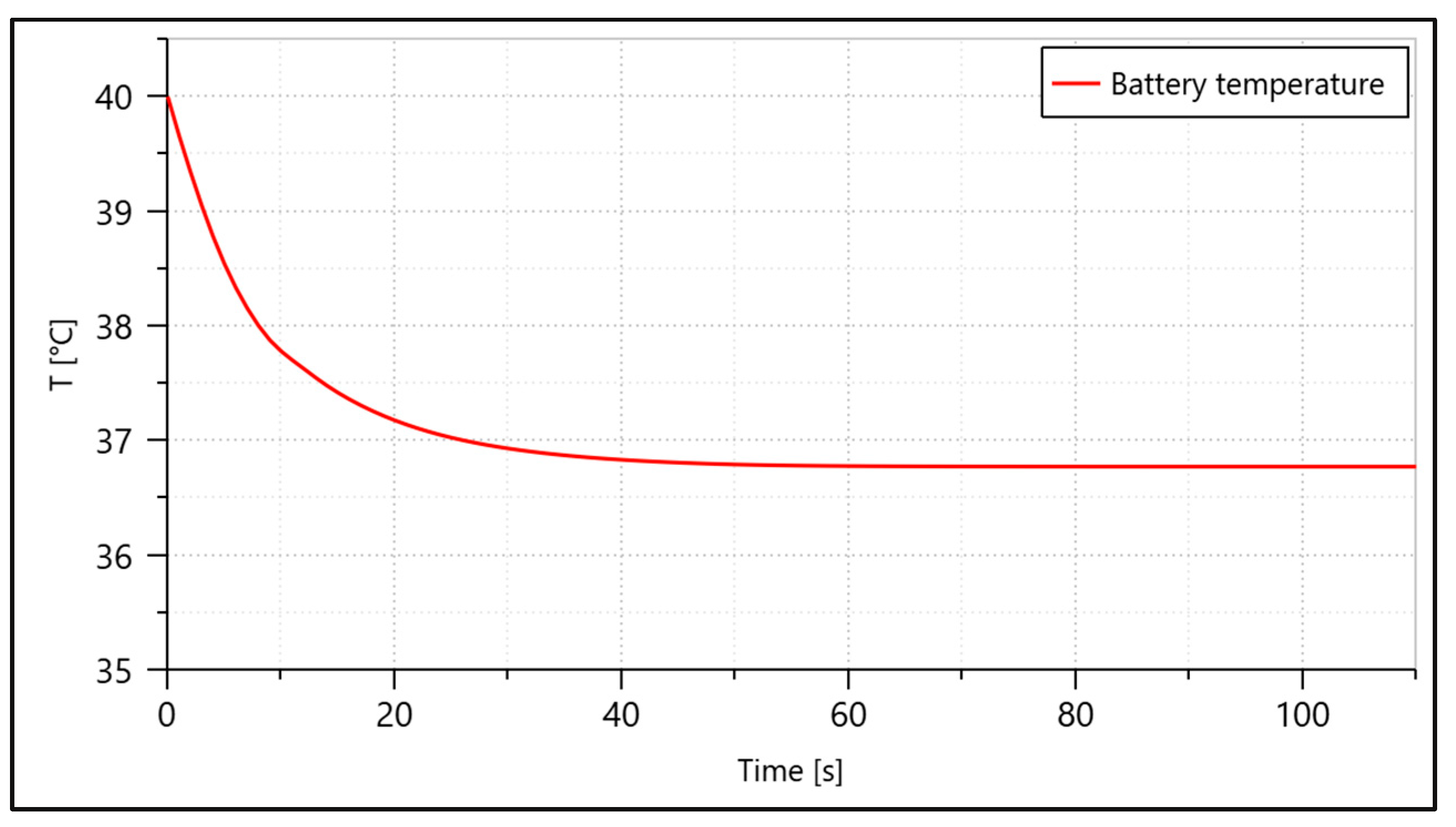
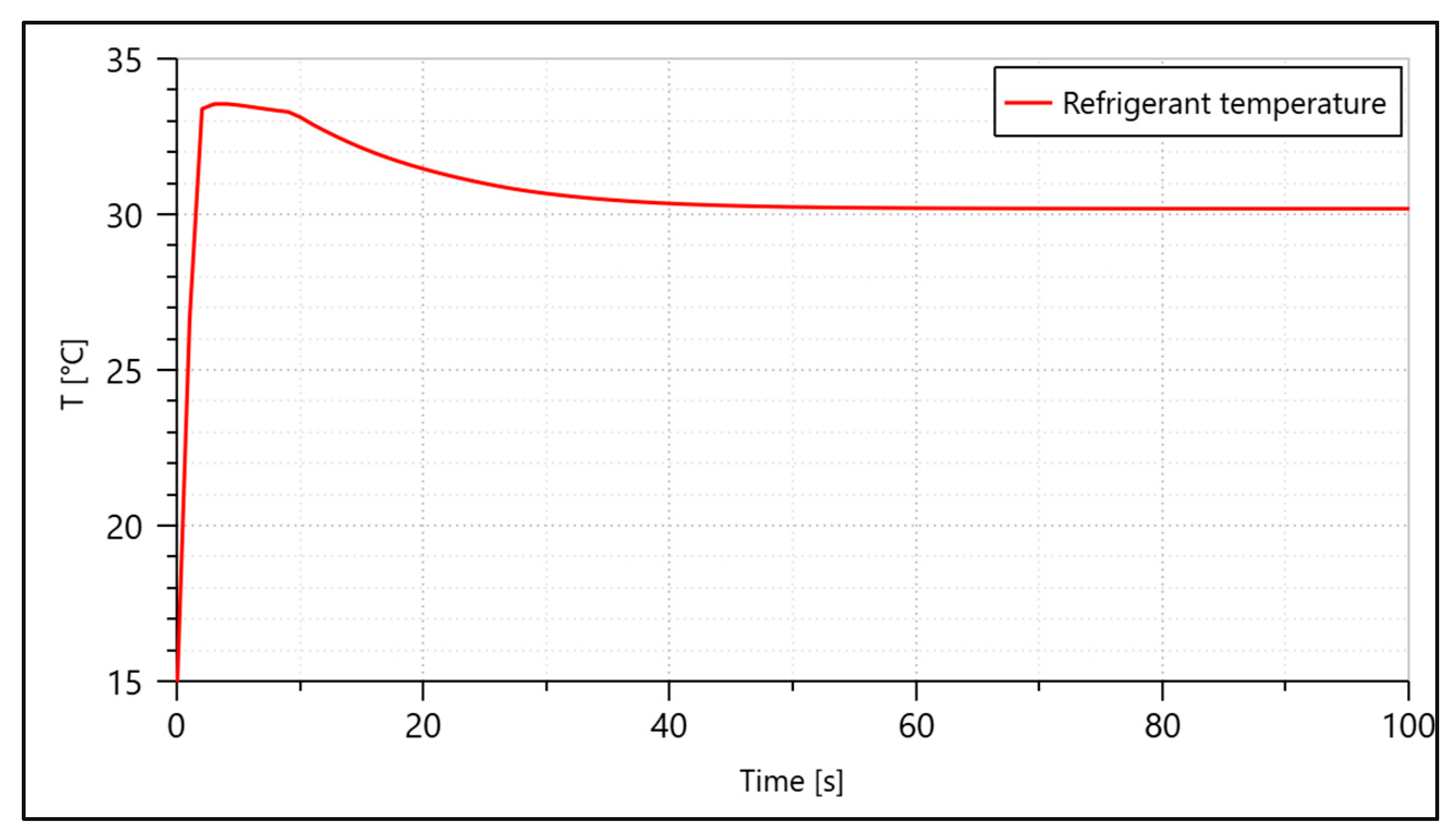
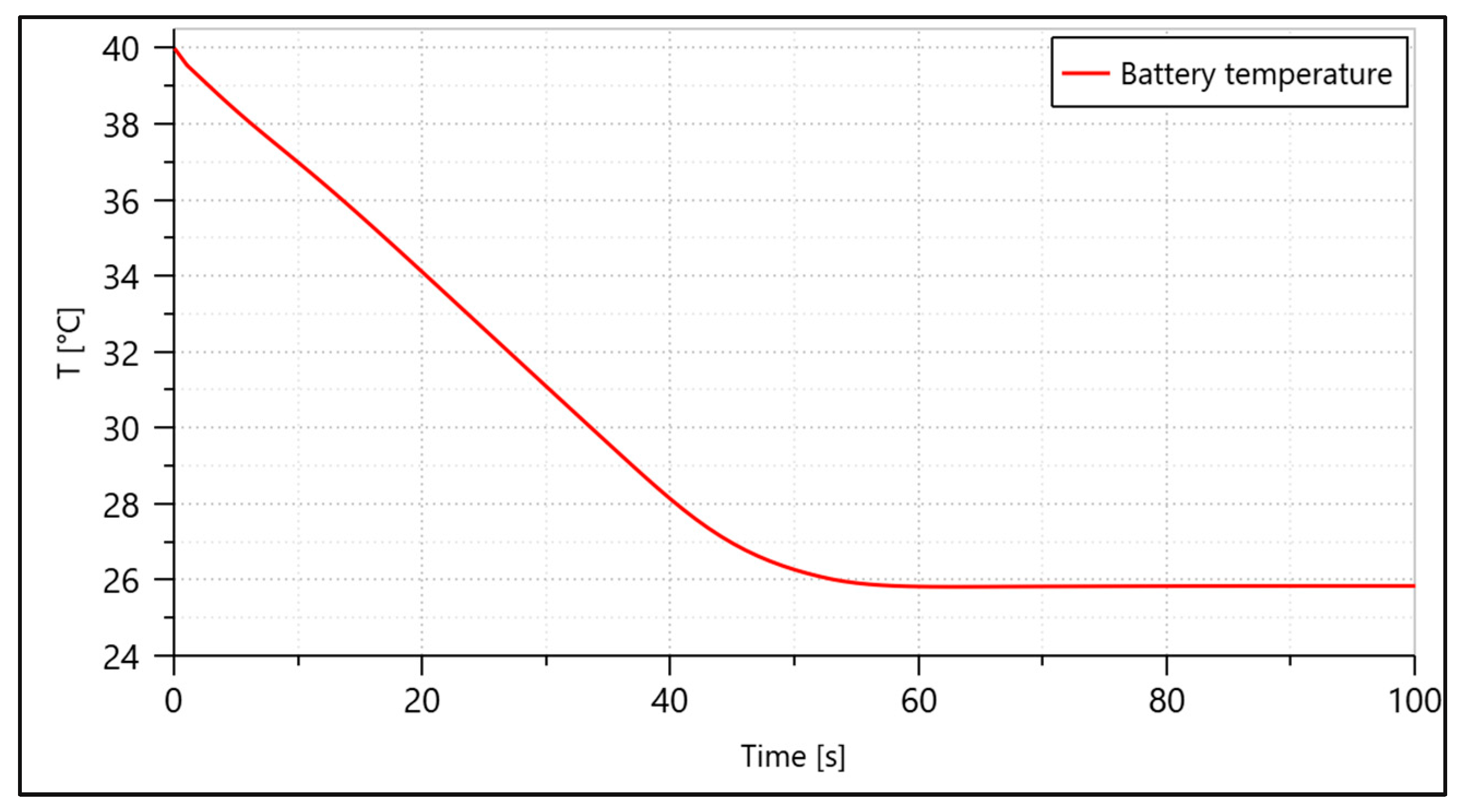
To prove the validity of the proposed model, a TMS able to maintain the 70 kW heat load released from the 1.4 MW battery that supplies power to the HEA below 40 °C was simulated and evaluated. The P2PL uses R450a refrigerant as the working fluid. The system’s functionality relies on the latent heat of the working fluid. The target fluid circulates in a cold plate, absorbing the heat load using latent heat and enabling efficient absorption. Meanwhile, the fluid shifts state from liquid to two-phase, continuing through the loop until it becomes condensate, at which point it is pumped again. In conventional cooling systems, heat is absorbed via specific heat, which is significantly lower than latent heat. For example, the specific heat of water used in air-cooled systems is 4.18 kJ/kg·K. However, the latent heat of the same fluid (water) is around 500 times greater, reaching approximately 2260 kJ/kg.

Section 2 outlines the methodology, which consists of a test case considering a 70 kW HEA battery heat load that should be maintained below 40 °C in three different environmental conditions. The second part covers the modularization and simulation model of the TMS. The proposed modeling uses Python code to estimate the size and weight of key system components, including the hydraulic diameter (Dh) of the cold plate and pipes and the condenser heat transfer area. The TMS is then simulated under three environmental conditions: a cold day, a standard day, and a hot day.

Section 3, the Results and Discussion, explains the outcomes of modeling the size and weight of components, while the simulation outcomes are defined for the three environmental conditions. The final battery temperature during cooling and the refrigerant condensation temperature are determined for cold and standard days, along with an analysis of the TMS operation under different system pressures. For the hot day, the maximum environmental battery temperature is defined as an outcome.

Section 4, Conclusion, summarizes the study and results obtained and outlines prospective future work.

2. Methodology

In this section, the case study is defined together with the environmental conditions, cold, standard, and hot day scenarios. The modeling and simulation of the thermal management system (TMS) are then introduced through a modular approach, and the system is evaluated under representative operating conditions.

2.1. Study Case

To prove the feasibility of the concept, a hybrid aircraft was used as a case study. The aircraft is targeted to be in service by 2030 based on the European directive, and it uses the battery as a second power source to support the takeoff and the rest of the mission profile of the aircraft to reduce polluting emissions. The power of the battery is assumed to be 1.4 MW, while its efficiency is 95%. The heat load generated by the battery is about 70 kW.

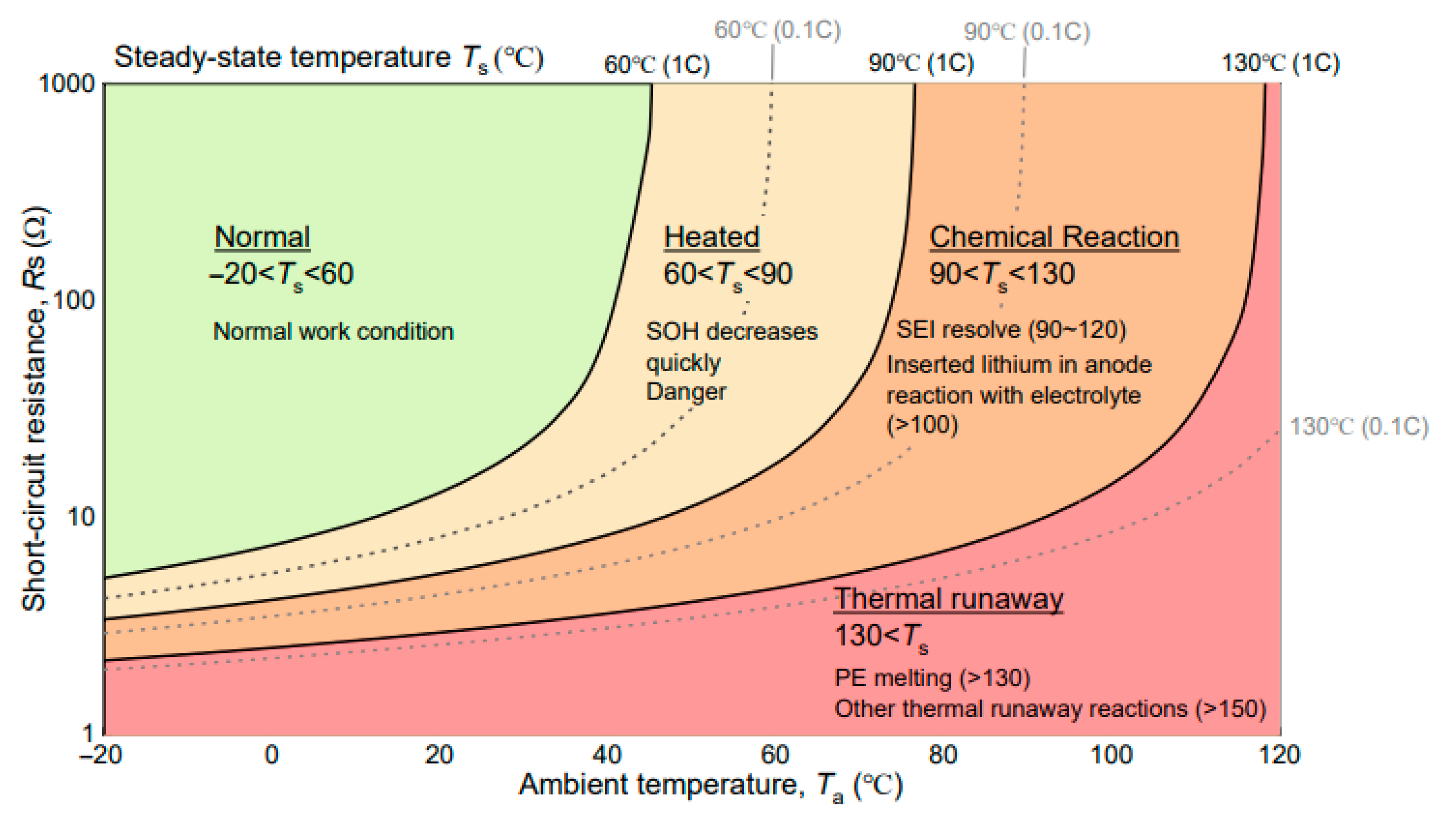
To properly design the TMS, it is important to take into account the battery temperature limitations. As mentioned in Figure 1, Li-ion batteries used in electric vehicles or aircraft can operate properly at a safe operational temperature between −20 °C and 60 °C, while the optimal working temperature is between 15 °C and 40 °C [28,29,30].

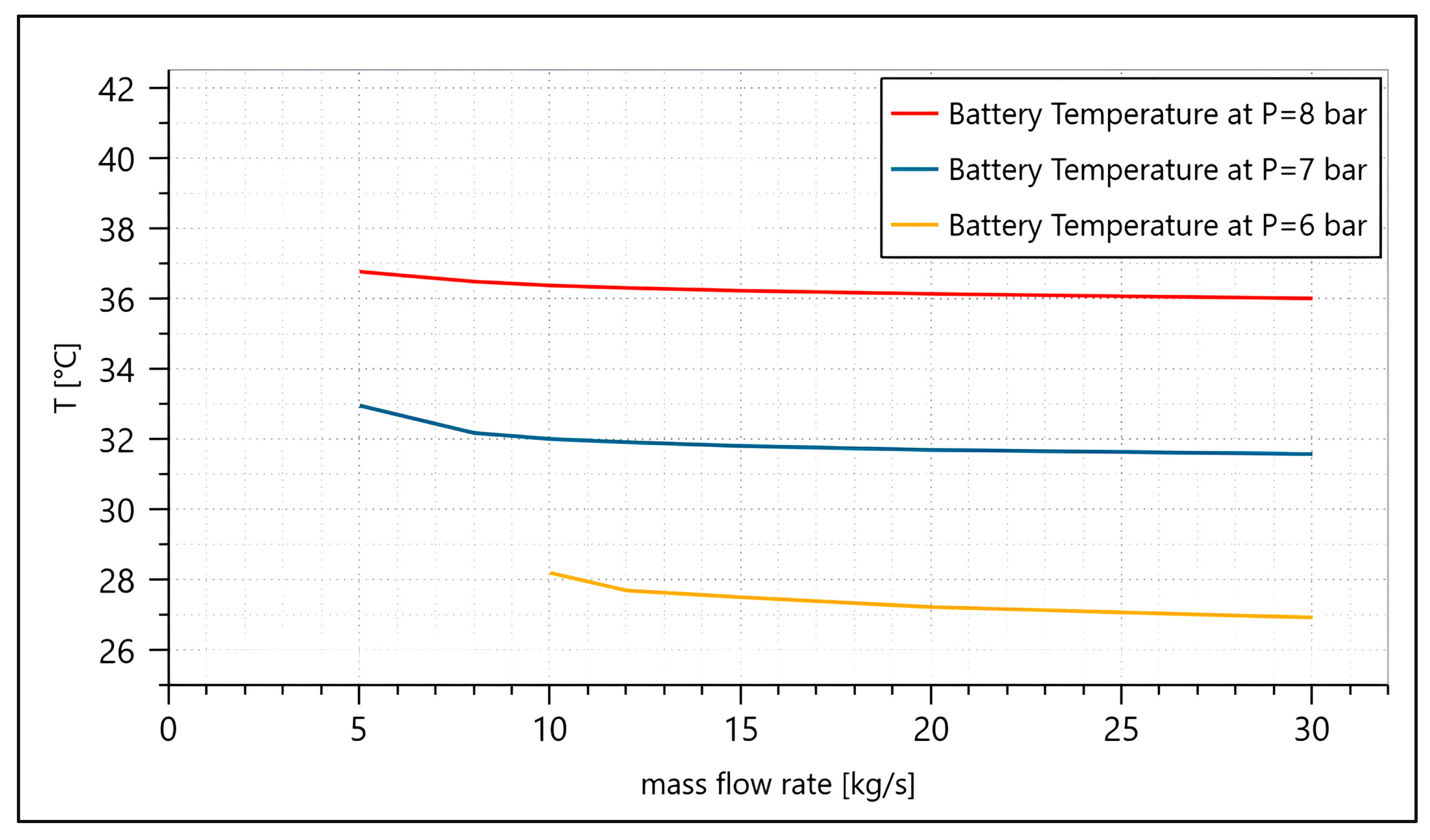
Another factor is the environmental conditions, which typically have a huge impact on system design. The design of the TMS components, especially the heat exchanger, will account for a hot day with a ground temperature of 40 °C. However, the proposed TMS is simulated under three conditions—standard day, hot day, and cold day, as shown in

Table 1. Temperature conditions used for the case study.

Condition	Cold Day	Standard Day	Hot Day
Temperature (°C)	−20	15	40

—to assess its performance across the entire temperature envelope of the aircraft.

2.2. Modulization and Simulation Model

The design utilizes a thermal model to dimension the key components. This process is based on a computational method implemented in Python code, which defines the required size of the key components, including the following:

• The required refrigerant mass flow rate;
• DH of the cold plate tubes;
• DH of the piping;
• The minimum heat transfer area of the heat exchanger.

Based on the given inputs—such as refrigerant characteristics, environmental conditions, fluid input temperatures, and heat exchanger core geometry—the code performs an iterative calculation to define the required sizes. The algorithm begins with an assumed small geometry and grows the part in three dimensions using mathematical correlations and equations for condensation, boiling, and pressure drop until the required design conditions are met. The model also estimates the weight of these components.

The modeling assumptions and boundary conditions are mentioned in

Table A1. Summary of governing modeling assumptions and boundary conditions.

Category	Assumption
Battery-Cold Plate Interface	Perfect thermal contact (zero contact resistance)
	Uniform heat flux distribution
	Battery modeled as single lumped thermal mass
Two-Phase Flow	Homogeneous flow model throughout
	Steady-state for sizing; quasi-steady for dynamics
	No flow maldistribution in parallel channels
Heat Transfer	Kandlikar correlation for evaporation
	Cavallini correlation for condensation
Pressure Drop	Homogeneous model for two-phase drops
	Minor losses = 2 × equivalent pipe length
Control System	Pressure regulated via accumulator
	Air flow rate constant per scenario
Environmental	Constant ambient temperature per simulation
	No altitude effects on air density

, while the input parameters for Python sizing algorithm can be found in

Table A2. Complete input parameters for Python sizing algorithm.

Parameter Category	Parameter	Value/Range	Note
System Requirements	Heat load (Q)	70 kW	Constant
	Battery power	1.4 MW	For efficiency calculation
	Battery efficiency	95%	Typical for Li-ion
	Target T_batt	≤40 °C (nominal)	Li-ion optimal range
Environmental	T_cold	−20 °C	Cold day
	T_standard	15 °C	Standard day
	T_hot	40 °C	Hot day (design point)
Refrigerant (R450A)	Source	NIST REFPROP	Via CoolProp library
	Latent heat (h_fg)	160–180 kJ/kg in 6–10 bar range
	Liquid density	~1150 kg/m3 at 7 bar
	Vapor density	~28 kg/m3 at 7 bar
Cold Plate Design	Tube material	Aluminum 6061	k = 167 W/m·K
	Wall thickness	1 mm	Standard for aviation
	Tube length	2 m	To achieve required area
	Contact surface	3 m	Battery size
	Number of tubes	Calculated	Based on D_h and area
Pipe Sizing	Material	Aluminum	Aviation standard
	Length (liquid line)	5 m	Aircraft layout
	Length (two-phase line)	3 m	Aircraft layout
Condenser Design	Type	Plate-fin	Compact HX standard
	Fin geometry	From [34]	3 mm pitch, 0.1 mm thickness
	Material	Aluminum	Lightweight
Convergence	Heat balance tolerance	1%	Standard for compact HX
	Max pressure drop	5 kPa/m	Exit criterion
	Max iterations	100	Prevent infinite loops

.

The results obtained from the model are used to build a simulation model in Siemens Simcenter Amesim software version 2310. This model is able to simulate the TMS performance across several environmental conditions.

2.2.1. Fluid Characteristics

The selection of the working fluids is the first step to start designing the system. To properly select the fluid, the following criteria must be fixed based on the case study:

• Latent heat;
• Boiling and condensation point;
• Low global warming potential (GWP)—non-toxic, non-flammable.

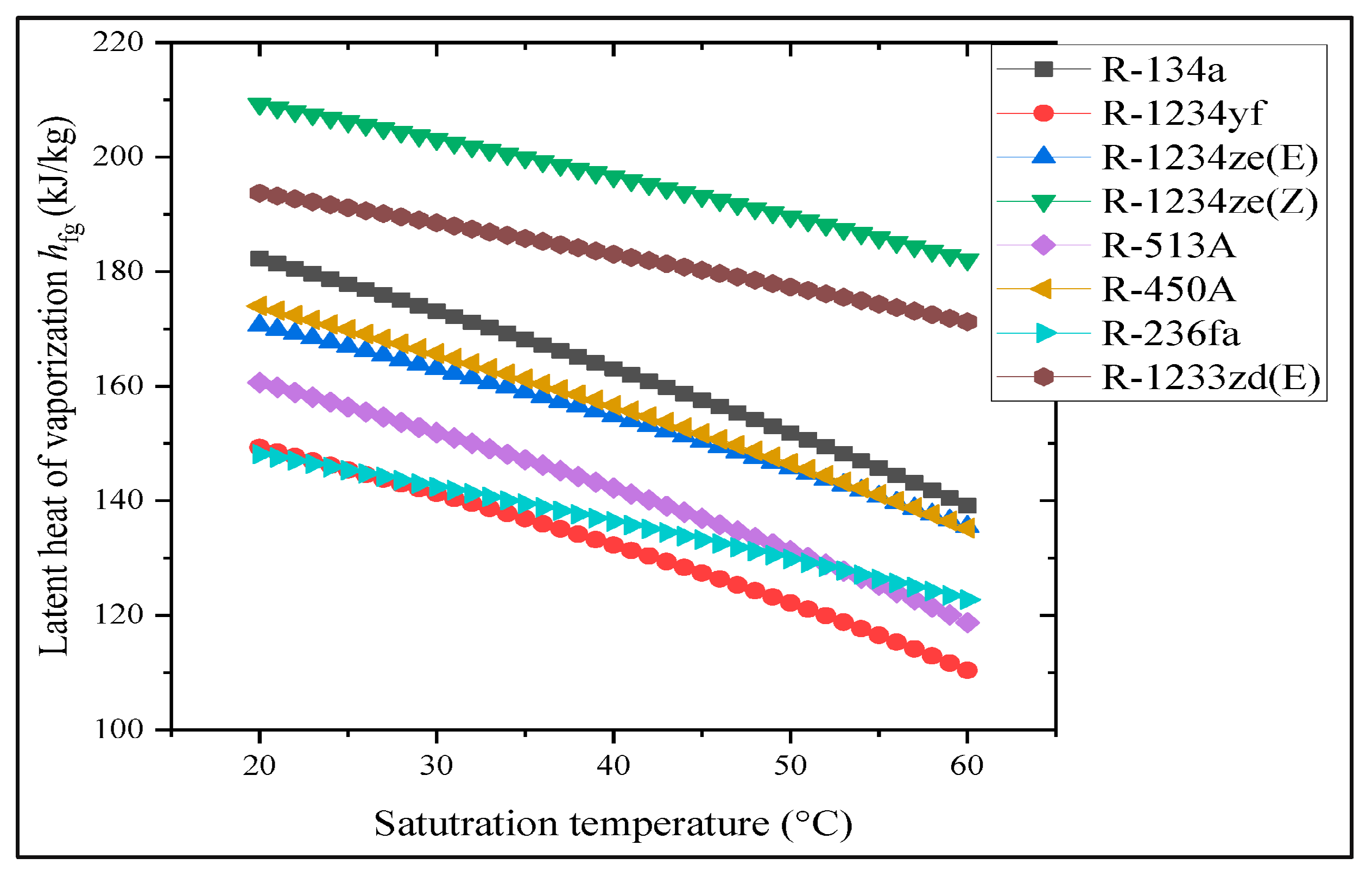
Several fluids demonstrate high efficiency, such as the widely used R134a, characterized by high performance. However, its high GWP leads to consideration of other fluids like R1233zd(E) and R1234ze(Z), noted for high latent heat. R450a is another refrigerant that follows these two in terms of latent heat, as demonstrated in Figure 2, which shows the latent heat of vaporization and saturation temperature for the considered fluids. These characteristics make them good alternatives to R134a.

Toxicity and flammability must be addressed. 1233zd(E) is ranked ASHRAE Safety Class A2L (low toxicity, mildly flammable), while R450a and R1234ze(Z) meet ASHRAE Safety Class A1 (non-toxic, non-flammable).

Besides safety class and latent heat, the boiling and condensation point is a critical selection criteria. In the P-h diagram, a comparison of these three refrigerants at fixed temperatures of 35 °C and 40 °C, represented in

Table 2. Saturation temperatures and pressure for the refrigerants.

Referent	P (bar) at 35 °C	P (bar) at 40 °C	ΔP (bar)
R450a	7.86	9.01	1.15
R1234ze(Z)	2.50	2.92	0.62
R1233zd(E)	1.8	2.15	0.85

, shows saturation pressures of approximately 2.5 bar and 2.92 bar for R1234ze(Z), 1.8 bar and 2.15 bar for R1233zd(E), and 7.86 bar and 9.01 bar for R450A, respectively. This difference represents a major performance advantage for R450A.

The high-pressure difference (ΔP ≈ 1.15 bar) between the evaporation and condensation temperatures enables more stable condensation even with significant pressure drops. In contrast, refrigerants like R1234ze(Z) or R1233zd(E) exhibit a very small pressure difference (ΔP ≈ 0.42 bar), increasing the risk of incomplete condensation and system instability. This behavior was confirmed during simulation tests, where high-latent-heat, low-pressure refrigerants failed to fully condense under equivalent conditions.

R450a represents a good option meeting all criteria. It is composed of 42% R134a and 58% R1234ze(E), achieving lower GWP than R134a while meeting ASHRAE Safety Class A1.

2.2.2. Hydraulic Diameter Sizing

The working fluid passes through the installation piping and then to the evaporator, which works as a cold plate. The remaining necessary geometry to be defined includes the DH for the installation piping, ensuring minimal pressure drop and, more importantly, the DH for the cold plate tubes required to achieve the proper refrigerant boiling point.

These diameters are calculated using the thermal model through the application of two-phase fluid boiling equations to define the heat transfer coefficient (HTC) and pressure drop. Starting with the evaporator’s latent heat equation, the required refrigerant mass flow rate is determined from Equation (1).

$$\dot{Q}=\dot{m}\times h_{fg}$$

(1)

where $\dot{Q}$ is the heat load rejected by the battery, $\dot{m}$ is the refrigerant mass flow, and $h_{fg}$ is the latent heat of the refrigerant.

The heat transfer coefficient (${\mathrm{h}}_{\mathrm{T}\mathrm{P}}$) for two-phase inside the cold plate is calculated using the general Kandlikar correlation for saturated two-phase flow boiling in horizontal tubes, applicable to widely used refrigerants [33].

$${\mathrm{h}}_{\mathrm{T}\mathrm{P}}={\mathrm{h}}_{\mathcal{l}}\times \left[\mathrm{D}1\right(\mathrm{C}\mathrm{o}{)}^{\mathrm{D}2}{\left(25{\mathrm{F}\mathrm{r}}_{\mathcal{l}}\right)}^{\mathrm{D}5}+\mathrm{D}3\left(\mathrm{B}\mathrm{o}{)}^{\mathrm{D}4}{\left(25{\mathrm{F}\mathrm{r}}_{\mathcal{l}}\right)}^{\mathrm{D}6}{\mathrm{F}}_{\mathrm{f}\mathcal{l}}\right]$$

(2)

where ${\mathrm{h}}_{\mathcal{l}}$ is the single-phase convective coefficient for liquids, calculated via the Dittus–Boelter correlation:

$${\mathrm{h}}_{\mathcal{l}}=0.023{\left({\displaystyle \frac{\mathrm{G}(1-\mathrm{x})\mathrm{D}}{{\mu }_{\mathcal{l}}}}\right)}^{0.8}{\mathrm{P}\mathrm{r}}_{\mathcal{l}}^{0.4}{\mathrm{k}}_{\mathcal{l}}/\mathrm{D}$$

(3)

$Bo$ is the boiling number for the nucleate boiling region:

$$Bo=q/\left(\begin{array}{c}G{h}_{fg}\end{array}\right)$$

(4)

And $C_o$is the convection number for the convective boiling region:

$$C_o={\left({\displaystyle \frac{1-x}{x}}\right)}^{0.8}{\left({\displaystyle \frac{{\rho }_g}{{\rho }_{\mathcal{l}}}}\right)}^{0.5}$$

(5)

The Froude number, Fr, of the possible effects of flow stratification in the horizontal flow is

$${\mathrm{F}\mathrm{r}}_{\mathcal{l}}={\mathrm{G}}^2/\left({\rho }_{\mathcal{l}}^2\mathrm{g}\mathrm{D}\right)$$

(6)

The two-phase total pressure drop $\mathsf{\Delta }{p}_{\mathrm{total}}$ inside the horizontal tube is represented by the sum of three terms.

$$\mathsf{\Delta }{p}_{\mathrm{total}}=\mathsf{\Delta }{p}_{\mathrm{static}}+\mathsf{\Delta }{p}_{\mathrm{a}}+\mathsf{\Delta }{p}_{\mathrm{frict}}$$

(7)

where $\mathsf{\Delta }{p}_{\mathrm{static}}$ = 0, the static pressure drop for a horizontal tube, and $\mathsf{\Delta }{p}_{\mathrm{a}}$is the acceleration pressure drop, calculated using the simplified homogeneous model in Equation (8):

$$\mathsf{\Delta }{p}_{\mathrm{a}}={\mathrm{G}}^2\left\{{\left[{\displaystyle \frac{\mathrm{x}}{{\rho }_G}}+{\displaystyle \frac{1-\mathrm{x}}{{\rho }_L}}\right]}_{\mathrm{out}}-{\left[{\displaystyle \frac{\mathrm{x}}{{\rho }_G}}+{\displaystyle \frac{1-\mathrm{x}}{{\rho }_L}}\right]}_{\mathrm{in}}\right\}$$

(8)

$\mathsf{\Delta }{p}_{\mathrm{frict}}$ is the frictional pressure drop, also calculated using a homogeneous model, as defined by Equation (9):

$$\mathsf{\Delta }{p}_{\mathrm{frict}}={\displaystyle \frac{{\mathrm{G}}^2}{2D{\rho }_{\mathrm{T}\mathrm{P}}}}{f}_{\mathrm{T}\mathrm{P}}$$

(9)

where $f_{\mathrm{T}\mathrm{P}}$ represents the friction factor, and ${\rho }_{\mathrm{T}\mathrm{P}}$ is the density averaged by the proportion of gas and liquid.

2.2.3. Condenser Sizing

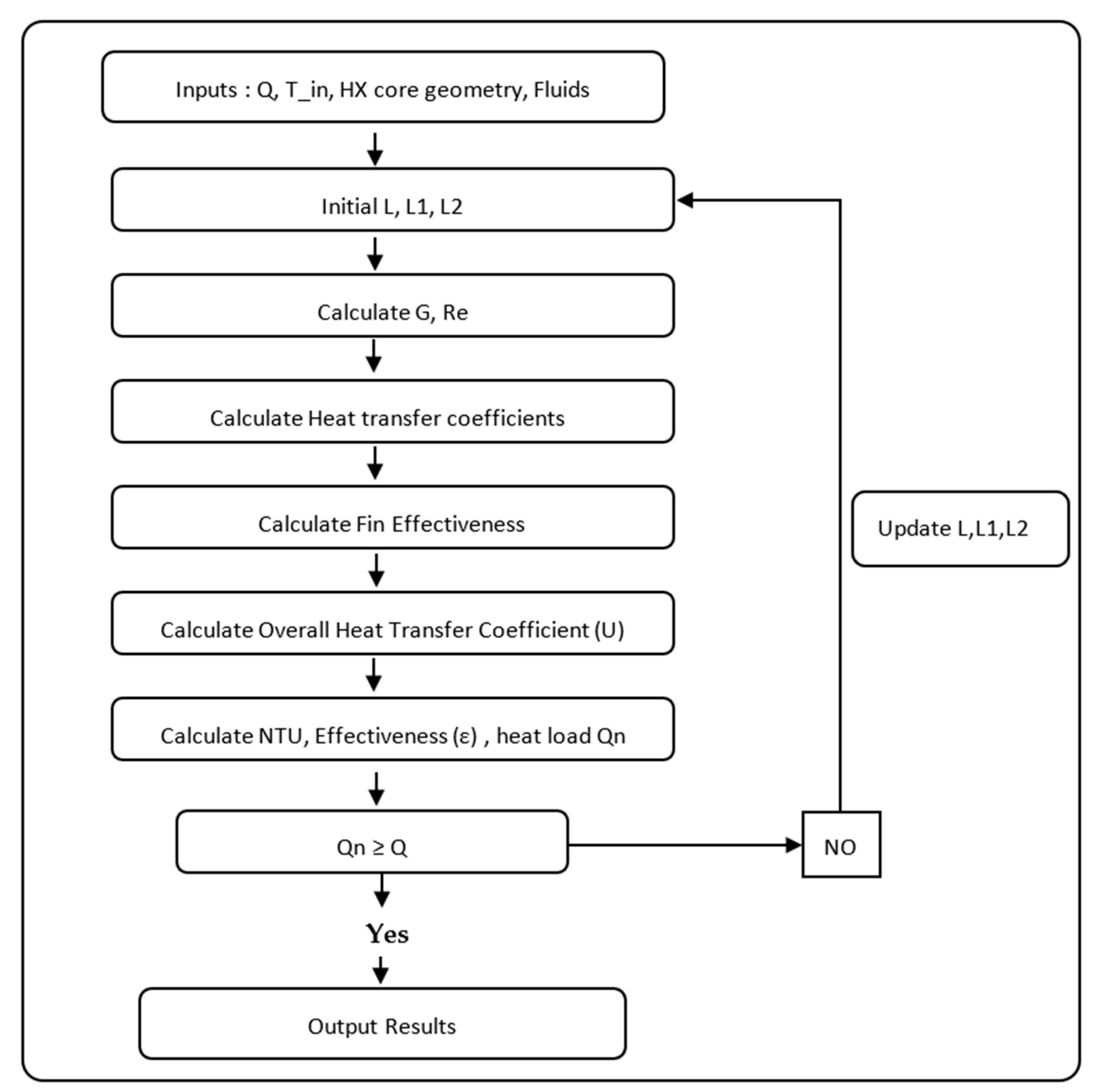
The condenser used is the plate fin heat exchanger. A predefined internal geometry is selected from the literature [34], while the final dimensions of the condenser are estimated using iterative calculation with a thermal model represented on a flowchart in Figure 3. The NTU method is utilized for calculation:

$$\epsilon =1-\mathrm{e}\mathrm{x}\mathrm{p}(-\mathrm{N}\mathrm{T}\mathrm{U})$$

(10)

$$\mathrm{N}\mathrm{T}\mathrm{U}=-\mathrm{l}\mathrm{n}(1-\epsilon )$$

(11)

$$U={\displaystyle \frac{NTU.A}{C_{min}}}$$

(12)

The condensation coefficient and HTC are calculated using the Cavallini correlation, which is validated for the R50a refrigerant [35].

$${\mathrm{h}}_{\mathrm{T}\mathrm{P}}={\displaystyle \frac{{\mathrm{k}}_{\mathcal{l}}}{\mathrm{D}}}0.05{\mathrm{R}\mathrm{e}}_{\mathrm{e}\mathrm{q}}^{0.8}{\mathrm{P}\mathrm{r}}^{0.33}$$

(13)

where ${\mathrm{R}\mathrm{e}}_{eq}$ is the equivalent Reynolds number, defined by

$${\mathrm{R}\mathrm{e}}_{eq}={\mathrm{R}\mathrm{e}}_v\left({\mu }_v/{\mu }_{\mathcal{l}}\right){\left({\rho }_{\mathcal{l}}/{\rho }_v\right)}^{0.5}+{\mathrm{R}\mathrm{e}}_{\mathcal{l}}$$

(14)

${\mathrm{R}\mathrm{e}}_v$ is defined as

$${\mathrm{R}\mathrm{e}}_v={\displaystyle \frac{GxD}{{\mu }_v}}$$

(15)

And ${\mathrm{R}\mathrm{e}}_{\mathcal{l}}$ is the liquid Reynold number:

$${\mathrm{R}\mathrm{e}}_{\mathcal{l}}={\displaystyle \frac{G(1-x)D}{{\mu }_{\mathcal{l}}}}$$

(16)

The pressure drop is calculated using the same simplified homogeneous model, Equation (8), as it is able to calculate pressure drop during both condensation and evaporation.

The condenser dry weight is calculated using Equation (17):

$$W_c={\rho }_{m}V(1-\sigma )$$

(17)

3. Results and Discussion

3.1. Thermal Model

The thermal model is designed to primarily define the size of key TMS components. This includes determining the DH for the installation piping and the internal tubes of the cold plate to ensure an effective boiling process. These results are represented in Table 3. The results indicate a required DH of 7.89 mm for the cold plate, which is validated via a comparison with other experimental studies investigating the boiling heat transfer of refrigerants similar to R450a under comparable hydraulic diameters, as presented in Table 4. For installation tubes, DH is 27 mm for the two-phase section and a reduced diameter of 15 mm for the fully liquid section. Furthermore, the model defines the required mass flow rate for the refrigerant (R450a) as 0.56 kg/s. This flow is delivered by a pump with a power rating of 22 W.

Table 3. Component size results.

Component	Value
Dh of two-phase pipes (mm)	15
Dh of liquid pipes (mm)	27
Dh of cold plate tubes (mm)	7.89
Refrigerant mass flow (Kg/s)	0.56
Pump power (w)	22

Table 3. Component size results.

Component	Value
Dh of two-phase pipes (mm)	15
Dh of liquid pipes (mm)	27
Dh of cold plate tubes (mm)	7.89
Refrigerant mass flow (Kg/s)	0.56
Pump power (w)	22

Table 4. Experimental studies on boiling heat transfer of R450a-like refrigerants at comparable hydraulic diameters.

Study	Refrigerant	T (°C)	q (kW/ m2)	G (kg/m2)	Dh (mm)
Current study	R450A	20	23	100	7.89
Mastrullo et al. 2024 [36]	R450A	30–50	10–20	150–400	6
Kundu et al. 2014 [37]	R134a, R410A, R407C	5–9	3–10	100–400	7
Liu et al. 2022 [38]	R515B, R450A, R1234ze(E)	30	10–50	50–400	6.14
Kedzierski et al. 2018 [39]	R1234yf, R450A, R134a	0–20	0.3–18	100–300	5.45

Table 4. Experimental studies on boiling heat transfer of R450a-like refrigerants at comparable hydraulic diameters.

Study	Refrigerant	T (°C)	q (kW/ m2)	G (kg/m2)	Dh (mm)
Current study	R450A	20	23	100	7.89
Mastrullo et al. 2024 [36]	R450A	30–50	10–20	150–400	6
Kundu et al. 2014 [37]	R134a, R410A, R407C	5–9	3–10	100–400	7
Liu et al. 2022 [38]	R515B, R450A, R1234ze(E)	30	10–50	50–400	6.14
Kedzierski et al. 2018 [39]	R1234yf, R450A, R134a	0–20	0.3–18	100–300	5.45

The condenser is designed based on an inlet air temperature of 15 °C and an air mass flow rate of 5 kg/s. A heat transfer area of 26.20 m² is defined for the condenser; this requirement is necessary to properly condense the refrigerant and reject the 70 kW heat load from the battery. The results of the condenser thermal model are presented in

Table 5. Condenser dimension results.

Condenser Dimension	Value
Length (mm)	430
Width (mm)	227
Heigh (mm)	200
$\mathrm{Heat}\mathrm{transfer}\mathrm{area}({\mathrm{m}}^2$)	26.20

.

The thermal model is able to estimate the weight of key components such as the condenser and piping. The refrigerant and pump weight is also extracted from the simulation model. The weight of each component and the total TMS weight are presented in

Table 6. Component weight results of TMS.

Component	Weight (kg)
Pump	2
Pipes	4
Condenser	12
Refrigerant	4
Total	22

.

The results obtained for P2PL HX weight, size, and pumping power confirm system compactness compared to other systems mentioned in Table 7, like VCS and liquid-to-air.

TMS compactness is not solely based on HX weight and size, but rather on overall system-level compactness, which includes power requirement, flow rate, and turbomachinery size.

The actual condenser dimensions are 0.430 m × 0.245 m × 0.200 m, with a 26.2 m² total heat transfer area, a frontal area of 0.020 m², and a dry weight of 12 kg. This is relatively small compared to condensers in previous studies. One study investigating thermal management for a hybrid-electric aircraft with a 96 kW heat load reported a heat exchanger volume of 0.06 m³ with dimensions of 0.48 m × 0.73 m × 0.18 m [40]. Another study using a similar HX design found a total heat transfer area of 20 m² for a smaller heat load of 45.9 kW from a hybrid-electric aircraft battery [20].

The major advantage of the proposed pumped two-phase loop (P2PL) system is its very low pumping power and refrigerant mass flow rate. The entire loop operates with a pump power of only 26 W and a refrigerant mass flow rate of 0.56 kg/s. For other similar TMS, such as liquid-to-air studies, the pump power is about 500 W to 4 kW, which adds significant weight. For VCS, the cooling system is much larger and more complex, exceeding 100 kg for the entire system due to the compressor [18,22].

This significantly reduces both the auxiliary power demand and the total system mass. In contrast, vapor compression systems (VCS) require a compressor that handles the system’s weight, volume, and complexity. This makes the P2PL system inherently more compact and energy-efficient.

Table 7. Different cooling technologies and their weights; adapted from [41].

Technology	COP	Mass (kg)
Air cycle machine	0.1–0.7	80–290
Vapor cycle machine	2.3–4.4	330–600
Expendable cooling	N/A	30–300
Vortex tube cooling	0.01–0.13	50–85
Thermoelectric cooler	0.2–1.2	10–30
Magnetocaloric cooler	0.5–9.7	340–610
Phase change material	N/A	400–510

Table 7. Different cooling technologies and their weights; adapted from [41].

Technology	COP	Mass (kg)
Air cycle machine	0.1–0.7	80–290
Vapor cycle machine	2.3–4.4	330–600
Expendable cooling	N/A	30–300
Vortex tube cooling	0.01–0.13	50–85
Thermoelectric cooler	0.2–1.2	10–30
Magnetocaloric cooler	0.5–9.7	340–610
Phase change material	N/A	400–510

A multi-level validation approach was required due to the absence of experimental data for a directly comparable MW-class aircraft battery P2PL. Consequently, the developed model was benchmarked against independent experimental studies. At the component level, the predicted optimal hydraulic diameter of 7.89 mm corresponds with findings from Mastrullo et al. [36] and Liu et al. [38], whose work identified 6–8 mm channels as optimal for R450a-like refrigerants. The condensation model also aligns with experimental data from Morrow and Derby [42].

For system-level validation, the implemented pressure-based control logic is corroborated by Liu et al. [43], who demonstrated that accumulator pressure regulation could maintain the saturation temperature within ±0.1 °C under variable loads. Furthermore, the system’s efficiency scaling is substantiated through comparison with the 20 kW aerospace P2PL developed by van Gerner et al. [44]. The model’s calculated pump power-to-heat load ratio of 0.00031 follows an established efficiency trend, showing improvement over the ratio of ~0.0015 for their 20 kW system and the ~0.09 ratio typical of older, smaller-scale units [44]. This progression confirms that the low pump power requirement in the present model is a direct physical outcome of scaling to MW-class thermal loads.

3.2. Simulation Model

The simulation model is built using the two-phase library, as shown in Figure 4. The model uses size data provided from the thermal model, including the DH of piping and condenser geometry. The system also requires a tank or accumulator with pressure regulation to maintain a stable pressure at the pump inlet. The Amesim simulation setup can be found in

Table A3. Amesim simulation setup.

Component	Model/Library Used	Key Parameters
Refrigerant Circuit	Two-Phase Fluid Library	R450A properties from NIST
Battery	Thermal Mass + Heat Source	C = 20 kJ/K, Q = 70 kW
Cold Plate	Tube Heat Exchanger	D_h = 7.89 mm, L = 2 m
Piping	Pipe Components	Liquid: D_h = 15 mm, Two-phase: D_h = 27 mm
Condenser	Plate Heat Exchanger	A = 26.2 m2, dimensions 430 × 227 × 200 mm
Pump	Centrifugal Pump	ΔP = 1.5 bar @ 0.56 kg/s
Accumulator	Tank with Pressure Regulator	V = 2 L, maintains saturation
Air Flow	Boundary Conditions	T_in = scenario, $\dot{\mathrm{m}}$ = 5 kg/s
Solver Settings	Fixed-step	Time step = 0.1 s
Initial Conditions	-	T = 15 °C, P = 7 bar, x = 0

.

The TMS is simulated in three environmental conditions: a cold day, a standard day, and a hot day. For each condition, the system response time, battery temperature, and condensation temperature data are extracted. Furthermore, an analysis of operational pressure is performed to assess the system’s flexibility in low-temperature conditions.

3.2.1. Standard Day Condition

The initial conditions of the system are set to an inlet air temperature of 15 °C to the condenser. With the system pressure elevated by the pump to 7 bar and an air mass flow rate of 5 kg/s, the system is successfully able to reduce the battery temperature to a stable value of 36.77 °C during the first 100 seconds, as shown in Figure 5. Meanwhile, the heat exchanger dissipates the heat load and condenses the refrigerant at 30.1 °C, as shown in Figure 6.

The condensation temperature and the associated heat transfer behavior are in line with the experimental data for R450A reported by Morrow and Derby [42], based on their investigation of condensation heat transfer coefficients at a saturation temperature of 40 °C. Under the present operating conditions (T_sat ≈ 30.1 °C and P_sat ≈ 7 bar), the system’s condensation performance follows the expected trends observed in their study. This study also validated the Cavallini correlation, which was used in the present model. Furthermore, the thermodynamic stability of R450A at these operating temperatures is consistent with experimental results at the system level found by Makhnatch et al. [45], demonstrating that R450A operates with stable pressure ratios and lower discharge temperatures than R134a within similar condensing temperature ranges (25–35 °C).

The maximum pressure the system can reach is limited by the battery temperature. At 40 °C, the pressure corresponding to the saturation curve of R450a is ≈9 bar. However, to maintain the battery below 40 °C, a pressure of 8 bar corresponds to a refrigerant temperature of 35 °C. This provides a sufficient temperature gap to maintain the battery below 40 °C while the refrigerant absorbs the heat load during its evaporation at 8 bar and 35 °C.

The minimum pressure depends on the environmental conditions and the ability of the condenser to condense the refrigerant to a temperature near the air inlet temperature. In this case, at an air temperature of 15 °C, and taking into consideration that the refrigerant is fully condensed at the same temperature as the inlet air, the pressure would be 4.32 bar. However, in reality, the refrigerant condenses at a higher temperature, which means the pressure should be higher. This is also controlled by varying the air mass flow to achieve higher efficiency and condense the refrigerant as close as possible to the air temperature.

The pressure analysis in Figure 7 shows the variation in battery temperature as a function of air mass flow rate at different system pressures, ranging from the minimum pressure of 6 bar to the maximum at 8 bar. The TMS is able to regulate the battery temperature to various setpoints based on operational needs. The minimum battery temperature that the TMS can achieve is 27 °C at a system pressure of 6 bar and an air mass flow rate of 30 kg/s, while the upper limit is 38 °C at 8 bar.

The results clearly show that the system pressure is the main factor that defines the final battery temperature, while the air mass flow is primarily responsible for ensuring the full condensation of the refrigerant. For example, at a system pressure of 8 bar, the battery temperature remains almost constant, with a variation of only 0.7 °C while the air mass flow rate changes from 5 kg/s to 25 kg/s. This is because the refrigerant is able to be fully condensed at an air mass flow of 5 kg/s; increasing this value does not lead to a decrease in battery temperature, as it is controlled by the boiling pressure and temperature of the refrigerant.

3.2.2. Cold Day Condition

Cold day conditions were evaluated at an ambient temperature of −15 °C. Under these conditions, the system demonstrates high performance and flexibility in regulating battery temperature. As established in the previous discussion, the lower inlet air temperature enables a lower refrigerant condensation point. This improves the heat rejection capability and enables precise thermal management of the battery across its entire operational range of 15 °C to 40 °C.

Figure 8 shows the time needed for the TMS to maintain the battery at a stable temperature. The system maintains a stable battery temperature within the first 60 s, which is faster than under standard conditions. As the system is flexible, the temperature is set to 25 °C (the ideal temperature for batteries), the system pressure is fixed at 6 bar, and the air mass flow rate is 5 kg/s.

3.2.3. Hot Day Condition

Hot day conditions of 40 °C are considered for the design. Under these hard conditions, the P2PL system maintains the battery within its operational temperature range. This range is considered between −20 °C and +60 °C for Li-ion batteries in electric vehicles [28,29,30].

The simulation of the system on a 40 °C hot day (Figure 9) shows that the P2PL system maintains the battery at 47.6 °C with a system pressure of 10 bar during the take-off phase, which lasts less than 20 min. A key advantage of this system is its ability to effectively mitigate the risk of battery thermal runaway, which typically begins at temperatures above 60 °C. The P2PL can function even in extreme hot conditions of 50 °C, keeping the battery below the 60 °C threshold at 57.45 °C, as shown in the simulation results in Figure 10.

However, while this peak temperature of 57.45 °C remains below the critical safety limit, we acknowledge that it exceeds the optimal operating range (15–40 °C). Prolonged operation at this temperature during extreme hot-day takeoffs may accelerate solid electrolyte interphase (SEI) formation and capacity fade. Therefore, this operating mode represents a trade-off where safety and mission completion are prioritized over long-term battery cycle life during rare, extreme environmental events.

This performance is a distinct characteristic of the P2PL system. The heat exchanger (HX) and pumping power are fixed; only the system’s saturation pressure changes. This pressure change directly adjusts the saturation temperature, which in turn regulates the battery temperature. This inherent feature provides a significant advantage over single-phase liquid-to-air cooling, which typically requires significantly higher flow rates and pumping power to handle such extreme ambient envelopes.

4. Conclusions

This study investigates the modeling and simulation of a thermal management system (TMS) for a hybrid-electric aircraft based on a P2PL cooling system. A thermal model is developed to determine the dimensions of the key components. The results show a total system mass of 22 kg and a condenser heat transfer area of 26.20 m². These results are used to create a simulation model for analyzing cooling performance under three environmental conditions and various system pressures. The system demonstrates good cooling performance under standard conditions, maintaining a constant battery temperature of 36 °C for the first 100 s at a system pressure of 8 bar. It also operates effectively at different pressure levels (6, 7, and 8 bar) and performs well in cold conditions.

The TMS results in hot conditions demonstrate that at a 40 °C ambient temperature, the P2PL system maintains the battery temperature at 47.6 °C. In an extreme hot condition of 50 °C, it keeps the battery at 57.45 °C during the short takeoff phase (less than 20 min); while this exceeds the optimal aging range, it remains safely below the critical limit (>60 °C), representing an acceptable trade-off where mission safety is prioritized over cycle life during rare extreme events.

Future work will investigate improvements to the thermal model and explore the application of the P2PL to other aircraft subsystems.