Design and Analysis of Combining Oil-Cooling Scheme of S-Shaped and End-Spraying Passages for Permanent Magnet Synchronous Motor

Abstract

The continuous pursuit of power density, efficiency, and miniaturization poses significant challenges to the heat dissipation and temperature-rise control of permanent magnet synchronous motor (PMSM) for new energy vehicles. This paper proposes a novel S-shaped axial return passage in the motor casing and a combined oil-cooling scheme integrating S-shaped and end-spraying passages. The geometric structure and parameters of the S-shaped passage and end-spraying passage were designed and optimized, and a finite-element temperature-field model of a PMSM equipped with the combined oil-cooling system is established. The results show that, compared with a traditional right-angle axial returning passage, the pressure loss of the new S-shaped returning passage is reduced by 50%, while the wall heat transfer coefficient remains comparable. At a cooling oil flow rate of 12 L/min, the highest temperature of the end winding is 92.6 °C, only 1.5 °C higher than that of the stator core under rated operating conditions. An experimental prototype was fabricated, and the measured results indicate that the simulated end-winding temperature shows close agreement with the experimental values, with a maximum deviation of only 3.8 °C. The proposed combined oil-cooling scheme efficiently enhances the cooling of both the stator core and end winding and significantly improves the temperature uniformity of the PMSM.

1. Introduction

Permanent Magnet Synchronous Motors (PMSMs) have become the core component of drive systems for new energy vehicles due to their high efficiency, high power density, and lightweight design [1,2]. However, as drive systems continue to evolve towards miniaturization and ultra-high power density, increasingly compact structural designs increasingly limit heat dissipation space, posing severe challenges to motor temperature-rise control [3,4]. Excessive operating temperatures can not only cause irreversible demagnetization of permanent magnets but also degrade winding insulation performance, thereby directly affecting vehicle safety and operational reliability [5,6]. Therefore, developing novel and efficient cooling systems has become a key research focus for further improving PMSM performance and overcoming thermal management bottlenecks.

Since the copper loss in the stator windings accounts for a large portion of the total losses, directly cooling the windings is more effective than other cooling methods [7,8]. Air-cooling is limited by its low convective heat transfer, resulting in high winding temperatures, whereas water-cooling channels can only be arranged near the stator core due to insulation constraints, leading to a restricted cooling area and reduced heat dissipation efficiency. Consequently, oil-cooling, which can directly remove heat from the windings and other critical regions, significantly lowers the maximum temperature (e.g., from 133 °C to 97 °C). Compared with air-cooling and water-cooling, oil-cooling, with its higher heat dissipation efficiency, is thus more suitable for meeting the thermal management requirements of high-power density PMSMs [9,10,11], and it also offers higher dielectric safety [12]. Currently, research on oil-cooling technology for PMSMs can be broadly categorized into two types:

The first category is cooling based on casing channels, primarily used for dissipating heat from the stator core. For example, Xie et al. [13] and Yang et al. [14] enhanced the uniformity of cooling oil distribution within the motor by designing circumferential stator channels and employing optimization algorithms to adjust their geometric parameters. Nevertheless, a major challenge associated with this approach is the trade-off between channel pressure loss and heat dissipation efficiency. Owing to the high viscosity of cooling oil, traditional complex channel layouts—such as dense spirals or multiple return structures—tend to induce significant flow resistance, thereby increasing pumping power consumption. Consequently, reducing channel pressure loss while maintaining high heat-transfer performance remains a critical issue in casing-based oil-cooling design.

The second category focuses on direct spray or immersion cooling of end windings, which are often the weak point in motor thermal management. Research by Yang et al. [15] and Park et al. [16] demonstrates that using oil-spray rings or arrayed nozzles for directional spraying on the end windings can effectively suppress hotspot temperatures in this region. Although such direct-contact cooling can significantly alleviate end-winding overheating, when applied alone, it is often insufficient to cool the interior of the stator core. Wang et al. [17] enhanced motor heat dissipation by directing cooling oil toward both the stator core and windings through channels formed in the shaft and rotor. Overall, direct oil-cooling techniques mainly include casing-flow cooling, end-nozzle spray cooling, and hollow-shaft oil-throwing. However, none of these methods provide comprehensive and uniform cooling for the stator, end windings, and rotor. Moreover, casing oil passages frequently experience substantial pressure loss due to the high viscosity of the cooling oil [18]. This can easily lead to uneven axial and radial temperature distribution within the motor and may induce additional mechanical losses, such as oil churning, or affect the air-gap magnetic field distribution.

In summary, existing studies primarily focus on single cooling structures, and there is a lack of integrated solutions capable of simultaneously minimizing flow resistance in casing channels while maintaining uniform motor temperature. To address this gap, this paper proposes a novel combined oil-cooling system for PMSMs. By designing an S-shaped axial returning passage, flow resistance is significantly reduced based on fluid dynamic principles, and this is integrated with an end-spraying system to achieve synergistic heat dissipation. The geometric parameters of both the S-shaped passage and the spray passage are optimized. Through establishing a fluid-solid coupled finite-element model and prototype experiments, the effectiveness and advantages of this combined scheme in reducing pressure drop, suppressing local temperature rise, and improving the overall temperature uniformity of the motor are verified.

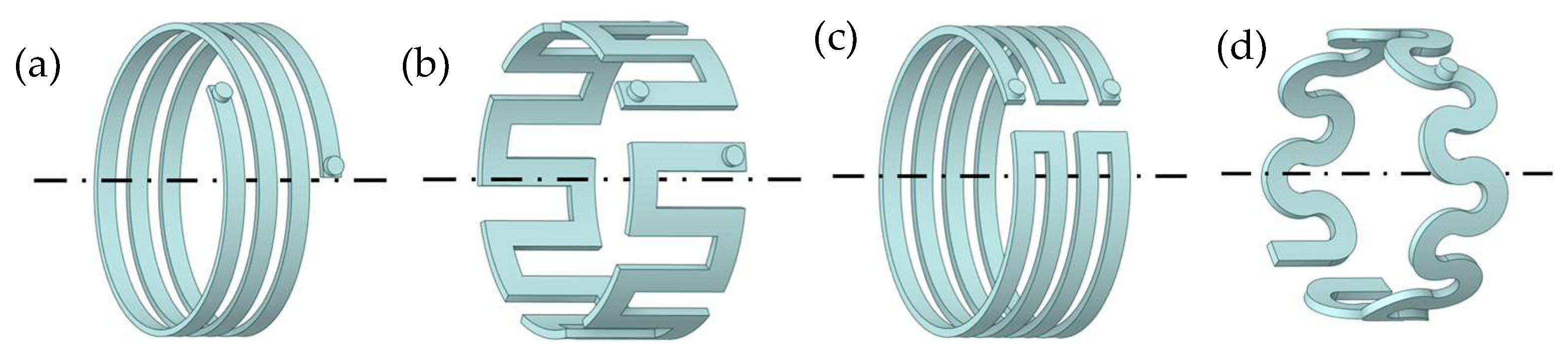
2. Design and Parameter Optimization of S-Shaped Axial Returning Passage

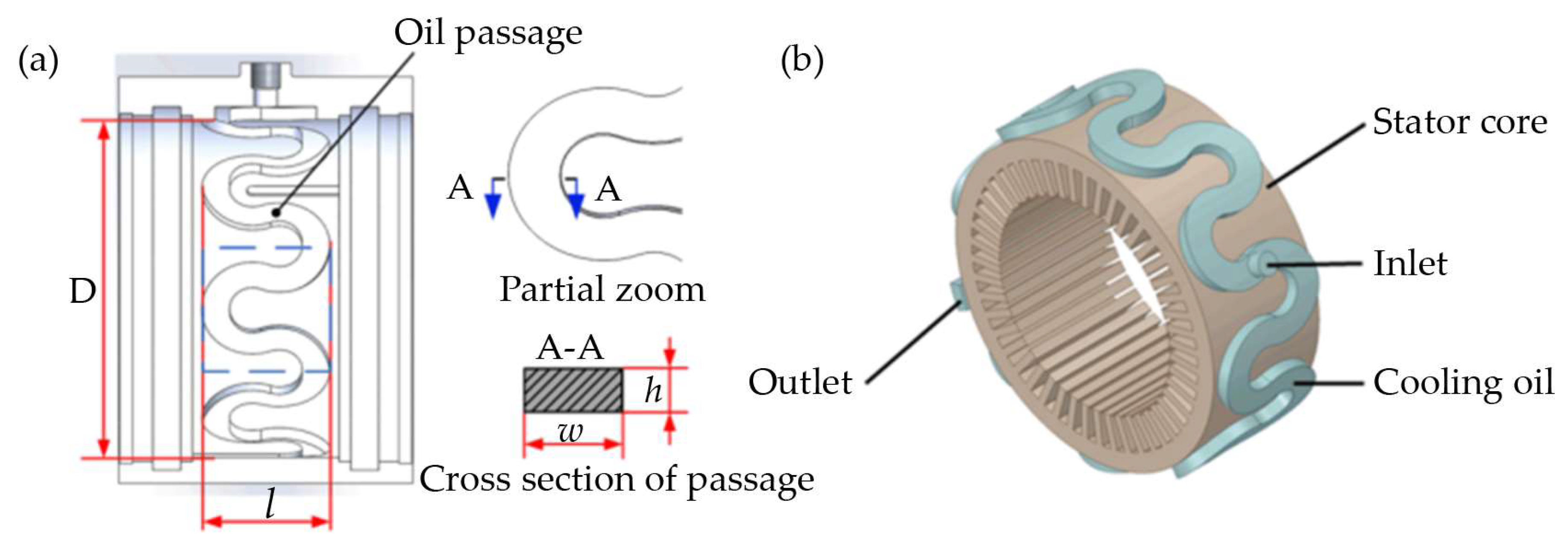
2.1. Design of the S-Shaped Axial Returning Passage

In practice, there are three main casing cooling passages for PMSM: spiral, axial returning, and circumferential returning passages, as shown in Figure 1a–c. Although the returning passage provides better cooling, it suffers from a large pressure drop; in contrast, the spiral passage incurs a smaller pressure drop but delivers lower cooling efficiency [19]. To achieve improved cooling performance with minimal pressure loss, a new S-shaped axial returning casing passage is proposed based on the advantages of both, as shown in Figure 1d.

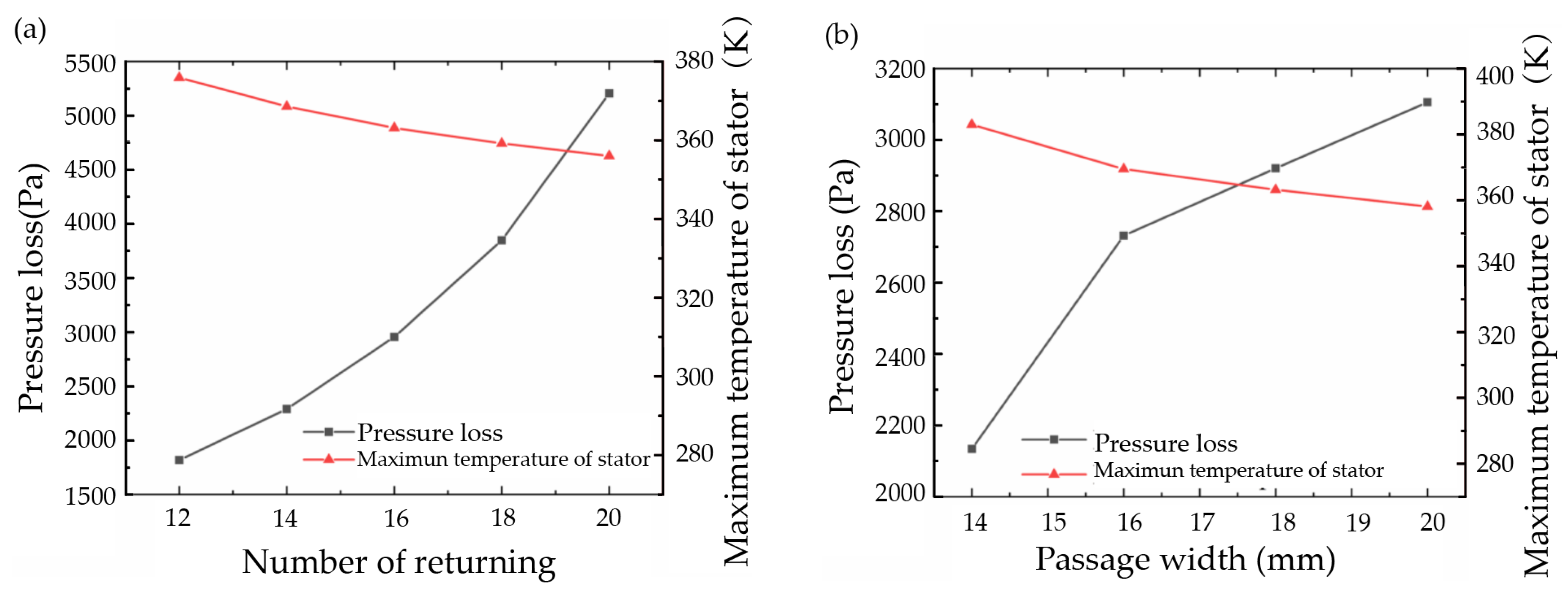
2.2. Geometric Parameter Optimization of the S-Shaped Passage

Figure 2a shows the structural diagram of the S-shaped axial returning passage. The passage section is rectangular, and the oil inlet is located in the middle of the passage to ensure that the length of the passage before and after the motor is equal. The geometric parameters of the S-shaped passage are the number of returning, length, and cross-sectional height and width. In Figure 2a, D is the inner wall diameter of the casing, w is the width, h the height, and l the axial length of the passage. To isolate the effects of the number of return passes and the cross-sectional dimensions of the S-shaped passage on pressure loss and the wall heat transfer coefficient, the model was simplified to include only the stator core and the flow passage, while other motor components were omitted. The heating power of the stator core is set as 600 W. The three-dimensional diagram of stator core and S-shaped passage is shown in Figure 2b. Based on literature analysis, it is known that higher oil flow rates generally improve convective heat transfer and reduce the temperatures of motor windings and core; however, when the flow velocity exceeds approximately 3 m/s, further increase in flow rate yields little improvement in cooling efficiency while significantly increasing pressure drop and pump power requirements [20]. Considering both the cooling performance and the size limitations of the PMSM, the axial returning passage is therefore designed with an axial length of 83 mm and a cross-sectional area of 153 mm². The radius of curvature the S-shaped passage was selected to balance convective heat transfer and pressure loss. A tighter bend increases local flow velocity and enhances heat transfer locally, but also causes higher pressure drop and may induce flow separation, reducing overall cooling uniformity. Conversely, a larger bend radius reduces hydraulic loss but slightly decreases local heat transfer. Based on the literature [21,22,23] and engineering experience, the chosen curvature ensures uniform oil distribution across the passage while keeping pressure loss moderate.

The inlet flow is set to 12 L/min (corresponding to a flow velocity of 1.31 m/s) with an inlet temperature of 40 °C. This setup provides sufficient cooling while maintaining moderate hydraulic loss [24]. The ambient temperature is 23 °C. The influence of the number of returning and cross-sectional width on heat dissipation and pressure loss is analyzed by finite-element simulation. Based on the cooling parameters, including cooling oil flow rate of 12 L/min and a pipe cross-sectional area of 153 mm² at 40 °C, the Reynolds number (Re) was calculated to evaluate the flow regime of the cooling fluid. The calculation yields Re = 1550, which is well below the critical threshold of 2300. Therefore, the flow of cooling oil in the returning passage falls in the laminar regime, rather than turbulent flow as in the water-cooling case.

Figure 3a illustrates the effect of the returning number of S-shaped passage on the pressure loss and the maximum temperature of the stator core, with a passage width of 18 mm. The maximum temperature of the stator core decreases as the returning number increases. Specifically, the maximum stator core temperature is 375.6 K when the returning number is 12 and decreases to 356 K when the returning number is 20. However, the pressure loss rises sharply with an increasing number of returning. When the returning number is 20, the pressure loss of the oil passage reaches 4382.2 Pa, which is 3.8 times that of the case with 12 returning. Therefore, considering both pressure loss and stator core temperature, the returning number of the S-shaped passage is selected as 16.

Figure 3b shows the influence of the cross-sectional width on the pressure loss and the maximum temperature of the stator core when the number of returning is 16 and at the same cross-sectional area. In Figure 3b, decreasing the oil passage width results in a weakened heat dissipation capability in the oil passage. The maximum temperature of the stator core under the cross-sectional width of 20 mm is 24.8 K lower than that with a width of 14 mm. However, under the same flow rate, the pressure loss of oil passage increases with the increase in oil passage width. The pressure loss of the oil passage with 20 mm width is 3186.4 Pa, which is 49.1% higher than that of the 14 mm passage. Considering both heat dissipation capacity and pressure loss, the oil passage width is selected as 18 mm.

2.3. Comparison Analysis of Pressure Loss and Heat Transfer Coefficient

To determine whether the S-shaped axial returning passage outperforms the conventional axial returning passage, the performance of the conventional axial returning passages with right-angle (Figure 4a) and round-corner (Figure 4b) were analyzed. The comparison results are presented in Figure 4c under the conditions of the same geometric parameters: cross-sectional height 8.5 mm, width 18 mm, the number of returning 16 and axial length 83 mm. From Figure 4c, the wall heat transfer coefficients of the three kinds of passages are close to each other. However, the pressure loss of the S-shaped passage is only 2275 Pa, compared to 4556 Pa and 3400 Pa for the right-angle and round-corner passages, respectively. Therefore, the pressure loss of the S-shaped passage is only half that of the right-angle passage and 33% lower than that of the round-corner passage, while maintaining comparable wall heat transfer.

3. Combining Oil-Cooling Scheme of S-Shaped and End-Spraying Passages

3.1. Introduction of Combining Oil-Cooling Scheme

The cooling oil flowing through the casing passage is directly in contact with the stator core, and the waste heat transmitted through the stator core can be dissipated efficiently. To further reduce the temperature of the end winding, a circular oil-spraying passage with arrayed nozzles is installed around the end winding. The oil-spraying passage is connected to the S-shaped casing passage, allowing the cooling oil to flow from the S-shaped axial returning casing passage to the circular oil-spraying passage, as shown in Figure 5a. The oil-spraying passage is composed of a rectangular groove machined on the inner wall of the casing and covered by an oil-spraying ring as cover, as shown in Figure 5b. Consequently, the heat generated at the end winding can be directly removed by the cooling oil. Therefore, the new combined cooling system is expected to cool both the stator core and the end winding more efficiently while maintaining low pressure loss.

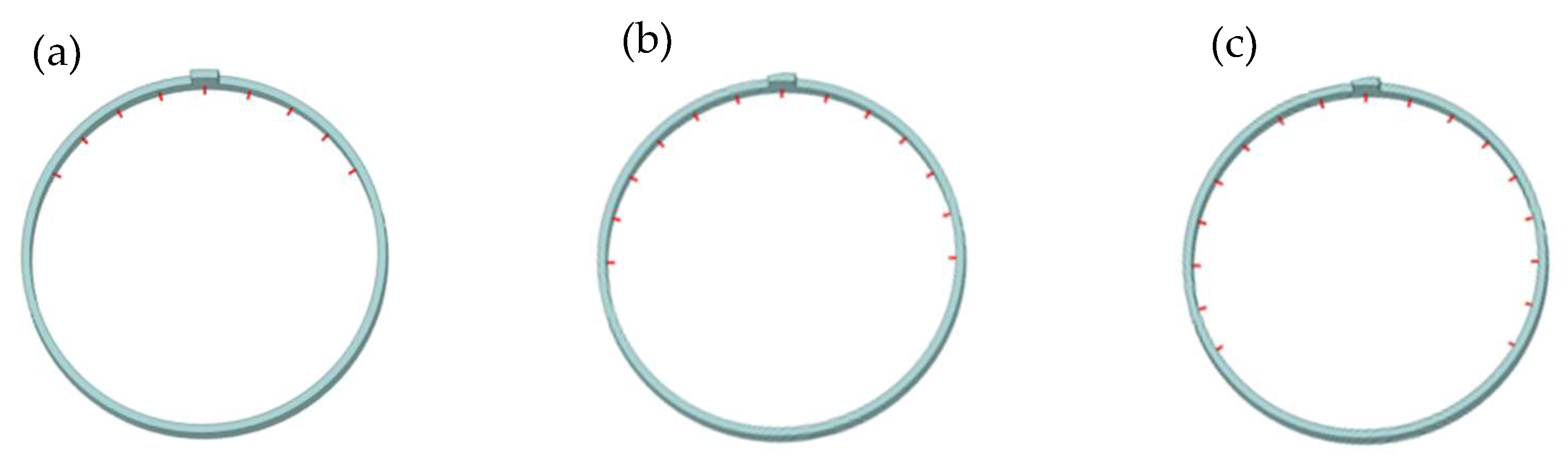
3.2. Nozzle Arrangements on the Oil-Spraying Ring

The oil-spraying passage consists of an open rectangular groove machined on the inner wall of the casing and an oil-spraying ring serving as the cover. The cooling oil is directly sprayed onto the end winding through the nozzles, effectively removing the heat from the winding. The cooling oil flows from top to bottom along the end winding under the combined action of pressure and gravity. Therefore, in order to make the motor cool uniformly and reduce the pressure loss of the oil-spraying passage, nozzles are generally not arranged at the bottom of the motor. Figure 6 shows three nozzle arrangements along the oil-spraying ring: 120°, 180°, and 240°. The height and width of the oil-spraying passage are set as 5 mm and 18 mm, respectively, due to the limitation of PMSM configuration size. The diameter of the nozzle is 1.5 mm, and the number of nozzles at 120°, 180° and 240° arrangements are 9, 13 and 17, respectively. The pressure loss and flow velocity of the three nozzle arrangements are analyzed numerically using Ansys (version 2024 R1, ANSYS Inc., Canonsburg, PA, USA). Each end winding is sheathed by a spraying ring. Thus, the inlet flow of the oil-spraying passage is set to half of the oil flow of the casing passage, which is 6 L/min, and the inlet temperature is 40 °C.

Figure 7 shows the pressure loss and velocity of spraying passage under the three nozzle arrangements. As shown in Figure 7, both the pressure loss and flow velocity decrease with increasing nozzle distribution angle. For the 240° nozzle arrangement, the pressure loss of the spraying passage is 10,938 Pa, and the maximum velocity is 3.4 m/s. Considering a relatively small velocity drop, the 240° arrangement with the lowest pressure loss is preferred in practice. Compared with the casing passage, the pressure loss in the spraying passage increases significantly. This can be attributed to the abrupt change in cross-sectional area at the nozzle, which results in a higher local pressure loss.

4. Structural Design and Temperature Distribution

4.1. Structure Design of PMSM with Combining Cooling System

Figure 8a shows the structure of a PMSM equipped with the combining oil-cooling system. To ensure practical applicability, the motor is based on a commercial POEV60 model. The S-shaped passage with rectangular cross-section is machined on the inner wall of the casing. According to the above study, the axial length and the returning number of passages are 83 mm and 16, respectively; the cross-sectional height and width are 8.5 mm and 18 mm. The motor casing with S-shaped passage and the oil-spraying ring are shown in Figure 8b,c, respectively. The S-shaped passage is formed by the interference fit between the casing and the stator, and the oil-spraying passage is formed by the interference fit between the casing and the spraying ring. Two oil-spraying rings, each with 17 nozzles arranged over a 240° circular arc, are installed on the two end windings. The sides of the oil-spraying passages are sealed with sealing rings. The cooling oil inlet is positioned at the midpoint of the casing passage. Cooling oil is pumped through the system, first directly cooling the stator within the casing passage, and then entering the oil-spraying passage to directly cool the end windings. Most of the heat is carried away by the cooling oil, and a very small part of heat is transferred to the casing. The detailed specifications of the PMSM are provided in

Table 1. Specifications of the prototype motor.

Parameter	Value	Parameter	Value
rated DC voltage (V)	380	number of stator slots	48
rated power (kW)	60	number of pole pairs	6
peak power(kW)	120	external diameter of stator (mm)	220
rated rotational speed (r/min)	3820	rotor geometry (mm)	143.2×78
peak rotational speed (r/min)	12,000	air-gap length (mm)	0.8
insulation class	H	rotor core material	Silicon steel
returning number of passages	16	magnet material (k)	NdFeB (k = 9 W/m·K)
nozzle arrangement (°)	240	passage shape	S-shape
length of stator (mm)	90	cross-sectional width of passage (mm)	18

.

4.2. Finite-Element Modeling and Simulation Setup

In this study, a fluid–solid coupled heat transfer method was adopted to calculate the motor temperature field. The temperature field is governed by the following equations:

(1).

Heat transfer function

The thermal conductivity differential equation for the temperature field of the oil-cooled motor is derived from the energy conservation equation and Fourier’s law of heat conduction, as shown in Equation (1);

$${\displaystyle \frac{\partial }{\partial x}}\left({\lambda }_x{\displaystyle \frac{\partial t}{\partial x}}\right)+{\displaystyle \frac{\partial }{\partial x}}\left({\lambda }_y{\displaystyle \frac{\partial t}{\partial x}}\right)+{\displaystyle \frac{\partial }{\partial x}}\left({\lambda }_z{\displaystyle \frac{\partial t}{\partial x}}\right)+q_v=0$$

(1)

where λ_x, λ_y, and λ_z are thermal conductivity coefficients in the x, y, and z directions and qv is the volumetric heat source at each point in the motor. The thermal differential equation and boundary conditions for the motor temperature field are expressed as follows in Equation (2);

$$\left\{\begin{array}{c}{\lambda }_x{\displaystyle \frac{{\partial }^{2}T}{\partial x^2}}+{\lambda }_y{\displaystyle \frac{{\partial }^{2}T}{\partial y^2}}+{\lambda }_z{\displaystyle \frac{{\partial }^{2}T}{\partial z^2}}=-q+c\rho {\displaystyle \frac{\partial T}{\partial \tau }}\\ -{\lambda {\displaystyle \frac{\partial T}{\partial n}}|}_{S_2}=0\\ -{\lambda {\displaystyle \frac{\partial T}{\partial n}}|}_{S_3}=\alpha \left(T-T_f\right)\end{array}\right.$$

(2)

where λ is thermal conductivity coefficients, T is the temperature, q is the volumetric heat source density, τ is time term, S₂ and S₃ represent the object boundaries, n is the normal vector on the boundary surface, T_f is the fluid temperature, and α is convective heat transfer coefficient on fluid–solid interface.

(2).

Fluid control equation

The working fluid in this study is considered incompressible. In addition to satisfying the three fundamental conservation equations, the general governing equation is employed in the calculation process [25]:

$${\displaystyle \frac{\partial \left(\rho \varphi \right)}{\partial \tau }}+{\displaystyle \frac{\partial \left(\rho v\varphi \right)}{\partial y}}+{\displaystyle \frac{\partial \left(\rho w\varphi \right)}{\partial z}}+{\displaystyle \frac{\partial \left(\rho u\varphi \right)}{\partial x}}={\displaystyle \frac{\partial }{\partial x}}\left(\Gamma {\displaystyle \frac{\partial \varphi }{\partial x}}\right)+{\displaystyle \frac{\partial }{\partial y}}\left(\Gamma {\displaystyle \frac{\partial \varphi }{\partial y}}\right)+{\displaystyle \frac{\partial }{\partial z}}\left(\Gamma {\displaystyle \frac{\partial \varphi }{\partial z}}\right)+S_c$$

(3)

where $\varphi$ is generalized variables, Γ is the diffusion function corresponding to $\varphi$, and $S_c$ is the generalized source term.

(3).

Establishment of simulation model

The thermal performances of the tested motors under different operating conditions were evaluated through CFD analysis conducted in Fluent. To simplify the model while ensuring computational efficiency and accuracy, the following assumptions were adopted:

(a).

The winding and iron core were treated as a single equivalent body with uniform heat generation and anisotropic thermal conductivity.

(b).

The cooling oil was supplied to the motor uniformly at a constant temperature and velocity.

(c).

Thermal radiation was neglected during the temperature-rise simulation.

(d).

Structural features such as ribs, filets, and grooves that have negligible influence on motor temperature rise were removed.

(e).

The heat transfer coefficient and thermal conductivity of all components were assumed to be constant.

The simplified motor model was discretized into numerous small elements using the finite-element method. An unstructured mesh was generated for the cooling-oil fluid domain. To improve calculation accuracy, numerical stability, and mesh convergence, all fluid–solid interface grids were enforced to share nodes. After meshing, the model contained 3,086,626 nodes and 12,023,685 elements, with an average skewness of 0.218.

(4).

Simulation Parameter Setting

When using Fluent for motor thermal simulation, it is necessary to apply heat generation to the heating components. The volumetric heat generation of each component is calculated according to Equation (4):

$$q={\displaystyle \frac{P_{loss}}{V}}$$

(4)

where P_loss denotes the heat loss power of each component and V represents the volume of the corresponding heating component.

Table 2. Heat loss and volumetric heating power of each motor component.

Rotational Speed		3000 r/min	3820 r/min	5000 r/min	3000 r/min	3820 r/min	5000 r/min
Heat Loss Rate		Loss (W)			Heat Volume Power (W/m3)
Name of part	end winds	3836.2	2157.8	1498.5	2,757,116	1,550,832	1,070,159
	stator	413.2	449	582.7	252,594	274,479	356,212
	rotor	50.8	46.2	56.7	4755	4324	5307

shows the loss of heat and volumetric heating power of the motor components, which were obtained from the electromagnetic analysis software ANSYS Maxwell (version 2023 R1, ANSYS Inc., Canonsburg, PA, USA).

Table 3. Thermal and physical properties of materials.

Material	Thermal Conductivity (W/(m·K))	Density (kg/m3)	Specific Heat Capacity (J/(kg·K))
aluminum	151	2700	963
silicon steel	axial: 4.43	7650	460
	radial: 39
copper	axial: 387	8520	385
	radial: 39
insulating paper	0.18	-	-
oil	0.22	870	1985
permanent magnet	9	7800	420

lists the thermal-physical properties of the selected materials.

The boundary conditions for the temperature-field analysis are defined as follows:

(a)

In the CFD model, the cooling oil was used as the working fluid, and a velocity inlet was specified according to the prescribed flow rates of 8 L/min, 12 L/min, and 16 L/min, with the inlet temperature maintained at 65 °C. The outlet was defined as a pressure boundary at standard atmospheric pressure. All fluid–solid interfaces, including the housing–oil and stator–oil contact surfaces, were modeled as conjugate heat transfer interfaces to allow heat exchange across domains, while the remaining walls were treated as adiabatic. A 0.3 mm insulation layer was assigned to the winding–stator interface to account for the thermal resistance of the actual structure.

(b)

Although the flow path includes S-shaped bends and narrow passages, the Reynolds number calculated based on the oil properties and hydraulic diameter indicates laminar flow; therefore, a laminar flow model was employed. The machined channel surfaces were assumed to be hydraulically smooth, consistent with conventional industrial practice.

(c)

A high-quality unstructured mesh was generated for the oil domain, and geometric features with negligible thermal influence were removed to improve mesh quality. Node sharing was enforced across all fluid–solid interfaces to ensure accurate heat transfer. The final mesh contained approximately 3.09 million nodes and 12.02 million elements, with an average skewness of 0.218. Mesh sensitivity was examined by progressively refining the mesh, and the results were considered mesh-independent when the variations in pressure drop and winding temperature were below 2%.

4.3. Temperature Distribution

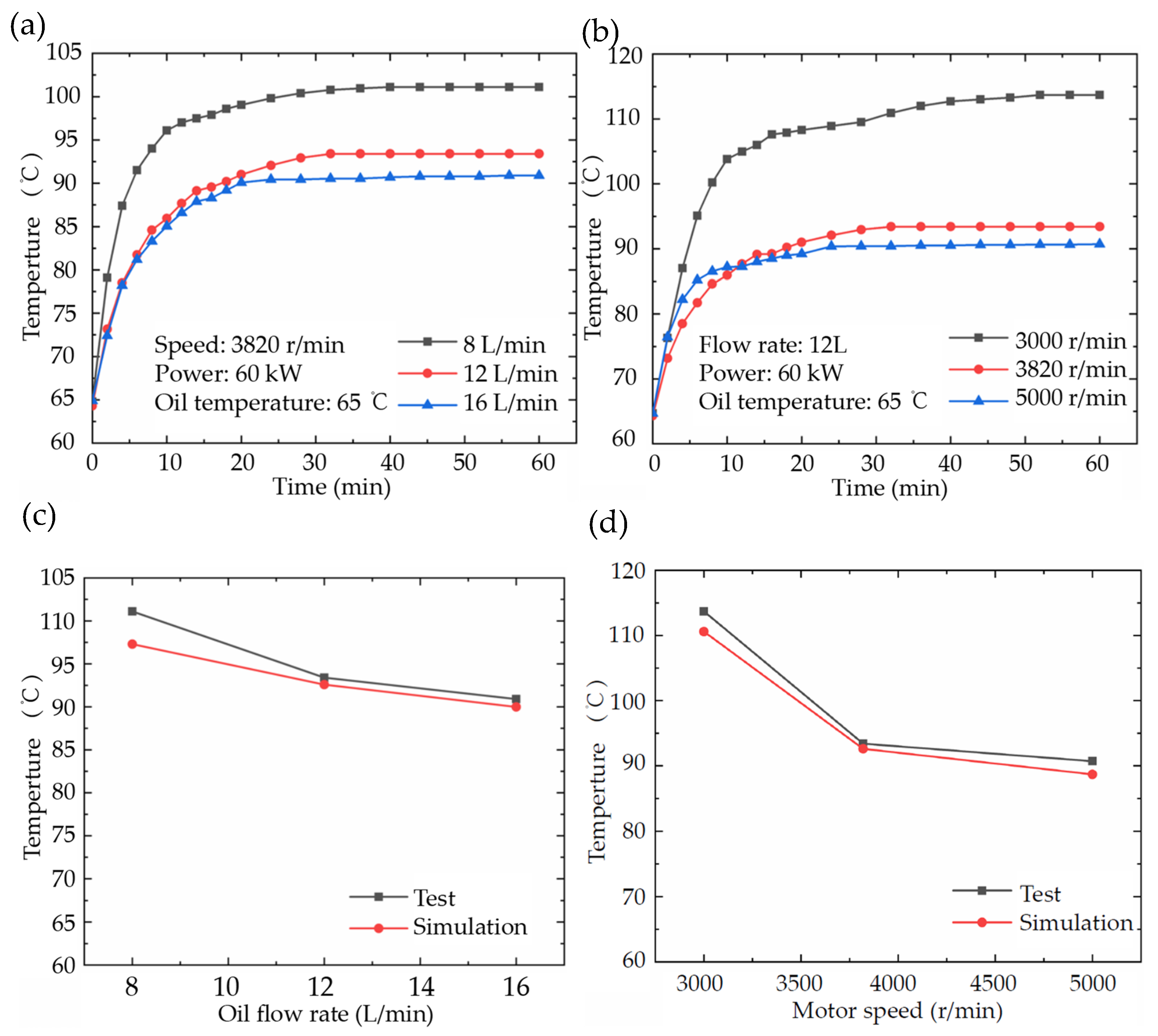
4.3.1. Effect of Flow Rate of Cooling Oil

Figure 9 shows the temperature distribution of axial cross-section and end winding under different cooling oil flow rates. As shown in Figure 9, the maximum temperature, located at the bottom of the end winding near the stator core, decreases with increase cooling oil flow. The higher temperature at the winding bottom under low flow is due to natural convection of the cooling oil under gravity. When the flow rate is 8 L/min, the motor temperature reaches the highest value of 97.3 °C. When the flow rate is 16 L/min, the maximum temperature of the motor is only 90.8 °C, which is 6.5 °C lower than that at 8 L/min, but only 1.6 °C lower than that at 12 L/min. This indicates that increasing the cooling oil flow enhances the motor’s heat dissipation; however, the improvement gradually diminishes at higher flow rates. Therefore, a cooling oil flow rate of 12 L/min is considered optimal. Furthermore, Figure 9b,e shows that at 12 L/min, the maximum temperature of the end winding is 92.6 °C, which is only 1.5 °C higher than the maximum temperature of the stator core. This indicates that the combined oil-cooling scheme significantly improves the heat dissipation of both the stator core and winding, thereby enhancing the uniformity of the temperature of the motor. In addition, with increasing cooling oil flow rate, the temperature distribution becomes more uniform, and the motor’s high temperature region diminishes.

4.3.2. Effect of Motor Rotational Speed

Figure 10 presents the temperature distribution of axial cross-section and end winding under the rated power of 60 kW, a cooling oil flow of 12 L/min, and different rotational speeds. As shown in Figure 10, the temperatures of both the windings and the stator core decrease with increasing rotational speed. The maximum end-winding temperature reaches 111.2 °C at a rotational speed of 3000 r/min, while the maximum temperatures are 92.4 °C and 87.5 °C at 3820 r/min and 5000 r/min, respectively. Furthermore, the high-temperature region shifts from the end winding toward the stator core and rotor, as illustrated in Figure 10a–c.

On one hand, the phase current decreases with the increase in rotational speed, resulting in a reduction in the corresponding coils. This behavior is attributed to the motor control strategy: Maximum Torque Per Ampere (MTPA) control is applied below the rated speed, and voltage-feedback flux-weakening control is employed above the rated speed. Since the motor operates at a constant rated power of 60 kW, the output torque decreases significantly as rotational speed increases (T = P/ω). Although the negative d-axis current increases to suppress back-EMF during flux-weakening, the q-axis current, which is proportional to the torque, decreases more substantially. Consequently, the vector sum of the total phase current decreases, leading to a reduction in copper losses. On the other hand, as rotational speed increases, iron losses in the motor increase while copper losses decrease, causing the high-temperature region to shift from the end winding to the stator core and rotor.

5. Experimental Analysis

5.1. Experimental Design

To verify the validity and reliability of the motor temperature-field simulation results, temperature rise experiments were conducted under the motor’s rated operating conditions. Two sets of experiments were designed, in which the coolant flow rate and the motor speed were treated as independent variables, respectively, to investigate the motor’s temperature-rise characteristics under different flow rates and rotational speeds. The test platform for motor temperature-rise measurement is shown in Figure 11. The experimental system primarily comprises the oil-cooling motor prototype, motor controller, power cabinet, oil-cooling system, water-cooling system, experimental bench, and test system console. It should be noted that the oil circulation system is used to cool the motor prototype, while the water circulation system is solely employed to cool the motor controller to ensure its normal operation.

During each test, the motor prototype was placed on a motor dynamometer (Chongqing KaRui Testing Equipment Co., Ltd., Chongqing, China). The controller converts DC voltages to AC power, and the torque and speed are adjusted via the console. Since the bottom of the end winding exhibits the highest temperature, this location was monitored using PT1000 platinum resistance thermometers (Shenzhen Yongyang New Energy Technology Co., Ltd., Shenzhen, China) with a measurement accuracy of ±0.15 °C at 100 °C. The test was terminated when the temperature fluctuation of the thermometer remained below 1 °C during a period of 15 min, or the temperature reached 160 °C to prevent damage to the insulation materials. The working conditions of the tested PMSM are summarized in

Table 4. Experimental parameters.

Rotational Speed (r/min)	Power/kW	Oil Temperature/°C	Oil Flow Rate/L/min	Annotation
3820	60	65	8	Comparison of oil flow
3820	60	65	12
3820	60	65	16
3000	60	65	12	Comparison of Rotational speed
3820	60	65	12
5000	60	65	12

.

5.2. Experimental Results

Figure 12 presents the experimental results showing the influence of cooling oil flow rate and rotational speed on the temperature rise in end winding. The end-winding temperatures reach steady state after 30 min of motor operation. The steady-state temperatures decrease with increasing cooling oil flow rate and rotational speed. Specifically, the steady temperature of end winding is 101.1 °C at a cooling oil flow rate is 8 L/min, while the steady temperatures are 93.4 °C and 90.9 °C at flow rates of 12 L/min and 16 L/min, respectively, as shown in Figure 12a. Comparing Figure 9 with Figure 12a, the simulation results of the maximum end-winding temperature closely match the experimental results, as shown in Figure 12c. Furthermore, comparing Figure 10 with Figure 12b, the simulation results of the maximum end-winding temperature under different rotational speeds also agree well with the experimental results, as shown in Figure 12d. From Figure 12c,d, the maximum deviation between the simulated and experimental results is only 3.8 °C, confirming the validity of the motor temperature-field model. The experimental and simulation results are also compared in

Table 5. Simulation and Experimental Results.

Cooling Oil Flow (L/min)	Sim Temp (°C)	Exp Temp (°C)	Deviation (%)
8	97.3	101.1	3.76
12	92.6	93.4	0.86
16	90.8	90.9	0.11

.

6. Conclusions

Focusing on the challenges of heat dissipation and temperature-rise control in high–power-density PMSMs for new energy vehicles, a combined oil-cooling scheme integrating an S-shaped axial returning passage with end-spraying cooling is proposed. Numerical simulations, together with experimental validation, lead to the following conclusions:

a.

The pressure loss of the S-shaped axial returning passage is only half of that of the right-angle axial returning passage and 33% lower than that of the round-corner axial returning passage, while the wall heat-transfer coefficients of all the three passage types are comparable.

b.

The optimal configuration of the S-shaped passage includes 16 returns with a width of 18 mm. For the end-spraying passage, a 240° nozzle arrangement is preferred due to its minimal pressure loss.

c.

The proposed combined oil-cooling scheme efficiently cools both the stator core and end winding and significantly improves the uniformity of motor temperature. At a cooling oil flow rate of 12 L/min, the maximum temperature of the end winding is 92.6 °C, only 1.5 °C higher than the maximum temperature of the stator core under rated operating conditions. The simulated end-winding temperature shows close agreement with the experimental measurements, with a maximum deviation of only 3.8 °C.

d.

Although experimentally validated on a 60 kW prototype, the findings possess wider applicability. The underlying mechanism of the S-shaped passage is rooted in fundamental fluid dynamics, rendering it effective for various casing-cooled motors irrespective of their specific dimensions. Additionally, the hybrid cooling strategy tackles the universal thermal bottleneck of end windings of end windings in high-power-density motors. Therefore, the proposed cooling structure and optimization methodology provide a scalable reference for thermal management of other PMSMs under diverse operating conditions.

In conclusion, the proposed combined oil-cooling scheme, integrating S-shaped and end-spraying passages, effectively reduces the temperature of both stator windings and core in high-power-density PMSMs. In practical EV traction systems, this scheme is suitable for motors with compact packaging and high thermal loads, where direct winding cooling is essential. However, several limitations should be considered: complex flow distribution may require careful pump and manifold design, system packaging constraints may limit implementation in certain motor layouts, and additional cost and complexity associated with the cooling system must be weighed against performance gains. Future research will focus on further optimizing the cooling passage geometry and evaluating transient and high-load operating conditions to enhance cooling efficiency and adaptability, providing guidance for practical implementation in next-generation EV motors.