Displacement Experiment Characterization and Microscale Analysis of Anisotropic Relative Permeability Curves in Sandstone Reservoirs

Abstract

As a critical parameter for describing oil–water two-phase flow behavior, relative permeability curves are widely applied in field development, dynamic forecasting, and reservoir numerical simulation. This study addresses the issue of relative permeability anisotropy, focusing on the seepage characteristics of two typical bedding structures in sandstone reservoirs—tabular cross-bedding and parallel bedding—through multi-directional displacement experiments. A novel anisotropic relative permeability testing apparatus was employed to conduct displacement experiments on cubic core samples, comparing the performance of the explicit Johnson–Bossler–Naumann (JBN) method, based on Buckley–Leverett theory, with the implicit Automatic History Matching (AHM) method, which demonstrated superior accuracy. The results indicate that displacement direction significantly influences seepage efficiency. For cross-bedded cores, displacement perpendicular to bedding (Z-direction) achieved the highest displacement efficiency (75.09%) and the lowest residual oil saturation (22%), primarily due to uniform fluid distribution and efficient pore utilization. In contrast, horizontal displacement exhibited lower efficiency and higher residual oil saturation due to preferential flow path effects. In parallel-bedded cores, vertical displacement improved efficiency by 18.06%, approaching ideal piston-like displacement. Microscale analysis using Nuclear Magnetic Resonance (NMR) and Computed Tomography (CT) scanning further revealed that vertical displacement effectively reduces capillary resistance and promotes uniform fluid distribution, thereby minimizing residual oil formation. This study underscores the strong interplay between displacement direction and bedding structure, validating AHM’s advantages in characterizing anisotropic reservoirs. By integrating experimental innovation with advanced computational techniques, this work provides critical theoretical insights and practical guidance for optimizing reservoir development strategies and enhancing the accuracy of numerical simulations in complex sandstone reservoirs.

1. Introduction

Energy is a key resource for modern societal development, with demand increasing rapidly during processes of industrialization and urbanization, particularly in developing countries [1]. As the world’s largest energy consumer and a major importer of fossil fuels, China relies heavily on oil and gas in its energy structure. In 2024, approximately 74% of China’s oil and 42% of its natural gas were imported, underscoring the country’s strong dependence on external hydrocarbon resources [2]. As shown in Figure 1, while China’s crude oil production has remained relatively stable in recent years, consumption has continued to rise, highlighting the critical role of oil development and utilization in supporting national growth. Sandstone oil and gas reservoirs play a pivotal role in global hydrocarbon exploitation, accounting for about 50–60% of global petroleum reservoirs. As the dominant type of conventional reservoirs, they make a significant contribution to worldwide oil and gas production [3]. The large variations in porosity and permeability, together with their widespread distribution, make sandstone reservoirs a primary target for petroleum exploration and development [4,5]. Reservoir sandstones exhibit anisotropy in both structure and properties. It is generally recognized that permeability anisotropy in reservoir sandstones is primarily caused by grain- or lamina-scale heterogeneities with preferential orientations, which is particularly pronounced in siliciclastic sandstones [6,7,8]. In China, sandstone reservoirs are mainly distributed in the Ordos, Songliao, Junggar, and Bohai Bay basins, while in the Sichuan Basin, sandstone reservoirs are predominantly gas-bearing. These reservoirs provide a crucial resource base for China’s petroleum production. Particularly under the backdrop of rising domestic oil demand, the exploitation of sandstone reservoirs holds strategic importance for reducing dependence on imports [9]. In the Ordos Basin, the development of Yanchang Formation sandstone reservoirs has advanced rapidly through the use of horizontal wells and hydraulic fracturing, with Chang 7 and Chang 9 being the major productive intervals [10]. The Songliao Basin’s Daqing Oilfield, though historically significant, has entered a high water-cut stage, with remaining oil largely distributed in poorly permeable sandstone bodies [11]. Both the Junggar and Bohai Bay basins exhibit promising development potential, with abundant sandstone resources, while in the Sichuan Basin, sandstone reservoirs are mainly gas-bearing [12]. However, significant production challenges remain. For example, the Ordos sandstone reservoirs face severe sand production problems, resulting in low recovery efficiency [13]. Reservoirs in the Songliao and Junggar basins are characterized by low permeability and strong heterogeneity, whereas those in the Bohai Bay and Sichuan basins are deeply buried, where overpressure risks are prevalent. Overpressure may alter pore structures and permeability, thereby impacting fluid flow properties [14]. Additionally, complex bedding structures, multiscale pore-throat systems, and microfractures result in tortuous fluid pathways, negatively affecting waterflood sweep efficiency [15]. To address these challenges, various enhanced recovery techniques such as cold production and hydraulic fracturing have been widely applied. However, these technologies are costly and their effectiveness is highly dependent on geological conditions [16]. Although advances in technology have partially mitigated issues such as sand production, low permeability, and overpressure risks, the inherent complexity of multiphase flow—particularly the directional interference and nonlinear behavior—remains unresolved. This highlights the necessity of investigating anisotropic relative permeability, which provides a quantitative description of multiphase flow capacity, interference, and pathways along different directions, thereby enabling more accurate reservoir modeling and prediction [17]. Heterogeneous conglomeratic sandstone exhibits anisotropic physical properties, rendering a comprehensive analysis of its physical processes challenging with experimental measurements [18].

Anisotropy in reservoirs is primarily manifested as the directional heterogeneity of petrophysical properties, such as permeability and porosity. Relative permeability, which reflects the flow capacity of oil and water phases in porous media, is commonly characterized by relative permeability curves. Reservoir anisotropy originates from both microscopic structures and macroscopic geological features, leading to different degrees of interference between multiphase fluids along different directions [19]. The anisotropy of relative permeability directly affects the dynamic behavior of multiphase fluids in reservoirs and plays a crucial role in optimizing development strategies. As a fundamental dataset, relative permeability curves are widely used to predict residual oil distribution and are essential for field development planning, dynamic performance analysis, and reservoir simulation [20,21]. Due to the complexity of anisotropy characterization under different conditions, anisotropy is often neglected in numerical simulations. One of the main challenges lies in the fact that relative permeability anisotropy is influenced by multiple factors, including fluid saturation and rock properties [22]. Research on the anisotropy of relative permeability has mainly focused on theoretical models, experimental methods, and practical applications. Early studies emphasized theoretical frameworks. For example, Pergament et al. (2012) applied numerical inversion to reconstruct the relative permeability tensor, revealing its misalignment with the absolute permeability tensor [23]. Experimental approaches include core testing and CT scanning. Clavaud et al. (2008) investigated permeability anisotropy using microscopic structural analysis [24]. In terms of practical applications, Li et al. (2021) [25] proposed a new measurement method for anisotropic relative permeability and applied it to numerical simulation, improving the understanding and description accuracy of multiphase flow in anisotropic reservoirs. Extensive research has been conducted on anisotropy in absolute permeability [25]. For instance, Ding et al. (2002) applied a three-dimensional, three-phase black-oil model to investigate well pattern performance and found that rectangular well patterns demonstrated advantages in waterflood development of low-permeability reservoirs with permeability anisotropy [26]. Li et al. (2018) established a pore-network model based on sandstone reservoir cores and showed that the distribution and morphology of residual oil are related to absolute permeability, capillary number, and microscopic heterogeneity [27]. However, research on the anisotropy of relative permeability remains limited, making it difficult to accurately reflect the degree of phase interference in different directions. Experimental evidence has confirmed the existence of relative permeability anisotropy in sandstone reservoirs. Liu et al. (2005) conducted experiments where fluids were allowed to flow radially in cylindrical cores, with flow distribution and pressure drop at the core surface used to determine anisotropy and the principal direction of maximum permeability [28]. However, simultaneous flow in multiple directions interfered with test accuracy. Ji et al. (2007) [29] proposed a capillary viscometer method suitable for measuring absolute permeability in tight cores within the range of 1 × 10⁻³ μm². This method stabilizes fluid flow, allows full penetration, and provides steady pressure values within a short time, thereby improving measurement accuracy. Nevertheless, it is mainly applicable to low-permeability cores, with limitations in high-permeability or strongly heterogeneous reservoirs, and does not account for multi-directional anisotropy [29]. Pei et al. (2024) considered the significant impact of core length-to-diameter ratio on end effects and employed staggered coring techniques to balance core properties and geometry, conducting relative permeability measurements in different directions on natural cores [30]. However, since the displacements were performed on different samples, inevitable errors arose, highlighting the importance of sample consistency in ensuring measurement accuracy. Current studies still face limitations, including interference in multi-directional testing, restricted applicability, and insufficient sample consistency, which prevent accurate characterization of phase interference in different directions. In this study, a novel anisotropic relative permeability testing apparatus is employed, integrating displacement experiments with nuclear magnetic resonance (NMR) and CT scanning to perform microscopic analyses of core interiors. This approach enables verification of multiphase flow characteristics and provides clear insights into the degree of interference between phases.

After experiments are completed, the acquired data must be processed to calculate relative permeability. The calculation methods can be broadly divided into explicit and implicit categories. Explicit methods include the steady-state technique and the unsteady-state Johnson–Bossler–Naumann (JBN) method, which is derived from the Buckley–Leverett theory of one-dimensional two-phase waterflood front propagation [31]. Implicit methods are represented by Automatic History Matching (AHM) [32,33]. During waterflooding, variations in oil–water saturation with time and distance constitute a transient process. The traditional JBN method has been widely applied because of its operational simplicity [34]. However, this method relies on idealized assumptions such as incompressible fluids and the neglect of capillary and gravitational forces. These assumptions are often invalid in real reservoirs—particularly in low-permeability and strongly heterogeneous formations. Furthermore, the calculation procedure of the JBN method is relatively complex and involves several approximations, which introduces significant uncertainties in interpreting relative permeability. Lishman, J.R. et al. (1970) verified the effectiveness of the JBN method in high-permeability reservoirs through core analysis but also pointed out its limitations in low-permeability systems [35]. Permeability anisotropy measured from core samples is controlled not only by the intrinsic rock fabric but also significantly influenced by sample geometry. Slender core plugs may introduce apparent or “pseudo” anisotropy, thereby leading to an overestimation of the degree to which vertical fluid flow is restricted in the reservoir [36]. In addition, numerical differentiation in the method is commonly replaced by finite difference schemes, which may lead to large errors. Considering the success of Johnson’s equations, Jones et al. (1978) proposed a graphical approach as a simplified alternative, though errors may arise in the tangent construction on the curves [32]. Huan et al. (1982) further improved the JBN equations by applying cubic smoothing curve fitting through the least-squares method to discrete experimental data, thereby reducing differentiation errors and improving the accuracy of relative permeability curves [37]. However, many modifications of JBN neglected capillary pressure, which may introduce errors in both wetting and non-wetting phase relative permeabilities, especially due to capillary discontinuity at the core outlet. To address this issue, Abdulmajeed et al. (2022) [38] proposed an improved JBN method that incorporates capillary pressure boundary conditions to correct for end effects, significantly reducing computational deviations in low-permeability reservoirs. Nevertheless, these improvements still face challenges, including the non-uniqueness of solutions, high sensitivity to experimental data, and insufficient consideration of reservoir anisotropy. As a result, they cannot accurately represent the directional interference between multiphase fluids in anisotropic formations [38].

In comparison, the Assisted History Matching (AHM) method optimizes model parameters iteratively to minimize the error between simulated results and actual observed data, demonstrating superior accuracy [39,40]. Although computer-implemented AHM methods first emerged in the 1950s, history matching methods with true “automatic” functionality were not applied until the mid-1960s [41]. Sigmund introduced least-squares optimization algorithms to AHM, successfully automating the fitting process while accounting for capillary pressure effects, thereby significantly enhancing fitting accuracy [42]. In the 1980s, advancements in computational technology enabled Watson et al. to introduce gradient-based optimization techniques, specifically the Gauss-Newton (GN) method, which linearized nonlinear least-squares problems to iteratively optimize reservoir model parameters, further improving fitting accuracy [43]. However, prior to the 1990s, AHM methods faced challenges such as high computational costs and a tendency to converge to local optima, leading to non-unique solutions. In the 1990s, researchers began exploring stochastic optimization methods, such as genetic algorithms and simulated annealing, which were capable of handling nonlinear reservoir models [44]. Nevertheless, these new methods still encountered increased computational demands and difficulties in quantifying parameter uncertainty. Evensen first proposed the Ensemble Kalman Filter (EnKF), which utilized an ensemble of reservoir models to achieve real-time data assimilation and uncertainty quantification, finding widespread application in reservoir production history matching [45,46,47]. Despite its superior performance, EnKF struggles with non-Gaussian distributions and high-dimensional parameter spaces and requires significant computational resources [48]. To address this, Gao et al. applied logarithmic or normalized score transformations to relative permeability parameters to meet EnKF’s Gaussian assumptions, thereby improving its applicability [49]. Li and Reynolds combined the Gauss-Newton method with transformed parameter spaces, iteratively optimizing transformed parameters to further enhance the accuracy of EnKF estimates [50]. Although AHM has evolved progressively, subsequent studies have mitigated some challenges through parameter transformations, gradient enhancement, and proxy models, reducing computational burdens and improving convergence [51,52]. However, significant research gaps remain, particularly in complex heterogeneous reservoirs, where AHM struggles to achieve efficient enhancement, real-time data assimilation, and uncertainty quantification [53], limiting its application in residual oil recovery and numerical simulation. In the computation of relative permeability curves, the conventional JBN method can only cover the saturation range of the two-phase co-flow region and fails to account for end effects and gravity at low flow rates, making it suitable only for one-dimensional unidirectional flow.

In this study, the AHM method was applied to the development of the QHD oilfield, yielding more accurate results compared to the JBN method, improving development strategies, and providing new insights for similar reservoir types. The QHD oilfield is currently in a high water-cut stage, characterized by a low reservoir dip angle and loose, sand-prone structures. To address this, core displacement experiments were conducted using natural sandstone outcrops with typical parallel and tabular cross-bedding to study the anisotropy of relative permeability. A novel anisotropic relative permeability testing apparatus was employed for displacement experiments, complemented by nuclear magnetic resonance (NMR) and computed tomography (CT) scanning of the experimental cores. In terms of computation, both the conventional JBN method and the AHM method were used to calculate relative permeability curves. Compared to the JBN method, the AHM method accounted for capillary pressure and reservoir heterogeneity, enabling the study of macroscopic petrophysical parameters and time-varying microscopic reservoir characteristics to elucidate the fluid flow behavior during waterflooding. This study reveals the differences between relative permeability anisotropy under different displacement directions and the intrinsic absolute permeability of the rock, and elucidates the formation mechanisms of relative permeability anisotropy. By characterizing the seepage capacity of multiphase fluids, it provides a basis for fluid distribution prediction and residual oil recovery, and offers important theoretical foundations and experimental support for optimizing waterflooding development strategies and improving the reliability of numerical simulations in complex sandstone reservoirs.

2. Experimental Investigation of the Mechanisms Underlying Anisotropic Relative Permeability Curves

2.1. Experimental Design

Displacement experiments are the primary method for obtaining relative permeability curves of immiscible fluids. In this study, sedimentary microfacies such as point bars, crevasse splays, and floodplains were selected as research objects, with particular emphasis on analyzing the effects of sedimentary structures characterized by tabular cross-bedding and parallel bedding on reservoir fluid flow behavior. By conducting anisotropic displacement experiments on core samples, the influence of rock anisotropy on fluid flow under different displacement directions was investigated, and the relative permeabilities of oil and water phases were subsequently determined. Furthermore, following oil and water flooding, nuclear magnetic resonance (NMR) and computed tomography (CT) scanning techniques were employed to evaluate pore-throat utilization and identify the optimal displacement direction, thereby improving displacement efficiency and providing guidance for field development.

2.1.1. Equipment and Experimental Samples

Laboratory measurements of relative permeability are typically conducted through steady-state and unsteady-state experiments on cylindrical rock samples (Abdulmajeed et al., 2022 [38]). Traditional core holders, which serve as the primary apparatus for relative permeability curve testing, come in various types. During laboratory experiments, core samples must be placed within the holder for testing. However, conventional anisotropic core holders are designed for one-dimensional testing; pressure is applied from a cylindrical interface into a cylindrical chamber, with injection at one end and production at the other, allowing only a single core sample in one orientation to be tested at a time. To measure samples in other directions, cores must be drilled in the corresponding orientations. This not only complicates the testing procedure but also compromises accuracy, as the samples are not identical.

Accurate characterization of pore structure anisotropy and relative permeability anisotropy can only be achieved by testing the same sample in multiple directions. In this study, a novel anisotropic relative permeability testing apparatus was employed (Figure 2 and Figure 3). This apparatus allows relative permeability curves to be measured along multiple directions using a single core sample, improving testing efficiency while ensuring accuracy (Li et al., 2021 [25]). The device accommodates cores measuring 5 × 5 × 5 cm, with a maximum displacement pressure of 32 MPa and a maximum confining pressure of 40 MPa. It supports multiphase fluid testing and can investigate two-phase displacement patterns under various injection-production schemes, including single-injection–multiple-production and multiple-injection–multiple-production, enabling the calculation of relative permeability. One core sample with parallel bedding (A-1) and one core sample with tabular cross-bedding (A-2) were selected to conduct anisotropic relative permeability displacement experiments. Some of the parameters are listed in

Table 1. Basic parameters of the core samples.

Core ID	Brine Salinity (ppm)	Crude Oil Viscosity (mPa·s)	Porosity (%)	Apparent Volume
A-1	4400	77	20.8	127.45
A-2	4400	77	20.8	129.73

.

Given that the anisotropic seepage experimental apparatus requires cubic core samples with dimensions of 5 cm × 5 cm × 5 cm, the cores available in the core repository could not satisfy the experimental requirements. In addition, the effects of different sedimentary facies and bedding architectures on oil–water flow behavior under reservoir conditions cannot be neglected. Therefore, as shown in Figure 4, natural sandstone cores exhibiting typical fluvial facies characteristics, including tabular cross-bedding and parallel bedding, were selected for this study. The samples have an average permeability of 732 mD and a porosity of 20.8%. After being cut and processed into cubic cores, displacement experiments were conducted in different flow directions to investigate anisotropic oil–water relative permeability.

The core samples are light gray to white in color and are composed predominantly of quartz with minor feldspar, indicating quartz sandstone. The displacement experiments were conducted at a designed flow rate of 0.2 mL/min. Sampling intervals were set according to the displacement duration at 2, 5, 10, and 30 min, and the total duration of each displacement experiment was 720 min.

The target layer is predominantly composed of point bar facies, and typical samples with tabular bedding and parallel bedding were selected to conduct anisotropic relative permeability experiments, as shown in Figure 5.

NMR and CT scanning devices, as shown in Figure 6 and Figure 7, based on different physical principles, accurately reveal the microstructure and fluid occurrence state within the core, providing critical data support for oil and gas resource evaluation and reservoir development planning.

The equipment was developed and manufactured by Suzhou Niumag Analytical Instrument Corporation (Niumag Corporation), Suzhou, China.

Figure 7. Nano Voxel 5000 CT Scanner.

Figure 7. Nano Voxel 5000 CT Scanner.

The equipment was designed, manufactured, and supplied by Tianjin Sanying Precision Instruments Co., Ltd., Tianjin, China.

2.1.2. Experimental Procedures

(1)

Core Displacement Experiments:

(1).

Core Preparation and Dry-State Characterization: Outcrop rock samples were cut into 5 × 5 × 5 cm cubic cores using wire cutting. The cores were cleaned to remove oil, water, salts, and soil impurities, then oven-dried and weighed. Bulk porosity was measured, and absolute permeability in the x, y, and z directions was determined in the dry state.

(2).

Water Saturation and Liquid-Phase Permeability Testing: The cleaned cores were placed in rubber sleeves and fully saturated with formation water. Liquid-phase permeability in the x, y, and z directions was measured, and differences among directions were recorded to preliminarily assess anisotropy.

(3).

Oil Displacement to Irreducible Water Saturation: Simulated crude oil was injected into the cores to displace water until irreducible water saturation (Swi) was reached. Outlet flow rates and time were recorded. The termination criterion was an outlet water cut below 0.1% and an injected pore volume (PV) greater than 30 PV. Under Swi conditions, effective oil-phase permeability was measured in x, y, and z directions. NMR and CT scans were performed to analyze pore structure and fluid distribution at Swi.

(4).

Directional Waterflooding Experiments: For each direction (x, y, z), water was injected at a constant rate for 30 PV. Outlet flow rates and times were recorded. The experiment was stopped when water cut exceeded 99.9% and injected PV exceeded 30, achieving residual oil saturation (Sor). Effective water-phase permeability was measured in all directions. NMR and CT scans were performed to analyze fluid distribution and pore changes at Sor. By adjusting the inlet and outlet of the core holder, the tests were sequentially completed for all three directions.

(5).

Data Analysis and Final Results: The cores were cleaned, oven-dried, and weighed again to verify mass changes. Based on the experimental data (flow rate, time, permeability, etc.), relative permeability curves for x, y, and z directions were calculated, and anisotropic characteristics were analyzed.

(2)

Nuclear Magnetic Resonance (NMR) Scanning:

(1).

Power on the NMR instrument, set the magnet control temperature, activate the condensation system, and preheat the instrument for at least 16 h.

(2).

Select pulse sequences to calibrate the scanning space and set scanning parameters.

(3).

Place the core in the NMR-specific PIC (Pressure Isolated Core holder) holder and position it at the center of the measurement chamber.

(4).

Select the pulse sequence, configure parameters, and start measurements.

(5).

Measurement parameters include echo spacing, full relaxation time, NECH (NMR Effective Porosity), NS (Number of Spins), RG (Relaxation Gradient), and others.

(3)

Computed Tomography (CT) Scanning:

(1).

Place the core sample into the Nano Voxel 5000 micro-CT system and adjust scanning parameters.

(2).

Reconstruct the scanned data into a digital 3D model using Phoenix Datosx 2 Acq X (v2.6) software. During reconstruction, geometric calibration values can be adjusted to reduce beam hardening artifacts.

(3).

Analyze the reconstructed 3D digital model using VOLUME GRAPHICS STUDIO MAX 2024.2 and AVIZO 9.0. Generate internal 3D visualizations and extract oil distribution within the core pores, with final images provided.

2.2. Relative Permeability Calculation Methods

The determination of relative permeability is a critical technique in reservoir development. With advances in oilfield development technologies, methods for estimating relative permeability have continuously evolved. Currently, two main approaches are used for calculating dynamic permeability: explicit methods and implicit methods. Explicit methods solve the Buckley–Leverett equation for two-phase water–oil flow using characteristic line theory, including the JBN method and its modified versions. Implicit methods, on the other hand, obtain dynamic data from displacement experiments and, combined with suitable relative permeability models and optimization algorithms, invert and fit reliable relative permeability curves.

2.2.1. JBN Calculation Method

The JBN method is based on the one-dimensional Buckley–Leverett theory for waterflood front propagation and the Welch integral approach. It uses unsteady-state coreflood data to obtain two-phase relative permeability curves. Relative permeability of the oil–water system is calculated using the JBN method based on the production rates of each fluid at the core outlet and the pressure difference along two sections of the core over time during the unsteady (waterflooding) process.

Assumptions:

(1).

Capillary pressure and gravity effects are neglected.

(2).

The two immiscible fluids are incompressible.

(3).

Oil and water saturations are uniform across any cross-section of the core.

The experiments were conducted using the constant-rate method. A core sample with length L (cm), diameter D (cm), and cross-sectional area A (cm²) was initially saturated with oil. Water was injected at a constant flow rate q (mL/h) from one end to displace the oil, and the cumulative injected volume was recorded as V(t) (mL). At the outlet end of the core, the produced fluids were collected, and the cumulative production of each phase was recorded as a function of time; the cumulative oil production is denoted as Vo(t) (mL). Meanwhile, the pressure differential across the core, ΔP(t) (0.1 MPa), was measured. Based on the above experimental measurements, the relative permeability of each phase can be calculated using the two-phase displacement theory of Buckley and Leverett [54] (1942).

Taking the inlet end of the core as the origin of the x-axis (x = 0), and considering incompressible two-phase fluids while neglecting gravity and capillary forces, the one-dimensional flow equation, continuity equation, and fractional-flow equation can be expressed as follows:

Equation of motion:

$$q_i=-A{\displaystyle \frac{k{k}_{r\mathrm{i}}}{{\mu }_i}}{\displaystyle \frac{\partial P}{\partial x}},i=o,w$$

(1)

Continuity equation:

$$-{\displaystyle \frac{\partial q_i}{\partial x}}=A\varphi {\displaystyle \frac{\partial S_i}{\partial t}}, i=o,w, S_w+S_i=1$$

(2)

Fractional-flow equation:

$$f_w={\displaystyle \frac{q_w}{q_w+q_o}}={\displaystyle \frac{k_{rw}/{\mu }_w}{k_{rw}/{\mu }_w+k_{ro}/{\mu }_o}}$$

(3)

Based on the principle of material balance, the Buckley–Leverett frontal-advance equation can be derived in a concise form as follows:

$$x={\displaystyle \frac{1}{\varphi A}}{\displaystyle \frac{d{f}_w(S_w)}{d{S}_w}}{\displaystyle {\int }_0^t{q}_t(t)dt=}{\displaystyle \frac{1}{\varphi A}}{\displaystyle \frac{d{f}_w(S_w)}{d{S}_w}}V(t)$$

(4)

For core samples, the cumulative injected water volume is generally expressed as an integer multiple of the pore volume, denoted as the injection multiple Q_i. Therefore, the above equation can be rewritten as follows:

$${\displaystyle \frac{1}{Q_i}}={\displaystyle \frac{\varphi AL}{V(t)}}={\displaystyle \frac{d{f}_w(S_{wL})}{d{S}_w}}={f^{\prime }}_{wL}$$

(5)

The above equation is the so-called Welge integral equation, whose physical meaning indicates that, during waterflooding in a core, the injection multiple is equal to the reciprocal of the derivative of water saturation.

• Relationship among the total two-phase resistance to flow Ω, the ratio of single-phase resistances, the apparent viscosity μ_app, and the injection multiple Q_i. Based on the above fundamental equations, and according to the equation of motion for two-phase flow:

  $$q(t)=q_o+q_w=-Ak({\displaystyle \frac{k_{ro}}{{\mu }_o}}+{\displaystyle \frac{k_{rw}}{{\mu }_w}}){\displaystyle \frac{\partial P}{\partial x}}$$

  (6)

The summation term in parentheses in the above equation has the dimension of viscosity and is defined as the apparent viscosity μ_app:

$${\mu }_{app}(S_w)={({\displaystyle \frac{k_{ro}}{{\mu }_o}}+{\displaystyle \frac{k_{rw}}{{\mu }_w}})}^{-1}$$

(7)

From Equation (6), the pressure distribution along the core is obtained as follows:

$$\Delta P(x)={\displaystyle \frac{q_t{\mu }_o}{Ak}}{{\displaystyle \underset{0}{\overset{x}{\int }}\frac{1}{{\mu }_o}(\frac{k_{ro}}{{\mu }_o}+\frac{k_{rw}}{{\mu }_w})}}^{-1}dx={\displaystyle \frac{q(t){\mu }_o}{Ak}}{\displaystyle \underset{0}{\overset{x}{\int }}\frac{{\mu }_{app}(S_w)}{{\mu }_o}}\cdot dx$$

(8)

If the value at the outlet end of the core is taken, and the above equation is differentiated with respect to x with the corresponding variable substitutions, then:

$$\Delta P(L)={\displaystyle \frac{q(t){\mu }_o}{Ak}}{\displaystyle \underset{0}{\overset{L}{\int }}\frac{{\mu }_{app}(S_w)}{{\mu }_o}}dx={\displaystyle \frac{q(t){\mu }_{o}L}{Ak{f^{\prime }}_{wL}}}{\displaystyle \underset{0}{\overset{{f^{\prime }}_{wL}}{\int }}\frac{{\mu }_{app}(S_w)}{{\mu }_o}}d{f^{\prime }}_w(S_w)$$

(9)

It can be simplified as:

$${\displaystyle \underset{0}{\overset{{f^{\prime }}_{wL}}{\int }}\frac{{\mu }_{app}(S_w)}{{\mu }_o}}d{f^{\prime }}_w(S_w)=\Omega ({f^{\prime }}_{wL})\cdot {f^{\prime }}_{wL}$$

(10)

It can be seen that:

$$\Omega ({f^{\prime }}_{wL})={\displaystyle \frac{\Delta P(L)}{q(t)}}{\displaystyle \frac{Ak}{{\mu }_{o}L}}$$

(11)

where Ω is the ratio of the total two-phase flow resistance to the single-phase flow resistance [37]. Substituting Equation (5) into Equation (10), and then differentiating both sides of the resulting equation, yields:

$${\displaystyle \frac{{\mu }_{app}(Q_i)}{{\mu }_o}}=\Omega (Q_i)-Q_i{\displaystyle \frac{d\Omega (Q_i)}{d{Q}_i}}$$

(12)

Based on the displacement data, the relationship between Ω and Q_i can be fitted, and accordingly, the relationship between μ_app and Q_i can be obtained.

2.

Relationship among the average water saturation $\overline{S}$, the outlet water saturation S_wL, and the injection multiple Q_i.

Assuming that the oil and water phases are incompressible, and based on the principle of material balance, the cumulative increase in water within the core is equal to the cumulative oil production at the outlet. Therefore, the average water saturation inside the core is ($\overline{S}$):

$$\overline{S}=S_{wc}+V_o/V_p,V_p=AL\varphi$$

(13)

If the saturation distribution between any two points in the core (between x₁ and x₂) is considered, the average water saturation can be expressed as:

$$\overline{S}={\displaystyle \frac{S_{w2}{x}_2-S_{w1}{x}_1}{x_2-x_1}}-{\displaystyle \frac{V(t)(f_{w2}-f_{w1})}{\varphi A(x_2-x_1)}}$$

(14)

This result originates from the work of Welge and is referred to as the Welge integral [55]. According to the specific boundary conditions of core displacement, the above equation can be transformed into:

$$\overline{S}=S_{wL}+Q_i(1-f_{wL})=S_{wL}+Q_i{f}_{oL}$$

(15)

In this equation, f_oL is the oil fractional flow at the outlet end of the core, which can be calculated using the following expression:

$$f_{oL}(S_{wL})=\underset{\Delta V\to 0}{\lim }{\displaystyle \frac{V_o(V+\Delta V)-V_o(V)}{\Delta V}}={\displaystyle \frac{d{V}_o}{dV}}={\displaystyle \frac{A\varphi L\cdot d\overline{S}}{dV}}={\displaystyle \frac{d\overline{S}}{d{Q}_i}}$$

(16)

Clearly, the calculation of the oil fractional flow at the outlet end of the core applies Equation (15). Furthermore, based on Equation (16), the water fractional-flow equation, as well as the outlet water fractional flow and water saturation of the core, can be derived as follows:

$$f_{wL}(S_{wL})=1-f_{oL}(S_{wL})=1-{\displaystyle \frac{d\overline{S}}{d{Q}_i}}$$

(17)

$$S_{wL}=\overline{S}-Q_i{\displaystyle \frac{d\overline{S}}{d{Q}_i}}=\overline{S}+\Phi {\displaystyle \frac{d\overline{S}}{d\Phi }},\Phi =1/Q_i$$

(18)

Using the above equations together with the experimental data, the relationships $\overline{S}$~Q_i, S_wL~Q_i can be obtained.

• Method for calculating oil–water relative permeability.

The fractional-flow equation for the waterflooding process can be expressed as:

$$f_{wL}={\displaystyle \frac{k_{rw}/{\mu }_w}{k_{rw}/{\mu }_w+k_{ro}/{\mu }_o}}={\displaystyle \frac{k_{rw}}{{\mu }_w}}{\mu }_{app}(S_{wL})$$

(19)

Rearranging the above equation and using Equation (17), the formulas for calculating the oil–water relative permeabilities are obtained as follows:

$$k_{rw}={\displaystyle \frac{{\mu }_w}{{\mu }_o}}{\displaystyle \frac{f_{wL}}{({\mu }_{app}/{\mu }_o)}}={\displaystyle \frac{{\mu }_w}{{\mu }_o}}{\displaystyle \frac{1-d\overline{S}/d{Q}_i}{({\mu }_{app}/{\mu }_o)}}={\displaystyle \frac{{\mu }_w}{{\mu }_o}}{\displaystyle \frac{1+{\Phi }^{2}d\overline{S}/d\Phi }{({\mu }_{app}/{\mu }_o)}}$$

(20)

$$k_{ro}={\displaystyle \frac{f_{oL}}{({\mu }_{app}/{\mu }_o)}}={\displaystyle \frac{d\overline{S}/d{Q}_i}{({\mu }_{app}/{\mu }_o)}}={\displaystyle \frac{-{\Phi }^{2}d\overline{S}/d\Phi }{({\mu }_{app}/{\mu }_o)}}$$

(21)

It has been found that $\gamma =(V_o+S_{wc})\Phi =S_{wavg}\Phi$, ΩΦ exhibits a linear correlation with the logarithm of Φ, and

$${\displaystyle \frac{{\mu }_w}{{\mu }_o}}\cdot {\displaystyle \frac{1+\frac{d\gamma }{d\Phi }\cdot \Phi -\gamma }{\frac{d\Omega \Phi }{d\Phi }}}={\displaystyle \frac{{\mu }_w}{{\mu }_o}}\cdot {\displaystyle \frac{1+(\frac{\Phi d{S}_{wavg}+S_{wavg}d\Phi }{d\Phi })\cdot \Phi -S_{wavg}\cdot \Phi }{\frac{\Omega d\Phi +\Phi d\Omega }{d\Phi }}}={\displaystyle \frac{{\mu }_w}{{\mu }_o}}\cdot {\displaystyle \frac{1+{\Phi }^2\frac{d{S}_{wavg}}{d\Phi }}{\Omega +\Phi \frac{d\Omega }{d\Phi }}}$$

(22)

Equation (22) is krw.

$${\displaystyle \frac{\gamma -\frac{d\gamma }{d\Phi }\cdot \Phi }{\frac{d\Omega \Phi }{d\Phi }}}={\displaystyle \frac{S_{wavg}\cdot \Phi -(\frac{\Phi d{S}_{wavg}+S_{wavg}d\Phi }{d\Phi })\cdot \Phi }{\frac{\Omega d\Phi +\Phi d\Omega }{d\Phi }}}={\displaystyle \frac{-{\Phi }^2\frac{d{S}_{wavg}}{d\Phi }}{\Omega +\Phi \frac{d\Omega }{d\Phi }}}$$

(23)

Equation (23) is kro.

Therefore, a new complex exponential fitting method is introduced here, which accounts for both the monotonicity of the experimental data and the accuracy of the fit. Its fundamental equation is:

$$\gamma =\exp [A_1\times \exp (-\ln (\Phi )/t_1)+A_2\times \exp (-\ln (\Phi )/t_2)+A_3\times \exp (-\ln (\Phi )/t_3)+A_0]$$

(24)

$$\Omega \Phi =\exp [a\times \ln (\Phi )+b]$$

(25)

Thus, based on Equations (22) and (23), the relative permeability calculation formulas can be obtained as follows:

$$\begin{array}{r}{k}_{rw}={\displaystyle \frac{{\mu }_{\mathrm{w}}}{{\mu }_{\mathrm{o}}}}{\displaystyle \frac{1-[\frac{A_1}{t_1}\cdot \exp (-\ln (\Phi )/t_1)+\frac{A_2}{t_2}\cdot \exp (-\ln (\Phi )/t_1)+\frac{A_3}{t_3}\cdot \exp (-\ln (\Phi )/t_2)+1]}{(a/\Phi )\cdot \exp (a\cdot \ln \Phi -b)}}\\ \cdot \exp [A_1\cdot \exp (-\ln (\Phi )/t_1)+A_2\cdot \exp (-\ln (\Phi )/t_2)+A_3\cdot \exp (-\ln (\Phi )/t_3)+A_0]\end{array}$$

(26)

$$\begin{array}{r}{k}_{r\mathrm{o}}={\displaystyle \frac{[\frac{A_1}{t_1}\cdot \exp (-\ln (\Phi )/t_1)+\frac{A_2}{t_2}\cdot \exp (-\ln (\Phi )/t_1)+\frac{A_3}{t_3}\cdot \exp (-\ln (\Phi )/t_2)+1]}{(a/\Phi )\cdot \exp (a\cdot \ln \Phi -b)}}\\ \cdot \exp [A_1\cdot \exp (-\ln (\Phi )/t_1)+A_2\cdot \exp (-\ln (\Phi )/t_2)+A_3\cdot \exp (-\ln (\Phi )/t_3)+A_0]\end{array}$$

(27)

where

• q—water injection rate
• μ—fluid viscosity
• ϕ—porosity
• f_w—water fractional flow
• f_wL—water fractional flow at the outlet end
• f_oL—oil fractional flow at the outlet end
• Sw—water saturation
• So—oil saturation
• S_wL—water saturation at the outlet end
• V—cumulative liquid production
• Vo—cumulative oil production
• Vp—pore volume

The basic principles of the JBN method and its modified approaches are essentially the same, and the calculation formulas can be derived from one another. However, due to differences in data processing, the error propagation coefficients vary, resulting in discrepancies in the calculated oil–water relative permeability. Explicit JBN methods and their modifications associate the relative permeability at the displacement front with saturation; therefore, the derived relative permeability curves are only applicable within the saturation range where two-phase flow is uniform, and the curve shapes are relatively coarse. Moreover, the fundamental assumption of explicit methods is that capillary forces and their end effects are neglected. While this assumption can be approximately satisfied at sufficiently high flow rates, it is often invalid in actual reservoirs, especially in strongly heterogeneous or low-permeability formations. Consequently, consideration of capillary pressure effects becomes essential.

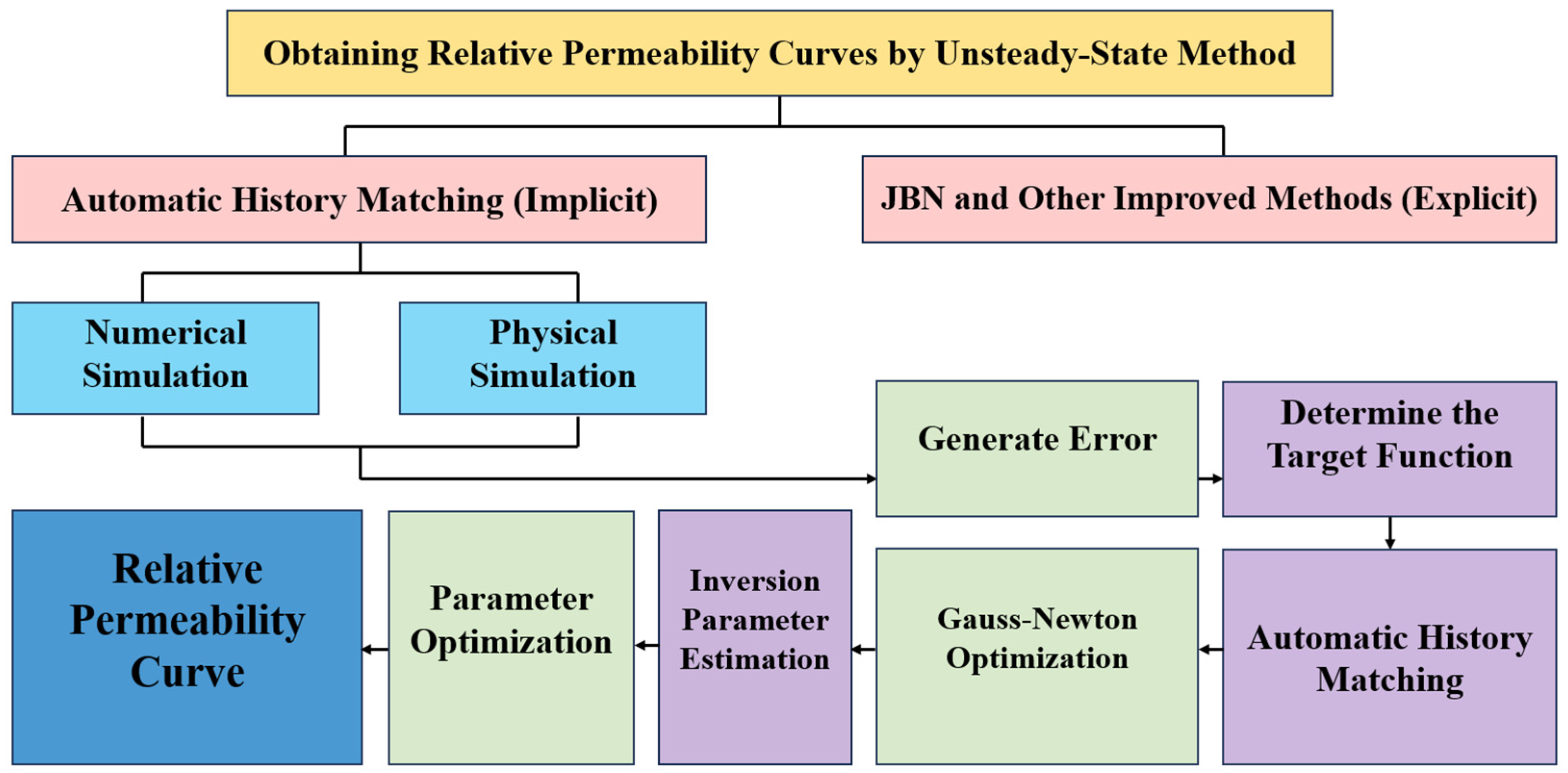
2.2.2. Relative Permeability Calculation Method Based on Automatic History Matching (AHM)

Automatic History Matching (AHM) is a method for calibrating relative permeability models by minimizing the discrepancy between simulation results and experimental data, thereby obtaining relative permeability curves that accurately reflect core behavior. The basic principle is as follows: First, it is assumed that oil–water relative permeability has a linear or nonlinear relationship with water saturation, forming a relative permeability model. This model contains a set of adjustable parameters, which are incorporated into the mathematical equations describing fluid flow within the core. Using finite element or finite difference methods under given conditions, simulated outputs such as cumulative oil production at the core outlet, pressure difference across the core, and recovery factor are obtained.

The objective function is defined as the sum of squared differences between experimental production data and model-calculated production data. The Gauss–Newton (GN) method is used to adjust model parameters, constructing an initial relative permeability curve and performing predictions, as illustrated in Figure 8. Simulation results are compared with experimental data, and optimization algorithms iteratively adjust parameters to reduce errors. The process continues until the error falls below a preset threshold or no longer significantly improves. The resulting relative permeability curve is considered the true representation of the core. The objective function plays a critical role in AHM, quantifying the discrepancy between predicted and actual data and providing a basis for optimizing model parameters.

A three-dimensional multiphase numerical model is constructed based on the geometric parameters of the experimental core (e.g., 5 × 5 × 5 cm³) and fluid properties (formation water and crude oil). The model accounts for physical effects such as capillary pressure, gravity, and fluid compressibility. The specific fitting steps are:

(1).

Parameter Initialization: Determine the required physical displacement experimental data.

(2).

Model Setup: Build a numerical model based on the physical core experiment.

(3).

Objective Function Definition: Compare simulated results with experimental data and calculate errors using appropriate formulas; this serves as the objective function.

(4).

Optimization Adjustment: Adjust the relative permeability model parameters according to the objective function using an optimization algorithm.

(5).

Iteration: Repeat the process until the error is below the preset threshold or no longer significantly decreases, indicating convergence and yielding a highly accurate fitted relative permeability curve.

The study fits cumulative oil production, injection–production pressure difference, water–oil ratio, and water cut from core experiments. Equations (28) and (29) are used as error functions for cumulative oil production, injection–production pressure difference, water–oil ratio, and water cut, respectively.

$${{\displaystyle \phi }}_1=\sum {\left({\displaystyle \frac{{{\displaystyle f}}_{1i}-{{\displaystyle f}}_{2i}}{{{\displaystyle f}}_{2i}}}\right)}^2$$

(28)

$${{\displaystyle \phi }}_2=\sum {\left({{\displaystyle f}}_{1i}-{{\displaystyle f}}_{2i}\right)}^2$$

(29)

Here, ${\phi }_1$ represents the error score for cumulative production, injection–production pressure difference, and water–oil ratio; ${\phi }_2$ represents the error score for water cut. $f_{1i}$ denotes the actual observed value, $f_{2i}$ denotes the numerical simulation result, and $i$ represents the corresponding time step for the data point.

3. Experimental Results and Discussion

Based on the aforementioned anisotropic coreflooding experimental methods, relative permeability tests were conducted on cores exhibiting typical depositional features, specifically parallel bedding and laminated cross-bedding, under different displacement directions. This study systematically analyzed the influence of the displacement direction and the bedding angle on flow characteristics. In this section, oil–water relative permeability curves obtained using both the JBN method and AHM technique are presented, and NMR and CT scanning are employed to further investigate how the angle between core bedding and displacement direction controls fluid migration patterns.

The study completed two sets of anisotropic relative permeability experiments on core samples with tabular cross-bedding and parallel bedding, eight sets of nuclear magnetic resonance (NMR) T₂ spectrum measurements, and six sets of NMR imaging experiments. In addition, a relative permeability inversion method based on automatic history matching was developed.

3.1. Displacement Experiment Analysis

3.1.1. Laminated Cross-Bedded Core

(1)

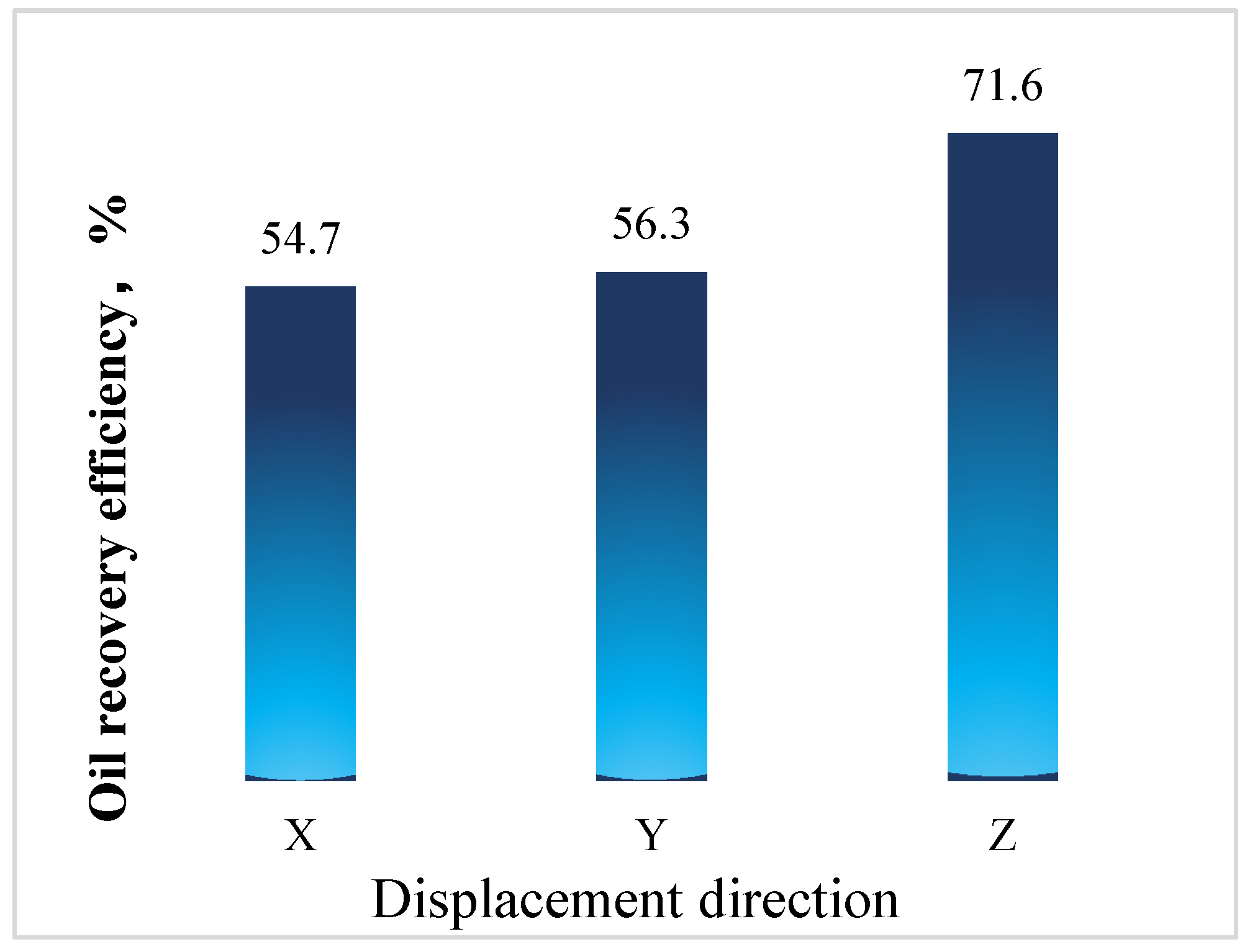
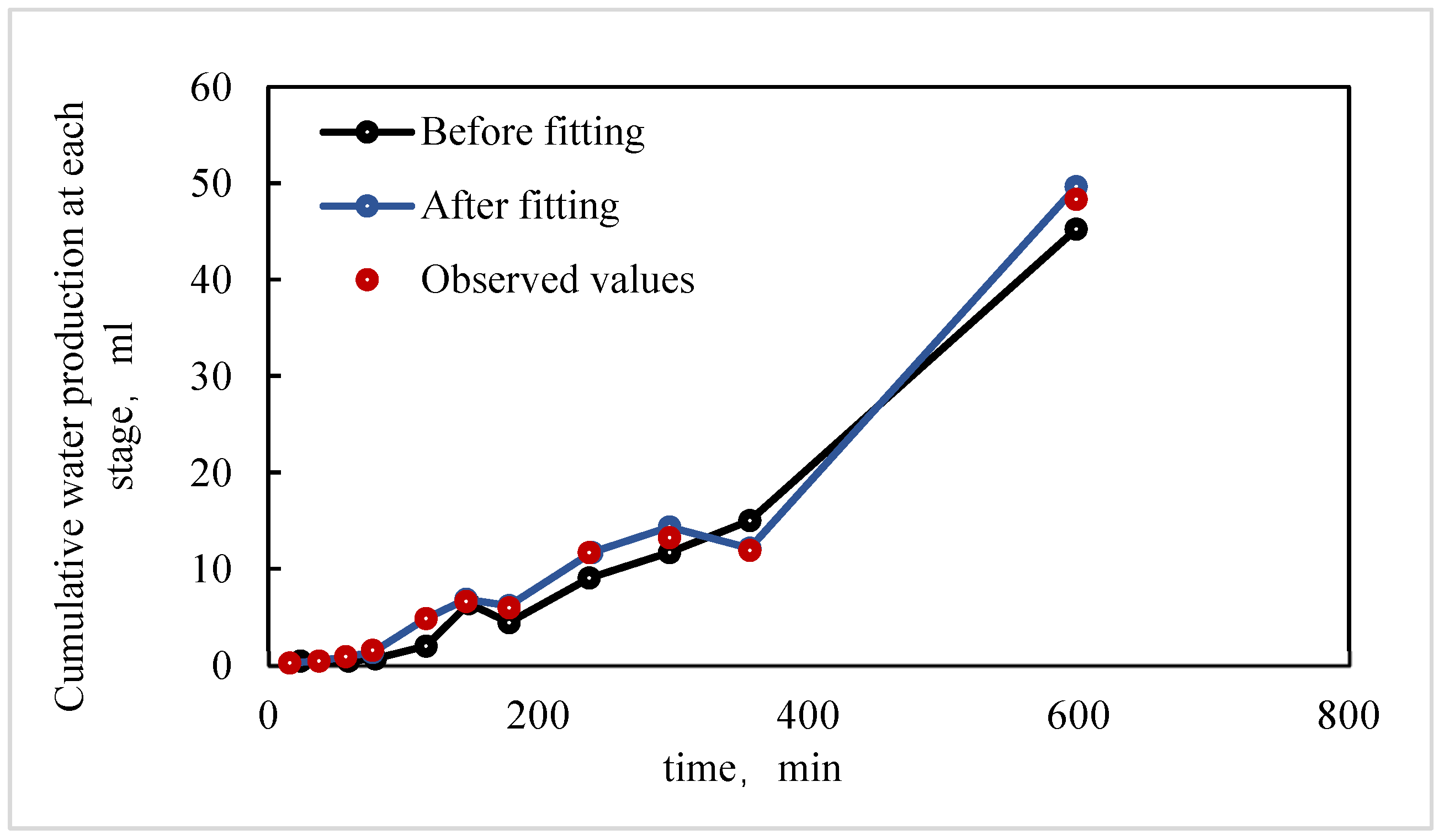
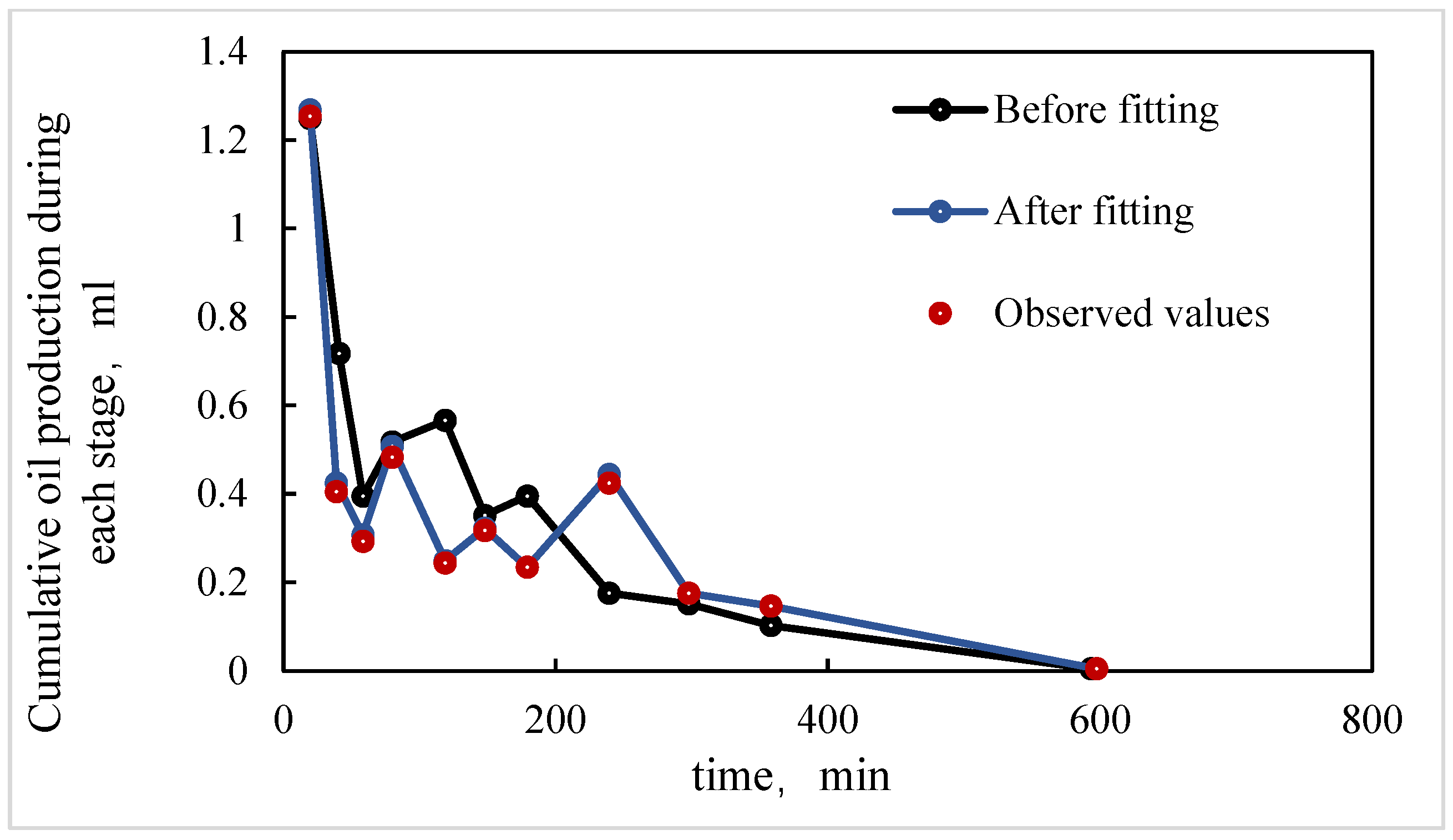
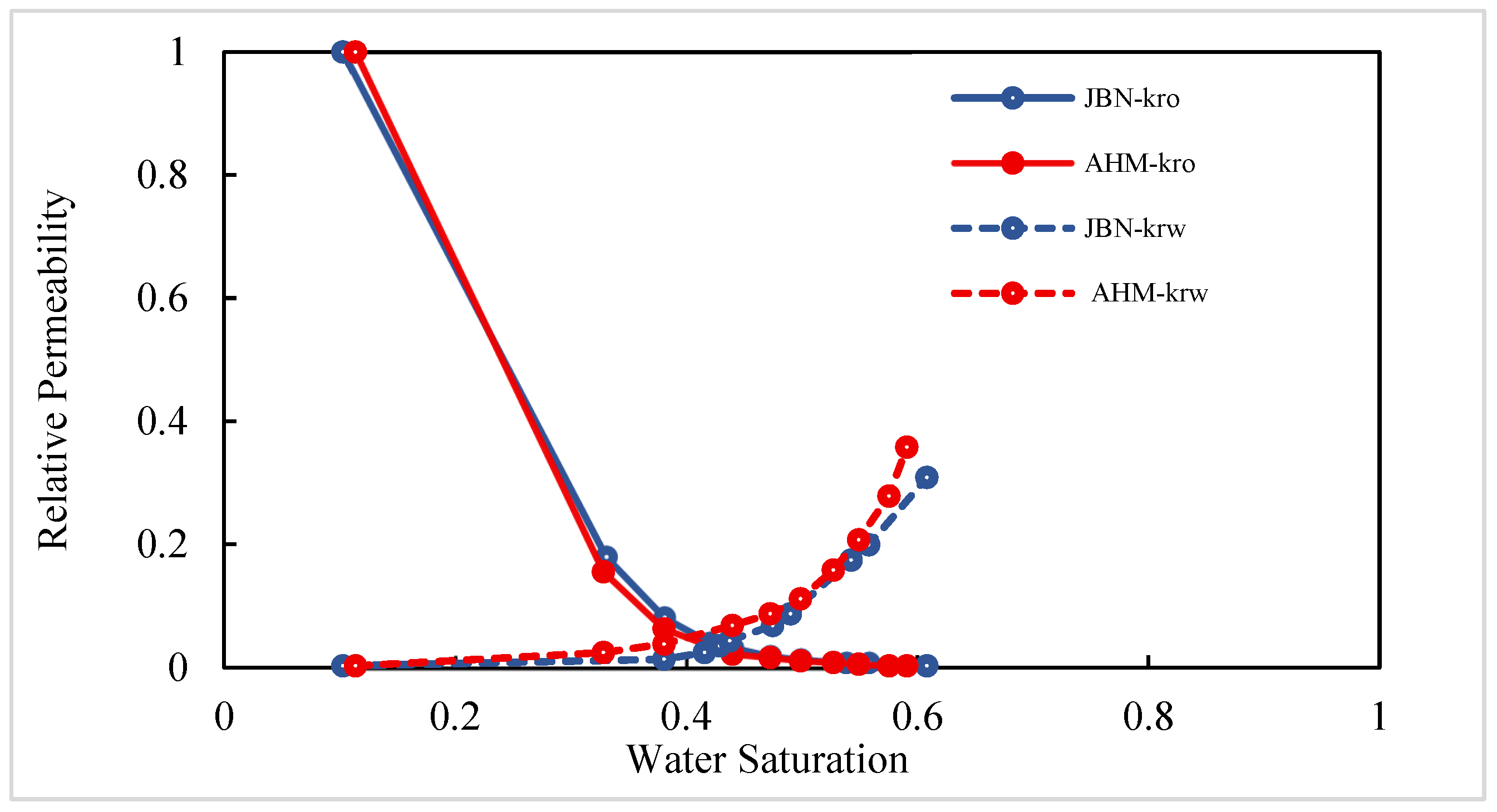
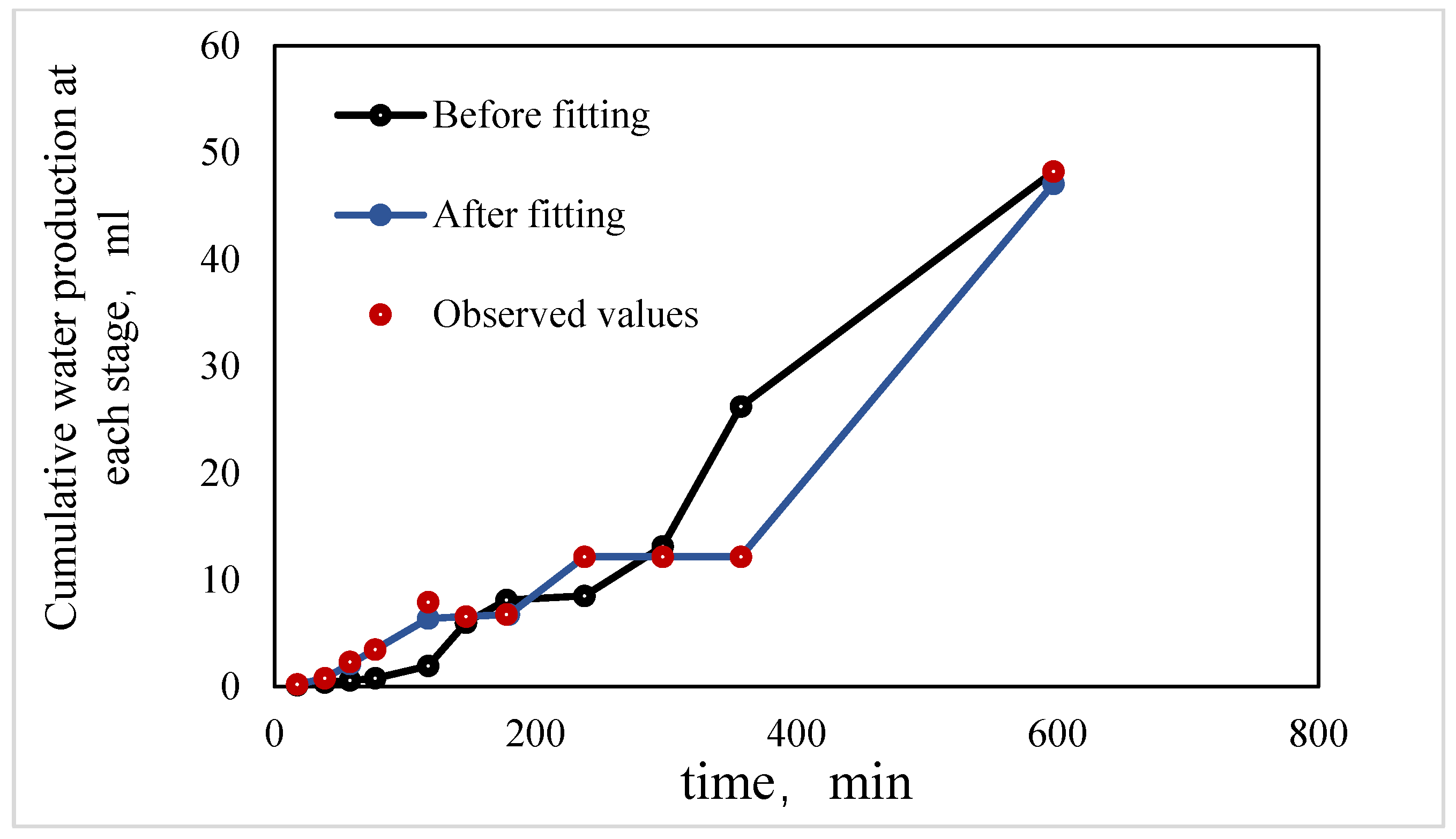
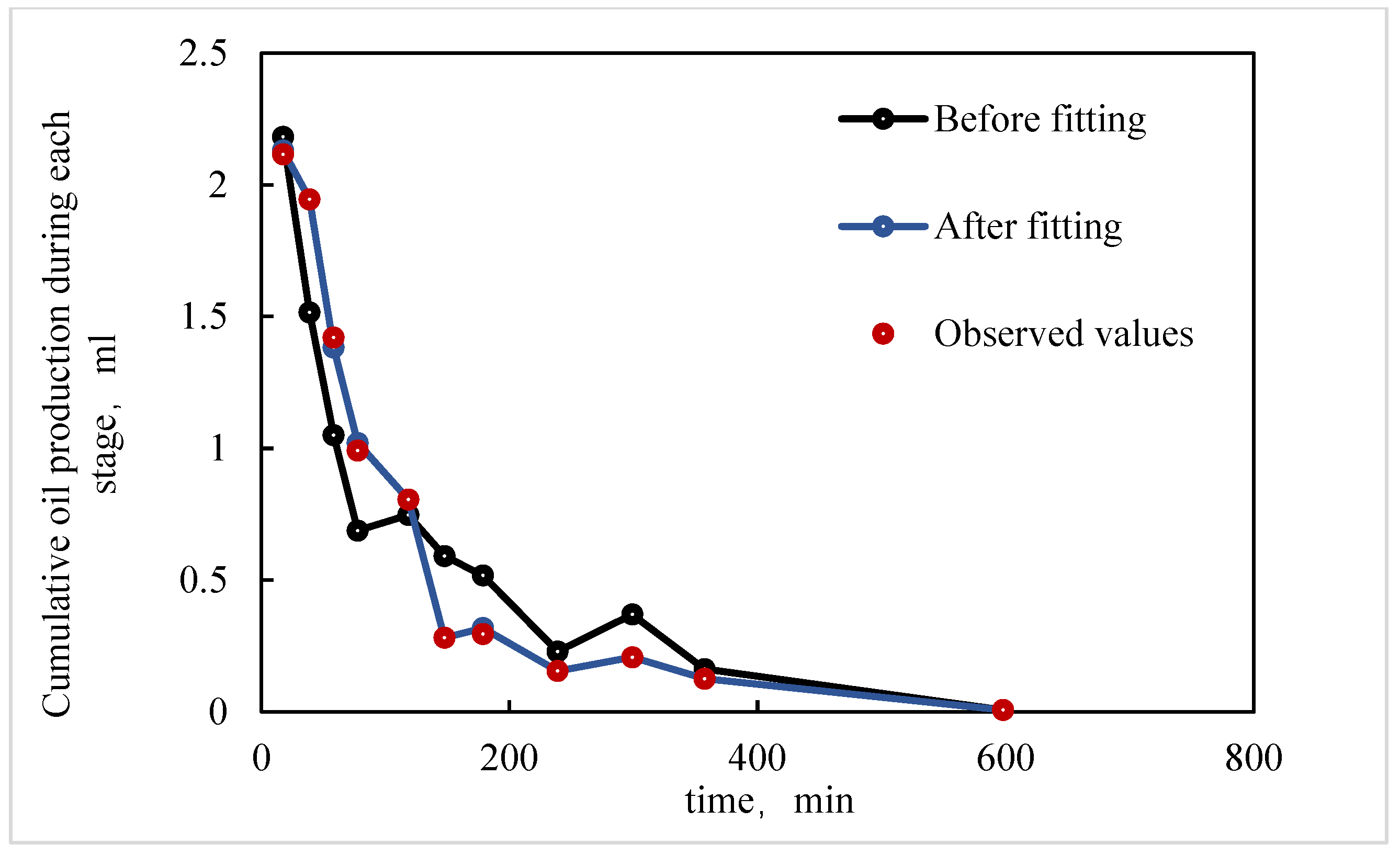
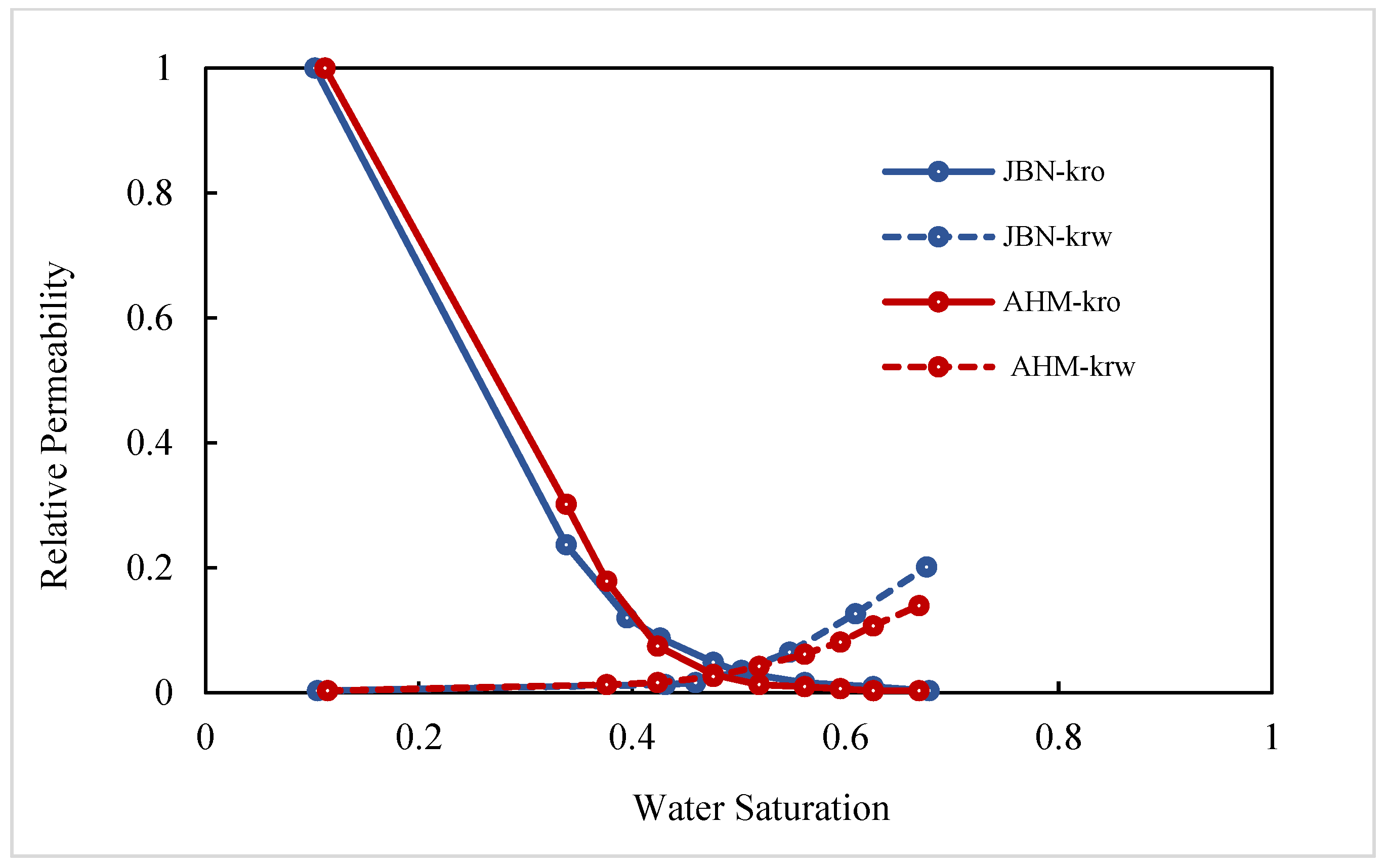
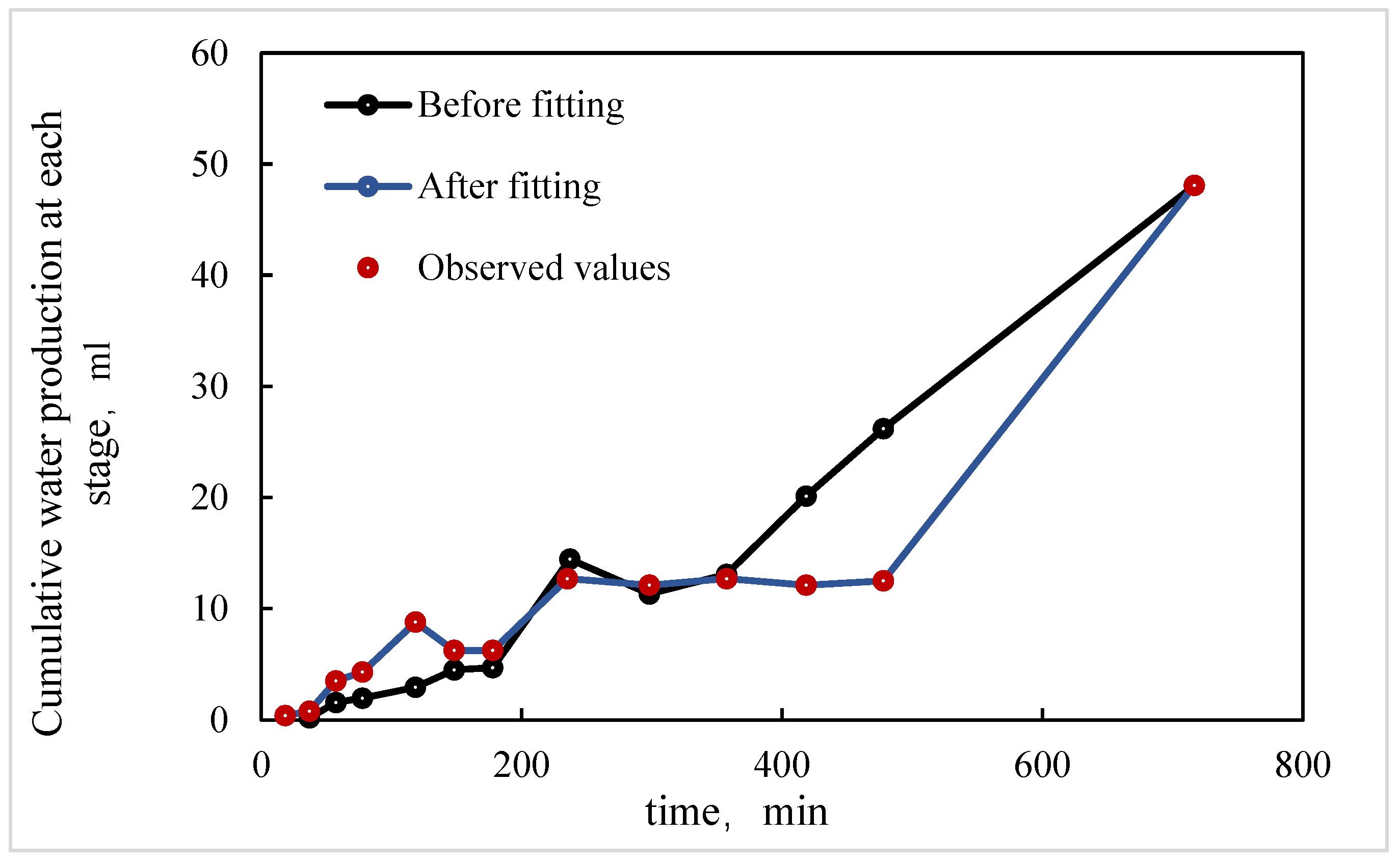
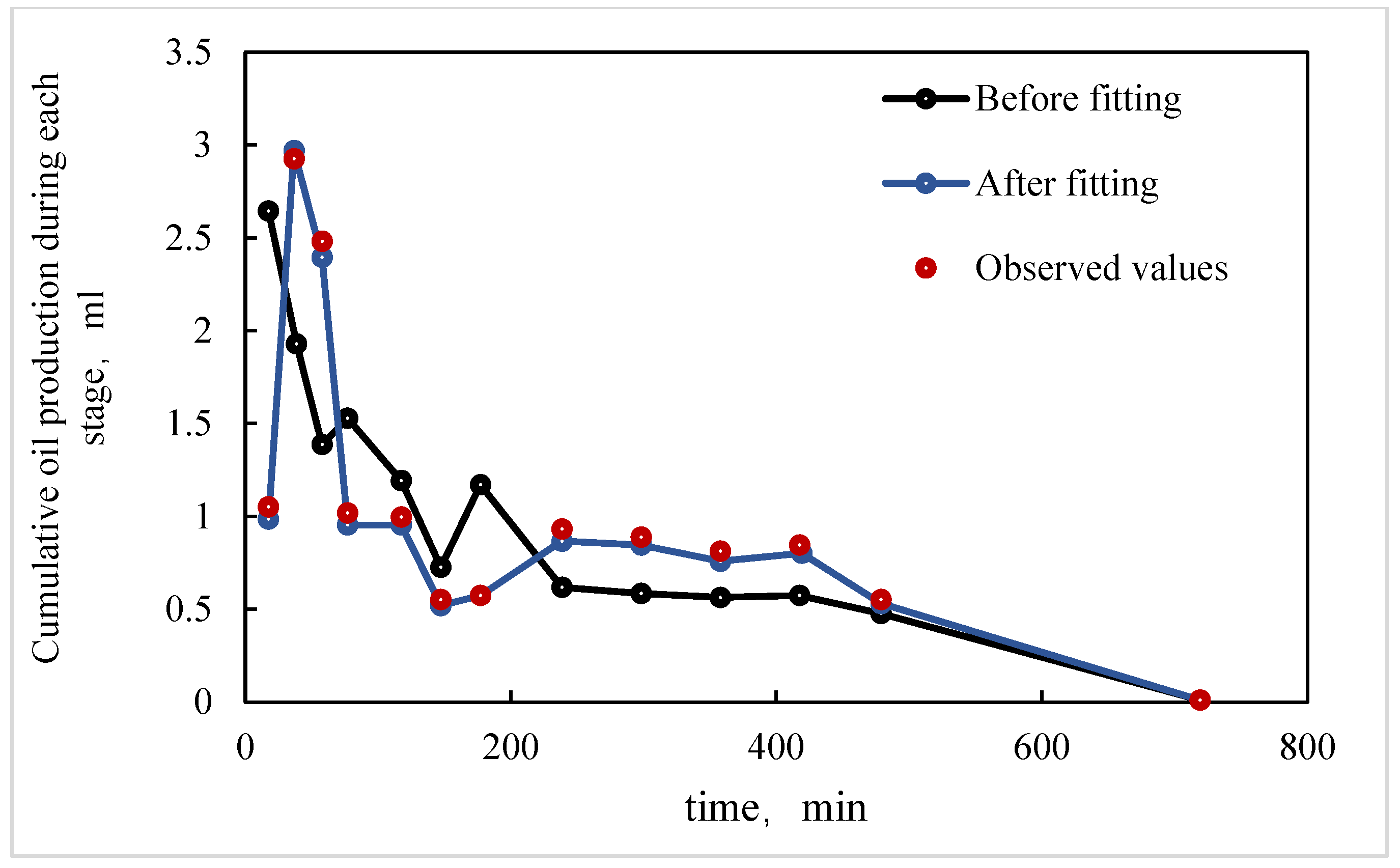
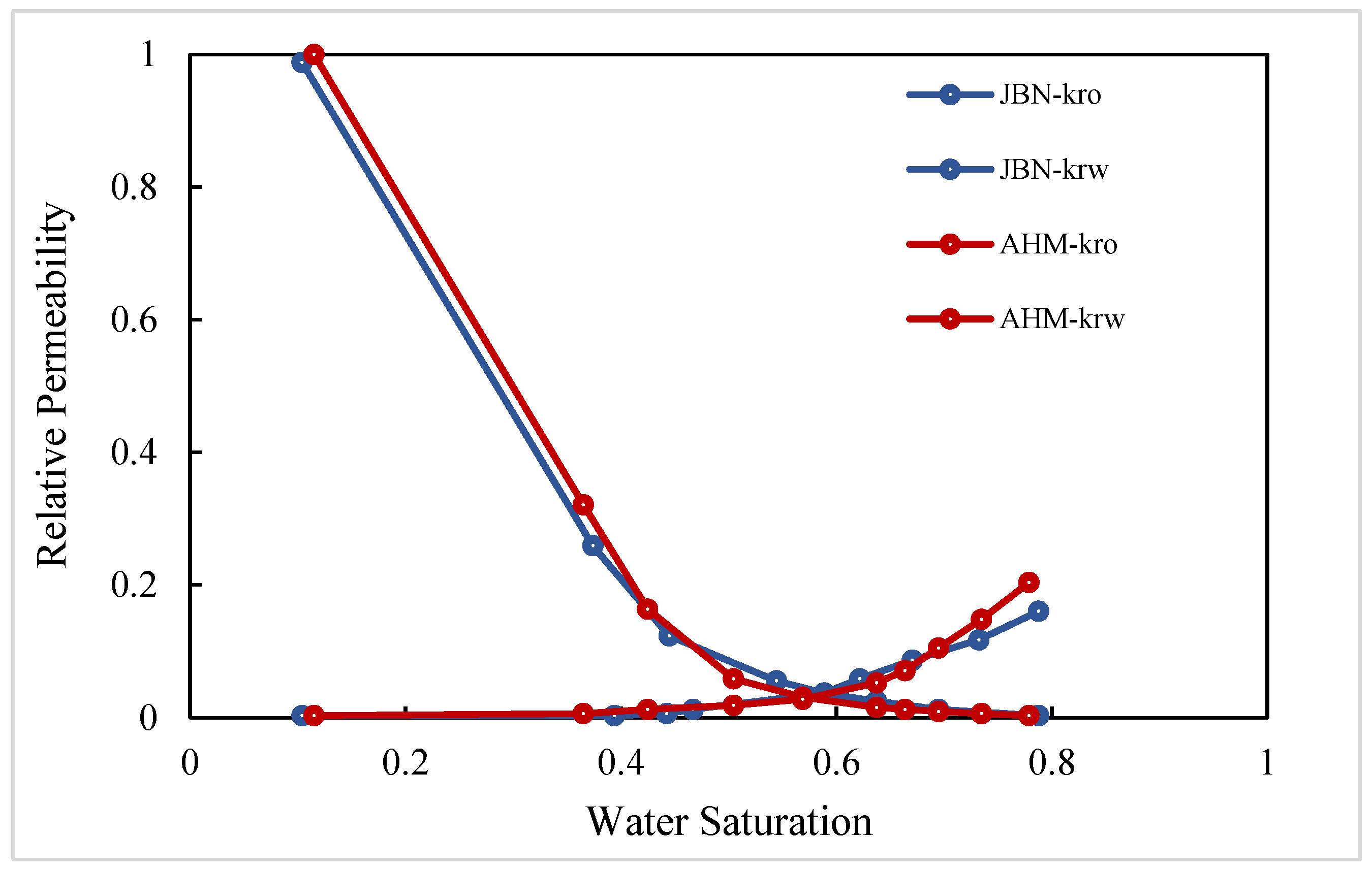
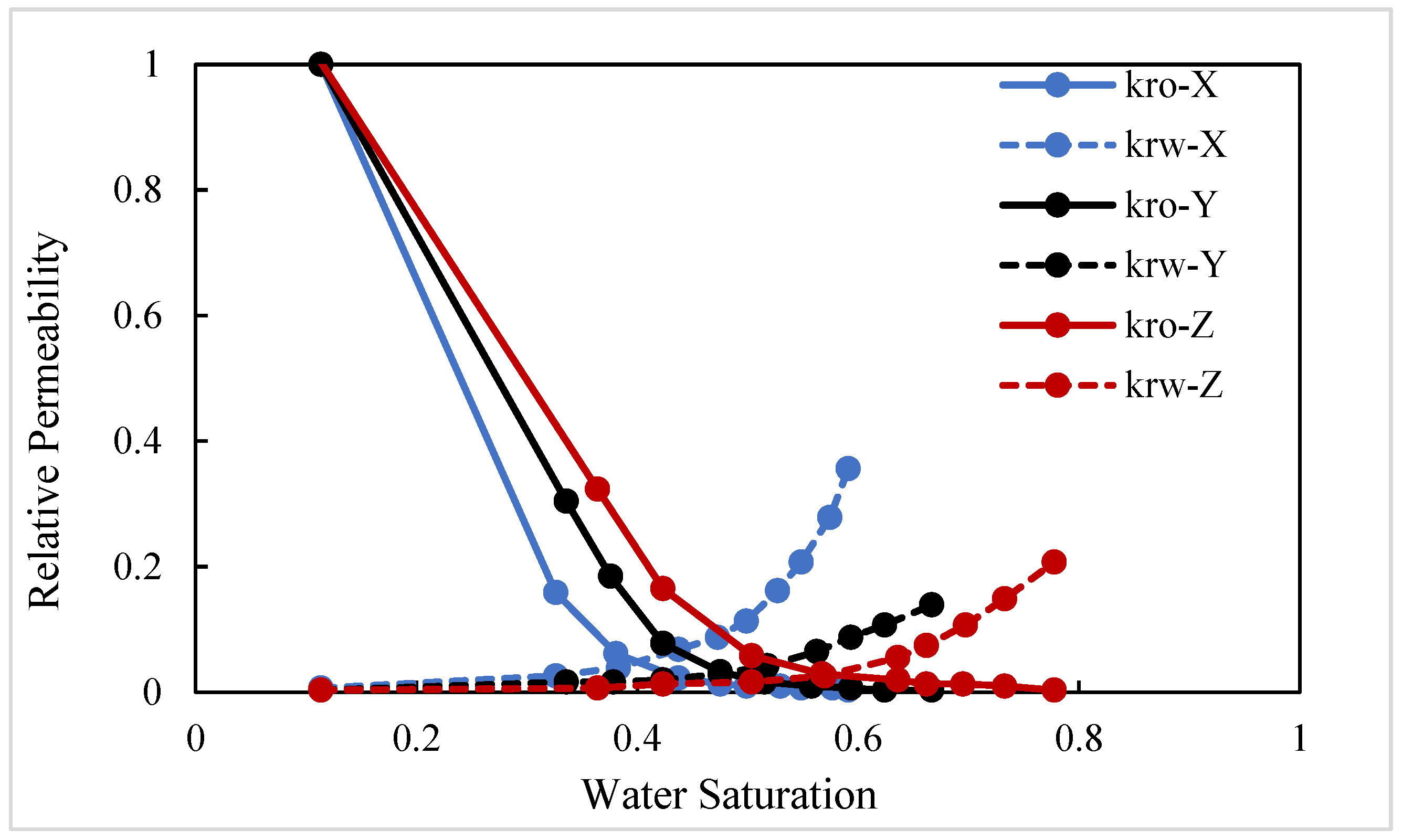
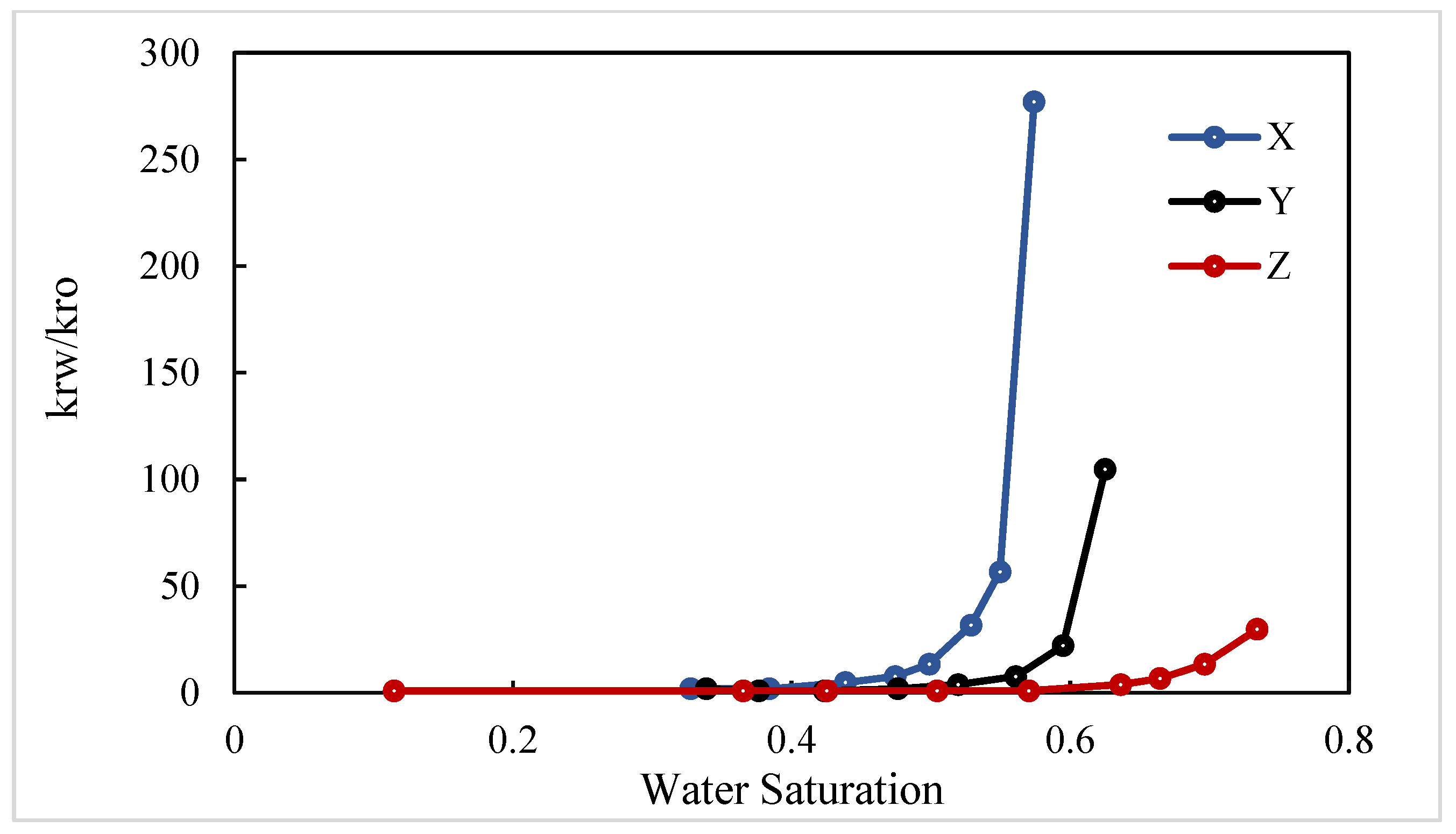
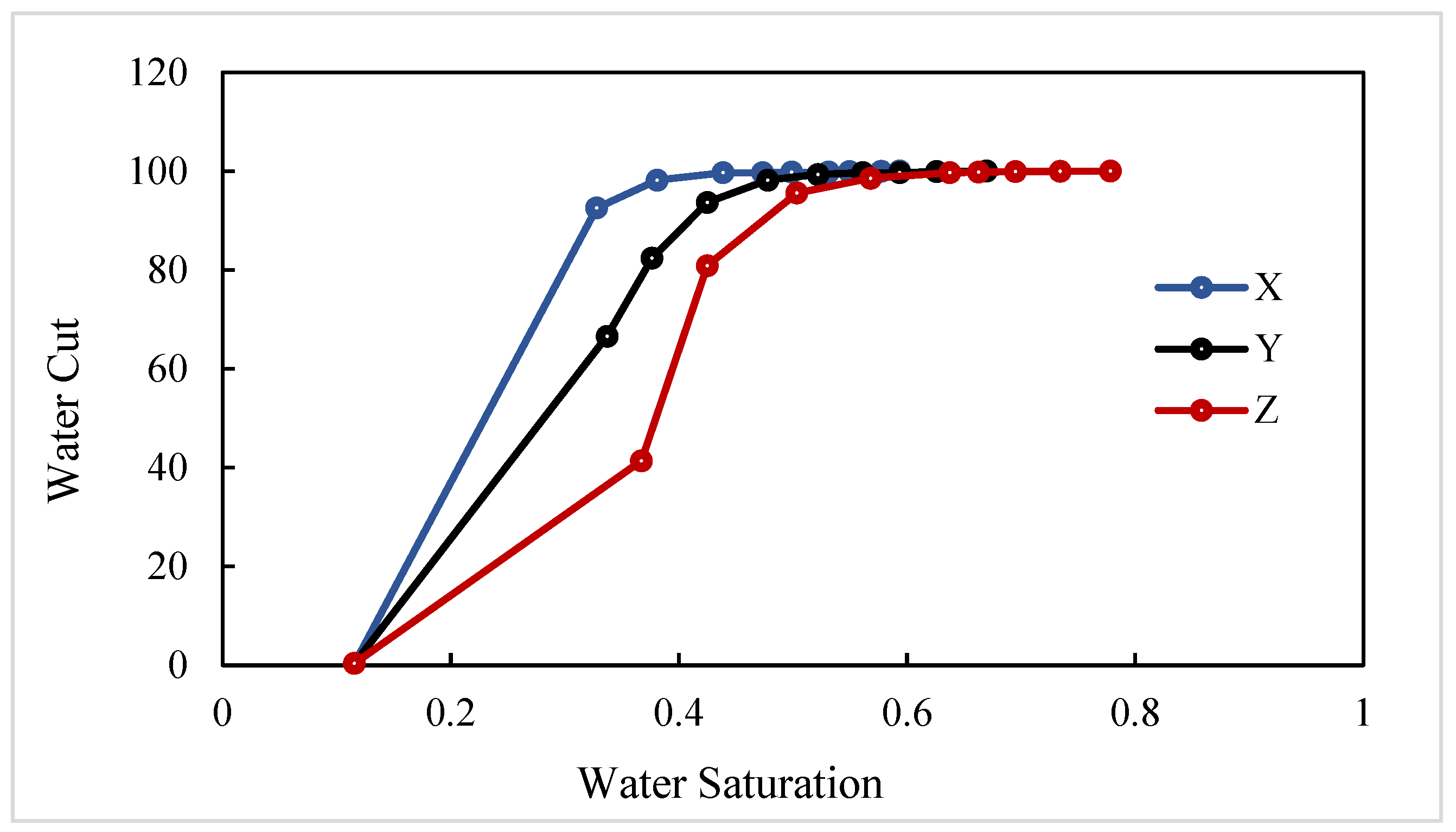
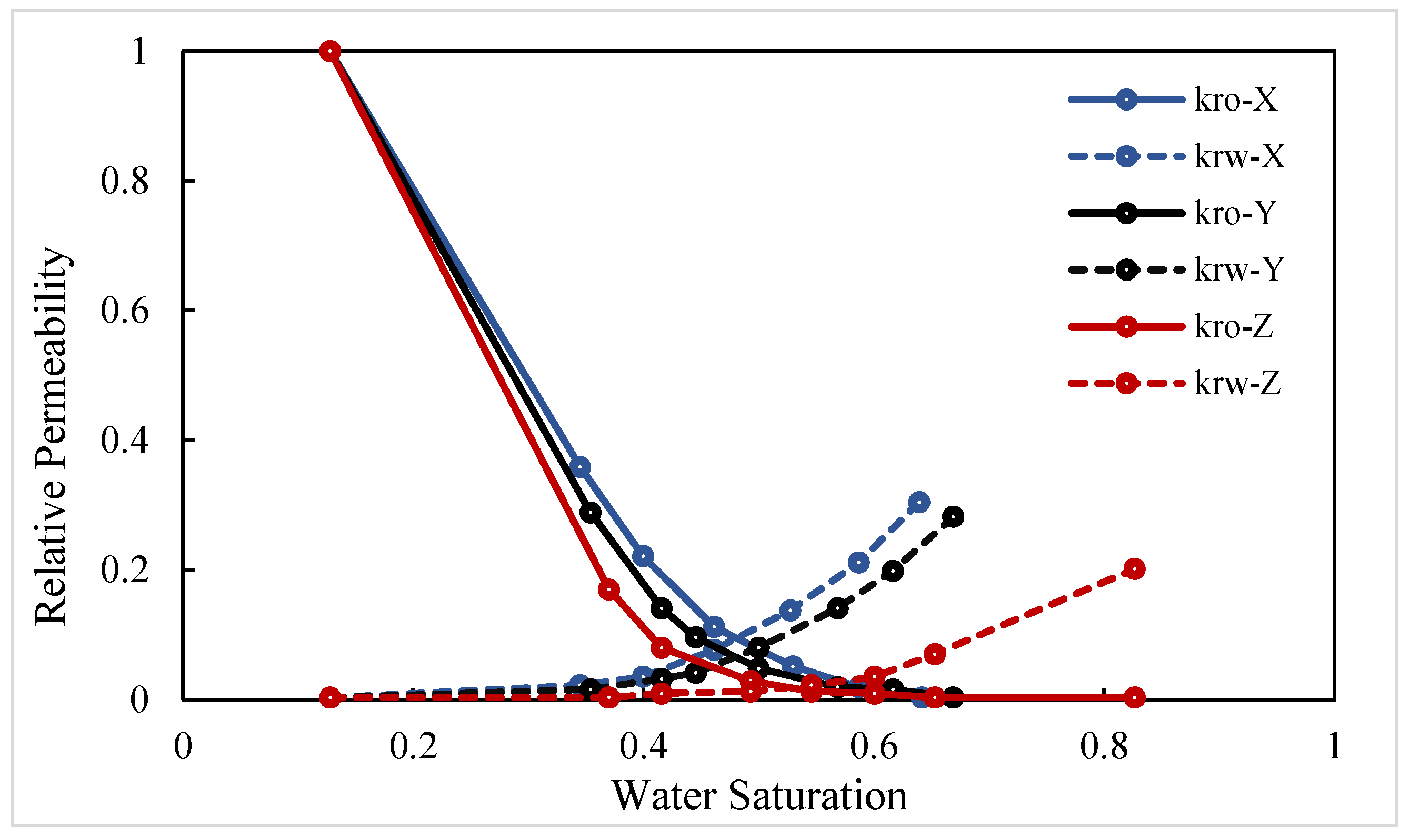
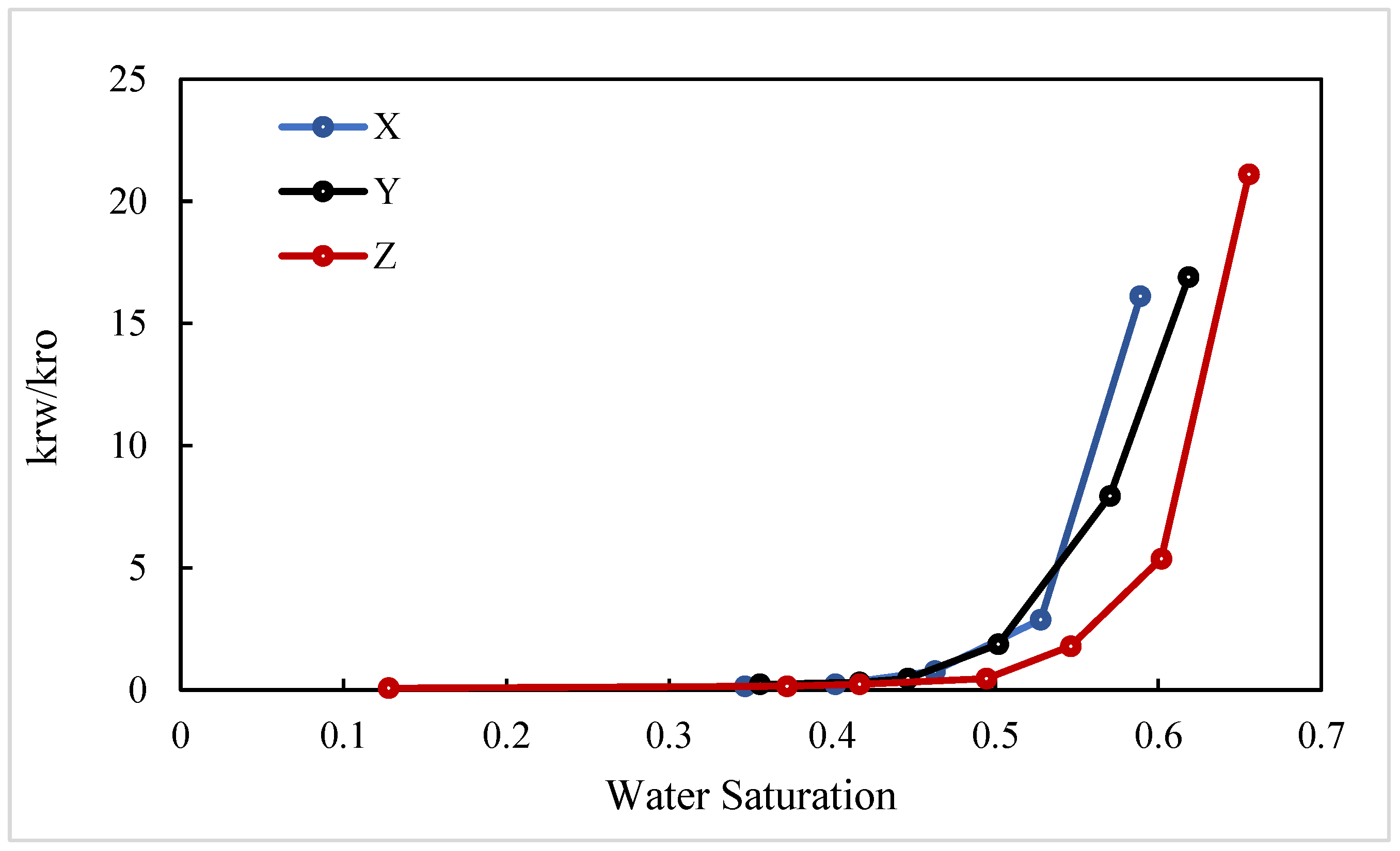
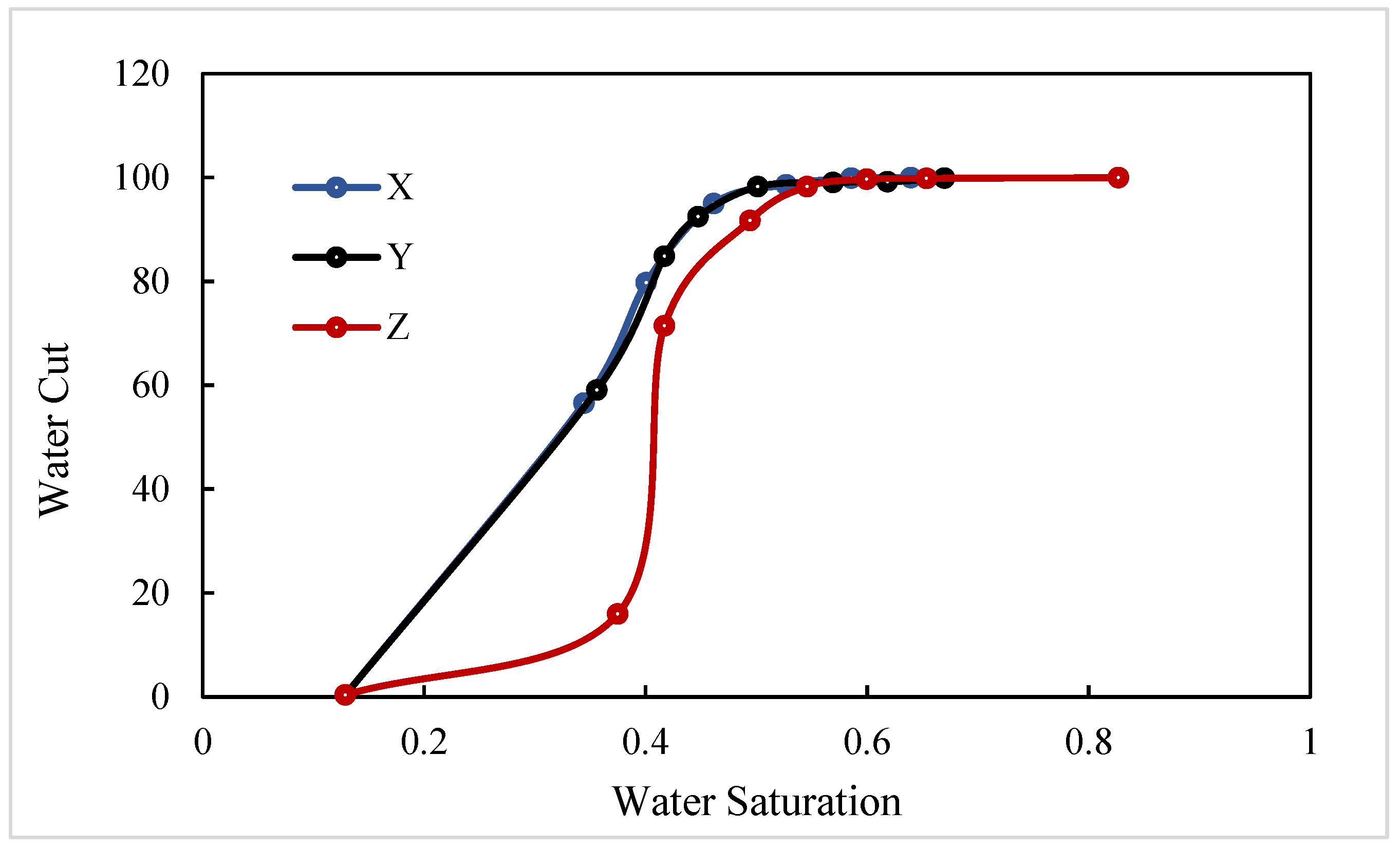
In the X direction, fluids flow parallel to the bedding planes, following relatively straight flow paths. With crude oil viscosity of 75 mPa·s, the waterflooding experiment shows a low connate water saturation of approximately 10% and a relatively high residual oil saturation of 40.6%. The endpoints of the relative permeability curves obtained using the JBN and AHM methods are consistent, yet notable differences appear in the co-permeability regions, reflecting the distinct capabilities of the two methods in capturing fluid–fluid interactions. Figure 9 and Figure 10 present comparative analyses of the dynamic water and oil production data at each experimental stage, demonstrating that the AHM method aligns more closely with the historically measured water production, particularly during high-water-cut periods, where prediction accuracy is significantly enhanced. The JBN method exhibits some deviations in describing oil-phase flow, whereas AHM, by accounting for reservoir heterogeneity and nonlinear fluid interactions, reproduces historical oil production curves more accurately. This is especially evident in regions with high residual oil saturation, indicating that AHM is more suitable for reservoirs with high-viscosity crude oil.

Figure 11 highlights the two-phase flow region and endpoint saturations, showing that water relative permeability is significantly higher than that of oil, with pronounced oil-phase trapping. The analysis suggests that the high water relative permeability in the X direction is likely associated with the bedding structure and pore-throat connectivity, leading to preferential water flow and oil trapping in low-permeability zones during waterflooding.

(2)

Core with plate-like cross-bedding in the Y direction (small angle relative to bedding), exhibiting flow across the bedding planes with a relatively complex pathway. The displacement in the Y direction has a slightly larger angle relative to the bedding compared to the X direction, reflecting variations in reservoir anisotropy. Figure 12 and Figure 13 present comparative analyses of stage-wise water and oil production in the Y direction. The data indicate that water production in the Y direction increases gradually over time, and the predictions from the automatic history-matching method align more closely with experimentally measured historical water production, particularly during high-water-cut periods, where prediction errors are significantly reduced. Residual oil saturation decreases from 40.6% in the X direction to 33% in the Y direction, indicating improved oil displacement efficiency.

Figure 14 shows the comparison of results before and after fitting. Compared with the X direction, oil recovery efficiency in the Y direction increases by 8.7%, while water saturation is relatively higher, reflecting the impact of bedding-angle variations on two-phase flow behavior. Analysis shows that relative permeability of the water phase in the Y direction is further enhanced, and oil phase retention is alleviated, which is associated with improved pore connectivity resulting from adjustments in the bedding orientation.

(3)

Core with plate-like cross-bedding in the Z direction (large angle relative to bedding), exhibiting cross-bedding flow with a complex pathway. In the Z-direction waterflooding experiments, the angle relative to the bedding further increases, reflecting a significant change in reservoir anisotropy. Figure 15 and Figure 16 present comparative analyses of stage-wise water and oil production in the Z direction. Water production in the Z direction shows a more pronounced upward trend over time, and predictions from the automatic history-matching method align more closely with experimentally measured historical water production, particularly during high-water-cut periods, where prediction errors are significantly reduced. Residual oil saturation decreases to 22%, and compared with the X direction, oil recovery efficiency in the Z direction improves by 21.14%, indicating that the further increase in bedding angle significantly enhances oil displacement. The JBN method exhibits certain deviations when describing oil-phase flow, whereas the automatic history-matching method, by accounting for reservoir heterogeneity and anisotropy in bedding orientation, better reproduces the historical oil production curve. This provides important support for predicting residual oil distribution and optimizing development strategies.

The curves in Figure 17 show enhanced oil-phase mobility; relative permeability of the water phase in the Z direction further increases, oil-phase retention is significantly alleviated, water saturation rises compared with the X and Y directions, and oil recovery efficiency is higher.

Figure 18 illustrates the displacement behavior of the laminated cross-bedded core in the X (along bedding), Y (small angle), and Z (large angle) directions. By comparing the relative permeability curves of the laminated cross-bedded core calculated using the JBN and AHM methods, the directional differences in X, Y, and Z were identified, with the AHM method more accurately matching historical production data. The curves generated by AHM outperform JBN in representing both the two-phase flow region and endpoint saturations. Through iterative optimization of model parameters, AHM captures capillary effects and reservoir heterogeneity, whereas JBN, being simpler, is suitable only for straightforward one-dimensional flow; it often exhibits errors such as distorted curve shapes, overestimated endpoints (e.g., residual saturation deviations of 10–20%), and insufficient coverage of the two-phase flow region, particularly misrepresenting interphase interactions at low saturations. This indicates that AHM better reflects the fluid dynamics in the Y direction, providing a scientific basis for optimizing injection-production strategies.

Figure 19 shows significant differences in horizontal relative permeability curves. The two-phase flow region expands with increasing water drive–bedding angle (39.7% < 47.8% < 57.1%). As the angle increases, oil recovery improves from 53.95% in the X direction to 75.09% in the Z direction, demonstrating that larger angles promote simultaneous two-phase flow and enhance oil displacement efficiency. Residual oil saturation decreases from 40.6% to 22%, corresponding to an increase in water saturation. Within the same core, water-phase relative permeability correlates positively with absolute permeability, and residual oil saturation is higher in high-permeability directions.

Results in Figure 20 further indicate that in high-permeability directions (e.g., X), the water/oil ratio is higher and water cut rises faster, confirming early water breakthrough. In contrast, the Z direction exhibits a lower water/oil ratio, suggesting more efficient oil mobilization. Figure 21 presents the relationship between water cut and water saturation; in the Z direction, water cut increases more slowly, indicating delayed water breakthrough and more uniform displacement, which is favorable for optimizing reservoir development.

3.1.2. Parallel-Laminated Core

Figure 22 illustrates the structural characteristics of the parallel-laminated core, marking the X, Y (horizontal), and Z (vertical) directions. Fluid flow in the horizontal directions is relatively uniform, whereas vertical flow is altered by lamination barriers, expanding the sweep area.

Figure 23 shows that the relative permeability curves in the horizontal directions (X and Y) exhibit minor differences, with two-phase co-flow zones smaller than in the vertical direction (47.6% < 51.5%). Horizontal flow demonstrates higher two-phase flow capacity, elevated relative permeability curves, and lower water saturation compared to the vertical direction, confirming that displacement efficiency is higher when flow is perpendicular to the laminations.

Figure 24 presents the dynamic water-to-oil ratio. Compared with horizontal flow, the vertical direction shows a significantly lower water-to-oil ratio, indicating that water movement is restricted by lamination barriers, allowing for more efficient oil mobilization. Experimental results show that oil recovery in the vertical direction is 18.06% higher than in the horizontal direction, consistent with piston-like displacement mechanisms when the flow is perpendicular to laminations. Water saturation rises more slowly, and water breakthrough is delayed, resulting in a more uniform displacement process, further supporting the conclusion of higher vertical displacement efficiency.

Figure 25 compares cumulative oil production between horizontal (X, Y) and vertical (Z) directions. The data indicate greater oil mobilization in the vertical direction, reduced residual oil saturation, and significantly improved oil recovery. In contrast, horizontal flow experiences faster water saturation increase and earlier water breakthrough, leading to lower displacement efficiency. These observations align with the results shown in Figure 23 and Figure 24, confirming that although vertical permeability is lower, lamination barriers optimize fluid distribution, achieving higher recovery. Relative permeability curves generated using the AHM method outperform the JBN method in representing two-phase flow regions, providing a reliable basis for refined reservoir characterization.

Note: Due to the limited number of anisotropic displacement experiments, and because these results are deterministic model outputs, uncertainty (error) bars are not provided.

3.2. Microscopic Mechanism Analysis of Anisotropic Relative Permeability Curves

To investigate the microscopic influence of bedding structure and displacement direction on oil–water flow behavior, the cubic core samples were first saturated with oil and subjected to constant-rate water flooding along a selected direction, with a displacement volume exceeding 30 PV. Before and after water flooding, the cores were scanned using NMR T₂ spectroscopy and CT imaging to obtain detailed information on fluid distribution and saturation changes within the pore space. The procedure was then repeated along the other two directions, allowing comparison of imaging results to analyze the distribution of residual oil under different flow orientations.

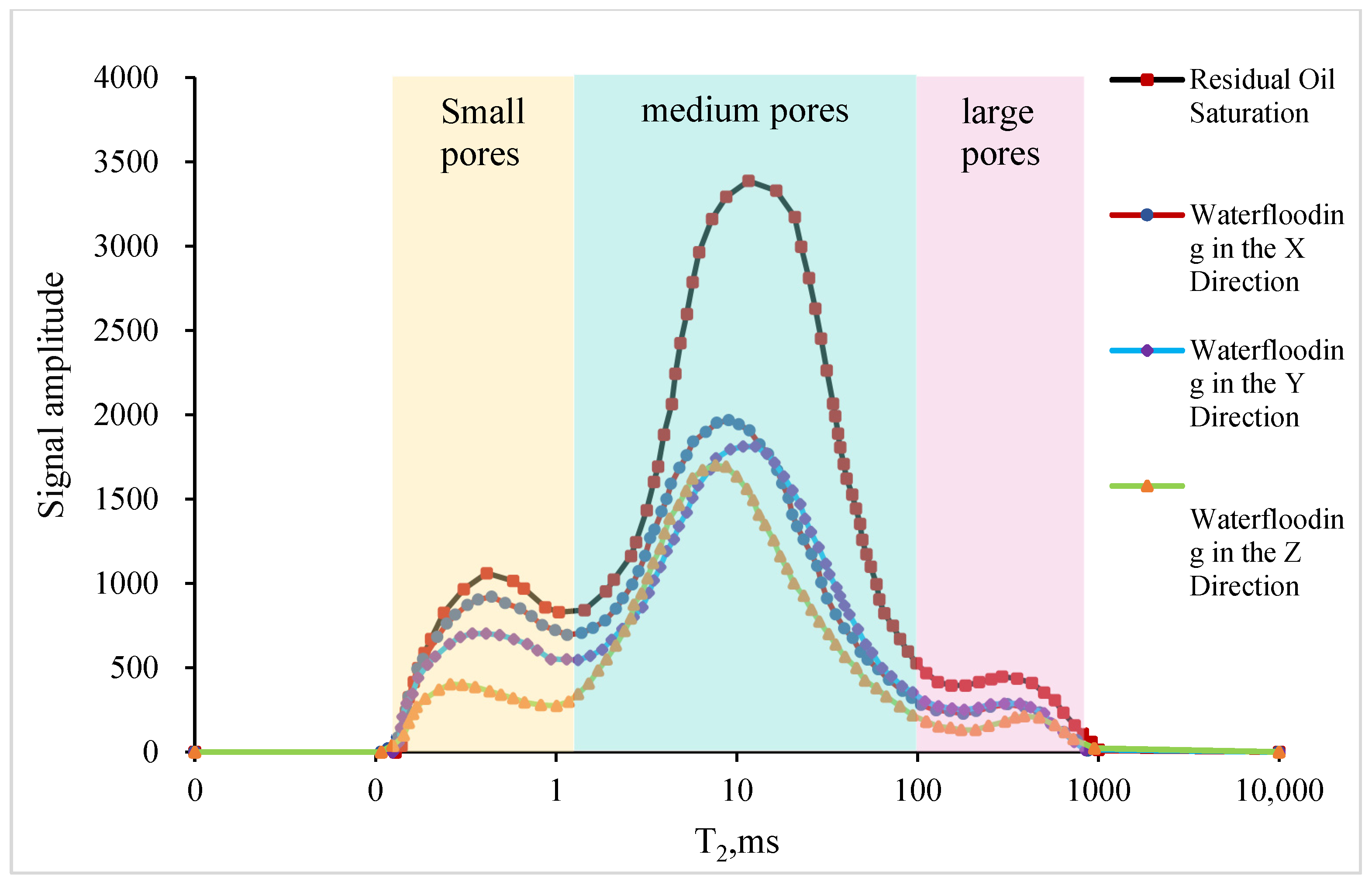
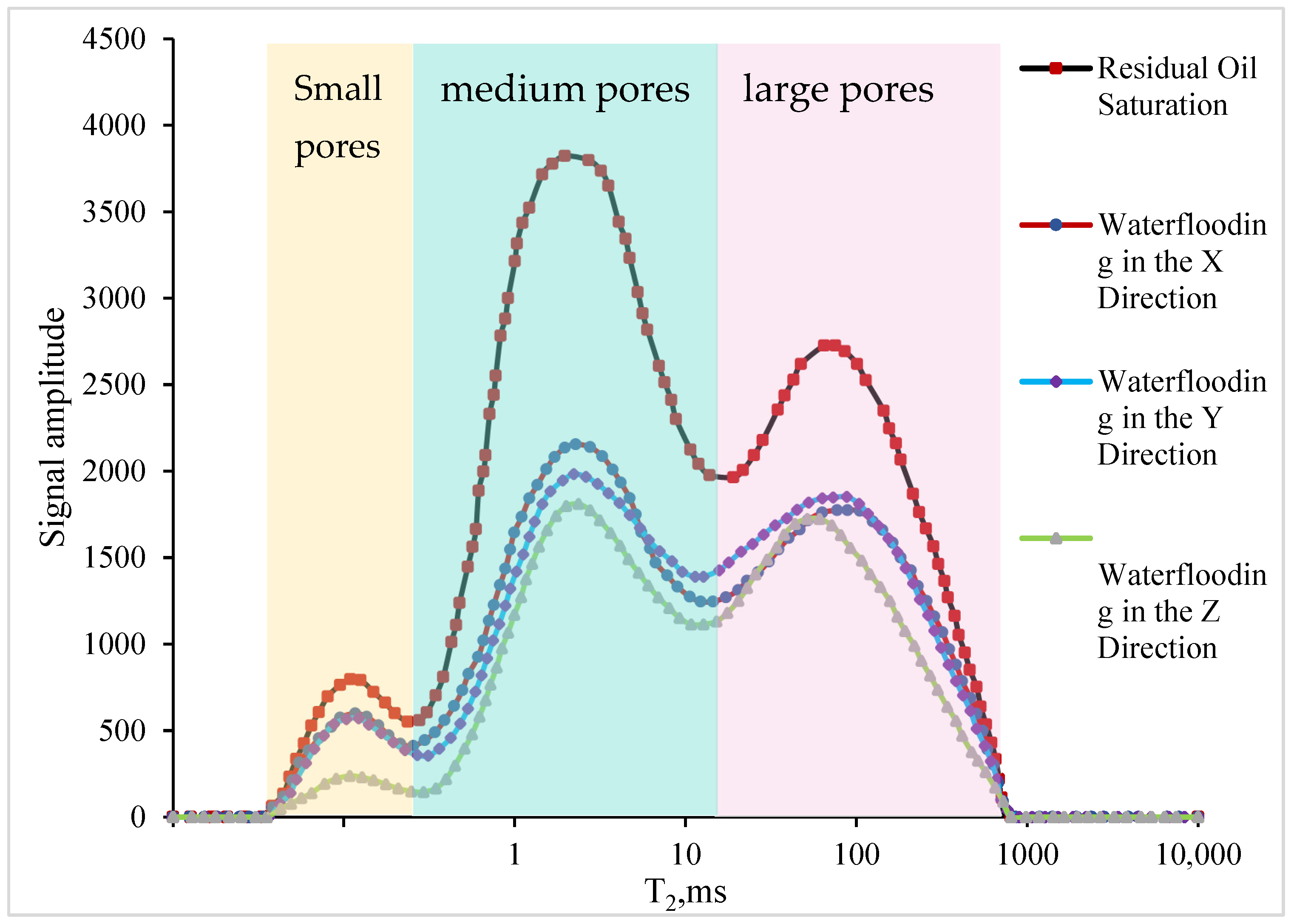
3.2.1. Analysis of NMR Results

The displacement process of the core with tabular cross-bedding is illustrated in Figure 26. Analysis of Figure 27 indicates that as the water-flooding direction increasingly deviates from the bedding orientation, the mobilization of residual oil in smaller pores is significantly enhanced. The amplitude of the T₂ spectral peaks corresponding to these small pores decreases markedly, demonstrating more effective displacement of residual oil. Overall residual oil saturation is significantly reduced, reflecting higher oil recovery efficiency. These results suggest that increasing the angle between the flooding direction and bedding promotes improved fluid mobility and displacement efficiency in small pore spaces.

Figure 28 NMR imaging results of the tabular cross-bedding core. The experiment demonstrates that core-scale heterogeneity significantly influences the distribution of residual oil; when the water flooding direction forms a larger angle with the bedding, the swept volume is more uniform, whereas at smaller angles, low-permeability layers near the bedding exhibit lower water saturation and higher residual oil saturation.

The displacement process of the parallel-laminated core is illustrated in Figure 29. Figure 30 shows that during water flooding along the horizontal direction, the distribution of residual oil in small, medium, and large pores exhibits minimal variation, with residual oil saturations tending to be uniform. In contrast, when water flooding is conducted perpendicular to the bedding planes, the mobilization of residual oil in small pores is significantly enhanced, resulting in an overall lower residual oil saturation compared to horizontal water flooding. The experimental results are highly consistent with this observation, confirming the reliability of the experiments and the accuracy of the model.

Figure 31 shows the NMR imaging results of the horizontally laminated core. The results indicate that after water flooding along the two horizontal directions, both the T₂ spectra and imaging exhibit minimal differences, suggesting that flow in the horizontal directions tends to channel through high-permeability pathways, leaving oil trapped in low-permeability zones such as small pores. In contrast, flooding perpendicular to the lamination results in a more uniform sweep; the T₂ spectra show significantly increased mobilization of oil in small pores, indicating that although the overall flow capacity is reduced, delayed water breakthrough enhances oil recovery efficiency.

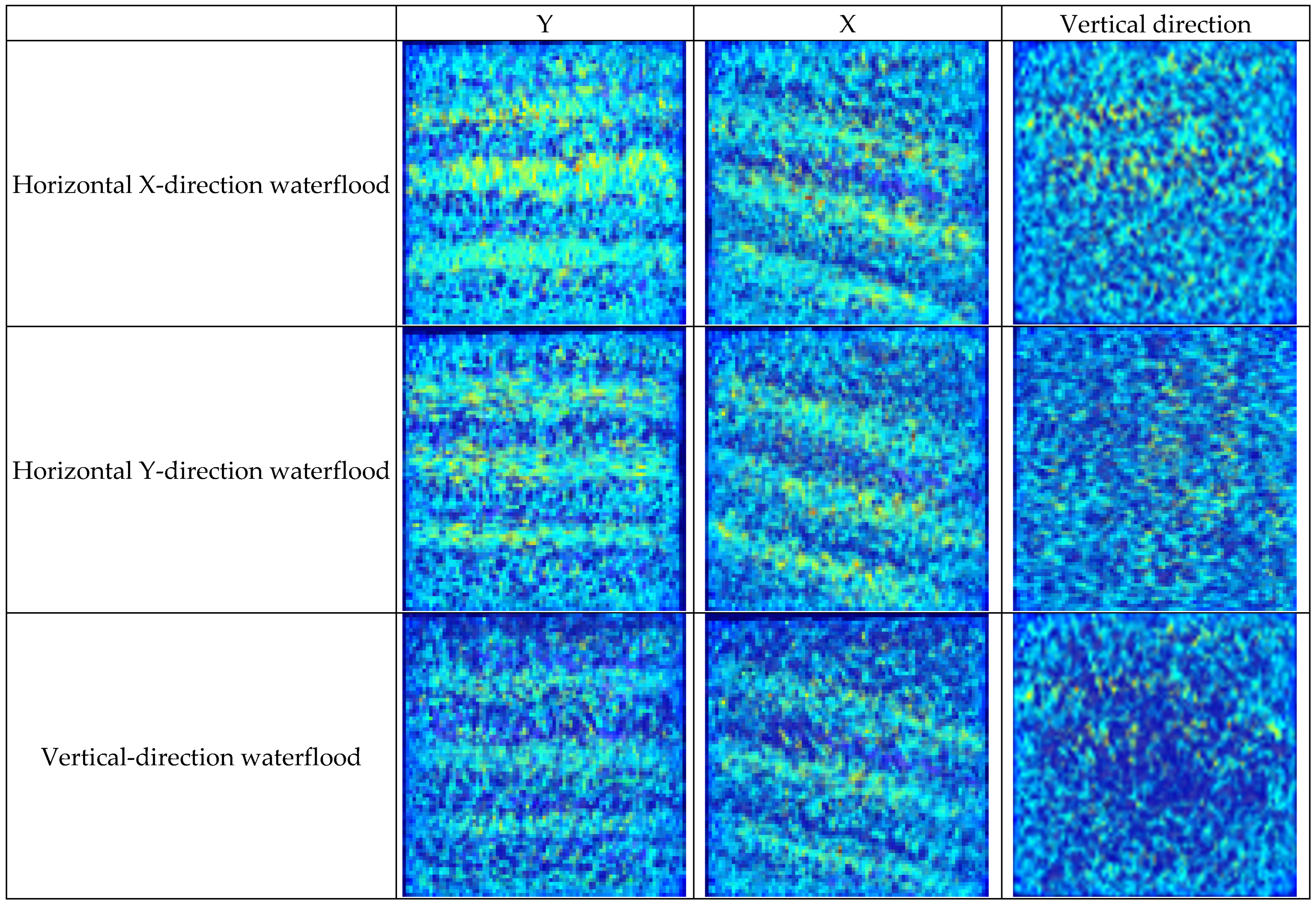
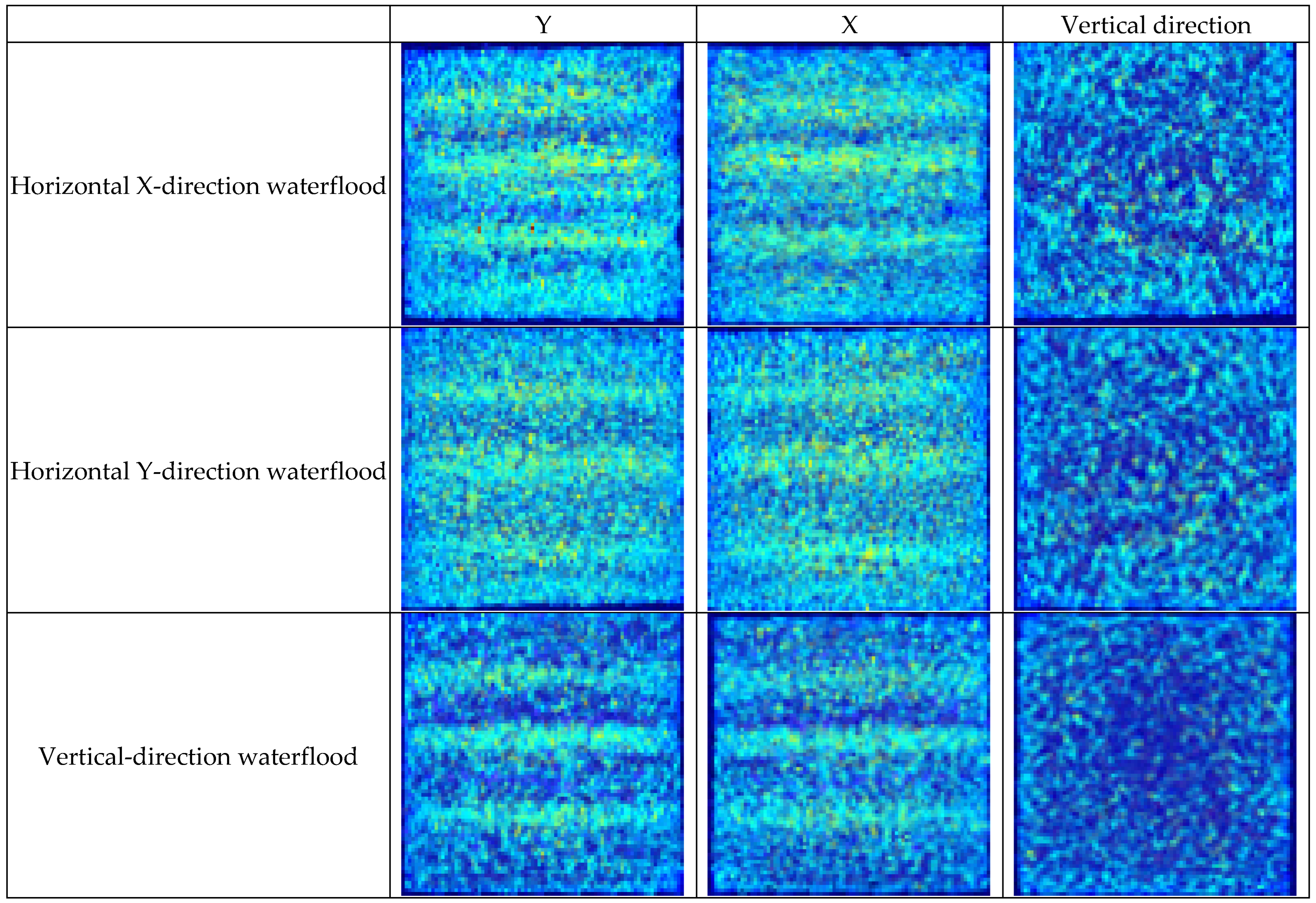
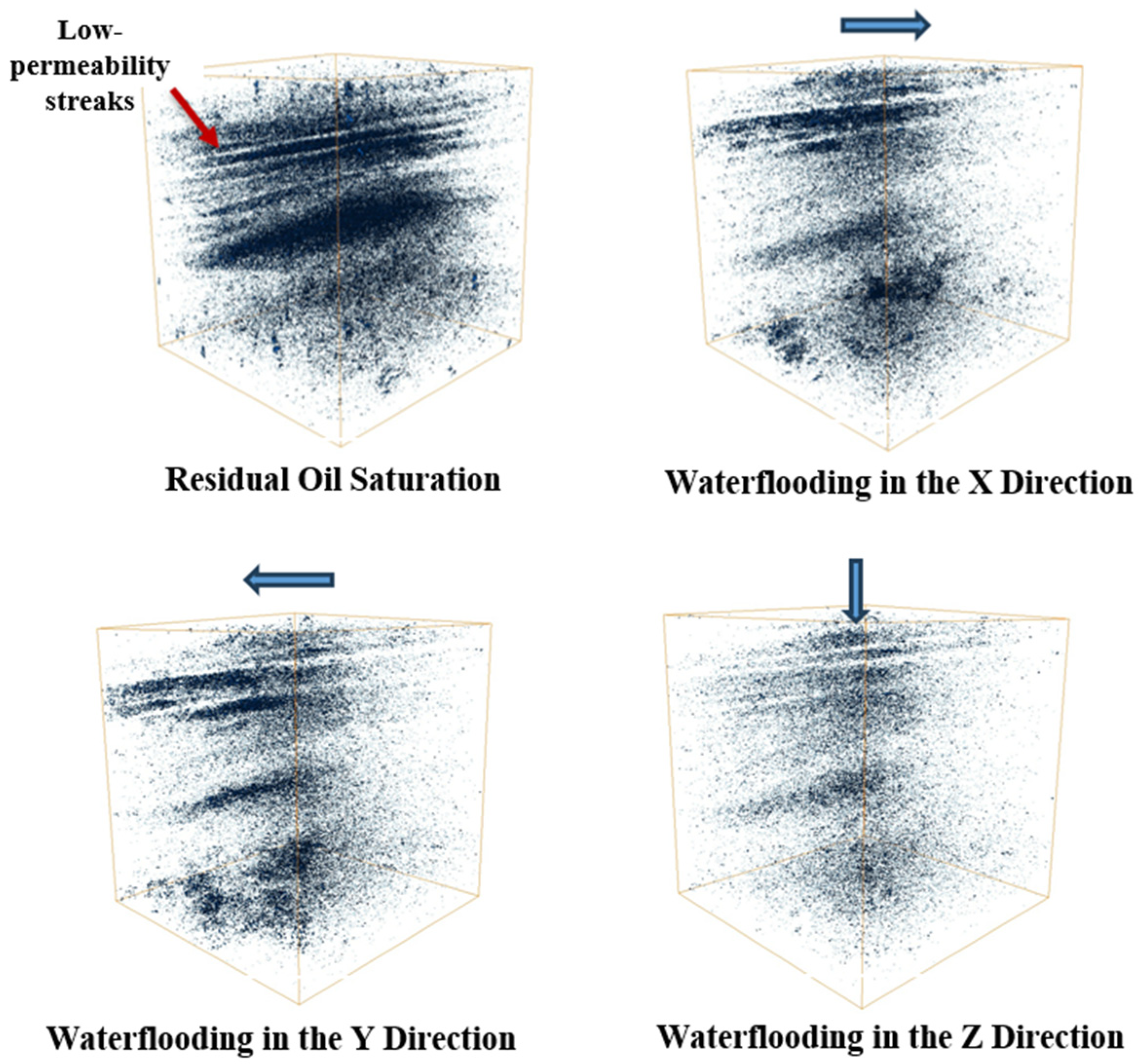
3.2.2. CT Scan Results Analysis

In summary, for both the laminated cross-bedded and parallel-bedded cores, displacement efficiency is highest along the direction perpendicular to the bedding planes (Z-direction), reaching 71.6%, with a wide sweep area and a relatively uniform residual oil distribution. Displacement efficiencies in the X and Y directions are 54.7% and 56.3%, respectively. Figure 32 presents the CT imaging results for different displacement directions, showing that residual oil tends to accumulate in low-permeability zones and exhibits a patchy distribution. This indicates that perpendicular-to-bedding displacement can overcome the limitations of capillary forces and permeability heterogeneity, enhancing oil phase mobility. Figure 33 compares displacement efficiencies, confirming that waterflooding in the Z-direction (perpendicular to bedding) achieves the highest oil recovery, consistent with the physical displacement experiments.

Note: The arrow indicates different displacement directions.

Figure 33. Comparison of oil recovery efficiency.

Figure 33. Comparison of oil recovery efficiency.

4. Conclusions

This study systematically investigated the effects of displacement direction and lamination angle on two-phase oil–water flow behavior and residual oil distribution by conducting anisotropic displacement experiments on interbedded and parallel laminated cores, combined with JBN and AHM relative permeability methods as well as NMR and CT imaging analyses. The main conclusions are as follows:

(1).

Significant influence of displacement direction on oil recovery: The experiments demonstrate that increasing the angle between the displacement direction and lamination significantly enhances oil recovery. In interbedded laminated cores, oil recovery in the Z-direction (perpendicular to lamination, 90° angle) reached 75.09%, markedly higher than the X-direction (along lamination, 53.95%). For parallel laminated cores, vertical displacement improved recovery by 18.06% compared to horizontal flow. Vertical displacement promotes fluid penetration across lamination intersections, mobilizes oil in small pores, and reduces residual oil saturation. NMR and CT imaging confirm the uniformity of vertical displacement, providing practical guidance for optimizing water injection directions.

(2).

AHM method improves relative permeability accuracy: Compared to the conventional JBN method, the AHM technique, through numerical simulation and optimization algorithms, significantly enhances the precision of anisotropic relative permeability curves. Fitted curves closely match historical production data, particularly in predicting two-phase co-flow regions and endpoint saturations. For interbedded laminated cores, the co-flow region in the Z-direction reached 57.1%, much higher than 39.7% in the X-direction. By accounting for capillary forces and permeability heterogeneity, the AHM method is well-suited for complex reservoirs and provides reliable parameters for reservoir numerical modeling.

(3).

Microscale imaging reveals pore-scale flow mechanisms: NMR T₂ spectra and CT scans indicate that displacement direction strongly affects pore-scale fluid distribution. Vertical-to-lamination displacement markedly increases oil mobilization in small pores, lowering residual oil saturation to 22% with more uniform distribution. Horizontal displacement favors channeling, leaving residual oil concentrated in low-permeability zones. CT imaging shows that vertical displacement overcomes capillary restrictions and enhances oil–water interfacial shear. These microscale insights provide direct evidence of anisotropic flow mechanisms, supporting optimized reservoir development strategies.

Limitations: The experimental samples are centimeter-scale, limiting direct extrapolation to field-scale reservoir management. Geological conditions in actual reservoirs may include fractures, heterogeneous deposition, and multi-layer interactions, which differ from the controlled laboratory environment. Moreover, lab-controlled temperature and pressure may not fully replicate field conditions, potentially introducing deviations in predictive applicability.