Numerical Improvement of Battery Thermal Management Integrating Phase Change Materials with Fin-Enhanced Liquid Cooling
Abstract
1. Introduction
2. Numerical Methodology
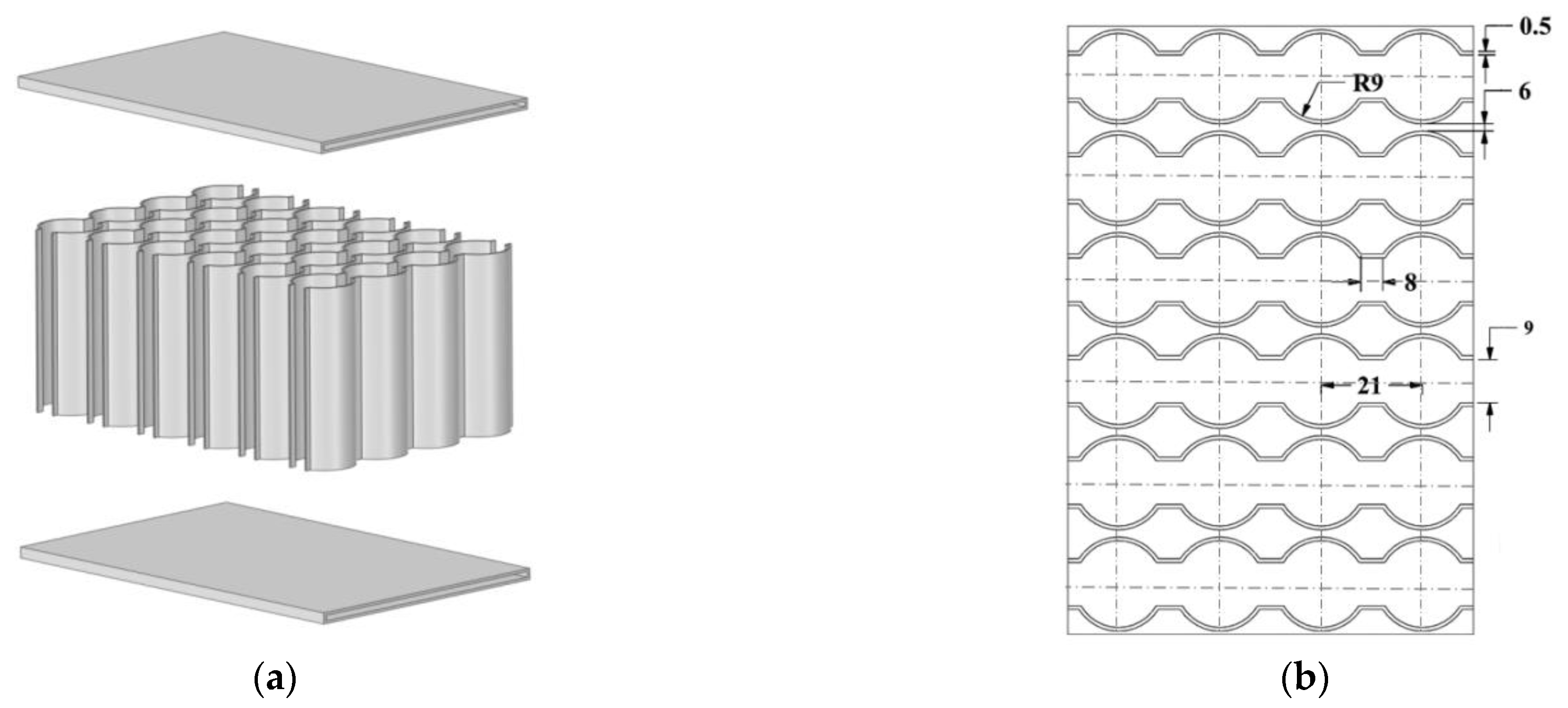
2.1. Physical Model
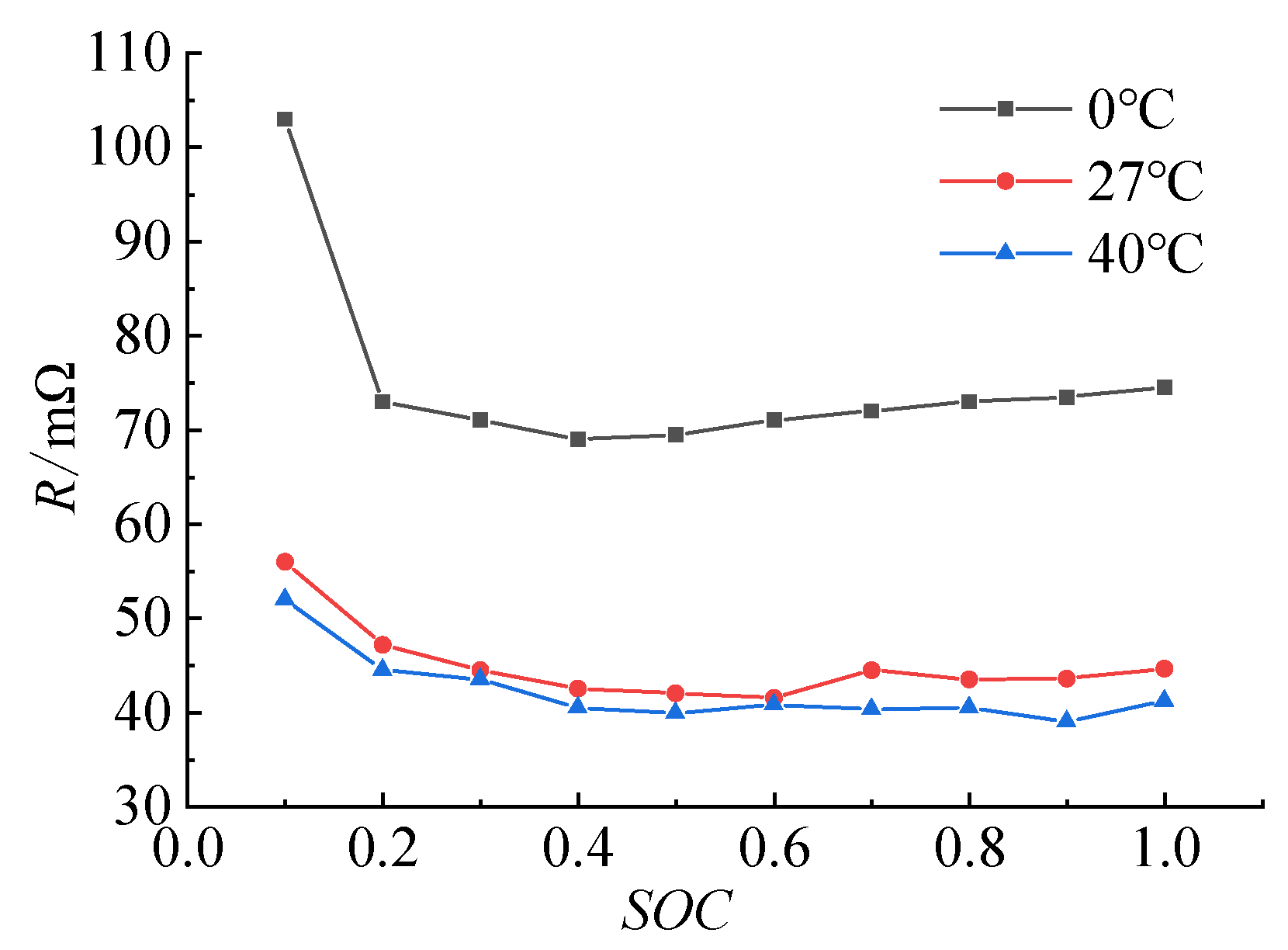
2.2. Battery Heat Generation Model
2.3. Heat Transfer Model and Boundary Conditions
- (a)
- The PCM has uniform and isotropic physical properties;
- (b)
- The specific heat capacity and thermal conductivity of the PCM are constant and independent of temperature;
- (c)
- The density and volume of the PCM remain unchanged during phase change;
- (d)
- The PCM remains stationary within the battery pack, and its internal heat conduction follows Fourier’s law, like solid materials;
- (e)
- Radiative heat transfer between the battery pack and the environment is negligible.
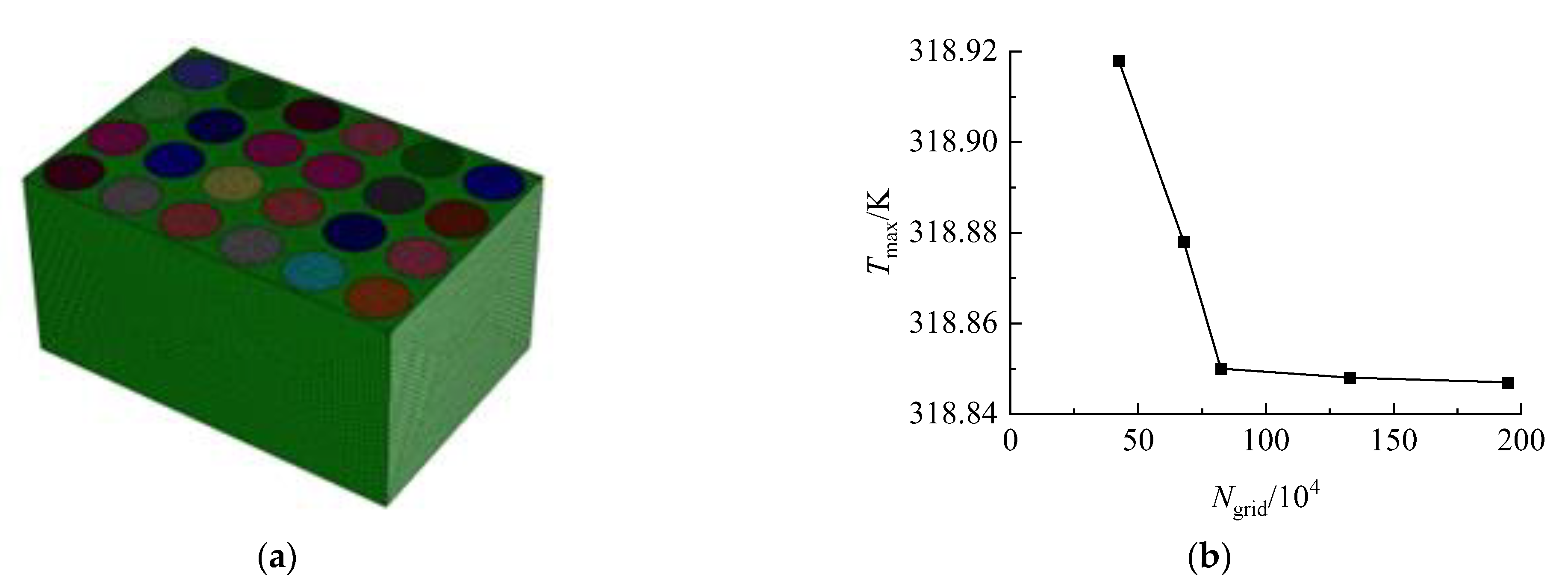
2.4. Mesh Model and Grid Independence Verification
2.5. Model Validation
3. Results and Analysis
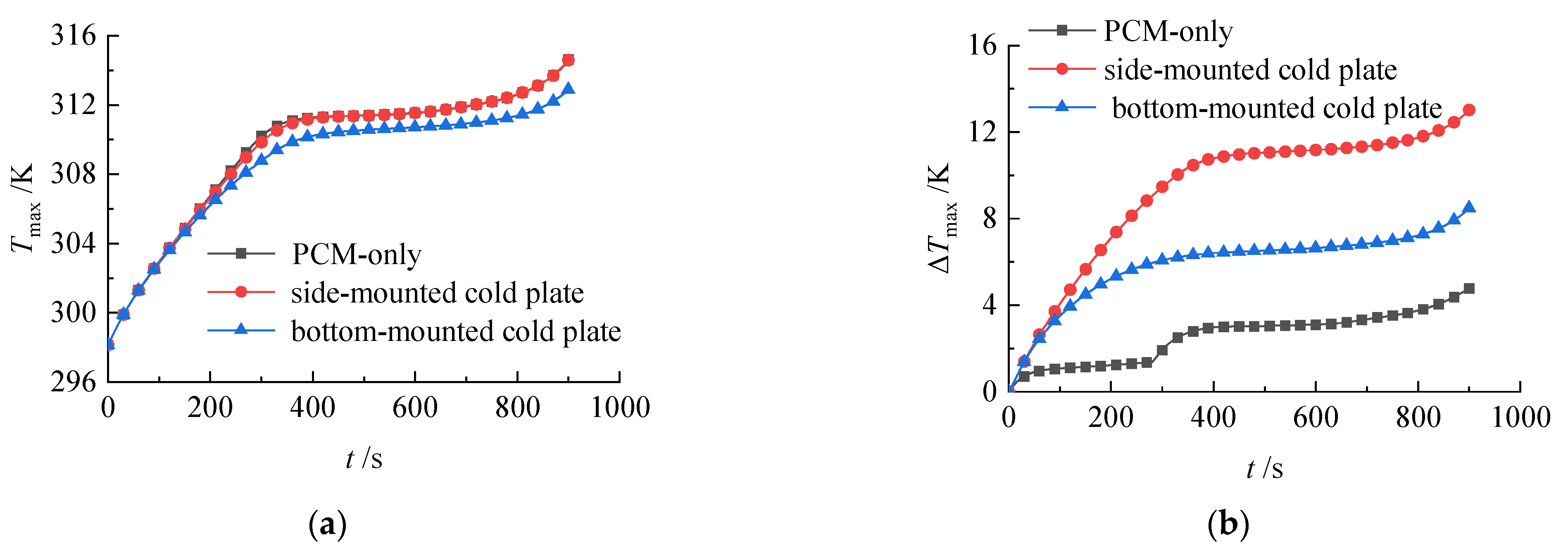
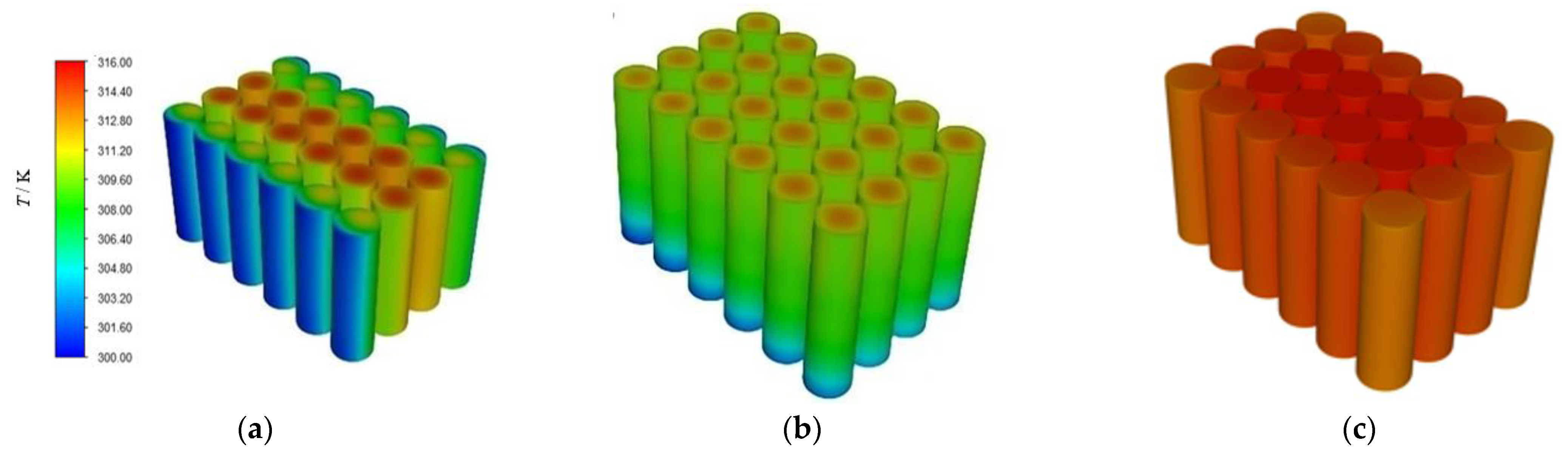
3.1. Thermal Management Performance of PCM–Conventional Liquid Cooling Hybrid System
3.2. Thermal Management Performance of PCM–Fin Enhanced Liquid Cooling Hybrid System
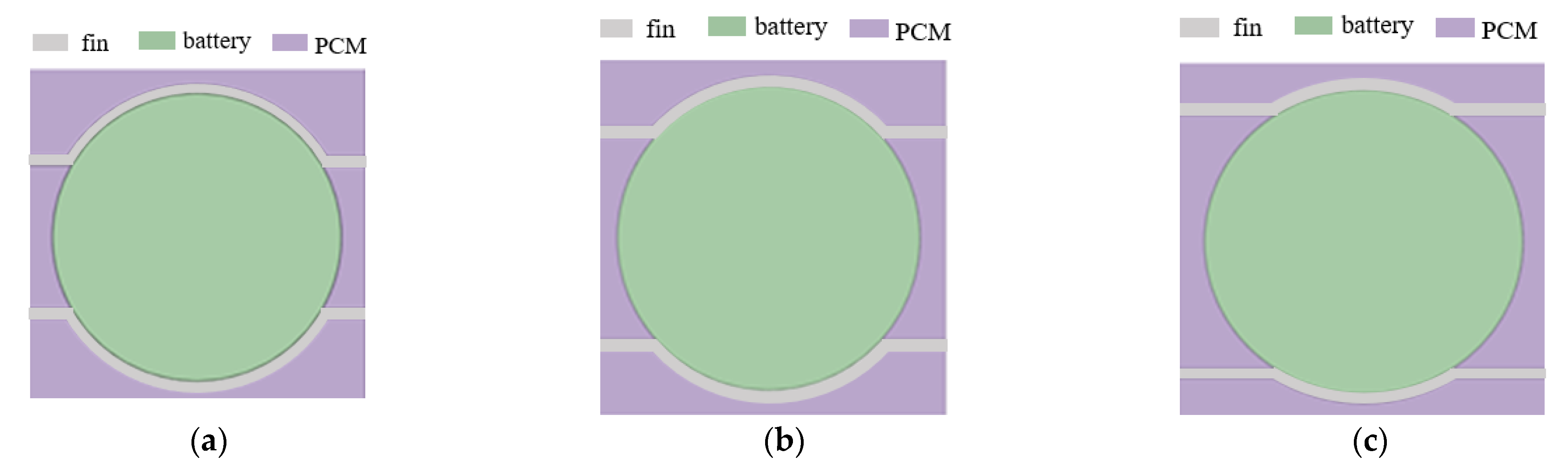
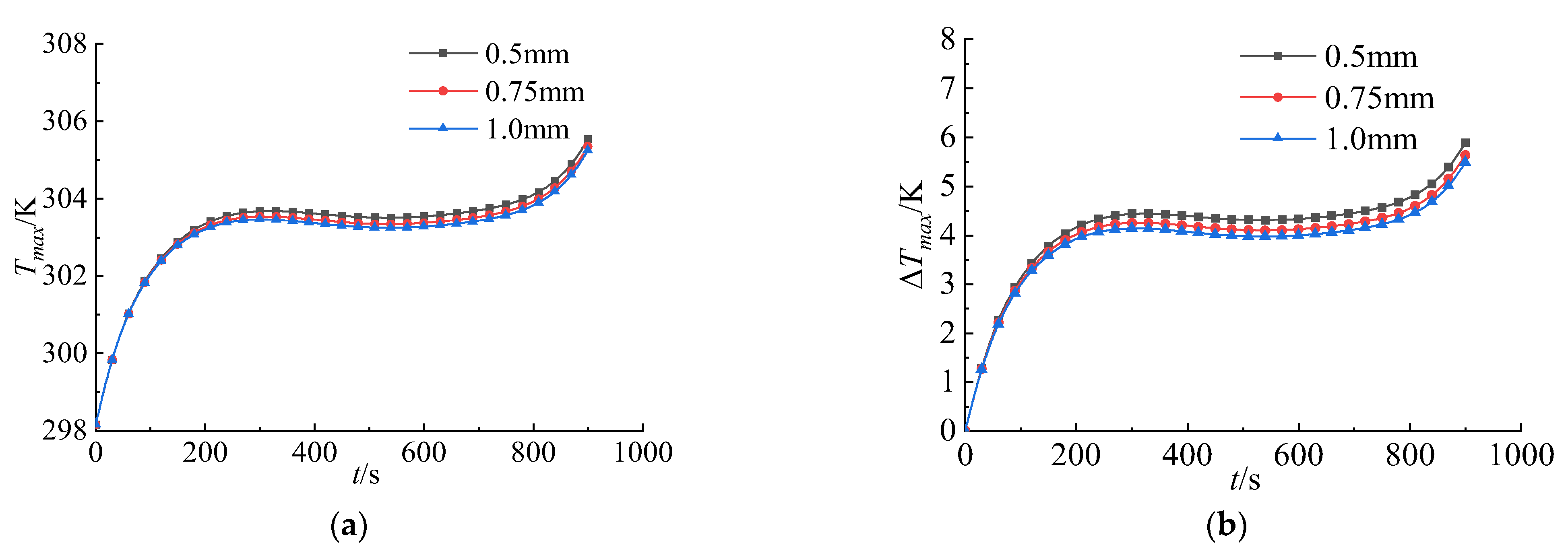
3.2.1. Influence of Fin Spacing and Fin Thickness on Temperature Distribution
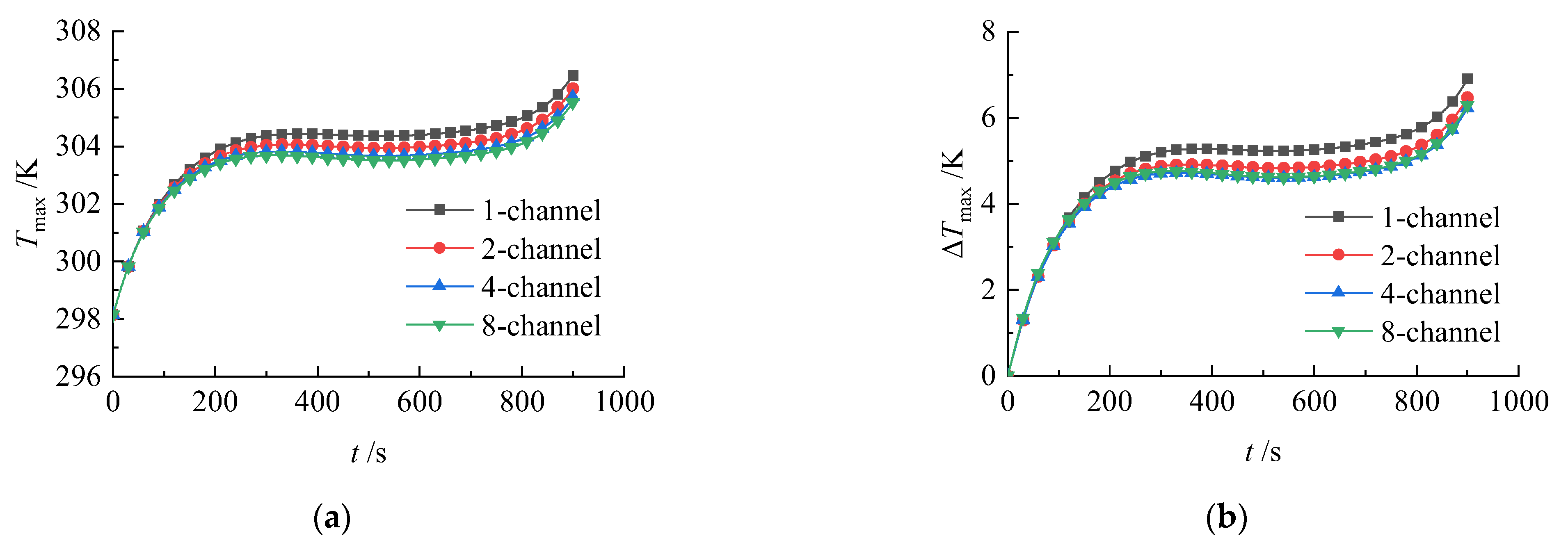
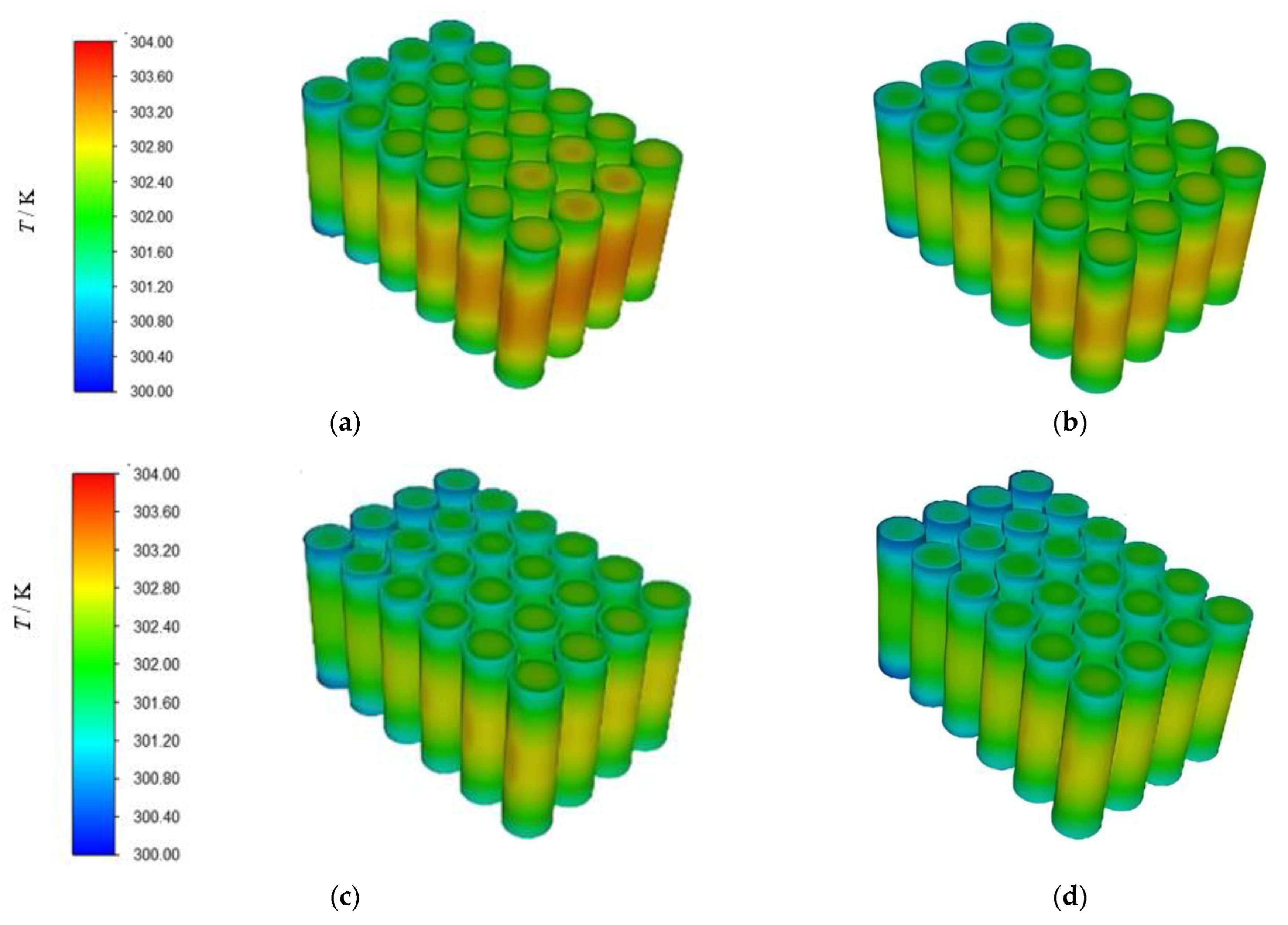
3.2.2. Effect of Channel Quantity on Battery Pack Temperature Distribution
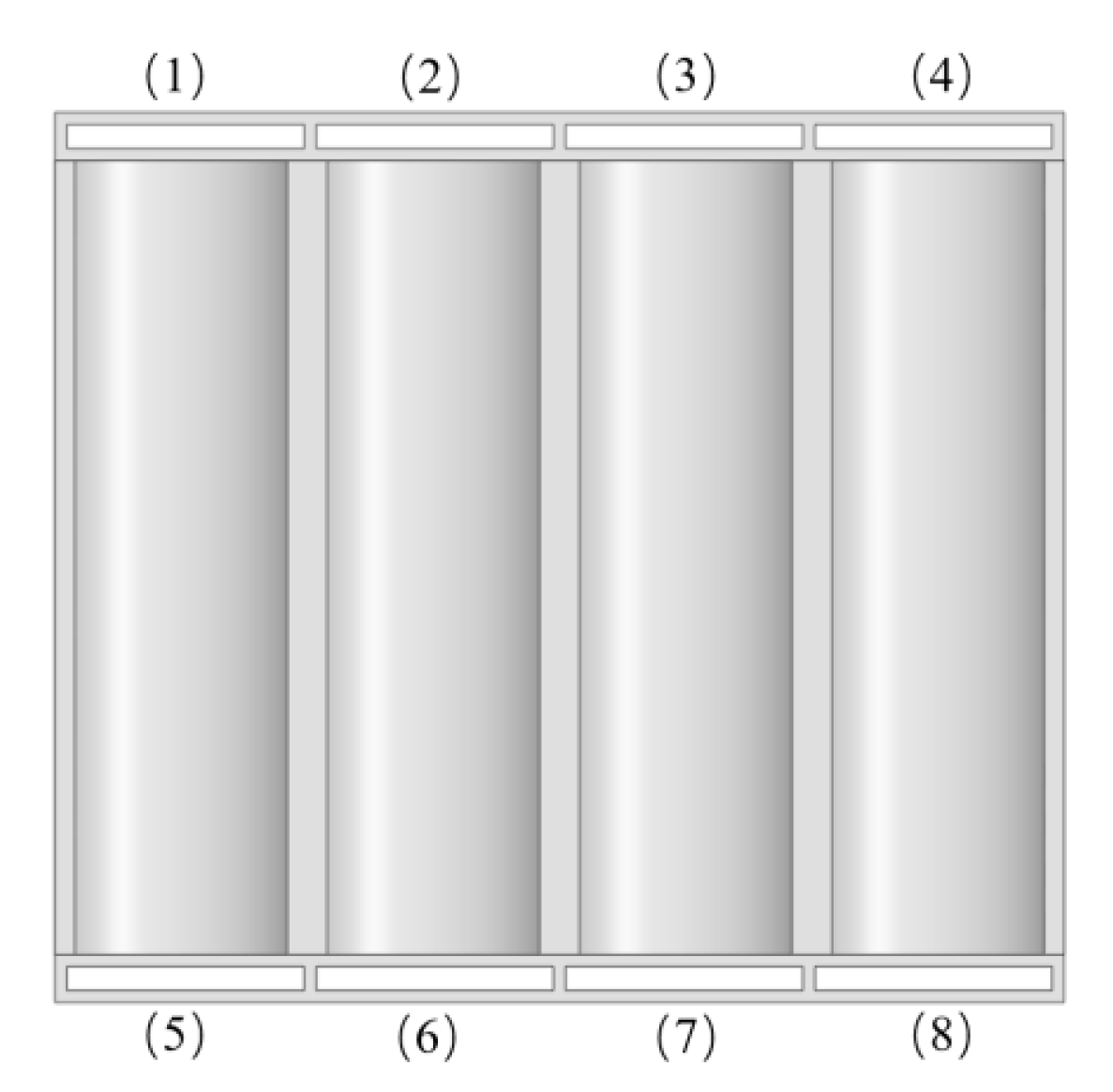
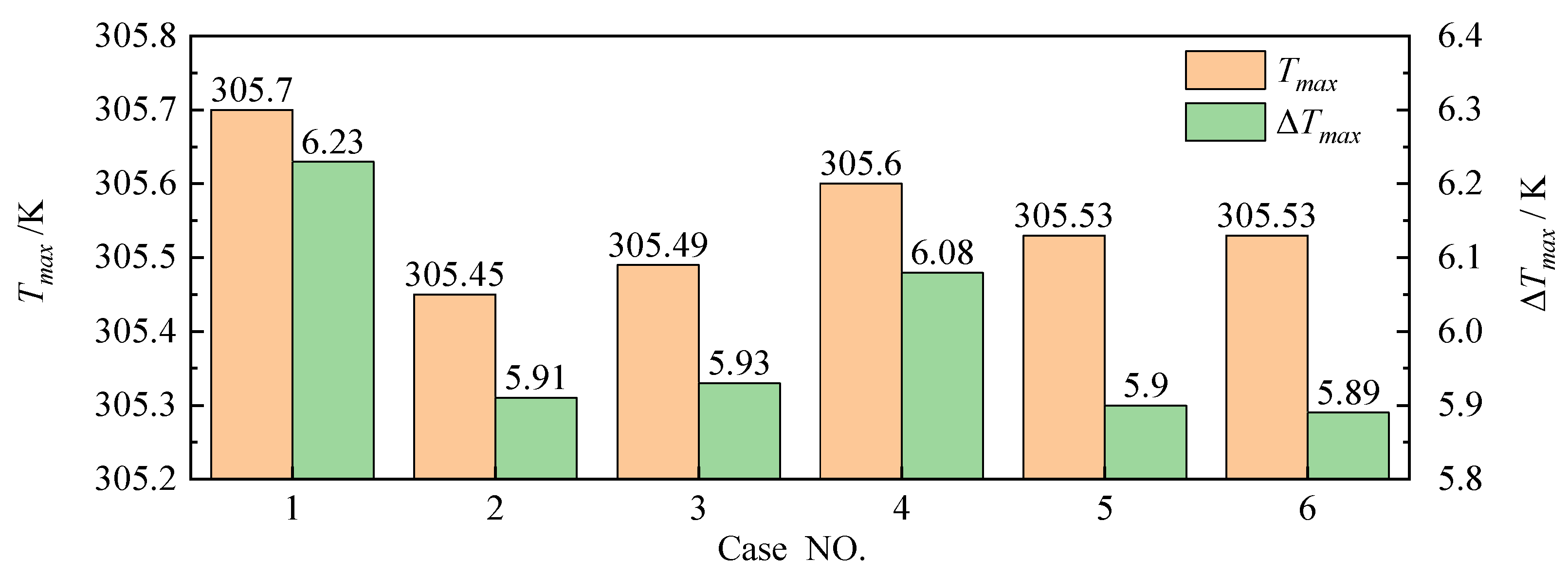
3.2.3. Effect of Coolant Flow Direction on Battery Temperature Distribution
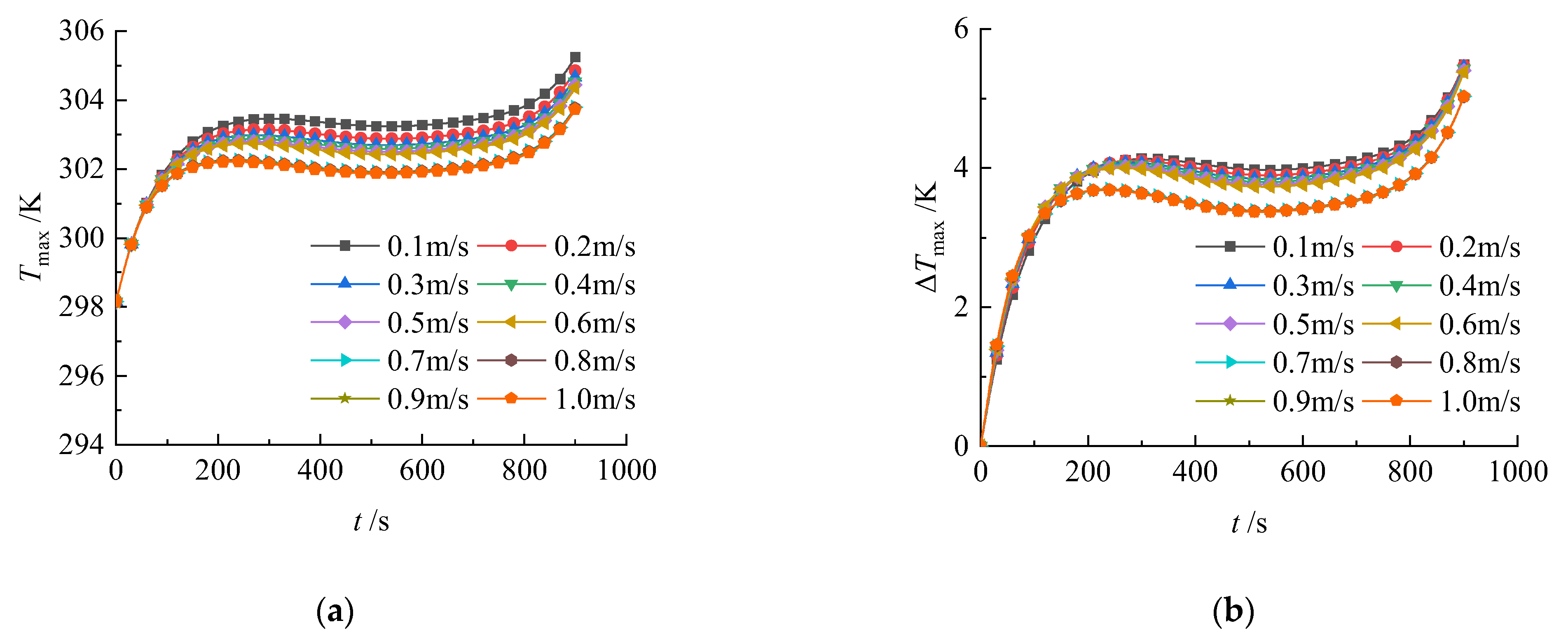
3.2.4. Effect of Coolant Flow Velocity on Battery Temperature Distribution
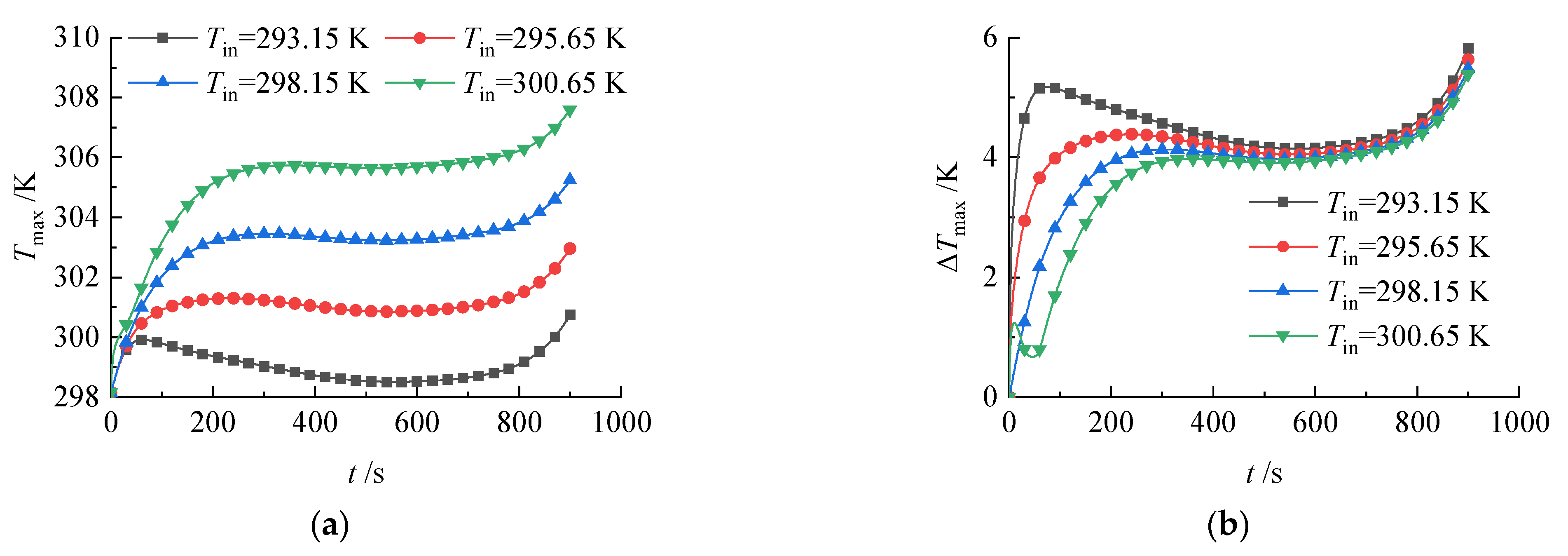
3.2.5. Effect of Coolant Inlet Temperature on Battery Temperature Distribution
4. Conclusions
- (1)
- Limited effectiveness of basic PCM–liquid cooling: During the 4C discharge process, when only side-mounted and bottom-mounted cold plates are added to the battery pack filled with phase change material (PCM), the maximum temperature of the battery pack decreases by merely 1.8 K. Concurrently, the temperature non-uniformity significantly intensifies, resulting in a maximum temperature difference exceeding 10 K within the battery pack.
- (2)
- Superior performance of fin-enhanced hybrid system: The aluminum heat dissipation fin dual cooling plates, with a thickness of 0.5 mm and spacing of 9 mm, optimize the heat transfer path through their design. This configuration reduces the maximum temperature to 305.58 K while lowering the maximum temperature difference to 5.99 K. Further optimized parameters, including alternating flow directions, four-channel cooling plates, and a flow velocity of 0.7 m/s, achieve greater performance enhancement, maintaining the maximum temperature difference below 5 K.
- (3)
- Diminishing returns at higher flow velocities: Increasing the flow rate enhances cooling efficiency up to 0.7 m/s. Beyond this, further increasing the coolant speed yields negligible improvements due to the inherent thermal conductivity limitations of the battery and PCM.
- (4)
- Trade-off in coolant temperature selection: While lower inlet temperatures reduced the maximum temperature among the batteries in the pack, excessively low temperatures could lead to higher temperature difference, particularly during early discharge stages. At an inlet temperature of 300.65 K, the maximum temperature is 310.01 K, and the maximum temperature difference is 5.38 K. In contrast, at an inlet temperature of 293.15 K, the maximum temperature is 299.91 K, and the maximum temperature difference is 5.82 K. Thus, a 7.5 K reduction in inlet temperature leads to a 10.1 K decrease in maximum temperature and a 0.44 K increase in maximum temperature difference.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Aneke, M.; Wang, M. Energy storage technologies and real life applications—A state of the art review. Appl. Energy 2016, 179, 350–377. [Google Scholar] [CrossRef]
- Zhao, R.; Gu, J.; Liu, J. Performance assessment of a passive core cooling design for cylindrical lithium-ion batteries. Int. J. Energy Res. 2018, 42, 2728–2740. [Google Scholar] [CrossRef]
- Zhao, R.; Gu, J.; Liu, J. An experimental study of heat pipe thermal management system with wet cooling method for lithium ion batteries. J. Power Sources 2015, 273, 1089–1097. [Google Scholar] [CrossRef]
- Zhang, S.T. Degradation Law and Failure Mechanism of Li-Ion Batteries Under High Temperature Conditions. Master’s Thesis, Harbin University of Science and Technology, Harbin, China, 2023. [Google Scholar]
- Mei, W.; Chen, H.; Sun, J.; Wang, Q.S. Numerical study on tab dimension optimization of lithium-ion battery from the thermal safety perspective. Appl. Therm. Eng. 2018, 142, 148–165. [Google Scholar] [CrossRef]
- Wang, M.M.; Sun, L.; Guo, P.Y.; Guo, D.L.; Zhao, L.T.; Jin, Y. Overcharge and thermal runaway characteristics of lithium iron phosphate energy storage battery modules based on gas online monitoring. High Volt. Eng. 2021, 47, 279–286. [Google Scholar]
- Zhou, G.; Huang, Q.; Zhang, Q.; Niu, C.X.; Lu, H.H.; Yang, S.Q.; Liu, Y.; Wei, Z.K.; Li, S.L.; Kong, Y. Thermal insulation phase-change hydrogel with enhanced mechanical properties for inhibiting thermal runaway propagation in lithium-ion battery module. J. Energy Storage 2024, 102, 114102. [Google Scholar] [CrossRef]
- Sun, Z.Y.; Wang, Z.P.; Liu, P.; Zhang, Z.S.; Chen, Y.; Qu, C.H. Overview of fault diagnosis in new energy vehicle power battery system. J. Mech. Eng. 2021, 57, 87–104. [Google Scholar]
- Liu, B.J.; Wang, L.W.; Wu, Y.Y.; Liu, Y.C.; Zhong, G.B.; Xiang, H.F. Advances in thermal management of lithium-ion batteries. CIESC J. 2024, 75, 4413–4431. [Google Scholar]
- Wang, B.; Sun, C.C.; Wang, Y.L.; Chen, X.Y.; Zhou, Q.P. Thermal insulation and preheating performance of lithium battery based on phase change material. Chem. Eng. 2022, 50, 23–28. [Google Scholar]
- Zhu, X.Q.; Wang, Z.P.; Wang, H.; Wang, C. Review of thermal runaway and safety management for lithium-ion traction batteries in electric vehicles. J. Mech. Eng. 2020, 56, 91–118. [Google Scholar]
- Jin, Z.H.; Yuan, Q.; Han, Z.N.; Xue, F. Thermal management performance analysis of lithium battery with flat heat pipe and liquid cooling. Chem. Eng. 2023, 51, 41–45. [Google Scholar]
- Hendrayanto, A.P.; Fathoni, M.A.; Aliefiansyah, S.M.; Nandy, P. Experimental study on start-up and heat transfer characteristics in loop heat pipes with dual heat sources for battery thermal management system. Therm. Sci. Eng. Prog. 2024, 55, 102980. [Google Scholar] [CrossRef]
- Lin, T.; Liu, Q.Y.; Yang, G.; Han, F.Q. Study on thermal management circuit and temperature control effect of power batteries. Chin. J. Power Sources 2019, 43, 849–852. [Google Scholar]
- Wen, K.; Fu, X.F.; Pei, F. Research on the thermal management safety of the fast-charging power battery management system. Energy Rep. 2023, 10, 3289–3296. [Google Scholar] [CrossRef]
- Deng, J.; Li, Z.; Chen, J. Experiment study of pseudo-passive heat removal system for power battery thermal runaway propagation inhibition. Appl. Therm. Eng. 2024, 253, 123777. [Google Scholar] [CrossRef]
- Sun, Y.; Tao, L.R.; Lei, L.X.; Tao, H. Simulation analysis of thermal management system of parallel liquid cooled battery. Agric. Equip. Veh. Eng. 2021, 59, 19–24. [Google Scholar]
- Zhang, Z.; Li, Y. Experimental study of a passive thermal management system using copper foam-paraffin composite for lithium-ion batteries. Energy Procedia 2017, 142, 2403–2408. [Google Scholar] [CrossRef]
- Ye, Y.H.; Saw, L.H.; Shi, Y.; Tay, A.A.O. Numerical analyses on optimizing a heat pipe thermal management system for lithium-ion batteries during fast charging. Appl. Therm. Eng. 2015, 86, 281–291. [Google Scholar] [CrossRef]
- Zhang, W.C.; Liang, Z.C.; Yin, X.X.; Ling, G.Z. Avoiding thermal runaway propagation of lithium-ion battery modules by using hybrid phase change material and liquid cooling. Appl. Therm. Eng. 2021, 184, 116380. [Google Scholar] [CrossRef]
- Yang, W.; Zhou, F.; Liu, Y.C.; Xu, S.; Chen, X. Thermal performance of honeycomb-like battery thermal management system with bionic liquid mini-channel and phase change materials for cylindrical lithium-ion battery. Appl. Therm. Eng. 2021, 188, 116649. [Google Scholar] [CrossRef]
- Afaynou, I.; Faraji, H.; Choukairy, K.; Khallaki, K.; Akrour, D. Effectiveness of a PCM-based heat sink with partially filled metal foam for thermal management of electronics. Int. J. Heat Mass Transf. 2024, 235, 126196. [Google Scholar] [CrossRef]
- Chen, M.Y. Research on 18650 Lithium-Ion Battery Compound Thermal Management System Based on Direct Liquid Cooling-Air Cooling. Master’s Thesis, Jiangsu University of Technology, Changzhou, China, 2022. [Google Scholar]
- Chen, H.F. Performance and Structural Optimization of Low-Temperature Thermal Management System for Lithium-Ion Batteries Based on Composite Phase Change Materials. Master’s Thesis, Lanzhou University of Technology, Lanzhou, China, 2023. [Google Scholar]
- Chen, C. Research on Heat Dissipation and Optimization Design of Square Power Lithium Battery for New Energy Vehicle. Master’s Thesis, Shanghai Institute of Technology, Shanghai, China, 2020. [Google Scholar]


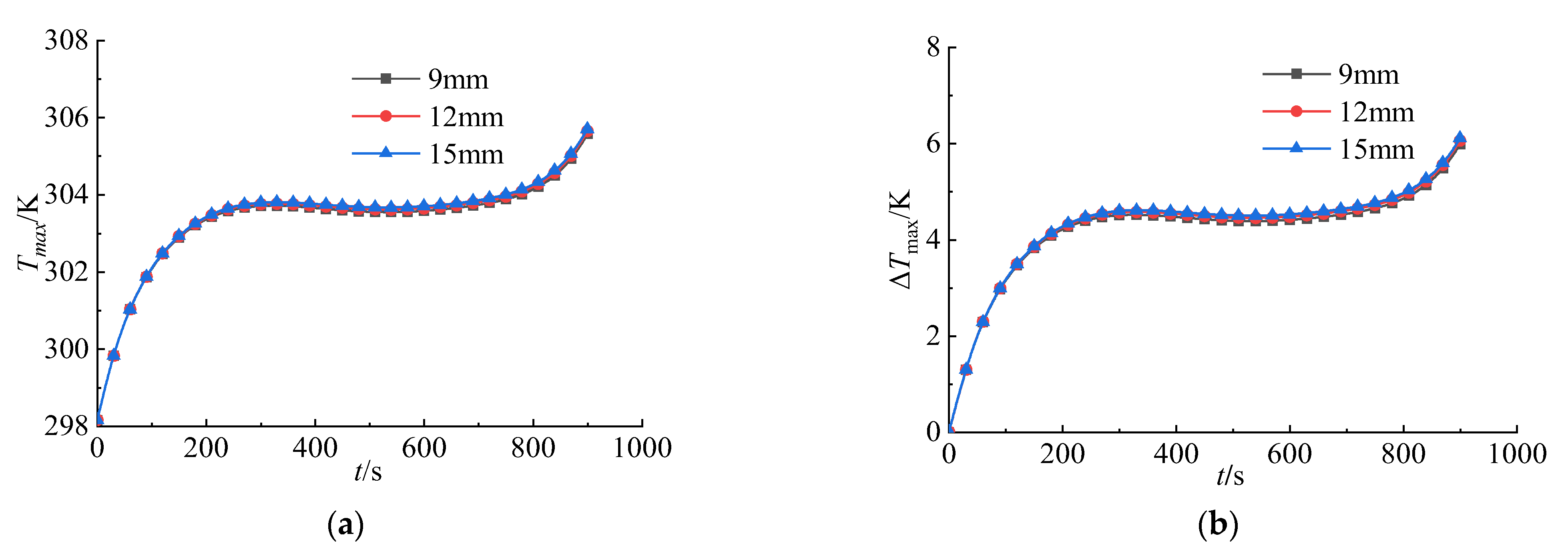


| ρb/(kg·m)−3 | Cp, b/(J kg−1·K−1) | λa, b/(W·m−1·K−1) | λr, b/(W·m−1·K−1) |
|---|---|---|---|
| 2673.55 | 1034.18 | 20.19 | 0.87 |
| ρpcm/(kg·m)−3 | Cp, pcm/(J kg−1·K−1) | Lpcm/(J·kg−1) | Tom, pcm/K | λpcm/(W·m−1·K−1) |
|---|---|---|---|---|
| 814 | 2150 | 182200 | 308.15 | 0.33 |
| T/°C | ζ1 | ζ2 | ζ3 | ζ4 | ζ5 | ζ6 | ζ7 |
|---|---|---|---|---|---|---|---|
| 0 | 5.764 | −20.740 | 29.810 | −21.850 | 8.616 | −1.734 | 0.209 |
| 27 | 2.608 | −8.614 | 11.180 | −7.299 | 2.578 | −0.493 | 0.086 |
| 40 | 2.799 | −9.076 | 11.560 | −7.389 | 2.525 | −0.458 | 0.079 |
| Channel No. | Case 1 | Case 2 | Case 3 | Case 4 | Case 5 | Case 6 |
|---|---|---|---|---|---|---|
| (1) | Inlet | Outlet | Outlet | Outlet | Outlet | Inlet |
| (2) | Inlet | Outlet | Outlet | Outlet | Inlet | Outlet |
| (3) | Inlet | Outlet | Inlet | Inlet | Outlet | Inlet |
| (4) | Inlet | Outlet | Inlet | Inlet | Inlet | Outlet |
| (5) | Inlet | Inlet | Inlet | Outlet | Outlet | Outlet |
| (6) | Inlet | Inlet | Inlet | Outlet | Inlet | Inlet |
| (7) | Inlet | Inlet | Outlet | Inlet | Outlet | Outlet |
| (8) | Inlet | Inlet | Outlet | Inlet | Inlet | Inlet |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, B.; Jiao, C.; Zhang, S. Numerical Improvement of Battery Thermal Management Integrating Phase Change Materials with Fin-Enhanced Liquid Cooling. Energies 2025, 18, 2406. https://doi.org/10.3390/en18092406
Wang B, Jiao C, Zhang S. Numerical Improvement of Battery Thermal Management Integrating Phase Change Materials with Fin-Enhanced Liquid Cooling. Energies. 2025; 18(9):2406. https://doi.org/10.3390/en18092406
Chicago/Turabian StyleWang, Bo, Changzhi Jiao, and Shiheng Zhang. 2025. "Numerical Improvement of Battery Thermal Management Integrating Phase Change Materials with Fin-Enhanced Liquid Cooling" Energies 18, no. 9: 2406. https://doi.org/10.3390/en18092406
APA StyleWang, B., Jiao, C., & Zhang, S. (2025). Numerical Improvement of Battery Thermal Management Integrating Phase Change Materials with Fin-Enhanced Liquid Cooling. Energies, 18(9), 2406. https://doi.org/10.3390/en18092406







