A Synergistic Planning Framework for Low-Carbon Power Systems: Integrating Coal-Fired Power Plant Retrofitting with a Carbon and Green Certificate Market Coupling Mechanism

Abstract

The intensifying impacts of climate change induced by carbon emissions necessitate the implementation of urgent mitigation strategies. Given that the power sector is a major contributor to global carbon emissions, strategic decarbonization planning in this sector is of paramount importance. This study proposes a synergistic planning framework for low-carbon power systems that integrates coal-fired power plants (CFPPs) and a carbon and green certificate market coupling mechanism, thereby facilitating a “security–economic–low-carbon” tri-objective transition in power systems. The proposed framework facilitates dynamic decision-making regarding the retrofitting of CFPPs, investments in renewable energy resources, and energy storage systems. By evaluating three distinct CFPP retrofitting pathways, the framework enhances economic efficiency and reduces carbon emissions, achieving reductions of 28.67% in total system costs and 2.96% in CO₂ emissions. Implementing the carbon–green certificate market coupling mechanism further unlocks the market value of green certificates, thereby providing economic incentives for clean energy projects and increasing flexibility in the allocation of carbon emission quotas for enterprises. Relative to cases that consider only carbon trading or only green certificate markets, the coupled mechanism reduces the total cost by 10.96% and 15.56%, and decreases carbon emissions by 27.10% and 47.36%, respectively. The collaborative planning framework introduced in this study enhances economic performance, increases renewable energy penetration, and reduces carbon emissions, thus facilitating the low-carbon transition of power systems.

1. Introduction

CO₂ emissions have become the primary driver of global climate change in recent years. According to the International Energy Agency’s 2025 Global Energy Review, global CO₂ emissions rose by 0.8% in 2024 compared with 2023, reaching a record 37.8 Gt [1]. The power sector contributes the most to these emissions [2]. Under the mandate of decarbonization, power systems are shifting from a binary focus on security and economy to a triadic equilibrium of security, economy, and low-carbon objectives [3,4,5]. This transition requires not only ensuring reliable and economically viable power supply, but also accelerating the deployment of clean energy technologies, improving energy efficiency, and further reducing carbon emissions to meet global climate targets.

Coal-fired power plants (CFPPs) are a major contributor to carbon emissions within modern power systems. Integrating large-scale renewable energy to replace high-emission coal generation is essential for the electricity sector’s low-carbon transition. However, the accelerated retirement of conventional CFPPs can significantly constrain grid stability. Moreover, the intermittency of renewable resources introduces operational uncertainties that may cause power shortfalls and frequency deviations, undermining system reliability. To mitigate the effects of high renewable penetration on grid stability, CFPPs must adjust their load profiles to maintain supply–demand equilibrium. Retrofitting CFPPs provides an effective means of reducing carbon emissions while preserving necessary operational flexibility.

Existing research on CFPP low-carbon retrofits primarily falls into four categories: carbon capture and storage (CCS) retrofitting, flexibility enhancements, Carnot battery (CB) integration, and operation with green iron [6,7,8,9,10]. Reference [10] assesses the potential of converting an existing modern coal-fired power plant to operation with iron. Reference [11] quantifies the system-level environmental and economic benefits of synergistic operations between flexible CCS-equipped power plants and variable renewable energy sources. Reference [12] presents a two-stage planning model for an electricity–gas coupled integrated energy system that optimizes the scale and placement of CCS and power-to-gas facilities. Case studies demonstrate the model’s efficacy in reducing carbon emissions and enhancing CCS profitability within the coupled electricity–gas system. Reference [9] develops a cost-effective, multi-technology flexibility retrofit scheduling method for long-term CFPP operation, formulating characteristic and relational models for typical retrofit options via MILP. Reference [13] proposes retrofitting CFPPs with electric heating units and molten salt thermal storage to enhance system flexibility and decarbonization. The integration of CBs has been identified as a promising approach for improving energy utilization efficiency [14]. Reference [15] introduces a joint planning model for CFPP conversion and battery energy storage integration with renewable resources, facilitating emission reduction, renewable absorption, and operational security in decarbonized power systems. These studies collectively demonstrate that CFPP retrofits can synergize economic viability with environmental sustainability during the power sector’s energy transition. However, current low-carbon dynamic planning frameworks lack comprehensive consideration of diverse CFPP transformation pathways.

Carbon emission trading (CET) and green certificate trading (GCT) markets play pivotal roles in promoting renewable energy deployment and reducing carbon emissions in the power sector. CET schemes provide market-based incentives for energy facilities to reduce carbon emissions. Reference [16] develops a low-carbon economic dispatch strategy for active distribution networks that incorporates carbon emission trading and accounts for supply- and demand-side uncertainties. Participation in the CET market yields synergistic economic and environmental benefits. Reference [17] investigates the use of concentrated solar power plants to replace combined heat and power units, thereby enhancing renewable energy integration via carbon trading mechanisms. GCT employs market instruments to facilitate renewable energy deployment and reduce emissions by optimizing the energy mix and carbon output [18,19,20]. Reference [21] proposes a multi-objective, dynamic environmental–economic dispatch model for a power system with integrated wind farms, based on a GCT mechanism, to promote wind power utilization and enhance economic performance. As CET and GCT markets mature, numerous studies examine their complementary interactions. Integrating CET and GCT markets has become an emerging industry trend. Reference [22] introduces an optimal dispatch model for a multi-energy complementary system that integrates carbon emission trading with green certificate markets. Green certificates can be converted into carbon emission allowances, indirectly engaging in the carbon market to achieve higher renewable energy utilization and lower carbon emissions. References [23,24] highlight the synergistic effects of CET and GCT, which facilitate power supply integration, reduce fossil fuel power generation capacity, and increase the share of renewable energy installations. The integration of carbon and green certificate market mechanisms into low-carbon power system planning, especially when assessing the transformation pathways of conventional thermal power plants (CFPPs), improves operational flexibility and economic performance.

To facilitate the energy transition processes aimed at achieving a “secure–economic–low-carbon” equilibrium in power systems, a synergistic planning strategy for low-carbon power systems is proposed. This strategy integrates the retrofitting of CFPPs with a carbon–green certificate market coupling mechanism. The retrofitting of CFPPs is designed to reduce system carbon emissions while maintaining stability and flexibility. Furthermore, the carbon–green certificate coupling mechanism is employed to further reduce carbon emissions and enhance the integration of renewable energy resources.

The primary contributions of this paper are summarized as follows:

• Considering that CFPPs are major contributors to carbon emissions in power systems, retrofitting strategies for CFPPs are incorporated into the low-carbon planning framework to reduce system carbon emissions while maintaining stability and economic efficiency.
• To further reduce system carbon emissions and improve the utilization of renewable energy resources, a carbon–green certificate market coupling mechanism is considered within the planning framework.
• A multi-stage planning model is proposed, which considers both CFPP retrofitting and the carbon–green certificate market coupling mechanism. This model facilitates dynamic decision-making regarding the retrofitting of CFPPs and investment in new energy and energy storage systems.

The remainder of this paper is organized as follows. Section 2 develops the mathematical model for CFPP retrofitting and the carbon–green certificate coupling mechanism. Section 3 formulates the multi-stage low-carbon planning model, integrating both CFPP retrofitting and the carbon–green certificate coupling mechanism, and specifies its objective function and constraints. Section 4 presents a case study that evaluates the proposed algorithm’s effectiveness and economic viability. Section 5 discusses the key findings and their implications. Finally, Section 6 concludes the paper and suggests future research directions.

2. Coal-Fired Power Plant Retrofitting Strategies and Carbon–Green Certificate Market Coupling Mechanism

This section presents the mathematical models for the retrofitting pathways of CFPPs and further elaborates on the models for the carbon emission trading market, the green certificate trading market, and the carbon–green certificate coupling mechanism.

2.1. Coal-Fired Power Plant Retrofitting Strategies

Current research on low-carbon retrofitting technologies for CFPPs primarily encompasses four pathways: CCS retrofitting, flexibility retrofitting, CB retrofitting, and green-iron retrofitting. CCS retrofitting benefits from national-level financial incentives, demonstrates technological maturity, and involves controllable risks. Flexibility retrofitting technologies are well established and can be rapidly implemented during routine maintenance windows. CB retrofitting integrates industrial waste-heat recovery with heat pump systems, has completed pilot-scale demonstrations, is compatible with existing thermal networks, and offers high thermal efficiency. Since green-iron retrofitting remains at the pilot stage, with its maturity and economic viability yet to be validated, this study focuses exclusively on the first three pathways: CCS retrofitting, flexibility retrofitting, and CB retrofitting, as illustrated in Figure 1.

2.1.1. CCS Retrofitting

The predominant carbon capture methodologies currently employed encompass pre-combustion capture, post-combustion capture, and oxy-fuel combustion. Post-combustion capture represents the most extensively utilized approach, and the carbon capture retrofitting considered herein adopts this methodology.

CCS retrofitting is effectuated through the integration of CCS apparatuses into conventional coal-fired power plants. During operation, the generating unit produces power and delivers electrical energy. The output power is bifurcated into two components: a portion is exported to the external power plant system, designated as the “net output power”, while the remainder is allocated to supply the energy consumption of the CCS equipment, as shown in Equation (1). The energy consumption of CCS equipment is categorized into fixed energy consumption and operational energy consumption, as delineated in Equation (2). The quantity of carbon captured within the CCS equipment must not exceed the specified limits, as delineated in Equations (3)–(5). The actual carbon emissions of the retrofitted coal-fired power plant are presented in Equation (6).

$$P_{j,k,t}^{\mathrm{c}\mathrm{f}\mathrm{p}\mathrm{p}}=P_{j,k,t}^{\mathrm{n}\mathrm{e}\mathrm{t}}+P_{j,k,t}^{\mathrm{c}\mathrm{c}\mathrm{s}}$$

(1)

$$P_{j,k,t}^{\mathrm{c}\mathrm{c}\mathrm{s}}=P_j^{\mathrm{c}\mathrm{c}\mathrm{s},\mathrm{f}\mathrm{i}\mathrm{x}\mathrm{e}\mathrm{d}}·y_{j,t}^{\mathrm{c}\mathrm{c}\mathrm{s}}+{\mu }_j·M_{j,k,t}^{\mathrm{c}\mathrm{c}\mathrm{s}}$$

(2)

$$0\le M_{j,k,t}^{\mathrm{c}\mathrm{c}\mathrm{s}}\le M_{j,k,t}^{\mathrm{c}\mathrm{c}\mathrm{s},\mathrm{m}\mathrm{a}\mathrm{x}}·y_{j,t}^{\mathrm{c}\mathrm{c}\mathrm{s}}$$

(3)

$$M_{j,k,t}^{\mathrm{c}\mathrm{c}\mathrm{s},\mathrm{m}\mathrm{a}\mathrm{x}}={\lambda }_j·M_{j,k,t}^{\mathrm{c}\mathrm{f}\mathrm{p}\mathrm{p}}$$

(4)

$$M_{j,k,t}^{\mathrm{c}\mathrm{f}\mathrm{p}\mathrm{p}}={\zeta }_j·P_{j,k,t}^{\mathrm{c}\mathrm{f}\mathrm{p}\mathrm{p}}$$

(5)

$$M_{j,k,t}^{\mathrm{c}\mathrm{f}\mathrm{p}\mathrm{p},\mathrm{a}\mathrm{c}\mathrm{t}}=M_{j,k,t}^{\mathrm{c}\mathrm{f}\mathrm{p}\mathrm{p}}-M_{j,k,t}^{\mathrm{c}\mathrm{c}\mathrm{s}}$$

(6)

where $P_{j,k,t}^{\mathrm{c}\mathrm{f}\mathrm{p}\mathrm{p}}$ represents the power output of CFPP $j$ at time $k$ within stage $t$; $P_{j,k,t}^{\mathrm{n}\mathrm{e}\mathrm{t}}$ denotes the net power output of CFPP $j$ at time $k$ within stage $t$; $P_{j,k,t}^{\mathrm{c}\mathrm{c}\mathrm{s}}$ signifies the power consumption of the CCS equipment at time $k$ within stage $t$ for CFPP $j$; $P_j^{\mathrm{c}\mathrm{c}\mathrm{s},\mathrm{f}\mathrm{i}\mathrm{x}\mathrm{e}\mathrm{d}}$ represents the fixed power consumption of the CCS equipment for CFPP $j$; $y_{j,t}^{\mathrm{c}\mathrm{c}\mathrm{s}}$ indicates the retrofitting status of CFPP $j$ during stage $t$, controlled by a binary variable (0–1), where 1 signifies retrofitting and 0 signifies no retrofitting; ${\mu }_j$ is the unit power consumption of the CCS equipment; $M_{j,k,t}^{\mathrm{c}\mathrm{c}\mathrm{s}}$ represents the CCS amount at time $k$ within stage $t$ for CFPP $j$; $M_{j,k,t}^{\mathrm{c}\mathrm{c}\mathrm{s},\mathrm{m}\mathrm{a}\mathrm{x}}$ denotes the upper limit of the CCS amount at time $k$ within stage $t$ for CFPP $j$; ${\lambda }_j$ represents the CCS rate of CFPP $j$; $M_{j,k,t}^{\mathrm{c}\mathrm{f}\mathrm{p}\mathrm{p}}$ signifies the carbon emissions at time $k$ within stage $t$ for CFPP $j$; ${\zeta }_j$ denotes the carbon emission rate of CFPP $j$; and $M_{j,k,t}^{\mathrm{c}\mathrm{f}\mathrm{p}\mathrm{p},\mathrm{a}\mathrm{c}\mathrm{t}}$ represents the actual carbon emissions at time $k$ within stage $t$ for CFPP $j$.

2.1.2. Flexibility Retrofitting

Conventional CFPPs exhibit substantial installed capacity and stable power output; however, they are characterized by limited operational flexibility, including constrained ramp rates and extended startup times. Flexibility retrofits aim to enhance the operational flexibility of existing coal-fired power plants by reducing the minimum stable generation level and improving the ramp-up rate through modifications to the boiler or steam turbine. The power output and ramp constraints of the retrofitted coal-fired power plant are represented by Equations (7)–(9).

$$\begin{array}{cc}\hfill P_j^{\mathrm{c}\mathrm{f}\mathrm{p}\mathrm{p},\mathrm{m}\mathrm{i}\mathrm{n}}·x_{j,k,t}^{\mathrm{c}\mathrm{f}\mathrm{p}\mathrm{p}}·& \left(1-y_{j,t}^{\mathrm{f}\mathrm{l}\mathrm{e}\mathrm{x}}\right)+P_j^{\mathrm{c}\mathrm{f}\mathrm{p}\mathrm{p},\mathrm{m}\mathrm{i}\mathrm{n},\mathrm{f}\mathrm{l}\mathrm{e}\mathrm{x}}·x_{j,k,t}^{\mathrm{c}\mathrm{f}\mathrm{p}\mathrm{p}}·y_{j,t}^{\mathrm{f}\mathrm{l}\mathrm{e}\mathrm{x}}\le P_{j,k,t}^{\mathrm{c}\mathrm{f}\mathrm{p}\mathrm{p}}\hfill \\ & \le P_j^{\mathrm{c}\mathrm{f}\mathrm{p}\mathrm{p},\mathrm{m}\mathrm{a}\mathrm{x}}·x_{j,k,t}^{\mathrm{c}\mathrm{f}\mathrm{p}\mathrm{p}}\hfill \end{array}$$

(7)

$$P_{j,k,t}^{\mathrm{c}\mathrm{f}\mathrm{p}\mathrm{p}}-P_{j,k-1,t}^{\mathrm{c}\mathrm{f}\mathrm{p}\mathrm{p}}\le {UR}_j·x_{j,k-1,t}^{\mathrm{c}\mathrm{f}\mathrm{p}\mathrm{p}}·\left(1-y_{j,t}^{\mathrm{f}\mathrm{l}\mathrm{e}\mathrm{x}}\right)+{UR}_j^{\mathrm{f}\mathrm{l}\mathrm{e}\mathrm{x}}·x_{j,k-1,t}^{\mathrm{c}\mathrm{f}\mathrm{p}\mathrm{p}}·y_{j,t}^{\mathrm{f}\mathrm{l}\mathrm{e}\mathrm{x}}$$

(8)

$$P_{j,k-1,t}^{\mathrm{c}\mathrm{f}\mathrm{p}\mathrm{p}}-P_{j,k,t}^{\mathrm{c}\mathrm{f}\mathrm{p}\mathrm{p}}\le {DR}_j·x_{j,k,t}^{\mathrm{c}\mathrm{f}\mathrm{p}\mathrm{p}}·\left(1-y_{j,t}^{\mathrm{f}\mathrm{l}\mathrm{e}\mathrm{x}}\right)+{DR}_j^{\mathrm{f}\mathrm{l}\mathrm{e}\mathrm{x}}·x_{j,k,t}^{\mathrm{c}\mathrm{f}\mathrm{p}\mathrm{p}}·y_{j,t}^{\mathrm{f}\mathrm{l}\mathrm{e}\mathrm{x}}$$

(9)

where $P_j^{\mathrm{c}\mathrm{f}\mathrm{p}\mathrm{p},\mathrm{m}\mathrm{i}\mathrm{n}}$ and $P_j^{\mathrm{c}\mathrm{f}\mathrm{p}\mathrm{p},\mathrm{m}\mathrm{a}\mathrm{x}}$ denote the lower and upper power output limits, respectively, for CFPP $j$; The binary variable $x_{j,k,t}^{\mathrm{c}\mathrm{f}\mathrm{p}\mathrm{p}}$ represents the on/off status of CFPP $j$ at time $k$ within stage $t$, where 0 signifies shutdown and 1 indicates operation; the binary variable $y_{j,t}^{\mathrm{f}\mathrm{l}\mathrm{e}\mathrm{x}}$ represents the flexibility modification status of CFPP $j$ during stage $t$; $P_j^{\mathrm{c}\mathrm{f}\mathrm{p}\mathrm{p},\mathrm{m}\mathrm{i}\mathrm{n},\mathrm{f}\mathrm{l}\mathrm{e}\mathrm{x}}$ denotes the minimum power output of CFPP $j$ following flexibility retrofits; ${UR}_j$ and ${DR}_j$ represent the ramp-up and ramp-down rates, respectively, for CFPP $j$; and ${UR}_j^{\mathrm{f}\mathrm{l}\mathrm{e}\mathrm{x}}$ and ${DR}_j^{\mathrm{f}\mathrm{l}\mathrm{e}\mathrm{x}}$ denote the ramp-up and ramp-down rates for CFPP $j$ subsequent to flexibility retrofits.

2.1.3. CB Retrofitting

The Carnot battery, also referred to as thermal energy storage (TES) with heat pump technology, comprises three primary components: power-to-heat (P2H), TES, and heat-to-power (H2P) conversion. A molten salt CB energy storage system, designed for retrofitting CFPPs, retains the existing power generation cycle as the H2P component. It integrates electric heating or a reverse-Brayton cycle as the P2H component, and incorporates low-cost molten salt thermal storage for large-scale energy storage. This system can utilize curtailed renewable energy or off-peak grid electricity, either directly or indirectly via a heat pump cycle, to heat the molten salt, converting electrical energy into high-temperature thermal energy for storage. Subsequently, the high-temperature molten salt and the boiler serve as a combined heat source to drive the steam turbine for power generation, thereby reducing or potentially replacing coal consumption. The structure of the CB is illustrated in Figure 2.

The mathematical formulation of the CB system is organized by categorizing the constraints according to three key operational phases: P2H, TES, and H2P. Specifically, the P2H process is described by Equations (10) and (11), while the H2P conversion is represented through Equations (12) and (13). The CB’s charge–discharge behavior is conditioned by a transformation rule (14), with mutual exclusivity of charging and discharging enforced by Equation (15). The TES dynamics are modeled starting with the energy balance in Equation (16), while the upper and lower thermal capacity bounds are given in Equation (17). Initial thermal state alignment is secured via Equation (18). Heat charging and discharging rates are constrained by Equations (19) and (20), with further ramp rate limitations specified in Equations (21) and (22). Additionally, Equations (23) and (24) govern the startup and shutdown timing of the CB system.

$$Q_{j,k,t}^{\mathrm{c}\mathrm{h}\mathrm{a}}={\varphi }_j^{\mathrm{c}\mathrm{b},\mathrm{c}\mathrm{h}\mathrm{a}}·P_{j,k,t}^{\mathrm{c}\mathrm{b},\mathrm{c}\mathrm{h}\mathrm{a}}$$

(10)

$$0\le P_{j,k,t}^{\mathrm{c}\mathrm{b},\mathrm{c}\mathrm{h}\mathrm{a}}\le P_j^{\mathrm{e}\mathrm{h}\mathrm{e}}·x_{j,k,t}^{\mathrm{c}\mathrm{b},\mathrm{c}\mathrm{h}\mathrm{a}}$$

(11)

$$P_{j,k,t}^{\mathrm{c}\mathrm{b},\mathrm{d}\mathrm{i}\mathrm{s}}={\varphi }_j^{\mathrm{c}\mathrm{b},\mathrm{d}\mathrm{i}\mathrm{s}}·Q_{j,k,t}^{\mathrm{d}\mathrm{i}\mathrm{s}}$$

(12)

$$P_j^{\mathrm{c}\mathrm{b},\mathrm{m}\mathrm{i}\mathrm{n}}·x_{j,k,t}^{\mathrm{c}\mathrm{b},\mathrm{d}\mathrm{i}\mathrm{s}}\le P_{j,k,t}^{\mathrm{c}\mathrm{b},\mathrm{d}\mathrm{i}\mathrm{s}}\le P_j^{\mathrm{c}\mathrm{b},\mathrm{m}\mathrm{a}\mathrm{x}}·x_{j,k,t}^{\mathrm{c}\mathrm{b},\mathrm{d}\mathrm{i}\mathrm{s}}$$

(13)

$$x_{j,k,t}^{\mathrm{c}\mathrm{b},\mathrm{c}\mathrm{h}\mathrm{a}}+x_{j,k,t}^{\mathrm{c}\mathrm{b},\mathrm{d}\mathrm{i}\mathrm{s}}\le y_{j,t}^{\mathrm{c}\mathrm{b}}$$

(14)

$$x_{j,k,t}^{\mathrm{c}\mathrm{b},\mathrm{c}\mathrm{h}\mathrm{a}}+x_{j,k,t}^{\mathrm{c}\mathrm{b},\mathrm{d}\mathrm{i}\mathrm{s}}\le 1$$

(15)

$$Q_{j,k,t}=Q_{j,k,t}+Q_{j,k,t}^{\mathrm{c}\mathrm{h}\mathrm{a}}·{\eta }_j^{\mathrm{c}\mathrm{b},\mathrm{c}\mathrm{h}\mathrm{a}}-Q_{j,k,t}^{\mathrm{d}\mathrm{i}\mathrm{s}}/{\eta }_j^{\mathrm{c}\mathrm{b},\mathrm{d}\mathrm{i}\mathrm{s}}$$

(16)

$$Q_j^{\mathrm{m}\mathrm{i}\mathrm{n}}\le Q_{j,k,t}\le Q_j^{\mathrm{m}\mathrm{a}\mathrm{x}}$$

(17)

$$Q_{j,0,t}=Q_{j,NK,t}$$

(18)

$$0\le Q_{j,k,t}^{\mathrm{c}\mathrm{h}\mathrm{a}}\le R_j^{\mathrm{c}\mathrm{b},\mathrm{c}\mathrm{h}\mathrm{a}}·x_{j,k,t}^{\mathrm{c}\mathrm{h}\mathrm{a}}$$

(19)

$$0\le Q_{j,k,t}^{\mathrm{d}\mathrm{i}\mathrm{s}}\le R_j^{\mathrm{c}\mathrm{b},\mathrm{d}\mathrm{i}\mathrm{s}}·x_{j,k,t}^{\mathrm{d}\mathrm{i}\mathrm{s}}$$

(20)

$$\left|Q_{j,k,t}^{\mathrm{c}\mathrm{h}\mathrm{a}}-Q_{j,k-∆k,t}^{\mathrm{c}\mathrm{h}\mathrm{a}}\right|\le R_j^{\mathrm{c}\mathrm{b},\mathrm{c}\mathrm{h}\mathrm{a}}·∆k$$

(21)

$$\left|Q_{j,k,t}^{\mathrm{d}\mathrm{i}\mathrm{s}}-Q_{j,k-∆k,t}^{\mathrm{d}\mathrm{i}\mathrm{s}}\right|\le R_j^{\mathrm{c}\mathrm{b},\mathrm{d}\mathrm{i}\mathrm{s}}·∆k$$

(22)

$$\left(X_{j,k-1,t}^{\mathrm{c}\mathrm{b},\mathrm{o}\mathrm{n}}-T_j^{\mathrm{c}\mathrm{b},\mathrm{o}\mathrm{n}}\right)·\left(x_{j,k-1,t}^{\mathrm{c}\mathrm{b},\mathrm{d}\mathrm{i}\mathrm{s}}-x_{j,k,t}^{\mathrm{c}\mathrm{b},\mathrm{d}\mathrm{i}\mathrm{s}}\right)\ge 0$$

(23)

$$\left(X_{j,k-1,t}^{\mathrm{c}\mathrm{b},\mathrm{o}\mathrm{f}\mathrm{f}}-T_j^{\mathrm{c}\mathrm{b},\mathrm{o}\mathrm{f}\mathrm{f}}\right)·\left(x_{j,k-1,t}^{\mathrm{c}\mathrm{b},\mathrm{d}\mathrm{i}\mathrm{s}}-x_{j,k,t}^{\mathrm{c}\mathrm{b},\mathrm{d}\mathrm{i}\mathrm{s}}\right)\ge 0$$

(24)

where $Q_{j,k,t}^{\mathrm{c}\mathrm{h}\mathrm{a}}$ and $Q_{j,k,t}^{\mathrm{d}\mathrm{i}\mathrm{s}}$ denote the charging and discharging thermal energy of CB $j$ at time $k$ within stage $t$, respectively; ${\varphi }_j^{\mathrm{c}\mathrm{b},\mathrm{c}\mathrm{h}\mathrm{a}}$ and ${\varphi }_j^{\mathrm{c}\mathrm{b},\mathrm{d}\mathrm{i}\mathrm{s}}$ represent the electrical-to-thermal and thermal-to-electrical efficiencies of CB $j$; $P_{j,k,t}^{\mathrm{c}\mathrm{b},\mathrm{c}\mathrm{h}\mathrm{a}}$ and $P_{j,k,t}^{\mathrm{c}\mathrm{b},\mathrm{d}\mathrm{i}\mathrm{s}}$ signify the charging and discharging power of CB $j$ at time $k$ within stage $t$, respectively; $P_j^{\mathrm{e}\mathrm{h}\mathrm{e}}$ denotes the rated capacity of the electrical heating device for CB $j$; $x_{j,k,t}^{\mathrm{c}\mathrm{b},\mathrm{c}\mathrm{h}\mathrm{a}}$ and $x_{j,k,t}^{\mathrm{c}\mathrm{b},\mathrm{d}\mathrm{i}\mathrm{s}}$ are binary variables indicating the charging and discharging states of CB $j$ at time $k$ within stage $t$; $P_j^{\mathrm{c}\mathrm{b},\mathrm{m}\mathrm{i}\mathrm{n}}$ and $P_j^{\mathrm{c}\mathrm{b},\mathrm{m}\mathrm{a}\mathrm{x}}$ define the lower and upper bounds of the discharging power for CB $j$; $y_{j,t}^{\mathrm{c}\mathrm{b}}$ is a binary variable denoting the retrofitting state of CB $j$ within stage $t$; $Q_{j,k,t}$ represents the TES level of CB $j$ at time $k$ within stage $t$; ${\eta }_j^{\mathrm{c}\mathrm{b},\mathrm{c}\mathrm{h}\mathrm{a}}$ and ${\eta }_j^{\mathrm{c}\mathrm{b},\mathrm{d}\mathrm{i}\mathrm{s}}$ denote the charging and discharging efficiencies of CB $j$; $Q_j^{\mathrm{m}\mathrm{i}\mathrm{n}}$ and $Q_j^{\mathrm{m}\mathrm{a}\mathrm{x}}$ define the lower and upper bounds of the TES for CB $j$; $R_j^{\mathrm{c}\mathrm{b},\mathrm{c}\mathrm{h}\mathrm{a}}$ and $R_j^{\mathrm{c}\mathrm{b},\mathrm{d}\mathrm{i}\mathrm{s}}$ represent the ramp rates for charging and discharging of CB $j$; $∆k$ denotes the time interval; $X_{j,k,t}^{\mathrm{c}\mathrm{b},\mathrm{o}\mathrm{n}}$ and $X_{j,k,t}^{\mathrm{c}\mathrm{b},\mathrm{o}\mathrm{f}\mathrm{f}}$ represent the continuous operational and downtime durations of CB $j$ at time $k$ within stage $t$; and $T_j^{\mathrm{c}\mathrm{b},\mathrm{o}\mathrm{n}}$ and $T_j^{\mathrm{c}\mathrm{b},\mathrm{o}\mathrm{f}\mathrm{f}}$ represent the minimum startup and shutdown times for CB $j$.

2.2. Carbon–Green Certificate Market Coupling Mechanism

2.2.1. Carbon Emission Trading Market

The CET market constitutes a market-based mechanism for emission reduction. This system establishes an aggregate emissions cap for greenhouse gases, which is subsequently divided into a defined quantity of emission allowances. These allowances are then allocated to various emission entities. These entities are then able to engage in the buying and selling of emission allowances within the market, contingent upon their respective emission profiles, as delineated in Equations (25) and (26).

$$M_t^{\mathrm{q}\mathrm{u}\mathrm{o}}=\beta ·\sum _{k\in \mathrm{N}\mathrm{K}}\sum _{i\in {\mathsf{\Omega }}_{\mathrm{l}\mathrm{o}\mathrm{a}\mathrm{d}}}{P}_{i,k,t}^{\mathrm{l}\mathrm{o}\mathrm{a}\mathrm{d}}$$

(25)

$$M_t^{\mathrm{a}\mathrm{c}\mathrm{t}}=M_t^{\mathrm{q}\mathrm{u}\mathrm{o}}-\sum _{k\in \mathrm{N}\mathrm{K}}\sum _{j\in {\mathsf{\Omega }}_{\mathrm{c}\mathrm{f}\mathrm{p}\mathrm{p}}}{M}_{j,k,t}^{\mathrm{c}\mathrm{f}\mathrm{p}\mathrm{p},\mathrm{a}\mathrm{c}\mathrm{t}}$$

(26)

where $M_t^{\mathrm{q}\mathrm{u}\mathrm{o}}$ represents the carbon allowance within stage $t$; $\beta$ denotes the carbon emission baseline value; $\mathrm{N}\mathrm{K}$ signifies the set of time periods; ${\mathsf{\Omega }}_{\mathrm{l}\mathrm{o}\mathrm{a}\mathrm{d}}$ represents the set of loads; ${\mathsf{\Omega }}_{\mathrm{c}\mathrm{f}\mathrm{p}\mathrm{p}}$ denotes the set of CFPPs; $P_{i,k,t}^{\mathrm{l}\mathrm{o}\mathrm{a}\mathrm{d}}$ represents the load power at node $i$ at time $k$ within stage $t$; and $M_t^{\mathrm{a}\mathrm{c}\mathrm{t}}$ represents the actual carbon emission trading volume within stage $t$.

2.2.2. Green Certificate Trading Market

The GCT market serves as a market-based mechanism designed to stimulate and facilitate the expansion of renewable energy sources. Governmental bodies allocate a specific quota of renewable energy certificates to enterprises. In instances where an enterprise’s renewable energy generation falls short of its allocated certificate quota, the acquisition of additional certificates is mandated to fulfill the requirement. Conversely, entities exceeding their quota may opt to sell their surplus certificates, thereby generating revenue, as delineated in Equations (27) and (28).

$$N_t^{\mathrm{q}\mathrm{u}\mathrm{o}}=\alpha ·\sum _{k\in \mathrm{H}\mathrm{o}\mathrm{r}\mathrm{i}\mathrm{z}\mathrm{o}\mathrm{n}}\sum _{i\in {\mathsf{\Omega }}_{\mathrm{l}\mathrm{o}\mathrm{a}\mathrm{d}}}{P}_{i,k,t}^{\mathrm{l}\mathrm{o}\mathrm{a}\mathrm{d}}$$

(27)

$$N_t^{\mathrm{a}\mathrm{c}\mathrm{t}}=N_t^{\mathrm{q}\mathrm{u}\mathrm{o}}-\sum _{k\in \mathrm{H}\mathrm{o}\mathrm{r}\mathrm{i}\mathrm{z}\mathrm{o}\mathrm{n}}\sum _{w\in {\mathsf{\Omega }}_{\mathrm{r}\mathrm{e}}}{P}_{w,k,t}^{\mathrm{r}\mathrm{e}}$$

(28)

where $N_t^{\mathrm{q}\mathrm{u}\mathrm{o}}$ denotes the green certificate quota within stage $t$; $\alpha$ signifies the responsibility weight for renewable energy consumption; $N_t^{\mathrm{a}\mathrm{c}\mathrm{t}}$ represents the actual number of green certificate transaction within stage $t$; ${\mathsf{\Omega }}_{\mathrm{r}\mathrm{e}}$ denotes the set of renewable energy installations; and $P_{w,k,t}^{\mathrm{r}\mathrm{e}}$ represents the output of renewable energy unit $w$ at time $k$ during stage $t$.

2.2.3. Carbon–Green Certificate Market Coupling

Green certificates contain all relevant information on the generation and consumption of renewable energy, while carbon emissions from conventional thermal power generation can be quantitatively calculated. Therefore, the carbon reduction achieved through the use of green electricity can be determined via green certificates. The portion of green certificates that offsets carbon emissions can indirectly engage in the carbon emissions market, effectively interacting with prices and quotas. By increasing the storage and use of renewable energy, green certificates can be obtained to offset carbon allowances, thereby reducing carbon trading costs. This incentivizes enterprises to expand clean energy storage capacity, reduce dependence on fossil fuels, lower carbon emissions, promote clean energy integration, and enhance the overall environmental benefits of the energy system, fostering low-carbon economic growth. The conversion relationship between green certificates and carbon allowances can be determined through the base trading prices of both, yielding the number of green certificates and carbon allowances to be offset. The calculation is illustrated in Equations (29)–(31).

$$M_t^{\mathrm{g}\mathrm{r}\mathrm{e}\mathrm{e}\mathrm{n}}=\varpi ·N_t^{\mathrm{j}\mathrm{o}}$$

(29)

$$M_t^{\mathrm{a}\mathrm{c}\mathrm{t},\mathrm{j}\mathrm{o}}=M_t^{\mathrm{a}\mathrm{c}\mathrm{t}}-M_t^{\mathrm{g}\mathrm{r}\mathrm{e}\mathrm{e}\mathrm{n}}$$

(30)

$$N_t^{\mathrm{a}\mathrm{c}\mathrm{t},\mathrm{j}\mathrm{o}}=N_t^{\mathrm{a}\mathrm{c}\mathrm{t}}-N_t^{\mathrm{j}\mathrm{o}}$$

(31)

where $M_t^{\mathrm{g}\mathrm{r}\mathrm{e}\mathrm{e}\mathrm{n}}$ represents the carbon emission trading rights offset by green certificates in stage $t$; $\varpi$ represents the conversion coefficient for offsetting carbon emission trading rights with green certificates; $N_t^{\mathrm{j}\mathrm{o}}$ represents the number of green certificates used to offset carbon emission trading rights within stage $t$; $M_t^{\mathrm{a}\mathrm{c}\mathrm{t},\mathrm{j}\mathrm{o}}$ represents the carbon emission trading rights after offsetting within stage $t$; and $N_t^{\mathrm{a}\mathrm{c}\mathrm{t},\mathrm{j}\mathrm{o}}$ represents the number of green certificates remaining after offsetting within stage $t$.

3. Low-Carbon Power System Planning Model with Coordinated Carbon–Green Certificate Market Coupling Mechanism and Coal-Fired Power Plant Retrofitting

This section formulates a low-carbon planning model for power systems, accounting for the retrofitting of CFPPs and the integration of a carbon–green certificate market coupling mechanism. This model makes decisions regarding the retrofitting of CFPPs and investment in renewable energy and energy storage systems.

3.1. Objective Function

The objective is to minimize the total costs over the planning period, encompassing the retrofitting costs of CFPPs, investment costs associated with renewable energy sources and energy storage systems, costs related to carbon market transactions, costs associated with green certificate market transactions, operational costs of CFPPs, penalties incurred from renewable energy curtailment, and costs resulting from load losses, as shown in Equations (32)–(44).

$$\begin{array}{cc}\hfill \min C={\displaystyle \sum _{t\in NT}}{\kappa }_t·& (C_t^{\mathrm{c}\mathrm{f}\mathrm{p}\mathrm{p},\mathrm{r}}+C_t^{\mathrm{r}\mathrm{e},\mathrm{i}\mathrm{n}\mathrm{v}}+C_t^{\mathrm{e}\mathrm{s}\mathrm{s},\mathrm{i}\mathrm{n}\mathrm{v}}+C_t^{\mathrm{c}\mathrm{a}\mathrm{r}\mathrm{b}\mathrm{o}\mathrm{n}}+C_t^{\mathrm{g}\mathrm{r}\mathrm{e}\mathrm{e}\mathrm{n}}+C_t^{\mathrm{c}\mathrm{f}\mathrm{p}\mathrm{p},\mathrm{o}\mathrm{p}}\hfill \\ & +C_t^{\mathrm{r}\mathrm{e},\mathrm{c}\mathrm{u}\mathrm{r}\mathrm{t}}+C_t^{\mathrm{l}\mathrm{o}\mathrm{a}\mathrm{d},\mathrm{c}\mathrm{u}\mathrm{r}\mathrm{t}})\hfill \end{array}$$

(32)

$${\kappa }_t=1/{\left(1+\epsilon \right)}^{t-1}$$

(33)

$$C_t^{\mathrm{c}\mathrm{f}\mathrm{p}\mathrm{p},\mathrm{r}}=C_t^{\mathrm{c}\mathrm{c}\mathrm{s}}+C_t^{\mathrm{f}\mathrm{l}\mathrm{e}\mathrm{x}}+C_t^{\mathrm{c}\mathrm{b}}$$

(34)

$$C_t^{ccs}=\sum _{j\in {\mathsf{\Omega }}_{\mathrm{c}\mathrm{f}\mathrm{p}\mathrm{p}}}{c}^{\mathrm{c}\mathrm{c}\mathrm{s}}·P_j^{\mathrm{m}\mathrm{a}\mathrm{x}}·\left(y_{j,t}^{\mathrm{c}\mathrm{c}\mathrm{s}}-y_{j,t-1}^{\mathrm{c}\mathrm{c}\mathrm{s}}\right)$$

(35)

$$C_t^{\mathrm{f}\mathrm{l}\mathrm{e}\mathrm{x}}=\sum _{j\in {\mathsf{\Omega }}_{\mathrm{c}\mathrm{f}\mathrm{p}\mathrm{p}}}{c}^{\mathrm{f}\mathrm{l}\mathrm{e}\mathrm{x}}·P_j^{\mathrm{m}\mathrm{a}\mathrm{x}}·\left(y_{j,t}^{\mathrm{f}\mathrm{l}\mathrm{e}\mathrm{x}}-y_{j,t-1}^{\mathrm{f}\mathrm{l}\mathrm{e}\mathrm{x}}\right)$$

(36)

$$C_t^{\mathrm{c}\mathrm{b}}=\sum _{j\in {\mathsf{\Omega }}_{\mathrm{c}\mathrm{f}\mathrm{p}\mathrm{p}}}\left(c^{\mathrm{e}\mathrm{h}\mathrm{e}}·P_j^{\mathrm{e}\mathrm{h}\mathrm{e}}+c^{\mathrm{t}\mathrm{e}\mathrm{s}}·Q_j^{\mathrm{t}\mathrm{e}\mathrm{s}}+c^{\mathrm{s}\mathrm{g}}·P_j^{\mathrm{m}\mathrm{a}\mathrm{x}}\right)·\left(y_{j,t}^{\mathrm{c}\mathrm{b}}-y_{j,t-1}^{\mathrm{c}\mathrm{b}}\right)$$

(37)

$$C_t^{\mathrm{r}\mathrm{e},\mathrm{i}\mathrm{n}\mathrm{v}}=\sum _{w\in {\mathsf{\Omega }}_{\mathrm{r}\mathrm{e}}}{c}^{\mathrm{r}\mathrm{e}}·P_w^{\mathrm{r}\mathrm{e},\mathrm{m}\mathrm{a}\mathrm{x}}·\left(y_{w,t}^{\mathrm{r}\mathrm{e}}-y_{w,t-1}^{\mathrm{r}\mathrm{e}}\right)$$

(38)

$$C_t^{\mathrm{e}\mathrm{s}\mathrm{s},\mathrm{i}\mathrm{n}\mathrm{v}}=\sum _{e\in {\mathsf{\Omega }}_{\mathrm{e}\mathrm{s}\mathrm{s}}}{c}^{\mathrm{e}\mathrm{s}\mathrm{s}}·P_e^{\mathrm{e}\mathrm{s}\mathrm{s},\mathrm{m}\mathrm{a}\mathrm{x}}·\left(y_{e,t}^{\mathrm{e}\mathrm{s}\mathrm{s}}-y_{e,t-1}^{\mathrm{e}\mathrm{s}\mathrm{s}}\right)$$

(39)

$$C_t^{\mathrm{c}\mathrm{a}\mathrm{r}\mathrm{b}\mathrm{o}\mathrm{n}}=c^{\mathrm{c}\mathrm{a}\mathrm{r}\mathrm{b}\mathrm{o}\mathrm{n}}·M_t^{\mathrm{a}\mathrm{c}\mathrm{t},\mathrm{j}\mathrm{o}}$$

(40)

$$C_t^{\mathrm{g}\mathrm{r}\mathrm{e}\mathrm{e}\mathrm{n}}=c^{\mathrm{g}\mathrm{r}\mathrm{e}\mathrm{e}\mathrm{n}}·N_t^{\mathrm{a}\mathrm{c}\mathrm{t},\mathrm{j}\mathrm{o}}$$

(41)

$$C_t^{\mathrm{c}\mathrm{f}\mathrm{p}\mathrm{p},\mathrm{o}\mathrm{p}}=\sum _{k\in NK}\sum _{j\in {\mathsf{\Omega }}_{\mathrm{c}\mathrm{f}\mathrm{p}\mathrm{p}}}{c}_j^{\mathrm{f}\mathrm{u}\mathrm{e}\mathrm{l}}·F_j\left(P_{j,k,t}^{\mathrm{c}\mathrm{f}\mathrm{p}\mathrm{p}}\right)$$

(42)

$$C_t^{\mathrm{r}\mathrm{e},\mathrm{c}\mathrm{u}\mathrm{r}\mathrm{t}}=\sum _{k\in NK}\sum _{w\in {\mathsf{\Omega }}_{\mathrm{r}\mathrm{e}}}{c}^{\mathrm{r}\mathrm{e},\mathrm{c}\mathrm{u}\mathrm{r}\mathrm{t}}·\left(P_{w,k,t}^{\mathrm{r}\mathrm{e},\mathrm{f}}-P_{w,k,t}^{\mathrm{r}\mathrm{e}}\right)$$

(43)

$$C_t^{\mathrm{l}\mathrm{o}\mathrm{a}\mathrm{d},\mathrm{l}\mathrm{o}\mathrm{s}\mathrm{s}}=\sum _{k\in NK}\sum _{i\in {\mathsf{\Omega }}_{\mathrm{l}\mathrm{o}\mathrm{a}\mathrm{d}}}{c}^{\mathrm{l}\mathrm{o}\mathrm{a}\mathrm{d},\mathrm{l}\mathrm{o}\mathrm{s}\mathrm{s}}·P_{i,k,t}^{\mathrm{l}\mathrm{o}\mathrm{s}\mathrm{s}}$$

(44)

where ${\kappa }_t$ represents the present value factor within stage $t$; $\epsilon$ represents the discount rate; $C_t^{\mathrm{c}\mathrm{f}\mathrm{p}\mathrm{p},\mathrm{r}}$ denotes the retrofitting expenses for CFPPs; $C_t^{\mathrm{r}\mathrm{e},\mathrm{i}\mathrm{n}\mathrm{v}}$ signifies the investment costs associated with renewable energy sources; $C_t^{\mathrm{e}\mathrm{s}\mathrm{s},\mathrm{i}\mathrm{n}\mathrm{v}}$ represents the investment costs for energy storage systems; $C_t^{\mathrm{c}\mathrm{a}\mathrm{r}\mathrm{b}\mathrm{o}\mathrm{n}}$ indicates the transaction costs within the carbon market; $C_t^{\mathrm{g}\mathrm{r}\mathrm{e}\mathrm{e}\mathrm{n}}$ denotes the trading costs of green certificates; $C_t^{\mathrm{c}\mathrm{f}\mathrm{p}\mathrm{p},\mathrm{o}\mathrm{p}}$ represents the operational expenses of CFPPs; $C_t^{\mathrm{r}\mathrm{e},\mathrm{c}\mathrm{u}\mathrm{r}\mathrm{t}}$ signifies the penalty costs for curtailment of renewable energy resources; $C_t^{\mathrm{l}\mathrm{o}\mathrm{a}\mathrm{d},\mathrm{l}\mathrm{o}\mathrm{s}\mathrm{s}}$ represents the penalty costs for load shedding; $C_t^{\mathrm{c}\mathrm{c}\mathrm{s}}$, $C_t^{\mathrm{f}\mathrm{l}\mathrm{e}\mathrm{x}}$, and $C_t^{\mathrm{c}\mathrm{b}}$ respectively represent the retrofitting costs for CCS, flexibility enhancements, and CB integration; $c^{\mathrm{c}\mathrm{c}\mathrm{s}}$ and $c^{\mathrm{f}\mathrm{l}\mathrm{e}\mathrm{x}}$, respectively, denote the unit retrofitting costs for CCS and flexibility enhancements; $P_j^{\mathrm{m}\mathrm{a}\mathrm{x}}$ represents the rated capacity of the CFPP $j$; $c^{\mathrm{e}\mathrm{h}\mathrm{e}}$, $c^{\mathrm{t}\mathrm{e}\mathrm{s}}$, and $c^{\mathrm{s}\mathrm{g}}$ represent the unit investment costs for electric heating devices, TES, and thermal-to-electric conversion units, respectively; $c^{\mathrm{r}\mathrm{e}}$ represents the unit investment costs for renewable energy resources; $P_w^{\mathrm{r}\mathrm{e},\mathrm{m}\mathrm{a}\mathrm{x}}$ represents the rated capacity of renewable energy resources; $y_{w,t}^{\mathrm{r}\mathrm{e}}$ represents the deployment status of renewable energy resources $w$ within stage $t$, controlled by a binary variable (0–1); $c^{\mathrm{e}\mathrm{s}\mathrm{s}}$ represents the unit investment costs for energy storage; $P_e^{\mathrm{e}\mathrm{s}\mathrm{s},\mathrm{m}\mathrm{a}\mathrm{x}}$ represents the rated capacity of energy storage; $y_{e,t}^{\mathrm{e}\mathrm{s}\mathrm{s}}$ represents the deployment status of energy storage, controlled by a binary variable (0–1); ${\mathsf{\Omega }}_{\mathrm{e}\mathrm{s}\mathrm{s}}$ represents the set of energy storage systems to be deployed; $c^{\mathrm{c}\mathrm{a}\mathrm{r}\mathrm{b}\mathrm{o}\mathrm{n}}$ denotes the unit carbon trading price; $c^{\mathrm{g}\mathrm{r}\mathrm{e}\mathrm{e}\mathrm{n}}$ denotes the unit green certificate price; $c_j^{\mathrm{f}\mathrm{u}\mathrm{e}\mathrm{l}}$ represents the fuel price; $F_j\left(·\right)$ represents the heat rate curve of the CFPP $j$; $c^{\mathrm{r}\mathrm{e},\mathrm{c}\mathrm{u}\mathrm{r}\mathrm{t}}$ represents the unit penalty cost for curtailment of renewable energy; $P_{w,k,t}^{\mathrm{r}\mathrm{e},\mathrm{f}}$ represents the predicted output of renewable energy resource $w$ at time $k$ within stage $t$; $c^{\mathrm{l}\mathrm{o}\mathrm{a}\mathrm{d},\mathrm{l}\mathrm{o}\mathrm{s}\mathrm{s}}$ represents the unit penalty cost for load shedding; and $P_{i,k,t}^{\mathrm{l}\mathrm{o}\mathrm{s}\mathrm{s}}$ represents the magnitude of load shedding at node $i$ at time $k$ within stage $t$.

3.2. Constraints

3.2.1. Investment Constraints

Each CFPP can only select one type of retrofitting pathway, and the post-retrofitting status remains unchanged, as shown in Equations (45)–(48). The status of renewable energy resources and energy storage systems remains unchanged after their construction, as indicated in Equations (49) and (50).

$$y_{j,t}^{\mathrm{c}\mathrm{c}\mathrm{s}}+y_{j,t}^{\mathrm{f}\mathrm{l}\mathrm{e}\mathrm{x}}+y_{j,t}^{\mathrm{c}\mathrm{b}}\le 1$$

(45)

$$y_{j,t}^{ccs}\le y_{j,t-1}^{ccs}$$

(46)

$$y_{j,t}^{\mathrm{f}\mathrm{l}\mathrm{e}\mathrm{x}}\le y_{j,t-1}^{\mathrm{f}\mathrm{l}\mathrm{e}\mathrm{x}}$$

(47)

$$y_{j,t}^{\mathrm{c}\mathrm{b}}\le y_{j,t-1}^{\mathrm{c}\mathrm{b}}$$

(48)

$$y_{w,t}^{\mathrm{r}\mathrm{e}}\le y_{w,t-1}^{\mathrm{r}\mathrm{e}}$$

(49)

$$y_{e,t}^{\mathrm{e}\mathrm{s}\mathrm{s}}\le y_{e,t-1}^{\mathrm{e}\mathrm{s}\mathrm{s}}$$

(50)

3.2.2. Operational Constraints

(1)

CFPP operation constraints

CFPP operation is subject to generation output upper and lower bounds, startup and shutdown times, and ramp-up constraints, as shown in Equations (51)–(55).

$$P_j^{\mathrm{c}\mathrm{f}\mathrm{p}\mathrm{p},\mathrm{m}\mathrm{i}\mathrm{n}}·x_{j,k,t}^{\mathrm{c}\mathrm{f}\mathrm{p}\mathrm{p}}\le P_{j,k,t}^{\mathrm{c}\mathrm{f}\mathrm{p}\mathrm{p}}\le P_j^{\mathrm{c}\mathrm{f}\mathrm{p}\mathrm{p},\mathrm{m}\mathrm{a}\mathrm{x}}·x_{j,k,t}^{\mathrm{c}\mathrm{f}\mathrm{p}\mathrm{p}}$$

(51)

$$\left(X_{j,k-1,t}^{\mathrm{c}\mathrm{f}\mathrm{p}\mathrm{p},\mathrm{o}\mathrm{n}}-T_j^{\mathrm{c}\mathrm{f}\mathrm{p}\mathrm{p},\mathrm{o}\mathrm{n}}\right)·\left(x_{j,k-1,t}^{\mathrm{c}\mathrm{f}\mathrm{p}\mathrm{p}}-x_{j,k,t}^{\mathrm{c}\mathrm{f}\mathrm{p}\mathrm{p}}\right)\ge 0$$

(52)

$$\left(X_{j,k-1,t}^{\mathrm{c}\mathrm{f}\mathrm{p}\mathrm{p},\mathrm{o}\mathrm{f}\mathrm{f}}-T_j^{\mathrm{c}\mathrm{f}\mathrm{p}\mathrm{p},\mathrm{o}\mathrm{f}\mathrm{f}}\right)·\left(x_{j,k,t}^{\mathrm{c}\mathrm{f}\mathrm{p}\mathrm{p}}-x_{j,k-1,t}^{\mathrm{c}\mathrm{f}\mathrm{p}\mathrm{p}}\right)\ge 0$$

(53)

$$P_{j,k,t}^{\mathrm{c}\mathrm{f}\mathrm{p}\mathrm{p}}-P_{j,k-1,t}^{\mathrm{c}\mathrm{f}\mathrm{p}\mathrm{p}}\le {UR}_j·x_{j,k-1,t}^{\mathrm{c}\mathrm{f}\mathrm{p}\mathrm{p}}$$

(54)

$$P_{j,k-1,t}^{\mathrm{c}\mathrm{f}\mathrm{p}\mathrm{p}}-P_{j,k,t}^{\mathrm{c}\mathrm{f}\mathrm{p}\mathrm{p}}\le {DR}_j·x_{j,k,t}^{\mathrm{c}\mathrm{f}\mathrm{p}\mathrm{p}}$$

(55)

where $X_{j,k,t}^{\mathrm{c}\mathrm{f}\mathrm{p}\mathrm{p},\mathrm{o}\mathrm{n}}$ and $X_{j,k,t}^{\mathrm{c}\mathrm{f}\mathrm{p}\mathrm{p},\mathrm{o}\mathrm{f}\mathrm{f}}$ represent the continuous operational and downtime durations of CFPP $j$ at time $k$ within stage $t$; and $T_j^{\mathrm{c}\mathrm{f}\mathrm{p}\mathrm{p},\mathrm{o}\mathrm{n}}$ and $T_j^{\mathrm{c}\mathrm{f}\mathrm{p}\mathrm{p},\mathrm{o}\mathrm{f}\mathrm{f}}$ represent the minimum startup and shutdown times for CFPP $j$.

(2)

Renewable energy resources operation constraints

The deployment of renewable energy resources is subject to operational constraints that must not surpass their forecasted values, as defined by Equation (56).

$$0\le P_{w,k,t}^{\mathrm{r}\mathrm{e}}\le P_{w,k,t}^{\mathrm{r}\mathrm{e},\mathrm{f}}·y_{w,t}^{\mathrm{r}\mathrm{e}}$$

(56)

(3)

Energy storage system operation constraints

The operation of the energy storage system is subject to constraints including charge/discharge limits, prohibition of simultaneous charging and discharging, energy transition processes, capacity upper and lower bounds, and consistency of initial and terminal energy levels, as expressed in Equations (57)–(62).

$$0\le P_{e,k,t}^{\mathrm{e}\mathrm{s}\mathrm{s},\mathrm{d}\mathrm{i}\mathrm{s}}\le P_e^{\mathrm{e}\mathrm{s}\mathrm{s},\mathrm{m}\mathrm{a}\mathrm{x}}·x_{e,k,t}^{\mathrm{e}\mathrm{s}\mathrm{s},\mathrm{d}\mathrm{i}\mathrm{s}}$$

(57)

$$0\le P_{e,k,t}^{\mathrm{e}\mathrm{s}\mathrm{s},\mathrm{c}\mathrm{h}\mathrm{a}}\le P_e^{\mathrm{e}\mathrm{s}\mathrm{s},\mathrm{m}\mathrm{a}\mathrm{x}}·x_{e,k,t}^{\mathrm{e}\mathrm{s}\mathrm{s},\mathrm{c}\mathrm{h}\mathrm{a}}$$

(58)

$$x_{e,k,t}^{\mathrm{e}\mathrm{s}\mathrm{s},\mathrm{d}\mathrm{i}\mathrm{s}}+x_{e,k,t}^{\mathrm{e}\mathrm{s}\mathrm{s},\mathrm{c}\mathrm{h}\mathrm{a}}\le 1$$

(59)

$$E_{e,k,t}^{\mathrm{e}\mathrm{s}\mathrm{s}}=E_{e,k-1,t}^{\mathrm{e}\mathrm{s}\mathrm{s}}+\left(P_{e,k,t}^{\mathrm{e}\mathrm{s}\mathrm{s},\mathrm{c}\mathrm{h}\mathrm{a}}·{\eta }_e^{\mathrm{e}\mathrm{s}\mathrm{s},\mathrm{c}\mathrm{h}\mathrm{a}}-P_{e,k,t}^{\mathrm{e}\mathrm{s}\mathrm{s},\mathrm{c}\mathrm{h}\mathrm{a}}/{\eta }_e^{\mathrm{e}\mathrm{s}\mathrm{s},\mathrm{d}\mathrm{i}\mathrm{s}}\right)$$

(60)

$$E_e^{\mathrm{e}\mathrm{s}\mathrm{s},\mathrm{m}\mathrm{a}\mathrm{x}}·{\rho }^{\mathrm{e}\mathrm{s}\mathrm{s},\mathrm{m}\mathrm{i}\mathrm{n}}·y_{e,t}^{\mathrm{e}\mathrm{s}\mathrm{s}}\le E_{e,k,t}^{\mathrm{e}\mathrm{s}\mathrm{s}}\le E_e^{\mathrm{e}\mathrm{s}\mathrm{s},\mathrm{m}\mathrm{a}\mathrm{x}}·{\rho }^{\mathrm{e}\mathrm{s}\mathrm{s},\mathrm{m}\mathrm{a}\mathrm{x}}·y_{e,t}^{\mathrm{e}\mathrm{s}\mathrm{s}}$$

(61)

$$E_{e,0,t}^{\mathrm{e}\mathrm{s}\mathrm{s}}=E_{e,\mathrm{H}\mathrm{o}\mathrm{r}\mathrm{i}\mathrm{z}\mathrm{o}\mathrm{n},t}^{\mathrm{e}\mathrm{s}\mathrm{s}}=E_e^{\mathrm{e}\mathrm{s}\mathrm{s},\mathrm{m}\mathrm{a}\mathrm{x}}·{\rho }^{\mathrm{e}\mathrm{s}\mathrm{s},\mathrm{i}\mathrm{n}\mathrm{i}}$$

(62)

where $P_{e,k,t}^{\mathrm{e}\mathrm{s}\mathrm{s},\mathrm{d}\mathrm{i}\mathrm{s}}$ and $P_{e,k,t}^{\mathrm{e}\mathrm{s}\mathrm{s},\mathrm{c}\mathrm{h}\mathrm{a}}$ represent the discharge and charge power of the energy storage system $e$ at time $k$ in stage $t$, respectively; $P_e^{\mathrm{e}\mathrm{s}\mathrm{s},\mathrm{m}\mathrm{a}\mathrm{x}}$ represents the upper limit of the discharge and charge power of the energy storage system $e$; $x_{e,k,t}^{\mathrm{e}\mathrm{s}\mathrm{s},\mathrm{d}\mathrm{i}\mathrm{s}}$ and $x_{e,k,t}^{\mathrm{e}\mathrm{s}\mathrm{s},\mathrm{c}\mathrm{h}\mathrm{a}}$ represent the discharge and charge states of the energy storage system $e$ at time $k$ in stage $t$, controlled by 0–1 variables; $E_{e,k,t}^{\mathrm{e}\mathrm{s}\mathrm{s}}$ represents the stored energy of the energy storage system $e$ at time $k$ in stage $t$; ${\eta }_e^{\mathrm{e}\mathrm{s}\mathrm{s},\mathrm{d}\mathrm{i}\mathrm{s}}$ and ${\eta }_e^{\mathrm{e}\mathrm{s}\mathrm{s},\mathrm{c}\mathrm{h}\mathrm{a}}$ represent the discharge and charge efficiencies of the energy storage system $e$, respectively; ${\rho }^{\mathrm{e}\mathrm{s}\mathrm{s},\mathrm{m}\mathrm{a}\mathrm{x}}$ and ${\rho }^{\mathrm{e}\mathrm{s}\mathrm{s},\mathrm{m}\mathrm{i}\mathrm{n}}$ represent the upper and lower limit coefficients of the energy storage system’s capacity, respectively; $E_e^{\mathrm{e}\mathrm{s}\mathrm{s},\mathrm{m}\mathrm{a}\mathrm{x}}$ represents the rated capacity of the energy storage system e; and ${\rho }^{\mathrm{e}\mathrm{s}\mathrm{s},\mathrm{i}\mathrm{n}\mathrm{i}}$ represents the initial capacity coefficient of the energy storage system.

(4)

Power balance constraints

The system must maintain real-time power balance, and the load shedding should not exceed the load, as shown in Equations (63)–(64).

$$\begin{gathered} \begin{array}{cc}\hfill {\displaystyle \sum _{j\in {\mathsf{\Omega }}_{\mathrm{c}\mathrm{f}\mathrm{p}\mathrm{p}}}}{P}_{j,k,t}^{\mathrm{n}\mathrm{e}\mathrm{t}}+& {\displaystyle \sum _{w\in {\mathsf{\Omega }}_{\mathrm{r}\mathrm{e}}}}{P}_{w,k,t}^{\mathrm{r}\mathrm{e}}+{\displaystyle \sum _{j\in {\mathsf{\Omega }}_{\mathrm{c}\mathrm{f}\mathrm{p}\mathrm{p}}}}\left(P_{j,k,t}^{\mathrm{c}\mathrm{b},\mathrm{d}\mathrm{i}\mathrm{s}}-P_{j,k,t}^{\mathrm{c}\mathrm{b},\mathrm{c}\mathrm{h}\mathrm{a}}\right)\hfill \\ & +{\displaystyle \sum _{e\in {\mathsf{\Omega }}_{\mathrm{e}\mathrm{s}\mathrm{s}}}}\left(P_{e,k,t}^{\mathrm{e}\mathrm{s}\mathrm{s},\mathrm{d}\mathrm{i}\mathrm{s}}-P_{e,k,t}^{\mathrm{e}\mathrm{s}\mathrm{s},\mathrm{c}\mathrm{h}\mathrm{a}}\right)\hfill \end{array} \\ ={\displaystyle \sum _{i\in {\mathsf{\Omega }}_{\mathrm{l}\mathrm{o}\mathrm{a}\mathrm{d}}}}\left(P_{i,k,t}^{\mathrm{l}\mathrm{o}\mathrm{a}\mathrm{d}}-P_{i,k,t}^{\mathrm{l}\mathrm{o}\mathrm{a}\mathrm{d},\mathrm{l}\mathrm{o}\mathrm{s}\mathrm{s}}\right) \end{gathered}$$

(63)

$$P_{i,k,t}^{\mathrm{l}\mathrm{o}\mathrm{a}\mathrm{d},\mathrm{l}\mathrm{o}\mathrm{s}\mathrm{s}}\le P_{i,k,t}^{\mathrm{l}\mathrm{o}\mathrm{a}\mathrm{d}}$$

(64)

3.3. Abstract Expression

For the purpose of facilitating discussion, the collaborative planning model is formulated in an abstract manner, as demonstrated in Equations (65)–(68). Specifically, ${\mathit{x}}_t$ denotes the binary decision variables for stage $t$, encompassing the selection of CFPP retrofitting pathways and investments in renewable energy resources and energy storage systems. The continuous variables, ${\mathit{y}}_t$, represent the optimal operational decisions for each stage, such as the output of CFPPs and the charging, discharging, and energy levels of energy storage systems. Notably, constraint (67) pertains to investment constraints, while all operational constraints that couple investment and operational decision variables are presented in (68).

$$\underset{\left\{\mathit{x},\mathit{y}\right\}}{\min }{\sum }_{t=1}^{NT}{\mathit{c}}_a^{\mathrm{T}}{\mathit{x}}_t+{\mathit{c}}_b^{\mathrm{T}}{\mathit{y}}_t$$

(65)

$$\mathrm{s}.\mathrm{t}.{\mathit{x}}_t\in \left\{0,1\right\}$$

(66)

$$\mathit{A}{x}_t\le {\mathit{c}}_{\mathit{l}}$$

(67)

$$\mathit{D}{\mathit{x}}_t+\mathit{E}{\mathit{y}}_t\le \mathit{f}$$

(68)

where ${\mathit{c}}_a$, ${\mathit{c}}_b$, ${\mathit{c}}_l$, $\mathit{f}$, and $\mathit{A}$, $\mathit{D}$, $\mathit{E}$ denote abstract vector and matrix representations of appropriate dimensions.

3.4. Collaborative Planning Model Considering Uncertainties of Renewable Energy Sources

The uncertainty of renewable energy poses a major challenge in the low-carbon transformation of power systems. To address this, a stochastic programming model for coordinated planning is proposed. In this model, the decision variables are divided into two parts: discrete investment decisions, which constitute the first stage; and flexible power and energy storage charging and discharging capacities, referred to as the second-stage variables. The first-stage variables remain fixed regardless of uncertainty, while the second-stage variables adjust in response to uncertainty. The Monte Carlo simulation method is used to generate a sufficient number of renewable energy uncertainty scenarios, which are then reduced using a reduction scheme technique to obtain a few representative scenarios, balancing computation speed and result accuracy [25]. As a result, Equations (65)–(68) can be rewritten as follows:

$$\underset{\left\{\mathit{x},\mathit{y}\right\}}{\min }{\sum }_{t=1}^{NT}\left({\mathit{c}}_a^{\mathrm{T}}{\mathit{x}}_t+{\sum }_{\varrho =1}^{RS}{p_{\varrho }\mathit{c}}_b^{\mathrm{T}}{\mathit{y}}_{t,\varrho }\left({\upsilon }_{t,\varrho }\right)\right)$$

(69)

$$\mathrm{s}.\mathrm{t}.{\mathit{x}}_t\in \left\{0,1\right\}$$

(70)

$$\mathit{A}{x}_t\le {\mathit{c}}_{\mathit{l}}$$

(71)

$$\mathit{D}{\mathit{x}}_t+\mathit{E}{\mathit{y}}_{t,\varrho }\left({\upsilon }_{t,\varrho }\right)\le \mathit{f}$$

(72)

where ${\upsilon }_{t,\varrho }$ represents the $\varrho$-th scenario, and $p_{\varrho }$ denotes the probability of scenario $\varrho$.

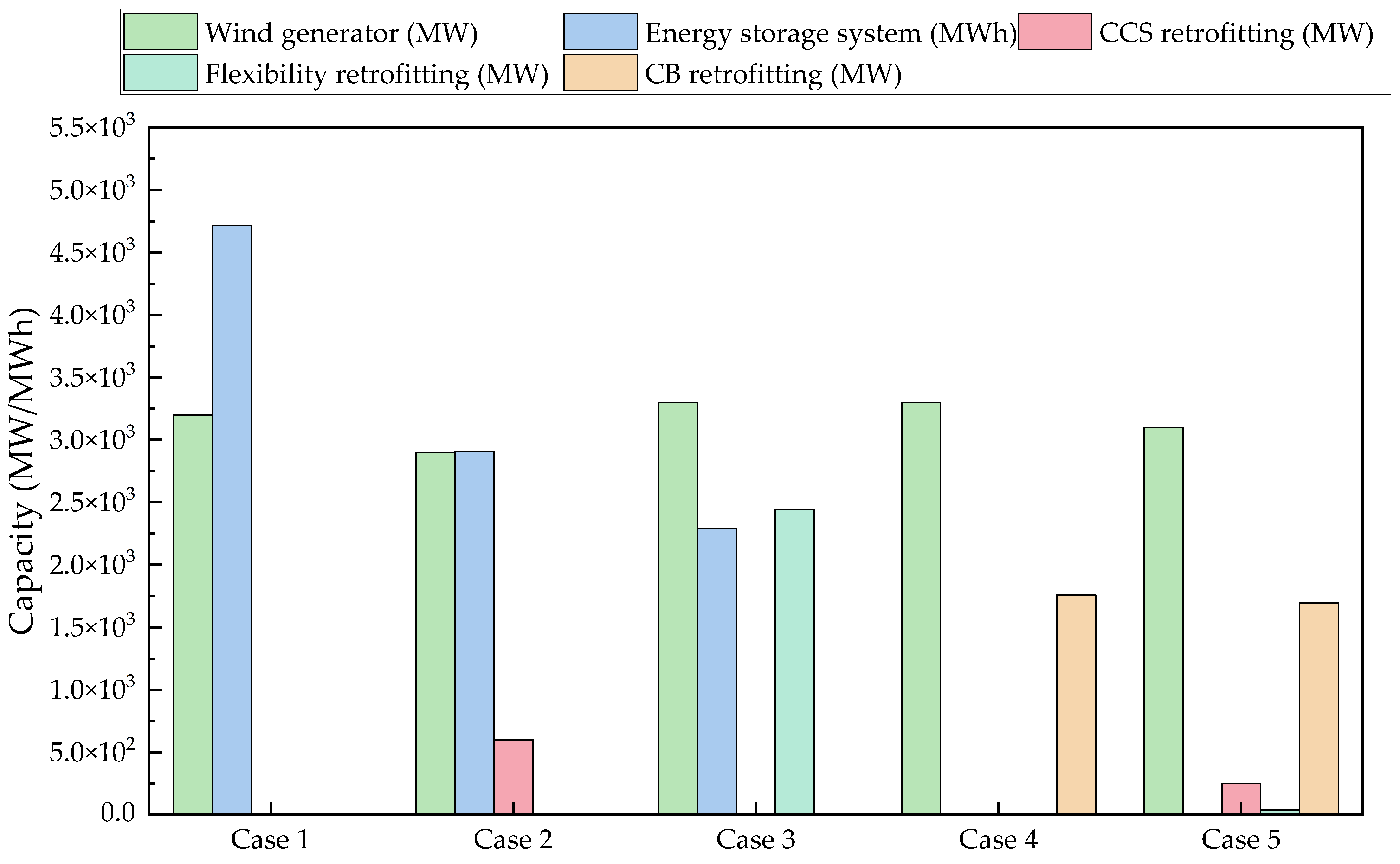
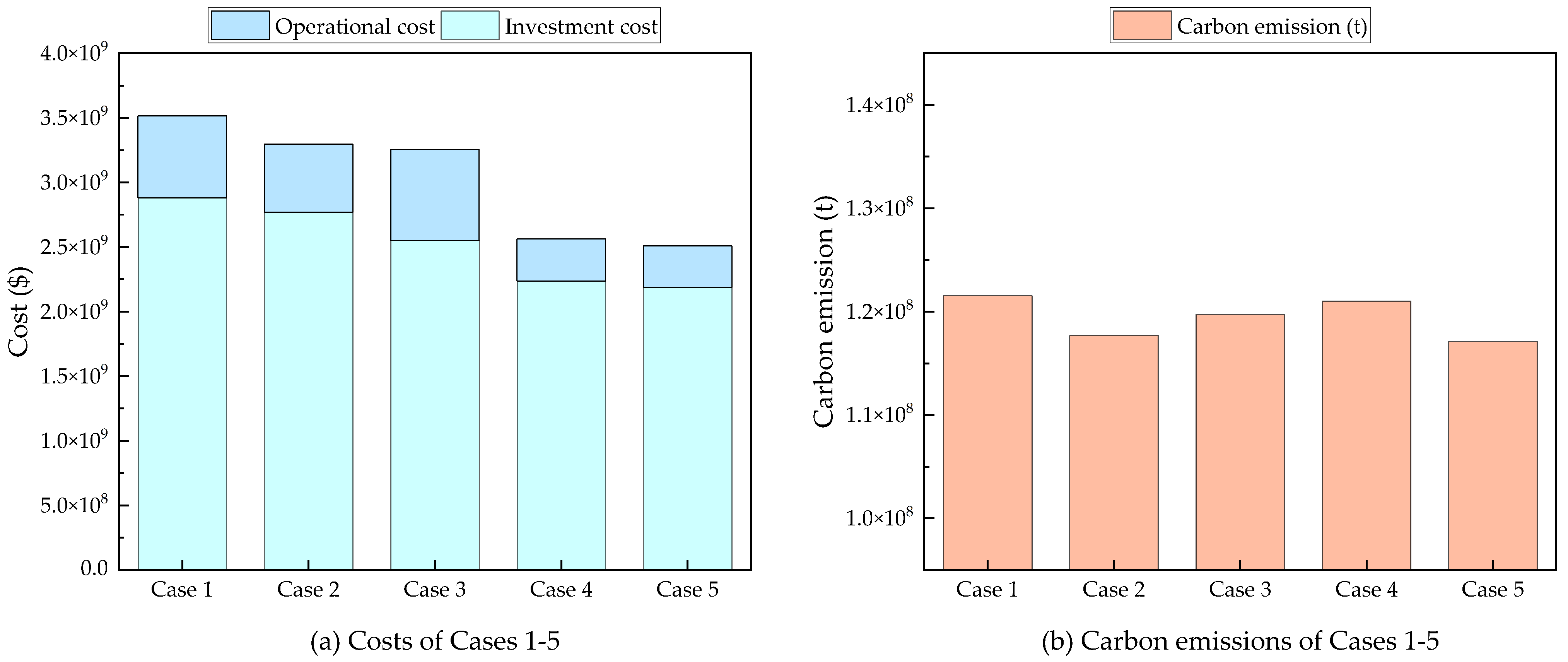
4. Case Studies

In this section, we describe how two test systems were used to verify the effectiveness of the proposed method. The proposed methodology was implemented in MATLAB R2022a with numerical optimization performed through Gurobi 11.0.2, with the optimality gap threshold set to 0.1%. All computational experiments were executed on a PC with an AMD Ryzen 9 7950X 16-core processor and 32 GB RAM.

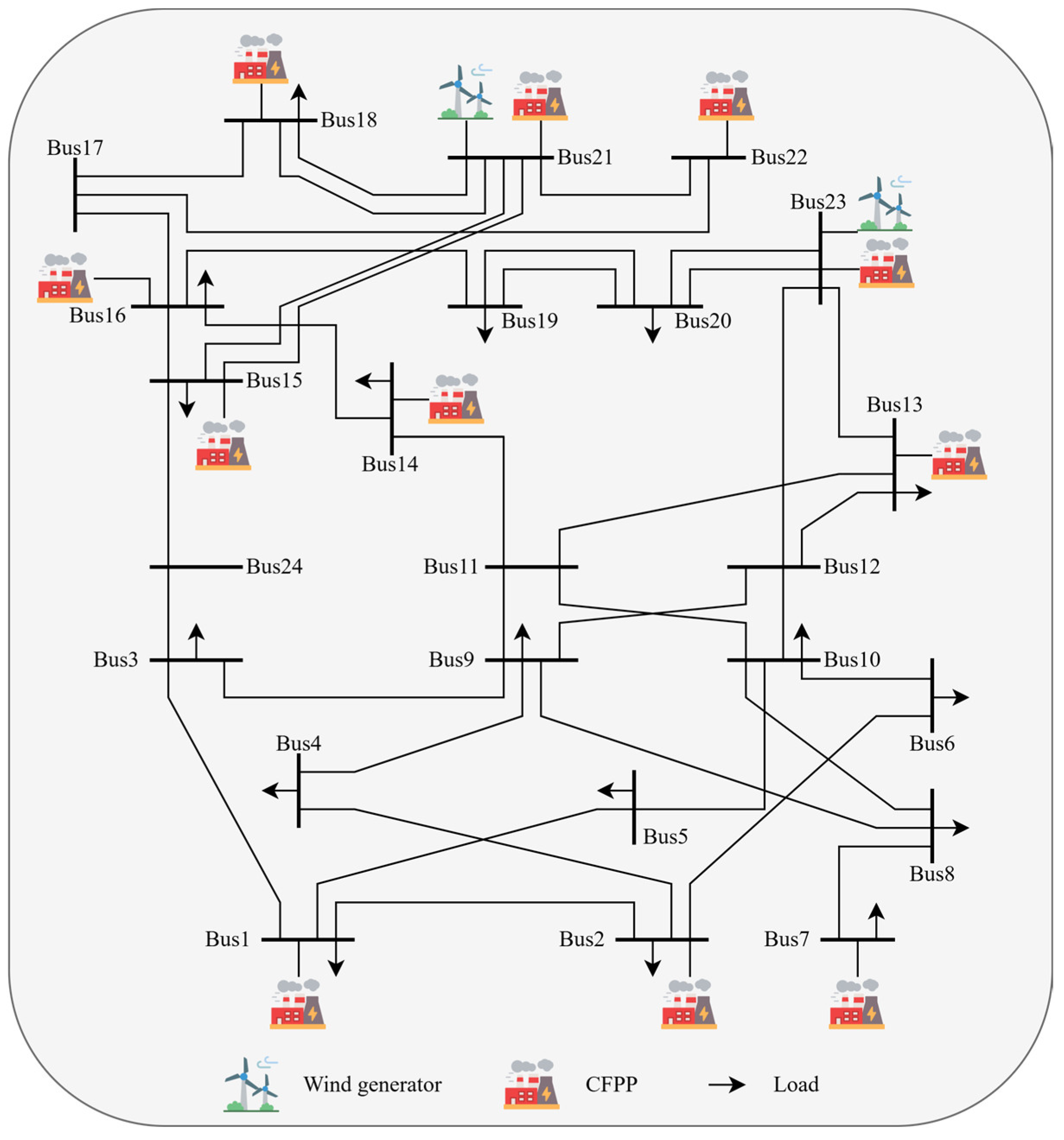
4.1. IEEE RTS 24-Bus Test System

The IEEE RTS 24-bus test system (as depicted in Figure 3) was employed to validate the efficacy of the proposed model [26]. This power system comprises 32 CFPPs, with a total capacity of 3650 MW, and four wind farms, totaling 400 MW [27,28]. To streamline the computation, the planning period was defined as a five-year interval. Investments in wind generators, energy storage systems, and the transformation of CFPPs were assumed to be completed within the initial year of each stage. The total planning horizon encompassed 15 years (NT = 3), with each stage represented by a single typical day of 24 h (NK = 24). The parameters associated with the coal-fired power plants are detailed in

Table 1. Parameters associated with CFPPs.

Parameters	Value	Parameters	Value
$c^{\mathrm{c}\mathrm{c}\mathrm{s}}$	607,730 $/MW	$c^{\mathrm{s}\mathrm{g}}$	100,000 $/MW
$c^{\mathrm{f}\mathrm{l}\mathrm{e}\mathrm{x}}$	155,000 $/MW	${\lambda }_j$	90%
$c^{\mathrm{e}\mathrm{h}\mathrm{e}}$	50,000 $/MW	${\mu }_j$	0.269 MWh/t
$c^{\mathrm{t}\mathrm{e}\mathrm{s}}$	30,000 $/MW	${\zeta }_j$	1.08 t/MWh

. The investment in renewable energy resources is limited to the deployment of wind turbine generators. Parameters pertinent to the renewable energy resources and energy storage systems are presented in

Table 2. Parameters associated with renewable energy resources and energy storage systems.

Parameters	Value	Parameters	Value
$c^{\mathrm{r}\mathrm{e}}$	1,097,900 $/MW	${\eta }_e^{\mathrm{e}\mathrm{s}\mathrm{s},\mathrm{c}\mathrm{h}\mathrm{a}}/{\eta }_e^{\mathrm{e}\mathrm{s}\mathrm{s},\mathrm{d}\mathrm{i}\mathrm{s}}$	0.9
$c^{\mathrm{e}\mathrm{s}\mathrm{s}}$	300,000 $/MW	${\rho }^{\mathrm{e}\mathrm{s}\mathrm{s},\mathrm{i}\mathrm{n}\mathrm{i}}$	0.4
$E_e^{\mathrm{e}\mathrm{s}\mathrm{s},\mathrm{m}\mathrm{a}\mathrm{x}}$	1 MWh	${\rho }^{\mathrm{e}\mathrm{s}\mathrm{s},\mathrm{m}\mathrm{a}\mathrm{x}}$	0.9
$P_e^{\mathrm{e}\mathrm{s}\mathrm{s},\mathrm{m}\mathrm{a}\mathrm{x}}$	0.2 MW	${\rho }^{\mathrm{e}\mathrm{s}\mathrm{s},\mathrm{m}\mathrm{i}\mathrm{n}}$	0.1

.

Case 1: Low-carbon power system planning without CFPP retrofitting.

Case 2: Low-carbon power system planning with CCS retrofitting (Reference [12]).

Case 3: Low-carbon power system planning with flexibility retrofitting (Reference [9]).

Case 4: Low-carbon power system planning with CB retrofitting (Reference [15]).

Case 5: Low-carbon power system planning with multiple CFPP retrofitting pathways.

Case 6: Case 5 with participation in the CET market (Reference [16]).

Case 7: Case 5 with participation in the GCT market (Reference [18]).

Case 8: Case 5 with participation in both the CET and the GCT markets (Reference [20]).

Case 9: Case 5 with the carbon–green certificate market coupling mechanism.

Case 1 (Baseline case): As illustrated in Figure 4 and Figure 5, the deployment includes 3200 MW of wind generators and 4719 MWh of energy storage systems, resulting in total costs of 3516 M$ and total carbon emissions of 121.3 Mt.

Case 2: This case examines the impact of a CCS retrofitting. Relative to Case 1, the wind generator capacity decreases by 300 MW and the CCS retrofitting capacity increases by 600 MW. Moreover, the energy storage system capacity declines by 1811 MWh. The total cost decreases by 6.24%, and carbon emissions decline by 2.55%. The CCS retrofitting enables the CFPP to continue generating power, reduce emissions, and provide grid-balancing flexibility.

Case 3: This case investigates the effect of flexibility retrofitting. Relative to Case 1, the wind generator capacity increases by 100 MW and the flexibility retrofitting capacity increases by 2441 MW. The energy storage system capacity declines by 2427 MWh. The total cost decreases by 7.43%, while carbon emissions decline by 1.21%. The flexibility retrofitting enhances the plant’s regulation capability and improves the integration of renewable energy. However, the requirement to maintain a minimum output for system stability constrains achievable emission reductions.

Case 4: This case evaluates CB retrofitting. Relative to Case 1, the wind generator capacity increases by 100 MW and the CB retrofitting capacity increases by 1758 MW. The energy storage system capacity decreases by 4719 MWh. The total cost decreases by 24.27%, and carbon emissions decline by 0.36%. The CB retrofit preserves grid-regulation flexibility and improves energy utilization efficiency. By replacing the need for separate storage, it lowers the total cost, although its lower round-trip efficiency limits emission reductions.

Case 5: This case investigates the combined implementation of all three CFPP retrofitting pathways. Compared to Cases 2 and 3, the total cost decreases by 23.92% and 22.94%, respectively; compared to Case 4, it decreases by 5.80%. Similarly, carbon emissions decline by 0.40%, 1.75%, and 2.60% relative to Cases 2, 3, and 4, respectively. This combined approach leverages the complementary benefits of CCS, flexibility, and CB retrofits, resulting in improved cost-effectiveness and enhanced operational flexibility for large-scale renewable integration.

Case 6: This case extends Case 5 by integrating the CET market. Figure 6a,b present the cost and emission results for Cases 5–7, while Figure 7 details the installed capacities. Compared to Case 5, the CCS retrofitting capacity increases by 1620 MW, resulting in a 7.97% reduction in total cost and a 27.52% decrease in carbon emissions. Investment costs increase by 412.8 M$, whereas operating expenses decrease by 612.6 M$ and emissions decline by 32.4 Mt. These changes enable the acquisition of surplus emission allowances, yielding a net financial benefit.

Case 7: This case examines the inclusion of the GCT market. Compared to Case 5, the wind generator capacity increases by 200 MW, the CCS retrofitting capacity decreases by 250 MW, and the flexibility retrofitting capacity increases by 90 MW. This leads to a 2.95% reduction in total costs, while carbon emissions increase by 0.42%. The increase in wind turbine capacity is primarily driven by the system’s ability to profit from trading surplus green certificates in the GCT market, thus improving the system’s economic feasibility. However, the expansion of renewable energy capacity increases the demand for system flexibility, necessitating a corresponding increase in flexibility retrofit capacity, which explains the increase in carbon emissions. Therefore, while the flexibility retrofit enhances the system’s capacity to accommodate renewable energy fluctuations, it also increases the operational demand of CFPPs, leading to a slight increase in carbon emissions.

Case 8: This case considers both the CET and the GCT market, excluding the offset mechanism. The results for Case 8 are presented in

Table 3. Planning results for Case 8 and Case 9.

Case	Total Cost	Carbon Emissions	Installed Capacity
			Wind Generator	CCS Retrofitting	Flexibility Retrofitting	CB Retrofitting
Case 8	2182 M$	69.39 Mt	3800 MW	100 MW	150 MW	2446 MW
Case 9	2055 M$	62.18 Mt	4700 MW	100 MW	-	3396 MW

. Compared to Case 6 and Case 7, Case 8 demonstrates significant improvements in both total costs and carbon emissions. Specifically, the total costs decrease by 5.47% and 10.35%, and the carbon emissions decline by 18.64% and 41.28%, respectively. The simultaneous consideration of both markets plays a crucial role in optimizing the energy mix and enhancing economic efficiency.

Case 9: The introduction of the carbon–green certificate market coupling mechanism is analyzed. According to the data in Table 3, compared to Case 8, the wind generator capacity increases by 900 MW, and the CB retrofit capacity increases by 950 MW. Consequently, the total costs decrease by 5.82%, and carbon emissions are reduced by 10.39%. The significant increase in wind generator and CB retrofit capacity not only reduces costs, but also improves the system’s carbon footprint. Furthermore, the enhanced CB retrofit capacity improves the system’s renewable energy absorption and storage capability, allowing for better regulation of fluctuating electricity demand. This transition significantly increases renewable energy utilization and mitigates the economic losses associated with energy fluctuations. Importantly, the carbon–green certificate market coupling mechanism facilitates the conversion of green certificates within the carbon market, providing additional economic incentives for green energy projects. This coupling mechanism offers greater flexibility and incentives in carbon quota allocation, enhancing low-carbon performance and economic efficiency.

To demonstrate the impact of green certificate prices and carbon emission allowance prices on the coordinated planning strategy, a sensitivity analysis was performed based on Case 9. Figure 8 and Figure 9 present the results of the sensitivity analysis.

As shown in Figure 8, when the carbon emission allowance price level increases from 0.5 to 1.5, the wind power installed capacity rises by 1000 MW, the CCS retrofitting capacity increases by 1042 MW, the flexibility retrofitting capacity decreases by 1050 MW, and the CB retrofitting capacity grows by 890 MW. Carbon emissions decrease from 116.34 Mt to 55.82 Mt, reflecting a reduction of 52.02%. The higher carbon emission allowance price accelerates CFPP retrofits and wind power unit construction, prioritizing CCS and CB retrofits to maintain power balance and significantly reduce carbon emissions.

As shown in Figure 9, when the green certificate price level increases from 0.5 to 1.5, the wind power installed capacity rises by 1600 MW, the CCS retrofit capacity declines by 1350 MW, the CB retrofit capacity grows by 1455 MW, and carbon emissions decrease by 31.7%. While the green certificate price change does not directly affect carbon emissions, the increase in green certificate prices results in the construction of more wind power units, thus lowering the system’s carbon emissions. The increase in CB retrofit capacity aims to provide adequate flexibility adjustment resources.

The conversion coefficient $\varpi$ is critical to the carbon–green certificate market coupling mechanism, as it affects the number of green certificates that can offset carbon emissions, thereby influencing the system’s carbon emissions. Therefore, a sensitivity analysis was conducted based on Case 9. The results are shown in

Table 4. Sensitivity analysis results for different conversion coefficients.

$\mathbf{Conversion} \mathbf{Coefficient} \mathit{\varpi }$	Total Cost	Carbon Emissions	Installed Capacity
			Wind Generator	CCS Retrofitting	Flexibility Retrofitting	CB Retrofitting
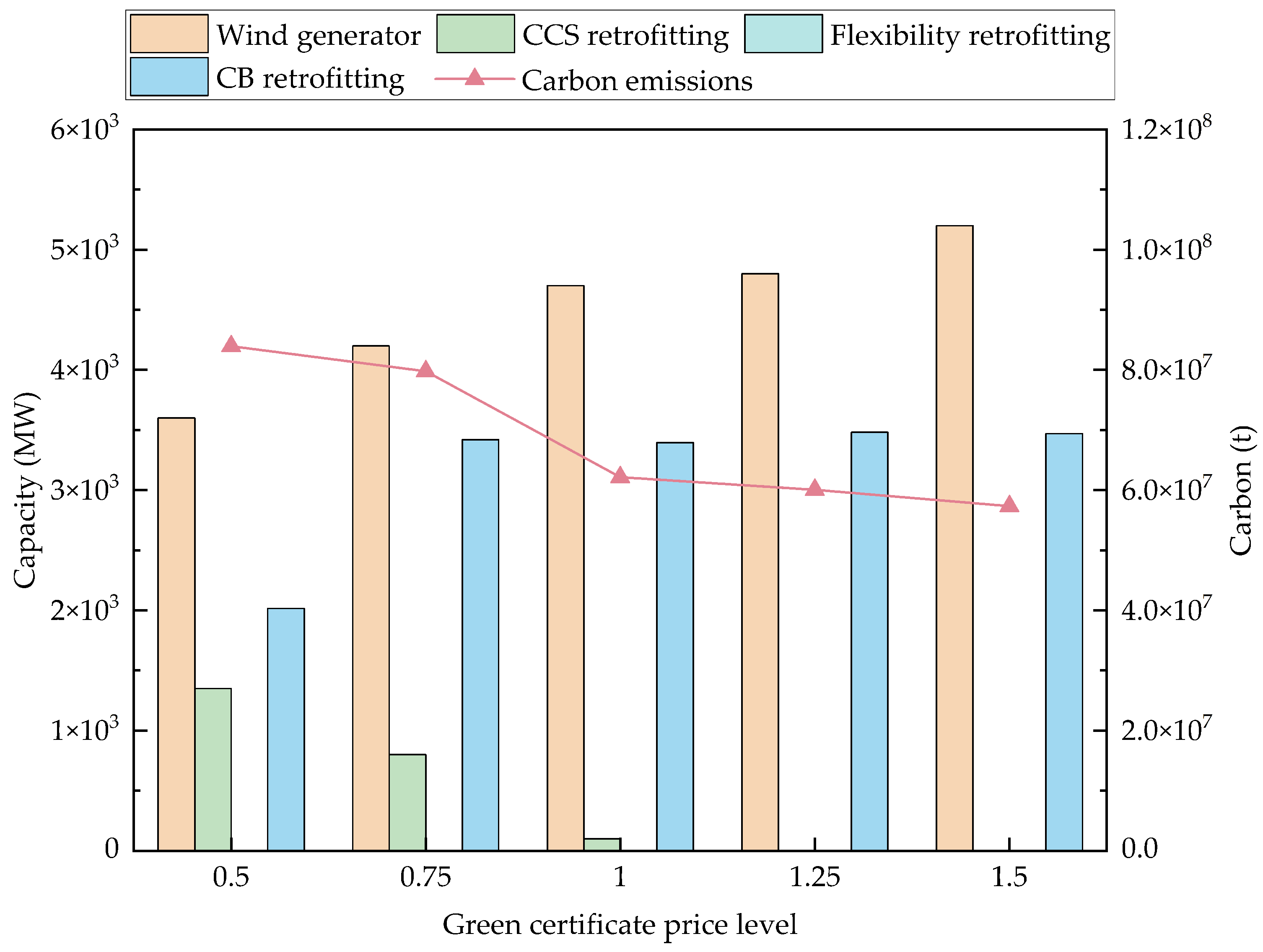
0.25	2261 M$	73.96 Mt	4100 MW	804 MW	40 MW	2692 MW
0.375	2172 M$	67.87 Mt	4500 MW	100 MW	40 MW	3086 MW
0.5	2055 M$	62.18 Mt	4700 MW	100 MW	-	3396 MW
0.625	1944 M$	65.25 Mt	4700 MW	100 MW	-	3396 MW
0.75	1819 M$	67.71 Mt	4900 MW	-	-	3446 MW

.

As shown in Table 4, as the conversion coefficient increases, the total system cost gradually decreases, while carbon emissions initially decrease and then increase, reaching a minimum at 0.5. The wind generator installed capacity continuously increases, and the CB retrofit capacity increases to accommodate more renewable energy integration.

The power generation of wind turbines is significantly affected by wind speed variations, exhibiting considerable volatility. In low-carbon power system planning, it is crucial to consider the uncertainty in wind turbine output. Therefore, an additional case was introduced.

Case 10: This case considers the uncertainty in wind turbine output based on Case 9.

Case 10: To simulate the uncertainty, 10,000 wind turbine scenarios were developed. After applying scenario reduction techniques to balance efficiency and accuracy, five scenarios were retained. The planning results for this scenario are shown in

Table 5. Planning results of Case 10.

Case	Total Cost	Carbon Emissions	Installed Capacity
			Wind Generator	CCS Retrofitting	Flexibility Retrofitting	CB Retrofitting
Case 10	2183 M$	64.71 Mt	4600 MW	100 MW	80 MW	3546 MW

. As shown in the table, after considering the uncertainty in wind turbine output, the wind turbine installed capacity decreases by 100 MW, the flexibility retrofit capacity increases by 80 MW, and the CB retrofit capacity increases by 150 MW. As a result, total costs increase by 5.86%, and carbon emissions rise by 3.91%. To address the uncertainty in wind turbine output, the system increases the flexibility retrofit and CB retrofit capacities to improve energy utilization efficiency and system regulation capability.

4.2. IEEE 118-Bus System

To further validate the efficacy of the proposed collaborative planning framework for large-scale system networks, this section presents simulations based on the IEEE 118-bus system. The IEEE 118-bus system comprises 54 CFPPs (7059 MW) and 10 wind farms (1000 MW) [28]. Similar cases were tested, and their costs and computational performance are presented in

Table 6. Planning results of Cases 1–10 in IEEE 118-node system.

Case	Investment Cost	Operational Cost	Total Cost	Carbon Emissions	Computation Time
Case 1	31.604 B$	1.081 B$	32.684 B$	335.93 Mt	467 s
Case 2	28.370 B$	0.911 B$	29.281 B$	280.67 Mt	542 s
Case 3	29.554 B$	1.342 B$	30.896 B$	325.01 Mt	617 s
Case 4	26.466 B$	0.586 B$	27.052 B$	334.22 Mt	593 s
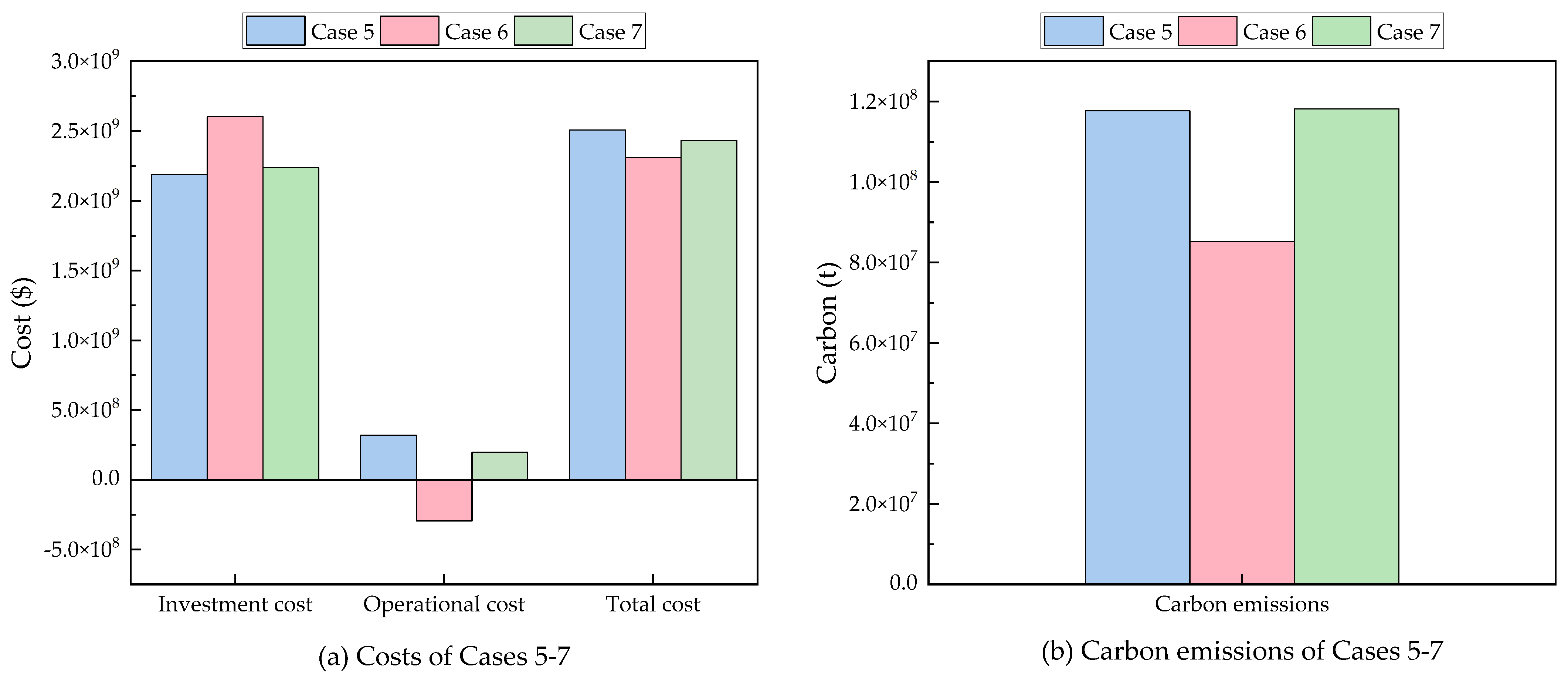
Case 5	24.008 B$	0.691 B$	24.699 B$	270.39 Mt	2668 s
Case 6	25.564 B$	−3.008 B$	22.556 B$	229.82 Mt	3101 s
Case 7	24.462 B$	0.136 B$	24.598 B$	270.81 Mt	2974 s
Case 8	19.762 B$	1.695 B$	21.457 B$	190.20 Mt	3238 s
Case 9	19.278 B$	1.241 B$	20.519 B$	174.67 Mt	3443 s
Case 10	20.633 B$	1.781 B$	22.414 B$	189.90 Mt	18,765 s

.

As shown in Table 6, the total cost and carbon emissions of Cases 2–4 decrease after considering various retrofitting pathways. Compared to Case 1, the integration of all three retrofitting pathways for CFPPs in Case 5 results in a 24.43% reduction in total cost and a 19.51% decrease in carbon emissions. These retrofits enhance both economic performance and low-carbon efficiency. With the inclusion of CET and GCT, Case 8 sees further reductions, with the total cost and carbon emissions decreasing by 13.13% and 29.66%, respectively, compared to Case 5. The introduction of the carbon–green certificate coupling mechanism in Case 9 further improves these outcomes, reducing the total cost by 0.938 B$ (from 21.457 B$ in Case 8) and lowering carbon emissions by 15.53 Mt. The carbon–green certificate coupling mechanism provides enhanced flexibility and stronger incentives for carbon reduction, thus improving both low-carbon performance and economic efficiency. However, when uncertainties are considered, the total cost increases by 8.45%, indicating that a more reliable and secure plan comes at the expense of economic efficiency.

Additionally, the calculation times for Cases 1–10 demonstrate that, after incorporating the transformation of coal-fired power plants and the carbon–green certificate market coupling mechanism, additional constraints and related variables are introduced, thereby increasing the computational burden of collaborative planning. Furthermore, the calculation time is notably longer when wind power uncertainty is considered. This is due to the collaborative planning model introducing a second phase to account for wind uncertainty alongside other variables and constraints, thus further extending the calculation time. While the increase in calculation time is evident, it remains acceptable for practical engineering applications [29]. Thus, the results above demonstrate the scalability of the proposed method in large-scale systems.

5. Discussion

(1) The retrofitting of CFPPs presents diverse pathways for future power system evolution, particularly in facilitating low-carbon transition strategies. The integration of CCS technologies enables the mitigation of greenhouse gas emissions, while preserving existing power generation capacity. Flexibility upgrades enhance grid stability and support the integration of renewable energy sources, thereby optimizing power system efficiency. Furthermore, the CB offers an efficient energy storage solution, with its high round-trip efficiency and rapid charge–discharge capabilities proving effective in addressing the intermittency challenges associated with renewable energy sources.

(2) The carbon–green certificate market coupling mechanism accelerates the energy transition by enhancing market flexibility and efficiency. By providing businesses with expanded emission reduction options and incentives for green energy procurement, this mechanism effectively promotes carbon emission reductions and the adoption of renewable energy, thereby contributing to global emission reduction targets and energy structure transformation.

(3) Both CFPP retrofitting and the carbon–green certificate coupling mechanism contribute to improved system economics, increased renewable energy utilization, and reduced carbon emissions. The former focuses on reducing carbon emissions from CFPPs, mitigating the risk of stranded assets. The latter emphasizes increasing the grid integration of renewable energy. Combining these strategies can further limit system carbon emissions and expand the integration of new energy sources without compromising system economics, thereby demonstrating the benefits of high renewable energy penetration and driving the power system towards a green, intelligent, and sustainable trajectory.

(4) This paper proposes a planning framework for the transformation of coal-fired power plants and the integration of the carbon–green certificate coupling mechanism. However, the proposed framework does not account for regional or national differences in carbon trading policies, renewable energy targets, emission reduction strategies, and infrastructure constraints. Additionally, the potential impacts of air pollution reduction and increased water resource use during carbon capture and storage are not considered. Therefore, future research will focus on developing a low-carbon integrated planning framework that incorporates regulatory challenges, infrastructure limitations, and synergies with other factors.

6. Conclusions

To mitigate carbon emissions within power systems, this paper introduces a low-carbon planning methodology that integrates CFPP retrofitting with a carbon–green certificate market coupling mechanism. We develop mathematical models for three distinct retrofitting pathways for CFPPs and the carbon–green certificate market coupling. Subsequently, a low-carbon planning model is formulated, incorporating both CFPP retrofitting and the carbon–green certificate market coupling mechanism. The simulation results demonstrate the following:

(1) The proposed low-carbon planning methodology, which considers CFPP retrofitting and a carbon–green certificate market coupling mechanism, facilitates dynamic decision-making regarding CFPP retrofitting, renewable energy resource investments, and energy storage system investments.

(2) Incorporating CFPP retrofitting enhances system economics and reduces carbon emissions. This approach achieves a 28.67% reduction in total costs and a 2.96% reduction in carbon emissions.

(3) The integration of the carbon–green certificate market coupling mechanism provides increased flexibility and incentives within the system. This not only improves the system’s low-carbon performance, but also significantly enhances the overall economic efficiency. Compared to scenarios considering only a single market, the total costs are reduced by 10.96% and 15.56%, respectively, while carbon emissions are reduced by 27.1% and 47.36%, respectively.