Modeling the Electricity Generation Processes of a Combined Solar and Small Hydropower Plant
Abstract
1. Introduction
2. A Review of Tasks and Methods for Modeling the Joint Operation of an SHPP and an SPP
- the dynamic behavior of systems;
- the integration of various energy sources;
- thermodynamic processes;
- electromechanical phenomena.
- increasing the efficiency of the operation of interlocked SHPP and SPP systems (by using SPP energy to replenish additional hydro resources for SHPP electricity production);
- large-scale electricity accumulation due to potential energy generated by the gravitational force of water.
3. Materials and Methods
3.1. Concept of Joint Operation of a Solar Power Plant and a Small Hydropower Plant
3.2. The Task Statement
3.3. Method of Solving Problems
- forming the current structure based on candidate models (model structure synthesis);
- estimating its parameters and verifying the adequacy of the model (parametric identification).
3.3.1. Initialization Phase
- LIMIT is the number of iterations before the depletion of the current candidate model structure;
- S is the total number of candidate models within a single iteration;
- is the maximum allowable number of structural elements in candidate models;
- is the current iteration number;
- MCN is the total number of iterations;
- F is the set of structural elements.
3.3.2. Worker Bee Phase
3.3.3. Explorer Bee Phase
3.3.4. Scout Bee Phase
| Algorithm 1. Algorithm for the Second Stage of Interval Model Identification |
| Step 1. Initialization: Input experimental data Read the current model structure (given as a set of structural elements of size ) from the first stage; Set initial values for the parameter vector ; Set initial values for the coefficients vector (usually set as: ); Input initial values for penalty function coefficients ; Form the objective function ; Set stopping criteria thresholds; Step 2. Iterative Optimization: While none of the stopping criteria are satisfied do: Step 2.1. Update the barrier function by Formula (25); Step 2.2. Compute the gradient of the barrier function (the direction of growth of the value of the barrier function): Step 2.6. Check stopping criteria; End While Step 3. Return parameter vector |
3.4. Models Hydropower and Solar Power Plants
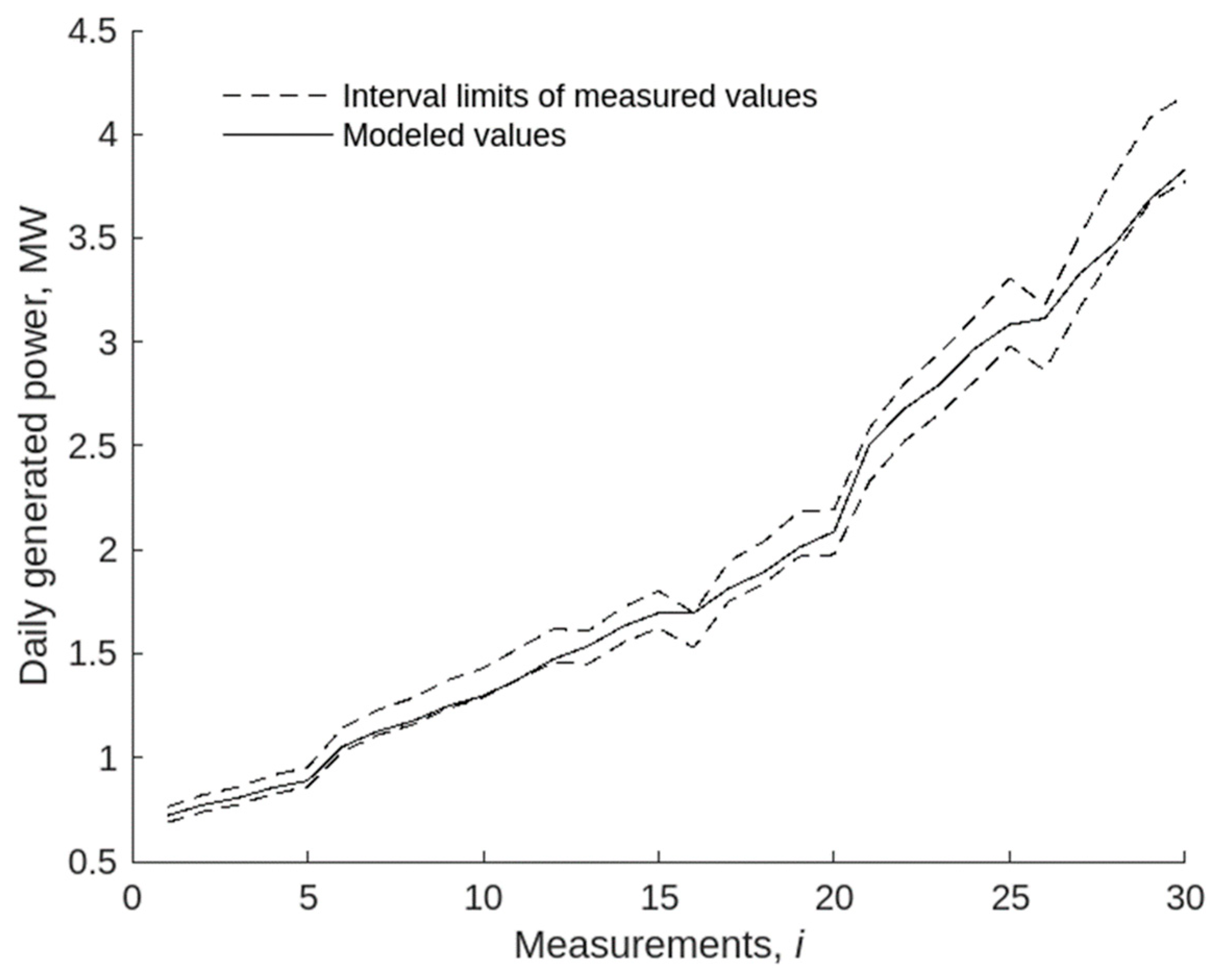
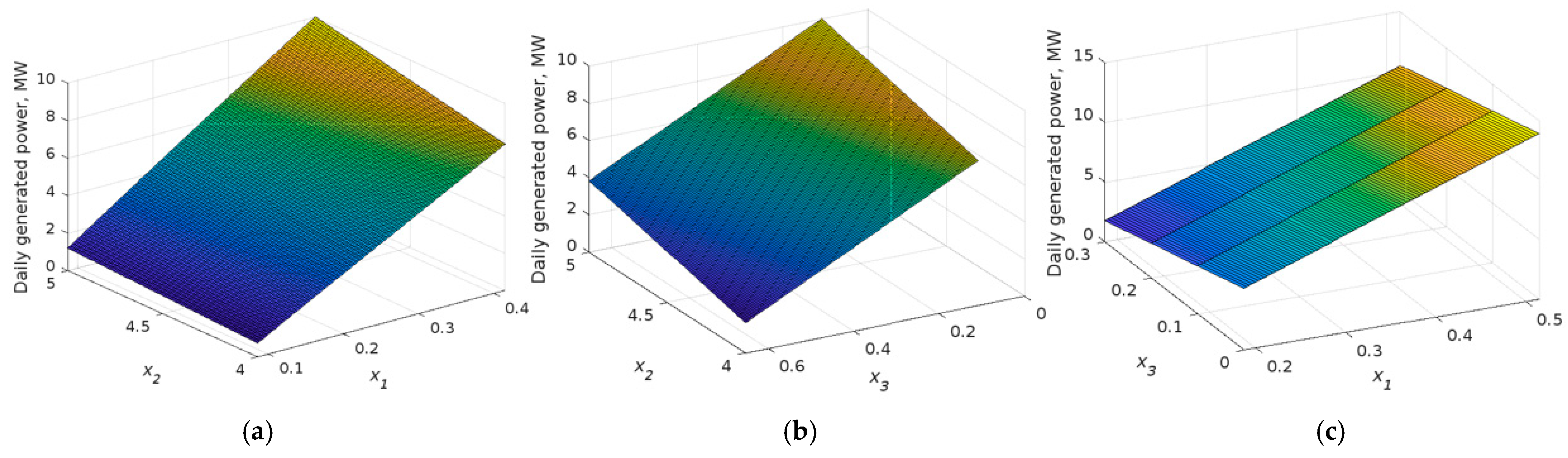
4. Results and Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| SHPP | Small Hydropower Plant |
| SPP | Solar Power Plant |
| DE | Discrete Equation |
| ISNAE | Interval System of Nonlinear Algebraic Equations |
References
- Adelekan, O.A.; Ilugbusi, B.S.; Adisa, O.; Obi, O.C.; Awonuga, K.F.; Asuzu, O.F.; Ndubuisi, N.L. Energy transition policies: A global review of shifts towards renewable sources. Eng. Sci. Technol. J. 2024, 5, 272–287. [Google Scholar] [CrossRef]
- Maka, A.O.M.; Alabid, J.M. Solar energy technology and its roles in sustainable development. Clean Energy 2022, 6, 476–483. [Google Scholar] [CrossRef]
- You, V.; Kakinaka, M. Modern and traditional renewable energy sources and CO2 emissions in emerging countries. Environ. Sci. Pollut. Res. 2022, 29, 17695–17708. [Google Scholar] [CrossRef] [PubMed]
- Deshmukh, M.K.G.; Sameeroddin, M.; Abdul, D.; Sattar, M.A. Renewable energy in the 21st century: A review. Mater. Today Proc. 2023, 80, 1756–1759. [Google Scholar] [CrossRef]
- Fernández, D.G.; Fajardo-Moreno, W.; Moreno-Monsalve, N. Analysis of Non-Conventional Renewable Energy Sources Projects in Colombia. In Proceedings of the 2023 IEEE Colombian Conference on Communications and Computing (COLCOM), Bogota, Colombia, 26–28 July 2023; pp. 1–4. [Google Scholar]
- Büyüközkan, G.; Karabulut, Y.; Mukul, E. A novel renewable energy selection model for United Nations’ sustainable development goals. Energy 2018, 165, 290–302. [Google Scholar] [CrossRef]
- Yousef, L.A.; Yousef, H.; Rocha-Meneses, L. Artificial Intelligence for Management of Variable Renewable Energy Systems: A Review of Current Status and Future Directions. Energies 2023, 16, 8057. [Google Scholar] [CrossRef]
- Koshlak, H. A Review of Earth-Air Heat Exchangers: From Fundamental Principles to Hybrid Systems with Renewable Energy Integration. Energies 2025, 18, 1017. [Google Scholar] [CrossRef]
- Ahmed, B.; Al Mubarak, M.; Khouj, M. Renewable Technologies: Solar Power and Wind Power Energy Utilization—Advantages and Disadvantages. In Technological Sustainability and Business Competitive Advantage. Internet of Things; Al Mubarak, M., Hamdan, A., Eds.; Springer: Cham, Switzerland, 2023. [Google Scholar]
- Rahman, A.; Farrok, O.; Haque, M.M. Environmental impact of renewable energy source based electrical power plants: Solar, wind, hydroelectric, biomass, geothermal, tidal, ocean, and osmotic. Renew. Sustain. Energy Rev. 2022, 161, 112279. [Google Scholar] [CrossRef]
- Idoko, I.P.; Ayodele, T.R.; Abolarin, S.M.; Ewim, D.R.E. Maximizing the cost effectiveness of electric power generation through the integration of distributed generators: Wind, hydro and solar power. Bull. Natl. Res. Cent. 2023, 47, 166. [Google Scholar] [CrossRef]
- Medina, J.C.L.; Concepción, V.H.; Zerpa, F.A.L.; Pino, C.A.M. Gran Canaria energy system: Integration of the chira-soria pumped hydroelectric power plant and analysis of weekly daily demand patterns for the year 2023. Renew. Energy 2024, 232, 121128. [Google Scholar] [CrossRef]
- Jurasz, J.; Tomczyk, P.; Bochenek, B.; Kuriqi, A.; Kasiulis, E.; Chen, D.; Ming, B. Solar-hydro cable pooling–Utilizing the untapped potential of existing grid infrastructure. Energy Convers. Manag. 2024, 306, 118307. [Google Scholar] [CrossRef]
- Fan, J.L.; Huang, X.; Shi, J.; Li, K.; Cai, J.; Zhang, X. Complementary potential of wind-solar-hydro power in Chinese provinces: Based on a high temporal resolution multi-objective optimization model. Renew. Sustain. Energy Rev. 2023, 184, 113566. [Google Scholar] [CrossRef]
- Nasir, J.; Javed, A.; Ali, M.; Ullah, K.; Kazmi, S.A.A. Sustainable and cost-effective hybrid energy solution for arid regions: Floating solar photovoltaic with integrated pumped storage and conventional hydropower. J. Energy Storage 2023, 74, 109417. [Google Scholar] [CrossRef]
- Zeidan, M.; Al-soud, M.; Dmour, M.; Alakayleh, Z.; Al-qawabah, S. Integrating a Solar PV System with Pumped Hydroelectric Storage at the Mutah University of Jordan. Energies 2023, 16, 5769. [Google Scholar] [CrossRef]
- Mamatha, G.; Verma, A.; Kulkarni, P.S. Proposing a Hybrid Solar Electrification for Already Existing Hydropower Plant. In Proceedings of the 2024 IEEE Students Conference on Engineering and Systems (SCES), Prayagraj, India, 21–23 June 2024; pp. 1–6. [Google Scholar]
- Lima, G.M.; Belchior, F.N.; Villena, J.E.N.; Domingos, J.L.; Freitas, M.A.V.; Hunt, J.D. Hybrid electrical energy generation from hydropower, solar photovoltaic and hydrogen. Int. J. Hydrogen Energy 2024, 53, 602–612. [Google Scholar] [CrossRef]
- Dyvak, M.; Melnyk, A.; Manzhula, V.; Petryshyn, N.; Brukhanskyi, R.; Tymets, V. The Approach to Modelling the Joint Operation of a Solar Power Plant and a Small Hydropower Plant. In Proceedings of the 2024 IEEE 17th International Conference on Advanced Trends in Radioelectronics, Telecommunications and Computer Engineering (TCSET 2024), Lviv, Ukraine, 8–12 October 2024; pp. 217–222. [Google Scholar]
- Dyvak, M. Parameters Identification Method of Interval Discrete Dynamic Models of Air Pollution Based on Artificial Bee Colony Algorithm. In Proceedings of the 2020 10th International Conference on Advanced Computer Information Technologies (ACIT), Deggendorf, Germany, 16–18 September 2020; pp. 130–135. [Google Scholar]
- Dyvak, M.; Pukas, A.; Oliynyk, I.; Melnyk, A. Selection the “Saturated” Block from Interval System of Linear Algebraic Equations for Recurrent Laryngeal Nerve Identification. In Proceedings of the 2018 IEEE Second International Conference on Data Stream Mining & Processing (DSMP), Lviv, Ukraine, 21–25 August 2018; pp. 444–448. [Google Scholar]
- Li, Y.; Ming, B.; Huang, Q.; Wang, Y.; Liu, P.; Guo, P. Identifying effective operating rules for large hydro–solar–wind hybrid systems based on an implicit stochastic optimization framework. Energy 2022, 245, 123260. [Google Scholar] [CrossRef]
- Gonzalez-Gonzalez, J.J.; Arenas-López, J.P.; Badaoui, M. Advancing towards zero emissions: Integrating floating photovoltaic systems in hydroelectric power plant reservoirs. Results Eng. 2024, 23, 102742. [Google Scholar] [CrossRef]
- Caldeira, M.J.V.; Ferraz, G.M.F.; Santos, I.F.S.D.; Filho, G.L.T.; Barros, R.M. Using solar energy for complementary energy generation and water level recovery in Brazilian hybrid hydroelectricity: An energy and economic study. Renew. Energy 2023, 218, 119287. [Google Scholar] [CrossRef]
- Glasnovic, Z.; Margeta, J. The features of sustainable Solar Hydroelectric Power Plant. Renew. Energy 2009, 34, 1742–1751. [Google Scholar] [CrossRef]
- Rauf, H.; Gull, M.S.; Arshad, N. Complementing hydroelectric power with floating solar PV for daytime peak electricity demand. Renew. Energy 2020, 162, 1227–1242. [Google Scholar] [CrossRef]
- Hoseinzadeh, S.; Ghasemi, M.H.; Heyns, S. Application of hybrid systems in solution of low power generation at hot seasons for micro hydro systems. Renew. Energy 2020, 160, 323–332. [Google Scholar] [CrossRef]
- Kougias, I.; Szabó, S.; Monforti-Ferrario, F.; Huld, T.; Bódis, K. A methodology for optimization of the complementarity between small-hydropower plants and solar PV systems. Renew. Energy 2016, 87, 1023–1030. [Google Scholar] [CrossRef]
- Silvério, N.M.; Barros, R.M.; Filho, G.L.T.; Redón-Santafé, M.; Santos, I.F.S.D.; de Mello Valério, V.E. Use of floating PV plants for coordinated operation with hydropower plants: Case study of the hydroelectric plants of the São Francisco River basin. Energy Convers. Manag. 2018, 171, 339–349. [Google Scholar] [CrossRef]
- Abdelhafidi, N.; Yılmaz, İ.H.; Bachari, N.E.I. An innovative dynamic model for an integrated solar combined cycle power plant under off-design conditions. Energy Convers. Manag. 2020, 220, 113066. [Google Scholar] [CrossRef]
- Bhayo, B.A.; Al-Kayiem, H.H.; Gilani, S.I.U.; Ismail, F.B. Power management optimization of hybrid solar photovoltaic-battery integrated with pumped-hydro-storage system for standalone electricity generation. Energy Convers. Manag. 2020, 215, 112942. [Google Scholar] [CrossRef]
- Wang, Z.; Fang, G.; Wen, X.; Tan, Q.; Zhang, P.; Liu, Z. Coordinated operation of conventional hydropower plants as hybrid pumped storage hydropower with wind and photovoltaic plants. Energy Convers. Manag. 2023, 277, 116654. [Google Scholar] [CrossRef]
- Temraz, A.; Alobaid, F.; Link, J.; Elweteedy, A.; Epple, B. Development and Validation of a Dynamic Simulation Model for an Integrated Solar Combined Cycle Power Plant. Energies 2021, 14, 3304. [Google Scholar] [CrossRef]
- Zhou, Y.; Chang, F.-J.; Chang, L.-C.; Lee, W.-D.; Huang, A.; Xu, C.-Y.; Guo, S. An advanced complementary scheme of floating photovoltaic and hydropower generation flourishing water-food-energy nexus synergies. Appl. Energy 2020, 275, 115389. [Google Scholar] [CrossRef]
- Zhang, Y.; Ma, C.; Lian, J.; Pang, X.; Qiao, Y.; Chaima, E. Optimal photovoltaic capacity of large-scale hydro-photovoltaic complementary systems considering electricity delivery demand and reservoir characteristics. Energy Convers. Manag. 2019, 195, 597–608. [Google Scholar] [CrossRef]
- Sachenko, A.; Kochan, V.; Turchenko, V.; Tymchyshyn, V.; Vasylkiv, N. Intelligent nodes for distributed sensor network. In Proceedings of the 16th IEEE Instrumentation and Measurement Technology Conference (Cat. No.99CH36309) (IMTC/99), Venice, Italy, 24–26 May 1999; Volume 3, pp. 1479–1484. [Google Scholar]
- Lytvyn, V.; Vysotska, V.; Pukach, P.; Nytrebych, Z.; Demkiv, I.; Senyk, A.; Malanchuk, O.; Sachenko, S.; Kovalchuk, R.; Huzyk, N. Analysis of the developed quantitative method for automatic attribution of scientific and technical text content written in Ukrainian. East.-Eur. J. Enterp. Technol. 2018, 6, 19–31. [Google Scholar] [CrossRef]
- Li, H.; Liu, P.; Guo, S.; Ming, B.; Cheng, L.; Yang, Z. Long-term complementary operation of a large-scale hydro-photovoltaic hybrid power plant using explicit stochastic optimization. Appl. Energy 2019, 238, 863–875. [Google Scholar] [CrossRef]
- León Gómez, J.C.; De León Aldaco, S.E.; Aguayo Alquicira, J. A Review of Hybrid Renewable Energy Systems: Architectures, Battery Systems, and Optimization Techniques. Eng 2023, 4, 1446–1467. [Google Scholar] [CrossRef]
- Bartolucci, L.; Cordiner, S.; Mulone, V.; Rocco, V.; Rossi, J.L. Hybrid renewable energy systems for renewable integration in microgrids: Influence of sizing on performance. Energy 2018, 152, 744–758. [Google Scholar] [CrossRef]
- Hassan, Q. Optimisation of solar-hydrogen power system for household applications. Int. J. Hydrogen Energy 2020, 45, 33111–33127. [Google Scholar] [CrossRef]
- Javed, M.S.; Zhong, D.; Ma, T.; Song, A.; Ahmed, S. Hybrid pumped hydro and battery storage for renewable energy based power supply system. Appl. Energy 2020, 257, 114026. [Google Scholar] [CrossRef]
- Calise, F.; Dentice d’Accadia, M.; Libertini, L.; Vicidomini, M. Thermoeconomic analysis of an integrated solar combined cycle power plant. Energy Convers. Manag. 2018, 171, 1038–1051. [Google Scholar] [CrossRef]
- Fedor, P.; Perdukova, D.; Bernat, P.; Štěpanec, L.; Fedák, V. Modeling of Electromagnetic Phenomena in Small Hydroelectric Plants. In Proceedings of the 2023 International Conference on Electrical Drives and Power Electronics (EDPE), The High Tatras, Slovakia, 25–27 September 2023. [Google Scholar]
- Dyvak, M.; Spivak, I.; Melnyk, A.; Manzhula, V.; Dyvak, T.; Rot, A.; Hernes, M. Modeling Based on the Analysis of Interval Data of Atmospheric Air Pollution Processes with Nitrogen Dioxide due to the Spread of Vehicle Exhaust Gases. Sustainability 2023, 15, 2163. [Google Scholar] [CrossRef]
- Dyvak, M.; Stakhiv, P.; Pukas, A. Algorithms of parallel calculations in task of tolerance ellipsoidal estimation of interval model parameters. Bull. Pol. Acad. Sci. 2012, 60, 159–164. [Google Scholar] [CrossRef]
- Ocheretnyuk, N.; Voytyuk, I.; Dyvak, M.; Martsenyuk, Y. Features of structure identification the macromodels for nonstationary fields of air pollutions from vehicles. Proceedings of International Conference on Modern Problem of Radio Engineering, Telecommunications and Computer Science, Lviv, Ukraine, 21–24 February 2012; p. 444. [Google Scholar]
- Darmorost, I.; Dyvak, M.; Porplytsya, N.; Shynkaryk, T.; Martsenyuk, Y.; Brych, V. Convergence Estimation of a Structure Identification Method for Discrete Interval Models of Atmospheric Pollution by Nitrogen Dioxide. In Proceedings of the 2019 9th International Conference on Advanced Computer Information Technologies (ACIT), Ceske Budejovice, Czech Republic, 5–7 June 2019; pp. 117–120. [Google Scholar]
- Mykola, D.; Krzysztof, G.; Janusz, Z.; Natalia, P.; Jacek, D.; Ewa, K. Mathematical Model of Dynamics of Generated Electric Power by Photovoltaic Installation Taking into Account a Seasonality Factor. In Proceedings of the 2020 10th International Conference on Advanced Computer Information Technologies (ACIT), Deggendorf, Germany, 16–18 September 2020. [Google Scholar]




| Turbine Type | Capacity of Turbine (kW) | Generator Model | Capacity of Generator (kW) | Net Head (M) | Discharge (Flow) Rate (m3/s) |
|---|---|---|---|---|---|
| Francis Voith (horizontal-axial) | 50 | SGD 12-24-12 | 125 | 3.5–5.0 | 0.7–2.0 |
| Francis Voith (vertical-axial) | 150 | SG 146-10 | 250 | 3.5–5.0 | 2.0–5.0 |
| Number | Daily Water Consumption, Million m3 | Head Difference, m | Daily Reactive Power, MW | Daily Generated Electricity, MW |
|---|---|---|---|---|
| i | ||||
| 1 | 0.0864 | 4 | 0.1088 | [0.6875; 0.7629] |
| 2 | 0.0864 | 4.3 | 0.1169 | [0.7390; 0.8201] |
| 3 | 0.0864 | 4.5 | 0.1224 | [0.7734; 0.8582] |
| 4 | 0.0864 | 4.8 | 0.1305 | [0.8249; 0.9154] |
| 5 | 0.0864 | 5 | 0.1360 | [0.8593; 0.9536] |
| 6 | 0.1296 | 4 | 0.1632 | [1.0312; 1.1443] |
| 7 | 0.1296 | 4.3 | 0.1754 | [1.1085; 1.2301] |
| 8 | 0.1296 | 4.5 | 0.1836 | [1.1601; 1.2873] |
| 9 | 0.1296 | 4.8 | 0.1958 | [1.2374; 1.3732] |
| 10 | 0.1296 | 5 | 0.2039 | [1.2890; 1.4304] |
| 11 | 0.1728 | 4 | 0.2175 | [1.3749; 1.5257] |
| 12 | 0.1728 | 4.3 | 0.2339 | [1.4590; 1.6191] |
| 13 | 0.1728 | 4.5 | 0.2447 | [1.4520; 1.6112] |
| 14 | 0.1728 | 4.8 | 0.2611 | [1.5551; 1.7257] |
| 15 | 0.2160 | 4 | 0.2719 | [1.6238; 1.8020] |
| 16 | 0.1728 | 5 | 0.2719 | [1.5290; 1.6968] |
| 17 | 0.2160 | 4.3 | 0.2923 | [1.7527; 1.9450] |
| 18 | 0.2160 | 4.5 | 0.3059 | [1.8386; 2.0404] |
| 19 | 0.2160 | 4.8 | 0.3263 | [1.9675; 2.1834] |
| 20 | 0.2160 | 5 | 0.3399 | [1.9776; 2.1946] |
| 21 | 0.3283 | 4 | 0.4133 | [2.3279; 2.5833] |
| 22 | 0.3283 | 4.3 | 0.4443 | [2.5238; 2.8007] |
| 23 | 0.3283 | 4.5 | 0.4650 | [2.6544; 2.9456] |
| 24 | 0.3283 | 4.8 | 0.4960 | [2.8124; 3.1210] |
| 25 | 0.3283 | 5 | 0.5167 | [2.9810; 3.3080] |
| 26 | 0.4147 | 4 | 0.5221 | [2.8637; 3.1778] |
| 27 | 0.4147 | 4.3 | 0.5613 | [3.1680; 3.5156] |
| 28 | 0.4147 | 4.5 | 0.5874 | [3.4278; 3.8039] |
| 29 | 0.4147 | 4.8 | 0.6265 | [3.6753; 4.0785] |
| 30 | 0.4147 | 5 | 0.6526 | [3.7739; 4.1879] |
| Time Discretization | Measurement Time | 15 July | 24 December | ||
|---|---|---|---|---|---|
| Percentage of Generated Electricity from Peak Power in the Model | Generated Electricity by the SPP with a Peak Capacity of 100 kW | Percentage of Generated Electricity from Peak Power in the Model | Generated Electricity by the SPP with a Peak Capacity of 100 kW | ||
| k | T | % | (кBт) | % | (кBт) |
| 1 | 4:30 | 0 | 0 | 0 | 0 |
| 2 | 4:45 | 0 | 0 | 0 | 0 |
| 3 | 5:00 | 0 | 0 | 0 | 0 |
| 4 | 5:15 | 0.2 | 0.2 | 0 | 0 |
| 5 | 5:30 | 0.6 | 0.6 | 0 | 0 |
| 6 | 5:45 | 0.8 | 0.8 | 0 | 0 |
| 7 | 6:00 | 1.1 | 1.1 | 0 | 0 |
| 8 | 6:15 | 2.2 | 2.2 | 0 | 0 |
| 9 | 6:30 | 2.8 | 2.8 | 0 | 0 |
| 10 | 6:45 | 3.6 | 3.6 | 0 | 0 |
| 11 | 7:00 | 6.2 | 6.2 | 0 | 0 |
| 12 | 7:15 | 7.6 | 7.6 | 0 | 0 |
| 13 | 7:30 | 10.2 | 10.2 | 0 | 0 |
| 14 | 7:45 | 12.4 | 12.4 | 0 | 0 |
| 15 | 8:00 | 10.6 | 10.6 | 0 | 0 |
| 16 | 8:15 | 12.8 | 12.8 | 0 | 0 |
| 17 | 8:30 | 14.1 | 14.1 | 0.2 | 0.2 |
| 18 | 8:45 | 18.2 | 18.2 | 1.2 | 1.2 |
| 19 | 9:00 | 16.5 | 16.5 | 2.7 | 2.7 |
| 20 | 9:15 | 14 | 14 | 6.9 | 6.9 |
| 21 | 9:30 | 32 | 32 | 7 | 7 |
| 22 | 9:45 | 38 | 38 | 9.4 | 9.4 |
| 23 | 10:00 | 40 | 40 | 11.7 | 11.7 |
| 24 | 10:15 | 46 | 46 | 16.8 | 16.8 |
| 25 | 10:30 | 54 | 54 | 29.5 | 29.5 |
| 26 | 10:45 | 58 | 58 | 34.8 | 34.8 |
| 27 | 11:00 | 60 | 60 | 42 | 42 |
| 28 | 11:15 | 64 | 64 | 40 | 40 |
| 29 | 11:30 | 68.2 | 68.2 | 41.2 | 41.2 |
| 30 | 11:45 | 69.3 | 69.3 | 45.4 | 45.4 |
| 31 | 12:00 | 73.2 | 73.2 | 48.5 | 48.5 |
| 32 | 12:15 | 74 | 74 | 54.2 | 54.2 |
| 33 | 12:30 | 81 | 81 | 53.8 | 53.8 |
| 34 | 12:45 | 86 | 86 | 56.4 | 56.4 |
| 35 | 13:00 | 77 | 77 | 52.3 | 52.3 |
| 36 | 13:15 | 78 | 78 | 48.4 | 48.4 |
| 37 | 13:30 | 76.8 | 76.8 | 41.4 | 41.4 |
| 38 | 13:45 | 83.2 | 83.2 | 29 | 29 |
| 39 | 14:00 | 75.8 | 75.8 | 14 | 14 |
| 40 | 14:15 | 78 | 78 | 7.2 | 7.2 |
| 41 | 14:30 | 77 | 77 | 4.7 | 4.7 |
| 42 | 14:45 | 75 | 75 | 3.1 | 3.1 |
| 43 | 15:00 | 76.3 | 76.3 | 2.6 | 2.6 |
| 44 | 15:15 | 74.2 | 74.2 | 1. 5 | 1. 5 |
| 45 | 15:30 | 75.1 | 75.1 | 0.9 | 0.9 |
| 46 | 15:45 | 73.5 | 73.5 | 0.5 | 0.5 |
| 47 | 16:00 | 68.9 | 68.9 | 0.2 | 0.2 |
| 48 | 16:15 | 66.5 | 66.5 | 0.1 | 0.1 |
| 49 | 16:30 | 62.4 | 62.4 | 0 | 0 |
| 50 | 16:45 | 57.6 | 57.6 | 0 | 0 |
| 51 | 17:00 | 54.7 | 54.7 | 0 | 0 |
| 52 | 17:15 | 52 | 52 | 0 | 0 |
| 53 | 17:30 | 46.2 | 46.2 | 0 | 0 |
| 54 | 17:45 | 40.4 | 40.4 | 0 | 0 |
| 55 | 18:00 | 35 | 35 | 0 | 0 |
| 56 | 18:15 | 28.4 | 28.4 | 0 | 0 |
| 57 | 18:30 | 22.5 | 22.5 | 0 | 0 |
| 58 | 18:45 | 18 | 18 | 0 | 0 |
| 59 | 19:00 | 15 | 15 | 0 | 0 |
| 60 | 19:15 | 6.3 | 6.3 | 0 | 0 |
| 61 | 19:30 | 2.1 | 2.1 | 0 | 0 |
| 62 | 19:45 | 1.4 | 1.4 | 0 | 0 |
| 63 | 20:00 | 0.8 | 0.8 | 0 | 0 |
| 64 | 20:15 | 1 | 1 | 0 | 0 |
| 65 | 20:30 | 1.2 | 1.2 | 0 | 0 |
| 66 | 20:45 | 0.6 | 0.6 | 0 | 0 |
| 67 | 21:00 | 0 | 0 | 0 | 0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dyvak, M.; Manzhula, V.; Melnyk, A.; Petryshyn, N.; Pan, T.; Banasik, A.; Pikiewicz, P.; Kempa, W.M. Modeling the Electricity Generation Processes of a Combined Solar and Small Hydropower Plant. Energies 2025, 18, 2351. https://doi.org/10.3390/en18092351
Dyvak M, Manzhula V, Melnyk A, Petryshyn N, Pan T, Banasik A, Pikiewicz P, Kempa WM. Modeling the Electricity Generation Processes of a Combined Solar and Small Hydropower Plant. Energies. 2025; 18(9):2351. https://doi.org/10.3390/en18092351
Chicago/Turabian StyleDyvak, Mykola, Volodymyr Manzhula, Andriy Melnyk, Nataliia Petryshyn, Tiande Pan, Arkadiusz Banasik, Piotr Pikiewicz, and Wojciech M. Kempa. 2025. "Modeling the Electricity Generation Processes of a Combined Solar and Small Hydropower Plant" Energies 18, no. 9: 2351. https://doi.org/10.3390/en18092351
APA StyleDyvak, M., Manzhula, V., Melnyk, A., Petryshyn, N., Pan, T., Banasik, A., Pikiewicz, P., & Kempa, W. M. (2025). Modeling the Electricity Generation Processes of a Combined Solar and Small Hydropower Plant. Energies, 18(9), 2351. https://doi.org/10.3390/en18092351









