Accurate Location Method for Abnormal Line Losses in Distribution Network Considering Topology Matching and Parameter Estimation in Grid
Abstract
1. Introduction
2. Distribution Network Topology Matching Model Based on SVM
2.1. Data Preprocessing
2.2. Parameter Optimization of SVM Based on Improved Grid Search Method
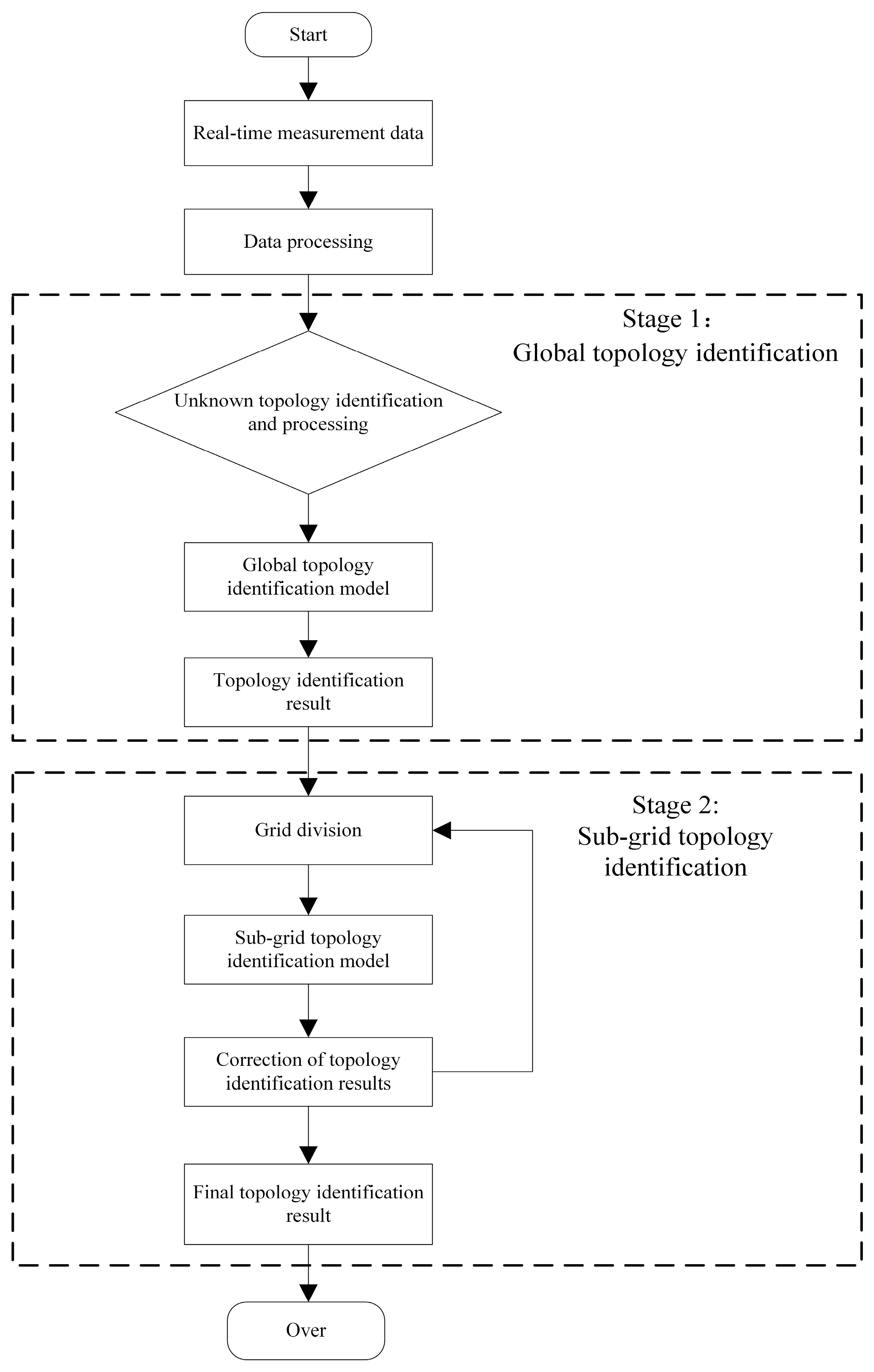
2.3. The Overall Process of the Distribution Network Topology Matching Method
3. Determination of the Aging Degree of Lines Based on Parameter Estimation
3.1. Parameter Estimation Model Combining Voltage Estimation and Power Estimation
3.2. Evaluation Method of Line Aging Degree
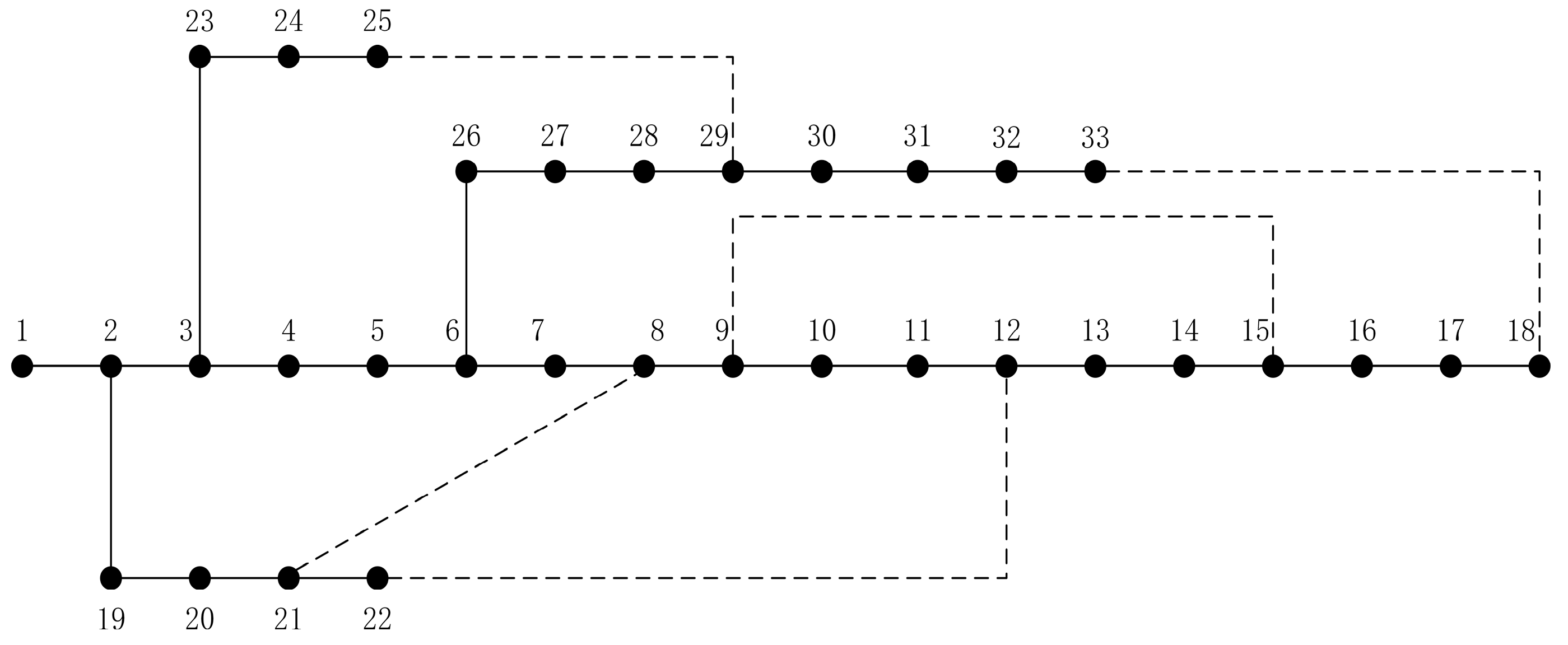
4. Case Study
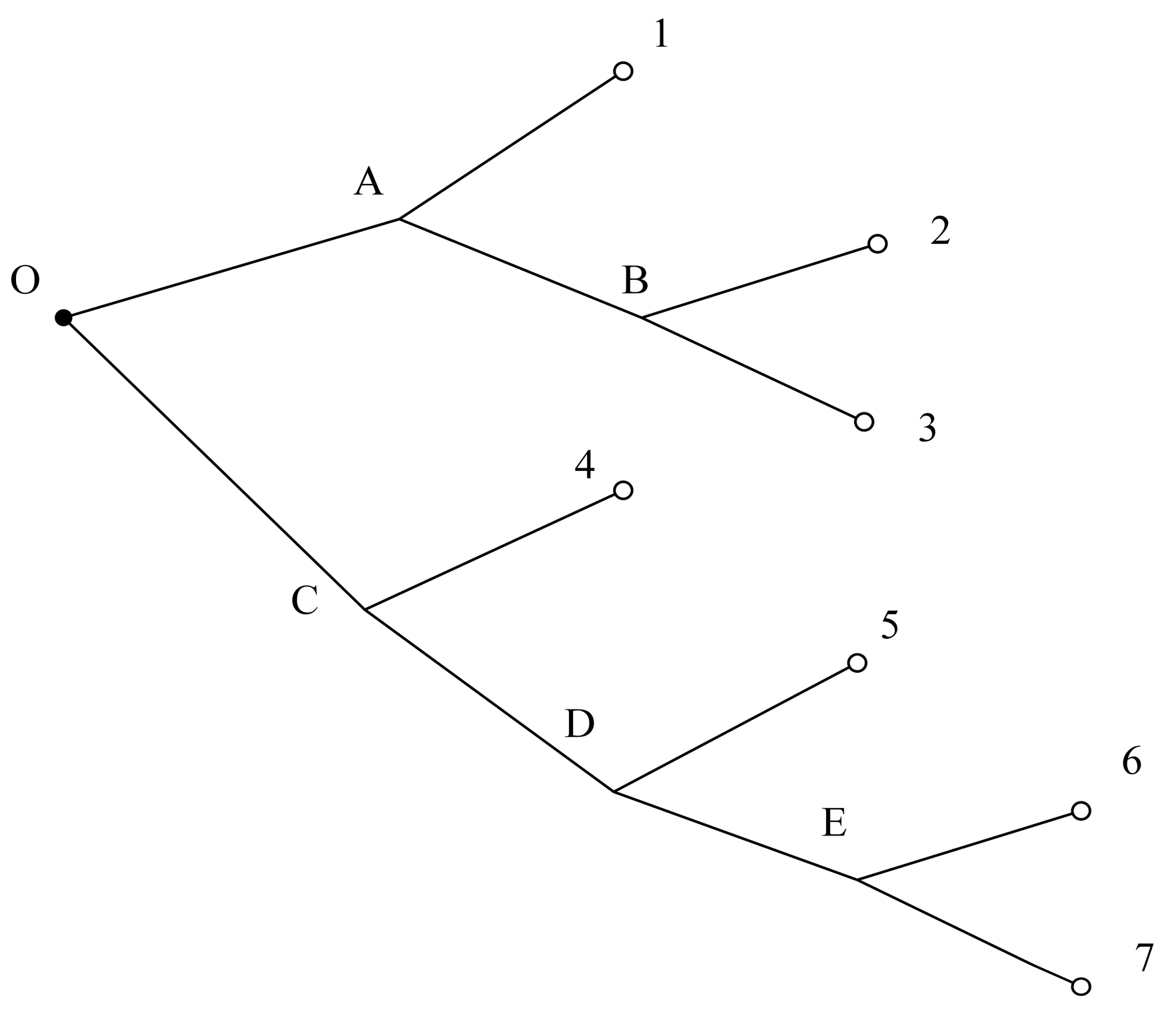
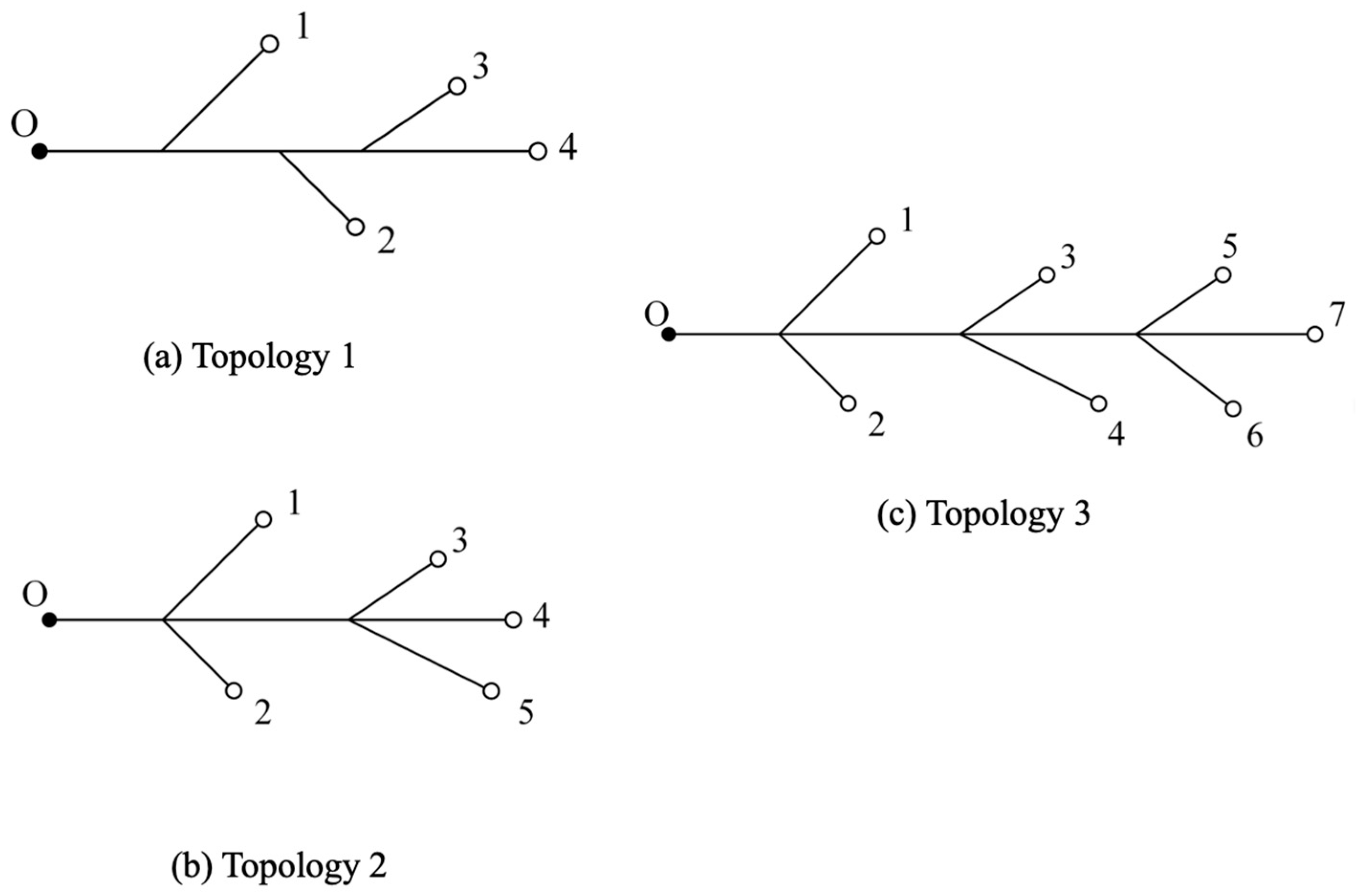
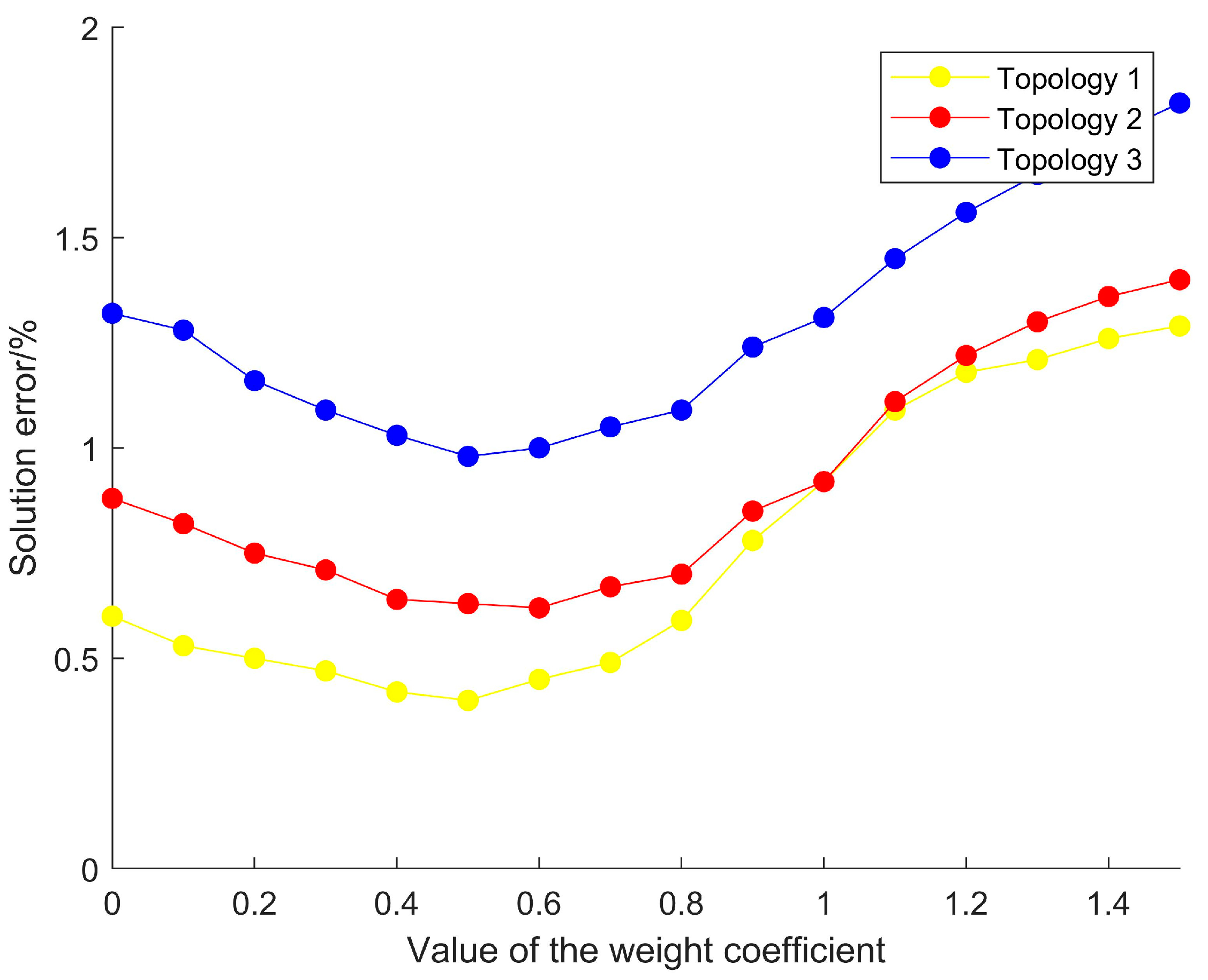
4.1. Topology Matching
4.2. Parameter Estimation
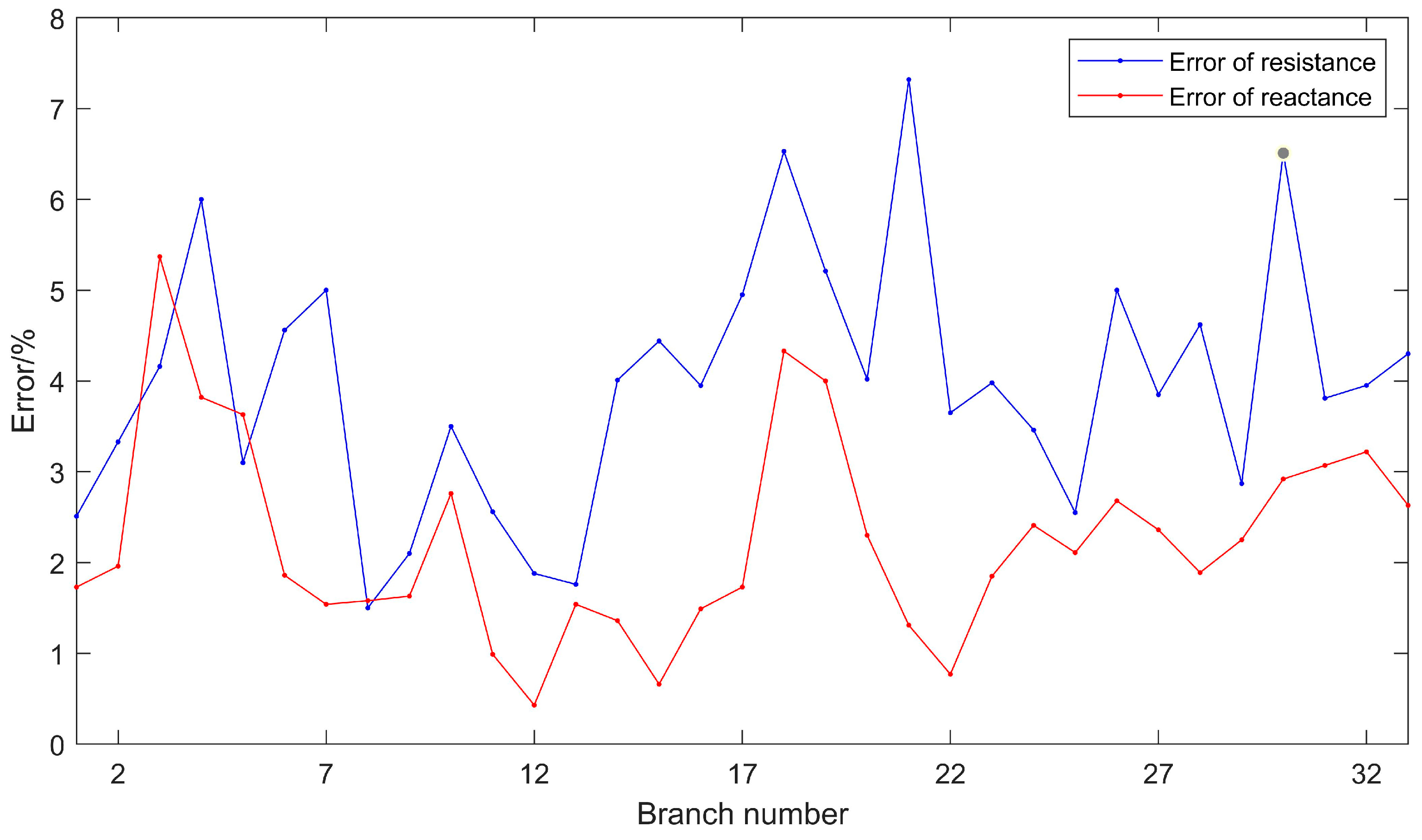
4.3. Location of Abnormal Line Loss Branches
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| SVM | Support vector machine |
| NTL | Non-technical loss |
| TL | Technical loss |
References
- Chen, H.; Xu, L.; Yang, L.; Jin, Y.; Fu, H.; Li, S. Research status and prospects on technical loss reduction of regional power grid. Power Syst. Technol. 2024, 49, 1–13. [Google Scholar]
- Sun, K. Lean Analysis of Transformer District Line Loss Based on Data Mining Applied Research. Master’s Theses, Zhengzhou University, Zhengzhou, China, 2021. [Google Scholar]
- Chen, G.; Zhang, S.; Yang, L.; Huang, W.; Nan, Y.; Zhang, Y.; Hao, S. Station line loss rate anomaly identification and accurate tracking method of associated users based on multi-dimensional scene division. Power Syst. Prot. Control 2024, 52, 162–177. [Google Scholar]
- Chen, C. Research on Abnormal Power Loss Detection and Combined Power Loss Reduction Strategy Optimization in the Distribution Network. Master’s Thesis, Southeast University, Nanjing, China, 2021. [Google Scholar]
- Wang, H.; Zhang, Y.; Yan, F.; Chen, Y.; Yang, L.; Chang, Q.; Zhang, Z.; Chen, Q.; Yuan, Q. The study of coal-to-electricity district line loss anomaly identification method based on deep neural network. Power Demand Side Manag. 2018, 20, 31–35. [Google Scholar]
- Zhang, C.; Xiao, X.; Zheng, Z. Electricity theft detection for customers in power utility based on real-valued deep belief network. Power Syst. Technol. 2019, 43, 1083–1091. [Google Scholar]
- Xiao, F.; Qian, A. Electricity theft detection in smart grid using random matrix theory. IET Gener. Transm. Distrib. 2018, 12, 371–378. [Google Scholar] [CrossRef]
- Huang, S.-C.; Lo, Y.-L.; Lu, C.-N. Non-Technical Loss Detection Using State Estimation and Analysis of Variance. IEEE Trans. Power Syst. 2013, 28, 2959–2966. [Google Scholar] [CrossRef]
- Amin, S.; Schwartz, G.A.; Cardenas, A.A.; Sastry, S.S. Game-Theoretic Models of Electricity Theft Detection in Smart Utility Networks: Providing New Capabilities with Advanced Metering Infrastructure. IEEE Control Syst. Mag. 2015, 35, 66–81. [Google Scholar]
- Guo, Y.; Yuan, Y.; Wang, Z. Distribution grid modeling using smart meter data. IEEE Trans. Power Syst. 2021, 37, 1995–2004. [Google Scholar] [CrossRef]
- Madbhavi, R.; Natarajan, B.; Srinivasan, B. Distribution System Topology Identification Using Graph Neural Networks. In Proceedings of the 2023 IEEE PES GTD International Conference and Exposition (GTD), Istanbul, Turkiye, 22–25 May 2023; pp. 151–155. [Google Scholar]
- Zelenskii, E.G.; Tuchina, D.S.; Kononov, Y.G.; Kozhevnikov, V.M. Mobile Laboratory for Identification of Radial Distribution Network Topology. In Proceedings of the 2022 IEEE International Multi-Conference on Engineering, Computer and Information Sciences (SIBIRCON), Yekaterinburg, Russia, 11–13 November 2022; pp. 2110–2115. [Google Scholar]
- Amoateng, D.O.; Yan, R.; Mosadeghy, M.; Saha, T.K. Topology detection in power distribution networks: A PMU based deep learning approach. IEEE Trans. Power Syst. 2021, 37, 2771–2782. [Google Scholar] [CrossRef]
- Liao, W.; Zhu, R.; Takiddin, A.; Tariq, M.; Ruan, G.; Cui, X. Transfer Learning-Driven Electricity Theft Detection in Small Sample Cases. IEEE Trans. Instrum. Meas. 2024, 73, 1–13. [Google Scholar] [CrossRef]
- Long, H.; Chen, C.; Gu, W.; Xie, J.; Wang, Z.; Li, G. A data-driven combined algorithm for abnormal power loss detection in the distribution network. IEEE Access 2020, 8, 24675–24686. [Google Scholar] [CrossRef]
- Bettiol, A.L.; Gomides, P.S.; Figueiredo, D.B.S.; Medeiros, R. Detection and Tracking of Atypical Billings Aiming at Minimizing Non-Technical Losses in Distribution Companies in Brazil. In Proceedings of the 2023 International Conference on Electrical, Computer and Energy Technologies (ICECET), Cape Town, South Africa, 16–17 November 2023; pp. 1–5. [Google Scholar]
- Liao, W.; Zhu, R.; Yang, Z.; Liu, K.; Zhang, B.; Zhu, S.; Feng, B. Electricity Theft Detection Using Dynamic Graph Construction and Graph Attention Network. IEEE Trans. Ind. Inform. 2024, 20, 5074–5086. [Google Scholar] [CrossRef]
- Larose, D.T.; Larose, C.D. Discovering Knowledge in Data: An Introduction to Data Mining; John Wiley & Sons: Hoboken, NJ, USA, 2014. [Google Scholar]
- Liao, Z.; Liu, Y.; Wang, B.; Tao, W. Topology Identification of Active Low-Voltage Distribution Network Based on Regression Analysis and Knowledge Reasoning. Energies. 2024, 17, 1762. [Google Scholar] [CrossRef]
- Wu, X.; Sun, F.; Li, F. Dynamic reactive power optimization of distribution network based on electric distance partition. J. Xi’an Shiyou Univ. (Nat. Sci. Ed.) 2023, 38, 94–99+128. [Google Scholar]
- Luan, W.; Wang, B.; Zhou, N.; Guo, Z. Modeling of LV distribution network based on metering data. Power Syst. Technol. 2015, 39, 3141–3146. [Google Scholar]
- Wang, X. A survey of gradient descent and optimization algorithms. Comput. Knowl. Technol. 2022, 18, 71–73. [Google Scholar]
- Wang, Q.S. A New Steepest Descent Method. Master’s Thesis, Jilin University, Jilin, China, 2021. [Google Scholar]
- Li, S.; Chen, H.; Qin, Y.; Guo, W.; Xu, X. Research on the influence of 10 kV line aging and high resistance grounding fault on line loss. Electr. Power Equip. Manag. 2021, 4, 185–186. [Google Scholar]
- Baran, M.E.; Wu, F.F. Optimal capacitor placement on radial distribution systems. IEEE Trans. Power Deliv. 1989, 4, 725–734. [Google Scholar] [CrossRef]
- Zimmerman, R.D.; Murillo-Sanchez, C.E.; Thomas, R.J. MATPOWER: Steady-state operations, planning, and analysis tools for power systems research and education. IEEE Trans. Power Syst. 2011, 26, 12–19. [Google Scholar] [CrossRef]
- Liu, Q. Online Analysis of Low Frequency Oscillation Identification Based on WAMS Light. Master’s Thesis, Shandong University, Shandong, China, 2014. [Google Scholar]

| Topology Matching Method | Accuracy/% | Time/s |
|---|---|---|
| Global topology matching method | 95.31 | 0.962 |
| The topology matching method combined with the grid | 97.46 | 2.412 |
| Measurement Error/% | Average Error of Impedance Parameters/% | ||
|---|---|---|---|
| The Model Established in This Paper | Voltage Estimation Model | Power Estimation Model | |
| 0.5 | 3.11 | 3.32 | 5.94 |
| 1 | 3.36 | 4.11 | 6.78 |
| 3 | 5.71 | 7.19 | 9.93 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
An, H.; Zhou, Q.; Wu, Q.; Liu, Y.; Huang, C.; Li, J. Accurate Location Method for Abnormal Line Losses in Distribution Network Considering Topology Matching and Parameter Estimation in Grid. Energies 2025, 18, 2324. https://doi.org/10.3390/en18092324
An H, Zhou Q, Wu Q, Liu Y, Huang C, Li J. Accurate Location Method for Abnormal Line Losses in Distribution Network Considering Topology Matching and Parameter Estimation in Grid. Energies. 2025; 18(9):2324. https://doi.org/10.3390/en18092324
Chicago/Turabian StyleAn, Haiyun, Qian Zhou, Qiuwei Wu, Yufang Liu, Cheng Huang, and Jiaxun Li. 2025. "Accurate Location Method for Abnormal Line Losses in Distribution Network Considering Topology Matching and Parameter Estimation in Grid" Energies 18, no. 9: 2324. https://doi.org/10.3390/en18092324
APA StyleAn, H., Zhou, Q., Wu, Q., Liu, Y., Huang, C., & Li, J. (2025). Accurate Location Method for Abnormal Line Losses in Distribution Network Considering Topology Matching and Parameter Estimation in Grid. Energies, 18(9), 2324. https://doi.org/10.3390/en18092324






