Research on Day-Ahead Optimal Scheduling of Wind–PV–Thermal–Pumped Storage Based on the Improved Multi-Objective Jellyfish Search Algorithm
Abstract
1. Introduction
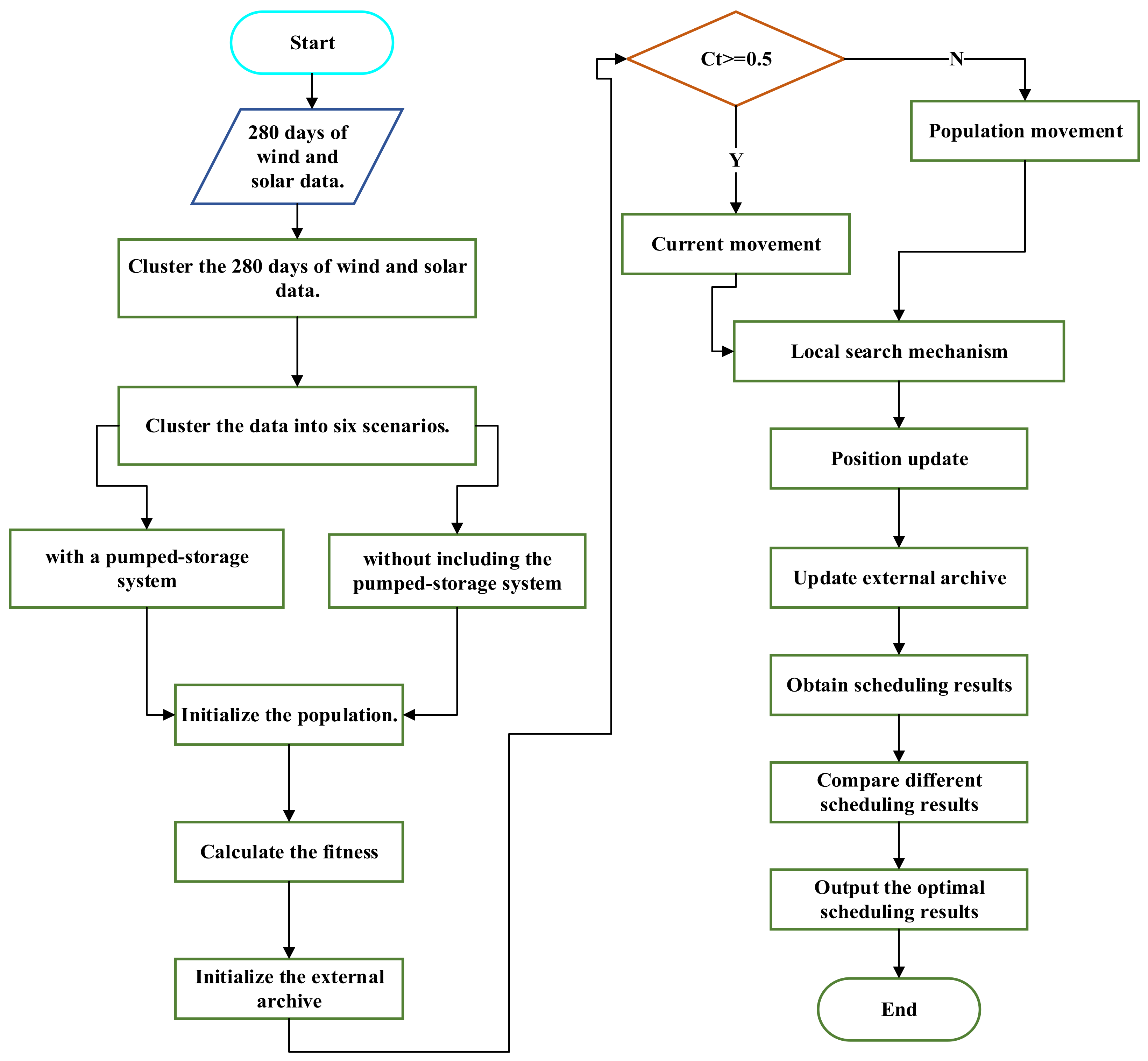
2. Typical Scenario Division
2.1. Mean Shift Clustering Algorithm
2.2. Clustering Scenarios
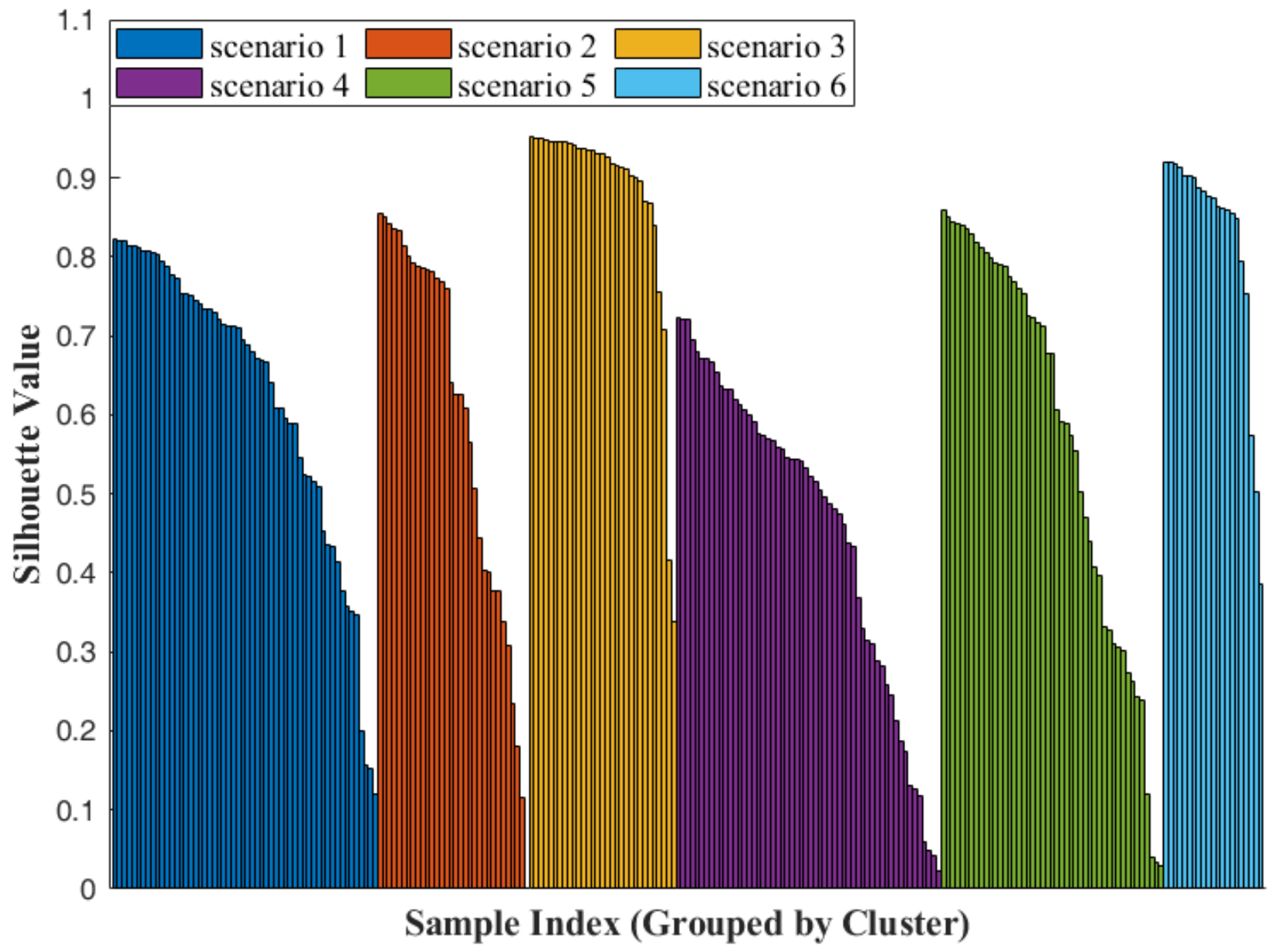
- Clustering Validity Analysis
- 2.
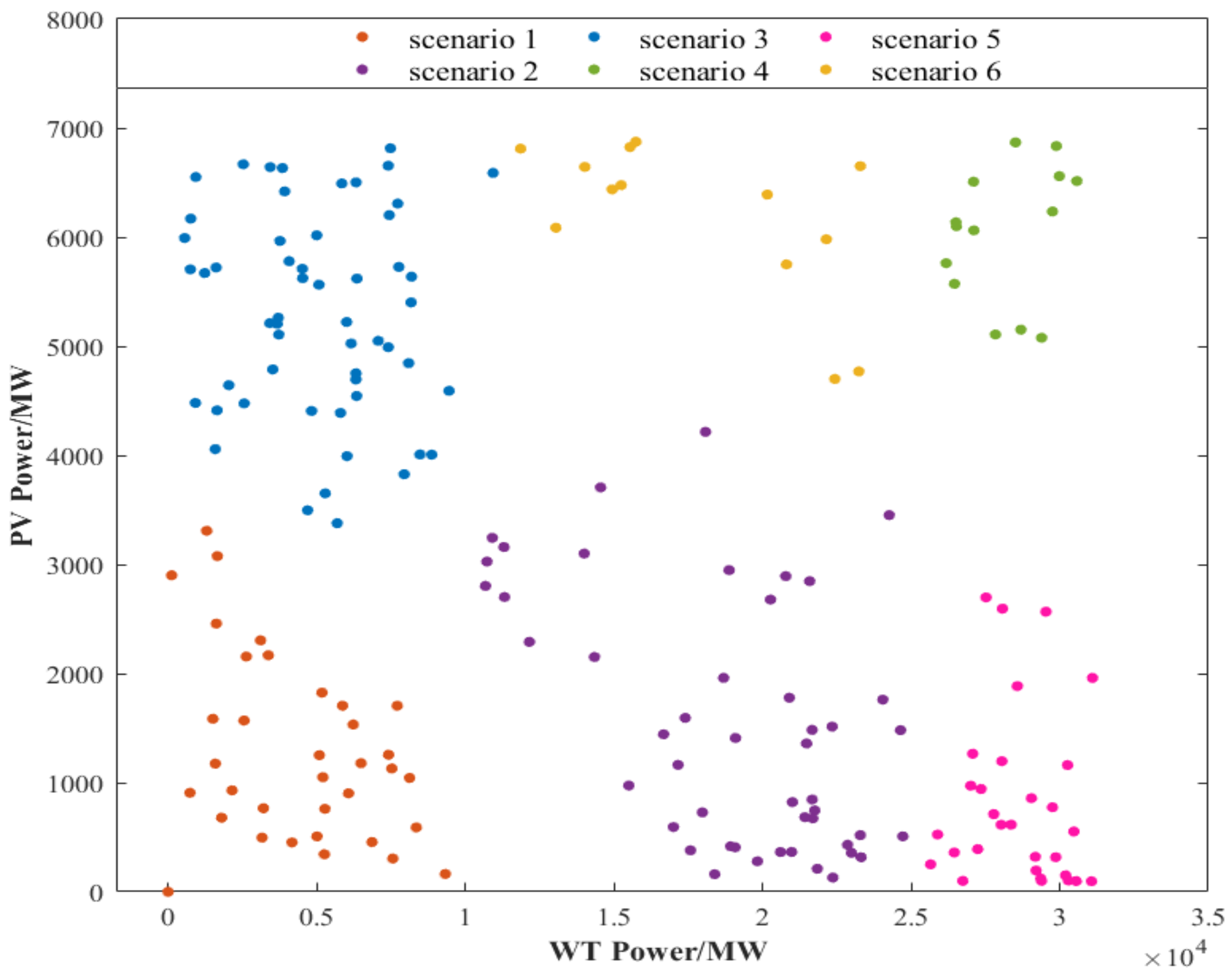
- Clustering Results Presentation
3. Improved Multi-Objective Jellyfish Search Algorithm
3.1. Multi-Objective Jellyfish Algorithm
- (1)
- Weak local search capability: The core mechanism of the JSA is centered around random drifting and current-following strategies. This results in limited capability for fine-tuning when approaching the Pareto front. In complex, multi-modal solution spaces, the algorithm faces difficulties in enhancing the convergence precision of the solution set through effective neighborhood search, often leading to a dispersed distribution of solutions or divergence from the true Pareto front.
- (2)
- The original Ct1 parameter employs a linear decay mechanism, leading to a lack of adaptability in transitioning between global exploration and local exploitation: the linear variation of (1 − t/T) causes the algorithm’s exploration capability to rapidly diminish in the early stages, potentially resulting in premature convergence to local optima. The uniform distribution of the random component (2*rand−1) leads to a fixed perturbation amplitude, preventing dynamic adjustment of the search step size according to the iteration stage. This rigidity hampers the algorithm’s ability to adapt to the evolving demands of complex multi-objective problems, resulting in insufficient global search time and persistent ineffective perturbations in later stages, thereby reducing optimization efficiency.
- (3)
- Insufficient diversity maintenance mechanism: The algorithm lacks an adaptive neighborhood design tailored to the multi-objective characteristics. For example, it does not dynamically adjust the search step size based on the correlation between objectives, which further reduces the effectiveness of the local search.
3.2. Algorithm Improvement
3.2.1. Improvement of Time Control Parameter
3.2.2. Local Search Mechanism
3.2.3. Weight Assignment and Optimal Solution Selection
- (1)
- Weight determination based on the Entropy Method
- (2)
- Optimal Solution Selection in TOPSIS
3.3. Simulation Experiments
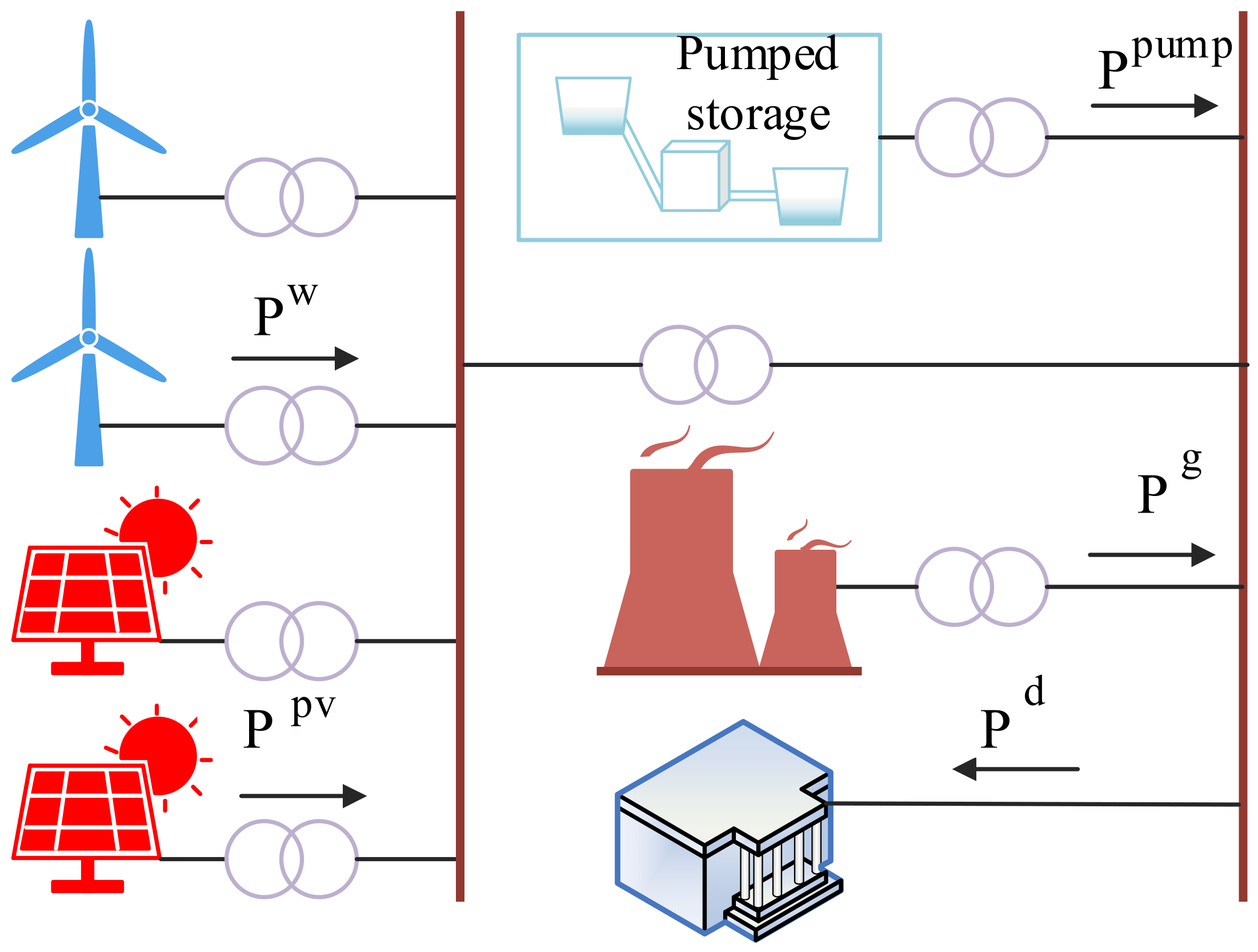
4. Wind–PV–Thermal–Pumped Storage System Model
4.1. Objective Function
4.2. Operating Cost
4.2.1. Coal Cost of Thermal Power Units
4.2.2. Pollutant Treatment Costs
4.2.3. Penalty Cost for Curtailing Wind and PV Power
4.2.4. Construction Cost
4.3. Constraints
4.3.1. System Power Balance Constraint
4.3.2. Constraints of Thermal Power Units
- (1)
- Output Constraints of Thermal Power Units [39]
4.3.3. Pumped Storage Station Constraints [40,41]
- (1)
- Operational Constraints of the Pumped Storage Station
- (2)
- Spinning Reserve Constraint
4.3.4. Wind Power Constraints
4.3.5. PV Power Constraints
5. Simulation Results and Analysis
5.1. Algorithm Solving Comparison for the Real Model
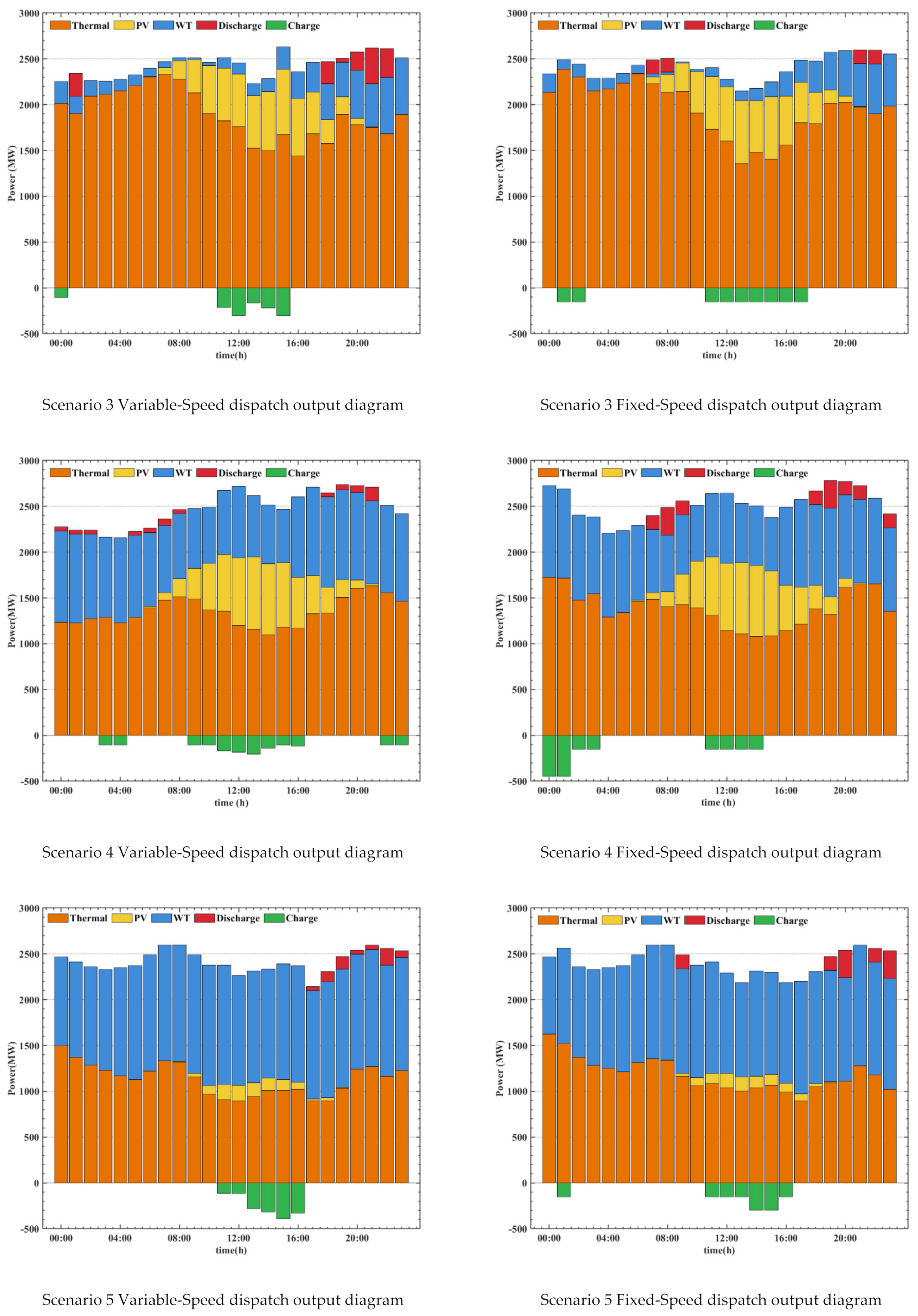
5.2. Joint Scheduling Model of Variable-Speed and Fixed-Speed Pumped Storage
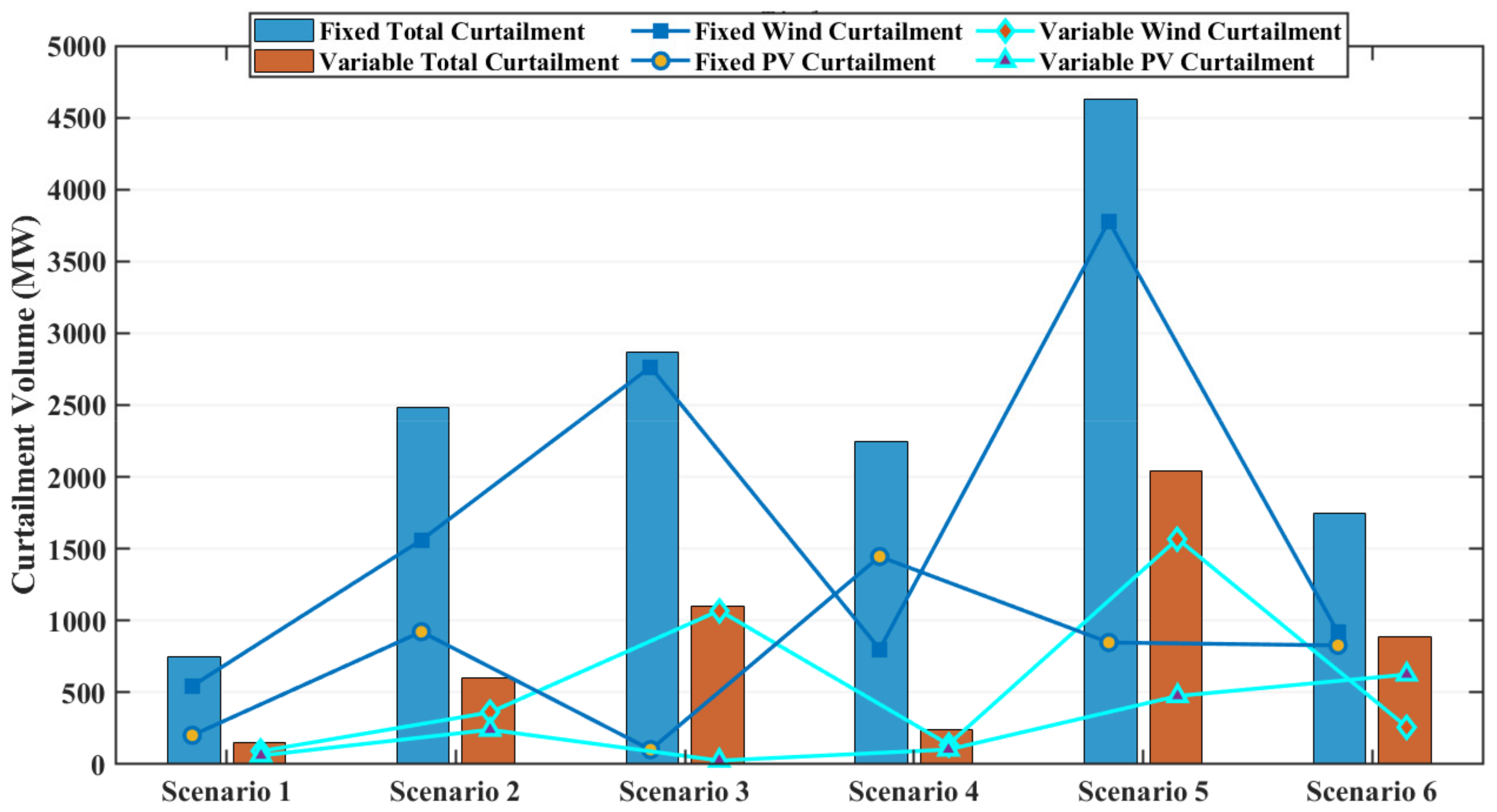
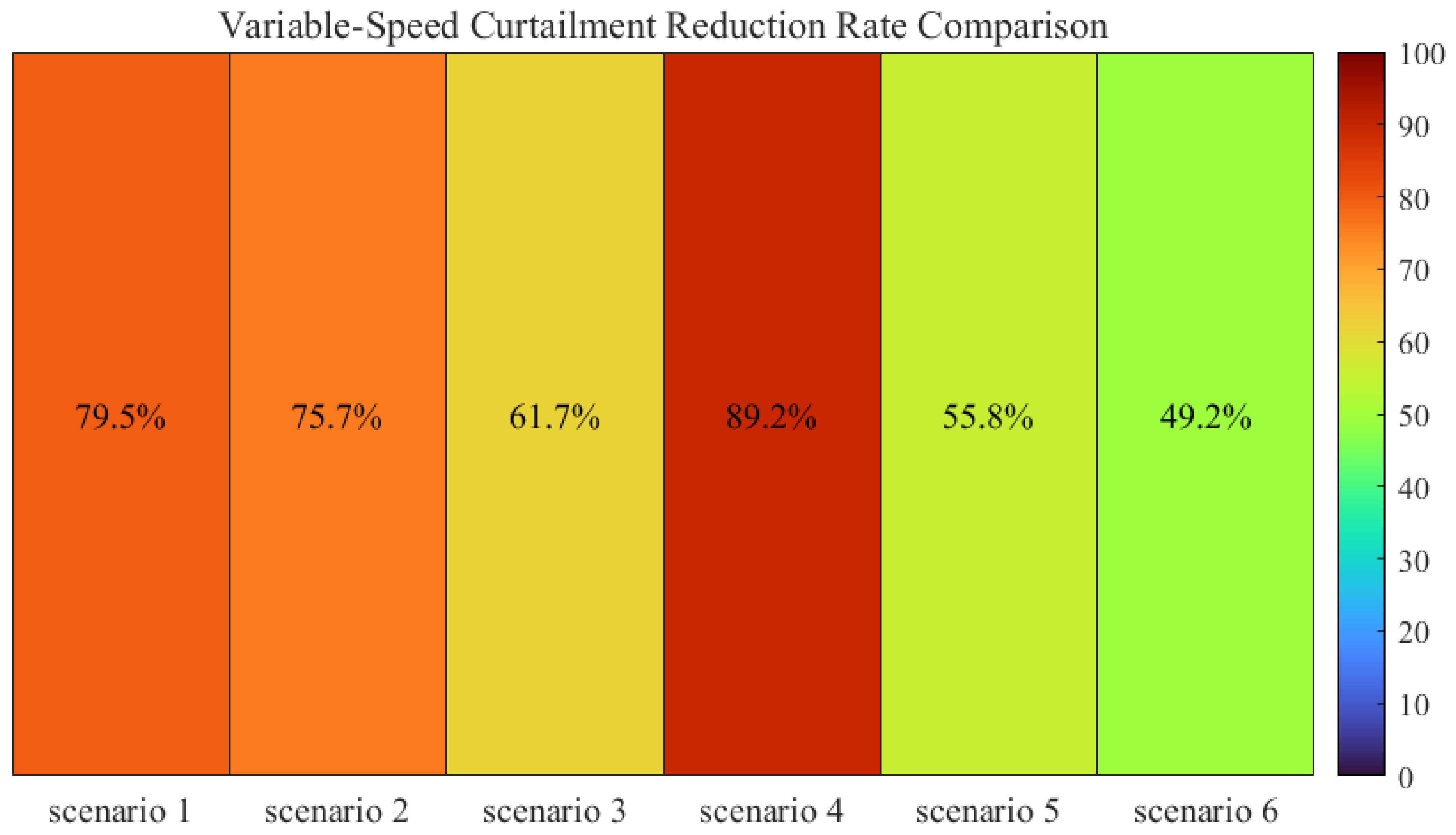
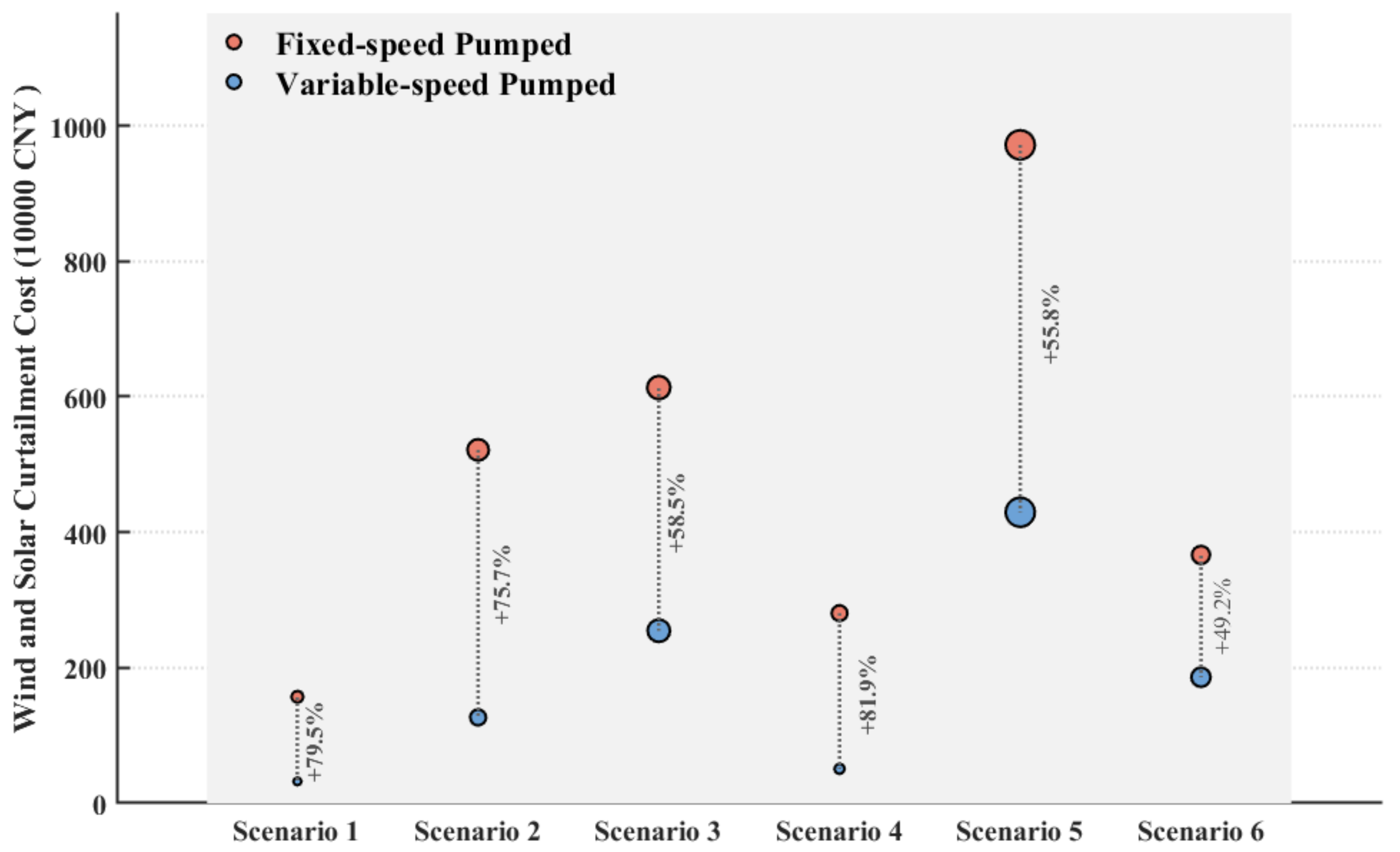
5.3. Wind and PV Curtailment Analysis
5.4. Operating Cost Analysis
6. Conclusions and Future Work
6.1. Conclusions
- (1)
- This paper establishes a data-driven scenario construction and classification model and proposes an annual operational scenario division method based on the mean shift clustering algorithm. The clustering algorithm divides 280 days of wind–PV output data into six typical scenario sets. Compared to traditional manual classification methods, this approach enhances credibility and reduces subjectivity.
- (2)
- A three-dimensional objective function system, including operational costs, carbon emissions, and thermal power output volatility, was developed. A pumped storage station was introduced as a flexible regulation unit to enhance the stability of the integrated energy system.
- (3)
- This paper proposes an improved nonlinear MOJS. This algorithm significantly improves convergence accuracy and the distribution of the Pareto front by introducing a dynamic adaptive mechanism and a local search mechanism. After 500 iterations, the Pareto front convergence index (GD) of IMOJS is 0.000245, which is better than MOJS (0.00118) and NSGA-III (0.000364), demonstrating stronger convergence performance. Moreover, IMOJS shows an overall performance improvement of 17% in the three-objective optimization problem in six different test scenarios.
- (4)
- The introduction of VS-PS plants effectively mitigates fluctuations in thermal power output and significantly reduces joint dispatch operating costs. Through the flexible power regulation of the VS-PS plants, wind and PV curtailment costs were reduced by an average of 62.3%, effectively increasing the stability of the joint dispatch system.
6.2. Future Work
- (1)
- The current study only considers variable-speed pumped storage as flexible regulation units on the power supply side. Future work should incorporate the uncertainty of renewable energy forecasting by establishing wind/PV prediction models that align with their generation characteristics. Subsequent research should develop rolling optimization models for renewable energy prediction and construct multi-timescale integrated energy scheduling models to reduce uncertainties and enhance grid stability.
- (2)
- The current fixed electricity pricing strategy obtains optimal time-of-use pricing through calculation. Future studies could develop real-time pricing strategies based on wind power characteristics while considering long-term regional load demand with refined user load classification. More precise demand response mechanisms can be achieved by conducting an in-depth analysis of user electricity consumption behavior to improve system economic efficiency and renewable energy utilization.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| Abbreviation | Full Name |
| IMOJS | Improved Multi-Objective Jellyfish Search Algorithm |
| LFC | Load Frequency Control |
| PV | Photovoltaic |
| KDE | Kernel Density Estimation |
| MOJS | Multi-Objective Jellyfish Search Algorithm |
| MCA | Musical Chairs Algorithm |
| BMCA | Binary version Musical Chairs Algorithm |
| NESTPSO | Nested Particle Swarm Optimization |
| JSA | The single-objective Jellyfish Search Algorithm |
| MOEA/D | Multi-Objective Evolutionary Algorithm based on Decomposition |
| SPEA2 | The Strength Pareto Evolutionary Algorithm 2 |
| HV | Hypervolume |
| GD | Generational Distance |
| IGD | Inverted Generational Distance |
| NSGA-III | Non-dominated Sorting Genetic Algorithm III |
| VS-PS | Variable-Speed Pumped Storage |
| FS-PS | Fixed-Speed Pumped Storage |
| TOPSIS | Technique for Order of Preference by Similarity to Ideal Solution |
Appendix A
| Test Function | Objectives | Iterations | IMOJS | NSGA-III | MOJS | MOEA/D | SPEA2 |
|---|---|---|---|---|---|---|---|
| DTLZ1 | 3 | 300 | 8.41 × 10−1 | 8.39 × 10−1 | 8.30 × 10−1 | 8.40 × 10−1 | 8.38 × 10−1 |
| 8.39 × 10−1 | 8.17 × 10−1 | 8.28 × 10−1 | 8.38 × 10−1 | 8.37 × 10−1 | |||
| 8.39 × 10−1 | 8.17 × 10−1 | 8.25 × 10−1 | 8.28 × 10−1 | 8.35 × 10−1 | |||
| 5 | 500 | 9.69 × 10−1 | 9.70 × 10−1 | 9.64 × 10−1 | 9.68 × 10−1 | 9.58 × 10−1 | |
| 9.63 × 10−1 | 9.53 × 10−1 | 9.18 × 10−1 | 9.60 × 10−1 | 9.55 × 10−1 | |||
| 9.60 × 10−1 | 9.05 × 10−1 | 9.18 × 10−1 | 9.56 × 10−1 | 9.53 × 10−1 | |||
| 8 | 800 | 9.86 × 10−1 | 8.31 × 10−1 | 9.44 × 10−1 | 9.69 × 10−1 | 0.00 × 100 | |
| 9.69 × 10−1 | 6.47 × 10−1 | 9.16 × 10−1 | 9.63 × 10−1 | 0.00 × 100 | |||
| 9.38 × 10−1 | 5.94 × 10−1 | 8.88 × 10−1 | 9.25 × 10−1 | 0.00 × 100 | |||
| DTLZ2 | 3 | 300 | 5.59 × 10−1 | 5.61 × 10−1 | 5.56 × 10−1 | 5.62 × 10−1 | 5.55 × 10−1 |
| 5.59 × 10−1 | 5.29 × 10−1 | 5.56 × 10−1 | 5.57 × 10−1 | 5.53 × 10−1 | |||
| 5.59 × 10−1 | 5.28 × 10−1 | 5.55 × 10−1 | 5.54 × 10−1 | 5.50 × 10−1 | |||
| 5 | 500 | 7.78 × 10−1 | 7.75 × 10−1 | 7.68 × 10−1 | 7.76 × 10−1 | 6.70 × 10−1 | |
| 7.78 × 10−1 | 7.81 × 10−1 | 7.66 × 10−1 | 7.74 × 10−1 | 6.65 × 10−1 | |||
| 7.77 × 10−1 | 7.71 × 10−1 | 7.66 × 10−1 | 7.73 × 10−1 | 6.40 × 10−1 | |||
| 8 | 800 | 9.14 × 10−1 | 8.68 × 10−1 | 7.86 × 10−1 | 8.65 × 10−1 | 0.00 × 100 | |
| 8.79 × 10−1 | 8.67 × 10−1 | 7.84 × 10−1 | 8.64 × 10−1 | 0.00 × 100 | |||
| 8.65 × 10−1 | 8.59 × 10−1 | 7.81 × 10−1 | 8.63 × 10−1 | 0.00 × 100 | |||
| DTLZ3 | 3 | 300 | 3.94 × 10−1 | 3.35 × 10−1 | 3.62 × 10−1 | 3.61 × 10−1 | 5.07 × 10−1 |
| 3.81 × 10−1 | 3.22 × 10−2 | 3.56 × 10−1 | 2.77 × 10−1 | 3.40 × 10−1 | |||
| 2.90 × 10−1 | 3.20 × 10−1 | 2.45 × 10−1 | 1.73 × 10−1 | 3.19 × 10−1 | |||
| 5 | 500 | 4.46 × 10−1 | 3.80 × 10−1 | 4.26 × 10−1 | 7.08 × 10−1 | 4.26 × 10−1 | |
| 4.27 × 10−1 | 3.68 × 10−1 | 3.78 × 10−1 | 3.92 × 10−1 | 4.19 × 10−2 | |||
| 3.88 × 10−1 | 3.33 × 10−1 | 3.53 × 10−1 | 1.48 × 10−1 | 2.15 × 10−2 | |||
| 8 | 800 | 5.36 × 10−1 | 3.64 × 10−1 | 1.76 × 10−1 | 6.39 × 10−1 | 0.00 × 100 | |
| 4.69 × 10−1 | 2.79 × 10−1 | 1.29 × 10−1 | 4.24 × 10−1 | 0.00 × 100 | |||
| 3.92 × 10−1 | 2.18 × 10−1 | 8.26 × 10−2 | 9.44 × 10−2 | 0.00 × 100 | |||
| DTLZ4 | 3 | 300 | 5.63 × 10−1 | 5.18 × 10−1 | 5.00 × 10−1 | 5.59 × 10−1 | 5.48 × 10−1 |
| 5.52 × 10−1 | 5.16 × 10−1 | 4.91 × 10−1 | 4.40 × 10−1 | 4.39 × 10−1 | |||
| 5.15 × 10−1 | 4.93 × 10−1 | 4.85 × 10−1 | 3.41 × 10−1 | 3.47 × 10−1 | |||
| 5 | 500 | 7.48 × 10−1 | 7.44 × 10−1 | 7.35 × 10−1 | 6.80 × 10−1 | 6.56 × 10−1 | |
| 7.46 × 10−1 | 7.34 × 10−1 | 7.32 × 10−1 | 5.69 × 10−1 | 6.18 × 10−1 | |||
| 7.35 × 10−1 | 7.24 × 10−1 | 7.27 × 10−1 | 5.15 × 10−1 | 5.99 × 10−1 | |||
| 8 | 800 | 8.38 × 10−1 | 8.27 × 10−1 | 8.32 × 10−1 | 7.79 × 10−1 | 0.00 × 100 | |
| 8.29 × 10−1 | 7.14 × 10−1 | 8.30 × 10−1 | 7.31 × 10−1 | 0.00 × 100 | |||
| 8.27 × 10−1 | 3.84 × 10−1 | 4.77 × 10−1 | 6.96 × 10−1 | 0.00 × 100 | |||
| DTLZ5 | 3 | 300 | 2.00 × 10−1 | 1.99 × 10−1 | 1.95 × 10−1 | 1.83 × 10−1 | 1.99 × 10−1 |
| 1.94 × 10−1 | 1.98 × 10−1 | 1.95 × 10−1 | 1.82 × 10−1 | 1.97 × 10−1 | |||
| 1.93 × 10−1 | 1.93 × 10−1 | 1.94 × 10−1 | 1.77 × 10−1 | 1.84 × 10−1 | |||
| 5 | 500 | 1.16 × 10−1 | 1.04 × 10−1 | 1.09 × 10−1 | 1.14 × 10−1 | 4.09 × 10−2 | |
| 1.14 × 10−1 | 1.03 × 10−1 | 1.07 × 10−1 | 1.13 × 10−1 | 3.54 × 10−2 | |||
| 1.15 × 10−1 | 1.02 × 10−1 | 1.04 × 10−1 | 1.07 × 10−1 | 2.07 × 10−2 | |||
| 8 | 800 | 9.19 × 10−2 | 8.49 × 10−2 | 8.99 × 10−2 | 9.03 × 10−2 | 0.00 × 100 | |
| 9.14 × 10−2 | 8.33 × 10−2 | 8.97 × 10−2 | 8.92 × 10−2 | 0.00 × 100 | |||
| 9.12 × 10−2 | 7.91 × 10−2 | 8.95 × 10−2 | 8.47 × 10−2 | 0.00 × 100 | |||
| DTL6 | 3 | 300 | 1.99 × 10−1 | 1.98 × 10−1 | 1.94 × 10−1 | 1.89 × 10−1 | 1.94 × 10−1 |
| 1.98 × 10−1 | 1.96 × 10−1 | 1.94 × 10−1 | 1.82 × 10−1 | 1.90 × 10−1 | |||
| 1.92 × 10−1 | 1.91 × 10−1 | 1.94 × 10−1 | 1.76 × 10−1 | 1.79 × 10−1 | |||
| 5 | 500 | 1.15 × 10−1 | 8.18 × 10−2 | 8.68 × 10−2 | 1.19 × 10−1 | 9.62 × 10−2 | |
| 1.14 × 10−1 | 7.61 × 10−2 | 8.57 × 10−2 | 1.12 × 10−1 | 6.77 × 10−2 | |||
| 1.11 × 10−1 | 7.49 × 10−2 | 8.01 × 10−2 | 1.03 × 10−1 | 5.40 × 10−2 | |||
| 8 | 800 | 9.12 × 10−2 | 4.39 × 10−2 | 5.47 × 10−2 | 9.10 × 10−2 | 0.00 × 100 | |
| 9.10 × 10−2 | 3.94 × 10−2 | 5.17 × 10−2 | 9.01 × 10−2 | 0.00 × 100 | |||
| 9.02 × 10−2 | 3.65 × 10−2 | 3.98 × 10−2 | 8.76 × 10−2 | 0.00 × 100 |
| Test Function | Objectives | Iterations | IMOJS | NSGA-III | MOJS | MOEA/D | SPEA2 |
|---|---|---|---|---|---|---|---|
| DTLZ1 | 3 | 300 | 3.25 × 10−4 | 7.45 × 10−4 | 6.33 × 10−2 | 7.52 × 10−4 | 5.45 × 10−4 |
| 2.80 × 10−4 | 4.46 × 10−4 | 1.22 × 10−2 | 3.58 × 10−4 | 3.84 × 10−4 | |||
| 2.45 × 10−4 | 3.64 × 10−4 | 1.18 × 10−3 | 2.53 × 10−4 | 3.62 × 10−4 | |||
| 5 | 500 | 1.69 × 10−3 | 6.66 × 10−2 | 1.50 × 10−1 | 1.70 × 10−3 | 5.42 × 10−2 | |
| 1.68 × 10−3 | 6.00 × 10−2 | 1.40 × 10−1 | 1.70 × 10−3 | 2.98 × 10−2 | |||
| 1.68 × 10−3 | 5.50 × 10−2 | 8.51 × 10−3 | 1.70 × 10−3 | 7.00 × 10−3 | |||
| 8 | 800 | 5.29 × 10−2 | 1.07 × 10¹ | 9.86 × 10−1 | 8.00 × 10−2 | 4.25 × 10¹ | |
| 3.75 × 10−2 | 9.04 × 100 | 9.51 × 10−1 | 7.03 × 10−2 | 4.01 × 10¹ | |||
| 3.56 × 10−2 | 7.54 × 100 | 7.75 × 10−1 | 6.43 × 10−2 | 3.89 × 10¹ | |||
| DTLZ2 | 3 | 300 | 5.06 × 10−4 | 1.31 × 10−3 | 6.29 × 10−4 | 5.09 × 10−4 | 1.11 × 10−3 |
| 5.05 × 10−4 | 1.24 × 10−3 | 5.98 × 10−4 | 5.06 × 10−4 | 1.07 × 10−3 | |||
| 5.03 × 10−4 | 1.23 × 10−3 | 5.76 × 10−4 | 5.02 × 10−4 | 9.39 × 10−4 | |||
| 5 | 500 | 5.25 × 10−3 | 1.26 × 10−2 | 5.44 × 10−3 | 5.40 × 10−3 | 1.74 × 10−2 | |
| 5.23 × 10−3 | 1.24 × 10−2 | 5.44 × 10−3 | 5.36 × 10−3 | 1.65 × 10−2 | |||
| 5.20 × 10−3 | 1.19 × 10−2 | 5.44 × 10−3 | 5.30 × 10−3 | 1.51 × 10−2 | |||
| 8 | 800 | 1.29 × 10−2 | 2.25 × 10−2 | 2.59 × 10−1 | 2.40 × 10−2 | 2.85 × 10−1 | |
| 1.29 × 10−2 | 2.18 × 10−2 | 2.55 × 10−1 | 2.39 × 10−2 | 2.84 × 10−1 | |||
| 2.21 × 10−2 | 1.24 × 10−2 | 2.55 × 10−1 | 2.39 × 10−2 | 2.82 × 10−1 | |||
| DTLZ3 | 3 | 300 | 1.26 × 10−1 | 1.42 × 10−1 | 4.08 × 10−1 | 4.87 × 10−1 | 3.54 × 10−1 |
| 1.25 × 10−1 | 1.37 × 10−1 | 3.50 × 10−1 | 1.81 × 10−1 | 2.51 × 10−1 | |||
| 4.27 × 10−3 | 5.32 × 10−2 | 3.01 × 10−1 | 1.19 × 10−1 | 1.15 × 10−1 | |||
| 5 | 500 | 3.65 × 10−1 | 4.25 × 10−1 | 9.06 × 100 | 3.78 × 10−1 | 1.29 × 10¹ | |
| 3.16 × 10−1 | 4.10 × 10−1 | 8.98 × 100 | 3.18 × 10−1 | 5.92 × 100 | |||
| 2.86 × 10−1 | 3.25 × 10−1 | 8.24 × 100 | 2.97 × 10−1 | 2.72 × 100 | |||
| 8 | 800 | 2.96 × 100 | 8.71 × 100 | 3.10 × 102 | 3.64E × 102 | 2.42 × 102 | |
| 2.45 × 100 | 6.64 × 100 | 2.93 × 102 | 2.63 × 102 | 2.36 × 102 | |||
| 2.34 × 100 | 6.45 × 100 | 1.93 × 102 | 1.83 × 102 | 2.28 × 102 | |||
| DTLZ4 | 3 | 300 | 4.75 × 10−4 | 5.47 × 10−4 | 1.32 × 10−3 | 5.07 × 10−4 | 1.27 × 10−3 |
| 4.62 × 10−4 | 4.96 × 10−4 | 1.23 × 10−3 | 4.81 × 10−4 | 1.10 × 10−3 | |||
| 4.41 × 10−4 | 4.96 × 10−4 | 1.23 × 10−3 | 4.64 × 10−4 | 1.06 × 10−3 | |||
| 5 | 500 | 5.10 × 10−3 | 5.15 × 10−3 | 1.23 × 10−2 | 5.61 × 10−3 | 2.84 × 10−2 | |
| 4.96 × 10−3 | 5.09 × 10−3 | 1.23 × 10−2 | 5.47 × 10−3 | 2.16 × 10−2 | |||
| 4.93 × 10−3 | 4.83 × 10−3 | 1.22 × 10−2 | 5.30 × 10−3 | 7.30 × 10−3 | |||
| 8 | 800 | 1.51 × 10−2 | 1.52 × 10−2 | 2.68 × 10−1 | 2.12 × 10−2 | 2.87 × 10−1 | |
| 1.43 × 10−2 | 1.40 × 10−2 | 2.67 × 10−1 | 1.77 × 10−2 | 2.84 × 10−1 | |||
| 1.37 × 10−2 | 1.40 × 10−2 | 2.65 × 10−1 | 1.60 × 10−2 | 2.82 × 10−1 | |||
| DTLZ5 | 3 | 300 | 2.40 × 10−4 | 2.79 × 10−4 | 2.74 × 10−4 | 2.40 × 10−4 | 2.62 × 10−4 |
| 2.39 × 10−4 | 2.37 × 10−4 | 2.60 × 10−4 | 2.35 × 10−4 | 2.41 × 10−4 | |||
| 2.38 × 10−4 | 2.36 × 10−4 | 2.48 × 10−4 | 2.27 × 10−4 | 2.11 × 10−4 | |||
| 5 | 500 | 8.99 × 10−2 | 9.49 × 10−2 | 1.85 × 10−1 | 1.05 × 10−1 | 2.06 × 10−1 | |
| 8.54 × 10−2 | 9.36 × 10−2 | 1.84 × 10−1 | 9.39 × 10−2 | 2.01 × 10−1 | |||
| 8.54 × 10−2 | 9.01 × 10−2 | 1.81 × 10−1 | 8.63 × 10−2 | 1.92 × 10−1 | |||
| 8 | 800 | 1.38 × 10−1 | 1.70 × 10−1 | 2.78 × 10−1 | 2.73 × 10−1 | 3.20 × 10−1 | |
| 1.35 × 10−1 | 1.68 × 10−1 | 2.77 × 10−1 | 2.35 × 10−1 | 3.17 × 10−1 | |||
| 1.34 × 10−1 | 1.67 × 10−1 | 2.77 × 10−1 | 2.12 × 10−1 | 3.14 × 10−1 | |||
| DTL6 | 3 | 300 | 4.76 × 10−6 | 5.05 × 10−6 | 4.63 × 10−6 | 7.15 × 10−6 | 5.15 × 10−6 |
| 4.62 × 10−6 | 5.00 × 10−6 | 4.55 × 10−6 | 5.42 × 10−6 | 4.96 × 10−6 | |||
| 4.48 × 10−6 | 4.95 × 10−6 | 4.51 × 10−6 | 4.95 × 10−6 | 4.57 × 10−6 | |||
| 5 | 500 | 3.11 × 10−1 | 3.40 × 10−1 | 3.40 × 10−1 | 3.58 × 10−1 | 1.06 × 100 | |
| 3.10 × 10−1 | 3.20 × 10−1 | 8.70 × 10−1 | 3.50 × 10−1 | 8.81 × 10−1 | |||
| 3.09 × 10−1 | 3.03 × 10−1 | 8.69 × 10−1 | 3.12 × 10−1 | 6.39 × 10−1 | |||
| 8 | 800 | 4.75 × 10−1 | 4.72 × 10−1 | 1.17 × 100 | 4.95 × 10−1 | 1.28 × 100 | |
| 4.52 × 10−1 | 4.70 × 10−1 | 1.16 × 100 | 4.92 × 10−1 | 1.21 × 100 | |||
| 4.48 × 10−1 | 4.56 × 10−1 | 1.14 × 100 | 4.87 × 10−1 | 1.17 × 100 |
| Test Function | Objectives | Iterations | IMOJS | NSGA-III | MOJS | MOEA/D | SPEA2 |
|---|---|---|---|---|---|---|---|
| DTLZ1 | 3 | 300 | 2.09 × 10−2 | 3.73 × 10−2 | 2.85 × 10−2 | 2.18 × 10−2 | 2.21 × 10−2 |
| 2.08 × 10−2 | 2.85 × 10−2 | 2.57 × 10−2 | 2.10 × 10−2 | 2.14 × 10−2 | |||
| 2.04 × 10−2 | 2.69 × 10−2 | 2.46 × 10−2 | 2.06 × 10−2 | 2.12 × 10−2 | |||
| 5 | 500 | 6.89 × 10−2 | 8.44 × 10−1 | 8.37 × 10−2 | 6.90 × 10−2 | 9.15 × 10−2 | |
| 6.85 × 10−2 | 5.02 × 10−1 | 7.37 × 10−2 | 6.89 × 10−2 | 8.81 × 10−2 | |||
| 6.84 × 10−2 | 3.90 × 10−1 | 7.35 × 10−2 | 6.80 × 10−2 | 8.12 × 10−2 | |||
| 8 | 800 | 1.34 × 10−1 | 1.81 × 10−1 | 1.99 × 100 | 1.64 × 10−1 | 2.38 × 102 | |
| 1.15 × 10−1 | 1.67 × 10−1 | 1.72 × 100 | 1.17 × 10−1 | 1.66 × 102 | |||
| 1.12 × 10−1 | 1.57 × 10−1 | 1.33 × 100 | 1.14 × 10−1 | 1.29 × 102 | |||
| DTLZ2 | 3 | 300 | 8.98 × 10−2 | 5.66 × 10−2 | 7.08 × 10−2 | 5.49 × 10−2 | 5.76 × 10−2 |
| 5.45 × 10−2 | 5.62 × 10−2 | 6.93 × 10−2 | 5.47 × 10−2 | 5.69 × 10−2 | |||
| 5.45 × 10−2 | 5.58 × 10−2 | 6.80 × 10−2 | 5.46 × 10−2 | 5.59 × 10−2 | |||
| 5 | 500 | 2.19 × 10−1 | 2.18 × 10−1 | 2.61 × 10−1 | 2.19 × 10−1 | 2.70 × 10−1 | |
| 2.15 × 10−1 | 2.17 × 10−1 | 2.57 × 10−1 | 2.17 × 10−1 | 2.60 × 10−1 | |||
| 2.12 × 10−1 | 2.15 × 10−1 | 2.54 × 10−1 | 2.13 × 10−1 | 2.58 × 10−1 | |||
| 8 | 800 | 4.42 × 10−1 | 5.43 × 10−1 | 2.15 × 100 | 4.89 × 10−1 | 2.50 × 100 | |
| 4.22 × 10−1 | 5.34 × 10−1 | 1.98 × 100 | 4.87 × 10−1 | 2.48 × 100 | |||
| 4.12 × 10−1 | 4.07 × 10−1 | 1.92 × 100 | 4.79 × 10−1 | 2.43 × 100 | |||
| DTLZ3 | 3 | 300 | 2.80 × 10−1 | 3.97 × 10−1 | 4.02 × 10−1 | 4.18 × 100 | 7.99 × 10−1 |
| 2.29 × 10−1 | 2.40 × 10−1 | 2.75 × 10−1 | 1.00 × 100 | 2.71 × 10−1 | |||
| 1.27 × 10−1 | 2.31 × 10−1 | 2.73 × 10−1 | 1.65 × 10−1 | 1.97 × 10−1 | |||
| 5 | 500 | 5.13 × 10−1 | 1.41 × 100 | 1.57 × 10¹ | 2.45 × 100 | 9.30 × 100 | |
| 4.22 × 10−1 | 9.67 × 10−1 | 1.06 × 10¹ | 7.66 × 10−1 | 5.31 × 100 | |||
| 3.95 × 10−1 | 5.99 × 10−1 | 8.12 × 100 | 5.91 × 10−1 | 2.15 × 100 | |||
| 8 | 800 | 2.45 × 100 | 3.87 × 100 | 8.30 × 102 | 5.84 × 100 | 1.72 × 103 | |
| 1.92 × 100 | 3.02 × 100 | 6.87 × 102 | 5.71 × 100 | 1.56 × 103 | |||
| 1.56 × 100 | 2.07 × 100 | 6.59 × 102 | 5.67 × 100 | 1.23 × 103 | |||
| DTLZ4 | 3 | 300 | 7.28 × 10−2 | 2.01 × 10−1 | 2.13 × 10−1 | 5.41 × 10−1 | 5.40 × 10−1 |
| 6.98 × 10−2 | 1.52 × 10−1 | 1.57 × 10−1 | 4.57 × 10−1 | 2.16 × 10−1 | |||
| 6.82 × 10−2 | 1.03 × 10−1 | 1.04 × 10−1 | 9.57 × 10−2 | 2.01 × 10−1 | |||
| 5 | 500 | 2.43 × 10−1 | 2.57 × 10−1 | 3.12 × 10−1 | 6.46 × 10−1 | 4.28 × 10−1 | |
| 2.34 × 10−1 | 2.56 × 10−1 | 3.03 × 10−1 | 4.03 × 10−1 | 3.68 × 10−1 | |||
| 2.24 × 10−1 | 2.23 × 10−1 | 3.00 × 10−1 | 3.04 × 10−1 | 2.68 × 10−1 | |||
| 8 | 800 | 4.96 × 10−1 | 5.32 × 10−1 | 2.03 × 100 | 6.82 × 10−1 | 2.56 × 100 | |
| 4.87 × 10−1 | 4.97 × 10−1 | 1.94 × 100 | 6.20 × 10−1 | 2.50 × 100 | |||
| 4.73 × 10−1 | 4.92 × 10−1 | 1.93 × 100 | 5.79 × 10−1 | 2.42 × 100 | |||
| DTLZ5 | 3 | 300 | 6.50 × 10−3 | 1.32 × 10−2 | 1.17 × 10−2 | 3.39 × 10−2 | 6.64 × 10−3 |
| 6.41 × 10−3 | 1.24 × 10−2 | 1.08 × 10−2 | 3.38 × 10−2 | 6.18 × 10−3 | |||
| 6.35 × 10−3 | 1.18 × 10−2 | 1.06 × 10−2 | 3.37 × 10−2 | 5.97 × 10−3 | |||
| 5 | 500 | 1.04 × 10−1 | 1.18 × 10−1 | 1.17 × 10−1 | 2.65 × 10−1 | 2.72 × 10−1 | |
| 1.03 × 10−1 | 1.17 × 10−1 | 1.05 × 10−1 | 2.57 × 10−1 | 2.49 × 10−1 | |||
| 9.89 × 10−2 | 1.06 × 10−1 | 1.04 × 10−1 | 2.52 × 10−1 | 2.13 × 10−1 | |||
| 8 | 800 | 2.73 × 10−1 | 2.80 × 10−1 | 2.98 × 10−1 | 2.87 × 10−1 | 2.47 × 100 | |
| 2.58 × 10−1 | 2.63 × 10−1 | 2.97 × 10−1 | 2.79 × 10−1 | 2.45 × 100 | |||
| 2.54 × 10−1 | 2.45 × 10−1 | 2.76 × 10−1 | 2.72 × 10−1 | 2.43 × 100 | |||
| DTL6 | 3 | 300 | 6.55 × 10−3 | 2.00 × 10−2 | 1.48 × 10−2 | 3.39 × 10−2 | 7.32 × 10−3 |
| 6.53 × 10−3 | 1.89 × 10−2 | 1.39 × 10−2 | 3.38 × 10−2 | 6.89 × 10−3 | |||
| 6.52 × 10−3 | 1.86 × 10−2 | 1.35 × 10−2 | 3.29 × 10−2 | 6.84 × 10−3 | |||
| 5 | 500 | 3.25 × 10−1 | 3.44 × 10−1 | 3.62 × 100 | 3.51 × 10−1 | 5.41 × 100 | |
| 2.85 × 10−1 | 3.25 × 10−1 | 3.57 × 100 | 2.99 × 10−2 | 4.64 × 100 | |||
| 2.78 × 10−1 | 2.64 × 10−1 | 3.37 × 100 | 2.57 × 10−2 | 3.38 × 100 | |||
| 8 | 800 | 7.09 × 10−1 | 7.06 × 10−1 | 5.97 × 100 | 7.21 × 10−1 | 1.10 × 10¹ | |
| 6.69 × 10−1 | 6.98 × 10−1 | 5.71 × 100 | 6.88 × 10−1 | 1.00 × 10¹ | |||
| 6.28 × 10−1 | 6.96 × 10−1 | 5.60 × 100 | 6.35 × 10−1 | 9.99 × 100 |
References
- Guo, Y.T.; Xiang, Y. Cost-benefit analysis of PV-storage investment in integrated energy systems. Energy Rep. 2022, 8, 66–71. [Google Scholar] [CrossRef]
- Kocaman, A.S.; Modi, V. Value of pumped hydro storage in a hybrid energy generation and allocation system. Appl. Energy 2017, 205, 1202–1215. [Google Scholar] [CrossRef]
- Koholé, Y.W.; Wankouo Ngouleu, C.A.; Fohagui, F.C.V.; Tchuen, G. A comprehensive comparison of battery, hydrogen, pumped-hydro and thermal energy storage technologies for hybrid renewable energy systems integration. J. Energy Storage 2024, 93, 112299. [Google Scholar] [CrossRef]
- Benato, A.; Stoppato, A. Pumped Thermal Electricity Storage: A technology overview. Therm. Sci. Eng. Prog. 2018, 6, 301–315. [Google Scholar] [CrossRef]
- Klumpp, F. Comparison of pumped hydro, hydrogen storage and compressed air energy storage for integrating high shares of renewable energies—Potential, cost-comparison and ranking. J. Energy Storage 2016, 8, 119–128. [Google Scholar] [CrossRef]
- Xu, B.; Chen, D.; Venkateshkumar, M.; Xiao, Y.; Yue, Y.; Xing, Y.; Li, P. Modeling a pumped storage hydropower integrated to a hybrid power system with PV-wind power and its stability analysis. Appl. Energy 2019, 248, 446–462. [Google Scholar] [CrossRef]
- Naval, N.; Yusta, J.M.; Sánchez, R.; Sebastián, F. Optimal scheduling and management of pumped hydro storage integrated with grid-connected renewable power plants. J. Energy Storage 2023, 73, 108993. [Google Scholar] [CrossRef]
- Hunt, J.D.; Al-Nory, M.T.; Slocum, A.H.; Wada, Y. Integrated seasonal pumped hydro, cooling, and reverse osmosis: A solution to desert coastal regions. Desalination 2025, 593, 118242. [Google Scholar] [CrossRef]
- Shyam, B.; Kanakasabapathy, P. Feasibility of floating PV PV integrated pumped storage system for a grid-connected microgrid under static time of day tariff environment: A case study from India. Renew. Energy 2022, 192, 200–215. [Google Scholar] [CrossRef]
- Liu, L.; Sun, Q.; Li, H.; Yin, H.; Ren, X.; Wennersten, R. Evaluating the benefits of Integrating Floating PV and Pumped Storage Power System. Energy Conv. Manag. 2019, 194, 173–185. [Google Scholar] [CrossRef]
- Bhayo, B.A.; Al-Kayiem, H.H.; Gilani, S.I.U.; Ismail, F.B. Power management optimization of hybrid PV PV-battery integrated with pumped-hydro-storage system for standalone electricity generation. Energy Conv. Manag. 2020, 215, 112942. [Google Scholar] [CrossRef]
- Li, J.; Zhao, Z.; Li, P.; Apel Mahmud, M.; Liu, Y.; Chen, D.; Han, W. Comprehensive benefit evaluations for integrating off-river pumped hydro storage and floating PV. Energy Conv. Manag. 2023, 296, 117651. [Google Scholar] [CrossRef]
- Ma, T.; Yang, H.; Lu, L.; Peng, J. Optimal design of an autonomous PV–wind-pumped storage power supply system. Appl. Energy 2015, 160, 728–736. [Google Scholar] [CrossRef]
- Zhao, Z.; Yuan, Y.; He, M.; Jurasz, J.; Wang, J.; Egusquiza, M.; Egusquiza, E.; Xu, B.; Chen, D. Stability and efficiency performance of pumped hydro energy storage system for higher flexibility. Renew. Energy 2022, 199, 1482–1494. [Google Scholar] [CrossRef]
- Liu, J.; Ma, T.; Wu, H.; Yang, H. Study on optimum energy fuel mix for urban cities integrated with pumped hydro storage and green vehicles. Appl. Energy 2023, 331, 120399. [Google Scholar] [CrossRef]
- Ren, Y.; Sun, K.; Zhang, K.; Han, Y.; Zhang, H.; Wang, M.; Jing, X.; Mo, J.; Zou, W.; Xing, X. Optimization of the capacity configuration of an abandoned mine pumped storage/wind/PV integrated system. Appl. Energy 2024, 374, 124089. [Google Scholar] [CrossRef]
- Zhu, Y.; Yao, S.; Zhang, Y.; Cao, M. Environmental and economic scheduling for wind-pumped storage-thermal integrated energy system based on priority ranking. Electr. Power Syst. Res. 2024, 231, 110353. [Google Scholar] [CrossRef]
- Connolly, D.; Lund, H.; Mathiesen, B.V.; Pican, E.; Leahy, M. The technical and economic implications of integrating fluctuating renewable energy using energy storage. Renew. Energy 2012, 43, 47–60. [Google Scholar] [CrossRef]
- Patwal, R.S.; Narang, N. Multi-objective generation scheduling of integrated energy system using fuzzy based surrogate worth trade-off approach. Renew. Energy 2020, 156, 864–882. [Google Scholar] [CrossRef]
- Yan, Y.; Wu, T.; Li, S.; Xie, H.; Li, Y.; Liu, M.; Zhao, Y.; Liang, H.; Zhang, G.; Xin, H. Optimal operation strategies of pumped storage hydropower plant considering the integrated AC grids and new energy utilization. Energy Rep. 2022, 8, 545–554. [Google Scholar] [CrossRef]
- Sun, H.; Ren, Q.; Hou, J.; Zhao, Z.; Xie, D.; Zhao, W.; Meng, F. Study on the performance and economy of the building-integrated micro-grid considering PV and pumped storage: A case study in Foshan. Int. J. Low-Carbon Technol. 2022, 17, 630–636. [Google Scholar] [CrossRef]
- Xu, Y.; Li, C.; Wang, Z.; Zhang, N.; Peng, B. Load Frequency Control of a Novel Renewable Energy Integrated Micro-Grid Containing Pumped Hydropower Energy Storage. IEEE Access 2018, 6, 29067–29077. [Google Scholar] [CrossRef]
- Xu, J.P.; Liu, T.T. Optimal Hourly Scheduling for Wind-Hydropower Systems with Integrated Pumped-Storage Technology. J. Energy Eng. 2021, 147, 04021013. [Google Scholar] [CrossRef]
- Pérez-Díaz, J.I.; Jiménez, J. Contribution of a pumped-storage hydropower plant to reduce the scheduling costs of an isolated power system with high wind power penetration. Energy 2016, 109, 92–104. [Google Scholar] [CrossRef]
- Wang, X.Y.; Bai, Y.P. The global Minmax k-means algorithm. Springerplus 2016, 5, 1665. [Google Scholar] [CrossRef]
- Chen, Q.Q.; He, L.J.; Diao, Y.A.; Zhang, K.B.; Zhao, G.R.; Chen, Y.M. A Novel Neighborhood Granular Meanshift Clustering Algorithm. Mathematics 2023, 11, 207. [Google Scholar] [CrossRef]
- Liao, Y.; Zhao, Y.; Fang, N.; Huang, J. A Study on Site Selection for Regional Air Rescue Centers Based on Multi-Objective Jellyfish Search Algorithm. Biomimetics 2023, 8, 254. [Google Scholar] [CrossRef]
- Wang, X.; Feng, Y.; Tang, J.; Dai, Z.; Zhao, W. A UAV path planning method based on the framework of multi-objective jellyfish search algorithm. Sci. Rep. 2024, 14, 28058. [Google Scholar] [CrossRef]
- Yang, B.; Yin, Y.; Gao, Y.; Wang, S.; Fu, G.; Zhou, P. Field-factory hybrid service mode and its resource scheduling method based on an enhanced MOJS algorithm. Comput. Ind. Eng. 2022, 171, 108508. [Google Scholar] [CrossRef]
- Tian, J.; Qian, C.Y. Improved Multi-Objective Jellyfish Search Algorithm for UAV 3D Trajectory Planning. J. Northwest Univ. Natl. (Nat. Sci.) 2024, 45, 41–55. [Google Scholar] [CrossRef]
- Zhang, L.; Wang, N.Y.; Mao, J.L.; Li, R.Q. Low carbon flexible job shop scheduling based on improved multi-objective jellyfish search algorithm. Mech. Electr. Eng. Mag. 2023, 40, 1086–1092. [Google Scholar] [CrossRef]
- Tao, X.J.; Mo, Y.B. Improved Artificial Jellyfish Search Algorithm in Equations with Multiple Roots and Engineering Application. Math. Pract. Theory 2023, 53, 160–173. [Google Scholar]
- Eltamaly, A.M.; Rabie, A.H. A Novel Musical Chairs Optimization Algorithm. Arab. J. Sci. Eng. 2023, 48, 10371–10403. [Google Scholar] [CrossRef]
- Eltamaly, A.M. A Novel Strategy for Optimal PSO Control Parameters Determination for PV Energy Systems. Sustainability 2021, 13, 1008. [Google Scholar] [CrossRef]
- Ma, L.; Wang, Z.; Lu, Z.; Lu, X.; Wan, F. Integrated Strategy of the Output Planning and Economic Operation of the Combined System of Wind Turbines-Pumped-Storage-Thermal Power Units. IEEE Access 2019, 7, 20567–20576. [Google Scholar] [CrossRef]
- Liu, P.; Wu, X.; Wang, Z.; Bo, Y.; Bao, H. Numerical simulation study on gas-solid flow characteristics and SO2 removal characteristics in circulating fluidized bed desulfurization tower. Chem. Eng. Process.-Process Intensif. 2022, 176, 108974. [Google Scholar] [CrossRef]
- Meng, Z.; Wang, C.; Wang, X.; Chen, Y.; Wu, W.; Li, H. Simultaneous removal of SO2 and NOx from flue gas using (NH4)2S2O3/steel slag slurry combined with ozone oxidation. Fuel 2019, 255, 115760. [Google Scholar] [CrossRef]
- Lyu, X.; Liu, T.Q.; Liu, X.; He, C.; Nan, L.; Zeng, H. Low-carbon robust economic dispatch of park-level integrated energy system considering price-based demand response and vehicle-to-grid. Energy 2023, 263, 125739. [Google Scholar] [CrossRef]
- Yang, Y.; Wei, Q.Y.; Liu, S.K.; Zhao, L. Distribution Strategy Optimization of Standalone Hybrid WT/PV System Based on Different PV and Wind Resources for Rural Applications. Energies 2022, 15, 5307. [Google Scholar] [CrossRef]
- Zhao, P.Y.; Nan, H.P.; Cai, Q.S.; Gao, C.Y.; Wu, L.C. A Data-Driven Predictive Control Method for Modeling Doubly-Fed Variable-Speed Pumped Storage Units. Energies 2024, 17, 4912. [Google Scholar] [CrossRef]
- Shi, Y.F.; Shi, X.J.; Yi, C.B.; Song, X.F.; Chen, X.G. Control of the Variable-Speed Pumped Storage Unit-Wind Integrated System. Math. Probl. Eng. 2020, 2020, 3816752. [Google Scholar] [CrossRef]



| Reference | VS-PS | Wind–PV Data Preprocessing | Algorithm Improvement | Large-Scale Power Generation System |
|---|---|---|---|---|
| [7] | √ | × | × | × |
| [8] | √ | × | √ | × |
| [9] | √ | × | × | × |
| [10] | × | × | × | × |
| [12] | √ | × | √ | × |
| [13] | √ | × | × | × |
| [14] | √ | √ | × | × |
| [15] | √ | √ | × | × |
| [16] | √ | × | × | × |
| [17] | × | × | × | √ |
| [20] | √ | × | × | √ |
| [21] | × | × | √ | × |
| [23] | √ | √ | × | × |
| Proposed | √ | √ | √ | √ |
| Index | Value |
|---|---|
| Mean Silhouette | 0.613 |
| Calinski–Harabasz | 710.7 |
| Davies–Bouldin | 0.542 |
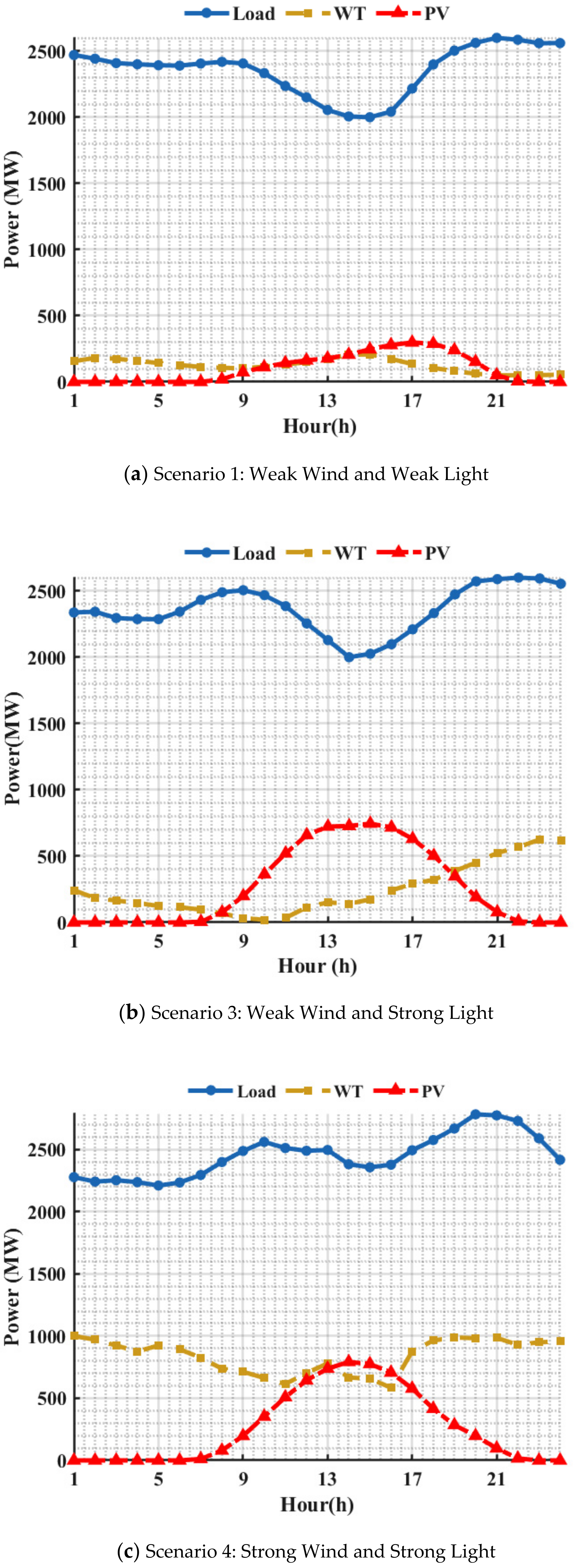
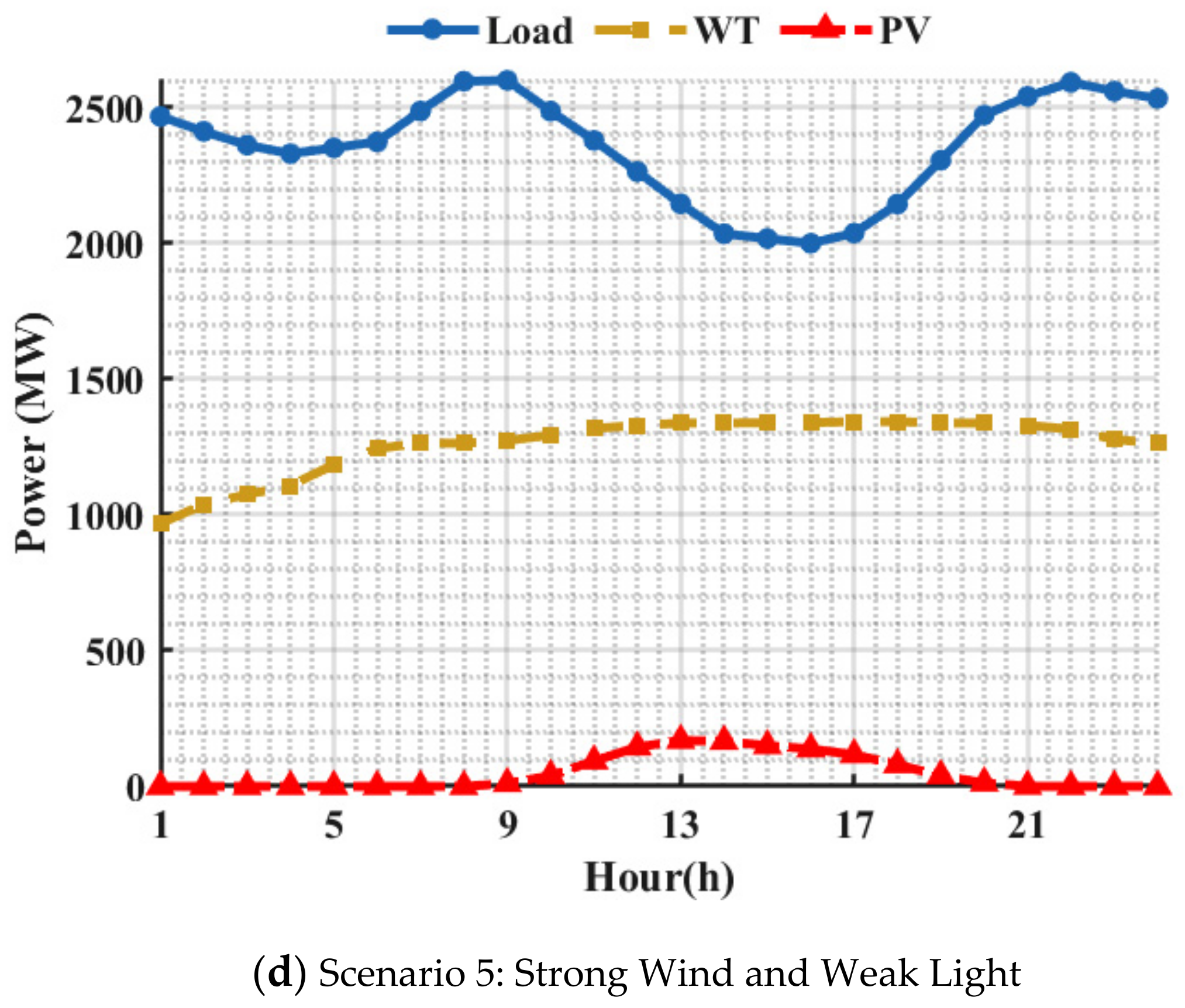
| Scenarios | Class Name | Date |
|---|---|---|
| Scenario 1 | Weak Wind and Weak Light | 28 June 2021 |
| Scenario 2 | Moderate Wind and Weak Light | 13 April 2021 |
| Scenario 3 | Weak Wind and Strong Light | 19 May 2021 |
| Scenario 4 | Strong Wind and Strong Light | 29 May 2021 |
| Scenario 5 | Strong Wind and Weak Light | 31 March 2021 |
| Scenario 6 | Moderate Wind and Strong Light | 26 August 2021 |
| Test Function | Objectives | Iterations | IMOJS | NSGA-III | MOJS | MOEA/D | SPEA2 |
|---|---|---|---|---|---|---|---|
| DTLZ1 | 5 | 500 | 9.69 × 10−1 | 9.70 × 10−1 | 9.64 × 10−1 | 9.68 × 10−1 | 9.58 × 10−1 |
| 9.63 ×10−1 | 9.53 × 10−1 | 9.18 × 10−1 | 9.60 × 10−1 | 9.55 × 10−1 | |||
| 9.60 × 10−1 | 9.05 × 10−1 | 9.18 × 10−1 | 9.56 × 10−1 | 9.53 × 10−1 | |||
| DTLZ2 | 3 | 300 | 5.59 × 10−1 | 5.61 × 10−1 | 5.56 × 10−1 | 5.62 × 10−1 | 5.55 × 10−1 |
| 5.59 × 10−1 | 5.29 × 10−1 | 5.56 × 10−1 | 5.57 × 10−1 | 5.53 × 10−1 | |||
| 5.59 × 10−1 | 5.28 × 10−1 | 5.55 × 10−1 | 5.54 × 10−1 | 5.50 × 10−1 | |||
| DTLZ3 | 3 | 300 | 3.94 × 10−1 | 3.35 × 10−1 | 3.62 × 10−1 | 3.61 × 10−1 | 5.07 × 10−1 |
| 3.81 × 10−1 | 3.22 × 10−1 | 3.56 × 10−1 | 2.77 × 10−1 | 3.40 × 10−1 | |||
| 2.90 × 10−1 | 3.20 × 10−1 | 2.45 × 10−1 | 1.73 × 10−1 | 3.19 × 10−1 | |||
| 5 | 500 | 4.46 × 10−1 | 3.80 × 10−1 | 4.26 × 10−1 | 7.08 × 10−1 | 4.26 × 10−1 | |
| 4.27 × 10−1 | 3.68 × 10−1 | 3.78 × 10−1 | 3.92 × 10−1 | 4.19 × 10−1 | |||
| 3.88 × 10−1 | 3.33 × 10−1 | 3.53 × 10−1 | 1.48 × 10−1 | 2.15 × 10−1 | |||
| 8 | 800 | 5.36 × 10−1 | 3.64 × 10−1 | 1.76 × 10−1 | 6.39 × 10−1 | 0.00 × 100 | |
| 4.69 × 10−1 | 2.79 × 10−1 | 1.29 × 10−1 | 4.24 × 10−1 | 0.00 × 100 | |||
| 3.92 × 10−1 | 2.18 × 10−1 | 8.26 × 10−2 | 9.44 × 10−2 | 0.00 × 100 | |||
| DTLZ4 | 8 | 800 | 8.38 × 10−1 | 8.27 × 10−1 | 8.32 × 10−1 | 7.79 × 10−1 | 0.00 × 100 |
| 8.29 × 10−1 | 7.14 × 10−1 | 8.30 × 10−1 | 7.31 × 10−1 | 0.00 × 100 | |||
| 8.27 × 10−1 | 3.84 × 10−1 | 4.77 × 10−1 | 6.96 × 10−1 | 0.00 × 100 | |||
| DTLZ6 | 5 | 500 | 1.15 × 10−1 | 8.18 × 10−2 | 8.68 × 10−2 | 1.19 × 10−1 | 9.62 × 10−2 |
| 1.14 × 10−1 | 7.61 × 10−2 | 8.57 × 10−2 | 1.12 × 10−1 | 6.77 × 10−2 | |||
| 1.11 × 10−1 | 7.49 × 10−2 | 8.01 × 10−2 | 1.03 × 10−1 | 5.40 × 10−2 |
| Test Function | Objectives | Iterations | IMOJS | NSGA-III | MOJS | MOEA/D | SPEA2 |
|---|---|---|---|---|---|---|---|
| DTLZ2 | 3 | 300 | 5.06 × 10−4 | 1.31 × 10−3 | 6.29 × 10−4 | 5.09 × 10−4 | 1.11 × 10−3 |
| 5.05 × 10−4 | 1.24 × 10−3 | 5.98 × 10−4 | 5.06 × 10−4 | 1.07 × 10−3 | |||
| 5.03 × 10−4 | 1.23 × 10−3 | 5.76 × 10−4 | 5.02 × 10−4 | 9.39 × 10−4 | |||
| 8 | 800 | 1.29 × 10−4 | 2.25 × 10−2 | 2.59 × 10−1 | 2.40 × 10−2 | 2.85 × 10−1 | |
| 1.29 × 10−4 | 2.18 × 10−2 | 2.55 × 10−1 | 2.39 × 10−2 | 2.84 × 10−1 | |||
| 2.21 × 10−4 | 1.24 × 10−2 | 2.55 × 10−1 | 2.39 × 10−2 | 2.82 × 10−1 | |||
| DTLZ4 | 3 | 300 | 4.75 × 10−4 | 5.47 × 10−4 | 1.32 × 10−3 | 5.07 × 10−4 | 1.27 × 10−3 |
| 4.62 × 10−4 | 4.96 × 10−4 | 1.23 × 10−3 | 4.81 × 10−4 | 1.10 × 10−3 | |||
| 4.41 × 10−4 | 4.96 × 10−4 | 1.23 × 10−3 | 4.64 × 10−4 | 1.06 × 10−3 | |||
| 8 | 800 | 1.51 × 10−2 | 1.52 × 10−2 | 2.68 × 10−1 | 2.12 × 10−2 | 2.87 × 10−1 | |
| 1.43 × 10−2 | 1.40 × 10−2 | 2.67 × 10−1 | 1.77 × 10−2 | 2.84 × 10−1 | |||
| 1.37 × 10−2 | 1.40 × 10−2 | 2.65 × 10−1 | 1.60 × 10−2 | 2.82 × 10−1 | |||
| DTL6 | 3 | 300 | 4.76 × 10−6 | 5.05 × 10−6 | 4.63 × 10−6 | 7.15 × 10−6 | 5.15 × 10−6 |
| 4.62 × 10−6 | 5.00 × 10−6 | 4.55 × 10−6 | 5.42 × 10−6 | 4.96 × 10−6 | |||
| 4.48 × 10−6 | 4.95 × 10−6 | 4.51 × 10−6 | 4.95 × 10−6 | 4.57 × 10−6 | |||
| 5 | 500 | 3.11 × 10−1 | 3.40 × 10−1 | 3.40 × 10−1 | 3.58 × 10−1 | 1.06 × 100 | |
| 3.10 × 10−1 | 3.20 × 10−1 | 8.70 × 10−1 | 3.50 × 10−1 | 8.81 × 10−1 | |||
| 3.09 × 10−1 | 3.03 × 10−1 | 8.69 × 10−1 | 3.12 × 10−1 | 6.39 × 10−1 | |||
| 8 | 800 | 4.75 × 10−1 | 4.72 × 10−1 | 1.17 × 100 | 4.95 × 10−1 | 1.28 × 100 | |
| 4.52 × 10−1 | 4.70 × 10−1 | 1.16 × 100 | 4.92 × 10−1 | 1.21 × 100 | |||
| 4.48 × 10−1 | 4.56 × 10−1 | 1.14 × 100 | 4.87 × 10−1 | 1.17 × 100 |
| Test Function | Objectives | Iterations | IMOJS | NSGA-III | MOJS | MOEA/D | SPEA2 |
|---|---|---|---|---|---|---|---|
| DTLZ2 | 3 | 300 | 8.98 × 10−2 | 5.66 × 10−2 | 7.08 × 10−2 | 5.49 × 10−2 | 5.76 × 10−2 |
| 5.45 × 10−2 | 5.62 × 10−2 | 6.93 × 10−2 | 5.47 × 10−2 | 5.69 × 10−2 | |||
| 5.45 × 10−2 | 5.58 × 10−2 | 6.80 × 10−2 | 5.46 × 10−2 | 5.59 × 10−2 | |||
| 5 | 500 | 2.19 × 10−1 | 2.18 × 10−1 | 2.61 × 10−1 | 2.19 × 10−1 | 2.70 × 10−1 | |
| 2.15 × 10−1 | 2.17 × 10−1 | 2.57 × 10−1 | 2.17 × 10−1 | 2.60 × 10−1 | |||
| 2.12 × 10−1 | 2.15 × 10−1 | 2.54 × 10−1 | 2.13 × 10−1 | 2.58 × 10−1 | |||
| 8 | 800 | 4.42 × 10−1 | 5.43 × 10−1 | 2.15 × 100 | 4.89 × 10−1 | 2.50 × 100 | |
| 4.22 × 10−1 | 5.34 × 10−1 | 1.98 × 100 | 4.87 × 10−1 | 2.48 × 100 | |||
| 4.12 × 10−1 | 4.07 × 10−1 | 1.92 × 100 | 4.79 × 10−1 | 2.43 × 100 | |||
| DTLZ5 | 3 | 300 | 6.50 × 10−3 | 1.32 × 10−2 | 1.17 × 10−2 | 3.39 × 10−2 | 6.64 × 10−3 |
| 6.41 × 10−3 | 1.24 × 10−2 | 1.08 × 10−2 | 3.38 × 10−2 | 6.18 × 10−3 | |||
| 6.35 × 10−3 | 1.18 × 10−2 | 1.06 × 10−2 | 3.37 × 10−2 | 5.97 × 10−3 | |||
| 8 | 800 | 2.73 × 10−1 | 2.80 × 10−1 | 2.98 × 10−1 | 2.87 × 10−1 | 2.47 × 100 | |
| 2.58 × 10−1 | 2.63 × 10−1 | 2.97 × 10−1 | 2.79 × 10−1 | 2.45 × 100 | |||
| 2.54 × 10−1 | 2.45 × 10−1 | 2.76 × 10−1 | 2.72 × 10−1 | 2.43 × 100 | |||
| DTLZ6 | 5 | 500 | 3.25 × 10−1 | 3.44 × 10−1 | 3.62 × 100 | 3.51 × 10−1 | 5.41 × 100 |
| 2.85 × 10−1 | 3.25 × 10−1 | 3.57 × 100 | 2.99 × 10−2 | 4.64 × 100 | |||
| 2.78 × 10−1 | 2.64 × 10−1 | 3.37 × 100 | 2.57 × 10−2 | 3.38 × 100 | |||
| 8 | 800 | 7.09 × 10−1 | 7.06 × 10−1 | 5.97 × 100 | 7.21 × 10−1 | 1.10 × 10¹ | |
| 6.69 × 10−1 | 6.98 × 10−1 | 5.71 × 100 | 6.88 × 10−1 | 1.00 × 10¹ | |||
| 6.28 × 10−1 | 6.96 × 10−1 | 5.60 × 100 | 6.35 × 10−1 | 9.99 × 100 |
| Pollutants | Emission/kg | Treatment Cost/(CNY·kg−1) |
|---|---|---|
| SO2 | 1.25 | 6 |
| NOx | 8 | 8 |
| TSP | 0.41 | 2.20 |
| Installed Capacity of Each Power Source and Pumped Storage Parameters | Data |
|---|---|
| Total Capacity of the Wind Farm | 1500 MW |
| Total Capacity of the PV Power Plant | 1000 MW |
| Total Capacity of the Pumped Storage Units | 1200 MW |
| Hydroelectric Conversion Efficiency | 0.75 |
| Reservoir Capacity Upper Limit | 2806.5 m |
| Reservoir Capacity Lower Limit | 2784 m |
| Total Installed Capacity of Thermal Power Plant | 3000 MW |
| a(t/MW2) | 0.00056 |
| b(t/MW) | 0.384 |
| c(t) | 2.2 |
| Scenario | Algorithm | System Operating Cost (Ten Thousand CNY) | CO2 Emissions (t) | Fluctuations in Thermal Power Generation |
|---|---|---|---|---|
| Scenario1 | IMOJS | 1652.4 | 25,867.3 | 159.3 |
| MOJS | 1826.4 | 27,024.5 | 226.4 | |
| NSGA-III | 1718.9 | 26,202.6 | 254.8 | |
| MOEA/D | 1697.2 | 26,110.4 | 267.6 | |
| SPEA-2 | 1807.5 | 26,924.1 | 314.5 | |
| Scenario 2 | IMOJS | 2503.6 | 38,133.7 | 241.2 |
| MOJS | 2604.7 | 38,468.3 | 319.2 | |
| NSGA-III | 2567.3 | 38,294.5 | 261.4 | |
| MOEA/D | 2658.9 | 38,599.1 | 258.7 | |
| SPEA-2 | 2692.5 | 38,652.2 | 245.3 | |
| Scenario 3 | IMOJS | 1588.2 | 19,917.4 | 174.0 |
| MOJS | 1757.9 | 20,296.5 | 181.9 | |
| NSGA-III | 1692.4 | 20,158.0 | 198.6. | |
| MOEA/D | 1638.7 | 20,029.6 | 185.3 | |
| SPEA-2 | 1782.6 | 20,379.2 | 189.5 | |
| Scenario 4 | IMOJS | 3245.3 | 51,396.5 | 213.6 |
| MOJS | 3425.9 | 52,637.9 | 228.4 | |
| NSGA-III | 3306.4 | 51,743.8 | 224.9 | |
| MOEA/D | 3372.6 | 51,826.3 | 238.7 | |
| SPEA-2 | 3406.8 | 52,489.6 | 220.1 | |
| Scenario 5 | IMOJS | 1801.1 | 21,861.3 | 269.2 |
| MOJS | 2213.7 | 22,399.1 | 278.3 | |
| NSGA-III | 1976.9 | 22,067.3 | 294.0 | |
| MOEA/D | 1899.6 | 21,985.7 | 311.8 | |
| SPEA-2 | 2344.5 | 22,518.5 | 307.4 | |
| Scenario 6 | IMOJS | 2921.3 | 43,950.5 | 298.7 |
| MOJS | 3018.9 | 44,207.6 | 308.4 | |
| NSGA-III | 2989.7 | 44,112.8 | 352.5 | |
| MOEA/D | 2997.4 | 44,197.1 | 322.2 | |
| SPEA-2 | 3242.4 | 44,814.3 | 314.0 |
| Scenario | Variable/Fixed Pumped Storage | System Operating Cost (Ten Thousand CNY) | CO2 Emissions (t) | Fluctuations in Thermal Power Generation |
|---|---|---|---|---|
| Scenario 1 | Variable | 1652.4 | 25,867.3 | 159.3 |
| Fixed | 1867.8 | 27,338.7 | 292.1 | |
| Scenario 2 | Variable | 2503.6 | 38,133.7 | 241.2 |
| Fixed | 2977.6 | 39,387.4 | 333.0 | |
| Scenario 3 | Variable | 1588.2 | 19,917.4 | 174.0 |
| Fixed | 1911.2 | 20,645.3 | 200.3 | |
| Scenario 4 | Variable | 3245.3 | 51,396.5 | 213.6 |
| Fixed | 3563.6 | 52,814.6 | 261.0 | |
| Scenario 5 | Variable | 1801.1 | 21,861.3 | 269.2 |
| Fixed | 2400.3 | 22,764.9 | 285.6 | |
| Scenario 6 | Variable | 2921.3 | 43,950.5 | 298.7 |
| Fixed | 3126.3 | 44,315.3 | 338.0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, Y.; Zhang, K.; Liu, S.; Wang, Z. Research on Day-Ahead Optimal Scheduling of Wind–PV–Thermal–Pumped Storage Based on the Improved Multi-Objective Jellyfish Search Algorithm. Energies 2025, 18, 2308. https://doi.org/10.3390/en18092308
Hu Y, Zhang K, Liu S, Wang Z. Research on Day-Ahead Optimal Scheduling of Wind–PV–Thermal–Pumped Storage Based on the Improved Multi-Objective Jellyfish Search Algorithm. Energies. 2025; 18(9):2308. https://doi.org/10.3390/en18092308
Chicago/Turabian StyleHu, Yunfei, Kefei Zhang, Sheng Liu, and Zhong Wang. 2025. "Research on Day-Ahead Optimal Scheduling of Wind–PV–Thermal–Pumped Storage Based on the Improved Multi-Objective Jellyfish Search Algorithm" Energies 18, no. 9: 2308. https://doi.org/10.3390/en18092308
APA StyleHu, Y., Zhang, K., Liu, S., & Wang, Z. (2025). Research on Day-Ahead Optimal Scheduling of Wind–PV–Thermal–Pumped Storage Based on the Improved Multi-Objective Jellyfish Search Algorithm. Energies, 18(9), 2308. https://doi.org/10.3390/en18092308





