Numerical Investigation of Sheet-Gyroid Structure Modifications for Mixing Application in Renewable Energy Technologies

Abstract

The presented study focuses on evaluating the mixing properties of structures derived from the so-called sheet-gyroid geometry and their modifications as advanced mixing elements in renewable energy technologies. Using numerical simulations based on computational fluid dynamics (CFD), the hydrodynamic characteristics of the basic sheet-gyroid structure and five geometric modifications were analyzed under laminar flow conditions simulating the mixing of water and ethylene glycol. The evaluation was conducted using the parameters mixing index and performance index, which express the efficiency of fluid homogenization and its associated energy demands. The results show that all tested geometries significantly improve the degree of mixing compared to an empty channel. The highest concentration homogeneity and best energy efficiency were achieved by the twisted sheet-gyroid structure. This geometric modification exhibits the highest value of the performance index, confirming its ability to achieve excellent mixing with minimal pressure losses. The results of the study demonstrated that, despite similar hydraulic losses among some of the structures, their fluid mixing performance differs, which highlights the importance of targeted geometric design of sheet-gyroid structures. These findings are essential for the design of efficient mixers in technological applications where intensive mixing combined with minimal energy consumption is a critical factor.

1. Introduction

Effective liquid mixing is crucial in various renewable energy sectors [1,2,3,4,5,6]. Liquid mixing is important in fuel cells for renewable energy sources by ensuring the homogeneity of liquid electrolytes, which guarantees consistent ionic conductivity and optimal performance. It aids in the removal of heat generated during reactions, thus contributing to the stability and lifespan of the cell. In humidification systems, mixing water with gases affects proper humidity. In direct liquid fuel cells, it ensures a uniform concentration of fuel delivered to the electrode, leading to more stable and efficient performance of the entire system [7,8]. In the field of renewable energy, liquid mixing in photobioreactors is crucial for the efficient production of biomass and biofuels from algae and cyanobacteria. It ensures uniform distribution of light, nutrients, and carbon dioxide in the cultivation medium, thereby optimizing the photosynthetic activity of microorganisms. Mixing prevents cell sedimentation, the formation of temperature gradients, and localized nutrient depletion, leading to higher productivity and biomass yield. Effective mixing thus directly influences the economic and environmental sustainability of processes based on photobioreactors [9,10]. In the production of biofuels, such as ethanol from biomass and biodiesel from vegetable oils, it ensures optimal contact between reactants and microorganisms, thereby increasing yield and reducing reaction time. Mixing is also essential in the co-processing of biomass with petroleum fractions in refineries. In solar thermal energy, it guarantees homogeneous properties of heat transfer fluids and optimizes the characteristics of molten salts for efficient heat transfer and storage. In energy storage systems, particularly in flow batteries, electrolyte mixing affects battery performance and lifespan [11]. In geothermal energy, mixing is used to improve heat transfer in heat pumps and to increase rock permeability in EGS systems. Although less widespread, mixing is also being explored in energy extraction from salinity gradients and in water electrolysis for green hydrogen production. One of the most advanced approaches to addressing this challenge is the application of sophisticated geometric configurations, including gyroid structures [12,13], which are explored in the present research. These complex spatially periodic surfaces exhibit unique hydrodynamic properties [14], which can be leveraged to achieve efficient and uniform fluid mixing even at lower energy levels of the flowing medium.

The gyroid belongs to the class of triply periodic minimal surfaces, characterized by zero mean curvature and a continuous interconnection of internal channels in all three spatial directions [15,16,17]. This unique geometry generates complex flow patterns within the moving fluid, promoting the development of turbulent and chaotic flow regimes even at relatively low velocities. Such flow behavior enhances mass and heat transfer, making the gyroid structure particularly suitable for applications where mixing is a critical factor influencing the performance and reliability of technology [18]. In the field of renewable energy, gyroid structures can be effectively applied, for example, in the design of advanced heat exchangers, where their high surface-to-volume ratio allows for a significant enhancement of heat transfer efficiency. They are also considered highly promising for the development of photobioreactors, in which optimal mixing of the cultivation medium has a decisive impact on the productivity of microbial biomass. Another important application area is gas mixing in hydrogen electrolyzes or fuel cells, where gyroid configurations may contribute to more efficient removal of reaction products and uniform delivery of reactants to the active surface.

The mixing performance of gyroid structures can be purposefully improved through various geometric modifications, including adjustment of wall thickness, changes in the periodic length of the unit cell, deformation of the basic unit cell, or addition and subtraction of spatial elements within the gyroid geometry. By altering these parameters, it is possible to achieve controlled manipulation of hydrodynamic characteristics, such as levels of turbulent kinetic energy, distribution of shear stress, or intensity of vorticity in the flowing medium. Further improvements can be achieved through the integration of secondary geometric elements or by transitioning to hybrid gyroid configurations, which combine different types of triply periodic minimal surfaces to enhance chaotic flow behavior and increase the efficiency of fluid mixing.

The process of liquid mixing is the subject of a wide range of published research, in which authors explore the performance of various types of mixing devices, either powered by external energy sources or operating as passive static mixers. These investigations are typically conducted using physical experiments or numerical simulations [19,20,21,22,23].

The presented research focuses on the use of alternative configurations of the sheet-gyroid structure as a static mixer under low Reynolds number (Re) conditions, with the efficiency of the mixing process evaluated based on results obtained from numerical simulation. Tripathi et al. [24] conducted a numerical analysis study the mixing of water and ethanol in a spiral micromixer across a Reynolds number (Re) range of 1 to 100, and the results were compared with those of serpentine and straight micromixers of equal flow length. The findings show that at low Re values, the mixing efficiency is comparable across all three designs. However, at higher Reynolds numbers, the spiral micromixer outperforms the others due to the formation of Dean vortices, which enhance mixing. In the case of the straight micromixer, mixing efficiency decreases with increasing Re, whereas in the spiral and serpentine designs, efficiency initially drops and then increases again. Pressure losses are similar at low Re, but at higher flow rates, they are slightly higher in the spiral and serpentine configurations compared to the straight micromixer. Raza et al. [25] compared ten typical passive micromixers from five different design categories based on the mixing index, pressure drop and mixing cost under identical flow conditions and channel length, across a Reynolds number range of 0.01–120. The analysis was performed numerically using the continuity equation, Navier–Stokes equations, and the convection–diffusion equation. The results showed that mixing mechanisms vary depending on the Reynolds number; therefore, different types of micromixers were recommended for specific Re ranges. For low Re values, 3D double-layer micromixers were identified as the most suitable, while for medium-to-high Reynolds numbers, the 2D Tesla micromixer demonstrated the best performance.

Hosseini et al. [26] designed and tested a four-wing static mixer intended for mixing Newtonian fluids at Reynolds numbers ranging from 700 to 6800. The mixer consists of four blades rotated by 45°, arranged in varying numbers (6, 8, and 10 elements), with each subsequent element also rotated by 45°. Mixing quality was evaluated using the coefficient of variation, which decreases with increasing energy input per unit mass—most significantly with 10 mixing elements, where a mixing efficiency greater than 95% was achieved. The experimentally determined friction factors were compared with existing models and were found to be lower across a wide range of Reynolds numbers than those associated with other types of static mixers.

The implementation of gyroid structures into static mixers was investigated by Alzoubi et al. [27,28] who, unlike the present study, employed skeletal-gyroid structures, whereas the current work utilizes sheet-gyroid structures. In their studies, Alzoubi and colleagues focused on enhancing T-micromixers using various 3D-printed gyroid configurations, including twisted, graded, and stochastic versions. The objective was to induce more chaotic flow patterns and thereby improve mixing performance while maintaining device compactness. The validated numerical model demonstrated that the twisted skeletal-gyroid structure achieved the best results, increasing the mixing index by up to 172% and simultaneously reducing the length of the mixing chamber by 41%. These findings highlight the potential of such designs for more efficient and compact microfluidic devices in chemical and pharmaceutical applications. Ouda et al. [29] compared novel static mixers based on triply periodic minimal surface geometries with the conventional mixer using CFD simulations and experimental validation. The results showed that in the case of a single mixing unit, triply periodic minimal surface structures such as gyroid, diamond, and IWP outperformed the conventional mixer in terms of energy efficiency while maintaining or even improving mixing performance. In multi-unit systems, the conventional mixer achieved slightly better mixing efficiency; however, triply periodic minimal surface-based solutions remained more energy-efficient. By modifying the design, including hybridization with conventional geometry, it was possible to achieve comparable mixing performance with at least 25% energy savings.

The aim of the present study is to investigate the hydrodynamic characteristics of geometrically modified sheet-gyroid structures through computational fluid dynamics at low liquid flow velocities, with a focus on their application as advanced mixers in renewable energy technologies. The results of this work are expected to contribute to a deeper understanding of how the geometric parameters of gyroid structures interact with flow dynamics, which may lead to further optimization and broader implementation of these promising structures in practical applications.

2. Materials and Methods

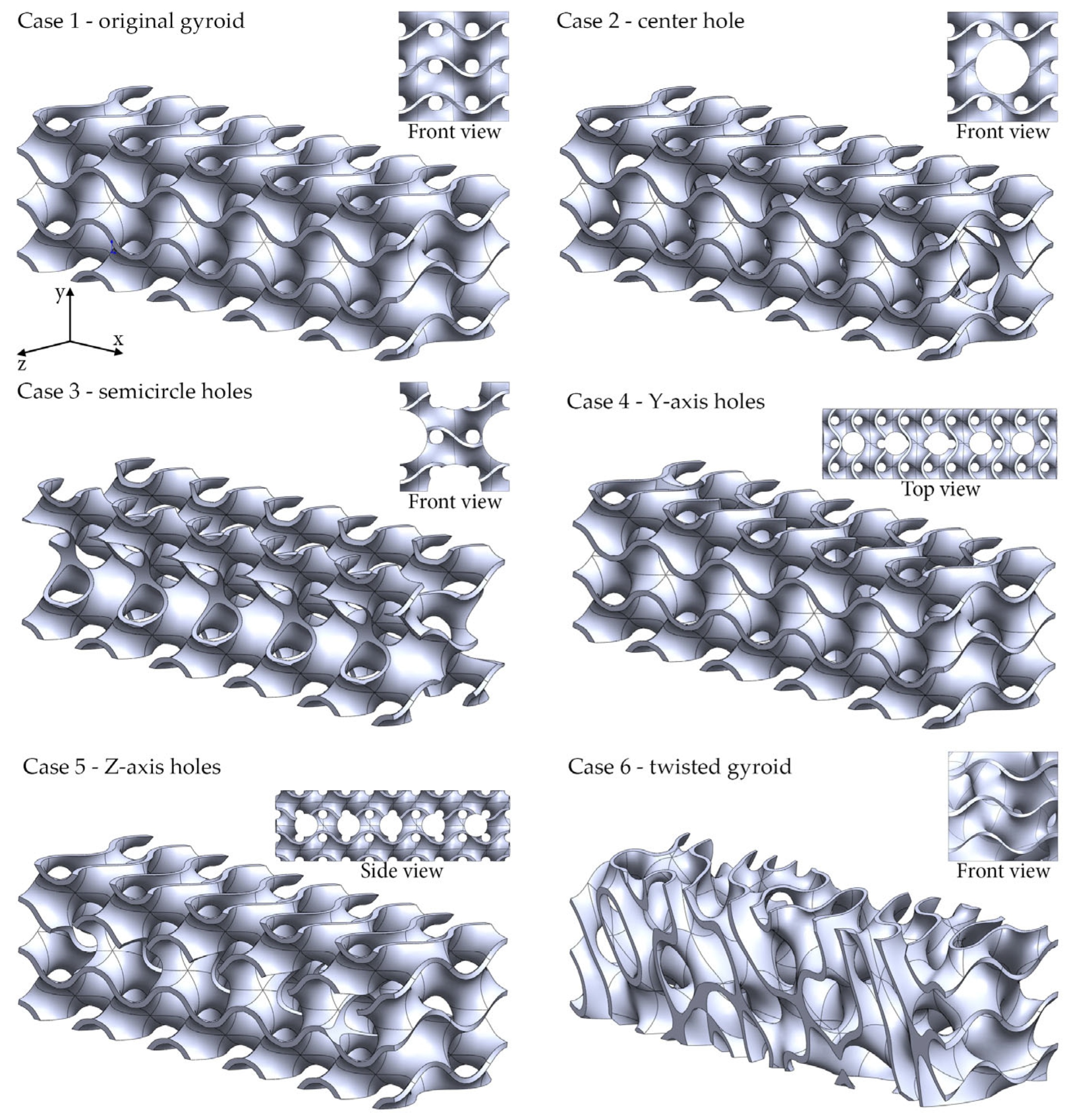
In the present study, a basic sheet-gyroid structure and five of its geometric modifications were used to thoroughly investigate the influence of structural alterations on the hydrodynamic and mixing properties during liquid flow. An overview of the tested structures is summarized in Figure 1. In total, six structural cases were analyzed, each with a specific geometric modification aimed at influencing flow behavior within the structure. For comparison purposes, a reference case with an empty channel was also evaluated to quantify the baseline condition.

The first case (Case 1—original gyroid) represents the unaltered sheet-gyroid structure with a regular, three-dimensionally periodic channel geometry, characterized by a uniform distribution of channels without additional design interventions. The mathematical definition of this geometry, as well as a detailed description of the procedure for constructing a 3D solid model suitable for CFD analysis, can be found in a broad range of scientific literature, including work by the authors of the present study [30,31]. Due to its geometric uniformity, this structure is widely used in devices focused on heat exchange applications. The uniform distribution of solid material within the structure ensures consistent heat transfer and contributes to the overall efficiency of the heat exchange process.

From the perspective of potential application in the mixing of liquids and gases, the sheet-gyroid geometry is less advantageous, as it tends to cause partial flow separation in the direction of the main axis due to the fluid passing through two distinct groups of channels. As a result, mixing occurs only to a limited extent. One option to eliminate this deficiency is to modify the basic geometry, thereby increasing its ability to mix different fluids, with only a minimal reduction in heat transfer efficiency or increase in pressure drop in the device.

The geometry labeled Case 2—center hole can be described as a sheet-gyroid structure with an added central open channel of diameter R = 1/4H, where H represents the total height and width of the structure. This modification is aimed at generating more pronounced central flow, which may promote enhanced mixing due to the formation of localized velocity changes and turbulence in the center of the unit cell. Case 3—semicircle holes consist of the base sheet-gyroid structure, from which volumes in the shape of cylinders with semicircular bases (radius R = 1/4H) have been subtracted. The centers of these semicircles are positioned on the peripheral edges of the structure at a distance of C = H/2 from the corners of the resulting square. These openings are intended to interconnect adjacent channels, thereby improving circulation and mass transfer between them, with the potential to increase overall mixing homogeneity. The fourth variant, Case 4—Y-axis holes, features openings oriented along the Y-axis, enabling selective interconnection of channels in that direction. This geometric modification may significantly reduce flow anisotropy and can be used to guide preferential flow paths within the structure. Five circular openings, each with a radius R = 1/6H, are aligned along the central Y-axis, with a spacing of B = 0.08L between them, where L is the total length of the structure.

Analogously, Case 5—Z-axis holes features openings distributed along the Z-axis. This configuration promotes horizontal flow components and enhances fluid exchange between the individual layers of the sheet-gyroid structure. The final configuration, Case 6—twisted gyroid, is based on the goal of maximizing the trajectory length of fluid particles as they move through the structure, thereby increasing residence time and improving mixing. This was achieved by twisting the structure around the X-axis so that the opposing square faces are rotated relative to each other by 360°. This modification strongly supports the formation of chaotic flow and turbulence, which can significantly increase the mixing efficiency compared to the original structure. All the described variants were thoroughly analyzed using computational fluid dynamics methods to determine their impact on hydrodynamic behavior and to identify geometries with optimal mixing performance.

The numerical simulation was performed in SolidWorks Flow Simulation 2024 as a steady-state analysis using the k-ε turbulence model [32]. The study was conducted using commercial software that integrates tools for computational aid design modeling, physical simulations, and result export suitable for additive manufacturing applications. During the simulation, no user-defined functions or custom scripts interfering with the solver algorithm were used. The solution was based on the finite volume method, with the convergence criterion set to 10⁻⁶. The flow calculations were derived from the fundamental mathematical equations—the Navier–Stokes equations system—which represent the conservation laws of mass, momentum, and energy [33].

$${\displaystyle \frac{\partial \mathsf{\rho }}{\partial \mathrm{t}}}+{\displaystyle \frac{\partial \left(\mathsf{\rho }{\mathrm{u}}_{\mathrm{i}}\right)}{\partial {\mathrm{x}}_{\mathrm{i}}}}=0,$$

(1)

$${\displaystyle \frac{\partial \left(\mathsf{\rho }{\mathrm{u}}_{\mathrm{i}}\right)}{\partial \mathrm{t}}}+{\displaystyle \frac{\partial }{\partial {\mathrm{x}}_{\mathrm{j}}}}\left(\mathsf{\rho }{\mathrm{u}}_{\mathrm{i}}{\mathrm{u}}_{\mathrm{j}}\right)+{\displaystyle \frac{\partial \mathrm{p}}{\partial {\mathrm{x}}_{\mathrm{i}}}}={\displaystyle \frac{\partial }{\partial {\mathrm{x}}_{\mathrm{j}}}}\left({\mathsf{\tau }}_{\mathrm{i}\mathrm{j}}+{\mathsf{\tau }}_{\mathrm{i}\mathrm{j}}^{\mathrm{R}}\right)+{\mathrm{S}}_{\mathrm{i}},$$

(2)

$${\displaystyle \frac{\partial \mathsf{\rho }\mathrm{H}}{\partial \mathrm{t}}}+{\displaystyle \frac{\partial \mathsf{\rho }{\mathrm{u}}_{\mathrm{i}}\mathrm{H}}{\partial {\mathrm{x}}_{\mathrm{i}}}}={\displaystyle \frac{\partial }{\partial {\mathrm{x}}_{\mathrm{i}}}}\left({\mathrm{u}}_{\mathrm{j}}\left({\mathsf{\tau }}_{\mathrm{i}\mathrm{j}}+{\mathsf{\tau }}_{\mathrm{i}\mathrm{j}}^{\mathrm{R}}\right)+{\mathrm{q}}_{\mathrm{i}}\right)+{\displaystyle \frac{\partial \mathrm{p}}{\partial \mathrm{t}}}-{\mathsf{\tau }}_{\mathrm{i}\mathrm{j}}^{\mathrm{R}}{\displaystyle \frac{\partial {\mathrm{u}}_{\mathrm{i}}}{\partial {\mathrm{x}}_{\mathrm{j}}}}+\mathsf{\rho }\mathsf{\epsilon }+{\mathrm{S}}_{\mathrm{i}}{\mathrm{u}}_{\mathrm{i}}+{\mathrm{Q}}_{\mathrm{H}},$$

(3)

where u is the fluid velocity, ρ is the density, S_i represents mass-distributed external forces (such as gravity or rotational forces), H = h + u²/2, h is the total enthalpy, with h being the specific enthalpy, Q_H denoting the volumetric heat source, τ_ij is the viscous stress tensor, τ^R_ij is the Reynolds stress tensor, and q_i is the diffusive heat flux. The indices imply summation over the three coordinate directions.

The comparison of the described structures in terms of fluid mixing efficiency was based on numerical simulations involving the mixing of two liquids: water (H₂O) and ethylene glycol (C₂H₆O₂). Figure 2 summarizes and graphically presents the boundary conditions used in the simulation. The computational domain consisted of a rectangular channel with a total length of 130 mm and a cross-section of 15 × 15 mm. The sheet-gyroid mixing structure, 50 mm in length, was placed in the central section of the channel, located 30 mm downstream from the fluid inlets.

At the channel inlet, two separate inlet regions were defined as velocity inlets, each 7.5 mm wide, designated for the supply of individual media: water (dynamic viscosity 1.002 mPa·s, density 998.29 kg/m³, pressure 101,325 Pa) and ethylene glycol (dynamic viscosity 19.831 mPa·s, density 1.15 kg/m³, pressure 101,325 Pa). The outlet face of the channel was defined as a pressure outlet, while the side walls of the channel were modeled as no-slip walls, implying zero velocity at the boundary.

The inlet velocities of the liquids were set at four distinct levels: 0.000067 m/s, 0.00334 m/s, 0.00669 m/s, and 0.01 m/s. These values were selected to correspond to different flow regimes characterized by Reynolds numbers (Re) of approximately 1, 5, 10, and 100. This range ensured coverage of low-speed laminar flow conditions, enabling a detailed analysis of the mixing performance of the designed sheet-gyroid structures.

In addition to the six sheet-gyroid configurations under investigation, a simulation was also carried out using an empty channel to establish a reference baseline. In total, twenty-eight numerical analyses were performed to comprehensively evaluate the influence of geometry and flow conditions on the mixing efficiency.

Based on the defined boundary conditions, a 3D model was created and subsequently converted into a computational mesh prior to the simulation. SolidWorks Flow Simulation employs a specific meshing method known as immersed body mesh. In this approach, the mesh is generated independently of the geometry’s shape, allowing cells to intersect the boundaries between solid and fluid phases. This system supports the implementation of a Cartesian grid composed of cuboidal (or rectangular) cells arranged along the axes of a Cartesian coordinate system and conforming to the boundaries of the computational domain. The mesh cells are categorized as solid, fluid, or partial; the latter intersects the interface between solid and fluid regions. A two-level wall function is applied to these partial cells, combining two numerical methods depending on the thickness of the boundary layer. This approach enables the solution of the Navier–Stokes equations within the control volumes defined by the mesh. A key step in verifying the accuracy of the simulation was the grid study, which examined the relationship between the number of mesh elements and the value of the monitored output parameter. In this case, the parameter was the area-weighted average concentration of ethylene glycol at the outlet of the computational domain (defined as a pressure outlet) at a flow velocity of 0.01 m/s. The results of the grid independence study are shown in Figure 3. During mesh generation, six different combinations of input parameters were tested, affecting both the size and distribution of mesh cells. The results indicated that from the fourth configuration onward, the output values became stable. This configuration was then selected for the main simulation, contributing to the optimization of computational time while ensuring reliable accuracy of the results.

To quantitatively compare the efficiency of the individual sheet-gyroid structures in mixing water and ethylene glycol, the concentrations of both fluids were analyzed at the outlet surface of the simulated domain (pressure outlet). On this surface, 45 measurement points were defined and evenly distributed across the entire area, ensuring representative sampling of the resulting concentrations and enabling an objective evaluation of the mixing homogeneity. The obtained concentration values were subsequently used to calculate the so-called mixing index, which quantifies the degree of homogeneity of the two-fluid mixture in the observed region. The mixing index parameter was calculated based on the formulation used in studies [34,35,36] expressed in the following form.

$${\mathrm{I}}_{\mathrm{M}}=1-{\displaystyle \frac{\mathsf{\sigma }}{{\mathsf{\sigma }}_{\mathrm{m}\mathrm{a}\mathrm{x}}}},$$

(4)

$${\mathsf{\sigma }}_{\mathrm{m}\mathrm{a}\mathrm{x}}=\sqrt{\overline{\mathrm{c}}·(1-\overline{\mathrm{c}})},$$

(5)

where σ is the standard deviation of concentration, ${\mathsf{\sigma }}_{\mathrm{m}\mathrm{a}\mathrm{x}}$ is the maximum standard deviation of concentration, and $\overline{\mathrm{c}}$ is the average mass fraction of medium. In addition, the performance index was calculated, which accounts for the mixing efficiency relative to the hydraulic losses in the system, as defined by Equation (6). The performance index formulation used in this study was adopted from Alzoubi et al. [27], where the cube root of the friction factor ratio was introduced to balance the trade-off between mixing efficiency and pressure drop in a non-linear fashion. The power of 1/3 reflects the diminishing returns in mixing performance with increasing pressure loss, as demonstrated by the numerical results therein.

$${\mathrm{I}}_{\mathrm{P}}={\displaystyle \frac{\left(\frac{{\mathrm{I}}_{\mathrm{M}\mathrm{s}}}{{\mathrm{I}}_{\mathrm{M}\mathrm{p}}}\right)}{{\left(\frac{{\mathrm{f}}_{\mathrm{D}\mathrm{s}}}{{\mathrm{f}}_{\mathrm{D}\mathrm{p}}}\right)}^{1/3}}},$$

(6)

where I_P is the performance index, I_Ms is the mixing index for the case with the implemented structure, IM_p is the mixing index for the case with an empty (plain) channel, f_ds is the Darcy friction factor for the case with the implemented structure, and f_dp is the Darcy friction factor for the case with the empty (plain) channel.

To provide a more detailed assessment of the hydraulic characteristics of the individual sheet-gyroid structures, the Darcy friction factor was calculated. In refs. [37,38], it was determined based on the pressure difference between the inlet (velocity-inlet) and outlet (pressure-outlet) surfaces, which enabled a comprehensive evaluation of the energy demands associated with flow through each structure and the identification of the most suitable geometry in terms of both mixing performance and energy efficiency.

$$\mathrm{f}={\displaystyle \frac{2∆\mathrm{p}{\mathrm{D}}_{\mathrm{h}}}{\mathrm{L}\mathsf{\rho }{\mathrm{u}}^2}},$$

(7)

where Δp is the pressure drop, i.e., the difference in pressure of the flowing medium between the inlet and outlet of the model, D_h is the hydraulic diameter, L is the length of the structure, ρ is the fluid density, and u is the fluid velocity.

3. Results

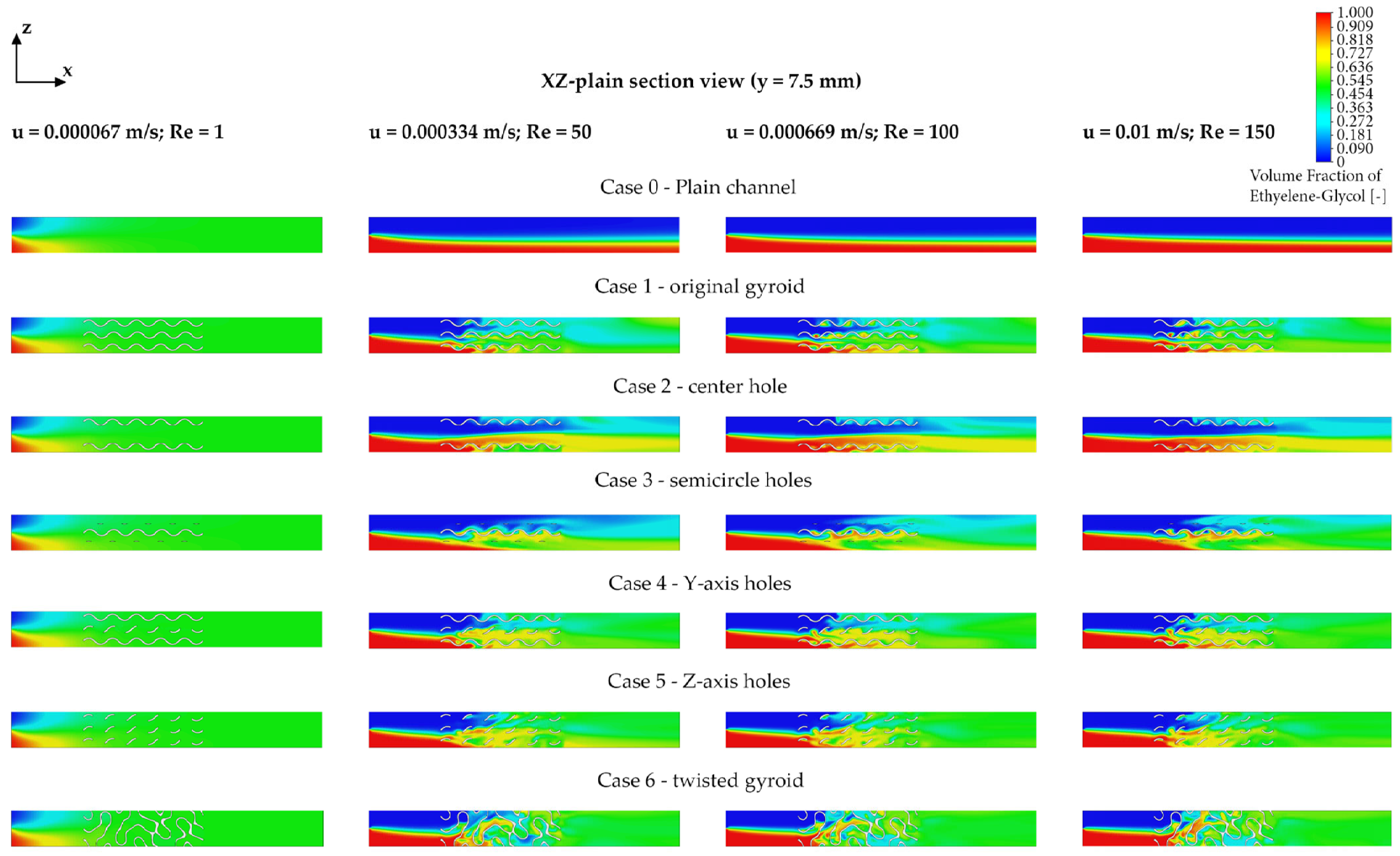
The results of the numerical simulations, presented as concentration distribution maps of ethylene glycol in a horizontal cross-section of the channel (Figure 4), clearly demonstrate the influence of the applied sheet-gyroid structures on the mixing of water and ethylene glycol at various Reynolds numbers (Re = 1, 50, 100, and 150). In the reference case (Case 0—empty channel), the flow remains strongly stratified, with both liquids clearly separated and minimal interfacial mixing. As the flow velocity increases, only a slight broadening of the interface is observed; even at the highest Reynolds number (Re = 150), significant homogenization does not occur. When the basic sheet-gyroid structure is introduced (Case 1—original gyroid), enhanced interaction between the fluid phases begins to appear within the region of the mixing element. At low Reynolds numbers, mixing remains limited due to the dominance of laminar flow. However, at Re = 100 and 150, an increase in turbulence and improved concentration homogeneity are evident. The original gyroid geometry induces complex flow trajectories that facilitate partial dispersion of ethylene glycol into the aqueous phase.

For the modified sheet-gyroid structures (Cases 2–6), it is evident that different geometric alterations significantly affect the mixing intensity and quality. The configuration with a central hole (Case 2—center hole) shows a modest improvement in mixing relative to the unmodified sheet-gyroid. Although concentration gradients are visibly altered, substantial enhancements become apparent only at higher Reynolds numbers, where distinct regions of intense mixing form around the central openings. A more pronounced improvement is observed in the case with quarter-circular openings (Case 3—semi holes), where the modified geometry promotes the formation of turbulent flow fields and chaotic vortices. These effects are particularly noticeable at higher Reynolds numbers, resulting in a more effective disruption of the laminar regime and enhanced ethylene glycol distribution across the channel. The variants with axis-aligned holes (Case 4—Y-axis holes and Case 5—Z-axis holes) exhibit similar trends, although the Z-axis configuration demonstrates slightly superior mixing performance. This suggests that the orientation of the perforations plays a crucial role in the flow dynamics, with Z-axis connectivity encouraging the formation of more complex vortex structures and stronger turbulence, thereby improving concentration homogenization. The most substantial enhancement in mixing is observed with the twisted sheet-gyroid configuration (Case 6—twisted gyroid). This modification significantly alters the flow characteristics, promoting the development of intense turbulent regions even at lower Reynolds numbers, and thus achieves the most effective mixing performance among all evaluated designs.

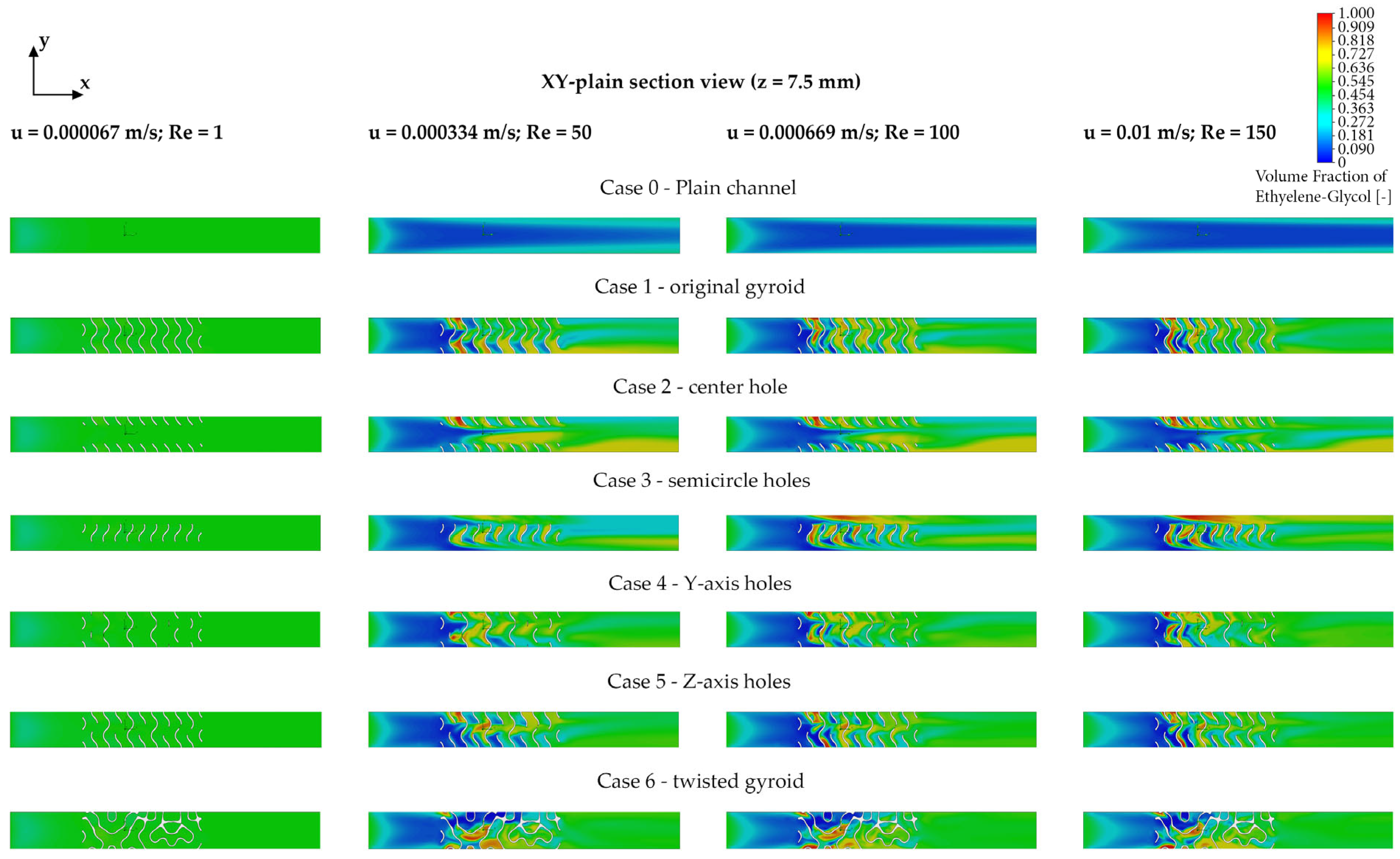
The results of the numerical simulations, presented as concentration distribution maps of ethylene glycol in a vertical cross-section of the channel within the XY plane (Figure 5), provide further detailed insights into the spatial concentration distribution for various sheet-gyroid structures and Reynolds numbers (Re = 1, 50, 100, and 150). In the reference case (Case 0—empty channel), a clear separation between the two fluid phases is again observed, with no significant development of turbulent structures or regions of intense mixing. The interface between water and ethylene glycol remains sharply defined, and increasing the Reynolds number does not lead to meaningful improvements in homogenization.

The introduction of the basic sheet-gyroid structure (Case 1—original gyroid) results in visibly enhanced mixing in the vertical section, particularly in the central part of the channel, where the geometric arrangement of the structure induces mild turbulence and local vortex formation. These effects intensify with increasing Reynolds number, promoting a more pronounced distribution of ethylene glycol throughout the cross-section. However, overall mixing remains relatively limited, especially at lower Reynolds numbers. In the case of the sheet-gyroid structure with a central hole (Case 2—center hole), localized zones of enhanced mixing appear primarily around the openings in the central region of the structure. This geometric modification slightly enhances vertical interaction between the flowing liquids; however, the overall improvement in mixing is still modest and becomes more apparent only at higher Reynolds numbers (Re = 100 and 150).

The structure with small quarter-circular holes (Case 3—semi holes) demonstrates a more significant enhancement in the vertical mixing of ethylene glycol across the entire cross-section. This configuration promotes the formation of stronger turbulent regions, facilitating better dispersion and fluid distribution. At higher flow velocities, these effects manifest as zones of increased concentration homogeneity. The geometries with oriented holes along the Y and Z axes (Case 4—Y-axis holes and Case 5—Z-axis holes) have distinct effects on vertical flow behavior. The Y-axis openings enhance vertical interaction between the fluids, particularly in specific regions of the channel. In contrast, the Z-axis openings lead to more uniform and intense mixing, as the axial orientation promotes the formation of complex vortical structures and stronger vertical flow fields. These turbulent regions substantially increase concentration homogeneity, particularly at higher Reynolds numbers. The most pronounced improvement in vertical mixing is clearly attributed to the twisted sheet-gyroid structure (Case 6—twisted gyroid). This geometric modification significantly alters the flow characteristics throughout the entire cross-section. Even at moderate Reynolds numbers (Re = 50), a marked increase in turbulence and effective vertical mixing is observed. At higher flow rates (Re = 100 and 150), the structure disrupts the original laminar regime entirely, generating intense turbulent vortices and enabling efficient ethylene glycol distribution throughout the channel volume.

The results of the numerical simulations presented in a cross-sectional view of the channel, taken immediately downstream of the inserted sheet-gyroid structure in the YZ plane (Figure 6), provide deeper insights into the spatial homogenization and distribution of ethylene glycol as influenced by the different sheet-gyroid configurations. This visualization clearly illustrates how the various geometric modifications affect the ethylene glycol concentration at the outlet of the simulated domain and how markedly they differ from the reference case without any mixing elements (Case 0). The reference case (Case 0—plain channel) exhibits a distinct and sharply defined separation between the two fluids, with the media remaining visually segregated. Even at higher Reynolds numbers, the interface appears only slightly diffused, and no effective mixing occurs. The absence of significant concentration blending, even at Re = 150, underscores the inefficiency of the empty channel configuration in promoting mixing without the use of any internal structures.

In the case of the original sheet-gyroid structure (Case 1—original gyroid), the resulting distribution of ethylene glycol differs significantly from the reference case. A more uniform dispersion of the liquid begins to emerge across the entire channel cross-section, with an increase in concentration homogeneity already visible at lower Reynolds numbers. At higher flow velocities (Re = 100 and 150), this effect becomes more pronounced, with clearly defined regions of localized vortices and intense mixing that substantially improve the distribution of ethylene glycol. Distinct fluid separation within the channels is observable, along with the formation of regularly recurring patterns corresponding to the concentration field. The sheet-gyroid structure with a central hole (Case 2—center hole) offers a modest improvement over the original configuration; however, overall mixing remains limited and uneven. Zones of both higher and lower concentration are visible at the outlet, indicating that this modification promotes localized regions of enhanced mixing rather than achieving homogeneous distribution across the entire cross-section.

A more significant improvement in ethylene glycol distribution is observed with the sheet-gyroid structure featuring small quarter-circular holes (Case 3—semi holes). This geometry induces intense vortex formation and turbulent zones, resulting in more uniform mixing of the two fluids. Even at moderate Reynolds numbers (Re = 50 and 100), a substantial improvement in concentration homogeneity is evident, which is further enhanced at higher flow velocities. Sheet-gyroid structures with holes oriented along the Y and Z axes (Case 4—Y-axis holes, Case 5—Z-axis holes) exhibit even greater homogeneity in the transverse cross-section. The Y-axis configuration results in well-defined turbulent regions that facilitate uniform distribution of ethylene glycol across the entire channel. The Z-axis configuration, however, yields even more intense mixing and better overall homogeneity, highlighting the advantage of axially oriented perforations in the design of sheet-gyroid-based mixing structures. The most pronounced effect on concentration uniformity and overall homogenization in the channel cross-section is observed with the twisted sheet-gyroid structure (Case 6—twisted gyroid). This modification significantly increases flow irregularity, with strong homogenization of ethylene glycol already occurring at lower Reynolds numbers. At the highest tested flow rate (Re = 150), the structure facilitates near-complete mixing, confirming its exceptional mixing capability in comparison to all other configurations analyzed.

Overall, the results demonstrate that geometric modification of sheet-gyroid structures can dramatically enhance mixing performance, with the most substantial improvements driven by the complexity and asymmetry of geometry. The twisted sheet-gyroid modification achieves the highest levels of turbulence and chaotic flow, resulting in superior mixing characteristics among all tested variants. These findings are directly applicable to the design of efficient static mixers in renewable energy technologies, where thorough component mixing is a critical factor influencing overall process efficiency.

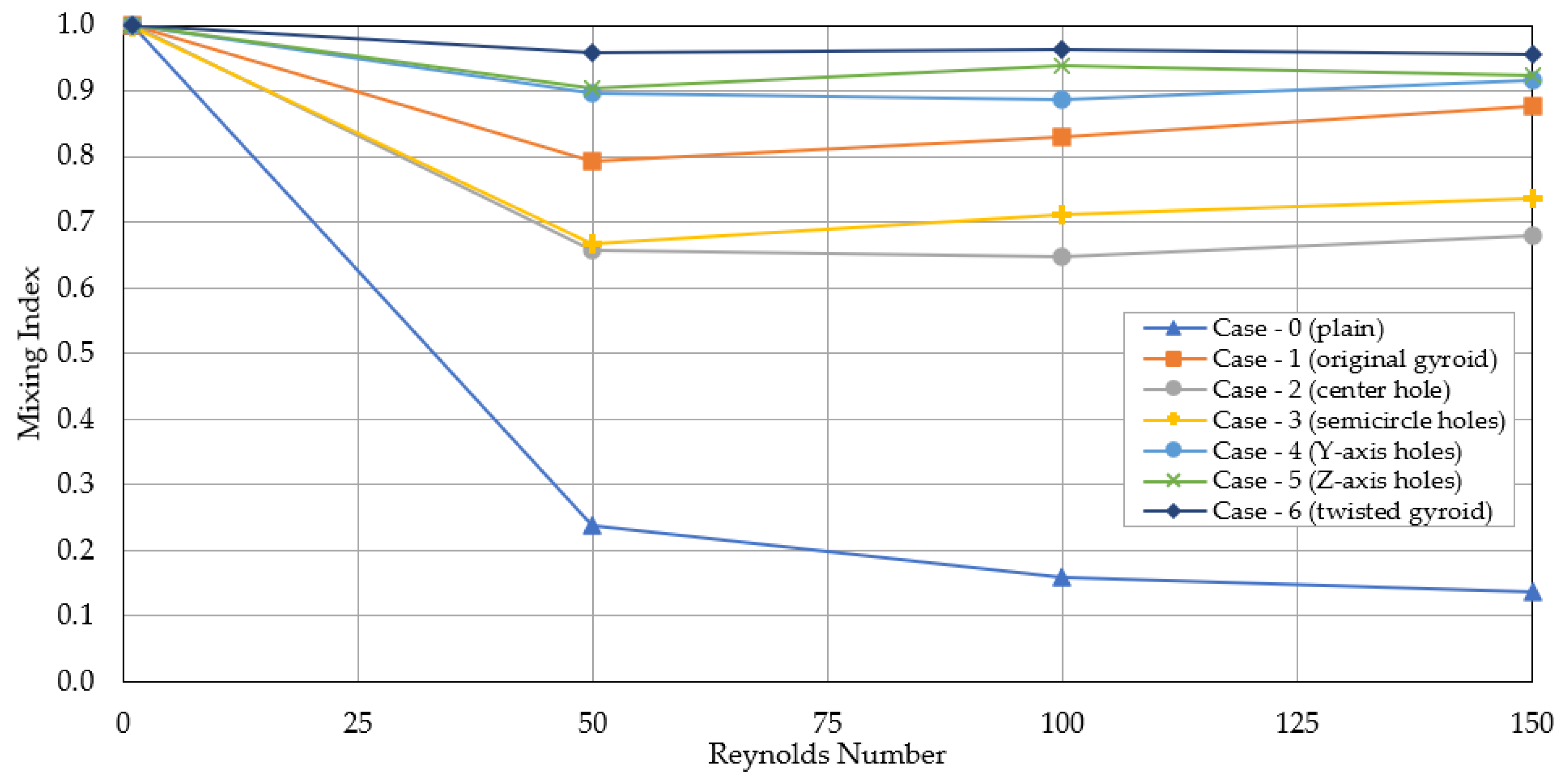
The effectiveness of the various sheet-gyroid structures in enhancing fluid mixing was also quantitatively evaluated using the mixing index parameter, the graphical representation of which is shown in Figure 7. This index characterizes the degree of homogeneity in the water–ethylene glycol mixture within the observed region and ranges from 0 to 1, where a value of 1 indicates perfect mixing, and a value of 0 corresponds to complete separation of the fluids. The obtained mixing index values for each analyzed configuration are plotted as a function of the Reynolds number, ranging from Re = 1 to Re = 150.

At the lowest Reynolds number (Re = 1), corresponding to very slow flow conditions, all cases—including the reference plain channel (Case 0)—exhibited mixing index values close to 1. This phenomenon is attributed to the dominance of molecular diffusion at low velocities, allowing near-complete homogenization of the fluids even in the absence of significant turbulence or structural intervention. As the Reynolds number increases, and thus the flow velocity rises, notable differences begin to emerge among the tested cases. The reference configuration without any mixing element (Case 0—plain channel) shows a sharp decline in mixing index, reaching approximately 0.4 at Re = 50 and remaining nearly constant with further increases in flow rate. This sharp drop is a result of the formation of a well-defined interface between the two fluids, without the onset of turbulence or chaotic flow, thereby limiting the effectiveness of mixing. In contrast, the original sheet-gyroid structure (Case 1—original gyroid) maintains relatively high mixing index values across the studied Reynolds number range. Although a slight decrease in the index is observed with increasing Re, it remains around 0.8 for Re = 50 to 150, indicating that the original sheet-gyroid geometry can sustain a high level of homogenization across varying flow conditions.

The sheet-gyroid configuration with a central hole (Case 2—center hole) follows a similar but slightly less favorable trend, with mixing index values around 0.7 at higher Reynolds numbers. This result suggests that the addition of a central opening provides only a marginal improvement in mixing performance and leads to a less uniform concentration distribution. Significantly better results were achieved with the structure featuring small quarter-circular holes (Case 3—semi holes). In this case, the mixing index remains above 0.8 even at the highest Reynolds numbers tested. This modified geometry clearly enhances turbulence and facilitates more effective fluid mixing. Both variants with axis-oriented perforations (Case 4—Y-axis holes, Case 5—Z-axis holes) demonstrate even stronger performance, maintaining consistently high mixing index values (above 0.9) throughout the entire range of flow velocities. These geometric adjustments promote the formation of more complex turbulent regions and support improved vertical and horizontal homogenization. The most notable enhancement in mixing performance is unequivocally observed in the twisted sheet-gyroid structure (Case 6—twisted gyroid). This configuration is the only one to maintain mixing index values near 1 across the entire range of Reynolds numbers. Even under relatively high flow conditions (Re = 100–150), the mixing index remains nearly unchanged at approximately 0.95, highlighting the exceptional ability of this geometry to ensure thorough homogenization under challenging flow regimes.

These results clearly demonstrate that geometric modifications to sheet-gyroid structures have a profound impact on mixing quality. The twisted sheet-gyroid configuration emerges as the most effective solution for achieving homogeneous concentration over a wide range of operating conditions. These findings offer practical value for the optimization of mixing devices, which are critical components in renewable energy technologies where effective fluid blending directly influences overall system efficiency.

The analysis was further extended by evaluating the efficiency of each structure using the performance index (I_P). This composite parameter is designed to balance two critical yet often opposing aspects of mixing devices: achieving a high degree of mixing homogeneity (expressed by the mixing index, I_M) and minimizing hydraulic losses (represented by the Darcy friction factor, f_D). The performance index is defined as the ratio of the mixing index to the friction factor for a given structure, normalized to the corresponding values of the reference case (i.e., the empty channel). The reference configuration has a performance index value of 1, serving as the baseline for comparing the effectiveness of the other geometries.

According to this definition, higher performance index values indicate greater structural efficiency; that is, improved fluid mixing with lower energy costs relative to the empty channel. Conversely, performance index values below 1 signify that the hydraulic losses outweigh the benefits of enhanced mixing, making the structure less advantageous than the baseline case. As shown in the accompanying graph in Figure 8, all analyzed sheet-gyroid structures exhibit performance index values significantly higher than the reference value (I_P = 1), indicating their potential to markedly improve mixing efficiency. The lowest performance index values were observed for the structure with a central hole (Case 2—center hole), though even in this case, the index remains well above 1, confirming its superiority over the plain channel configuration.

The original sheet-gyroid structure (Case 1—original gyroid) and the design with quarter-circular holes (Case 3—semicircle holes) both yielded considerably better results, with their performance index values increasing steadily up to approximately 6 at the highest Reynolds number (Re = 150). This suggests that these geometries offer an excellent compromise between mixing quality and energy demand. Even better performance was observed for the structures with axis-aligned perforations (Case 4—Y-axis holes and Case 5—Z-axis holes), both of which achieved performance index values exceeding 6 at high Reynolds numbers. These geometries proved to be more efficient than the base configuration and the semicircle-hole variant, providing strong homogenization with relatively low pressure drop. The highest performance index of all tested configurations was achieved by the twisted sheet-gyroid structure (Case 6—twisted gyroid), which exceeded a value of 7 at Re = 150. This design demonstrated an exceptional ability to efficiently mix fluids while minimizing energy losses, establishing it as the optimal choice for practical implementation in various technological systems.

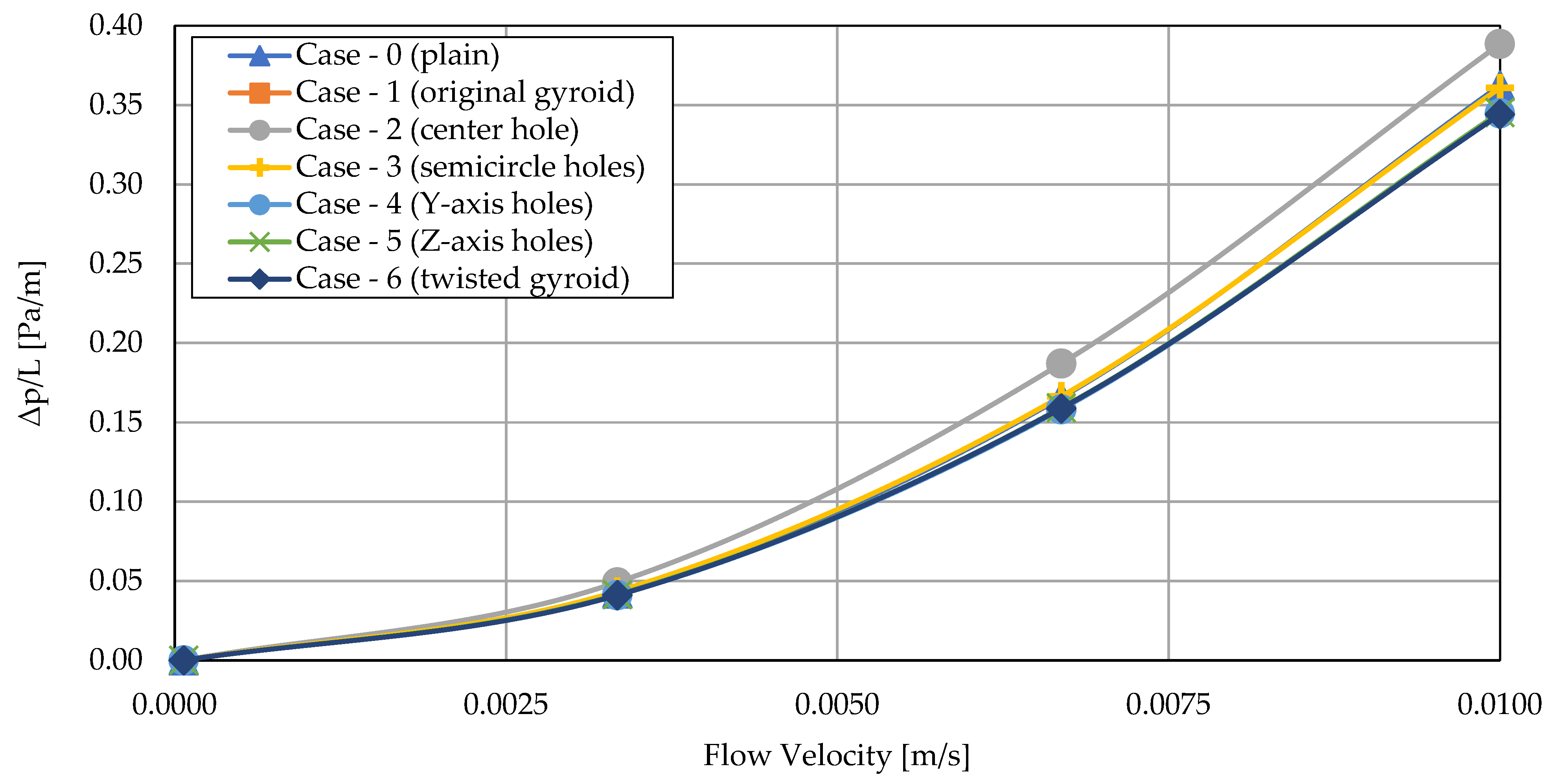
The numerical simulation results were further supplemented by an assessment of the pressure losses generated by the individual sheet-gyroid structures. These losses were quantified using the parameter Δp/L, representing the pressure drop per unit length of the structure. The corresponding graph illustrates the dependence of pressure drop on flow velocity for all analyzed cases over a velocity range from 0.000067 m/s to 0.01 m/s. The results in Figure 9 reveal that pressure loss is strongly dependent on flow velocity, with a distinctly nonlinear relationship. At low flow velocities (0.000067 m/s), pressure losses are practically negligible, which corresponds to very low Reynolds numbers and laminar flow conditions. However, as flow velocity increases to 0.01 m/s, pressure losses rise sharply in all cases. The highest values are observed for the structure with a central hole (Case 2—center hole), indicating that, despite its modest benefit in mixing performance, this geometric modification introduces considerable hydraulic resistance, which negatively impacts the overall efficiency of the structure in terms of energy consumption.

In contrast, the remaining sheet-gyroid configurations—including the sheet-original gyroid (Case 1), the version with quarter-circular holes (Case 3—semicircle holes), and those with Y-axis (Case 4) and Z-axis (Case 5) oriented perforations, as well as the twisted sheet-gyroid (Case 6)—exhibit similar pressure drop values that are lower than those recorded for the central-hole configuration. The differences among them are minimal, suggesting that these geometries impose comparable energy demands under identical operating conditions. Interestingly, despite the similar pressure losses among these modified structures, their mixing performance (evaluated via the mixing index and performance index) varies considerably. The twisted sheet-gyroid structure (Case 6) stands out as particularly advantageous, achieving significantly higher mixing efficiency while maintaining pressure losses on par with the other geometries. Based on the presented results, it can be concluded that, except for the central-hole configuration, all analyzed sheet-gyroid structures offer a favorable balance between mixing efficiency and hydraulic losses. The twisted sheet-gyroid represents the optimal solution, delivering the highest level of homogenization while maintaining relatively low flow resistance. This makes it a strong candidate for use in energy-efficient mixing applications in renewable energy systems and related technological processes.

These findings clearly demonstrate that through appropriate geometric modification of sheet-gyroid structures, significant improvements in mixing performance can be achieved while maintaining relatively low-pressure losses. This balance is crucial for the design of efficient equipment in renewable energy applications and other industrial processes where both mixing quality and energy efficiency are paramount.

4. Conclusions

This study focused on the numerical evaluation of sheet-gyroid structures and their selected geometric modifications to assess their suitability as advanced mixing elements for technologies utilizing renewable energy sources. The results of computational fluid dynamics simulations demonstrated a significant influence of geometric alterations on the mixing efficiency of two fluids—water and ethylene glycol—while also enabling the evaluation of the energy demands of each configuration. All analyzed sheet-gyroid structures, including both the original and modified variants, exhibited higher mixing efficiency compared to the reference case of an empty channel. Quantitative analysis using the mixing index showed that at low flow velocities, near-complete mixing occurred across all tested cases. However, with increasing flow velocity and Reynolds number, the differences between the structures became more pronounced. In this context, the twisted sheet-gyroid structure emerged as the most effective, maintaining a high mixing index even at elevated Reynolds numbers. When evaluated using the performance index—a parameter that accounts for both mixing quality and hydraulic losses—the twisted sheet-gyroid structure again proved to be the most advantageous. It achieved the highest values of this parameter, indicating an optimal balance between mixing performance and energy consumption. These findings support the hypothesis that targeted geometric modification of sheet-gyroid structures can significantly enhance fluid mixing efficiency while minimizing energy costs. From a practical standpoint, the manufacturability of these structures must also be considered. Sheet-gyroid structures, particularly complex or twisted variants, are challenging to fabricate using conventional manufacturing methods such as machining or casting. Therefore, additive manufacturing techniques, such as 3D printing, represent a promising alternative. AM enables the production of highly complex geometries that are difficult to achieve using traditional techniques while maintaining high precision and geometric fidelity. For the fabrication of sheet-gyroid structures, the most suitable technologies include Selective Laser Sintering, Selective Laser Melting, and Stereolithography. These methods allow to produce detailed structures with excellent accuracy and repeatability and support the use of materials that meet the chemical and mechanical requirements of various energy-related applications. Nevertheless, the advantages of additive manufacturing must be weighed against certain limitations, such as higher production costs, longer build times for large batches, and challenges associated with support structures during the fabrication of complex geometries. These factors must be carefully considered during the design of mixers intended for industrial applications. In conclusion, the twisted sheet-gyroid structure represents a highly efficient solution for fluid mixing applications, particularly within the field of renewable energy technologies. Its practical implementation, however, requires careful optimization of the manufacturing process using advanced additive manufacturing methods. Future research should focus on the refinement of fabrication techniques, reduction of production costs, and validation of the performance of these mixers under real operating conditions.