Characteristics of High-Pressure Hydrogen Jet Dispersion Along a Horizontal Plate

Abstract

Creating and updating safety regulations and standards for industrial processes and end-uses related to hydrogen demand a solid scientific foundation, which requires extensive research on unignited hydrogen releases from high-pressure systems across different situations. This study focuses on high-pressure hydrogen releases along a horizontal plate to investigate the surface effects on hydrogen dispersion. Hydrogen releases from high-pressure sources up to 30 MPa were modeled using a computational fluid dynamics (CFD) method, with the CFD models validated by experimental data. The hydrogen dispersion characteristics along the plate were studied for various source pressures and leak nozzle diameters. The results show that the maximum flammable extent along the plate increases linearly with both the source pressure and nozzle diameter, while the combustible mass increases to the power of 1.5 with the increase in leakage flow rate. The locations where the jet centerline attach to the plate are identical (about 0.41 m away from the nozzle exit in the axial direction) for different source pressures (10~30 MPa) and nozzle diameters (0.5~1.5 mm). The flow region was divided into pre-attachment and attachment zones by the attachment point, and the self-similarity characteristics of both zones were analyzed. Finally, correlations for the centerline and lateral concentration distributions were developed for both the pre- and post-attachment zones. The results can help users quickly assess safety distance when hydrogen leaks along the plate.

1. Introduction

Hydrogen has emerged as a promising alternative to fossil fuels, thanks to its high energy density and environmental benefits [1,2,3]. As the simplest and most abundant element in the universe, hydrogen offers the potential for a clean future built on sustainable energy. Recognizing this potential, many countries have released their national hydrogen roadmaps, outlining ambitious strategies for the development and expansion of hydrogen technologies [4,5]. These roadmaps emphasize the critical role of hydrogen in achieving carbon neutrality, enhancing energy security, and fostering economic growth. However, the small molecular size and high diffusivity of hydrogen present significant challenges in its storage and transport, particularly with regard to leakage through small orifices from high-pressure vessels. High-pressure hydrogen leaks pose several risks, including flammability, explosion hazards, and the potential for asphyxiation in confined spaces [6]. Understanding the mechanisms of high-pressure hydrogen leakage through small orifices in various scenarios is essential for the design of secure containment systems and the development of effective leak detection technologies.

When the pressure ratio of hydrogen exceeds the critical pressure ratio (approximately 1.9), which corresponds to a stagnation pressure exceeding 1.9 bar, the leakage of hydrogen results in under-expanded jets. Recently, the leakage of high-pressure hydrogen, which leads to the development of under-expanded jets, has been extensively studied. High-pressure gas leakage generates under-expanded jets, with complex shock wave structures forming outside the leak point [7]. Free under-expanded hydrogen jets have been well investigated through both experimental and numerical studies to characterize shock wave structures [8,9,10]. The flow characteristics of hydrogen downstream of shock wave regions have shown that the centerline concentration and velocity decays of momentum-dominated jets follow hyperbolic decay laws, while the radial concentration and velocity profiles exhibit Gaussian distributions [11,12,13,14,15,16]. Unintended hydrogen releases in real-world scenarios have also been studied, including in hydrogen refueling stations [17,18,19,20], hydrogen workshops [21], fuel cell vehicles [22,23,24,25], and garages [26,27]. These studies have primarily used computational fluid dynamics (CFD) methods to examine the effects of leak source parameters (pressure and diameter), wind (direction and speed), and ventilation (location and number) on hydrogen dispersion characteristics and flammable volume. For example, Li et al. [21] reduced the hazard area of hydrogen diffusion in a hydrogen workshop by 41.10% after vent configuration. Given the complexity of spatial structures in real-world scenarios that have complex shapes, layouts, sizes, etc., empirical correlations for the rapid calculation of hydrogen concentration distributions can only be derived in a few specific cases [28].

In real-world scenarios, potential leak points may be surrounded by obstacles such as the ground, buildings, and equipment. The leakage and dispersion of high-pressure hydrogen may be affected by obstacle walls. Sposato et al. [29] studied the flammable volume of a hydrogen horizontal jet impacting a vertical wall. The results show that when the flammable cloud is mainly distributed in the radial direction, the flammable volume decreases as the distance between the vertical wall and the nozzle increases. Conversely, when the flammable cloud is mainly distributed in the axial direction, the flammable volume increases with the increasing distance between the vertical wall and the nozzle. Tchouvelev et al. [30] simulated a horizontal hydrogen jet impacting a vertical wall using the PHOENICS software, and their results show that the ideal gas equation of state significantly overestimates the hypothetical hydrogen cloud volumes for LFL or fractions of LFL compared with the Abel–Nobel equation of state. Hu et al. [31] found that the concentration conforms to the Gaussian distribution along the centerline of the vertical wall.

Many studies have shown that a wall parallel to the nozzle increases the flammable distance. The gas jet near the wall surface exhibits a wall-attachment phenomenon due to the Coanda effect [32], which complicates the flow and diffusion of the gas. Hourri et al. [33,34] modeled hydrogen jets along horizontal walls at various nozzle heights (0~10 m) and pressures (100~700 bar) to investigate the effects on hydrogen dispersion. The results showed that the wall extended the combustible range, consistent with measurements by Hall et al. [35], and when the nozzle height was 0.077 m, the combustible range was increased by 48% compared with that of free jets. Bénard et al. [36] then developed an empirical correlation to predict the flammable extent of hydrogen and methane along horizontal surfaces and validated the correlation with experimental data from Defence Research and Development Canada (DRDC). Previous studies on methane jets have also shown that adjacent surfaces extend the flammable range of methane jets [37,38].

In summary, existing studies have demonstrated that the leakage of flammable gases along horizontal walls increases their flammable range. However, research on hydrogen jets adjacent to horizontal walls has primarily focused on calculating the maximum flammable range along the jet axis, with few studies addressing the decay pattern of gas concentration and the changes in the mass of flammable clouds. This study investigates the dispersion characteristics of high-pressure hydrogen jets influenced by a horizontal plate. Unlike previous studies that have primarily focused on calculating the maximum flammable range along the jet axis, this work quantifies the flammable mass of hydrogen and establishes a correlation between the flammable mass and leakage flow rate. Additionally, the concentration distribution patterns of hydrogen jets along the plate for different source pressures and nozzle diameters were studied, leading to the development of empirical correlations for the decay of streamwise and lateral hydrogen concentrations. These findings provide a more comprehensive understanding of hydrogen jet behavior near horizontal plates, offering valuable insights into flammable range expansion and gas concentration dynamics, which have been underexplored in the existing literature.

2. Methodology

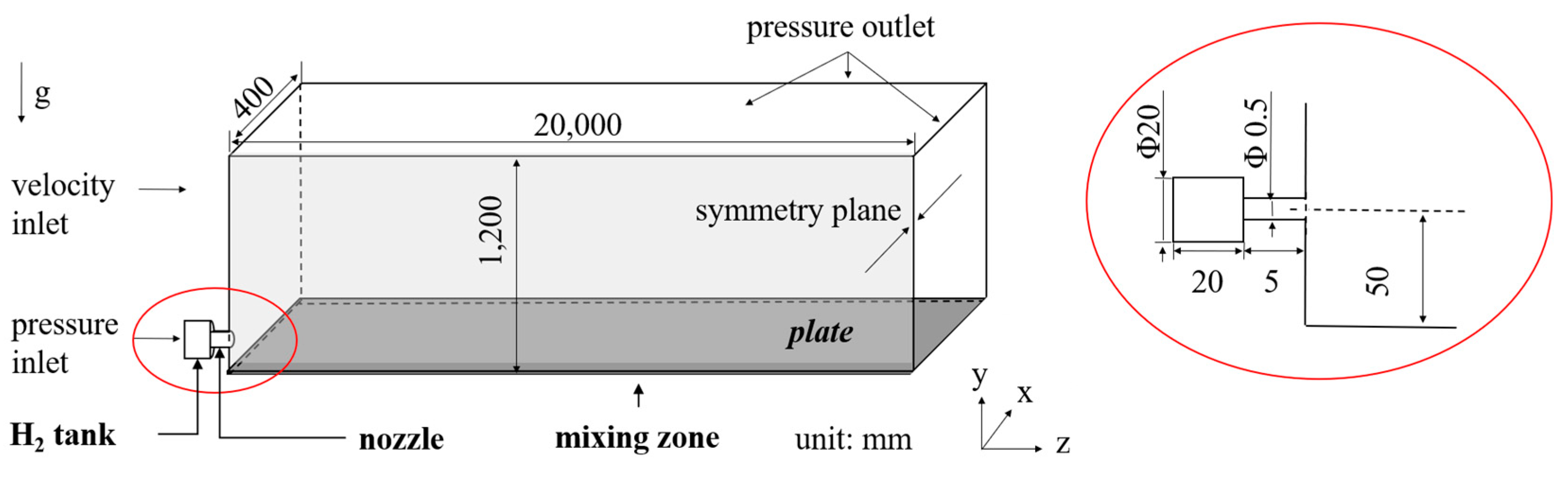
2.1. Geometry

The geometric model used in the study is reflection-symmetric, allowing half of the flow field region to be used as the computational domain, thereby reducing the computational load. The computational domain includes the hydrogen storage tank, nozzle, and mixing region. Hydrogen leaks from the H₂ tank through the nozzle into the mixing zone. The mixing zone, which is the main computational domain, is assumed to be a rectangular prism with sufficiently large dimensions to avoid effects on the jet flow from the outlet boundary. The main dimensions and boundary conditions are shown in Figure 1. The dimensions of the mixing zone are 20,000 mm × 400 mm × 1200 mm, which are designed to minimize the impact of the outlet boundary condition on the jet flow. The specific boundary conditions used in the CFD model include one pressure inlet, one velocity inlet, and one symmetry plane, all of which are annotated in Figure 1. The remaining boundary conditions for the H₂ tank and nozzle are all no-slip adiabatic walls. The plate is also a no-slip adiabatic wall. The remaining boundary conditions of the mixing zone are pressure outlets, with the pressure equal to the ambient pressure.

2.2. Numerical Model

The high-pressure hydrogen jets were modeled using the CFD software Ansys Fluent 19.2, with a three-dimensional steady-state solver. In the species transport model, the mixture was defined as hydrogen–air, and the density was calculated using the real gas equation of state. The Redlich–Kwong equation of state (R-K equation) is capable of yielding satisfactory results for calculating the pressure, volume, and temperature (p, v, T) properties of nonpolar or weakly polar fluids (e.g., hydrogen, which is a nonpolar molecule), and even some polar fluids, over a wide range of pressures. The Soave–Redlich–Kwong equation of state (R-K-S equation) further improves the accuracy of the R-K equation while retaining its ease of application. Therefore, the R-K-S equation is adopted. The coupling between pressure and velocity was solved using the Coupled algorithm, which solved the momentum- and pressure-based continuity equations together. The full implicit coupling is achieved through an implicit discretization of pressure gradient terms in the momentum equations and an implicit discretization of the face mass flux, including Rhie–Chow pressure dissipation terms. The second-order upwind scheme was applied for the convective terms. The mole fraction of hydrogen in the storage tank and nozzle regions was set to 1. Gravity was oriented perpendicular and downwards to the jet direction. The k-ω Shear Stress Transport (SST) turbulence model was used to combine the advantages of the k-ε and k-ω models and account for the transport of the turbulence shear stress in the definition of the turbulent viscosity, thus exhibiting more accurate results in the calculation of leakage and diffusion [39]. Other similar studies use the SST model to simulate high-pressure gas impinging on obstacles [37,38]. The y⁺ values along the plate surface were all less than 6. The transport equations for turbulent kinetic energy (k) and the specific dissipation rate (ω) are given by

$${\displaystyle \frac{\partial (\rho k)}{\partial t}}+{\displaystyle \frac{\partial \left(\rho U_{i}k\right)}{\partial x_i}}={\displaystyle \frac{\partial }{\partial x_j}}\left({\Gamma }_k{\displaystyle \frac{\partial k}{\partial x_j}}\right)+G_k-Y_k+S_k$$

(1)

$${\displaystyle \frac{\partial (\rho \omega )}{\partial t}}+{\displaystyle \frac{\partial \left(\rho U_i\omega \right)}{\partial x_i}}={\displaystyle \frac{\partial }{\partial x_j}}\left({\Gamma }_{\omega }{\displaystyle \frac{\partial \omega }{\partial x_j}}\right)+G_{\omega }-Y_{\omega }+D_{\omega }+S_{\omega }$$

(2)

where $G_k$ is the production of turbulent kinetic energy (TKE) due to mean velocity gradient, $G_{\omega }$ is the generation of ω, ${\Gamma }_k$ and ${\Gamma }_{\omega }$ are the effective diffusivity of k and ω, $Y_k$ and $Y_{\omega }$ represent the dissipation of k and ω due to turbulence, $D_{\omega }$ is the cross-diffusion term, and $S_k$ and $S_{\omega }$ are user-defined source terms. Time-dependent terms were neglected in this study.

Considering the actual hydrogen storage pressures involved in hydrogen production or hydrogen refueling stations [40], the pressure range of 10~30 MPa was adopted. The simulated source pressures (P₀) were 10, 20, and 30 MPa, with nozzle diameters (d) of 0.5, 0.7, and 1.0 mm. The ambient temperature (T_∞) was 300 K and the ambient pressure (P_∞) was 0.1013 MPa. The mole fraction of hydrogen in the H₂ tank and nozzle were set to 1, assuming that the H₂ tank and nozzle are filled with hydrogen during initialization. The mixing zone is filled with air. The velocity of the air velocity inlet was set to 0.1 m/s, while the hydrogen pressure inlet was specified as a pure hydrogen inlet. Monitoring points along the centerline of the plate were set to monitor the mass fraction of hydrogen. Calculations for all cases were assumed to be converged only after residuals were sufficiently small (the residual of energy smaller than 1 × 10⁻⁶ and the continuity equation smaller than 1 × 10⁻³) and the concentration at monitoring points stabilized.

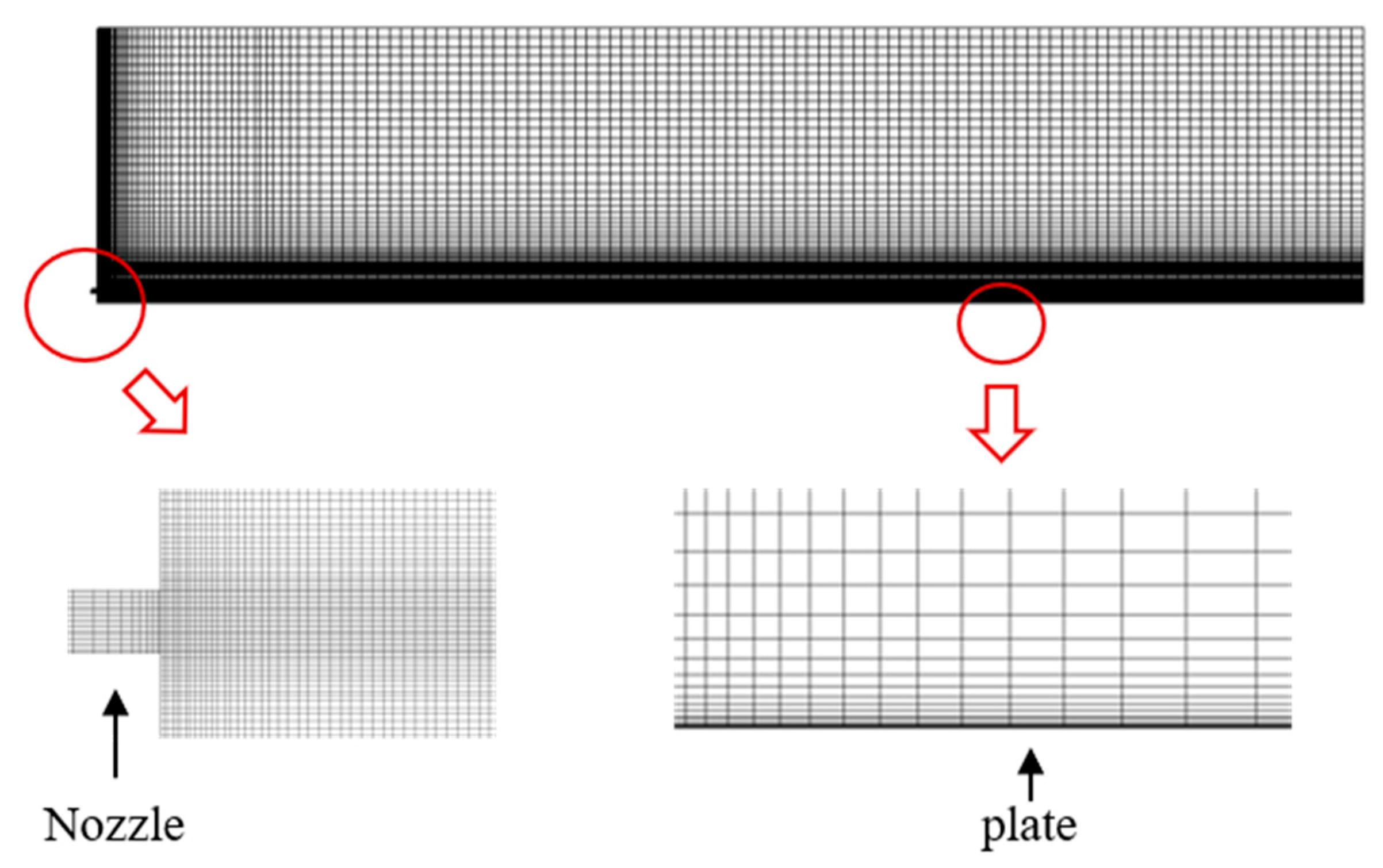
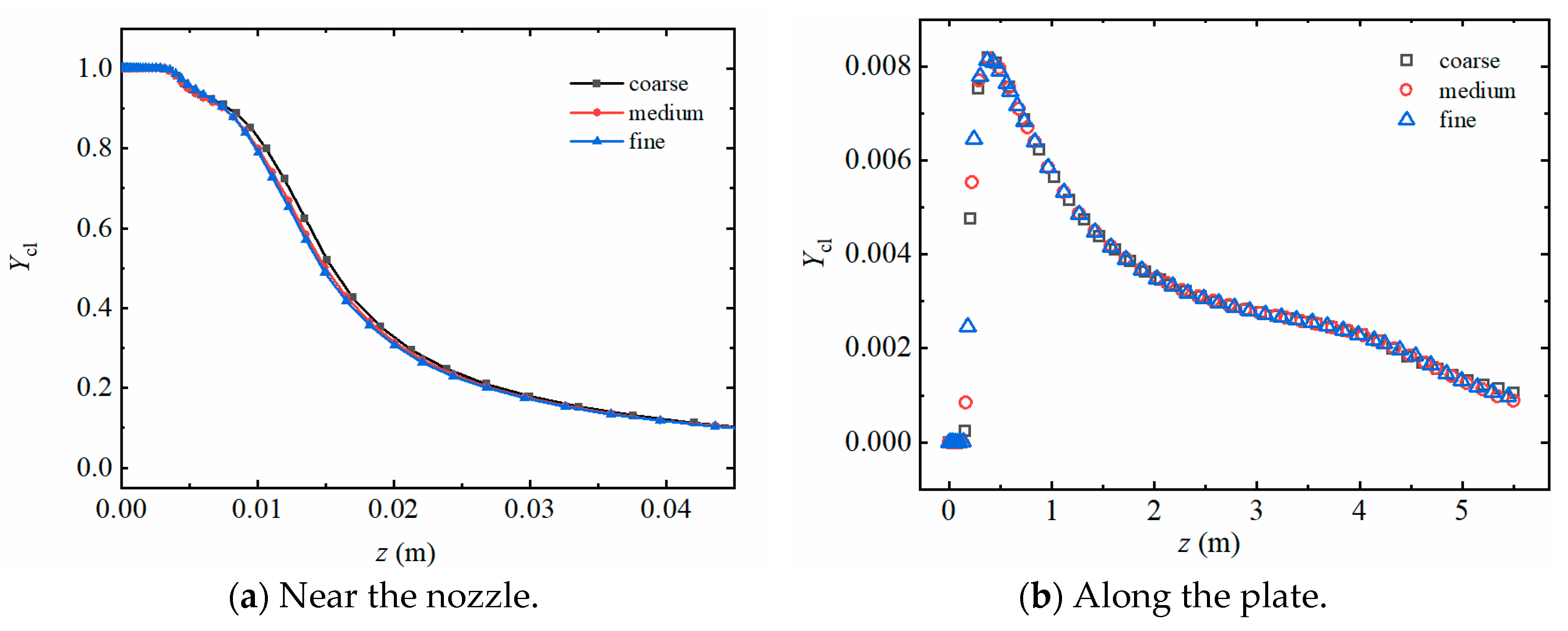
2.3. Grid Sensitivity

The computational domain was discretized into hexahedral elements to enhance stability and convergence. The smallest element size was 0.02 mm, appearing at the nozzle exit, and the largest element size was 50 mm, appearing at the pressure outlet of the mixing zone. The mesh near the plate was also refined, with the smallest element size being 0.06 mm. The mesh growth rate of the mixing zone was 1.1, while the mesh growth rates of the H₂ tank and nozzle regions were 1.2, since the study focused on the results of the mixing zones. The refinement of mesh for critical areas is shown in Figure 2. Three meshes were used to evaluate the effects of grid size on computational accuracy: coarse mesh with 999,725 elements, medium mesh with 1,208,768 elements, and fine mesh with 1,778,081 elements. The calculated jet centerline hydrogen mass fraction (Y) distributions near the nozzle and along the plate for the case of P₀ = 10 MPa and d = 0.5 mm are shown in Figure 3. The results show that the calculated hydrogen mass fractions along the plate are similar among the three meshes, while the calculated hydrogen mass fraction of the coarse mesh near the nozzle is slightly higher than that of the other two meshes. The medium mesh was used for the remaining simulations.

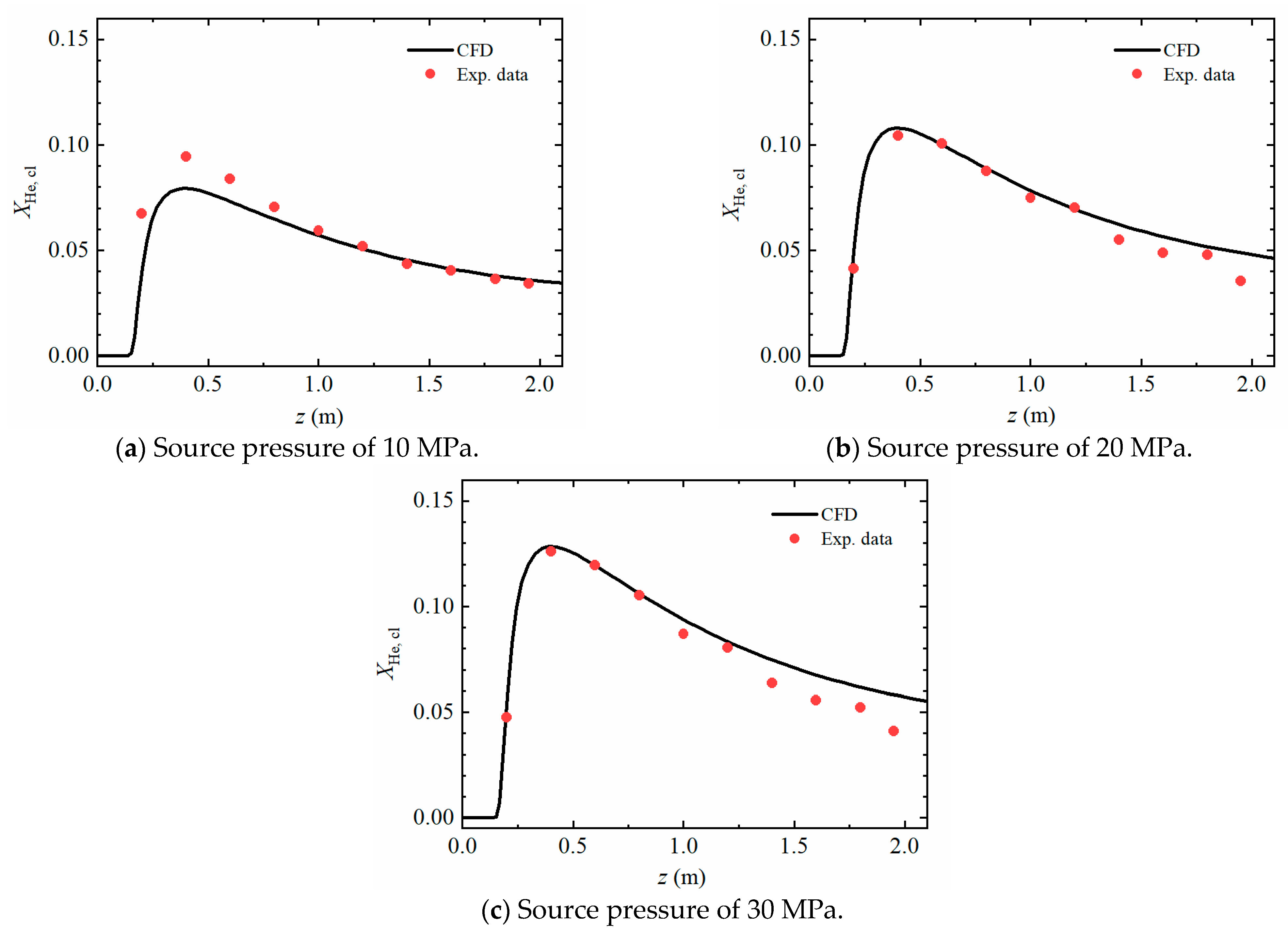
2.4. Validation

An experimental system was built to validate the model, as shown in Figure 4. Helium was used as a substitute for hydrogen due to safety concerns and the gases having similar physical properties (density significantly lower than air), resulting in buoyancy effects that dominantly governed the flow behavior. Swain et al. [41] validated the feasibility of using helium as a substitute for hydrogen in leakage characteristics research. Compressed helium was released from a circular nozzle with a 0.5 mm diameter. A flat plate, 2 m long and 0.5 m wide, was placed 0.05 m below the nozzle. Ten XEN-TCG3880Pt mini-thermal conductivity sensors with inaccuracies of ±2%FS, which are manufactured by Xensor Integration (Delfgauw, The Netherlands), were used as gas sensors to measure the helium concentration. Ten sensors were mounted every 0.2 m along the jet centerline projection on the plate, with the tops of the sensors flush with the plate surface. The Agilent 34970A data acquisition unit, produced by Keysight (Santa Rosa, CA, USA), was used to record the output voltage signals. The voltage signals were then converted into mole fractions using calibration correlations obtained by calibrating the sensors with helium/air mixtures of known concentrations. Further details of the experimental system are described in a previous work [31].

Horizontal helium jets with source pressures of 10, 20, and 30 MPa were measured. The average of the measurement results from three replicate experiments was taken as the final outcome. The measured helium concentration along the centerline of the flat plate and the simulation results are shown in Figure 5, where X represents the mole fraction, the subscript “He” indicates helium, and the subscript “cl” indicates the centerline of the jet. The results show that the simulation aligns well with the experimental data, with an overall prediction accuracy of 90.4%.

3. Results and Discussion

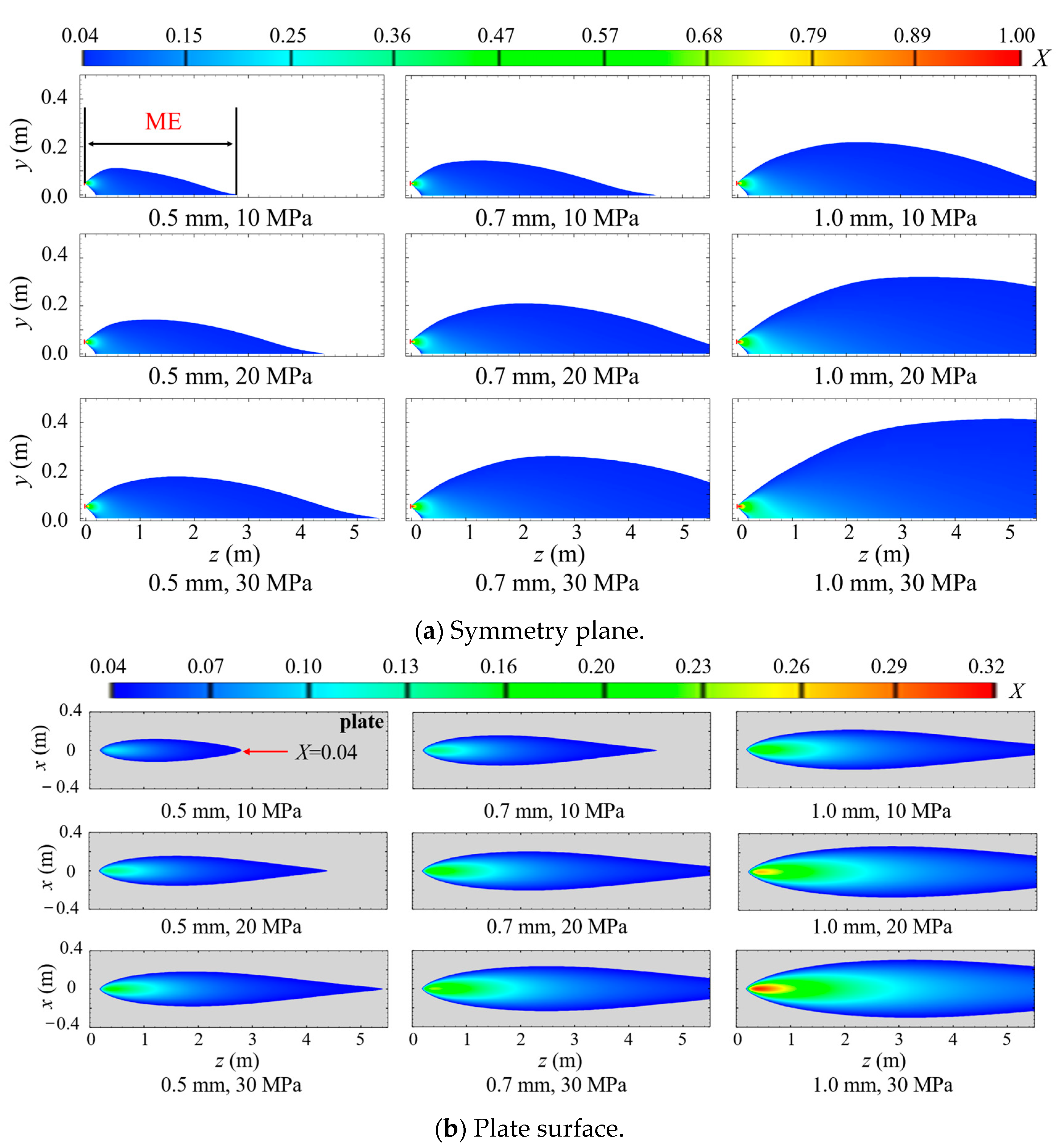
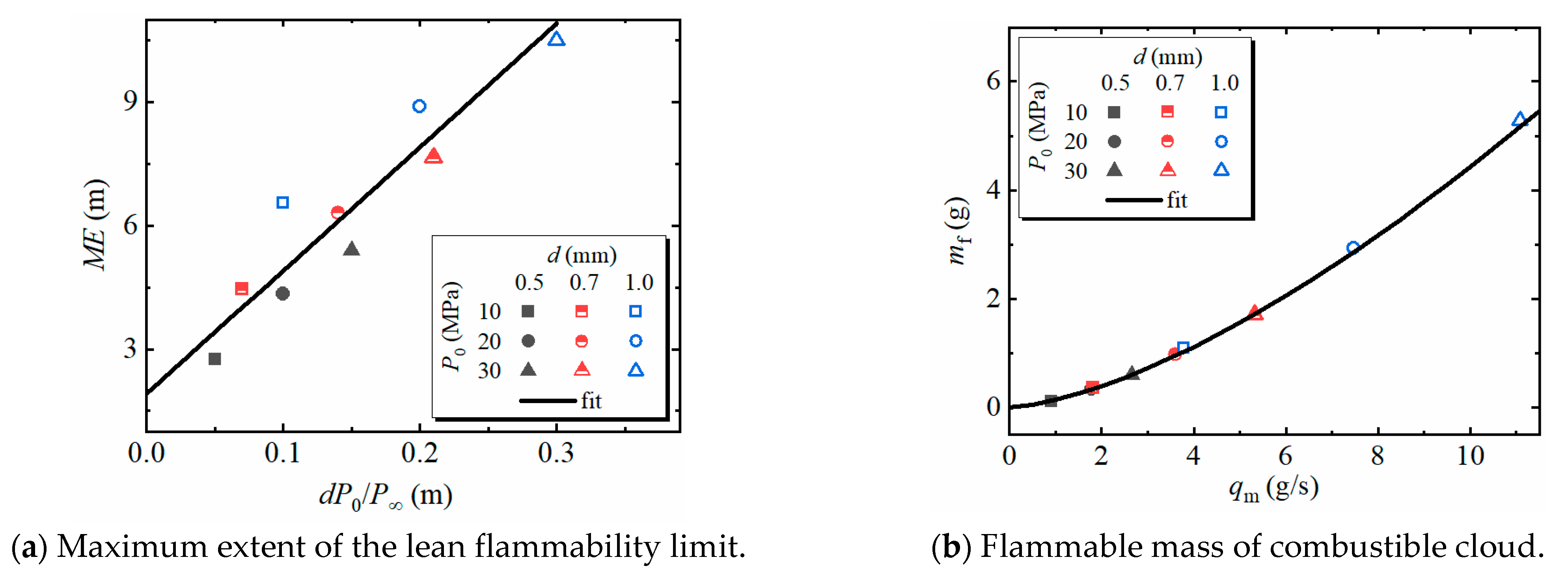
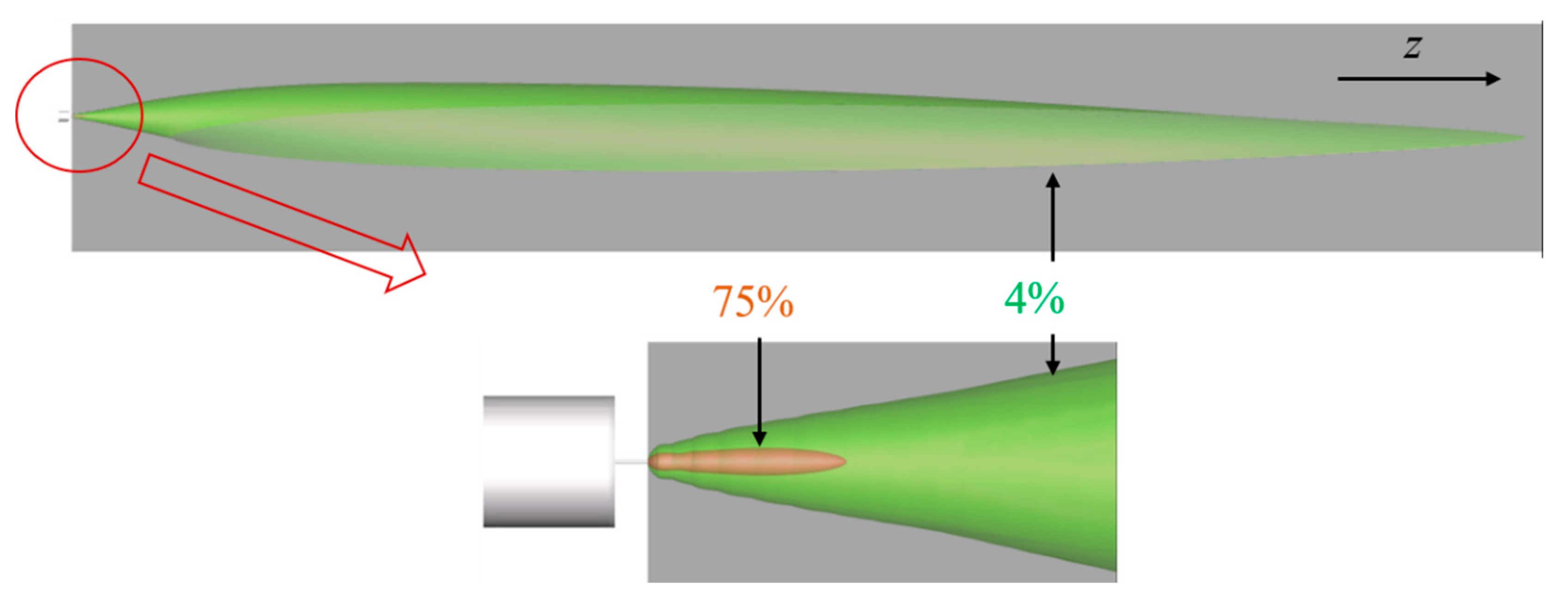
3.1. Combustible Cloud

The calculated hydrogen mole fraction distributions on the symmetry plane for various cases are shown in Figure 6a. In all cases, the hydrogen flammable clouds are attached to the plate. As the high-momentum hydrogen jet exits the nozzle and entrains the surrounding air, low-pressure zones form on both sides of the jet. The air in the low-pressure zone between the jet and the plate, however, cannot be replenished as quickly as on the opposite side due to the blockage caused by the plate. This creates a pressure difference between the upper and lower sides of the jet, which forces the jet to bend downward and attach to the plate surface. In this study, the pressure difference is sufficiently large to force the hydrogen flammable clouds to adhere to the plate and follow its curvature, thus preventing the hydrogen flammable clouds from floating. Similar wall attachment phenomena also exist in other studies [33,34,35,36], where hydrogen jets attach to the horizontal plate at higher heights of h = 0.5 m, 1 m, and 2 m under a pressure of 284 bar. This phenomenon, known as the Coanda effect [42], is accurately captured in the simulations. The results confirm that the hydrogen jets attach to the plate surface within a short distance from the nozzle across all cases. The hydrogen mole fraction distributions on the plate surface are shown in Figure 6b. Only the hydrogen mole fraction contours higher than the lean flammability limit (LFL, which is defined as X = 0.04) are shown in Figure 6, demonstrating that the volume of the combustible cloud increases with both nozzle diameter and source pressure.

The maximum extents (ME) of the combustible cloud on the symmetry plane, which are obtained via the linear fitting of the simulation data using Tecplot 360 EX 2022 R1 software, are analyzed for all cases to evaluate the hazardous range, as shown in Figure 7a. The maximum extent increases linearly with both nozzle diameter and source pressure, consistent with the mole fraction contours in Figure 6. An empirical equation was developed to correlate the maximum extent with the nozzle diameter and source pressure, as given by

$$ME=30d{\displaystyle \frac{P_0}{P_{\infty }}}+1.91$$

(3)

The error between calculated ME from Equation (3) and the experimental data is 23%, which is acceptable for a quick evaluation for practical use. For a choked flow, the mass flow rate (q_m) at the nozzle exit can be calculated using the following equation if the ideal gas equation of state is applied:

$$q_m=C_1{d}^2{P}_0$$

(4)

where C₁ is a coefficient determined by the specific heat ratio and the stagnation temperature. Substituting Equation (4) into Equation (3) yields

$$ME=C_2{q}_m^{0.5}+1.91=C_3{q}_m+1.91$$

(5)

where C₂ is a coefficient determined by P₀ and C₁, and C₃ is a coefficient determined by d and C₁. Therefore, the maximum extent of the combustible cloud increases with the square root of mass flow rate for a given pressure, and increases linearly with the mass flow rate for a given diameter.

The combustible cloud is prone to fire or explosion when exposed to an ignition source. In the event of an explosion, which represents the worst-case scenario of hydrogen safety accidents, the destructive power is directly related to the flammable mass of combustible cloud. An example of a 3D plot showing the volume of the combustible cloud is presented in Figure 8.

The flammable mass was obtained using a Custom Field Function (CFF) that multiplies the local hydrogen mass fraction by the density and then integrates this over the flammable volume to determine the total flammable mass. The results show that the flammable mass increases rapidly with the mass flow rate raised to the power of 1.5, as shown in Figure 7b, which can be correlated using the following equation:

$$m_f=0.14{\left(q_m\right)}^{1.5}=0.14{\left(C_1{P}_0\right)}^{1.5}{d}^3$$

(6)

where m_f is the flammable mass.

According to Equations (5) and (6), the flammable mass of the combustible cloud increases with the leakage mass flow rate much more rapidly than the maximum flammable extent along the plate. Specifically, for a given pressure, the flammable mass is proportional to the cube of the maximum extent of the combustible cloud. This implies that the explosive power may increase drastically with even a small increase in the maximum extent of the combustible cloud, which should be carefully considered in the risk assessment process.

3.2. Streamwise Concentration Profiles

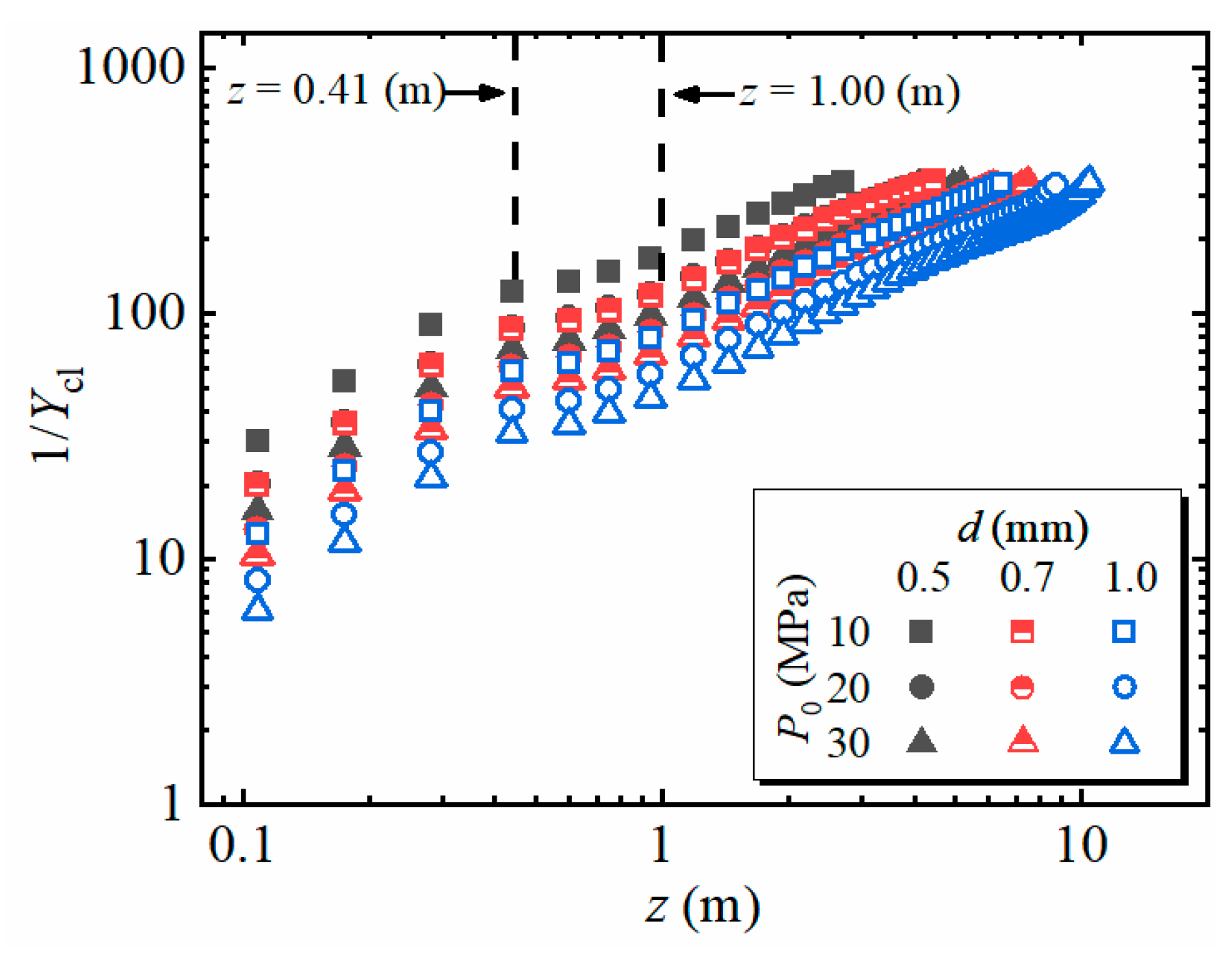
3.2.1. Jet Centerline

For the jet released from a circular nozzle, the hydrogen concentration at a given horizontal location peaks at the jet centerline. However, unlike a free jet, the jet centerline attaches to the plate surface at a short distance downstream of the nozzle due to the pressure difference between the upper and lower sides of the jet. As an example, the jet centerline at the symmetry plane for the case of d = 0.5 mm and P₀ = 10 MPa is shown in Figure 9.

The jet centerlines on the symmetry plane for various cases are plotted in Figure 10. In the present study, the horizontal distances of the attachment point (z_AP) are nearly the same, with a value of 0.41 m for all cases. One possible explanation is that, although jets with higher momentum tend to cause the attachment point to move downstream, the higher flow velocity also leads to a greater pressure difference on both sides of the jet, causing the attachment point to move upstream. Therefore, under these two opposing effects, the position of the attachment point remains relatively fixed.

The inverse hydrogen mass fraction (1/Y_cl) distributions along the jet centerline are shown in Figure 11. The results show that the hydrogen mass fraction at a given horizontal position increases with both nozzle diameter and source pressure, as expected. The attachment point divides the jet into pre-attachment and attachment zones, where the hydrogen concentration decay laws deviate significantly.

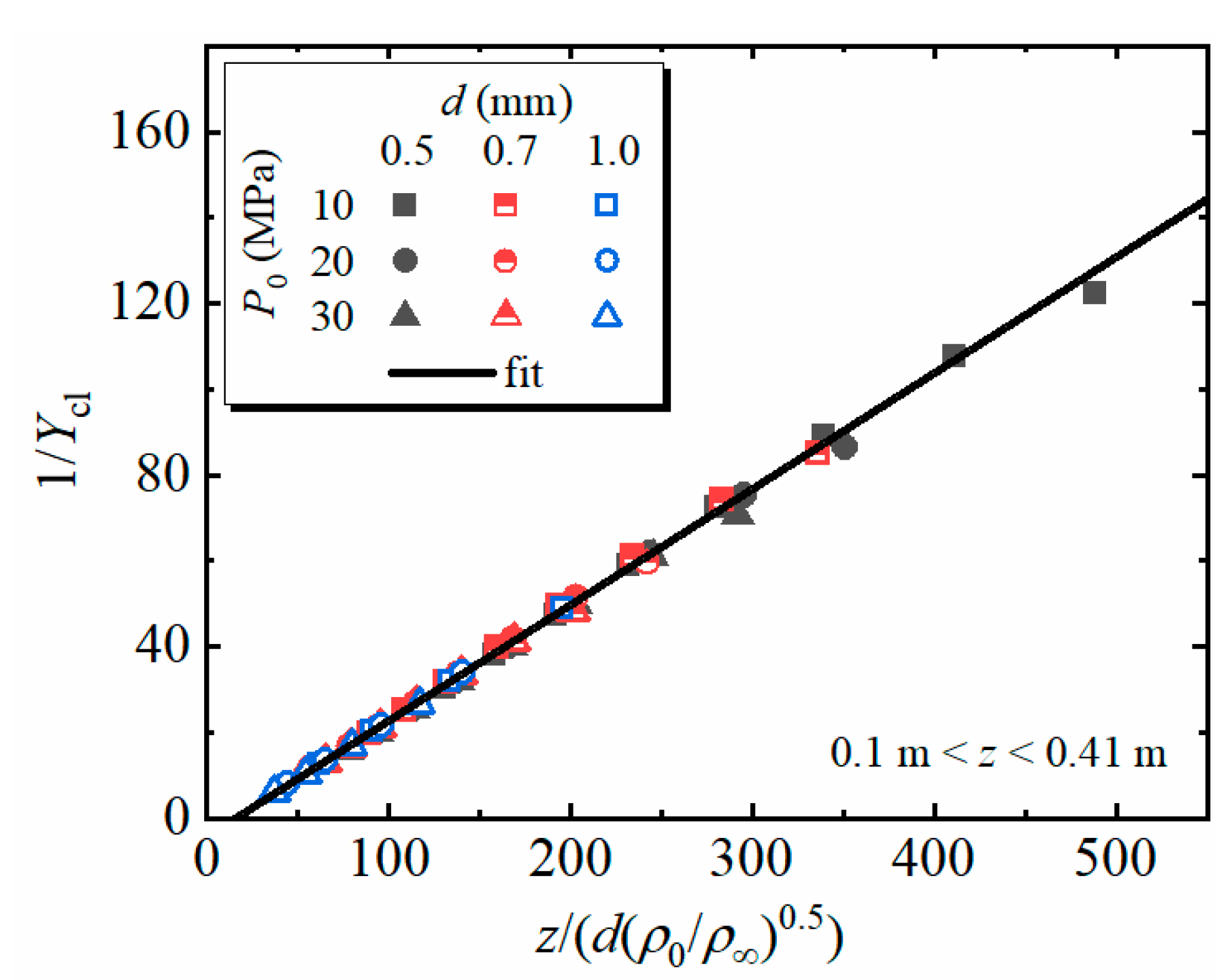
3.2.2. Pre-Attachment Zone

Studies on free jets have confirmed that the jet centerline concentration decay follows the canonical hyperbolic decay law [11,12,14,16]. The inverse jet centerline mass fraction can be calculated using the following empirical equation:

$${\displaystyle \frac{1}{Y_{cl}}}=C_d{\displaystyle \frac{z-z_0}{d\sqrt{{\rho }_N/{\rho }_{\infty }}}}$$

(7)

where C_d is the decay rate, z₀ is a constant representing the position of a pseudo-origin, ρ_N is the gas density at the nozzle exit calculated by Fluent software, and ρ_∞ is the ambient air density.

The inverse hydrogen mass fraction distributions in the pre-attachment zone for various cases are shown in Figure 12, where the horizontal distance is normalized by $d\sqrt{{\rho }_N/{\rho }_{\infty }}$. The results show that the jet centerline concentration decay law in the pre-attachment zone is similar to that of a free jet. The decay rate of the pre-attachment zone is 0.27, which is within the range of 0.21~0.27 of free jets concluded by Hecht et al. [43].

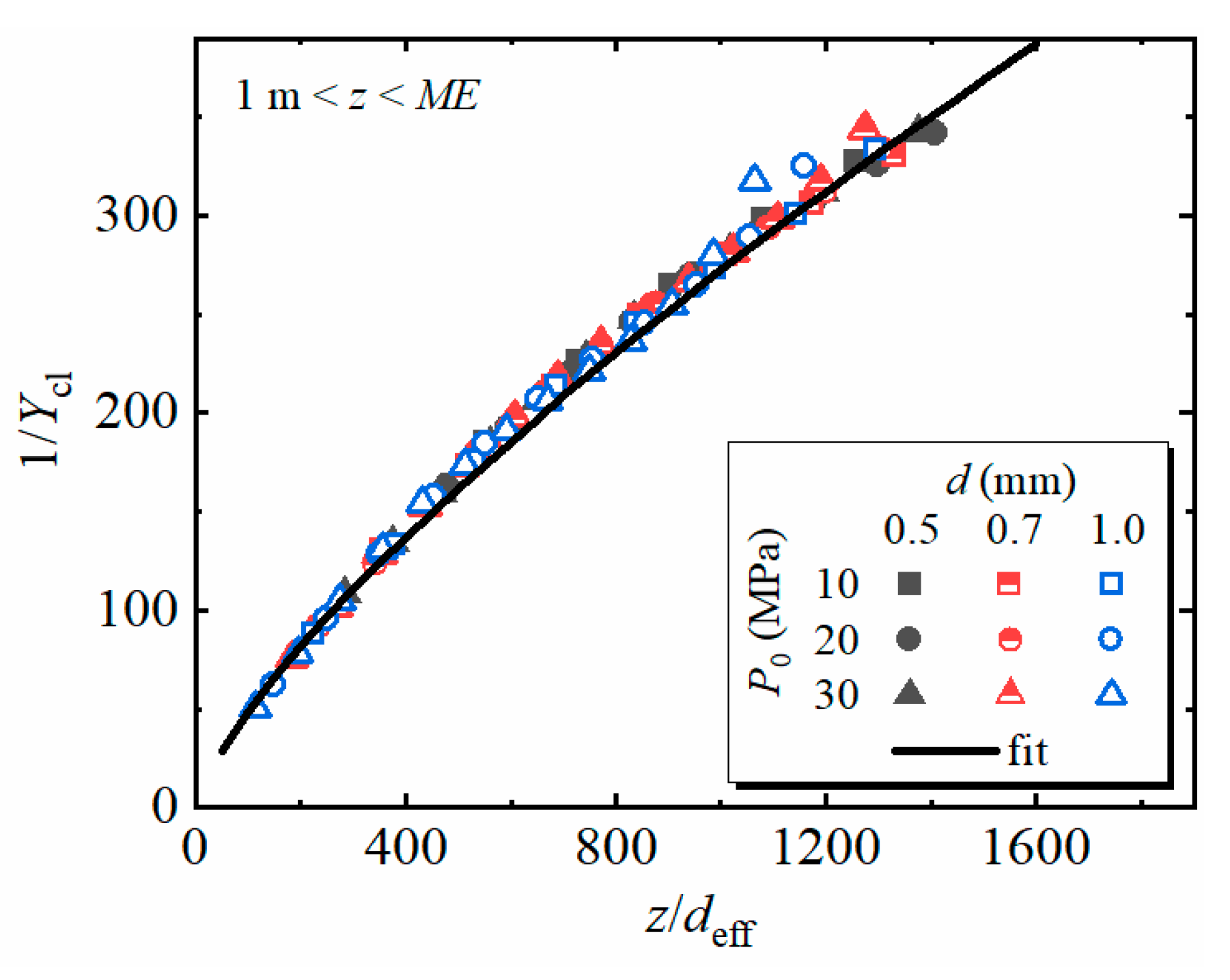
3.2.3. Post-Attachment Zone

Hydrogen dispersion in the attachment zone is influenced by both jet momentum and the surface, making the decay law in this zone more complex than in the pre-attachment zone. A transition zone forms around the attachment point, where the flow transitions from a free jet to an attached jet. Complex interactions between the jet and the surface significantly complicate the flow pattern in this region. As the jet flows downstream along the surface, the flow develops into a relatively stable region (z > 1 m), known as the post-attachment zone. The jet centerline concentration distribution exhibits self-similar features in this zone. An effective diameter, d_eff, was defined to account for the influences of both jet momentum and the plate surface:

$$d_{eff}=d{\left({\displaystyle \frac{d}{h}}\right)}^{0.3}{\left({\displaystyle \frac{P_0}{P_{\infty }}}\right)}^{0.6}$$

(8)

where h is the height of the nozzle above the plate surface.

The mass fraction data for all cases collapse onto a single power–law curve when the horizontal distance is normalized using the effective diameter defined in Equation (8), as shown in Figure 13. The results confirm that the hydrogen concentration distribution is self-similar, and the inverse mass fraction along the jet centerline in the post-attachment zone can be correlated using the following empirical equation:

$${\displaystyle \frac{1}{Y_{cl}}}=1.53{\left({\displaystyle \frac{z}{d_{eff}}}\right)}^{0.75}$$

(9)

The coefficient of determination (R²) is 0.987, which shows that the fitting curve agrees well with the numerical data.

According to Equations (7) and (9), the centerline concentration decay rate in the post-attachment zone is significantly lower than in the pre-attachment zone for a given nozzle diameter and source pressure. These results indicate that the surface near the leak point can substantially enlarge the hydrogen flammable extent, consistent with findings in the literature [33,34,35,36].

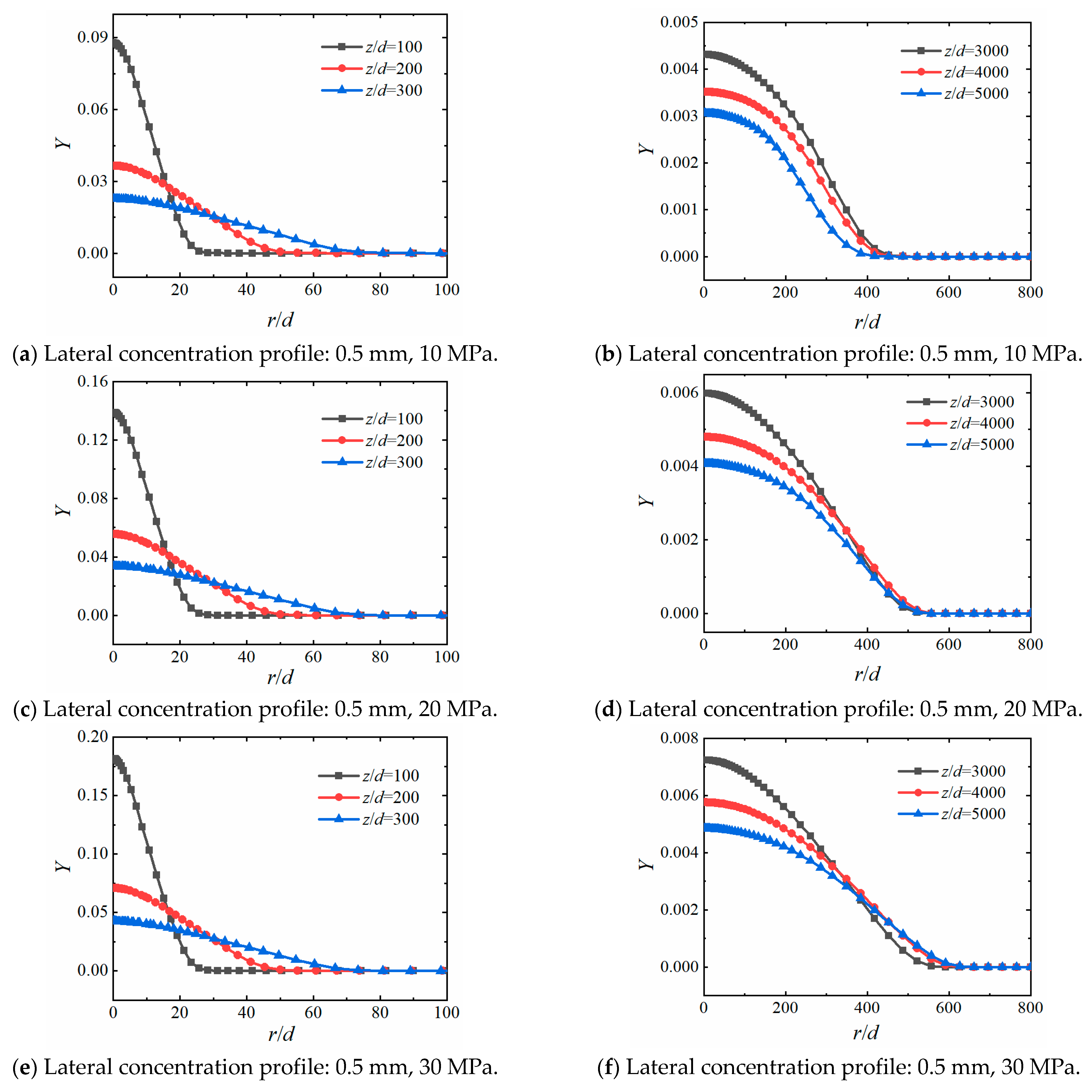
3.3. Lateral Concentration Profiles

The lateral concentration profiles at various streamwise locations along the jet centerline are shown in Figure 14, where only the case with a nozzle diameter of 0.5 mm is shown in the figure as an example. The results show that the concentration peaks at the jet centerline for both the pre- and post-attachment zones. In the pre-attachment zone, the lateral concentration distribution is Gaussian, similar to that of a free jet. In the post-attachment zone, the lateral concentration distribution follows a generalized Gaussian distribution with a wider bell shape. This is mainly due to the viscous resistance of the plate boundary layer, which hinders the lateral concentration decay of hydrogen, thus indicating a slower lateral concentration decay compared to the pre-attachment zone. The wider bell shape indicates a greater dispersion of values near r/d = 0. The broader the curve, the wider the distribution of data points.

All the data collapse onto a single curve for both the pre- and post-attachment zones when the lateral mass fraction (Y) is normalized by the centerline mass fraction (Y_cl) and the lateral distance (r) is normalized by the half width (r_0.5), as shown in Figure 15. The half width is defined as the distance between the peak of the profile and the point where the concentration is half of the peak concentration. These results further confirm that the lateral concentration distributions are self-similar in the pre- and post-attachment zones. The following empirical correlations can be used to fit the data for all cases:

Pre-attachment zone:

$${\displaystyle \frac{Y}{Y_{\mathrm{cl}}}}=\exp \left(-0.74{\left({\displaystyle \frac{r}{r_{0.5}}}\right)}^2\right)$$

(10)

Post-attachment zone:

$${\displaystyle \frac{Y}{Y_{\mathrm{cl}}}}=\exp \left(-0.75{\left({\displaystyle \frac{r}{r_{0.5}}}\right)}^3\right)$$

(11)

The factor before (r/r_0.5) in Equation (10), 0.74, is slightly larger than the factor (0.69) of a free jet in the literature [44]. In Equations (10) and (11), the power of (r/r_0.5) is called the scale parameter, which controls the kurtosis (peakedness and tail behavior) [45,46]. A higher-scale parameter results in a wider bell shape, which is consistent with the data shown in Figure 14 and Figure 15.

4. Conclusions

High-pressure hydrogen jets released from small nozzles near a plate surface were studied for nozzle diameters ranging from 0.5 to 1 mm and source pressures from 10 to 30 MPa. Three-dimensional CFD models were used and an experimental system was established to investigate the effects of the adjacent surface on the combustible cloud and the concentration decay of the jet.

The results show that the maximum extent of the combustible cloud increases linearly with both nozzle diameter and source pressure. Further analysis indicates that the maximum extent of the combustible cloud increases with the square root of the mass flow rate for a given pressure, and increases linearly with the mass flow rate for a given diameter. The flammable mass increases with the leakage mass flow rate raised to the power of 1.5. Consequently, the growth of the flammable mass in the combustible cloud outpaces the expansion of its maximum flammable extent along the plate.

The simulation results also show that the horizontal position of the jet centerline attachment points is nearly identical at z = 0.41 m across all cases. The attachment point divides the jet into pre-attachment and post-attachment zones. In the pre-attachment zone, the centerline concentration decay follows a pattern similar to that of a free jet, with a decay rate of 0.27. The attachment zone includes a brief transition zone where the flow pattern is highly complex and a post-attachment zone where the jet centerline concentration distribution exhibits self-similar characteristics. In the post-attachment zone, the inverse centerline mass fraction can be correlated using a power–law equation when the horizontal distance is normalized by an effective diameter that accounts for the influences of both jet momentum and the plate surface.

Furthermore, the lateral concentration distributions are self-similar in both the pre- and post-attachment zones. The lateral mass fraction distribution follows a Gaussian distribution in the pre-attachment zone and a generalized Gaussian distribution with a wider bell shape in the post-attachment zone. Consequently, the lateral concentration decay is slower in the post-attachment zone compared to the pre-attachment zone.

This study provides an effective method for determining safety distances for hydrogen leakage along flat walls, which are commonly found in real-world industrial and commercial hydrogen facilities. The developed empirical equations for calculating the combustible mass of hydrogen can also be applied in subsequent calculations of overpressure caused by hydrogen explosions, providing a valuable tool in process engineering design and practice. Due to the potential of a horizontal surface to extend the flammable distance of leaking hydrogen, hydrogen-related components in practical scenarios, especially joints and valves that are prone to leakage, should be positioned far away from any surface such as the ground if possible. Furthermore, the influencing factors in actual hydrogen-related scenarios are complex, such as the shape of obstacles, the height of the leakage source, and the ambient wind speed. Future work can focus on the effects of these factors to build a comprehensive scientific basis for predicting safety distances in hydrogen-related scenarios.