Fault Equivalence and Calculation Method for Distribution Networks Considering the Influence of Inverters on the Grid Side and the Distribution Network Side
Abstract
1. Introduction
- (1)
- An integrated grid-side source model and a parameter identification method for distribution network faults are proposed, both of which can accurately reflect the impact of the IBRs on the grid side of the distribution network containing DGs. The key parameters are identified based on the port electrical quantities, using the genetic algorithm.
- (2)
- A fault calculation method that takes into account the impact of IBRs on the grid side and distribution network side is proposed which can accurately calculate the electrical quantities of the distribution network and provide a reliable basis for fault characteristic analysis and protection settings.
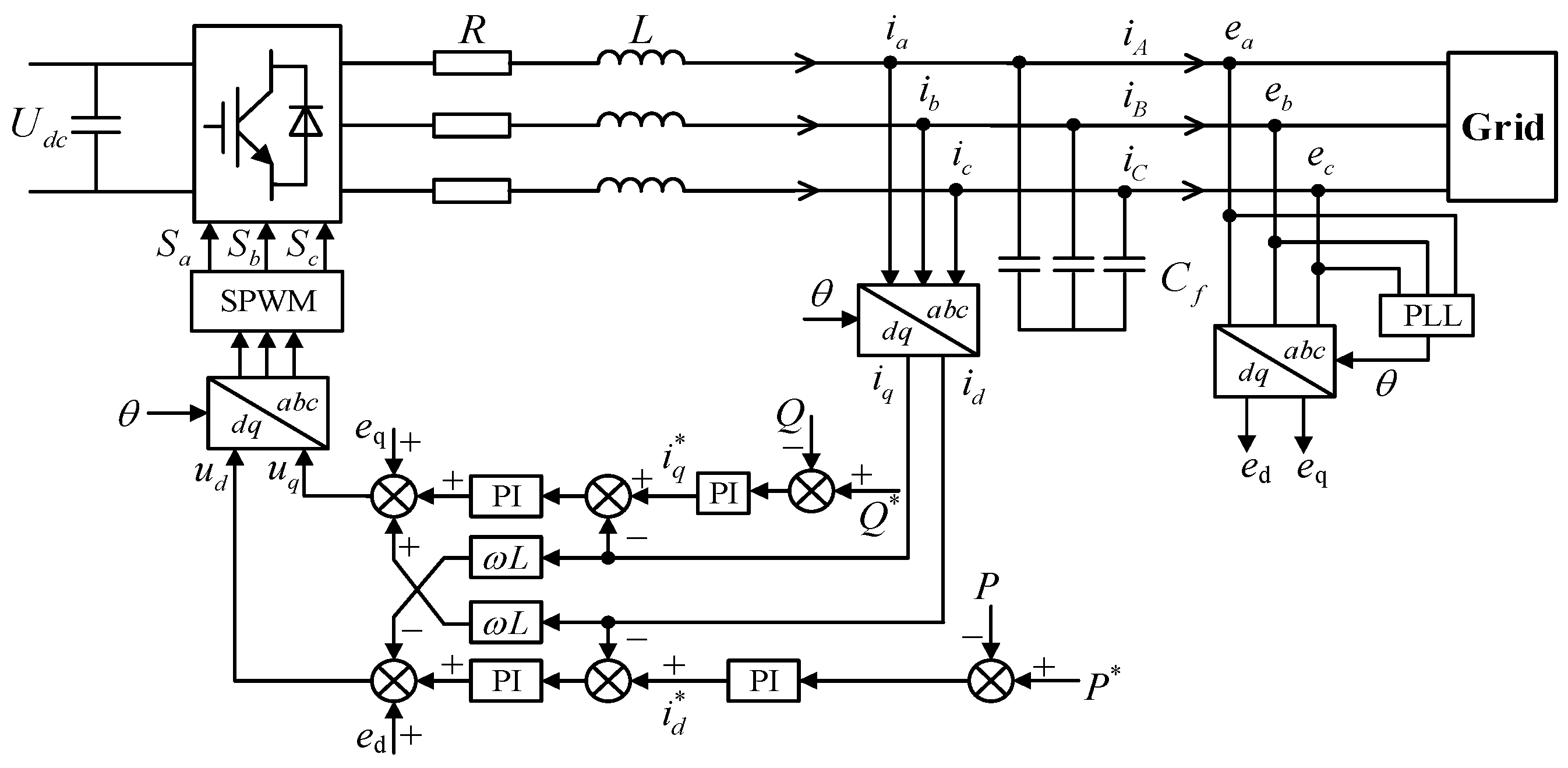
2. Typical Control Strategies and Current Features of IBRs
2.1. Control Strategy During Normal Operation
2.2. Control Strategy for Low-Voltage Ride-Through Periods
3. Equivalent Model of the Grid Side Containing a High Proportion of IBRs
3.1. Integrated Source Model
3.2. Parameter Identification Method
4. Fault Calculation Method for Distribution Networks with IBRs on Both Grid and Distribution Sides
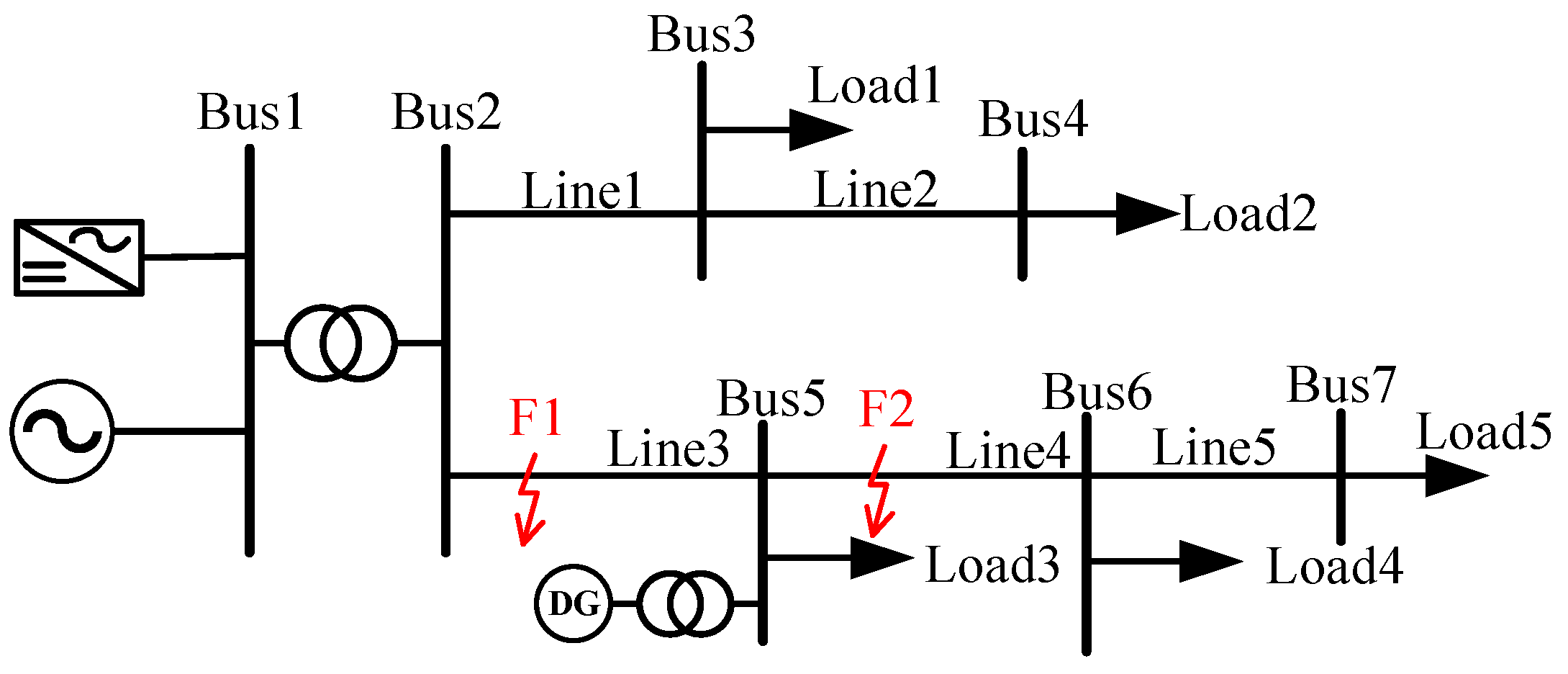
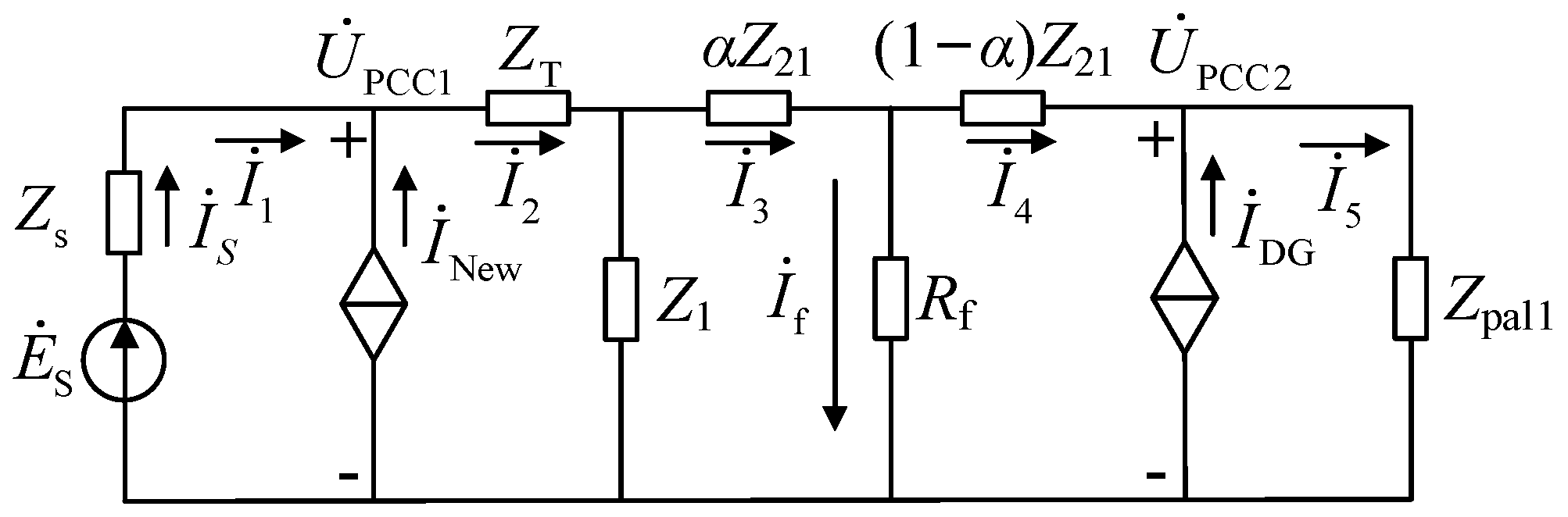
4.1. Fault-Equivalent Model of Distribution Networks
4.2. Fault Calculation Process for Distribution Networks
5. Simulation and Verification
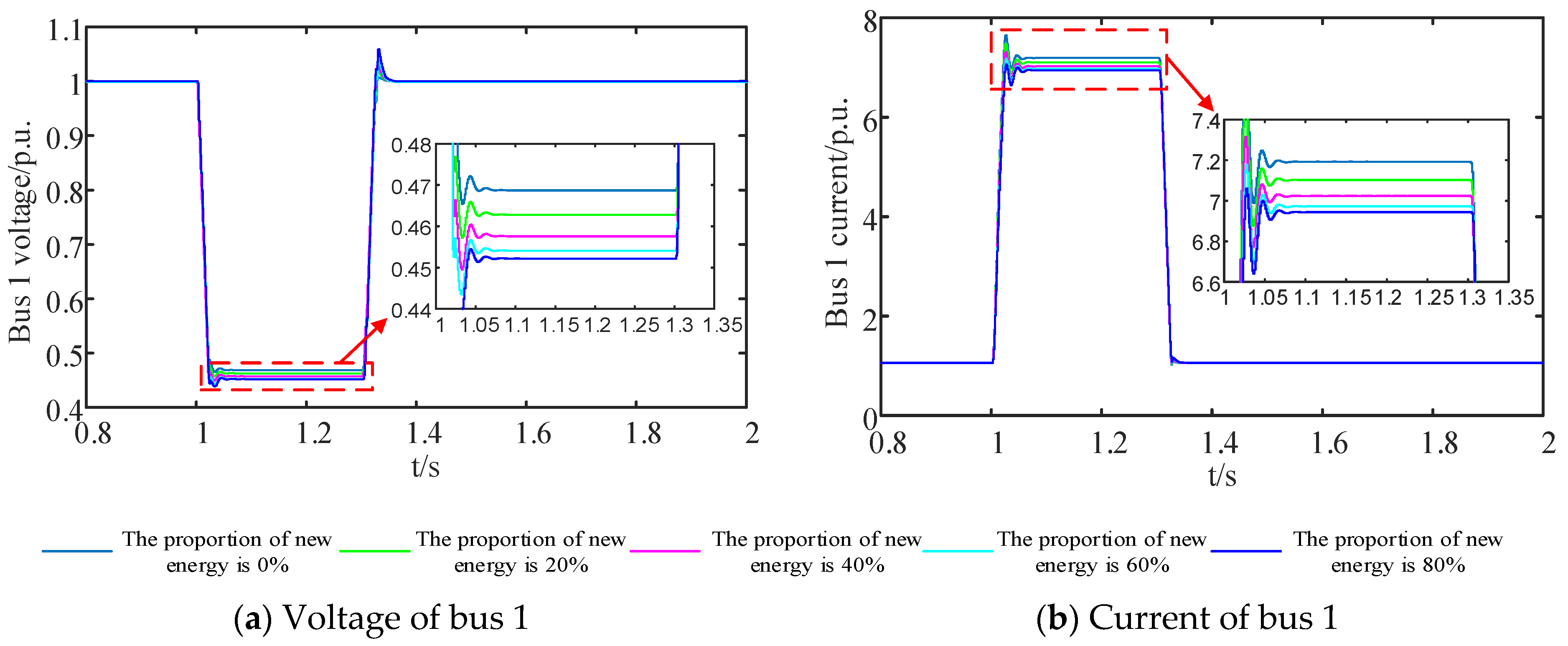
5.1. Verification of Integrated Source Model for the Grid Side
5.1.1. Impact of the Grid-Side IBR on the Fault Characteristics of Distribution Networks
5.1.2. Verification of the Parameter Identification Method
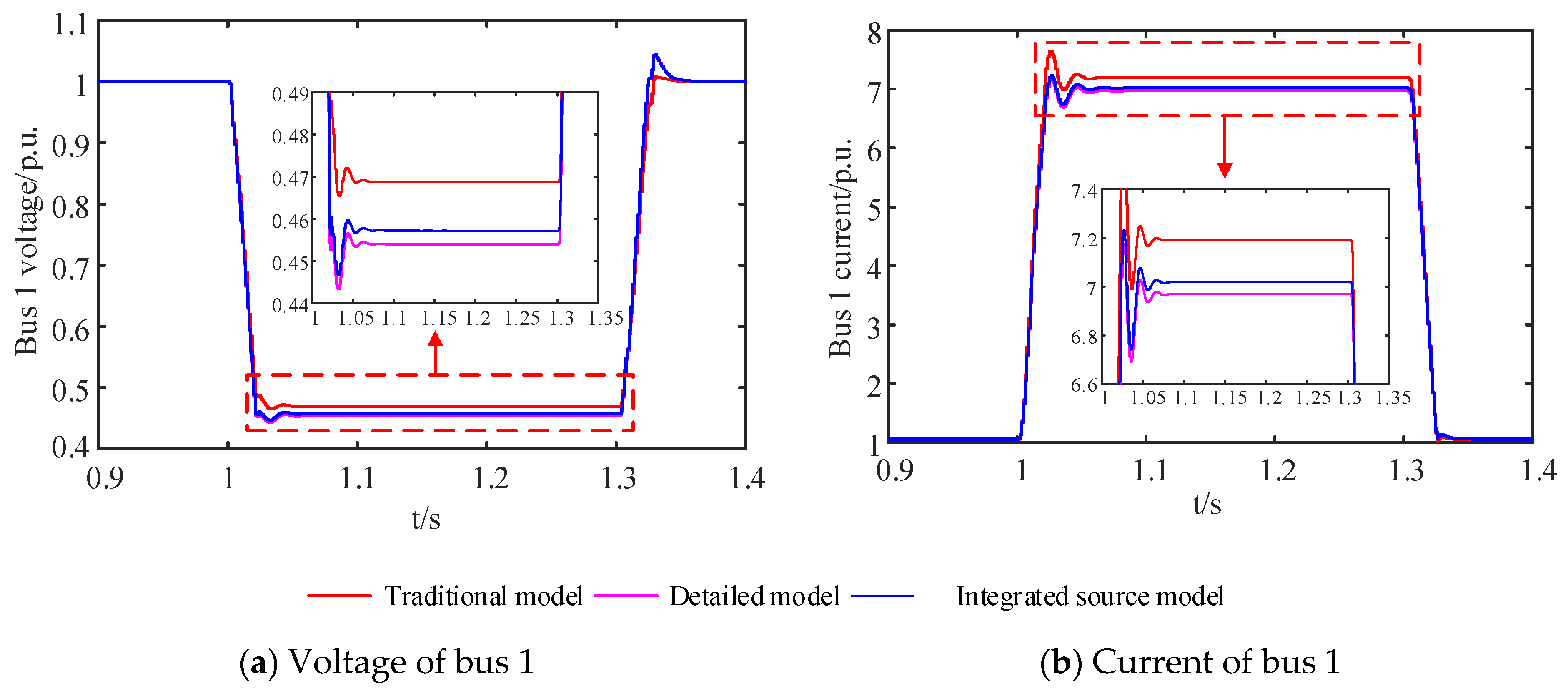
5.1.3. Performance Comparison of Different Models
- (a)
- Three-phase faults
- (b)
- Phase-to-phase faults
5.1.4. Convergence and Sensitivity to Initial Conditions
5.1.5. Performance of Different Parameter Identification Methods
5.2. Verification of the Fault Calculation Method
6. Conclusions
- (1)
- Compared to the single connection of a synchronous generator source, the addition of the grid-side IBRs leads to a decrease in the grid-side port voltage and a reduction in the fault current output to the distribution network during distribution network faults.
- (2)
- The proposed grid-side integrated source model uses the parallel connection form of ideal voltage sources with series impedance and voltage-controlled current sources, and the genetic algorithm can accurately identify the integrated source model parameters based on the voltage and current at the grid-side ports during normal operation. The model can effectively reflect the impact of the grid-side IBRs on the distribution network during faults.
- (3)
- Based on the simplified model of the network, the proposed distribution network fault calculation method uses the iterative calculation error of the PCC voltage as a benchmark. Then, accurate calculation of the electrical quantities during distribution network faults can be performed by the relationship between the voltage and output current of IBRs. The amplitude errors are within 1%, and the phase angle errors are within 4°.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| IBR | Inverter-based resources |
| PCC | Point of common coupling |
| DG | Distributed generator |
| GFL | Grid-following |
| GFM | Grid-forming |
| AC | Alternating current |
| KCL | Kirchhoff’s current law |
References
- Ma, X.; Zhen, W.; Ren, H.; Zhang, G.; Zhang, K.; Dong, H. A Method for Fault Localization in Distribution Networks with High Proportions of Distributed Generation Based on Graph Convolutional Networks. Energies 2024, 17, 5758. [Google Scholar] [CrossRef]
- Chen, G.; Liu, Y.; Yang, Q. Impedance Differential Protection for Active Distribution Network. IEEE Trans. Power Deliv. 2020, 35, 25–36. [Google Scholar] [CrossRef]
- Banerjee, G.; Hachmann, C.; Lipphardt, J.; Wiese, N.; Braun, M. Adaptive Hybrid Overcurrent Protection Scheme with High Shares of Distributed Energy Resources. Energies 2024, 17, 6422. [Google Scholar] [CrossRef]
- Yin, X.; Zhang, Z.; Xiao, F.; Yang, H.; Yang, Z. Study on Short-Circuit Calculation Model of Distributed Generators and Fault Analysis Method. Power Syst. Prot. Control 2015, 43, 1–9. [Google Scholar]
- Chang, Z.; Song, G.; Wang, X.; Guo, S.; Zhang, W.; Jin, X. Analysis on Asymmetric Fault Current of Inverter Interfaced Distributed Generator. In Proceedings of the 2016 China International Conference on Electricity Distribution (CICED), Xi’an, China, 10–13 August 2016; pp. 1–6. [Google Scholar]
- Dong, Z.; Liu, K.; Zhang, B. A General Fault Current Calculation Method for Distribution Network with Distributed Generation. Power Syst. Prot. Control 2019, 47, 161–168. [Google Scholar]
- Xu, Y.; Wu, T.; Hu, P.; Wang, N. Fault Recovery Method for Distributed Distribution Network Based on Island Partition. J. Electr. Eng. Technol. 2025, 20, 23–35. [Google Scholar] [CrossRef]
- Gao, Y.; Shi, H.; Wu, S.; Kong, D.; You, H.; Chen, J.; Xu, S.; Chen, J.F. A Practical Approach for Short-Circuit Current Calculation in IIDG-Integrated Distribution Grid. In Proceedings of the 2022 China International Conference on Electricity Distribution (CICED), Changsha, China, 7–8 September 2022; pp. 1477–1483. [Google Scholar]
- Pan, G.; Zeng, D.; Wang, G.; Zhu, G.; Li, H. Fault Analysis on Distribution Network with Inverter Interfaced Distributed Generations Based on PQ Control Strategy. Proc. CSEE 2014, 34, 555–561. [Google Scholar]
- Dai, Z.; Li, C.; Jiao, Y. Low-Voltage Ride Through Model of Inverter-Interfaced Distributed Generator and Its Application to Fault Analysis of Distribution Network. Proc. CSU-EPSA 2018, 30, 16–23. [Google Scholar]
- Shi, S.; Huang, Z.; Zhang, Y. Improvement of Short-circuit Calculation for distribution network with distributed generation. In Proceedings of the 2021 IEEE 4th Advanced Information Management, Communicates, Electronic and Automation Control Conference (IMCEC), Chongqing, China, 18–20 June 2021; pp. 21–24. [Google Scholar]
- Wang, Q.; Zhou, N.; Ye, L. Fault Analysis for Distribution Networks with Current-Controlled Three-Phase Inverter-Interfaced Distributed Generators. IEEE Trans. Power Deliv. 2015, 30, 1532–1542. [Google Scholar] [CrossRef]
- Ye, R.; Wang, H.; Zhang, Y. GCN-Based Short-Circuit Current Calculation Method for Active Distribution Networks. IEEE Access 2023, 11, 140092–140102. [Google Scholar] [CrossRef]
- Shuai, Z.; Shen, C.; Yin, X.; Liu, X.; Shen, Z.J. Fault Analysis of Inverter-Interfaced Distributed Generators with Different Control Schemes. IEEE Trans. Power Deliv. 2018, 33, 1223–1235. [Google Scholar] [CrossRef]
- Zhu, G.; Sheng, J. Equivalent Modeling of External Network in New Energy Power Grid Taking Voltage Support into Consideration. J. South China Univ. Technol. Nat. Sci. Ed. 2017, 45, 1–7. [Google Scholar]
- Xie, D.; Xiao, S. Short-Circuit Calculation Equivalent of External Power Grid Including Inverter Interfaced Distributed Generator and Analysis of Influencing Factors. Power Syst. Techol. 2024, 48, 2967–2976. [Google Scholar]
- Wang, X.; Wu, H.; Wang, X.; Dall, L.; Kwon, J.B. Transient Stability Analysis of Grid-Following VSCs Considering Voltage-Dependent Current Injection During Fault Ride-Through. IEEE Trans. Energy Convers. 2022, 37, 2749–2760. [Google Scholar] [CrossRef]
- Zhang, C.; Wu, X.; Xie, X. Research on Low Voltage Ride Through of DG Characteristics Based on GB/T33593 standard. Power Syst. Prot. Control 2019, 47, 76–83. [Google Scholar]
- She, B.; Li, F.; Cui, H.; Shuai, H.; Oboreh-Snapps, O.; Bo, R. Inverter PQ Control with Trajectory Tracking Capability for Microgrids Based on Physics-Informed Reinforcement Learning. IEEE Trans. Smart Grid 2024, 15, 99–112. [Google Scholar] [CrossRef]
- Cheng, L.; Xu, P.; Zhang, Q.; Wang, Y. Improved PQ Control Mothod for PV System. In Proceedings of the 2019 IEEE Symposium Series on Computational Intelligence (SSCI), Xiamen, China, 6–9 December 2019; pp. 2914–2920. [Google Scholar]
- Wei, C.; Shi, X.; Zhou, B.; Liu, Y. Fault Model of Inverter Interfaced Distributed Generator Adopting PQ Control Strategy Considering Current Tracking Capability of Converter. In Proceedings of the 2019 IEEE Innovative Smart Grid Technologies—Asia (ISGT Asia), Chengdu, China, 21–24 May 2019; pp. 1419–1424. [Google Scholar]
- Li, B.; Mu, R.; He, J.; Wang, W.; Yao, C.; Zhang, Y. Transient Fault Current Calculation Method for the PV Grid-Connected System Considering Dynamic Response of PLL. IEEE Trans. Ind. Appl. 2024, 60, 7537–7547. [Google Scholar] [CrossRef]
- Han, B.; Li, H.; Wang, G.; Zeng, D.; Liang, Y. A Virtual Multi-Terminal Current Differential Protection Scheme for Distribution Networks with Inverter-Interfaced Distributed Generators. IEEE Trans. Smart Grid 2018, 9, 5418–5431. [Google Scholar] [CrossRef]
- Liu, H.; Xu, K.; Zhang, Z.; Liu, W.; Ao, J. Research on Theoretical Calculation Methods of Photovoltaic Power Short-Circuit Current and Influencing Factors of Its Fault Characteristics. Energies 2019, 12, 316. [Google Scholar] [CrossRef]
- Wang, L.; Gao, H.; Zou, G. Modeling Methodology and Fault Simulation of Distribution Networks Integrated with Inverter-Based DG. Prot. Control. Mod. Power Syst. 2017, 2, 1–9. [Google Scholar] [CrossRef]
- Hasan, M.S.; Kamalasadan, S. Optimization of DER Integrated Distribution System by Sequential Quadratic Programming (SQP). In Proceedings of the 2022 IEEE Global Conference on Computing, Power and Communication Technologies (GlobConPT), New Delhi, India, 23–25 September 2022; pp. 1–6. [Google Scholar]
- Ekinci, S.; Izci, D.; Yilmaz, M. Simulated Annealing Aided Artificial Hummingbird Optimizer for Infinite Impulse Response System Identification. IEEE Access 2023, 11, 88627–88636. [Google Scholar] [CrossRef]






| Reference | DG Model | Grid-Side Model | Key Findings | Limitations |
|---|---|---|---|---|
| [8] | Constant voltage in series with a constant impedance | New energy sources are not mentioned | Calculate the fault current in the active distribution network; the fault calculation error is less than 5% | The impacts of grid-side IBRs are not considered; the calculation error is relatively large |
| [9] | Voltage-controlled current sources | Ideal current source in parallel with admittance | Improve the fault calculation accuracy compared to the case where DGs are not considered | The impacts of grid-side IBRs are not considered |
| [10] | Voltage-controlled current sources | Ideal voltage source in series with impedance | Propose a fault ride-through control strategy to enhance the efficiency of DGs and calculate the fault electrical quantities based on this strategy | The impacts of grid-side IBRs are not considered |
| [11] | Voltage source in series with an impedance | New energy sources are not mentioned | Calculate the fault electrical quantities by forming a new admittance matrix | The impacts of grid-side IBRs are not considered |
| [12] | Sequence component voltage-controlled current source | Ideal voltage source in series with impedance | Propose a fault calculation method for asymmetrical faults based on the composite sequence network | The impacts of grid-side IBRs are not considered; injection of the negative-component current for IBRs is not common |
| [13] | No physical model is available | No physical model is available | Propose a graph convolutional neural network-based calculation method to improve accuracy and computational speed | The impacts of grid-side IBRs are not considered; there is a lack of physical models as the theoretical basis |
| [14] | Voltage-controlled current sources (PQ control) and voltage source (VF control) | Ideal voltage source in series with impedance | Analyze the fault currents under different IBR control strategies | The impacts of grid-side IBRs are not considered |
| [15] | DG is not taken into consideration | Ideal voltage source in series with impedance | Use the equivalent potential method to reflect the voltage support role of the external grid containing new energy | The impacts of distribution network-side IBRs are not considered; the characteristics of distribution network are not analyzed |
| [16] | Ideal current source in parallel with admittance | No specific explanation is available, but it can refer to the DG model | Analyze the impact of high new energy penetration on the calculation of short-circuit currents | The impacts of the grid-side IBR on the distribution network are not considered |
| Percentage of New Energy/% | Parameter | Set Value/p.u. | Identified Value/p.u. | Error/% |
|---|---|---|---|---|
| 20 | z | 0.092 | 0.091 | 1.087 |
| IPW | 0.200 | 0.196 | 2.000 | |
| 40 | z | 0.097 | 0.097 | 1.031 |
| IPW | 0.400 | 0.395 | 1.250 | |
| 60 | z | 0.104 | 0.104 | 1.818 |
| IPW | 0.600 | 0.595 | 0.833 | |
| 20 | z | 0.110 | 0.108 | 1.818 |
| IPW | 0.800 | 0.797 | 0.375 |
| Detailed Model/p.u. | Traditional Model/p.u. | Integrated Source Model/p.u. | Error 1% | Error 2% | |
|---|---|---|---|---|---|
| Voltage | 0.764 | 0.761 | 0.766 | 0.393 | 0.262 |
| Current | 3.630 | 3.814 | 3.653 | 5.069 | 0.634 |
| Detailed Model/p.u. | Traditional Model/p.u. | Integrated Source Model/p.u. | Error 1% | Error 2% | |
|---|---|---|---|---|---|
| Voltage | 0.295 | 0.262 | 0.293 | 11.186 | 0.678 |
| Current | 2.842 | 3.04 | 2.865 | 6.967 | 0.809 |
| Initial Condition | ||||||
|---|---|---|---|---|---|---|
| Percentage of New Energy/% | Number of Iterations | Iteration Time/s | Number of Iterations | Iteration Time/s | Number of Iterations | Iteration Time/s |
| 20.0 | 76 | 0.198 | 75 | 0.200 | 128 | 0.273 |
| 40.0 | 79 | 0.198 | 75 | 0.200 | 105 | 0.235 |
| 60.0 | 83 | 0.203 | 80 | 0.209 | 88 | 0.213 |
| 80.0 | 88 | 0.212 | 85 | 0.214 | 93 | 0.220 |
| Percentage of New Energy/% | Parameters | Set Value/p.u. | Identification Value/p.u. | Error/% | Number of Iterations | Iteration Time/s |
|---|---|---|---|---|---|---|
| 20.0 | z | 0.092 | 0.091 | 1.087 | 60 | 0.18 |
| Ipw | 0.200 | 0.196 | 2.000 | |||
| 40.0 | z | 0.097 | 0.096 | 1.031 | 86 | 0.201 |
| Ipw | 0.400 | 0.395 | 1.250 | |||
| 60.0 | z | 0.104 | 0.102 | 1.818 | 64 | 0.178 |
| Ipw | 0.600 | 0.595 | 0.833 | |||
| 80.0 | z | 0.110 | 0.108 | 1.818 | 80 | 0.190 |
| Ipw | 0.800 | 0.797 | 0.375 |
| System Parameters | SQP [26] | SA [27] | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Percentage of New Energy/% | Parameters | Set Value/p.u. | Identification Value/p.u. | Error/% | Number of Iterations | Iteration Time/s | Identification Value/p.u | Error/% | Number of Iterations | Iteration Time/s |
| 20.0 | z | 0.092 | 0.091 | 1.087 | 43 | 0.040 | 0.094 | 2.455 | 1078 | 22.212 |
| Ipw | 0.200 | 0.196 | 2.000 | 0.201 | 0.738 | |||||
| 40.0 | z | 0.097 | 0.096 | 1.031 | 36 | 0.047 | 0.093 | 3.483 | 2246 | 33.769 |
| Ipw | 0.400 | 0.394 | 1.500 | 0.473 | 18.36 | |||||
| 60.0 | z | 0.104 | 0.102 | 1.818 | 40 | 0.158 | 0.098 | 5.754 | 1593 | 25.585 |
| Ipw | 0.600 | 0.595 | 0.833 | 0.583 | 2.800 | |||||
| 80.0 | z | 0.110 | 0.106 | 3.636 | 42 | 0.071 | 0.103 | 6.757 | 1022 | 13.808 |
| Ipw | 0.800 | 0.797 | 0.375 | 0.770 | 3.767 | |||||
| Rf | IS (kA) | IDG (kA) | If (kA) | UPCC1 (kV) | UPCC2 (kV) | |
|---|---|---|---|---|---|---|
| 0.5 Ω | Calculated result | 0.3870∠−28.9618° | 0.1732∠−121.7635° | 4.2197∠−62.9923° | 25.7404∠−16.7803° | 2.1474∠−64.8885° |
| Simulation result | 0.3863∠−28.9409° | 0.1736∠−118.4739° | 4.2083∠−62.6828° | 25.7605∠−16.5524° | 2.1448∠−64.4551° | |
| Magnitude error | 0.18% | 0.23% | 0.27% | 0.78% | 0.12% | |
| Phase angle error | −0.02° | −3.29° | −0.31° | −0.23° | −0.43° | |
| 0.7 Ω | Calculated result | 0.3600∠−22.7974° | 0.1732∠−100.7185° | 3.9394∠−55.9138° | 32.0985∠−13.8148° | 2.7795∠−56.9737° |
| Simulation result | 0.3594∠−22.8358° | 0.1736∠−98.3580° | 3.9237∠−55.6943° | 32.0614∠−13.6414° | 2.7706∠−56.6945° | |
| Magnitude error | 0.17% | 0.23% | 0.40% | 0.12% | 0.32% | |
| Phase angle error | 0.04° | −2.36° | −0.22° | −0.17° | −0.28° |
| Rf | IS (kA) | IDG (kA) | If (kA) | UPCC1 (kV) | UPCC2 (kV) | |
|---|---|---|---|---|---|---|
| 0.5 Ω | Calculated result | 0.2210∠−19.4515° | 0.1732∠−92.4823° | 2.5495∠−51.3567° | 43.4365∠9.5583° | 2.1397∠−35.4237° |
| Simulation result | 0.2214∠−19.6275° | 0.1736∠−89.5513° | 2.5383∠−51.1788° | 43.3088∠9.6054° | 2.1328∠−35.2608° | |
| Magnitude error | 0.18% | 0.23% | 0.44% | 0.29% | 0.32% | |
| Phase angle error | 0.18° | −2.93° | −0.1779° | −0.05° | −0.16° | |
| 0.7 Ω | Calculated result | 0.2110∠−16.2110° | 0.1732∠−84.2697° | 2.4049∠−47.8867° | 45.5659∠9.6577° | 2.4914∠−34.9844° |
| Simulation result | 0.2104∠−16.3237° | 0.1736∠−81.5819° | 2.4002∠−47.6408° | 45.5461∠9.7954° | 2.4887∠−34.7417° | |
| Magnitude error | 0.28% | 0.23% | 0.20% | 0.43% | 0.11% | |
| Phase angle error | 0.11° | −2.69° | −0.25° | −0.14° | −0.24° |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lu, J.; Zhao, R.; Fang, Y.; Gao, Y.; Gan, K.; Chen, Y. Fault Equivalence and Calculation Method for Distribution Networks Considering the Influence of Inverters on the Grid Side and the Distribution Network Side. Energies 2025, 18, 2111. https://doi.org/10.3390/en18082111
Lu J, Zhao R, Fang Y, Gao Y, Gan K, Chen Y. Fault Equivalence and Calculation Method for Distribution Networks Considering the Influence of Inverters on the Grid Side and the Distribution Network Side. Energies. 2025; 18(8):2111. https://doi.org/10.3390/en18082111
Chicago/Turabian StyleLu, Jiangang, Ruifeng Zhao, Yueming Fang, Yifan Gao, Kai Gan, and Yizhe Chen. 2025. "Fault Equivalence and Calculation Method for Distribution Networks Considering the Influence of Inverters on the Grid Side and the Distribution Network Side" Energies 18, no. 8: 2111. https://doi.org/10.3390/en18082111
APA StyleLu, J., Zhao, R., Fang, Y., Gao, Y., Gan, K., & Chen, Y. (2025). Fault Equivalence and Calculation Method for Distribution Networks Considering the Influence of Inverters on the Grid Side and the Distribution Network Side. Energies, 18(8), 2111. https://doi.org/10.3390/en18082111




