Abstract
This study presents an advanced method for modeling energy consumption in electric trucks by incorporating regenerative braking probability into conventional modeling equations. Traditional models typically assume uniform regenerative energy recovery, ignoring the variability introduced by differing driving behaviors and braking scenarios. To address this gap, the proposed method explicitly integrates regenerative probability, capturing the dynamic interactions between driving conditions and regenerative braking events. The research involves systematic data preprocessing techniques, including outlier detection and correction, to ensure high data integrity. Moreover, a genetic algorithm is employed to optimize critical features such as aerodynamic drag coefficient, rolling resistance, and regenerative braking efficiency and probability, aiming to minimize discrepancies between predicted and actual energy consumption. The validation results demonstrate that the enhanced model provides a significantly improved accuracy in predicting energy recovery and state-of-charge estimations, supporting more effective and sustainable energy management practices for electric truck operations.
1. Introduction
The rapid expansion of electric vehicle (EV) technology has underscored the necessity for precise energy consumption estimation models that can accurately reflect real-world driving conditions. Traditional models often struggle to account for the multifaceted variables influencing energy usage, such as driving behavior, road conditions, and vehicle dynamics. Recent research has highlighted the importance of integrating advanced parameters into these models to enhance their predictive capabilities. Among these parameters, regenerative braking plays a critical role in energy recovery during vehicle operation, yet its effectiveness can vary significantly based on driving scenarios and environmental factors [1,2].
Studies have demonstrated that accurately modeling regenerative braking can lead to substantial improvements in energy efficiency and range predictions for EVs [3,4]. Furthermore, optimization algorithms such as genetic algorithm (GA) have been shown to fine-tune model parameters, minimizing discrepancies between estimated and actual energy consumption [5]. To further enhance energy consumption models for electric trucks, this study introduces regenerative probability, a critical parameter that quantifies the likelihood of regenerative braking events occurring during a journey. Traditional models often assume a uniform energy recovery rate, overlooking variations in braking behavior. This study introduces regenerative probability, a key factor that quantifies the likelihood of regenerative braking events, improving the accuracy of energy recovery predictions and optimizing route-based SoC estimation.
This study aims to address these challenges by developing a route-based optimization (RBO) approach that incorporates key factors influencing energy consumption, including road grade, speed, and regenerative probability. By leveraging these advanced modeling techniques, this research seeks to improve the accuracy of energy consumption predictions for EVs, contributing to more efficient and sustainable energy management practices in real-world applications.
2. Literature Reviews
2.1. Overview of Energy Consumption Models for Electric Vehicles
The modeling of energy consumption in EVs is a critical area of research that addresses the growing need for efficient and sustainable transportation solutions. As the adoption of EVs increases, understanding the factors that influence their energy consumption becomes paramount for optimizing their performance and extending their operational range. Various models have been developed to estimate their energy consumption.
One significant approach to energy consumption modeling involves the use of artificial intelligence algorithms. In [6], predictive artificial intelligent models that analyze factors affecting EV operation, including energy management strategies, are discussed. This approach highlights the potential of machine learning techniques to enhance the accuracy of energy consumption predictions by leveraging real-world data and optimizing energy management systems. Another perspective is provided by Zhao et al. [7], who focus on the energy consumption characteristics of EVs in relation to traffic conditions and driving behavior. Their study emphasizes the importance of developing energy consumption estimation models that account for specific driving scenarios, thereby facilitating a better understanding of how EVs can contribute to energy savings and emissions reductions. Similarly, Luin et al. [8] utilize vehicle power-based models to estimate energy consumption, demonstrating the applicability of established models from internal combustion engines to EVs. This multifaceted approach is echoed in the work of Hendrix et al. [9], who evaluate energy consumption under standard driving cycles, emphasizing the need for models that can adapt to real-world driving conditions. The influence of environmental factors on energy consumption is also a critical consideration. Graba et al. [10] highlight how traffic and weather conditions significantly affect the energy consumption of battery electric vehicles (BEVs) and plug-in hybrid electric vehicles (PHEVs). Their findings underscore the necessity of incorporating external variables into energy consumption models to achieve more accurate predictions. Similarly, B.V. Sunanda et al. [11] conduct a sensitivity analysis to explore how different environmental factors impact energy consumption, further supporting the notion that EV energy models must be adaptable to varying conditions. In addition to these approaches, several studies have focused on the integration of microscopic driving parameters into energy consumption models.
Overall, the literature reveals a rich tapestry of research aimed at understanding and modeling energy consumption in electric vehicles. As the field continues to evolve, the integration of advanced modeling techniques, real-world data, and AI-driven approaches will be essential for enhancing the accuracy and reliability of energy consumption predictions, contributing to the development of more efficient and sustainable electric vehicle technologies.
2.2. Integration of Regenerative Braking in Energy Models
The integration of regenerative braking into energy models for EVs represents a significant advancement in enhancing energy efficiency and overall vehicle performance. Regenerative braking systems allow EVs to recover kinetic energy during braking, converting it into electrical energy that can be stored in the battery for later use. This process not only improves the vehicle’s energy efficiency, but also extends its driving range, making it a critical component of modern EV design. One of the key studies in this area is by Xu et al. [12], who present two braking regenerative energy optimization controllers specifically designed for in-wheel motor electric vehicles. Their research employs a model predictive control (MPC) method to optimize the distribution of brake torque between hydraulic and in-wheel motors, considering the efficiencies of both systems. This approach demonstrates how the effective management of regenerative braking can significantly enhance energy recovery during deceleration, thereby improving overall energy consumption models. In a similar vein, Wang et al. [13] develop an energy consumption model that incorporates a regenerative braking component alongside other critical factors such as road load and powertrain losses. Their model, validated through real-world driving evaluations, highlights the importance of including regenerative braking in energy consumption predictions, as it directly influences vehicles’ operational efficiency. This comprehensive modeling approach underscores the necessity of integrating regenerative braking into energy models to achieve accurate predictions of energy usage. Kropiwnicki and Furmanek [14] further emphasize the role of regenerative braking in urban traffic conditions, analyzing how traffic dynamics affect energy recovery. Their findings suggest that traffic management systems should account for regenerative braking capabilities to optimize energy recovery processes. This research aligns with the broader goal of enhancing urban mobility through improved energy efficiency in electric vehicles. Moreover, the work of Hamit Solmaz et al. [15] proposed a developed EV dynamic model which created by MATLAB/Simulink. The model is simulated based on NEDC and WLTP speed profile which the authors demonstrate a braking strategies can reduce energy consumption up to 8%. Chang et al. [16] introduce a systematic approach to instantaneous power consumption modeling that includes regenerative braking as a critical component. Their model accounts for factors such as vehicle weight, speed, and road slopes, illustrating how regenerative braking can be effectively integrated into comprehensive energy consumption models. Additionally, William Wood et al. [17] explore the dynamics of electric vehicle models that incorporate regenerative braking, emphasizing the need for the accurate modeling of both longitudinal vehicle dynamics and motor dynamics. Their findings suggest that a well-structured model can significantly enhance the accuracy of energy consumption predictions, particularly when regenerative braking is factored in. Ahmed G. Osman et al. [18] and Nathan Ewin et al. [19] develop an EV energy consumption model considering regenerative braking, demonstrating a high accuracy. Their study highlights precise estimation, though incorporating real-world driving conditions could further improve its applicability. Moreover, refs. [20,21] develop a robust energy consumption model based on a physical framework, effectively incorporating regenerative braking with fixed environmental parameters. While well-suited for net energy modeling, further optimization of the parameters and the consideration of regenerative probability could enhance realism in estimating regenerative contributions.
The integration of regenerative braking into energy models for electric vehicles is essential for optimizing energy efficiency and enhancing overall vehicle performance. Through various modeling approaches and empirical studies, researchers have demonstrated the significant impact of regenerative braking on energy consumption predictions.
2.3. Research Gaps and Objectives
Our objective was to find research gaps. The literature review presented in Table 1 highlights gaps in energy consumption models, particularly in regenerative probability consideration, which most studies neglect. While some models include regenerative power, they lack optimization. Methods vary between data-driven, physical, and hybrid approaches applied to personal cars, electric buses, and electric trucks. The proposed method is unique in integrating both regenerative probability and power using a hybrid approach for electric trucks, addressing key limitations in existing models.

Table 1.
Literature review on challenges in energy consumption model.
Despite the extensive body of literature on energy consumption modeling for EVs, several critical gaps persist, as follows:
- While regenerative braking is widely recognized as a critical factor, most models do not incorporate the probabilistic nature of regenerative braking events, which can significantly impact energy recovery.
- Few studies effectively integrate optimization techniques to adjust a comprehensive set of variables, including aerodynamics, rolling resistance, and novel parameters like regenerative probability.
To address these gaps, this study offers the following key contributions: it develops a comprehensive energy consumption model incorporating regenerative probability, employs GA optimization, and validates the model using real-world driving conditions.
- The development of an alternative model that integrates dynamic factors such as road grade, speed, regenerative braking efficiency, and regenerative probability, enhancing prediction accuracy.
- The establishment of regenerative probability as an innovative parameter, capturing the likelihood of regenerative braking events to improve energy recovery estimations.
- The validation of the proposed model against diverse real-world driving conditions to ensure its reliability, scalability, and practical relevance.
3. Methodology
The methodology outlined in this study aims to develop a robust and accurate energy consumption model for heavy-duty vehicles (HDVs) under various driving conditions. The process is divided into five key stages, each designed to address specific aspects of the modeling and optimization framework. Beginning with the design of a comprehensive framework, the methodology progresses through systematic data acquisition and preprocessing to ensure the quality and relevance of input data. Following this, an energy consumption model is formulated using physics-based principles and empirical relationships, capturing the critical variables influencing energy usage. To optimize the model’s accuracy, a GA is employed, enabling the fine-tuning of essential parameters to minimize errors. Finally, the model is evaluated using validation metrics, ensuring its reliability and practical applicability. This structured approach ensures the development of an effective model capable of addressing the challenges of energy consumption optimization in HDVs.
3.1. Framework Design
The methodology adopted in this study is designed to optimize an energy consumption model for HDVs under varying driving scenarios. The framework consists of the following three key stages: dataset collection and preprocessing, variable optimization and testing, and model validation between location A to B, as shown in Figure 1.
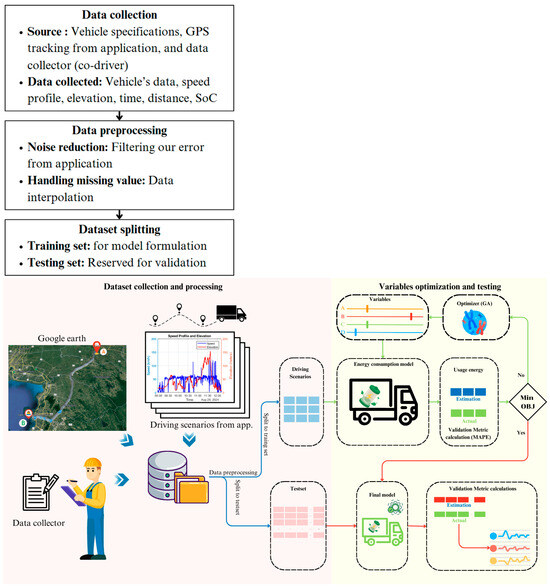
Figure 1.
Model’s parameters estimation frameworks.
3.2. Data Acquisition and Preprocessing
The E-truck used in this study is characterized by its high-capacity battery, powerful motor, and optimized weight distribution. It features a 618.24 V, LiFePO4 battery, a motor rated at 220 kW (360 kW peak) with up to 3400 Nm torque, and a maximum speed of 89 km/h. These specifications provide a foundation for analyzing its energy consumption and performance, as summarized in Table 2.

Table 2.
E-truck’s parameters.
Driving scenario data were collected from real-world sources such as GPX file, capturing essential variables such as speed, elevation, time, and distance. However, these measurements may have had inaccuracies due to uncertain factors, such as sensor measurement errors and random environmental variations. The dataset was preprocessed to eliminate noise and manage missing values. This ensured that the data were ready for training and testing purposes. The preprocessed dataset was then split into training and test subsets, with the training data used for model formulation and the test data reserved for evaluation, as shown in Figure 1. Outlier detection and correction were applied to the speed and elevation datasets to enhance data reliability.
Figure 2a shows the speed preprocessing, where 136 outliers caused by sensor noise or transmission errors were identified and replaced with interpolated values. The cleaned data are shown in blue. Figure 2b illustrates elevation correction, where 57 anomalies were removed using threshold boundaries, ensuring realistic road gradient estimation. This preprocessing improved the data quality, preventing errors from affecting the energy modeling, vehicle dynamics, and predictive simulations.
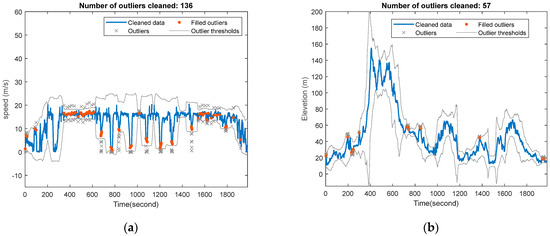
Figure 2.
Data Preprocessing: (a) outlier detection and cleaning for speed data and (b) outlier detection and cleaning for elevation data.
3.3. Model Formulation
The energy consumption model is formulated based on fundamental physics and empirical data relationships. The model incorporates key parameters such as air density, vehicle mass, rolling resistance, and the power consumption of auxiliary systems. The goal is to accurately estimate energy consumption under different driving scenarios while accounting for the influence of dynamic conditions such as acceleration, elevation, and speed.
An equation for the HDV energy consumption model typically considers several key factors, including vehicle parameters, driving conditions, and energy losses. Here, we present a generalized equation to model the energy consumption of a Joule unit consisting of aero resistance (Eaero), rolling resistance (Erolling), gradient (Egrade), accessory system (Eaccessory), and regenerative energy (Eregen) [20], as shown in (1)–(9).
where ρ is air density (kg/m3), Cd is the coefficient of aerodynamic drag, A is the frontal area of the vehicle (m2), Cr is the coefficient of rolling resistance, v is the vehicle speed (m/s), t is the time duration (s), m is the vehicle mass (kg), g is the acceleration due to gravity (9.81 m/s2), θ is the road grade angle (radians), vinitial is the initial velocity (m/s), vfinal is the final velocity (m/s), Pacc is the power consumption of auxiliary systems (W), ηregen is the efficiency of regenerative braking (%), pregen is the regeneration probability, Nregen is the number of regeneration events in a round, and Nbrake is the number of braking events in a round.
Etotal = Eaero + Erolling + Eaccel + Egrade + Eaccessory – Eregen,
Eaero = 0.5 ∙ ρ ∙ Cd ∙ A ∙ v3 ∙ t,
Erolling = Cr ∙ m ∙ g ∙ v ∙ t,
Eaccel = 0.5 ∙ m ∙ (v2final – v2initial),
Egrade = m ∙ g ∙ sin(θ) ∙ v ∙ t,
Eaccessory = Pacc ∙ t,
Eregen = pregen ∙ ηregen ∙ Ebrake,
EBrake = 0.5 ∙ m ∙ (v2initial – v2final),
3.4. Optimization via Genetic Algorithm
To enhance the model’s performance, a GA is employed to optimize critical variables. The GA iteratively searches for the optimal set of parameters that minimize the mean absolute percentage error (MAPE) between the estimated and actual energy consumption, as shown in Table 3.

Table 3.
Psudo code of optimization process.
The optimization process ensures that the model is both accurate and adaptable to various driving scenarios. Parameters such as the coefficient of aerodynamic drag, rolling resistance, and regenerative braking efficiency are fine-tuned during this stage. The objective function is derived directly from the error metric calculated in (10)–(18).
Subject to
Obj.: Minimize(ω1 ∙ MAPE+ ω2 ∙ errormean_p75to100 + ω3 ∙ errormax),
ρmin ≤ ρ ≤ ρmax
Cd,min ≤ Cd ≤ Cd,max
Cr, min ≤ Cr ≤ Cr, max
Pacc, min ≤ Pacc ≤ Pacc, max
ηregen, min ≤ ηregen ≤ ηregen, max
pregen, min ≤ pregen ≤ pregen, max
SoC min ≤ SoC ≤ SoC max
Pregen < Plimit
3.5. Model Evaluation
The final model, optimized using the GA, is evaluated using the test dataset, with validation metrics such as MAPE computed to assess accuracy and reliability. Additional metrics, including root mean squared error (RMSE), which emphasizes larger errors, and mean absolute error (MAE), which provides a straightforward measure of the average absolute differences, are used to provide a more comprehensive evaluation of the model’s performance. The Max Error highlights the largest deviation between the actual and predicted values, serving as an indicator of extreme cases, while the coefficient of determination (R2) quantifies how clearly the model explains the variability in the actual data, with values closer to 1 indicating a better fit. The comparison between the estimated and actual energy consumption offers valuable insights into the model’s applicability in real-world scenarios, confirming its robustness and identifying areas for potential refinement. This evaluation framework ensures a reliable and systematic approach to assessing the performance and practical utility of the proposed model.
where and are the actual value and estimation, respectively. is the number of samples. I is the time step. is the mean of the actual value.
4. Results and Discussion
In this section, the outcomes of the optimization, the accuracy of the resulting predictions, and the subsequent output analysis are presented, providing a comprehensive examination of the methodology’s performance.
4.1. Optimization Outcomes
In Figure 3a,b, both plots how the GA refines key parameters for the EV energy consumption model over successive generations, using different route scenarios. In each panel, the horizontal axis is the generation count, while the left vertical axis tracks the best fitness found so far and the right vertical axis shows maximum error and average. In both (a) and (b), the best fitness steadily decreases, indicating an improved model accuracy, and the error metrics drop sharply and then level out at low values, reflecting more reliable predictions of battery state of charge. The main distinction is that Figure 3b begins at a higher fitness value but converges similarly within about 10–15 generations, demonstrating that, despite different initial conditions (outbound vs. return), the route-based GA optimization yields significant reductions in estimation errors for both test cases.
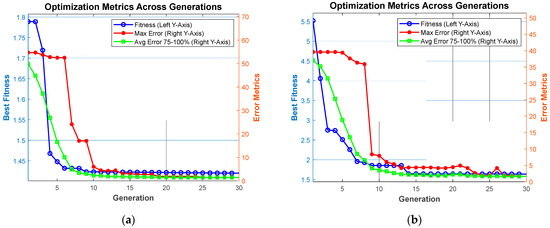
Figure 3.
Convergence curve of hyperparameter optimization, (a) outbound trip and (b) return trip.
4.2. Prediction Accuracy
To evaluate the proposed predictive model’s accuracy, battery state of charge estimates are compared with real-world data and discrepancies are quantified using MAPE and other validation metrices. These results confirm the model’s reliability for accurate EV range prediction and energy consumption analysis.
In Figure 4, these plots compare the simulation-predicted state of charge profiles (blue lines) against actual logged SoC data as a function of distance travel, clearly illustrating the model’s accuracy in capturing real-world battery depletion. The mean absolute percentage error is below 2% in both tests, 0.90% for the round trip and 1.89% for the second trip, demonstrating very close agreement overall. In both cases, the final predicted SoC values (52.67% vs. 54.16%, 23.34% vs. 23.75%) differ from the measured SoC by only about 1–2%. These small deviations arise from transient factors not modeled in perfect detail. Nonetheless, the general alignment between the simulated and actual SoC curves confirms that the proposed battery and vehicle model is robust enough for accurate range prediction and energy consumption analysis in electric vehicle applications.
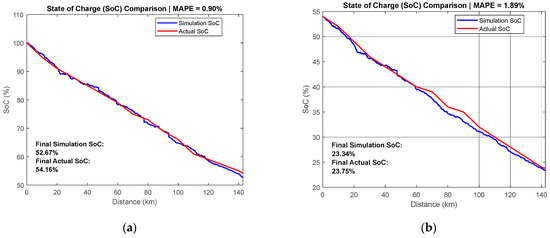
Figure 4.
Prediction results, (a) outbound trip and (b) return trip from proposed method.
Table 4 compares the average validation metrics for SoC estimation across different methodologies and trip conditions, considering RBO, pregen, and time classification. For time-based classification, off-peak trips achieve a lower MAPE and RMSE (1.308% and 1.149% for outbound, 1.291% and 0.509% for return), while peak trips show slightly higher errors, indicating the influence of traffic and energy recovery conditions. The method-based comparison highlights the effectiveness of the proposed approach, which integrates RBO and pregen, achieving an MAPE of 1.32%. In contrast, the traditional equation with RBO results in a lower MAPE of 0.96%, but its net regenerative energy is significantly higher (67.15 kWh), suggesting an overestimation of energy recovery. The traditional equation without RBO performs poorly (MAPE: 3.09%, RMSE: 2.39%), showing inaccurate SoC estimation. Net regenerative energy emphasizes the impact of optimization. The proposed method provides a more realistic estimation in terms of SoC accuracy and energy recovery, balancing efficiency while preventing overestimation (16.90 kW). Figure 5 visualizes these results, with (a) showing the cumulative energy consumption from the traditional equation and (b) depicting the regenerative braking power from the proposed equation. The traditional method exhibits continuous energy demand with minimal recovery distinction, while the proposed method presents a more structured and realistic regenerative braking profile. This improved energy recovery trend aligns with Table 3, confirming that RBO enhances SoC estimation and supports a more balanced EV energy model. Furthermore, uncertainties such as extreme weather conditions, including rainstorms and high temperatures, are expected to cause changes in energy consumption. Additional power may be required for climate control, although accessory loads represent only a small fraction of the cumulative energy shown in Figure 5. Similarly, as vehicle components age, a decline in battery performance and reductions in regenerative braking efficiency are anticipated. As a result, the trends observed in both cumulative energy consumption and regenerative braking power in Figure 5 are predicted to be altered.

Table 4.
Comparison of average validation metrics for tested case with SoC estimation.
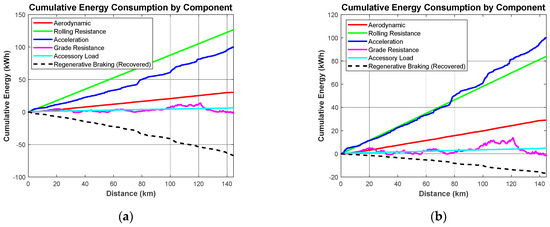
Figure 5.
Power visualization from model estimation, (a) cumulative energy consumption by traditional equation and (b) regenerative braking power profile by proposed equation.
The collected data confirm the validity of the regenerative probability and energy regeneration trends, supporting the proposed estimation approach. The distribution of regenerative probability shows that most values range between 0.05 and 0.2, indicating a realistic likelihood of regenerative braking events. Similarly, the total regenerative power is primarily concentrated between 5 and 25 kWh, demonstrating a reasonable variation in energy recovery. These findings align with Table 3 and Figure 6, reinforcing that the proposed method provides a balanced and accurate estimation of regenerative braking effects, preventing overestimation while improving SoC prediction and energy recovery analysis. The results validate the feasibility of incorporating regenerative probability into energy consumption models for more realistic EV performance assessments.
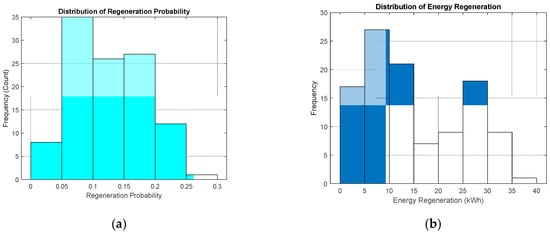
Figure 6.
Distribution of collected 109 data, (a) regeneration probability and (b) total regenerative power.
The analysis confirms the relationship between regenerative energy recovery, probability, and driving conditions, providing insights into the efficiency of energy recuperation in electric vehicles. Figure 7a illustrates regenerative energy and probability by segment, showing fluctuations in the total regenerative energy along different distance segments. The regenerative probability, represented by the red line, remains relatively stable across segments, indicating consistent braking events. Higher peaks in regenerative energy suggest sections of the route with more braking or downhill conditions, reinforcing the impact of terrain on energy recovery. Figure 7b presents the current and elevation variations along the route, highlighting the interaction between road gradient and energy demand. The elevation profile shows significant variations, particularly from 0 to 50 km and from 100 to 140 km, where steep inclines and declines occur. The positive current and negative current indicate periods of energy consumption and regenerative braking, respectively. High negative current values align with downhill segments, confirming effective regenerative braking utilization. These findings validate the importance of integrating elevation and regenerative probability into energy consumption models. The results emphasize that a route-based optimization approach improves SoC estimation accuracy, ensuring a more realistic representation of regenerative energy recovery in electric trucks.
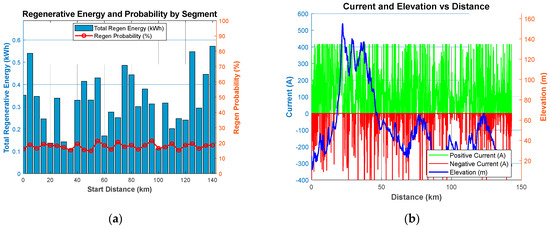
Figure 7.
Result analysis: (a) regenerative energy and probability by segmentation and (b) current and elevation.
4.3. Sensitivity Analysis
After establishing the framework for the electric truck’s energy consumption and regeneration estimator, a sensitivity analysis is conducted to identify the factors that most influence its accuracy. This study focuses on various GRWs, as shown in Table 5.

Table 5.
Sensitivity analysis of energy model parameters under varying GRWs.
Table 5 presents a sensitivity analysis of the energy model parameters under different GRW conditions for an HDV, comparing results with and without the inclusion of pregen. The analysis indicates that considering pregen improves the model’s representation of regenerative braking. Notably, ηregen remains consistently high and stable across various GRW values, indicating its robustness. This consistency enhances the reliability of the model’s energy recovery predictions and contributes to maintaining a low MAPE. Overall, the findings suggest that incorporating regenerative dynamics and adjusting parameters based on GRW can improve the accuracy and stability of energy consumption models.
5. Conclusions
This study introduced a route-based optimization method to improve the accuracy of energy consumption estimates for electric trucks. By incorporating road grade, speed, regenerative braking, and the probability of energy recovery, the proposed model provided a precise and realistic assessment of power usage. The use of optimization techniques significantly reduced errors in estimating battery charge levels, bringing predictions closer to actual energy consumption. The results highlight the importance of regenerative probability in refining energy recovery modeling, ensuring a balanced and reliable estimation. This approach enhances accuracy while preventing overestimations. Validation with real-world driving data confirms its effectiveness and that can be used for fleet management, energy efficiency planning, and route optimization in electric truck operations.
In future work, data from various electric truck types will be incorporated and datasets from different regions and seasons will be collected to evaluate the model under diverse operational conditions. The expanded experimental framework is intended to enhance the generalizability, reliability, and persuasiveness of our findings. Additionally, applications to other vehicle types will be explored, real-time control adjustments will be integrated, and external influences such as traffic flow will be considered. Advances in predictive modeling and data analysis are expected to further refine energy efficiency strategies and improve the operational effectiveness of electric vehicles.
Author Contributions
Conceptualization, N.J., G.S., and K.C.; methodology, N.J.; software, N.J.; validation, N.J., G.S., and K.C.; formal analysis, N.J.; investigation, N.J., S.P., and G.S.; resources, N.J. and S.P.; data curation, N.J. and S.P.; writing—original draft preparation, N.J., G.S., and K.C.; writing—review and editing, N.J., G.S., and K.C.; visualization, N.J. and G.S.; supervision, K.C.; project administration, N.J.; funding acquisition, K.C. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Suranaree University of Technology development fund.
Data Availability Statement
Data will be available on request.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Janpoom, K.; Suttakul, P.; Achariyaviriya, W.; Fongsamootr, T.; Katongtung, T.; Tippayawong, N. Investigating the influential factors in real-world energy consumption of battery electric vehicles. Energy Rep. 2023, 9, 316–320. [Google Scholar] [CrossRef]
- Chen, Y.; Zhang, Y.; Sun, R. Data-driven estimation of energy consumption for electric bus under real-world driving conditions. Transp. Res. Part D: Transp. Environ. 2021, 98, 102969. [Google Scholar] [CrossRef]
- Huda, N.; Kaleg, S.; Hapid, A.; Kurnia, M.R.; Budiman, A.C. The Influence of the Regenerative Braking on the Overall Energy Consumption of a Converted Electric Vehicle. SN Appl. Sci. 2020, 2, 606. [Google Scholar] [CrossRef]
- Vigneshwar, A.S.; Kavitha, N.; Sureshbabu, J.; Chellam, S.; Chandrasekar, P.; Kalaiarasi, K. The Future Charged: Optimizing Electric Vehicle Performance through Advanced Power Management Strategies. In Proceedings of the 2024 7th International Conference on Circuit Power and Computing Technologies (ICCPCT), Kollam, India, 8–9 August 2024; pp. 775–780. [Google Scholar]
- Hasan, M.S.; Tarequzzaman, M.; Moznuzzaman, M.; Ahad Juel, M.A. Prediction of Energy Consumption in Four Sectors Using Support Vector Regression Optimized with Genetic Algorithm. Heliyon 2025, 11, e41765. [Google Scholar] [CrossRef] [PubMed]
- Mądziel, M.; Campisi, T. Predictive Artificial Intelligence Models for Energy Efficiency in Hybrid and Electric Vehicles: Analysis for Enna, Sicily. Energies 2024, 17, 4913. [Google Scholar] [CrossRef]
- Zhao, H.; He, R.; Yin, N. Modeling of Vehicle CO2 Emissions and Signal Timing Analysis at a Signalized Intersection Considering Fuel Vehicles and Electric Vehicles. Eur. Transp. Res. Rev. 2021, 13, 5. [Google Scholar] [CrossRef]
- Luin, B.; Al-Mansour, F.; Šemrov, D. Estimate of Traffic Energy Consumption From Vehicle Fleet Distribution Forecast. E3s Web Conf. 2019, 116, 00046. [Google Scholar] [CrossRef]
- Hendrix, E.M.T.; Rocha, A.M.A.C.; García, I. On Trajectory Optimization of an Electric Vehicle. In Proceedings of the Computational Science and Its Applications–ICCSA 2019: 19th International Conference, Saint Petersburg, Russia, 1–4 July 2019; pp. 249–260. [Google Scholar]
- Graba, M.; Mamala, J.; Bieniek, A.; Augustynowicz, A.; Czernek, K.; Krupińska, A.; Włodarczak, S.; Ochowiak, M. Assessment of Energy Demand for PHEVs in Year-Round Operating Conditions. Energies 2023, 16, 5571. [Google Scholar] [CrossRef]
- Sunanda, B.V.; Parchure, R. An Economic Assessment of Electric Two-wheeler and Impact of Policy Instruments in Indian Sub-nationals. J. Dev. Policy Pract. 2024, 10, 24551333241294145. [Google Scholar] [CrossRef]
- Xu, W.; Chen, H.; Wang, J.; Zhao, H. Velocity Optimization for Braking Energy Management of in-Wheel Motor Electric Vehicles. IEEE Access 2019, 7, 66410–66422. [Google Scholar] [CrossRef]
- Wang, J.J.; Besselink, I.I.; Nijmeijer, H. Electric Vehicle Energy Consumption Modelling and Prediction Based on Road Information. World Electr. Veh. J. 2015, 7, 447–458. [Google Scholar] [CrossRef]
- Kropiwnicki, J.; Furmanek, M. Analysis of the Regenerative Braking Process for the Urban Traffic Conditions. Combust. Engines 2019, 178, 203–207. [Google Scholar] [CrossRef]
- Kıyaklı, A.O.; Solmaz, H. Modeling of an Electric Vehicle With MATLAB/Simulink. Int. J. Automot. Sci. Technol. 2018, 2, 9–15. [Google Scholar] [CrossRef]
- Chang, N.; Baek, D.; Hong, J. Power Consumption Characterization, Modeling and Estimation of Electric Vehicles. In Proceedings of the 2014 IEEE/ACM International Conference on Computer-Aided Design (ICCAD), San Jose, CA, USA, 2–6 November 2014. [Google Scholar]
- Wood, W.; Zamora, D.; Sabzehgar, R.; Rasouli, M. Simulation-Based Comparative Analysis of Extractable Energy from Various Commercial Electric Vehicles During Regenerative Braking. In Proceedings of the 2024 IEEE 21st International Power Electronics and Motion Control Conference (PEMC), Pilsen, Czech Republic, 30 September–3 October 2024; pp. 1–6. [Google Scholar]
- Osman, A.; Tawfik, M.; Ali, A.M.; Asfoor, M.S. Evaluation of Electric Vehicle Performance Based on High-Fidelity Modeling and Experimental Testing. In Proceedings of the 2024 6th Novel Intelligent and Leading Emerging Sciences Conference (NILES), Giza, Egypt, 19–21 October 2024; pp. 50–55. [Google Scholar]
- Miri, I.; Fotouhi, A.; Ewin, N. Electric Vehicle Energy Consumption Modelling and Estimation—A Case Study. Int. J. Energy Res. 2020, 45, 501–520. [Google Scholar] [CrossRef]
- Sakulphaisan, G.; Son-In, S.; Junhuathon, N.; Muankhaw, T. Speed Profile Optimization for Autonomous Electric Bus in Urban Area: Based on Service Route Parameter in Thailand. In Proceedings of the 2023 International Conference on Power, Energy and Innovations (ICPEI), Phrachuap Khirikhan, Thailand, 18–20 October 2023; pp. 149–154. [Google Scholar]
- Junhuathon, N.; Chayakulkheeree, K. Comparative Analysis of Electrification Technologies in Heavy-Duty Vehicles: A Case Study of Thailand. In Proceedings of the 2024 IEEE/IAS Industrial and Commercial Power System Asia (I&CPS Asia), Pattaya, Thailand, 9–12 July 2024; pp. 719–724. [Google Scholar]
- Zubair, M.; Chen, S.; Ma, Y.; Ong, G.P.; Pang, Q. Explore Driving Factors to Energy Consumption of Electric Vehicles Based on Structural Equation Modeling. Int. J. Green Energy 2024, 21, 1–11. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).