Influence of Potential Well Depth on the Dual−Coupling Beam Energy Harvester: Modeling and Experimental Validation
Abstract
1. Introduction
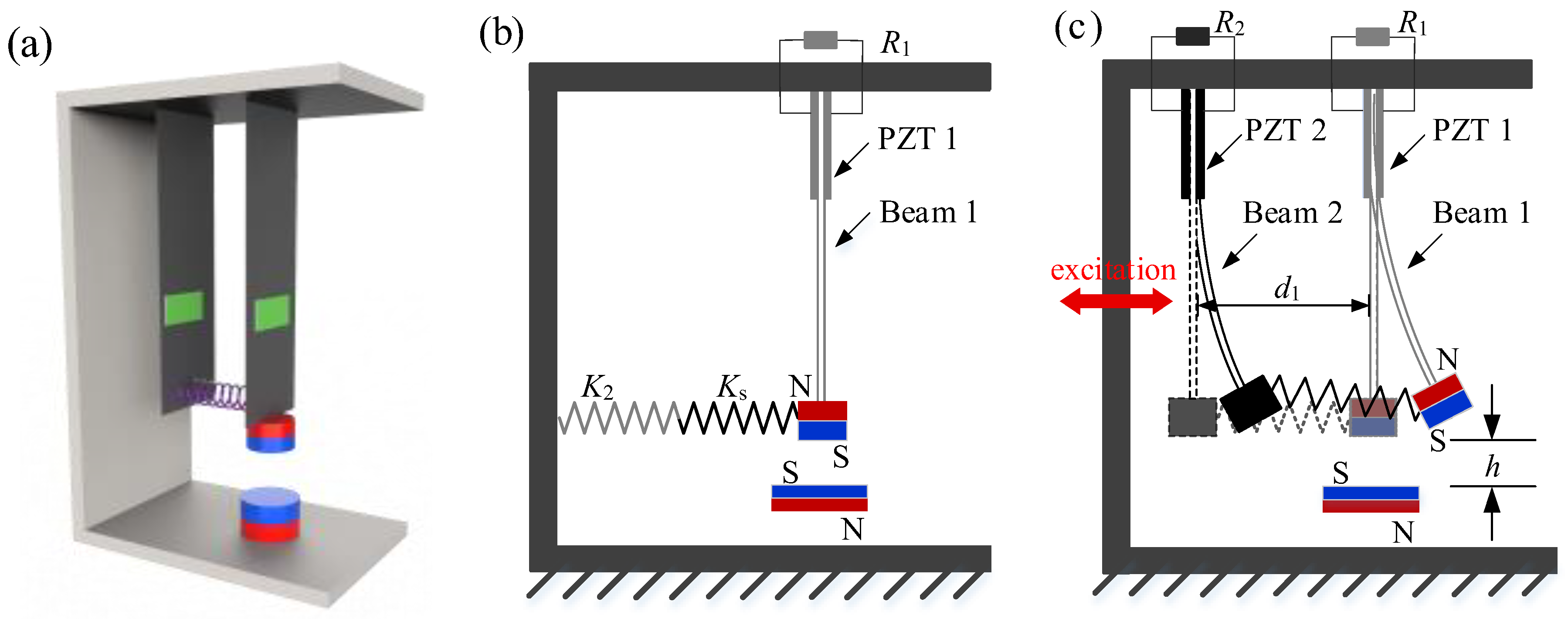
2. Structure and Mathematical Model of DEH
3. Experiment Setup and Parameter Identification
3.1. Experiment Setup
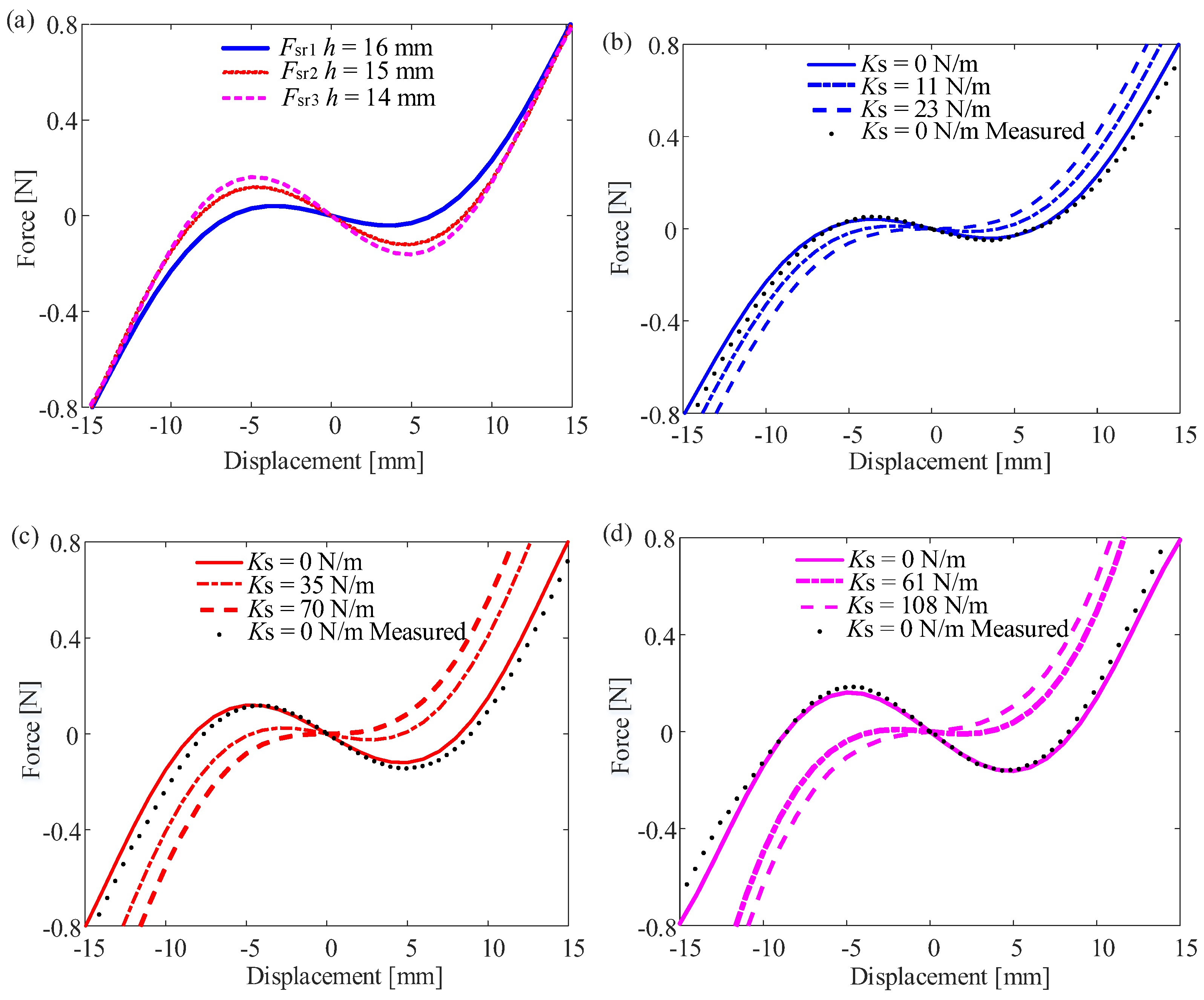
3.2. Nonlinear Restoring Forces and Potential Energy for Beam 1
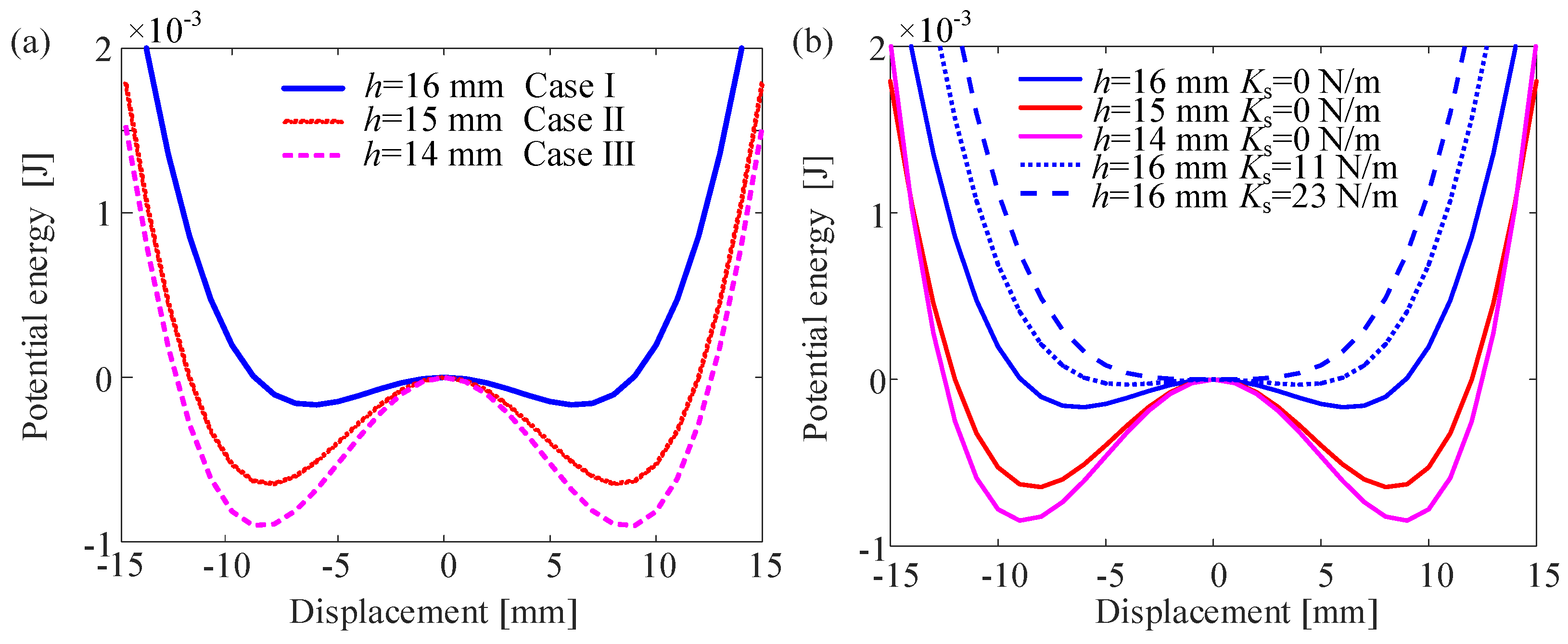
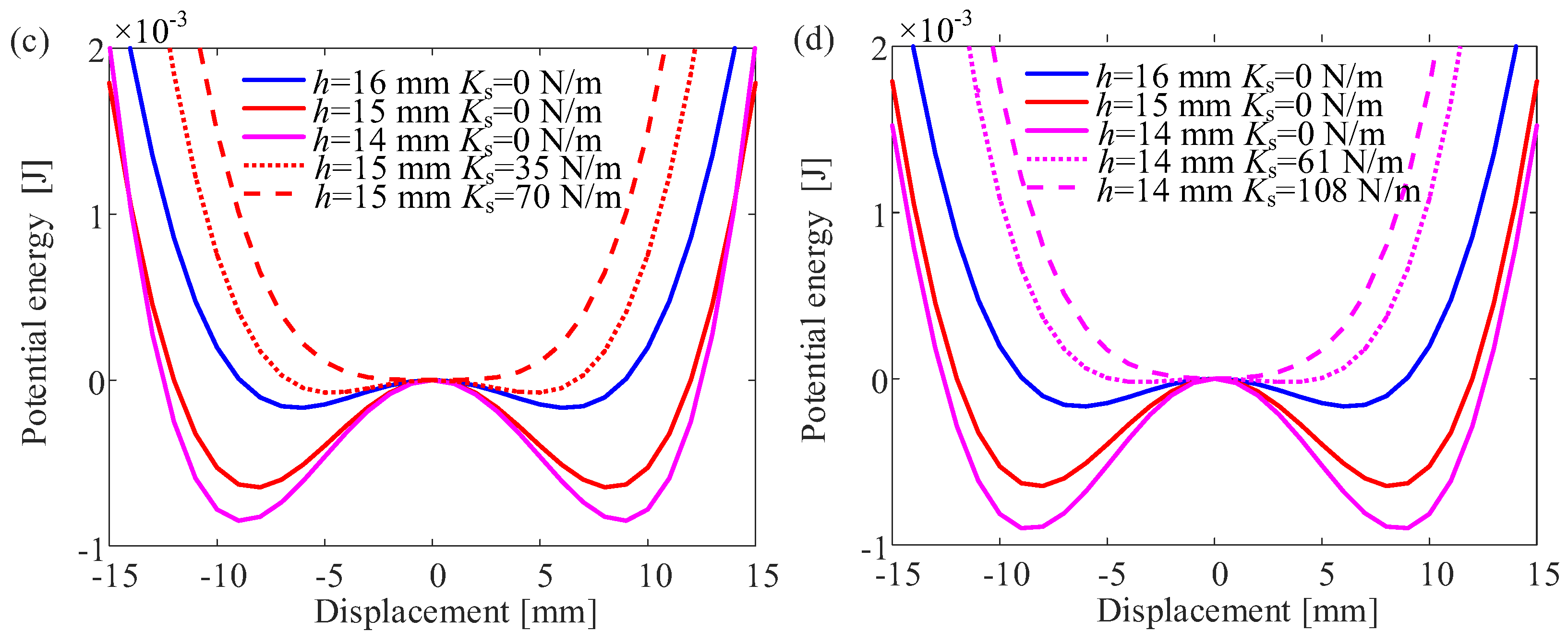
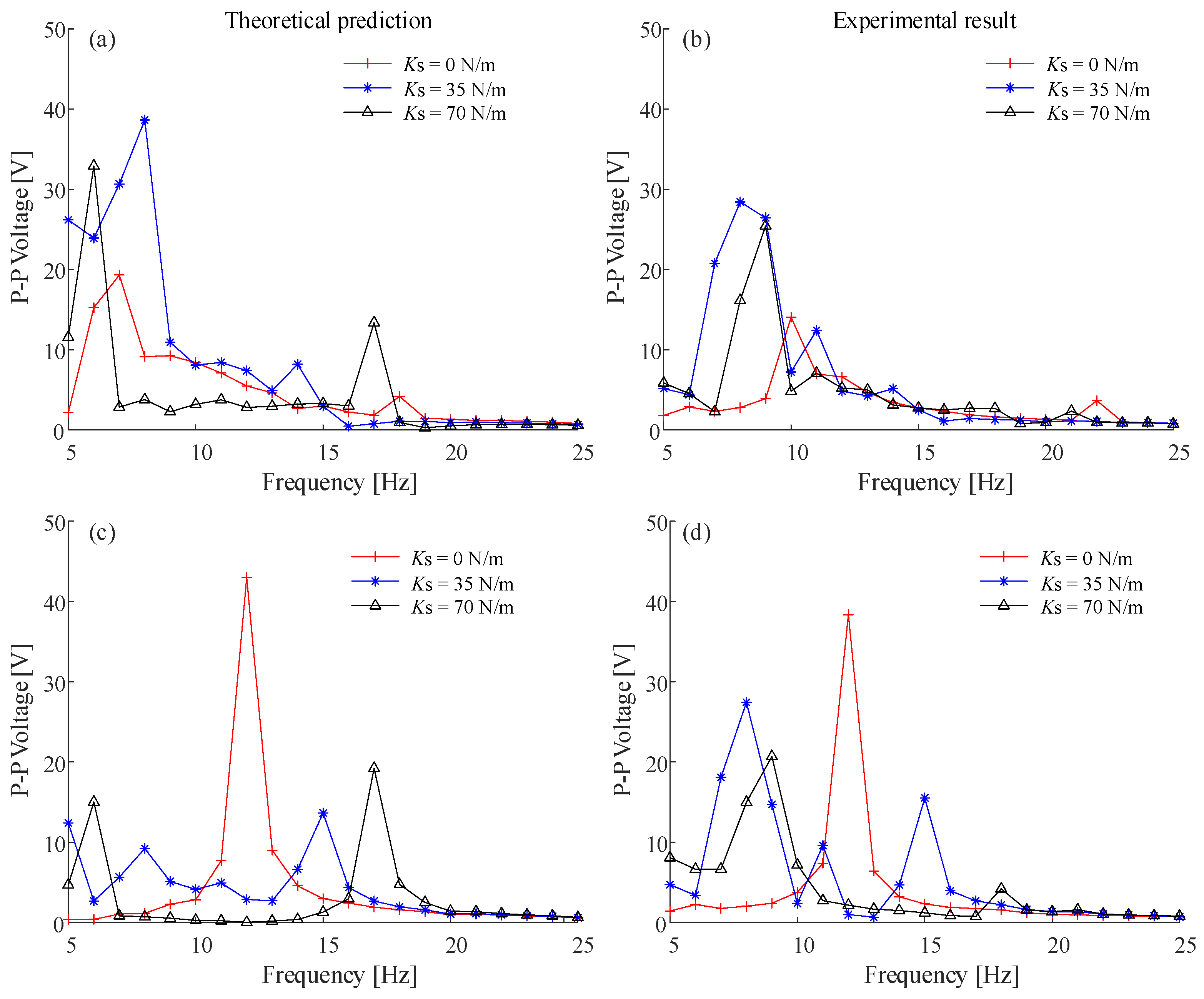
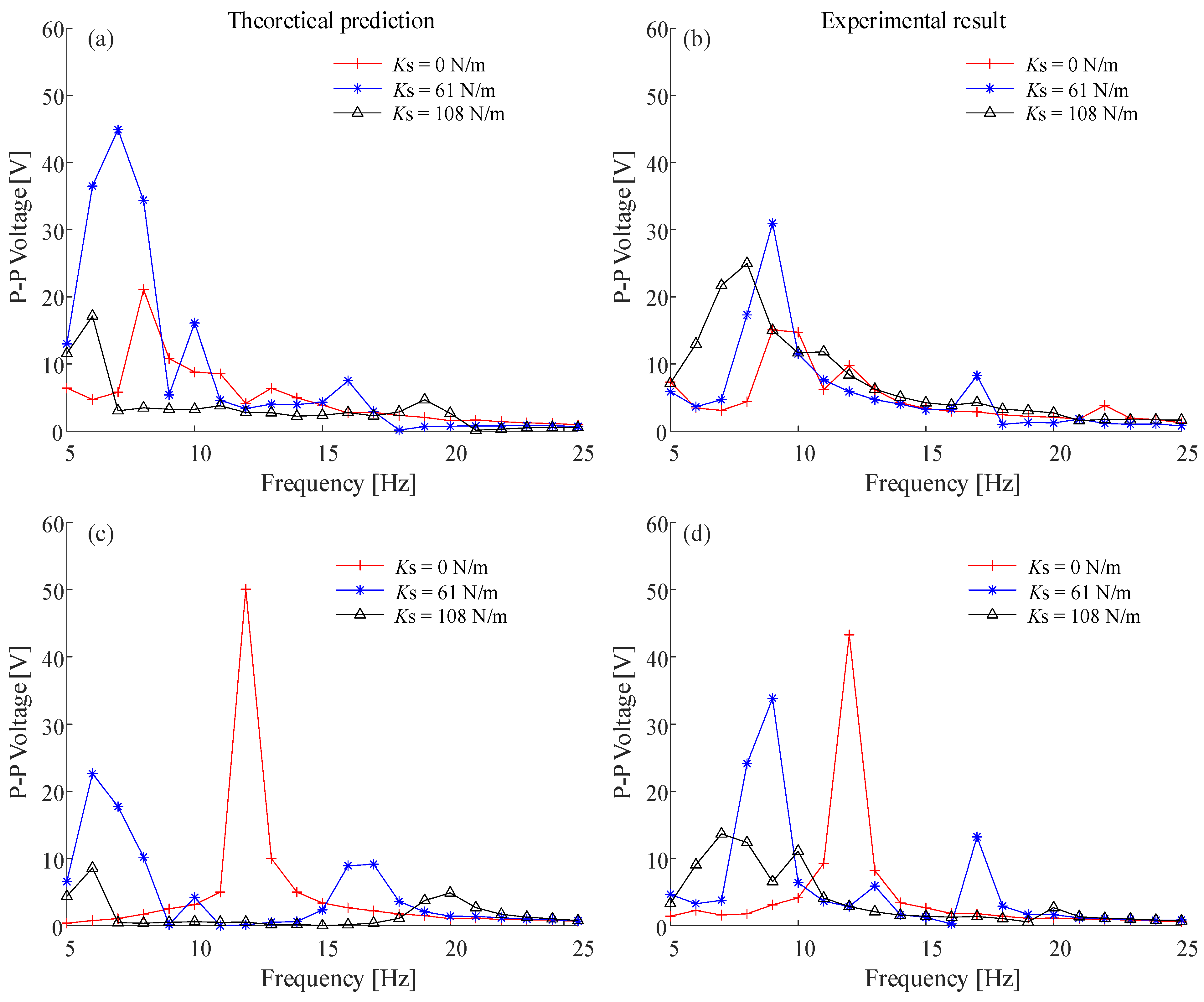
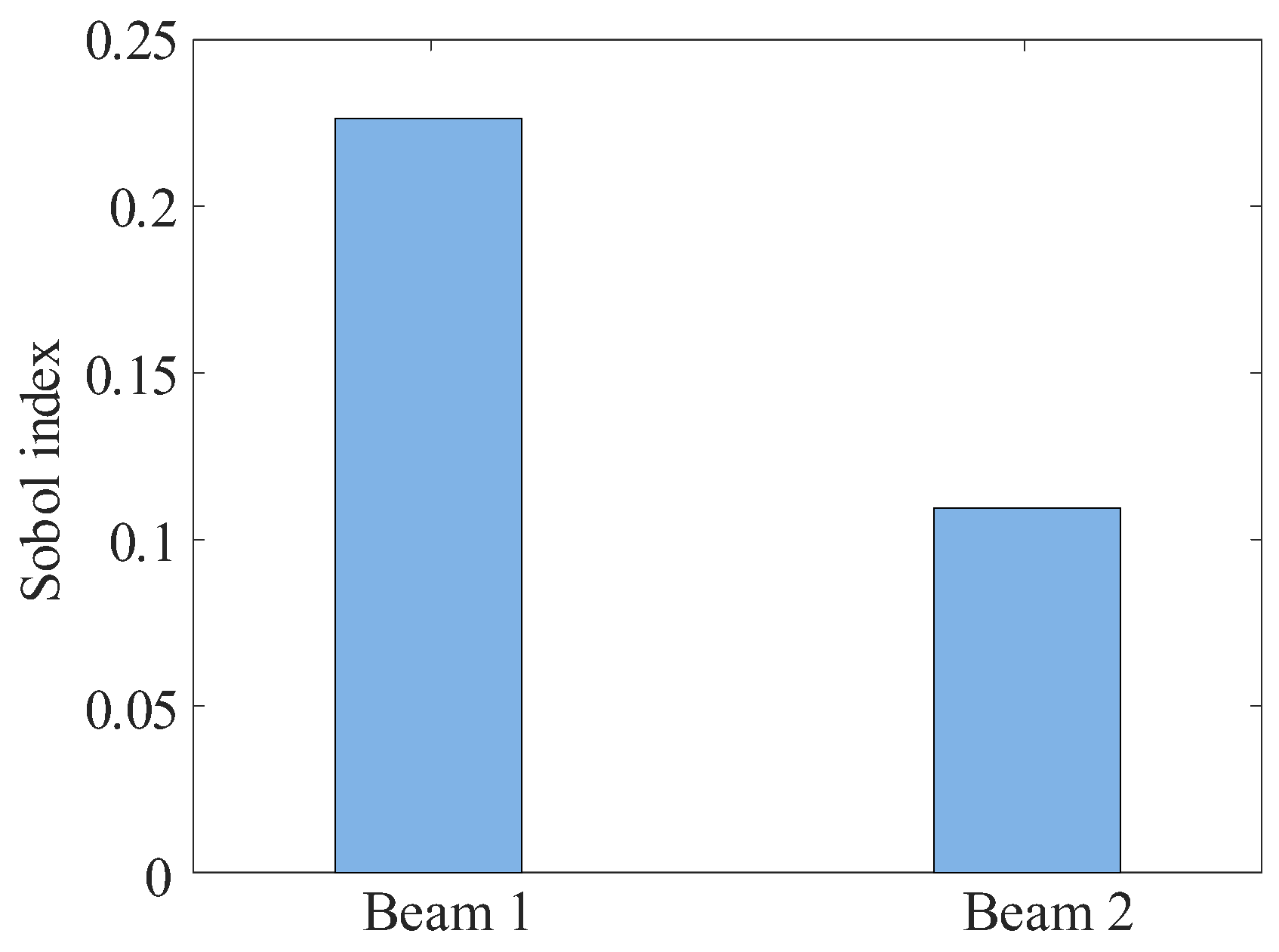
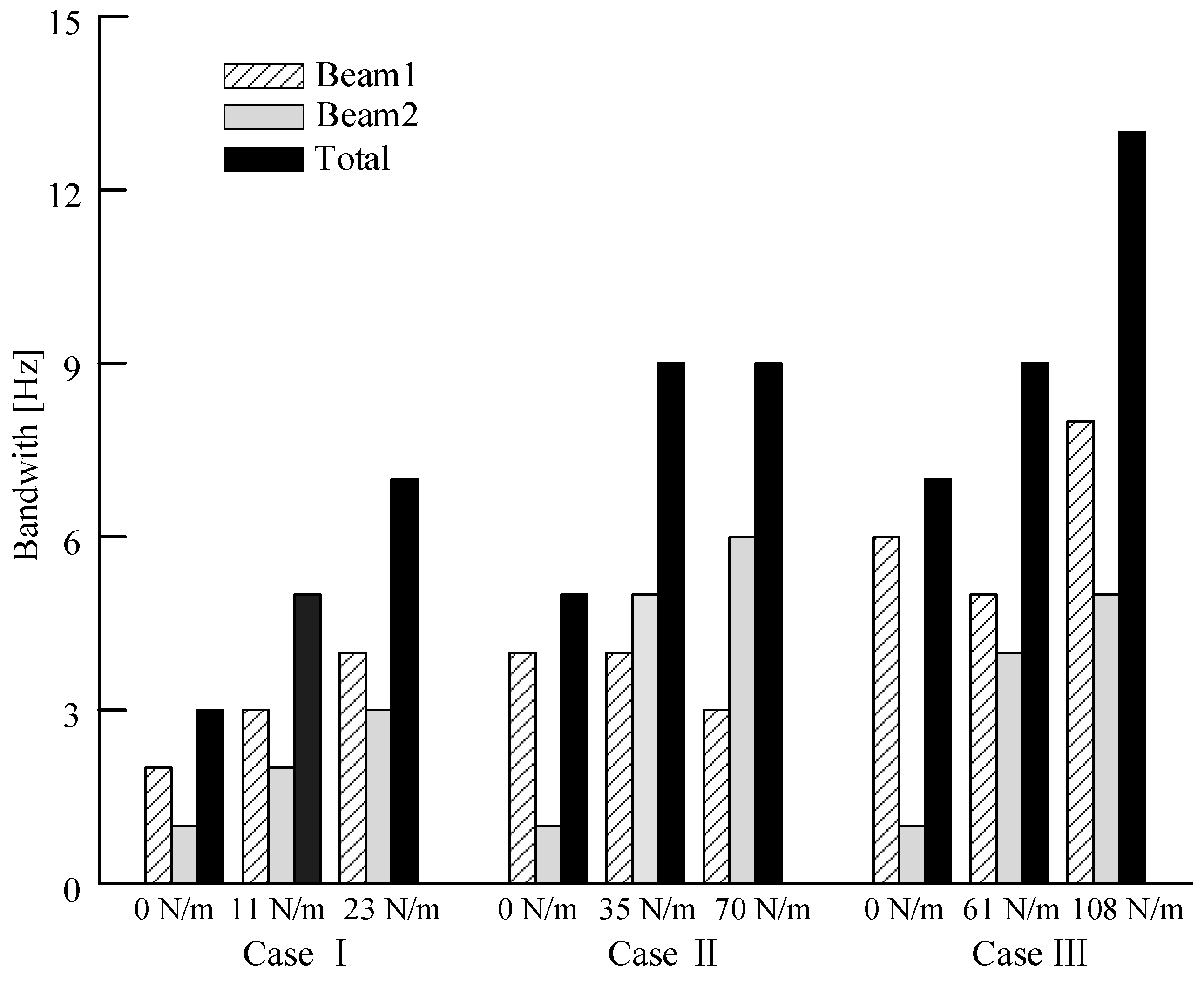
4. Influence of Varying Potential Well Depths on the DEH
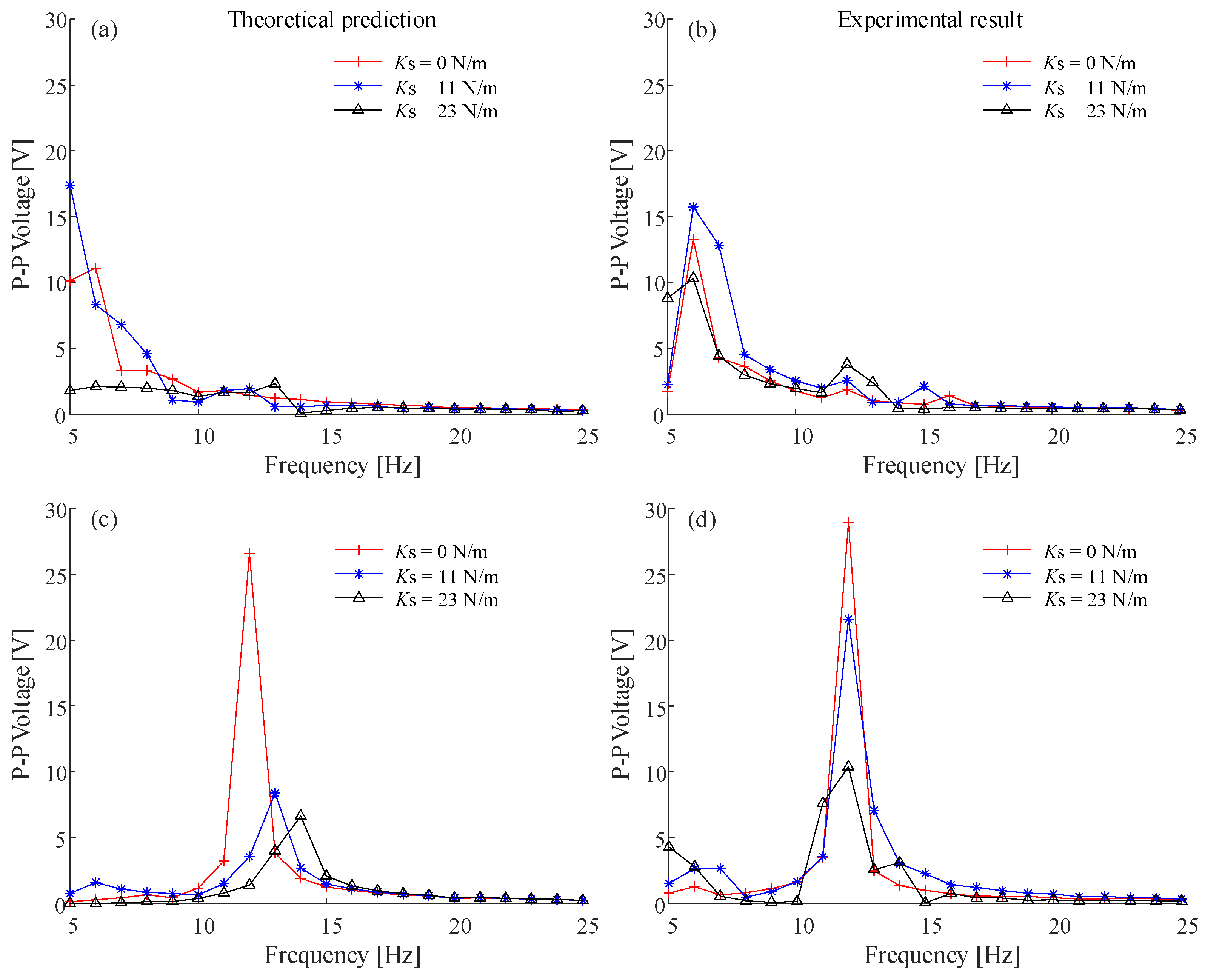
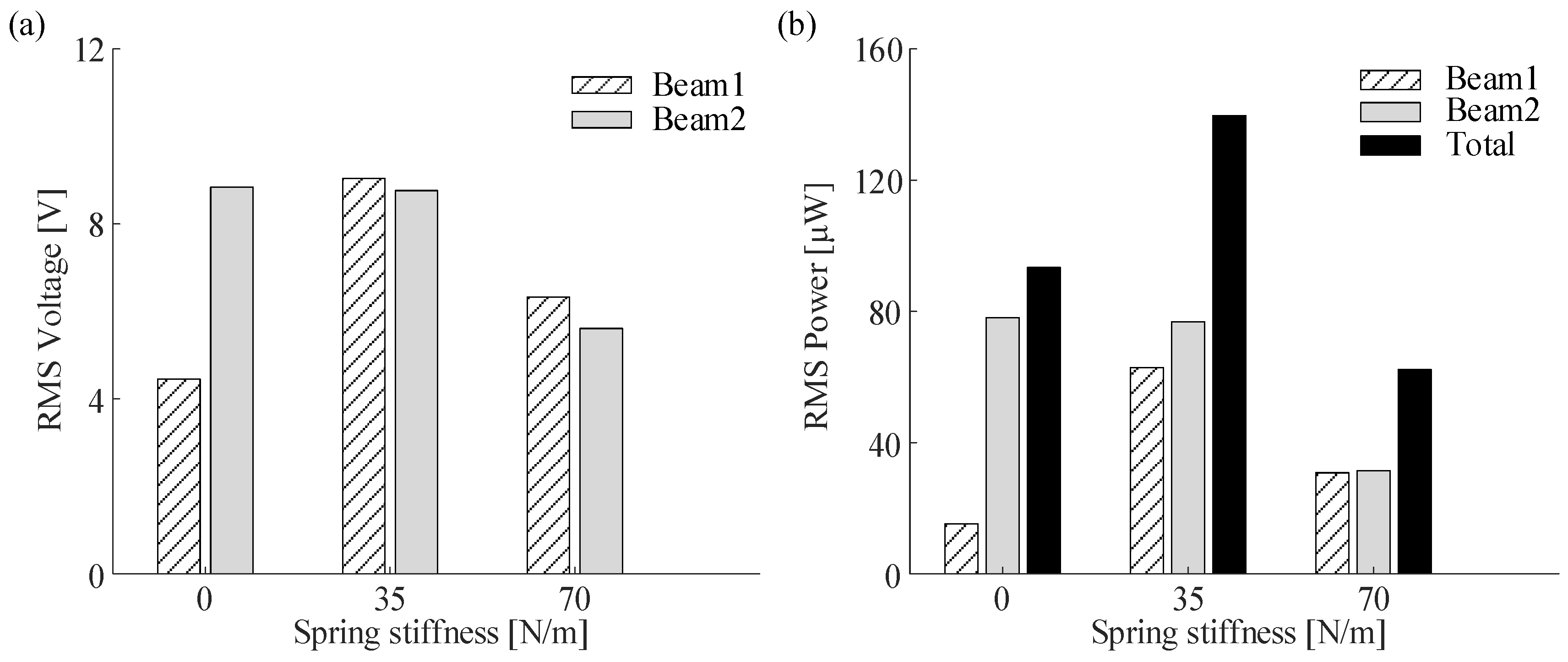
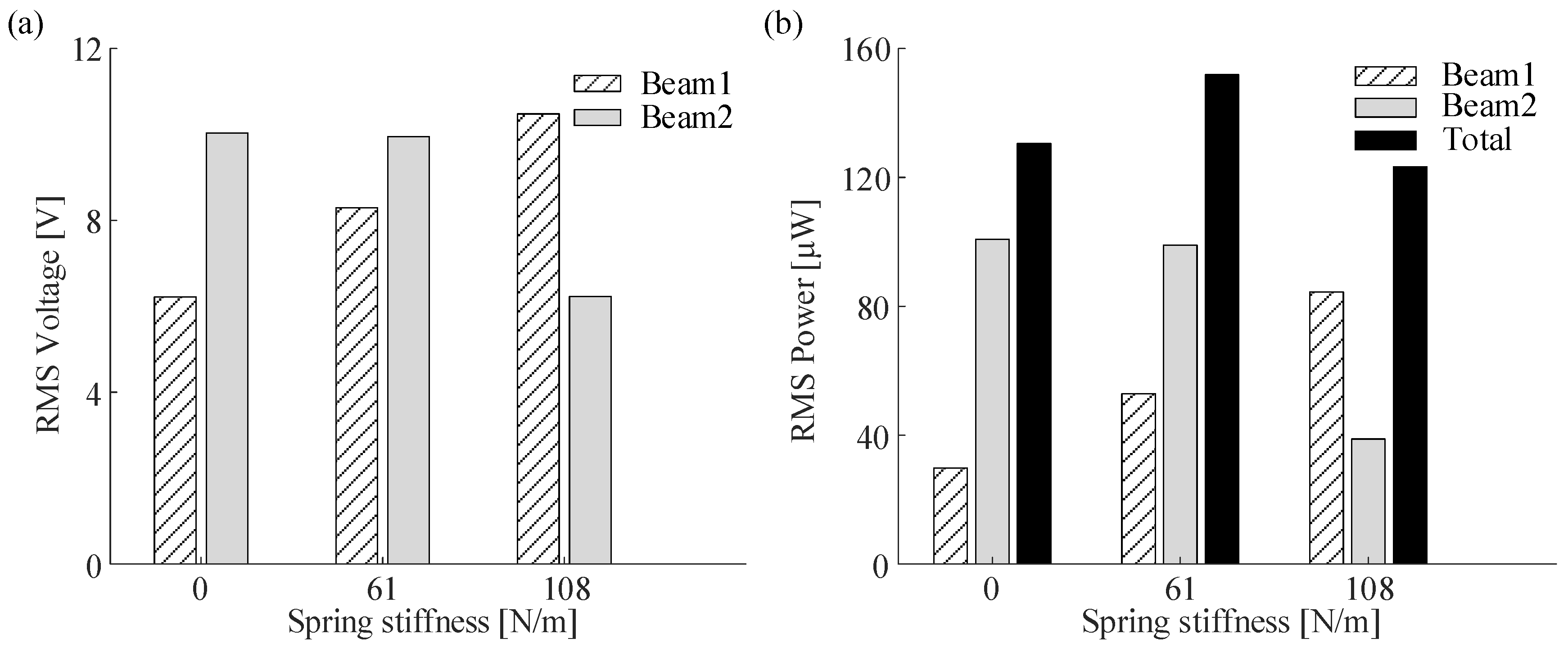
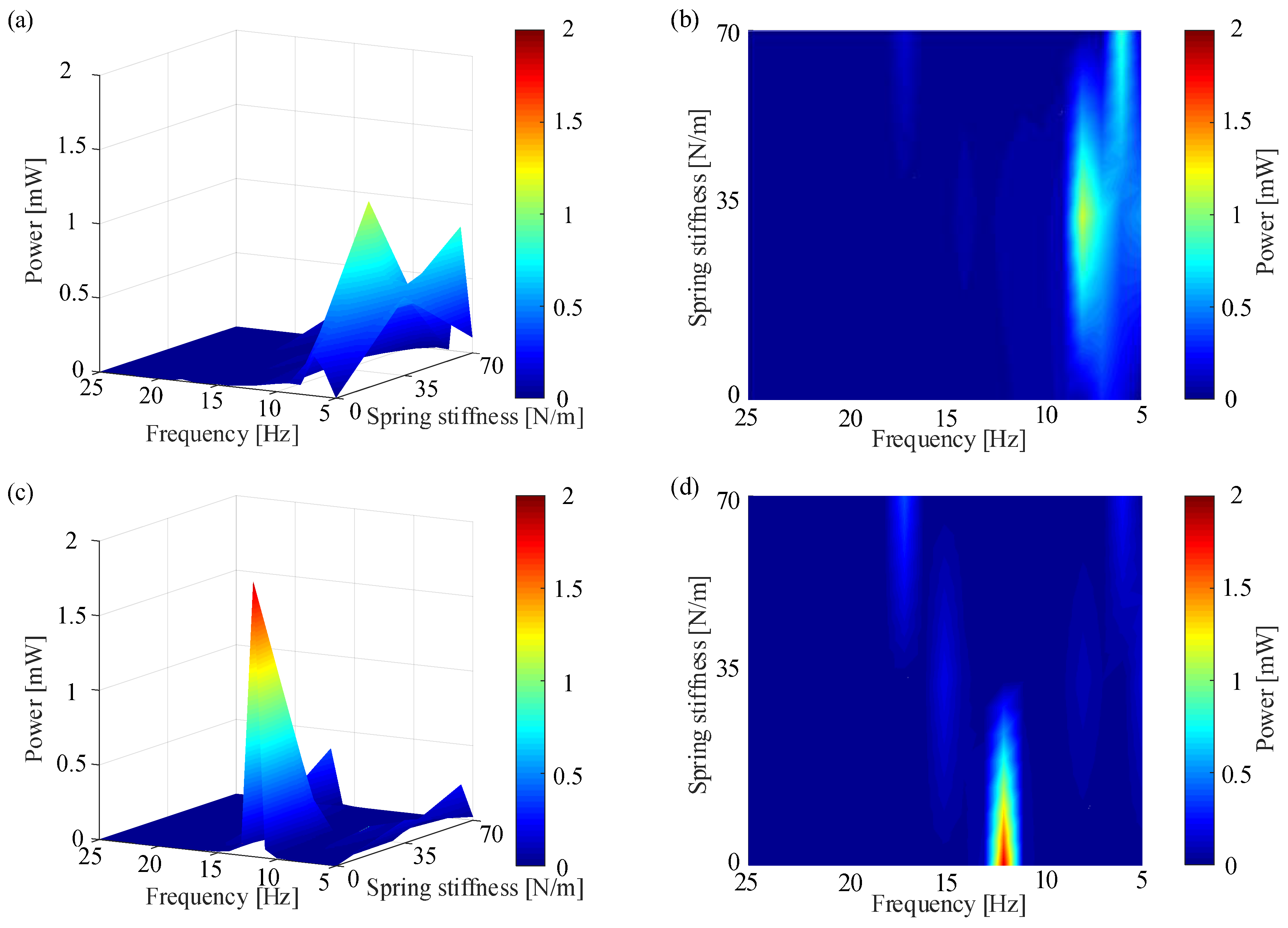
4.1. Numerical Simulation Under Constant Frequency Excitation
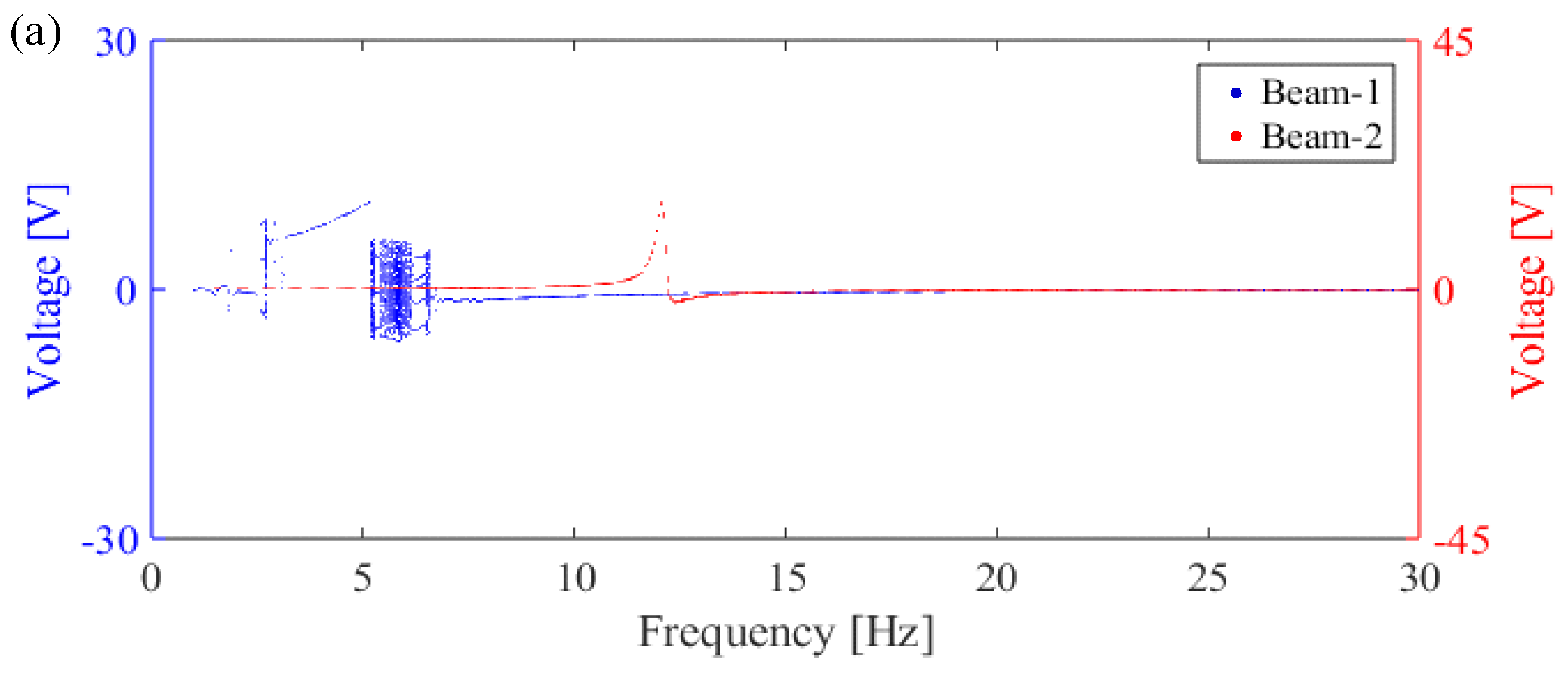
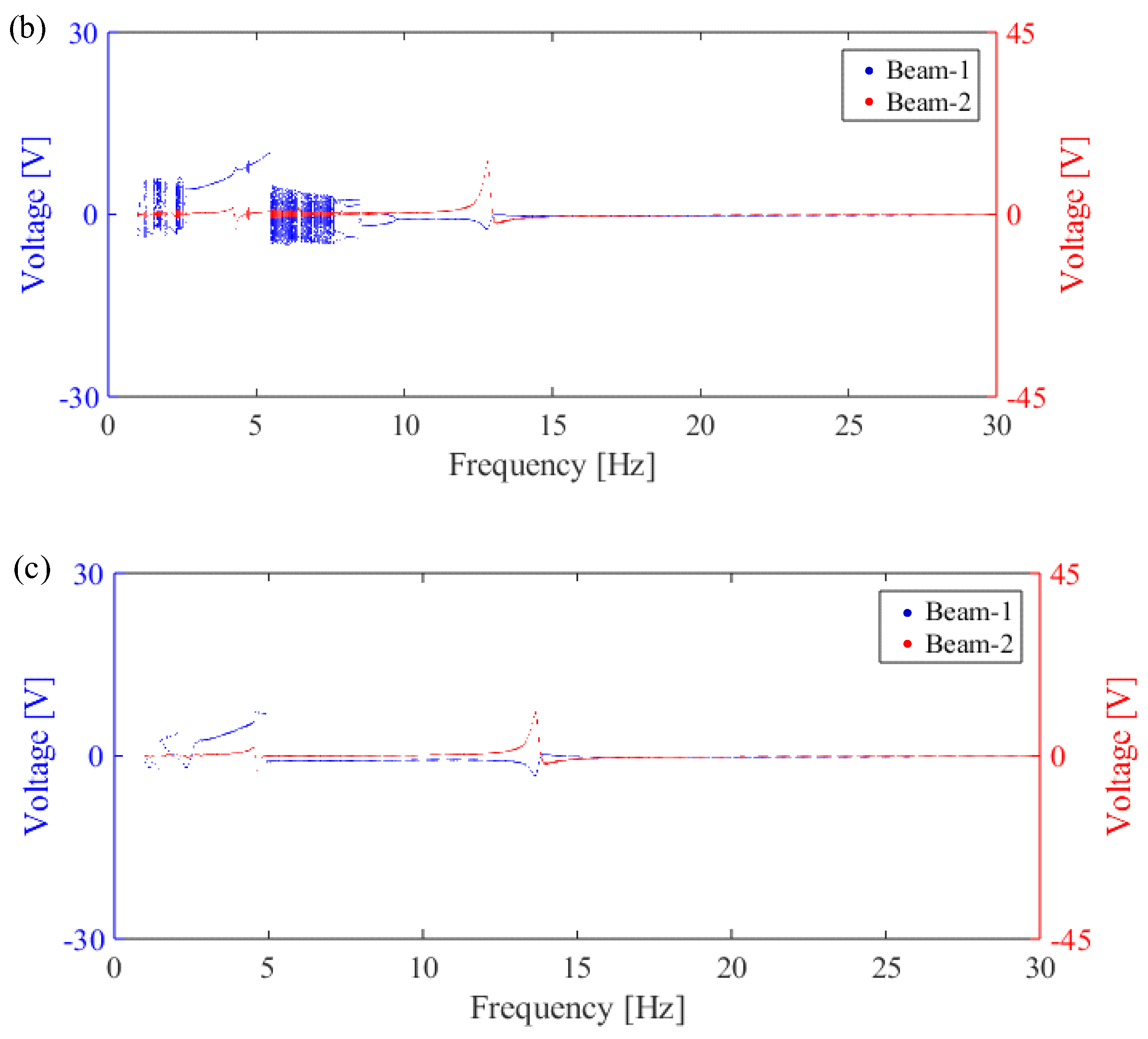
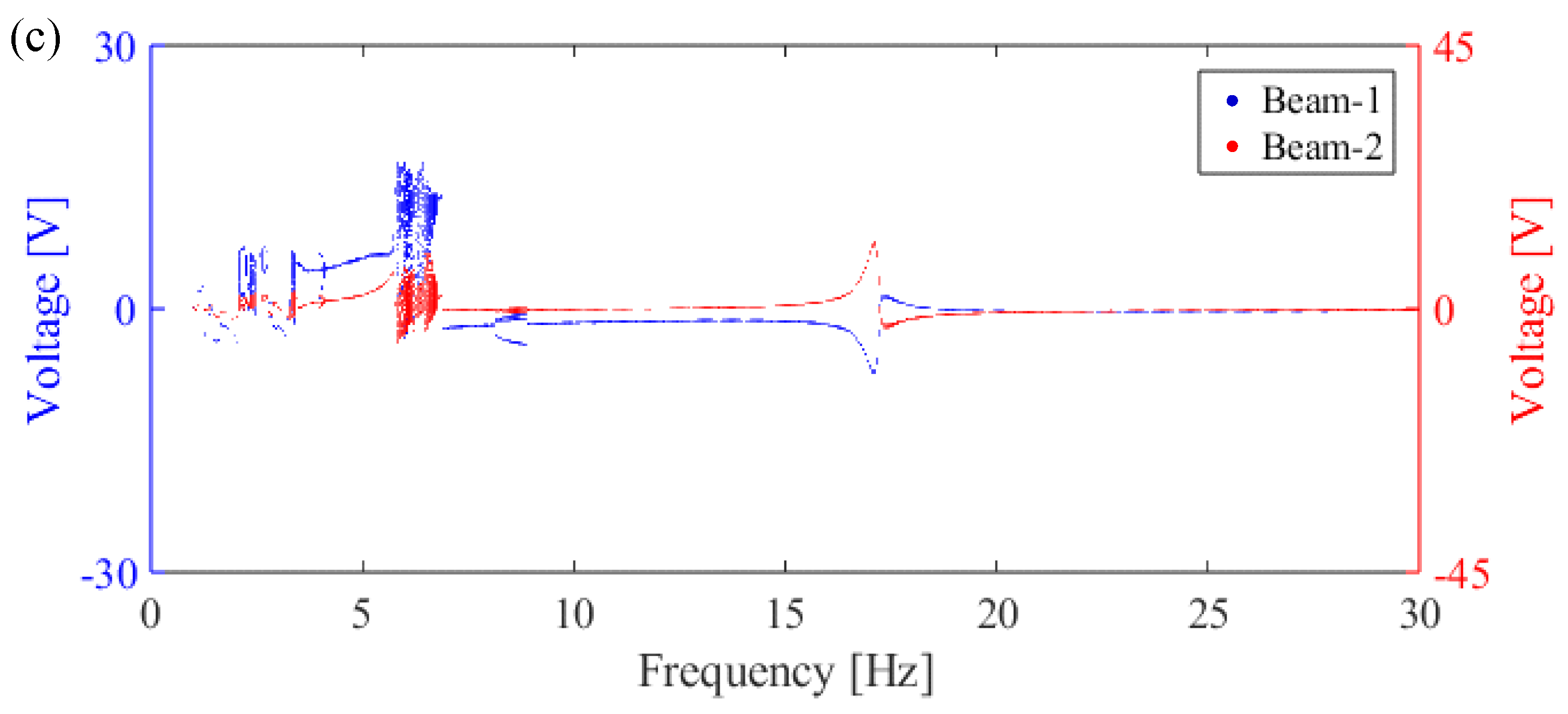
4.2. Experimental Verification of Constant Frequency Excitation
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Lai, Z.; Xu, J.; Bowen, C.R.; Zhou, S. Self-powered and self-sensing devices based on human motion. Joule 2022, 6, 1501–1565. [Google Scholar] [CrossRef]
- Yang, Z.; Zhou, S.; Zu, J.; Inman, D. High-performance piezoelectric energy harvesters and their applications. Joule 2018, 2, 642–697. [Google Scholar] [CrossRef]
- Zhang, Y.; Cao, J.; Zhu, H.; Lei, Y. Design, modeling and experimental verification of circular Halbach electromagnetic energy harvesting from bearing motion. Energy Convers Manag. 2019, 180, 811–821. [Google Scholar] [CrossRef]
- Fan, K.; Hao, J.; Wang, C.; Zhang, C.; Wang, W.; Wang, F. An eccentric mass-based rotational energy harvester for capturing ultralow-frequency mechanical energy. Energy Convers Manag. 2021, 241, 114301. [Google Scholar] [CrossRef]
- Zhu, J.; Fan, K.; Wang, W.; Zhai, K.; Zhang, L.; Zhou, J.; Li, C.; Li, Y.; Li, J.; Liu, Y.; et al. A robust hybrid nanogenerator strategy achieved by regenerative motion transmission toward wind energy harvesting and self-powered sensing. Nano Energy 2025, 135, 110697. [Google Scholar] [CrossRef]
- Zhao, H.; Fan, K.; Zhao, S.; Wu, S.; Zhang, X.; Hou, Z. Lightweight energy harvesting backpack achieved with a slingshot-inspired flexible accelerator. Appl. Energy 2025, 379, 124993. [Google Scholar] [CrossRef]
- Zhang, H.; Zhou, S.; Zhang, J.; Ma, H.; Zhou, S. A sustainable and enhanced-performance vibration energy harvester for application on railway bridge: Design, modeling, and analysis. Mech. Syst. Signal Process. 2025, 225, 112279. [Google Scholar] [CrossRef]
- Li, Z.; Lyu, W.; Gong, C.; Zhou, S.; Li, C. Experimental investigation and dynamic analysis of a novel electromagnetic energy harvester based on airfoil flutter. Energy Convers. Manag. 2025, 326, 119471. [Google Scholar] [CrossRef]
- Li, Q.; He, L.; Lv, X.; Liu, Z.; Li, Z.; Fan, W. A piezoelectric energy harvester based on center of gravity shift. Appl. Energy 2025, 377, 124394. [Google Scholar] [CrossRef]
- Zhou, S.; Cao, J.; Erturk, A.; Lin, J. Enhanced broadband piezoelectric energy harvesting using rotatable magnets. Appl. Phys. Lett. 2013, 102, 173901. [Google Scholar] [CrossRef]
- Huguet, T.; Badel, A.; Lallart, M.; Druet, O. Drastic bandwidth enhancement of bistable energy harvesters: Study of subharmonic behaviors and their stability robustness. Appl. Energy 2018, 226, 607–617. [Google Scholar] [CrossRef]
- Fang, S.; Chen, K.; Xing, J.W. Liao. Tuned bistable nonlinear energy sink for simultaneously improved vibration suppression and energy harvesting. Int. J. Mech. Sci. 2021, 212, 106838. [Google Scholar] [CrossRef]
- Xue, H.; Hu, Y.; Wang, Q.M. Broadband piezoelectric energy harvesting devices using multiple bimorphs with different operating frequencies. IEEE Trans. Ultrason. Ferroelectr. Freq. Control. 2008, 55, 2104–2108. [Google Scholar] [CrossRef] [PubMed]
- Sun, R.; Li, Q.; Yao, J.; Scarpa, F.; Rossiter, J. Tunable, multi-modal, and multidirectional vibration energy harvester based on three-dimensional architected metastructures. Appl. Energy 2020, 264, 114615. [Google Scholar] [CrossRef]
- Dhote, S.; Yang, Z.; Zu, J. Modeling and experimental parametric study of a tri-leg compliant orthoplanar spring based multi-mode piezoelectric energy harvester. Mech. Syst. Signal Process. 2018, 98, 268–280. [Google Scholar] [CrossRef]
- Toyabur, R.M.; Salauddin, M.; Park, J.Y. Design and experiment of piezoelectric multimodal energy harvester for low frequency vibration. Ceram. Int. 2017, 43, S675–S681. [Google Scholar] [CrossRef]
- Challa, V.R.; Prasad, M.G.; Shi, Y.; Fisher, F.T. A vibration energy harvesting device with bidirectional resonance frequency tunability. Smart Mater. Struct. 2008, 17, 015035. [Google Scholar] [CrossRef]
- Podder, P.; Constantinou, P.; Mallick, D.; Amann, A.; Roy, S. Magnetic tuning of nonlinear MEMS electromagnetic vibration energy harvester. J. Microelectromech. Syst. 2017, 26, 539–549. [Google Scholar] [CrossRef]
- Wu, Y.; Li, S.; Fan, K.; Ji, H.; Qiu, J. Investigation of an ultra-low frequency piezoelectric energy harvester with high frequency up-conversion factor caused by internal resonance mechanism. Mech. Syst. Signal Process. 2022, 162, 108038. [Google Scholar] [CrossRef]
- Stanton, S.C.; McGehee, C.C.; Mann, B.P. Nonlinear dynamics for broadband energy harvesting: Investigation of a bistable piezoelectric inertial generator. Phys. D Nonlinear Phenom. 2010, 239, 640–653. [Google Scholar] [CrossRef]
- Liu, Q.; Qin, W.; Yang, Y.; Zhou, Z. Harvesting weak vibration energy by amplified inertial force and multi-stable buckling piezoelectric structure. Mech. Syst. Signal Process. 2023, 189, 110125. [Google Scholar] [CrossRef]
- Liu, Q.; Qin, W.; Yang, T.; Deng, W.; Zhou, Z. Harvesting weak vibration energy by amplified inertial force and super-harmonic vibration. Energy 2023, 263, 125948. [Google Scholar] [CrossRef]
- Ma, X.; Ma, H.; Zhou, S. Nonlinear analysis and response identification of tristable energy harvesters under wind and base excitations. Int. J. Non-Linear Mech. 2025, 173, 105052. [Google Scholar] [CrossRef]
- Fang, S.; Chen, K.; Lai, Z.; Zhou, S.; Liao, W. Snap-through energy harvester with buckled mechanism and hierarchical auxetic structures for ultra-low-frequency rotational excitations. Appl. Phys. Lett. 2023, 122, 93901. [Google Scholar] [CrossRef]
- Tian, L.; Shen, H.; Yang, Q.; Song, R.; Bian, Y. A novel outer-inner magnetic two degree-of-freedom piezoelectric energy harvester. Energy Convers. Manag. 2023, 283, 116920. [Google Scholar] [CrossRef]
- Chen, K.; Gao, F.; Liu, Z.; Liao, W. A nonlinear M-shaped tri-directional piezoelectric energy harvester. Smart Mater. Struct. 2021, 30, 045017. [Google Scholar] [CrossRef]
- Xing, J.; Fang, S.; Fu, X.; Liao, W.H. A rotational hybrid energy harvester utilizing bistability for low-frequency applications: Modelling and experimental validation. Int. J. Mech. Sci. 2022, 222, 107235. [Google Scholar] [CrossRef]
- Xiang, X.; Chen, K.; Yang, Q.; Shen, H. Reversible nonlinear energy harvester tuned by titling angle or clamping distance. Sens. Actuators A Phys. 2024, 366, 115009. [Google Scholar] [CrossRef]
- Chen, J.; Bao, B.; Liu, J.; Wu, Y.; Wang, Q. Piezoelectric energy harvester featuring a magnetic chaotic pendulum. Energy Convers. Manag. 2022, 269, 116155. [Google Scholar] [CrossRef]
- Li, H.; Qin, W. Dynamics and coherence resonance of a laminated piezoelectric beam for energy harvesting. Nonlinear Dyn. 2015, 81, 1751–1757. [Google Scholar] [CrossRef]
- Zhang, H.; Ma, T. Adaptive energy harvesting from low-level ambient vibrations. Appl. Mater. Today 2023, 34, 101911. [Google Scholar] [CrossRef]
- Vocca, H.; Neri, I.; Travasso, F.; Gammaitoni, L. Kinetic energy harvesting with bistable oscillators. Appl. Energy 2012, 97, 771–776. [Google Scholar] [CrossRef]
- Wang, H.; Zhao, Q.; Song, R.; Guo, J.; Chang, W.; Yang, X.; Zhang, L. Design and performance study of low frequency magnetic coupling bistable piezoelectric and electromagnetic energy harvester. Energy 2025, 320, 135178. [Google Scholar] [CrossRef]
- Ma, X.; Litak, G.; Zhou, S. Using 0–1 test to diagnose periodic and chaotic motions of nonlinear vortex-induced vibration energy harvesters. Chaos Solitons Fractals 2025, 192, 116036. [Google Scholar] [CrossRef]
- Harne, R.L.; Wang, K.W. A review of the recent research on vibration energy harvesting via bistable systems. Smart Mater. Struct. 2013, 22, 23001. [Google Scholar] [CrossRef]
- Deng, H.; Wang, Z.; Du, Y.; Zhang, J.; Ma, M.; Zhong, X. A seesaw-type approach for enhancing nonlinear energy harvesting. Appl. Phys. Lett. 2018, 112, 213902. [Google Scholar] [CrossRef]
- Zhou, S.; Cao, J.; Inman, D.J.; Lin, J.; Liu, S.; Wang, Z. Broadband tristable energy harvester: Modeling and experiment verification. Appl. Energy 2014, 133, 33–39. [Google Scholar] [CrossRef]
- Zhou, S.; Zuo, L. Nonlinear dynamic analysis of asymmetric tristable energy harvesters for enhanced energy harvesting. Commun. Nonlinear Sci. Numer. Simul. 2018, 61, 271–284. [Google Scholar] [CrossRef]
- Wang, C.; Zhang, Q.; Wang, W.; Feng, J. A low-frequency, wideband quad-stable energy harvester using combined nonlinearity and frequency up-conversion by cantilever-surface contact. Mech. Syst. Signal Process. 2018, 112, 305–318. [Google Scholar] [CrossRef]
- Lan, C.; Qin, W. Enhancing ability of harvesting energy from random vibration by decreasing the potential barrier of bistable harvester. Mech. Syst. Signal Process. 2017, 85, 71–81. [Google Scholar] [CrossRef]
- Mei, X.; Zhou, S.; Yang, Z.; Kaizuka, T.; Nakano, K. Enhancing energy harvesting in low-frequency rotational motion by a quad-stable energy harvester with time-varying potential wells. Mech. Syst. Signal Process. 2021, 148, 107167. [Google Scholar] [CrossRef]
- Ma, X.; Li, H.; Zhou, S.; Yang, Z.; Litak, G. Characterizing nonlinear characteristics of asymmetric tristable energy harvesters. Mech. Syst. Signal Process. 2022, 168, 108612. [Google Scholar] [CrossRef]
- Xu, H.; Zhou, S. Theoretical analysis and potential engineering application of an energy harvester. Int. J. Mech. Sci. 2024, 275, 109284. [Google Scholar] [CrossRef]
- Margielewicz, J.; Gąska, D.; Caban, J.; Litak, G.; Dudziak, A.; Ma, X.; Zhou, S. Double-Versus Triple-Potential Well Energy Harvesters: Dynamics and Power Output. Sensors 2023, 23, 2185. [Google Scholar] [CrossRef]
- He, Q.; Daqaq, M.F. Influence of potential function asymmetries on the performance of nonlinear energy harvesters under white noise. J. Sound Vib. 2014, 333, 3479–3489. [Google Scholar] [CrossRef]
- Erturk, A.; Inman, D.J. Broadband piezoelectric power generation on high-energy orbits of the bistable Duffing oscillator with electromechanical coupling. J. Sound Vib. 2011, 330, 2339–2353. [Google Scholar] [CrossRef]
- Fang, S.; Fu, X.; Liao, W. Modeling and experimental validation on the interference of mechanical plucking energy harvesting. Mech. Syst. Signal Process. 2019, 134, 106317. [Google Scholar] [CrossRef]
- Lan, C.; Qin, W. Vibration energy harvesting from a piezo electric bistable system with two symmetric stops. Acta Phys. Sin. 2015, 64, 210501. [Google Scholar] [CrossRef]
- Fan, Y.; Niu, M.; Ghayesh, M.H.; Amabili, M.; Chen, L. Nonlinear vibration energy harvesting via parametric excitation: Snap-through with time-varying potential wells. Mech. Syst. Signal Process. 2024, 220, 111625. [Google Scholar] [CrossRef]
- Tang, L.; Yang, Y.; Soh, C.K. Improving functionality of vibration energy harvesters using magnets. J. Intell. Mater. Syst. Struct. 2012, 23, 1433–1449. [Google Scholar] [CrossRef]
- Chen, K.; Zhang, X.; Xiang, X.; Shen, H.; Yang, Q.; Wang, J.; Litak, G. High performance piezoelectric energy harvester with dual-coupling beams and bistable configurations. J. Sound Vib. 2023, 561, 117822. [Google Scholar] [CrossRef]
- Sobol, I.M. Global sensitivity indices for nonlinear mathematical models and their Monte Carlo estimates. Math. Comput. Simul. 2001, 55, 271–280. [Google Scholar] [CrossRef]
- Liang, H.; Hao, G.; Olszewski, O.Z.; Pakrashi, V. Ultra-low wide bandwidth vibrational energy harvesting using a statically balanced compliant mechanism. Int. J. Mech. Sci. 2022, 219, 107130. [Google Scholar] [CrossRef]




| Description | Material | Value (mm) |
|---|---|---|
| Beam 1, Beam 2 | Stainless steel (Jiangsu Naite Stainless Steel Co., Ltd., Nantong, China) | 100 × 30 × 0.4 |
| Piezo element | PZT−5H (Baoding Hongsheng Acoustic Electronic Equipment Co., Ltd., Baoding, China) | 20 × 10 × 0.5 |
| Spring | Stainless steel (Ningde Li Spring Manufacturing Company, Dongguan, China) | Ф10 × 31 |
| Magnet A, Magnet B | NdFeB (Shanghai Tianyu Magnetic Material Company, Shanghai, China) | Ф15 × 5, Ф25 × 10 |
| Tip−mass | Brass (Biling Hardware products Co., Ltd., Changsha, China) | 15 × 12 × 10 |
| Description | Symbol | Value |
|---|---|---|
| Equivalent mass | M1, M2 | 18.9, 16.6 (g) |
| Equivalent damping | C1, C2 | 6.48 × 10−2 (Ns/m) 2.4 × 10−2 (Ns/m) |
| Equivalent stiffness | K1, K2 | 104, 96 (N/m) |
| Equivalent capacitance | Cp1, Cp2 | 12.2, 11.5 (nF) |
| Load resistance | R1, R2 | 1.3, 1 (MΩ) |
| Equivalent electromechanical coupling coefficient | θ1, θ2 | 2.76 × 10−5 (N/V) 1.8 × 10−5 (N/V) |
| Potential Well Depth | Case I | Case II | Case III |
|---|---|---|---|
| Initial depth (mJ) | 0.17 (Ks = 0 N/m) | 0.64 (Ks = 0 N/m) | 0.9 (Ks = 0 N/m) |
| Depth 1 (mJ) | 0.03 (Ks = 11 N/m) | 0.075 (Ks = 35 N/m) | 0.02 (Ks = 61 N/m) |
| Depth 2 (mJ) | 0 (Ks = 23 N/m) | 0 (Ks = 70 N/m) | 0 (Ks = 108 N/m) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ren, S.; Tian, L.; Shen, H. Influence of Potential Well Depth on the Dual−Coupling Beam Energy Harvester: Modeling and Experimental Validation. Energies 2025, 18, 1984. https://doi.org/10.3390/en18081984
Ren S, Tian L, Shen H. Influence of Potential Well Depth on the Dual−Coupling Beam Energy Harvester: Modeling and Experimental Validation. Energies. 2025; 18(8):1984. https://doi.org/10.3390/en18081984
Chicago/Turabian StyleRen, Shuangchen, Libin Tian, and Hui Shen. 2025. "Influence of Potential Well Depth on the Dual−Coupling Beam Energy Harvester: Modeling and Experimental Validation" Energies 18, no. 8: 1984. https://doi.org/10.3390/en18081984
APA StyleRen, S., Tian, L., & Shen, H. (2025). Influence of Potential Well Depth on the Dual−Coupling Beam Energy Harvester: Modeling and Experimental Validation. Energies, 18(8), 1984. https://doi.org/10.3390/en18081984






