Applicability Analysis of Reduced-Order Methods with Proper Orthogonal Decomposition for Neutron Diffusion in Molten Salt Reactor
Abstract
1. Introduction
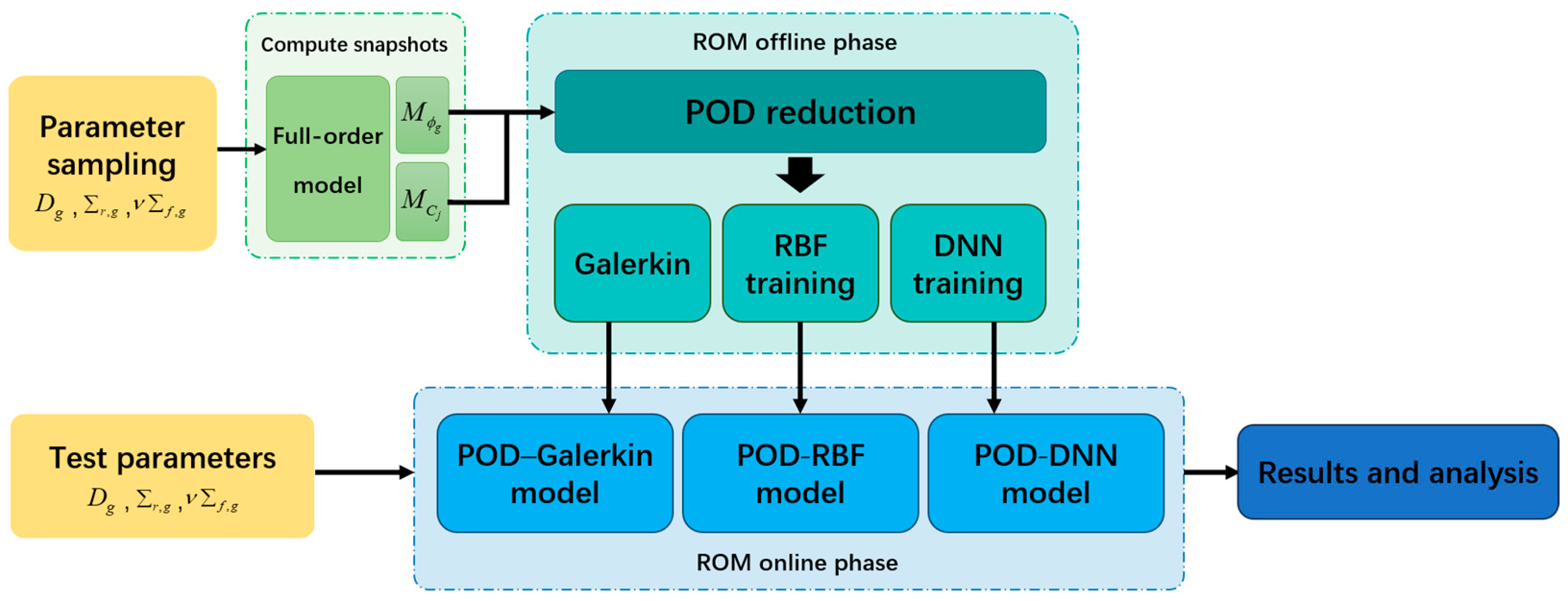
2. Methods
2.1. Full-Order Models
2.2. Reduced-Order Model Approaches
2.2.1. The POD–Galerkin Method
2.2.2. The POD-RBF Method
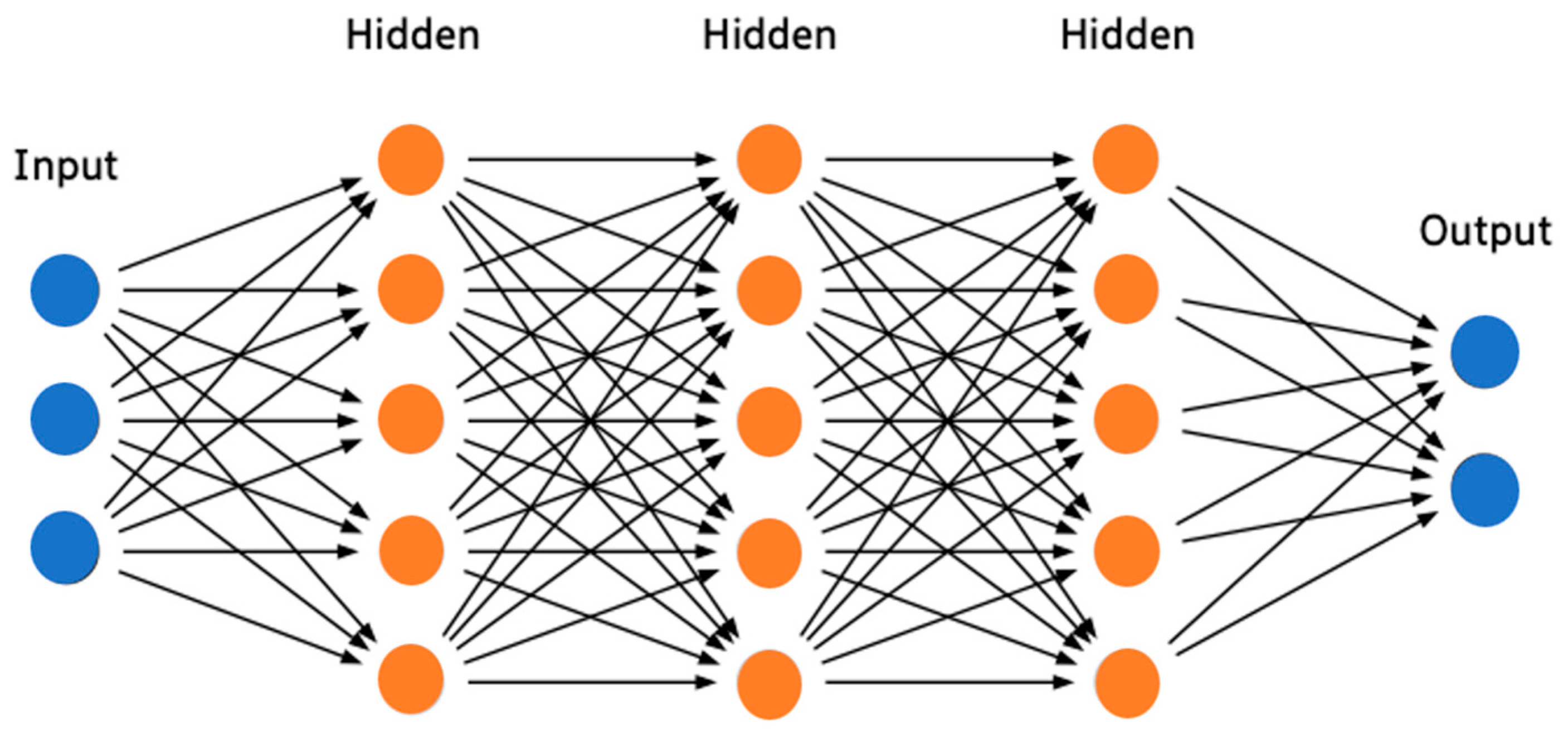
2.2.3. The POD-DNN Method
2.3. Error Analysis
3. Results and Discussion
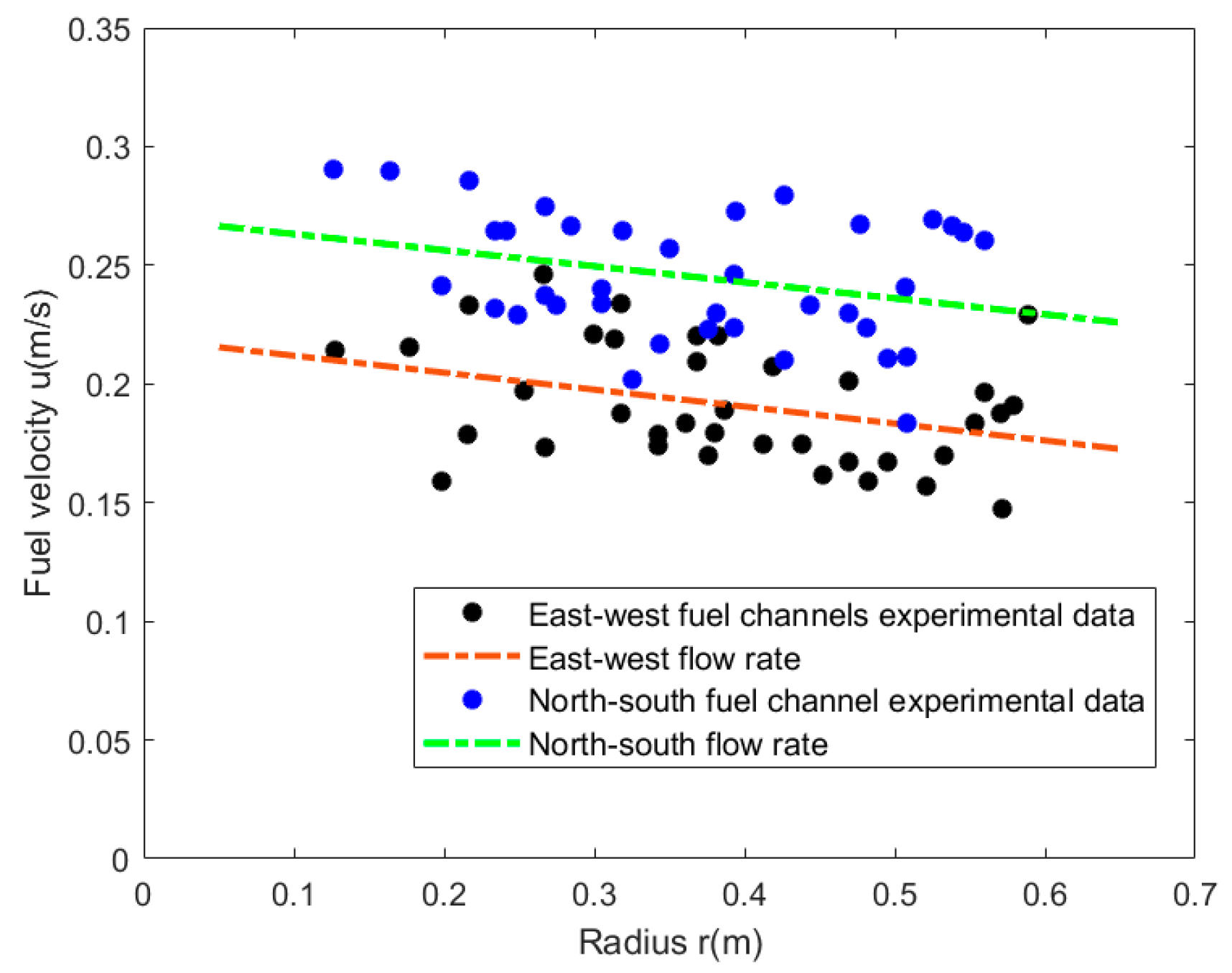
3.1. Benchmark Description
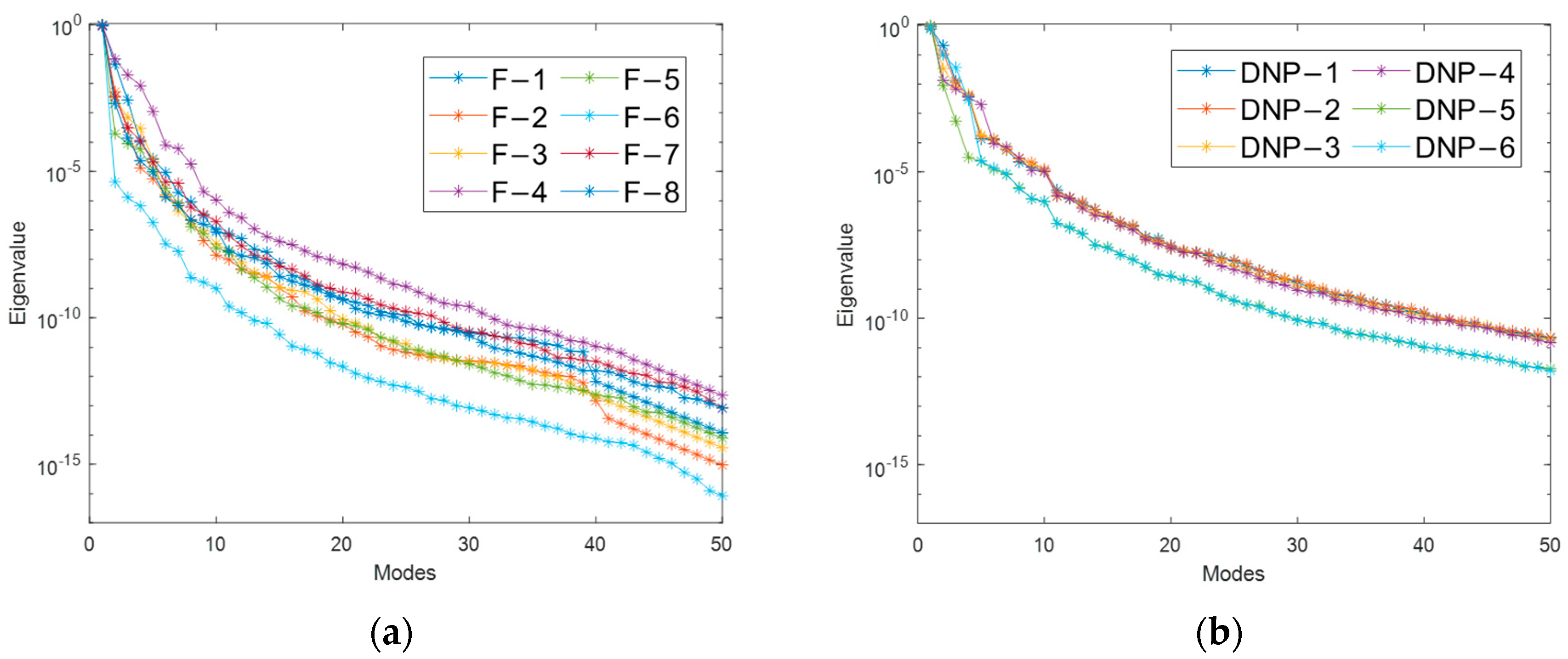
3.2. ROM Parameter Analysis
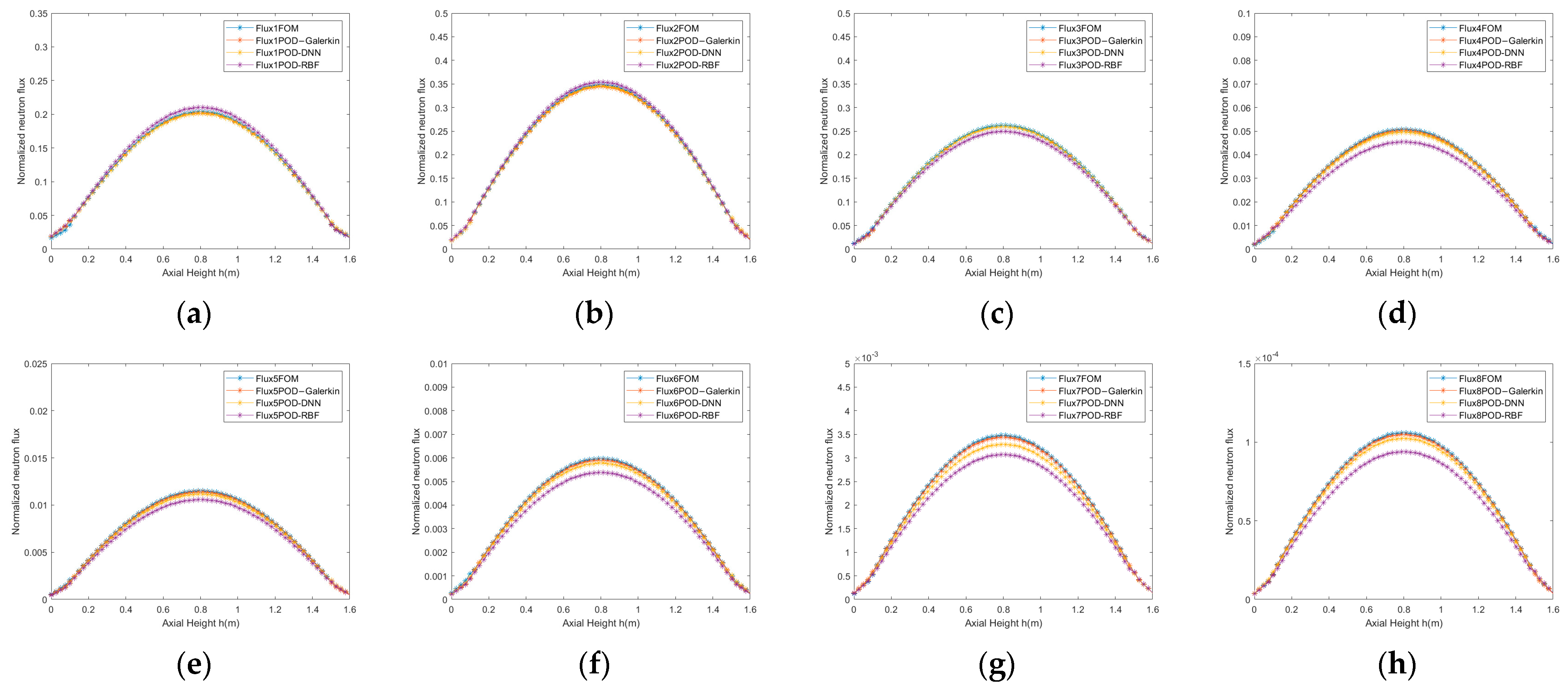
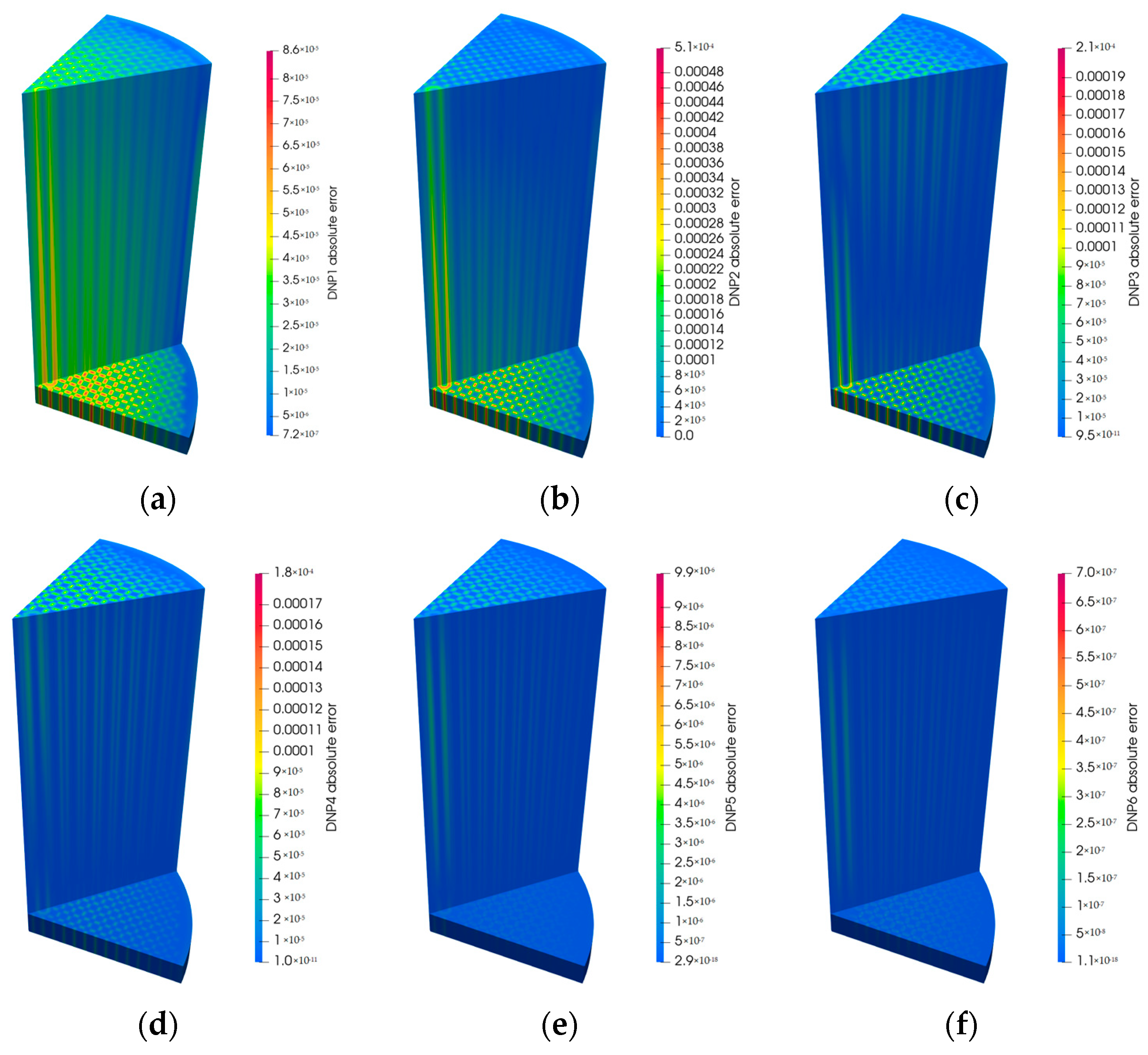
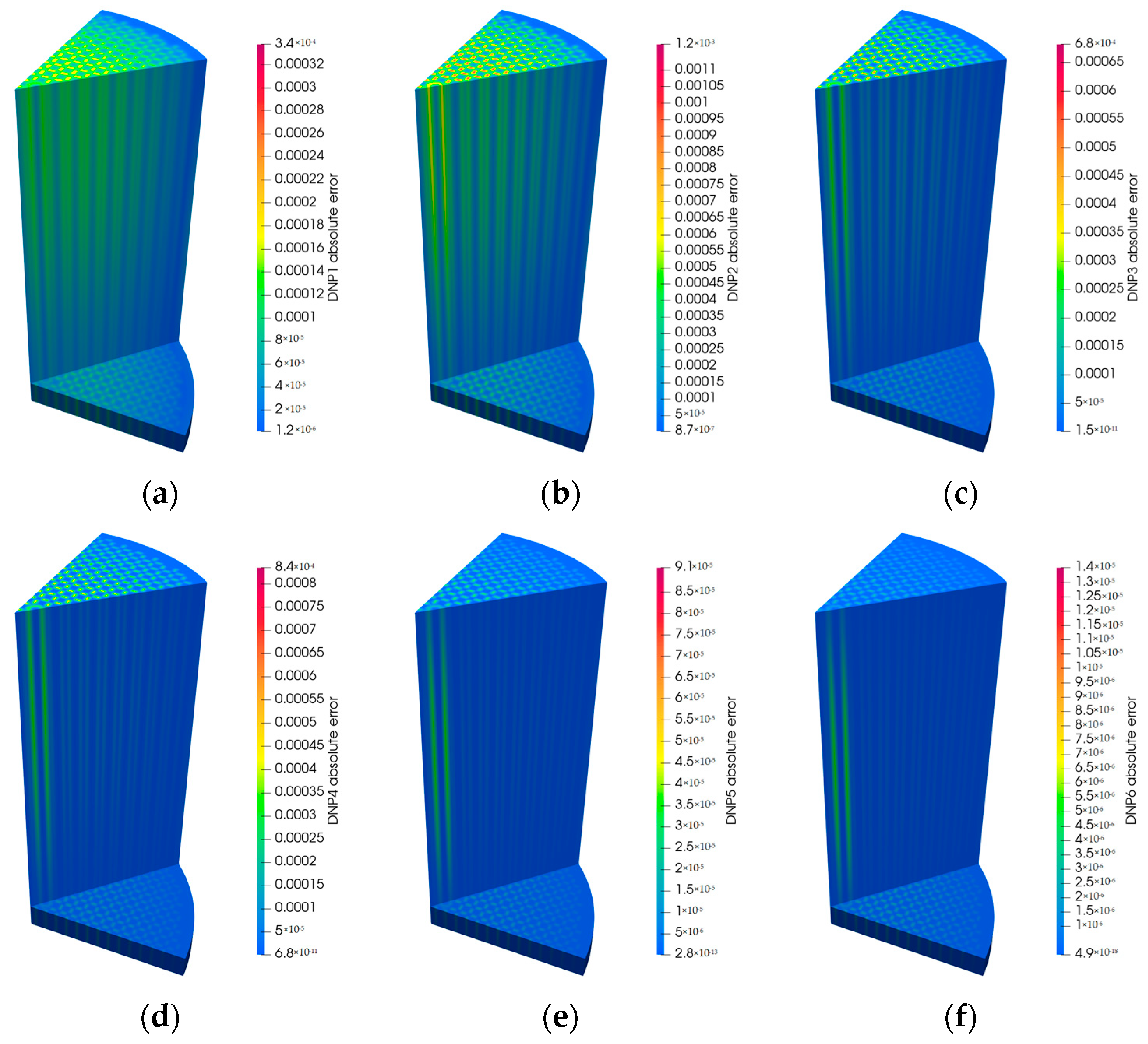
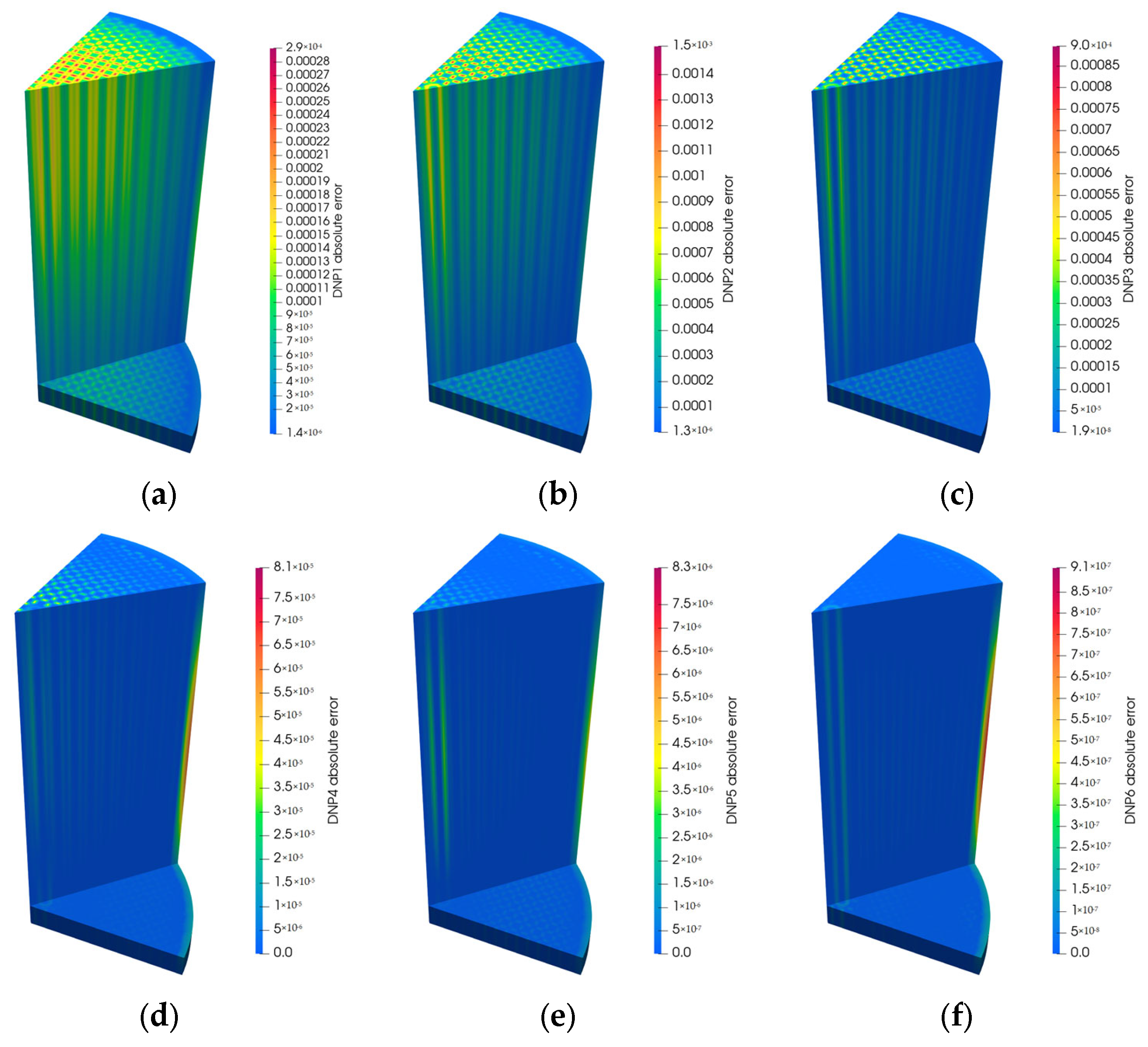
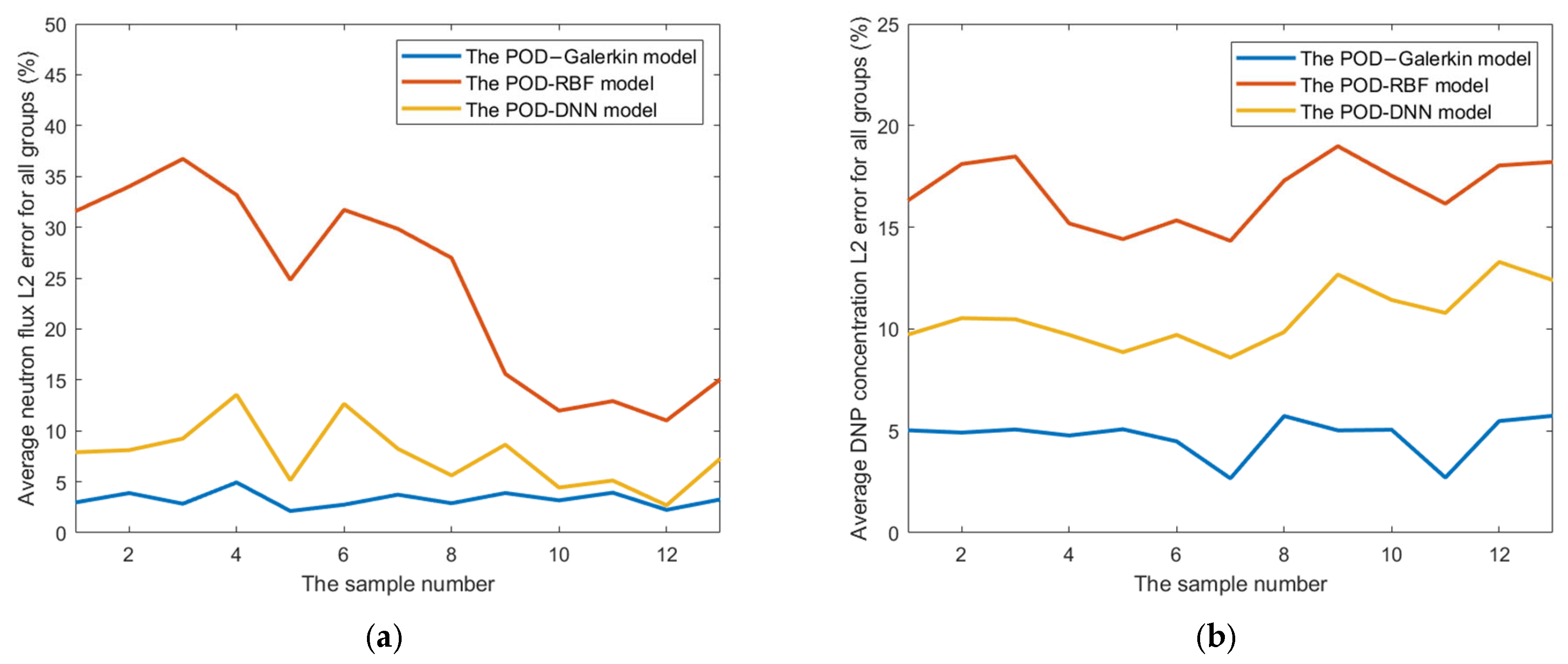
3.3. Accuracy and Performance Analysis
4. Conclusions
- For reduced-order calculations of the neutron flux and DNP concentration under small-sample conditions, the POD–Galerkin model demonstrates superior computational accuracy compared to the POD-RBF and POD-DNN models, with average L2 errors of less than 0.00658% for the neutron flux and 1.01% for the DNP concentration. And the POD–Galerkin model exhibits excellent extrapolation capabilities and maintains an L2 error of less than 6.04% when the test samples exceed the range of the snapshot samples.
- All three reduced-order models can effectively improve the computational efficiency, and the POD–Galerkin model has an acceleration ratio of about 1800.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| POD | Proper Orthogonal Decomposition |
| RBF | Radial basis function |
| DNN | Deep Neural Network |
| ROM | Reduced-order model |
| FOM | Full-order model |
| DNP | Delayed neutron precursors |
| MM | Modal Method |
| ESNII | European Sustainable Nuclear Industrial Initiative |
| ESFR | European Sodium Fast Reactor |
| MSFR | Molten Salt Fast Reactor |
| MSRE | Molten Salt Reactor Experiment |
| ORNL | Oak Ridge National Laboratory |
References
- Song, S.; Cheng, M.; Lin, M. Development and application of multi-scale thermal fluid coupling program for molten salt cooled fast reactor based on RELAP5 and sub-channel program. Nucl. Tech. 2022, 45, 070602. [Google Scholar] [CrossRef]
- Zong, Z.-W.; Cheng, M.-S.; Yu, Y.-C.; Dai, Z.-M. A multithreaded parallel upwind sweep algorithm for the SN transport equations discretized with discontinuous finite elements. Nucl. Sci. Tech. 2023, 34, 200. [Google Scholar] [CrossRef]
- Guo, Z.; Zhou, J.; Zhang, D.; Chaudri, K.S.; Tian, W.; Su, G.; Qiu, S. Coupled neutronics/thermal-hydraulics for analysis of molten salt reactor. Nucl. Eng. Des. 2013, 258, 144–156. [Google Scholar] [CrossRef]
- Zuo, X.-D.; Cheng, M.-S.; Dai, Y.-Q.; Yu, K.-C.; Dai, Z.-M. Flow field effect of delayed neutron precursors in liquid-fueled molten salt reactors. Nucl. Sci. Tech. 2022, 33, 96. [Google Scholar] [CrossRef]
- Mathieu, L.; Heuer, D.; Brissot, R.; Garzenne, C.; Le Brun, C.; Lecarpentier, D.; Liatard, E.; Loiseaux, J.M.; Méplan, O.; Merle-Lucotte, E.; et al. The thorium molten salt reactor: Moving on from the MSBR. Prog. Nucl. Energy 2006, 48, 664–679. [Google Scholar] [CrossRef]
- Lin, M.; Cheng, M.; Cai, X.; Dai, Z.-M. Applicability analysis of reduced order modeling methods for fluid dynamics in molten salt reactor. Nucl. Tech. 2024, 47, 090604. [Google Scholar] [CrossRef]
- Berkooz, G.; Holmes, P.; Lumley, J.L. The Proper Orthogonal Decomposition in the Analysis of Turbulent Flows. Annu. Rev. Fluid Mech. 1993, 25, 539–575. [Google Scholar] [CrossRef]
- Noack, B.R. Turbulence, Coherent Structures, Dynamical Systems and Symmetry. AIAA J. 2013, 51, 2991. [Google Scholar] [CrossRef]
- Abrate, N.; Dulla, S.; Pedroni, N. A non-intrusive reduced order model for the characterisation of the spatial power distribution in large thermal reactors. Ann. Nucl. Energy 2023, 184, 109674. [Google Scholar] [CrossRef]
- Benner, P.; Gugercin, S.; Willcox, K. A Survey of Projection-Based Model Reduction Methods for Parametric Dynamical Systems. SIAM Rev. 2015, 57, 483–531. [Google Scholar] [CrossRef]
- Raffel, C.; Shazeer, N.; Roberts, A.; Lee, K.; Narang, S.; Matena, M.; Zhou, Y.; Li, W.; Liu, P.J. Exploring the limits of transfer learning with a unified text-to-text transformer. J. Mach. Learn. Res. 2020, 21, 140. [Google Scholar] [CrossRef]
- Bei, X.; Dai, Y.; Yu, K.; Cheng, M. Three-Dimensional Surrogate Model Based on Back-Propagation Neural Network for Key Neutronics Parameters Prediction in Molten Salt Reactor. Energies 2023, 16, 4044. [Google Scholar] [CrossRef]
- Buchan, A.G.; Pain, C.C.; Fang, F.; Navon, I.M. A POD reduced-order model for eigenvalue problems with application to reactor physics. Int. J. Numer. Methods Eng. 2013, 95, 1011–1032. [Google Scholar] [CrossRef]
- Sartori, A.; Baroli, D.; Cammi, A.; Chiesa, D.; Luzzi, L.; Ponciroli, R.; Previtali, E.; Ricotti, M.E.; Rozza, G.; Sisti, M. Comparison of a Modal Method and a Proper Orthogonal Decomposition approach for multi-group time-dependent reactor spatial kinetics. Ann. Nucl. Energy 2014, 71, 217–229. [Google Scholar] [CrossRef]
- German, P.; Ragusa, J.C. Reduced-order modeling of parameterized multi-group diffusion k-eigenvalue problems. Ann. Nucl. Energy 2019, 134, 144–157. [Google Scholar] [CrossRef]
- Prince, Z.M.; Ragusa, J.C. Parametric uncertainty quantification using proper generalized decomposition applied to neutron diffusion. Int. J. Numer. Methods Eng. 2019, 119, 899–921. [Google Scholar] [CrossRef]
- Ostrowski, Z.; Białecki, R.A.; Kassab, A.J. Solving inverse heat conduction problems using trained POD-RBF network inverse method. Inverse Probl. Sci. Eng. 2008, 16, 39–54. [Google Scholar] [CrossRef]
- Das, A.; Khoury, A.; Divo, E.; Huayamave, V.; Ceballos, R.; Eaglin, R.; Kassab, A.; Payne, A.; Yelundur, V.; Seigneur, H. Real-Time Thermomechanical Modeling of PV Cell Fabrication via a POD-Trained RBF Interpolation Network. Comput. Model. Eng. Sci. 2020, 122, 757–777. [Google Scholar] [CrossRef]
- Elzohery, R.; Roberts, J. Exploring Transient, Neutronic, Reduced-Order Models using DMD/POD-Galerkin and Data-Driven DMD; EDP Sciences: Les Ulis, France, 2020. [Google Scholar]
- Hasan, M.D.A.; Balasubadra, K.; Vadivel, G.; Arunfred, N.; Ishwarya, M.V.; Murugan, S. IoT-Driven Image Recognition for Microplastic Analysis in Water Systems using Convolutional Neural Networks. In Proceedings of the 2024 2nd International Conference on Computer, Communication and Control (IC4), Indore, India, 8–10 February 2024; pp. 1–6. [Google Scholar]
- Kang, H.; Tian, Z.; Chen, G.; Li, L.; Wang, T. Application of POD reduced-order algorithm on data-driven modeling of rod bundle. Nucl. Eng. Technol. 2022, 54, 36–48. [Google Scholar] [CrossRef]
- Massone, M.; Gabrielli, F.; Rineiski, A. A genetic algorithm for multigroup energy structure search. Ann. Nucl. Energy 2017, 105, 369–387. [Google Scholar] [CrossRef]
- Wei, C.; Ooka, R.; Zhang, B.; Zhou, Q. Predicting Unsteady Indoor Temperature Distributions by POD-DNN. E3S Web Conf. 2022, 356, 04028. [Google Scholar] [CrossRef]
- Kiegiel, K.; Chmielewska-Śmietanko, D.; Herdzik-Koniecko, I.; Miśkiewicz, A.; Smoliński, T.; Rogowski, M.; Ntang, A.; Rotich, N.K.; Madaj, K.; Chmielewski, A.G. The Future of Nuclear Energy: Key Chemical Aspects of Systems for Developing Generation III+, Generation IV, and Small Modular Reactors. Energies 2025, 18, 622. [Google Scholar] [CrossRef]
- Panico, D.M. Development of a C++ tool for Reduced Order Modelling of Molten Salt Fast Reactor multiphysics: Sensitivity Analysis application. Doctoral Dissertation, Politecnico di Torino, Turin, Italy, 2019. [Google Scholar]
- Qian, H.; Chen, G.; Liu, D.; Yu, Y.; Zhang, Y.; Zhang, L.; Li, J. Development of a non-intrusive ROM for 5 × 5 rod bundles of PWR using small sample data. Ann. Nucl. Energy 2025, 217, 111347. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, W.; Peng, S.; Li, J.; Wang, T.; He, Q.; Wang, T.; Lu, H.; Zeng, L. Enhancing uncertainty analysis: POD-DNNs for reduced order modeling of neutronic transient behavior. Nucl. Eng. Des. 2025, 435, 113969. [Google Scholar] [CrossRef]
- Sirovich, L. Turbulence and the dynamics of coherent structures. II. Symmetries and transformations. Q. Appl. Math. 1987, 45, 573–582. [Google Scholar] [CrossRef]
- Liang, Y.C.; Lin, W.Z.; Lee, H.P.; Lim, S.P.; Lee, K.H.; Sun, H. Proper Orthogonal Decomposition and its Applications—Part II: Model Reduction for Mems Dynamical Analysis. J. Sound Vib. 2002, 256, 515–532. [Google Scholar] [CrossRef]
- Haubenreich, P.N.; Engel, J.R.; Prince, B.E.; Claiborne, H.C. Msre Design and Operations Report. Part III. Nuclear Analysis; Oak Ridge National Lab. (ORNL): Oak Ridge, TN, USA, 1964; p. 204.
- Romano, P.K.; Forget, B. The OpenMC Monte Carlo particle transport code. Ann. Nucl. Energy 2013, 51, 274–281. [Google Scholar] [CrossRef]
- Romano, P.K.; Horelik, N.E.; Herman, B.R.; Nelson, A.G.; Forget, B.; Smith, K. OpenMC: A state-of-the-art Monte Carlo code for research and development. Ann. Nucl. Energy 2015, 82, 90–97. [Google Scholar] [CrossRef]
- Kępisty, G.; Oettingen, M.; Stanisz, P.; Cetnar, J. Statistical error propagation in HTR burnup model. Ann. Nucl. Energy 2017, 105, 355–360. [Google Scholar] [CrossRef]
- Oettingen, M.; Kim, J. Detection of Numerical Power Shift Anomalies in Burnup Modeling of a PWR Reactor. Sustainability 2023, 15, 3373. [Google Scholar] [CrossRef]
- Vieira, T.A.S.; Carvalho, Y.M.; Gonçalves, R.C.; de Almeida Carvalho, K.; Silva, V.V.A.; Barros, G.P.; Santos, A.A.C.d. Proposition of a small molten salt modular reactor utilizing fine-mesh 1:1 coupled calculations—Part I. Ann. Nucl. Energy 2025, 213, 111079. [Google Scholar] [CrossRef]
- Cheng, M.-S.; Dai, Z.-M. Development of a three dimension multi-physics code for molten salt fast reactor. Nucl. Sci. Tech. 2014, 25, 66–76. [Google Scholar] [CrossRef]
- Naha, S.; Das, D.K. Radial basis function neural network controller for power control of molten salt breeder reactor of nuclear power plant. Ann. Nucl. Energy 2024, 195, 110160. [Google Scholar] [CrossRef]
- Foad, B.; Elzohery, R.; Novog, D.R. Demonstration of combined reduced order model and deep neural network for emulation of a time-dependent reactor transient. Ann. Nucl. Energy 2022, 171, 109017. [Google Scholar] [CrossRef]
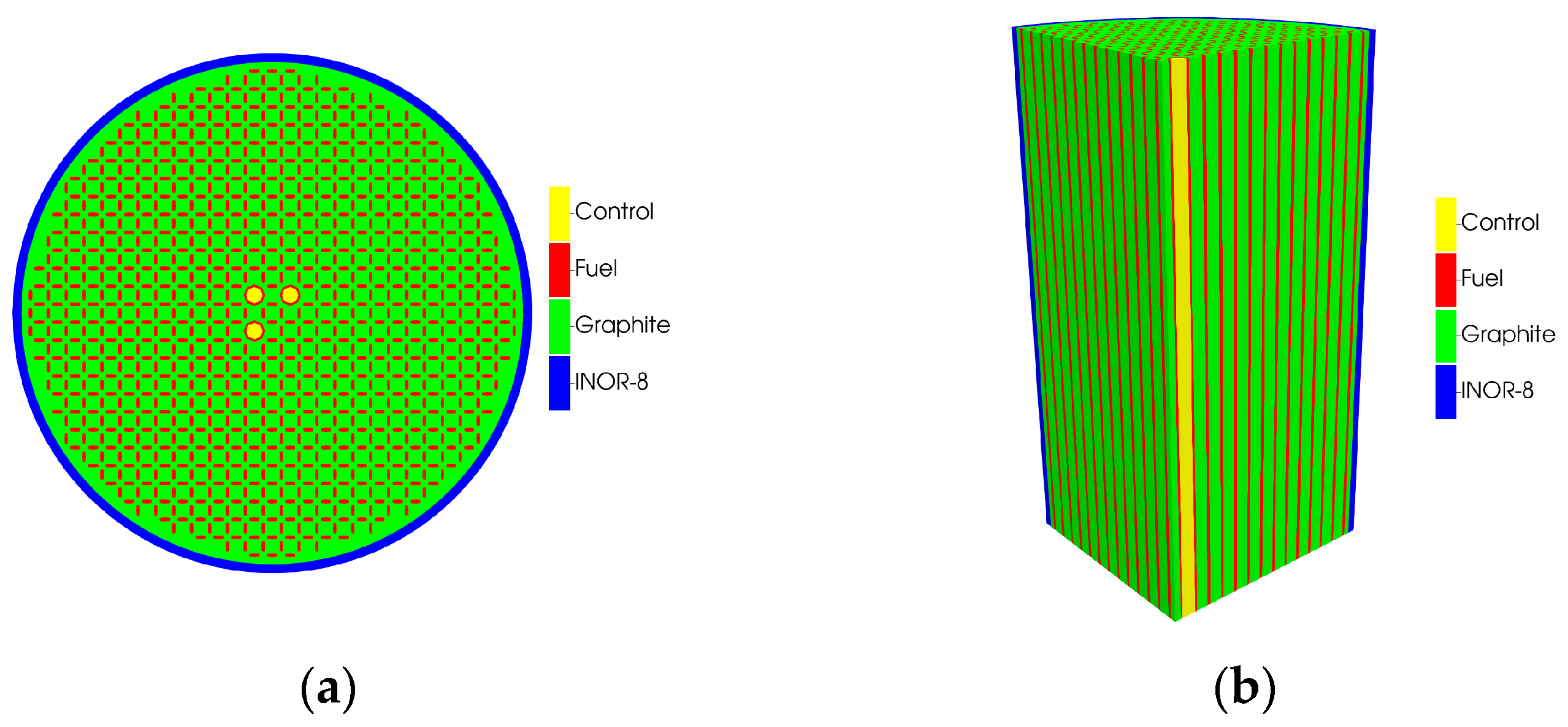
| Parameter | Value (cm) |
|---|---|
| Total height of the model | 160.02 |
| Graphite part radius | 71.12 |
| Outer reactor vessel radius | 73.66 |
| Fuel channel thickness | 1.016 |
| Fuel channel width | 2.032 |
| Cutout radius at fuel channel corners | 0.508 |
| Control rod channel radius | 2.347 |
| Radius of fuel channel out of control rod | 3.048 |
| Total | Group 1 | Group 2 | Group 3 | Group 4 | Group 5 | Group 6 | ||
|---|---|---|---|---|---|---|---|---|
| U-235 | 640.5 | 21.1 | 140.2 | 125.4 | 252.8 | 74.0 | 27.0 | |
| - | 0.0124 | 0.0305 | 0.111 | 0.301 | 1.14 | 3.01 |
| Item | Value | Item | Value |
|---|---|---|---|
| Hidden layer (neutron flux/ DNP concentration) | [128, 128, 64]/[128, 128, 64] | Activation function | Swish |
| Epochs | 2000 | LR decay strategy | Exponential decay |
| Batch size | 16 | Validation split | 20% |
| Learning rate (LR) | 0.001 | Early stopping | 50 epochs |
| Dropout rate | 0.2 | Optimizer | Adam |
| L2 regularization | 0.001 |
| Parameter | Group | Number of POD Modes |
|---|---|---|
| Neutron Flux | 1 | 13 |
| 2 | 12 | |
| 3 | 12 | |
| 4 | 15 | |
| 5 | 15 | |
| 6 | 18 | |
| 7 | 21 | |
| 8 | 23 | |
| DNP concentration | 1 | 18 |
| 2 | 17 | |
| 3 | 16 | |
| 4 | 14 | |
| 5 | 17 | |
| 6 | 16 |
| Parameter | Method | Max (%) | Min (%) | Avg (%) |
|---|---|---|---|---|
| POD–Galerkin | 1.21 × 10−2 | 3.68 × 10−3 | 6.58 × 10−3 | |
| POD-RBF | 2.68 | 1.98 × 10−1 | 4.08 × 10−1 | |
| POD-DNN | 2.25 | 3.03 × 10−2 | 7.55 × 10−1 | |
| POD–Galerkin | 2.95 | 2.25 × 10−1 | 1.01 | |
| POD-RBF | 4.58 | 2.52 × 10−1 | 2.36 | |
| POD-DNN | 3.24 | 9.81 × 10−2 | 1.68 |
| Method | FOM Calculation Time (s) | ROM Calculation Time (s) | Acceleration Rate |
|---|---|---|---|
| POD–Galerkin | 649.72 | 0.358 | 1814 |
| POD-RBF | 649.72 | 0.627 | 1036 |
| POD-DNN | 649.72 | 0.75 | 866 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, Z.; Lin, M.; Cheng, M.; Dai, Y.; Zuo, X. Applicability Analysis of Reduced-Order Methods with Proper Orthogonal Decomposition for Neutron Diffusion in Molten Salt Reactor. Energies 2025, 18, 1893. https://doi.org/10.3390/en18081893
Zhou Z, Lin M, Cheng M, Dai Y, Zuo X. Applicability Analysis of Reduced-Order Methods with Proper Orthogonal Decomposition for Neutron Diffusion in Molten Salt Reactor. Energies. 2025; 18(8):1893. https://doi.org/10.3390/en18081893
Chicago/Turabian StyleZhou, Zhengyang, Ming Lin, Maosong Cheng, Yuqing Dai, and Xiandi Zuo. 2025. "Applicability Analysis of Reduced-Order Methods with Proper Orthogonal Decomposition for Neutron Diffusion in Molten Salt Reactor" Energies 18, no. 8: 1893. https://doi.org/10.3390/en18081893
APA StyleZhou, Z., Lin, M., Cheng, M., Dai, Y., & Zuo, X. (2025). Applicability Analysis of Reduced-Order Methods with Proper Orthogonal Decomposition for Neutron Diffusion in Molten Salt Reactor. Energies, 18(8), 1893. https://doi.org/10.3390/en18081893






