Evaluating the Balancing Properties of Wind and Solar Photovoltaic System Production

Abstract

This research evaluates how wind and solar PV systems balance together. Increasing the share of stochastic renewable energy production in electricity and hot turning reserve deficit are welcome compensation issues. This research used weather station data from an open seashore from the last 10 years, 2014–2023, on the Estonian island Saaremaa’s west coast to evaluate yearly fluctuations. We used the indicator demand cover factor to estimate the coincidence of wind generation and solar PV system electricity. For clarity, the initial data were prepared by assuming the equality of production and consumption annual data by scaling the obtained data. This study demonstrates that the best compensating possibilities are the share of wind generation and solar PV electricity mix, respectively, equal to 0.7/0.3 and 0.8/0.2, reaching a demand cover factor of 0.62. This study evaluated the demand cover factor’s dependence on increased production compared to consumption. This study used different batteries to research the influence of these demand cover factors. Furthermore, this research makes a significant contribution by showcasing how to turn weather station data into real wind generator and PV panel production data.

1. Introduction

The increasing share of renewable energy sources in electricity generation is essential for achieving a sustainable and low-carbon energy system [1]. Among the most widely used renewable energy technologies, wind power (wind) and solar photovoltaic (solar PV) systems stand out due to their availability, scalability, and decreasing costs; however, both sources exhibit stochastic production patterns, leading to challenges in balancing supply and demand within a power grid. Understanding the relationship between these two sources is essential for optimizing energy generation, minimizing curtailment, and ensuring a stable electricity supply [2,3].

The balance between wind and solar PV system production has become a key concern in energy system planning, particularly in regions with a high penetration of variable renewable energy. While wind and solar PV systems are complementary to some extent, their combined production characteristics must be thoroughly analysed to determine the optimal mix that maximizes electricity generation while minimizing reserve deficits. The main challenge arises from the intermittent nature of these energy sources, requiring effective strategies to enhance grid stability and self-sufficiency [4].

There has been a slight setback in the development of green technologies recently. For example, the USA plans to withdraw from green agreements, and Europe has begun to realize the negative economic impact of overly rapid clean energy development plans. Despite everything, the development of renewable energy—specifically wind and solar—continues regardless of the wishes of top executives. The driving force behind this is humanity’s pursuit of a cleaner environment for future generations. There have not been many studies in recent years specifically on the compensatory properties between wind and solar PV generation equipment and their practical applicability.

Wind and solar PV systems have been combined, with biomass also included, proposed in [5]; however, it does not analyse the interaction between wind and solar PV systems. Moreover, batteries are listed alongside energy sources such as wind and solar PV systems, which is incorrect. The seasonal variations in solar and wind energy are analysed in the Commonwealth of Kentucky, USA. When considering daily patterns, the wind was found to follow solar generation with an offset [6]. The results indicate the potential of solar and wind energy across most African regions and emphasize the importance of considering solar, wind, or their combined energy mix for local energy planning and storage solutions [7]. The use of flexible solar and wind fleets as a secondary reserve, combined with an implicit storage technique, has been proposed [8]. Integrating multiple energy sources into a single hybrid renewable energy system effectively addresses challenges like intermittency and geographical limitations associated with individual renewable systems. Therefore, the continuous development and implementation of an energy management system are crucial for achieving key objectives such as energy efficiency, resilience, stability, and sustainability [9]. Several studies related to this field have been reviewed and are summarized as follows:

Benato et al. [10] examined the integration of energy storage systems with photovoltaic power plants, showing that the virtual power plant (VPP) model effectively smooths PV power peaks and enhances supply stability. Niu and Luo [11] explored economic efficiencies of distributed PV systems and storage solutions, revealing that optimized storage frameworks enhance grid adaptability and stability. Ho-Tran and Fiedler [12] studied seasonal extreme events in Germany’s renewable production, highlighting the increased risk of low power production in summer due to stationary cyclonic weather patterns. Fasihi et al. [13] investigated the potential of green ammonia production using hybrid PV–wind plants, identifying cost-competitive scenarios by 2040. Dietrich [14] analysed zero-energy buildings in different climates, emphasizing land-use trade-offs and optimized renewable integration strategies. Salkuti [15] proposed optimal railway electrification using renewable sources, demonstrating cost benefits and enhanced grid integration.

Chen et al. [16] examined land-use conflicts in renewable energy deployment in Northern Europe, concluding that offshore wind expansion could reduce land demands. Silva et al. [17] proposed a stochastic approach for optimizing renewable energy market participation, showing significant profit gains and imbalance reductions. Nnodim et al. [18] analysed wind and solar integration into electricity grids, recommending curtailment and storage for effective intermittency management. Al-Dahidi et al. [19] developed machine learning models for PV power predictions, improving forecasting accuracy for better grid management. Santos-Alamillos et al. [20] studied wind–solar spatiotemporal balancing in the Iberian Peninsula, concluding that colocation reduces generation variability. Veluchamy [21] introduced an optimization algorithm for microgrid energy management, achieving cost reductions in distributed networks. Velosa et al. [22] developed an open-source simulator for energy community power demand and generation scenarios, facilitating the testing of optimization strategies. Lippert [23] discussed lithium-ion energy storage in wind farms, demonstrating effective output control and ancillary service provision. Tafarte et al. [24] investigated bioenergy’s role in mitigating fluctuations from wind and solar PV systems, concluding that flexible bioenergy operation enhances grid stability. Schmidt et al. [25] analysed Brazil’s hydrothermal system, highlighting the benefits of wind–PV expansion in reducing thermal backup needs. Carbajales-Dale et al. [26] assessed storage energy costs for wind and solar PV systems, revealing that wind energy can support large-scale storage while PV systems are limited in terms of storage affordability. Haegel and Kurtz [27] tracked global PV adoption trends, showing rapid expansion and increasing storage integration.

Hadi et al. [28] proposed a demand response algorithm to optimize renewable penetration in microgrids, reducing peak demand and enhancing system balance. Stamatakis et al. [29] examined energy management in super-tankers, demonstrating CO₂ reductions through PV–wind–hydrogen integration. Shepherd et al. [30] developed feasibility tools for green ammonia production, assessing storage needs and balancing strategies. Hou et al. [31] analysed climate change impacts on solar power generation, identifying changes in seasonal production variability. Madiba et al. [32] optimized under-frequency load shedding in microgrids, improving reliability through renewable integration. Coles et al. [33] studied tidal stream power’s impact on energy system security, demonstrating its role in supply–demand balancing. Jiang et al. [34] applied machine learning for energy management in grid-connected microgrids, achieving cost reductions and efficiency improvements. The following table summarizes the methodologies, objectives, and results from relevant studies.

From the literature overview, it becomes evident that different measures are used to try to achieve balancing activities in the presence of renewables: using a virtual power plant model, producing green ammonia, engaging energy storage elements, using machine learning models to predict solar PV production, etc. (

Table 1. Comparison of some highly related studies.

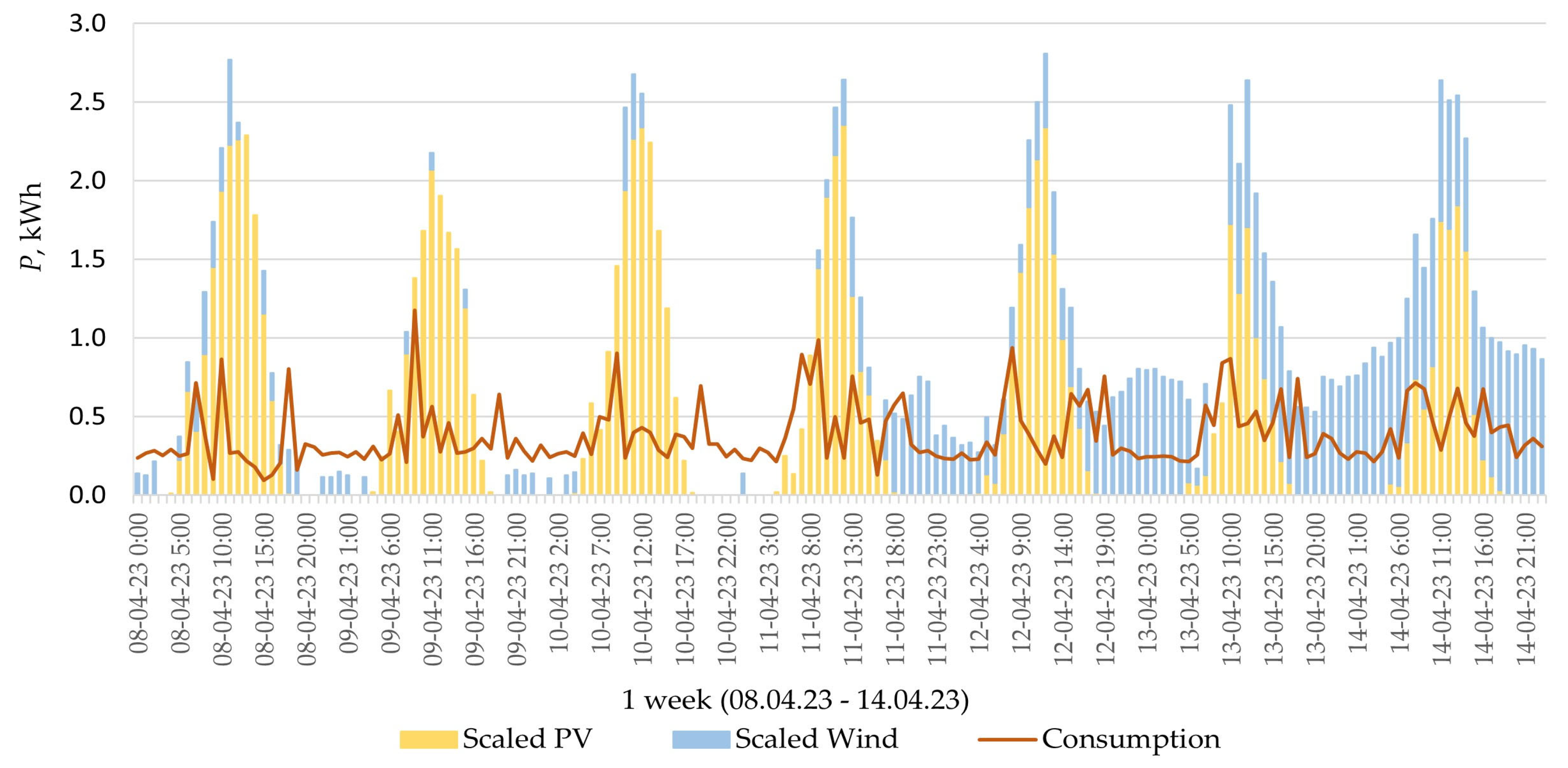
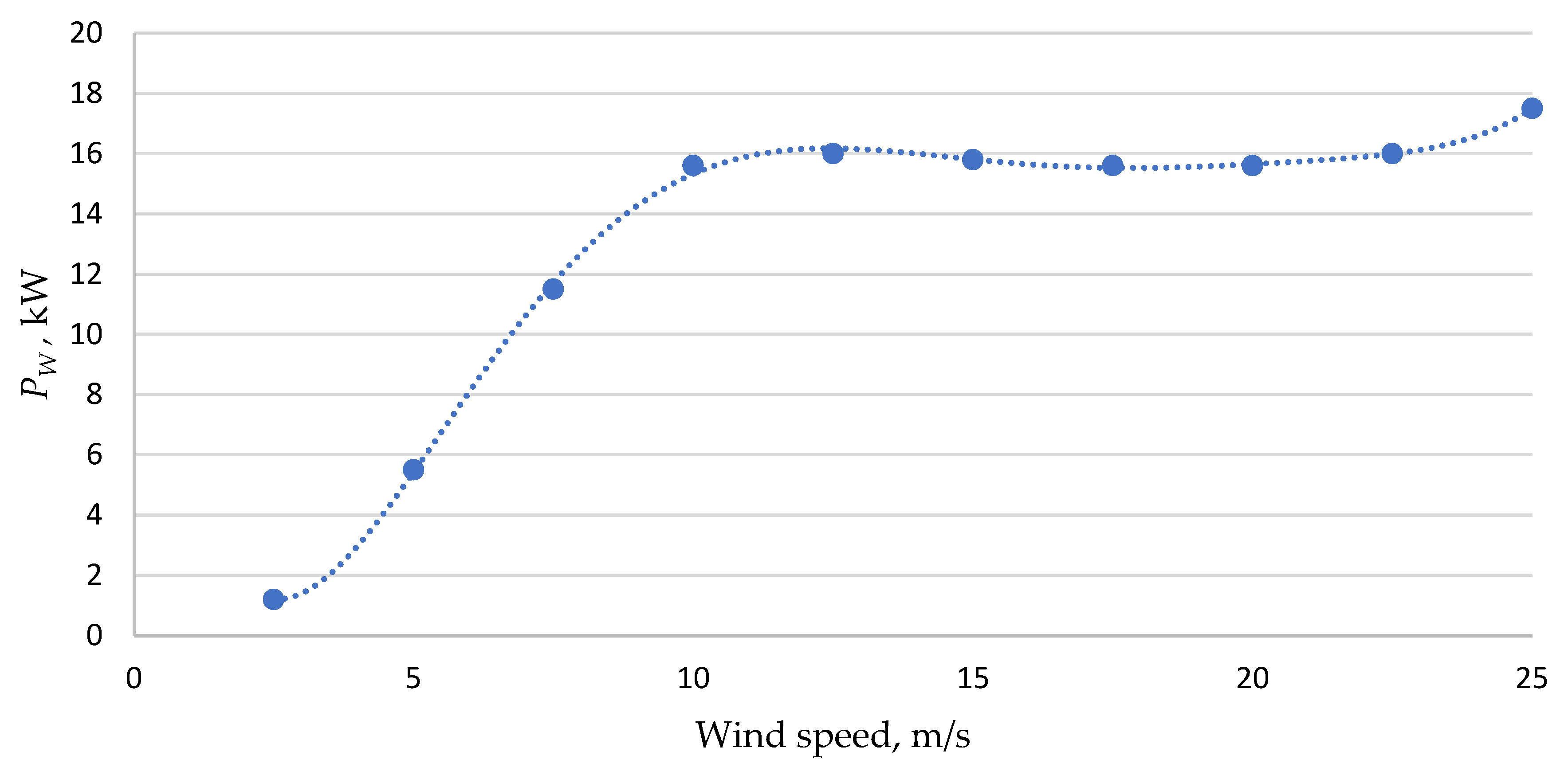
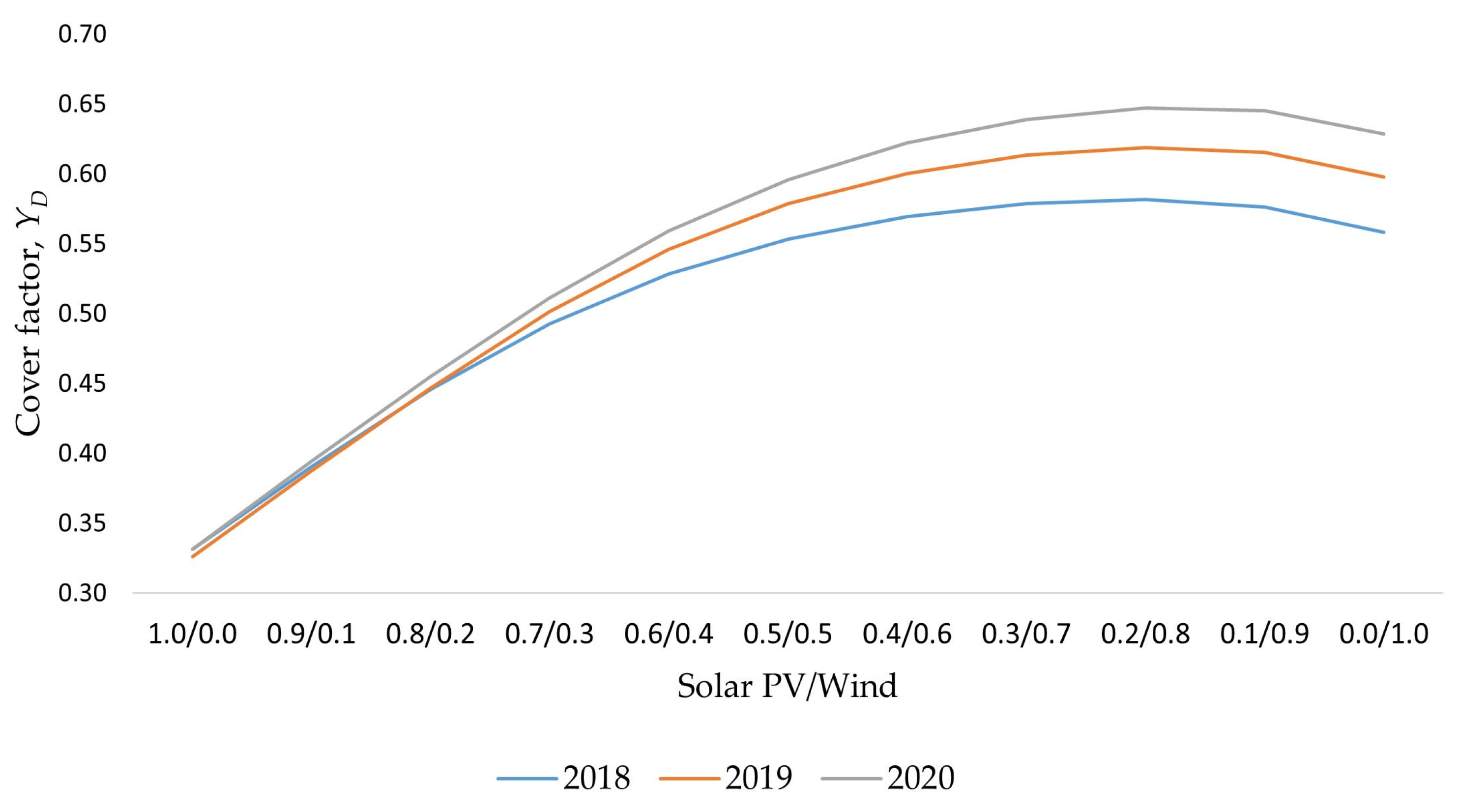
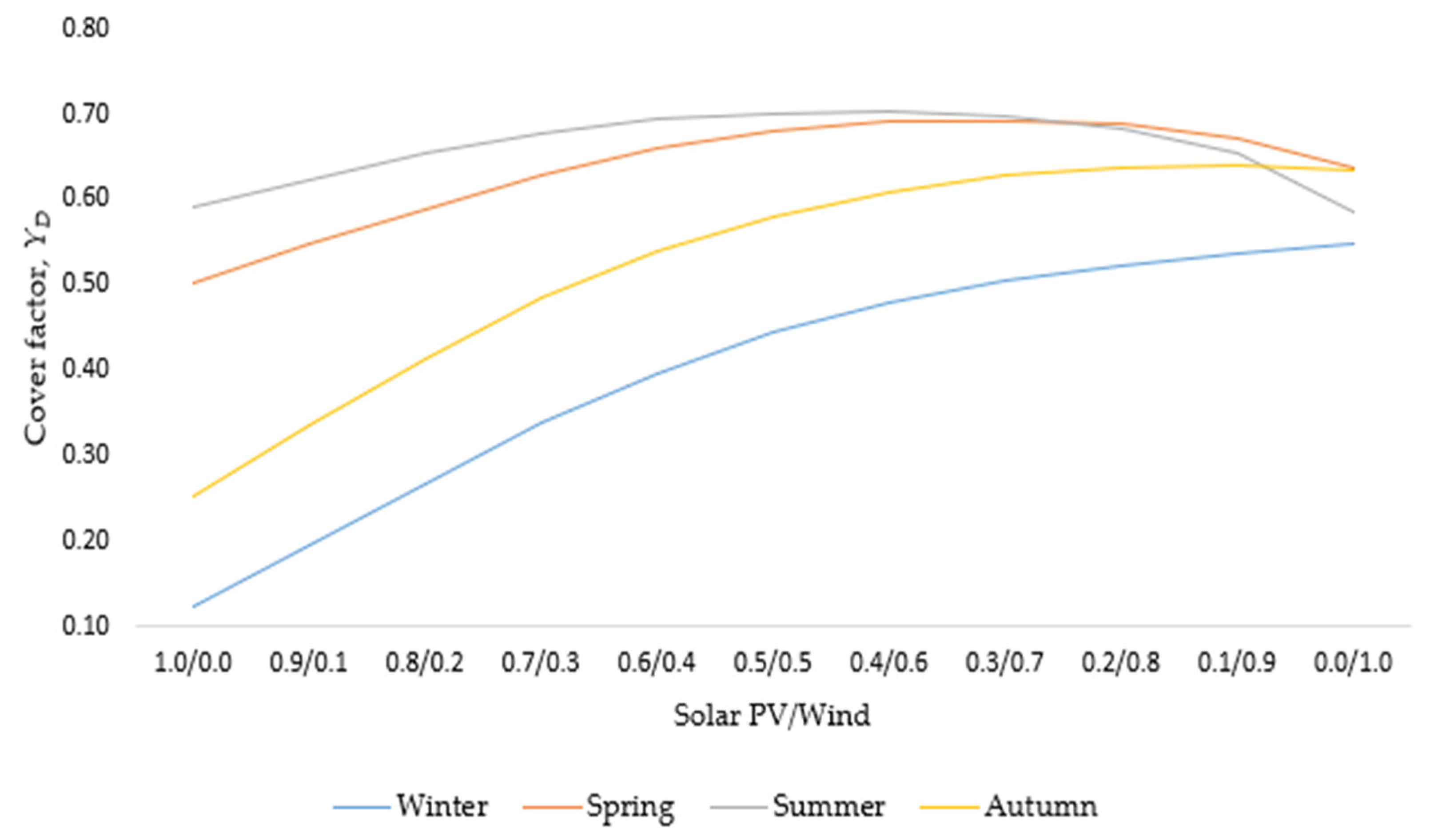
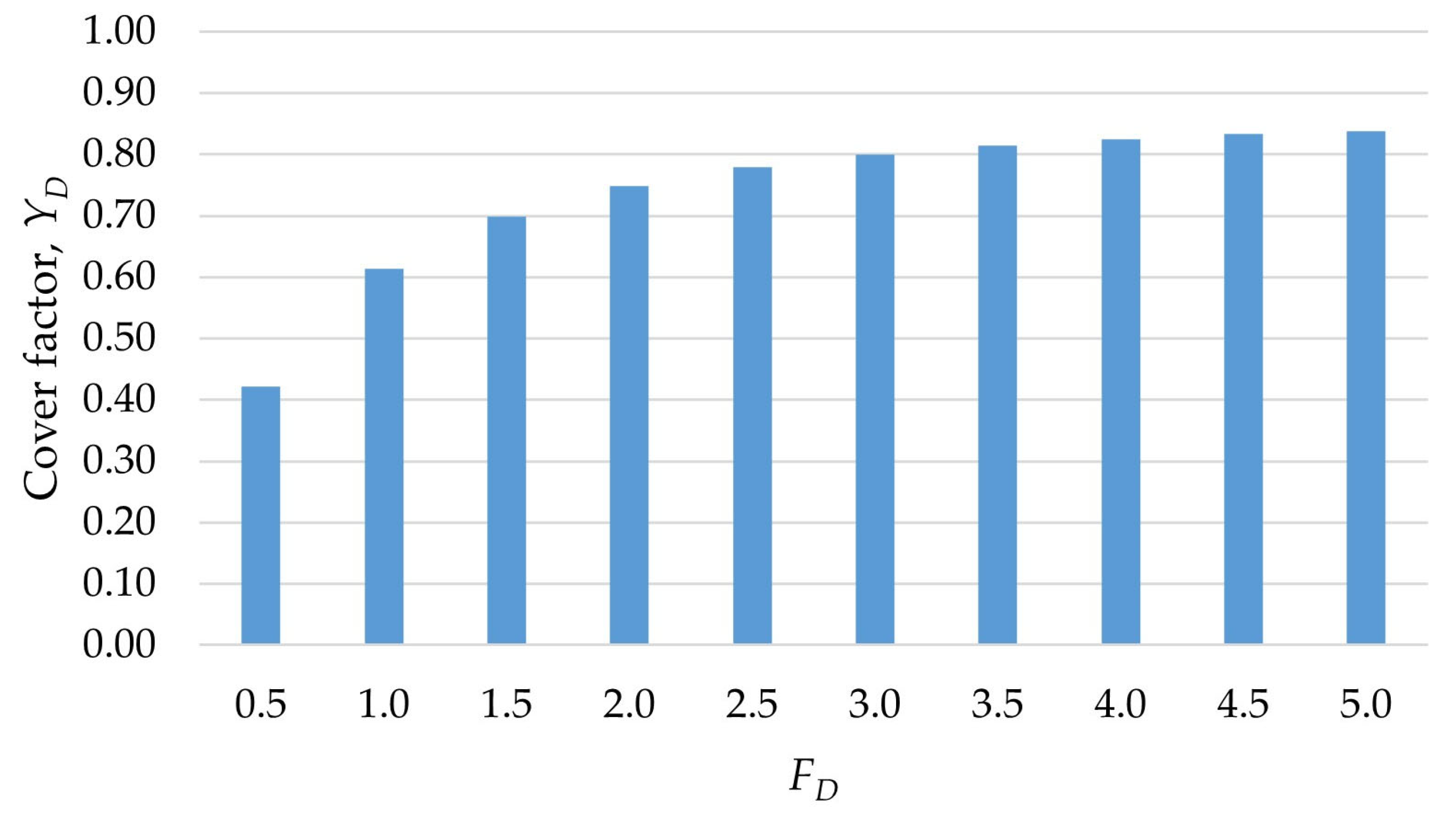
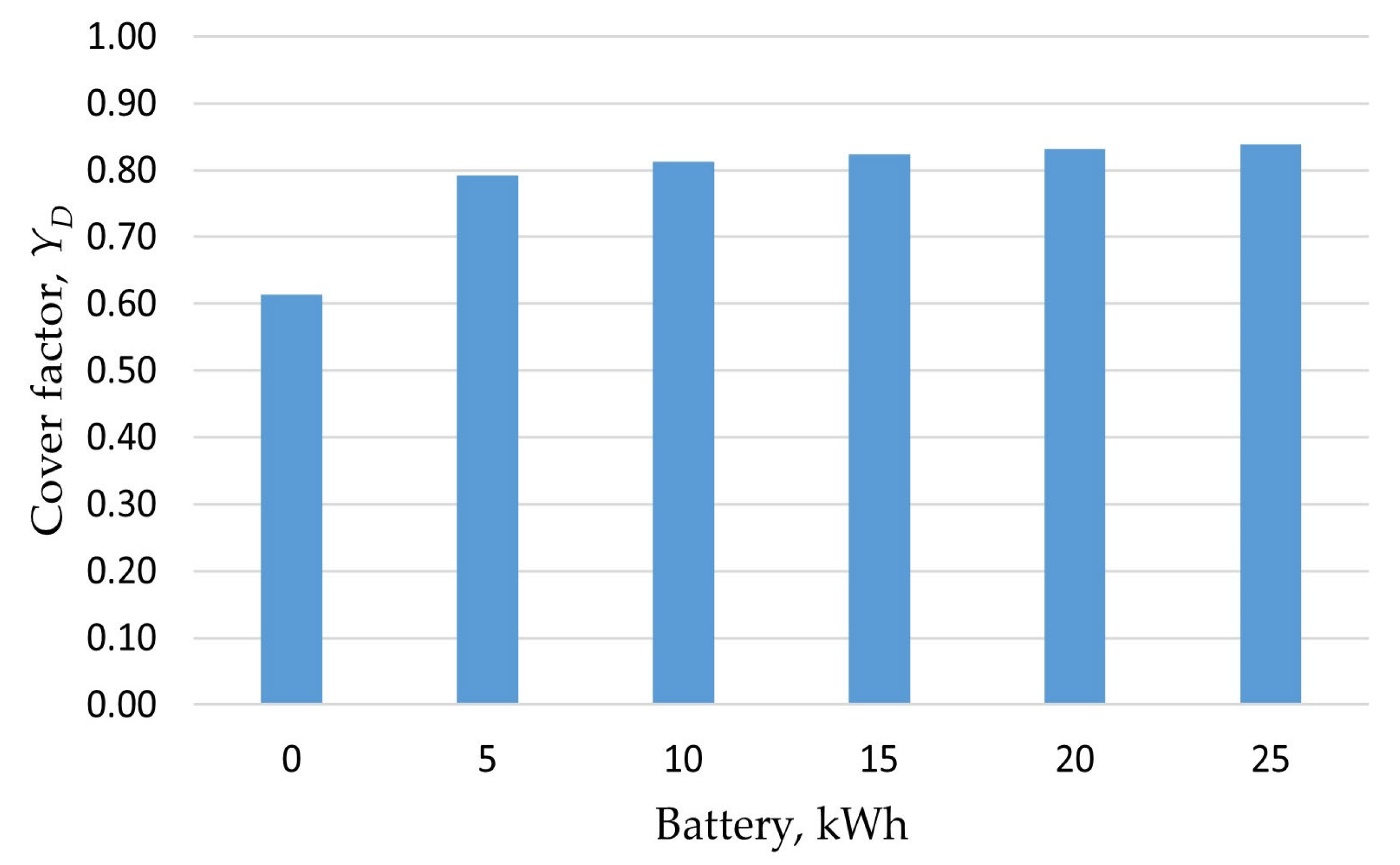
Study	Methodology	Objectives	Results
Benato et al. [10]	Integration of energy storage with PV systems	Optimize power output stabilization	Virtual power plant model improved power stability
Niu and Luo [11]	Economic analysis of distributed PV systems and storage	Evaluate grid adaptability and storage efficiency	Optimized framework enhanced stability and reliability
Frank et al. [35]	Analysis of seasonal renewable production in Germany	Study extreme low-power events	Identified increased risk of summer production deficits
Fasihi et al. [13]	Green ammonia production with hybrid PV–wind systems	Assess cost competitiveness	Found feasible cost levels for green ammonia by 2040

). All these measures are prioritized for more significant profit, and the second output is balancing properties with renewables. The third aspect is lessening the environmental impact. Wind and solar PV production often accompany each other. The shortcoming that is revealed from the previous literature review is that different methods are used for balancing renewables, but marginal attention has been paid to the possibility of using self-balancing possibilities between wind and solar.

Unlike previous studies focusing on hourly based yearly datasets over ten years, our research provides a site-specific analysis by examining real-world data from Saaremaa, Estonia, offering localized insights into wind and PV system integration. The use of a decade-long dataset (2014–2023) ensures robustness in assessing renewable energy balancing, making our findings more reliable. Furthermore, this study applies the demand cover factor indicator to quantitatively evaluate the effectiveness of wind–PV system synergy in covering local electricity consumption, a methodology that is rarely explored in the existing literature. While previous studies primarily analyse wind and PV systems separately, our research uniquely assesses the role of different battery storage solutions in influencing the demand cover factor. Additionally, our findings provide practical recommendations for policymakers and grid operators in Estonia and similar regions, contributing to renewable energy policy advancements.

The core objective of this research is to identify the most effective combination of wind and solar PV system generation that enhances energy balance and minimizes reliance on external energy sources. It presents a comprehensive analysis of the balancing issues between wind and solar PV system production, emphasizing the significance of data-driven approaches in optimizing renewable energy generation. This study highlights the importance of selecting an appropriate energy mix, utilizing advanced forecasting techniques, and incorporating battery storage solutions to achieve a more reliable and sustainable energy supply. The insights derived from this research will be valuable for informing future renewable energy policies and strategies, particularly in regions with similar climatic and geographical conditions.

This article consists of five parts. The first part is the introduction, which gives the literature overview and sets the objectives. The second part gives an overview of the data treatment objectives used and describes the modelled equipment. The third chapter consists of the results of modelling and the influence of wind/solar PV share on the demand capacity factor in different conditions. The fourth chapter is the conclusion, where an explanation for issues that are not handled in the main chapters is given. The conclusion provides the principal results and generalizations. This article also has one appendix with a description of the measurement devices.

2. Data and Methods

In this study, the settlement of Roomassaare on the west coast of Saaremaa was chosen as the location for the wind generator and PV panels described in this article. This choice was primarily due to good wind conditions and the simultaneous availability of PV and wind speed data at the measuring station. Another factor in favour of this choice was that the location is on an island and at the same time in a remote area with a foreseeable weak electricity grid. This study interpreted the wind and solar PV system production data using hourly wind speed and total solar radiation data from the Roomassaare weather station (N 58°13′05″; E 22°30′3″) [36]. It used 10 years of hourly data from 2014 to 2023. Wind speed data were measured at the weather station at a height of 10 m.

The anemometer WAA151 measured wind speed from 4 December 2007 to 26 May 2015, and the anemometer WAA151 and windvane WAV151 measured wind direction during this period (Appendix A,

Table A1. Anemometer WAA151 specifications [37].

Parameter	Indication
Sensor/Transducer type	Cup anemometer/Optico-chopper
Measuring range	0.4…75 m/s
Starting threshold	<0.5 m/s
Accuracy (within 0.4…60 m/s), with characteristic transfer function	±0.17 m/s
With “simple transfer function” Ut = 0.1 × R	±0.5 m/s

and

Table A2. Wind vane WAV151 specifications [37].

Parameter	Indication
Sensor/Transducer type	Vane/Optical code disc
Measuring range	0…360°
Starting threshold	<0.4 m/s
Resolution	5.6°
Accuracy	Better than ±3°
Setting time after power turn-on	<100 µs
Dealy distance	0.4 m

[37]). A Kipp & Zonen pyranometer CMP-21 (Delft, The Netherlands) measured solar total irradiation (Appendix A,

Table A3. Specifications of pyranometer KippjaZonen CMP21 [38].

Parameter	Indication
Spectral range (50% points)	285 to 2800 nm
Sensitivity	7 to 14 µV/W/m2
Response time (95%)	<5 s
Zero ofset A	<±7 W/m2
Zero ofset B	<±2 W/m2
Directional response (up to 80° with 1000 W/m2 beam)
Temperature response (−20 to ±50 °C)	<±1%
Operational temperature	−40 °C to +80 °C
Maximum solar irradiance	4000 W/m2
Fielf of view	180°

[38]). From 27 May 2015 to now, the Ultrasonic Wind Sensor WMT700 has been used to measure wind speed and direction (Appendix A, Table A1, [39]). Vaisala (Vantaa, Finland) produces all wind sensors.

Figure 1 shows that the wind generator and solar PV system production data are sometimes summarized and sometimes exist alone. Spring is the best time for following the coincidence of wind and solar PV system production data.

Scaling wind generator production and solar PV system data means that the sums of both annual datasets equal the sum of yearly consumption.

Wind speed from a height of 10 m was extrapolated to 18 m as the initial data of the wind generator TUGE 20 [40] using a logarithmic equation [41]:

$$V_2=V_1·{\displaystyle \frac{ln·\left(\frac{h_2}{z_0}\right)}{ln·\left(\frac{h_1}{z_0}\right)}},$$

(1)

where V₂ is the extrapolated wind speed at a height of 18 m, m/s;

V₁ is the measured wind speed at a height of 10 m, m/s;

h₂ is the wind generator hub height, 18 m;

h₁ is the height of the measured wind speed in the weather station, 10 m;

z₀ is the roughness coefficient; for a flat landscape, z₀ = 0.03.

TUGE 20 power curve data [40] were interpolated by Formula (2), R₂ = 0.9994:

$$P=7·{10}^{-6}·V_0^6-0.0006·V_0^5+0.022·V_0^4+0.3904·V_0^3+3.3587·V_0^2-10.894·V_0+12.753,$$

(2)

where P is the wind generator output capacity, kW;

V₀ is the scaled wind speed at a height of 18 m.

The power curve described by Formula (2) is present in Figure 1.

Figure 2 shows that the sixth-order polynomial is described quite well for the power curve, R₂ = 0.9994. As the cut-in wind speed for TUGE 20 is 3.5 m/s, power values below 3.5 m/s were removed. It is a typical small-wind-generator power curve.

The approximation of the solar irradiation data from the weather station horizontal-plane measurements for real PV panels’ output data (angle to the ground: 35°, azimuth: 180°, efficiency: 0.213, panel size a’= 2297 × 1134 mm, quantity: 10, Ja Solar JAM72S30 550W (Beijing, China), monocrystal) begins from the angle of incidence calculations by Formula (3) [42]:

$$A_f=\cos \left({\theta }_z\right)·\cos \left(\beta \right)+\mathrm{s}\mathrm{i}\mathrm{n}\left({\theta }_z\right)·\mathrm{s}\mathrm{i}\left(\beta \right)·\cos \left({\gamma }_s-\gamma \right),$$

(3)

where A_f is the angle of incidence, °;

Ѳ_z is the zenith angle, °;

ß—the slope, the angle between the plane of the surface in question and horizontal, °;

ϒ_s is the solar azimuth angle, °;

ϒ is the surface azimuth angle, °.

Clear sky index [43]:

$$K_t={\displaystyle \frac{GHI}{G_0·\mathrm{c}\mathrm{o}\mathrm{s}\left(Z_s\right)}},$$

(4)

where K_t is the clearness index;

GHI is the total sun solar irradiation on a horizontal surface in the Roomassaare weather station, W/m²;

G₀ is the solar constant, 1367 W/m²;

Z_s is the zenith angle, °.

Diffuse horizontal irradiance—DHI [43]:

$$DHI=GHI·\left(1-F\right),$$

(5)

where F is as follows:

$$F=\left\{\begin{array}{c}1-0.249·K_t,when{K}_t<0.35\\ 1.577-1.84·K_t,when0.35\le K_t<0.75\\ 0.1,when{K}_t\ge 0.75\end{array}\right.,$$

(6)

Direct normal irradiance—DNI:

$$DNI={\displaystyle \frac{GHI-DHI}{\mathrm{c}\mathrm{o}\mathrm{s}\left(Z_s\right)}},$$

(7)

Direct solar irradiance—G_dir:

$$G_{dir}=DNI·A_f,$$

(8)

Solar diffused irradiation—G_dif:

$$G_{dif}=DHI·{\displaystyle \frac{(1+\cos \left(\beta \right))}{2}},$$

(9)

Solar irradiation reflection—G_ref:

$$G_{ref}=GHI·{\displaystyle \frac{(1-\cos \left(\beta \right))}{2}},$$

(10)

Total irradiation—G_total:

$$G_{total}=G_{otse}+G_{dif}+G_{ref},$$

(11)

PV panel production—P:

$$P=G_{total}·S·\eta ,$$

(12)

where P is the PV panel produced capacity, W;

S is the total panel area, m²;

η is the PV panel efficiency.

The modelled family size in a private house is two people and an area of 90 m². The consumption schedule was measured in 2023, and the yearly consumption was 3276 kWh. Estonia is very close to the EU average in 2022 of 1584 kWh electricity consumption per capita [44]. The current case’s consumption is 3276 kWh, slightly more than the EU average of 3168 kWh for such households. The model features a typical household location in the countryside. The household has wood log stoves, electrical floor heating in the WC, two refrigerators, and an electric stove. There are no heat pumps. The yearly consumption graph is supposed to be close for all years from 2014 to 2023. New devices were not obtained during these ten years in this private house.

Calculations in this article scaled the wind generator and PV panels’ annual productions to equal the yearly consumption. PV panel production scaled by consumption was as follows:

$$P_{PV}^{\prime }\left(h\right)=K_{PV}·P_{PVh},$$

(13)

where $P_{PV}^{\prime }\left(h\right)$ is the scaled annual production graph equal to the sum of consumption, kWh;

P_PVh is the hourly production of PV panels, kW;

K_VP is the scaling coefficient for PV panels:

$$K_{PV}={\displaystyle \raisebox{1ex}{$W_{cy}$}\!\left/ \!\raisebox{-1ex}{$W_{PVy}$}\right.},$$

(14)

where W_cy is the yearly sum of the consumption graph, kWh;

W_PVy is the sum of yearly PV panel consumption, kWh.

Wind generator production by consumption:

$$P_W^{\prime }\left(h\right)=K_W·P_{Wh},$$

(15)

where $P_w^{\prime }\left(h\right)$ is the scaled wind generator annual production equal to the sum of consumption, kWh;

P_Wh is the hourly production of the wind generator, kW;

K_W is the scaling coefficient for the wind generator:

$$K_W={\displaystyle \raisebox{1ex}{$W_{cy}$}\!\left/ \!\raisebox{-1ex}{$W_{Wy}$}\right.},$$

(16)

where W_wy is the sum of the yearly wind generator production, in kWh.

Total power graph, which is equal to the consumption:

$$P_{total}\left(h\right)=a·P_{PV}^{\prime }\left(h\right)+b·P_W^{\prime },$$

(17)

where a = percentage 0… 1, and b = (1 − a).

The indicator being modelled is the self-consumption rate or, in other words, the demand cover factor Y_D [45,46,47,48]:

$$Y_D={\displaystyle \frac{{\int }_{t_0}^{t_1}{P}_{D}dt+{\int }_{t_1}^{t_2}{P}_{S}dt}{{\int }_{t_0}^{t_2}{P}_{D}dt}},$$

(18)

where P_S is the local power supply, and P_D is the local power demand. The time when P_D (t) ≤ P_S (t) is denoted as t₀… t₁, and t₁… t₂ is the time when P_D (t) ≥ P_S (t) [45]. The demand cover factor is defined as the ratio in which the local supply covers the energy demand and indicates the “self-generation” [42,45].

This article investigates whether there may be differences in the best wind and PV electricity in different years when self-consumption is the highest. It finds the margins of the fluctuation and evaluates the optimal battery size.

This article is used to compare production capabilities among years in terms of the capacity factor (CF) [49]:

$$CF={\displaystyle \frac{{\int }_0^{8760}Pdt}{P_{rated}·t}},$$

(19)

where P is the annual production graph hourly capacities, kW;

P_rated is the rated capacity of the production device, kW;

t is the hours per year, t = 8760 h.

The capacity factor is the quotient between annual actual production, conceivable production, and the yearly permanent rated production.

The multiplication coefficient, F_D, is calculated as follows [50]:

$$F_D={\displaystyle \frac{W_{prod}}{{\int }_{t_0}^{t_2}{P}_{D}dt}},$$

(20)

where W_prod is the actual wind generator and PV panel production mix, kWh;

${\int }_{t_0}^{t_2}{P}_{D}dt$ is the yearly consumed electricity, kWh.

3. Results

This section presents results for calculating wind and solar PV system balancing properties together.

Table 2. Yearly properties of production devices.

Year	Capacity CFwind	Factors CFPV	Vavg m/s	Pwind kW	PPV kW
2023	0.363	0.120	5.13	7.26	0.66
2022	0.367	0.117	5.21	7.35	0.65
2021	0.382	0.116	5.37	7.65	0.64
2020	0.488	0.118	6.48	9.77	0.65
2019	0.398	0.116	5.53	7.96	0.64
2018	0.346	0.121	4.91	6.91	0.66
2017	0.397	0.111	5.54	7.95	0.61
2016	0.372	0.114	5.24	7.44	0.63
2015	0.443	0.117	5.96	8.87	0.64
2014	0.394	0.115	5.48	7.88	0.64
Average	0.395	0.116	5.49	7.90	0.64

presents capacity factors CF_wind and CF_PV as annual capacity factors for wind generators and PV panels, respectively, V_avg is the average wind speed by year, and P_wind and P_PV are the average yearly scaled wind generator and PV panel capacities, respectively. CF_wind is desirably high for this site. CF_PV is similar in all places in Estonia: at the seashores and lakeshores, it is a little higher, similarly to what is presented here, and inland, it keeps near 0.11. The fluctuations are higher with CF_wind due to the nature of the wind conditions. In conclusion, the analysis of CF_wind and CF_PV representatives separated the average year, 2019, minimum, 2018, and maximum, 2020, when both capacities were similarly average, minimum, or maximum.

This means that, when yearly solar irradiation is high, the potential output of wind generators is high too; more energy from the sun induces more energy in the wind. P_wind and P_PV denote the average annual capacity by 100% of production, separately.

Figure 3 presents the demand cover factor, Y_D, in terms of different energy mixes. Energy mixes are annual electricity productions.

Figure 3 depicts the Y_D dependence of different wind and solar PV energy mixes. The highest value of 2019, Y_D = 0.62, was achieved for the energy mix values 0.2/0.8 and 0.3/0.7 simultaneously, as well as solar PV and wind systems. In this area, the curve is very smooth; it lowers rapidly on the side of a 100% solar PV system, Y_D = 0.33, and the opposite side of the figure when the wind share is 100%, Y_D = 0.6. This means that wind generation has more influence on the Y_D than solar PV systems do.

Figure 4 presents the demand cover factor, Y_D, in terms of different energy mixes, which are seasonal electricity productions.

Figure 4 depicts the Y_D dependence of different wind and solar PV energy mixes by season. The highest value is found in summertime, Y_D = 0.7, was achieved for the energy mix values 0.2/0.8 and 0.3/0.7 simultaneously, as well as solar PV and wind systems. The worse Y_D = 0.5 by the same energy mix is found in winter. In wintertime, the expected 100% solar PV value is Y_D = 0.12. With 100% wind, have less influence is present, and a relatively high value, Y_D = 0.6… 0.7, is maintained.

Figure 5 depicts the influence of the multiplicity, F_D, of production on consumption in 2019 in terms of the 0.2/0.8 energy mix.

According to analyses supported by Figure 5, some conclusions can be made. The Y_D is significantly reduced by reducing production to half of consumption, according to expectations. Y_D growth slackens by increasing F_D over one, reaching the value F_D = 2.5 when Y_D reaches 0.78. This means that Y_D no longer grows proportionally when F_D increases beyond 2.5. More precisely, the limit could be considered as F_D = 2.

Figure 6 depicts the influence of adding batteries to the solution by F_D = 1 in 2019, using an energy mix of 0.2/0.8.

Figure 6 depicts logic similar to that of the previous figure. Increasing the battery volume by over 10 kWh is no longer effective. It is identical to the asymptotic function, like in Figure 4. Upon switching the battery in the system to one that is 10 kWh, the Y_D reaches 0.82.

4. Discussion

This calculation does not take battery efficiency and ageing parameters into account. The authors assume that modern lithium batteries have high efficiency and that ageing parameters remain within the range uncertainty. The calculated Y_D appears relatively high compared to previous results [50]. Earlier calculations used a wind generator with CF_wind = (0.05… 0.08); now, it is around 0.4. Solar PV CF was a little lower, too. Previously, different consumer data [45] were used at night with zero consumption; the current consumption data form an unbroken chart. There is less consumption at night and more in the daytime; however, consumption is still lower at night.

Different indicators of the optimal wind and solar PV energy mix are considered worldwide, but the results are similar to ours. In the US, the optimal energy mixes for balancing generation and daily load consist of approximately 80% wind energy and 20% solar PV due to the nighttime gap in solar production [51]. Again, in the US computing expected load-carrying capability, the best results were obtained in the 75/25 mix of wind and solar PV [52]. For instance, the initial statistical analysis of the Japanese data indicates that the optimal mix of hydrothermal, geothermal, and biomass energy that minimizes the standard deviation of mismatch, and the theoretical energy storage capacity is a combination of 75% solar and 25% wind power [53]. This means that this mix might be the opposite when in combination with other renewable energy sources. In contrast, a scenario with an 80/20 wind–solar energy mix reduces the overall surplus and offers an excellent opportunity for arbitraging the remaining surplus [54]. In conclusion, the available sources are rather old, and the optimal energy mix depends on the methodology and the accompaniment of other renewable sources.

As depicted in Figure 5 and Figure 6, Y_D is calculated using the average value in 2019. If minimum and maximum year values are used, Y_D changes between margins 0.59 and 0.65. The uncertainty is less than ±5%.

Wind speed and total solar irradiation are often measured at weather stations, but how can these measurements be interpolated into technical production data? This article addresses this question. Although it appears to be a case study, it provides insights that can be scaled up or down for other solutions.

Preventing the oversizing of wind and solar PV production equipment when planning small distributed networks is essential. The best option is to have a high self-consumption level. This has an economic effect. Less electricity purchased from the grid lessens the environmental impact. Electricity obtained from the grid is generated largely by fossil fuels. The ecological effect is expressed only by the choice of production equipment: wind generators and solar PV. Hydroelectricity in Estonia is not spread due to the flat terrain. Other ways are to purchase electricity from the grid and use a CHP (cogeneration heat plant), gas turbines or motors, or, in the worst case, only electrical generators that use fossil liquid fuels.

5. Conclusions

This study provides significant insight into balancing wind and solar PV system production research in small-scale regions like Estonia. This article’s novelty lies in its study of wind and solar PV balancing in good wind conditions in Estonia. In good wind conditions, the Y_D maximum is broader, and the impact of wind and solar separately on the individual result is more significant.

We used self-consumption, measured as a demand cover factor, Y_D, as an indicator for evaluating wind, and solar PV system balancing potential together. A smooth peak appears on the demand cover factor curve and wind and solar PV system production, particularly in shares of 30/70 and 20/80 for solar PV systems and wind, respectively. The maximum Y_D at the peak is 0.62, and maintaining a high level of Y_D favours wind generation, where 100% wind production yields a Y_D of 0.6, compared to only 0.33 for 100% solar PV energy. The production capacity needed to be increased relative to consumption to achieve optimal results, with the best outcomes occurring at F_D = 2.5 and Y_D = 0.78. By increasing F_D over 2.5, the growth speed of Y_D significantly slows down. Adding battery storage further improved capacity utilization, with a 10 kWh battery achieving a Y_D of 0.82. It is important to note that wind conditions with a high CF, as presented in this study, provide only a small balancing effect between wind and solar PV system production, whereas lower CF values for wind enhance the impact of balancing.

Finally, this article presents a method for calculating the actual output of production devices based on measured weather, wind, and total solar irradiation data. The best balancing shares of wind and solar PV are generalized at least to the northern hemisphere and by different CF values of wind and solar PV.